Cross-Scale Mechanical Contact Analysis from Asperities to Rough Surfaces: A Critical Review

1. Introduction

In the context of accelerated industrialisation, engineering equipment forms the material foundation, engineering equipment serves as an important material basis for supporting national defense security and promoting the development of the national economy. Various complex pieces of equipment are assembled from a wide variety of parts and components, and they are mainly assembled through different forms of connection structures. The joint interface transmit loads and energy. During the entire life cycle of a product, under the influence of vibration and impact loads, behaviors such as friction, wear, slip, collision, and separation will occur at the contact parts of the joint interface, giving rise to phenomena like the decline of interface pre-tightening forces and structural damage or failure [1,2,3]. By establishing contact models for joint interface to gain an in-depth understanding of the mechanical behaviors of joint interface, the overall performance of the equipment can be improved and its service life can be extended.

With the development of disciplines such as contact mechanics, tribology and plastic mechanics, there are mainly two types of nonlinear dynamics reduced-order modeling methods for establishing contact models of joint interface: the "top-down" approach based on data-driven methods and the "bottom-up" approach based on physical mechanisms. [4].

The meaning of "top-down" refers to a modeling approach (data-driven modeling) that is based on the form of phenomenological mathematical models, utilizes the dynamic responses at the macro scale of the connection structure, and then establishes the contact model of the joint interface by using the nonlinear system identification method. The meaning of "bottom-up" refers to a modeling approach that is based on the micro- and meso-scale morphological features of rough surfaces and the contact mechanism to establish the contact model of the rough joint interface. This method starts from the stick-slip friction contact behavior of individual micro-asperities at the micro- and meso-scale for modeling, and adopts the cross-scale methods based on mathematical statistics theory or fractal theory to describe the nonlinear dynamic characteristics of the joint interface. Compared with the "top-down" modeling approach, this approach can more realistically reflect the contact mechanisms on the contact interfaces, better characterize the influence of roughness on stick-slip behaviors, and most of the parameters in the model have clear physical meanings [5].

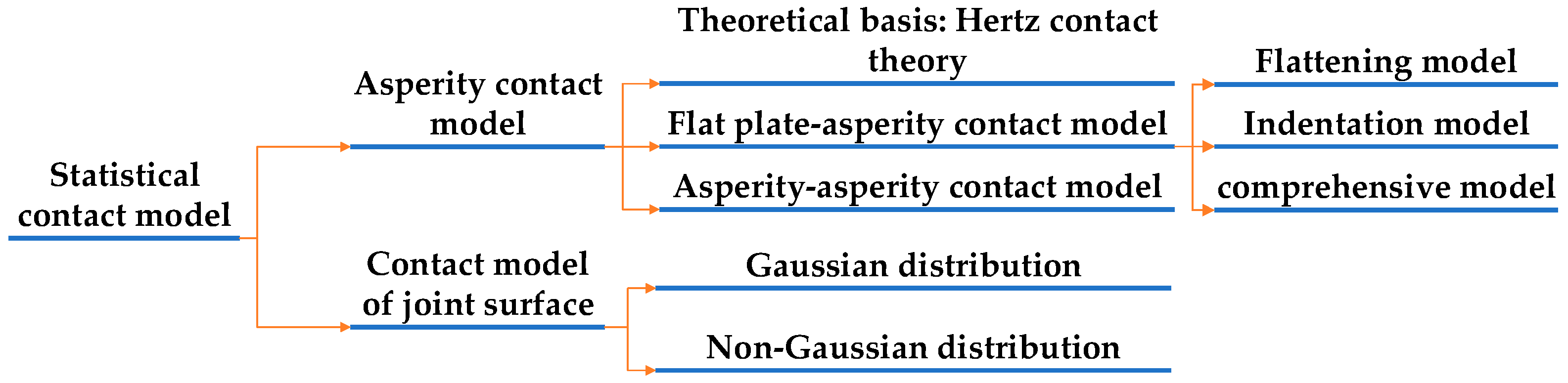
Figure 1. The main research contents of the statistical contact model.

Figure 1. The main research contents of the statistical contact model.

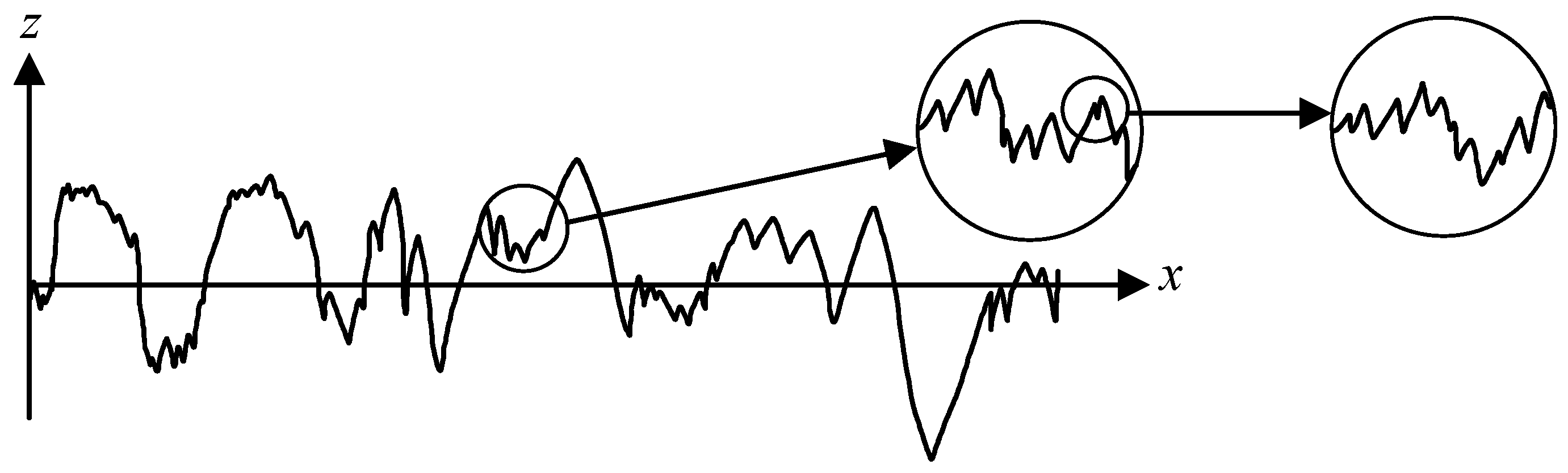
The models under the "bottom-up" modeling approach mainly include fractal contact models and statistical contact models. The microscopic morphology of the rough contact interfaces of connection structures has fractal characteristics such as cross-scale, disorder, irregular randomness and self-similarity. When the joint interface is magnified infinitely, the distribution properties of the rough interface at each magnitude level show similarities. These distribution properties are mainly manifested in being multi-scale, discontinuous, and having mathematical features such as being non-differentiable and statistically self-affine [6], as shown in Figure 2, which enables the rough contact model to have the conditions for modeling with fractal thinking.

The fractal contact models, grounded in fractal geometry theory, exhibit multi-scale characteristics that facilitate the cross - scale study of the microscopic topography of rough surfaces... By using fractal parameters to characterize the properties of rough surfaces, it doesn't need to rely on the sampling length and instrument resolution, and its accuracy can be guaranteed. However, not all engineering surfaces possess fractal characteristics, so the fractal contact model has relatively poor universality. It is still uncertain whether it can be applied to the research on hysteresis behavior under tangential cyclic loading. Therefore, the applicable range of the fractal contact model is relatively narrow and has certain limitations.

The Statistical contact models employ geometric and physical parameters to be constructed and thus possess relatively strong universality. It is conducive to explaining the stiffness of the contact interface and the damping energy dissipation characteristics from a microscopic perspective, and its research and development are also more comprehensive. The statistical contact model of rough surfaces generally requires first establishing an asperity contact model and then using the statistical summation theory to extend the asperity contact model to the entire rough surface, thus forming the statistical contact model of rough surfaces. According to the modeling steps of the statistical contact model, this paper will summarize from two aspects, namely the asperity contact model and the development status of the statistical contact model of the joint interface, so as to provide references and suggestions for the in-depth research on the statistical contact model in the future.

2. Research on Asperity Contact Model

On the microscopic level, asperities are randomly distributed on rough surfaces. Therefore, the actual contact between two rough surfaces is actually the mutual contact of asperities on a microscopic scale, which results in the fact that the actual contact area is always smaller than the nominal contact area [7,8]. Hence, the fundamental issue in studying the contact model of rough surfaces is to study the contact problem of asperities on rough surfaces under the action of tangential or normal loads. Establishing an appropriate asperity contact model has become a major research approach.

2.1. Elastic Contact Theory and Classification of Asperity Contact Models

2.1.1. Elastic Contact Theory

The deformation law of asperities on a rough surface is known as point - contact or Hertz contact [9], which is the most important problem in contact mechanics and has attracted the attention of scholars for more than a century. Hertz contact theory is the basis of the classical contact model and analyzes and solves the contact stress of various common elastic bodies theoretically. According to Hertz theory, when two spheres with radii R₁ and R₂ are in elastic contact, the contact area $A_e$, contact load $N_e$, maximum contact pressure $p_{em}$ , and average contact pressure $p_{ea}$ can be expressed as functions of the deformation amount $\omega$.

$$A_e=\pi R_{12}\omega ,$$

(1)

$$N_e={\displaystyle \frac{4}{3}}E{R_{12}}^{{\displaystyle \frac{1}{2}}}{\omega }^{{\displaystyle \frac{3}{2}}},$$

(2)

$$p_{em}=({\displaystyle \frac{2E}{\pi }})({\displaystyle \frac{\omega }{R_{12}}}){\displaystyle \frac{1}{2}},$$

(3)

$$p_{ea}={\displaystyle \frac{2}{3}}{p}_{em}=({\displaystyle \frac{4E}{3\pi }}){({\displaystyle \frac{\omega }{R_{12}}})}^{{\displaystyle \frac{1}{2}}},$$

(4)

In Equations (1)-(4), the relation $R_{12}^{-1}=R_1^{-1}+R_2^{-1}$ is satisfied, where $R_{12}$ is the relative curvature; $E$ satisfies the relation $E^{-1}=\left(1-{{\nu }_1}^2\right)\times E_1^{-1}+\left(1-{{\nu }_2}^2\right)\times E_2^{-1}$ ($E_1$, $E_2$, ${\nu }_1$, and ${\nu }_2$ are the elastic moduli and Poisson's ratios of the two contacting bodies, respectively), and $E$ is the equivalent elastic modulus.

Hertz contact theory contains some assumptions:

(1) The material of asperities is uniformly distributed and isotropic.

(2) Asperities only undergo small, completely elastic deformations.

(3) Only the stress condition of a single asperity is considered, without taking into account the interaction between asperities.

(4) Asperities are only subjected to normal contact loads, without considering tangential loads.

Hertz contact theory is a classic theory in elastic contact mechanics. It is aimed at the contact of ideal elastic bodies. Through rigorous elastic mechanics analysis and mathematical derivations, it provides a precise mathematical analysis and physical model description. When the asperities in the asperity contact model are in the elastic contact stage, Hertz contact theory offers theoretical support for analyzing the contact behavior of a single pair of asperities. Subsequently, the contact theory in elastic mechanics has also evolved into contact theories that consider friction (such as the Cartwright – Lund theory), contact theories that take into account adhesion and friction (such as the JKR theory[10], DMT theory, etc.), contact theories for multi-layered media, and dynamic contact theories.

2.1.2. Classification of Asperity Contact Models

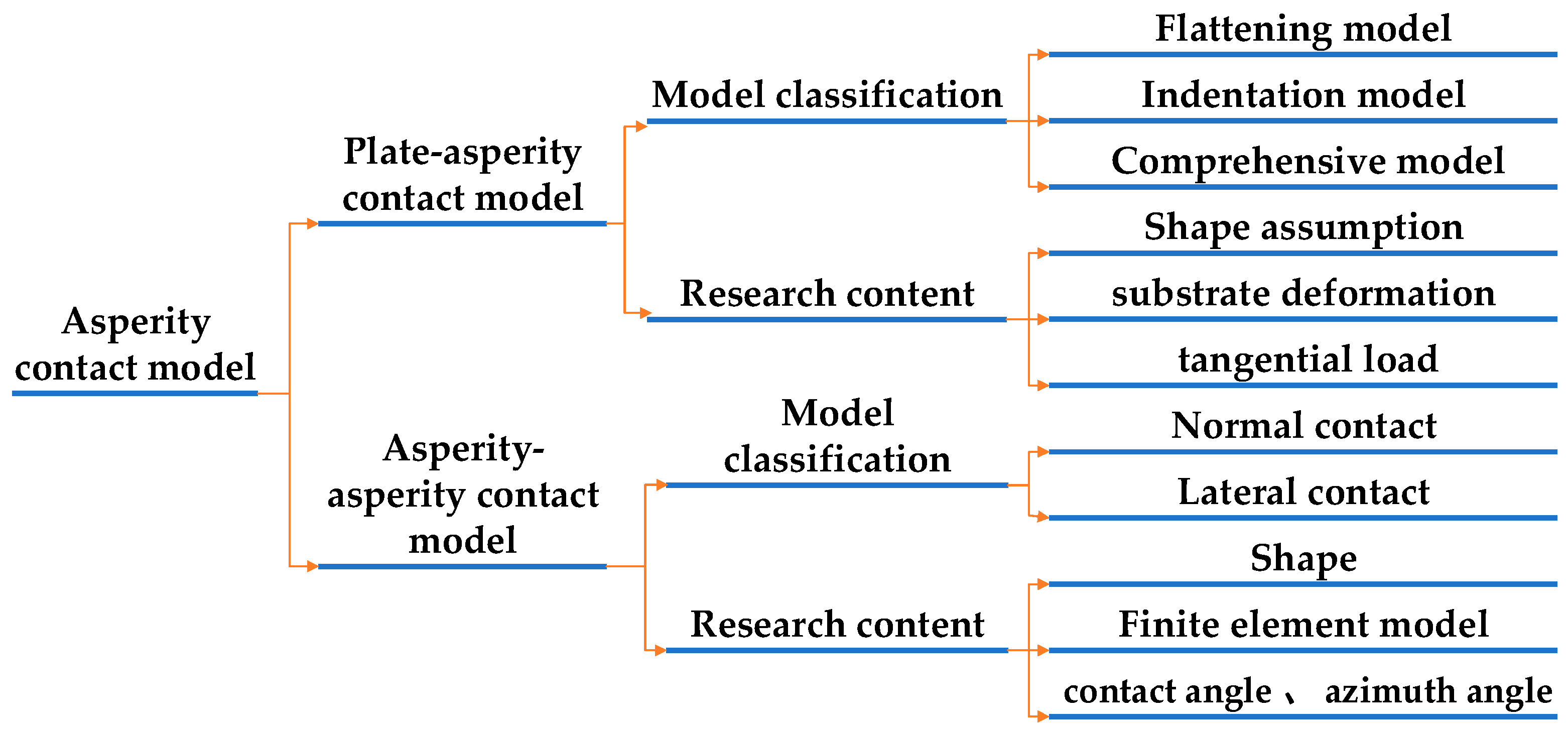
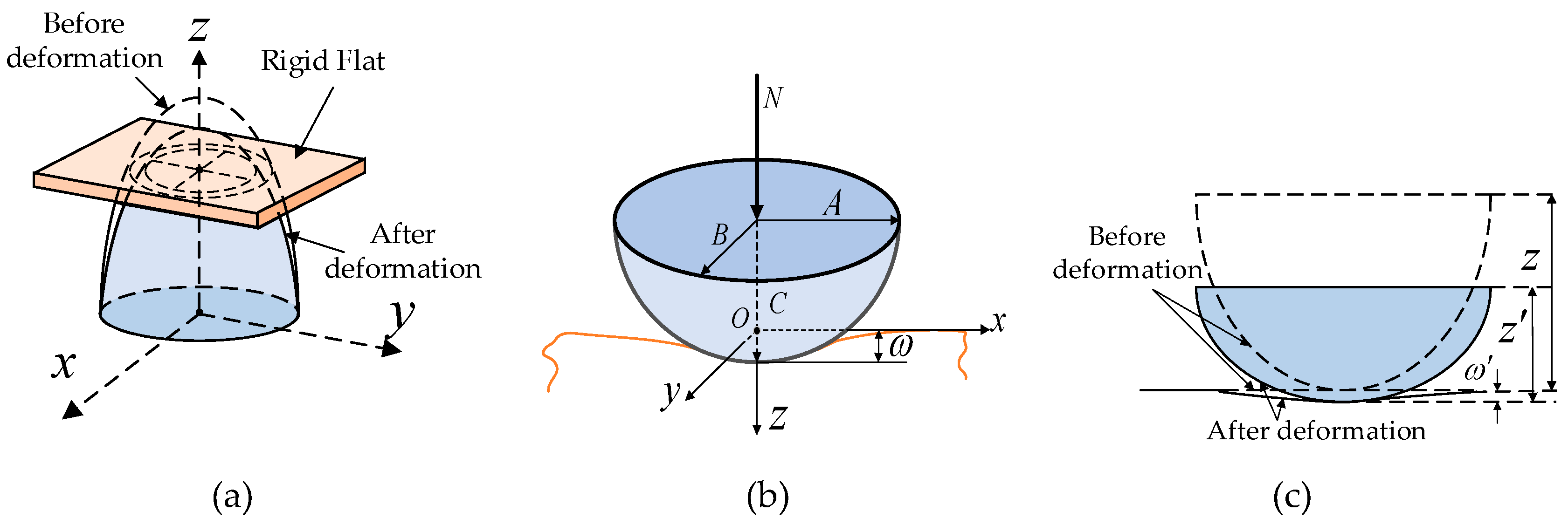
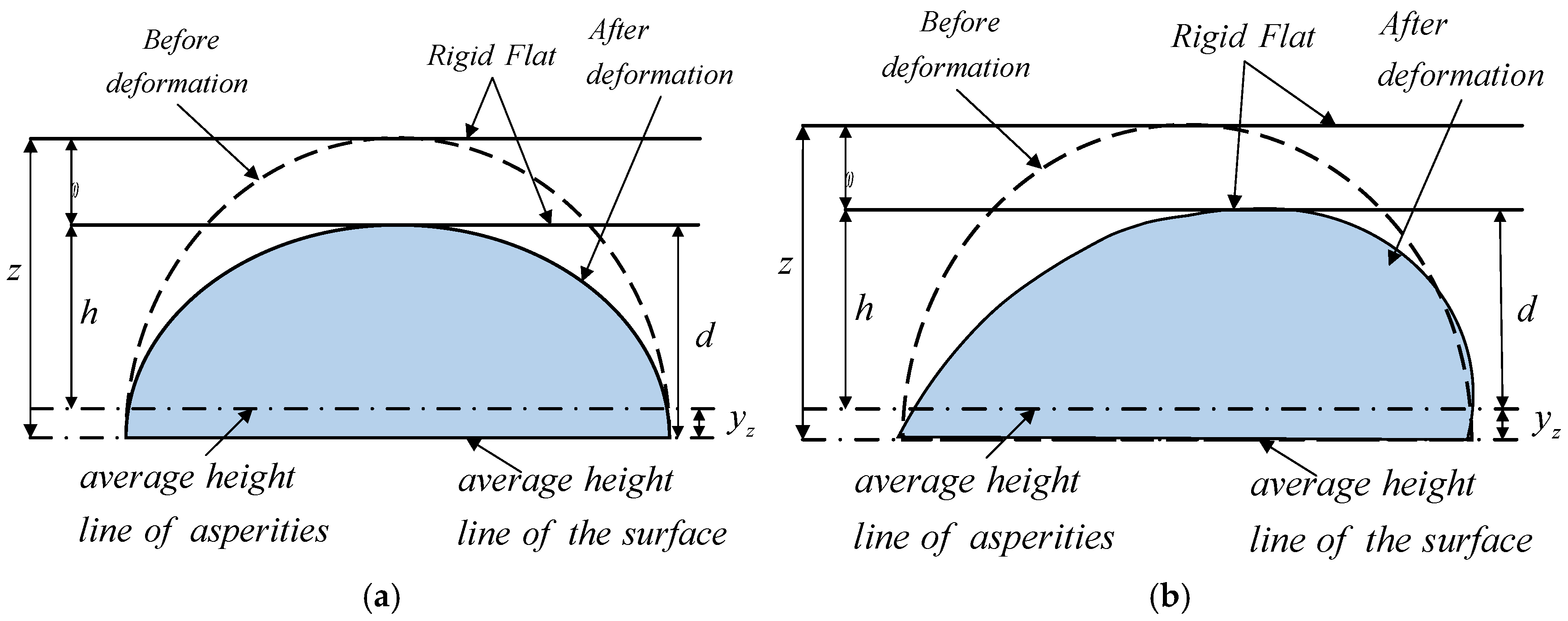
At present, there are two common methods for studying the asperity contact model. The first is the flat - asperity contact model, in which the contact surface is regarded as the contact between a rough surface and a smooth flat plate. The deformation and contact mechanical characteristics of the asperities under load are analyzed, as shown in

Figure 3. Classification and Research Content of Asperity Contact Models.

Figure 3. Classification and Research Content of Asperity Contact Models.

Figure 4. Comparison diagram of the flat plate-asperity contact model before and after loading.

Figure 4. Comparison diagram of the flat plate-asperity contact model before and after loading.

Many models adopt this method to simplify the models and apply the finite element method or a combination of the elastic contact theory and approximate solutions to simulate this kind of contact. This research idea was first put forward by Sinclair and Follansbee [11,12]. Such contact models can be divided into three major categories [9] , as shown in Figure 5: namely, the flattening model, the indentation model and the comprehensive model. In the flattening model, the smooth flat plate is regarded as a rigid plane and only the asperities undergo deformation. In the indentation model, the asperities are considered to be rigid and only the smooth flat plate undergoes deformation. In the comprehensive model, both the asperities and the smooth flat plate are considered to be deformable.

The three types of flat - asperity contact models each have their own applicable scenarios and limitations. The flattening model enables a more detailed analysis of the geometric shape changes and stress distribution patterns of asperities during the contact process. In particular, it provides an intuitive means for studying the influence of geometric parameters such as asperity height and shape on the contact behavior. In situations where the accuracy requirements are not extremely high and the focus is mainly on factors related to the deformation of asperities themselves, a simplified model that only considers the deformation of asperities can quickly conduct theoretical derivations and preliminary estimations. However, in engineering applications that require precise analysis of the interaction between the two contacting surfaces and demand a high level of accuracy for the overall contact performance, the applicability of this model is limited. In some practical situations, for example, when the hardness of asperities is much higher than that of the flat plate material, or when the flat plate is relatively thin and more prone to deformation, the indentation model can better reflect the dominant role of the flat plate's deformation during the contact process, thus being more suitable for such specific actual contact scenarios. However, in most conventional cases of rough surface contact, the deformation of asperities and the flat plate are often interrelated and jointly affect the contact effect. The integrated model can more comprehensively reflect the essence of contact and has a wide range of applicability. It is suitable for contact problems under various combinations of different materials, different surface roughnesses, and different load conditions. However, this model has a relatively high level of complexity, and it is rather difficult to obtain and calibrate the parameters.

The flat - asperity contact model constitutes a significant part of the research on asperity contact models. It includes aspects such as the study of asperity shapes, the research on contact mechanics considering substrate deformation, and the research on contact mechanics considering tangential loads.

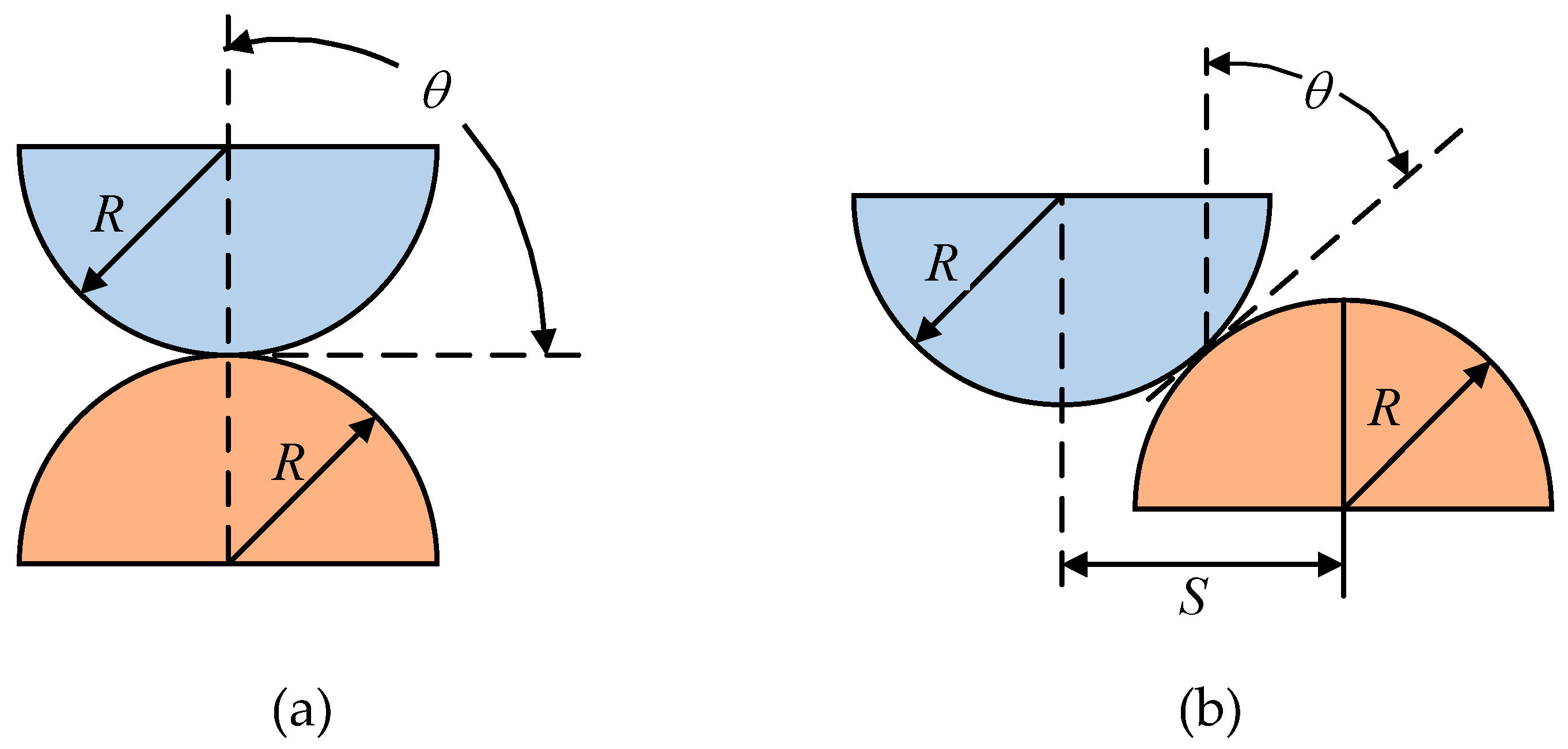
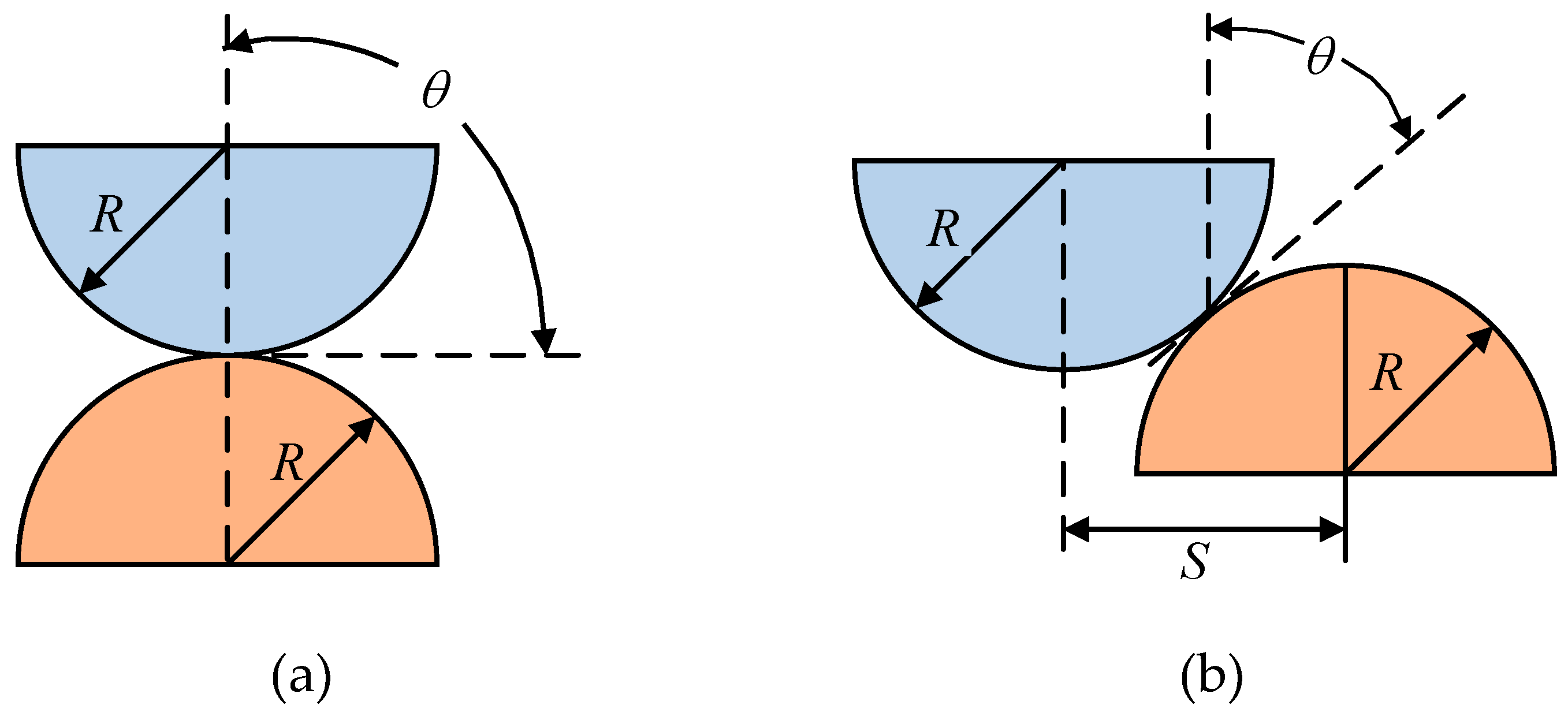
The second research method is to regard both contacting surfaces as rough surfaces. The asperities on the upper and lower surfaces come into contact with each other under the action of force and both undergo deformation. The contact forms are mainly divided into normal contact and lateral contact, where normal contact can be regarded as a special case of lateral contact, as shown in Figure 6.

The asperity - asperity contact model focuses on the contact behavior between asperities. It can describe the interaction between rough surfaces in more detail, reflecting the microscopic characteristics during the contact process. This is helpful for a deep understanding of the microscopic physical mechanisms in the contact process, such as the formation and development of contact points. Compared with the flat - asperity contact model, the asperity - asperity contact model can more realistically simulate the contact phenomena of rough surfaces in actual engineering, improving the accuracy and reliability of the model. Its drawback is that since it is necessary to consider multiple factors such as the geometric shapes, distribution laws, and material properties of asperities, the process of establishing and solving the model is relatively complex, and the calculation cost is also relatively high. With the development of computer technology, the use of finite element analysis methods can effectively solve a series of problems such as high complexity and large computational amount.

The research content of the asperity - asperity contact model mainly includes aspects such as the study of asperity shapes, the research on the probability distribution functions of contact angles and contact azimuth angles, and the research on finite element models.

2.2. Flat Plate - Asperity Contact Model

During the establishment of the statistical contact model, it is necessary to first establish the asperity contact model. The Hertz theory is the foundation of classical contact mechanics. Hertz established the asperity contact model based on the flat plate - asperity contact assumption and was the first to derive the analytical solution for the elastic contact of curved surfaces. The research on the contact model of asperities under normal and tangential loads aims to describe the contact state between rough contact surfaces more comprehensively and accurately. As such models are widely used in the study of the contact characteristics of rough surfaces, it is of great significance to optimize the models reasonably.

In the research on the flat - asperity contact model, scholars carry out innovative research in different directions according to various requirements and research focuses. This involves optimizing assumptions regarding aspects such as the shape of asperities, whether the substrate undergoes deformation, and whether tangential loads are taken into account.

2.2.1 Shapes of Asperities

In practical engineering, rough surfaces are generally highly anisotropic, that is, the surfaces under consideration have obvious textures in certain directions. For such surfaces, the major axis direction of asperities needs to be consistent with the texture direction. Therefore, scholars have begun to assume that the shape of asperities is a non-single-curvature shape for modeling, such as an ellipsoidal shape. Bush [13]et al. chose highly eccentric ellipsoids with the major axis along the texture direction to represent asperities and established the BGT model. They analyzed the conditions for the transition from the elastic contact stage to the plastic contact stage. However, the deformation state of asperities was only limited to the elastic contact stage in their research. So and Liu [14] combined the maximum principal stress yield criterion to analyze the elastoplastic contact between rough surfaces and planes, and extended the ellipsoidal asperity model to the elastoplastic and plastic deformation stages. Greenwood [15] verified that most of the asperity peaks were only slightly elliptical by extending Nayak's theory. By using the approximate solution of elliptical Hertz contact based on the geometric mean value of the peak curvature, a new ellipsoidal contact model on rough surfaces was established. This model can reproduce the results of the BGT model in a simpler and more accurate manner.

Horng [16] et al. introduced the concept of the ratio of the radius in the principal direction to that in the secondary direction of asperities, extended the CEB model [17] to ellipsoidal asperities and established the JH model. Similar to the CEB model, this model fails to take into account the elastoplastic transition stage. The JW contact model of elastoplastic ellipsoidal asperities established by Jeng and Wang [18] has improved the deficiencies of the JH model and the ZMC model. Buczkowski et al. [19] combined the BGT model, the CEB model and the ZMC model to establish a new statistical model for rough surfaces.

Chung [20] assumed that asperities were in the shape of ellipsoids and established a finite element model. This model successfully simulated the contact pressure distribution and the evolution of the plastic region of ellipsoids with different ellipticities under different deformation amounts. For the first time, it conducted a detailed analysis of the elastic - plastic deformation behavior between ellipsoids with different ellipticities and a rigid flat plate, filling the gap in this field. JENG [21] studied the variation of the friction coefficient of a contact surface with elliptical asperities under different parameters. It was found that the friction coefficient increased with the increase of the plastic index but decreased with the increase of the effective radius ratio.

Some scholars believe that it is more in line with the actual situation to assume the asperities shape as the sinusoidal shape. It seems logical to use the sinusoidal contact model instead of the spherical contact model [18,22]. Their measurement and research on rough surfaces found that sinusoidal contact can simulate the asperity contact better than hemispherical contact. Jackson [23] et al. found through research that for light-load contact, the behavior of sinusoidal contact may be very similar to that of a sphere. However, as the load increases and the contact approaches completion, the behavior of the sinusoidal curved surface is quite different from that of the spherical surface.

By assuming the shape of asperities to be a half-period cosine curve of revolution, An Qi et al. [24] established a contact model that can effectively simulate the asperities on ground surfaces. Shang [25] et al. proposed a method of using a parabolic body of revolution to equivalent asperities and derived the calculation equation for the normal contact stiffness of rough surfaces in the elastic contact stage. Li Ling [26] et al., based on the rough surface topography measurement experiments, put forward a method of using a parabolic body of revolution to equivalent asperities, established the analytical relationship between the contact radius of asperities and the contact deformation amount, and according to the geometric model, re-derived the contact expressions of a single asperity in the three deformation stages of elasticity, elastoplasticity and full plasticity.

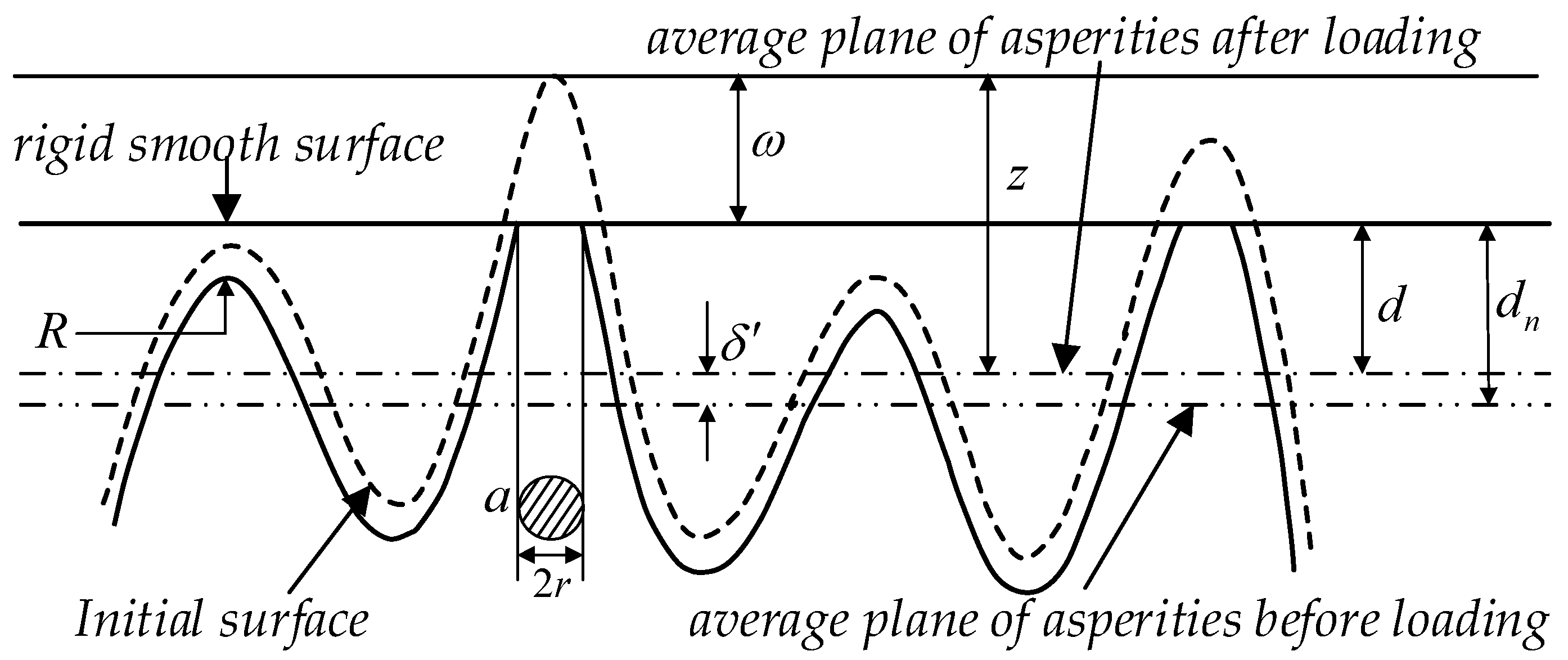
2.2.2. Substrate Deformation

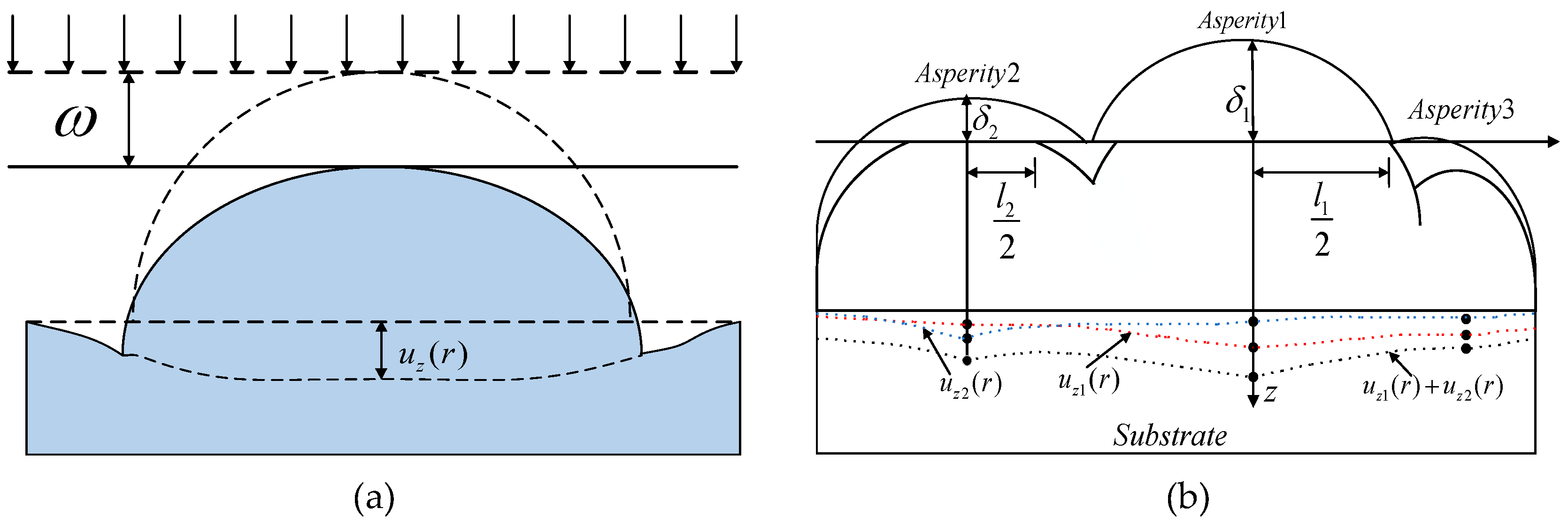
Traditional contact models often neglect the substrate deformation or the interaction among asperities, resulting in a relatively low prediction accuracy for contact characteristics [27]. Since asperities are located on a continuous substrate, the deformation of one asperity will change the height of adjacent asperities through the deformation of the substrate, thus affecting the contact situation of the entire joint interface, as shown in Figure 7. When the ratio of the actual contact area to the nominal contact area of two rough surfaces is small, the influence of asperity interaction can be neglected. For example, the Greenwood-Williamson (GW) model provides relatively good prediction results for contacts under low load conditions [28,29]. However, when the contact load is relatively large, the distance between asperities will gradually decrease, and adjacent asperities will interact with each other and thus affect the contact characteristics of the contact interface. Therefore, the study of the contact characteristics of the contact interface should also take into account the asperity interaction and the deformation of the substrate.

Zhao and Chang [30] based on the ZMC model, combined the Saint-Venant's principle and Love's formula with the deformation amount of asperities for the first time. They assumed that the area at the bottom of each asperity was proportional to the load it bore and established a substrate deformation model, namely the ZC model. Jeng and Peng [31] also based on the Saint-Venant's principle and Love's formula, analyzed the influence of asperity interaction on the average spacing and contact area between rough surfaces where the asperity height had a non-Gaussian distribution. Ciavarella [32] and others improved the GW theory. They regarded the contact pressure as being uniformly distributed on the nominal contact area. This modification was equivalent to adding a parameter proportional to the nominal pressure to the effective separation distance of the average plane, resulting in the reduction of the "true" contact area and the total load at a given separation distance. The improved GW theory was able to predict the numerical contact response at intermediate load levels.

Vakis [33] combined the total substrate deformation generated by the interaction with the KE model and proposed a new substrate deformation model. Tang et al. [34] introduced the substrate deformation of asperities themselves and the interaction among adjacent asperities to predict the closure behavior of rock joints under compressive loads. Song [35] et al. utilized the deformation response of three-dimensional single asperities, took into account the interaction effect of asperities through substrate deformation, and conducted statistical calculations on the contact characteristics of rough surfaces. Zhang Lihua [36] explored the relationship between the total substrate deformation with and without considering the interaction among asperities, and introduced the surface asperity area density function to establish a rough surface contact model that takes into account the interaction among asperities. Li [37] et al. considered the elastic deformation of surface asperities and the nonlinear deformation effect of the substrate, and proposed a modified elastic contact stiffness model. They mainly studied the influence of substrate deformation on contact stiffness in rough surface contact. This model shows higher adaptability than the traditional Hertz model in dealing with high-stress conditions and can provide more accurate predictions of contact stiffness. Its main drawback lies in its high sensitivity to material parameters, requiring precise parameter measurements during the experiment.

2.2.3. Research on Contact Mechanics Under Tangential Loads

During the normal operation of the equipment, the joint interface will be simultaneously subjected to the combined action of normal and tangential loads. As a result, complex behaviors such as friction, slip, and sliding will occur at the joint interface, and energy dissipation will be generated at the contact interface, which also has an impact on the contact stiffness and contact damping. Therefore, when studying the contact behavior of joint interfaces, the tangential load is also an influencing factor that cannot be ignored. Among them, the exploration of the tangential load-displacement relationship of joint interfaces has always been regarded as one of the rather challenging problems [38,39,40,41].

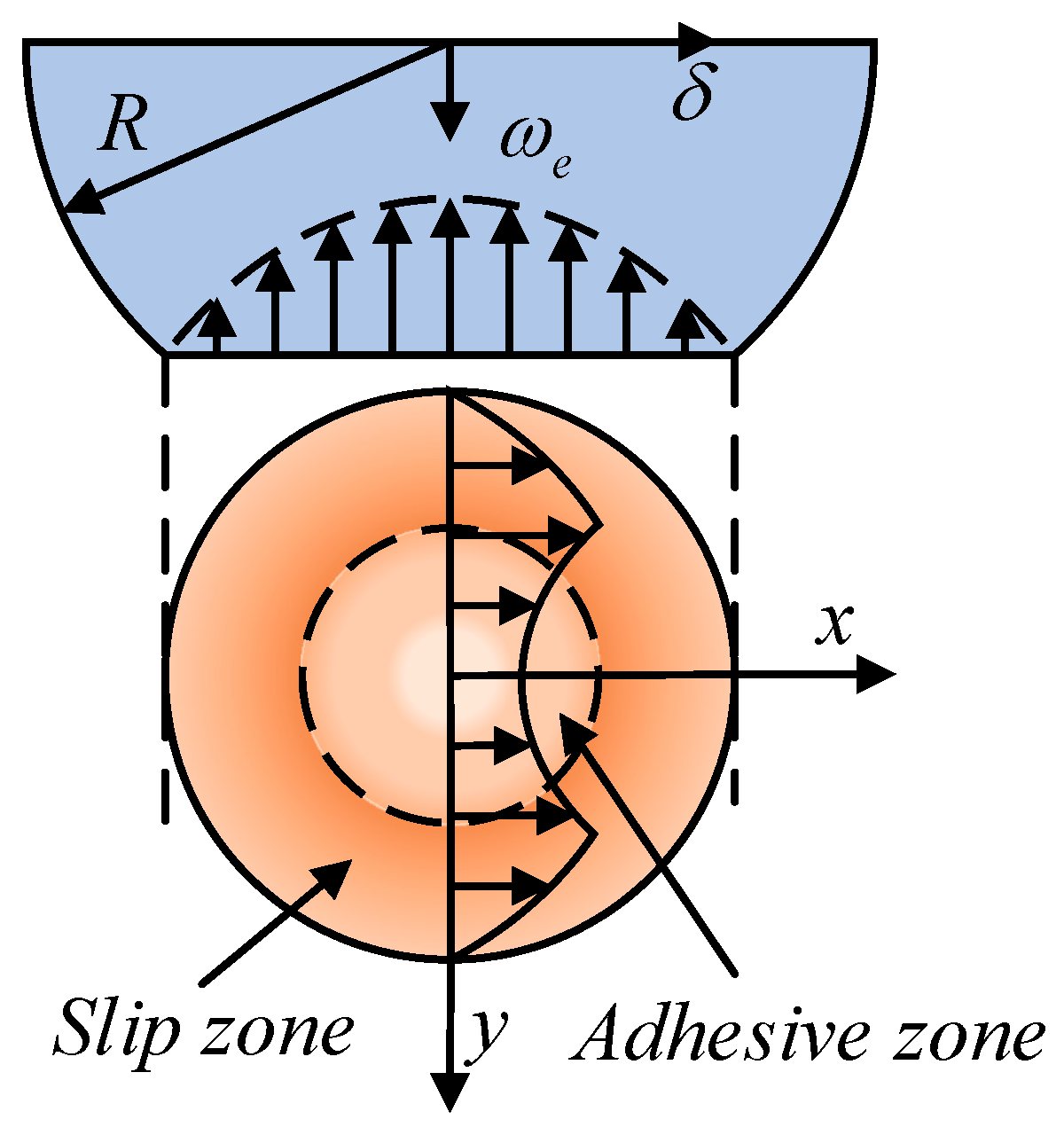
Figure 8(a) shows the contact between a single asperity and a rigid smooth flat plate without tangential force. Figure 8(b) shows contact that considering tangential force. Many experimental results indicate [42] that the tangential force will cause the contact area to become larger compared to the contact area without tangential force.

Mindlin [43] was the first to theoretically explore the slip-sliding behavior of two asperities under the combined action of normal and tangential loads. Mindlin assumed that asperities only underwent elastic deformation, the contact satisfied Coulomb's friction law, and the friction coefficient was a constant value. He then derived the nonlinear relationship between the interfacial tangential load and the tangential displacement. According to Mindlin's theory, when the tangential load borne by the contact interface is less than the critical force for macroscopic sliding, there is no sliding in the central area of the contact, and only microscopic slip occurs at the edge of the contact area. When the tangential load increases, the area of the slip zone also increases until the tangential load reaches the critical value for macroscopic sliding, at which point the entire contact interface will experience macroscopic sliding.

As shown in Figure 9, Mindlin's theory presents the distribution laws of normal and tangential forces on the elastic contact interface, as well as the relationship between the tangential load and the relative displacement as follows:

$$T_e=\left\{\begin{array}{cc}f{N}_e[1-{(1-\delta /{\delta }_e)}^{3/2}]\hfill & \delta \le {\delta }_e\hfill \\ f{N}_e\hfill & \delta >{\delta }_e\hfill \end{array}\right.,$$

(5)

$${\delta }_{ｅ}={\displaystyle \frac{3f{N}_e}{16G{r}_e}}$$

(6)

In the formula: $f$ is the friction coefficient; $\delta$ is the tangential relative displacement; $T_e$ is the tangential load acting on the elastic asperity; $N_e$ is the normal load acting on the elastic asperity; ${\delta }_e$ is the tangential relative displacement when the elastic asperity undergoes macroscopic sliding; $r_e$ is the radius of the actual contact area of the asperity; $G$ is the equivalent shear modulus, where $G=G_1/(2-{\nu }_1)$, $G_1$ is the shear modulus of the asperity material, and ${\nu }_1$ is the Poisson's ratio of the asperity material.

Johnson's experimental results [44] show that under large loads, the asperities undergo plastic deformation, which leads to the final fatigue and fretting of the surface in the high-stress annulus region. The energy consumed is quantitatively consistent with the results calculated by Mindlin, providing considerable support for Mindlin's theoretical analysis.

Kogut [45] analyzed a sphere that underwent completely elastic and completely plastic deformations under the load of a rigid plane by using the finite element analysis method. He defined the "internal static friction coefficient" and gave simple analytical expressions for both elastic and plastic cases. Wang Dong et al. [46] introduced a new load-displacement relationship for plastically contacted asperities and drew on the probabilistic and statistical analysis method of the GW model to derive the relationship between the tangential load and displacement of the entire rough surface. Xu Gang et al. [47] combined the two modeling methods of rough surface contact models, namely the constitutive model and the phenomenological model, and proposed a rough surface tangential contact model based on the KE normal contact theory and the Iwan model. By considering the constitutive equation for tangential motion occurring between rough surfaces and comparing it with the Iwan model, they derived a probability distribution function of the critical slip force of friction plates based on measurable physical parameters.

Under the action of tangential loads, due to the factor of tangential friction, the contact shape is different from that under a single normal load, and the contact area also changes at the same time. In practical engineering applications, joint interfaces usually transmit both normal and tangential loads simultaneously. Therefore, when establishing a joint interface contact model that is more in line with the actual situation according to the actual working conditions of the joint interface, the coupling effect of normal and tangential loads should be taken into account.

2.3. Asperity - Asperity Contact Model

Adopting the flat plate - asperity contact assumption method in the Hertz contact theory greatly simplifies the complexity of the model and reduces the amount of calculation. However, some important parameters are also ignored in this way, and there are deviations between the established model and the actual contact situation [48]. In order to be more in line with the real contact behavior of rough surfaces, some scholars have chosen to use the asperity - asperity contact assumption to conduct research on the asperity contact model, as shown in Figure 10.

2.3.1. Shapes of Asperities

The contact behavior of asperity - asperity can be classified into normal contact and lateral contact. Normal contact means that the tops of two asperities are in contact with each other. Lateral contact is the form of contact among the vast majority of asperities, and normal contact can also be regarded as a special case of lateral contact. In the flat plate - asperity model, scholars have made innovations and improvements in the shape of asperities. In the asperity - asperity model, scholars have also explored the contact behaviors of asperities with different shapes.

Jager [49] studied the lateral contact behavior between two spheres and proposed a calculation method for estimating the energy consumption due to friction. However, this model only considered the elastic deformation stage of asperities and ignored the elastoplastic and plastic stages. Faulkner and Arnell [50] assumed the shapes of asperities to be cylinders and spheres respectively and established finite element models to explore the influence of roughness on the overall friction coefficient. It was found that the friction coefficient of a rough surface with spherical asperities was smaller than that with cylindrical asperities.

Kogut and Etsion [45,51] modified the deformation stage of asperities based on the ZMC model by using the finite element method. They removed the limitation of volume conservation in the asperity deformation stage and divided the elastoplastic stage of asperities into the first elastoplastic and the second elastoplastic, enabling all the deformation stages to be connected more smoothly into a whole. Thus, they obtained contact models for elastic, elastoplastic and fully plastic deformations and established the KE model.

Sepehri and Farhang [52] established the SF contact model. Based on the asperity constitutive relationship derived from the KE model, they deduced the governing equations for asperity contact and developed approximate equations in closed form for contact force components and contact area. Li and Hong [53] et al. combined the KE model and the SF model to establish an oblique impact contact model for ellipsoidal asperities on double rough surfaces. They discussed the contact behavior during the elastoplastic deformation stage of a single asperity and applied it to the research on predicting the contact resistance of electrical components.

Jamshidi and Ahmadian et al. [54] established an oblique contact model for spherical asperities on double rough surfaces. They studied the frictional contact hysteresis behavior between two planes. By analyzing the partial slip and total slip on rough surfaces, they modified Mindlin's spherical elastic contact solution and developed an improved contact model using the double rough surface contact theory. However, this model only took the elastic deformation stage into consideration.

2.3.2. Contact Angle and Contact Azimuth Angle

In the process of expanding the asperity - asperity contact model to the rough surface contact model by using statistical methods, the research on key parameters such as the contact angle between asperities, the contact azimuth angle, and the height distribution function of asperities is of great significance. When two rough surfaces are in contact, lateral contact is mainly affected by the contact angle, and the uniformity of the contact azimuth angle determines the degree of interfacial anisotropy, while the height distribution of asperities determines the roughness of the surface. Therefore, in the process of establishing the rough surface contact model, how to select the distribution functions of the contact angle, the contact azimuth angle, and the height of asperities among asperities has become one of the research directions that scholars pay attention to.

Gorbatikh [48] based on the lateral contact of asperities, assumed the distribution function of the contact angle and studied the characteristics of the lateral contact between asperities by using statistical methods. A new statistical contact model for the contact interface was established, but the theoretical basis for this angle distribution function was not provided. Gao Zhiqiang [55] studied the contact characteristics of asperities in the three deformation stages of elasticity, elastoplasticity and plasticity based on the lateral contact and interaction of asperities. By adopting the contact angle distribution function assumed by Gorbatikh [48], a contact interface contact model (GZQ model) that reflects the normal and tangential contact energy consumption of asperities was established. However, the contact angle distribution function cited in this model has no exact theoretical or experimental basis. Misra and Huang [56,57] creatively introduced the joint probability density function of the contact angle and azimuth angle during the lateral contact of asperities. Combining the calculation schemes of asperity contact sliding and stress-displacement increment, and coupling the tangential and normal contact stiffnesses, they studied the sliding behavior of asperities in lateral contact.

Shi et al. [58] established a three-dimensional lateral contact model using two elastoplastic spherical asperities. They described the initial offset state of the lateral contact by using two parameters, namely the contact azimuth angle and the contact angle, and found that the load ratio of asperities is mainly determined by the Young's modulus of the material and the interfacial shear strength, while the maximum force on asperities during the unloading stage is mainly related to the contact angle of asperities. However, this model only conducted the force analysis and modeling research on asperities and was not extended to the study of the contact characteristics of rough surfaces. Gao and Fu [59] based on the joint distribution function of the contact angle and the contact azimuth angle proposed by Misra and Huang [56,57], combined with the KE model, the ZC model and the adhesion-slip theory, established an anisotropic rough surface contact model (GF model) considering the lateral contact and interaction of asperities. They analyzed the adhesion and slip conditions of the contact surface under the action of tangential force and the influence of the standard deviation of asperity height and asperity contact angle on the contact surface. Jamshidi et al. [54] defined the contact state according to the relative positional relationship when asperities are in contact, and at the same time modified Misra's contact angle function. Thus, they established the HJ model with the coupling of the normal load and the shear force on the contact interface.

Fan Lingsong et al. [60,61] studied the horizontal distance distribution of adjacent asperities on rough surfaces and found that the horizontal distance follows the Gaussian distribution law. For the first time, they replaced the assumed contact angle distribution function with the distribution law of the horizontal distance of asperities. According to the statistical theory, they established the FLS model containing the normal and tangential contact characteristics, breaking through the theoretical bottleneck that the contact angle distribution function still needs to be assumed when building the lateral contact model.

2.3.3. Numerical Contact Models of Asperities

The more closely the contact model conforms to the actual situation, the greater its complexity will be. For complex rough surface contact problems, it is necessary to conduct research and calculations with the help of the finite element method and experiments. The finite element model can accurately simulate and calculate contact parameters such as pressure distribution, deformation amount or load when a single asperity or multiple asperities are under pressure and deformed. Experiments can verify the correctness of previous models and the proposed new calculation results and calculation fitting formulas, and intuitively and accurately analyze these contact problems. Finite element simulation is an important means of simulating and testing the effect of the model, and it is also an important method for studying contact characteristics.

The elastoplastic hemispherical finite element contact model established by Jackson [62], namely the JG model, verified the correctness of the Hertz contact theory under the extremely small deformation amounts. It was also pointed out that when the contact deformation amount is too large, the final result is not the same as the fully plastic contact of the AF model. In the elastoplastic contact deformation stage, the JG model is closer to the simulation results than the KE model and the ZMC model. It can effectively study the contact behavior of asperities and also has a certain degree of adaptability to macroscopic contact.

Jackson [63] et al., based on the initial state of asperities on rough surfaces being lateral contact, derived empirical formulas for the average tangential force and the average normal force of spherical asperities in the sliding state through semi-analytical methods and finite element simulation analysis respectively.

Mulvhill [64] et al., based on the condition of asperity lateral contact, established an elastoplastic interaction finite element model for the contact between cylindrical asperities and spherical asperities. The difference between this model and the models established by predecessors lies in that it allows a greater overlap of asperities in the heigh, has a higher interfacial viscous shear strength, and allows the occurrence of material failure.

Chandrasekar [65] et al. improved the analytical model of asperity interaction based on the finite element method and proposed that the surface roughness density is an important parameter for determining the influence of asperity interaction on the contact interface.

Zhu Linbo [66] added the elastoplastic deformation stage of asperity lateral contact on the basis of predecessors who only considered the elastic deformation stage and the plastic deformation stage, and established the ZLB model. Compared with the original elastic-plastic contact models of the contact interface, this model is closer to the finite element results. Zhao [67] et al. established an analytical contact model for the interaction of multiple asperities applying power-law hardening materials by considering the position, height and radius of curvature of asperities on rough surfaces, and studied the influence of the material properties of power-law hardening materials on the interaction of asperities.

Finite element analysis (FEA) is a numerical simulation technique used to predict how materials will perform under given conditions and has a very wide range of application scenarios. It solves complex engineering problems by decomposing complex structures into many small and simple parts. By increasing the number of elements in the model, the accuracy of the calculation results can be improved. This enables engineers to conduct extremely detailed analyses of designs, thereby ensuring the safety and reliability of products. Compared with traditional test methods, virtual testing using FEA can significantly reduce the number of physical prototypes, thus cutting down time and cost. The application of FEA in micromechanical analysis is gradually becoming an important analytical method in the fields of materials science and engineering, especially in the fields of multi-scale modeling and nonlinear analysis. Although numerical simulation provides a powerful prediction tool, this method involves a large number of ideal conditions compared to experiments, and experimental verification remains the key to ensuring the reliability of the model. Therefore, the future development trend of finite element model verification methods will be to strengthen the combination of experiments and simulations, form a closed-loop feedback mechanism, and continuously improve and refine the finite element model.

In the asperity - asperity contact models, the shapes of asperities are mostly assumed to be ellipsoids, cylinders and other shapes at present. In the future, they may be expanded in the directions of paraboloids, revolving bodies of trigonometric functions and other shapes, so as to establish contact models that are more in line with the actual situation. With the progress of the finite element algorithm, it will also be applicable to the fitting calculations of more complex contact models. The combination of finite element analysis and experimental verification has gradually become an important method for studying the complex contact behaviors of rough surfaces. Besides using the two parameters of contact angle distribution and contact azimuth angle to characterize the anisotropy of asperities, using the horizontal distance distribution of asperities for characterization is also a new approach.

3. Statistical Contact Model of Rough Surfaces

Moreover, its research and development are more comprehensive. The GW model [68,69] is the earliest rough surface contact model established by the method based on statistical analysis. The GW model has obtained the relationships among the contact pressure, contact area and deformation amount of rough surfaces by studying the heights of asperities and the their characteristics of distribution.

Figure 11. GW model.

Figure 11. GW model.

In order to facilitate model establishment and derivation calculations, the GW model makes the following assumptions: (1) The shape of asperities is spherical, with a radius of an average value, and their heights are randomly distributed; (2) Asperities are evenly distributed on the rough surface and have no directionality; (3) During the contact process, only asperities undergo deformation, the substrate does not deform, and the deformations among asperities do not affect each other; (4) The upper and lower asperities are in tip-to-tip contact, and lateral contact behaviors are not considered.

As a typical representative of statistical contact analysis, the GW model has laid a milestone foundation for the contact theory between rough surfaces. Up to now, this model is still accepted and used by researchers.

As a seminal contribution, the GW model established fundamental principles for subsequent surface contact research. Based on this, scholars have continuously conducted in-depth research on the statistical contact model and established models that can describe the actual contact behaviors of rough surfaces more accurately.

In the process of expanding the asperity contact model to the rough surface contact model by means of the statistical summation method, one of the core steps is to determine the height distribution function of the asperities on the rough surface. The GW model regards the height distribution of asperities on the rough surface as a random function that obeys the Gaussian distribution. Therefore, most models also adopt the Gaussian distribution. In the gradual development of contact models, there have also been some attempts to use non-Gaussian distributions for height. This chapter will classify and discuss the development and research status of contact models according to different height distributions.

3.1. Surface Contact Model Based on Gaussian Distribution

Since Greenwood and Williamson established the classic GW model, Chang et al. [17] studied the deformation situations of asperities on rough surfaces beyond the elastic contact stage based on the GW model. They took into account the volume conservation law of asperities in the plastic deformation stage and extended the GW model to plastic deformation, thus establishing the CEB model. Horng [16] et al. extended the CEB model to ellipsoidal asperities and established the JH model. However, just like the CEB model, its shortcoming is that it didn't study the elastoplastic transition stage. Jeng and Wang [18] established the JW contact model for elastoplastic ellipsoidal asperities in order to make up for the defect that the plastic transition stage wasn't considered in the JH model. They took into account the assumed mutation in the transition process from elastic deformation to fully plastic deformation and improved the deficiencies of the JH model and the ZMC model.

The research on the elastoplastic contact stage is to study the contact state of the joint interface of engineering equipment when the load changes from low to high during actual assembly and operation, which has important engineering significance. Under high load conditions, the fully plastic flow of asperities has a significant impact on the contact stiffness, and the stress distribution within the contact area has a nonlinear relationship with the load. How to achieve a smooth transition of contact parameters from the elastic contact stage to the plastic contact stage in the model is a major difficulty.

The team led by Zhao Yongwu and other scholars have conducted in-depth research on the transition stage to the elastoplastic state for rough surface contact models based on the Gaussian distribution. In 2000, Zhao et al. [70] studied the discontinuity problem at the critical point from elastic to plastic deformation by using the function interpolation and fitting method, proposed the ZMC model, and established a complete deformation model for asperities on rough surfaces. However, the ZMC model has some shortcomings due to the limitations of the interpolation function properties. For example, the fitted average contact pressure is not smooth at the critical points of elastic, elastoplastic and plastic deformations, and the critical point of fully plastic deformation has not been determined. In 2001, Zhao and Chang [30] based on the ZMC model, assumed that the area at the bottom of each asperity is proportional to the load it bears, combined the Saint-Venant's principle and the Love formula with the deformation amount of asperities, derived the interaction formula, and established the substrate deformation model, namely the ZC model. In 2007, Zhao Yongwu et al. [71] aimed at the problem that the ZMC model is not smooth at the critical points and the critical point of fully plastic deformation has not been determined. They used the function interpolation and fitting method to establish a new model with continuous and smooth critical points. This model solved the problem that the critical point of plastic deformation has not been determined and achieved a smooth transition from elasticity to elastoplasticity. In 2019, Wang and Zhang [72] et al., aiming at the problem of discontinuous elastoplastic deformation of asperities, adopted the improved Hermite interpolation method, combined with the GW model and the AF model on the basis of other assumptions, and established an improved ZMC model.

Li Ling [73] et al. established a new polynomial function to describe the relationship between the contact deformation amount and the contact area according to the fact that both the real contact area of asperities and the transformation of contact load satisfy the continuous and smooth conditions at the critical point of the deformation state transformation. This has solved the problem that the contact mechanism in the elastoplastic region of the contact interface is difficult to determine.

Nayak [74] put forward a new method, that is, using three important parameters related to the power spectral moments, namely the root mean square of asperity height, the root mean square of surface gradient and the root mean square of asperity radius of curvature, to characterize a random and isotropic Gaussian surface. And he pointed out three simple methods for obtaining these parameters from the rough surface profile, as well as the method for expanding this theory to non-isotropic Gaussian surfaces.

Li [75] proposed a contact stiffness model combining continuous smooth characteristics and asperity interaction by introducing a surface smoothness parameter, which makes the prediction of contact stiffness more accurate. The drawback of this model is its relatively high complexity and large amount of calculation, so it is applicable to small-scale high-precision engineering designs. Xu Gang [47] derived a probability distribution function of the critical slip force of friction plates based on measurable physical parameters by comparing the constitutive equation of tangential motion occurring between rough surfaces with the Iwan model, and proposed a tangential contact model for rough surfaces based on the KE normal contact theory and the Iwan model. Zhang Wei et al. [76] based on the GW statistical contact model, derived expressions for the normal contact load and stiffness of the contact interface when considering the substrate deformation or interaction of asperities separately. They took into account the substrate deformation and the interaction of adjacent asperities, but ignored the elastoplastic deformation stage and the plastic deformation stage of asperities.

Li Ling [26] put forward a method of using revolving bodies of quadratic functions to equivalent asperities. She re-derived the contact equations of a single asperity in the three deformation stages of elasticity, elastoplasticity and full plasticity, and established a microscopic contact model for rough surfaces. This model provided new ideas for establishing the contact model of the joint interface. Yakovenko and Goryacheva [77] established a model considering the mutual influence of asperities by using the localization method. The constructed contact model can study the dependence of contact characteristics on the applied pressure, and within a wide range of nominal pressures, it can display the experimentally observed real contact area and the saturation effect of the additional compliance caused by roughness.

All of the above models assume that the height distribution of asperities follows a Gaussian distribution. During the statistical summation process, their forms are simple. Therefore, currently, the Gaussian distribution assumed by the GW model is still adopted for the asperity height distribution in most statistical contact models. However, it is not easy to obtain analytical solutions for contact models under the Gaussian distribution. Through the exploration of some scholars, it has been found that similar analytical results can be obtained by adopting other non-Gaussian distribution assumptions[78,79,80], and it is easier to obtain analytical solutions. In subsequent research, it has also been discovered that, at a more microscopic level, the height of asperities does not always follow a Gaussian distribution[81,82]. Thus, scholars have launched research on rough surface contact models under the assumption that the asperity height distribution is other non-Gaussian distributions.

3.2. Surface Contact Model Based on Non-Gaussian Distribution

The experiments of GW show that the height distribution of asperities on engineering surfaces mostly follows a Gaussian distribution. However, adopting the Gaussian distribution is not conducive to obtaining the analytical solutions of the contact parameters of the contact interface. On the basis of GW's pioneering work, researchers selected the exponential distribution as the height distribution of asperities when obtaining simplified closed-form solutions. Hess and Soom [78,79] as well as Hess and Wagh utilized the exponential distribution of asperity heights in their dynamic friction modeling work. Etsion and Front [80] also adopted the exponential distribution in their static seal structure modeling work. Polycarpou and Etsion [81] modified the exponential distribution and used a modified exponential distribution with two additional constants to approximate the Gaussian distribution, obtaining simple analytical expressions with acceptable accuracy. You Jinmin and Chen Tianning [83] established a new contact model to analyze the influence of different height distributions on the calculation results of contact parameters under three different random distributions of asperity heights, namely the Gaussian distribution, the simple exponential distribution and the modified exponential distribution. The results indicate that the modified exponential distribution has a relatively good approximation to the Gaussian distribution, while the error between the simple exponential distribution and the Gaussian distribution is relatively large. Goryacheva and Yakovenko [84] assumed the asperity height distribution to be the exponential distribution and the single-stage distribution to study the influence of the interaction of asperity parameters on the macroscopic contact characteristics, and pointed out that ignoring the interaction among the asperities on the contact surface in the discrete contact model will lead to significant errors when determining the contact characteristics on both the macroscopic and microscopic scales.

Borodich and Pepelyshev [82] found that on the nanometer and micrometer scales, the height distributions of the studied surfaces were not Gaussian distributions. This once again proved that the normal distribution is not applicable to the description of the topography of all rough surface asperities. When studying rough surfaces on a more microscopic scale, they also pointed out that the Markov surface proposed by Whitehouse [85] is more suitable for the description of rough surfaces.

Li Ling [29] pointed out that since the Gaussian distribution function and the exponential distribution function have no upper limit and do not conform to the actual variation range of asperity height, adopting a new distribution with the same standard deviation as that of the Gaussian distribution can solve the drawback that the asperity height in the Gaussian distribution and the exponential distribution has no upper limit, which is more in line with the actual situation. Li Ling introduced the triangular distribution function to characterize the height distribution of surface asperities. On the basis of improving the GW model, a new elastic contact stiffness model was established, revealing the influence laws of the distribution function, substrate deformation and surface roughness on the contact characteristics of the contact interface. The results showed that the triangular distribution function can effectively characterize the height distribution of surface asperities. However, there is currently no more literature to support the universality of the triangular distribution. Therefore, it is still not mature enough to use the triangular distribution to study rough surface contact models.

Some scholars assume that the height distribution of asperities follows a Weibull distribution. This distribution has high flexibility. By adjusting the shape parameter and the scale parameter, various distribution curves with different shapes can be obtained, which can well fit different distribution patterns in many actual data. McCool [86,87] suggested using the Weibull probability density function to simulate the distribution of asperity height. The two-parameter Weibull distribution is different from the commonly assumed symmetric Gaussian model. It can explain the skewness in the roughness height distribution, whether it is positive or negative. In addition, the contact between two Weibull surfaces can be approximated as the contact between an equivalent single Weibull surface and a smooth flat plate. Reference [88] considered extending the GW model with a two-parameter Weibull distribution to make it applicable to different types of roughness height distributions. Reference [89] studied the influence of the Weibull height distribution on the evolution of the real contact area in elastic, frictionless and non-adhesive contacts.

Besides assuming that the height distribution of asperities is a certain known typical distribution function, it is also possible to directly generate rough surfaces with different height distributions through algorithms. In 1996, Kotwal [90] proposed a statistical analysis method for non-Gaussian surfaces: by using the Pearson frequency curve system based on the method of moments to provide a group of curves to generate a distribution equation with the first four moments known, so as to obtain the probability density function of a distribution with known average, standard deviation, skewness and kurtosis. For example, non-Gaussian sequences can be obtained from Gaussian sequences by using transformation systems of the Johnson type or the Pearson type. Reference [91] utilized the mapping relationship between the height and curvature of asperities in the Johnson distribution and the Gaussian distribution to carry out corresponding conversions on rough surfaces with non-Gaussian distributions, and applied the mapping relationship between Gaussian and non-Gaussian roughness height distributions to the asperity height distribution. A contact model of a rough distribution model that can predict the distribution of surface asperities only through basic roughness parameters was established.

The algorithms adopted in References [92,93,94,95,96,97,98] can essentially be regarded as improvements on the same concept mentioned above. The algorithms used to generate surfaces with non-Gaussian height distributions are still not as versatile, robust or widely applied as those for Gaussian distributions. And as Francisco and Brunetière [99] pointed out, this method has some limitations, including issues regarding stability and accuracy. Nevertheless, after a series of improvements, today's algorithms allow the specification of skewness and kurtosis, thus being able to offer a considerable degree of flexibility [100].

To sum up, the Gaussian distribution has a simple form, but it is difficult to obtain analytical solutions during the calculation process. In the case of slight contact on rough surfaces, the exponential distribution can be adopted for the height distribution of asperities. The exponential distribution can make it easier to obtain analytical solutions. However, the error between the simple exponential distribution and the Gaussian distribution is relatively large, and it needs to be modified before it can be used as an approximation of the Gaussian distribution. Moreover, in the case of high loads, the exponential distribution will no longer be applicable. Since the traditional Gaussian model is symmetric about its average, this means that the traditional Gaussian model cannot accurately describe the skewness characteristics of surface roughness. The two-parameter Weibull distribution can solve this problem well. It can explain the skewness in the roughness height distribution, whether it is positive or negative. The Weibull distribution can reflect asymmetry well, and its parameters can be calculated based on the given root mean square value and the dimensionless skewness value of the asperity height distribution. In addition, the contact between two Weibull surfaces can be equivalent to the contact between a single Weibull surface and a smooth plane, which simplifies the calculation process. However, the parameter estimation of the Weibull distribution is complex, and since the Weibull distribution does not have the additivity property, this increases the computational burden in practical applications. Using algorithms to generate non-Gaussian distributions allows for more freedom when generating non-Gaussian surfaces. This method performs well in specifying commonly used height probability distributions and power spectra, and can handle particularly difficult height probability distributions, having quite high versatility. However, as the requirement for calculation accuracy increases, the computational complexity of the algorithms also increases correspondingly, requiring more computational costs. With the development and optimization of relevant algorithms, using algorithms to generate height distributions of asperities on rough surfaces that are more in line with the real situation is also a trend.

4. Discussion

This review mainly focuses on the current research status of the multi - scale contact models of connection interfaces from the microscopic to the macroscopic scale. Based on the rough surface contact model, the multi - scale model of two rough contact surfaces in the connection structure is introduced. The phenomenological contact models of rough surfaces have been developed and applied quite maturely, but there is still much room for development in the constitutive models based on the microscopic contact mechanism.

Asperities are the basic components of rough surfaces. There are still many assumptions in the establishment of asperity contact models. For example, relatively regular geometric shapes are selected for asperities, while the asperities on real rough surfaces have non - unique and irregular shapes. Currently, most asperity contact models are built based on the assumption of asperity shapes. Integrating surface topography measurement technology into the research of asperity contact models and conducting modeling based on the microscopic topography measurement of rough surfaces is one of the trends in the research of asperity contact models. With the in - depth research of asperity contact models, considering the substrate deformation and the combined action of normal and tangential loads simultaneously is also a trend.

The asperity height distribution is crucial for the research of statistical contact models. Compared with the traditional Gaussian distribution, obtaining a more realistic height distribution through the analysis and fitting of topography measurement data is an important trend. As a new technology, generating general rough surfaces using algorithms will also be better integrated into the research of rough surface contact models with the development of computer algorithms.

5. Conclusions

There are a large number of complex large-scale mechanical equipment in industries such as aerospace, mechanical processing and transportation. The components of these equipment are mainly assembled through different forms of connection structures, such as bolts, flanges, wedge rings and so on. Due to the strong nonlinearity of the contact stiffness and contact damping of their joint interfaces, in order to improve the overall performance of the equipment and extend its service life, it is necessary to establish joint interface contact models to accurately predict their contact characteristics. This paper mainly focuses on the current research status of statistical contact models and summarizes and elaborates from two aspects: asperity contact models and rough surface contact models respectively. It summarizes the current research status of asperity contact models under the two modeling methods of flat plate-asperity and asperity-asperity, as well as the current research status of rough surface contact models under different height distribution assumptions. It also summarizes the previous work and points out some research trends. Based on the previous research, it is found that there are still some problems that need to be solved urgently in the research field of joint interface contact models.

Problems Urgently to Be Solved:

1. Utilize more precise surface detection methods and signal processing methods to detect real surfaces, so as to explore the assumption methods for the shape of asperities and the height distribution of asperities that are universally applicable to different materials under different processing techniques.

2. The mainstream method for characterizing the anisotropy of the contact interface is to characterize it by assuming the distribution of contact angles and the distribution of contact azimuth angles, which lacks a practical basis. It is necessary to explore characterization methods with a practical basis to make the research results more convincing and realistic.

3. Establish contact models that take into account the normal load and tangential load with inclined angles and coupled dynamic changes, so as to establish contact models that are more in line with the actual working conditions of the equipment and conduct theoretical analysis on the contact mechanism of the joint interface more clearly.