1. Introduction
Sewing machine case is the assembly benchmark component of sewing equipment, and its processing and assembly accuracy directly determines the quality level and service life of sewing equipment. Sewing equipment manufacturing enterprises are mainly small and medium-sized enterprises, which leads to the problems of scattered manufacturing resources and insufficient industrial collaboration in the processing of core components such as sewing machine cases, which seriously hinders the high-quality development of sewing equipment manufacturing enterprises in the agglomeration area and restricts the production efficiency of sewing equipment. Network collaborative manufacturing, as a new intelligent manufacturing mode [
1], can make full use of the idle manufacturing resources in the industrial agglomeration area [
2], realize the optimal allocation of industrial resources in the manufacturing of machine cases [
3], and shorten the manufacturing cycle of machine cases. And how to efficiently realize the optimization of the composition of sewing machine case manufacturing resources is the key to realize the optimal allocation technology of sewing machine cases [
4].
Manufacturing service composition optimization is one of the key issues in realizing optimal allocation technology [
5]. And the research of manufacturing resource composition optimization method in collaborative manufacturing environment is of great importance to the implementation and development of collaborative manufacturing. Liu et al. [
6] proposed a method for optimal selection of guide roller cloud manufacturing resources based on a composite algorithm of extensible clustering and fuzzy analytic hierarchy process (FAHP), which utilizes an improved extended clustering algorithm in combination with FAHP to achieve the selection of optimal collaborative manufacturing resources for the production equipment of the optimal guide rollers; Li et al. [
7] proposed a combination of service preferences based on an extended Gale-Shapley algorithm Li [
8] and others constructed a multi-objective preference model with service matching degree and execution time as the preference objectives, and solved the model using an improved particle swarm optimization algorithm to realize the combination recommendation of manufacturing services; Fazeli [
9] and others combined the characteristics of multiple heuristic algorithms and proposed a flexible and extensible resource combination optimization method to achieve the optimal resource selection of guide roll production equipment. expandable resource combination optimization method, which realizes the recommendation of the optimal resource combination scheme. In service composite optimization problem solving, meta-heuristic algorithms have become mainstream in recent years, and the common ones are Multi-objective Genetic Algorithm [
10] (NSGA-II), Improved Strength Pareto Evolutionary Algorithm [
11] (SPEA2), Zebra Optimization Algorithm [
12], Particle Swarm Optimization (PSO) [
13], and Harris Hawk Optimization algorithm [
14], etc. Liang et al. [
15] proposed a Qos-Aware collaborative manufacturing service composition selection method based on deep reinforcement learning algorithms, and achieved optimal recommendation of manufacturing service compositions through model training; Huang et al. [
16] proposed a two-dimensional preference mechanism and method of manufacturing services, which solves the problems of personalization, cost, and response time in the process of providing on-demand services. The coupling and contradiction problems in terms of personalization, cost and response time in the process of on-demand service provision are solved, and the efficiency of collaborative manufacturing is improved.
In summary, there are some key problems in sewing machine case manufacturing service composition optimization:
the feature information of the case equipment manufacturing resources is complex, and the model applicable to sewing machine case manufacturing service composition optimization has not yet been established;
the existing solution algorithms are less efficient and prone to fall into local optimum when solving large-scale service composition optimization problems.
Aiming at the above problems, this paper proposes a service composition optimization method for sewing machine case manufacturing in collaborative manufacturing environment. Firstly, we analyze the structure and process flow of sewing machine case, realize the task decomposition at process level, and put forward the evaluation index system of collaborative manufacturing service composition optimization for sewing machine case; secondly, we construct the mathematical model of sewing machine case manufacturing composition optimization based on the interests of the demand side of sewing machine case manufacturing service and the service side of sewing machine case manufacturing resources as the upper and lower layers of the bi-level programming model; lastly, we construct the mathematical model of sewing machine case manufacturing composition optimization based on NSGA-II algorithm to solve the large-scale service composition optimization problem. Finally, based on NSGA-II algorithm, the solution of the bi-level programming model of case manufacturing service composition optimization is completed.
2. Materials and Methods
2.1. Materials
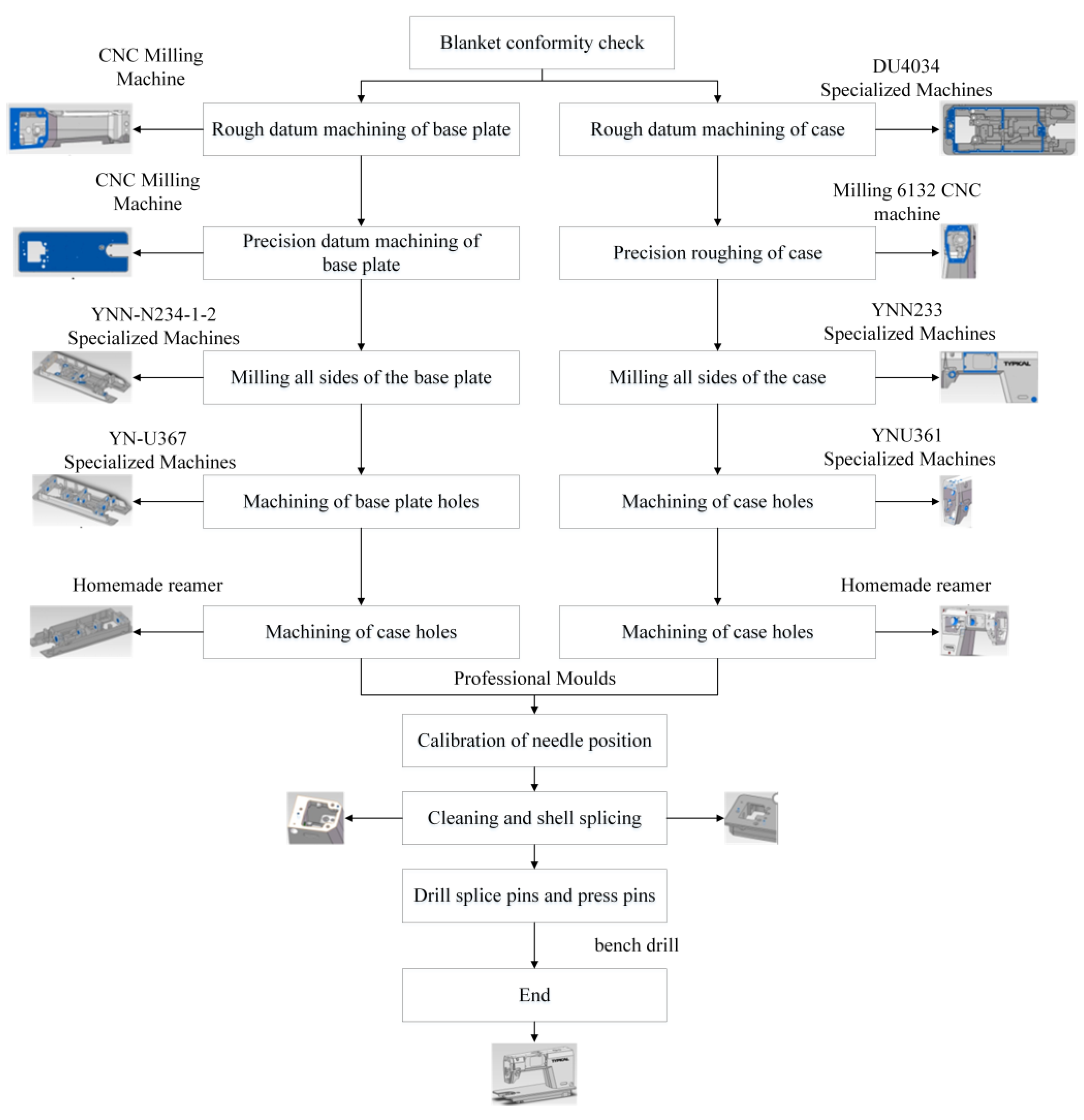
This paper centers on the most common sewing machine case. Combined with industrial site research and literature combing, the fine machining process and assembly process of sewing machine cases are summarized with a focus on fine machining of the cases, as shown in
Figure 1. The main processes of case processing and manufacturing include rough milling of the head, fine milling of the head, drilling of the head, rough milling of the base, fine milling of the base, drilling of the base and assembling and molding, etc., which involves more than 20 machine tools for rough milling, fine milling, drilling and assembling and more than 30 processes.
2.2. Service Composition Optimization Problem Analysis
Manufacturing service composition selection is one of the key issues in realizing the optimal allocation technology. Collaborative manufacturing service composition is to select suitable manufacturing services from the cloud pool of manufacturing services with different processing capabilities, compose them into manufacturing service compositions to perform manufacturing tasks, and construct large-grained part-level manufacturing resource services by combining multiple process-level manufacturing resource services to satisfy the complex needs of the demand side of the manufacturing resources and realize the optimal allocation of resources for the sewing machine case manufacturing industry. Optimized allocation of resources in the manufacturing industry.
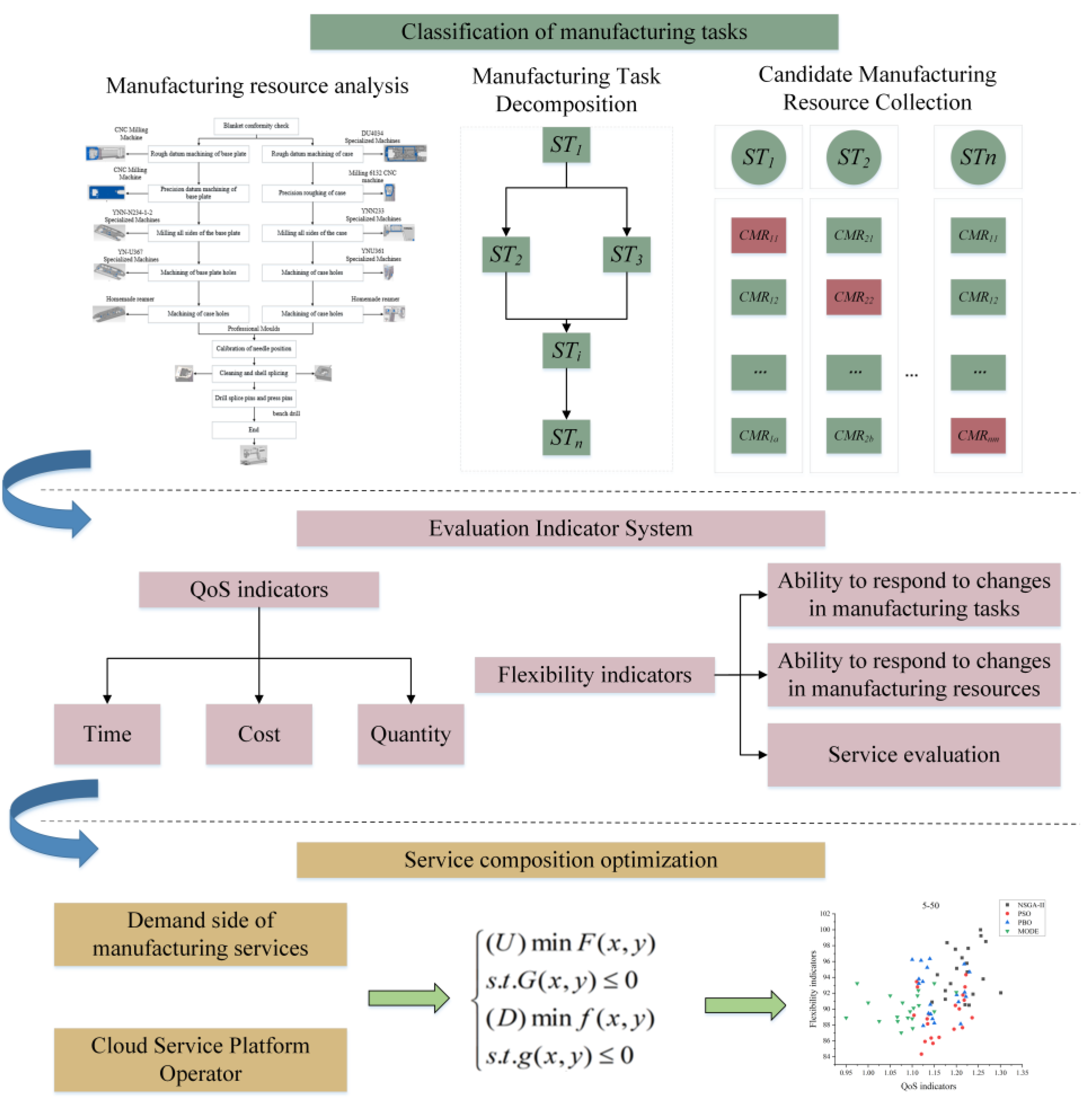
The task demand in collaborative manufacturing is continuous and personalized, when the manufacturing demand is submitted to the cloud platform, it will be transformed into a manufacturing task, the cloud platform will decompose the manufacturing task into multiple sub-tasks according to the process flow, and each sub-task corresponds to a set of candidate manufacturing services capable of completing the sub-task; and after that, a manufacturing resource is selected from each set of candidate manufacturing resources to form the combination of manufacturing services, and the optimal optimization goal that meets the goal is obtained according to the selected optimization goal. After that, a manufacturing resource is selected from each candidate manufacturing resource set to form a manufacturing service composition, and according to the selected optimization objective, the optimal manufacturing service composition that meets the objective is obtained. The manufacturing service composition optimization process is shown in
Figure 2.
Manufacturing resource analysis and task decomposition: when a demand-side user submits a manufacturing demand to the collaborative manufacturing platform, the demand is first transformed into a manufacturing task T. At the same time, on the basis of researching and analyzing the manufacturing resources required for the manufacturing task, the manufacturing task is decomposed into n sub-tasks (ST1, ST2, ..., STi, ..., STn). For each sub-task STi, there exist mi manufacturing resources that can satisfy the demand, therefore, the sub-task STi, its corresponding set of candidate manufacturing resources is CMRi={CMRi1, CMRi2,..., CMRim};
Constructing combination optimization evaluation indicator system: the construction of composition optimization evaluation indicator system is a key step to realize the construction of the composition optimization model. Considering the interests of the service demand side and the platform operator, we construct the composition optimization evaluation indicator system from the aspects of QoS indicators and flexibility indicators;
Modeling and solving of manufacturing service compositions optimization: the idea of bi-level programming is introduced into the field of manufacturing service compositions optimization, and the mathematical model of manufacturing service compositions optimization for sewing machine cases is constructed by taking the QoS indexes and the flexibility indexes as the optimization objectives of the upper and lower levels, respectively. The solution of manufacturing service combination optimization problem is an NP-Hard level problem, which needs to be solved by global optimal Pareto solution to meet the demand.
2.3. Sewing Machine Case Manufacturing Service Composition Optimization Method
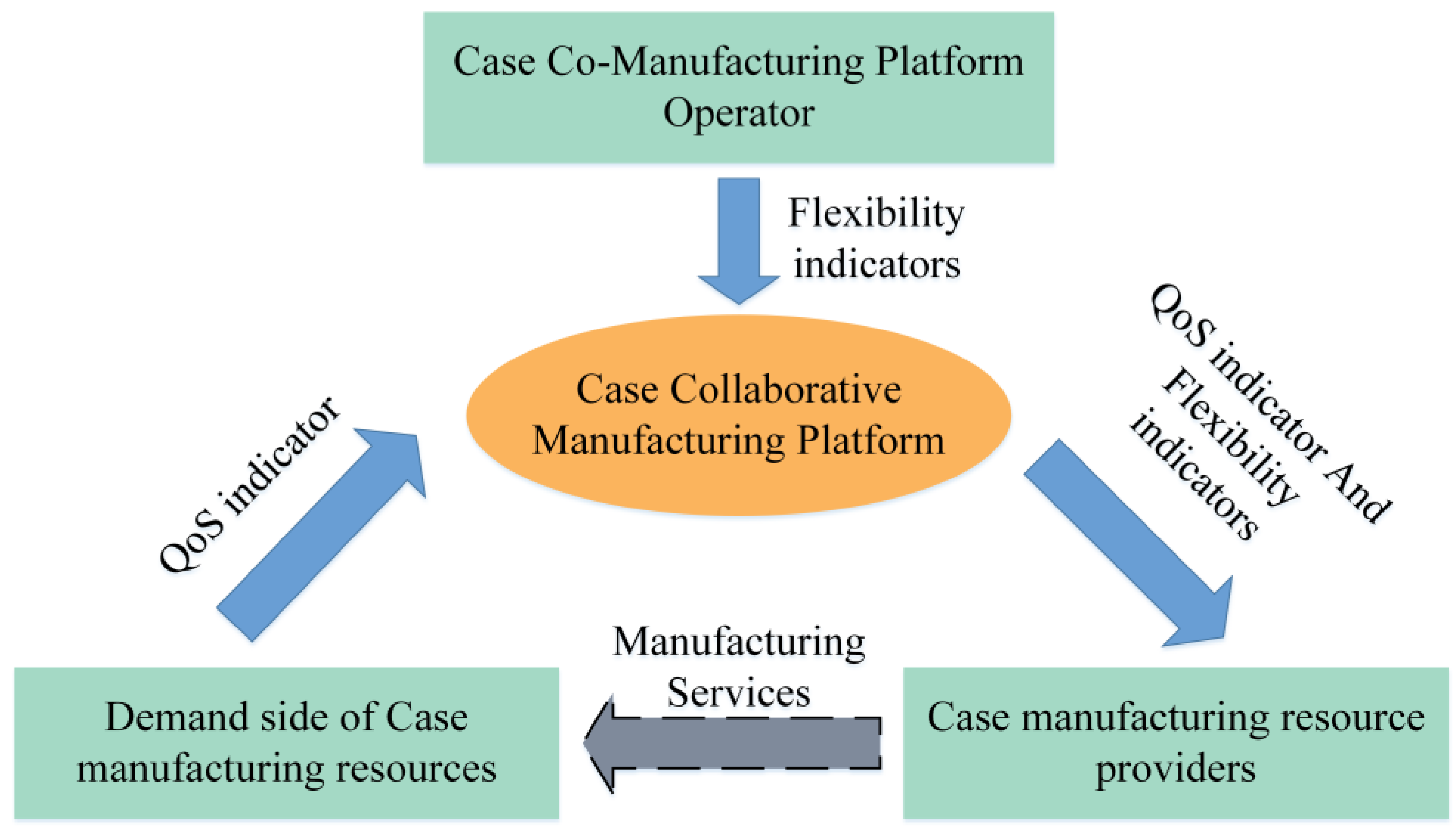
The realization of collaborative manufacturing of sewing machine case is composed of collaborative platform management, collaborative manufacturing service demand side and collaborative manufacturing service provider, and the three together decide the result of case manufacturing service composition optimization, and the establishment of manufacturing service composition optimization evaluation index system is the basis for the realization of the above composition optimization. Therefore, in the process of establishing the evaluation index system of manufacturing service composition optimization. Firstly, the service quality requirements of the demand side of collaborative manufacturing services should be considered; and secondly, the flexibility indexes of the management side of the collaborative platform for the combination preference of sewing machine case manufacturing services should also be considered. According to the above requirements, the evaluation indexes and decision-making process of sewing machine case manufacturing service composition optimization are obtained, as shown in
Figure 3.
2.4. Sewing Machine Case Manufacturing Service Composition Optimization Evaluation Index System
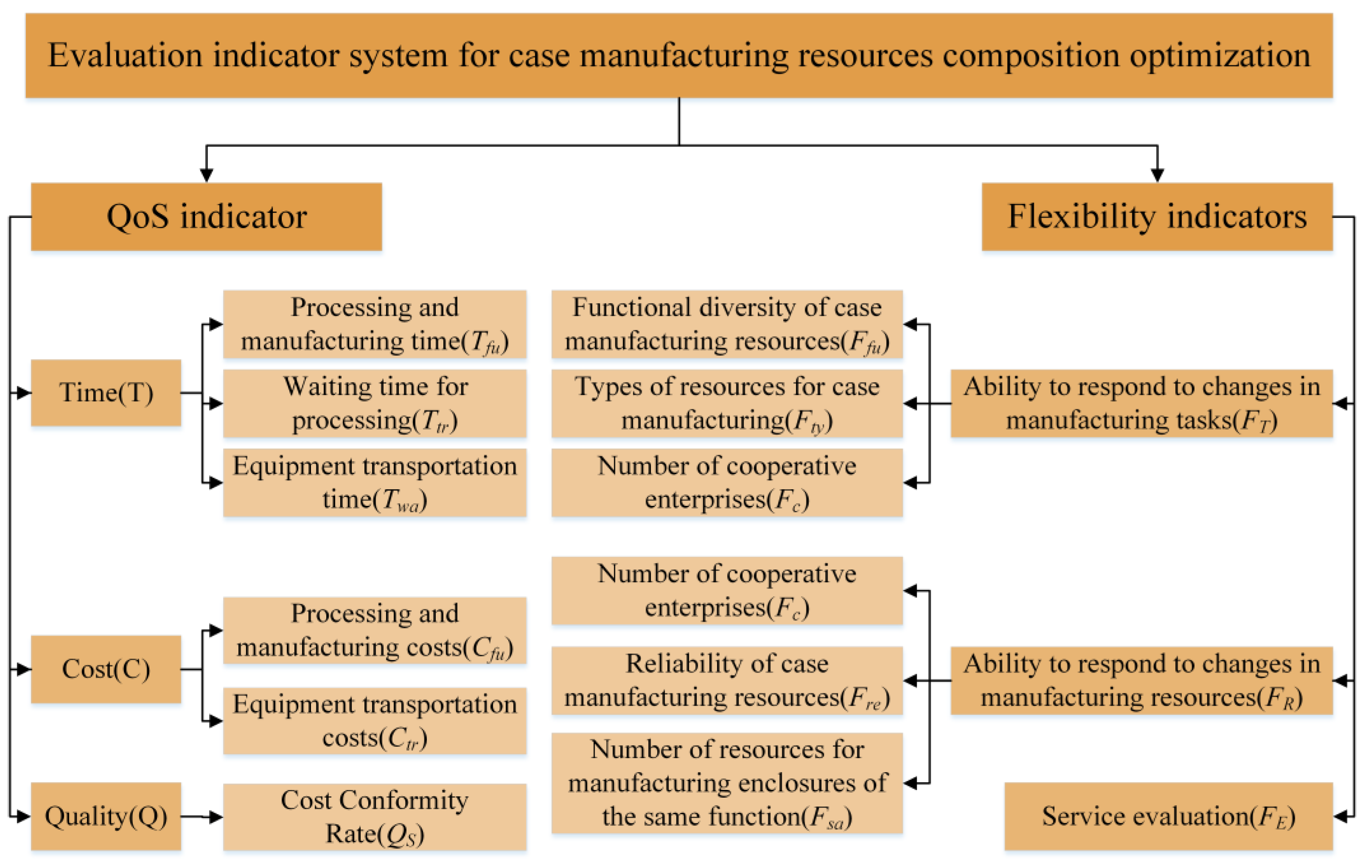
In the process of completing the collaborative manufacturing tasks of sewing machine cases, the demand side of the collaborative manufacturing services of sewing machine cases mainly focuses on the total time spent on the collaborative manufacturing tasks, the total cost, and the quality of the core indicators, i.e., to complete the collaborative tasks of the case of the preferred composition of the manufacturing resources of the quality of the service factors; the management side of the collaborative manufacturing platform of the case mainly focuses on the preferred composition of the collaborative manufacturing services of the case of the collaborative manufacturing tasks. Flexibility indicators, i.e., the response ability of the collaborative manufacturing service provider in the case of changes in manufacturing tasks and manufacturing resources, also includes indicators such as the evaluation of the case collaborative manufacturing services. According to the above requirements, this paper establishes the evaluation index system for the optimization of the service composition of sewing machine shell manufacturing resources under the cooperative manufacturing environment, as shown in
Figure 4.
The QoS metrics of the sewing machine case collaborative manufacturing service composition evaluation index system include time T, cost C, and quality Q, as follows:
Time indicator T: includes processing and manufacturing time Tfu, processing waiting time Ttr and equipment transportation time Twa;
Cost indicator C: includes processing and manufacturing costs Cfu and equipment transportation costs Ctr;
Quality indicator Q: The quality indicator for the portfolio of manufacturing services is expressed in terms of the average quality pass rate of the individual manufacturing services Qs, i.e., the quality pass rate of the manufacturing service provider in accomplishing the relevant tasks.
In addition to QoS metrics, manufacturing services are also affected by the status of the service provider during the completion process, therefore, this paper proposes sewing machine case collaborative manufacturing service composition optimization flexibility metrics, including the sewing machine case manufacturing service provider's ability to cope with changes in the manufacturing task FT, the ability to cope with changes in the manufacturing resources FR, and the service evaluation FE, which are detailed as follows:
Response capacity in case of changes in manufacturing tasks FT: including functional diversity of case manufacturing resources Ffu, types of case licensing resources Fty and number of cooperating companies Fc;
Response capacity in case of changes in manufacturing resources FR: including the number of cooperative enterprises Fc, the reliability of case manufacturing resources Fre, and the number of case manufacturing resources of the same function Fsa.
2.5. Mathematical Modeling of Sewing Machine Case Manufacturing Service Composition
The multi-objective composition optimization problem of sewing machine case manufacturing resources involves the interests of the management of the collaborative manufacturing platform and the demand side of the collaborative manufacturing services, and in the process of composition optimization, both sides will aim at improving their own interests, and there is also the problem of mutual influence between the variables of the two sides. Therefore, the multi-objective compositional optimization problem of chassis manufacturing resources needs a better method to be solved.
Bi-level programming [
17] is an important concept in the field of operations research, in the bi-level programming model, there usually exists an upper level and a lower level decision maker, the two sides of the decision-making have their own objective function and constraints, and there is a mutual influence relationship between them. The upper decision maker makes the optimal decision, the lower decision maker finds the optimal solution according to its own objective function and constraints on the basis of the optimal decision of the upper layer, and feeds back the decision result to the upper decision maker to find the global optimal solution of the problem.
According to the concept and definition of bi-level programming, the mathematical expression of the bi-level programming model for housing manufacturing resource composition optimization established in this paper is shown in Equation ((1):
Where U is the upper level of the programming model; L is the lower level of the programming model; F is the objective function of the upper level of the programming model; x is the decision variable of the upper level of the programming model; G is the constraints on the decision variable x; f is the objective function of the lower level of the programming model; y is the decision variable of the lower level of the programming model, y = y(x); and g is the constraints on the decision variable y.
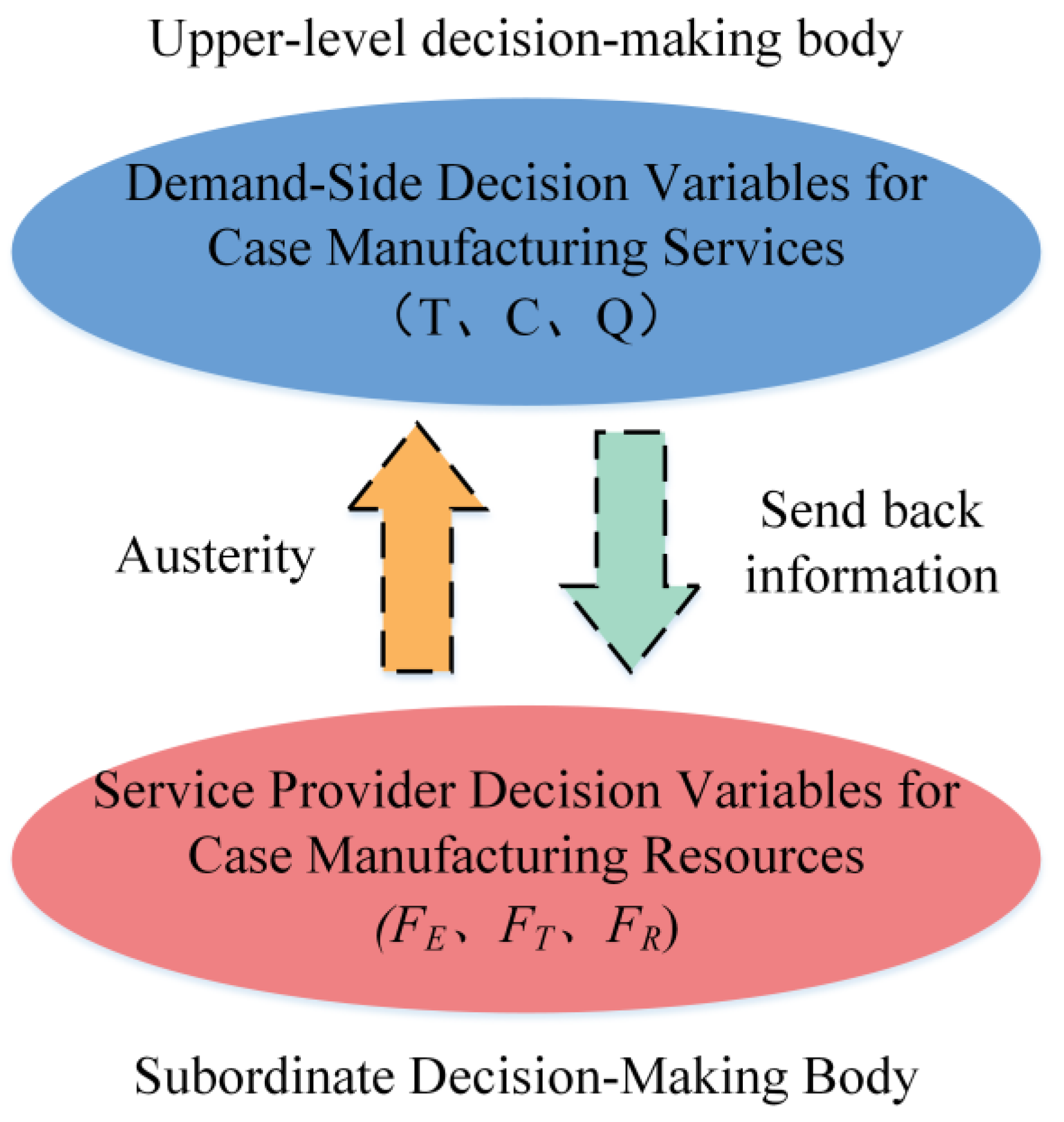
In the bi-level programming model for optimization of the composition of sewing machine case manufacturing resources, the upper and lower levels of the preference problem are independent of each other, but there is a certain connection in the process of compositions optimization, which not only pays attention to the demand side of the demand side of the service of the case manufacturing resources, but also pays attention to the risk that the management side of the collaborative manufacturing service platform is dealing with. Therefore, the idea of bi-level programming is applied to the case collaborative manufacturing to solve the composition optimization problem of the case manufacturing resources, and the realization principle is shown in
Figure 5.
- 2.
Lower tier programming model, the lower level flexibility metrics optimization objectives for the sewing machine case manufacturing service composition include optimal coping capacity when manufacturing tasks change, optimal coping capacity when manufacturing resources change, and the highest evaluation of capable services:
- 3.
Construction of bi-level programming model for enclosure manufacturing resource composition optimization under demand preference. To summarize, the bi-level planning model for case manufacturing resource composition optimization under collaborative manufacturing environment:
Where Wt, Wc and Wq denote the weighting coefficients of time, cost and quality, respectively. Tmax, Cmax and Qmax represent the constraints of the demand side of manufacturing resources on time, cost and service quality, respectively, and Qmax=1-Qmin. Ffumin, Ftymin, Fremin and Fsamin denote the constraints of the operator of the platform on the service indicators, respectively. Fcomin denotes the minimum number of cooperative enterprises, and FEmin denotes the minimum service evaluation value required by the platform manager.
2.6. Solving a Bi-level Programming Composition Optimization Model for Sewing Machine Case Manufacturing Resources
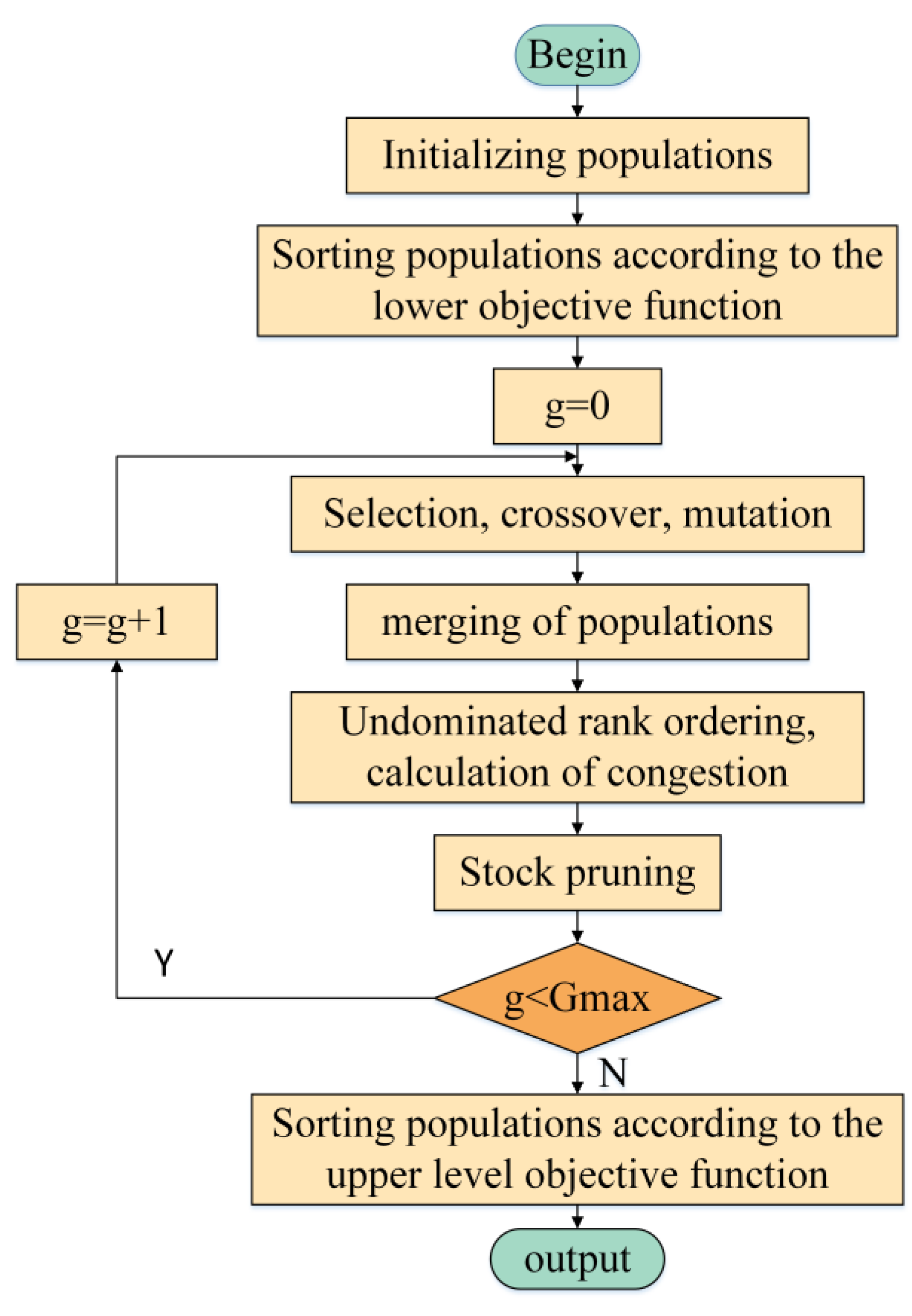
Under the collaborative manufacturing environment, the solution of the case manufacturing resources composition optimization problem, as the key to realize collaborative manufacturing, determines the fundamental interests of multiple parties, such as the demand side of manufacturing resources, the service side of manufacturing resources and the management side of the collaborative manufacturing platform. Evolutionary multi-objective optimization, as an effective search method, can realize the composition optimization of case manufacturing resources by algorithmically solving the Pareto optimal solution set of the mathematical model, and has been widely used in the field of multi-objective optimization. With the evolution of evolutionary multi-objective optimization algorithms, the fast non-dominated sorting genetic algorithm with elite strategy (NSGA-II) is proposed as one of the most excellent evolutionary multi-objective optimization algorithms so far, and this paper will also be based on the NSGA-II algorithm, and the process of solving the bi-level programming model using the NSGA-II algorithm is shown in
Figure 6.
Genetic coding of resource compositions for case manufacturing, under the constraints of the upper and lower objective functions of the bi-level programming model for case manufacturing resource composition optimization, the search space of the NSGA-II algorithm is determined and the case manufacturing resource compositions are coded to form the corresponding individual genes. The result of decimal coding with a random composition of manufacturing resources (CMR1,5、CMR2,3、CMR3,1、CMR4,4、CMR5,2) is 5-3-1-4-2;
Initializing the population of manufacturing resource composition of sewing machine case, randomly generate the initial population Pg of the manufacturing resource composition with the number of individuals N. Sort each individual in the population according to the non-dominated rank, complete the division of individuals into different ranks, and calculate the dominated set of individuals, the number of dominated individuals sorted and the degree of crowding;
The cross mutation generates a new population of sewing machine case manufacturing resource composition, and the binary tournament is utilized to select the excellent individuals of the case manufacturing resource composition from the population Pg, and the cross mutation operation is carried out to generate the progeny population Qg with the number of N;
Merge the sire and daughter sewing machine case manufacturing resource composition populations, and merge the case manufacturing resource composition populations Pg and Qg to form a new population Rg with a number of 2N;
Non-dominated rank ordering, calculation of crowding, and fast non-dominated ordering of the sewing machine case manufacturing resource composition population Rg and calculation of inter-individual crowding;
Sewing machine case manufacturing resource composition population pruning, using the elite retention strategy as a criterion, optimization of the highest rated N sewing machine case manufacturing resource compositions, and fusion of these N case manufacturing resource compositions to generate a new population Pg+1;
Repeatedly iterating the composition of sewing machine case manufacturing resources, repeating the steps of non-dominated sorting, congestion calculation, selection, crossover and mutation, and setting the stopping conditions, such as reaching the maximum number of iterations or convergence, the Pareto-optimal set of solutions for the upper level objective function is obtained;
Calculate the optimal solution of the lower objective, take the optimal solution of the upper objective function as the feasible solution set of the lower objective function, use the results of the calculation of the objective function value to complete the sewing machine case manufacturing resource composition advantages and disadvantages of sorting, sorting of the first composition of the manufacturing resources that is the optimal solution of the bi-level programming model.
3. Results
In order to verify the superiority and feasibility of NSGA-II algorithm to solve the bi-level programming model, the algorithm performance comparison, arithmetic analysis and specific examples are designed respectively. The experimental validation is completed using MatLab software, the operating system is windows 10 and the running space is 16GB.
3.1. Algorithm Performance Comparison
The Hypervolume Metric (
HV) [
18], measures the volume of the target space constituted between the set of nondominated solutions and a reference point, with the expression shown in Equation (5).where is the Lebesgue measure used to measure the volume;
S denotes the set of non-dominated solutions;
|S| denotes the number of non-dominated solutions;
vi denotes the hypervolume formed by the reference point and the
i solution in the solution set;
- 2.
Generation Distance (GD) is a kind of index for evaluating the convergence of multi-objective optimization algorithm, the smaller the value of GD indicates that the solution is closer to the real Pareto solution set, and the better the convergence performance, the specific expression is shown in Equation (6).where P is the set of non-dominated solutions on the frontier derived by the algorithm, P* denotes the solutions distributed on the optimal Pareto frontier, d(a,b) denotes the minimum Euclidean distance between the two decision-making subjects of the game, and P is the total number of solutions on the Pareto frontier obtained;
In this paper, using the self-constructed dataset of the group, we simulate the manufacturing resource combination selection process for sewing machine case manufacturing requirements, and analyze the effectiveness of NSGA-II algorithm on sewing machine case manufacturing resource combination optimization by comparing the evaluation indexes of the selected algorithms. PSO [
19], PBO [
20], MODE [
21] are introduced to compare the algorithms with NSGA-II, and the initial conditions of various algorithms are set in the same experimental environment as shown in
Table 1.
The demand side of the sewing machine case manufacturing service publishes its own part demand in the case collaborative manufacturing platform, and the collaborative manufacturing platform completes the above process-level task splitting of the case part manufacturing, and at the same time, it uses this as an arithmetic example of the bi-level programming model to decompose the case manufacturing resources and service demand matching task. The five process-level manufacturing tasks of the case header can be decomposed into five processes: header finishing milling, header drilling, base rough milling, base finishing milling and base drilling, and assuming that each process corresponds to 50 candidate services, the instances of the manufacturing tasks of the case header of the sewing machine can be expressed as (5-50), so in order to further validate the applicability of the NSGA-II to the problems of different scales of the manufacturing of the case of the sewing machine, this case study is extended to include nine sewing machine case manufacturing problems of different scales, denoted as {(5-50), (5-100), (5-150), (10-50), (10-100), (10-150), (15-50), (15-100), (15-150)}, each algorithm was run independently for 30 times and calculated according to Equation (5, 6, and 7), and the specific data obtained are shown in Tables (2 and 3).Results of GD and HV metrics for all algorithms. The optimal results of the different algorithms are marked in bold, and (Mean/Std) indicates the mean and standard deviation.Combining the data in Tables (2 and 3), the statistical results are as follows. In terms of GD metrics, the NSGA-II algorithm performs best in all scales except (5-100) and (5-150), while PBO obtains the best GD value only in the scale of (5-100). The best GD value is obtained by PBO only on the (5-100) scale, and MODE achieves the best result only on the 10-150 scale, while the other algorithms do not achieve the best average value. In terms of HV metrics, NSGA-II achieved the best values on all nine scales for the sewing machine case manufacturing problem.
Table 2.
GD indicator results.
Table 2.
GD indicator results.
| GD |
|
5-50 |
5-100 |
5-150 |
10-50 |
10-100 |
10-150 |
15-50 |
15-100 |
15-150 |
| PSO |
Mean |
4.48E-02 |
4.25E-02 |
2.04E-01 |
6.65E-02 |
4.25E-01 |
8.65E-02 |
1.99E-01 |
8.26E-01 |
4.52E-02 |
| Std |
3.36E-02 |
1.31E-02 |
2.69E-02 |
8.52E-02 |
8.49E-02 |
1.52E-02 |
5.23E-02 |
9.34E-02 |
6.77E-03 |
| PBO |
Mean |
5.36E-02 |
3.25E-01 |
5.23E-01 |
5.86E-01 |
2.26E-01 |
3.59E-01 |
2.26E-01 |
2.72E-01 |
1.59E-01 |
| Std |
4.35E-03 |
2.48E-02 |
5.26E-02 |
3.40E-01 |
5.81E-03 |
1.29E-02 |
2.23E-02 |
5.91E-02 |
9.32E-03 |
| MODE |
Mean |
7.98E-02 |
5.98E-01 |
3.43E-01 |
3.99E-01 |
3.65E-01 |
1.17E-02 |
4.64E-01 |
5.67E-01 |
1.49E-01 |
| Std |
2.26E-02 |
2.94E-03 |
2.24E-02 |
4.57E-01 |
1.18E-01 |
2.75E-03 |
8.69E-02 |
1.24E-01 |
8.98E-03 |
| NSGA-II |
Mean |
2.37E-02 |
5.69E-01 |
2.46E-01 |
2.33E-01 |
1.48E-01 |
2.56E-02 |
1.79E-02 |
2.32E-01 |
1.14E-01 |
| Std |
5.69E-02 |
3.89E-02 |
9.23E-02 |
6.66E-02 |
2.80E-02 |
1.93E-01 |
1.45E-03 |
1.80E-01 |
1.27E-02 |
Table 3.
HV indicator results.
Table 3.
HV indicator results.
| HV |
|
5-50 |
5-100 |
5-150 |
10-50 |
10-100 |
10-150 |
15-50 |
15-100 |
15-150 |
| PSO |
Mean |
2.78E-02 |
3.68E-02 |
1.99E-01 |
5.88E-02 |
9.53E-02 |
1.19E-02 |
1.35E-01 |
5.11E-01 |
9.56E-02 |
| Std |
4.22E-03 |
3.68E-02 |
9.48E-02 |
6.68E-02 |
2.48E-02 |
1.68E-03 |
1.68E-02 |
1.99E-01 |
1.58E-02 |
| PBO |
Mean |
5.56E-02 |
3.11E-02 |
1.17E-01 |
3.54E-03 |
3.21E-01 |
4.22E-02 |
1.47E-02 |
6.72E-02 |
6.34E-01 |
| Std |
6.55E-03 |
2.44E-02 |
5.68E-02 |
3.68E-01 |
5.81E-03 |
1.58E-02 |
2.22E-03 |
5.91E-02 |
9.32E-03 |
| MODE |
Mean |
7.22E-02 |
3.68E-02 |
1.14E-01 |
6.67E-03 |
6.35E-02 |
4.37E-02 |
1.58E-01 |
9.64E-02 |
5.29E-02 |
| Std |
2.38E-02 |
2.59E-02 |
2.98E-02 |
5.89E-03 |
1.68E-01 |
1.76E-03 |
8.68E-02 |
2.28E-01 |
5.34E-03 |
| NSGA-II |
Mean |
6.58E-01 |
4.25E-02 |
2.04E-01 |
6.65E-02 |
4.25E-01 |
4.69E-02 |
1.99E-01 |
5.26E-01 |
6.46E-01 |
| Std |
3.98E-02 |
6.31E-02 |
2.69E-02 |
7.36E-02 |
8.48E-02 |
1.36E-02 |
5.69E-02 |
9.35E-02 |
9.48E-03 |
3.2. Arithmetic Analysis
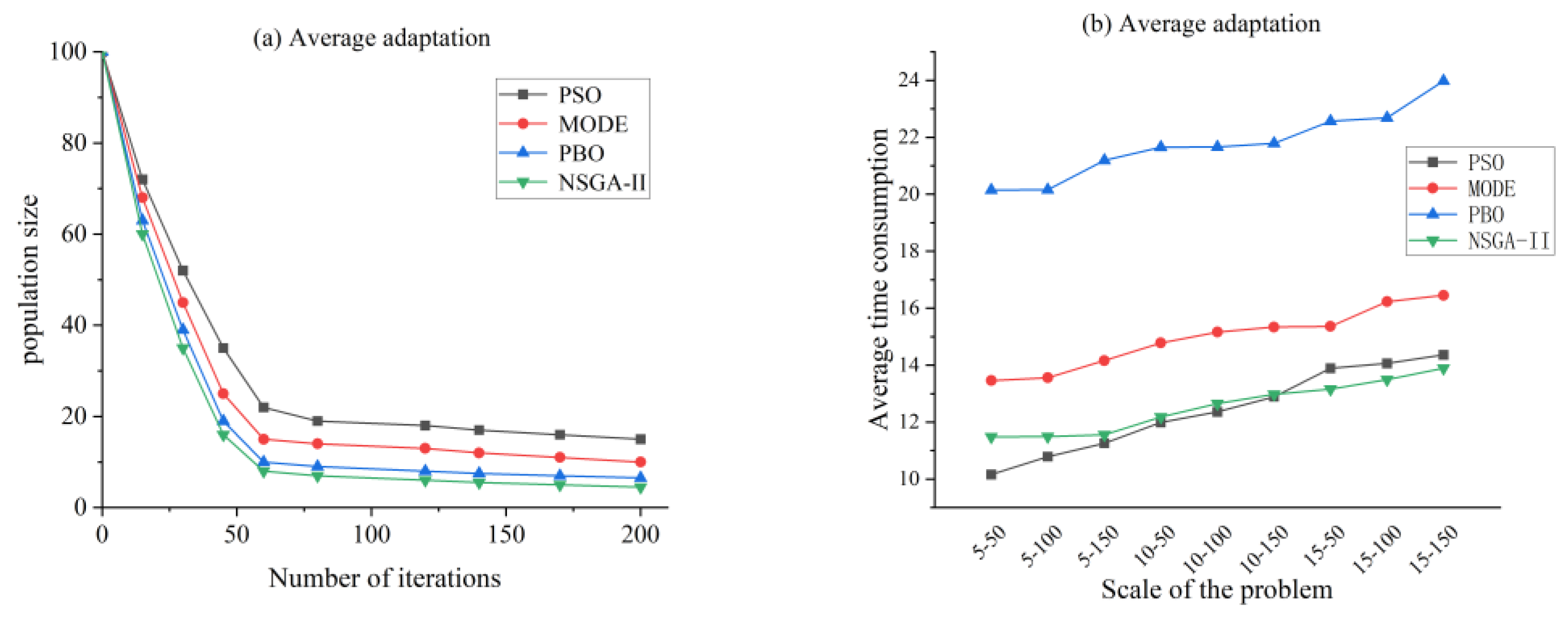
A quantitative analysis of the four algorithms of different sizes was carried out by comparing their average fitness statistics and computational time consumption statistics on 20 sewing machine case heads manufacturing composition optimization problems, as shown in
Figure 7.
Figure 7a shows the best average fitness of the four algorithms under the conditions of population size of 100 and iteration number of 200, and it can be seen that the fitness all tends to level off when the number of iterations is 65, and it can be seen by observing the green curve that the NSGA-II algorithm has the lowest value of best fitness and the fastest speed of convergence in dealing with the sewing machine case head manufacturing composition optimization problem, which can show that the NSGA-II algorithm performance is better than the performance of the remaining three algorithms. From
Figure 7b, the convergence time of NSGA-II algorithm is slightly less than PSO algorithm for small scale sewing machine case head manufacturing composition optimization problem, but less than PBO algorithm for larger scale sewing machine case head manufacturing composition optimization problem, whereas MODE algorithm consumes more time than both algorithms, PBO algorithm consumes the longest time and is almost as fast as the other three algorithms. The PBO algorithm consumes the longest time, which is almost three times the time consumed by the NSGA-II algorithm.
3.3. Specific Examples
In order to more intuitively compare the performance of each algorithm in terms of solving the optimal QoS scheme, a self-built database is used to obtain the data distribution graph shown in
Figure 8.
Figure 8 shows the distribution of the optimal QoS solutions obtained by the four algorithms on the 20 sewing machine case header manufacturing composition optimization problems..Most of the red data points obtained by the NSGA-II algorithm are located in the uppermost region, which indicates that the NSGA-II algorithm can achieve better quality metrics in dealing with the problem of composition optimization of sewing machine case heads manufacturing, and for the time metrics and the cost metrics, the NSGA-II algorithm can always be located in the region of relatively small values as well. It is noteworthy that as the problem size increases, the NSGA-II algorithm consistently generates solutions that are distributed in the uppermost region. This phenomenon also demonstrates the applicability of the NSGA-II algorithm when dealing with large-scale sewing machine case heads manufacturing composition optimization problems.
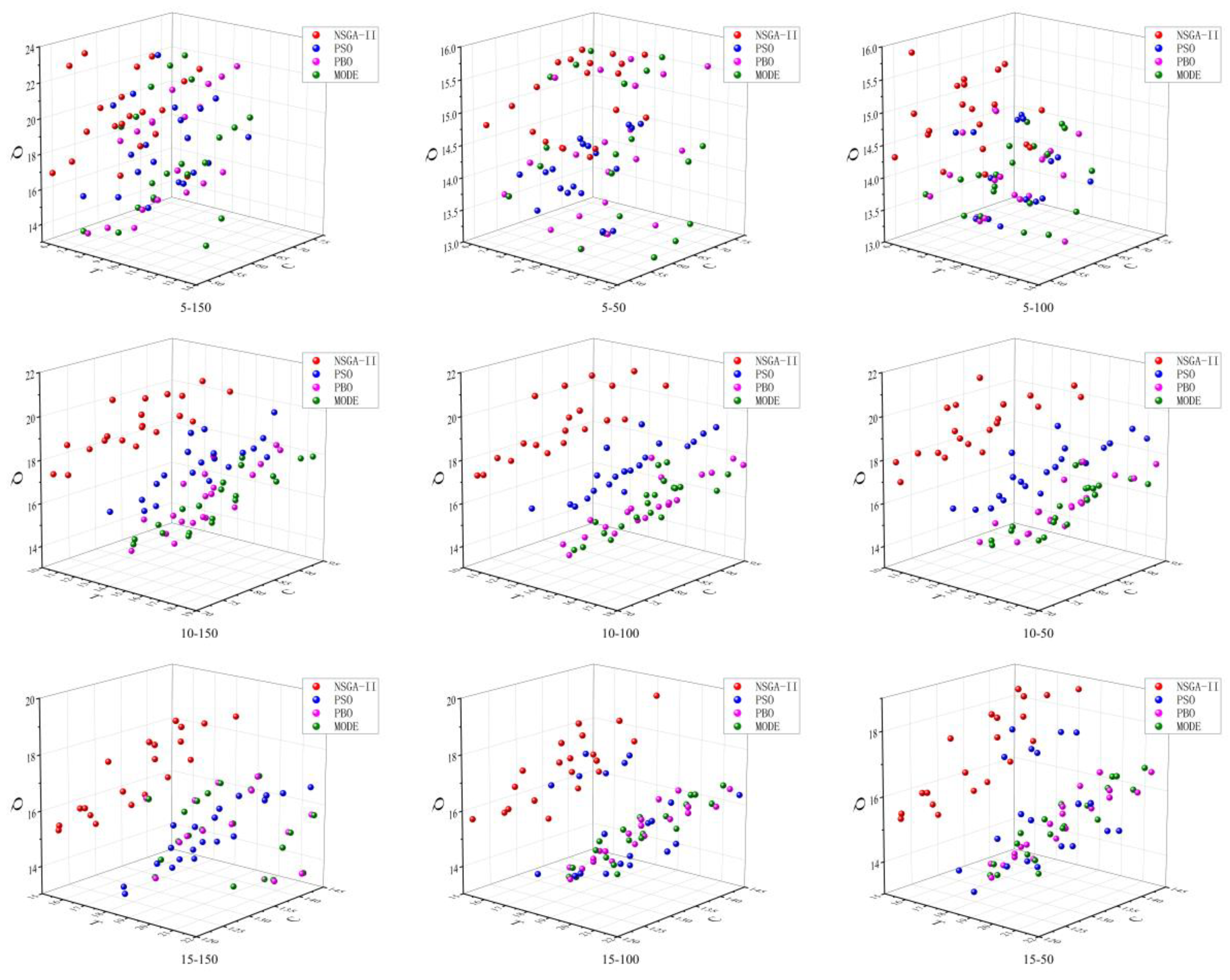
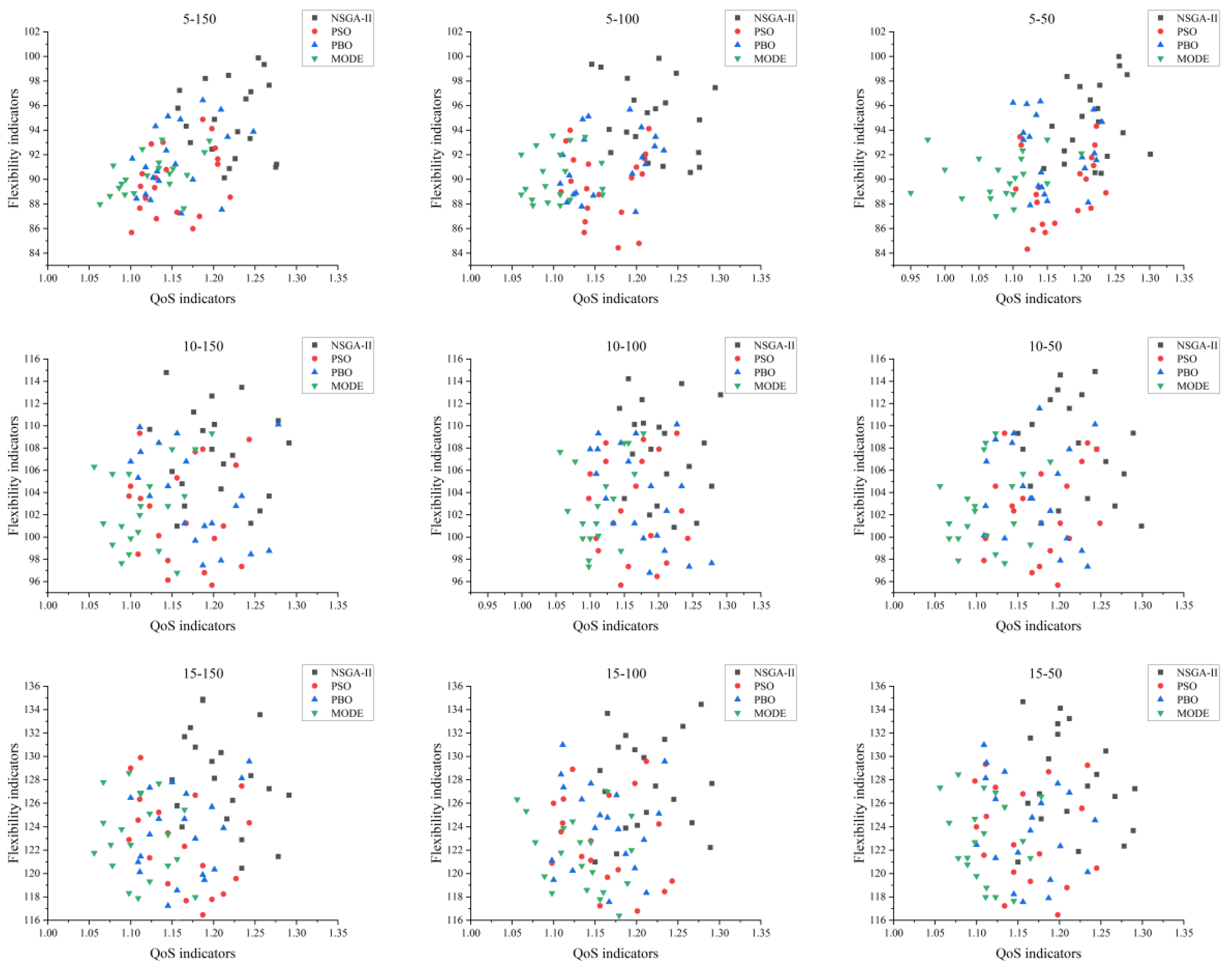
By introducing the QoS normalization formula in Equation (7) and the flexibility indicators in the evaluation index system, the distribution of the solutions of the four algorithms at different scales on the 20 sewing machine case head manufacturing composition optimization problems can be obtained as shown in
Figure 9.
Figure 9 shows the solutions of the four algorithms in different scales on the 20 sewing machine case head manufacturing composition optimization problems, it can be clearly seen that in the results of different scales of composition optimization, the solutions solved by NSGA-II algorithm are always located in the upper right side of the statistical chart, which indicates that the NSGA-II algorithm has some advantages in solving the bi-level programming model, and it can always give the optimal solution. . However, the MODE algorithm gives worse results than the other algorithms in solving bi-level programming models, and the PSO algorithm and PSO algorithm give comparable results between the NSGA-II algorithm and the MODE algorithm in solving bi-level programming problems of different sizes.
The effectiveness and efficiency of NSGA-II algorithm for solving the sewing machine case cooperative manufacturing service composition optimization problem is verified through the three parts of algorithm performance comparison, case analysis and specific examples. It can effectively solve the problem of low efficiency and easy to fall into local optimum in large-scale service composition optimization problems.
4. Discussion
In the results section, the set of manufacturing resources corresponding to each process is obtained by splitting the process-level tasks of sewing machine case part manufacturing. Meanwhile, the effectiveness and efficiency of NSGA-II algorithm for solving the sewing machine case collaborative manufacturing service composition optimization problem is verified through the three parts of algorithm performance comparison, case analysis and specific examples. It can effectively solve the problem of low efficiency and easy to fall into local optimum when large-scale service composition optimization problem. However, for other manufacturing parts, performing process-level task splitting may result in more process numbers than the 15 process numbers experimented in this paper, as well as matching more manufacturing resource sets, which points out the direction for subsequent research.
The composition optimization problem of sewing machine case manufacturing resources in network collaborative manufacturing environment has many evaluation indexes, complex composition model and difficult to solve model, which belongs to the typical multi-objective optimization problem, therefore, this paper introduces the bi-level programming decision-making to solve the multi-objective optimization problem, which needs to consider the interests of the management of collaborative manufacturing platform and the demand side of the collaborative manufacturing services in the process of the composition optimization at the same time.
For the part of establishing the evaluation index system for optimization of sewing machine case manufacturing service composition, the demand side of sewing machine case collaborative manufacturing service mainly focuses on the core indexes such as the total time spent on collaborative manufacturing tasks, the total cost, and the quality; while the management side of sewing machine case collaborative manufacturing platform mainly focuses on the flexibility indexes of the sewing machine case collaborative manufacturing service composition optimization in the process of the collaborative manufacturing tasks. The QoS and flexibility indicators are used to establish the optimization evaluation index system of sewing machine shell manufacturing service composition, and the NSGA-II algorithm is used to solve the bi-level programming model of sewing machine case manufacturing resource composition optimization by using the variables of all kinds of evaluation indicators as the constraints. In addition, for the solution of the algorithm, it is recommended to take more initial populations of the algorithm to get more optimal composition programs if the conditions allow.
5. Conclusions
This paper focuses on the optimization of manufacturing service composition under the collaborative manufacturing environment of sewing machine case, analyzes the structure and manufacturing process of sewing machine case, and realizes the process-level task decomposition of sewing machine case manufacturing tasks; under the premise of comprehensively considering the interests of the service demand side, the resource provider, and the platform operator, it puts forward the evaluation index system of manufacturing service composition that combines the QoS indicators and the flexibility indicators, and introduces the idea of bi-level programming to establish a mathematical model of sewing machine case manufacturing service composition optimization; based on the NSGA-II algorithm, it realizes the solution of the composition optimization decision model, and realizes the composition optimization of the case manufacturing services by using NSGA-II algorithm, and establishes the combination optimization model by using the case manufacturing services. The idea of bi-level programming is introduced to establish a mathematical model for the optimization of the composition of sewing machine case manufacturing services; based on the NSGA-II algorithm, the solution of the decision model for the composition optimization is realized, the composition optimization of sewing machine case manufacturing services is realized, and the effectiveness of the method is verified by using sewing machine case manufacturing resource data.
Author Contributions
Conceptualization, G.S. and S.L.; methodology, G.S. and K.S.; software, G.S. and K.S.; validation, Z.G. and L.Z.; formal analysis, G.S.; investigation, G.S.; resources, G.S. and J.Z.; data curation, J.Z.; writing—original draft preparation, G.S.; writing—review and editing, G.S. and S.L.; visualization, G.S.; supervision, K.S.; project administration, G.S. and Z.G.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mou, J. Multi-Objective Optimization for Resource Allocation in Intelligent Manufacturing. International Journal of Simulation Modeling, 2024, 23, 359–370. [Google Scholar] [CrossRef]
- Wei, X. Optimized Configuration of Manufacturing Resources for Middle and Lower Batch Customization Enterprises in Cloud Manufacturing Environment. Complexity. 2020, 2020, 5619758. [Google Scholar] [CrossRef]
- Xian, C.; Ming, Y.; Zhou, Z. Research on optimal selection of services and optimal allocation of resources in cloud manufacturing environment. Journal of Physics: Conference Series. 2019, 1314, 012167. [Google Scholar] [CrossRef]
- Song, C.; Zheng, H.; Han, G. Cloud edge collaborative service composition optimization for intelligent manufacturing. IEEE Transactions on Industrial Informatics. 2022, 19, 6849–6858. [Google Scholar] [CrossRef]
- Jing, W.; Zhao, C.; Miao, Q. QoS-DPSO: QoS-aware task scheduling for cloud computing system. Journal of Network and Systems Management. 2021, 29, 1–29. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Z.; Jiang, X. An Optimal Selection Method of Cloud Manufacturing Resource for Guide Roller based on Combination Algorithm. Journal of Imaging Science & Technology 2024, 68. [Google Scholar] [CrossRef]
- Li, F.; Zhang, L.; Liu, Y. QoS-aware service composition in cloud manufacturing: A Gale–Shapley algorithm-based approach. IEEE Transactions on Systems, Man, and Cybernetics: Systems. 2018, 50, 2386–2397. [Google Scholar] [CrossRef]
- Li, Y.; Yao, X.; Liu, M. Multiobjective optimization of cloud manufacturing service composition with improved particle swarm optimization algorithm. Mathematical Problems in Engineering. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Fazeli, M.; Farjami, Y.; Nickray, M. An ensemble optimisation approach to service composition in cloud manufacturing. International Journal of Computer Integrated Manufacturing. 2019, 32, 83–91. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE access. 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Gu, Q.; Chen, S.; Jiang, S. Improved strength Pareto evolutionary algorithm based on reference direction and coordinated selection strategy. International Journal of Intelligent Systems. 2021, 36, 4693–4722. [Google Scholar] [CrossRef]
- Trojovská, E.; Dehghani, M.; Trojovský, P. Zebra optimization algorithm: A new bio-inspired optimization algorithm for solving optimization algorithm. Ieee Access. 2022, 10, 49445–49473. [Google Scholar] [CrossRef]
- Geng, Z.; Kong, W.; Wang, X. Adaptive search based Grey Wolf optimization algorithm for multi-objective optimization of ethylene cracking furnace. Swarm and Evolutionary Computation. 2025, 92, 101810–101810. [Google Scholar] [CrossRef]
- Zhou, G.; Du, J.; Guo, J. A novel hippo swarm optimization: for solving high-dimensional problems and engineering design problems. Journal of Computational Design and Engineering. 2024, 11, 12–42. [Google Scholar] [CrossRef]
- Liang, H.; Wen, X.; Liu, Y. Logistics-involved QoS-aware service composition in cloud manufacturing with deep reinforcement learning. Robotics and Computer-Integrated Manufacturing. 2021, 67, 101991. [Google Scholar] [CrossRef]
- Huang, S.; Gu, X.; Zhou, H. Two-dimensional optimization mechanism and method for on-demand supply of manufacturing cloud service. Computers & Industrial Engineering. 2018, 117, 47–59. [Google Scholar]
- Wang, G.; Zou, Q.; Zhao, C. A highly efficient approach for bi-level programming problems based on dominance determination. Journal of Computing and Information Science in Engineering. 2022, 22, 041006. [Google Scholar] [CrossRef]
- Xu, B.; Lv, J.; Liu, J. Manufacturing Cloud Service Composition Optimization Based on Usability Analysis. Industrial Engineering and Management. 2024, 29, 1–11. [Google Scholar]
- Coello, C.; Pulido, G.; Lechuga M, S. Handling multiple objectives with particle swarm optimization. IEEE Transactions on Evolutionary Computation. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Połap, D.; Woźniak, M. Polar bear optimization algorithm: Meta-heuristic with fast population movement and dynamic birth and death mechanism. Symmetry, 2017, 9, 203. [Google Scholar] [CrossRef]
- Babu, B.; Anbarasu, B. Multi-objective differential evolution (MODE): an evolutionary algorithm for multi-objective optimization problems (MOOPs). Proceedings of international symposium and 58th annual session of IIChE. 2005.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).