Theoretical Aspects of Thin Film Optical Spectra: Underlying Models, Model Restrictions and Inadequacies, Algorithms, and Challenges

1. Introduction

Today, there is a large variety of commercial software available that provides calculation routines for both design and characterization tasks arising in research and technology of thin solid films and optical (multilayer) coatings. Examples of commonly used software packages are Film Wizard [1], FilmStar [2], Essential Macleod [3], OptiLayer [4] and OTF Studio [5]. Those software solutions strongly differ in menu organisation and interface appearance and comfortability, and also in the efficiency of the mathematics used for performing the concrete calculations. But as a matter of fact, the physical model ideas that are hidden behind the different mathematical routines are very similar. As a consequence of this surprising convergence, the user has to provide practically identical information to any chosen software before he (or she) can start with the calculation. Such information usually includes the angle of incidence, the polarization state of the light, and a spectral target that naturally includes information about the spectral range of interest. And at least in a design task, information about the optical properties of available materials must be provided, in terms of the wavelength dependence of two material quantities: the refractive index $n$, and the extinction coefficient $K$ for each material.

It is however more interesting, which kind of (usually accessible) information is NOT needed for the calculation. Thus, the intensity of the incident light is usually not a parameter of interest. The same concerns spatial beam extensions, or geometrical information about the angular distribution of light ray directions in focused or defocused incident radiation. The reason is in the specifics of the underlying physical thin film model, and this is what this paper shall be about.

In order to avoid misunderstandings: We recognize that the title of our paper has some similarity to the title of the excellent paper by A.V. Tikhonravov: “Some theoretical aspects of thin-film optics and their applications”, published in 1993 [6]. It is by no means our purpose to copy the strategic approach of that publication. What we are discussing here is focused on

• Physical modelling of both the system geometry and the material parameters
• Forward search tasks concerning the calculation of spectrophotometric quantities only, no inverse problems
• Specific effects arising from violations of the model assumptions in practice.

We therefore start with the description of what one could call the standard model of thin film optics. We note that this is usually rather a matter discussed in relevant textbooks, and would like to explicitly refer to those which had explicit impact on this study [7,8,9,10].

It is our opinion that a critical view on the underlying model assumptions is essential for any user of commercial thin film design and characterization software in order to develop a realistic view on the practical significance of any calculation result. Knowledge on the thin film optical models should already been imparted in corresponding university courses, where thin film optics may be taught as a special chapter of applied optics with clear interfaces to physical optics, electrodynamics, quantum physics and solid state physics [10].

2. Basic Model Assumptions in Conventional Thin Film Optics

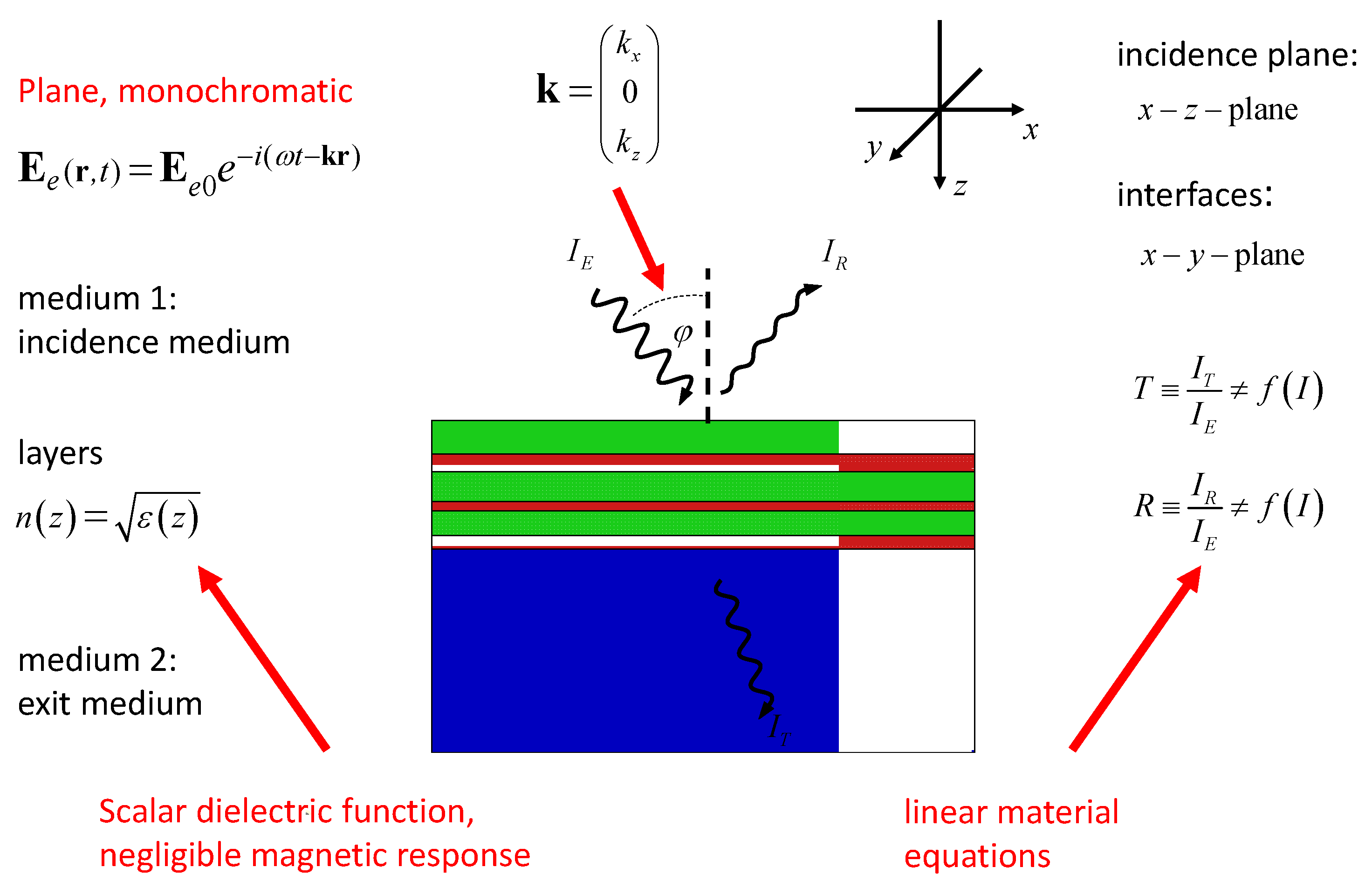
2.1. System Geometry

Let us shortly summarize basic model assumptions concerning system and illumination geometry characteristic in thin film optics [9,10]:

• We assume stratified media only. Consequently, the optical properties of the media shall depend on one coordinate (here the z-coordinate, compare Figure 1) only. The optical parameters describing the materials may exhibit a discontinuous z-dependence, and in this case, the discontinuities in the optical parameters describe what we will further call interfaces. The interfaces are perpendicular to the z-axis.
• Consequently, the model system extends to infinity along the x- and y-axes.
• We further assume optical isotropy of all media. In addition, any magnetic response is neglected in our model.
• The semispace above the stratified medium is filled with a homogenous medium, called the incidence medium. As a postulate, light propagation in the incidence medium should be free of damping. On its bottom, the stratified medium faces a semispace filled with a further homogeneous medium, called the exit medium.
• It is assumed, that a plane monochromatic electromagnetic wave is incident (from the incidence medium) on the stratified medium. In this case, an incident wavevector may be unambiguously defined. On this basis, an incidence angle may be introduced, which is zero for the particular case of normal incidence.
• At oblique light incidence, the wavevector of the incident wave and the z-axis allow defining an incidence plane.
• We further assume a three-wave scenario. That means, that the incident wave gives rise to the generation of two other plane waves, propagating either in the exit medium (the transmitted wave), or in the incidence medium (the reflected wave).
• The materials are described in terms of linear optical constants only. As a consequence, reflectances and transmittances may be introduced that do not depend on the light intensity.

The set of requirements I–VIII defines what we will further call the standard model of thin film optics (compare Fig. 1) In many situations, the exit medium is associated with the substrate material. We further note that sometimes the incidence medium is called the superstratum. Note that in this article, we will not explicitly consider the back side of the substrate (compare [10,11]).

2.2. Material Description

2.2.1. Dispersion Models

When restricting on electric dipole interaction in optically isotropic materials (i.e. neglecting any magnetic response), the light-matter interaction results in the induction of a macroscopic polarization of the medium according to [10,12,13,14]:

$$\mathit{P}\left(t\right)={\epsilon }_0{\int }_0^{\infty }\kappa \left(\xi \right)\mathit{E}\left(t-\xi \right)d\xi$$

(1)

Here, $\mathit{P}$ is the polarisation of the medium, ${\epsilon }_0$ the vacuum permittivity, $\mathit{E}$ the electric field in the medium and $\kappa$ the real response function of the medium. $t$ is the time, and the integration variable $\xi$ stands for the time delay.

From the response function, the dielectric function $\epsilon \left(\omega \right)$ (with $\omega$ - angular frequency of the incident light) of the medium is straightforwardly calculated according to:

$$\epsilon =1+{\int }_0^{\infty }\kappa \left(\xi \right)e^{i\omega \xi }d\xi =1+{\int }_0^{\infty }\kappa \left(\xi \right)\left(\cos \omega \xi +i\sin \omega \xi \right)d\xi =\epsilon \left(\omega \right)$$

(2)

Note that according to (2), the dielectric function must depend on the light frequency (so-called dispersion) and is necessarily a complex quantity. For any real response function $\kappa \left(\xi \right)$, from (2) we immediately find:

$$\mathrm{Re}\epsilon \left(-\omega \right)=\mathrm{Re}\epsilon \left(\omega \right);\mathrm{Im}\epsilon \left(-\omega \right)=-\mathrm{Im}\epsilon \left(\omega \right)$$

(3)

In terms of the formulated model assumptions III and VIII, the optical constants n (the refractive index) and K (the extinction coefficient) are obtained from the complex dielectric function according to (4):

$$n\left(\omega \right)+iK\left(\omega \right)\equiv \sqrt{\epsilon \left(\omega \right)}\Rightarrow \left\{\begin{array}{c}n\left(\omega \right)=\mathit{Re}\sqrt{\epsilon \left(\omega \right)}\\ K\left(\omega \right)=\mathit{Im}\sqrt{\epsilon \left(\omega \right)}\end{array}\right.$$

(4)

2.2.2. Commonly Used Dispersion Models

There is a large amount of dispersion models used in the modern scientific literature, compare for example [15,16,17,18,19,20,21,22,23,24,25]. Many of these models arise from making use of quantum mechanical features of the light-matter interaction, while in classical physics; there are basically three different dispersion models. We can only shortly present a selection of those models and start with the basic classical models:

When classifying the electrons in a solid into free and bound electrons [26,27], three basic polarization mechanisms may be identified, which are presented in the following scheme:

Here we have further introduced the resonance frequency ${\omega }_0$, the damping constant $\gamma$, and the “plasma angular frequency” ${\omega }_p=\sqrt{{\displaystyle \frac{N{q}^2}{{\epsilon }_{0}m}}}$ of the considered free or bound charge carriers (here electrons), respectively. $q$ and $m$ are charge and mass of the charge carriers, and $N$ stands for their concentration in the medium. The subscript “stat” denotes the static value of a given quantity.

Typically, none of the three mentioned models is applied in its pure form, because real matter has a tremendous number of degrees of freedom, all contributing to the full polarization of the medium under the action of an incident light wave. Therefore, the three basic models are usually properly superimposed to achieve a satisfying description of a realistic optical behavior. Some popularity has the multi-oscillator model [27,28], but we will further focus on two special cases, namely the Brendel model [17] as well as the beta-distributed oscillator model (ß_do model [18,19]).

Brendel model: It pursues the specifics of optical materials, which are characterized by fluctuations in the resonance frequencies within the material and thus provide an inhomogeneous line broadening mechanism. When assuming a Gaussian distribution of angular resonance frequencies $\Omega$ around a central frequency ${\bar{\omega }}_0$, an approximate calculation of the “averaged” dielectric function is performed by the equation

$$\epsilon \left(\omega \right)=1+{\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}{\int }_{-\infty }^{\infty }\exp \left[-{\displaystyle \frac{{\left(\Omega -{\bar{\omega }}_0\right)}^2}{2{\sigma }^2}}\right]{\displaystyle \frac{{\omega }_p^2}{{\Omega }^2-{\omega }^2-2i\gamma \omega }}d\Omega$$

(5)

Here, $\sigma$ is the standard deviation of the assumed Gaussian distribution, which defines the inhomogeneous contribution to the width of the absorption line defined by the imaginary part of ε. The shape of the absorption line is defined by the relation between $\sigma$ and $\gamma$. In the case of $\sigma \gg \gamma$, a Gaussian lineshape will be observed, while for $\sigma \ll \gamma$, we will find a rather Lorentzian behavior. When both linewidth contributions are comparable to each other, we have $\sigma \approx \gamma$, and then we obtain a so-called Voigt line.

The beta-distributed oscillator (β_do) model: In the β_do model it is the assumed, that the envelope of the mentioned multiplicity of individual absorption lines is formed by a Beta-distribution being given by

$$w_{\beta \_\mathrm{do}}\left(\omega \right)=\left\{\begin{array}{c}{\displaystyle \frac{{\left(\omega -{\omega }_a\right)}^{A-1}{\left({\omega }_b-\omega \right)}^{B-1}}{{\int }_{{\omega }_a}^{{\omega }_b}{\left(\omega -{\omega }_a\right)}^{A-1}{\left({\omega }_b-\omega \right)}^{B-1}d\omega }};A,B>0;\omega \in \left({\omega }_a,{\omega }_b\right)\\ 0;\omega \notin \left({\omega }_a,{\omega }_b\right)\end{array}\right.$$

(6)

The real parameters $A$, $B$, ${\omega }_a$ and ${\omega }_b$ are free parameters within the β_do model. The dielectric function is then given by:

$$\epsilon \left(\omega \right)=1+{\displaystyle \frac{J}{\pi }}{\int }_{{\omega }_a}^{{\omega }_b}{w}_{\beta \_\mathrm{do}}\left(\xi \right)\left[{\displaystyle \frac{1}{\xi -\omega -i\gamma }}+{\displaystyle \frac{1}{\xi +\omega +i\gamma }}\right]d\xi$$

(7)

Here $J$ is a further model parameter, which has the sense of an oscillator strength. Figure 2 shows an example on the optical constants dispersion as described in terms of the β_do model. The total of 6 free parameters provides some flexibility in modelling various (in particular asymmetric) absorption features, in particular in modelling what is called an absorption edge, defined by the parameter (or threshold frequency or absorption onset frequency) ${\omega }_a$ in (6).

As already mentioned, there is a tremendous amount of further dispersion models, particularly accounting for the quantum mechanical nature of light-matter interaction [13,14,15,20,21,22,23,24,25,29,30,31,32,33,34,35]. We will shortly mention the Tauc-Lorentz, Cody-Lorentz, as well as the Forouhi-Bloomer models, because of their ability to model the threshold character of light absorption in dielectric or semiconductor coatings by introducing an absorption edge.

In the Tauc-Lorentz model, the imaginary part of the dielectric function of a single oscillator model is merged together with the Tauc edge [30,31,32] to generate the imaginary part of the dielectric function of the Tauc Lorentz model according to [20,21] (8):

$$\mathrm{Im}\epsilon \left(\omega \right)\propto {\displaystyle \frac{{\left(\hslash \omega -E_g\right)}^2\theta \left(\hslash \omega -E_g\right)+{\left(\hslash \omega +E_g\right)}^2\theta \left(-\hslash \omega -E_g\right)}{\omega \left[{\left({\omega }_0^2-{\omega }^2\right)}^2+4{\omega }^2{\gamma }^2\right]}}$$

(8)

Here, $E_g$ is the absorption edge described in terms of the Tauc optical gap. Compared to the usual writing, (8) is generalized to negative frequency arguments in order to comply with (3). The corresponding real part is calculated in terms of a Kramers-Kronig relation (see later point 2.2.3). Explicit expressions can be found, for example, in [20,33].

The introduction of the Tauc gap in amorphous semiconductor optics is connected to the assumption of a constant (frequency-independent) transition matrix element of the momentum operator. If, on the contrary, constancy of the electric dipole moment operator is presumed, one arrives at the Cody-description of light absorption in the vicinity of the absorption gap, which results in the definition of the Cody gap [35]. With corresponding modifications in (8), the Cody-Lorentz model may be formulated [22]. To our knowledge the Tauc-Lorentz model is more frequently used in practice than its counterpart, the Cody-Lorentz relation.

In the Forouhi Bloomer model (we restrict here on the version for amorphous solids [23]), explicit expressions for n and K are derived according to:

$$\begin{gathered} K\left(\omega \right)={\displaystyle \frac{A{\left(\omega -{\omega }_{gap}\right)}^2}{{\omega }^2-B\omega +C}} \\ n\left(\omega \right)=n_{\infty }+{\displaystyle \frac{B_0\omega +C_0}{{\omega }^2-B\omega +C}} \end{gathered}$$

(9)

The $A$-, $B$- and $C$-values are constants. For uniformity reasons, (9) is written here in terms of the angular frequency, which is in contrast to the original publication where the photon energy was used. What appears rather strange is the asymptotic behavior for $K(\omega \to \infty )\to A\ne 0$. This has been recognized early and gave rise to corresponding criticism ([20]). Nevertheless, the model is frequently applied to spectra analysis in the vicinity of the fundamental absorption edge.

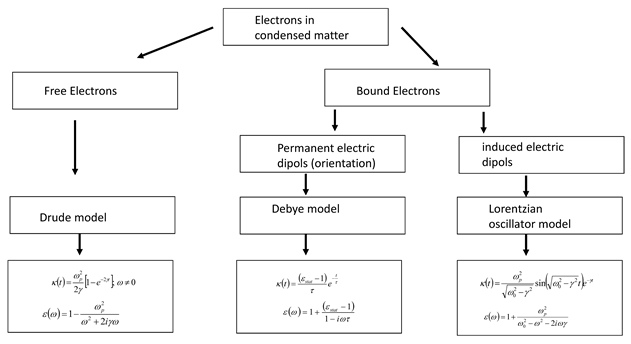
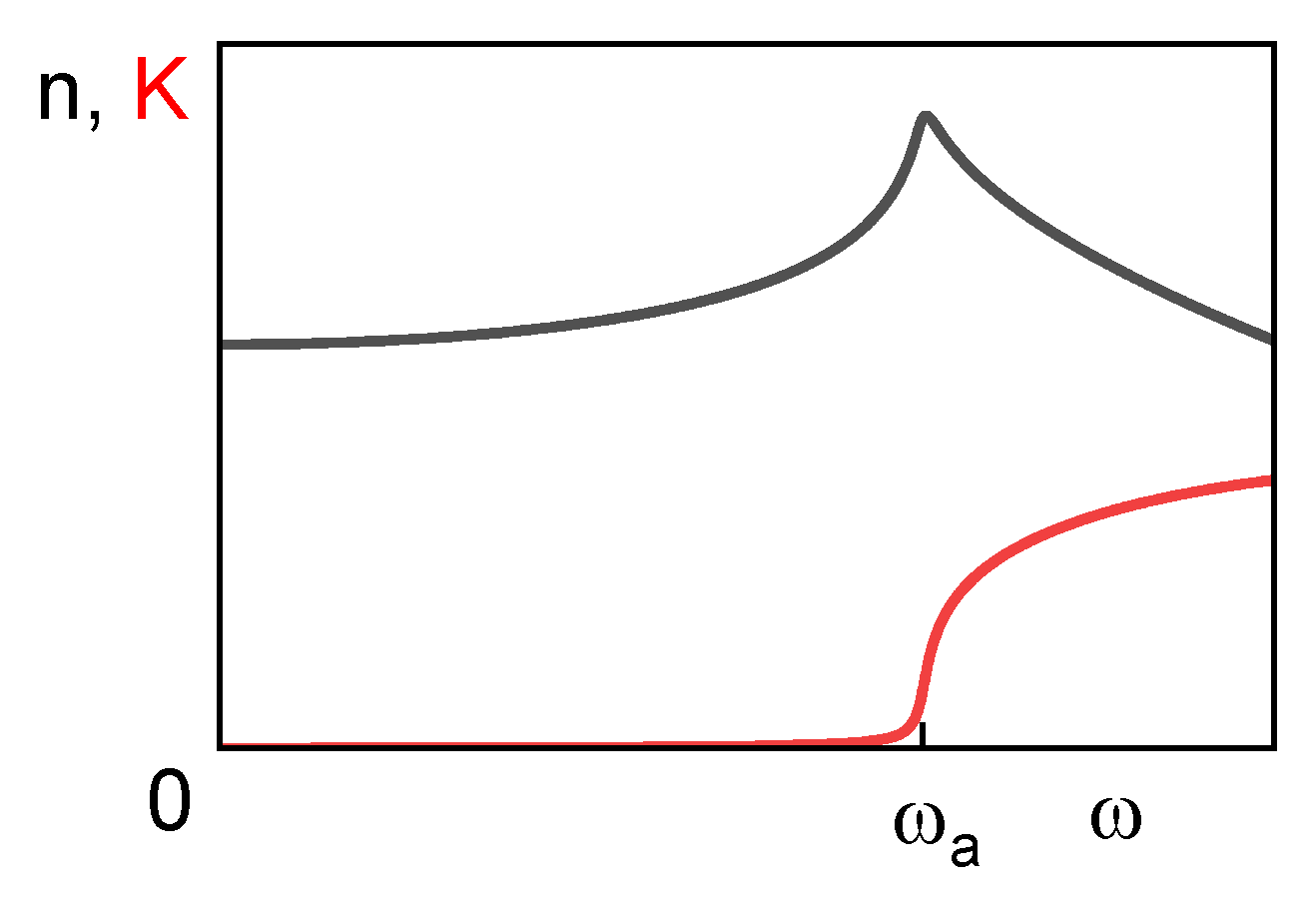
2.2.3. Kramers-Kronig Consistency

Any physically reasonable dielectric function must suffice the Kramers-Kronig relations [10,12,13]:

$$\mathrm{Re}\epsilon \left(\omega \right)=1+{\displaystyle \frac{1}{\pi }}VP{\int }_{-\infty }^{\infty }{\displaystyle \frac{\mathrm{Im}\epsilon \left({\omega }_2\right)d{\omega }_2}{{\omega }_2-\omega }}=1+{\displaystyle \frac{2}{\pi }}VP{\int }_0^{\infty }{\displaystyle \frac{\mathrm{Im}\epsilon \left({\omega }_2\right){\omega }_{2}d{\omega }_2}{{\omega }_2^2-{\omega }^2}}$$

(10)

$$\begin{gathered} \mathrm{Im}\epsilon \left(\omega \right)=-{\displaystyle \frac{1}{\pi }}VP{\int }_{-\infty }^{\infty }{\displaystyle \frac{\left[\mathrm{Re}\epsilon \left({\omega }_2\right)-1\right]d{\omega }_2}{{\omega }_2-\omega }}+{\displaystyle \frac{{\sigma }_{stat}}{{\epsilon }_0\omega }} \\ =-{\displaystyle \frac{2\omega }{\pi }}VP{\int }_0^{\infty }{\displaystyle \frac{\left[\mathrm{Re}\epsilon \left({\omega }_2\right)-1\right]}{{\omega }_2^2-{\omega }^2}}d{\omega }_2+{\displaystyle \frac{{\sigma }_{stat}}{{\epsilon }_0\omega }} \end{gathered}$$

(11)

With VP–Cauchys principal value of the improper integral, and ${\omega }_2$ - integration variable. The term ${\displaystyle \frac{{\sigma }_{stat}}{{\epsilon }_0\omega }}={\displaystyle \frac{{\omega }_p^2}{2\gamma \omega }}$ in (11) arises from the singularity in the Drude function at $\omega =0$ and is only relevant in electric conductors with a static electric conductivity ${\sigma }_{stat}\ne 0$. The Drude-, Debye-, and oscillator models are consistent with (10) and (11), and so are their linear superpositions. As a special case, the β_do model is Kramers-Kronig consistent as well. The situation is a bit more complicated with the Brendel model [36] because the dielectric function according to (5) contains a contribution with a vanishing resonance frequency, which becomes equivalent to a Drude-like term and therefore requires an addendum to (11) similar to what we have in the case of conductors. The problem may be overcome when using an appropriately apodised Gaussian function in (5) instead.

The Campi-Coriasso-Model [37,38] seems to be the first Kramers-Kronig consistent model combining the oscillator model with Tauc’s law [39]. It uses the same number of parameters with the same meaning as the Tauc-Lorentz model, but its parametrization is different and it is far less common. In the original work no analytical expression for the real part of the dielectric function is provided but can be found in [39], where also a good overview on models combining Tauc’s law and Lorentz model is given. The author of [39] conclude on the Kramers-Kronig-consistency of both the Tauc-Lorentz and Cody-Lorentz approaches, while the Forouhi-Bloomer model is claimed as Kramers-Kronig inconsistent.

In [40] a different physically consistent model combining the oscillator model with Tauc’s law is presented. It is called Advanced Dispersion Model and is a precursor of the Universal Dispersion Model [24]. In contrast to the latter, it requires a priori information about the physical and chemical structures of the films since the model contains physical parameters specific for the material, such as atomic fractions.

In concluding this paragraph, let us mention that the Kramers-Kronig relations represent a rather general quantitative formulation of the physical connection between light refraction and absorption phenomena. In fact those connections are intuitively used by any coating practitioner. It is well known from coating practice that materials with a large refractive index tend to have smaller optical gaps than materials with a smaller refractive index. These correlations are formulated in semi-empirical rules like the Moss- and Ravindra-rules [41], and represent a useful guide in any realistic coating design procedure.

3. Model Violations

3.1. General

In this article, we will separately deal with model violations concerning geometrical features of our “standard model”, and those concerning modelling the optical material constants. Concerning geometry, so it is clear that the idealized model requirements I–VIII as formulated in section 2.1 will never be fulfilled in practice, and therefore, model violations are unavoidable in practice. Therefore, we will discuss prominent examples, effects and their possible application potential. To a certain extent, this also concerns modelling of materials, because no real material is absolutely homogeneous, isotropic, electrically insulating and so on. What we will not discuss here are specific effects arising from the use of Kramers-Kronig inconsistent dispersion models in practical modelling the coating optical response in broad spectral regions. We see no real necessity to make use of inconsistent models, because there are enough Kramers-Kronig consistent dispersion models available, and it is hard to recognize the generation of new application ideas from the use of physically inconsistent models.

3.2. Geometry

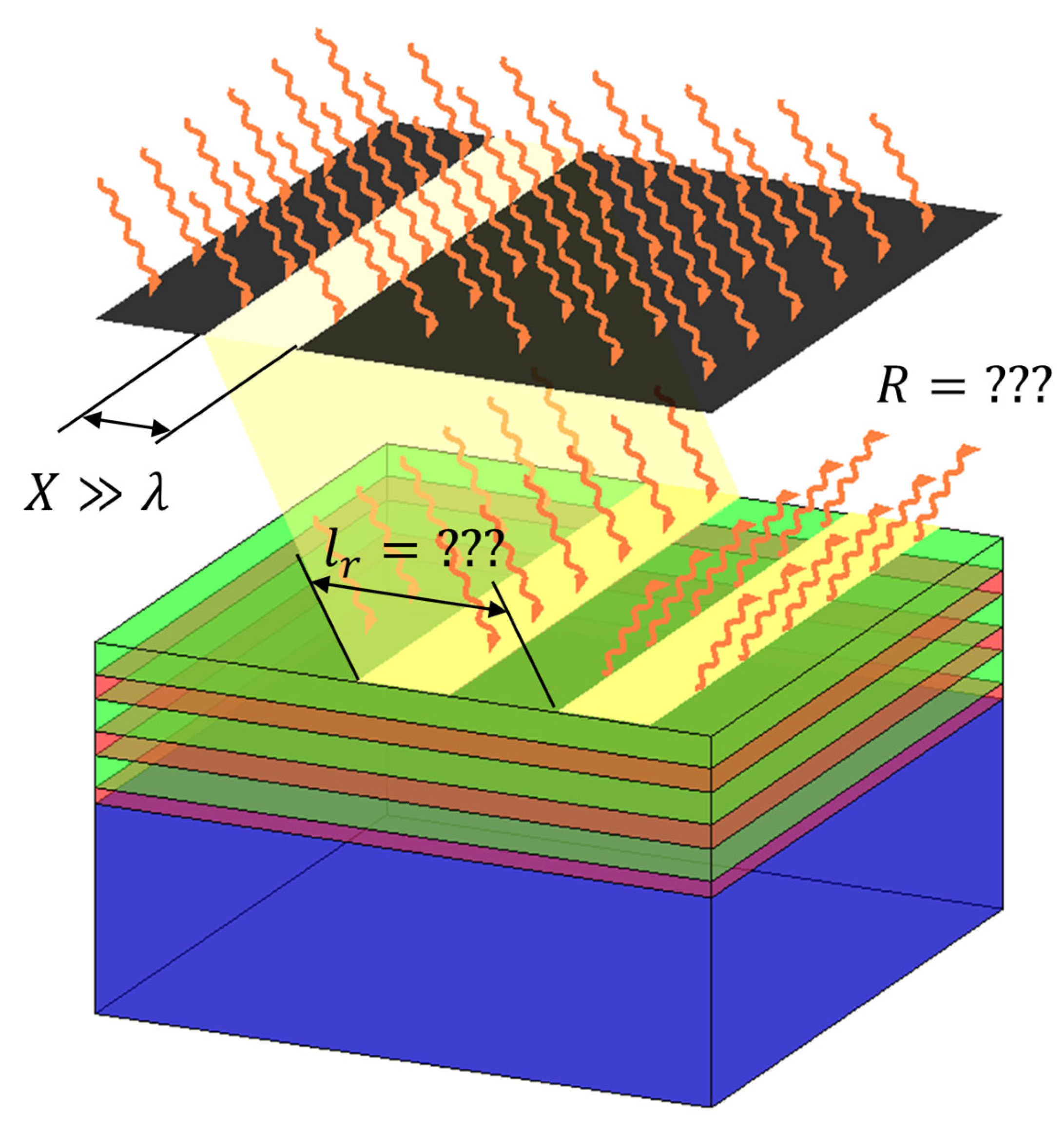
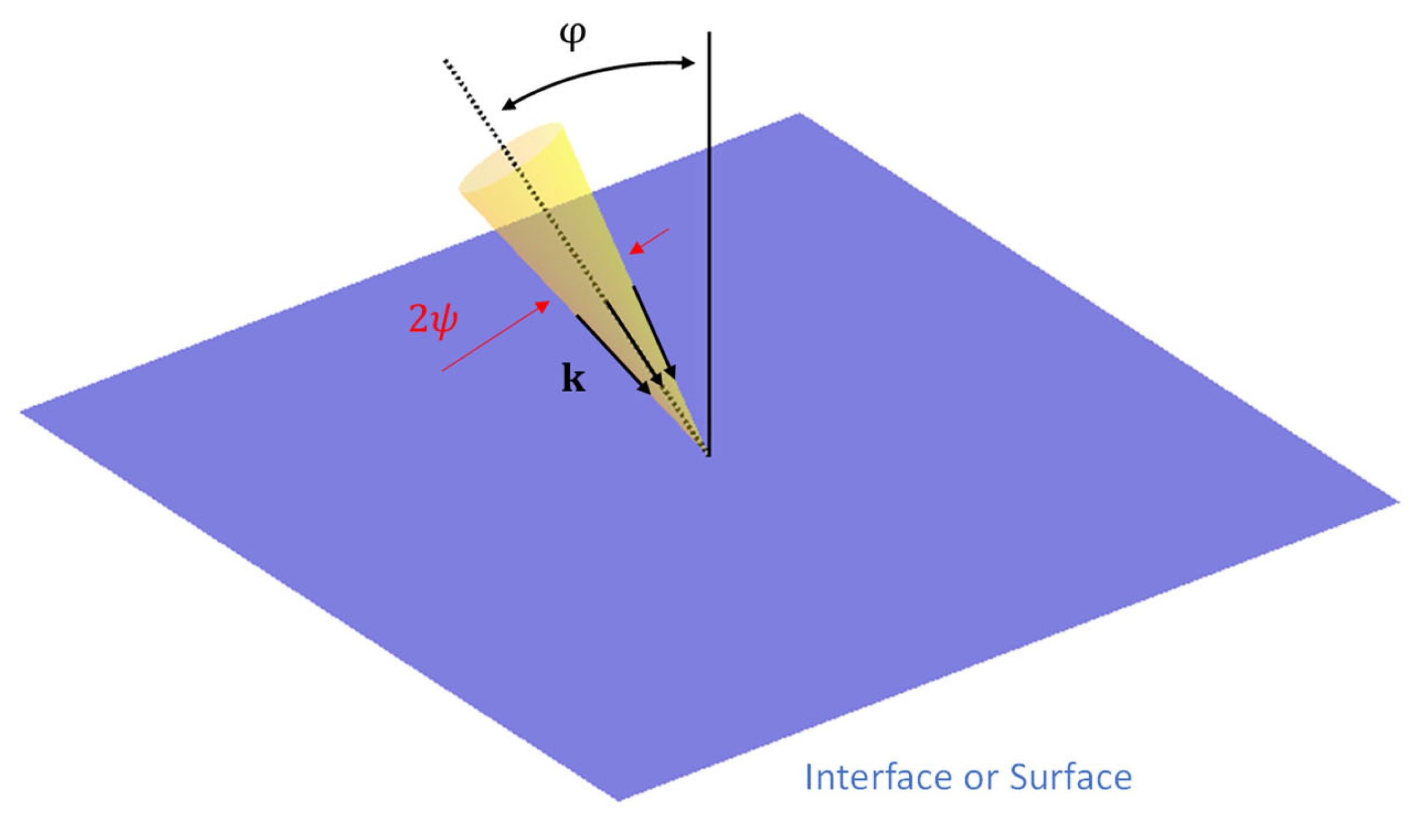
3.2.1. Restricted Beam Dimensions

We return to our standard model (Figure 1) and turn to the discussion of selected model assumption violations. Within this section, we shortly discuss a phenomenon called the Goos-Hänchen shift [42] for historical reasons.

In this context we consider a situation, that in contrast to model assumption V, the illumination area is spatially restricted. In particular, we assume some kind of illumination slit that is elongated along the y-axis while being spatially restricted along the x-axis (Figure 3).

Clearly, even in this modified illumination geometry, the incident light beam may be reflected or transmitted at the sample surface. Once we have a spatially restricted illumination spot, it makes sense to ask, where the light leaves the sample.

Historically, this was first investigated in internal total reflection conditions at a single interface. As a matter of fact, the totally reflected light beam turns out to be laterally shifted along the x-axis with respect to the incident light beam for a characteristic distance l_r. This is the so-called Goos-Hänchen shift [42,43]. It turned out later that this phenomenon is however not restricted to surfaces in total internal reflection conditions. In optical coatings, lateral shifts up to the sub-millimeter range have been experimentally established [44].

In [43], Kurt Artmann was able to show that the value of the Goos-Hänchen shift depends on the first derivative of the phase ${\delta }_r$ of the complex reflection coefficient with respect to the incidence angle $\phi$. The idea behind his model is that the spatially restricted illumination area is equivalent to relaxing the model requirement V. Hence, he assumed a certain distribution of incident plane waves with different incidence angles, and the lateral shift $l_r$ is then obtained as:

$$l_r=-{\displaystyle \frac{d{\delta }_r}{d{k}_x}}={\displaystyle \frac{\lambda }{2\pi n_1\cos \phi }}{\displaystyle \frac{d{\delta }_r}{d\phi }}$$

(12)

Here, $n_1$ denotes the refractive index of the incidence medium.

Again, the effect is not only relevant in total internal reflection conditions [10]. It has been found in the vicinity of the Brewsters angle with p-polarized light [45], at interfaces between transparent and absorbing media [45,46,47,48,49], as well as at metal surfaces [48,49].

Artmanns argumentation is general enough to be applicable to thin film stacks as well [44,50]. Correspondingly, lateral shifts in transmission ($t$) and reflection ($r$) are estimated in terms of (13):

$$\begin{gathered} r=\left|r\right|e^{i{\delta }_r}\Rightarrow l_r=-{\displaystyle \frac{\lambda }{2\pi }}{\displaystyle \frac{1}{n_1\cos \phi }}{\displaystyle \frac{d{\delta }_r}{d\phi }} \\ t=\left|t\right|e^{i{\delta }_t}\Rightarrow l_t=-{\displaystyle \frac{\lambda }{2\pi }}{\displaystyle \frac{1}{n_1\cos \phi }}{\displaystyle \frac{d{\delta }_t}{d\phi }} \end{gathered}$$

(13)

The lateral shift according to (13) depends on the wavelength of the incident light. Potential applications therefore pursue wavelength demultiplexing tasks [51,52].

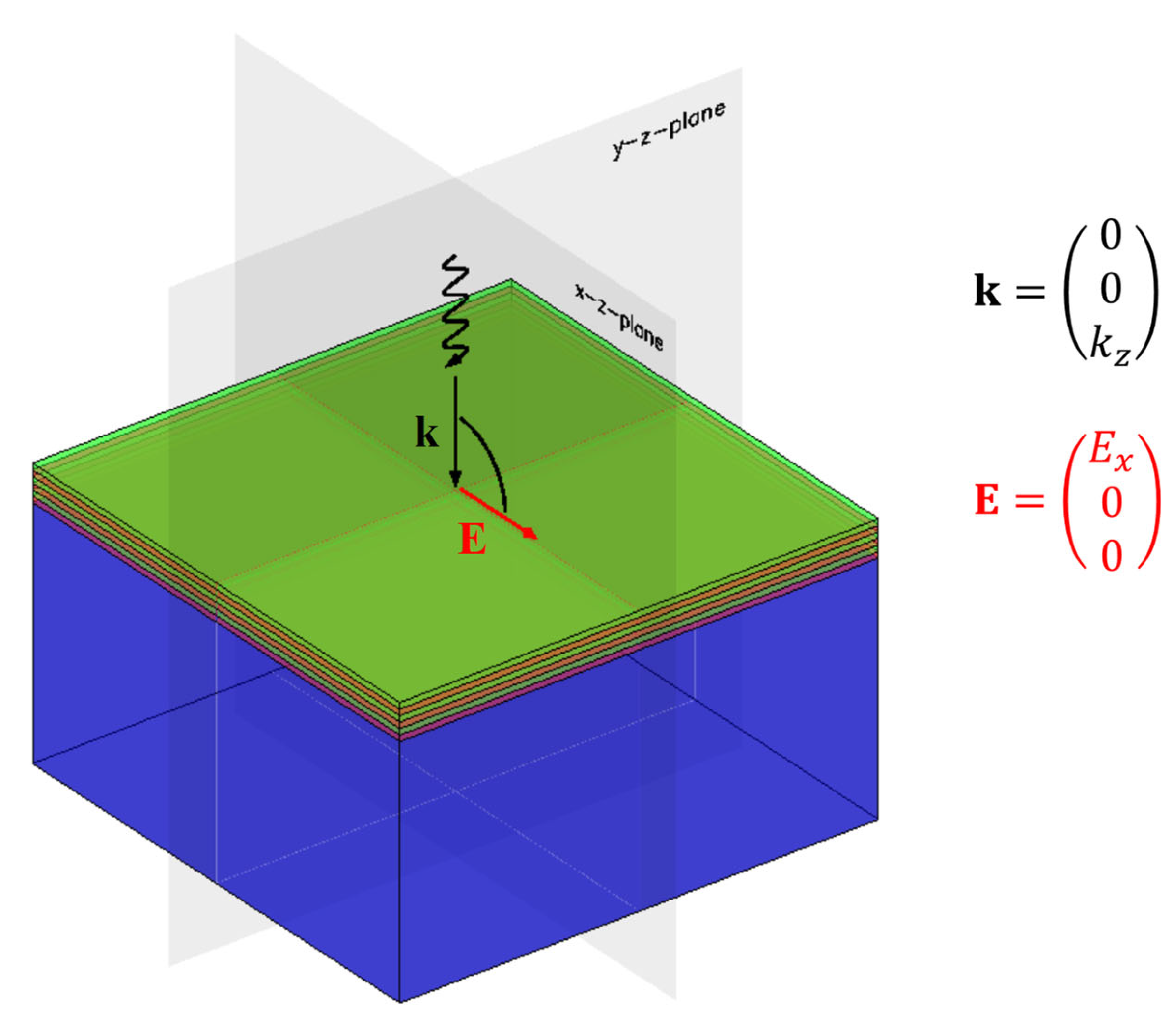
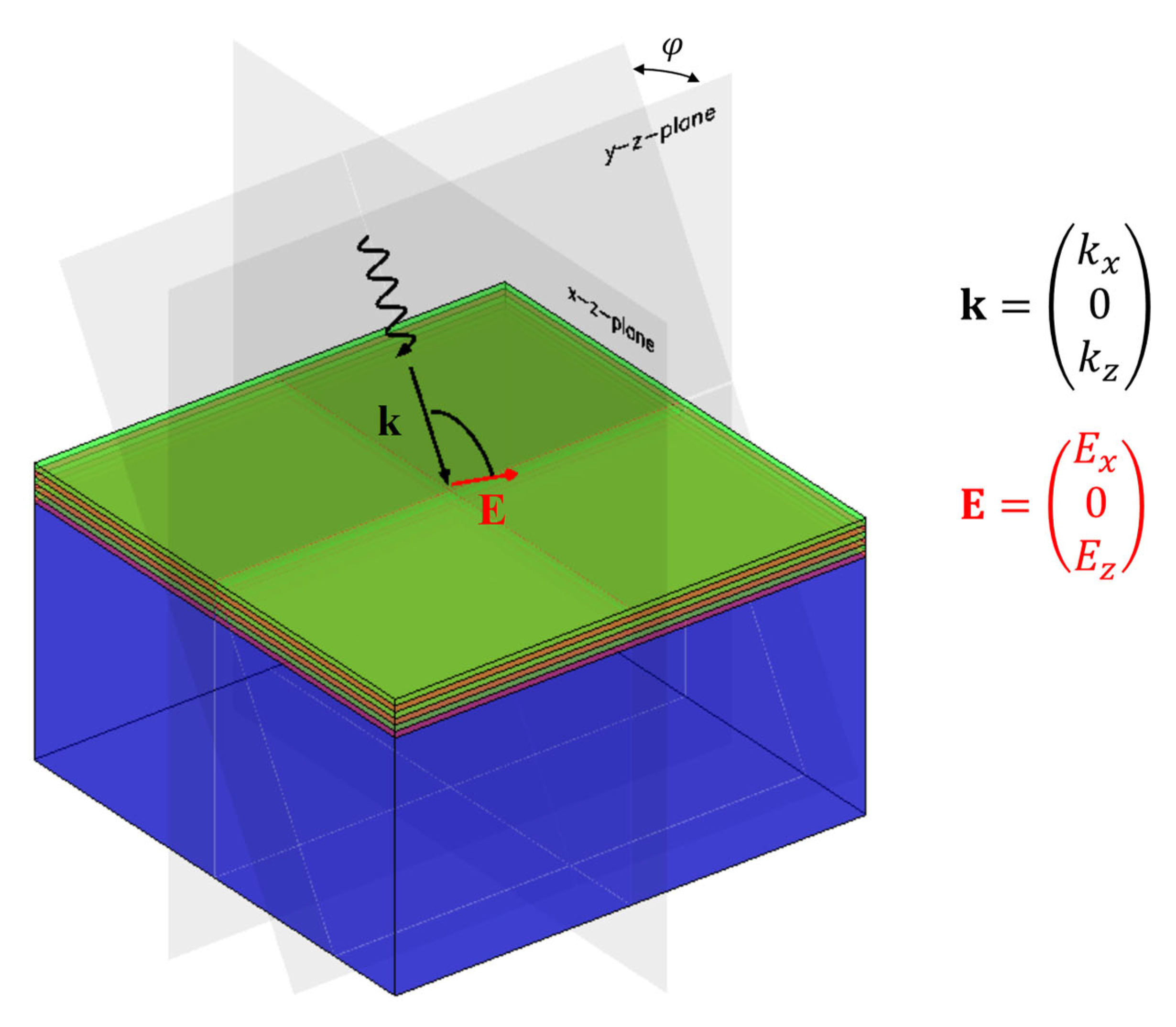
3.2.2. Polarization Leakage

In this section, we discuss consequences of a violation of model requirement VI (no unambiguously defined incidence plane). Let us imagine a situation, where the assumed plane sample surface is illuminated by light consisting of many different rays with different individual wavevectors. Let us further restrict on a simple model case, where all incident wavevectors are confined in a cone characterized by an apex-semiangle $\Psi$ (Figure 4) [53]. The angle $\phi$ now denotes the angle between the surface normal and the symmetry axis of the cone. The described situation may correspond to oblique incidence of focused or defocused light.

However, because of the assumed conical light incidence geometry, it is now no more possible to define an incidence plane in the strong sense. Indeed, each of the light rays that form the cone defines an individual incidence plane, and consequently, the termini of s- and p-polarization [10] use their assumed strong sense. Indeed, for example, light that is s-polarized with respect to the nominal incidence plane defined by the symmetry axis of the cone, is not necessarily s-polarized for the individual incidence planes relevant for other k-vectors, instead, it may contain p-polarized components. The result is an effect called the polarization leakage. It is rather disturbing in any real experiment performed with linearly polarized light and, in particular, destroys the performance of thin film light polarizers.

While a general theory of the polarization leakage is developed in [54], a somewhat simpler but less general treatment restricted to a Lambertian intensity distribution results in the manageable expression (14) (compare [53]):

$$leakage\approx {\displaystyle \frac{{\Psi }^2}{4{\tan }^2\phi }}$$

(14)

In deriving (14), $\Psi \ll \phi$ is assumed.

Note that the leakage is determined by the illumination geometry only, the apex- semiangle is given in radians. Therefore, improvements of the coating design have no effect on the polarization leakage.

As it turns out from (14), the polarization leakage may be reduced by enlarging the angle $\phi$. In practice, that gave rise for the development of completely new types of thin film polarizers, working at incidence angles substantially larger than the usually applied incidence at 45° [55]. The working principle of these polarizers is based on attenuated total internal reflection at certain internal interfaces, and thus represents an example of the development of completely new optical components stimulated by the emergence of an originally disturbing effect like the polarization leakage.

3.2.3. Rough Surfaces

Rough surfaces, as well as any laterally structured coatings, violate the model assumption I defined in section 2.1 because they introduce an additional $x$- and/or $y$-dependence of the dielectric function. Indeed, any surface profile is usually defined in terms of a surface height function $h\left(x,y\right)$. The rms surface roughness $\sigma$ is then defined through:

$$\sigma ={\displaystyle \frac{1}{L}}\sqrt{{\int }_0^L{\int }_0^L{\left[h\left(x,y\right)-⟨h⟩\right]}^{2}dxdy};⟨h⟩={\displaystyle \frac{1}{L^2}}{\int }_0^L{\int }_0^{L}h\left(x,y\right)dxdy$$

(15)

where $L$ is a characteristic length scale. Usually, in a practical situation, the surface profile is not exactly known. Let us for simplicity consider the situation of a one-dimensional surface height profile $h\left(x\right)$ that is assumed to be known on a certain length interval $L$ in a number of $N$ points. That interval may then periodically continued, so that it can be approximated by [56]:

$$h\left(x\right)=\sum _{l=-N}^N{h}_l{e}^{{\displaystyle \frac{2i\pi lx}{L}}}$$

(16)

In this case, the rms surface roughness can be written as:

$${\sigma }_{rms}=\sum _{l=-N}^N{\left|h_l\right|}^2$$

(17)

From here we obtain the expressions for the so-called small scale roughness ${\sigma }_{small}$ and large scale roughness ${\sigma }_{large}$ via:

$${\sigma }_{small}=\sum _{\left[l>>{\displaystyle \frac{L}{\lambda }}\right]}{\left|h_l\right|}^2$$

(18)

$${\sigma }_{large}=\sum _{\left[l<<{\displaystyle \frac{L}{\lambda }}\right]}{\left|h_l\right|}^2$$

(19)

Small-and large scale roughnesses have a different impact on the optical properties of a coating. Large scale roughness gives rise to diffuse light scattering and thus provides an optical loss mechanism. Small scale roughness, on the contrary, rather acts like an antireflection coating. A small scale roughness is usually modelled by introducing a fictive mixture layer on the surface, making use of a mixing model like the Lorentz-Lorenz or the Maxwell Garnett approach. This calculation strategy is well established and incorporated today in commercially available film characterization software, particularly for ellipsometry purposes [57]. The introduction of an (optically homogeneous) mixture model eliminates the x- and y-dependence of the optical properties from the system, so that the calculation of the optical properties may again be performed in terms of the model assumptions formulated in section 2.1.

The situation is different in the case of a large scale roughness. Different approximation formulas have been proposed to incorporate the scatter losses into the optical model. A crucial point is that the effect of the roughness on the thin film spectra is now twofold: The surface roughness may not only change the propagation direction of the incident light through elastic scatter, but has also an impact on the coherence of light trains superimposing as a result of multiple internal reflections at the interfaces of the film system. Therefore, at the moment, no unique generally accepted manageable approach is available, but there exists a large diversity of different approaches, (as examples, we cite [56,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91]) all having their individual strength and shortcomings. As seen from the references, surface roughness in optical coatings is a hot topic from the sixtieth of the last century of the previous millennium until today.

A detailed discussion of the available literature is beyond the frames of this review. Clearly, a rigorous electrodynamic treatment of wave propagation through a system with a specified surface geometry will provide the necessary information, but in thin film practice, any practitioner will seek for a couple of manageable formulas that allow for a quick-and-dirty estimation of the effect of roughness on a spectrum that is otherwise calculated in the usual way. We therefore limit the discussion of large scale roughness to the presentation of a set of estimation formulas, that have proven useful for estimating the roughness-induced changes in specular reflectance and transmittance at interfaces compared to the ideally flat surface model (Table 1). Thereby, the model for large scale roughness by A. V. Tikhonravov [56] is limited to normal light incidence and non-absorbing materials only. It can be extended to the case of oblique light incidence, as exemplified in [58,79]. Table 1 summarizes several proposed versions of scatter factors S relevant for reflection (r) and transmission (t). In the calculations, these scatter factors appear as prefactors to the usual Fresnel field transmission and reflection coefficients.

3.2.4. Coherence

In thin film optics, a loss in coherence between multiply internally reflected waves is usually caused by either a coating thickness that increases the coherence length of the incident light, or by the loss of phase information of the wave when passing rough interfaces (compare section 3.2.3.) In this section, our focus will be on the first mechanism.

In optical multilayer systems with smooth interfaces, a distinction is usually made in the description between the extreme cases of incoherent (e.g. substrate with consideration of the back side) and coherent light propagation [11]. In the case of incoherent light propagation, no phase information is included, because the coherence length of the light is assumed to be smaller than the layer thickness. Therefore, no interference effects occur and only the wave amplitudes are relevant and geometrical optics can be used for modelling.

In the case of coherent light propagation, the coherence length is assumed to be significantly larger than the layer thickness. For this reason, the phase information remains important and interference effects between multiply reflected waves will occur. Therefore, the wave optic is the corresponding theoretical model here.

Optical coatings containing both types of layers can be modelled with the general transfer matrix method outlined in many textbooks (e.g. [92]). In the case of anisotropic layers, a generalized method is proposed in [93].

In the intermediate regime, when the layer thickness is in the range of the coherence length, the two mentioned extreme cases are of no relevance, and an adapted theoretical approach based on partial coherence is required.

Bearing in mind that the coherence length is affected by spectral resolution and wavelength of the light source, a given sample may appear either “coherent” or “incoherent”, depending on the illumination conditions [10]. When an optical coating is measured in a sufficiently broad spectral range, the transition from “coherent” to “incoherent” may even be observed within a single transmission or reflection spectrum. As a result, the loss in coherence may be observed by a depletion of the amplitude of the interference fringes usually observed in both transmission and reflection spectra.

Let us finish this section with a short literature review. Initially, the theoretical description of partial coherence was limited to single layer coatings at normal incidence [94], but later these limitations could be eliminated in a more general theory [95]. In this approach a complex degree of coherence (cdc) has been introduced. The limiting cases of the absolute values are |cdc| = 0 for incoherent and |cdc| = 1 for coherent light propagation. In [77] a simpler coherence function is proposed and spectral averaging over an interval is used.

In [96] partially coherent light propagation is also modelled with the transfer matrix method, but the transition from coherent to incoherent propagation is achieved by introducing a random phase of increasing intensity. In [97] the coherence length is considered using a Fourier transform of a randomly generated partially-coherent wave. Thereby, the statistical field distribution of partially coherent light is modelled using a rigorous coupled wave analysis.

In [72] and [75] a generalized matrix method is presented, where interface roughness has been addressed as a special case of partially coherent light propagation. The phase-shift integration method in [98] provides an alternative mathematical approach for the modelling and is used to derive an analytical expression for irradiance at an arbitrary depth of the multilayer stack. The method is advantageous for gradient optimization methods because analytical layer thickness derivatives are provided.

In [99] the net-radiation method is adapted for modeling the reflectance, transmittance and absorption depth profile of thin-film multilayer structures such as solar cells. Thereby, an arbitrary multilayer structure with coherent, partly coherent and incoherent layers can be simulated more accurately at much lower computational cost.

A generalized transmission line method (TLM) is outlined in [100] and applied to thickness determination of individual layers of an organic light-emitting diode. Additionally, the approach is used for calculation of the external quantum efficiency of an organic photovoltaic with partially coherent rough interfaces between the layers.

3.2. Materials

3.2.1. Optically Anisotropic Materials

In fact, optical material anisotropy and its relation to optical thin film theory and practice is well understood and documented in the realm of (variable angle) spectroscopic ellipsometry [101,102,103]. Software packages for ellipsometry data analysis therefore usually allow modelling certain types of optical anisotropy [104,105]. Therefore, there is no principal difficulty to generalize the thin film model to anisotropic materials. We mention that anisotropic film materials allow designing and manufacturing of novel superior polarizing components, as already demonstrated in the field of Giant Birefringent Optics (GBO [106,107]).

3.2.2. Time-Dependent Material Properties

The corresponding basics have already been developed in the 50^th of the previous century [108,109]. Instead of (1) and (2), we now have:

$$\kappa =\kappa \left(t,\xi \right)\Rightarrow \mathit{P}\left(t\right)={\epsilon }_0\underset{0}{\overset{\infty }{\int }}\kappa \left(t,\xi \right)\mathit{E}\left(t-\xi \right)d\xi \Rightarrow \epsilon \left(t,\omega \right)=1+{\int }_0^{\infty }\kappa \left(t,\xi \right)e^{i\omega \xi }d\xi$$

(20)

This way we have introduced what may be called a “time-dependent dielectric function”, while relaxing the natural requirement of time homogeneity.

Let us in a short manner note some specifics of wave propagation in the presence of time inhomogeneity [110]. It is well known that spatial inhomogeneity preserves the light frequency but changes the wavelength. Time-inhomogeneity, on the contrary, changes the light frequency while preserving the wavelength. This is a direct conclusion from Noethers theorems [10,111,112].

A temporal interface is defined as a discontinuity in $\epsilon \left(t\right)$, while a spatial (i.e. usual) interface results from a discontinuity in $\epsilon \left(z\right)$. Both kinds of interface result in the generation of a backtravelling (reflected) wave when an incident wave arrives at the interface. However, at a temporal interface, the sum of transmittance and reflectance may exceed 1, which is in contrast to the situation at a spatial interface between two passive media [109,110].

The combination of several temporal interfaces allows constructing temporal coatings [113]. Even more futuristic, the combination of temporal and spatial interfaces in an optical component leads us to the concept of a time-varying metamaterial [114].

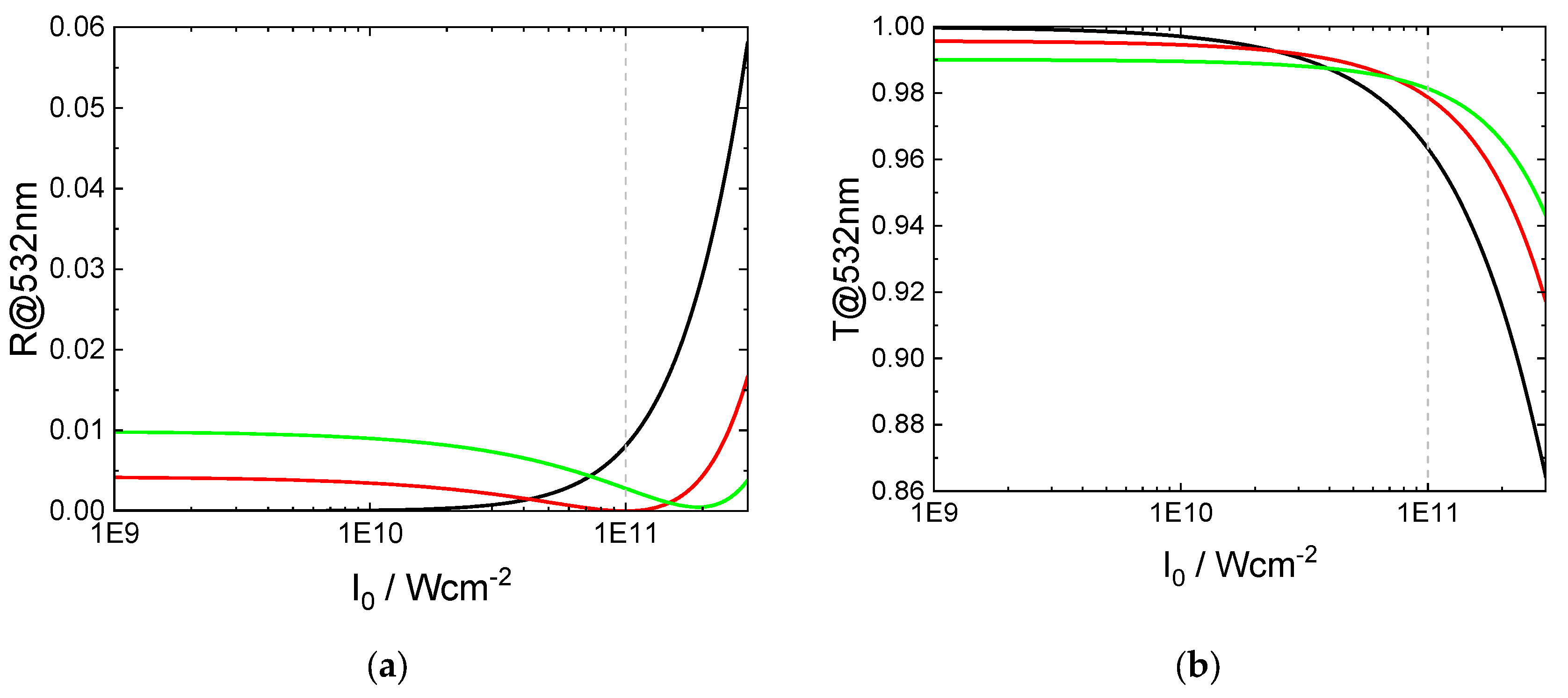
3.2.3. Non-Linear Response

According to model assumption VIII, T and R are independent of the incident light intensity. However, T and R may become intensity dependent, provided that (1) is replaced by its non-linear counterpart according to [115]:

$$\begin{gathered} P\left(t\right)=P^{\left(1\right)}+P^{\left(2\right)}+P^{\left(3\right)}+...={\epsilon }_0{\int }_0^{\infty }{\kappa }^{\left(1\right)}\left(\xi \right)E\left(t-\xi \right)d\xi + \\ {\epsilon }_0{\int }_0^{\infty }{\int }_0^{\infty }{\kappa }^{\left(2\right)}\left({\xi }_1,{\xi }_2\right)E\left(t-{\xi }_1\right)E\left(t-{\xi }_1-{\xi }_2\right)d{\xi }_{1}d{\xi }_2+ \\ {\epsilon }_0{\int }_0^{\infty }{\int }_0^{\infty }{\int }_0^{\infty }{\kappa }^{\left(3\right)}\left({\xi }_1,{\xi }_2,{\xi }_3\right)E\left(t-{\xi }_1\right)E\left(t-{\xi }_1-{\xi }_2\right)E\left(t-{\xi }_1-{\xi }_2-{\xi }_3\right)d{\xi }_{1}d{\xi }_{2}d{\xi }_3+... \end{gathered}$$

(21)

In the more familiar frequency domain (21) may be written in the simplified manner:

$$P=P^{\left(1\right)}+P^{\left(2\right)}+P^{\left(3\right)}+...={\epsilon }_0{\chi }^{\left(1\right)}E+{\epsilon }_0{\chi }^{\left(2\right)}{E}^2+{\epsilon }_0{\chi }^{\left(3\right)}{E}^3+...$$

(22)

As it is evident from (21) or (22), non-linear optical effects become significant only at rather large light intensities. Relevant with respect to thin film optics examples include harmonic generation as well as the observation of intensity-dependent transmittances or reflectances [116,117,118,119,120]. In ultrashort light pulses, peak intensities may become rather large [121]. In such a constellation, the reflectance of a thin film reflector may be significantly reduced when comparing to what is expected from the standard (linear) theory. The physical process behind is called non-linear absorption. Let us mention for completeness, that the second harmonic generation is related to second order terms in (21) and (22), while the third harmonic generation as well as nonlinear absorption result from the third-order terms.

As an example, Figure 5 shows the simulated normal incidence reflectances and transmittances of three fictive antireflection coatings depending on the intensity of the incident light. For details of the simulation algorithm see [122,123,124], but let us shortly mention that the calculation of T and R is based on the solution of a system of equations as:

$$\begin{gathered} {\displaystyle \frac{dE}{dz}}=-i{\mu }_0\omega H \\ {\displaystyle \frac{dH}{dz}}=-i{\epsilon }_0\epsilon \omega E-{\displaystyle \frac{3}{4}}i{\epsilon }_0\omega {\chi }^{\left(3\right)}{\left|E\right|}^{2}E \end{gathered}$$

(23)

Here, for simplicity, normal incidence is assumed. $E$ stands for the electric, and $H$ for the magnetic field strength. This is a non-linear system of equations which needs to be solved numerically for the assumed z-dependence of $\epsilon$ and ${\chi }^{\left(3\right)}$. Note that in the special case of ${\chi }^{\left(3\right)}=0$, (23) becomes linear and coincides with the system of equations relevant for calculating the linear response of any stratified medium (compare [9,10,26]). In particular, the well-known matrix formalism may be directly derived from the linear version of (23).

After having solved (23) with proper boundary conditions, the electric field transmission and reflection coefficients (Fresnel-coefficients $t$ and $r$) are obtained from:

$$t={\displaystyle \frac{2}{E(z=0)-\sqrt{\frac{{\mu }_0}{{\epsilon }_0}}H(z=0)}};r={\displaystyle \frac{E(z=0)+\sqrt{\frac{{\mu }_0}{{\epsilon }_0}}H(z=0)}{E(z=0)-\sqrt{\frac{{\mu }_0}{{\epsilon }_0}}H(z=0)}}$$

(24)

Here, air is assumed as incidence medium. The interface between air and the stratified medium is at $z=0$.

Assuming now ${\chi }^{\left(3\right)}\ne 0$, all materials are characterized by four optical constants. Indeed, in addition to the linear optical constants $n$ and $K$, the real as well as the imaginary parts of ${\chi }^{\left(3\right)}$ have to be taken into consideration. As a result, the calculated transmittance and reflectance turn out to be intensity-dependent.

Let us finish this small section with a model calculation (see Figure 5). We start from a simple V-coating [7,8] that might be in use as antireflection coating at a wavelength of 532 nm (black line). In addition, the red line in Figure 5 shows the performance of a modified V-coating optimized for smallest reflectance at an incident intensity of 10¹¹ Wcm^-2 taking nonlinear susceptibilities into account, while the green line corresponds to the performance of a design optimized for highest transmittance at 10¹¹ Wcm^-2. Basic design parameters are summarized in Table 2.

Obviously, at low light intensities, the traditional V-coating is best in antireflection performance. However, the picture changes at larger light intensities. Therefore, in nonlinear optics, new optical coating design solutions may have to be developed.

Thus, in nonlinear optics, optical coating design tasks are of increased complexity when comparing with the linear case. Particularly, we mention the increased number of optical material parameters that need to be known and considered in the design calculation.

The intensity dependence of the optical performance of the coating is a direct consequence. A design that is optimized for a certain light intensity is not necessarily a good choice for application at other intensities (compare Figure 5).

Compared to the linear task, the determination of non-linear optical parameters needs much more complex and expansive equipment, as well as a considerable larger measurement effort [125]. We note that it might be prospective to make use of parametrized dispersion laws for non-linear optical constants [126], calibrated by a restricted set of experimental data. We also mention that there exists a couple of estimation formulas for realistic non-linear refractive indices [127,128,129], based on the generalized Millers rule [130].

3.2.4. Thickness-Dependent Optical Constants

The basic concept of optical thin film theory described so far relies on the possibility to perform a clear separation between material parameters (optical constants) and geometrical parameters (thicknesses) from each other [16]. This is a fundamental requirement, and it allows, for example in a coating design task, combining optical constants and film thicknesses in an arbitrary manner. In fact, this is not always possible. Once the optical constants represent macroscopic parameters, obtained after averaging the atomic or molecular responses in a thermodynamically relevant volume fraction, this concept may collapse when the film thickness becomes too small. Thus, atomic or molecular monolayers are more reliably modeled in terms of the microscopic polarizability [131,132]. This is clearly an extreme example, but a “thickness-dependence” of optical constants is also obtained in thin metal films, when the thickness becomes smaller than the mean free path of the conduction electrons in the metal [133,134,135]. Also, a clear separation between effective optical constants and thickness of a metal island film is problematic [136]. In a more recent publication, Willey [137] proposed a design procedure for metal-island-film based coatings while taking the thickness dependence of their effective optical constants into account explicitly.

Presently, research is also directed on making use of nanolaminates as versatile building blocks in optical coatings design [138,139,140,141,142]. The hope is that because of quantum confinement effects [143,144], new combinations of optical gap and refractive index may become accessible, thus overcoming the restrictions emerging from the Moss or Ravindra rules [41]. However, those nanolaminates are strongly anisotropic (compare Figure 6 and Figure 7), and the efficient exploitation of confinement effects may be restricted to special illumination and polarization geometries. Thus, in the case of normal incidence (Figure 6), the electric field strength vector $\mathit{E}$ is in the x-y-plane and cannot induce electric dipole transitions along the z-axis (i.e. between different discrete energy levels of the electron moving along the confinement direction in the quantum well, compare the selection rules discussed in [144]). At oblique incidence and p-polarization, however, such transitions shall be possible, because the electric field strength vector has a non-vanishing component along the z-axis. Hence, even the absorption behaviour of such nanolaminates is expected to be strongly anisotropic, which offers new development directions in the field of polarizing absorptive optics.

4. Summary and Challenges

We have reviewed important facets of the typical thin film optical model. According to our primary intention, idealized model assumptions have first been formulated, and then opposed to real geometry and measurement conditions that give rise to model assumption violations in practice. We emphasize that knowledge of these possible model violations and their effects is important for at least three reasons.

• They enable the user of commercial optical film calculation software to critically evaluate the practical value of a calculation result
• They enable the practitioner to understand the reason for discrepancies between the promised and measured performance of purchased thin film optical components.
• They define important topics for the design of university courses on applied thin film spectroscopy.

In addition to this, we tried to demonstrate that the effects caused by certain model violations had a stimulating impact on the development of novel optical components. Examples are provided by new demultiplexing devices, Giant Birefringent Optics, as well as new thin film polarizer, dielectric reflector, antireflection coating and absorber coating designs.