1. Introduction
PMSM has gained significant traction in industrial automation and electric vehicle applications due to their exceptional efficiency, high power density, and superior dynamic performance. The PMSM drive system represents a typical dual time-scale system. Among the most efficient control designs for PMSM is the cascade structure, which incorporates a rapid inner loop responsible for armature current control while employing a slower outer loop intended to adjust angular velocity by generating appropriate current reference signals. However, achieving the desired control performance for PMSM applications presents challenges. Including issues such as parameter variations, external disturbances, and system nonlinearity. In reference [
1], it is pointed out that the permanent magnetic flux linkage can vary by 20% of its nominal value, while the stator resistance can vary by 200% of its nominal value." In practical applications, researchers often aim to employ a stable and highly accurate control strategy that can effectively achieve rapid response and robustness in the presence of uncertain parameters. However, conventional proportional-integral (PI) controllers prove inadequate for tracking the outer loop velocity when motor parameter uncertainties arise. Consequently, researchers have explored diverse advanced control techniques to address the velocity servo problem, encompassing model predictive control (MPC), robust control, adaptive control, fuzzy control, disturbance rejection control, sliding mode control, prediction-based model-free control as well as deep learning and reinforcement learning-based controls. The paper [
2] proposes a robust model predictive current control method based on nonlinear extended state observation to enhance the control performance of PMSM in the presence of parameter variations. The paper [
3] presents a robust adaptive model predictive speed control method based on recurrent neural network to tackle the speed control problem of permanent magnet synchronous motors under parameter mismatch conditions.
The paper [
4] presents a universal control framework that utilizes an observer to estimate both the system state and disturbances, while establishing a predictive current controller based on an enhanced system model. The paper [
5] introduces a motor-parameter-free model predictive voltage control strategy for permanent magnet synchronous motor drive systems. Its fundamental concept aims at reducing dependence on motor parameters in PMSM control, thus enhancing the robustness of this control strategy. The literature [
6,
7,
8,
9,
10] employs the MPC algorithm to mitigate torque fluctuations in PMSM drive systems induced by interturn faults (ITF). It simplifies the complexity of control methods for PMSM drives considering ITF by incorporating an adaptive compensation current approach.
In the field of robust adaptive control, the compensator based on the extended state observer proposed in reference [
11] effectively addresses the issue of excessively high switching gains required for disturbance rejection. Reference [
12] introduced a system transformation method that effectively converts a PMSM system with current constraints into an unconstrained system, thereby streamlining the controller design process. Reference [
13] proposed an observer scheme utilizing neural networks along with a sensorless robust optimal control approach to address the speed and current tracking challenges in partially unknown PMSM systems under disturbances and saturation voltages. The paper [
14] integrates the adaptive integral sliding mode method and employs a self-regulation approach to adjust the amplitude of the sliding mode function as well as compensate for load disturbances, thereby enhancing the dynamic performance of the system. The paper [
15,
16,
17,
18,
19] utilizes deep reinforcement learning(DRL) to solve the control problem of PMSM. By introducing artificial intelligence algorithms into the traditional parameter optimization process, a DRL model is constructed that can automatically optimize and adjust parameters in different application scenarios, thereby achieving optimal control effects in various environments.
In the domain of prediction-based control strategies, reference [
20] introduces an advanced model-free active disturbance rejection dead-zone predictive current control approach specifically designed for permanent magnet synchronous motors. This approach is based on a data-driven methodology, aiming to address the issue of parameter mismatch in dead-zone prediction current control and improve the performance of PMSM control systems. The paper [
21] introduces a model-free predictive current control drive system that incorporates an extended Kalman filter to address performance degradation in model predictive control due to variations in motor parameters. The paper [
22] introduces a model-free predictive current control strategy for the drive system of PMSM in electric vehicles. This innovative approach effectively mitigates performance limitations caused by inaccurate inertia estimation through real-time dynamic adjustment of inertia parameters. The paper [
23] presents a novel speed control strategy that combines an adaptive speed controller with a radial basis function neural network for precise speed regulation of PMSM. This approach effectively mitigates the impact of parameter uncertainties and load variations on system performance. The paper [
24] utilizes a linear-nonlinear switching active disturbance rejection control strategy to design speed and current controllers for PMSM in servo systems, aiming to improve the disturbance rejection performance of the PMSM speed and current controllers. The paper [
25] presents an optimal tracking control strategy for PMSM systems characterized by partially unknown dynamics, voltage saturation, and varying speed and current. By integrating an advanced feedforward control input, the conventional velocity and current tracking challenges are redefined as novel optimal control problems within a cascaded framework. Experimental results demonstrate that both tracking, and approximation errors are uniformly bounded.
In the vector control system of a three-phase PMSM, the conventional PI regulator is widely adopted as the speed controller due to its simplicity and robustness. However, the PMSM exhibits nonlinear dynamics and strong coupling among multiple variables. In the presence of external disturbances or variations in internal parameters, the traditional PI control method struggles to meet stringent control requirements. To improve the dynamic performance of the PMSM speed regulation system, it is crucial to implement a control strategy that remains insensitive to external disturbances and parameter changes while ensuring rapid response and high accuracy. Furthermore, achieving high-performance control for a PMSM requires precise rotor position and speed information within the magnetic field-oriented vector control framework. The use of mechanical sensors for this purpose, however, increases system cost, size, and weight, and imposes strict operating environment constraints. Sensorless control technology addresses these challenges by monitoring electrical signals within the motor windings and employing advanced algorithms to accurately estimate rotor position and speed, thereby enhancing the robustness and reliability of the PMSM vector control system. This paper introduces an energy-optimized speed control algorithm based on the TD3 for PMSM drive systems. The main contributions are summarized as follows.
●The TD3-based optimal control reduces the design difficulty of the speed tracking controller for nonlinear PMSMs.
●Adding energy consumption optimization control to the traditional control objective of steady, accurate and fast effectively improves the efficiency of the motor.
●The better generalization of the algorithm enables the motor to exhibit better control performance under different operating conditions.
2. Description of the Control Problem
2.1. Control Cbject Model
The motion equation of PMSM can be described as follows:
Among them,
,
,
and
represent the mechanical angular velocity, moment of inertia, damping coefficient, and load torque of the motor respectively. To facilitate controller design in a synchronous rotating coordinate system
for PMSM models are commonly established. The stator voltage equation can be expressed as equation (3).
The stator magnetic flux equation is given by equation (4).
The substitution of equation (4) into equation (3) yields the stator voltage equation as (5).
Among them:
are the components of the stator voltage on the
axis, while
are the components of the stator current on the
axis,
represents the stator resistance.
are the X-axis components of the stator magnetic flux.
represents the angular velocity of electricity,
are the inductance components of the
axis,
represents the magnetic flux of a permanent magnet. In addition, it is important to pay attention to the relationship between variables in equation (6) when constructing a PMSM simulation model.
Where:
represents the mechanical angular velocity of the motor (
), and
represents the motor speed (
). The common methods of traditional vector control include
control and maximum torque current ratio control,The control method where the
-axis inductance of surface-mounted PMSM is equal, i.e.,
and
, is mainly applicable to three-phase surface-mounted PMSMs. In this case, equation (2) can be rewritten as equation (7).
For surface-mounted three-phase PMSM, control and maximum torque current ratio control are equivalent.
2.2. Speed Loop Control
Assuming the motor starts with no load, i.e.,
, when adopting control strategy
, the active damping is defined as equation (8).
The combination of equation (1) and equation (2) yields equation (9), thereby establishing a comprehensive relationship.
Reposition the poles of equation (9) at the desired closed-loop bandwidth
, and apply a Laplace transform to derive the transfer function representing motor speed in relation to shaft current as equation (10).
The
represents the desired bandwidth of the speed control loop. The coefficient
of active damping, as derived from the comparison between equation (9) and equation (10), is presented in equation (11).
The speed loop controller can be mathematically represented as equation (12) when employing a conventional PI controller.
Where .
2.3. Current Loop Control
The current equation for the
-axis, which corresponds to equation (13), can be obtained by rewriting equation (5).
The complete decoupling of
and
yields equation (14).
The substitution of equation (5) into equation (14) results in the derivation of equation (15).
where
are the
-axis and
-axis voltages after current decoupling, respectively. Using the conventional PI controller and combining with the feed-forward decoupling control strategy, the
-axis voltage can be obtained as Eq. (16).
where is the proportional gain of the PI regulator and is the integral gain of the PI regulator.
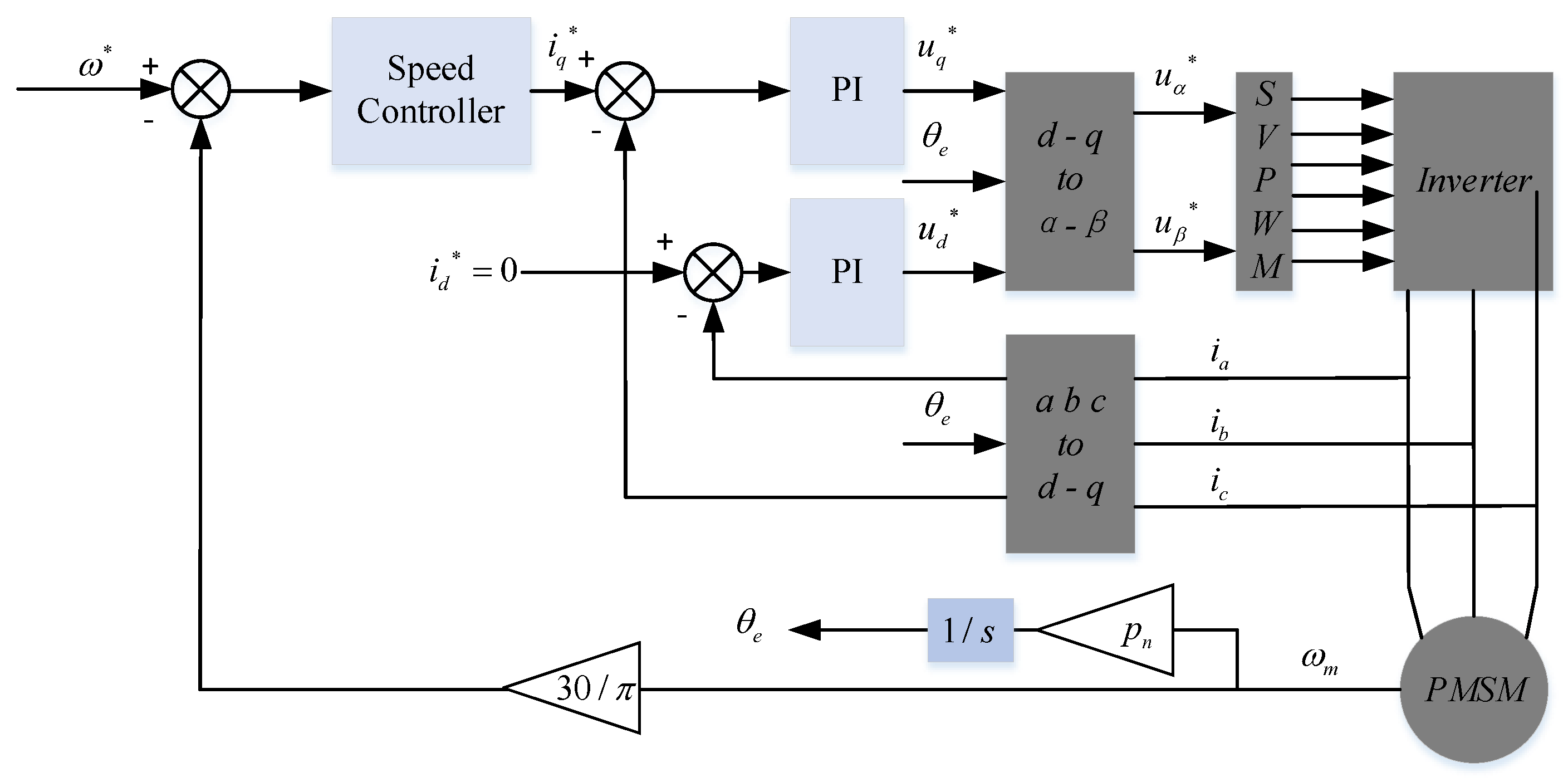
The block diagram in
Figure 1 illustrates the three-phase PMSM vector control employing the method with
. It is evident from the figure that three-phase PMSM vector control primarily comprises of three components, namely a speed loop PI controller, a current loop PI controller, and the Space Vector Pulse Width Modulation (SVPWM) algorithm.
3. TD3 OF PMSM
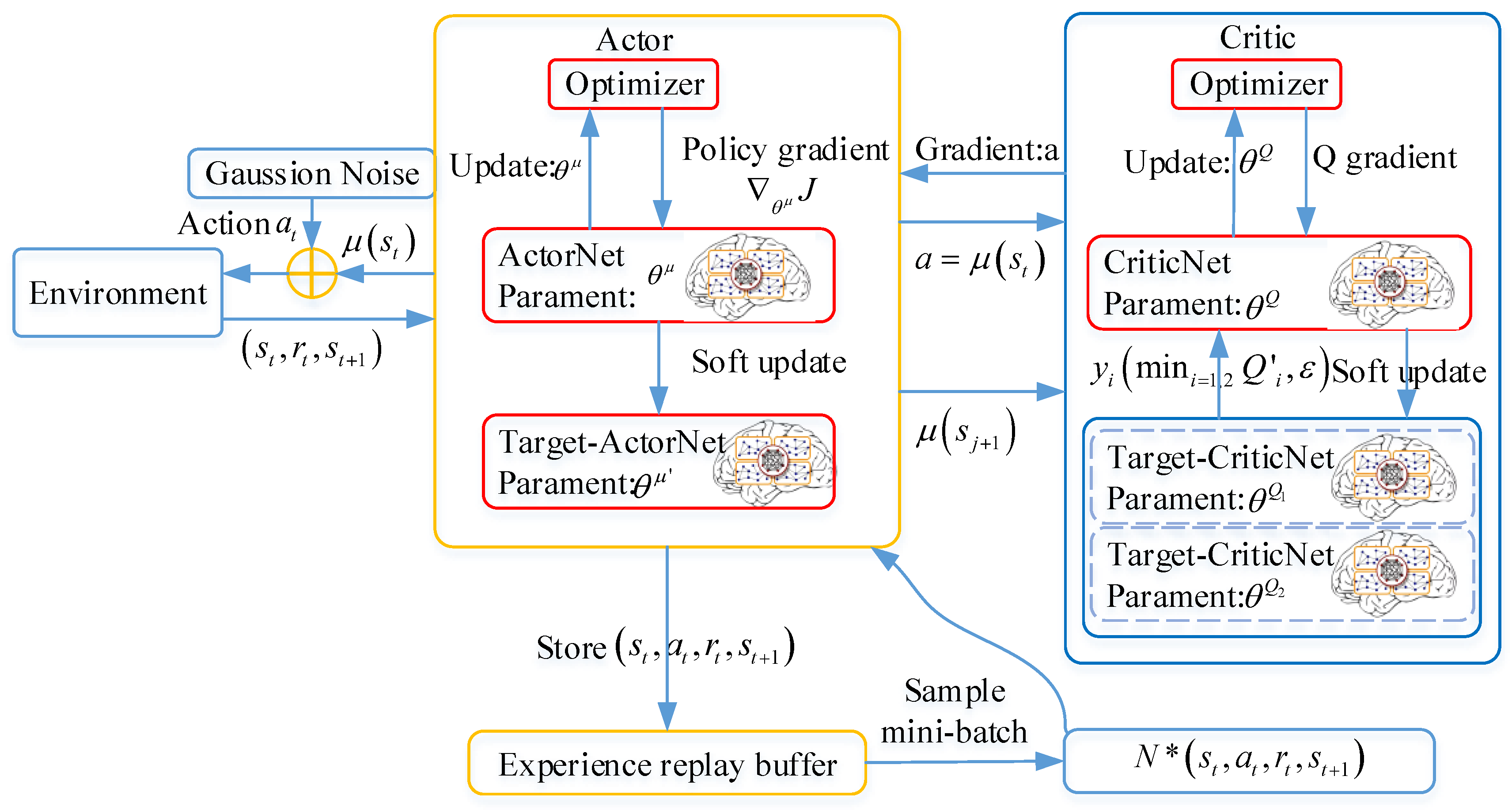
The TD3 algorithm proposes three key enhancement techniques based on the -deep deterministic policy gradient(DDPG) algorithm, as delineated below. (1)Double network refers to the utilization of two Critic networks, wherein the smaller one is employed for computing the target value in order to mitigate potential issues related to overestimation.(2)Target policy smoothing regularization: Incorporate perturbations to the action in the subsequent state while calculating the target value, aiming to enhance the precision of value evaluation.(3) Following multiple updates of the Critic network, subsequent updates are made to the Actor network to enhance training stability.
Figure 2 shows the structure of TD3 algorithm.
The update process of the TD3 algorithm is not significantly different from that of the DDPG algorithm, except for the distinction in how the target values are computed. The Actor network updates by maximizing the cumulative expected return through deterministic policy gradient, while both Critic1 and Critic2 networks update by minimizing the error between the evaluation value and the target value using mean squared error. All target networks are updated using an exponential moving average (EMA) soft update method. During the training phase, a batch of data is sampled from the Replay Buffer with a specific batch size. Assuming one sample is denoted as
, the update process for all networks follows. The updating procedure for Critic1 and Critic2 networks entails employing the Target Actor network to calculate the action
in state
. Subsequently, target policy smoothing regularization is implemented, and noise
is incorporated into the target action
.
Building upon the concept of dual networks, equation (18) is employed for the computation of the target value
.
The gradient descent algorithm is ultimately employed to minimize the error between the evaluation value and the target value, thereby facilitating parameter updates in both Critic1 and Actor network update process.
After updating the Critic1 and Critic2 networks for d steps, initiate an update of the Actor network) Employ the Actor network to compute action for state . Where .
It is crucial to emphasize that there is no necessity to introduce noise after computing the action, as our objective is for the Actor network to update towards the direction of maximum value. Adding noise would be inconsequential in this context. Subsequently, we employ either Critic1 or Critic2 network to assess the state-action pair, assuming utilization of Critic1 network . The optimization is ultimately achieved by employing a gradient ascent algorithm to facilitate updates in the Actor network.
The target network is updated using a soft update method, wherein a learning rate
is introduced to calculate the weighted average between the old parameters of the target network and their corresponding new parameters. Subsequently, these averaged parameters are assigned to the target network (equation 20).
where
, The value of t is usually set to 0.005. The reward at each time step is:
Here, are the coefficients of each term, is the d-axis current error, is the q-axis current error, are the actions from the previous time step.
4. Results and Analysis
The parameters of the motor utilized in the simulation presented in this paper are detailed in
Table 1.
In this article, simulation experiments and data analysis employ per unit (pu) values. Per unit values are a dimensionless indicator commonly utilized in power systems to represent the ratio between actual values and reference values. This enables relative comparisons among different systems, electrical quantities, or engineering parameters, facilitating quantitative analysis and research. The reference values used in this article can be found in
Table 2.
To evaluate the effectiveness and robustness of the algorithm, simulation experiments were conducted under two representative PMSM operating conditions.
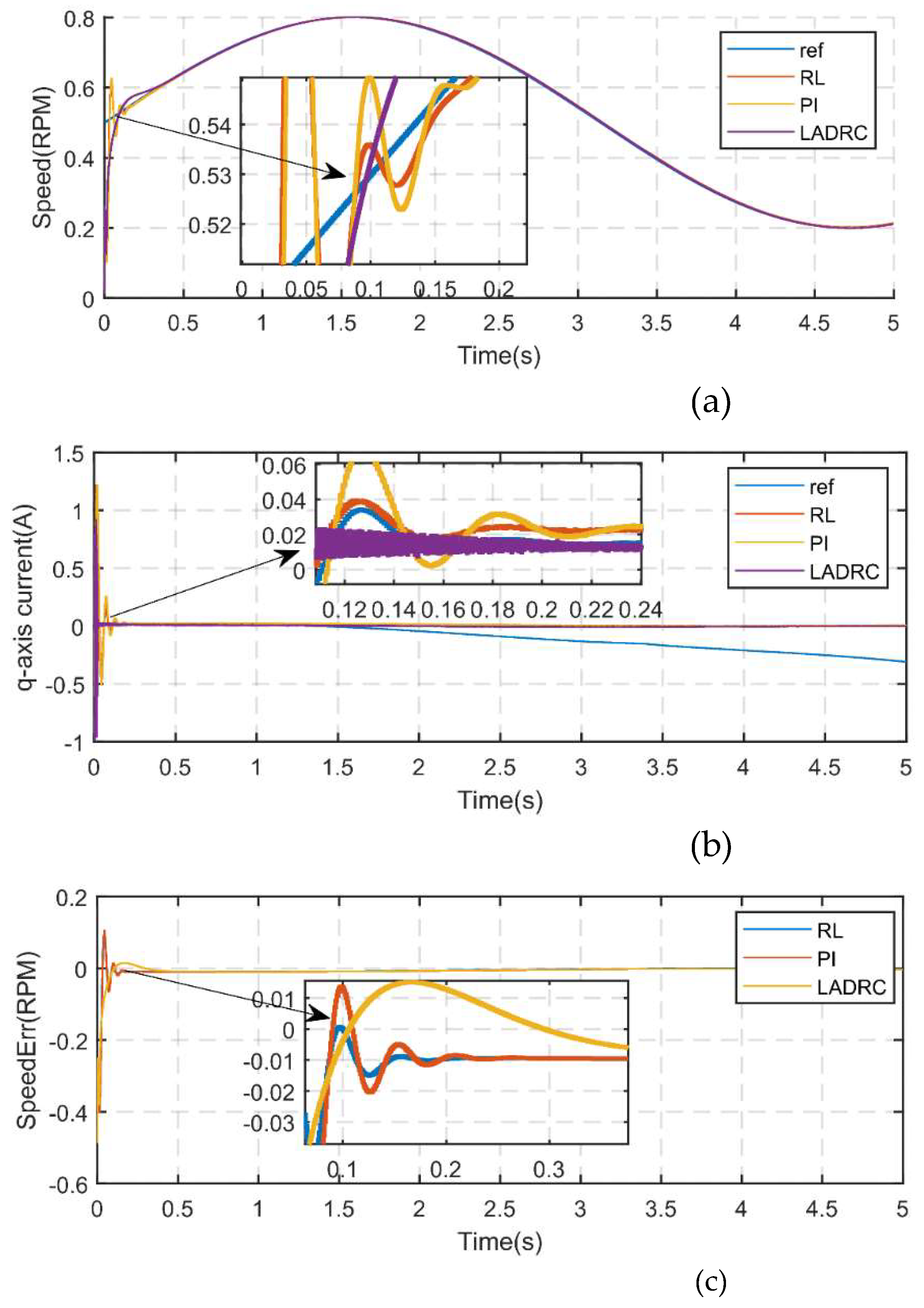
Working condition 1. PMSM load is constant, the starting moment is given 0.5pu, the reference speed trajectory is a sinusoidal signal,
, no-load startup, the experimental results are shown in
Figure 3.
From
Figure 3(a), it is evident that the TD3 algorithm of this design achieves faster tracking of the upper reference trajectory speed with minimal overshoot compared to the other controllers. The traditional PI controller exhibits significant overshoot, whereas the LADRC controller requires a longer time to reach steady state. From
Figure 3(b), it can be observed that the TD3-based controller stabilizes the q-axis current closer to the reference value more rapidly and with less fluctuation. In contrast, the PI controller shows substantial overshoot, and the LADRC controller experiences greater fluctuations. From
Figure 3(c), it is clear that the TD3 algorithm, as a reinforcement learning approach, demonstrates the smallest speed tracking error and superior stability.
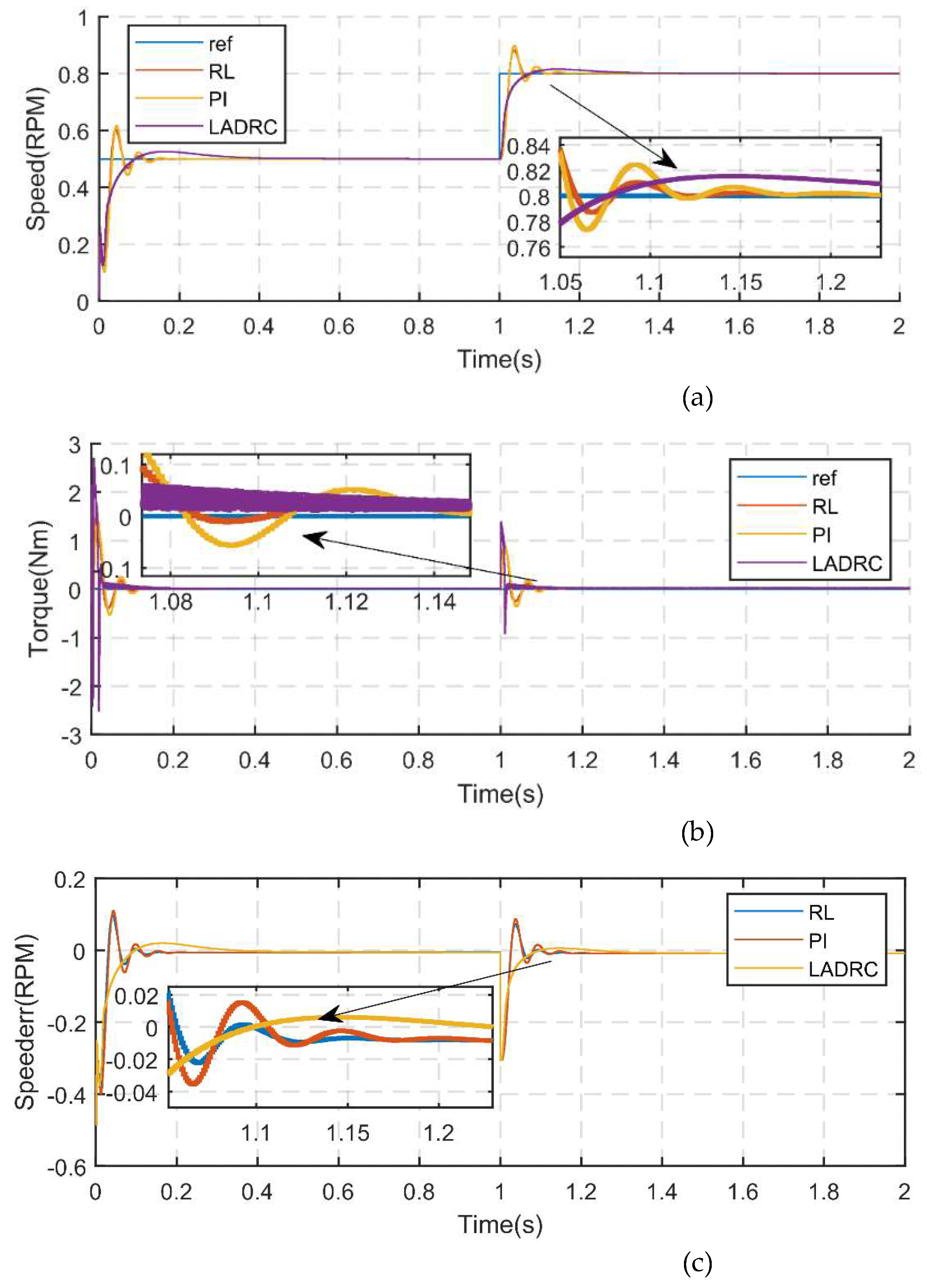
Working condition 2. The PMSM speed is suddenly increased, the load is constant, the given speed is 0.5pu at the starting moment, and it is suddenly changed to 0.8pu at 1 second, and the no-load is started, the experimental results are shown in
Figure 4.
From
Figure 4(a), it is evident that the controller using the LADRC algorithm exhibits the smallest overshoot but requires the longest time to reach steady state. In contrast, the RL algorithm achieves the fastest return to steady state with significantly less overshoot compared to the PI algorithm. From
Figure 4(b), it can be observed that the torque fluctuation caused by a sudden change in rotational speed is also minimized. Furthermore, as shown in
Figure 4(c), the proposed algorithm demonstrates the smallest overall rotational speed tracking error.
Table 3 summarizes the performance comparison of the three algorithms over a 1-second period.
From
Table 3, it is evident that the RL algorithm demonstrates superior adaptability to sudden speed changes. It can rapidly return to a steady state, with the overshoot remaining within an acceptable range.
5. Conclusions
The PMSM drive system is a typical dual time-scale system characterized by control challenges such as parameter variations, external disturbances, and nonlinearities. In this paper, we propose a TD3-based optimal control method aimed at minimizing the energy consumption of PMSM drive systems. We conduct simulation experiments under two typical operating conditions to validate the effectiveness and robustness of the proposed algorithm. The experimental results demonstrate that the TD3 algorithm surpasses both the traditional PI controller and the linear active disturbance rejection control (LADRC) algorithm in terms of reference trajectory tracking accuracy, q-axis current regulation, and speed tracking error minimization. This study offers a novel approach to PMSM drive system control, significantly enhancing motor efficiency and system robustness through the integration of deep reinforcement learning.
Author Contributions
Conceptualization, Y.Z. (Yingjie Zhang); methodology, and writing—original draft preparation, Z.H.; software, M.L.; validation, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was jointly funded by National Key Research and Development Program of China, grant number 2019YFE0105300, Hunan Provincial Regional Joint Fund Project, grant number 2024JJ7179
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Krishnan R. Electric Motor Drives: Modeling, Analysis, and Control. Upper Saddle River, NJ, USA: Prentice-Hall, 2001.
- Zhang Z.; Liu Y.; Liang X.; Guo H. and Zhuang X. Robust Model Predictive Current Control of PMSM Based on Nonlinear Extended State Observer. IEEE Journal of Emerging and Selected Topics in Power Electronics. 2023, 11,862-873. [CrossRef]
- Yang C.; Meng F.; Zhang H.; Zhao J.; Wang H. and Zhou L. Optimal Coordinated Control for Speed Tracking and Torque Synchronization of Rigidly Connected Dual-Motor Systems. IEEE/ASME Transactions on Mechatronics. 2023,28, 2609-2620. [CrossRef]
- Li X.; Tian W.; Gao X. A Generalized Observer-Based Robust Predictive Current Control Strategy for PMSM Drive System. IEEE Transactions on Industrial Electronics. 2022,69-2. [CrossRef]
- Wang Y.; Fang S.; Hu J. and Huang D. A Novel Active Disturbance Rejection Control of PMSM Based on Deep Reinforcement Learning for More Electric Aircraft. IEEE Transactions on Energy Conversion. 2023,38,1461-1470. [CrossRef]
- Wang Y.; Fang S. and Hu J. Active Disturbance Rejection Control Based on Deep Reinforcement Learning of PMSM for More Electric Aircraft. IEEE Transactions on Power Electronics. 2023,38,406-416. [CrossRef]
- Jiang X.; Yang Y.; Fan M.; Ji A. et al. An Improved Implicit Model Predictive Current Control With Continuous Control Set for PMSM Drives. IEEE Transactions on Transportation Electrification. 2022,8,2444-2455. [CrossRef]
- Xu B.; Jiang Q.; Ji W. and Ding S. An Improved Three-Vector-Based Model Predictive Current Control Method for Surface-Mounted PMSM Drives. IEEE Transactions on Transportation Electrification. 2022,8,4418-4430. [CrossRef]
- Wang X. et al. Fault-Tolerant Control of Common Electrical Faults in Dual Three-Phase PMSM Drives Fed by T-Type Three-Level Inverters. IEEE Transactions on Industry Applications. 2021,57,481-491. [CrossRef]
- Sun Z.; Deng Y.; Wang J.; Yang T.; Wei Z. and Cao H. Finite Control Set Model-Free Predictive Current Control of PMSM With Two Voltage Vectors Based on Ultralocal Model. IEEE Transactions on Power Electronics. 2023,38,776-788. [CrossRef]
- Ma Y.; Li D.; Li Y. and Yang L. A Novel Discrete Compound Integral Terminal Sliding Mode Control With Disturbance Compensation For PMSM Speed System. IEEE/ASME Transactions on Mechatronics. 2022,27,549-560. [CrossRef]
- Zhang J.; Ren W. and Sun X. Current-Constrained Adaptive Robust Control for Uncertain PMSM Drive Systems: Theory and Experimentation. IEEE Transactions on Transportation Electrification. 2023,9,4158-4169. [CrossRef]
- Tan L.; Cong T. and Cong D. Neural Network Observers and Sensorless Robust Optimal Control for Partially Unknown PMSM With Disturbances and Saturating Voltages. IEEE Transactions on Power Electronics. 2021,36,12045-12056. [CrossRef]
- Li Z.; Wang F.; Ke D.; Li J. and Zhang W. Robust Continuous Model Predictive Speed and Current Control for PMSM With Adaptive Integral Sliding-Mode Approach. IEEE Transactions on Power Electronics. 2021,36,14398-14408. [CrossRef]
- Wang Y.; Fang S.; Hu J. and Huang D. A Novel Active Disturbance Rejection Control of PMSM Based on Deep Reinforcement Learning for More Electric Aircraft. IEEE Transactions on Energy Conversion. 2023,38,1461-1470. [CrossRef]
- Wang Y.; Fang S. and Hu J. Active Disturbance Rejection Control Based on Deep Reinforcement Learning of PMSM for More Electric Aircraft. IEEE Transactions on Power Electronics. 2023,38,406-416. [CrossRef]
- Zhao J.; Yang C.; Gao W. and Zhou L. Reinforcement Learning and Optimal Control of PMSM Speed Servo System. IEEE Transactions on Industrial Electronics. 2023,70,8305-8313. [CrossRef]
- Attestog S.; Senanayaka J.; Khang H. and Robbersmyr K. Robust Active Learning Multiple Fault Diagnosis of PMSM Drives With Sensorless Control Under Dynamic Operations and Imbalanced Datasets. IEEE Transactions on Industrial Informatic. 2023,19,9291-9301. [CrossRef]
- Wang Y.; Fang S.; Hu J. and Huang D. Multiscenarios Parameter Optimization Method for Active Disturbance Rejection Control of PMSM Based on Deep Reinforcement Learning. IEEE Transactions on Industrial Electronics. 2023,70,10957-10968. [CrossRef]
- Wang Y.; Fang S. and Huang D. An Improved Model-Free Active Disturbance Rejection Deadbeat Predictive Current Control Method of PMSM Based on Data-Driven. IEEE Transactions on Power Electronics. 2023, 38, 9606-9616. [CrossRef]
- Luo L.; Huang W.; Huang M. and Fan Q. Model-Free Predictive Current Control of Sensorless PMSM Drives with Extended Kalman Filter. In 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 2023, 2369-2374. [CrossRef]
- Wei Y.; Men S.; Wei Y.; Qi H. and Wang F. A Model-Free Predictive Current Control for PMSM Driving System of EV with Adjustable Low Inertia. In 2022 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Haining, China, 2022, 1-7. [CrossRef]
- Jie H.; Zheng G.; Zou J.; Xin X. and Guo L. Speed Regulation Based on Adaptive Control and RBFNN for PMSM Considering Parametric Uncertainty and Load Fluctuation. IEEE Access. 2020, 8, 190147-190159. [CrossRef]
- Lin P.; Wu Z.; Liu K. and Sun X. A Class of Linear–Nonlinear Switching Active Disturbance Rejection Speed and Current Controllers for PMSM. IEEE Transactions on Power Electronics. 2021, 36, 14366-14382. [CrossRef]
- Tan L. and Pham T. Optimal Tracking Control for PMSM With Partially Unknown Dynamics, Saturation Voltages, Torque, and Voltage Disturbances. IEEE Transactions on Industrial Electronics. 2022, 69, 3481-3491. [CrossRef]
- Vrabie D.; Vamvoudakis K.; Lewis F. Optimal Adaptive Control and Differential Games by Reinforcement Learning Principles. IEEE Control Systems, 2014, 34, 80-82. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).