Ultra-Local Model-Based Adaptive Enhanced Model-Free Control for Pmsm Speed Regulation

1. Introduction

Permanent magnet synchronous motor (PMSM) offer high power density, efficiency, and low maintenance, making them widely used in applications such as radar, photoelectric detection systems [1]. In PMSM speed control system, a double closed-loop structure is commonly used, consisting of an outer speed loop and an inner current loop. The speed controller plays a key role in ensuring precise speed tracking and effective suppression of load disturbances.

Proportional-integral (PI) control is widely used in PMSM drive systems due to its simplicity, clarity, and effectiveness [2,3]. However, practical challenges such as motor parameter uncertainties, and unknown load disturbances limit its speed control performance. To address these issues, advanced control methods, including internal model control [4], sliding mode control [5], adaptive control [6], fuzzy control [7], and model predictive control (MPC) [8], have been applied to speed loops.

A key challenge in sliding mode control is the buffeting phenomenon caused by high-frequency switching. High-order sliding mode control techniques have been developed to mitigate this issue [9]. Adaptive sliding modes enhance the robustness of the system in the face of uncertainty and parameter variations, but increase the complexity and computational effort of the system [10]. Adaptive control is more complex than traditional methods, and although adaptive controllers can gradually adapt to changes in parameters, they often struggle to respond quickly to sudden changes [11,12].

Disturbance/uncertainty estimation and attenuation (DUEA) [13] control enhances system robustness by estimating and compensating for disturbances and uncertainties in real time. Since the 1960s, various DUEA techniques based on different estimation methods have been developed. Among these, disturbance observer-based control (DOBC) and extended state observer-based control (ESOC, known as ADRC) are the most widely studied and applied in AC motor drives. As a key component of DOBC, DOB was first proposed by Ohnishi [14] in the 1980s to enhance the disturbance rejection capability and robustness of DC motor drives. In DOBC, the disturbances/uncertainties are estimated by the observer and compensated by the estimated disturbances/ uncertainties [15,16]. ADRC was introduced by Han in the 1990s as a practical control method to replace classical PID controllers [17]. To simplify ADRC design, a linear extended state observer (LESO) is proposed [18]. LESO is often combined with other control methods, and the robustness of PMSM system can be improved by feedforward compensation of lumped disturbance estimated by LESO [19,20].

Recently, ultra-local model (ULM)-based model-free control (MFC), proposed by Fliess and Join [21], has gained significant attention in areas such as PMSM, autonomous vehicle trajectory, and energy system management. MFC is a control strategy that does not require a precise mathematical model of the system, but uses the input and output data of the system to adjust in real time. Compared to ADRC, MFC has fewer control parameters and does not need knowledge of the system’s order. In [22], a model-free control strategy based on ultra-local models is proposed for current control in PMSM and later extended to speed control [23]. However, both methods face issues with complex lumped disturbance estimation and long computation times. To address this, a new observer was designed based on the model-free current control strategy for PMSM, which significantly reduces design parameters and computational complexity [24,25,26]. MFC has some limitations, including its reliance on data quality. Since MFC depends on real-time data, it is sensitive to measurement noise and sensor accuracy. Inaccurate or noisy data can reduce performance and potentially lead to system instability or loss of control accuracy.

The control gain $\alpha$ in the ULM serves as a critical parameter determining closed-loop system performance. In ULM-based model-free control, $\alpha$ appears in the denominator of the control law. Too small an $\alpha$ value may induce tracking error oscillations and control input chattering, while an excessively large $\alpha$ can degrade control precision. Consequently, developing effective gain tuning strategies for ULM-based model-free control remains crucial [27]. To enhance ULM control performance, several variable-gain model-free approaches have been developed [28,29]. For instance, an online method was proposed to estimate the control gain using previous-step command signals [28]. Alternatively, in [29], the differential Riccati equation used for online gain adaptation was introduced. While these adaptive techniques have improved the overall performance of model-free control, the systematic tuning of gains for optimal performance requires further investigation.

In this study, the Nonlinear Disturbance Observer (NDO) and PD control law were integrated into a generalized model-free feedback controller to enhance the speed regulation performance of PMSMs. An $\alpha$-adaptive method based on gradient descent was developed to achieve optimal tracking performance, while a parameter estimation approach was designed to optimize the selection of $\alpha$’s initial value. These methodologies collectively enabled the proposed controller to achieve superior performance through accurate lumped disturbance estimation, input gain adaptation, and rapid response times.The main contributions of this work are summarized as follows:

• Compared to conventional lumped disturbance estimation methods, the incorporation of NDO eliminated steady-state errors caused by load torque variations. The integration of PD control law into the generalized model-free controller effectively reduced speed overshoot, while the dead-zone method mitigated control signal oscillations induced by sensor noise.
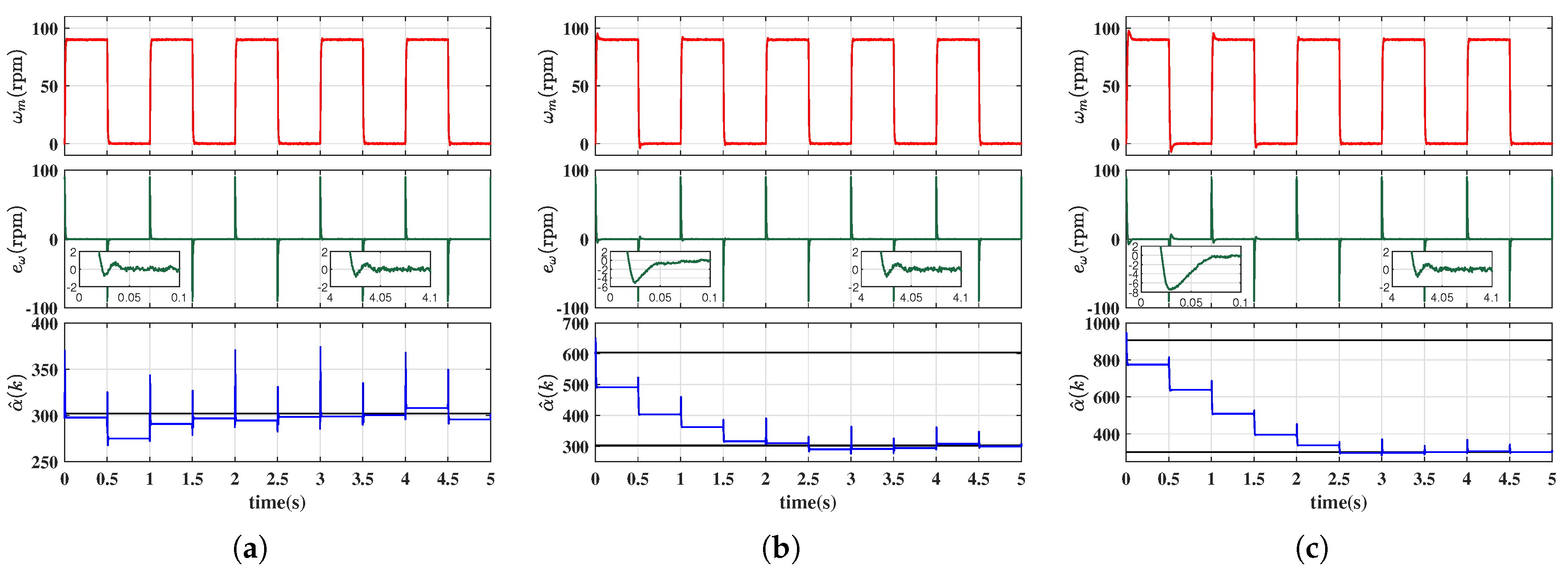
• The proposed $\alpha$ online adaptive estimation law ensured rapid convergence to the true $\alpha$ value, significantly improving speed tracking accuracy.
• The algebraic framework-based linear parameter identification method enabled high-precision estimation of the true $\alpha$ value, eliminating arbitrariness in initial value selection and enhancing transient performance during startup phases.

The remainder of this paper is structured as follows: Section 2 presents the PMSM dynamic model and conventional model-free speed control strategies. Section 3 details the novel enhanced model-free speed control (EMFSC) framework and the proposed input gain identification methodology. Comparative analysis of simulation and experimental results is provided in Section 4. Finally, the conclusions are presented in Section 5.

2. Conventional Model-Free Speed Control Based on Ultra-local Model

2.1. Mathematical Model of SMPMSM Direct Drive System

Considering the parametric uncertainties and unknown external disturbance, the electromechanical equation of PMSM complex direct drive system is given as

$$\left\{\begin{array}{c}{J}_n{\displaystyle \frac{d{\omega }_m}{dt}}=T_e-T_L-B_n{\omega }_m-d_n-f_t,\hfill \\ T_e={\displaystyle \frac{3n_p}{2}}({\phi }_n{i}_q+(L_d-L_q)i_d{i}_q),\hfill \end{array}\right.$$

(1)

where ${\omega }_m$ is rotor mechanical rotational speed; $J_n$ and $B_n$ express the nominal values of rotational inertia and the friction coefficient, respectively; $T_e$ stands for the electromagnetic torque; $T_L$ denotes the load torque; $d_n$ is the constant disturbance; $f_t$ express disturbance induced by the parametric uncertainties and other unknown disturbance; $n_p$ is the pole pair number; ${\phi }_n$ express the nominal values of permanent-magnet flux linkage; $i_d$ and $i_q$ represent d- and q-axes currents, respectively; $L_d$ and $L_q$ are the stator inductances of the d- and q-axes, respectively.

For the surface-mounted PMSM, the d- and q-axes inductances are equal ($L_d=L_q$). Then, the electromagnetic torque $T_e$ can be represented as follows:

$$T_e={\displaystyle \frac{3n_p{\phi }_n{i}_q}{2}}.$$

(2)

From Equation (1), the motion dynamics can be expressed as

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\omega }_m}{dt}}=& {\displaystyle \frac{1}{J_n}}{T}_e+{\displaystyle \frac{1}{J_n}}\left(-T_L-B_n{\omega }_m-d_n-f_t\right)\hfill \\ \hfill =& {\displaystyle \frac{3n_p{\phi }_n}{2J_n}}{i}_q+{\displaystyle \frac{1}{J_n}}\left(-T_L-B_n{\omega }_m-d_n-f_t\right).\hfill \end{array}$$

(3)

2.2. Principle of Conventional ULM-Based Model-Free Control

The first-order ultra-local model of a single-input single-out system is expressed as [21]

$$\dot{y}=F+\alpha u,$$

(4)

where y and u are output and control variables, respectively; $\alpha$ represents a nonphysical scaling factor selected by the designer; and F represents the known and unknown part of the system. Defining tracking error $e=y_d-y$, the error dynamic can be gotten as

$$\dot{e}={\dot{y}}_d-F-\alpha u,$$

(5)

where $y_d$ is the desired output. To converge the tracking error e, a generalized model-free feedback controller is proposed as

$$u={\displaystyle \frac{-F+{\dot{y}}_d+C\left(e\right)}{\alpha }},$$

(6)

where $C\left(e\right)$ denotes the error convergence law.

In [23], the principle of model-free control based on ultra-local model with algebraic parameter identification is applied to the speed control of a SMPMSM drive and the corresponding controller is called "conventional MFSC" (MFSC-API). The reference of torque is calculated as

$$T_e^{*}\left(k\right)={\displaystyle \frac{-{\widehat{F}}_{\Omega }\left(k\right)+{\dot{\omega }}_m^{*}\left(k\right)+K_{p}e\left(k\right)}{{\alpha }_{\Omega }}},$$

(7)

where ${\widehat{F}}_{\Omega }\left(k\right)$ donates the estimated value of the lumped disturbance $F_{\Omega }\left(k\right)$, ${\omega }_m^{*}\left(k\right)$ is the desired speed, the symbol "(k)" represents value of above variable at the (k)th control period, $K_P$ represents the parameter of the controller. For the mechatronic system described in (3), in the presence of a mismatch between the controller’s initial parameters and the true machine parameters, the lumped disturbance $F_{\Omega }$ can be mathematically characterized as

$$F_{\Omega }=({\displaystyle \frac{1}{J_n}}-{\alpha }_{\Omega })T_e+{\displaystyle \frac{1}{J_n}}\left(-T_L-B_n{\omega }_m-d_n-f_t\right).$$

(8)

Within a sufficiently "small" time interval, $F_{\Omega }\left(k\right)$ is treated as a constant parameter and estimated through an algebraic parameter identification technique (API) [30], expressed as:

$$\begin{array}{cc}\hfill {\widehat{F}}_{\Omega }\left(k\right)=& -{\displaystyle \frac{3}{T_F^3}}{\int }_0^{T_F}\left[\left(T_F-2\delta \right){\omega }_m\left(\delta \right)+{\alpha }_{\Omega }\delta \left(T_F-\delta \right)T_e^{*}\left(\delta \right)\right]d\delta \hfill \\ \hfill =& -{\displaystyle \frac{3}{n_F^3}}{T}_s\sum _{m=1}^{n_F}\left[\left(n_F-2\left(m-1\right)\right)\times {\omega }_m\left(m-1\right)\right.\hfill \\ \hfill & +{\alpha }_{\Omega }\left(m-1\right)T_s\left(n_F-\left(m-1\right)\right)\times T_e^{*}\left(m-1\right)\hfill \\ \hfill & \left.+\left(n_F-2m\right)\times {\omega }_m\left(m\right)+{\alpha }_{\Omega }m{T}_s\left(n_F-m\right)\times T_e^{*}\left(m\right)\right],\hfill \end{array}$$

(9)

where $T_F$ is the data window and $T_F=n_F{T}_s$; $n_F$ is the data window length; $\left[0,T_F\right]$ is a sliding data window.

According to the ultra-local model, $\alpha$ should be designed to keep $\dot{y}$ and $\alpha u$ in the same order of magnitude. The control performance of the system may be adversely affected by improper selection of the $\alpha$ parameter. Given this, the tuning of the input gain $\alpha$ has a significant impact on the stability and tracking accuracy of control system.

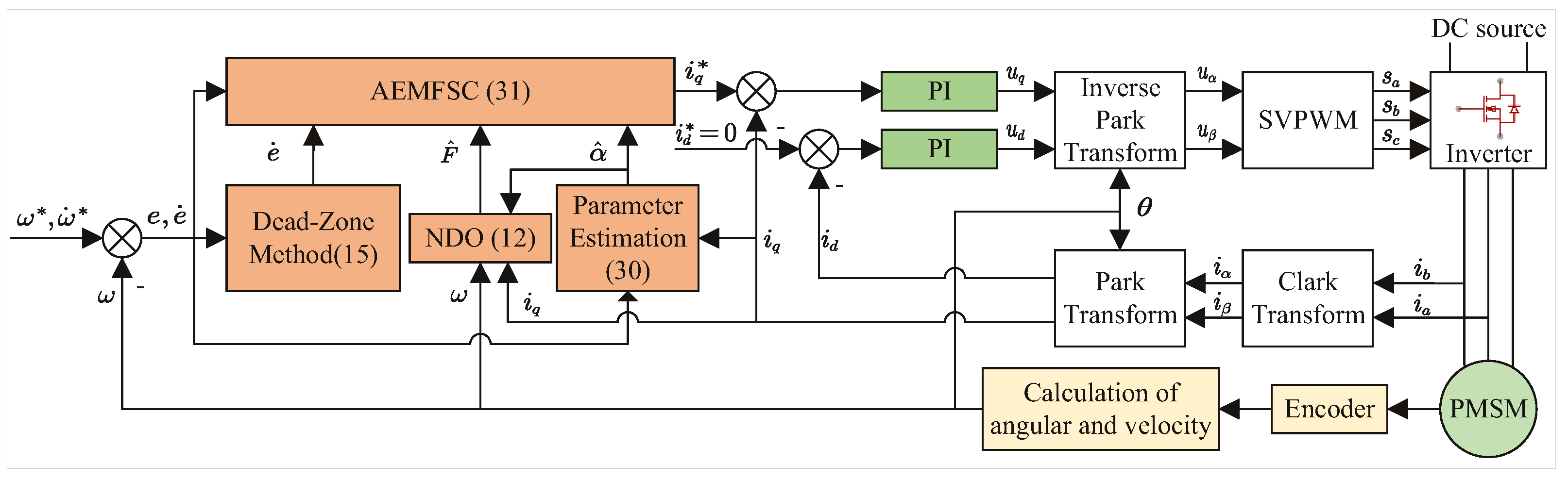
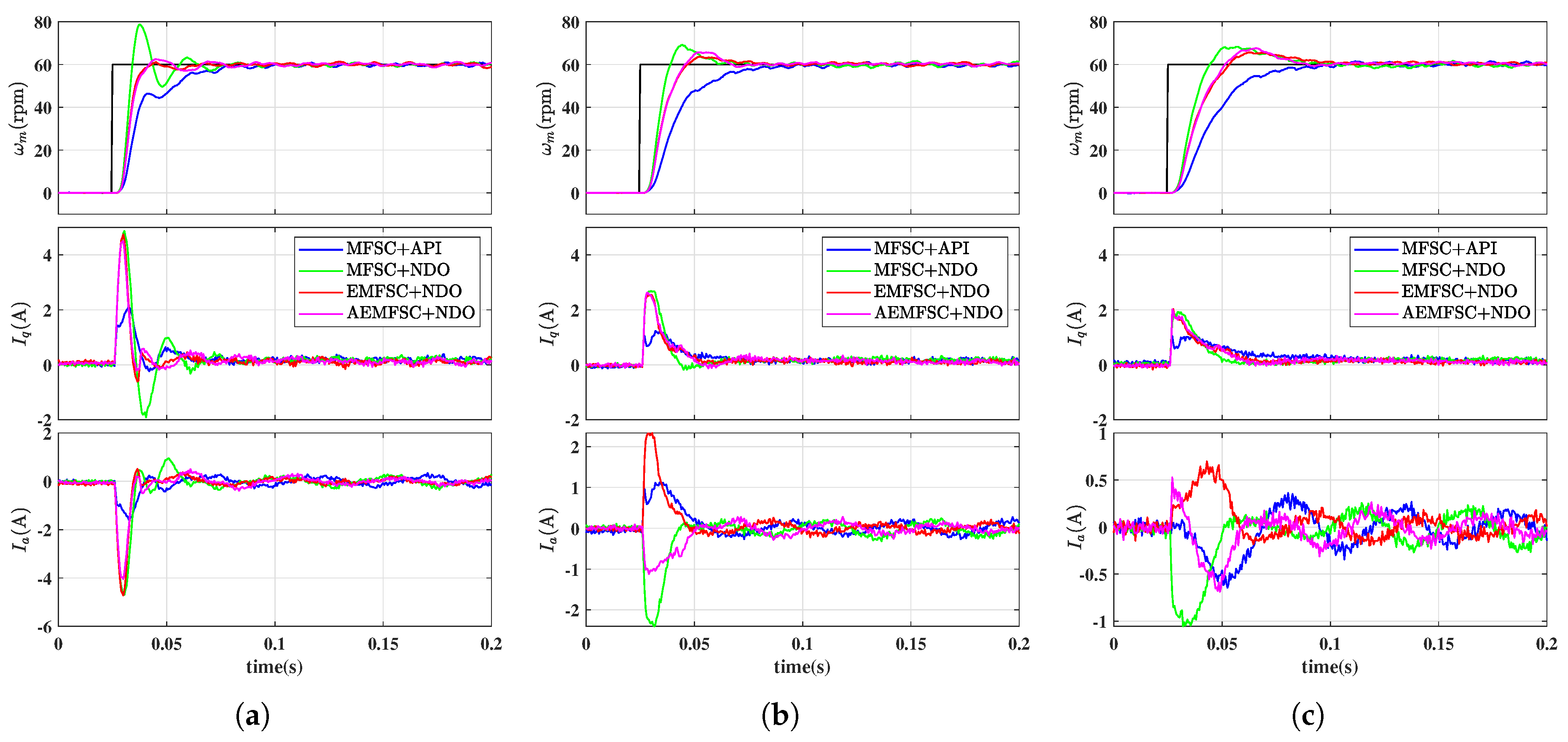
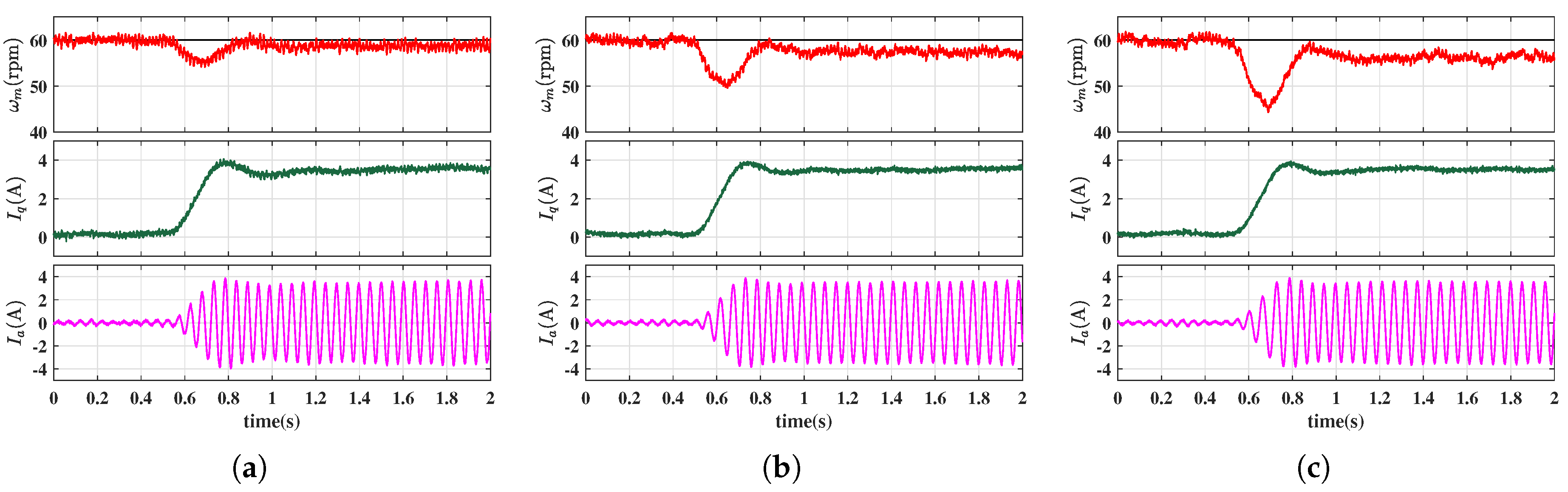
3. Principle of the Proposed AEMFSC-NDO

In this section, an adaptive enhanced model-free speed control framework based on the ultra-local model is developed. First, a nonlinear disturbance observer (NDO)-enhanced model-free controller (EMFSC-NDO) is developed by integrating a nonlinear disturbance observer with proportional-derivative (PD) control architecture. Subsequently, an adaptive law for the control input gain is derived via gradient descent method, resulting in an adaptive EMFSC-NDO method (AEMFSC-NDO). Finally, an initial value determination method for the control input gain is derived based on algebraic differentiation techniques.

3.1. Enhanced Model-Free Speed Control via Nonlinear Disturbance Observer

In this article, according to (3), considering the SMPMSM q-axis current as output variable, the ideal ultra-local mathematical model of SMPMSM can be expressed as

$$\dot{y}={\alpha }_{e}u+F_1,$$

(10)

where the output $y={\omega }_m$, the input $u=i_q$, the theoretical control gain ${\alpha }_e=3n_p{\phi }_n/\left(2J_n\right)$, and the lumped disturbance $F_1=\left(-T_L-B_n{\omega }_m-d_n-f_t\right)/J_n$.

The practical difficulty in obtaining accurate machine parameters leads to a parametric mismatch between the designed ultra-local model and the true system dynamics. Therefore, the practically realized ultra-local model takes the following form:

$$\dot{y}=\alpha u+F_2,$$

(11)

where the lumped disturbance $F_2=({\alpha }_e-\alpha )u+F_1$. With model (11) as the basis, the model-free feedback control scheme (6) is subsequently deployed. However, the existence of $F_2$ results in control law (6) not being implemented. To achieve precise and rapid real-time estimation of $F_2$, the nonlinear disturbance observer (NDO) is designed as follows [31]:

$$\left\{\begin{array}{c}\dot{Z}=-Lz-L(p+\alpha u)\hfill \\ p=Ly\hfill \\ {\widehat{F}}_2=Z+p.\hfill \end{array}\right.$$

(12)

where Z is an auxiliary variable, L is the positive gain of the nonlinear disturbance observer, ${\widehat{F}}_2$ is the estimated value of the lumped disturbance.

Take the derivative of the observer error ${\tilde{F}}_2=F_2-{\widehat{F}}_2$, and using (11), then yields

$$\begin{array}{cc}\hfill {\dot{\tilde{F}}}_2=& \dot{F_2}-{\dot{\widehat{F}}}_2\hfill \\ \hfill =& \dot{F_2}-(\dot{Z}+L\dot{y})\hfill \\ \hfill =& \dot{F_2}-(-L(z+Ly+\alpha u)+L(\alpha u+F_2))\hfill \\ \hfill =& \dot{F_2}-L(-{\widehat{F}}_2+F_2)\hfill \\ \hfill =& \dot{F_2}-L{\tilde{F}}_2.\hfill \end{array}$$

(13)

Considering that the total disturbance $F_2$ and ${\dot{F}}_2$ are bounded, which is ${lim}_{t\to \infty }{\dot{F}}_2=0$. According to the principle of Lyapunov function stability, the nonlinear disturbance observer system is progressively stable.

To enhance the transient tracking performance of the speed control system, a PD control law is employed to ensure the convergence of the tracking error. Therefore, the enhanced model-free controller is proposed as

$$u={\displaystyle \frac{-{\widehat{F}}_2+{\dot{y}}_d+k_{p}e+k_d\dot{e}}{\alpha }}.$$

(14)

where $k_p,k_d\in {\mathbb{R}}^{+}$ are the control parameters.

To prevent amplification of high-frequency noise in speed tracking error differentiation, which may cause control signal chattering and potential system instability, a dead-zone method is implemented in the controller. This approach suspends error derivative calculation when the error magnitude falls below a predefined threshold. Specifically, the dead-zone implementation follows as

$$\dot{e}\left(k\right)=\left\{\begin{array}{cc}{\displaystyle \frac{e\left(k\right)-e\left(k-1\right)}{T_s}},\hfill & \left|e\left(k\right)\right|⩾\delta \hfill \\ 0,\hfill & \left|e\left(k\right)\right|<\delta ,\hfill \end{array}\right.$$

(15)

where $\delta$ is the error threshold.

Taking the control law (14) into the tracking error dynamics (5) based on (10), one has the following error equation:

$$\begin{array}{cc}\hfill \dot{e}=& {\dot{y}}_d-{\alpha }_{e}u-F_1\hfill \\ \hfill =& {\dot{y}}_d-F_1-{\displaystyle \frac{{\alpha }_e}{\alpha }}(-{\widehat{F}}_2+{\dot{y}}_d+k_{p}e+k_d\dot{e})\hfill \\ \hfill =& {\dot{y}}_d-F_1-\rho (-{\widehat{F}}_2+{\dot{y}}_d+k_{p}e+k_d\dot{e})\hfill \\ \hfill =& -\rho k_{p}e-\rho k_d\dot{e}+D_r\hfill \end{array}$$

(16)

where $b_e/b=\rho$, $\rho >0$, the residual disturbance $D_r=-F_1+\rho {\widehat{F}}_2+(1-\rho ){\dot{y}}_d$. Then, rewrite above equation as follow:

$$\dot{e}=-Ae+B{D}_r,$$

(17)

where

$$A={\displaystyle \frac{\rho k_p}{1+\rho k_d}}>0,B={\displaystyle \frac{1}{1+\rho k_d}}>0.$$

(18)

The Lyapunov function is defined as $V=P{e}^2$, where $P\in {\mathbb{R}}^{+}$ denotes a positive real number. Taking the derivative of V, it yields

$$\begin{array}{cc}\hfill \dot{V}=2Pe\dot{e}=& -2PA{e}^2+2PB{D}_{r}e\hfill \\ \hfill ⩽& -2PA{e}^2+2PBsup|D_r\left|\right|e|.\hfill \end{array}$$

(19)

where $sup|D_r|$ represents the upper bound of $D_r$. Obviously, when $\left|e\right|⩾A^{-1}Bsup\left|D_r\right|$, $\dot{V}⩽0$ can be guaranteed. Furthermore, one gets

$$\underset{t\to \infty }{lim}\left|e\right|⩽{\displaystyle \frac{Bsup|D_r|}{A}}={\displaystyle \frac{sup|D_r|}{\rho k_p}}.$$

(20)

Thus, the closed-loop system is asymptotic stability and the tracking error is uniformly ultimately bounded.

3.2. Adaptive Enhanced Model-Free Speed Controller Design

The gain $\alpha$ critically determines both the closed-loop stability and speed regulation quality in PMSM drives. This work proposes a gradient descent-based online auto-tuning scheme to optimize this essential parameter.

The above (11) can be discretized as follows:

$$\begin{array}{cc}\hfill y\left(k\right)=& y(k-1)+T_s\alpha u(k-1)+T_{s}F(k-1),\hfill \\ \hfill y(k-1)=& y(k-2)+T_s\alpha u(k-2)+T_{s}F(k-2),\hfill \end{array}$$

(21)

where $T_s$ is the sampling time. since the change period of the lumped disturbance F is much larger than the period of the sampling time $T_s$ , it can be considered that the lumped disturbance is unchanged in the adjacent sampling period, namely

$$F(k-1)=F(k-2).$$

(22)

On this basis, we have

$$y\left(k\right)=2y(k-1)-y(k-2)+T_s\alpha \Delta u(k-1),$$

(23)

with $\Delta u(k-1)=u(k-1)-u(k-2)$

Then, the output error can be expressed as

$$e\left(k\right)=y_d-y\left(k\right)=y_d-2y(k-1)+y(k-2)-T_s\alpha \Delta u(k-1).$$

(24)

Consider the following index function:

$$J={\displaystyle \frac{1}{2}}{e}^2\left(k\right).$$

(25)

Then, the gradient of the index function with respect to $\alpha$ is given by:

$${\nabla }_{\alpha }J=e\left(k\right){\displaystyle \frac{\partial e\left(k\right)}{\partial \alpha }}=-T_s\Delta u(k-1)e\left(k\right).$$

(26)

The presence of measurement noise $n\left(t\right)$ in the error signal $e\left(t\right)$ can corrupt the gradient estimation, causing the parameter $\alpha$ to oscillate randomly around or deviate cumulatively from its true value. To enhance the adaptation law, a dead-zone technique is introduced to suppress noise effects by disabling updates during small-error conditions. The implementation details are as follows:

$${\nabla }_{\alpha }J=\left\{\begin{array}{cc}-T_s\Delta u(k-1)e\left(k\right),\hfill & \left|e\left(k\right)\right|⩾\delta \hfill \\ 0,\hfill & \left|e\left(k\right)\right|<\delta ,\hfill \end{array}\right.$$

(27)

where $\delta$ is the error threshold. Therefore, the update law for $\alpha$ is given as follows

$$\widehat{\alpha }\left(k\right)=\widehat{\alpha }(k-1)-\eta {\nabla }_{\alpha }J=\left\{\begin{array}{cc}\widehat{\alpha }(k-1)+\eta T_s\Delta u(k-1)e\left(k\right),\hfill & \left|e\left(k\right)\right|⩾\delta \hfill \\ \widehat{\alpha }(k-1),\hfill & \left|e\left(k\right)\right|<\delta ,\hfill \end{array}\right.$$

(28)

where $\eta$ is the learning rate.

To prevent instability in parameter adaptation caused by excessively large or small control inputs $\Delta u(k-1)$, a nonlinear modulation scheme is applied to the learning rate. The learning rate $\eta$ is dynamically adjusted based on the input variation $\Delta u(k-1)$, as specified below

$$\eta T_s=\mu \to {\displaystyle \frac{\mu }{1+\mu {\left(\Delta u(k-1)\right)}^2}}.$$

(29)

By incorporating this nonlinear modulation scheme into the standard gradient update law, the final adaptation rule can be gotten as

$$\widehat{\alpha }\left(k\right)=\left\{\begin{array}{cc}\widehat{\alpha }(k-1)+\mu {\displaystyle \frac{1}{1+\mu {\left(\Delta u(k-1)\right)}^2}}\Delta u(k-1)e\left(k\right),\hfill & \left|e\left(k\right)\right|⩾\delta \hfill \\ \widehat{\alpha }(k-1),\hfill & \left|e\left(k\right)\right|<\delta ,\hfill \end{array}\right.$$

(30)

where $\mu$ is the adaptive coefficient, ${\alpha }_0$ is the initial value of $\widehat{\alpha }\left(k\right)$.

Combining nonlinear disturbance observer (12), enhanced model-free speed control law (14), and adaptive gain law (30) based on gradient descent method, the final adaptive enhanced model-free speed controller (AEMFSC) is designed as

$$u={\displaystyle \frac{-{\widehat{F}}_2+{\dot{y}}_d+k_{p}e+k_d\dot{e}}{\widehat{\alpha }}}.$$

(31)

The block diagram of the proposed PMSM speed control strategy is shown in Figure 1.

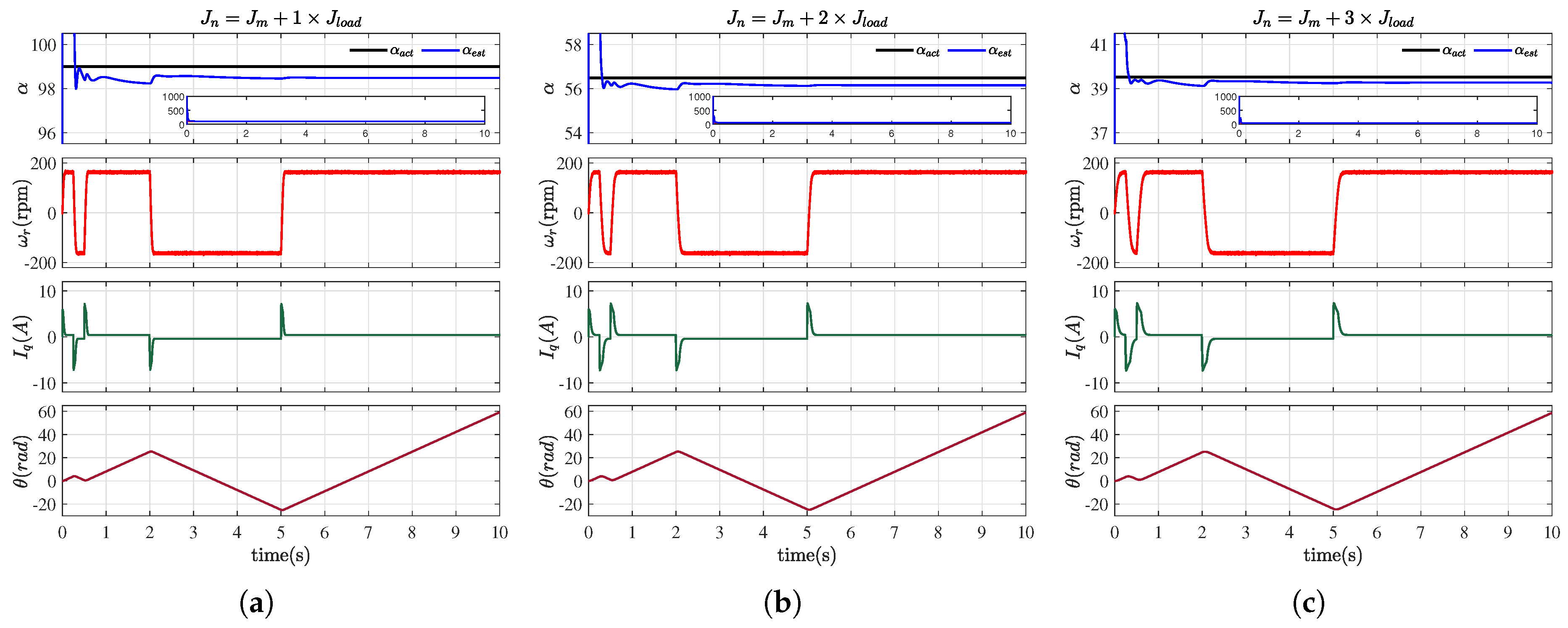
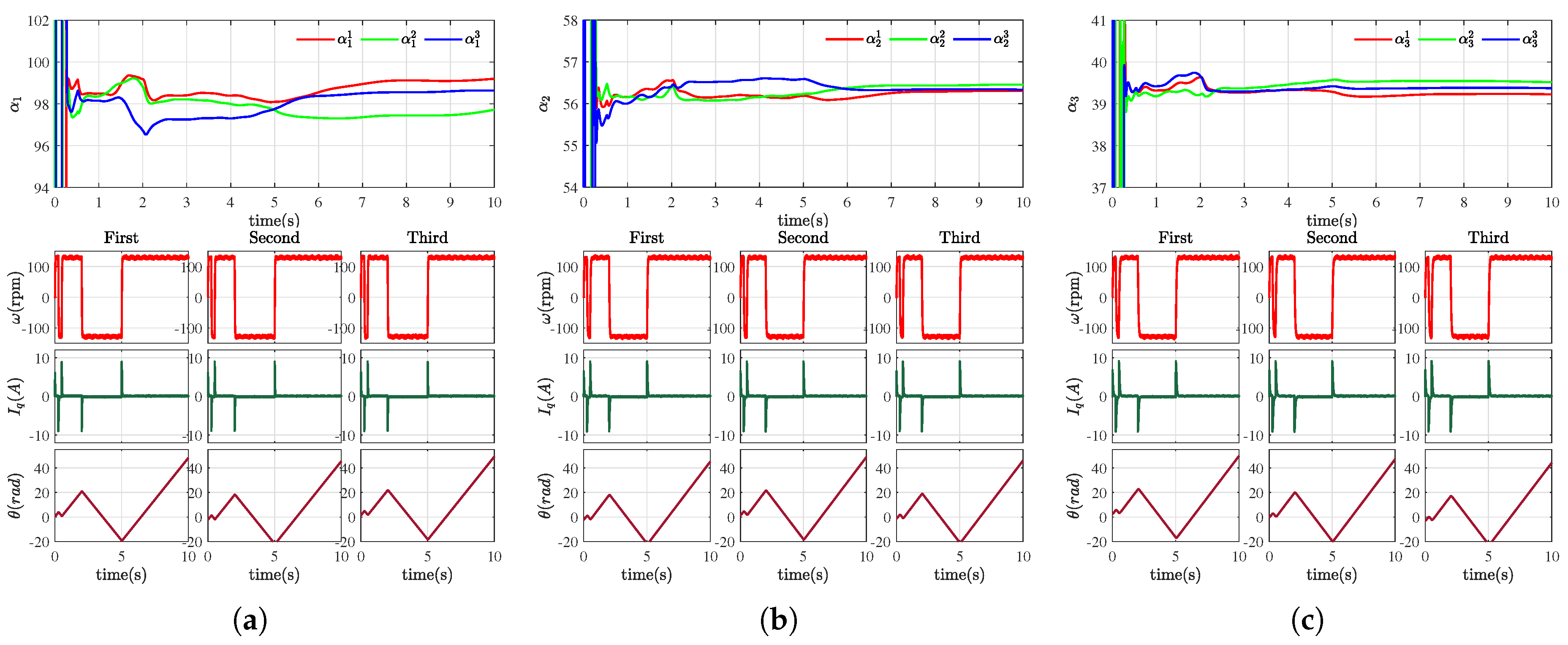
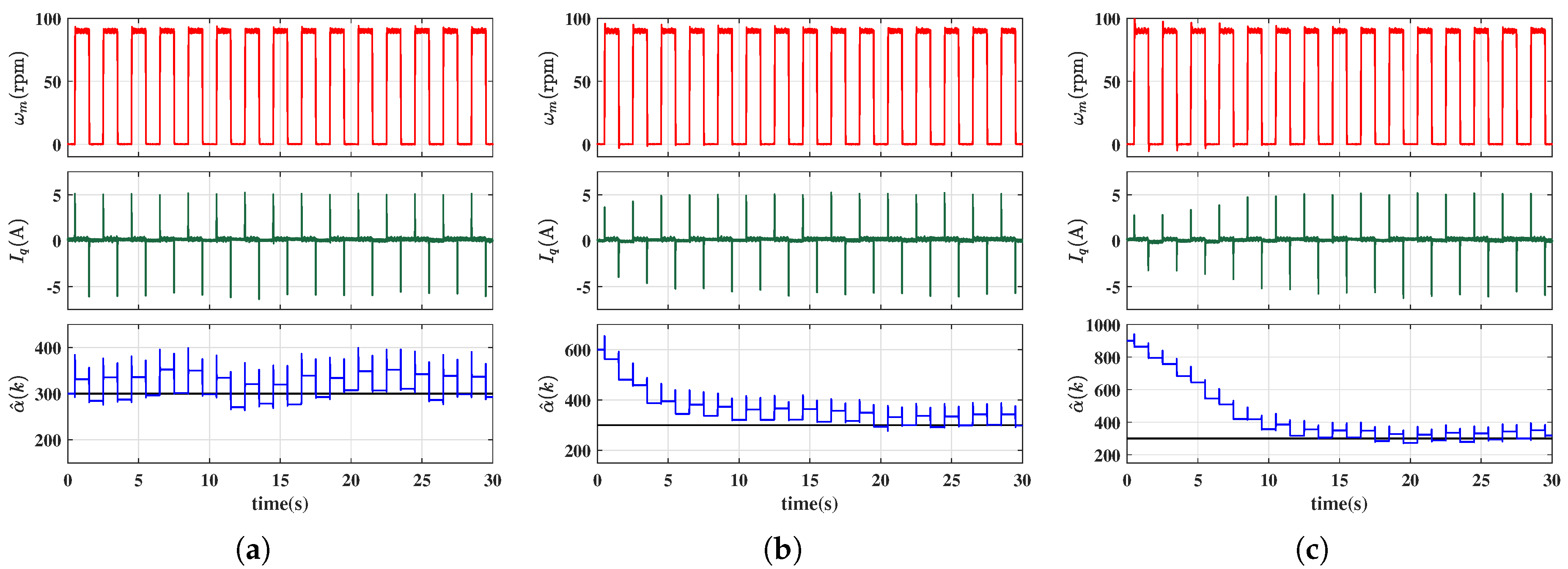
3.3. Initial Value Estimation Method for the Input Gain

In practical motor applications, two major challenges exist: (1) inaccuracies or missing specifications of flux linkage parameters and torque coefficients on nameplates, and (2) considerable difficulties in accurately estimating moment of inertia under complex loading conditions, resulting in significant deviations between calculated ${\alpha }_0$ and actual ${\alpha }_e$ values.

For constant-load motor systems, employing a fixed ${\alpha }_0$ value effectively reduces computational overhead in embedded systems. For variable-load systems, appropriate initial ${\alpha }_0$ values substantially enhance transient tracking performance during the startup phase. This subsection consequently presents an algebraic framework-based linear identification method for high-precision ${\alpha }_0$ identification.

The electromechanical equation (3) of SMPMSM drive system can be expressed as

$$\ddot{\theta }+a\dot{\theta }=b{i}_q+A_0,$$

(32)

where $\theta$ is the rotor mechanical angle, $\dot{\theta }={\omega }_m$, $a=B_n/J_n$, $b=3n_p{\phi }_n/\left(2J_n\right)$, and $A_0=\left(-T_L-d_n-f_t\right)/J_n$. The constant parameters $a,b\in \mathbb{R}$ are unknown, and the $A_0\in \mathbb{R}$ is considered to be a constant load perturbation [32]. Then (32) in S-domain is given as

$$(s^2+as)\theta =b{i}_q+s{\theta }_0+{\dot{\theta }}_0+a{\theta }_0+A_0/s.$$

(33)

Introduce a first order low pass filter, given by

$${\theta }_f={\displaystyle \frac{{\omega }_c}{s+{\omega }_c}}\theta ,$$

(34)

where the known constant parameters ${\omega }_c\in \mathbb{R}$ is strictly positive. Thus

$$(s^2+as)(s+{\omega }_c){\theta }_f={\omega }_c(b{i}_q+s{\theta }_0+{\dot{\theta }}_0+a{\theta }_0+A_0/s)$$

(35)

Multiplying both sides of (35) by s yields:

$$s(s^2+as)(s+{\omega }_c){\theta }_f={\omega }_c(bs{i}_q+s^2{\theta }_0+s{\dot{\theta }}_0+as{\theta }_0+A_0)$$

(36)

Derive both sides three times with respect to s, in order to eliminate the unknown parameter $A_0$, and the initial conditions ${\theta }_0$, ${\dot{\theta }}_0$:

$$\begin{array}{cc}\hfill & 24s{\theta }_f+36s^2{\displaystyle \frac{d{\theta }_f}{ds}}+12s^3{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}+s^4{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}+6{\omega }_c{\theta }_f+18{\omega }_{c}s{\displaystyle \frac{d{\theta }_f}{ds}}+9{\omega }_c{s}^2{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}+{\omega }_c{s}^3{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}\hfill \\ \hfill & +6a{\theta }_f+18as{\displaystyle \frac{d{\theta }_f}{ds}}+9a{s}^2{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}+a{s}^3{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}+6a{\omega }_c{\displaystyle \frac{d{\theta }_f}{ds}}+6a{\omega }_{c}s{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}+a{\omega }_c{s}^2{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}\hfill \\ \hfill & ={\omega }_c\left(3b{\displaystyle \frac{d^2{i}_q}{d{s}^2}}+bs{\displaystyle \frac{d^3{i}_q}{d{s}^3}}\right).\hfill \end{array}$$

(37)

Then multiply both sides by $s^{-4}$ for avoiding derivations with respect to time:

$$\begin{array}{cc}\hfill & a\left(6s^{-4}{\theta }_f+18s^{-3}{\displaystyle \frac{d{\theta }_f}{ds}}+9s^{-2}{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}+s^{-1}{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}+6{\omega }_c{s}^{-4}{\displaystyle \frac{d{\theta }_f}{ds}}+6{\omega }_c{s}^{-3}{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}+{\omega }_c{s}^{-2}{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}\right)\hfill \\ \hfill & +b\left(-3s^{-4}{\omega }_c{\displaystyle \frac{d^2{i}_q}{d{s}^2}}-{\omega }_c{s}^{-3}{\displaystyle \frac{d^3{i}_q}{d{s}^3}}\right)=-24s^{-3}{\theta }_f-36s^{-2}{\displaystyle \frac{d{\theta }_f}{ds}}-12s^{-1}{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}-{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}\hfill \\ \hfill & -6{\omega }_c{s}^{-4}{\theta }_f-18{\omega }_c{s}^{-3}{\displaystyle \frac{d{\theta }_f}{ds}}-9{\omega }_c{s}^{-2}{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}-{\omega }_c{s}^{-1}{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}.\hfill \end{array}$$

(38)

The remaining negative powers of s correspond to iterated time integrals. The corresponding formulae in the time domain are easily deduced thanks to the correspondence between $d^v/d{s}^v,v⩾0$, and the multiplication by ${(-t)}^v$ in the time domain. Equation (38) in time domain can be obtained as

$$a{\pi }_1\left(t\right)+b{\pi }_2\left(t\right)=q\left(t\right)$$

(39)

with

$$\begin{array}{cc}\hfill {\pi }_1\left(t\right)=& -\int t^3{\theta }_{f}dt+{\int }^2\left(9t^2{\theta }_f-{\omega }_c{t}^3{\theta }_f\right)dt+{\int }^3\left(-18t{\theta }_f+6{\omega }_c{t}^2{\theta }_f\right)dt\hfill \\ \hfill & +{\int }^4\left(6{\theta }_f-6{\omega }_{c}t{\theta }_f\right)dt,\hfill \\ \hfill {\pi }_2\left(t\right)=& {\int }^3{\omega }_c{t}^3{i}_{q}dt-{\int }^{4}3{\omega }_c{t}^2{i}_{q}dt,\hfill \\ \hfill q\left(t\right)=& \int \left(-12t^2{\theta }_f+{\omega }_c{t}^3{\theta }_f\right)dt+{\int }^2\left(36t{\theta }_f-9{\omega }_c{t}^2{\theta }_f\right)dt\hfill \\ \hfill & +{\int }^3\left(-24{\theta }_f+18{\omega }_{c}t{\theta }_f\right)dt-{\int }^{4}6{\omega }_c{\theta }_{f}dt+t^3{\theta }_f.\hfill \end{array}$$

(40)

We have denoted by ${\int }^{\left(n\right)}\varphi \left(t\right)$ the quantity ${\int }_0^t{\int }_0^{{\beta }_1}\dots {\int }_0^{{\beta }_{n-1}}\varphi \left({\beta }_n\right)d{\beta }_n\dots d{\beta }_{2}d{\beta }_1$. Moreover, $\int \varphi \left(t\right)={\int }_0^t\varphi \left({\beta }_1\right)d{\beta }_1$.

Integrating the expression (40) one time, leads to the following system of linear equations for the estimates $a_e$, $b_e$ of the unknown parameters:

$$\left[\begin{array}{cc}{P}_{11}\left(t\right)& P_{12}\left(t\right)\\ P_{21}\left(t\right)& P_{22}\left(t\right)\end{array}\right]\left[\begin{array}{c}a\hfill \\ b\hfill \end{array}\right]=\left[\begin{array}{c}{Q}_1\left(t\right)\hfill \\ Q_2\left(t\right)\hfill \end{array}\right],$$

(41)

with

$$P_{11}={\pi }_1\left(t\right),P_{12}={\pi }_2\left(t\right),Q_1\left(t\right)=q\left(t\right),P_{21}=\int {\pi }_1\left(t\right),P_{22}=\int {\pi }_2\left(t\right),Q_2\left(t\right)=\int q\left(t\right).$$

After a time interval of the form $\left[0,t\right]$, the estimates a and b can be obtained by solving the previous expression. Then the input gain ${\alpha }_0=b$ can be used in the proposed EMFSC (14) or AEMFSC (31).

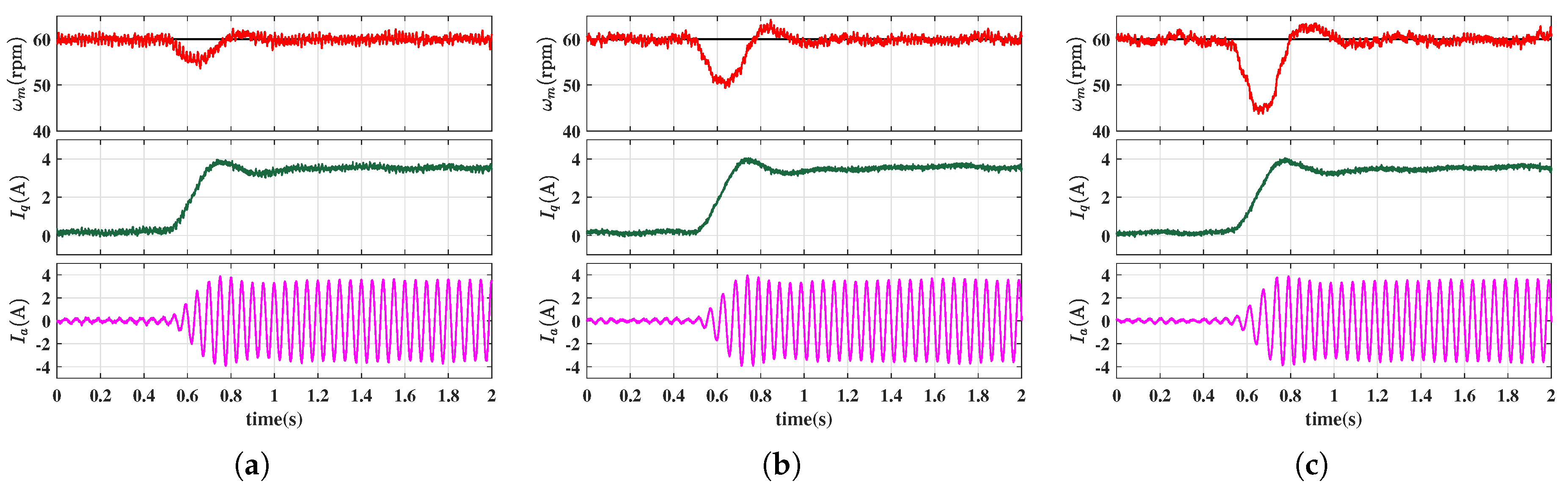
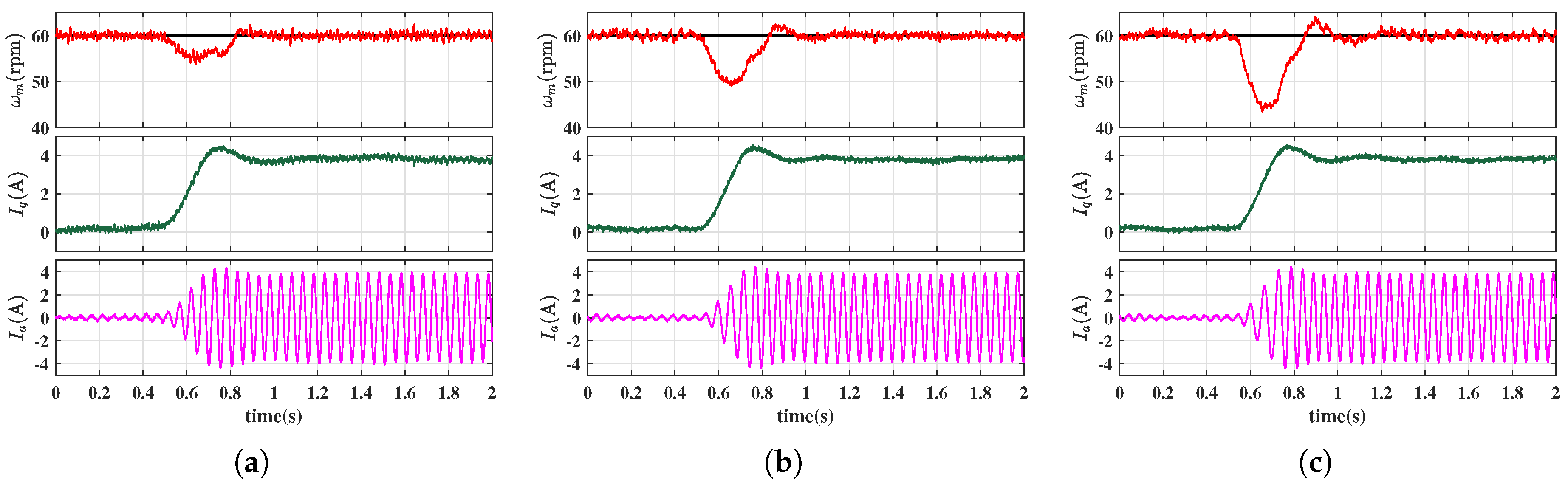
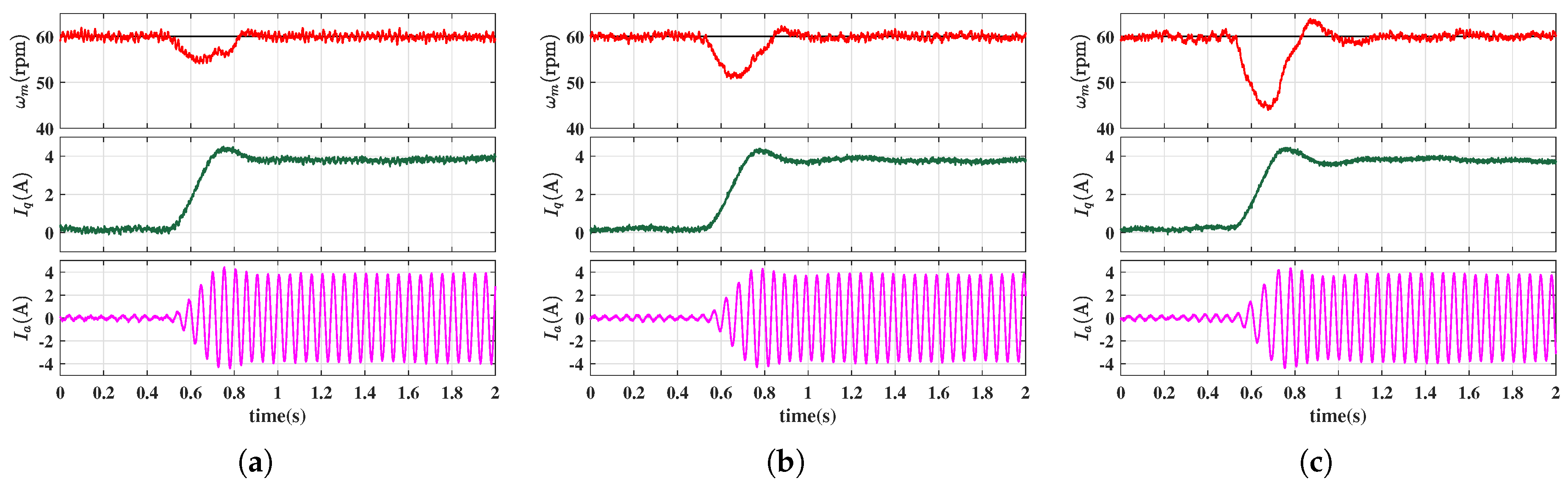
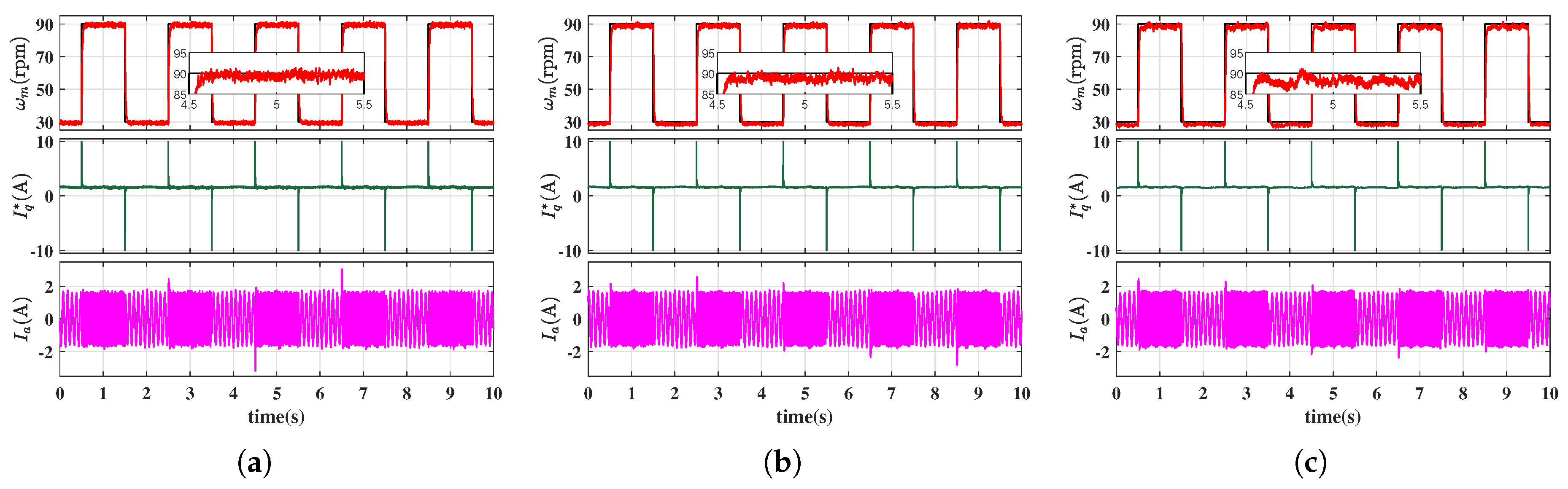
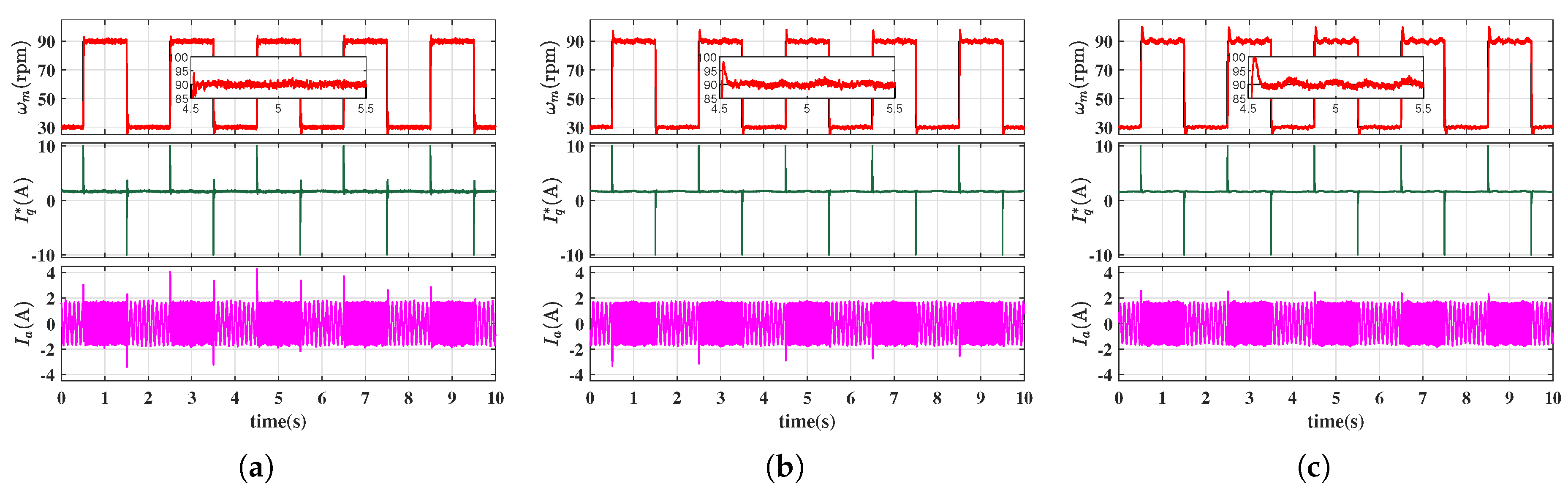
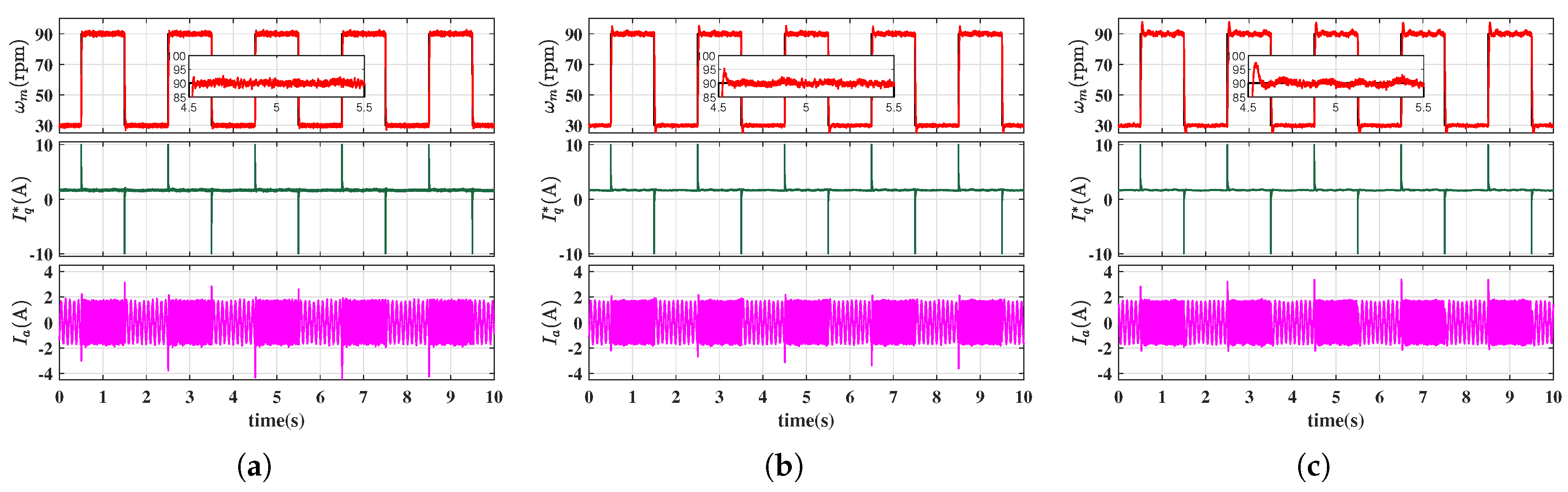
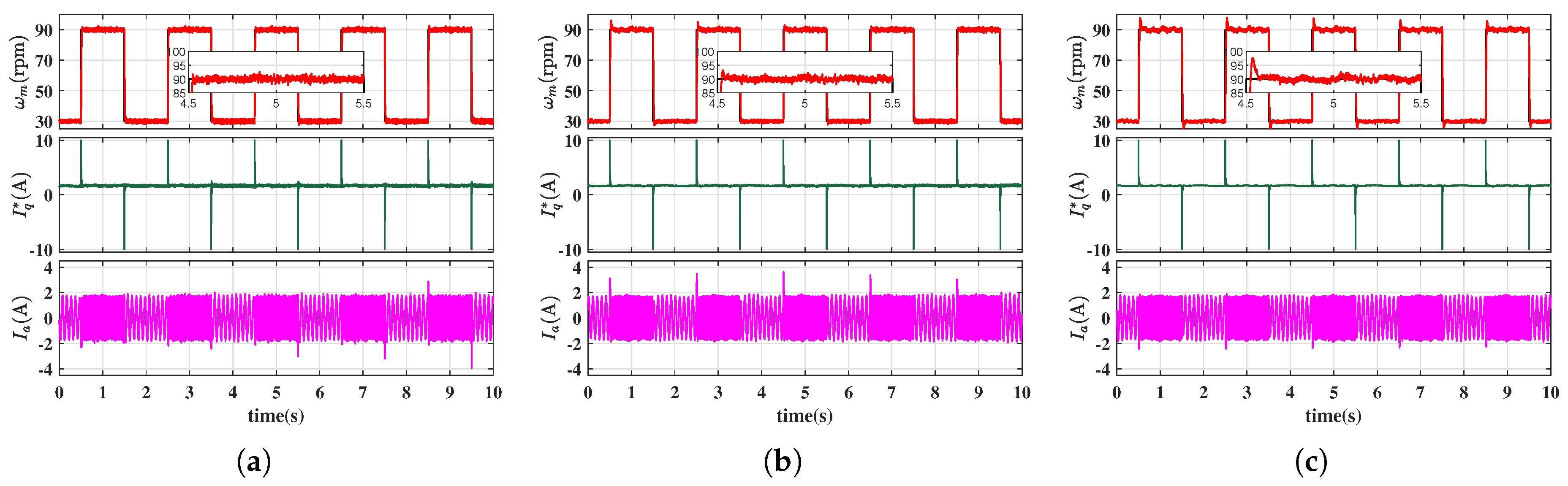
4. Simulation and Experimet Results

This section conducts a rigorous comparative evaluation of the proposed EMFSC-NDO (14) and AEMFSC-NDO (31), comparing them with two control methods: conventional MFSC-API [23] and MFSC-NDO (7). The assessment examines transient response, steady-state accuracy, and disturbance rejection capabilities under identical operating conditions.

Both simulation and experimental studies are performed on a SMPMSM drive system, utilizing a two-level voltage source inverter with SVPWM at 10 kHz switching frequency. The dead-time is set as 0.5$\mu$s. Decoupled PI regulators are adopted in the current loop, and these controllers are employed in the speed loop. The speed loop frequency is 2 kHz. Table 1 lists the specification of the SMPMSM used in the digital simulation and experimental tests.

All control parameters are optimized through systematic trial-and-error procedures to ensure optimal tracking performance and disturbance rejection capabilities. Notably, the simulation model incorporates realistic encoder quantization effects by superimposing discrete position measurement noise.

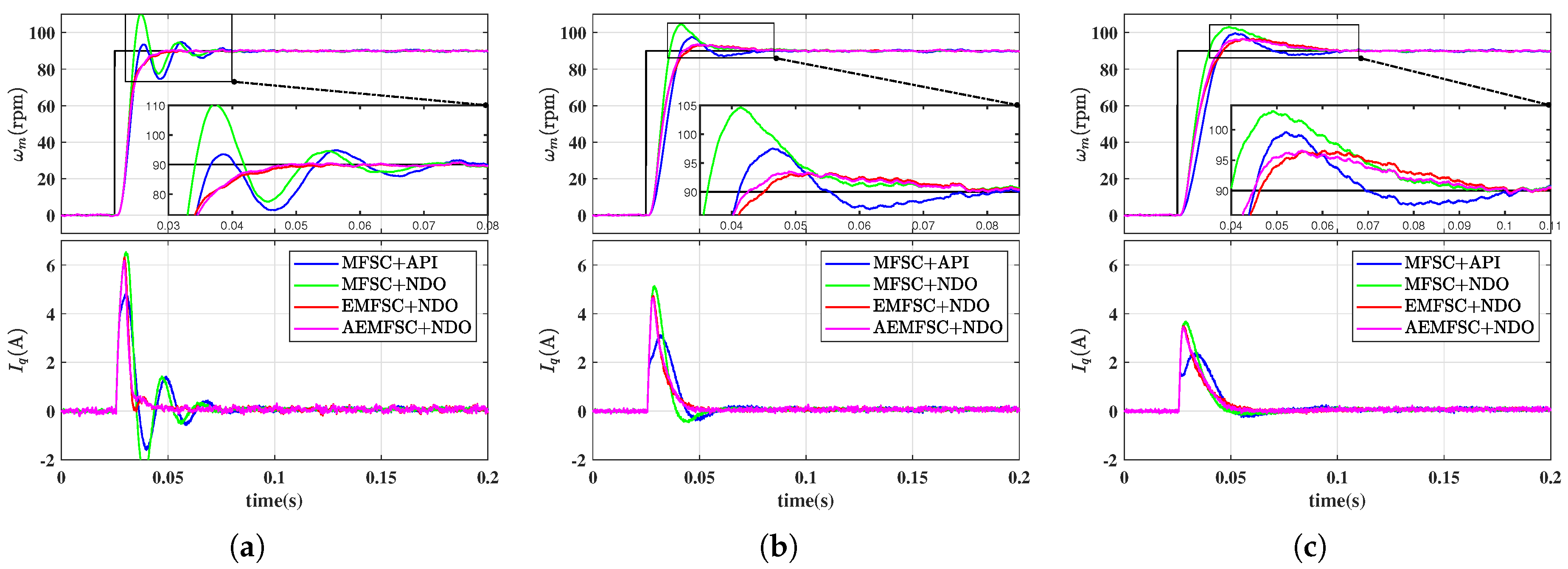
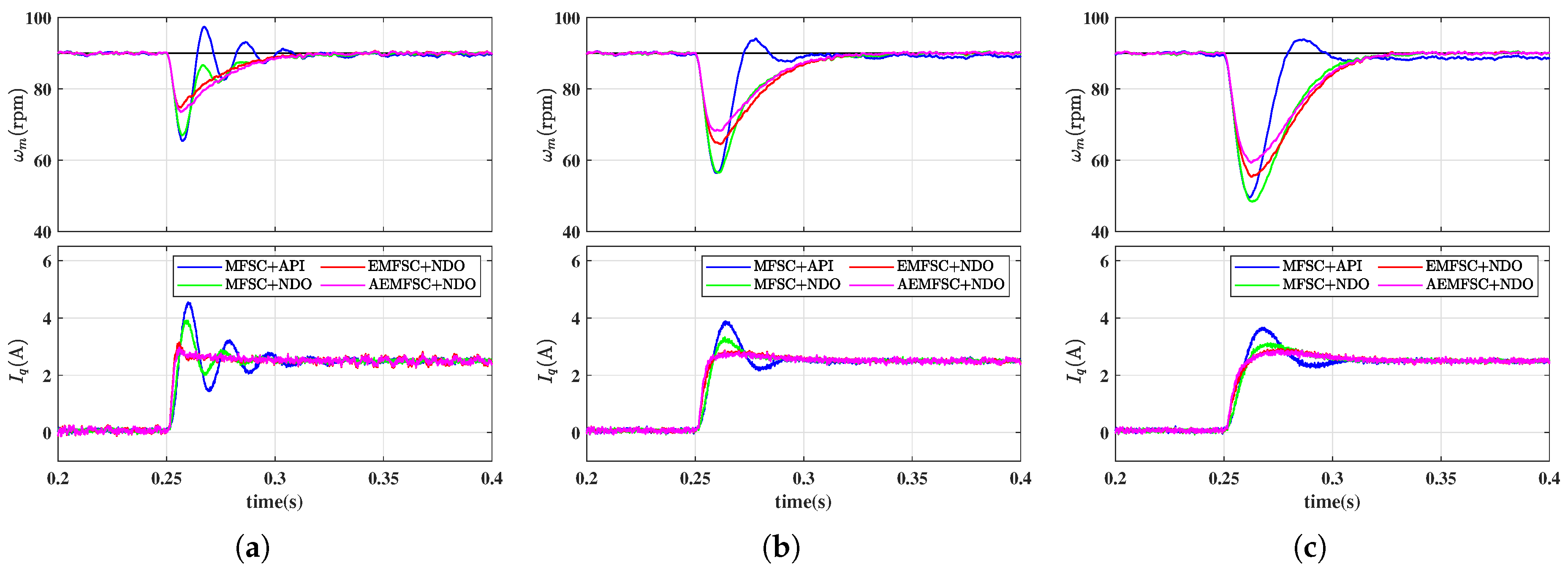
4.1. Simulation Results

Numerical simulations of the PMSM speed regulation system are conducted using MATLAB/Simulink, with the control algorithm executed in discrete-time domain at 2 kHz sampling rate.

The parameters of MFSC-API, MFSC-NDO, EMFSC-NDO, and AEMFSC-NDO controllers are chosen as follows: $k_p$ = 160, $n_F$ = 10 for MFSC-API controller, $k_p$ = 400, L = 50 for MFSC-NDO controller, $k_p$ = 400, $k_d$ = 1, L = 50, $\delta$ = 0.3 rad/s for EMFSC-NDO controller, and $k_p$ = 400, $k_d$ = 1, L = 50, $\delta$ = 0.3 rad/s, $\mu$ = 20 for AEMFSC-NDO controller. The reference speed is 90 rpm, and the inertia of the load is chosen as $J_{load}$ = 0.00134 kg·m². Therefore, the theoretical ture value of input gain ${\alpha }_e=1.5n_p{\phi }_n/(J_m+J_{load})=302.07$.

Figure 2 shows the startup responses of the MFSC-API, MFSC-NDO, EMFSC-NDO, and AEMFSC-NDO controllers at the reference speed of 90 rpm. The load torque is initially set to zero, so the PMSM can be assumed to be load-free. Figure 2 clearly demonstrates that both the EMFSC-NDO and AEMFSC-NDO controllers exhibit superior dynamic performance, achieving minimal overshoot and the fastest settling time among all compared methods. However, when the selected input gain and the theoretical true input gain mismatched, the performance of PMSM system will deteriorate.

Figure 3 presents a comparative analysis of disturbance rejection capabilities among the four control schemes. The results demonstrate that the proposed AEMFSC-NDO controller exhibits superior load disturbance rejection, with merely 18.4% speed drop during sudden load torque application (4.0 N·m step change at t=0.25s), compared to 25.7% for the MFSC-NDO method. Furthermore, parameter mismatch analysis reveals that input gain variations can degrade the system’s disturbance rejection performance .

To validate the effectiveness of the $\alpha$ adaptation algorithm, three distinct initial value conditions were experimentally tested. As demonstrated in Figure 4, the results show that: (i) the estimated input gain converges to its theoretical actual value within several square-wave cycles, and (ii) the automatic adjustment of parameter $\alpha$ significantly reduces transient tracking errors.

The preceding analysis reveals that while the proposed AEMFSC-NDO demonstrates exceptional robustness and rapid tracking performance, inappropriate initial values of $\alpha$ can adversely affect transient tracking during startup and potentially destabilize the system. To obtain accurate $\alpha$ values, the algebraic framework-based linear identification method is employed for precise input gain estimation. The estimation procedure, validated under three distinct load inertia conditions ($J_n=J_m+n{J}_{load},n=1,2,3,J_{load}=0.01254$), operates as follows: (a) Initialize with an overestimated $\alpha$ value (e.g., $\alpha$=1000); (b) Execute maximum-speed square-wave rotation; (c) Compute $\alpha$ via (41) using measured position and q-axis current. Figure 5 confirms high estimation accuracy across all test cases. Notably, this computationally intensive method may require offline implementation on resource-constrained DSPs after data acquisition.

4.2. Experimental Results

To further verify the effectiveness of the proposed control scheme, some real-time experiments are carried out. Figure 6 depicts the experimental test platform, which is governed by a TMS320F28379D digital signal processor (DSP). The control circuit is composed of power supply (RU-36-10036), SPMSM (J155LWX001), two-level inverter, and measurement circuit.

A MOSFET module inverter is fed by a programmable DC power supply, set at 34V in the experiments. The rotor position sensor is a 19-bit electromagnetic encoder (EAB42-0M19S-8-B) and the current sensor is a CC6920B-10A current sensor. The nominal parameters of the motor, the sampling time and all the parameters of the current controller are the same as in the simulation.

To mitigate sensor noise amplification and prevent motor oscillations, practical controller implementations employ smaller parameter values compared to simulation environments. The parameters of MFSC-API, MFSC-NDO, EMFSC-NDO, and AEMFSC-NDO controllers are chosen as follows: $k_p$ = 80, $n_F$ = 10 for MFSC-API controller, $k_p$ = 300, L = 50 for MFSC-NDO controller, $k_p$ = 300, $k_d$ = 1, L = 50, $\delta$ = 0.3 rad/s for EMFSC-NDO controller, and $k_p$ = 300, $k_d$ = 1, L = 50, $\delta$ = 0.3 rad/s, $\mu$ = 10 for AEMFSC-NDO controller.

For systems with uncertain load inertia and motor parameters, an algebraic framework-based linear identification method can be employed to achieve precise identification of the input gain. Figure 7 displays the estimation results of parameter $\alpha$ derived from three experimental trials under distinct load conditions. The initial angle position of the motor is different each time. The inertia of each load disk is $J_{load}=0.01254$. The estimated values exhibit remarkable consistency across all trials, aligning closely with the simulation outcomes. This agreement further validates the efficacy of the algebraic framework-based linear estimation method in accurately determining the input gain parameter $\alpha$. The estimated gain value can be directly employed as the fixed parameter $\alpha$ in the EMFSC-NDO approach or serve as the initial value for $\alpha$ in the adaptive AEMFSC-NDO scheme.

Applying the aforementioned algebraic framework-based linear identification method, the input gain is identified as ${\alpha }_e$=300 when the load is a magnetic powder brake. Figure 8 compares the startup responses of MFSC-API, MFSC-NDO, EMFSC-NDO, and AEMFSC-NDO controllers under no-load conditions at 60 rpm reference speed. As demonstrated in Figure 8(a) with accurate input gain, the proposed EMFSC-NDO and AEMFSC-NDO controllers exhibit superior transient performance. Although the MFSC-API controller generates lower q-axis current peaks, it has a longer settling time. These results conclusively establish the advantages of EMFSC-NDO and AEMFSC-NDO controllers in PMSM speed transient regulation.

Figure 8(b)-(c) reveal significant sensitivity to input gain variations. When $\alpha =3{\alpha }_e$, both EMFSC-NDO and AEMFSC-NDO exhibit excessive speed overshoot, while MFSC-NDO shows relative improvement. Notably, elevated gain values universally prolong the settling time across all four controllers, potentially degrading system performance during rapid speed transitions. Table 2 quantitatively compares key performance indicators: (i) speed overshoot, and (ii) settling time, further validating the proposed controllers’ robustness against parameter mismatches.

The disturbance rejection capability is evaluated during steady-state operation by applying an 8 N·m load torque disturbance. Figure 9, Figure 10, Figure 11 and Figure 12 present the experimental results under this loading condition. As revealed in Figure 9(a), while the MFSC-API controller exhibits smaller speed drops, it suffers from significant steady-state errors that degrade control performance. Comparative results in Figure 10(a), Figure 11(a) and Figure 12(a) demonstrate that the proposed EMFSC-NDO and AEMFSC-NDO schemes achieve superior disturbance rejection compared to MFSC-NDO. The comparison between MFSC-API and MFSC-NDO further reveals inherent limitations of the algebraic parameter identification approach in estimating lumped disturbances during abrupt load changes.

Experimental results with different input gain values ($\alpha =2\alpha$ and $\alpha =3\alpha$ ) show substantially increased speed deviations and prolonged settling times. This confirms that excessive input gain values severely deteriorate the system’s disturbance rejection capability. In this scenario, the proposed AEMFSC-NDO control strategy consistently outperforms both MFSC-NDO and EMFSC-NDO approaches. This superiority stems from its adaptive $\alpha$ adjustment capability during load transients, which actively enhances disturbance rejection performance. It should be noted that when the controller input satisfies the persistent excitation condition, the AEMFSC-NDO can recover its nominal anti-disturbance performance through $\alpha$ adaptation, even with initial parameter mismatch. Quantitative performance metrics under load torque variations are systematically compared in Table 3.

Figure 13, Figure 14, Figure 15 and Figure 16 present the square-wave speed tracking performance under 4 N·m load torque, with reference speeds ranging from 30 to 90 rpm. While the conventional MFSC-API controller exhibits steady-state errors as previously analyzed, the other three controllers achieve rapid and accurate speed tracking. However, elevated input gain values are observed to degrade the tracking performance, particularly during square-wave transitions.

Quantitative evaluation using Root Mean Square Value (RMSE, entire process) and Integral Absolute Error (IAE, steady-state phase) metrics is summarized in Table 4. With matched $\alpha$ values, the EMFSC-NDO strategy demonstrates superior tracking accuracy and steady-state performance. Under parameter mismatch conditions, the AEMFSC-NDO’s adaptive mechanism effectively suppresses speed overshoot and maintains better high-speed tracking performance, owing to its self-tuning capability.

The effectiveness of the proposed $\alpha$-adaptation algorithm is validated through three distinct initial conditions, with experimental results presented in Figure 17. The data demonstrate that the estimated $\alpha$ converges to the vicinity of its true value within several square-wave cycles. It should be noted that choosing a smaller value of $\mu$ will reduce the oscillation amplitude of the input gain, but this comes at the cost of a longer convergence time.

5. Conclusions

This paper has developed an NDO-based EMFSC control algorithm for PMSM systems to achieve high tracking performance under external disturbances and unknown load torque. Compared with conventional MFSC-API and MFSC-NDO methods, the proposed EMFSC-NDO eliminates steady-state errors, reduces speed overshoot, and demonstrates faster settling time with enhanced disturbance rejection capability. Furthermore, two parameter identification methods have been designed to online estimate the true input gain values, effectively addressing input gain mismatch issues. The effectiveness and superiority of the proposed approach have been thoroughly validated through both simulation and experimental results. Future work will focus on improving the convergence speed and estimation accuracy of NDO for lumped disturbances, as well as developing more advanced input gain identification techniques.