1. Introduction
Advances in power electronics and modern control techniques are facilitating the integration of more electrical subsystems into aircrafts, reinforcing flight control and improving passenger and cargo comfort [
1]. The transition from hydraulically, pneumatically, and mechanically powered subsystems to electrically driven systems—known as the “More Electric Aircraft” (MEA) concept—has gained traction due to its potential to reduce weight, maintenance costs, and carbon emissions while improving fuel efficiency. As the MEA concept continues to evolve, onboard power demand and generator capacity have risen significantly, increasing from a few hundred kilovolt-amperes before World War II to megavolt-amperes in recent decades [
2].
Increasing the power capacity of aircraft electrical systems inevitably adds weight and volume due to larger machines, drives, and thicker transmission lines. Even when inactive, this added weight increases fuel consumption. Therefore, minimizing size and weight while maintaining efficient power generation is a key priority. Permanent magnet (PM) machines are widely preferred in aerospace due to their high efficiency, reduced losses, and compact design. Unlike electrically excited machines, PMs eliminate excitation losses , simplifying thermal management and improving overall performance [
3]. They also eliminate mechanical components like brushes and commutators, reducing maintenance and sparking risks [
4,
5]. PMSMs are categorized by back-EMF waveform into sinusoidal and trapezoidal types, where sinusoidal PMSMs offer smooth torque when harmonics are well-filtered, but they require of high switching frequencies which in turn result in increased losses. Trapezoidal PMSMs are cost-effective but suffer from core losses at high speeds. Based on magnet placement, PMSMs are classified as surface-mounted (SPMSM), insert-type, or interior-mounted. SPMSMs are particularly suited for aerospace applications due to their superior power density, efficiency, and reliability [
2]. Their high torque-to-weight ratio is crucial for minimizing aircraft weight while maintaining performance. The absence of excitation windings enhances efficiency and thermal management, which is critical in aerospace environments with limited cooling options. Additionally, their fast dynamic response, smooth torque, and brushless design ensure mechanical stability, reduced maintenance, and long-term reliability under extreme conditions such as high vibrations and temperature variations.
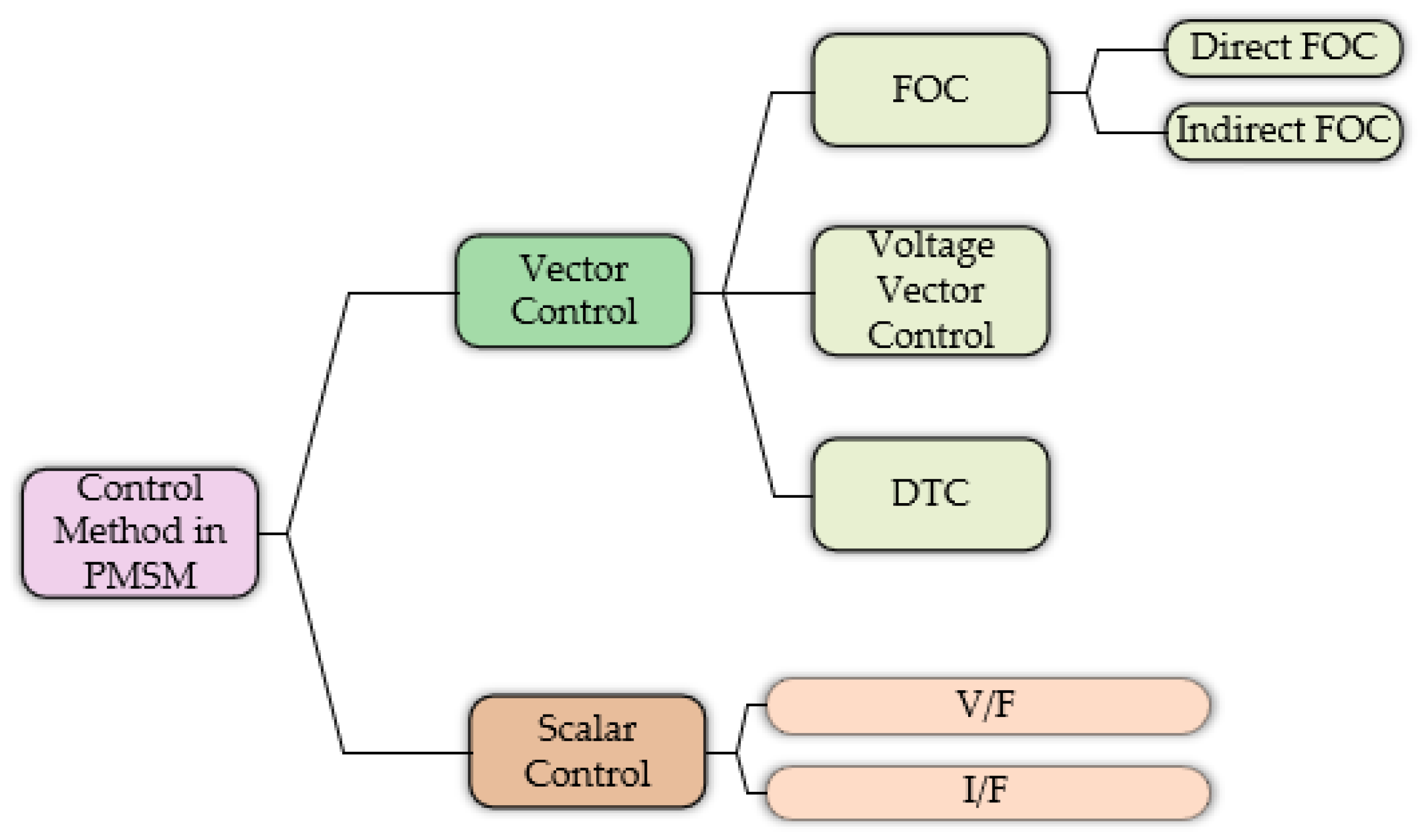
Various drive control strategies as shown in
Figure 1 have been proposed for SPMSM drives, including Field-Oriented Control (FOC), Direct Torque Control (DTC), constant volt-per-frequency control (V/F) and constant current-per-frequency control (I/F). Among these, FOC is the most commonly employed due to its high state performance. FOC decouples torque and flux, enabling independent control of these parameters. This approach enables smooth torque and speed regulations by using Proportional Integral(PI) controllers to manage the currents in the d- and q- axis frame [
6], where Pulse Width Modulation is typically employed to implement the control. Direct Torque Control (DTC) is a control strategy that directly regulates the motor’s torque and flux by selecting appropriate voltage vectors. It employs hysteresis controllers to ensure that torque and flux remain within a predefined bound. By continuously measuring the stator flux and torque, the system selects the optimal voltage vector from a predefined lookup table to restore the torque and flux to their desired range. Unlike the FOC, DTC does not rely on current control loops, simplifying its computational requirements. However, a drawback of DTC is its tendency to produce a higher torque ripple[
7].
MPC has recently emerged as a powerful strategy in motor drives systems, enabled by the advancement in faster microprocessors with enhanced computational capabilities. Its key features such as simplicity in design, ease of implementation, explicit handling of constraints and capacity to manage complex, non-linear dynamics have facilitated its widespread application particularly in power electronics.
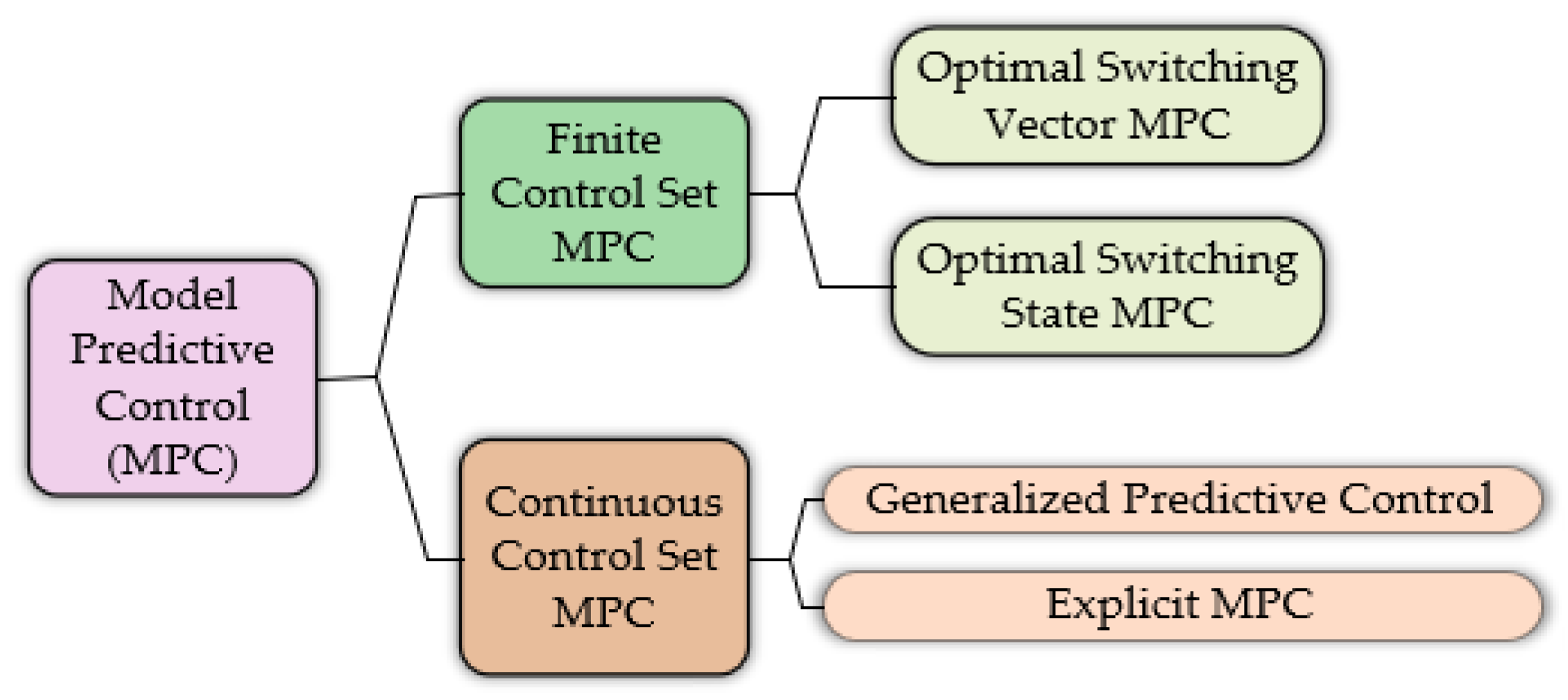
MPC can be classified into Continuous control set MPC (CCS-MPC) and finite Control set MPC (FCS-MPC) as shown in
Figure 2. The CCS-MPC computes a continuous control signal, which is then processed through modulation to generate the desired output voltage for the power converter. The modulation strategy choice depends on the converter topology, a notable advantage of CCS-MPC is its ability to maintain a fixed switching frequency, a critical requirement in power electronic applications. Two widely used CCS-MPC strategies are the generalised predictive control (GPC) and Explicit Model Predictive Control (EMPC). The former is well suited for linear and unconstrained problems while the latter is designed for systems with nonlinear dynamics and constraints. However, both face challenges in their formulation particularly when applied to power converters due to the inherent complexity of these systems [
8]. FCS-MPC, also known as direct MPC, simplifies the control process by leveraging the discrete nature of power converters and eliminating the need for an external modulator [
9]. This approach directly incorporates the system’s hybrid nature making it conceptually straightforward. Like CCS-MPC, FCS-MPC is also categorized into two sets which are the Optimal Switching Vector (OSV-MPC) and Optimal Switching Sequence MPC (OSS-MPC). The former is the most widely used method in power electronics, OSV-MPC employs the discrete output voltage vectors of the converter as its control set. The optimization process is reduced to a simple enumerated search, where one voltage vector is applied per switching period, but this leads to variable switching frequency unless additional constraints are imposed. To address the variable switching frequency limitation of OSV-MPC, OSS-MPC evaluates a limited switching sequence within each control period. By treating switching times as additional decision variables, OSS-MPC enhances control performance and mitigates the drawback associated with OSV-MPC [
10].
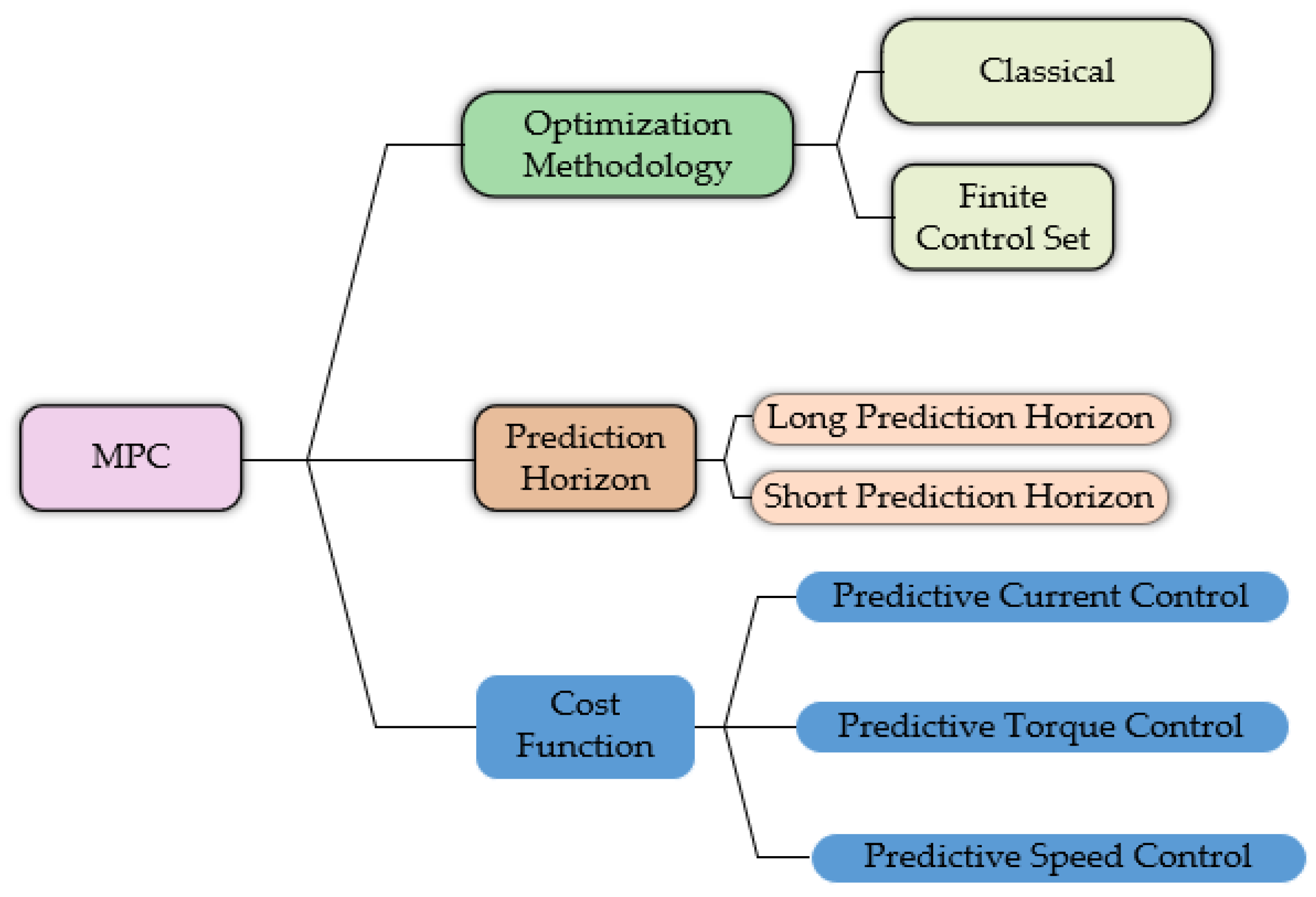
MPC optimizes motor performance by predicting future system behavior. It defines control actions by minimizing a cost function that represents the desired system performance, offering precise control and improved flexibilty for modern drive applications. MPC has been applied with FOC to control the internal stator current (MPCC) and also in DTC to directly control the machine’s torque and flux (MPTC). MPC can also be classified into single-step MPC and multi-step MPC / Long Prediction Horizon (LPH) as shown in
Figure 3. FCS-MPC has been widely applied to drives, demonstrating substantial benefits from incorporating a long prediction horizon (LPH) in terms of steady state operation and reduced current distortions. In this sense, Li et.al., [
11] confirmed that LPH enhances steady state performance of three phase drive systems, while Dorfling et.al.,[
12] validated the advantages of LPH-FCS-MPC for three level neutral point clamped converters with RL loads. Moreover, LPH-FCS-MPC significantly improves performance in higher-order systems, particularly by reducing harmonic distortions [
13]. While the multi-step offers superior performance compared to the single-step approach, it comes with a significantly higher computational burden. To address this a modified sphere decoding algorithm was proposed in [
14] significantly reducing computational load but introducing unpredictability in execution time for each sampling interval. To overcome this unpredictability the K-best SDA was introduced in [
15] providing fixed computational burden per sampling instant. A comparative analysis in [
16] demonstrates that the K-best approach provides fixed computational burden per sampling instant with tuneable Kb value but the modified sphere decoding algorithm provides better performance providing lowest THD.
The application of Model Predictive Control (MPC) in PMSM faces several challenges with its performance heavily reliant on the accuracy of the motor’s mathematical model. Key issues include variations in motor parameters such as its internal resistance, which is influenced by temperature, its inductance, which can vary as a function of current and permanent flux linkage which in turn is affected by environmental conditions, and additionally, manufacturing errors that may result in parameter inaccuracies either at runtime or during initial measurements. These factors collectively degrade the performance of MPC systems. To address parameter uncertainties, model-free approaches have been introduced in [
17] to mitigate the impact of inaccurate motor parameters. However, this method has two notable drawbacks; firstly, two current measurements are required in each sampling period for the detection of current spikes and secondly, it suffers from the issue of stagnant current variation updates, where the switching state can be unchanged for several sampling periods, adversely affecting current prediction performance. Nonetheless, these drawbacks can be eliminated while retaining the merits of a model-free predictive control approach [
18]. Alternative methods have also been explored, for instance, an improved current MPC for parameter mismatch in [
19] introduced a novel current update mechanism. Unlike earlier methods, where the current variation did not update within each control period (causing spikes at high speeds and impairing id and iq current tracking), this mechanism ensures that the predicted and measured stator currents are updated during each control period significantly improving performance.
In [
11] the effect on parameter mismatch on PMSM was comprehensively analyzed, this study implemented a moving horizon estimator as a disturbance observer, enabling estimation of external disturbances and their integration into the direct control problem. This approach enhanced the robustness of FCS-MPC across a wide range of operating conditions. In [
20], the effect of positive and negative parameter mismatch on the THD and Switching Frequency was studied on a conventional MPC and the proposed velocity model formulated by adding an integrator to the control problem without augmenting the states. In [
21], the trade-off between switching frequency and THD was studied for induction motors using monte carlo simulations (10,000 random samples), but the comparison was only based on the fitted results, with the effects of sampling time and weighing factor not being fully disclosed. Likewise, in [
22] another comparison for switching frequency and THD was presented, which did not consider the effect of sampling time and the weighing factor. In [
13] the comparison between 1-norm and 2-norm approach was carried out, considering various prediction horizons from
to
for different switching frequencies for an induction machine, but a clear comparison between the sampling time and the weighing factor effect on the THD and switching frequency was missing. In this sense, to the best of our knowledge, none of the above references have looked at the direct and complete mapping from these two variables (sampling time and weighing factor) to the control performance (THD and Switching Frequency). This is the main gap that is being fulfilled in this paper, where a comprehensive comparison between the SDA and FCS-MPC for SPMSM is presented, looking at the effects of parameter mismatch on the compared models.
2. Problem Formulation for LPH PMSM Control
2.1. Performance Metrics
In this work, two primary performance metrics are employed: total harmonic distortion (THD) and switching frequency. These metrics provide a quantitative basis for evaluating both the quality of the output waveform and the dynamic behavior of the control strategy.
2.1.1. Total Harmonic Distortion (THD)
THD quantifies the extent to which a waveform deviates from its fundamental sinusoidal component. Consider a signal
represented as:
where the amplitude of the fundamental component is determined by first computing its cosine and sine coefficients:
The amplitude of the fundamental is then given by:
The root-mean-square (RMS) value of the entire waveform is computed as:
and therefore, the Total Harmonic Distortion (THD) is subsequently defined by:
This metric effectively measures the relative contribution of higher harmonics in the signal.
2.1.2. Switching Frequency
The switching frequency
reflects the average number of switching events per unit time. It is defined by the formula:
where
represents the change in the control signal at time step
k,
is the sampling period, and
is the number of power semiconductor switches in the power converter of interest which is 3.
is the converter dependent correction factor which is
for two level converter [
13]. This metric allows us to assess the dynamic behavior and efficiency of the control strategy, particularly with respect to the operation of the power converter.
2.2. Model Predictive Control Formulation for PMSM Drive
2.2.1. SPMSM Mathematical Model
In [
23], several assumptions were made regarding the SPMSM were adopted in this article: magnetic saturation, cogging torque, and cross-saturation effects in [
24] were neglected. This implies that the d-axis inductance is approximately equal to the q-axis inductance, as well as to the inductance in the stationary alpha and beta axes.
The mathematical model of the PMSM drive in the dq axis can be presented as:
where:
and are the currents on the d- and q-axis, respectively.
and are the d-axis and q-axis voltage inputs.
2.2.2. Model Predictive Current Control
MPC consist of three components: a prediction model which is a mathematical or state space representation of the system, a cost function and an optimisation algorithm. The current dynamics of a Permanent Magnet Synchronous Motor (PMSM) in the d-q reference frame are given by:
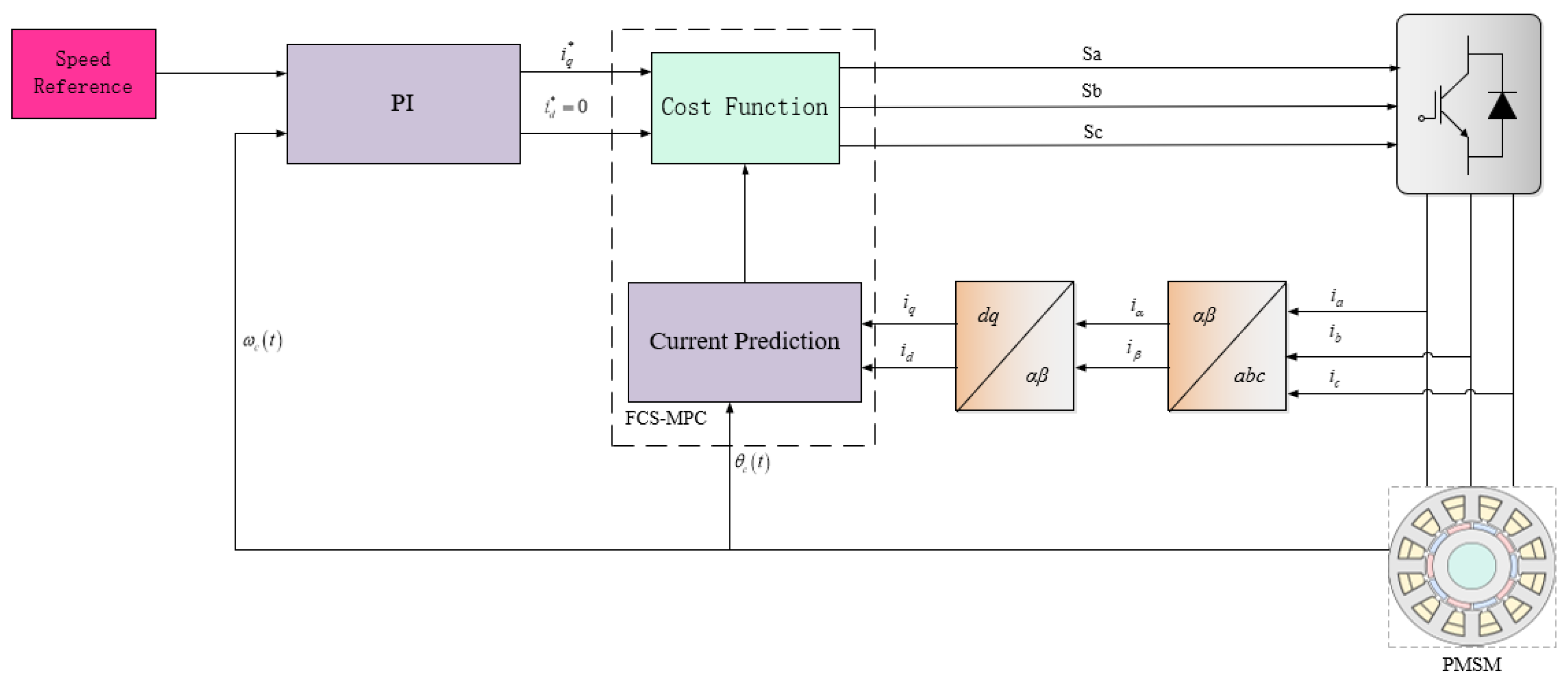
The FCS-MPC in
Figure 4 follows a conventional single step prediction, which uses Equation (
11) and Equation (
12) as its prediction model using the forward Euler discretization method, thus the design has to be done in the discrete time domain. The forward Euler discretization is given by:
Because the mechanical time constant of the SPMSM is much larger than the electromagnetic time constant,the motor rotor speed can be considered as constant during two control periods namely
. In addition, according to the first order forward euler discretization, the next instant
can simply be obtained as
. At this stage, the desired control targets are incorporated into a cost function
, also known as the objective function. This function forecasts the system’s behavior over a finite prediction horizon
N, expressing it in terms of tracking errors. For single-step Model Predictive Control (MPC), the prediction horizon is set to
, and the cost function is referred to as
J.
Many works in power electronics use the
-norm of the error vector for its computational simplicity [
25,
26,
27,
28], although recent literature suggests the
-norm for improved closed-loop performance, resulting in closer reference tracking and reduced ripple [
13,
29]. Another common criterion in cost function design is minimizing the control effort. This criterion recognizes that control actions not only impact system output but also come with costs, such as switching effort in power converters. A weighting factor
is introduced to balance this trade-off. A smaller value for
(close to but not zero) results in faster system dynamics. When the error term in the cost function approaches zero (i.e., when the measured output closely matches the reference), the second term, related to control effort, becomes more dominant, guiding the system towards the desired steady-state behavior.
This type of cost function in Equation (
16), when used in FCS-MPC, can ensure system stability and improve closed-loop performance. The most common implementation of Finite Control Set MPC (FCS-MPC) considers a one-step prediction horizon, where the stage cost does not include the control effort term, as seen in several references [
25,
26,
27,
28,
30,
31].
The computational stage in Equation (
15) is more efficient when using the
-norm instead of the
-norm. This is advantageous from a computational perspective, particularly because Model Predictive Control (MPC) must operate in real time, often within a few tens of microseconds. Consequently, much of the literature focuses on the
-norm. However, as noted in [
13], using an
-norm ensures closed-loop stability (or practical stability). In contrast, the
-norm can lead to closed-loop instability unless
. Setting
is not advisable as it results in the converter operating at its maximum switching frequency, and then, the stated switching frequency is limited to the chosen sampling interval. Moreover, operating at maximum switching frequency does not guarantee better performance, as demonstrated in Table 2 of [
16], the comparison involved two MPC formulations: one using the
-norm with
, and the other an unconstrained solution where
.
Results using
Figure 4 with Equation (
15) and Equation (
16) are presented in
Table 1 and
Table 2, respectively, showing sampling frequency and THD values for various sampling times. Results in
Table 1 were operating at maximum switching frequency as
, and in
Table 2 control effort was set to
.
Simulations were conducted for
Figure 4 with Equation (
15) and Equation (
16), respectively, with a prediction horizon corresponding to
and control effort tuning ranging from 0 to 4, incremented in steps of 0.01, in a bid to control the average switching frequency. Stability was lost for the 1-norm formulation(Equation (
15)) when
exceeded 2.53.
The cost function in Equations (
15) and (
16) is evaluated for all possible control input values in
Figure 5. However, as the prediction horizon increases, the number of possible values grows exponentially, making this approach computationally demanding. As previously discussed, increasing the prediction horizon offers benefits such as improved closed-loop stability and reduced THD. To balance these advantages with computational efficiency, the optimization problem is reformulated as follows.
2.3. Long Prediction Horizon MPC Formulation for PMSM Drive
The
Figure 6 represents the reformulated optimization problem for long prediction with the cost function block illustrated in
Figure 4 incorporated in the sphere decoding algorithm block. Here, the system model is formulated as a continuous-time prediction model in a state space form by solving the set of equations:
where the matrices
and
are the system and input matrices in continuous-time, with dimensions of
and
, respectively. The matrices A and B defined are dependent on the system and can be considered to be both time-variant or time-invariant. Moreover, the output matrix
is time-invariant with a dimension of
, which is used to define
y from the available
x. Here,
x stands for the plant state vector consisting of
number of system states
that fully defines the dynamics of the system.
The controlled plant-input vector, u, comprises number of control plant-input which are the manipulated variables that belong to an integer-valued finite control set (FCS), , which is expressed as =. The output vector, y, is composed of output variables of the system which are a function of the state variables . Then, the called feed-forward matrix D is neglected or assumed to be zero, as in most power electronics control applications this direct relationship is generally absent without any loss of generality.
Thus, the PMSM system in state-space form can be represented by the following matrices:
As stated earlier the MPC controller is in the discrete time-domain, therefore the above matrices are discretised using the forward Euler approximation such that:
Matrix B is multiplied by the Clarke and Park transforms in the dq frame, where the Park transform (
) is given by:
and the Clarke transform (
) by:
By inserting Equation (
17) into Equation (
18), we obtain:
where the matrices
and
are defined as :
Recalling that the cost function in Equation (
16) has two parts, the tracking and the control effort for the tracking effort, the tracking effort is represented as
:
Similarly, the second term in the cost function (Equation (
16)), the control effort can be rewritten as:
Where matrices
S and
E are defined as:
Summing up Equation (
21) and Equation (
20) yields the cost function in vector notation:
Then, the cost function can be reformulated according to [
14,
32] as:
where:
and,
The term
is independent of
and has no effect on the optimal solution, thus can be omitted. Therefore, when substituting back into the , it gives:
also subject to the constraint conditions
, and
.
The solution obtained from Equation (
27) without considering these constraints is known as the unconstrained solution. While this solution may not be directly applicable to the converter due to disregarding the system constraints, it serves as a starting point for finding the constrained solution given by:
The matrix
H being symmetric and positive definite (
), ensures its Cholesky factorization exists and yields to a unique lower triangular matrix
V. This property is crucial for the optimization process, as it allows for efficient computation of the constrained solution. Cholesky factorization decomposes the positive definite matrix
H into the product of a lower triangular matrix
V and its transpose,
[
33], i.e., with
.
The cost function can then be expressed in terms of
V and
as:
Geometrically, the matrix V serves as a lattice generator matrix, defining a discrete space where the optimal solution resides. This transformation allows us to represent the optimization problem in a new space where the constraints are simplified and the problem becomes computationally tractable for long prediction horizons. In this transformed space, the optimization problem involves finding the control sequence that minimizes the distance J to the unconstrained solution , while satisfying all system constraints. Operating in the transformed space reduces the computational complexity of the optimization problem, making it feasible for practical applications in power converters.
2.4. Sphere Decoding Algorithm Implementation for the PMSM Drive
The challenge in Equation (
29) which relates to finding the shortest distance between two vectors, is known as the closest point problem, where several conventional algorithms have been already addressed in [
34].
Two algorithms are highlighted, known as the Pohst and Kannan algorithms, with the former using a hypersphere for the devising of methods regarded as sphere decoders such as the SDA although it was been primarily applied in communication theory. Nonetheless, in the context of power electronics, specifically in addressing the Long Prediction Horizon (LPH)-FCS-MPC problem for power converters, a modified sphere decoding algorithm has been developed and adapted [
14],this approach tailors the SDA to suit the requirements of power converter control. This problem can be interpreted as minimizing the hypersphere of radius
, which corresponds to the value of the cost function, centered at
. The Sphere Decoding Algorithm (SDA) evaluates only those candidate solutions that lie within the computed hypersphere, selecting the one with the smallest cost function as the optimal solution. Specifically, the optimal solution
is the
n-dimensional lattice point that has the minimum Euclidean distance from the unconstrained solution
as shown in
Figure 5. Equivalently, this solution is the unique lattice point enclosed within the smallest hypersphere centered at
with radius
.
A key advantage of SDA is that it ensures optimality with significantly higher computational efficiency compared to the exhaustive enumeration used in
Figure 7, coupled with the fact that it does not need to evaluate every possible control input, reducing the exponential computational burden when the prediction horizon is increased. The efficiency of SDA is largely dependent on the initial choice of
, which must be small enough to minimize the number of evaluated nodes, but not too small as to exclude all possible solutions. The initial radius is computed as proposed in [
35]:
where
and,
These radii are based on two different approximations: the “
Babai estimate”
and the “
educational guess”
. The Babai estimate represents the rounded unconstrained solution to the nearest integer vector:
whereas the educational guess is given by the previously applied optimal solution
shifted by one time step. Once
is determined, following the receding horizon policy, only its first element is applied by the converter, while the remaining elements are discarded. The process then repeats at the next time step over a shifted prediction horizon, incorporating updated measurements and estimates.
After determining the initial radius, the algorithm explores the search tree, evaluating one switching element at a time, effectively reducing the problem to a one-dimensional search at each step. The distance of the first selected element from the unconstrained solution is calculated, and if it falls within the sphere’s boundary, the algorithm proceeds with that branch. Otherwise, the entire branch is discarded, as no further elements from that branch can contribute to a feasible solution within the sphere. This pruning mechanism is fundamental to the SDA and makes it well-suited for long prediction horizons.
Once a feasible solution is found, the radius is recalculated and updated, further refining the search space. This iterative process continues, progressively tightening the sphere’s boundary, thereby eliminating more suboptimal solutions. The final solution obtained at the end of this process is declared optimal.
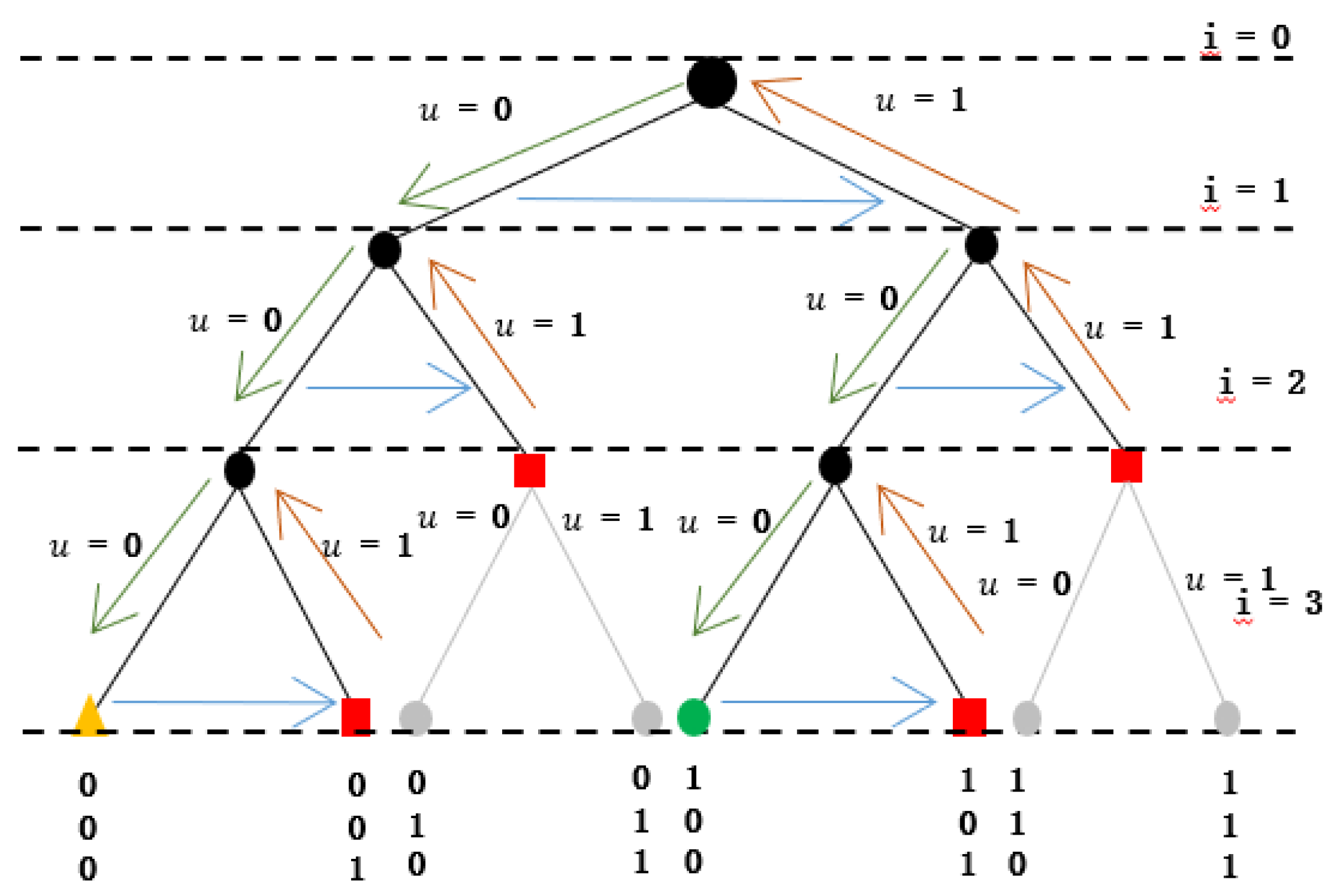
Figure 8 illustrates the operation of the sphere decoding algorithm for
. At each node in the search tree, the algorithm calculates the cumulative squared deviation up to the current step, and then compares it against the squared radius. If the current node’s cost exceeds the radius (yellow triangle), the branch is pruned (grey) and the algorithm backtracks (orange arrow) to explore other nodes. This simplifies the verification process and enhances computational efficiency, ensuring that the sphere decoding algorithm can quickly and effectively prune branches of the search tree that cannot lead to a valid solution within the prescribed radius. When the algorithm reaches a bottom node and finds a candidate solution within the current sphere, it tightens the sphere around this solution. The process is repeated over and over, further tightening the sphere to fewer and fewer candidate solutions, thus refining the search. The SDA terminates when the entire search tree has been explored; only at this point can the algorithm guarantee that the found solution is optimal (green circle) having examined all possible candidate solutions within the defined sphere.
4. Conclusions
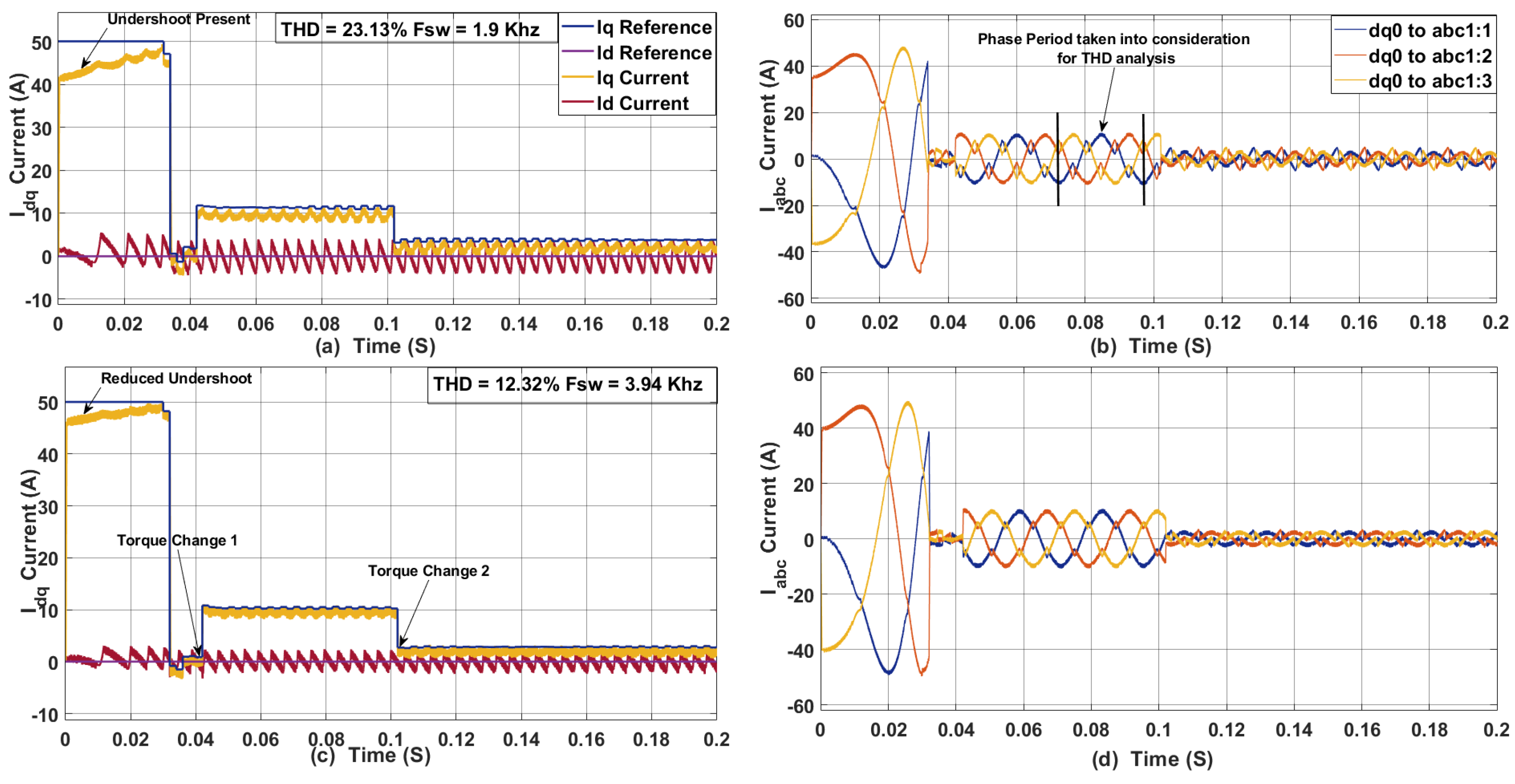
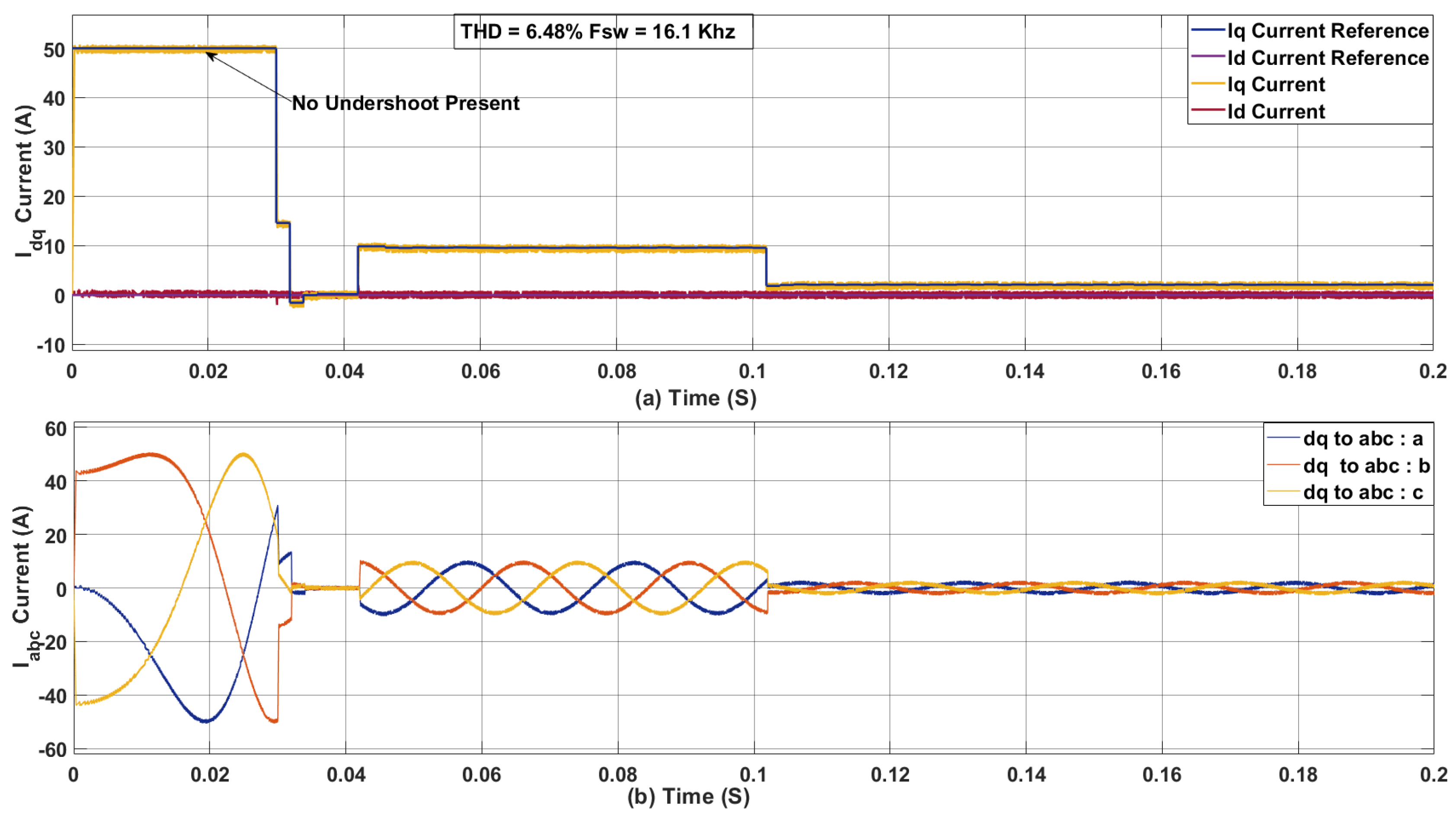
In this paper, we investigated the performance of a Sphere Decoding Algorithm (SDA)-based Finite Control Set Model Predictive Control (FCS-MPC) for PMSM drives, with a particular focus on the effects of sampling time, control effort weighting, and parameter mismatches. Our simulation results demonstrate that at longer sampling times (40 and 80 , significant undershoot occurs in the current response. As the sampling time is reduced below 40 the undershoot gradually diminishes and disappears entirely at a 10 ampling time. At this shorter sampling time, while the inclusion of a control effort term successfully reduces the switching frequency, a small undershoot remains, indicating that the predicted output closely follows the reference but does not perfectly align with the midpoint of the desired waveform. Furthermore, our investigation into parameter mismatches revealed that variations in resistance and flux linkage have a negligible effect on the system’s THD and switching frequency. In contrast, inductance mismatches significantly impact the controller’s performance. Depending on the magnitude of the inductance error, the system sometimes compensates by increasing the switching frequency; however, for severe mismatches, the system can become unstable. This outcome underscores the critical importance of accurate inductance estimation in ensuring effective current tracking and maintaining low THD.
From an aerospace perspective, achieving low torque ripple and high efficiency is paramount for PMSM applications in electric propulsion and actuation systems. The findings suggest that optimizing the prediction horizon and control effort weighting can significantly improve dynamic performance, reducing electromagnetic interference and enhancing system reliability in aircraft environments where precise control is essential. Looking ahead, future research should focus on enhancing the robustness of the SDA-based FCS-MPC approach in the presence of parameter mismatches. One promising direction is the integration of Recursive Least Squares (RLS) for real-time parameter estimation. RLS can continuously update key parameters such as resistance, inductance, and flux linkage, mitigating the adverse effects of mismatches and enabling the controller to maintain optimal performance despite variations due to temperature, aging, or manufacturing tolerances. Additionally, exploring hybrid adaptive estimation methods, such as combining RLS with an Extended Kalman Filter, may further improve noise rejection and estimation accuracy. Experimental validation on a physical PMSM setup under various operating conditions, including thermal and load variations, will be sought in future studies to confirm the practical viability of the proposed solutions in aerospace applications.
Author Contributions
Conceptualization, all authors; methodology, J.A., Y.G., and S.V.; software, J.A., and X.Y.; validation, J.A., Y.G., X.Y., and S.V.; formal analysis, all authors; investigation, J.A., and Y.G.; resources, J.A., Y.G., and H.S.R.; data curation, J.A., and Y.G.; writing—original draft preparation, J.A.; writing—review and editing, all authors; supervision, Y.G., S.V., and H.S.R.; project administration, Y.G., and H.S.R. All authors have read and agreed to the published version of the manuscript.
Figure 1.
Different Control Methods for Motor Drvies
Figure 1.
Different Control Methods for Motor Drvies
Figure 2.
Categories of MPC
Figure 2.
Categories of MPC
Figure 3.
Different Aspects in MPC
Figure 3.
Different Aspects in MPC
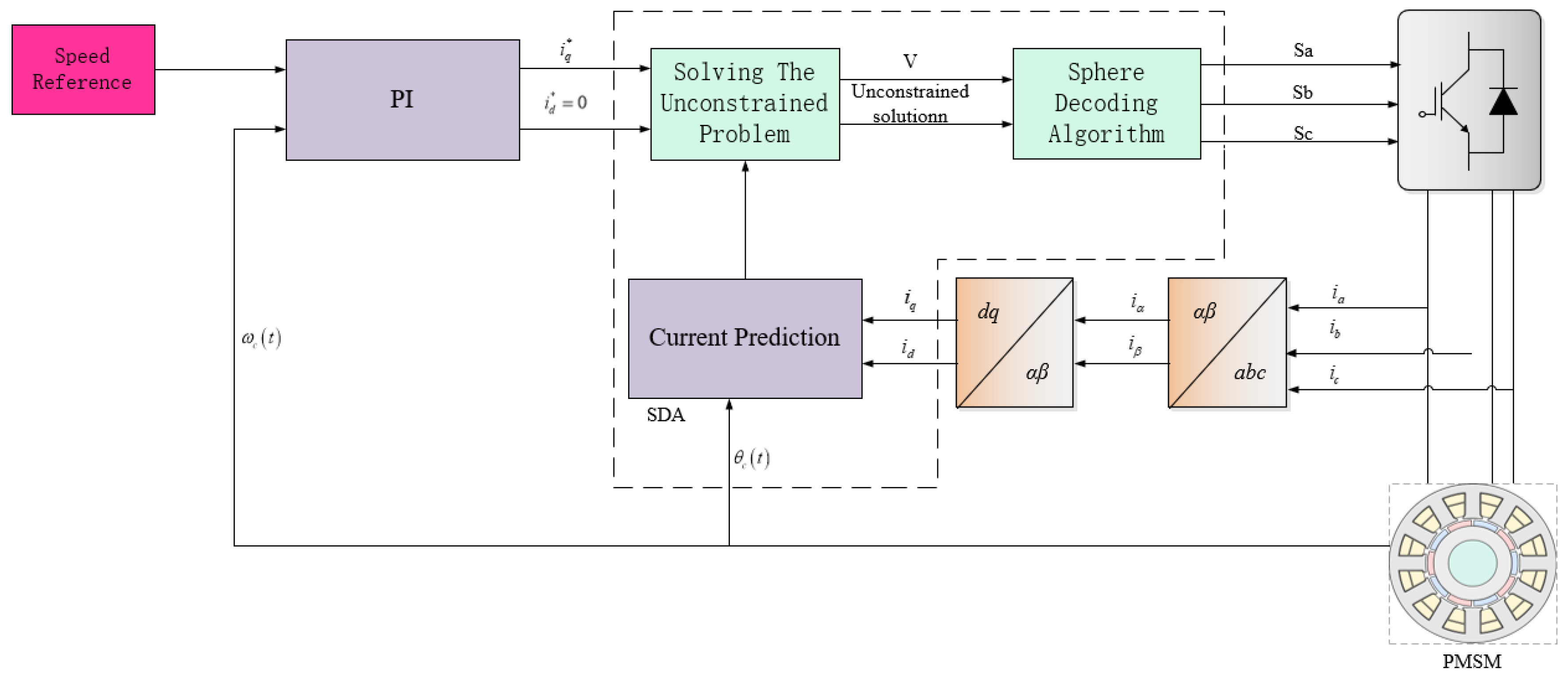
Figure 4.
Illustration of FCS-MPC for PMSM Drive
Figure 4.
Illustration of FCS-MPC for PMSM Drive
Figure 5.
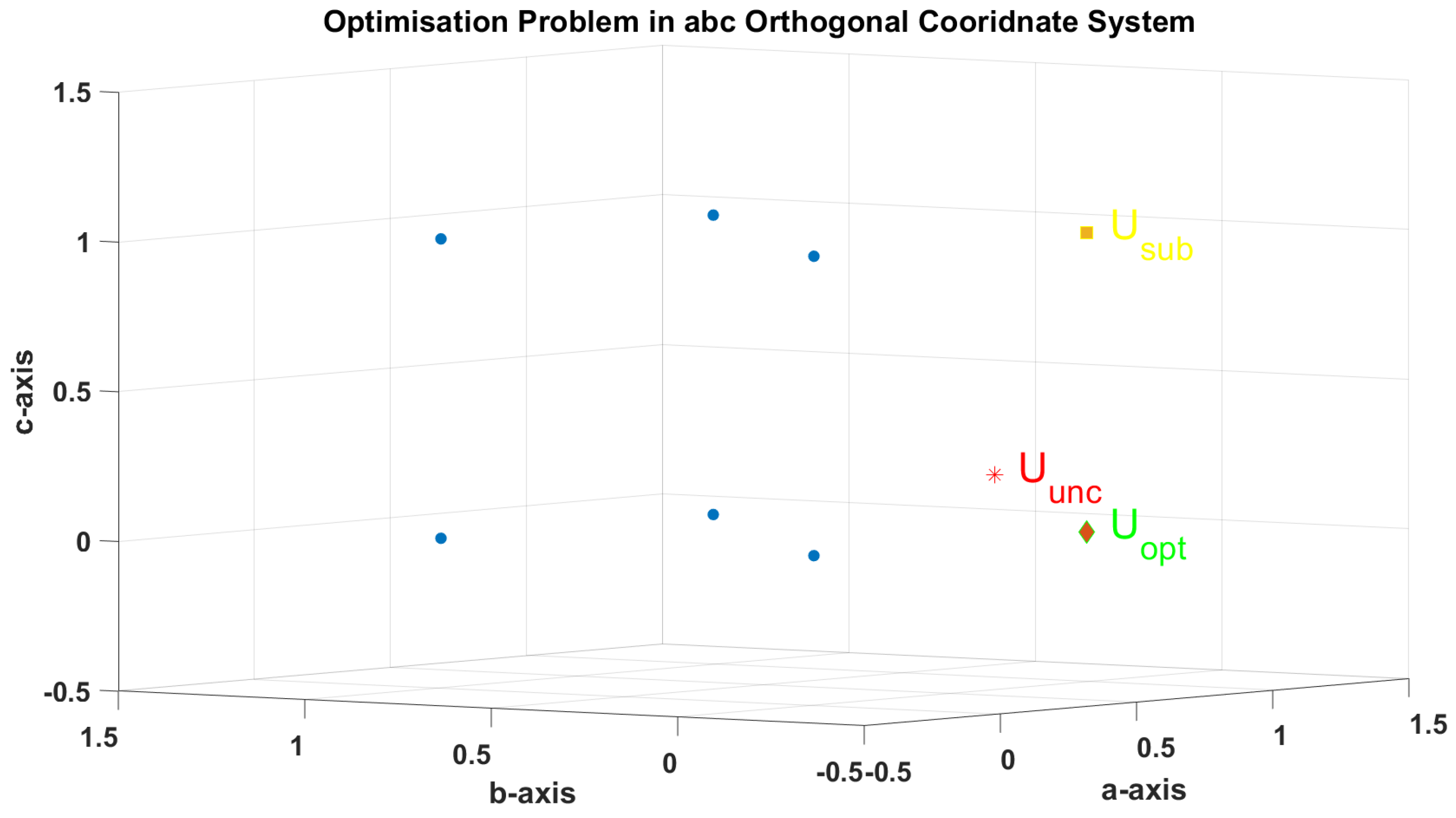
Visualization of FCS-MPC problem with in the original abc axis, the unconstrained solution is shown in red, the suboptimal solution shown in yellow, and the optimal solution is shown in green.
Figure 5.
Visualization of FCS-MPC problem with in the original abc axis, the unconstrained solution is shown in red, the suboptimal solution shown in yellow, and the optimal solution is shown in green.
Figure 6.
Illustration of Sphere Decoding Algorithm for PMSM Drive.
Figure 6.
Illustration of Sphere Decoding Algorithm for PMSM Drive.
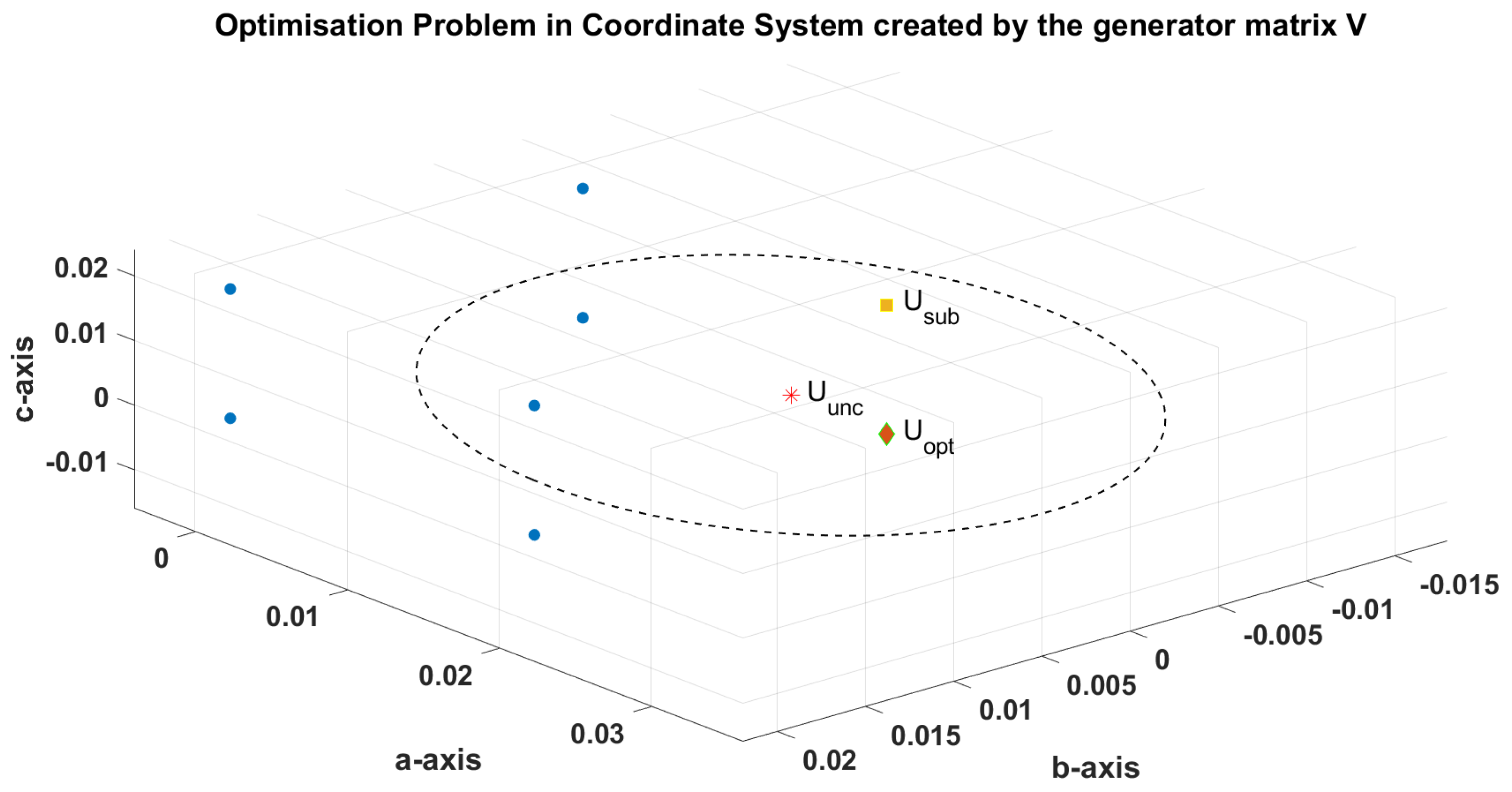
Figure 7.
Visualization of FCS-MPC problem with in abc plane transformed by generator matrix V.
Figure 7.
Visualization of FCS-MPC problem with in abc plane transformed by generator matrix V.
Figure 8.
One step horizon search tree for a three phase two-level inverter explored by the SDA algorithm. Blue arrows indicates side tracking, orange arrow indicates backtracking, green arrow depth first search progessing to the bottom layer. Current incumbent solution (yellow triangle), green circle (Optimal Solution).
Figure 8.
One step horizon search tree for a three phase two-level inverter explored by the SDA algorithm. Blue arrows indicates side tracking, orange arrow indicates backtracking, green arrow depth first search progessing to the bottom layer. Current incumbent solution (yellow triangle), green circle (Optimal Solution).
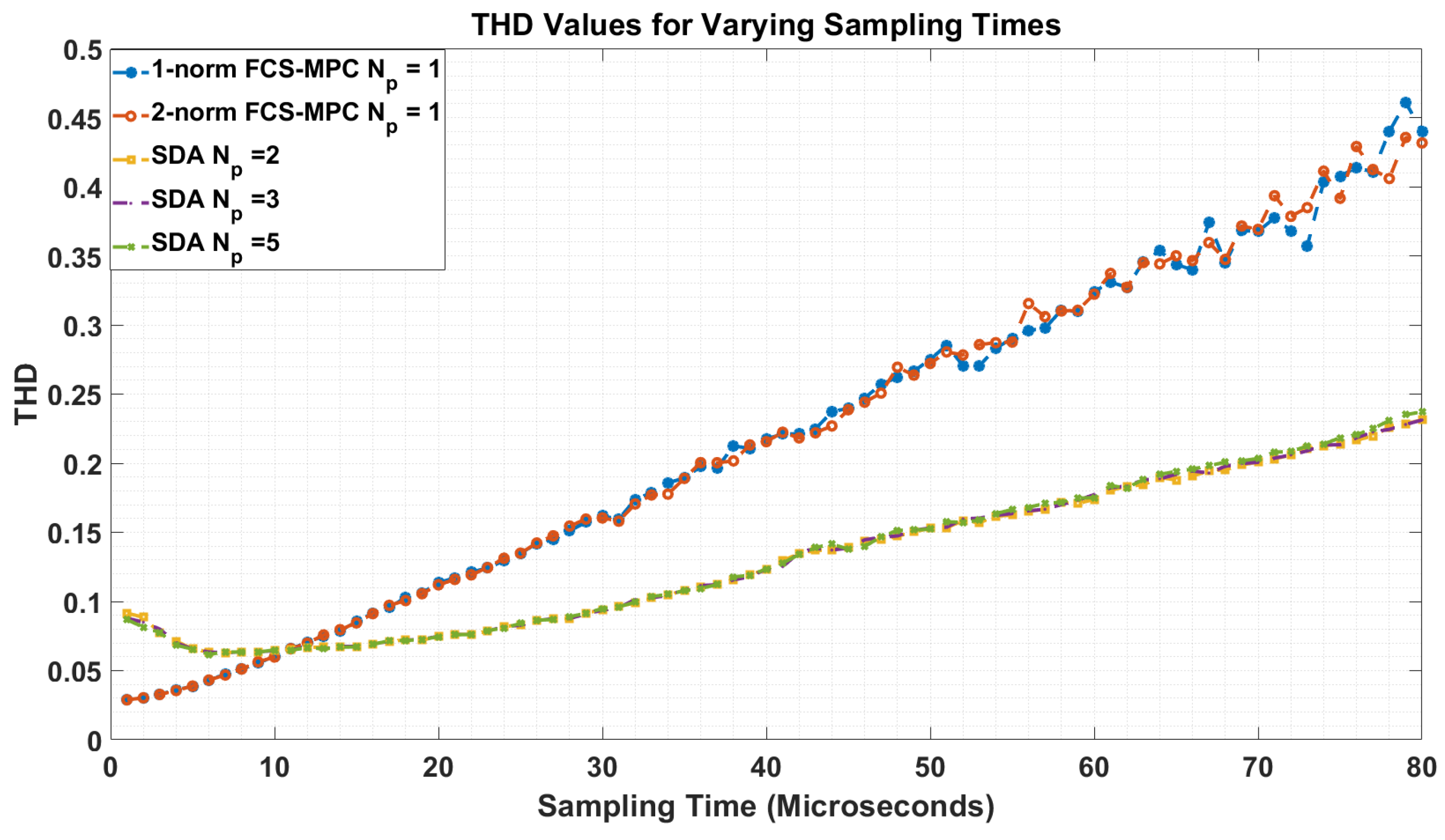
Figure 9.
THD for Various Sampling Times for FCS-MPC and SDA with .
Figure 9.
THD for Various Sampling Times for FCS-MPC and SDA with .
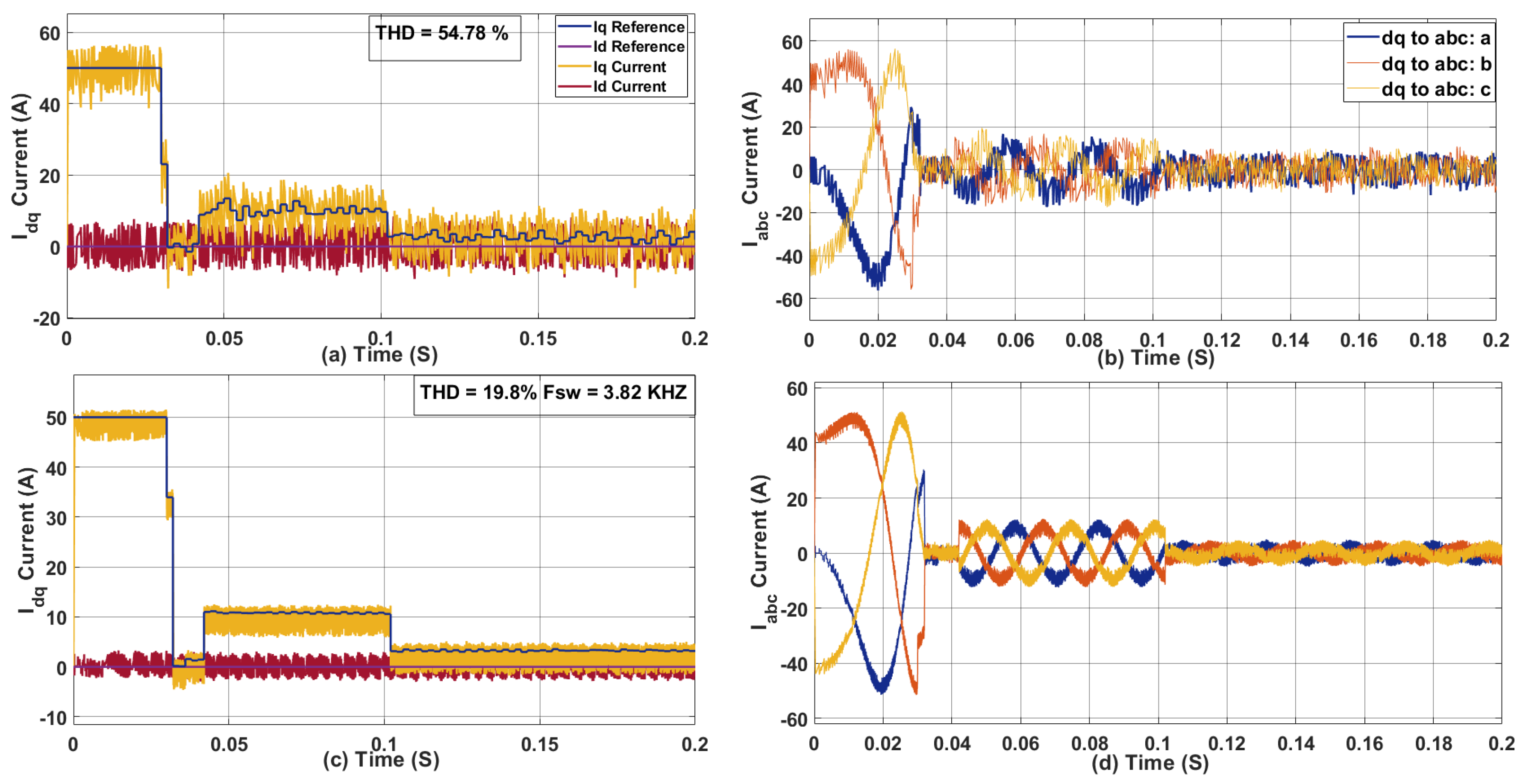
Figure 10.
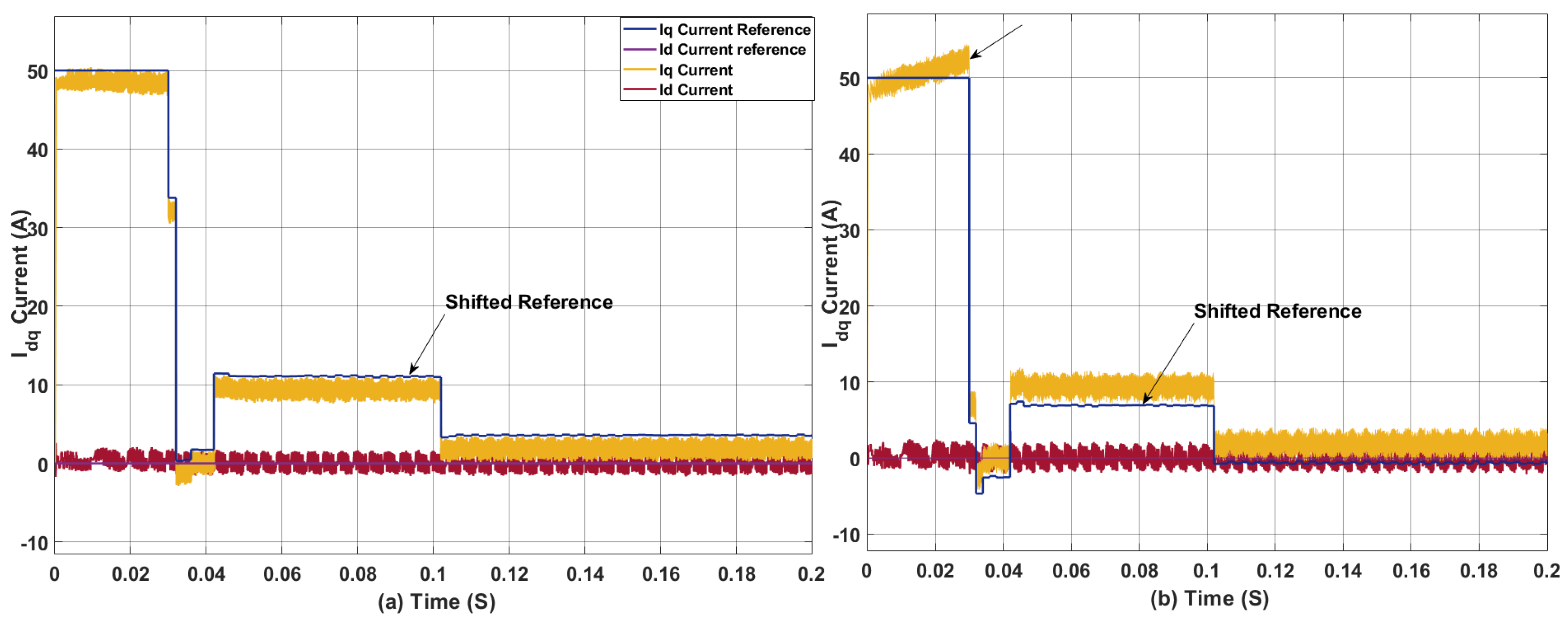
(a) Current in dq axis for 80 ith . (b) Current in abc axis for 80 (c)Current in dq axis for 40 ith .(d) Current in abc axis for 40
Figure 10.
(a) Current in dq axis for 80 ith . (b) Current in abc axis for 80 (c)Current in dq axis for 40 ith .(d) Current in abc axis for 40
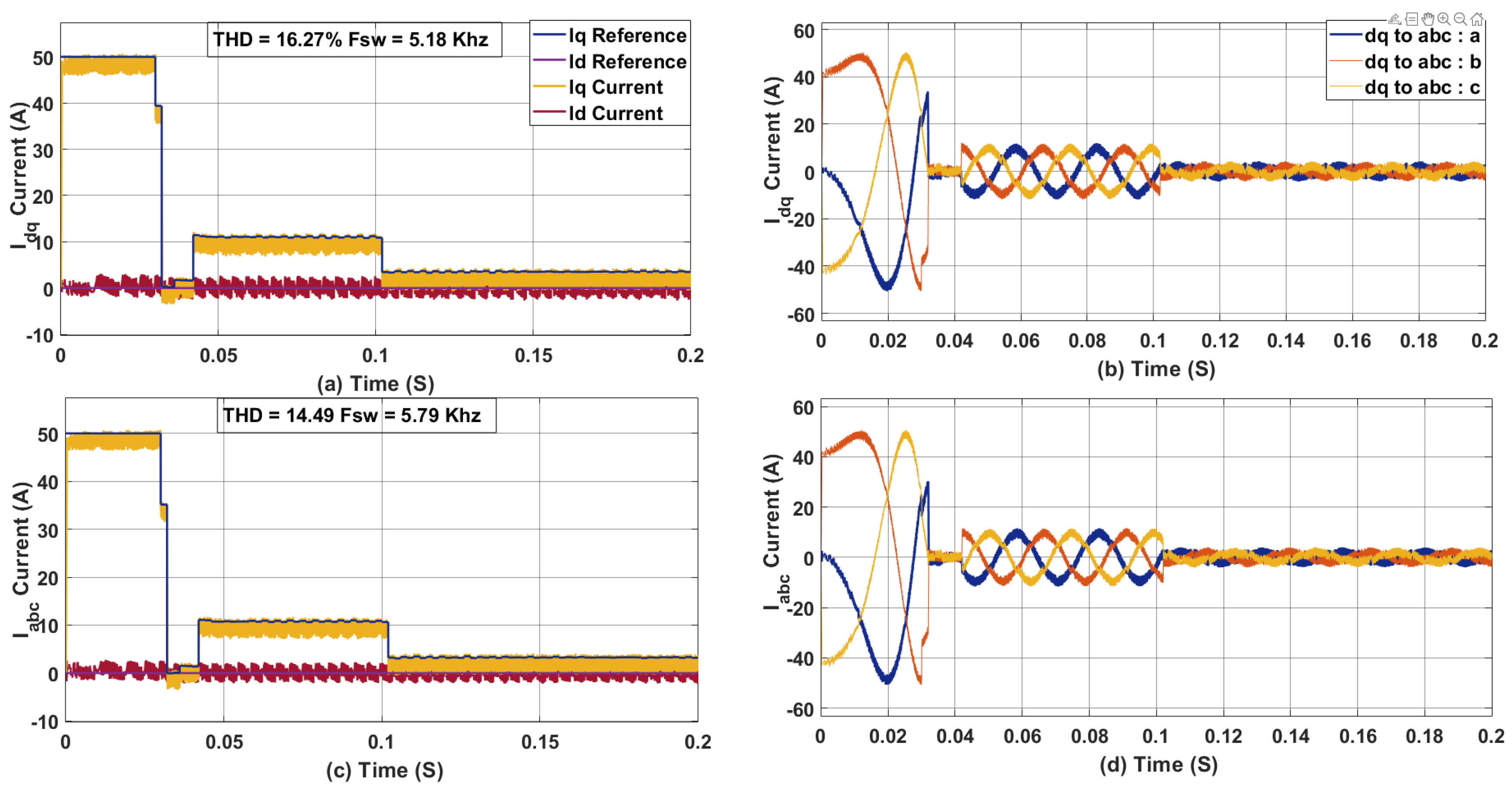
Figure 11.
(a) dq axis Current for a two SDA with for 10 (b) abc axis current for a two SDA with for 10
Figure 11.
(a) dq axis Current for a two SDA with for 10 (b) abc axis current for a two SDA with for 10
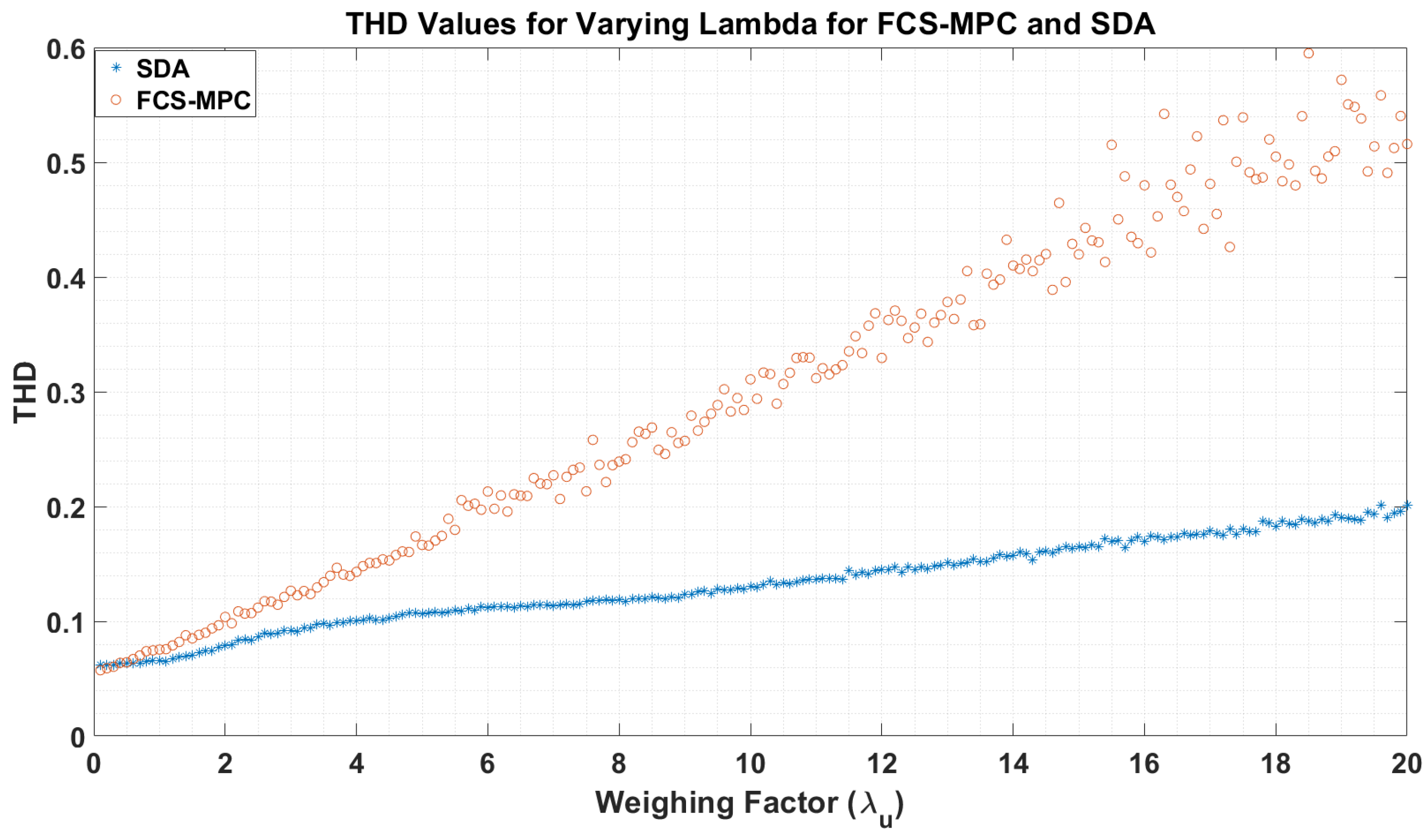
Figure 12.
Effect of Weighing Factor on FCS-MPC with 2-norm and SDA with .
Figure 12.
Effect of Weighing Factor on FCS-MPC with 2-norm and SDA with .
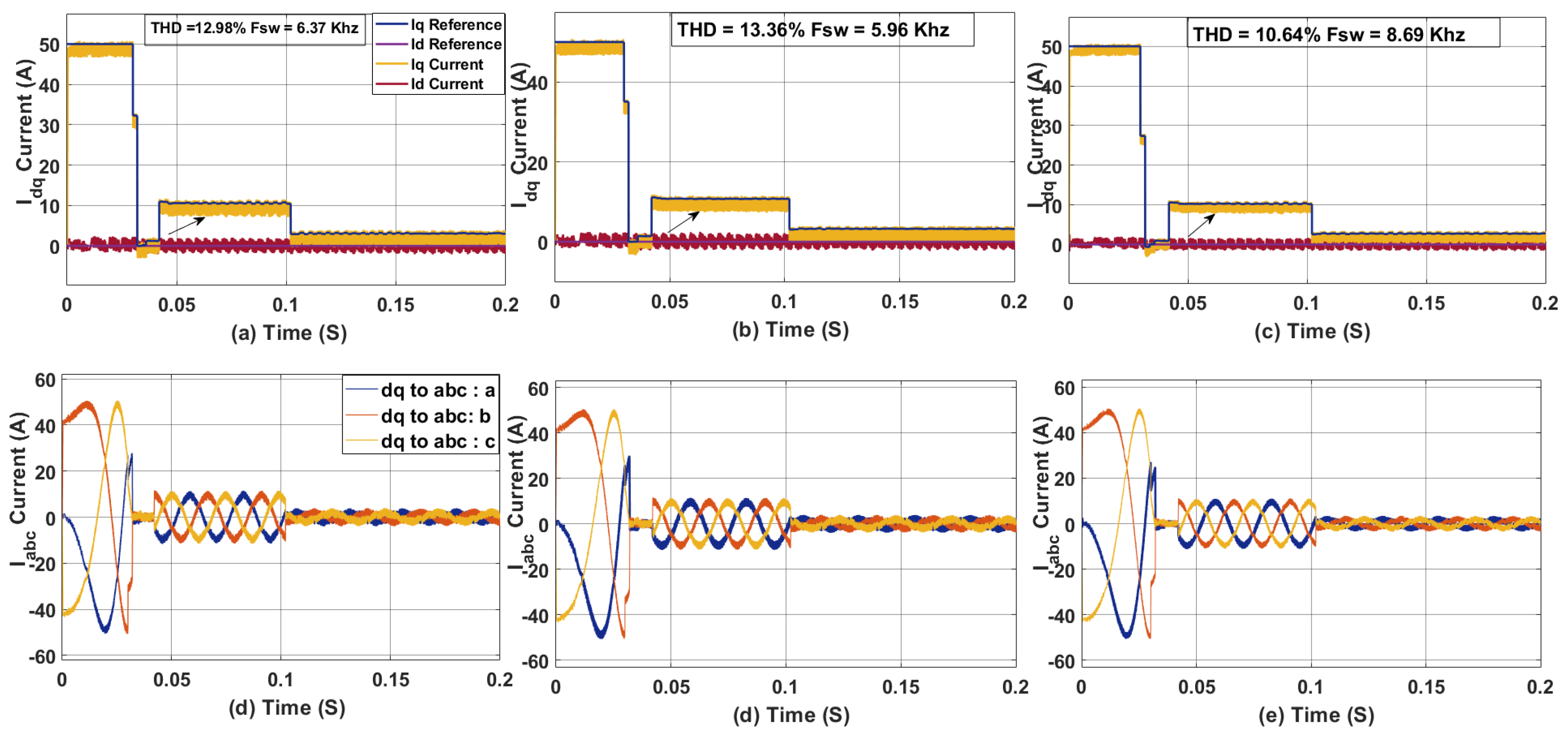
Figure 13.
(a) Current in dq axis for 10 ith for a single step FCS-MPC with 2-norm(b) Current in abc axis for 10 ith for a single step FCS-MPC with 2-norm. (c) Current in dq axis for 10 ith for a two step SDA(d) Current in abc axis for 10 ith for a two step SDA.
Figure 13.
(a) Current in dq axis for 10 ith for a single step FCS-MPC with 2-norm(b) Current in abc axis for 10 ith for a single step FCS-MPC with 2-norm. (c) Current in dq axis for 10 ith for a two step SDA(d) Current in abc axis for 10 ith for a two step SDA.
Figure 14.
(a) Current in dq axis for 10 ith for a three step SDA(b) Current in abc axis for 10 ith for a three step SDA. (c) Current in dq axis for 10 ith for a five step SDA(d) Current in abc axis for 10 ith for a five step SDA.
Figure 14.
(a) Current in dq axis for 10 ith for a three step SDA(b) Current in abc axis for 10 ith for a three step SDA. (c) Current in dq axis for 10 ith for a five step SDA(d) Current in abc axis for 10 ith for a five step SDA.
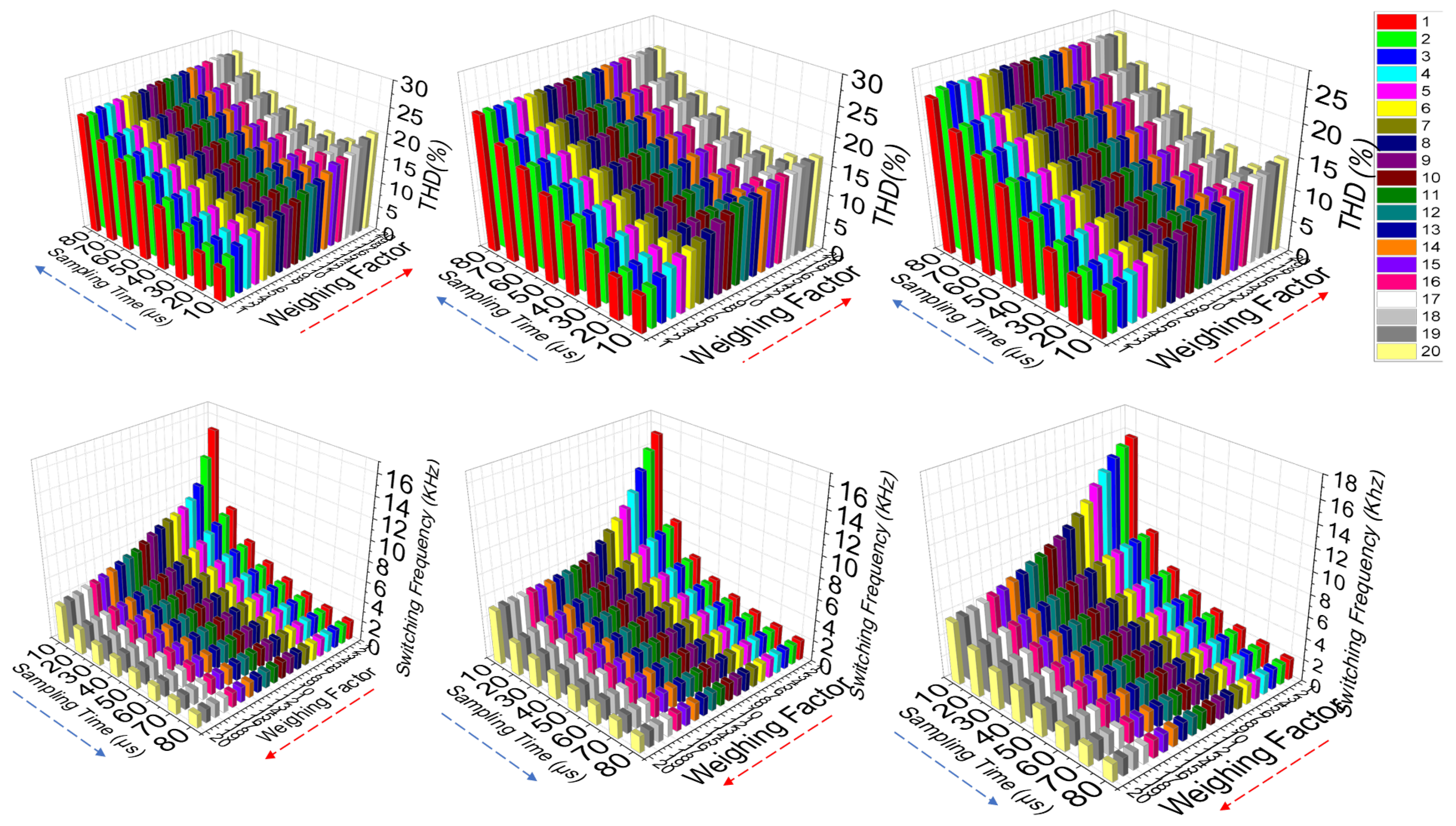
Figure 15.
(a) Top and Bottom Figure (left): Effect of Sampling time and weighing factor effect on a two step prediction SDA THD and average switching frequency . (b)Top and Bottom Figure (Middle): Effect of Sampling time and weighing factor effect on a three step prediction SDA THD and average switching frequency(c)Effect of Sampling time and weighing factor effect on a five step prediction SDA THD and average switching frequency.
Figure 15.
(a) Top and Bottom Figure (left): Effect of Sampling time and weighing factor effect on a two step prediction SDA THD and average switching frequency . (b)Top and Bottom Figure (Middle): Effect of Sampling time and weighing factor effect on a three step prediction SDA THD and average switching frequency(c)Effect of Sampling time and weighing factor effect on a five step prediction SDA THD and average switching frequency.
Figure 16.
(a) Current in dq axis for 10 ith for a two step SDA(b) Current in abc axis for 10 ith for a two step SDA. (c) Current in dq axis for 10 ith for a three step SDA(d) Current in abc axis for 10 ith for a three step SDA. (e) Current in dq axis for 10 ith for a five step SDA(f) Current in abc axis for 10 ith for a five step SDA.
Figure 16.
(a) Current in dq axis for 10 ith for a two step SDA(b) Current in abc axis for 10 ith for a two step SDA. (c) Current in dq axis for 10 ith for a three step SDA(d) Current in abc axis for 10 ith for a three step SDA. (e) Current in dq axis for 10 ith for a five step SDA(f) Current in abc axis for 10 ith for a five step SDA.
Figure 17.
This is a figure. Schemes follow the same formatting. If there are multiple panels, they should be listed as: (a) Current in dq axis for 10 ith for a two step SDA with paramter mismatch (b) Current in dq axis for 10 ith for a two step SDA with paramter mismatch .
Figure 17.
This is a figure. Schemes follow the same formatting. If there are multiple panels, they should be listed as: (a) Current in dq axis for 10 ith for a two step SDA with paramter mismatch (b) Current in dq axis for 10 ith for a two step SDA with paramter mismatch .
Table 1.
Sampling , Switching Frequency and THD for a norm cost function
Table 1.
Sampling , Switching Frequency and THD for a norm cost function
| Sampling Time
|
Sampling Frequency (KHz) |
Switching Frequency (KHz) |
THD(%) |
| 20 |
50 |
9.87 |
10.67 |
| 40 |
25 |
4.94 |
21.16 |
| 80 |
12.5 |
2.51 |
41.85 1
|
Table 2.
Sampling , Switching Frequency and THD for a norm cost function
Table 2.
Sampling , Switching Frequency and THD for a norm cost function
| Sampling Time
|
Sampling Frequency (KHz) |
Switching Frequency (KHz) |
THD(%) |
| 20 |
50 |
9.84 |
10.75 |
| 40 |
25 |
4.76 |
21.04 |
| 80 |
12.5 |
2.39 |
42.32 1
|
Table 4.
Resistance Parameter Mismatch
Table 4.
Resistance Parameter Mismatch
| Prediction Horizon
|
5*
|
0.2*
|
10*
|
| 2-Step |
12.97 (6.995
|
13.01 (7.034
|
13.13(6.97
|
| 3-Step |
13.00 (6.545
|
12.99 (6.547
|
13.38(6.325
|
| 5-Step |
10.15(9.543
|
10.08(9.543
|
10.14(9.3607 1
|
Table 5.
Flux Mismatch
| Prediction Horizon
|
0.1*
|
0.5*
|
2*
|
5*
|
| 2-Step |
13.05 (6.98
|
12.81 (7.0282
|
12.69(7.0051) |
13.07 (7.0355
|
| 3-Step |
13.10 (6.585
|
13.22 (6.6065
|
13.19 (6.5679
|
13.13 (6.5767
|
| 5-Step |
10.27(9.4064
|
9.97(9.5314
|
9.70 (9.4994
|
10.07 (9.4714 ( 1
|
Table 6.
Inductance Parameter Mismatch
Table 6.
Inductance Parameter Mismatch
| Prediction Horizon
|
0.1*
|
0.5*
|
2*
|
5*
|
| 2-Step |
29.72 (1.58
|
12.85 (8.4147
|
18.37(4.4052) |
39.60 (3.108kHZ) |
| 3-Step |
29.67 (1.62
|
11.20 (10.448
|
12.48 (7.0995kHZ) |
22.22(4.3292
|
| 5-Step |
29.37(1.6717
|
9.57(13.647
|
13.20 (7.0751
|
12.09 (7.3826 ( 1
|