Economic Value Creation of Artificial Intelligence in Supporting Variable Renewable Energy Integration: A Systematic Review of Power System Applications

1. Introduction

The global energy landscape is transforming significantly with the increasing penetration of Variable Renewable Energy (VRE) sources such as wind, solar, geothermal, hydro, ocean, bioenergy, hydrogen, and hybrid systems [1,2,3]. This shift towards Renewable Energy Resources (RERs) is driven by the urgent need to reduce greenhouse gas emissions, combat climate change, and achieve sustainable development goals [4,5,6]. However, integrating VRE into existing power systems presents several economic and operational challenges, primarily due to these energy sources’ intermittent and variable nature [7,8].

Artificial Intelligence (AI) has emerged as a powerful tool for addressing these challenges, offering innovative solutions to optimize the integration of VRE into power systems [9]. AI technologies, including machine learning, neural networks, and optimization algorithms, can potentially enhance the economic efficiency and operational reliability of renewable energy systems [10,11]. By leveraging AI, power systems can improve generation and demand forecasting [12,13], market design [14], demand response [15,16], storage solutions [17,18], power quality [19], and predictive maintenance [20,21].

Despite the growing body of literature on AI applications in RERs, there is a notable gap in systematic reviews focusing on the economic aspects of VRE integration. This paper aims to bridge this gap by conducting a comprehensive review of the role of AI in creating economic value in the context of VRE integration. The review spans literature from 2014 to 2024, providing insights into AI-driven advancements, opportunities, and limitations in the renewable energy sector. The contributions of this review are given as:

• Identification and Evaluation of AI Use Cases

  This paper systematically identifies and evaluates use cases where AI tools create economic value in the electricity sector, specifically concerning VRE integration. By analyzing these use cases, we aim to provide a comprehensive understanding of how AI can be exploited to enhance economic efficiency in the integration process.

• Economic Impact Analysis

  This review assesses the estimated economic impact of various AI applications in VRE integration. We explore the challenges in measuring the value created by AI in reducing integration costs, providing a detailed analysis of the potential economic benefits and limitations.

• Emphasis on Economic Value Creation

  Unlike previous studies, primarily focused on performance metrics, this work emphasizes the importance of economic value creation of AI tools. We highlight how AI contributes to cost reduction, improved operational efficiency, and overall economic sustainability in the power sector.

By addressing these contributions, this paper seeks to highlight AI’s critical role in VRE integration optimization, ultimately facilitating a more resilient and economically sustainable energy landscape. The findings of this review aim to inform policymakers, researchers, and industry stakeholders about the potential of AI in transforming the renewable energy sector.

The remaining sections of this study are structured as follows: Section 2 is dedicated to scope and methodology, Section 3 elaborates on the role of AI in renewable energy systems, Section 4 describes the economic aspect of AI fostering the integration of VRE in power systems, Section 5 discusses the future challenges and limitations of AI, and Section 6 presents the conclusion.

2. Scope and Methodology

2.1. Scope of the Review

This review paper aims to examine and clarify the potential economic value of AI in supporting the integration of VRE sources. The study focuses on the economic aspects of VRE integration, an area that has received limited attention in previous literature despite its importance for decarbonization efforts. The review systematically analyzes how AI can effectively foster VRE integration, using an economic model from existing literature. Identification and evaluation of use cases are done where AI tools create economic value in the electricity sector, specifically concerning VRE integration. The scope also includes an analysis of the estimated economic impact of these use cases and an exploration of the challenges in measuring the value created by AI in reducing VRE integration costs. This study emphasizes the economic value creation of AI tools, rather than merely improvements in performance metrics. The literature considered spans from 2014 to 2024 and includes only English language sources.

2.2. Methodology

2.2.1. Literature Search Strategy

A systematic literature review approach has been employed by adapting the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) methodology. The web databases used for literature search include Google Scholar, Science Direct, and IEEE Xplore and various keywords have been used for joint search such as "artificial intelligence," "machine learning," "electricity," "value creation," "renewable energy," "variable energy sources," and "integration cost." To ensure comprehensive coverage, we also reviewed relevant references from identified articles, as well as sectorial reports and technology blogs.

2.2.2. Selection and Screening Process

The initial search yielded 827 articles after sorting the duplicates followed by an abstract screening, which reduced the pool to 200 articles by excluding those not related to VRE integration costs in the energy sector. A subsequent full-text review further narrowed the selection based on three key criteria: focus on reducing VRE integration costs, alignment with our AI definition (presented in Section 1 of the paper), and inclusion of information about AI tool value creation. We excluded articles that focused solely on improving performance metrics without relating to value creation. This rigorous process resulted in a final selection of 41 references for in-depth analysis.

2.2.3. Data Analysis and Synthesis

The selected articles are categorized using a framework of integration costs, which is presented in Section 3. The synthesis of findings addresses key questions regarding AI use cases, their economic impact, and challenges in value measurement. To aid in presentation and analysis, key findings are summarized in various tables that present the key references discussed throughout the article.

2.2.4. Limitations and Bias Considerations

We acknowledge potential selection biases in our review process. These include subjectivity in determining whether tools align with our AI definition, as presented in Section 1 of the paper. Moreover, the possibility of low representation of negative outcomes or value-destroying cases in the published literature is also acknowledged. These limitations are considered in the analysis and conclusions to ensure a balanced and critical review of the available evidence.

3. AI in Renewable Energy System

The application of AI in RERs is becoming very common for design, estimation, optimization, distribution, management and policy. This section details the applications of AI for the most commonly used RERs [21,22,23,24,25].

3.1. AI in Wind Energy

In pertinent literature, several reviews discuss the use of AI in wind energy [26,27,28,29,30]. In [26,27], a brief overview of existing statistical, physical, correlation and neural network approaches for power and wind speed estimation is presented. An overview of data mining methods used for the estimation of wind power is provided in [28]. In this work, the extremely short, intermediate, medium, and long-term wind power estimations are covered in four categories. Similarly, [30] examined data mining techniques for forecasting short-term wind speed and power. Three categories of probabilistic models: short, medium, and long term, for forecasting wind power are listed in [29].

Relevant research indicates three main categories of AI used in wind energy: neural, statistical, and evolutionary learning. These categories are integrated to create hybrid AI methods [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59]. Many studies focus on wind power and speed prediction using AI neural learning techniques [31,32,33]. Mabel et al. estimate wind output over three years from seven wind farms using a neural network with feed-forward backpropagation (BPNN) [31]. The training and test data sets’ Root Mean Square Errors (RMSEs), for the BPNN, are 0.0070 and 0.0065, respectively, indicating excellent prediction accuracy. Three different ANN approaches, Radial Basis Function Neural Network (RBFNN), BPNN, and Adaptive Linear Element Network (ADALINE) have been used to estimate wind speed from the two locations. There has also been a comparison of the three models’ performances [32]. While the effectiveness of ANN approaches varies depending on the location of wind farms, the RBF approach yields the best results (minimum RMSE of 1.444) for a single site. The BPNN yields RMSE of 1.254 at minimum for a single site. Through trial and error, Mabel et al. [33] improved the BPNN setup for wind power estimation. With relative humidity, generation hours and wind speed as inputs, a 3-5-1 ANN yields the optimal estimating results (Mean Square Error (MSE) of $7.6\times {10}^{-3}$).

Since ANN techniques’ performances are inconsistent, certain changes have been recommended to increase their efficiency [34]. In certain studies, additional methods have also been incorporated for comparison [35,36,37,38,39]. Recurrent high-order neural networks, an advanced kind of ANN, were used for wind power estimation by Karnataka’s et al. [34]. The ANN model’s performance is juxtaposed with the Naïve Bayes (NB) approach. The lowest RMSE of 4.2 is achieved by the ANN in comparison to the NB. For the years 1993–1997, the Marmara’s wind speed was spatially forecasted using the BPNN approach [35]. A comparison is made between the efficiency of the ANN model and the Trigonometric Point Cumulative Semi Variogram (TPCSV) method. For the majority of months and sites, ANN yields an increased coefficient of correlation between predicted and actual wind speed. For instance, in January, for the Canakkale site, the correlation coefficients for ANN and TPCSV were 0.95 and 0.88, respectively. According to Alexiadis et al.’s research [36], the BPNN approach significantly increases wind speed and wind power estimation accuracy by $20-40\%$ when compared to the persistent forecasting model. To anticipate wind speed from the two wind farms, the Bayesian Combination (BC) methodology, ADALINE, BPNN, and RBFNN techniques were used by Li et al. [37]. When compared to ANN approaches, the BC method yields a more reliable and superior result estimation (RSME of 1.5). The analysis of twelve estimating strategies, with the non-linear ANN methods of Neural Logic Networks (NLN) and the Auto Regressive Moving Averages (ARMA) approaches, has been reported [38]. The approaches applied wind speed data having hourly resolution. Compared to other approaches, NLN demonstrates the best results (RMSE improvement of 4.9%). During two years, from 2004 to 2005, Cadenas et al. [39] employed BPNN to forecast wind speed with information gathered from Mexico’s Chetumal wind farm in Quintana Roo. The ANN and Single Exponential Smoothing (SES) methods’ performances are compared. Compared to the SES approach (MAE of 0.5617), the earlier approach works better (MAE of 0.5251).

Fuzzy logic [40] and its integration with ANN approaches were also investigated in various papers [40,41,42] for wind power forecasting. Simoes et al. [40] designed a wind generation system of 3.5 kW using fuzzy logic. The designed system can be implemented in the field and performs well. The combination of fuzzy logic with ANN, and RBFNN approaches was applied by Sideratos et al. [41] for wind power estimation. Findings are useful for the operational planning of wind farms, one to forty-eight hours in advance. Monfared et al. [42] have estimated the wind speed using the fuzzy and BPNN techniques. The suggested methods perform better than the conventional ones (RMSE of 3.27 and 3.30 for two strategies, respectively, in one situation).

Several statistical techniques were covered in [43,44]. A probabilistic approach for estimating short-term wind output was presented by Juban et al. [43]. The process yields a predictive probability density function for estimation based on the kernel density function. The model’s reliability is within the range of 2 to $4\%$, consistent with findings from related studies. Mohandes et al. [44] employed the Support Vector Machines (SVM) approach to estimate wind speed utilizing at Madina, Saudi Arabia, wind data. Additionally, a comparison is made between the Multilayer Perceptron (MLP) neural networks and SVM performance. Compared to the ANN approach (MSE of 0.0078), SVM achieves worse estimation accuracy (MSE of 0.009).

Several studies [45,46,47,48] have employed the Adaptive-Neuro-Fuzzy-Inference-System (ANFIS), a combination of fuzzy and neural approaches, to enhance the performance of the ANN method. Potter et al. [45] use the wind data from the Australian state of Tasmania along with ANFIS to predict wind power on an extremely short basis. When wind data is examined from a session in a different year, the MAE is consistently less than eight. Based on the speed of wind data at altitudes of 10, 20, 30, and 40 meters, Mohandes et al. [46] computed wind speed up to a height of 100 meters using ANFIS. Compared to the actual speed of wind at the same height, the ANFIS projected wind speed at 40 m has a 3% Mean-Absolute Percentage Error (MAPE). Yang et al. [47] interpolate the information about the lost wind calculated from China’s twelve wind farms using the ANFIS approach. The actual observed wind speed and the ANFIS forecasted wind speed had an RMSE of 0.22. Maximum-power-point-tracking (MPPT) has been designed by Meharrar et al. [48] using an ANFIS wind generator. As an input, wind speed is used by the ANFIS to estimate the rotational speed of wind turbines. In training, the ANFIS performs effectively with an error of 0.005.

In addition to ANFIS, ANN is also combined with other techniques to improve prediction performance [30,49,51,52]. For example, Yang et al. [49] used BPNN along with Wavelet Analysis (WT) to diagnose faults in the wind turbine gearbox, successfully identifying two typical situations, three fault situations, one severe fault situation, and two light fault situations. To choose the input parameters and variables of the ANN and the closest neighbor techniques used to estimate wind power in the short-term and network traffic analysis, Jursa et al. [50] implemented two evolutionary algorithms: Differential Evolution (DE) and Particle Swarm Optimisation (PSO). Prediction accuracy is 2.8% higher with the PSO-optimized ANN than with the manually structured ANN. An enhanced version of the FNN and the Empirical Mode Decomposition (EMD) technique for wind speed estimate has been created by Guo et al. [51]. The performance of the improved EMD&FNN is better (MSE of 0.1647) than that of the FNN (MSE of 0.1512) and EMD-FMM (MSE of 0.1295). Pourmousavi et al. [52] have presented an ANN-Markov chain (MC) technique for short-term wind speed forecasting. For larger margins, the ANN-MC has a lower error (94.83) than the ANN (96.04).

Hybrid AI techniques are described in detail [53,54,55,56,57,58,59]. Fuzzy techniques based on the two GA models (real-coded GA and binary-coded GA) were developed by Damousis et al. [53] for wind power and speed prediction. When the statistics about wind energy from a remote site were analyzed by applying wireless modems, the fuzzy approach produced higher accuracy than the persistent technique for the next hour and longer, respectively, by 29.7% and 39.8%. The SVM and EEMD approaches are combined by Hu et al. [54] to construct and evaluate a hybrid forecasting method. Using the suggested hybrid method, the monthly average wind speed measured at three different locations in China was determined. When EEMD is placed against two conventional time series approaches; Seasonal Autoregressive Integrated Moving Average (SARIMA) and Autoregressive Integrated Moving Average (ARIMA); EMD-SVM and SVM yield an MAE of 0.12. Cadenas et al. [55] created a novel hybrid model that combined BPNN and ARIMA techniques to forecast wind speed at three distinct locations in Mexico. In comparison to the ARIMA (MSE of 4.1) and ANN (MSE of 5.65), the hybrid approach has an MSE of 0.49. For short-term wind speed prediction, a hybridized ANN approach with the fifth-generation Mesoscale Model (MM5) has been proposed by Salcedo-Sanz et al. [56]. By using the MM5 output, the ANN technique yields higher accuracy in estimating, with MAE ranging from $1.45-2.2m{s}^1$ for varying hidden layer neuron counts (9-5) and wind turbine sites. Liu et al.’s [57] proposed a hybrid AI method with WT, GA, SVM, and deep quantitative analysis. The GA is applied for the modification of SVM parameters. The WT, SVM, GA model fared improved (MAE of 0.6168) than the persevering method (MAE of 0.8355) and SVM-GA (MAE of 0.7844). Kong et al. [58] developed a novel hybrid model for forecasting wind speed using PSO and PCA for SVM parameter optimization, and a refined form of SVR called Reduced Support Vector Machine (RSVM). Effective estimating accuracy is demonstrated by the RSVM. In Rahmani et al.’s [59] proposed hybrid intelligence technology, PSO and Ant Colony Optimisation (ACO), for the hourly wind power forecast for 43 data using temperature and wind speed as external variables. The hybrid approach produces the best MAPE of 3.50% when compared to PSO (MAPE of 10.50%) and ACO (MAPE of 5.8%). Pousinho et al. [60] have developed a hybrid approach for risk optimization in trading wind energy that combines WT, PSO, and ANFIS. Portugal uses this hybrid approach to analyze data from wind farms. The predicted profit was accurately projected to be between 18719 and 18487 euros for various levels of risk values between 1 and 0. An outline of the studies discussed above is shown in Table 1.

3.2. AI in Solar Energy

There has been much discussion in the literature about the significance of AI in solar energy applications [61,62]. The specific uses of ANN techniques in solar energy, including building heating load calculations and solar system design and modeling, are described in [61]. Mellita et al. evaluated the use of AI in weather data modeling and on and off-grid PV system size [62,63] in addition to discussing its applications in PV system modeling, simulation, and control. In particular, [61] provides a summary of the specific uses of ANN approaches in design and modeling, building heating load, etc. A brief overview of the research conducted by Mellita et al. on applying AI to meteorological data modeling, PV system sizing, control and simulation is provided in [62]. The application of AI approaches to the dimensions of standalone and grid-connected photovoltaic systems has also been reviewed by Mellita et al. [63]. A compilation of building energy consumption estimation techniques utilizing AI and statistics are found in [63]. Dounis et al. [61] gave an overview of the use of agent-based intelligent automation systems for building energy management. AI is being applied in both single and hybrid approaches to solar energy research [64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102]. The most popular approach in solar energy research is ANN. It is utilized in PV connected to the grid to anticipate solar irradiance [64,65,66,67,68,69,70,71,72,73,74,75]. It is possible to attain a correlation in comparison with the actual and expected solar radiations of 98-99% and 94-96% on sunny days and gloomy days, respectively. Using temperature and humidity as inputs, the BPNN forecasts Global Solar Radiation (GSR) for the years 1998–2002 [64]. The RMSE value between the actual and BPNN forecasted GSR was $2.823\times {10}^{-4}$. Kalogirou et al. [65] employ BPNN to estimate the performance of heating systems based on solar water. The improved performance of BPNN is confirmed by the higher coefficient of determination values ($R^2$ of 0.9808 and 0.9914 for the maximum temperature rise and extracted energy, respectively). Using the BPNN, beam solar irradiance was calculated by examining data from eleven distinct stations. The radiation model’s projected values and actual values had an RMSE of $2.69$ to $2.79\%$[66]. The daily ambient temperature is estimated with a BPNN of $3\times 6\times 1$, with an RMSE of 1.96 [67]. The BPNN was used to estimate the daily sun irradiation with an RMSE of 5.5-7.5% [68]. With an RMSE of 3.29%, a High Concentration Photovoltaic (HCPV) system with the maximum power was estimated using the BPNN [69]. The BPNN was used to estimate the average monthly solar radiation around the globe, and the relation between the predicted and real solar irradiation was 0.97 [70]. Using the BPNN, hot water quantity and solar energy production were calculated and the results showed $R^2$ values of 0.9973 and 0.9978, respectively [71].

Several studies in research [72,73,74,75] compare the effectiveness of the BPNN model to various methods. Tasadduq et al. [72] utilize BPNN to estimate the ambient temperature 24 hours in advance, and they compare the effectiveness of BPNN with batch-learning ANN. Using BPNN for three years, the Mean Percentage Deviation (MPD) values attained were 3.16, 4.17, and 2.13. Alam et al. [73] forecast diffuse solar radiation, both hourly and daily, with an RMSE of 4.5% using the BPNN, in contrast to 37.4% for alternative empirical techniques. Tymvios et al. [74] predicted worldwide solar radiation using Ångström’s linear techniques and BPNN. Ångström’s linear technique and the BPNN method perform similarly (RMSE of 5.67–6.57%). The eight Chinese cities’ GSR estimates from 1995 to 2004 were estimated using the BPNN approach, and the results were compared to those obtained using empirical regression techniques. With a minimum RMSE of 0.867, the BPNN outperforms empirical regression techniques [75]. For solar energy analysis, a few more techniques were employed in addition to ANN [76,77,78]. The SVM approach, for example, is compared to the AR and RBFNN in terms of performance when used to predict short-term solar power [76]. The SVM approach (MAE of 33.72 $W{m}^{-2}$) outperforms the AR (MAE 62 $W{m}^{-2}$) and RBF (MAE of 43 $W{m}^{-2}$) approaches. Li et al. [77] examined the performance of SVR and ANN for estimating solar PV energy production. The two approaches’ RMSEs were nearly identical. When estimating solar electricity generation, the RBF-SVM method performs better than the two forecasting techniques currently in use, PPF and Cloudy. Compared to the other two methods, SVM shows a 27% greater estimation accuracy [78].

Applications for solar energy have also made use of several evolutionary AI techniques [79,80,81]. Mashohor et al. [79] proposed GA in solar tracking to enhance PV system performance. The optimal GA-solar system is produced by a GA with an initial population size of 100, 50 epochs, and probabilities of crossover and mutation of 0.7 and 0.001, respectively. The generating gain’s low standard deviation (1.55), which indicates higher system efficiency, further supports this claim. The best possible design for a solar water heating system takes advantage of GA. In particular, the GA is used to optimize the plate collector area to 63 $m^2$, which yields a solar fraction value of 98% [80]. Tracking PV arrays’ MPPT coupled to batteries was implemented by Kumar et al. [81] using GA. The conventional Perturb and Observe (PO) algorithm’s performance is compared with the GA. The 400-line voltage is attained by the boost converter.

It has also been observed that combining AI techniques improves prediction efficiency [82,83,84,85,86,87,88]. The ANN and TRNSYS are combined to forecast the performance of an Integrated Collector Storage (ICS) solar water heater, with an $R^2$ value of 0.9392 [82]. GA was used by Monteiro et al. [83] to optimize the parameters of the Historical Similar Mining (HISIMI) model, which is used to estimate PV system power. The performance of the modal of GA-HISIMI (RMSE of 283.89) is compared with that of the classical persistence (RMSE of 445.48) and BPNN (RMSE of 286.11) approaches. In Algeria, the optimization of PV system size is achieved using the amalgamation of limitless impulsive response (IIR) filter and RBFNN [84]. The RBF-IIR approach was used to estimate the optimal sizing coefficients, and its performance was compared with the MLP-IIR approach, BPNN, RBFNN, and classical models. Using the RBF-IIR approach, the sizing coefficients were computed with high accuracy (correlation of 98%). For the forecasting of solar radiation levels, WT and BPNN were combined [85]. WT-BPNN outperformed the traditional approaches (ARMA, AR, MTM), recurrent, BPNN and RBFNN methods in terms of accuracy (97%) and performance. Without using exogenous inputs, GA-optimized BPNN is used to anticipate solar power output [86]. GA-BPNN’s performance is compared with that of the k-nearest neighbor (KNN), ARIMA, BPNN, and persistent model techniques. The minimal RMSE of 72.86 kW is obtained using the GA-BPNN. To estimate PV system power, Mandal et al. [87] combined WT and RBFNN and evaluated the results against, RBF, BPNN and WT-BPNN. The minimum RMSE for the WT-RBF is 0.23. The economic benefits of solar energy are optimized by the application of NN and GA in the group method of data handling (GMDH) [88]. The ideal solution increases life cycle savings by 3.1-4.9%. Multiple studies [89,90,91,92,93,94] have employed the ANFIS method. These include modeling a PV power supply system with an accuracy rate of 98% [89], satellite image data for the prediction of hourly global radiation [90], average temperature and length of sunshine to predict solar radiation [91], simulating a PS power supply [92], and forecasting a solar chimney power plant’s performance [93].

A variety of hybrid AI approaches have also been employed by solar energy systems [94,95,96,97,98]. The following are a few of these: ARMA and Time Delay Neural Network (TDNN) are used to predict solar radiation [96], For GSR prediction, a hybrid of the SVM and Firefly algorithm (FFA) is created, and its effectiveness is compared with that of the BPNN and Genetic Programming (GP) approaches (RMSE of 1.8661 for SVM-FFA), and PV connected to the grid power prediction is achieved through a hybrid of SVM and SARIMA methods [97]. Table 2, provides an overview of the results of AI approaches, discussed above, for solar energy systems. 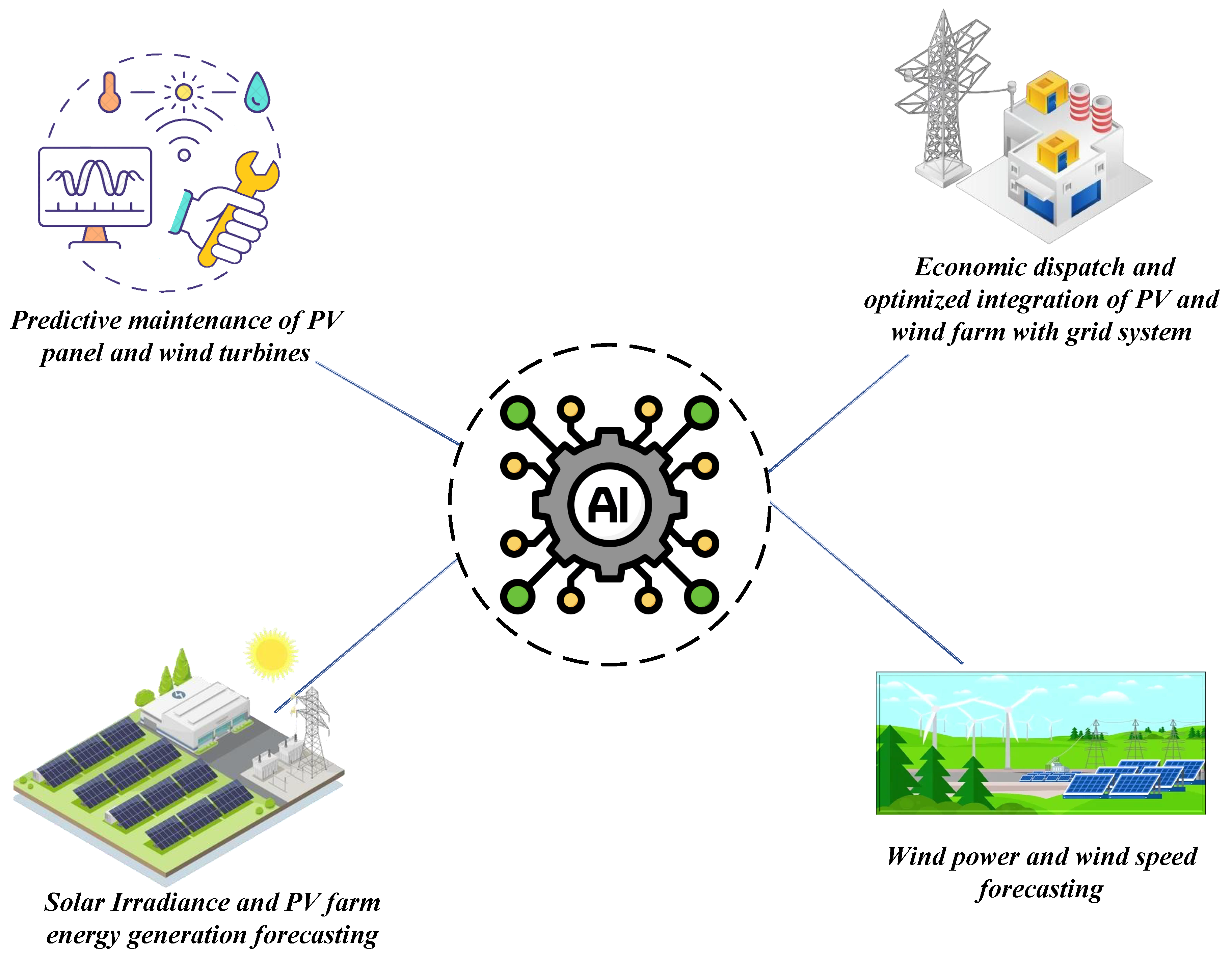Figure 1 illustrates the application of AI for solar and wind energy resources.

3.3. AI in Geothermal Energy

Studies [99,100,101,102,103] provide an overview of the use of AI approaches in geothermal applications. The authors in [99] have given a brief overview of the potential applications of AI approaches with sensors and robots in geothermal well drilling design, control, optimization, computer modelling, and simulation of geothermal reservoir and its impact on the advancement of geothermal energy. Additional evaluations [100] examine numerical models for geothermal reservoirs and enhanced geothermal systems by O’Sullivan et al. [101,102]. Study [103] also provides a synopsis of the development of numerical modeling for geothermal reservoirs. Table 3 outlines the use of AI in geothermal energy-related applications, both in standalone and hybrid forms [104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123]. To forecast the performance of Vertical Ground Coupled Heat pump (VGCHP) systems, Esen et al. [104] employed BPNN with the Levenberg-Marguardt (LM), Pola-Ribiere Conjugate Gradient (PRCG), and Scaled Conjugate Gradient (SCG) algorithms. Better prediction efficiency is achieved with the eight neurons in the hidden layer of the LM-based BPNN (RMS of 0.0432). To predict the geothermal well’s Static Formation Temperature (SFT), LM-based BPNN was used by Bassam et al. [105]. With five neurons in the buried layer of the BPNN, the prediction error is less than $\pm 5\%$. The best operating conditions for a geothermal well are determined using BPNN (with LM, CGP, and SCG) in [106]. Using the temperature and vapor fraction of geothermal water with the ammonia fraction as inputs, the best-predicted values of generated and circulatory pump power are obtained by the seven-neuron BPNN hidden layer (RMSE of 1.5289). The ANN and BPNN (with CGP, LM, and SCG) are utilized for power cycle optimization, similar to ORC-Binary [107]. For generating and needed pump circulation power, with 14–16 neurons in a hidden layer, the LM-based BPNN produced the greatest results (RMSE of 0.0001 for the $s_1$ and $s_2$ cycles). The cycle $s_1$ input variable is comparable to the one outlined in [106], but the cycle $s_2$ analysis includes an extra input variable called outlet pressure. Using the real values for the 96.5% of data points, BPNN is utilized to generate a geothermal map at various depths with less than a 5% variance [108]. In the Afyonkarahisar Geothermal District Heating System (AGDHS), thermal performance and energy destructions are predicted using the LM-based BPNN with good accuracy (RMSE of 0.0053) [109]. Using eight distinct input parameters, the geothermal well’s Void Percent (VF) data were forecasted using BPNN, which has a foundation with the LM training approach. With an RMSE of 0.0966, six neurons in the hidden layer of BPNN produce the best forecast accuracy [110]. The VF-ANN is used for predicting the stormwater treated by geothermal energy’s Biochemical Demand for Oxygen (BOD), nitrate-nitrogen, ortho-phosphate-phosphorus, ammonia and nitrogen. The QN-based BPNN yields the best accuracy for predicting ammonia and nitrogen [111]. The AGDHS PID controller, which increases energy efficiency by 13%, is tested using BPNN [112]. Greater accuracy in ORC-Binary geothermal plant modeling is achieved by using BPNN with LM for the $o_2$ and $o_3$ cycles (20 and 22 neurons in the hidden layer, respectively) and for the $b_3$ type cycle [113]. The site placements planning model [114] makes use of geographic information data with the BPNN, which depends on the LM and SCG algorithms. With BPNN, conductivity maps of the ground can be created more accurately (83% of projected data have deviations of less than 10%) [115]. With the use of the wellbore production database, BPNN, which is based on the LM algorithm, showed improved pressure drop prediction efficiency in geothermal wells [116].

In certain investigations, the study of the geothermal system also used fuzzy logic and EA [117,118,119,120]. For VGSHP, Sayyaadi et al. [117] used multi-objective optimizations with the EA and single-objective thermodynamic and Thermos Economic (TE) optimizations. Six EAs (two DE, GA, PSO Monte-Carlo random search) were used in another study [118] to determine the ideal location of Borehole Heat Exchangers (BHEs). In Recirculation Aquaculture Systems (RAS), for geothermal heat [119] and to control water temperature for maximum RAS output [120], it has been possible to create a fuzzy logic controlled (FLC) system. Some analytical studies on geothermal energy [121,122,123] used ANFIS and hybrid AI approaches. For example, VGSHP performance is assessed using ANFIS, and the results are compared with BPNN techniques (SCG, LM, and CGP algorithms). In this instance, ANFIS is more effective than BPNN techniques [121]. ANFIS is also used to assess the AGDHS system (forecast of energy and energy rates) and compare it with BPNN techniques [122]. In geothermal reservoir temperature prediction, GMDHNN based on GA and Singular Value Decomposition (SVD) is used and the results reveal that ANFIS outperforms BPNN approaches [123].

3.4. AI In Hydro Energy

Different studies discussed the application of AI approaches in the hydro energy sector. Kishor et al. [124] focused on the planning and management of hydropower facilities using both conventional techniques and contemporary AI methodologies such as GA, ANN, Fuzzy, ANFIS, etc. Nourani et al. discussed the importance and use of hybrid AI techniques based on wavelet pre-processors in hydro-climatology [125], particularly in the assessment of the importance of hydrologic cycle operations. In hydro energy applications, Table 4 summarises the utilization of both the single and hybrid AI approaches [126,127,128,129,130,131,132,133,134,135,136,137,138,139,140].

In Taiwan, eight reservoirs are utilized to optimally schedule hydropower plant operations using the BPNN technique [126]. Compared to Differential Dynamic Programming (DDP) and K-Nearest Neighbor (KNN), the BPNN is more economical. For linear and non-linear reservoirs, the discharge peak and peak time must be estimated. Smith et al. [127] employed the BPNN technique in their modeling of the rainfall-runoff process. When predicting peak discharge for non-linear reservoirs and time to peak for linear reservoirs, BPNN achieves higher accuracy. For seventeen years, the San Juan River basin’s steam flow has been accurately predicted using the BPNN model in two distinct seasons [128]. The most important components in the generation of hydroelectric power are the potential head and flow of water. Moreover, Kisi et al. [129] investigated river flow modeling with the BPNN and gradient descent (GD) and compared the results with the autoregressive (AR) approach. Approximations using BPNN are more precise than those using AR. Estoperez et al. [130] estimate the monthly power outage in advance (RMSE of 0.061) and used BPNN for micro-hydro power plant scheduling. In the research of hydro energy, the GA [131,132,133] and fuzzy [134] methodologies have also been employed. To plan a hydrothermal power system in Brazil, for instance, Carneiro et al. [135] employed GA, and they compared the outcomes with those of a traditional non-linear programming (NP) optimization technique. For the years 1971–1973, the GA’s operating costs (726,742.2 MW) are lower than the NP’s (745,020 MW). For a comparable application, Gil et al. [132] created a new GA (with the help of a group of skilled operators) and assessed how well it performed in comparison to other GA implementations. A new kind of GA known as Chaotic Hybrid (CH)-GA has been created by Yuan et al. [133] to solve the issue of the short-term hydrogenation schedule being hampered by the water delay time. When compared to the conventional S-GA and NP, the CHGA yields a higher profit. Adhikary et al. [134] examine the use of a fuzzy logic-based method to determine which of the four penstock materials, asbestos cement, steel, and GRP, is best for hydro turbines. The best material with the highest degree of index was determined to be GRP.

ANFIS and hybrid AI techniques’ role in the production of hydropower has also been covered in a few research [135,136,137,138,139,140]. In Taiwan, the Shihmen reservoir is controlled by the ANFIS approach, which predicts the release of water. The M-5 rule curves are also used to compare the method’s performance [135]. The ANFIS performs better (there is less water scarcity) than the M-5 rule curves. Firat et al. [136] estimated the Menderes River’s flow effectively using the ANFIS model. Multiple Regressions (MR) and ANN are used to compare ANFIS’s performance (the minimum relative error for ANFIS is 0.073). An ANN is integrated with an expert system through the use of Learning Vector Quantization (LVQ) and ART-MAP for hydropower plant predictive maintenance (PM) and Acoustic Prediction (AP) [137]. The AP and PM come up with more accurate projections. GA and PSO-adjusted FLC have been developed by Sinha et al. [138] regarding Automated Generation Control (AGC) in hydroelectric systems. In terms of settling time and peak overshoot, the GA-FLC and PSO-FLC outperform the conventional FLC. An AI hybrid approach for estimating river flow known as case-based reasoning (CBR) has been created making use of Elman ANN, modular ANN, Fourier Frequency Transform (FFT) and Hierarchical Clustering (HC) [139]. The models’ performances are compared with CBR (minimum MAE of 17. 11 for CRB). The hydraulic energy production in Turkey is predicted by BPNN using the Artificial Bee colony (ABC) model (ABC is used to optimize BPNN) with a relative error of 0.23 [140]. 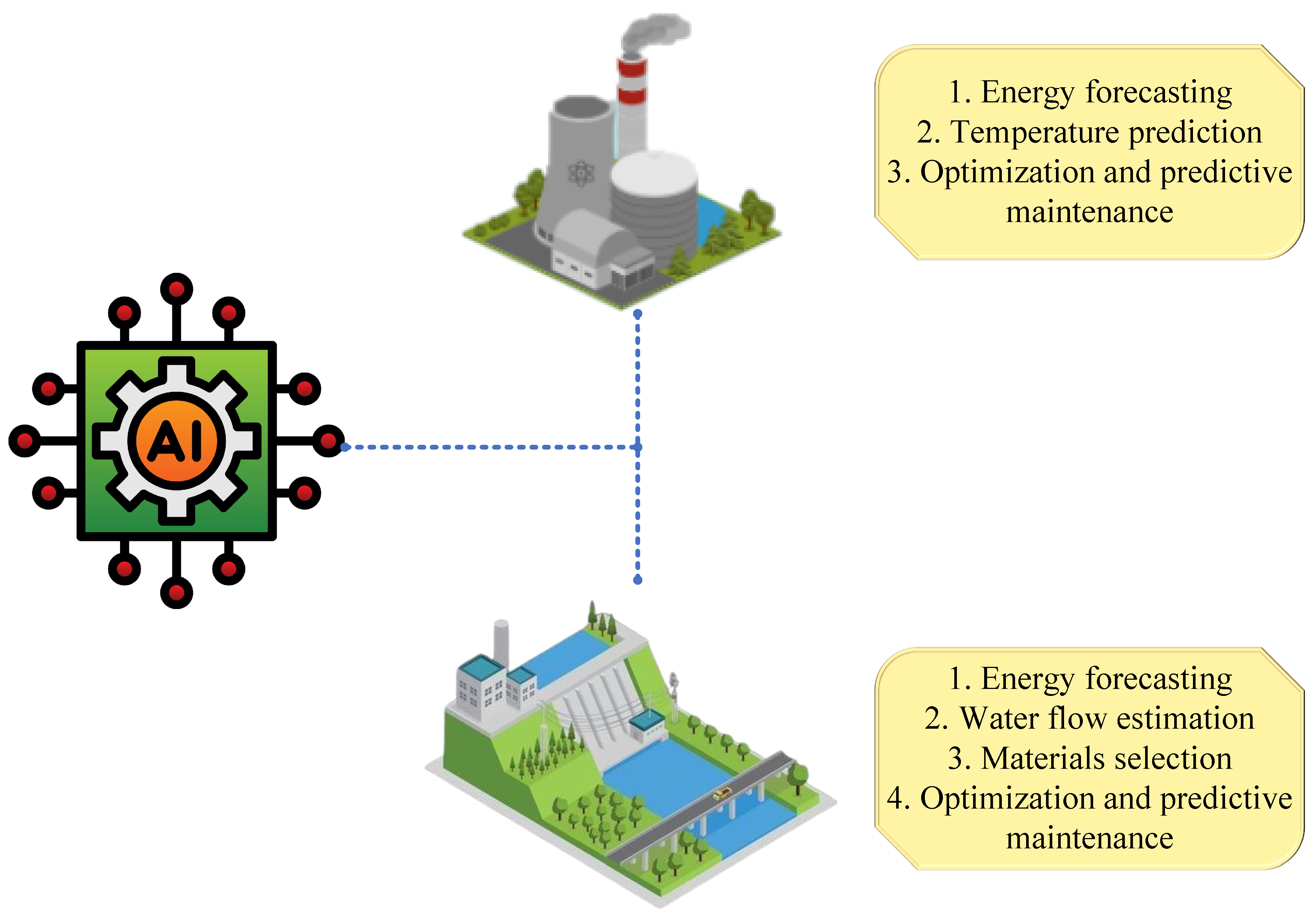Figure 2 depicts AI applications for geothermal and hydro energy resources.

3.5. AI in Ocean Energy

The studies [141,142,143,144] provide a summary of how various AI approaches are being used for ocean energy. Essentially, [141] discusses AI’s involvement in generating energy from oceans, while Aartrijk et al. [142] provide an overview of AI’s role in ocean energy. According to Jain et al., [143], there are numerous ocean engineering applications of ANN. The availability of renewable energy resources has been extensively covered by Iglesias et al. Authors of [144] have discussed the potential of wave farms producing energy located in the Canary Islands, which will eventually be one of the first islands to run exclusively on renewable energy.

The studies [145,146,147,148,149,150,151,152,153] discuss the involvement of several single and mixed AI techniques for ocean energy and the Table 5 summarizes the key findings. The sea level variation along Western Australia’s coast is forecasted using a three-layer BPNN approach (correlation coefficient of 0.7–0.9) [145]. The BPNN algorithm with six different options for number of neurons in the layer has been used by Londhe et al. [146] to estimate ocean wave conditions for one day with decent precision (for lead times of 12 hours, there is a 67% correlation between the predicted wave height). Three architects analyzed data obtained from Tasmania between 1985 and 1993 ($R^2$ of 0.92) to forecast wave parameters using the BPNN approach, which takes the coastal environment factors as input [147]. Using sixty datasets and thirty US rivers, the longitudinal dispersal coefficient in streams was predicted. A study by Toprak et al. [148] employed the RBFNN, BPNN, and Generalized Regression Neural Network (GRNN). The FLC has been created by Chen et al. [149] to lessen the effects of external wave force in the ocean and the proposed method demonstrates good stability. Ghorbani et al. [150] predict sea level using the GP and ANN. The GP prediction accuracy (MSE of 22.5–28.2) outperformed the LM algorithm-based BPNN.

To increase the prediction accuracy, mixed AI methods [152,153] and ANFIS [154] approaches have also been employed. Karimi et al.’s investigation [153] highlights the effectiveness of eleven different ARMA model variants, BPNN (LM), BPNN (CG), BPNN (GD), and ANFIS (five variations, each with a unique membership function) in sea level prediction. Results from ANFIS and ANN approaches are nearly identical, however they outperform ARMA techniques. For wave hindcasting, a hybrid method combining the Numerical Wave Model (NWM) and BPNN is employed [151]. In comparison to the BPNN and NWM methods, the hybrid strategy performs better. The authors in [152] have developed a hybrid intelligence system that utilizes SVR and case-based reasoning to improve $C{O}_2$ flux prediction and investigate the understanding of how air and ocean interact. 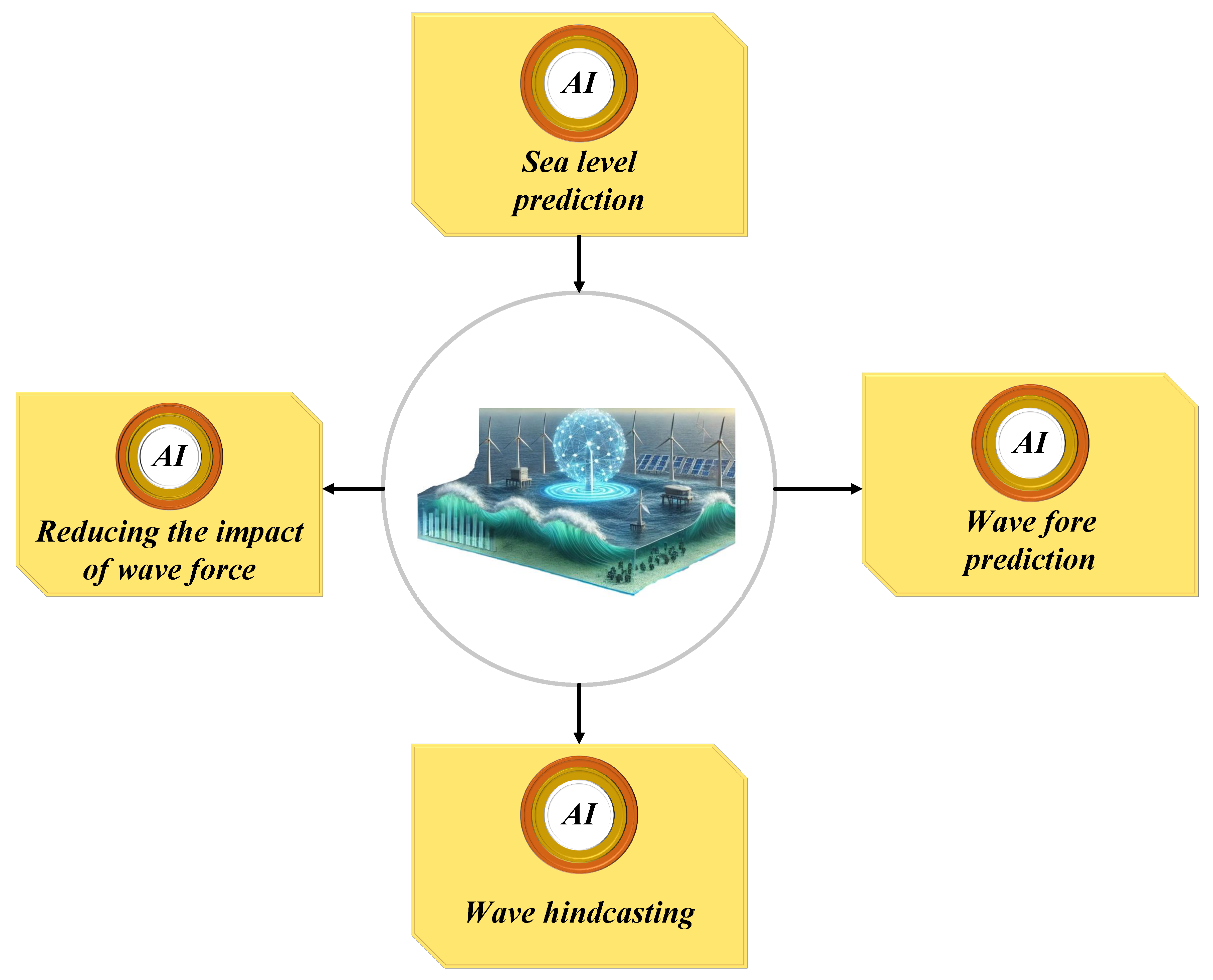Different applications of AI in ocean energy are demonstrated in Figure 3

3.6. AI in Bioenergy

Shabani et al. [154] provide a succinct overview of predictable and stochastic mathematical models for foresting biomass energy, optimization and the ideal supply chain architecture in renewable energy generation. Several studies [155,156,157,158,159,160,161,162,163,164,165,166,167] describe the usage of both standalone and combined AI systems for analysis of bioenergy, which is summarized in Table 6. Studies [155,156,157,158,159,160] about bioenergy use ANN architectures. Yang et al. [155] forecasts the density and fuel’s cetane number for diesel using BPNN, RBFNN, GRNN, and Recurrent Neural Network (RNN) to detect the fatty acid composition (BPNN performs best in this case). To measure the amount of methane in biomass from bioreactors by using temperature, alkalinity, conductivity, pH, sulfate, BOD, and chloride as input parameters, ten different kinds of BPNN are analyzed in [156,157,158,159](RMSE ranges from 0.00263-0.00250). The RBFNN trained with inputs of pressure, blend, load, compression ratio, and injection time (accuracy range 69–96%) for the performance of biodiesel engines (engine emissions, exhaust temperature, and thermal efficiency/energy consumption of the break) is examined in [160]. To estimate the density, viscosity, water and methanol content, and other properties of biodiesel, the polynomial and Spline Partial Least Squares Regression (SPLS), Principal Component Regression (PCR), Multiple Linear Regression (MLR) are studied and compared with the BPNN (the BPNN performed better than the other approaches) [159]. Apart from SVM and KNN [161], PSO [162], and GP [163], ANN has also been applied in bioenergy analysis work. Based on Near-Infrared (NIR) data, Balabin et al. [161] classified biodiesel into ten categories (based on origin) using regularized discriminant evaluation, KNN, SPLS, and SVM algorithms. The SVM produces an accuracy for classification that is superior to the other three approaches. To optimize the biomass supply chain (flows from the producing sources), an improved version of PSO is used [162]. A comparison is made between the performance of the current Higher Heating Value (HHV) models and biomass fuels estimated HHV utilized by GP and BPNN [163]. The GP and BPNN forecasted accuracy is superior to that of the traditional models (RMSE of 0.942 and 0.987, respectively).

Hybrid AI techniques are also applied in the investigation of bioenergy [164,165,166,167]. For the years 1964–2006, Koutroumanidis et al. [164] estimated fuelwood costs in Greece using ARIMA, ANN, and a hybrid of ANN-ARIMA. Compared to the ANN and ARIMA approaches separately, the ANN-ARIMA model predicts better estimation (MAPE of 14%). A hybrid system that maximizes heat transfer and enhances biomass boiler cleaning using fuzzy logic and ANN saves 12-gigawatt hours annually [165]. Methane may be produced from waste digesters using a hybrid AI method based on BPNN and GA [166]. The hybrid approach produces 6.9% more methane when the settings are optimized. Similar hybrid technology is applied in a different study [167] to optimize the production of biogas from cow manure, banana stems, rice bran, paper waste, and sawdust which resulted in produciton of $10.280$$d{m}^3$ of biogas. 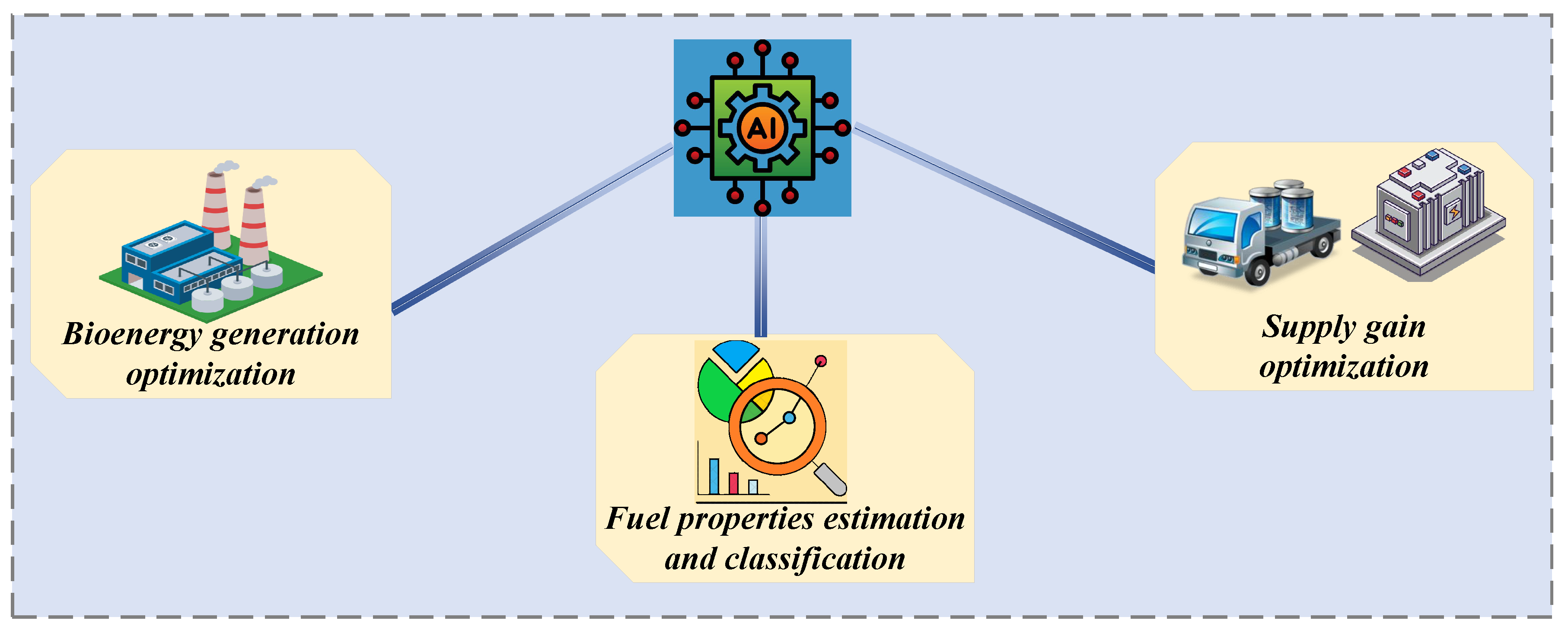Various fields of bioenergy resources in which AI can play an active role are demonstrated in Figure 4.

3.7. AI in Hydrogen Energy

Petrone et al. [168] summarized model-based machine learning methods for proton exchange membranes fuel cell system (PEMFC) diagnosis. Similarly, for a related topic, three sorts of non-modal-based methods, including statistics, signal processing, and AI techniques, are described in [169]. A summary of scientific approaches consisting of AI techniques in hydrogen energy is provided in Table 7 and is documented in multiple studies [40,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194]. The ANN is a commonly used technique in the hydrogen energy industry [40,170,171,172,173,174,175,176,177,178]. Three AI techniques, namely BPNN, MGGP, and SVR are employed to forecast the output voltage of Microbial Fuel cells (MFCs), with MGGP yielding the highest accuracy [170]. The $C{O}_2$ hydrogenation activity is predicted by BPNN [171]. BPNN with eleven training approaches are used to forecast the impact of hydrogen vehicle engine operating parameters on $C{O}_2$, carbon monoxide, $N{O}_x$, and hydrocarbon emissions [172] and record 100% accuracy in the carbon emission prediction. The PEM fuel cell’s stability and fault detection are observed using the Bayesian method and LM with BPNN [173]. The cathode temperature and voltage of the fuel cell with a Polymeric Electrolyte Membrane (PEMFC) are predicted with good precision [174]. Using two inputs, throttle position and engine speed, the parameters of hydrogen engines (mass airflow (MAF)) are forecasted with the twelve distinct training techniques of BPNN [195]. Moreover, BPNN is used in other studies [175,176,177,178] to forecast the Solid Oxide Fuel Cell (SOFC) stack voltage [177], parameters, emissions of the hydrogen engine [175] (RMSE of ±$4\%$), the MFC power density (RMSE of $4.89\times {10}^{-4}$ for a single configuration), and the hydrogen-functionalized graphene tensile strength prediction [176].

Hydrogen energy analysis has also been carried out using fuzzy logic methods [179,180,181] and EU techniques [182,183,184]. Fuel Cell Hybrid Vehicles (FCHV) employ a parameter-based fuzzy logic controller optimized with GA to regulate the amount of hydrogen consumed [181]. The SOFC’s current density properties are modeled by a recurrent fuzzy system [180], and the ignition time of a hydrogen automobile is predicted using a fuzzy logic technique utilizing three distinct kinds of membership functions [179]. The PSO is used in addition to fuzzy logic and GA for FCHV energy optimization [182]. Nath et al. [183] reviewed the use of GA, PCA, and BPNN in modelling of hydrogen generation. The Bird Mating Optimization (BMO) method for modeling the PEMFC system is proposed by Askarzadeh et al. [184].

Studies [185,186,187,188,189,190,191,192,193,194] described the ANFIS and other hybrid AI methods. ANFIS is utilized in the forecast of various safety parameters of hydrogen (such as hydrogen pressure, flow rate and explosive limit), applied with ten input requirements [186]. Based on various training procedures, the effectiveness of ANFIS is compared with different types of eleven BPNN (RMS of 1.4 in the ANFIS-powered hydrogen pressure forecast). The parameters of Stack Current and Voltage (SOFC) are predicted using ANFIS and the results are compared with the ANN approach (RMSE of less than 2 for ANFIS forecast). Emissions (CO, $C{O}_2$, HC and $N{O}_x$) from the hydrogen automobile were forecasted using ANFIS and BPNN-LM. The BPNN performs better than ANFIS in this regard (HC emission RMSE of 1.58% using the BPNN) [187]. The performance of the PEM electrolyzer ($H_2$ flow rate, system, and stack efficiencies) is predicted using ANFIS (the predicted inaccuracy of hydrogen flow rate is 1.06%) [188]. Effective PEMFC cell voltage prediction is possible using ANFIS [189]. A hybrid AI method based on full logic and wavelet technique has been applied to decrease HEV energy usage (0.06962 kMol $H_2$), and the findings are compared with RBFNN and BPNN [190]. High precision temperature forecasting of the hydrogen reactor is achieved by using a hybrid technique based on SVR and PSO, and its performance is compared with that of SVR and BPNN [190]. When compared to PSO and GA, the hybrid ABC algorithm outperforms other approaches in terms of minimizing the Sum of Squared Errors (SSEs) for parameteric prediction of PEMFC [194]. Combining GA and BPNN results in a 54 ml/g increase in biohydrogen output [193]. A similar set of techniques is applied in different research [192] to maximize the SOFC cell characteristics (1.705% standard error of prediction achieved).

3.8. AI in Hybrid Renewable Energy

In [196,197,198], a brief discussion about the application of AI techniques in the hybrids RERs is presented. An overview of the methods developed for ideal sizing has been provided by Luna Rubio et al. [196]. Zhau et al. [197] presented the design techniques for the solar-wind hybrid system, and [198] provides an overview of the various EA approaches used in optimization. Table 8 compiles a few hybrid RER applications using both the single and hybrid AI techniques [199,200,201,202,203,204,205,206,207,208,209,210]. For a hybrid RER system based on a water power source, BPNN is utilized to predict generator state (on/off) and power [199]. FLC has been employed by Chavez-Ramirez et al. [200] for energy management, while the BPNN technique was used for hybrid RE power prediction. A different study [201] used PSO in conjunction with the FLC and Cuckoo Search (CS) algorithms to investigate the energy control of a hybrid renewable energy system (with the CS and a levelized energy cost of 2.01$). Hakimi et al. [202] use PSO to optimize the hybrid RER system’s size in an attempt to cut expenses. The hybrid RER system’s operation is optimized using an improved GA, which outperforms the conventional GA approach [203]. The hybrid RER system’s performance parameters (energy cost, net current cost, and generating cost) are optimized using the bee algorithm [204]. GA has been used by Khatib et al. [205] to maximize the storage capability, size of PV array, and windmill size of hybrid wind-photovoltaic system. In hybrid energy (photo voltaic, fuel cell, windmill) systems, the optimization of size and distribution is carried out using a multi-objective ABC method [206], which produces a high voltage stability index. The hybrid wind-PV-diesel system’s size optimization is done by Markov-based GA [207].

According to [208], four methods, PSO, Simulated Annealing (SA), Tabu Search (TS) and Harmony Search (HS), perform better concerning wind-PV-battery and wind-PV-FC system size optimization. The PSO performs better than the other three techniques. In hybrid AI approaches, the wind-PV-battery system size is optimized using ANFIS to minimize production costs. Additionally, the hybrid optimization (HO)-GA and the hybrid renewable energy optimization model for electric power are compared with ANFIS’s performance [209]. Fuzzy logic-based and ANN controllers are devised as hybrid AI technology to manage power flow between energy and storage units of hybrid RER systems and to generate high storage of charge [210].

The ANFIS is also used for estimating wind power [211], biodiesel modeling [212], and radiation of solar [213]. The ARIMA-SVR is used for tidal energy real-time estimation in [214]. For solar radiation forecast, empirical decomposition, wavelet decomposition, ANN, and autoregressive approaches are used [215]. In PV system load estimation, enhanced and hybrid ANN are used [216]. Several recent studies [217,218,219,220,221,222,222] have also covered the specific applications of AI methods, including solar PV system power tracking [218], estimation of wind and solar energy [218,219], decision systems in RER [221], PV solar systems controllers [223], and energy management [222].

4. AI Fostering the Integration of VRE in Power Systems: Economic Aspect

Table 9 lists the primary strategies that have previously been examined and have the potential to affect the three categories of integration expenses described in the preceding section. As previously stated, every action can have a complex impact on the electrical system and may directly or indirectly impact several integration cost components. For instance, as demonstrated by models based on various situations, numerous steps can yield significant cost reductions by enhancing overall power system adaptability [225,226]. To keep things simple, this study associates each metric with the component of integration cost that has the greatest potential for value generation, as the literature has discussed. Next, it discusses these steps and gives an example of an AI system that can facilitate them. The applications of AI that are covered here highlight AI’s ability to provide value to costs associated with VRE integration, although they are by no means exhaustive as that would be impracticable. The present work provides the potential efficiency improvements from certain AI applications, these metrics can vary in the literature and are often difficult to identify and organize. Table 9 provides a synopsis of the covered use cases.

4.1. Mitigating Balancing Costs

In the energy system, supply and demand must always be equal, however, short-term uncertainties surrounding VRE generation lead to deviations from contracted positions. This will result in unintentional changes within a day of traditional power plants with increasing system costs [237,288,289,290]. Improved prediction or more effective market operations can reduce balancing costs by increasing liquidity and enabling traders to adjust their places in the market before unbalancing of the system. Nowadays, demand forecasting [291,292,293], VRE generation forecasting [294,295,296], and markets balancing strategies [297,298,299] are all supported by AI.

4.1.1. Generation Forecasting

Scholars have primarily used model-based simulations to forecast solar and wind power that may provide values to companies [227,228,229]. To demonstrate the forecasting of day-ahead solar power generation and its value creation, the authors performed a simulation on the ISO New England system operator in the US [227]. This was done under different situations with varying saturation levels and advances in solar power prediction. Solar power prediction were demonstrated to increase consistently for different prediction levels up to perfect prediction (i.e., 100% consistent improvement). A 25% improvement in forecasting led to cost reductions of USD 0.33/MWh and USD 0.5/MWh for the production of solar electricity at penetration levels of 9% and 18%, respectively. A 50% improvement in forecasting resulted in cost reductions of USD 0.95/MWh and USD 0.62/MWh for solar power generation at penetration levels of 9% and 18%, respectively. Overall, it has been elaborated that cost savings increase with forecasting accuracy and solar power generation penetration level, however, the marginal benefit of an improvement in prediction accuracy of more than 50% has decreased.

Several meteorological models have also been combined using machine learning to increase the precision of forecasts for solar and wind power generation using the data from the US National Renewable Energy Laboratory (NREL) and IBM’s Thomas J. Watson Research Centre [228]. These results were verified over a longer time frame at various US locations. The meteorological condition categorization characteristics (column integrated cloud water content, solar zenith angle, etc.) are included in their model because the forecast bias error of a single physical model is "localized," or dependent on these parameters. The machine learning based model blending technique was frequently demonstrated to lessen the "localized" inaccuracy of individual models when compared to predictions based on the most accurate specific meteorological model, resulting in an accuracy gain of over 30% for solar power forecasts. AI has also been used by the UK’s National Grid Electricity System Operator [229] to enhance VRE generation predictions. In collaboration with the Alan Turing Institute, it has produced a system that improved solar power predictions by 33% using 80 input factors.

Even though wind generation forecasting is more sophisticated than solar power forecasting, AI can still improve it since wind generation forecasting employs techniques comparable to meteorological forecasting, which has grown significantly in recent decades [300]. For instance, machine learning algorithms were employed by DeepMind and Google [234] to predict the capacity of wind power 700 MW in the USA. Their models have increased the value of wind energy by almost 20% when compared to a baseline situation, forecasting wind power output for 36 hours before the actual generating time.

4.1.2. Demand Forecasting

Demand forecasting is just as important to maintaining grid balance as generation forecasting. The availability of data on power usage has greatly expanded, primarily as a result of the widespread installation of smart meters [235], which has improved demand prediction. Hernandez et al. [233] examined earlier research and compared several techniques with general linear versus non-linear energy demand prediction models. With 2.04% of the average error for linear models, 3.20% for ANN-based models and 3.14% for ANN-based hybrid models, in a national or regional geographic setting, it has been shown that linear models perform better than non-linear ones [233]. On the other hand, linear models appear to be comparatively less reliable at the smart grid level in smart cities (average error for hybrids based on ANNs is 2.28%, whereas for linear it is 4.71%). Previous work [233] only employed non-linear models (average error of 4.82%) to forecast energy usage in smart buildings and microgrids, as distributed generation introduces additional complexity and uncertainty, particularly when VRE generation is involved. These findings also point to the potential benefits of AI, especially in the form of ANN-based extremely nonlinear forecasting models, for improved demand prediction in complicated environments and at progressively lower geographic and market scales. In this instance, Saxena et al.’s hybrid model [236] for forecasting peak electric load also incorporates an ANN model to facilitate demand response activities. For a year during the testing phase, the suggested model properly forecasted 70% of the real days of peak load and suggested that a US institution may save close to USD $80,000.

4.1.3. More Efficient Market Design

A better market structure can help lower balancing costs in addition to predicting generation and demand [237]. AI can enhance the effectiveness of market balancing by accounting for the pace and complexity of activities. Bidding procedures that maximize profits were demonstrated to cut balancing expenses by 50% [239]. For instance, an algorithm called EUPHEMIA has been created [231,232] to allocate energy and set day-ahead electricity pricing across Europe as well as to distribute cross-border transmission capacity. With matched offers valued at an average of each day exceeding EUR 200 million, the system is utilized to estimate day-ahead electricity costs for 25 European nations. Although the algorithm currently relies on several rules and optimization models instead of using machine learning, it may be feasible to make it better in the future by combining machine learning and optimization to forecast parameters in advance or taking robustness into account, as has recently been done with techniques at the intersection of machine learning and optimization [245]. Market-generating companies were modeled in a different study by Kiran et al. [241] as agents that pick up on the market environment. The data handling capacity of a multi-agent reinforcement learning method from the electrical market and simulated ideal power flow was examined. By optimizing the generating businesses’ profits, the agents reduced transmission line congestion and increased net earnings by 15 to 20%.

4.2. Mitigating Profile Cost

Profile expenses are mostly brought on by the long-term and decreased use of pricey conventional backup generation capacity to offset the unpredictable supply of VRE. To reduce the need for costly backup energy generation equipment, they can be primarily controlled by making the power system more flexible. The classification and evaluation of the many components of integration costs can be complicated. However, some authors suggest that profile costs are the largest value pool that can be affected by various strategies, including demand response and storage solutions [301]. AI can further boost this as discussed next, even if it is already evident that storage technologies [302,303] and demand response techniques [304,305] might be beneficial.

4.2.1. Demand Response

Demand response, which describes adjustments to end-users’ consumption habits, through monetary rewards or enhanced usage optimization to match the power supply more closely, is becoming more and more common within power networks [242,306,307,308,309]. In addition to profile costs, it has complex effects [302] on integration costs generally, which makes it relevant for other cost components. Demand response can reduce profile costs over time by reducing peak demand, maximizing capital utilization, and delaying the need for network improvements. This can also have an impact on integration costs associated with the grid. It may also have an immediate influence on balancing expenses since it affects the electrical markets [310,311]. Digital solutions, smart infrastructure, and AI are used [243] to increase the volume of demand response by 185 GW until 2040, creating an estimated value of USD 270 billion, by avoiding investments in new electricity infrastructure, such as power generation capacity, transmission, and distribution. By 2040, 1 billion residential buildings and 11 billion linked household appliances are predicted to make up the majority of the global demand response volume. This estimate may be overly optimistic or wrong, but it does show possibilities for the future.

Demand response can be supported by AI in several ways [244], including demand and future power price predictions, load scheduling and management at the aggregator and customer levels, incentive scheme design, and customer segmentation [312]. For instance, evolutionary game theory and agent-based simulations were presented by Ramchurn et al. [245] to estimate the energy use of every single dwelling. Typical load profiles for 26 million homes were employed in the simulation, which included 5000 dwellings in the UK. The approach that was demonstrated decreased demand peaks and, consequently, the grid’s required capacity by as much as 17% and 6% in carbon emissions. Rocha et al. describe [246] a novel approach to energy planning for smart homes that is based on AI approaches. This work presents an estimation of distributed generation while taking into account variations in the price of power, a battery bank, operational cycles, and equipment priority. When comparing smart homes with and without battery banks and distributed generation, the efficiency of the system revealed a 51.4% cost savings. A machine learning method for a demand-side management strategy that is both rule and prediction-based implementation in the residential sector was compared by Pallonetto et al. [247]. The rule-based algorithm and the predictive algorithm resulted in savings of 20.5% and 41.8%, respectively, on electricity end-use expenditures as associated with the baseline situation. For utility generation expenses, savings for both methods fell into the same range.

Data centers are a viable domain of application for demand response, further showcasing the possibilities of these methods [248,249]. Data centers used about 1% of the world’s electricity in 2019 [250]. Because they are highly automated, have sensors installed, can continuously monitor their IT equipment, and can schedule many of their tasks to be completed ahead of schedule, they allow for very flexible management of power demand through the use of cutting-edge technology [248]. The extent of demand responsiveness of data centers might vary depending on how much they engage with the electrical market [249]. The first level is to optimize energy consumption without considering the power markets. Monitoring the price signals of the electrical markets to lower energy prices can lead to a more sophisticated demand response. When the computational effort is split among several geographically separated data centers, a third level can be reached [251,252] to benefit from potential variations in the cost of electricity. For example, an energy-efficient, geographically distributed, sustainable data center optimizer utilizing deep learning was proposed by Kang et al. [253]. The suggested optimizer with deep learning guaranteed service quality requirements while reducing the energy of data center costs by around 25% on average when associated with the traditional rank-based genetic technique. All three levels may benefit from the application of AI, which can help lower profile expenses.

Data center cooling is a crucial factor to consider when optimizing energy consumption because it accounts for a considerable amount of the energy used [254]. A deep reinforcement learning framework is used by Li et al. [255] to solve a problem of energy cost reduction including temperature constraints in data centers. An assessment network is trained to predict an energy cost counter that is penalized by the DC room’s cooling condition, and a policy network is trained to predict the ideal control options. When tested on a simulation platform, the performance of their algorithm demonstrated an 11% reduction in cooling costs compared to a physically built reference line control method. While not tested in an actual data center setting, genuine data-based results showed a 15% decrease in cooling expenses. Among the data centers, Google provides a real-world example of how AI can be used to optimize energy consumption. There DeepMind Inc. [256,257] trained an ANN to predict average Power Usage Effectiveness (PUE) which is the proportion of the total energy used in buildings to that of information technology. The solution successfully decreased PUE by 15% and the amount of energy consumed for cooling by 40%. Based on its ability to predict the pressure and temperature of the data center one hour in advance, DeepMind has been able to offer suggestions for consumption control. As of 2018, DeepMind’s AI has direct control of a cooling system, requiring human involvement only, when necessary, rather than humans implementing its recommendations. Multiple Google data centers now host the scaled version of the system.

4.2.2. Storage Solutions

As the cost of storage technology declines, storage solutions, which may also become a crucial source of adaptability with quick reaction times, can help to decrease profile expenses by the integration of VRE sources in addition to demand response techniques. For example, the cost of lithium-ion battery storage decreased by 85% between 2010 and 2018 [258]. A bottom-up analysis of manufacturing and material costs further illustrates [259] that significant additional capital cost reductions for storage systems are possible.

According to International Energy Agency (IEA) projections, battery storage capacity will increase from 8 GW in 2019 to 330–550 GW by 2040, primarily as a result of cost-effectiveness [250]. According to IEA projections, battery storage renewable curtailment in the EU may be reduced by 45 TWh by 2040, primarily with the help of digital technologies, and by an additional 22 TWh with demand response enabled by digital means [243]. This would prevent around 30 Mt of $C{O}_2$ emissions and restrict the curtailment of wind and solar PV power from 7% to 1.6%.

In the future, electric automobiles may potentially make innovative storage solutions possible. Since Electric Vehicles (EVs) are both users of power and mobile battery storage services, they can modify their consumption patterns with relative ease, which presents a unique use case for demand response. This could have an impact on profile prices. These EVs have the potential to be crucial in the future in terms of giving the grid flexibility, and AI can greatly help achieve this [260]. To minimize the overall cost of energy for an electric vehicle, various machine learning-based algorithms can also be created to control the charging of EVs in reaction to pricing in real-time. To decide whether to charge EVs during connection sessions, Lopez et al. [261] presented intelligent charging approaches based on various machine learning techniques (decision trees, random forests, SVM, and neural networks). They computed cost savings through a variety of methods, demonstrating that deep neural networks performed best and machine learning approaches generally had the major effect. Globally, there were about 5.1 million EVs in 2018, however, the IEA [262] projects that by 2030, there will be between 135 and 250 million of them. The flexibility offered by "smart charging" might save between USD 100 and USD 280$ billion in new power infrastructure investments between 2016 and 2040, based on how many EVs will be sold in the future [243]. Based on a 2025 California simulation [263], it is projected that through vehicle-to-grid solutions, EVs could save between USD 12.8 and USD 15.4$ billion in stationary electricity storage expenditures.

AI possesses the potential to expedite and simulate battery system development, manufacture, and optimization [264,265,266,267]. Using data-driven tools to illustrate and comprehend battery storage systems’ capacity degradation can also help to reduce expenses. By using machine learning, commercial graphite-lithium-iron phosphate cells may be categorized and predicted based on their cycle life. For instance, based on a dataset from cycling 124 cells under various fast-charging settings, Severson et al. [264] showed that the cycle life prediction error improved by 9.1% when utilizing the first 100 cycles and a classification error by 4.9% when using the first 5 cycles.

AI is being used more and more to support energy management to increase efficiency [269], which is a crucial prerequisite to guarantee the financial sustainability of storage, and optimal system configuration [268]. Mahmoud et al. [268] proposed an online monitoring system with AI assistance to test a current commercial type-load profile linked to Western Australia’s South West Interconnected System distribution network, to optimize the battery storage system’s size and lower the associated microgrid’s operating expenses. As per the simulated outcomes, the intelligence included in the control of battery storage in the grid-connected without export, islanded, and grid-connected with export functionality resulted in an annual generation cost reduction of 6.5%, 7.6%, and 11.5%, respectively. To address issues with management, control, and real-time economic operations, Samuel et al. [270] created a deep convolutional neural network for multi-micro grids’ energy management system. The suggested model takes renewable energy, demand loads, energy storage devices, and current power pricing into account. It was suggested that the best scheduling strategy be used to minimize the overall daily operational expenses for several microgrids. As a result, the microgrid’s operating expenses can drop by as much as 87.86%.

Based on previous optimal operation mode training datasets, supervised machine learning was applied in [271] to forecast the real-time operating mode of the upcoming period of operation for PV battery systems installed in homes. As a benchmark, various machine-learning-based algorithm types were compared and assessed with a predictive control method based on a model-based economy. The effectiveness of the algorithms was evaluated using real data sets gathered from 50 homes. The outcomes demonstrated that the algorithms for machine learning were more accurate, which described into greater savings throughout several assessments.

The Hornsdale Power Reserve is a similar development, which Tesla constructed in 2017 and which has 129 MWh of storage capacity. It is the biggest stationary battery energy storage system made of lithium-ion batteries in the world [272]. The Tesla-developed auto-bidder has enabled the system to function and has made a substantial contribution to Southern Australia’s grid stability. A US software business called Advances Microgrid Solution (AMS) also creates innovative AI-based energy storage technologies based on the lessons learned from the Hornsdale Power Reserve. According to AMS, AI-powered smart battery trading systems are five times more effective than the most skilled human traders [273]. In a similar development, Tesla constructed the Hornsdale Power Reserve in 2017, making it the biggest energy storage system for stationary lithium-ion batteries in the world with 129 MWh of storage [272]. The system, which runs on an auto-bidder created by Tesla, greatly improves Southern Australia’s grid stability. Furthermore, flexible "smartened" electric heating on the demand side may be capable of storing energy and releasing it as required, giving the power system flexibility [313]. In the future, all of these might present more chances for AI use cases. To sum up, data-intensive technologies and AI have the potential to reduce profile costs by improving consumption optimization or enhancing power system flexibility through improved management of the rapidly expanding, extremely extensive networks of dispersed storage devices, like EVs or storage services. Since profile costs make up a significant portion of integration expenses, future value creation and research in this area should concentrate on mitigating these costs.

4.3. Mitigating Grid-Related Costs

The conclusions examine how AI can affect grid-related expenses, mostly due to the necessity of fortifying the electrical grid because of VRE fluctuations and the higher costs associated with transmission infrastructure resulting from the generally remote locations of VRE generation sites [226]. Keep in mind that the cost of constructing grid access for offshore windmills will probably be higher than the cost of establishing a grid connection between solar PV fields, as grid-related expenses vary depending on the VRE technology [314]. Forecasting the turbine position and line connection topology using AI and other modeling tools allowed for the optimization of the initial investment costs of large-scale offshore wind farms in the past [315]. To keep the cost of the circuit layout as low as possible, an ant colony algorithm was used in conjunction with other techniques in that study to establish the wind farm’s internal line connection topology.

4.3.1. Power Quality Disturbance

The VRE integration may cause significant disturbances to the power system, power quality and distributed generation sources [274]. The VRE generation, particularly solar PVs, can result in the power system’s behaviour from unidirectional to bidirectional, depending on power quality measures in the grid [275]. AI techniques can assist in enhancing the grid’s power quality, which will increase the system’s financial gains [276]. For instance, Singh et al.[277] used AI approaches to identify power system conflicts and achieved an accuracy of 98.57% for forecast accuracy based on real conflicts and 99.93% for simulated results. Kumar et al. [278] presented that the solar PV power filter could use AI to enhance power quality.

4.3.2. Predictive Maintenance

It will be particularly crucial to schedule maintenance or stop power grid failures in VRE-intensive areas where it is difficult to physically access the grid infrastructure for repair, in addition to the costs associated with the investment. By providing improved predictive maintenance solutions, AI can be used to optimize maintenance and reduce grid-related expenses. The literature examines the application of AI-supported predictive maintenance along the value chain for electricity, with a focus on power lines [279,280,281,282], as well as VRE [283,284,285] and conventional generating [286]. The partnership between Columbia University and New York City’s Con Edison to build the city’s electrical grid with a predictive maintenance system based on machine learning [281] is an illustration of how AI is affecting predictive maintenance. A basic procedure that aims to forecast the likelihood of component and system failures was created using previous electrical grid data models. After the system was implemented, 1468 out of 4590 network days were failure-free, as opposed to 908 days that were failure-free before. This represents a significant improvement. As an additional illustration, Gao et al. [287] optimized the distribution network using an algorithm based on reinforcement learning, primarily to boost hosting capacity, lower network line losses, and decrease VRE curtailment. Without requiring any interaction with the real physical network, which is expensive and fraught with security risks, the algorithm was trained using past data from network reconfigurations. The algorithm greatly reduces the weekly operating costs of the behaviour policy for most of the datasets from the past. The model can result in weekly operational cost savings of up to 60%, depending on the network architecture.

More broadly, E. ON has created the predictive analytics for wind Turbines (PredATur) system [284] to improve personnel scheduling and maintenance. The PredATur integrates the output of two complementary approaches using sensor data from wind turbines. In the meanwhile, the machine learning strategy expands upon a digital doppelganger of the wind turbines that simulates every sensor output, the park-average approach checks the state of the turbines by comparing them with those of nearby turbines. Currently, PredATur keeps an eye on about 1,800 turbines. The projected annual EBITDA impact for PredATur detections in 2017 is €3.2–5.7 million based on value estimates.

5. Discussion

The integration of VRE sources into power systems presents a host of economic and operational challenges, which AI promises to mitigate through various innovative applications. This section critically examines the findings of the systematic review, highlighting the strengths and limitations of AI-driven approaches, and identifying areas for future research and improvement.

5.1. Economic Value Creation of AI in VRE Integration

AI’s potential to create economic value in VRE integration is evident across multiple applications. Generation and demand forecasting, and market design improvements are particularly impactful in mitigating balancing costs. AI-driven forecasting models increase the accuracy of VRE generation predictions, thereby reducing the need for costly balancing actions. However, the economic benefits are highly contingent on the quality and granularity of the data used to train these models. Inadequate data quality or insufficient data points can lead to suboptimal predictions, limiting the economic benefits AI can offer.

Moreover, AI’s ability to enhance market design, particularly in the context of balancing markets, has significant implications for economic efficiency. AI algorithms can optimize bidding strategies, reduce market inefficiencies, and ultimately lower balancing costs. However, the implementation of AI in market design also raises concerns about fairness, transparency, and market manipulation. Ensuring that AI-driven market mechanisms are designed with robust safeguards and regulatory oversight is essential to prevent potential exploitation and ensure equitable outcomes for all market participants.

5.2. Enhancing Demand Response and Storage Solutions

AI also plays a crucial role in enhancing demand response and optimizing storage solutions, both are vital for mitigating profile costs. Demand response strategies, supported by AI, allow for more efficient consumption patterns and load management, reducing peak demand and associated costs. Furthermore, AI-driven algorithms for managing battery storage systems and EVs charging can significantly improve system efficiency and reduce operational costs. Despite these advantages, the economic viability of AI in demand response and storage solutions depends on the scalability of these technologies and the regulatory frameworks governing energy markets. Additionally, the initial investment required for AI implementation in these areas can be a barrier to widespread adoption.

The potential of AI to optimize the integration of Distributed Energy Resources (DERs) through advanced demand response and storage solutions cannot be overstated. By enabling real-time monitoring and dynamic management of DERs, AI can facilitate the seamless integration of these resources into the grid, enhancing overall system flexibility and resilience. However, the complexity of managing a diverse array of DERs, coupled with the need for robust cybersecurity measures, presents significant challenges. Addressing these challenges will be crucial to unlock the full economic potential of AI-driven demand response and storage solutions.

5.3. Addressing Grid-Related Costs Through AI

AI’s capability to enhance predictive maintenance and improve power quality is essential for addressing grid-related costs. Predictive maintenance, enabled by machine learning and data analytics, can foresee potential failures of power grid infrastructure, thereby reducing downtime and maintenance costs. Similarly, AI techniques can optimize power quality by identifying and mitigating disturbances, thus ensuring a stable and reliable power supply. However, the effectiveness of these AI applications relies heavily on the integration of advanced sensing technologies and real-time data processing capabilities. The high cost of deploying these technologies and the complexity of integrating AI systems with existing grid infrastructure remain significant challenges.

Additionally, AI can play a pivotal role in optimizing the planning and operation of power grids. By leveraging AI for grid management, operators can enhance grid stability, optimize power flows, and reduce transmission losses. Advanced AI algorithms can also facilitate the efficient integration of renewable energy sources by dynamically adjusting grid parameters in response to real-time data. Nevertheless, the successful deployment of AI in grid management necessitates significant investments in digital infrastructure and skilled personnel. Ensuring that grid operators have the necessary expertise to implement and manage AI technologies will be critical to realizing the full benefits of AI in grid-related applications.

5.4. Challenges and Limitations

While AI offers substantial benefits, several challenges and limitations must be acknowledged. Figure 5 illustrates the limitation’s of AI which hinder its practical deployment and widespread adoption. The reliability and transparency of AI models have concerns, particularly in safety-critical applications such as power systems. AI models are often perceived as black boxes, making it difficult to interpret their decision-making processes. This lack of transparency can hinder trust and acceptance among stakeholders. Moreover, the cybersecurity risks associated with AI systems are a growing concern, as they could be potential targets for cyberattacks, jeopardizing the stability and security of power systems. Furthermore, the success of AI applications in VRE integration is closely tied to the availability of high-quality data. Inconsistent or inaccurate data can lead to false predictions and suboptimal decisions, undermining the economic benefits of AI. There is also a need for standardized methodologies to evaluate the economic impact of AI applications, as current approaches vary widely, making it challenging to compare results across different studies. Ethical considerations also play significant role in the deployment of AI in energy systems. Ensuring that AI algorithms are designed and implemented in a manner that is fair, unbiased, and respects privacy is essential. Addressing these ethical considerations will require ongoing collaboration between AI developers, energy sector stakeholders, and policymakers to establish clear guidelines and standards.

5.5. Future Research Directions

Future research should focus on several key areas to fully harness AI’s potential in VRE integration. First, developing transparent and interpretable AI models is crucial to gaining stakeholder trust and facilitating widespread adoption. Efforts should be made to enhance the explainability of AI algorithms to ensure that their decisions can be understood and validated by human operators. Second, addressing the cybersecurity risks associated with AI systems is imperative. Future work should also explore the robust security frameworks and protocols to protect AI-driven power systems from cyber threats. Collaboration between AI researchers, cybersecurity experts, and energy sector stakeholders will be essential in this endeavor. Third, advancing data collection and processing techniques will significantly improve the accuracy and reliability of AI applications. Investment in advanced sensing technologies and real-time data analytics will provide the high-quality data necessary for optimal AI performance. Additionally, developing standardized evaluation methodologies will enable more consistent and comparable assessments of AI’s economic impact across different studies.

Finally, policy and regulatory frameworks should be developed to support the integration of AI in the energy sector. Policymakers should create an enabling environment that encourages innovation while ensuring the safe and secure deployment of AI technologies. Incentives for choosing AI-driven solutions and guidelines for data sharing and privacy protection will be critical in this regard. To further improve the economic value of AI in VRE integration, interdisciplinary research that combines insights from computer science, economics, and energy engineering will be essential. Such collaborative efforts can lead to the development of innovative AI-driven solutions that address the multifaceted challenges of VRE integration. AI has tremendous potential for enhancing the economic efficiency and operational reliability of VRE integration. While significant progress has been made, addressing the challenges and limitations identified in this discussion will be crucial for realizing AI’s full potential. Continued research, investment, and policy support are essential to foster a resilient and economically sustainable energy landscape powered by AI-driven innovations.

6. Conclusions

This systematic review has comprehensively explored the potential of AI to enhance the economic efficiency and operational reliability of VRE integration into power systems. The increasing penetration of VRE is driven by the urgent need to mitigate climate change and achieve sustainable development goals, however, it is associated with significant economic and operational challenges. AI has emerged as a promising solution to address these challenges through its applications in generation and demand forecasting, market design, demand response, storage solutions, power quality enhancement, and predictive maintenance. Key findings from this review include:

• AI-driven models significantly enhance the accuracy of VRE generation and demand forecasts, leading to reduced balancing costs and improved grid stability. However, the economic benefits of these models are contingent on the quality and granularity of input data. Ensuring high-quality, comprehensive datasets is crucial for maximizing the economic impact of AI applications.
• AI algorithms optimize market bidding strategies, reduce inefficiencies, and lower balancing costs. However, the implementation of AI in market design must address issues of fairness, transparency, and potential market manipulation to ensure equitable outcomes for all participants.
• AI enhances demand response strategies and optimizes the management of battery storage systems and EVs charging, resulting in significant cost savings and improved system efficiency. The scalability of these techniques, and supportive regulatory frameworks are essential for their widespread adoption and economic viability.
• AI techniques improve power quality by identifying and mitigating disturbances and enhance predictive maintenance by forecasting potential failures of power grid infrastructure. The integration of advanced sensing technologies and real-time data processing capabilities is crucial for the effectiveness of these applications.
• The reliability and transparency of AI models, cybersecurity risks, data quality, and ethical considerations are significant challenges to be addressed. Developing transparent and interpretable AI models, robust security frameworks, and standardized evaluation methodologies are essential for getting stakeholders’ trust and ensuring successful AI deployment in VRE integration.
• Future research should focus on enhancing the explainability of AI algorithms, addressing cybersecurity risks, advancing data collection and processing techniques, and evolving policy and regulatory frameworks to support AI integration in the energy sector. Interdisciplinary research that combines insights from computer science, economics, and energy engineering will be critical for developing innovative AI-driven solutions.