A Comprehensive Review of Optimal Power Flow in Integrated Energy Systems: A Shift from Traditional to Data-Driven Technologies

1. Introduction

Energy is fundamental to human society's production and operation. As the global economy develops, the shortage of traditional fossil fuels and the deterioration of the ecological environment have become focal points of concern. There is an urgent need for an efficient and green energy utilization system [1]. Additionally, as society progresses, humanity's satisfaction with traditional and singular power supply is waning, with forms of energy such as cooling, heating, and gas playing increasingly important roles [2]. 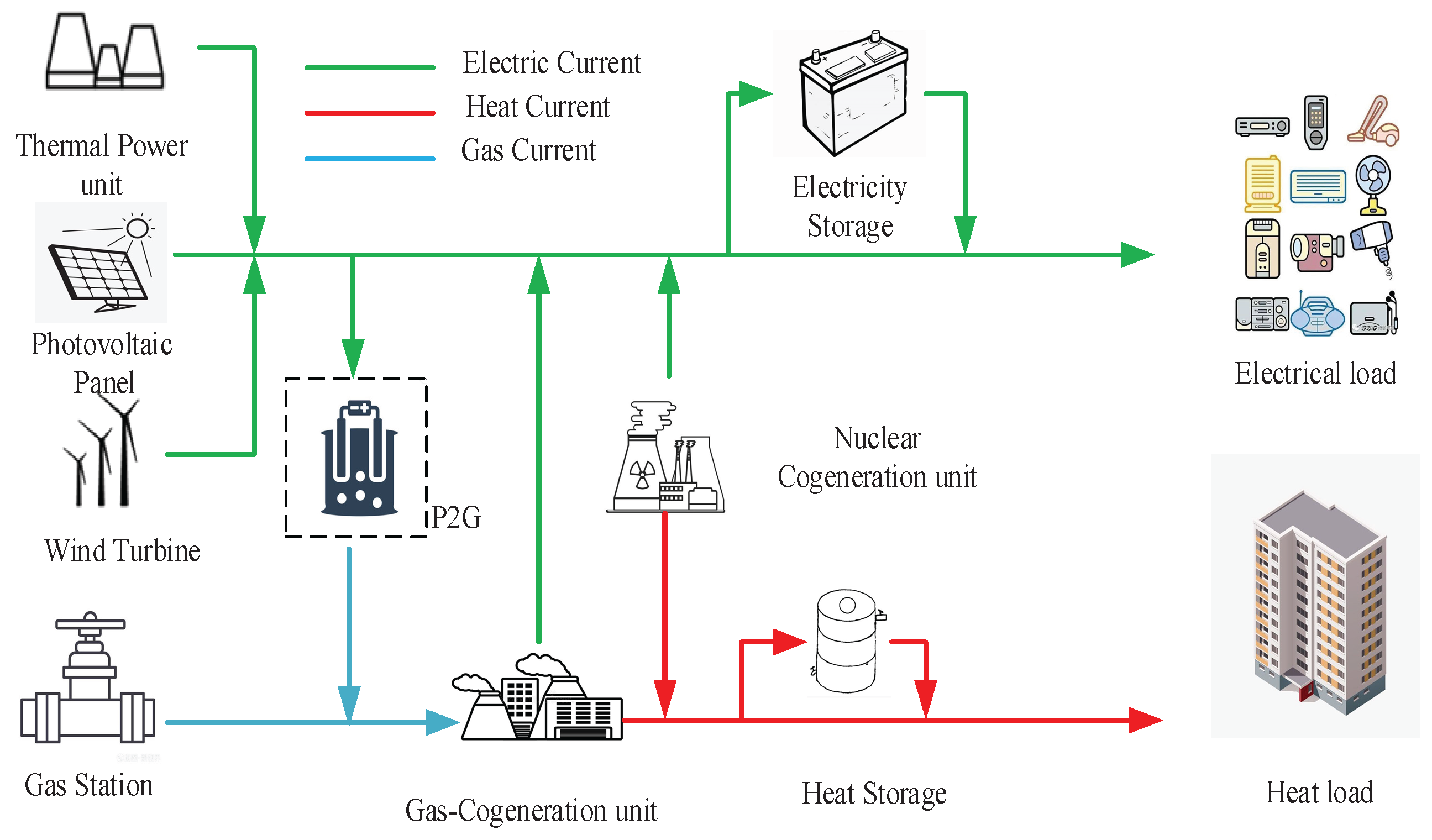In response to these challenges, integrated energy systems (IESs) have emerged as a comprehensive solution [3], as illustrated in Figure 1 [4].

Amid rapid economic development in China, the tension between the escalating demand for fossil fuels and their diminishing reserves is intensifying. Coupled with significant environmental challenges like excessive carbon emissions, reliance on traditional fossil resources is increasingly inadequate to meet the demands of modern energy conservation, environmental protection, and high societal energy needs [5,6]. In many urban energy systems across China, electricity, natural gas, and heat networks operate independently without the ability for unified control, leading to inefficiencies and opaque system operations [7,8,9]. This often results in energy wastage or load shedding due to imbalances between supply and demand, consequently lowering energy utilization rates and causing economic losses [10,11].

The United States pioneered the development of Integrated Energy Systems (IES) in 2001 [12], introducing the concept of the Energy Internet in 2011, which blends distributed energy with internet technology [13]. This initiative evolved under the "Future Renewable Electric Energy Delivery and Management Systems" project, focusing on constructing a digital energy network [14,15]. In Europe, the concept of IES originated from studies on information transmission within energy systems [16], while Japan, facing energy resource scarcity, has been exploring IES since 2009, setting national goals to create a comprehensive energy framework [17]. Despite a late start, China has made significant strides in researching energy interconnection and smart grids, emphasizing the integration of energy and information through energy internet technologies [18,19,20,21].

The IES model employs advanced information technology and innovative management to integrate the production, supply, and consumption of electricity, heat, cooling, and gas within a region, enhancing the synergy between various energy forms and breaking traditional energy network silos [25,26,27]. This integration supports sustainable development by fostering a low-carbon, open energy future and upgrading energy system structures [28].

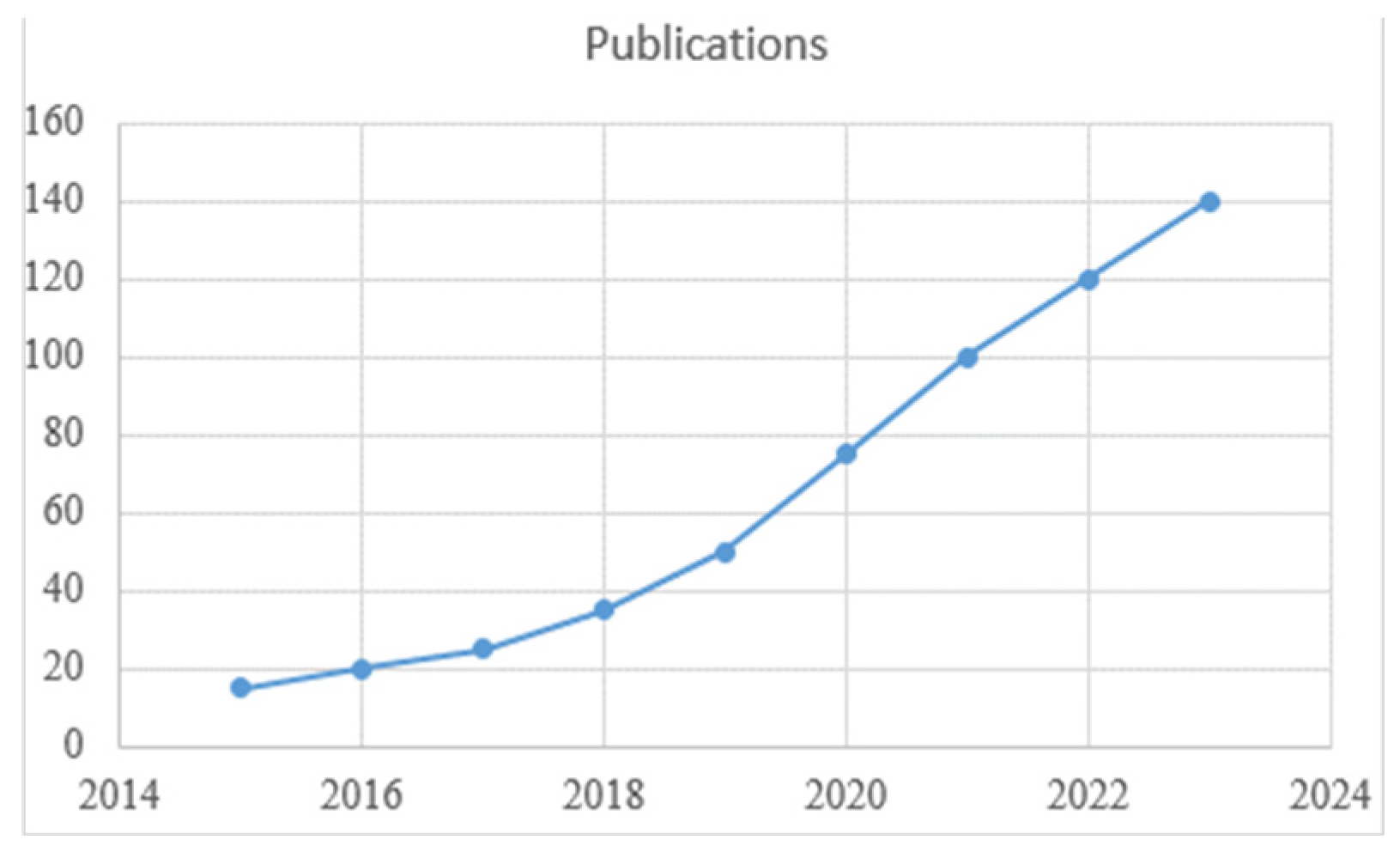
This paper explores the evolution of optimal power flow (OPF) techniques in IESs, transitioning from traditional to advanced data-driven models, and addresses challenges in OPF calculations to enhance the planning, operation, and management of these complex systems [29]. IES OPF has become a research hotspot, with a rapid increase in scholarly outputs in recent years, as depicted in Figure 2.

Traditional OPF models, often constrained by linear approximations and static conditions, fail to capture the dynamic interactions in the system efficiently [30]. Recent advancements in data-driven methodologies, leveraging machine learning and real-time data analytics, promise enhanced accuracy and adaptability in modeling the complex behaviors of multi-energy systems. These data-driven approaches, by harnessing the vast amounts of data generated by modern energy systems, offer not only more precise predictive capabilities but also adaptive control mechanisms that can significantly optimize energy distribution and usage in real-time, thus addressing many of the challenges posed by traditional methodologies.

This review aims to explore the evolution from traditional OPF models to modern data-driven approaches within integrated energy systems. By examining both the historical methodologies and the cutting-edge techniques currently shaping the industry, this paper seeks to highlight the pivotal role of data-driven innovations in the future of IES optimization.

2. Power Flow and OPF Calculations in IESs

IESs encompass a diverse range of energy supply networks and coupling components, creating a complex framework where the management of energy flow is critical. This section outlines the nuances between power flow calculations and OPF, their importance in IESs, and how advancements in data-driven technologies are enhancing these processes.

2.1. Distinction of Power Flow and OPF

Power flow calculations in IESs involve determining the routes and amounts of electricity that flow through the network under given operating conditions. The basic equations for power flow in IESs, including the balance of power at different nodes, which could be represented by [31]:

$$P_{G_i}-P_{L_i}=V_i{\displaystyle \sum }_{j=1}^N{V}_j\left(G_{ij}\cos \left({\theta }_i-{\theta }_j\right)+B_{ij}\sin \left({\theta }_i-{\theta }_j\right)\right)$$

(1)

$$Q_{G_i}-Q_{L_i}=V_i{\displaystyle \sum }_{j=1}^N{V}_j\left(G_{ij}\sin \left({\theta }_i-{\theta }_j\right)-B_{ij}\cos \left({\theta }_i-{\theta }_j\right)\right)$$

(2)

where $P_{G_i}$​​ and $P_{L_i}$​​ are the active powers of generator and load power at bus i, $Q_{G_i}$​​ and $Q_{L_i}$​​ are the reactive powers of generator and load power at bus i, $V_i$​ and $V_j$ are the voltages at buses i and j, $G_{ij}$ and $B_{ij}$ are the real and imaginary parts of the admittance between buses i and j, and ${\theta }_i$​ and ${\theta }_j$ are the angles of the voltages.

These calculations are essential for ensuring the physical and operational integrity of the energy network. Traditional methods like the Newton-Raphson and Gauss-Seidel methods have been extensively used due to their effectiveness in stable and predictable environments.

Optimal power flow, however, extends these calculations by introducing optimization goals which may include cost reduction, efficiency enhancement, and emission controls. OPF is particularly critical in IESs as it needs to coordinate multiple forms of energy—electrical, thermal, and gas—ensuring that the energy supply meets varied demands optimally. The OPF in IESs can be formulated by:

$$\begin{array}{l}\min f(\mathit{x},\mathit{u})\\ \mathrm{s}.\mathrm{t}. \left\{\begin{array}{l}\mathit{g}(\mathit{x},\mathit{u})=0\\ \mathit{h}(\mathit{x},\mathit{u})\le 0\end{array}\right.\end{array}$$

(3)

where, x denotes state variables including voltages, phase angles, node pressures in natural gas systems, and temperatures in thermal systems, u represents control variables such as generator outputs and transformer tap settings in power systems, compressor ratios in gas systems, and operational settings in thermal systems. The objective function $f(\mathit{x},\mathit{u})$ relates to energy inputs and flow equations, aiming for cost efficiency and minimum losses, depicted through system flows. The equality constraint

$\mathit{g}(\mathit{x},\mathit{u})=0$involves balancing equations at energy hubs and mixed flow equations, challenging due to the complexities of energy coupling. The inequality constraint $\mathit{h}(\mathit{x},\mathit{u})\le 0$covers equipment limitations, operational restrictions, and specific constraints of the IES. For example, the cost minimization objective might look like:

$$\min {\displaystyle \sum }_{i=1}^n{c}_i\left(P_{G_i}\right)$$

(4)

where $c_i$​ is the cost function associated with generator i and $P_{G_i}$​​ is the power output.

2.2. IES Power Flow Calculations

Traditional power flow methods often assume steady-state conditions and linear relationships, which are increasingly inadequate for the dynamic and complex nature of IESs, where energy inputs and demands are variable and interconnected. The complexity escalates due to the diverse nature of energy sources and the dynamic interactions between them, making traditional methods less effective at scalability and real-time processing.

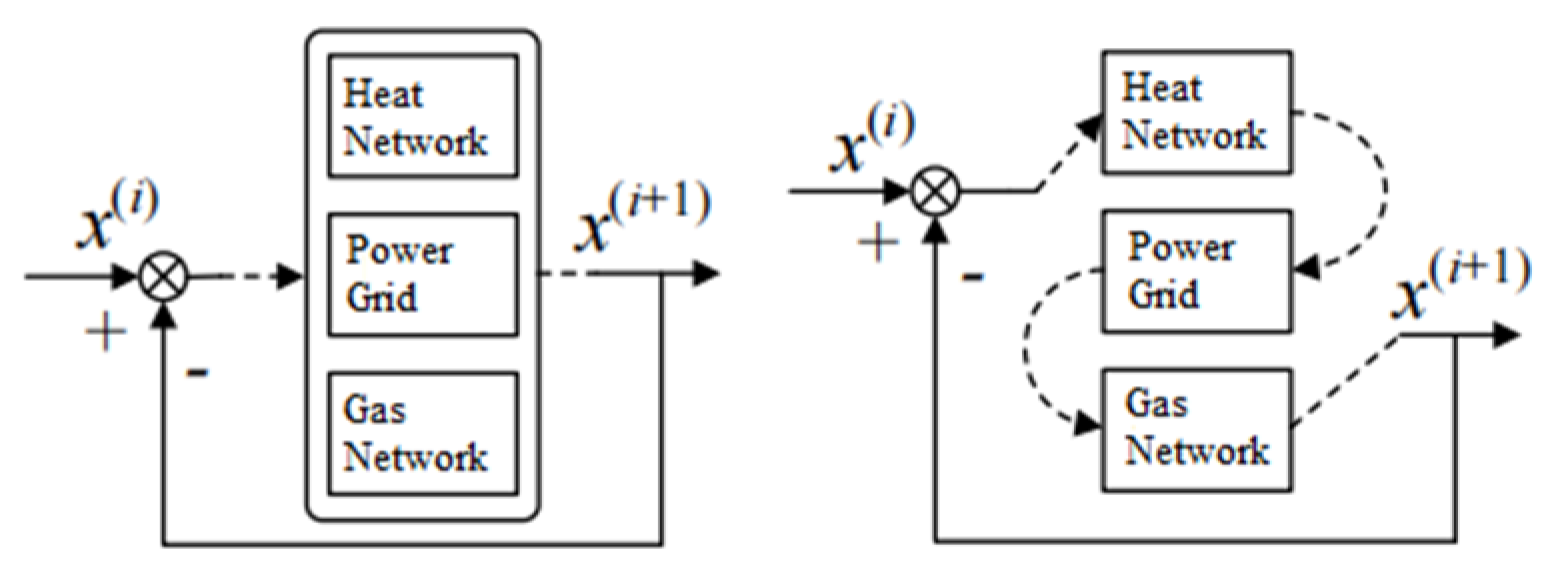
To be specific, the simultaneous solution method traditionally treats the electrical, gas, and heating networks as a whole, forming a system of unbalanced equations for the integrated network, and then deriving the Jacobian matrix of electrical, gas, and heat coupling. As illustrated in Figure 2, this method typically employs Newton's method for solving. On the other hand, the alternate iterative method solves for each subsystem independently, allowing each subsystem to use its own suitable power flow calculation method [32]. Such as, the electricity and gas networks might use Newton's method, while the heating network might use the forward-backward substitution method; coupling nodes are equated based on the characteristics and classifications of subsystem nodes, such as cogeneration units acting as PV nodes in the electrical network and as heat source nodes in the heating network.

2.3. Modern Approaches and Data-Driven Solutions

Research in power flow within integrated energy systems increasingly incorporates advanced modeling and analytical techniques to improve accuracy and adaptability. For instance, Reference [33] developed a method combining electric and thermal models for distribution networks, employing forward/backward iterations with high precision and robustness. Reference [34] utilized affine algorithms for interval power flow calculations in electric-thermal systems, enhancing the analysis of uncertainties such as load fluctuations and renewable energy integration.

In addition, enhancements focus on refining Newton's method [35,36], adapting it for broader applications within diverse energy networks. Reference [37] applied Newton's method to natural gas networks, demonstrating its versatility. Moreover, Reference [38] addressed complex, interconnected systems using Newton's method, which occasionally faces convergence challenges due to the dynamic nature of IESs. These advancements signify a shift towards integrating machine learning and artificial intelligence, revolutionizing traditional power flow calculations. This integration enables more dynamic system management, adapting to and optimizing energy flows within the complexities of integrated systems.

2.4. Data-Driven Enhancements in OPF

Data-driven enhancements in OPF are addressing traditional method limitations. Reference [39] introduced a step-size adaptation algorithm for more reliable initial settings in variable natural gas and thermal networks. This dynamic adjustment of iteration steps significantly enhances computation speed and accuracy, reducing Newton's method's sensitivity to initial values and ensuring more consistent outcomes. Then, Reference [40] developed a multi-energy flow initial value convergence theorem to strategically place initial values away from convergence boundaries, improving stability and speeding up the process.

Beyond these enhancements, the integration of machine learning and artificial intelligence is transforming OPF within IESs. These technologies effectively predict and adapt to changes in energy demand and supply, enhancing the precision and efficiency of OPF calculations. This shift not only improves the calculation precisions but also enhances the system's ability to optimize performance efficiently and reliably. These data-driven enhancements are pivotal in advancing the capabilities of OPF, marking a significant evolution from traditional methods.

2.5. Necessity and Impact of Advanced Data-Driven Techniques

As integrated energy systems become more complex, the necessity for data-driven approaches escalates. Advanced techniques like deep learning are crucial for adapting to and managing the dynamic nature of these systems. They utilize historical data and real-time inputs to predict and optimize power flow, showcasing a significant shift towards more adaptive and intelligent systems. This evolution in energy management technologies is vital for future-proofing energy infrastructures against the challenges posed by the unpredictable variability of renewable energy sources and the growing demands for energy efficiency. Such advancements not only enhance operational adaptability but also ensure that energy systems can sustain performance amidst increasing complexities and regulatory expectations.

3. Research Status in IES OPF

OPF is essential in integrated energy systems for the complementary and synergistic optimization among diverse energy subsystems, crucial for their safe, stable, and economical operation. Research on OPF in these systems is still emerging. Most studies have centered on electric-heat or electric-gas combinations, with fewer focusing on more complexly coupled systems like electric-heat-gas. Algorithmically, integrated energy systems have seen fewer multi-energy flow optimization algorithms compared to those for electrical systems alone. Most OPF research in integrated systems typically targets single-objective optimizations, such as minimizing economic or environmental costs, rather than multi-objective optimization.

Existing and potential algorithms for OPF in integrated energy systems are categorized into classical and intelligent algorithms. Classical algorithms encompass linear programming, mixed-integer programming, quadratic programming, Newton's method, and interior-point methods. Meanwhile, intelligent algorithms include genetic algorithms, neural networks, fuzzy algorithms, particle swarm optimization, and reinforcement learning algorithms.

Classical algorithms in integrated energy systems have seen significant applications and advancements. For instance, Reference [41] developed a dynamic OPF model for gas-electric systems by integrating transient natural gas and steady-state electric power flows, resulting in a single-stage linear programming problem that enhances operational strategies for both systems. The effectiveness of this model was validated through simulations, showcasing its utility in coordinated gas and electricity planning. Reference [42] addressed multi-period energy flow and pricing in carbon-conscious integrated systems involving electricity, natural gas, and centralized heating, establishing foundational flow models and using linearization to optimize scheduling and determine locational marginal prices, factoring in carbon emissions.

The interior-point method, known for its robust convergence, has been effectively applied to various OPF challenges. Reference [43] utilized it to evaluate the environmental impacts in a gas-electric integrated system, while Reference [44] used it in an electric-heat model focusing on minimizing coal consumption with promising simulated results.

Despite the efficacy of classical algorithms, their limitations include potential non-convergence with discontinuous objectives and challenges in handling complex, non-convex problems. In contrast, intelligent algorithms, inspired by natural and social phenomena, offer adaptive solutions to optimization challenges without requiring strict convexity or continuity, effectively handling uncertainties in data. However, their theoretical foundations need further development, and optimality of solutions can sometimes be uncertain. Reference [45] introduced a generalized intelligent optimization method for coupled multi-energy flows, employing a multi-agent genetic algorithm to break down complex problems into manageable OPF challenges, demonstrating robustness and applicability. Additionally, References [46] and [47] explored advanced genetic and particle swarm algorithms for optimizing multi-energy flows in IESs, further underscoring the potential of intelligent algorithms in complex energy system optimization.

4. Traditional OPF Models in IESs

OPF calculations play a pivotal role in the management of IESs, ensuring efficient, reliable, and sustainable energy distribution across various interconnected networks [48,49,50]. Traditional optimization models, developed over decades, are fundamental to understanding and solving OPF problems within these complex systems. These models provide structured frameworks to handle a myriad of challenges associated with energy generation, distribution, and consumption, adapting to the evolving landscapes of modern energy systems [51].

4.1. Optimization Problem Types

4.1.1. Linear Programming

Linear programming (LP) is an essential tool in the field of OPF calculations for IESs, particularly effective in scenarios where the relationships and constraints are linear. LP offers a clear computational advantage due to its simplicity and efficiency, which makes it exceptionally useful for initial feasibility studies, preliminary analyses, and systems characterized by straightforward and predictable resource allocations [52,53].

The primary utility of LP in IES OPF lies in its ability to provide quick, scalable solutions that can be crucial for operational planning and decision-making. LP models are used to optimize the cost of energy production and distribution by simplifying complex problems into linear relationships. This can involve minimizing costs or maximizing efficiency within operational limits defined by linear constraints.

However, the simplicity of LP also introduces limitations, especially in handling the complexities inherent in IESs. Most energy systems exhibit nonlinear behaviors—such as those arising from the physics of power flows in electrical grids or the response curves of energy storage systems—which cannot be accurately modeled using linear approximations. When LP is applied to such systems, it can result in suboptimal solutions that do not effectively capture the trade-offs and operational constraints, potentially leading to decisions that are not only economically inefficient but also technically infeasible [54]. Additionally, the integration of renewable energy sources like solar and wind, which are inherently variable and unpredictable [55], introduces further complexities that exceed the modeling capabilities of LP. These sources often require sophisticated decision-making tools that can adapt to rapid changes in input conditions, something that linear models typically struggle with.

Despite these challenges, LP remains a foundational tool in the OPF toolbox. Its effectiveness in certain applications—such as in systems with limited variability and well-defined linear interactions—continues to make it a valuable initial approach in multi-stage optimization frameworks. In these contexts, LP can provide baseline solutions that are refined through more complex nonlinear optimization methods as needed. This staged approach allows system operators to harness the simplicity and speed of LP where applicable, while reserving more computationally intensive methods for stages of the planning and operation process where they are most needed.

4.1.2. Nonlinear Programming

Nonlinear Programming (NLP) is crucial for effectively addressing the complex nonlinear dynamics typical of IESs. Unlike linear programming, NLP is adept at handling the intricate interactions within energy systems, such as the nonlinear voltage-current relationships in electrical networks, the efficiency curves of generators and transformers, and the thermodynamic properties in heating and cooling systems. These are common scenarios in IESs where energy sources, storage systems, and loads interact in ways that are inherently nonlinear and dynamic [56,57,58].

NLP methods are tailored to model these complexities accurately, allowing for the optimization of power flows that reflect the true physical and technical constraints of energy systems. This modeling capability is essential for devising optimal strategies that enhance system reliability, efficiency, and sustainability. For instance, NLP can optimize the dispatch of generation units in a way that minimizes fuel consumption while respecting environmental constraints, or it can be used to determine the optimal settings of network components that reduce losses and maintain voltage levels within safe operational limits.

However, the power of NLP comes with increased demands on computational resources. Solving NLP problems typically requires advanced mathematical techniques and powerful computational tools, including gradient methods, Newton-like algorithms, and interior-point methods, which are more complex and computationally intensive than those used in linear programming. These methods need to iteratively converge to a solution, often requiring numerous evaluations of derivatives and solving of large systems of equations [59]. Moreover, the use of NLP in IES OPF presents challenges such as ensuring global optimality and managing the convergence of solutions, especially in large-scale systems with multiple types of energy carriers and complex network topologies. The potential for multiple local minima or saddle points in NLP problems necessitates the use of sophisticated initialization strategies and robust algorithmic enhancements to improve solution quality and computational efficiency.

Despite these challenges, the application of NLP in IES OPF is growing, driven by advances in computational algorithms and increasing computational power. Moreover, as energy systems continue to integrate more renewable sources and become more interconnected, the ability of NLP to handle non-linearities becomes increasingly important. This makes NLP not just a tool for problem-solving, but a critical component in the planning and operation of modern energy systems, ensuring they can operate efficiently under a wide range of conditions and configurations [60,61].

4.1.3. Quadratic Programming

Quadratic Programming (QP) is an invaluable optimization tool within the realm of IESs, particularly when addressing OPF calculations where the objective functions—such as cost functions or power loss equations—naturally form quadratic relationships. This is frequently the case in power systems where the relationship between the power output and the associated costs or losses can be effectively modeled as quadratic curves, which better represent the actual performance and economic characteristics of energy generation and distribution systems.

QP provides several significant advantages for energy management. Firstly, it enhances the precision of modeling economic factors and technical losses within energy systems. By accurately representing the quadratic nature of these elements, QP enables more effective optimization of system operations. This includes minimizing operational costs, optimizing fuel consumption, and efficiently allocating resources across various types of energy inputs and outputs [62,63,64]. For instance, in electricity markets, QP can be used to determine the most cost-effective generation dispatch that meets demand while minimizing transmission losses and adhering to regulatory constraints. Moreover, QP formulations allow for the incorporation of various constraints that ensure the stability and reliability of the energy grid. These constraints might include generation capacity limits, network load capacities, and regulatory requirements for renewable energy utilization. The ability of QP to handle such constraints under quadratic cost functions makes it especially suitable for complex energy systems where multiple factors and interactions must be balanced [65].

However, despite its strengths, QP also comes with its set of challenges. The main challenge lies in solving the quadratic equations, especially when the problem size increases as more nodes, links, and alternative energy sources are integrated into the system. This can lead to an increase in the computational complexity, necessitating the use of advanced algorithms and high-performance computing solutions [66].

The integration of QP in IES OPF not only supports better economic and operational outcomes but also aligns with the increasing complexity and sophistication of modern energy systems. As the energy sector continues to evolve towards more integrated and dynamic systems, the role of QP remains crucial in ensuring that these systems are not only economically viable but also capable of meeting the increasing demands for energy reliability and sustainability.

4.1.4. Sequential Quadratic Programming

Sequential quadratic programming (SQP) excels in addressing the complex challenges of IESs, particularly for OPF problems involving multiple energy types and intricate interactions. As a robust optimization technique, SQP iteratively solves quadratic subproblems that approximate the original nonlinear OPF problem, offering high precision and adaptability essential for managing the dynamic nature of IESs [67].

SQP is adept at handling complex constraints and nonlinear relationships more effectively than other methods. It refines the approximation of nonlinearities in each iteration, progressively achieving solutions that meet operational constraints and optimization goals. This adaptability is crucial for responding to changes such as fluctuations in energy demand or renewable energy production [68].

In practical applications, SQP optimizes the integration and operation of diverse energy sources—electricity, heat, gas, and renewables—within an IES. It adjusts settings for generators, transformers, and storage units, balancing energy production costs, environmental impact, and system reliability. The inclusion of real-time data in each iteration enhances SQP's effectiveness, enabling it to update calculations based on the latest system state, thereby improving decision-making and system efficiency [69].

Despite its benefits, SQP's computational intensity, especially in large-scale systems with thousands of variables and constraints, requires substantial computational resources and sophisticated software tools. Nevertheless, SQP remains a key method for nonlinear OPF challenges in IESs, facilitating energy optimization amidst evolving technologies and market conditions. Its iterative and adaptable approach makes it vital for developing efficient, reliable, and sustainable energy systems [70,71,72].

4.2. Optimization Algorithms

4.2.1. Interior-Point Method

The interior-point method (IPM) is a sophisticated optimization technique employed in solving both linear and nonlinear programming problems within IESs [73]. The main principles of the IPM are encapsulated by its use of barrier functions to maintain solutions within feasible boundaries, combined with an optimization path that ensures convergence from any starting point within the feasible region [74,75,76]. The path-following IPM is valued for its robustness and ability to maintain feasible iterations, making it highly effective for optimizing large-scale power systems.

The fundamental equations governing the Interior-Point Method are outlined as follows:

a) Barrier Function: Central to the IPM is the use of a barrier function to modify the original optimization problem, ensuring that the solution avoids violating constraints. The typical modified objective function for problems with inequality constraints is:

$$\underset{x\in {ℝ}^n}{\min }f\left(x\right)-\mu {\displaystyle \sum }_{i=1}^m\ln \left(-g_i\left(x\right)\right)$$

(5)

Here, f(x) is the primary objective function, $g_i\left(x\right)\le 0$represents the constraints, and μ is a small, positive barrier parameter that controls the influence of the barrier term.

b) Karush-Kuhn-Tucker Conditions: At optimality, the solutions must satisfy the Karush-Kuhn-Tucker (KKT) conditions, which integrate the barrier term:

$$\mathrm{Primal} \mathrm{Feasibility}\text{:} g_i\left(x\right)\le 0$$

(6)

$$\mathrm{Dual} \mathrm{Feasibility}\text{:} {\lambda }_i\ge 0$$

(7)

$$\mathrm{Complementarity}\text{:} {\lambda }_i{g}_i\left(x\right)\le 0$$

(8)

$$\mathrm{Stationarity}\text{:} \nabla f\left(x\right)+{\displaystyle \sum }_{i=1}^m{\lambda }_i\nabla g_i\left(x\right)=0$$

(9)

c) Central Path and Newton's Method: The iterative approach of IPM follows the central path, a trajectory defined by points that satisfy the perturbed KKT conditions for diminishing values of μ. Newton’s method is typically used to compute the next iterate:

$$\left(\begin{array}{cc}{\nabla }^{2}f\left(x\right)& A^T\\ A& 0\end{array}\right)\left(\begin{array}{c}\Delta x\\ \Delta \lambda \end{array}\right)=\left(\begin{array}{c}-\nabla f\left(x\right)\\ -Ax+b\end{array}\right)$$

(10)

where A represents the matrix of gradients of the constraints, and b denotes the right-hand side of the constraints.

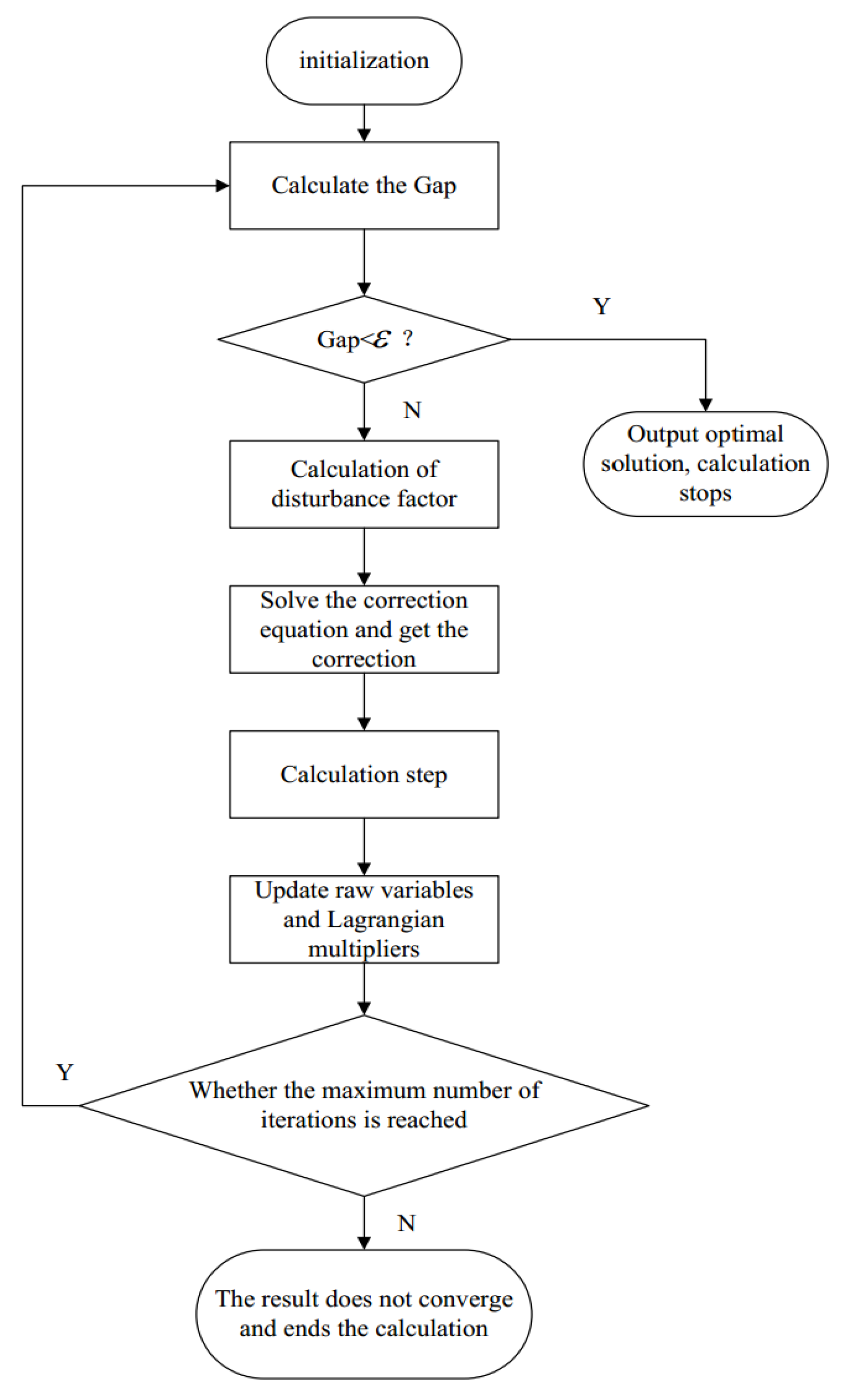
Recent advancements have significantly improved the interior-point method by incorporating data-driven analytics, enhancing its application in complex integrated energy systems. Adaptive step-size adjustments, informed by predictive analytics, reduce computation times and increase solution accuracy [77]. In response, new software tools have been developed to assist engineers and researchers in managing intricate energy optimization tasks, providing greater analytical detail and control for efficient energy management [78,79]. The process for addressing optimal energy flow problems using the IPM is detailed in Figure 3 [80].

4.2.2. Dual Decomposition

Dual decomposition is a vital optimization strategy within the field of OPF calculations for IESs. This technique addresses the daunting scalability challenges that arise when managing complex energy systems that encompass multiple energy types and extensive geographical areas [81]. Key formulas of this approach are as below:

a) Objective Function Decomposition: The general optimization problem in IESs can be expressed as:

$$\underset{x}{\min }f\left(x\right) \mathrm{subject} \mathrm{to} Ax=b,x\in X$$

(11)

Here, f(x) represents the objective function aimed at optimizing system operations, Ax=b are the constraints ensuring system stability and legality, and X denotes the feasible set of solutions. Decomposing the objective function is crucial for managing the complexity inherent in IESs.

b) Lagrangian Function: The Lagrangian for dual decomposition is formulated as:

$$L\left(x,\lambda \right)=f\left(x\right)+{\lambda }^T\left(Ax-b\right)$$

(12)

This incorporates the constraints into the objective function via Lagrange multipliers λ, which play a critical role in allowing the decoupling and independent solving of sub-problems.

c) Subproblem Formation: The main problem is divided into smaller subproblems, each solvable independently:

$$\underset{x_i}{\min }{f}_i\left(x_i\right)+{\lambda }^T{A}_i{x}_i$$

(13)

for each subproblem i. This breakdown not only simplifies the computational process but also localizes problem-solving, enhancing operational efficiency at various subsystem levels.

d) Dual Function and Optimization: The dual function, essential for optimizing the Lagrange multipliers, is given by:

$$g\left(\lambda \right)=\underset{x\in X}{\inf }\left(f\left(x\right)+{\lambda }^T\left(Ax-b\right)\right)$$

(14)

The optimization of this function involves maximizing:

$$\underset{\lambda }{\max }g\left(\lambda \right)$$

(15)

Solving the dual problem optimizes the entire system's performance by finding the best possible adjustments for the Lagrange multipliers.

e) Update Rule for Lagrange Multipliers: The Lagrange multipliers are updated iteratively to ensure convergence and alignment with global objectives:

$${\lambda }^{\left(k+1\right)}={\lambda }^{\left(k\right)}+{\alpha }^{\left(k\right)}\left(A{x}^{\left(k\right)}-b\right)$$

(16)

where ${\alpha }^{\left(k\right)}$ is the step size at iteration k. These updates are critical for iteratively refining the solutions to achieve the best possible global system performance.

Dual decomposition separates complex optimization problems into independent components, making it particularly effective for Integrated Energy Systems (IESs) where subsystems like electrical grids, heating networks, and gas pipelines operate under distinct constraints and dynamics [82,83]. This parallel optimization accelerates computation by distributing workloads across processors or computational nodes, while enabling tailored solutions for each subsystem—such as cost minimization, energy output maximization, or supply-demand balancing. This granularity is vital for integrating renewables with unpredictable outputs into the broader system [84,85,86].

In practice, dual decomposition alternates between solving local subproblems for each subsystem and updating global variables to coordinate system-wide energy balance, iterating until convergence criteria are met [87]. Despite its advantages in managing complex OPF challenges, achieving global convergence and optimality can be challenging. Independent subproblem solutions must be aligned with overall system objectives, often requiring additional control mechanisms like Lagrangian multipliers [88,89,90]. While dual decomposition improves computational efficiency and manageability, it demands sophisticated software and skilled operators to handle decomposition and reintegration complexities. Its success depends on the precise design of decomposition schemes and efficient algorithms. As IESs grow in scale and complexity, dual decomposition is becoming critical for efficient energy management [91,92,93].

4.3. Challenges and Opportunities

4.3.1. Challenges

Traditional models in OPF calculations for IESs face challenges in complexity and scalability. These approaches often struggle with the vast scale and intricacy of modern IESs, requiring substantial computational resources and advanced algorithms to handle diverse energy sources and consumption patterns effectively [94,95,96].

Another critical issue is adaptability. Traditional models may not adequately adapt to rapid changes in energy demand or supply, especially given the unpredictable nature of renewable energy sources such as wind and solar power [97]. These energy sources can vary dramatically due to environmental conditions, and traditional models often lack the flexibility to adjust to such fluctuations in real-time, potentially leading to inefficiencies or system instabilities.

Integration challenges further complicate OPF in IESs. The diverse energy types—electrical, thermal, gas, and renewables—demand seamless integration strategies [98,99,100]. Traditional models often struggle to manage interactions across these carriers, especially when optimizing systems with differing operational characteristics and regulatory constraints.

Lastly, data sensitivity is a substantial concern. The effectiveness of traditional OPF models heavily depends on the quality and accuracy of the input data. Inaccuracies in initial data can significantly impact the feasibility and reliability of the solutions provided by these models. This sensitivity to data quality means that any errors in data collection or processing can lead to suboptimal decision-making and potentially costly outcomes.

4.3.2. Opportunities

Despite these challenges, there are significant opportunities for advancing traditional models in the context of IES OPF. The development of hybrid approaches that combine traditional deterministic models with modern data-driven techniques offers a promising avenue. These hybrid models can enhance predictability and system adaptability, better handling the uncertainties and variability associated with renewable energy sources [101,102,103].

Advances in computing power and algorithms offer opportunities to address scalability and complexity challenges in traditional methods. Enhanced computational capabilities enable the handling of larger datasets and more complex models, supporting sophisticated simulation and optimization techniques for improved energy system management [104]. Additionally, regulatory support for renewable energy integration and smart grid development fosters the adoption of advanced modeling approaches, aligning traditional methods with modern IES requirements.

While traditional models in IES OPF face several challenges, the evolving landscape of energy systems and technology offers numerous opportunities to refine and enhance these models [105,106,107]. By leveraging advancements in computational techniques and embracing hybrid modeling approaches, it is possible to significantly improve the planning, operation, and optimization of integrated energy systems, leading to more sustainable and efficient energy management.

5. Data-Driven OPF Calculation in IESs

The transition to data-driven approaches in managing optimal power flow within IESs marks a pivotal shift, empowering systems to be more responsive, efficient, and intelligent [108]. By integrating analytics, machine learning, and artificial intelligence, these methodologies redefine how energy networks operate in real-time and how they adapt to evolving demands and energy landscapes [109,110,111].

5.1. Overview of Data-Driven Techniques in Energy Systems

Data-driven techniques transform energy management by leveraging extensive datasets to perform complex simulations and optimizations that traditional models cannot handle effectively [112,113,114]. These techniques analyze data from diverse sources such as satellite imagery for solar potential, sensor data from smart devices, and operational data from power plants to provide a holistic view of the energy ecosystem [115]. This wealth of information supports sophisticated forecasting models that can anticipate energy trends, optimize asset use, and reduce wastage.

5.2. Machine Learning Models in IES OPF

The integration of machine learning (ML) into IES OPF calculations represents a significant advancement in optimizing and managing complex energy systems [116]. These models enhance the predictive accuracy, operational efficiency, and adaptive capacity of IESs through sophisticated data analysis and algorithmic innovation.

5.2.1. Enhanced Forecasting Models

In the context of IES OPF, machine learning models significantly enhance predictive capabilities by utilizing sophisticated time series forecasting and regression analysis to anticipate fluctuations in energy demand and supply, particularly from renewable sources [117,118,119]. These models harness extensive historical datasets, which include past energy usage, weather conditions, economic indicators, and operational metrics from energy facilities. This comprehensive data foundation is critical for training the models to recognize and predict complex patterns and trends [120].

Techniques such as AutoRegressive Integrated Moving Average (ARIMA), Seasonal ARIMA (SARIMA), and Long Short-Term Memory (LSTM) networks are particularly adept at handling seasonal variations and nonlinear patterns typical in energy data. These methods are essential for accurately predicting future energy needs, enabling energy systems to plan and adjust their operations proactively.

Advanced regression models, including linear and polynomial regression, are employed to predict continuous variables that directly affect the energy systems. These models play a crucial role in determining optimal energy generation levels in response to variable inputs such as price fluctuations and changes in consumer behavior [121,122]. Furthermore, these predictive tools are instrumental in forecasting the variable outputs of renewable energy sources. The integration of these unpredictable energy sources into the grid is made seamless through accurate and timely predictions [123].

The real-time predictive capabilities of modern ML models allow for dynamic adjustments in electricity flow, maintaining system balance and enhancing economic efficiency [124,125,126]. These capabilities enable more informed decisions on energy market bidding, maintenance scheduling, and load management, all of which contribute to more robust and responsive energy systems. Moreover, these forecasting models play a vital role in risk management by identifying potential failures or disruptions in the supply chain, thereby ensuring reliability and continuity in power supply [127,128].

The continuous evolution of these technologies significantly boosts the operational and economic efficiency of IESs. By adapting to the ever-changing dynamics of energy demand and supply, machine learning models lead to the development of more adaptive, efficient, and resilient energy systems [129]. This ongoing advancement in forecasting technology underpins the reliability and sustainability of modern integrated energy systems [130].

5.2.2. Optimization Algorithms

In IES OPF, machine learning algorithms play a crucial role in optimizing complex, multi-source energy distributions [131,132,133]. These algorithms employ both traditional optimization techniques and advanced metaheuristic methods such as genetic algorithms and particle swarm optimization. Each method is tailored to address the unique challenges presented by IESs, which include the integration of heterogeneous energy sources like solar, wind, hydro, and fossil fuels, each characterized by distinct availability patterns and operational characteristics [134].

The integration of these diverse energy sources necessitates a delicate balance between economic efficiency and environmental sustainability [135,136,137]. This balance further complicates the optimization process, as it requires dynamic solutions that can swiftly adapt to changing conditions and priorities. ML algorithms are particularly adept in this area, automating the decision-making process and significantly enhancing the system’s ability to manage and optimize energy flows efficiently [138]. This automation is critical not only for maintaining system stability but also for managing the intermittent nature of renewable energy sources, whose outputs can fluctuate due to environmental factors [139,140,141].

By leveraging the computational power of ML algorithms, IESs can achieve a more harmonious balance between supply and demand, ensuring optimal energy distribution and minimizing wastage [142]. The sophisticated nature of these algorithms aids in meeting economic and environmental targets, facilitating the operation of energy systems that are both cost-effective and environmentally responsible [143]. Moreover, these systems are capable of self-adjusting in real time to unforeseen changes or disruptions, thereby ensuring continuous and reliable energy delivery across diverse geographical and consumer landscapes [144,145,146].

The use of ML algorithms in energy optimization not only supports the sustainability of energy systems but also contributes to their resilience. This enhanced resilience is crucial in an era where energy systems must be flexible enough to adapt to rapid changes in both generation capacity and consumption patterns, ensuring stability and reliability for all stakeholders involved [147].

5.2.3. Condition Monitoring and Predictive Maintenance

Machine learning models are indispensable in the realm of condition monitoring and predictive maintenance [148]. Serving as crucial tools, they ensure the health and longevity of the complex infrastructure that underpins modern energy systems. These models utilize real-time data gathered from an extensive network of sensors deployed across the IES [149,150,151]. By analyzing this data, ML models identify patterns and anomalies that could indicate potential equipment failures or inefficiencies.

Sophisticated algorithms such as neural networks and anomaly detection techniques are central to these ML models [152,153,154]. They enable the prediction of potential failures, forecasting not only when and where equipment might fail but also indicating when maintenance should be scheduled. This ability to preemptively address issues before they escalate allows for interventions that prevent costly repairs and avoid possible instability [155,156]. Such proactive maintenance strategies not only help in reducing maintenance costs but also significantly prolong the operational lifespan of critical infrastructure components [157].

Moreover, the predictive capabilities of these models facilitate the scheduling of maintenance activities at optimal times, which minimizes their impact on system operations and ensures continuous energy supply. This strategic integration of ML into maintenance practices transforms traditional reactive maintenance into a proactive component of system management, substantially enhancing both reliability and operational efficiency.

Through continuous monitoring and sophisticated analysis, ML models contribute significantly to the resilience of IESs. They adapt maintenance needs to the actual conditions and performance of the system, moving away from reliance on fixed maintenance schedules. This approach not only optimizes resource use but also plays a crucial role in maintaining the overall health of the energy grid, ensuring it operates at peak efficiency and with minimal disruption [158].

5.2.4. Renewable Energy Integration

Machine learning is revolutionizing the integration of variable renewable energy sources, such as wind and solar, into IESs [159,160,161]. These sources are inherently unpredictable due to their dependence on environmental conditions, posing significant challenges for traditional energy management systems [162]. ML models excel in this aspect by utilizing advanced forecasting techniques to predict energy outputs accurately. These predictions are critical for planning and managing the integration process, allowing for the adjustment of energy flow in real-time to accommodate the variable nature of renewable outputs. This capability significantly enhances both the stability and the efficiency of the energy grid [163,164,165].

By employing regression models, neural networks, and time-series analysis, ML can analyze historical weather data alongside real-time environmental inputs to predict the availability of wind and solar energy [166]. This predictive power enables utilities to balance these intermittent sources with more stable energy forms, such as hydroelectric or thermal power, optimizing the overall energy mix. Additionally, ML-driven optimization algorithms can dynamically adjust grid operations, such as rerouting power or controlling storage systems, to absorb excess energy during peak production times or to release energy during demand spikes [167].

The strategic integration of renewable energy facilitated by ML not only helps in reducing carbon footprints and meeting sustainability goals but also enhances economic efficiency by maximizing the utilization of generated renewable energy. Furthermore, ML models contribute to the development of smart grids that are capable of self-adjusting to changes in energy production and consumption patterns, thereby improving resilience against potential disruptions and ensuring a reliable power supply [168,169,170]. This integration of renewable sources is essential for the future of energy systems as it promotes a cleaner, more sustainable, and economically viable energy landscape. Machine learning's role in this process underscores its potential to transform energy management practices, making them more adaptive and forward-thinking [171,172].

5.2.5. System Resilience Enhancement

ML models significantly bolster the resilience of IESs by enhancing their ability to dynamically respond to a range of operational challenges [173,174,175]. These challenges include sudden disruptions in the energy supply, unexpected demand surges, or faults within the grid infrastructure. ML models achieve this by utilizing real-time data analysis and predictive capabilities to swiftly adjust energy flows and maintain equilibrium within the system [176].

The resilience-enhancing capability of ML models lies in their ability to process vast datasets from grid sensors, weather stations, and usage patterns to predict and address potential issues before they escalate [177]. For instance, ML can forecast energy deficits caused by weather-induced renewable output fluctuations and compensate by adjusting output from other sources or managing demand through demand response. Reinforcement learning algorithms further enable real-time energy distribution decisions, optimizing responses to grid conditions and enhancing reliability [178].

ML models also coordinate distributed energy resources like solar panels, battery storage, and electric vehicles as active grid assets. By intelligently managing charging, discharging, and energy consumption, these models reduce grid stress during peak times and ensure stability [179]. By boosting system resilience, ML not only ensures a stable and reliable energy supply but also protects infrastructure from damage, extending its lifespan and reducing costs. This adaptability is essential for modern energy systems, supporting sustainability goals and securing energy supply in a dynamic landscape [180].

5.3. Challenges and Opportunities

Expanding the implementation of data-driven OPF within IESs uncovers both challenges and significant opportunities.

5.3.1. Challenges

1) Data Quality and Scalability

Ensuring the quality, completeness, and timeliness of data is crucial, as discrepancies or gaps can severely impact the accuracy of predictions and the effectiveness of OPF calculations. Additionally, the increasing complexity and scale of energy systems demand scalable solutions that can manage vast datasets and provide real-time actionable insights, necessitating sophisticated algorithms [181,182].

2) Cybersecurity and Privacy Concerns

With the increasing reliance on digital technologies, energy systems are more vulnerable to cyber-attacks and privacy breaches [183,184,185]. Ensuring robust security measures and considering privacy-preserving techniques like federated learning are essential to protect sensitive data and maintain system integrity [186,187,188,189].

3) Uncertainty from Renewable Energies

The high penetration of variable renewable energy sources introduces significant uncertainty in power generation [190], complicating the management of energy flows and requiring more robust forecasting and optimization strategies [191,192,193].

4) Electric Vehicle Integration

The increasing adoption of electric vehicles (EVs) introduces significant challenges for power systems, particularly in managing load demands and optimizing distribution networks [194,195,196]. Advanced modeling is essential to accurately predict and effectively manage the impacts of EV charging on the main grid, ensuring stability and efficiency across the network [197].

5) Power electronics integration

Integrating power electronics into IES presents challenges but significantly enhances grid reliability by facilitating connections to dispersed renewable sources. This integration requires sophisticated control strategies for seamless interactions with existing AC systems, leveraging the flexible and rapid response capabilities of modern power electronics technology [198,199]. These interactions necessitate advanced, data-driven frameworks capable of managing the dynamic behaviors between AC and DC grids to ensure stability and efficiency. Furthermore, power electronics play a crucial role in providing grid support services such as voltage control and fault management, essential for maintaining resilience in highly renewable-integrated energy systems [200].

5.3.2. Opportunities

1) Enhanced System Efficiency and Reliability

Leveraging predictive analytics and real-time data, data-driven OPF can significantly improve the efficiency and reliability of IESs, enabling more precise and dynamic management of energy flows [201,202].

2) Economic and Operational Optimization

Advanced ML models offer substantial benefits in optimizing economic aspects such as energy trading, dynamic pricing, and cost-effective maintenance scheduling, enhancing the profitability and operational efficiency of energy providers [203].

3) Innovative Services and Customer Engagement

The insights provided by data-driven approaches not only enable the development of innovative services, such as personalized energy management and proactive customer engagement strategies [204], but also enhance demand response initiatives [205]. These initiatives engage customers in modifying their power usage during peak times using incentives, improving load management and flexibility auxiliary service [206], and enhancing customer relationships and satisfaction with energy services.

4) Informing Policy and Regulation

Data-driven insights not only guide policy and regulatory frameworks but also enhance governance and support for sustainable energy policies. By analyzing energy usage patterns and system performance, these insights shape policies promoting energy efficiency and renewable adoption [207]. Moreover, they inform regulatory developments to ensure sustainability and market equity, supporting a transition towards a more sustainable energy future [208,209].

6. Future Directions

As the fields of integrated energy system management and data-driven optimization continue to evolve, future advancements are expected to harness emerging technologies and develop new methodologies that enhance efficiency, accuracy, and resilience. Reflecting on the discussions in sections 4 and 5, several key areas are poised for significant development:

1)

Quantum Computing

Quantum computing emerges as a transformative technology with the potential to solve complex OPF problems far more efficiently than classical computers [210]. Quantum algorithms could exponentially speed up the processing of large-scale, complex optimization tasks associated with IESs, providing a groundbreaking tool for real-time energy management and decision-making [211].

2)

Hybrid Models

The integration of machine learning models with traditional optimization methods, such as the interior-point method explored in Section 4, highlights the potential for creating hybrid models. These models would leverage the predictability and reliability of deterministic models while incorporating the adaptability and learning capabilities of ML algorithms from Section 5. Such hybrid approaches could offer more robust solutions to energy optimization by effectively handling the variability and uncertainties of renewable energy sources and the dynamic demands of modern energy grids.

3)

Global Grid Management

Reflecting the visionary ideas from Section 5 regarding the utilization of AI, there is a clear trajectory towards the development of a global energy management platform. This platform would employ advanced data analytics and AI to optimize energy flows not just locally but across continents in real-time. The goal would be to maximize the utilization of renewable resources on a global scale, enhancing grid stability and energy sharing between nations and continents, thus contributing to global energy sustainability.

4)

Enhanced Security and Privacy Solutions

With the increasing integration of data-driven solutions and the potential for cyber threats discussed in Section 5, future directions must also include the development of enhanced cybersecurity measures. This includes the implementation of more advanced encryption methods and the use of federated learning models to ensure data privacy while still benefiting from collective insights.

5)

Regulatory and Policy Innovations

Future advancements should also focus on influencing regulatory frameworks and policies to support the widespread adoption of these advanced technologies. Effective policy measures could facilitate the integration of decentralized renewable energy sources [212], support the implementation of IESs, and promote cross-border energy exchanges underpinned by data-driven insights [213].

7. Conclusions

This review thoroughly traces the evolution of power flow calculations in Integrated Energy Systems (IESs), marking a significant transition from traditional methods to sophisticated, data-driven approaches. Traditional models, foundational yet limited, struggle to cope with the dynamic and complex nature of modern IESs. The integration of data-driven technologies, harnessing extensive datasets and advanced machine learning algorithms, has propelled energy management into a new era of enhanced efficiency and adaptability. These innovations not only bolster forecasting and optimization efforts but also significantly increase the resilience and flexibility of energy system operations.

Looking forward, research should persist in fusing and refining these technologies, exploring the potential of emerging fields like quantum computing and crafting hybrid models that merge the reliability of traditional methods with the agility of modern solutions. This progressive integration is essential for optimizing energy flow, reducing waste, and fostering a sustainable energy future, thus improving the economic and environmental performance of energy systems worldwide.