1. Introduction
Sound wave analysis is necessary to understand music because it is not just a sensory pleasure, but also contains very complex structures and patterns in terms of science and technology. Through sound wave analysis, we can deeply understand the components of music, and through this, we can use them for music creation, learning, and research [
1,
2,
3].
Acoustic analysis tools have evolved to enable humans to better understand and utilize sound. These tools started from simple auditory evaluation in the past and have evolved into advanced systems that utilize precise digital signal processing technology [
4].
In the early stages of the development of acoustic analysis tools, subjective evaluation using human hearing was the main focus. Using an oscillograph or an analog spectrum analyzer, most of all mechanical devices could do was visually analyze the waveform or frequency of sound waves [
5,
6,
7].
However, with the advent of the digital age, we began to analyze sound data using computers and software.
Fast Fourier Transform (FFT) has become a key technology in frequency domain analysis, and improved precision has made it possible to pinpoint the temporal and frequency characteristics of sound [
8,
9].
Recently, with the development of machine learning and AI-based analysis, technology is also being used to recognize patterns of sound, separate voice and instruments, and analyze emotions. Real-time sound analysis is possible through mobile devices and cloud computing, and thanks to 3D sound analysis, three-dimensional analysis is also possible by considering spatial sound information.Extending this to another application is expected to lead to infinite pioneering in a variety of fields, including healthcare (hearing testing), security (acoustic-based authentication), and environmental monitoring (noise measurement).
But there are also obvious limitations. First, the technical limitation is that analysis accuracy in complex environments is poor. It is difficult to extract or analyze specific sounds in noisy or resonant environments. In addition, it is difficult to process various sound sources, making it difficult to accurately separate sound sources with different characteristics such as musical instruments, human voices, and natural sounds [
10]. Another limitation is the lack of versatility: there are many tools optimized for a particular domain, but no general-purpose system is built to handle all acoustic data.The biggest limitation is the gap between human hearing. Due to the difficulty in quantifying subjective sound quality assessments, it is difficult to fully quantify or replace a person’s subjective listening experience, and techniques to elaborately analyze human cognitive responses to sound (emotion, concentration, etc.) are still in their infancy [
11].
Therefore, it is necessary to strengthen the technology to separate specific sound sources even in complex environments, and multimodal analysis should be developed to integrate various data such as video and text in addition to sound so that sound can be analyzed.
It also requires the development of models that better mimic the way the human hearing system works and acoustic calibration techniques tailored to individual hearing characteristics [
12].
To sum up, acoustoassay tools are moving beyond just their role as technical tools to gain a deeper understanding of humans and their environment and provide a better experience. Future developments depend on integrating technology with human sensory and cognitive elements [
13].
In this paper, we have developed a software that focuses on the quantification of subjective sound quality evaluation and present a method for analyzing various sound sources in various ways.
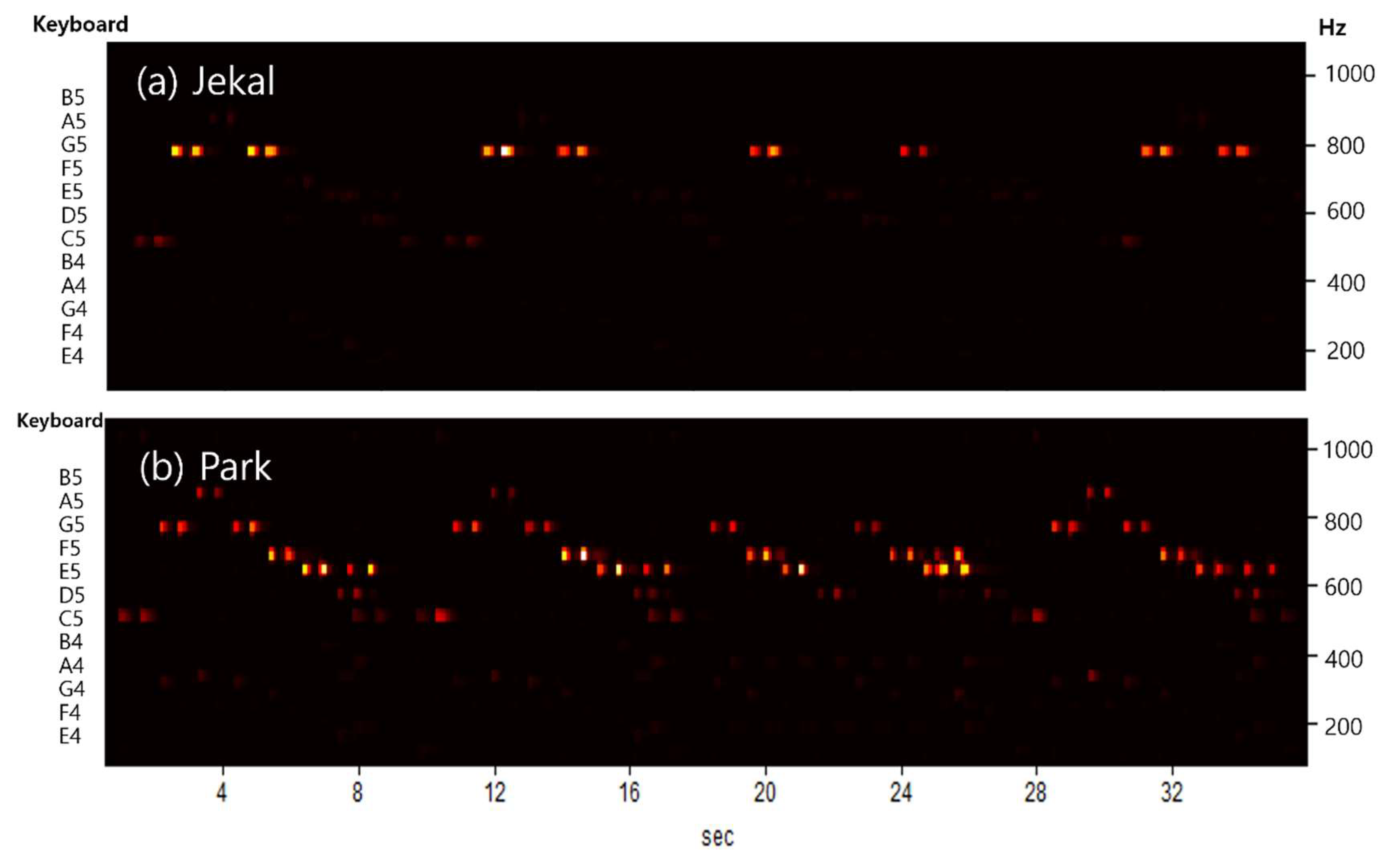
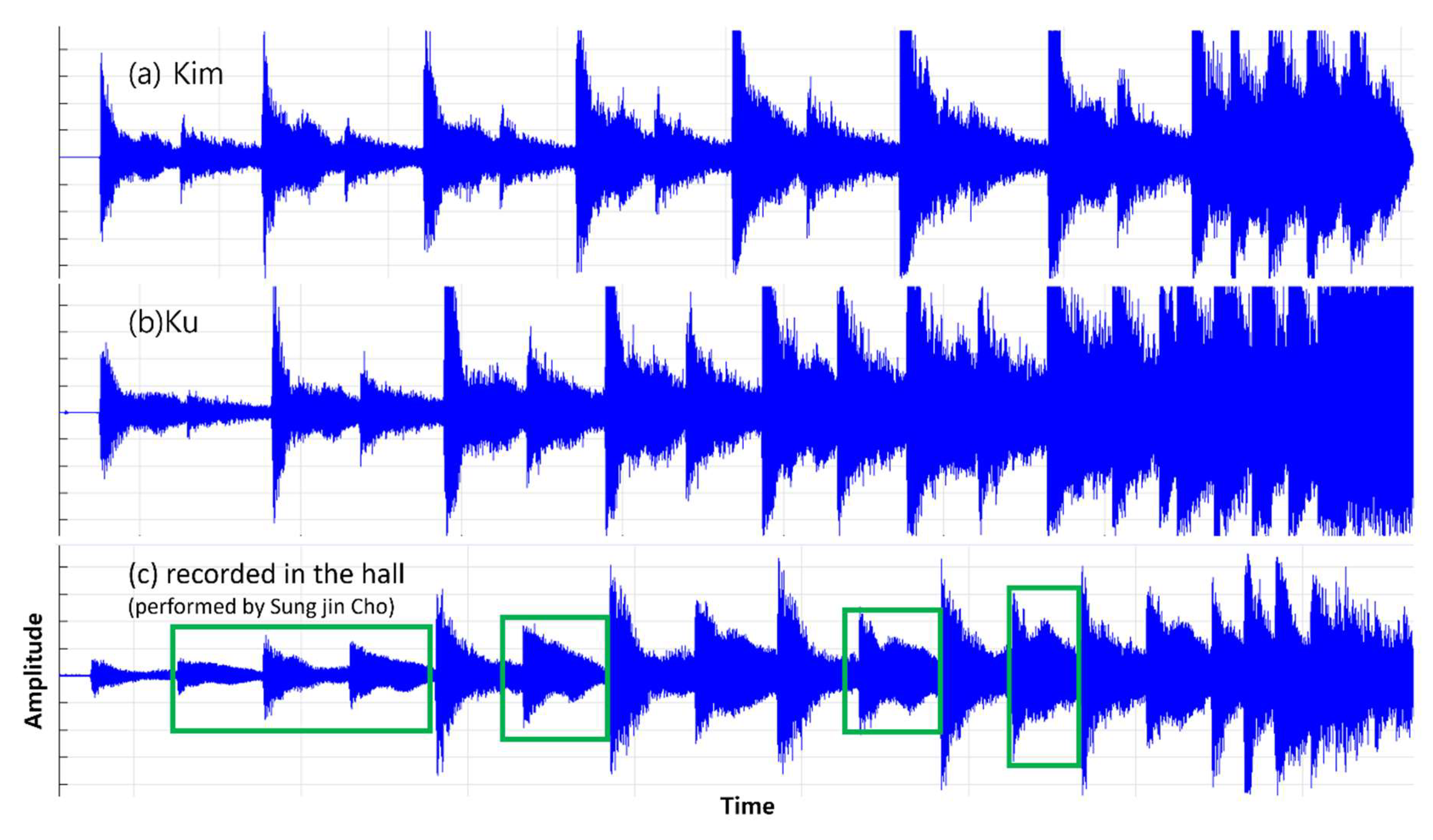
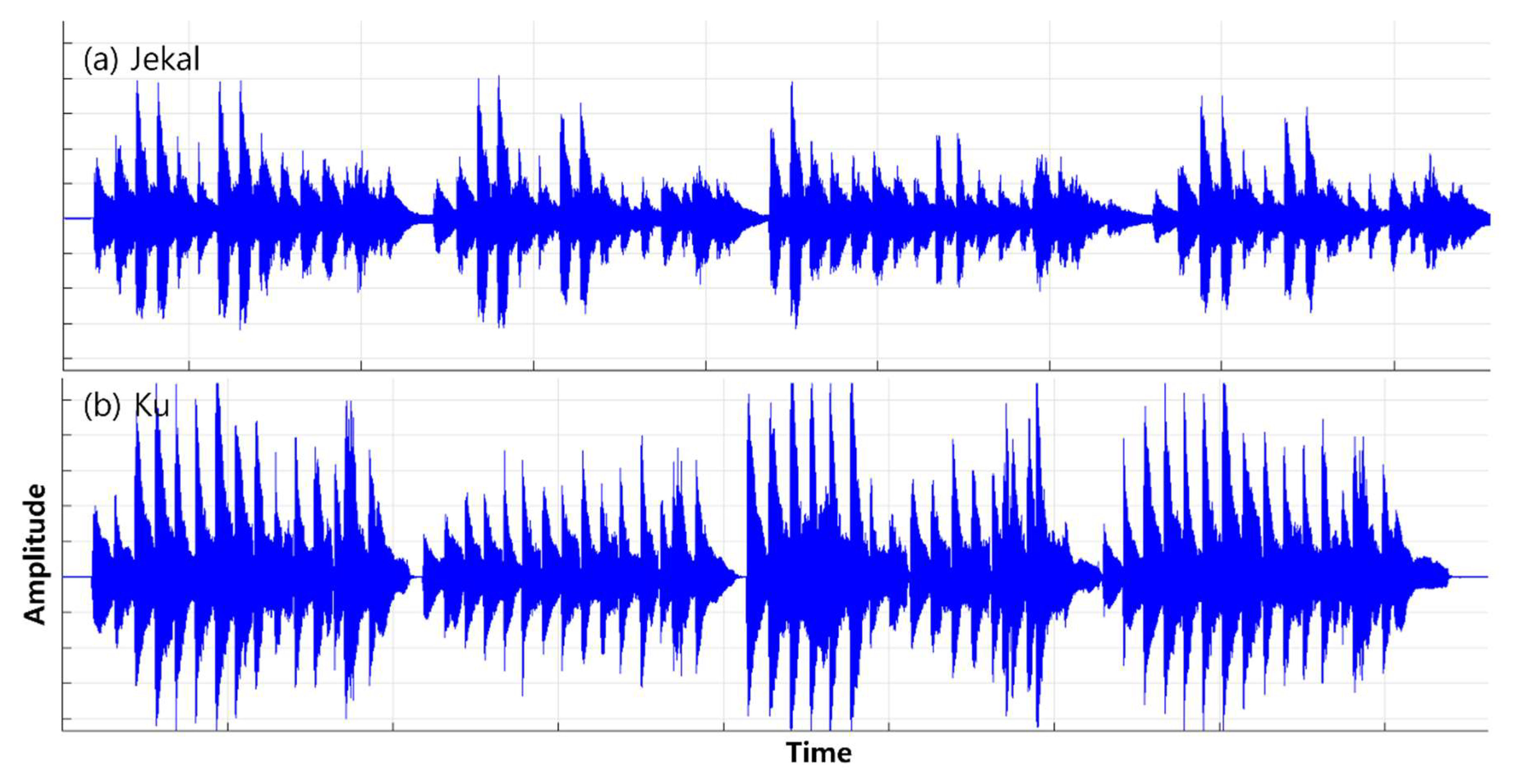
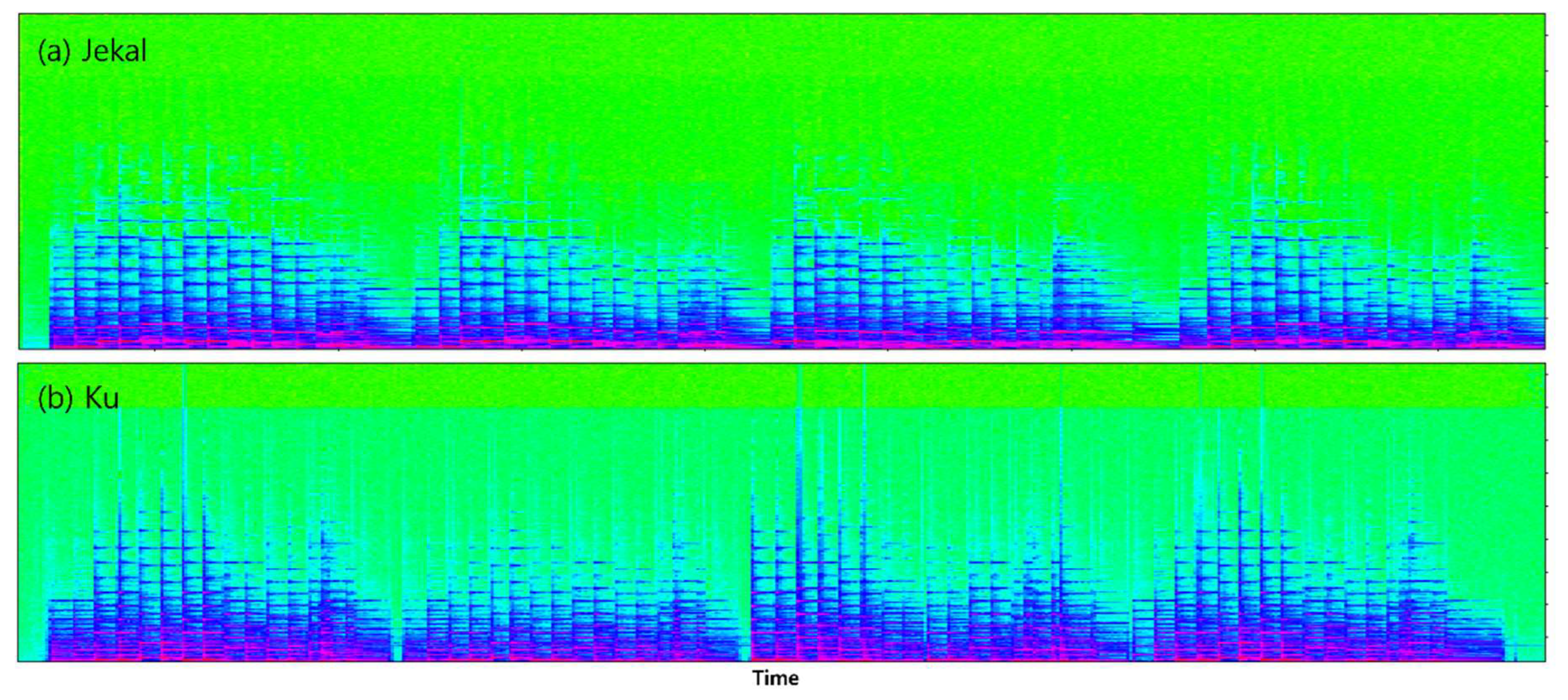
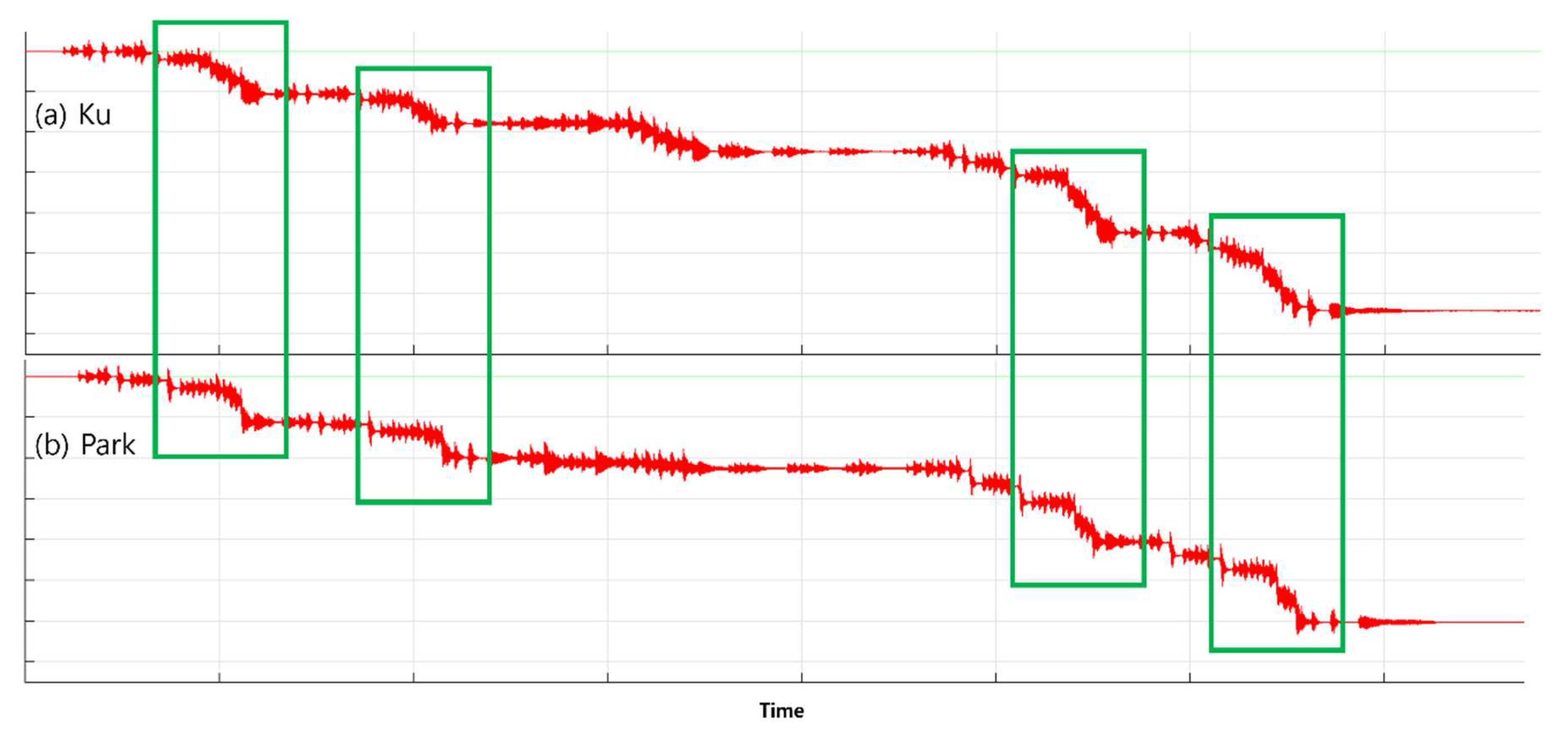
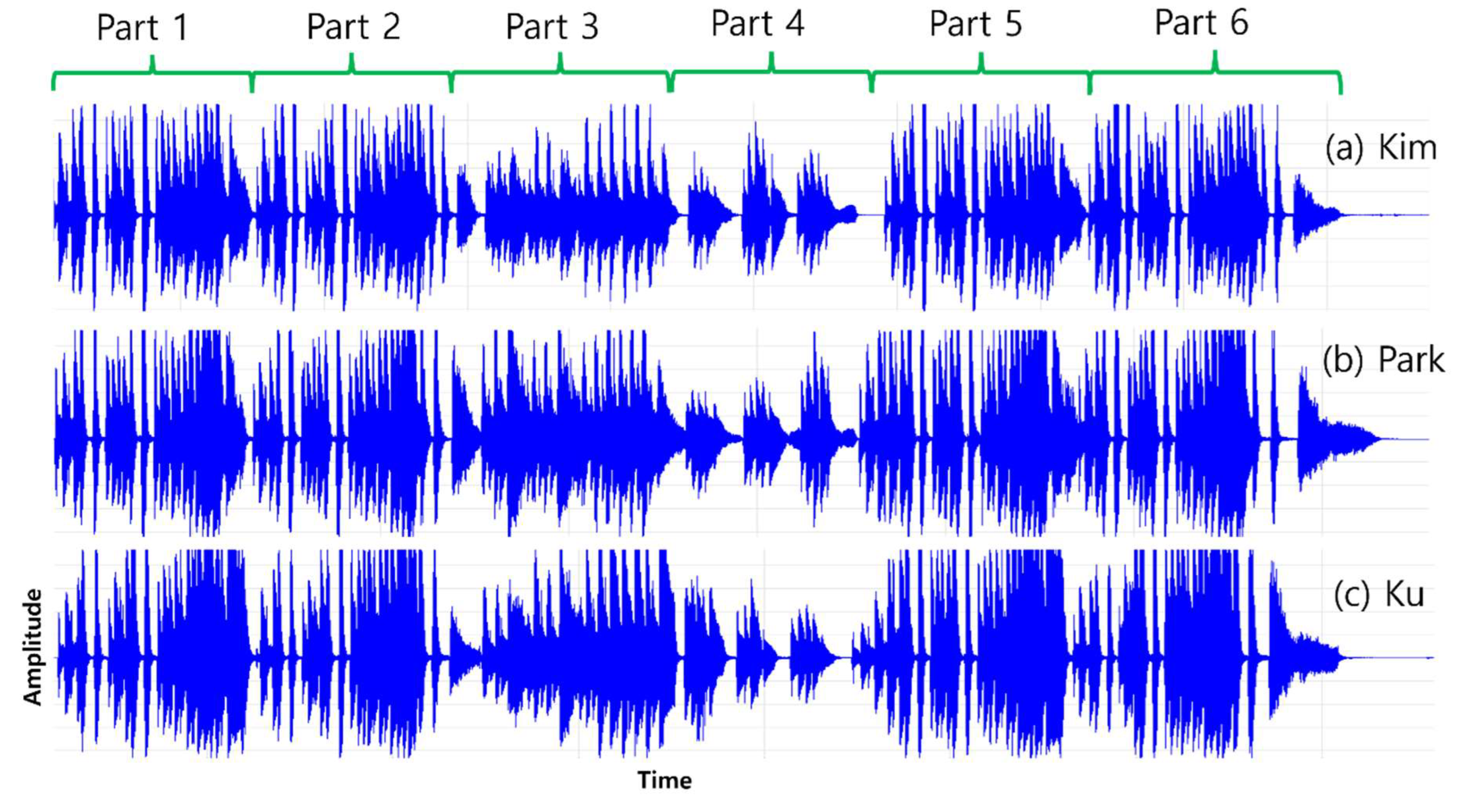
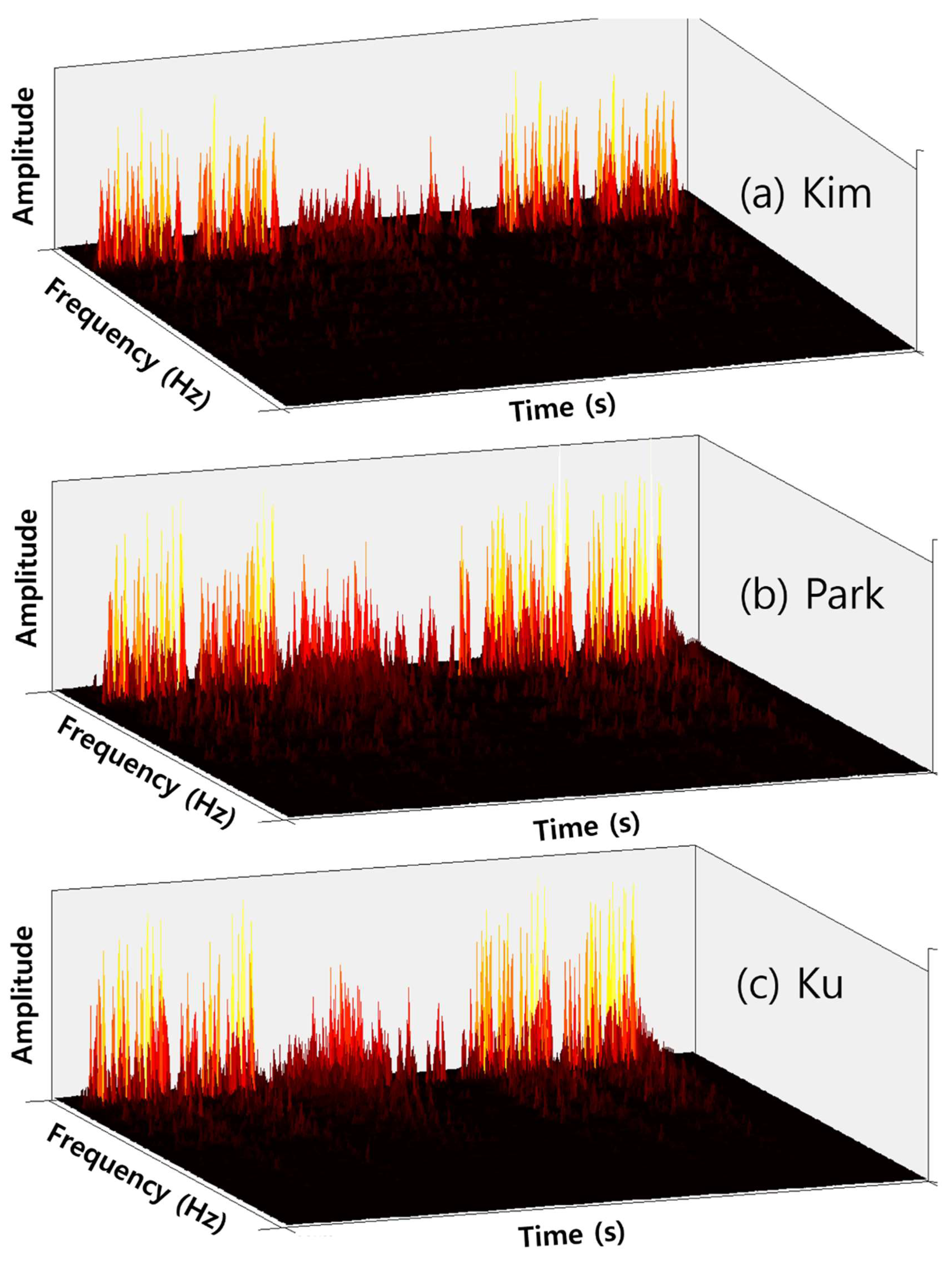
We also cognitively analyzed the performance of each of the three pianists (Younju Kim, Juhyun Ku, and Hyoen Park) for versatility evaluation and proof.
3. Prior studies
3.1. A Way of Expressing Sound
There are many ways in which sound is expressed, but it is mainly explained by physical principles such as vibration, waves, and frequency. Sound is a pressure wave that is transmitted through air (or other medium) as an object vibrates. Let’s take a closer look at it.
Sound is usually produced by an object vibrating. For example, when a piano keyboard is pressed, the strings vibrate, and the vibrations are transmitted into the air to be recognized as sound. This vibration is caused by an object moving and compressing or expanding air particles.
And this sound is transmitted through a medium (air, water, metal, etc.). The particles of the medium vibrate, compress and expand to each other, and sound waves are transmitted. At this time, the important concepts are pressure waves and repetitive vibrations.
Compression is a phenomenon in which the particles of the medium get close to each other, and re-action is a phenomenon in which the particles of the medium get away, and the sound propagates by repeating these two processes, through which we hear the sound.
These sounds can be distinguished by many characteristics. Mainly, the following factors play an important role in defining sounds.
(1) Frequency
The frequency represents the number of vibrations of the sound.
At this time, the frequency is measured in Hertz (Hz). For example, 440 vibrations per second are 440 Hz.
The higher the frequency, the higher the pitch, and the lower the pitch, the lower the pitch. Human ears can usually hear sounds ranging from 20 Hz to 20,000 Hz.
(2) Amplitude
The amplitude represents the volume of the sound, the larger the amplitude, the louder the sound, and the smaller the amplitude, the smaller the sound.
Amplitude is an important determinant of the “strength” of sound waves. A larger amplitude makes the sound louder, and a smaller amplitude makes it sound weaker.
(3) Wavelength
The wavelength is the distance that a vibration in a cycle occupies in space.The longer the wavelength, the lower the frequency, and the shorter the frequency, the higher the frequency.
(4) Timbre (Timbre)
Timbre is a unique characteristic of sound, formed by combining various elements in addition to frequency and amplitude.
For example, the reason why the piano and violin make different sounds even if they play the same note is that each instrument has different tones.
As in this study, in order to analyze sound with software, sound must be digitally expressed, and when expressing sound digitally, the sound is converted into binary number and stored.
Digital sound samples analog signals at regular intervals, converts the sample values into numbers, and stores them, which are used to store and reproduce sounds on computers.
In summary, sound is essentially a physical vibration and a wave that propagates through a medium. There are two main ways of expressing this, analog and digital, and each method produces a variety of sounds by combining the frequency, amplitude, wavelength, and tone of sound.
3.2. Traditional Method of Sound Analysis
Frequency analysis is a method of identifying the characteristics of a sound by decomposing the frequency components of the sound. It mainly uses Fourier Transform techniques.
Fourier transform is a mathematical method of decomposing a complex waveform into several simple frequency components (sine waves). This transform allows us to know the different frequencies that sound contains.
These Fourier Series and Fourier Transform allow us to analyze sound waves in the frequency domain.
Secondly, spectral analysis is a visual representation of the frequency components obtained through Fourier transform. This analysis visually shows the frequency and intensity of sound.
A spectrogram is a graph that shows the change in frequency components over time, and can visually analyze how sound changes over time.
In addition, time analysis is a method of analyzing sound waveforms over time. This method can track changes in the amplitude of sound over time.
Analyzing the waveform analysis at this time allows you to determine the sound volume, temporal change, and occurrence of specific events.
The waveform is a linear representation of the temporal variation of an analog signal or digital signal, and amplitude and periodicity can be observed.
You can also track the volume change by analyzing the amplitude of a sound over time. For example, you can determine the beginning and end of a specific sound, or you can analyze the state of attenuation and amplification of the sound.
Further in waveform analysis, characteristic waveform characteristics can also be extracted, which is particularly important for classification or characterization of acoustic signals.
3.3. The Characteristics of Piano Sound
The piano is a system with a built-in hammer corresponding to each key, and when the key is pressed, the hammer knocks on the string to produce a sound. The length, thickness, and tension of the string, and the size and material of the hammer are the main factors that determine the tone of the piano. Each note is converted into sound through vibrations with specific frequencies.
Frequency is an important factor in determining the pitch of a note. Piano notes range from 20 Hz to 4,000 Hz. They range from the lowest note of the piano, A0 (27.5 Hz), to the highest note, C8 (4,186 Hz).
The pitch is directly related to the frequency, and the higher the frequency, the higher the pitch, and the lower the frequency, the lower the pitch.
The piano’s scale consists of 12 scales, separated by octaves. For example, the A4 is 440 Hz, and the A5 doubles its frequency to 880 Hz.
Tone is an element that makes sounds different even at the same frequency. In other words, it can be said to be the “unique color” of a sound.
The tone generated by the piano is largely determined by its structure of harmonics. Since the piano can produce non-sinusoidal waveform sounds, each note contains several harmonics in addition to the fundamental frequencies. This pattern of tone makes the piano’s tone unique.
For example, the mid-range of the piano has a soft and warm tone, the high-pitched range has clear and sharp characteristics, and the low-pitched range has deep and strong characteristics.
Dynamic is the intensity of a sound, or the volume of a sound. In a piano, the volume varies depending on the intensity of pressing the keyboard. The piano is an instrument that allows you to delicately control decremental and incremental dynamics.
For example, the piano (p) is a weak sound, and the forte (f) is a strong sound. In addition to this, medium-intensity expressions such as mezzoforte (mf) and mezzo piano (mp) are possible.
In addition, the sound of the piano depends on the temporal characteristics such as attack, duration, and attenuation.
Attack is a rapid change in the moment a note begins. The piano’s note begins very quickly, and the volume is determined when the hammer hits the string.
The piano’s attack is instantaneous and gives a faster reaction than other instruments. For example, the pitch on the piano pops out right away, and the other instruments, such as string or woodwind, can start more smoothly.
Duration is a characteristic of how long a sound lasts after it is played. The piano strings gradually decay when they make a sound, because the string’s vibration gets weaker and weaker due to friction with the air or other factors. The length, thickness, and tension of the strings affect the duration of the sound at this time. If you use a pedal, you can increase the duration of the sound, but when you press the damper pedal, the strings continue to ring without stopping the vibration, making the sound longer.
If you look at the waveform, the piano is an instrument that generates non-sine sound. This is a complex waveform, not a sine wave, and several frequency components are mixed to create a rich tone.
The sound waves on the piano are rich in harmonics, so they have various tones and rich characteristics. For example, more low-frequency components are included in the lower register, and high-frequency components are more prominent in the upper register.
The notes generated by the piano can be divided into low, medium, and high notes, each range having the following characteristics.
-Blow (A0 to C4): It contains deep, rich, and strong low-frequency components. For example, Blow C1 has a very low frequency of 32.7 Hz.
-Middle tones (C4 to C5): range similar to the human voice, which is the key range of the piano. The mid tones of the piano have a balanced sound and a warm tone.
-High note (C6 to C8): It has a sharp, clear sound, and a clearer sound is produced at a fast tempo or high note.
In conclusion, the characteristics of the sound produced by the piano are influenced by a combination of several factors, including frequency, tone, attack and duration, dynamic, and attenuation. The piano is an instrument with very rich and complex harmonics, and its sound is characterized by fast attacks and various dynamic controls. In addition, the tone is determined by the characteristics of the strings used and the material of the hammer, which makes the piano sound a unique and distinctive sound.
3.4. Characteristics of Classical Piano Music
Piano classical music usually includes classical and romantic music, and its style has characteristic elements in musical structure, dynamics, emotional expression, and technical techniques.
First, complex chords and colorful tones are important features in piano classical music. Since the piano can play multiple notes at the same time, it is excellent at expressing different chords.
The way chords are created is the synthesis of sound waves, which combine several frequency components to create more complex and rich notes. In this process, each note has its own harmonics, which provides a touching and colorful tone to the music.
The second feature is that it delicately controls the dynamics. It can express dramatic changes and subtle emotions by crossing the piano(p) and the forte(f). It also expresses the rhythm and melody by using various technical techniques such as precise rhythms and arpeggios, trills, and scales.
These techniques require fast and repetitive vibrations, resulting in more complicated waveform fluctuations.
Lastly, classical piano music focuses on expressing emotional depth, and deals with epic development and emotional flow. The music delicately utilizes the dynamics and rhythm in expressing dramatic contrast or emotional height.
When viewed from the perspective of a scientific wave, the notes of classical piano music are not just sine waves but complex non-sinusoidal waveforms. Because of this, the piano’s sound includes harmonics, making it richer and more colorful in tone. This sonic quality is very important in classical music.
(1) Complex waveform structure
The waveform consists of a fundamental frequency and multiple overtones. For example, the piano’s sound vibrates according to its harmonic series, which means that in addition to the fundamental frequency, the background sounds such as 2x frequency, 3x frequency, and 4x frequency are also present.
Piano tones have frequencies higher than the basic notes, and they enhance or distort the characteristics of the basic notes. The tone of a piano is formed by the way these tones are nonlinearly combined.
For example, there are many and strong tones at lower notes, and relatively few and microscopic tones at higher notes.
(2) Quick attack and sudden waveform changes
In a piano, notes begin quickly, which is a part called an attack. The moment a note begins, the waveform undergoes a drastic change.
For example, the sound pressure on a piano rise very quickly as soon as the hammer hits the string, and then it attenuates rapidly. This causes a drastic change in the waveform.
The attack part is very short, producing an abnormal waveform indicating a spike with a fast frequency change. The waveform at this moment takes the form of a sharp peak and then a quick decrease in amplitude.
(3) Nonlinearity
The sound of classical piano music has nonlinear characteristics, forming unexpected waveforms through multiple nonlinear interactions, even at the same frequency.
For example, the moment a hammer hits a string, complex nonlinear oscillations can occur depending on the hammer’s mass, speed, and string tension. This results in a mixed waveform in addition to the fundamental frequency, which forms its own tone.
To sum up, the characteristics of piano classical music are very complex and colorful, ranging from its musical composition to the physical characteristics of the sound. Musically, it is characterized by complex chords and various dynamics, and it deals with emotional expression as important. These musical characteristics are physically revealed through the wave peculiarities of sound—complex waveforms, fast attacks, dynamic frequency changes, etc., and the singularity is well represented by the piano’s tonal structure and nonlinear waves. The sound waves of the piano are very rich and complex, which contribute to expressing the emotional depth and emotion that classical music is trying to convey well.