The Way To Solve ‘Dark Energy’ Problem Use Black Hole Property Without Ad Hoc Dark Energy Solution

1. Introduction

Dark energy is a mysterious component of the universe responsible for its accelerated expansion. Despite its significance, the fundamental properties of dark energy remain poorly understood. Current models often rely on the cosmological constant or other ad hoc solutions, which lack a clear connection to fundamental physics.

In this paper, we propose an alternative explanation for dark energy based on the properties of black holes. Specifically, we argue that the contribution of black hole energy tensors to the total energy-momentum tensor of the universe has been overlooked. This oversight can account for the observed effects of dark energy, including its isotropic nature and its role in cosmic expansion.

2. Theory

For almost a century, we have considered the curvature of the universe and its expansion. However, the biggest problem is that we have never accounted for the effect of black holes. Usually, black holes are considered negligible because they do not directly affect us on small scales. However, on a universal scale, if we ignore their pressure and curvature, our results become inaccurate. Most importantly, if we disregard the positive energy tensor of black holes, the effects can appear as dark energy—positive curvature, negative pressure, and a negative total energy tensor.

Mathematical Explanation

At the cosmological scale, the total energy-momentum tensor Tμν should be conserved. This is expressed mathematically as:

∇μTμν = 0

Here,

∇μ represents the covariant derivative, which is fundamental in the framework of general relativity. Even though different detectors might define energy differently based on their positions, local energy conservation holds.

However, in actual observations, we can only measure the observable part of the energy-momentum tensor Tμν_obs ,while ignoring the contribution from inside black holes,there are Tμν_BH,

Thus, the total energy-momentum tensor can be written as:

Tμν = Tμν_obs + Tμν_BH

Substituting this into the conservation equation, we can get:

∇μTμν_obs + ∇μTμν_BH = 0

The first term represents the conservation of the observable energy-momentum tensor, while the second term represents the conservation of the ignored black hole energy-momentum tensor.

Since we neglect ∇μTμν_BH in actual observations, the conservation equation for the observable energy-momentum tensor becomes:

∇μTμν_obs = - ∇μTμν_BH

This equation shows that the conservation of the observable energy-momentum tensor deviates from true global conservation, with the difference depending on the ignored black hole energy-momentum tensor ∇μTμν_BH.

In simpler terms, by ignoring the contribution of the black hole energy-momentum tensor, the observed average energy-momentum tensor is less than the true total value. This discrepancy could explain the effects attributed to dark energy.

3. Paradox

A paradox arises when we consider something beyond our worldline that cannot be detected. In this case, what exists beyond the worldline itself becomes a cause. For example, when we consider the energy tensor inside a black hole (which is, of course, beyond our light cone and worldline)

4. Exploring the Logic Paradox in Observability and Existence

The theory can be simply explained as follows: we have ignored the energy tensor of black holes, the tensor conservation, and we have a paradox here, that is [then when we consider things beyond our world line, since we cannot detect it, then what is beyond our world line, itself becomes a cause]. So when we consider the energy tensor in the black hole [of course, it is beyond our light cone and world line], the local is no longer applicable. This means that the dark energy effect is not limited by c, which explains why dark energy is so [average]. Note the action-reaction formula, in 6, they show that we are confident in their relationship, which makes sense, which means that using this formula, we ignore the tensor of the black hole, the pressure of the observable universe will be reduced--and consider the principle of positive energy, this is how it generates dark energy, which explains the data relationship between black hole growth and cosmic expansion let me try to build a mathematical model to describe the proposed self-referential logical paradox.

We cannot simply stay at the level that A ∉ U itself does not constitute a paradox, we also need to consider the causal relationship between the result "A cannot be observed" and A ∉ U, because the result "A cannot be observed", although it seems reasonable, is actually caused by the fact that A ∉ U, and according to relativity, A ∉ U should not be the causal "reason" for any thing within U.

This supplementary problem is crucial.

Define the spacetime manifold

Record the entire spacetime manifold as M

The observable region where the observer is located as U ⊂ M

Introduce the existence function of things

Define the observation restriction function

Define the observation restriction function f: U → {0, 1}

If x ∈ U, then f(x) = 1, indicating that x can be observed

If x ∉ U, then f(x) = 0, indicating that x cannot be observed

Describe the self-referential relationship

Consider an object A that satisfies A ∉ U

Since A ∉ U, so f(A) = 0, that is, A cannot be observed

However, since A ∉ U, it cannot be the "reason" for any thing within U

Therefore, A ∉ U itself cannot be a reasonable "reason" for A not being observed

The spacetime manifold M:

Represents the complete set of the entire spacetime

Observable region U:

Satisfying U ⊂ M, representing the region where the observer is located

Observation restriction function f(x):

f(x) = 1, when x ∈ U (observable )

f(x) = 0, when x ∉ U (unobservable)

Now let's consider a specific object A. According to the previous definitions, we have:

When A ∉ U, f(A) = 0 (1)

This means that if A is not within the observable region U, then A cannot be observed.

Now the problem arises, if A ∉ U cannot be reason, how can it become unobservable (f(A) = 0)? This creates a logical paradox.

[noticed detect things f(A) = 0 ,not included if we detected light from A that the light release when f(A)=1]

We can further analyze this paradox. Suppose there is a self-referential proposition "A ∉ U". If this proposition is true, then according to (1), we have f(A) = 0 , which means that A cannot be observed.

However, if A cannot be observed, according to the principle of causality in relativity, A ∉ U should not become the "reason" for any thing within U. Therefore, the proposition " f(A) = 0" itself should not hold.

This forms a logical loop that cannot be reconciled. It can be expressed mathematically as:

"A ∉ U" ⇒ f(A) = 0 ⇒ A cannot be the "reason" for any thing within U ⇒ "f(A) = 0" does not hold (3)

In summary, the core problem we face is: if an object A does not exist in the spacetime manifold U at all (A ∉ U), why is it still considered unobservable (f(A) = 0)? This seems to constitute a logical paradox. Gödel's incompleteness theorem may be the problem: Assuming the proposition "A ∉ U" is provable:

Based on this assumption, according to the definition we can obtain f(A) = 0, that is, A cannot be observed.

However, according to the principle of causality in relativity:

If A ∉ U, that is, A is not within the observable region,

Then A cannot be the "reason" for any thing within U.

This creates a contradiction:

On the one hand, we assume that f(A) = 0 is provable,

But on the other hand, this leads to the conclusion that A cannot be the "reason" for any thing within U,

This is contradictory to the premise that "A ∉ U" is a valid proposition.

Therefore, we can conclude:

If we assume the proposition "f(A) = 0" is provable,

It will lead to a logical contradiction, violating the principle of causality in relativity.

Conclusion:

If A is not the reason, then the fact that it is unobservable has no reason....

This shows that the self-referential proposition "f(A)=0"

is unprovable within the given theoretical framework,

Thus consistent with the situation described by Gödel's incompleteness theorem.

in fact ,that explain why dark energy is isotropic,because this effect if limit by position ,that mean …That mean i can disprove something if it prove this,correct?That mean the effect of this situation must be isotropic and instant [because if not that so,we can prove the cause and effect relationship by several measure...if it is not instant,that mean we can prove by serval measure time to check this [effect][actually not] is limit by c,to prove it is is cause and effect[because if we can know f(A) = 0 show up with A ∉ U ,and if we also know this ‘ causality’ follow the limit of c ,that mean we prove they are reason and effect relationship,but it betray what we have just prove] and in the isotropic part ,if the different part of universe change of energy tensor effect different,that mean …[because distance is definite by time[d=ct]so if it is instant,that mean their ‘distance’ to this effect is the same ,if ‘distance’ is same,[and notice they are all zero because t is zero placed in d=ct mean distance is zero too,so there are not possible to have degree and direction too]that mean it will be isotropic][Also notice even it cause indirectly,that make it broke causality also ,because in this process[if it indirect,there must be something inside black hole cause to outside]

And we can use this explain why black hole grow so fast too,because the energy tensor go into black hole is nearly not disappear[consider isotropic make it almost cant be detected]

in fact,maybe this paradox can solve quantum explain in parallel universe ,because if we use this paradox may be can explain why some time quantum show as over light speed,[because parallel universe is out of our lightcone ,of course that just a thought ,you can ignore this part.

5. Logic

In fact,the way to make dark energy property is simple–because total energy tensor is conservation and we can not detect black hole[and outside universe too,but they are related to black hole ignore cause universe expand too]energy tensor,our detectable energy tensor will drop,and consider paradox we have mentioned,this ignore effect can not limit by cause and effect by relativity,so it wont limit by distance and in every light cone outside this black hole ,instantly have that dark energy effect…?[need more support]and if that make sense ,then with positive energy principle and because it is isotropic so there will not possible to have momentum ,that is how it fit dark energy property[possible energy density but negative pressure and no momentum,isotropic]

6. Data Support

Ducan Farrah et al. (2023) found that within the cosmological time range of 0 < z ≤ 2.5, the mass of supermassive black holes (SMBHs) in elliptical galaxies grew 8-20 times compared to the stellar mass, with a median growth factor of 15.7±2.5. The authors further analyzed and found that the SMBH mass exhibits a power-law dependence on the cosmological redshift z, which can be expressed as MSMBH ∝ (1+z)3.1±0.3 . This redshift dependence is consistent with a model with a cosmological coupling strength of k ≈ 3,an in contrast to the traditional Kerr black hole solution (k = 0), which was excluded with a probability as high as 99.98% [Observational Evidence for Cosmological Coupling of Black Holes and its Implications for an Astrophysical Source of Dark Energy.][paper name] From The Astrophysical Journal Letters,

The formula this paper give is

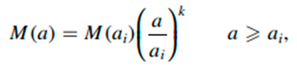
where ai is the scale factor at which the object becomes cosmologically coupled and k bigger or equal to zero is the cosmological coupling strength

Kevin S. Croker et al.[2024]’s Observations of supermassive black holes (SMBHs) in elliptical galaxies suggest their masses grow cosmologically in proportion to m ∝ a³, consistent with the predictions of this model. This growth cannot be fully explained by accretion or mergers alone. Recent results from the DESI (Dark Energy Spectroscopic Instrument) collaboration show that dark energy evolves with time, deviating from a pure cosmological constant (Λ). The time-evolution of dark energy density predicted by cosmologically coupled black holes closely follows DESI's results for redshifts z ≲ 3

It also give Statistical Evidence that The model fits observational data from DESI, supernovae, and the cosmic microwave background (CMB) with fewer parameters than alternative dark energy models like the w₀wₐ parameterization.For example, the model predicts a Hubble constant of H₀ = 69.94 ± 0.81 km s⁻¹ Mpc⁻¹, which reduces the tension between early-universe (Planck) and late-universe (SH0ES) measurements.

Those papers support black hole growth has a relation between dark energy density so they give strong evidence we can prove black hole and dark energy ,universe expand is related

7. Another Explanation

In other paper’,Can black holes be a source of dark energy?’by Serge Parnovsky ,they once use black hole still conservation that the dark energy is not ,but they not consider all our data base in observable and part 2 appearly reject this.And the point it have no negative pressure make a mistake at first that dark energy is happen in outside the black hole but not inside ,that is actually a misunderstanding confusion.[by part 4,negative pressure property actually because of the paradox

8. Conclusions

In this work, we have proposed a novel explanation for the nature of dark energy by considering the often-overlooked contributions of black hole energy-momentum tensors to the total energy-momentum tensor of the universe. Through mathematical analysis, we demonstrated that neglecting these contributions can result in observable effects that mimic the properties of dark energy, such as negative pressure, isotropy, and instantaneous influence.

Furthermore, we explored a logical paradox involving observability and causality, showing that the exclusion of black hole tensors introduces self-referential inconsistencies. These inconsistencies align with the isotropic and universal nature of dark energy, providing a potential theoretical basis for its effects beyond the framework of the cosmological constant.

Finally, we grounded our hypothesis in observational evidence, such as the cosmological coupling of supermassive black holes (SMBHs), their growth rates, and their relationship to cosmic expansion. These findings suggest that black holes may play a critical role in the evolution of the universe and the effects attributed to dark energy.

While this work is an early exploration, it opens new possibilities for understanding dark energy without relying on ad hoc solutions. Further research is needed to refine the mathematical framework, test predictions, and explore the broader implications of this hypothesis. If validated, this approach could bridge the gap between black hole physics and cosmology, addressing one of the greatest mysteries of modern science.