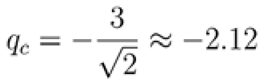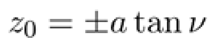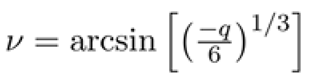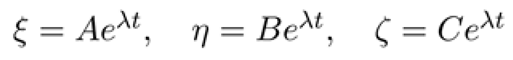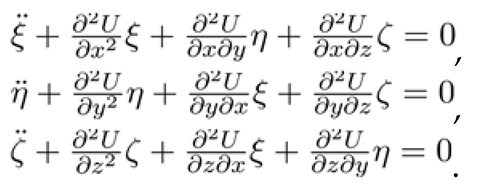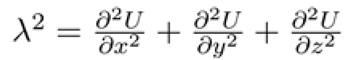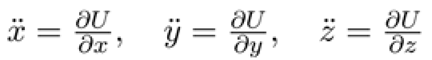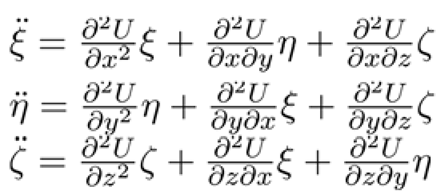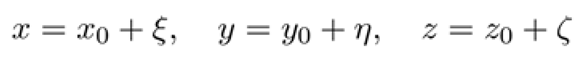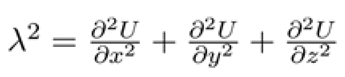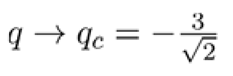1. Introduction
The restricted eight-body problem is a fascinating extension of classical celestial mechanics, providing insights into the intricate dynamics of systems influenced by gravitational and radiative forces. This model features a radiating central primary surrounded by six peripheral primaries in circular motion, creating a unique framework for studying out-of-plane equilibrium points, which are located along the z-axis and exhibit critical behaviors under varying radiation factors.
Recent work has highlighted the significance of out-of-plane dynamics in multi-body systems. Work in [
1] explored these dynamics within the circular restricted eight-body framework, identifying symmetrical equilibrium points and analyzing their stability. Similarly, research in [
2] proposed a low-voltage CMOS rectifier for biomedical implantable devices, showcasing advancements in energy harvesting and efficiency optimization. Studies in [
3,
4,
5] investigated light bending in the galactic halo, autonomous Hamiltonian systems, and the size of the galactic halo, respectively, providing insights into gravitational effects and the utility of Hamiltonian methods in celestial mechanics. Additionally, research in [
6] utilized SpinalNet for the morphological classification of galaxies, indirectly aiding in understanding the large-scale dynamics of celestial systems. This formulation builds upon the foundational work of Maxwell (1859) and further extensions by Kalvouridis and Hadjifotinou (2011). Building on these findings, this study delves deeper into the existence and alignment of these points at critical radiation values and examines the associated periodic orbits. By investigating the interplay of gravitational and radiative effects, this research contributes to a comprehensive understanding of celestial mechanics in complex systems. These equations originate from the analysis of Maxwell-type n-body systems and are a continuation of studies into the influence of radiation pressure on equilibrium dynamics.
2. Mathematical Framework and Formulas
The restricted eight-body problem involves a radiating central primary (μ0) and six peripheral primaries (μ) revolving in a circular orbit of radius a around the central primary. The equations of motion for a test particle (ε) are given by:
where the potential function includes both gravitational and radiative components. The general form of the potential function is expressed as:where represent the coordinates of the six peripheral primaries.
Critical Radiation Value
At the critical radiation value , the equilibrium points align precisely along the z-axis at a distance equal to the orbital radius of the peripheral primaries. This critical value determines the boundary condition where equilibrium points transition in their alignment
| Radiation Factor (q) |
) |
Observation |
| −<< |
|
Points lie outside the radius aaa. |
|
|
|
Points align exactly at aaa. |
|
|
Points lie within the radius aaa. |
Linear Stability Analysis
The stability of the equilibrium points is analyzed by introducing small perturbations () around the equilibrium positions. Let the perturbations be:
where λ are the characteristic roots of the system. The variational equations for these perturbations are derived from the linearized equations of motion:
The determinant of the Jacobian matrix formed by these partial derivatives determines the eigenvalues λ:
For the range of radiation factors −6<q<0 the eigenvalues satisfy
indicating that the equilibrium points are linearly unstable. This instability implies that small deviations from the equilibrium points grow exponentially over time, leading to chaotic dynamics around these points [
1,
2].
Role of Eigenvalues (λ) in Stability Analysis
Eigenvalues (λλ) are mathematical quantities derived from the system of linearized equations around an equilibrium point. They provide critical information about the stability of the system by describing how small perturbations evolve over time.
Linearized Equations of Motion: Eigenvalues are derived from the
linearization of the system around equilibrium points [
4]. By approximating the system's potential
U(x,y,z) with a second-order Taylor expansion about the equilibrium point, the resulting variational equations form a matrix. The eigenvalues of this matrix determine how perturbations (ξ,η,ζ) evolve over time.
Dynamic Behavior: Eigenvalues dictate whether perturbations grow (instability), decay (stability), or oscillate (neutral stability). This is crucial in identifying whether the system remains near the equilibrium or diverges away:
Positive Real Eigenvalues: Indicate exponential divergence, leading to an unstable system.
Negative Real Eigenvalues: Indicate exponential decay, leading to a stable system.
Complex Eigenvalues: Indicate oscillatory behavior, which may be stable if the real parts are negative.
Mathematical Interpretation
Given the eigenvalue equation:
the stability conditions are determined by the sign of
If λ2 > 0, λ is real, and the system is unstable.
If λ is imaginary, and the system exhibits oscillatory stability.
Applications of Eigenvalue Analysis
Predicting Orbital Stability: Eigenvalue analysis helps in identifying regions of instability near celestial bodies influenced by radiation and gravitational forces. This can inform trajectory planning for spacecraft.
Understanding Resonance Regions: Unstable equilibria often act as boundaries between different dynamical regimes, such as resonance regions, where orbits are quasi-periodic or chaotic.
Design of Orbital Maneuvers: By identifying unstable equilibrium points, spacecraft can utilize these regions for efficient orbital transfers or transitions.
Astrophysical Systems: In multi-body astrophysical systems, eigenvalues provide insights into long-term stability and evolution, especially in radiation-dominated environments.
Overall,Eigenvalues (λ) serve as a fundamental tool in stability analysis, offering a precise mathematical framework to study the dynamic behavior of celestial systems. In the restricted eight-body problem, their role highlights the inherent instability of out-of-plane equilibrium points, providing valuable insights into the complex interplay of gravitational and radiative forces in multi-body systems [
7].
Practical Implications in the Restricted Eight-Body Problem
| Aspect |
Observation |
Implication |
| Unstable Dynamics |
>0 for -6<q<0 |
Equilibrium points are unstable. |
| Divergence |
Exponential divergence of trajectories. |
Indicates chaotic behavior. |
| Radiation Factor |
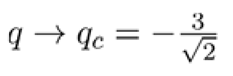 |
Points align on z-axis, instability persists |
| Orbital Mechanics |
Unstable regions predict trajectories. |
Useful for navigation and orbital transfers |
The eigenvalue analysis and resulting stability conditions underscore the dynamic complexity of the restricted eight-body problem. [
8]By characterizing the system's stability through λ2\lambda^2λ2, this study provides valuable insights into the interplay of gravitational and radiative forces in multi-body systems. These findings pave the way for further exploration of nonlinear effects and chaotic dynamics in celestial mechanics.
Literature Review
The study of the restricted eight-body problem is deeply rooted in celestial mechanics, focusing on understanding the complex dynamics of multi-body systems under gravitational and radiative forces. This review highlights key contributions from prior research, establishing a foundation for the exploration of out-of-plane equilibrium points and their stability.
Dynamics of Multi-Body Systems. The restricted eight-body problem builds upon the classical works of Maxwell [
6] and later extended by Kalvouridis and Hadjifotinou, who analyzed the Maxwell ring problem. Maxwell’s pioneering study on the stability of Saturn's rings [
6] laid the groundwork for understanding gravitational interactions in ring-like formations. Moser [
7] expanded these insights, incorporating stability and randomness into celestial systems, bridging the gap between theoretical mechanics and real-world applications. Idrisi et al. [
1,
10] specifically focused on out-of-plane dynamics in the restricted eight-body problem, introducing the concept of symmetrical equilibrium points along the z-axis. Their work provided a mathematical framework for analyzing the stability of these points, emphasizing the influence of the radiation factor q. Damour et al. [
9] contributed to the understanding of general-relativistic celestial mechanics by redefining reference systems for multi-body systems. This work underscores the importance of accurately modeling gravitational and radiative effects, which play a critical role in the restricted eight-body problem. Mahato et al. [
11] examined the effect of external perturbations, such as a planetesimal belt, on the dynamics of restricted multi-body systems. Their findings highlight the sensitivity of equilibrium points to additional forces, offering parallels to the influence of radiation in the eight-body framework.
Stability Analysis and Machine Learning Approaches. Stability analysis forms the core of understanding equilibrium points. Bhattacharya et al. [
3,
4] explored the application of the Rindler-Ishak method to light bending in galactic halos, emphasizing the interplay of gravitational forces and instability. Shaiakhmetov et al. [
5] utilized machine learning, specifically SpinalNet, to classify galactic morphologies, demonstrating the potential of computational techniques in analyzing complex celestial systems. Khan et al. [
8] advanced this approach by applying machine learning to software quality testing, illustrating how computational models can aid in stability prediction and analysis. These methods, although distinct in application, offer valuable insights for the predictive modeling of celestial systems.
Applications to Restricted Eight-Body Dynamics Idrisi et al. [
1,
10] provided comprehensive insights into out-of-plane dynamics, revealing that equilibrium points are inherently unstable due to the combined effects of gravitational and radiative forces. Their work serves as the cornerstone of this study, offering both theoretical and numerical perspectives on the restricted eight-body problem. Mahato et al. [
11] further expanded on perturbative effects, underscoring the importance of external forces in shaping equilibrium dynamics. Their findings align with the inherent instability observed in the eight-body problem, contributing to a broader understanding of multi-body interactions.
Conclusions
This study presents a detailed exploration of out-of-plane equilibrium points in the restricted eight-body problem, emphasizing their dynamics and stability under the influence of gravitational and radiative forces. By identifying two symmetrical equilibrium points along the z-axis, this research highlights the critical role of the radiation factor in determining their positions and behavior. Despite aligning precisely along the z-axis at the critical radiation value, these points exhibit inherent instability across all valid ranges of the radiation factor. The analysis underscores the complex interplay between gravitational attraction and radiation pressure, resulting in exponential divergence of small perturbations and confirming the chaotic nature of such systems. This instability provides insights into the sensitivity of multi-body dynamics, with significant implications for celestial navigation, orbital mechanics, and astrophysical modeling.
References
- Idrisi, M.J., Ullah, M. S., Tenna, W., Khan, M. T., Khan, M. F., Kamal, M.: Out-of-plane dynamics: a study within the circular restricted eight-body framework. New Astron. 102260 (2024). [CrossRef]
- Low Voltage CMOS Rectifier at 32 nm for Harvesting Energy in Implantable Devices.
- Bhattacharya, A., Isaev, R., Scalia, M., Cattani, C., & Nandi, K. K. (2010). Light bending in the galactic halo by Rindler-Ishak method. Journal of Cosmology and Astroparticle Physics, 2010(09), 004. [CrossRef]
- Bhattacharya, A., Isaev, R., Scalia, M., Cattani, C., & Nandi, K. K. (2010). Light bending in the galactic halo by Rindler-Ishak method. Journal of Cosmology and Astroparticle Physics, 2010(09), 004. [CrossRef]
- Shaiakhmetov, D., Mekuria, R. R., Isaev, R., & Unsal, F. (2021, November). Morphological classification of galaxies using SpinalNet. In 2021 16th International Conference on Electronics Computer and Computation (ICECCO) (pp. 1-5). IEEE.
- Brush, Stephen G; Everitt, C. W. F. (C. W. Francis), 1934-; Garber, Elizabeth; Maxwell, James Clerk, 1831-1879. On the stability of the motion of Saturn's rings.
- Moser, J. (2001). Stable and random motions in dynamical systems: With special emphasis on celestial mechanics (Vol. 1). Princeton university press.
- Khan, A., Mekuria, R. R., & Isaev, R. (2023, April). Applying Machine Learning Analysis for Software Quality Test. In 2023 International Conference on Code Quality (ICCQ) (pp. 1-15). IEEE.
- Damour, T., Soffel, M., & Xu, C. (1991). General-relativistic celestial mechanics. I. Method and definition of reference systems. Physical Review D, 43(10), 3273. [CrossRef]
- Idrisi, M. J., Ullah, M. S., Tenna, W., Khan, M. T., Khan, M. F., & Kamal, M. (2024). Out-of-Plane Dynamics: A Study within the Circular Restricted Eight-Body Framework. New Astronomy, 102260.
- Mahato, G., Pal, A. K., Alhowaity, S., Abouelmagd, E. I., & Kushvah, B. S. (2022). Effect of the Planetesimal Belt on the Dynamics of the Restricted Problem of 2+ 2 Bodies. Applied Sciences, 12(1), 424.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).