Submitted:
22 October 2024
Posted:
24 October 2024
You are already at the latest version
Abstract
Keywords:
1. Motivation
2. Method
3. Applications
3.1. Table 1
3.2. Table 2
3.3. General Properties
| Global | Local | Phase | Equivalent | Libration | Multibody | |
| Row | MMRs | MMR Pairs | Angle | Form of | Centers (°) | System |
| Index | (1) | (2) | (3) | (4) | (5) | (6) |
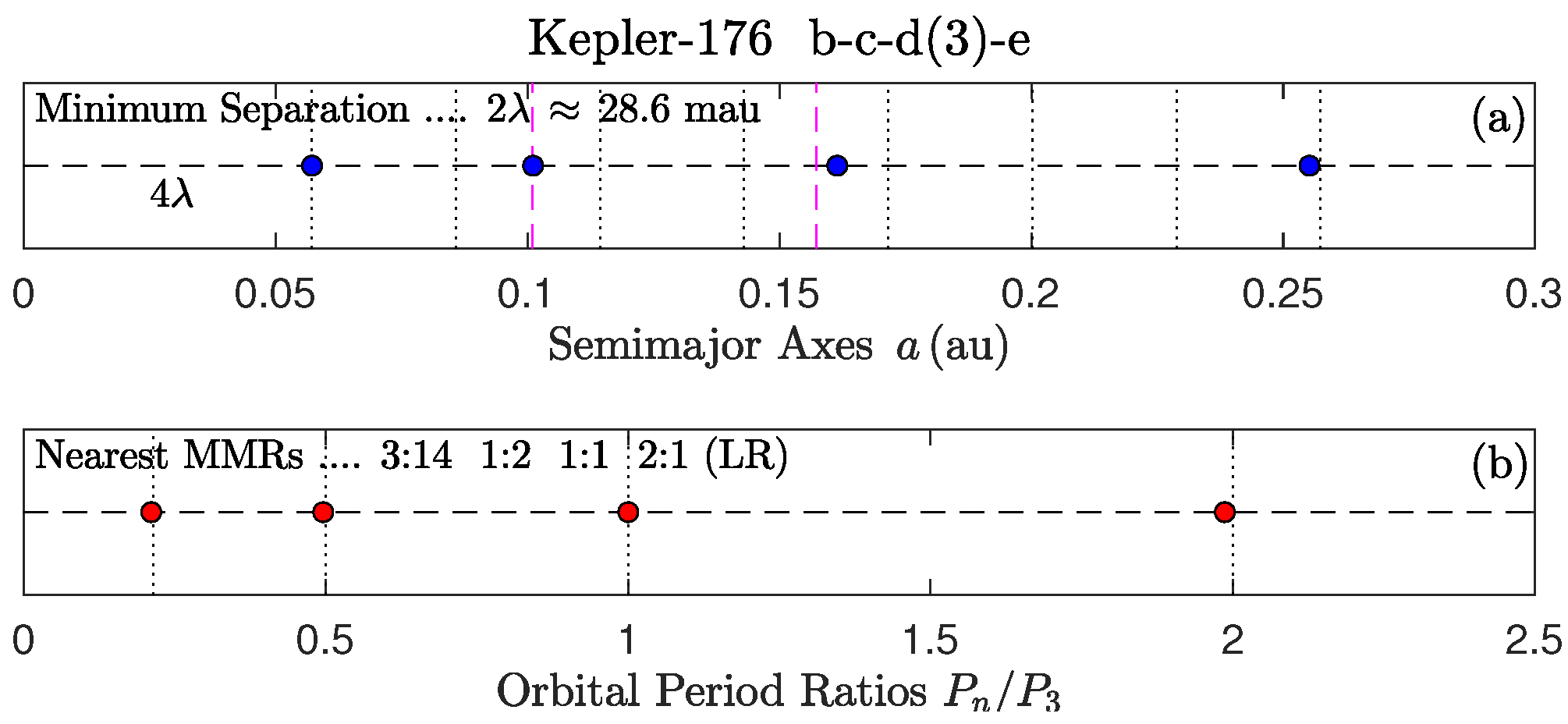
| 1 | 1/2 : 1 : 2/1 | 2:1 & 2:1 | 0 | GJ 876, HR 8799, HR 8832, Kepler-176 (Paper I) | ||
| 2 | 1/4 : 1/2 : 1 | 2:1 & 2:1 | 180 | HIP 41378, Io-Europa-Ganymede | ||
| 3 | 1 : 3/2 : 2/1 | 3:2 & 4:3 | HD 110067 | |||
| 4 | 2/3 : 1 : 4/3 | 3:2 & 4:3 | Kepler-223, TOI-178 | |||
| 5 | 1/2 : 3/4 : 1 | 3:2 & 4:3 | Kepler-90, TOI-1136, TRAPPIST-1 | |||
| 6 | 2/3 : 1 : 2/1 | 3:2 & 2:1 | None | TOI-1136, Kepler-20 (::); no librations | ||
| 7 | 3/4 : 1 : 3/2 | 4:3 & 3:2 | TOI-1136, HIP 41378, Kepler-223, HD 23472, TRAPPIST-1 | |||
| 8 | 4/5 : 1 : 4/3 | 5:4 & 4:3 | , | Kepler-60 | ||
| 9 | 2/3 : 1 : 3/2 | 3:2 & 3:2 | Kepler-11, K2-138, HD 110067, TRAPPIST-1 | |||
| 10 | 1/2 : 1 : 3/2 | 2:1 & 3:2 | Kepler-32, Kepler-82, Umbriel-Titania-Oberon | |||
| 11 | 3/4 : 1 : 5/4 | 4:3 & 5:4 | 180 | Not yet observed | ||
| 12 | 3/4 : 1 : 2/1 | 4:3 & 2:1 | None | Not yet observed, no librations | ||
| 13 | 4/5 : 1 : 2/1 | 5:4 & 2:1 | None | Not yet observed, no librations | ||
| 14 | 1 : 5/3 : 5/2 | 5:3 & 3:2 | TRAPPIST-1 (::), Kepler-11 (::1), HD 40307 | |||
| 15 | 5/8 : 1 : 5/3 | 8:5 & 5:3 | TRAPPIST-1 (::) |
- Notes:
- Three-body Definitions and Relations:
- , , , and , .
- Remarks and Comparisons:
- (1) Inspecting the Laplace-like angles in column 3 (rows 6-13): (1a) Three angles depend on but not on (rows 6, 12, 13); all three circulate. (1b) Two angles depend on both and (rows 7, 8); both librate. (1c) Three angles depend on but not on (rows 9-11); all three librate. (1d) In general, in the absence of , angle signals libration of (rows 9-11), whereas signals circulation of (rows 6, 12, 13); but terms added to induce librations (rows 7, 8).
- (2) Comparing the forms of in columns 3 and 4 (rows 6-11): (2a) If a term is present in both forms, then angle is as good a libration tracer as (rows 9-11). (2b) If an term is present in both forms, then librates, otherwise circulates (rows 6-8); equivalently, when terms are added to circulating (or more terms are added to ), they induce libration (rows 7, 8).
- (3) Turning to the local MMR pairs in column 2: (3a) The classical LR pair (2:1 & 2:1) shows librations of (rows 1, 2). (3b) The pairs with trailing MMR 2:1 and leading MMR other than 2:1 (rows 6, 12, 13) all show circulations; evidently, the trailing 2:1 MMR is responsible for this outcome. (3c) No such circulating primary MMRs have been observed in (extra)solar subsystems (rows 12, 13), and the (::) chain of TOI-1136 in row 6 is only a secondary triple that does not include the most massive planet (see note c below Table 1); therefore, no such primary MMRs (with a trailing 2:1 MMR) have been observed in (extra)solar subsystems at all. This is compounding evidence that the primary global 2:1 MMR must be vacant, except in LRs and Laplace-like multiples, such as those listed in rows 1 and 3.
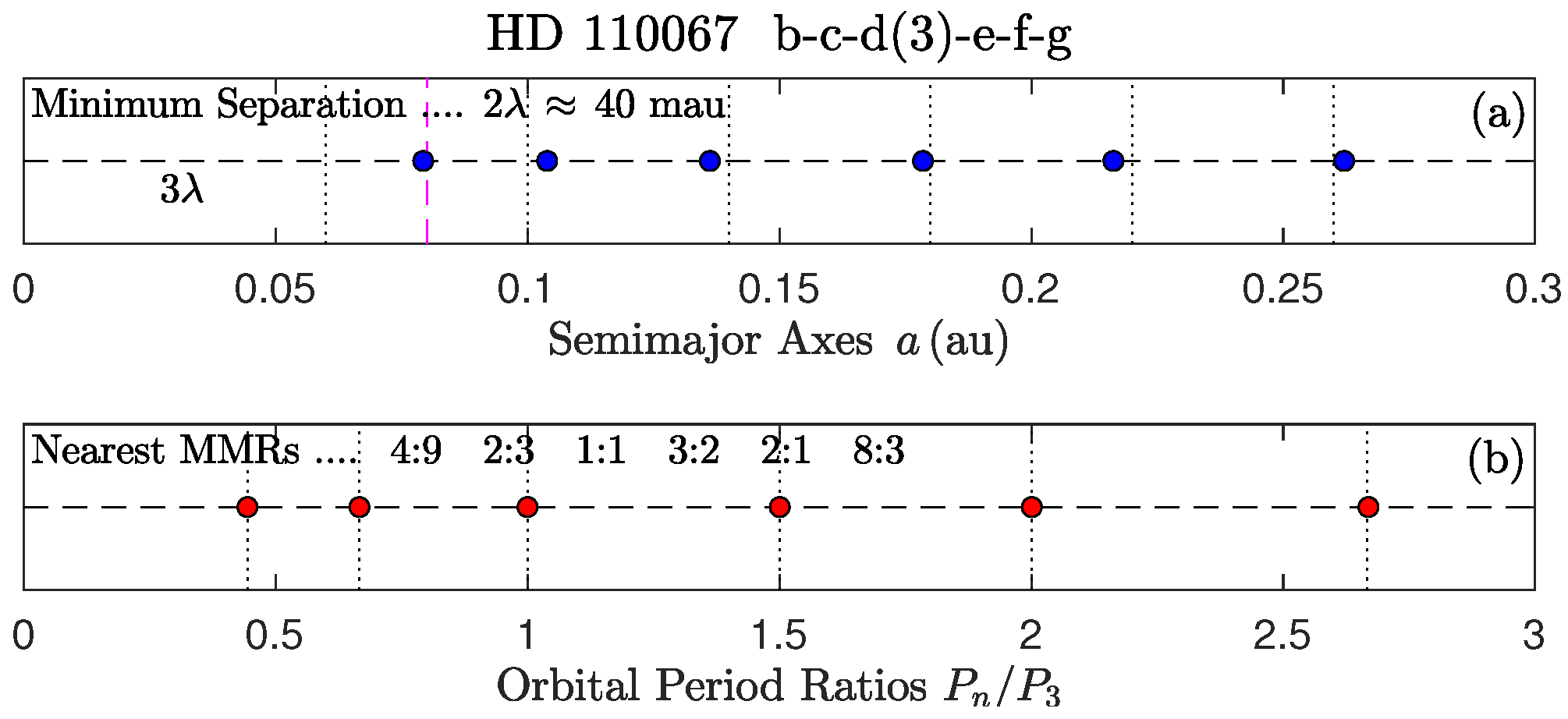
- (4) Focusing on the two MMR chains observed in HD 110067 (rows 3, 9): Planets c-d-e-f show an extended sequence of local first-order MMRs of the form (3:2 & 3:2 & 4:3) in which planet d is the most massive body ([38]). Both triples should librate according to the models of SF21. For this extended sequence of planets (indexed by 1-4), we find two corresponding phase angles, and (see Appendix A), that ought to be checked for librations individually. Their sum and difference also point to librations: for planets 1-3, and for planets 2-4. These angles are 2× the librating angles listed in rows 9 and 3, respectively. The particular 2× scaling is universal in four-body MMR chains; we derive it also for the planets b-c-d-e in Kepler-223 (with global MMR ::1:; rows 7 and 4, respectively) in Appendix B.3 from the observations and modeling of Mills et al. [3].
- (5) Focusing on the three secondary MMR chains (not involving planet g) of mostly mixed order observed in TRAPPIST-1 (rows 9, 14, 15): All secondary MMRs librate, just as the primary MMRs (e-f-g, f-g-h) listed in rows 5 and 7, respectively. This is because all consecutive local pairs are individually locked in resonance (including the innermost 8:5 & 5:3 pair) [12,13,39].
- (i)
- (ii)
- (iii)
- This scenario also signifies that the same global MMR may or may not be librating in individual systems, as the incorporated -difference may or may not be locked in local resonance. The location of the most massive planet (i.e., the 1:1 orbit) in the MMR chain, as well as perturbations from neighboring planets outside of the resonance, may play an important role in determining the outcome of early dynamical evolution.
- (iv)
- The angles of five mostly mixed-order MMRs at the bottom half of Table 1 (HD 40307, PSR B1257+12, Kepler-90, VET, RTH) combine even multiples of with either or . If the terms could possibly be set aside for a moment, then the librations of angles would be determined solely by the single local -pair present in the phase angle. If the presumption in item (ii) holds for mixed/high-order MMRs as well, then the (5:3 & 8:5) MMR in Kepler-90 f-g-h and the (8:5 & 8:5) VET MMR that depend on should show circulating phases. Some local MMRs of mixed order (but not quite those listed in Table 1) have been studied numerically in the recent past (see, e.g., Refs. [5,6,25,34,40]).
- (v)
4. Conclusions
- (a)
- We call principal resonant orbits those in the MMR set with . The principal MMRs are available for orbiting bodies to settle in safely, although the 2:1 MMR appears to be vacant (except in LRs and Laplace-like chains). High-order MMRs of this type provide shelter to orbiting bodies, especially to small distant planets, dwarf planets, and minor moons. For instance, Mercury and Pluto occupy the 1:50 and 21:1 MMRs of Jupiter, respectively; and Pan and Kiviuq occupy the 1:28 and 28:1 MMRs of Titan, respectively, in the Saturnian system.
- (b)
- Besides principal MMRs, very few rational outer MMRs :p and their reciprocal inner MMRs are common in multibody (sub)systems, and even fewer MMRs with appear scarcely. Our survey of 73 exosystems and solar subsystems is mapped out in Table 3. The scarce MMRs (, ) are enclosed in parentheses. An intriguing feature in this chart is that the MMRs commonly appear in reciprocal pairs. The three exceptional cases (4:5, 2:7, 8:3) are also interesting in their own right.
- (c)
- Extending Table 3 out to and , we find only the 9:2 MMR in exosystems. Surprisingly, this MMR is common in systems that contain complete LRs (HIP 41378 d, HR 8799 b) or uncompleted (would-be) LRs (Kepler-48 d, Kepler-332 d). In the former case, two overlapping LRs are avoided (see also item 8 above); in the latter case, classical LRs are not assembled, and the global 2:1 MMR (that would have formed the LR) remains vacant.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EGC | Europa-Ganymede-Callisto |
| LR | Laplace Resonance |
| MMR | Mean-Motion Resonance |
| MVE | Mercury-Venus-Earth |
| RTH | Rhea-Titan-Hyperion |
| SF21 | Siegel and Fabrycky (2021), Ref. [8] |
| VET | Venus-Earth-Toro |
Appendix A. Four-Planet Laplace-Like Phase Angles in HD 110067
Appendix B. Overlapping First-order Four-body MMRs
Appendix B.1. Four-body Phase Angles
Appendix B.2. The Classical Double LR with rj = 1
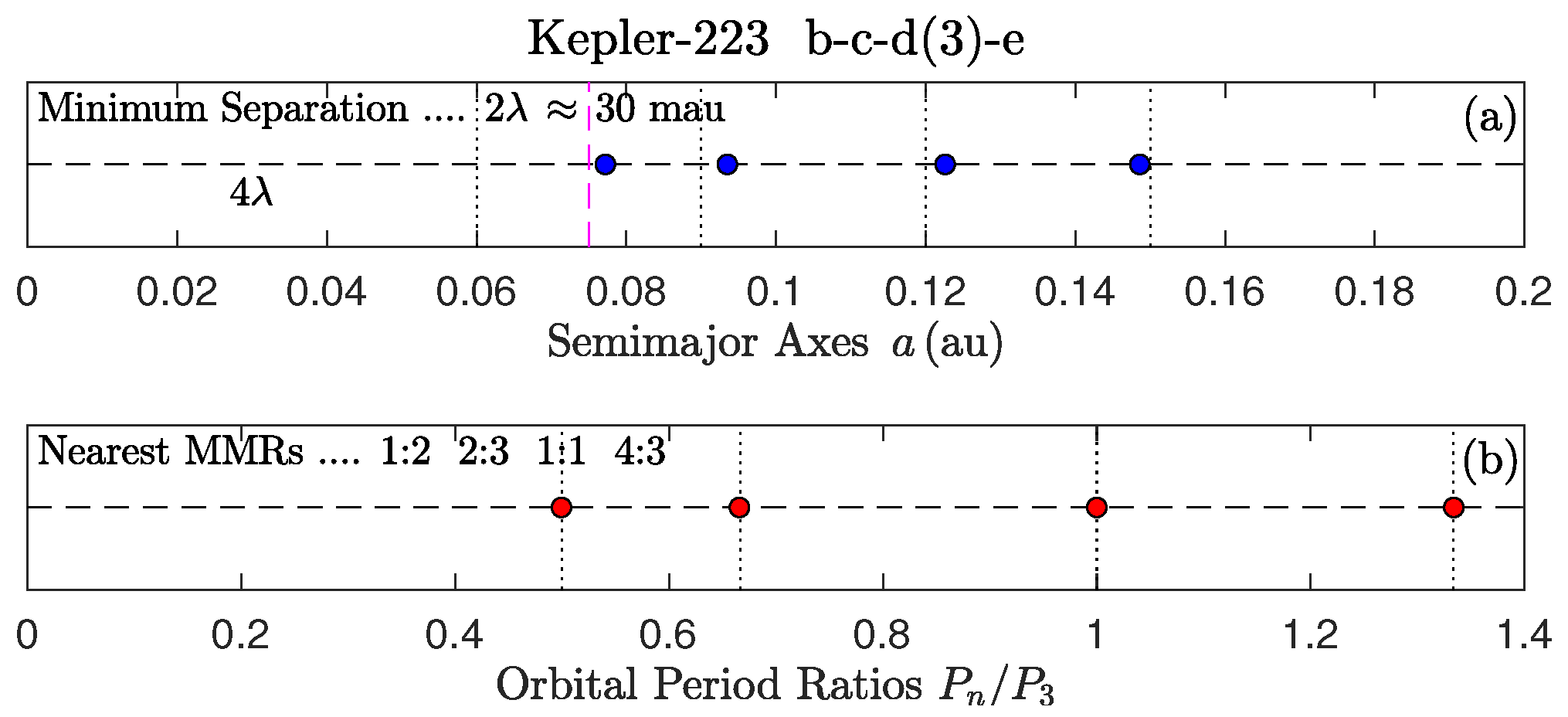
Appendix B.3. Application to Kepler-223
References
- Papaloizou, J. C. B. 2015, Three body resonances in close orbiting planetary systems: Tidal dissipation and orbital evolution, IJAsB, 14, 291. [CrossRef]
- Goździewski, K., Migaszewski, C., Panichi, F., & Szuszkiewicz, E. 2016, The Laplace resonance in the Kepler-60 planetary system, MNRAS, 455, L104. [CrossRef]
- Mills, S. M., Fabrycky, D. C., Migaszewski, C., et al. 2016, A resonant chain of four transiting, sub-Neptune planets, Nature, 533, 509. [CrossRef]
- Delisle, J. B. 2017, Analytical model of multi-planetary resonant chains and constraints on migration scenarios, A&A, 605, A96. [CrossRef]
- Charalambous, C., Martí, J. G., Beaugé, C., & Ramos, X. S. 2018, Resonance capture and dynamics of three-planet systems, MNRAS, 477, 1414. [CrossRef]
- Morrison, S. J., Dawson, R. I., & MacDonald, M. 2020, Chains of planets in mean motion resonances arising from oligarchic growth, ApJ, 904, 157. [CrossRef]
- Jontof-Hutter, D., Ford, E. B., Rowe, J. F., et al. 2021, Erratum: “Secure TTV mass measurements: Ten Kepler exoplanets between 3 and 8 M⊕ with diverse densities and incident fluxes”, ApJ, 911, 154.
- Siegel, J. C., & Fabrycky, D. 2021, Resonant chains of exoplanets: Libration centers for three-body angles, AJ, 161, 290 (SF21). [CrossRef]
- MacDonald, M. G., Feil, L., Quinn, T., & Rice, D. 2022, Confirming the 3:2 resonance chain of K2-138, AJ, 163, 162. [CrossRef]
- MacDonald, M. G., Polania Vivas, M. S., D’ Angiolillo, S., et al. 2023, exoMMR: A new python package to confirm and characterize mean motion resonances, AJ, 166, 94. [CrossRef]
- Quinn, T., & MacDonald, M. G. 2023, Confirming resonance in three transiting systems, AJ, 166, 58. [CrossRef]
- Luger, R., Sestovic, M., Kruse, E., et al. 2017, A seven-planet resonant chain in TRAPPIST-1, Nature Astronomy, 1, 0129. [CrossRef]
- Mah, J. 2018, MSc Thesis, University of Hong Kong (Hong Kong: Pokfulam).
- Brasser, R., Barr, A. C., & Dobos, V. 2019, The tidal parameters of TRAPPIST-1b and c, MNRAS, 487, 34. [CrossRef]
- Agol, E., Dorn, C., Grimm, S. L., et al. 2021, Refining the transit-timing and photometric analysis of TRAPPIST-1: Masses, radii, densities, dynamics, and ephemerides, PSJ, 2, 1. [CrossRef]
- Lari, G., Saillenfest, M., & Fenucci, M. 2019, The Galilean satellites’ evolution toward a 4-body mean motion resonance, EPSC Abstracts, Vol. 13, EPSC-DPS2019-2017-1, EPSC-DPS Joint Meeting 2019.
- Christodoulou, D. M., Sorabella, N. M., Bhattacharya, S., et al. 2024, I. An Exceptional Multiplanetary Resonant Chain in TOI-270 and an Exact Laplace-like Resonance in HD 110067, Galaxies, submitted (Paper I).
- Murray, C. D., & Dermott, S. F. 1999, Solar System Dynamics (Cambridge: Cambridge Univ. Press), pp. 364-371, 396-399.
- Lieske, J. H. 1998, Galilean satellite ephemerides E5, A&A Supl. Ser., 129, 205. [CrossRef]
- Musotto, S., Varadi, F., Moore, W., & Schubert, G. 2002, Numerical simulations of the orbits of the Galilean satellites, Icarus, 159, 500. 10.1006/icar.2002.6939.
- Forgács-Dajka, E., Sándor, Zs., & Érdi, B. 2018, A fast method to identify mean motion resonances, MNRAS, 477, 3383. [CrossRef]
- Lainey, V., Duriez, L., & Vienne, A. 2006, Synthetic representation of the Galilean satellites’ orbital motions from L1 ephemerides, A&A, 456, 783. [CrossRef]
- Lari, G., & Saillenfest, M. 2024, The nature of the Laplace resonance between the Galilean moons, Cel. Mech. Dyn. Astr., 136, 19. 10.1007/s10569-024-10191-6.
- Batygin, K., & Morbidelli, A. 2013, Analytical treatment of planetary resonances, A&A, 556, A28. [CrossRef]
- Celletti, A., Karampotsiou, E., Lhotka, C., et al. 2021, Laplace-like resonances with tidal effects, A&A, 655, A94. [CrossRef]
- Wolszczan, A., & Frail, D. A. 1992, A planetary system around the millisecond pulsar PSR1257+12, Nature, 355, 145. [CrossRef]
- Konacki, M., & Wolszczan, A. 2003, Masses and orbital inclinations of planets in the PSR B1257+12 system, ApJL, 591, L147. [CrossRef]
- Wolszczan, A. 2012, Discovery of pulsar planets, NewAR, 56, 2. [CrossRef]
- Goździewski, K., Konacki, M., & Wolszczan, A. 2005, Long-term stability and dynamical environment of the PSR 1257+12 planetary system, ApJ, 619, 1084. [CrossRef]
- Günther, M. N., Pozuelos, F. J., Dittman, J. A., et al. 2019, A super-Earth and two sub-Neptunes transiting the nearby and quiet M dwarf TOI-270, Nat. Astron., 3, 1099. [CrossRef]
- Kaye, L., Vissapragada, S., Günther, M. N., et al. 2022, Transit timings variations in the three-planet system: TOI-270, MNRAS, 510, 5464. [CrossRef]
- Mikal-Evans, T., Madhusudhan, N., Dittman, J., et al. 2023, Hubble Space Telescope transmission spectroscopy for the temperate sub-Neptune TOI-270 d: A possible hydrogen-rich atmosphere containing water vapor, AJ, 165, 84. [CrossRef]
- Danielsson, L. 1978, The orbital resonances between the asteroid Toro and the Earth and Venus, The Moon and the Planets, 18, 265. [CrossRef]
- MacDonald, M. G., Ragozzine, D., Fabrycky, D. C., et al. 2016, A dyamical analysis of the Kepler-80 system of five transiting planets, AJ, 152, 105. [CrossRef]
- Ćuk, M., El Moutamid, M., & Tiscareno, M. S. 2020, Dynamical history of the Uranian system, PSJ, 1, 22. [CrossRef]
- Jacobson, R. A. 2014, The orbits of the Uranian satellites and rings, the gravity field of the Uranian system, and the orientation of the pole of Uranus, AJ, 148, 76. [CrossRef]
- Jacobson, R. A. 2022, The orbits of the main Saturnian satellites, the Saturnian system gravity field, and the orientation of Saturn’s pole, AJ, 164, 199. [CrossRef]
- Luque, R., Osborn, H. P., Leleu, A., et al. 2023, A resonant sextuplet of sub-Neptunes transiting the bright star HD 110067, Nature, 623, 932. [CrossRef]
- Gillon, M., Triaud, A. H., Demory, B.-O., et al. 2017, Seven temperate terrestrial planets around the nearby ultracool dwarf star TRAPPIST-1, Nature, 542, 456. [CrossRef]
- Rivera, E. J., Laughlin, G., Butler, R. P., et al. 2010, The Lick-Carnegie exoplanet survey: A Uranus-mass fourth planet for GJ 876 in an extrasolar Laplace configuration, ApJ, 719, 890. [CrossRef]
- Mills, S. M., & Fabrycky, D. C. 2017, Mass, density, and formation constraints in the compact, sub-Earth Kepler-444 system including two Mars-mass planets, ApJL, 838, L11. [CrossRef]
- Weiss, L. M., Isaacson, H., Howard, A. W., et al. 2024, The Kepler Giant Planet Search. I. A decade of Kepler planet-host radial velocities from W. M. Keck Observatory, ApJS, 270, 8. [CrossRef]
- Barros, S. C. C., Demangeon, O. D. S., Alibert, Y., et al. 2022, HD 23472: a multi-planetary system with three super-Earths and two potential super-Mercuries, A&A, 665, A154. [CrossRef]
- Díaz, R. F., Ségransan, D., Udry, S., et al. 2016, The HARPS search for southern extra-solar planets. XXXVIII. Bayesian re-analysis of three systems. New super-Earths, unconfirmed signals, and magnetic cycles, A&A, 585, A134. [CrossRef]
- Tuomi, M., Anglada-Escudé, G., Gerlach, E., et al. 2013, Habitable-zone super-Earth candidate in a six-planet system around the K2.5V star HD 40307, A&A, 549, A48. [CrossRef]
- Rambaux, N., Van Hoolst, T., & Karatekin, Ö. 2011, Librational response of Europa, Ganymede, and Callisto with an ocean for a non-Keplerian orbit, A&A, 527, A118. [CrossRef]
- Lari, G., Saillenfest, M., & Fenucci, M. 2020, Long-term evolution of the Galilean satellites: the capture of Callisto into resonance, A&A, 639, A40. [CrossRef]
- Downey, B. G., Nimmo, F., & Matsuyama, I. 2020, Inclination damping on Callisto, MNRAS, 499, 40. [CrossRef]
- Goldreich, P. 1965, An explanation of the frequent occurrence of commensurable mean motions in the solar system, MNRAS, 130, 159. [CrossRef]
- Hamilton, D. P., & Burns, J. A. 1992, Orbital stability zones about asteroids: II. The destabilizing effects of eccentric orbits and of solar radiation, Icarus, 96, 43. [CrossRef]
- Judkovsky, Y., Ofir, A., & Aharonson, O. 2024, Kepler multitransiting system physical properties and impact parameter variations, AJ, 167, 103. [CrossRef]
- Goździewski, K., & Migaszewski, C. 2020, An exact, generalized Laplace resonance in the HR 8799 planetary system, ApJL, 902, L40. [CrossRef]
- Zurlo, A., Goździewski, K., Lazzoni, C., et al. 2022, Orbital and dynamical analysis of the system around HR8799. New astrometric epochs from VLT/SPHERE and LBT/LUCI, A&A, 666, A133. [CrossRef]
| Global | Local | Pair | Multibody | |
| MMRs | MMR Pairs | Angle | System | |
| (1) | (2) | (3) | (4) | (5) |
| 1 : 3/2 : 2 | 3:2 & 4:3 | 1 | HD 110067 (most recently found LR multiple; Paper I) | |
| 2/3 : 1 : 4/3 | 3:2 & 4:3 | 1 | Kepler-223, TOI-178 | |
| 1/2 : 3/4 : 1 | 3:2 & 4:3 | 1 | Kepler-90, TOI-1136, TRAPPIST-1 | |
| 2/3 : 1 : 3/2 | 3:2 & 3:2 | 1 | Kepler-11, K2-138, HD 110067, TRAPPIST- | |
| 2/3 : 1 : 5/3 | 3:2 & 5:3 | M | HD 23472 (discussed in Section 3.3(d) in relation to Kepler-444) | |
| 2/3 : 1 : 2/1 | 3:2 & 2:1 | 1 | TOI-1136,c Kepler-20 (::); no | |
| 2/3 : 1 : 5/1 | 3:2 & 5:1 | M | HD 34445 | |
| 3/4 : 1 : 3/2 | 4:3 & 3:2 | 1 | TOI-1136, HIP 41378,d Kepler-223,e HD 23472,e TRAPPIST-1 | |
| 3/4 : 1 : 5/3 | 4:3 & 5:3 | M | Kepler-90 | |
| (3/4 : 1 : 5/4) | (4:3 & 5:4) | (1) | (Not observed; discussed in Section 3.3(d) and in Table 2) | |
| 1/3 : 1 : 4/3 | 3:1 & 4:3 | M | HD 10180 | |
| 1/3 : 1 : 3/2 | 3:1 & 3:2 | M | Kepler-80 | |
| 1/2 : 1 : 3/2 | 2:1 & 3:2 | 1 | Kepler-32, Kepler-82 (::1), Umbriel-Titania-Oberon (Uranus)(U) | |
| 1/2 : 1 : 5/3 | 2:1 & 5:3 | M | HD 40307 | |
| 1/2 : 1 : 2/1 | 2:1 & 2:1 | 1 | GJ 876, HR 8799, HR 8832, Kepler-176 (Paper I) | |
| 1/4 : 1/2 : 1 | 2:1 & 2:1 | 1 | HIP 41378, Io-Europa-Ganymede (Galilean LR) (Paper I) | |
| 1/4 : 5/8 : 1 | 5:2 & 8:5 | 3 | Mercury-Venus-Earth (MVE) secondary MMR | |
| 1/2 : 1 : 7/3 | 2:1 & 7:3 | M | Europa-Ganymede-Callisto (EGC) MMR, no librations | |
| 1/5 : 1/2 : 1 | 5:2 & 2:1 | M | HD 40307 | |
| 2/5 : 1 : 3/2 | 5:2 & 3:2 | M | PSR B1257+ (although :1: is a strong alternative) | |
| 3/5 : 1 : 8/5 | 5:3 & 8:5 | M | Kepler- | |
| 3/5 : 1 : 2/1 | 5:3 & 2:1 | M | TOI- (and Ariel-Umbriel-Titania ::1 MMR in Uranus)(U) | |
| 3/5 : 1 : 9/4 | 5:3 & 9:4 | M | HD 108236 | |
| 4/5 : 1 : 4/3 | 5:4 & 4:3 | 1 | Kepler-60 | |
| 5/8 : 1 : 7/4 | 8:5 & 7:4 | 3 | TOI-700 | |
| 5/8 : 1 : 8/5 | 8:5 & 8:5 | 3 | Venus-Earth-Toro (VET) secondary | |
| 2/7 : 1 : 4/3 | 7:2 & 4/3 | M | Rhea-Titan-Hyperion (RTH) (Saturn)(S) (Section 3.3(g) and Paper I) | |
| 4/7 : 1 : 9/4 | 7:4 & 9/4 | M | Kepler-20 |
- Notes:
- aM: Mixed order of the pair [25]; absence of order-2 MMRs is notable.
- cIn TOI-1136, the innermost chain :: is recast to :1:2.
- dIn HIP 41378, the outermost chain :6:9 is recast to :1:.
- eIn Kepler-223, the innermost chain ::1 is recast to :1:. Similarly for the middle chain ::1 in HD 23472.
- gIn Kepler-90, the outermost chain ::1 is recast to :1:. But the planets (f-g-h) are too far apart to possibly develop librations.
- iOnly the trailing 8:5 MMR librates (amplitude ∼ 32°), although Venus leverages the orbital elements of asteroid 1685 Toro [33]. For the leading MMR, we did not adopt the commonly-quoted 8:13 ratio; we argue that 13 is not a small integer and that the order 5 is too high for such an MMR to be effectual. Besides 8:3 (Kepler-90, HD 110067), the only order-5 weak MMRs seen in exosystems are the 9:4 trailing MMRs in HD 108236 and Kepler-20. By the same token, order-4 MMRs either do not exist (e.g., :p with p odd and ) or do not librate because the two bodies are too far apart (e.g., 7:3 of Callisto with Ganymede and 5:1 of Iapetus with Titan).
- (**) These angles were found to librate (mostly about ) in type-I first-order MMR models (SF21).
- (***) Many MMR triples were found to be librating in Kepler-80 [34].
-
(‡) An identity relation: (see also Section 3.3(e) for more identities).(∦) No librations were seen in 30 type-I first-order (3:2 & 2:1) MMR models (SF21).
- (S)Ref. [37].
| q | ||||||
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | 1:2, 2:1 | 1:3, 3:1 | 1:4, 4:1 | 1:5, 5:1 | 1:6, 6:1 | |
| 2 | 2:3, 3:2 | —– | 2:5, 5:2 | —– | 2:7 | |
| p | 3 | 3:4, 4:3 | 3:5, 5:3 | —– | 3:7, 7:3 | 8:3 |
| 4 | 4:5 | —– | (4:7, 7:4) | —– | (4:9, 9:4) | |
| 5 | —– | (5:7) | (5:8) | —– | —– | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





