Origin of Gravitational Force — Model of Self-Forming Electric Dipoles with Dynamically Self-Calibrating Constant Mutual Attraction

Shangqing Liu

doi:10.20944/preprints202412.2082.v7

Submitted:

19 October 2025

Posted:

20 October 2025

You are already at the latest version

Abstract

Gravitational force is extremely important because it dominates the formation and evolution of the universe. However, its physical origin and intrinsic nature have not been clearly understood for a long time. Certain observed phenomena, along with those newly discovered by the Hubble and James Webb telescopes, cannot be well explained by existing theories. Furthermore, general relativity and quantum mechanics, which are the current mainstream theories explaining the gravitational force, are incompatible with each other. This situation strongly points to the need for a better or even novel theory of the gravitational force. Here, based on the classical space-time perspective, a different yet solid understanding of the gravitational force is introduced. The author has realized that the gravitational force originates from none other than the electric force, but it is a synthetic electric force produced by a large number of electric charges, and thus shows very different characteristics from simple electric force. Generally speaking, in any objects, there are a large number of free and inducible net electric charges. Due to various reasons, including unavoidable fluctuations of microscopic or subatomic particles, non-uniform charge distribution in the object is normal. The Earth, the Moon, and the Sun are all typical examples of such. The non-uniform charge distribution within an object will almost certainly turn that object into an electric dipole or a generalized electric dipole. Thus, almost any object can be regarded as an electric dipole because of self-forming. Furthermore, through dynamically self-calibrating, the interacting electric force produced between two objects will quickly change to an attractive force, and such force can be maintained constantly when two objects rotate to each other. In other words, although the electric force direction of an electric dipole is anisotropic, because the direction of the electric dipole, which is determined by non-uniform charge distribution, can change dynamically and quickly, an electric dipole can always maintain attraction to another electric dipole moving around it, similar to an object exhibiting isotropic attraction to its surrounding object. The dynamically self-calibrating process can also cause multiple electric dipoles, or even multiple groups of electric dipoles, to mutually and continuously attract each other, since every dipole or dipole group has a non-uniform charge distribution too, albeit on different scales. This is the true origin of the gravitational force. Calculation has shown that, under certain conditions, the change rate of the strength of the gravitational force derived from the dipole model closely follows the law of inverse square of the distance. This understanding can explain confusing phenomena effectively, such as flat galaxies, filamentary nebulae, the formations of the Solar System and Milky Way galaxy, unusual trajectories of ‘Oumuamua and 3I/ATLAS, and dark matter and dark energy. This understanding also naturally unifies the gravitational and electromagnetic forces and opens a key door for the final unification of the four fundamental forces of nature.

Keywords:

gravitational force

;

formations of the Solar system and Milky Way galaxy

;

dark matter

;

dark energy

;

unification of the gravitational and electromagnetic forces

;

classical space-time

Subject:

Physical Sciences - Particle and Field Physics

Introduction

For modern science, physics is the most fundamental branch, which is the study of matter, motion, and force interactions basically. Among four fundamental forces of nature, the gravitational force is the most significant for the macrocosm because it dominates the formation and evolution of the universe. Without the gravitational force, there would be no Earth and universe.

However, what is the gravitational force? What are its physical origin and intrinsic qualities? These questions have not yet clearly explained. From Newton theory of gravity to Einstein general relativity, and then to Higgs particle and field, the theories of the gravitational force are constantly developing. However, there are still discrepancies between observed phenomena and established theories. Furthermore, with scientific and technological progress, more inexplicable phenomena have been discovered. Compared to the other three fundamental forces, questions about the gravitational force are especially difficult because of its strange and mysterious behaviors.

For example, stars on the outskirts of galaxies move much faster than estimated based on their normal matter quantities [1]. Many galaxies within galaxy clusters move similarly. Thus, some people supposed that there is a large amount of dark matter present to provide the necessary attractive forces. However, after extensive searching, no sign of the dark matter has been found.

Another example is the accelerated expansion of the universe [2]. It seems that the velocity at which a distant galaxy recedes from us is continuously increasing. Therefore, unknown dark energy should dominate the universe. Otherwise, how can we explain the accelerated expansion of the universe? However, similarly, no dark energy has been detected until now either.

The Hubble Space Telescope has captured images of nebulae showing rope-like filaments [3]. The current explanation is that shock waves are very thin, appearing filamentous when their shells are viewed edge-on. However, why the shock waves are very thin and how so many of their shells are coincidentally viewed edge-on remain unanswered.

The James Webb Telescope has astonishingly discovered superfast matured massive galactic structures that should not have occurred in the early stages of the universe [4]. On the other hand, some distant stars are still accumulating mass from surrounding clouds [4]. These phenomena contradict the theory of the universe having a definite age starting from an explosion, as the maturities of these stars and galaxies should be consistent with the age of the universe.

In recent years, some strange comets have entered the solar system, such as ‘Oumuamua¹ to ‘Oumuamua³, and 3I/ATLAS, etc. Their trajectories are so unusual that they cannot be explained by Newton’s law of universal gravitational force.

The current mainstream theories of the gravitational force are based on Einstein general relativity and quantum mechanics. Einstein believed gravitational force originates from space-time curvature [5], while quantum mechanics posits that the gravitational force comes from the exchange of quantum particles [6]. Because the general relativity describes gravity as a smooth, continuous distortion of space-time, but quantum particles are discrete and discontinuous energy packets. The general relativity is incompatible with the quantum mechanics. In addition, this contradiction makes the unification of the four fundamental forces of nature impossible.

To solve these problems, people have made numerous attempts. However, despite arduous efforts over a long time, the physical origin and intrinsic nature of the gravitational force still lack satisfactory explanations. This situation strongly indicates the need for a better or even novel theory to explain the gravitational force in different ways.

This paper introduces a different yet solid understanding of the gravitational force.

The author has realized that the gravitational force originates from none other than the electric force, but it is a synthetic electric force produced by a large number of electric charges. The behavior and characteristics of this synthetic force are very different from those of a simple electric force. The author also suggests that the origin of the gravitational force is not complicated but requires insight to recognize it through its confusing appearances.

This new understanding considers any object as an electric dipole, and any two electric dipoles will interact with and ultimately attract each other. This electrical attractive force forms the gravitational force between any two objects. This attraction mechanism is also applicable to multiple dipoles or multiple groups of electric dipoles, as each electric dipole or group of electric dipoles has a single or combined non-uniform charge distribution too. In the following, detailed analyses and calculations will show that. As the electrical attractive force of electric dipole, the gravitational force has the following properties:

The gravitational force is anisotropic because the dipole electric field extends only along the dipole moment direction.
The strength of the gravitational force depends on the net electric charge quantities and the length of the electric dipole moment of the object; it does not depend solely on the so-called mass of the object.
Due to dynamically self-calibrating process, any object can always attract its surrounding object, no matter that object rotates around it or not, as if any object has an isotropic attractive force.
Although the strength of the electric field of an electric dipole is inversely proportional to the cube of the distance from the dipole, under certain conditions, the newly deduced law of the gravitational force based on the dipole model also shows that the gravitational force strength is inversely proportional to the square of the distance from the object. Thus, the new deduced law remains highly consistent with the results of precise measurements of the gravitational force by modern technology. This result reveals a truth: the Newton’s laws, where the strength of the gravitational force is inversely proportional to the square of the distance, is a high-precision approximation of the real physical fact under certain conditions.

Based on this understanding, the aforementioned confusing phenomena can be explained effectively. The flat galaxies and filamentary nebulae are caused by gravitational force anisotropy. The Solar System and Milky Way galaxy can operate stably because celestial bodies with heavy so-called masses can attract others through seemingly isotropic attraction. The ultra-fast movements of stars on the outskirts of galaxies and galaxies within galaxy clusters are maintained by increased attraction forces. The possible continually increasing velocity of distant galaxies may be produced by continually increasing attraction forces, while the slow growth of distant stars is due to decreased attraction forces. The strange trajectories of some comets entering the solar system are caused by unusual charge distributions within these celestial bodies.

Note that the strength of an object’s gravitational force may change with the electric charge distribution in that object and is not solely and constantly dependent on the object’s “fixed” so-called mass.

This new understanding is based on the classical space-time perspective and substantially electromagnetic principles. Thus, the strange behaviors of the gravitational force can be completely understood with common sense. Below, this new understanding will be introduced in detail.

Observation of Gravitational Force

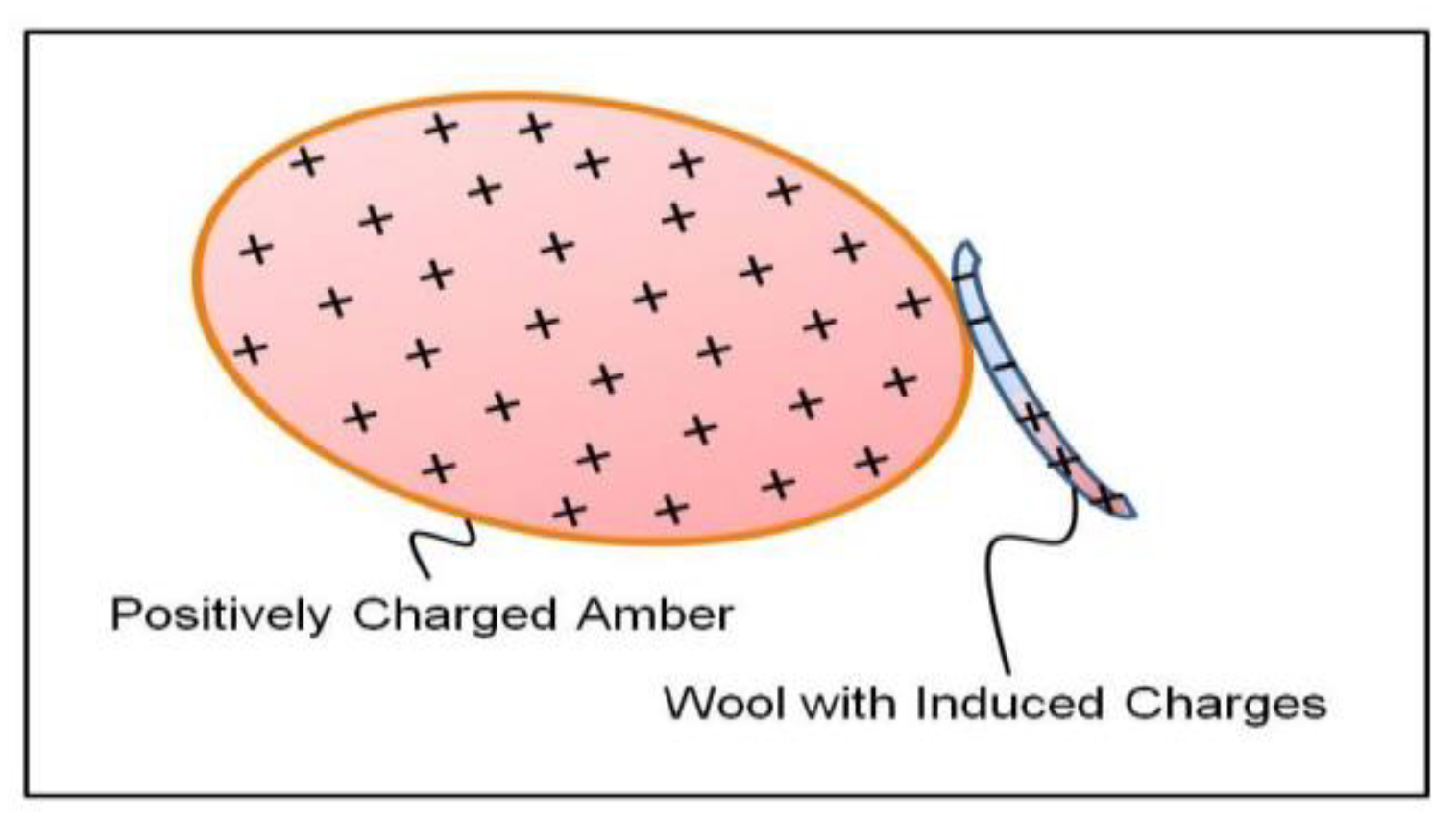
In the physics textbook, there is a description of the early discovery of electric charge and the attractive and repulsive forces between two charges [7]. As early as 600 BC, the ancient Greeks discovered that if amber was rubbed, it would attract other light objects, such as wool. Today we know that the amber has acquired net electric charges or has become “charged,” and these net charges on the amber would attract the wool. When we rub a plastic rod with fur and rub a glass rod with silk, you can find that the rubbed plastic rod and rubbed glass rod all have become “charged”, and then they can attract other light objects too.

In experiments involving rubbing a plastic rod with fur and rubbing a glass rod with silk, we can see that a plastic rod can be attracted by a glass rod. However, two plastic rods rubbed with fur, or two glass rods rubbed with silk, will repel each other. Today we know there are two kinds of electric charges. They are negative and positive, respectively. Rubbing the plastic rod with fur produces negative charges on the rod, while rubbing the glass rod with silk produces positive charges on the rod. After rubbing, the fur and silk also become “charged.” When the signs of the net charges on the rods are the same, the rods repel each other. When the signs of the net charges on the rods are opposite, the rods attract each other. Today we know that the signs of the net charges on the rubbed plastic rod and silk are negative. The signs of the net charges on the rubbed glass rod and fur are positive.

When you see wool being attracted by “charged” amber, you need to think more. The wool is not rubbed with any material; thus, it has not acquired any net charge. An “uncharged” object should be electrically neutral and should not be attracted or repelled by a “charged” object. So, why does the “charged” amber attract the “uncharged” wool?

This involves the generation and influence of induced net electric charges. In an object, there are free electric charges. If an external electric field exerts a force on the object, the free charges will move, changing the distribution of the total charges in the object. This change in charge distribution affects the electric fields inside and outside the object. Thus, the regional distribution of the charges in the object and the spatial distribution of the field out the object will affect each other and the last equilibrium of the charge and field distributions will be determined by both of the electric charges and electric field.

Additionally, many objects contain polar molecules having equal amounts of positive and negative charges but a lopsided distribution. In these molecules, the excess positive and negative charges are concentrated on opposite sides, making the molecule become an electric dipole. The dipole moment direction may change with the external electric field. In the object, there are also non-polar molecules. Under the external electric field, the positive and negative charge centers of these non-polar molecules may shift from a concentric status to a non-concentric status, causing these non-polar molecules to become induced polar molecules. Furthermore, electrically neutral atoms will also produce atomic polarization under the external electric field, with the positive and negative charge centers shifting from a concentric status to a non-concentric status.

The movements of free charges, the changes of dipole directions of polar molecules, and the polarizations of non-polar molecules and atoms will form induced net electric charges in the object. These induced charges will alter the regional distribution of electric charges in the object and the spatial distribution of electric fields in and out the object.

The amount of free and induced net electric charges depends on the number of molecules and atoms in the object. Thus, generally speaking, when an object has more molecules and atoms, this object will have more mass and more free and induced net electric charges.

Under an external electric field, the redistribution of electric charges, including free and induced net charges in the object, is the key reason that “charged” amber can attract “uncharged” wool. Regardless of whether an object is electrically neutral or has net positive or net negative charges, its electric charge distribution will change under the influence of an external electric field.

Suppose the “charged” amber is close to the “uncharged” wool. If the amber has net positive charges, it will exert a positive electric field on the wool, attracting the free negative charges in the wool to the side close to the amber. Since the amounts of positive and negative charges in electrically neutral wool are equal due to conservation of electric charge, the increase of net negative charges near the amber equals the increase of net positive charges far from the amber. Because the net negative charges are closer to the amber than the net positive charges, the attractive force of the amber on the net negative charges is slightly larger than its repulsive force on the net positive charges. Thus, the net force exerted by the amber on the wool is attractive, enough to lift light objects like wool, as shown in Figure 1.

At the same time, under the positive electric field of the amber, in the wool, the distribution center of all induced net negative charges will be close to the amber, while the distribution center of all induced net positive charges will be far from the amber. The location difference between these two induced charge distribution centers makes the amber attractive force slightly larger than its repulsive force to the wool too, helping to pick up the wool. About the two types of electric charge centers in a non-uniform electric charge distribution, more explicit definitions will be provided below.

The attractive force between the amber and wool is a synthetic electric force produced by a large number of electric charges in both the amber and wool. Although the wool is small, it contains a large number of molecules and atoms, and thus a large number of free and induced net electric charges.

If the amber is replaced by a negatively “charged” plastic rod, it can also pick up the “uncharged” wool. In this case, the rod will attract net free positive charges and distribution center of induced net positive charges close to the rod, and will repel net free negative charges and distribution center of induced net negative charges far from the rod. Thus, the net force of the plastic rod on the wool will remain a small attractive force too, sufficient to lift the lightweight wool. Therefore, whether an object has net positive or net negative charges, the “uncharged” wool will always be attracted to the “charged” object.

Here, it must be stated that the non-uniform charge distribution within any object is primarily generated spontaneously, see detailed explanation below. The role of an external electric field is mainly to redistribute the non-uniform charges within the object. That is, the external electric field is mainly to change the direction of the electric dipole of the object. The main reason is that, in most cases, because the distances between atoms and molecules within the object are very short, the electric field strength inside the object is much greater than the external electric field strength.

The author explained why a small “uncharged” paper piece can be attracted by a “charged” object in an electromagnetism examination at university with such details while young, but did not think further at that time. Thus, the author was unaware that understanding this phenomenon approached the realization of the origin of the gravitational force.

Origin of Gravitational Force

From understanding that a “charged” object can attract an “uncharged” object to understanding origin of the gravitational force, that is, an attractive force can originate spontaneously between any two “uncharged” objects, the key step is to recognize that non-uniform charge distribution can emerge spontaneously in any seemingly electrically neutral object.

In any electrically neutral object, an initial variation in charge distribution can disrupt charge distribution uniformity, causing net positive or net negative charges to appear. Many factors can cause such variation, including different movements of free charges, different thermal vibrations of polar and non-polar molecules and atoms, various collisions among microscopic or subatomic particles, different densities of polar and non-polar molecules and atoms, and any other differences of various physical and chemical characteristics in different regions of the object including substance composition, state, form, temperature, pressure, fluidity, and electric and thermal conductivity, etc. These myriad causes make the presence of net electric charges in some regions in an object unavoidable and normal. The common cognition that the electric charge distribution in an “uncharged” object is always uniform is wrong.

For example, Earth is a typical object with spontaneous non-uniform distributions of electric charge and electric field. These are caused by various substance compositions with different physical and chemical properties in different regions, especially at different depths in Earth’s interior. Furthermore, these non-uniform distributions are continuously changing. Measurements have indicated the presence of an electric field surrounding the Earth [8]. The field magnitude is about 100 volts per meter at ground level, and the field direction is downward. The surface of the Earth is negatively charged with many charge states [9]. It is also known that the Earth has a strong magnetic field. The Earth’s magnetic field should result from the continuous flow of a huge number of net electric charges in Earth’s interior.

In addition, astronomical observations and detections have shown that both the Moon and the Sun have their own electric fields. The Moon has an electric field near its surface, especially when it’s full and passes through Earth’s magnetotail, and the nightside lunar surface is negatively charged [10]. The Sun’s electromagnetic fields are complex and constantly changing, mainly generated by the movements of charged particles (plasma) in its interior, and these electromagnetic fields are also influenced by the Sun’s rotation and temperature [11].

Events occurring on the Earth, the Moon, and the Sun may occur on other celestial bodies. Some events that occur in large objects like the Moon, the Earth, and the Sun may also occur in small objects. At least, for example, the non-uniform distribution of electric charge may occur in small objects such as wool. For free electrons, polar molecules, non-polar molecules and atoms, small objects like wool are sufficiently large.

Therefore, when two objects approach each other, the two electric fields generated by the non-uniform charge distribution within two objects will influence each other, causing the charges within these two objects to redistribute. Another situation is that, if the electric field of one object, such as the object 1, is relatively weak, the relatively strong electric field of another object, such as the object 2, will affect the object 1. Thus, the object 2 will alter the charge distribution in object 1 to increase its electric field. The strength increased new electric field of the object 1 will exert back on object 2. Consequently, the non-uniformities of the charge distributions in both objects will increase, resulting in stronger and stronger electric fields both within and outside the two objects. These electric fields will interact each other. Thus, the electric interaction force between the two objects can start spontaneously and grow from weak to strong.

There is, of course, a limitation for the force strength of this electric interaction. With continual moving of the free charges within each object, the net negative charges will increase in some regions within each object, and the net positive charges will increase in some other regions within each object. The increases of the amounts of the net positive and net negative charges in different regions will enhance the repulsive forces to the charges with the same signs to enter these regions further. Thus, these increased repulsive forces will gradually reduce further moving of the free charges in each object. Similar limitations apply to two kinds of induced net charges from polar molecules and non-polar molecules and atoms in each object. Eventually, the electric charge and field distributions in the two objects will reach equilibrium states, and the electrical interaction force between the two objects will be stabilized.

Such electrical interaction forces can be created between any two objects. These objects can range from as large as galaxies and galaxy clusters to as small as molecules and atoms because even atoms can become tiny electric dipoles when they are polarized to have separated positive and negative charge centers. Furthermore, the following analysis and calculation will explain that such electrical interaction forces will almost always become attractive force eventually. Such electrical attractive force is just the gravitational force. It is the origin of the gravitational force.

Understanding how an attractive force can arise spontaneously between two initially electrically neutral objects may be challenging. However, if a non-uniform charge distribution can be induced in electrically neutral wool by an external electric field, why can’t a non-uniform charge distribution be induced in a seemingly neutral object by an inevitable initial charge variation? Additionally, if a “positively charged” amber or a “negatively charged” plastic rod can attract “uncharged” wool, why can’t the Earth, which has a downward electric field on its surface, attract the “uncharged” objects on its surface, including every one of us? Compared to an amber or plastic rod and wool, a person to the Earth is much smaller than wool to the amber or plastic rod. Therefore, similar to a charged amber attracting uncharged wool, the Earth, having net negative charges on its surface, will certainly attract a person on its ground. In the following section, we will explain this further.

In reality, the spontaneous appearances of net electric charges and non-uniform charge distribution are common in seemingly electrically neutral objects. The misconception about this has long prevented people from discovering the true origin of the gravitational force.

The actual non-uniform charge distributions in objects are very complex. However, the author emphasizes that no matter how complex the charge distribution within an object is, that object will almost always turn into an electric dipole.

First, in most situations, when an object has a non-uniform charge distribution, it is almost impossible for the center of the total net positive charge distribution and the center of the total net negative charge distribution to be exactly at the same point. Thus, such non-uniform charge distributions will certainly make that object an electric dipole.

Second, even in a few spherical objects, if the net positive and net negative charges are uniformly located within different spherical layers at different depths in the sphere’s interior, and the amounts of the total net positive and total net negative charges are equal, the center of the total net positive charge distribution will be exactly at the same center as the total net negative charge distribution. Thus, the charge distribution in such a sphere cannot make it become an electric dipole.

However, even if such objects really exist in nature, when any one or multiple external fields are applied to such an object, its electric charge distribution, with centripetal or centrifugal electric field, will change, losing its central symmetry. Such objects may be referred to as generalized electric dipoles. This situation is a bit like the Earth.

The creation process of the electric attraction force between any two objects cannot be seen visibly because the formation or reformation of the non-uniform charge distribution are caused by moving of free charges and the polarization of polar molecules, non-polar molecules and atoms. These movements and polarizations (shifts of charge distribution centers) have very fast speeds, possibly close to the light speed, and cannot be seen visibly. Therefore, because these processes can start spontaneously, grow and finish instantly and cannot be seen visibly, the generation of the gravitational force is strange and mysterious.

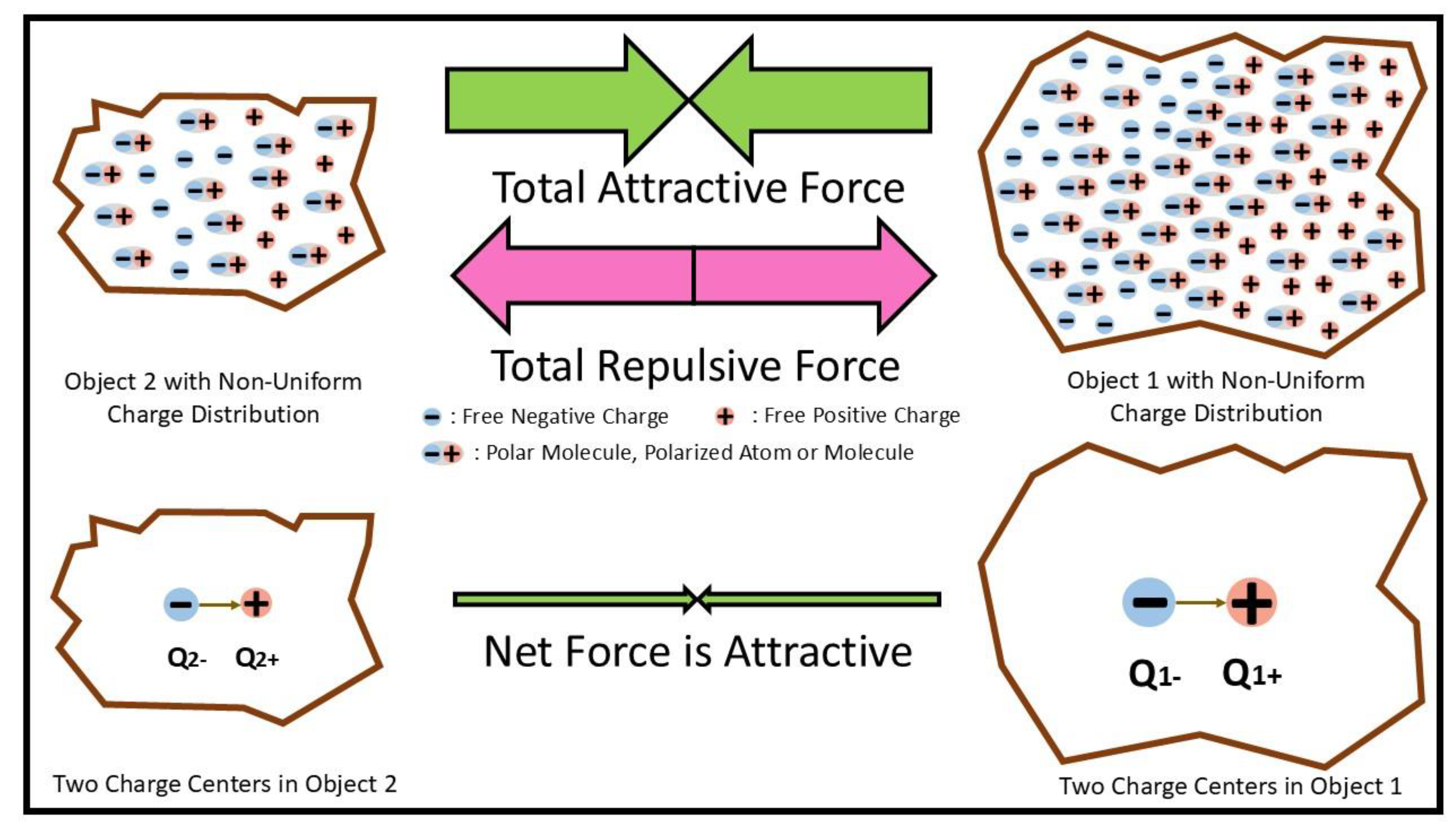
In interactions involving a large number of positive and negative electric charges, most electrical attractive forces are canceled by electrical repulsive forces due to the opposite signs of the electric charges, as shown in Figure 2.

Thus, the net electric interaction force is weak, and so although the gravitational force is the electric force, its strength is much smaller than the electric force. This is why the gravitational force strength is about 37 orders of magnitude smaller than the electric force strength, even though both have the same extremely long interaction distances and extremely fast interaction time (much faster than the light speed). This is another difficulty for many people to understand the strange behavior of the gravitational force.

More atoms and molecules in an object can provide more free and induced net electric charges and can produce a stronger electric field and electrical attractive force. It is why the object with more so-called mass can produce larger gravitational force.

What is the mass? This question has not been clearly answered. In physics, the concept of mass has two meanings: gravitational mass and inertial mass. Based on the new understanding of the gravitational force, an object’s gravitational mass represents the strength of the attractive force exerted on the object by the synthetic electric field of the Earth’s total electric charges when the object is motionless relative to the Earth. The object’s inertial mass represents the strength of the attractive force exerted on the object by the synthetic electric field of the total electric charges distributed in the space through which the object is moving. On or near the Earth, whether an object is in motion or motionless, the synthetic electric field exerted on that object is almost entirely generated by the Earth’s total electric charge. As a result, the gravitational mass and inertial mass of an object are always equal. Here, we addressed the well-known problem of why the gravitational mass and inertial mass of an object are always equal. Thus, the large and small metal balls with different so-called masses could fall at the same speed from the Leaning Tower of Pisa, as demonstrated by Galileo. Since the similar reason, in the absence of air resistance, a feather and a metal block may fall simultaneously on the lunar surface, as demonstrated by a U.S. astronaut in 1971. Therefore, the newly introduced understanding of the gravitational force can not only establish the equivalence principle but also provide a substantive reason for its establishment.

This new understanding also provides the real physical explanation for the Einstein mass-energy conservation law

E = m C^{2}

. Since both the gravitational mass and the inertial mass of an object are expressions of the interaction force strengths exerted on it, the change in motion energy of an object caused by an external force will naturally cause the so-called mass of that object to change. In other words, the real physical meaning of Einstein’s mass-energy conservation law is that it just expresses the transformation relationship between the gravitational force exerted by Earth on an object and the action force (or ability) of that object on another object.

Calculation of Gravitational Force

In an object, the non-uniform charge distribution may be very complicated, making the analysis and calculation of the produced electric field difficult. To simplify this, two net “charge centers,” similar to the “mass center” used in mechanics, are defined.

Regardless of the complexity of the net positive and net negative charge distributions, all electric forces generated by all net positive charges can be synthesized into a single positive electric force. The point from which this synthetic force is exerted on other object is the net positive “charge center.” Similarly, the net negative “charge center” is defined.

With this simplification, any object with non-uniform charge distribution can be regarded as having a net “positive charge center” and a net “negative charge center.” All net positive charges are considered concentrated at the “positive charge center,” and all net negative charges are considered concentrated at the “negative charge center.” As emphasized above, because these two charge centers are almost never at the same point for almost any object, and the two kinds of the electric charges have equal or almost equal amount in any object, nearly any object with a non-uniform charge distribution can be regarded as an electric dipole.

The theoretical electric dipole is a pair of two points electric charges with equal magnitude |

q

| and opposite signs, where |

q

| is the absolute value of electric charge

q

. A small distance

\vec{l}

is between the two points charges. The electric dipole moment

\vec{p}

is the product of the distance

\vec{l}

and the charge

q

.

\vec{p} = q \vec{l},

(1)

where

\vec{P}

and

\vec{l}

are vectors. The direction of the dipole moment

\vec{P}

is from the negative point charge to the positive point charge. The electrical field strength

\vec{E}

of the electric dipole at the distance of R is [12]

\vec{E} = \frac{1}{4 π ϵ_{0} R^{3}} [3 (\vec{P} \cdot \vec{R}) \vec{R} - \vec{P}] .

(2)

In Eq. (2),

\vec{R}

is unit distance vector along the R direction.

ϵ_{0}

is the electric constant. Note that, in deduction of Eq. (2), the terms in

l^{2}

and higher order terms are neglected. This approximation is justified if

l / R \to 0

keeping the product

P = q l

finite [13], where

l

, R and P are absolute values of the vectors

\vec{l}

,

\vec{R}

and

\vec{p}

. This approximation is used for calculating the gravitational force easily and quickly.

Sometimes, the distance

l

between the net “positive charge center” and net “negative charge center” may not be small. However, if the size of the object is much smaller than the scale related to the problem being considered, such as considering the attraction between a planet and a star in the universe, the size and shape of the object are less important because

R ≫ l

. Thus, the distance between the net positive and net negative “charge centers” in the object may be treated as enough small, and such objects with non-uniform charge distributions may be reasonably regarded as ideal electric dipoles.

From Eq. (2), we know that when the direction of the vector

\vec{R}

changes, the electric field strength

\vec{E}

changes too. When the direction of

\vec{P}

is the same as or opposite to the direction of

\vec{R}

, the electric field strength

\vec{E}

becomes

E_{S}

or

E_{O}

E_{S} = \frac{2 P}{4 π ε_{0} R^{3}} .

(3)

E_{O} = \frac{- 2 P}{4 π ε_{0} R^{3}} .

(4)

The

E_{S}

in Eq. (3) is positive, which expresses a repulsive force away from the dipole to a positive point charge. The

E_{O}

in Eq. (4) is negative, which expresses an attractive force toward the dipole to a positive point charge. When the direction of the dipole moment is perpendicular to the direction of

\vec{R}

, the electric field strength

\vec{E}

becomes

E_{P}

E_{P} = \frac{- P}{4 π ε_{0} R^{3}} .

(5)

The

E_{P}

in Eq. (5) is negative. Please note that

E_{P}

is a deflective force.

Then, a problem arises: if the electric field strength of an object with non-uniform charge distribution is not isotropic, why we have not observed that the gravitational force between two objects varies with their relative direction? For instance, why are many planetary orbits around stars nearly circular? In other words, why is the gravitational force always attractive?

The reason is that while the electric field of an electric dipole may exert repulsive, attractive, or deflective forces on another electric dipole, in most cases, the repulsive and deflective forces will quickly change to attractive force. When the interaction between two electric dipoles is repulsive, both dipoles are in states of highest electric potential energy, which is unstable. Any change in the charge distribution of one object will produce a deflective force between the two dipoles. This deflective force will rotate the dipoles, eventually making the force between them attractive.

The process by which repulsive and deflective forces become attractive forces, that is, the rotations of electric dipole moments, can occur automatically and continuously. This is a continuous self-calibrating process due to the mutual influence of the electric fields of two electric dipoles. As mentioned above, the change in direction of the electric dipole only requires the redistribution of the non-uniform charge within the object, and doesn’t require the rotation of the macroscopic object. Since the movements of free electric charges and the shifts of charge distribution centers occur at very high speeds and are not visible, this process can happen dynamically and be completed almost instantly. Consequently, the interaction force between two objects may always appear to be attractive, whether they rotate around each other or not, resulting in a seemingly isotropic gravitational force between them.

Of course, in some cases, the gravitational force between the two objects is still affected by their relative direction, which is one of the reasons why some planetary orbits around stars are elliptical, and some comets have strange trajectories.

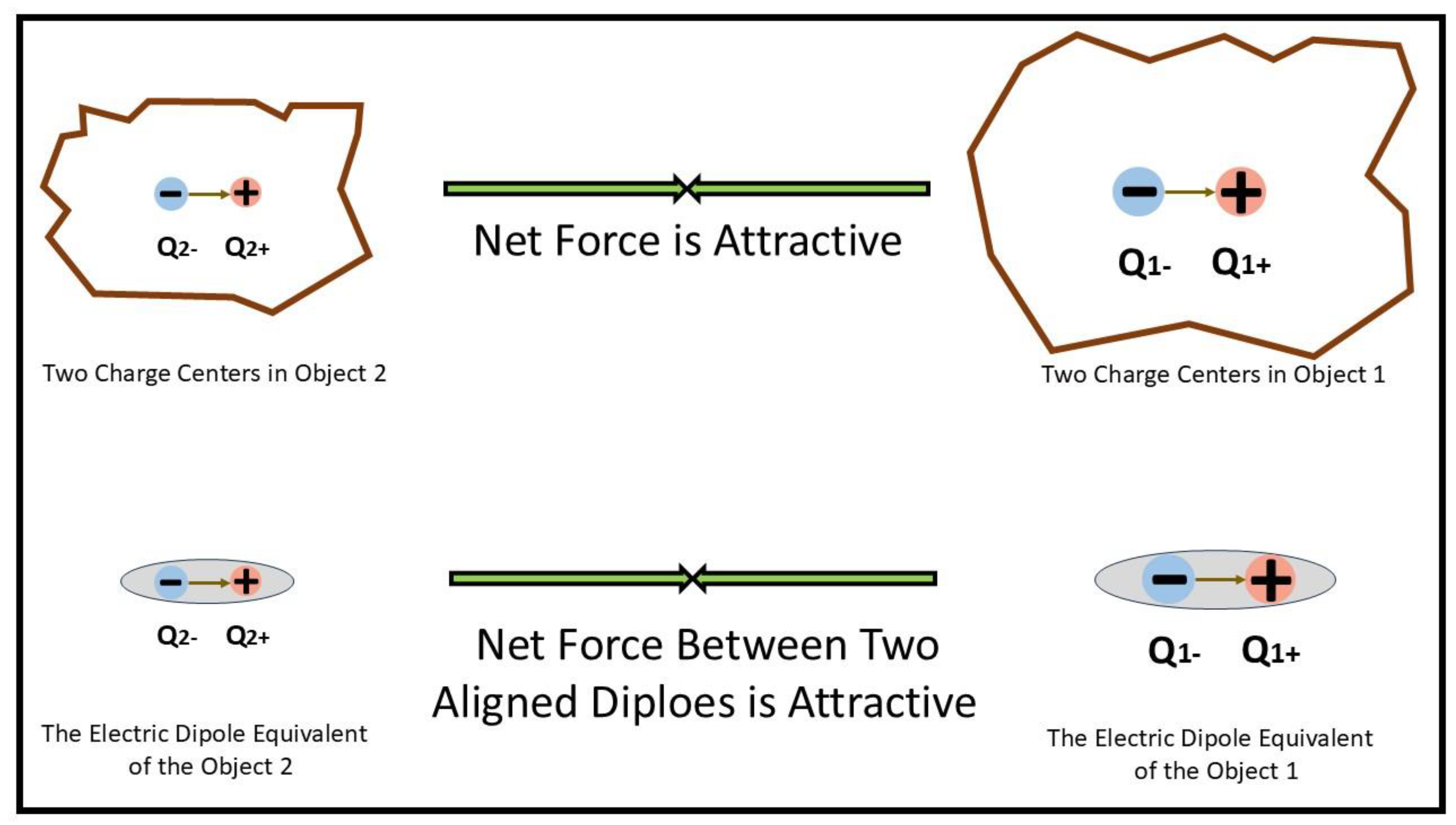
Therefore, any two objects can be regarded as two macroscopic electric dipoles. When these two macroscopic electric dipoles are aligned in the same direction along a straight line, they will attract each other, as shown in Figure 3.

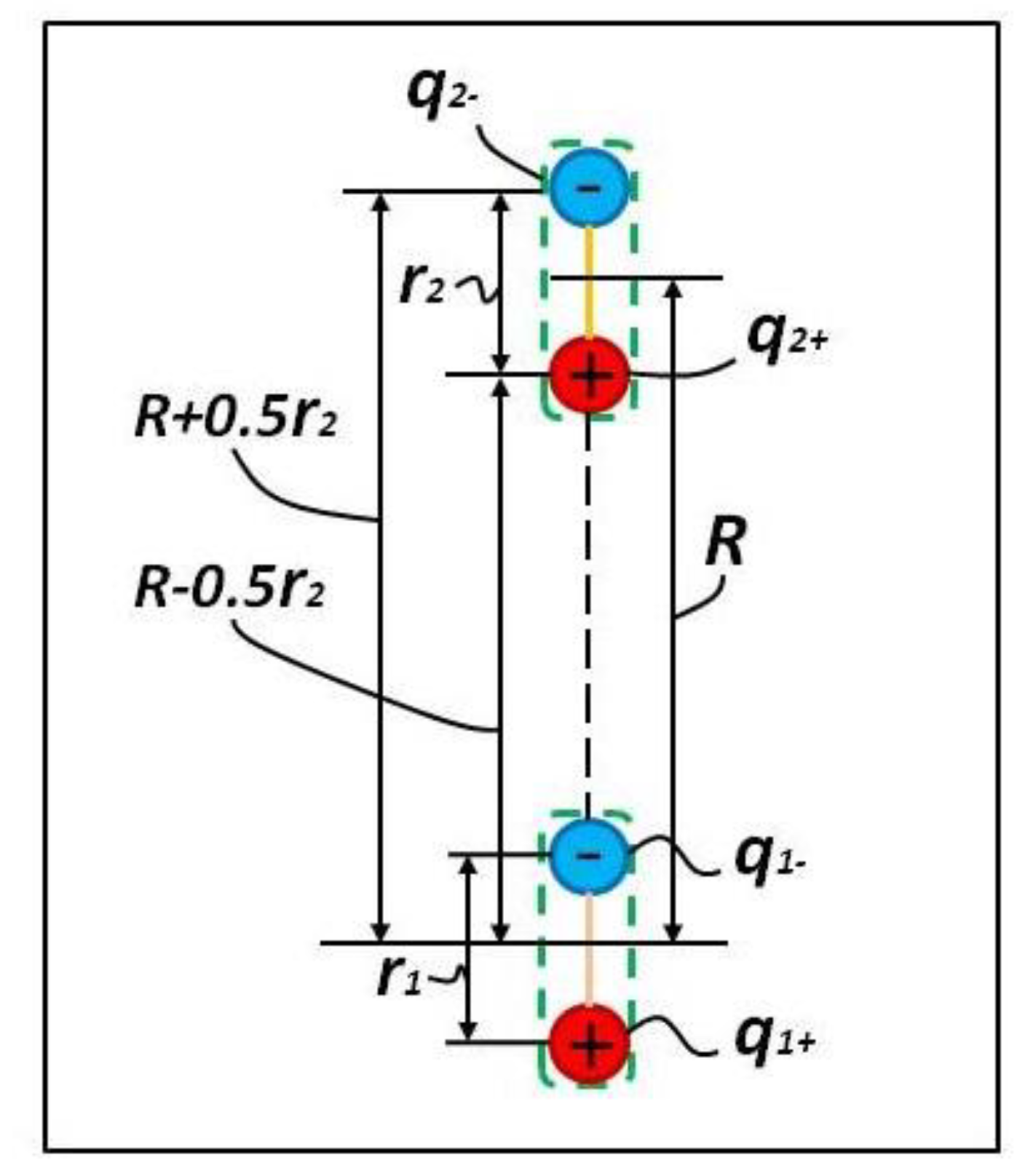
Below, the interaction force between two electric dipoles is calculated. First, considering the case when the directions of two dipole moments are the same. In Figure 4, the first dipole moment

{\vec{P}}_{1}

consists of positive pinot charge

q_{1 +}

and negative point charge

q_{1 -}

. The second dipole moment

{\vec{P}}_{2}

consists of positive pinot charge

q_{2 +}

and negative point charge

q_{2 -}

. The length of the first dipole moment

{\vec{P}}_{1}

is

r_{1}

. The length of the second dipole moment

{\vec{P}}_{2}

is

r_{2}

. The distance between the centers of two dipoles is R.

From Eq. (2), the first electric dipole will produce the electrical field

{\vec{E}}_{1}

at the distance R from its center

{\vec{E}}_{1} = \frac{1}{4 π ε_{0} R^{3}} [3 ({\vec{P}}_{1} ∙ \vec{R}) \vec{R} - {\vec{P}}_{1}] .

(6)

In the electrical field

{\vec{E}}_{1}

, the positive point charge

q_{2 +}

of the second dipole will feel a force

{\vec{F}}_{q 2 +}

as

{\vec{F}}_{q 2 +} = q_{2 +} {\vec{E}}_{1} = \frac{2 q_{2 +} {\vec{P}}_{1}}{4 π ε_{0} {(R - 0.5 r_{2})}^{3}}

(7)

The direction of force

{\vec{F}}_{q 2 +}

is along the direction of

\vec{R}

. The negative point charge

q_{2 -}

of the second dipole will feel a force

{\vec{F}}_{q 2 -}

as

{\vec{F}}_{q 2 -} = q_{2 -} {\vec{E}}_{1} = \frac{2 q_{2 -} {\vec{P}}_{1}}{4 π ε_{0} {(R + 0.5 r_{2})}^{3}} .

(8)

The direction of force

{\vec{F}}_{q 2 -}

is also along the direction of

\vec{R}

.

Because the absolute values of

q_{1 +}

and

q_{1 -}

are equal, and the absolute values of

q_{2 +}

and

q_{2 -}

are also equal, when

R ≫ r_{1}

and

{R ≫ r}_{2}

, the total force felt by the second dipole in the electric field

{\vec{E}}_{1}

is

{\vec{F}}_{D}

approximately

{\vec{F}}_{D} = \vec{F}_{q 2 +} + {\vec{F}}_{q 2 -} ≐ \frac{{6 r}_{1} r_{2}}{R^{2}} \frac{1}{4 π ε_{0}} \frac{{q_{1} q}_{2}}{R^{2}} \vec{R} .

(9)

In Eq. (9), if

\frac{\sqrt{6} r_{1} q_{1}}{R}

is replaced by

m_{1}

,

\frac{\sqrt{6} r_{2} q_{2}}{R}

is replaced by

m_{2}

，and

\frac{1}{4 π ε_{0}}

is replaced by a constant

G^{'}

, then Eq. (9) becomes

{\vec{F}}_{D} = G^{'} \frac{m_{1} m_{2}}{R^{2}} \vec{R} .

(10)

We can see that Eq. (10) is very similar to Newton’s gravitational law

{\vec{F}}_{G} = G \frac{{M_{1} M}_{2}}{R^{2}} \vec{R} .

(11)

Eqs. (9) and (10) show that the physical essence of the mysterious mass is the amount of electric charge. More strictly speaking, the mass is another expression of the amount of the electric charge multiplied by the length of the related electric dipole and divided by the distance between the two related dipoles.

Compare Newton’s law of the gravitational force

{\vec{F}}_{G}

with Coulomb’s law of the electric force

{\vec{F}}_{E}

{\vec{F}}_{E} = K \frac{q_{1} q_{2}}{R^{2}} \vec{R}

(12)

We can see that their expressions are very similar. Eqs. (10) and (11) express the attractive gravitational forces generated by two point-like objects with masses of

m_{1}

or

M_{1}

and

m_{2}

or

M_{2}

. Eq. (12) expresses the attractive electric force generated by two points electric charges of

q_{1}

and

q_{2}

.

G^{'}

or

G

is gravitational constant. K is Coulomb’s constant. Their numerical values depend on the system of the units used. If two charges in Eq. (12) are replaced by two masses in Eq. (10) or (11), then Eq. (12) becomes Eq. (10) or (11), and both

G^{'}

or

G

and K have the same numerical value and dimension. Thus, we profoundly see the physical rationality of the understanding that gravitational force is originated from the electric force.

The striking similarity between Eq. (10) or (11) and Eq. (12) strongly hints that the gravitational force is the electric force, because if the natures of two physical forces are different, their expressions should be significantly different. However, where else can we find such similarity between the expressions of two different physical forces?

When the directions of two dipole moments are opposite or perpendicular, the interaction forces between two dipoles become repulsive or deflective because both of the dipoles are pushed by repulsive electric fields, expressed by Eq. (3), or twisted by deflective electric fields, expressed by Eq. (5).

However, as explained above, in most cases, two interacting electric dipoles cannot push or twist each other for long. As soon as an electric dipole is affected by a deflective force, even if small, its dipole moment direction will rotate and eventually align with the direction of that force. The rotation of the electric dipole doesn’t require the rotation of the real physical body of the object. It only needs a change in the distribution of net electric charges, including free and induced net charges in the object. Such changes are easy, very fast and cannot be seen visibly. This explains why the gravitational force is always attractive. Thus, when considering the interaction force between two objects, because the directions of two electric dipoles are almost always the same, the interaction force, that is, the gravitational force between the two objects, can be expressed by Eq. (9) or (10) only. These two electric dipoles, equivalent to the two objects, will always attract each other, even when one rotates around the other, as shown in Figure 5.

When three objects interact with each other, the free and induced net charges in each object are redistributed in response to the electric fields generated by other two objects. If each object is simplified as an electric dipole, it will interact with the electric dipoles of the other two objects. Thus, the redistribution of charges in each object may be regarded as forming two electric dipoles. Each dipole in one object responds to an external dipole in one of the two other objects, leading to the analysis of interactions among six electric dipoles. When more objects are involved, the gravitational force analysis becomes more complex. However, the redistribution of net charges in each object may still be regarded as forming multiple electric dipoles, each responding to a dipole in each of the multiple other objects.

The dynamically self-calibrating process may apply to multiple electric dipoles, or even multiple groups of electric dipoles, causing them to mutually and continuously attract each other, whether they rotate around each other or not. The attractions between multiple electric dipoles, or even multiple groups of electric dipoles, may be understood from a different perspective too. This is because all of the charge distributions of the multiple electric dipoles or multiple groups of electric dipoles can form a larger combined charge distribution. As long as this larger combined charge distribution is non-uniform, it will still act as a synthetic electric dipole. Thus, any other electric dipole will be attracted to this synthetic electric dipole. The other electric dipole may be any individual electric dipole, including anyone within or outside the mentioned multiple electric dipoles or multiple groups of electric dipoles. Therefore, based on the introduced self-forming and dynamically self-calibrating electric dipole model, multiple electric dipoles, or even multiple groups of electric dipoles, can continuously attract each other.

Eq. (9) or (10) expresses the interactional electric force between two electric dipoles when the dipoles have the same direction. This electric force is the gravitational force between two objects. According to Eq. (9) or (10), the gravitational force has the following properties:

First, since the gravitational force is produced by net electric charges

q_{1}

and

q_{2}

, the gravitational field is actually the electric field.

Second, the strength of the gravitational force depends on the direction of the electric dipole, meaning that the gravitational force is essentially anisotropic. However, due to the aforementioned dynamically self-calibrating process, a constant and seemingly isotropic attraction can be maintained between two objects, whether they are rotate around each other or not. In other words, although at any given moment, the gravitational force is anisotropic, however, after successive and numerous micro self-calibrating with very fast speed, the overall performance of the gravitational force will appear as if it has an isotropic attraction capacity.

Third, replacing

\frac{\sqrt{6} r_{1} q_{1}}{R}

with

m_{1}

and replacing

\frac{\sqrt{6} r_{2} q_{2}}{R}

with

m_{2}

in Eqs. (9), because in most cases,

R ≫ r_{1}

and

R ≫ r_{2}

, so the magnitudes of

m_{1}

and

m_{2}

are much smaller than the magnitudes of

q_{1}

and

q_{2}

. This is why, although the gravitational force is the electric force, the strength of the gravitational force is much smaller than the strength of the electric force. Another reason for the gravitational force being much smaller than the electric force is that the attractive force is largely canceled out by the repulsive force, as mentioned above.

Fourth, the values of

r_{1}

,

r_{2}

,

q_{1}

and

q_{2}

in Eq. (9) are not fixed because they are determined by net charge distributions in two objects. Since variations of charge distributions in two objects can change the values of

r_{1}

,

r_{2}

,

q_{1}

and

q_{2}

, the gravitational force between two objects is not fixed even their so-called masses don’t change.

Fifth, while the strength of the electric field of an electric dipole is inversely proportional to the cube of the distance from the dipole (the terms in

l^{2}

and higher order terms are neglected), the strength of the gravitational force of an object, under certain conditions, may be closely inversely proportional to the square of the distance from the object. This is highly consistent with the results of precise measurements of the gravitational force via modern technology. In the following, quantitative calculation and detailed explanation will be provided.

Eq. (9) states that the gravitational force strength between two objects depends on their net electric charges, electric dipole moment lengths and their separate distance. Thus, the gravitational force between two objects appears to be an easily variable quantity. However, according to our usual understanding, the gravitational force is considered an invariant quantity, because their masses are assumed to be constant and independent of other bodies.

This understanding has limitations. The reason for this is that we typically observe the gravitational force between objects, or the weight of objects, just on the Earth’s surface or in near-Earth space. In this context, the net charge distribution within the object is mainly determined by the physical structure and states of all atoms and molecules within the object, as well as the influence of the Earth’s electric field on it. Since the change of overall strength of the Earth’s electric field acting on an object on the Earth’s surface is minimal usually, and the physical structure and states of all atoms and molecules within an object on the Earth’s surface also undergo no enough large changes, the so-called mass of an object on the Earth’s surface, or the weight of an object on the Earth’s surface, can be considered constant.

Change Rate of Gravitational Force

Newton’s law of the gravitational force states that the strength of the gravitational force is inversely proportional to the square of the distance from the object. This change rate was established by Newton based on the long-term observations of predecessors like Kepler, and has been confirmed by modern precise measurements. Therefore, any new theory of the gravitational force must conform to this quantitative characteristic. If a new theory can also explain its physical cause, the new theory would be of greater significance.

In the above descriptions, the introduced gravitational force expression Eq. (9) seems to say that the so-called mass

m_{1} = \frac{\sqrt{6} r_{1} q_{1}}{R}

or

m_{2} = \frac{\sqrt{6} r_{2} q_{2}}{R}

of an object changes inversely and linearly with the distance

R

from the object. Thus, the gravitational force strength described by Eq. (9) is inversely proportional to the fourth power of the distance

R

, which is clearly in contradiction with the inverse square law of the gravitational force, which is generally acknowledged.

In fact, this contradiction does not exist. The reason is that the values of

p_{1} = r_{1} q_{1}

and

p_{2} {= r}_{2} q_{2}

in Eq. (9), i.e., the numerical values of the electric dipole moments

{\vec{p}}_{1} = {\vec{r}}_{1} q_{1}

and

{\vec{p}}_{2} = {\vec{r}}_{2} q_{2}

are not fixed. They are determined by the non-uniform charge distribution within the two objects. When the distance

R

between the two objects changes, the internal non-uniform charge distributions in two objects will also change under the influence of each other’s electric field, causing changes in the values of

p_{1}

and

p_{2}

.

In the most ideal situation, if the values of

p_{1}

and

p_{2}

can change completely linearly and proportionally with

R

, then the so-called masses

m_{1}

and

m_{2}

would become fixed and do not change with distance

R

. In this case, the gravitational force strength derived from the dipole model would be able to change precisely inversely with the square of

R

, thus precisely matching Newton’s law.

Of course, this ideal situation cannot occur. However, investigation has found that under certain conditions, the values of

p_{1}

and

p_{2}

can change approximately synchronously with

R

, and when the conditions are ideal, the degree of approximation is very high.

In the universe, any independent object or substance system is composed of atoms and molecules, or electrons and ions with separated positive and negative charges. Within such an object or substance system, due to various macroscopic and microscopic reasons, the distribution of the electric charges is always non-uniform, i.e., there is an inherent original charge disorder in any independent object or substance system. When such an object or substance system is influenced by an external electric field, particularly a single external electric field, because the distances between the atoms and molecules, or electrons and ions within the object or substance system are generally very short, the strengths of the interaction electric fields among these atoms and molecules, or electrons and ions are very strong, making the strengths of these internal electric fields much larger than that of the external electric field. Thus, the main effect of the external electric field is not to excite or increase the internal disorder of the object or substance system, but rather to regularize the internal disorder of the object or substance system, that is, to regularize the internal non-uniform charge distribution of the object or substance system from more disorder to less disorder.

This physical mechanism may be further explained. In the universe, within a completely isolated object or substance system, due to completely absence of external constraints, its internal charge distribution is in a state of the most extreme disorder. Although the most extreme disorder does not necessarily result in a large electric dipole moment, the extremely disordered charge distribution is certainly highly sensitive to external electric fields. Therefore, the external electric field can more easily cause the isolated object or substance system to form a large electric dipole and induce large dipole moment value. The degree of independence of an object or substance system is determined by its distance from another object or substance system. The farther apart the two objects or substance systems are, the larger the original disorder of the charge distribution within them, and thus the greater their sensitivities to the external electric fields. Therefore, when the electric fields of these two objects or substance systems interact, the induced effects are stronger. As a result, the values of

p_{1}

and

p_{2}

of the two objects or substance systems not only change with variation of

R

, but the greater the distance

R

between them is, the greater the change rates of the values of

p_{1}

and

p_{2}

are.

Under this physical mechanism, for two mutually attracting objects, assuming their physical compositions, states, and environments are not significantly different (for example, both objects are in a solid state), quantitative calculations show that the values of

p_{1}

and

p_{2}

can indeed change approximately in direct proportion to the distance

R

. Under ideal physical conditions, the degree of approximation can be so high that it approaches or even exceeds the measurement error limits of modern technology. In other words, under ideal physical conditions, the so-called mass of an object, based on the dipole model, is highly approximately invariant, and the change rate of the gravitational force strength is highly approximated to be inversely proportional to the square of the distance

R

. Therefore, it can be said that Newton’s law of the gravitational force is only a highly approximate description of the change rate of the true gravitational force strength in nature under certain physical conditions. The quantitative proof of this conclusion is given below.

Since too many factors affect the interaction between two macroscopic objects, such as the kinds, quantities, spatial compositions, densities, and temperatures of the atoms and molecules contained in the two objects, the mathematical model can only be simplified, and so the calculation results are approximated. But, this does not affect the substantial conclusion.

The method of proof is first to demonstrate that the so-called mass of the object is constant; that is, the so-called mass of the object is not related to the distance R between two mutually interacting objects. If the so-called mass cannot remain completely unchanged, then the amount of change should be as small as possible, at least smaller than the measurement error limits of the modern technology. Therefore, our first step is to calculate the relative change rate

χ_{1}

or

χ_{2}

of the so-called mass

m_{1}

or

m_{2}

of one of the two objects after a distance change of

R = L

.

χ_{1}

or

χ_{2}

is defined below

χ_{1} = \frac{m_{1 L} - m_{11}}{m_{11}}

(13)

χ_{2} = \frac{m_{2 L} - m_{21}}{m_{21}}

(14)

In Eqs. (13) and (14),

m_{1 L}

or

m_{2 L}

is the so-called mass of object 1 or object 2 at the distance of

R = L

meters,

m_{11}

or

m_{21}

is the so-called mass of object 1 or object 2 at the distance of

R = 1

meter. Obviously, when the distance change

L

is larger and the relative change rate

χ_{1}

or

χ_{2}

is smaller, the so-called mass

m_{1}

or

m_{2}

changes less with distance

R

, so the value of mass

m_{1}

or

m_{2}

is closer to be constant. In other words, when the value of

L

is larger and the value of

χ_{1}

or

χ_{2}

is smaller, the change rate of the gravitational force strength of an object, predicted by the dipole model, is closer to be inversely proportional to the square of the distance

R

from that object.

Let the dipole moment of the object 1 be

{\vec{p}}_{1}

, then under the electric field

{\vec{E}}_{2}

, which is produced by the dipole moment of the object 2, the

{\vec{p}}_{1}

becomes

{\vec{p}}_{1} = {\vec{p}}_{1 \infty} + α {\vec{E}}_{2}

(15)

In Eq. (15),

{\vec{p}}_{1 \infty}

is the value of

{\vec{p}}_{1}

when the electric field

{\vec{E}}_{2} = 0

. Because only when the distance

R

between the two objects approaches infinity (

R \Rightarrow \infty

), the value of

{\vec{E}}_{2}

can be zero,

{\vec{p}}_{1 \infty}

is also the value of

{\vec{p}}_{1}

when the distance

R

approaches infinite.

α

(SI units:

C m^{2} / V

) is polarizability of the object 1. When

{\vec{p}}_{1}

and

{\vec{p}}_{2}

have the same direction and are aligned with a line, from Eqs. (3) and (15), we have

p_{1} = p_{1 \infty} + α E_{2} = p_{1 \infty} + \frac{α p_{2}}{2 π ε_{0} R^{3}}

(16)

If the physical characteristics and external environments of the two objects are not significantly different, then

p_{2} \approx γ p_{1}

，where

γ

is a dimensionless proportional constant. Thus, from Eq. (16), a self-consistent equation for calculating

p_{1}

can be obtained

p_{1} = p_{1 \infty} \frac{2 π ε_{0} R^{3}}{2 π ε_{0} R^{3} - α γ}

(17)

Since the so-called mass of object 1 is

m_{1} = \frac{\sqrt{6} p_{1}}{R}

, we have

m_{1} = \sqrt{6} p_{1 \infty} \frac{2 π ε_{0} R^{2}}{2 π ε_{0} R^{3} - α γ}

(18)

When

R^{3} = \frac{α γ}{2 π ε_{0}}

,

p_{1} = \infty

,

m_{1} = \infty

, Eqs. (17) and (18) encounter singularities. At singularities, the physical approximation on which the Eqs. (17) and (18) are based fails, resulting in the Eqs. (17) and (18) becoming invalid. Additionally, Eq. (18) shows when

R \Rightarrow \infty

，

m_{1} \Rightarrow 0

. This is because, based on the dipole model, both the gravitational mass and inertial mass of an object represent the strength of the attraction force experienced by another object (see above descriptions). If an object is located at infinity, the attraction force exerting on other object by that object is zero, and thus its so-called mass

m_{1}

becomes zero.

In Eq. (18), the polarizability

α

describes how the electric field generated by one macroscopic object affects the non-uniform charge distribution within another macroscopic object in manner and rate. First, the mutual influence between two objects depends on strengths of electric fields of two objects, which in turn depends on the distance between tow object, thus,

α

should be a function of

R

. Second, the redistribution speed of the non-uniform charge of the object also depends on distance

R

, because as previously explained, the farther the distance

R

between the two objects, the more sensitive the redistribution of the internal non-uniform charges to the external electric field in either of two objects, that is,

α

changes at different rates at different distances

R

, so

α

should be larger when the distance

R

is larger.

α

cannot be a linear function of the distance

R

.

Since there are too many factors that can affect the mutual influence between two macroscopic objects, to avoid overly complex calculations, we may temporarily assume

α

to be an exponential function of the distance

R

, that is,

α = {β R}^{N}

.

In equation

α = {β R}^{N}

,

β

(SI unit:

C / V m

) is a proportional constant.

N

is an integer or natural number and should be less than or equal to 3, because the electric field strength of an ideal electric dipole is inversely proportional to the cube of the distance

R

from the dipole (see Eq. (2)).

The value of

γ

depends mainly on the mass ratio of the two objects considered, so its minimum value is 1. When considering the attraction between a star and a planet within the solar system, such as the Earth and the Sun, since the mass of the Sun is

1.989 ⨯ 10^{30} k g

, and the mass of the Earth is

5.972 ⨯ 10^{24} k g

, the value of

γ

is

3.3 ⨯ 10^{5}

. When considering the attraction between the Earth and a measurement sample on the Earth’s surface for testing gravitational force change accuracy, since the Earth’s mass is

5.972 \times 10^{24}

kg, and the mass of a normal sample can’t exceed 1000kg, the value of γ is 5.97⨯

10^{21}

.

Then, simply considering three cases of

N = 1, 2, 3

. After substituting

α = β R

，

α = {β R}^{2}

and

α = β R^{3}

into Eq. (18), the calculation results show that when

α = {β R}^{2}

, the relative change rate of

m_{1}

with

R

is minimal, that is, in this case, the calculation results are closest to the observed physical reality.

When

α = {β R}^{2}

, Eq. (18) becomes

m_{1} = \sqrt{6} p_{1 \infty} \frac{2 π ε_{0}}{2 π ε_{0} R - β γ}

(19)

Estimating the polarizability value of a macroscopic object is difficult. Du to polarizability values of various atoms composing any object range from ~0.6 to ~60, for example, hydrogen (H) is 0.667, iron (Fe) is 8.4, sodium (Na) is 24.11, potassium (K) is 43.06, and cesium (Cs) is 59.6 (SI units:

C m^{2} / V

) [14], and any number of the polarizability value within the range of 0.6 to 60 does not substantially affect the calculation results, a typical value of

β = 16

is roughly assumed. After substituting this value and

ε_{0} = 8.854187818 ⨯ 10^{- 12} F / m

into Eq. (19), the relative change rates

χ_{1}

of the mass

m_{1}

of the object 1 with different distance changes

L

can be obtained, as shown in Table 1, Table 2 and Table 3. In Table 1,

γ = 1

, in Table 2,

γ = 10^{5}

, in Table 3,

γ = 10^{21}

, and the unit of distance

L

is km.

From Table 1, Table 2, and Table 3, it can be seen that when the mass ratio

γ

of the two objects is 1, the relative change rate

χ_{1}

of the mass

m_{1}

does not exceed one ten-thousandth (

χ_{1}

<

10^{- 4}

) within the range of distance change

L

from 1 meter to ten thousand kilometers (

L = 10^{4} k m

). When the mass ratio

γ

of the two objects is 100,000

(γ = 10^{5})

, the relative change rate

χ_{1}

of the mass

m_{1}

does not exceed one ten-thousandth (

χ_{1}

<

10^{- 4}

) within the range of distance change

L

from 1 meter to one billion kilometers (

L = 10^{9} k m

). When the mass ratio

γ

of the two objects is

10^{21}

(γ = 10^{21})

, the relative change rate

χ_{1}

of the mass

m_{1}

does not exceed one billionth (

χ_{1}

<

10^{- 9}

) within the range of distance change

L

from 1 meter to one hundred billion billion kilometers (

L = 10^{21} k m

).

If the maximum corresponding distance where the relative change rate

χ_{1}

of object mass

m_{1}

is less than a certain value, such as one ten-thousandth (

χ_{1}

<

10^{- 4}

), is defined as the “effective” distance

R_{E}

, where the inverse square law holds highly approximately, then from Table 1, Table 2, and Table 3, it can be seen that when

γ = 1

, the “effective” distance is ten thousand kilometers (

R_{E} = 10^{4} k m

); when

γ = 10^{5}

, the “effective” distance is one billion kilometers (

R_{E} = 10^{9} k m

); and when

γ = 10^{21}

, the “effective” distance is much longer than one hundred billion billion kilometers (

R_{E} ≫ 10^{21} k m

). Please note that, for the Sun, the relation of

p_{2} \approx γ p_{1}

should not no longer strictly hold, because the physical characteristics of the Sun differ significantly from other normal objects, including the Earth.

So far, precise measurements of the gravitational force change by humans were conducted on the Earth’s surface, with the highest precision being about

10^{- 9}

[15]. As mentioned above, the mass ratio γ between the Earth and a possible measurement sample is not greater than 5.97⨯

10^{21}

. Therefore, in the physical environment on the Earth’s surface, the accuracy of the change rate of the gravitational force established based on the dipole model is far higher than the measurement error limits of modern technology. Thus, the introduced gravitational theory is entirely consistent with the law of the gravitational force change obtained through long-term human observation and precise measurement. It should be noted that, so far, human observations and measurements of the gravitational force change rate were conducted on the Earth’s surface and in the Earth’s nearby space.

From Eq. (18), the gravitational force based on the dipole model has the following characteristics:

The change rate of gravitational force strength, which is inversely proportional to the square of the distance, or the so-called mass of an object being constant, depends on the distance between the interacting objects. This means there is an "effective" distance for these conditions to hold true.
The “effective” distance depends on the mass ratio of the two mutually attracting objects; the larger the mass ratio, the farther the “effective” distance;
The “effective” distance also depends on the polarizabilities of the two mutually attracting objects, and thus is related to the physical characteristics of the two objects, including composition, density, state, temperature, etc.
When $R \Rightarrow \frac{β γ}{2 π ε_{0}}$ , the so-called mass of the interaction body increases very fast and nonlinearly, and when $R ≫ \frac{β γ}{2 π ε_{0}}$ , the so-called mass of interaction body approaches zero. It may be a additional possible way to solve the mystery of dark matter and why celestial systems have finite sizes. First, because when the distance $R$ is great, the so-called mass of the interaction object increases rapidly, the celestial bodies on the far outskirts of a rotating galaxy will not be thrown out of the galaxy due to excessive rotational speed. Thus, although the required amounts of the masses of the celestial bodies on the far outskirts of a rotating galaxy are not found, the dark matter may still not be required. Second, objects that are too far from the center of the galactic system will have their so-called mass decrease rapidly, causing them to leave the galactic system. Therefore, any galactic system may only capture celestial bodies within a certain distance, resulting in a finite size. Certainly, there are other reasons contributing to the dark matter mystery. For example, celestial bodies located at the far outskirts of the rotating galaxies have distinctly different physical components, states, structures, pressures, temperatures, etc., that more easily lead to larger non-uniform charge distributions, resulting in larger electric dipole moment values. Further discussion is provided below.

The above description also explains the physical cause of the change rate of the gravitational force strength being inversely proportional to the square of the distance. The inverse square rate was initially obtained based on the observations and measurements, including the initial observations of planets orbiting stars, the later Cavendish experiment, and modern precise measurements. Previous discussions on the cause of the inverse square rate are only considered it to be due to the spherical divergence of a uniform field emanating from an ideal point in three-dimensional space, thus naturally so. But this paper gives real physical explanation for its cause.

Perhaps there is a question: why to chose

α = {β R}^{N}

and N=2 or N≈2, is it true in the real world? Now, apart from what has been explained above, the author cannot provide more reasons. However, one thing is certain: the calculated change rate of the gravitational force based on electric dipole model indeed align precisely with the physical facts.

Of course, if Eq. (19) is used to calculate the weight difference of the same object on the Earth’s surface and the Moon’s surface, it will be found that the calculation results have an error of nearly one order of magnitude. For Eq. (19), which is a very simplified formula established under many approximate assumptions, having only one order of magnitude error in celestial calculations on a cosmic scale should already be quite good, though Eq. (19) needs further optimization.

In summary, the electric dipole model should be a good model. It not only naturally explains various characteristics and related phenomena of the gravitational force but also accounts for numerous bizarre cosmic anomalies (see detailed descriptions below). Where else can we find a more reasonable, effective, and commonsensical theory of the gravitational force? It should be noted that humanity has been exploring this for hundreds of years.

It should be said a little more: according to the dipole model, the so-called mass of an object is no longer fixed. However, for the so-called mass of an object to undergo “sufficient and necessary” change, that is, for the overall external effect of the non-uniform charge distribution within an object to undergo “sufficient and necessary” change, the internal physical structure of the object and/or the external physical environment must undergo corresponding “sufficient and necessary” changes. This “sufficient and necessary” is measured from the broad perspective of the universe. The intense physical changes we generally observe on the Earth’s surface, such as temperature changes from tens to hundreds of degrees, density changes by several to dozens of times, and pressure changes from a few to dozens of atmospheres, do not reach the “sufficient and necessary” level on the “universal” scale. Therefore, in general natural environments, such as on or near the Earth’s surface, the so-called mass of an object is highly approximately constant.

Above-described properties make the gravitational force exhibit strange and mysterious behaviors, causing confusing phenomena observed in the universe. Some of these phenomena have puzzled humans for a long time. However, by using new understandings of the gravitational force, these confusing phenomena can be explained effectively. On the other hand, these phenomena may be regarded as indirect evidences of the correctness of this introduced new understanding.

Truths of the Confusing Phenomena

1. Formation of the Solar System and Milky Way Galaxy

Based on the electric dipole model, we can explain the centripetal attraction of the Earth to everything on its surface, as well as the formation of the Earth-Moon system, the Solar system, and the Milky Way galaxy effectively.

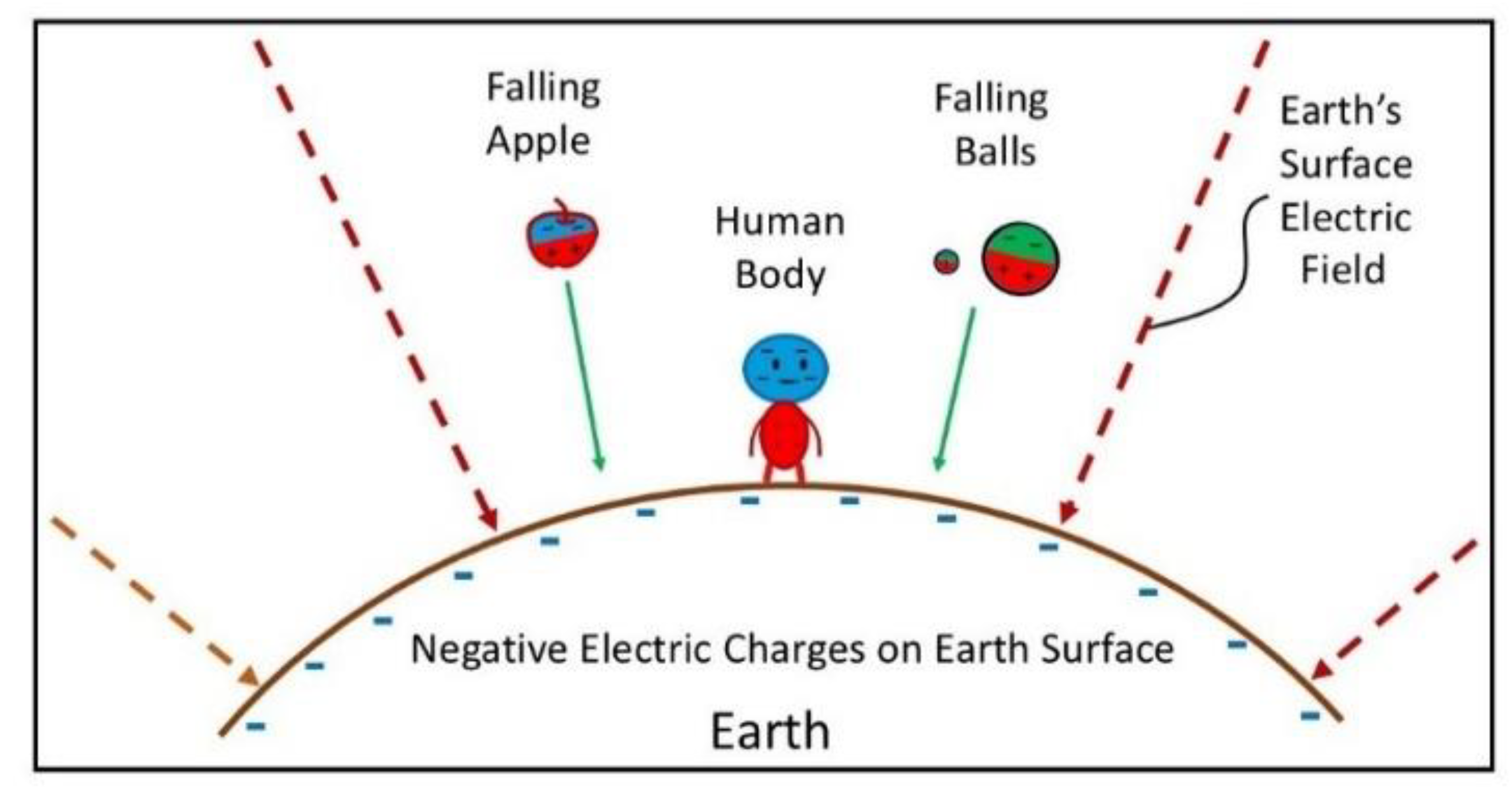
First, as indicated above, measurements have shown that the Earth’s surface is negatively charged, resulting in a downward electric field surrounding it, that is, a centripetal electric field is surrounding the Earth. The magnitude of this field is about 100 volts per meter at ground level. Thus, for any object on the Earth’s surface, whether it is initially electrically neutral or charged, the Earth’s electric field will induce a non-uniform distribution of free and induced net electric charges in that object, as shown in Figure 6.

Since the Earth’s surface field is toward the Earth’s center, in every object on the Earth’s surface, the free positive charges will be pushed toward the ground, and the free negative charges will be pulled away from the ground, causing the net positive and net negative charges to be distributed in the red and blue regions in the object, respectively. Additionally, the distribution center of all induced net positive charges will move close to the ground, while the distribution center of all induced net negative charges will move farther from the ground.

Please note that not all net negative charges within any object on the Earth's surface move to the blue region of the object, and not all net positive charges move to the red region within the object. This is because, in the most polar molecules, polarized atoms and molecules, although the positive and negative charges move under the Earth’s electric field, still remain within these atoms and molecules. Please refer to Figure 2. The blue and red regions in Figure 6 are a figurative representation.

Thus, in every object on the Earth’s surface, the non-uniform distribution of the free and induced net electric charges will make this object become an electric dipole with its moment directed toward the Earth’s center. Therefore, every object, as a small electric dipole, will be attracted by the Earth’s surface negative charges, that is, the Earth’s gravitational force. Such objects include everything on Earth’s surface, including every person standing on the ground, the two metal balls thrown from the Leaning Tower of Pisa by Galileo, and the apple that fell from the tree and hit Newton.

The Earth’s surface electric field is not uniform. The strength of the electric field on the Earth’s surface changes with the height of the measured location; that is, the farther a location is from the Earth’s surface, the weaker the electric field strength. Measurements have shown that the Earth’s atmospheric electric field strength decreases significantly with increasing height due to the conductivity of the upper atmosphere and the concentration of charge at lower altitudes [16]. Thus, although an ideal electric dipole has equal positive and negative charges, the Earth’s electric field strengths at the induced positive and negative charge centers of an object on the Earth’s surface are different. As a result, the Earth’s attractive and repulsive forces exerted on an object cannot be canceled, and the attractive force is larger than the repulsive force. The distances of the induced positive and negative charge centers of the object on the Earth’s surface from the Earth’s center are different as well. This difference also helps to increase the attraction between the Earth and the object on its surface, similar to the previously described attraction between charged amber and wool.

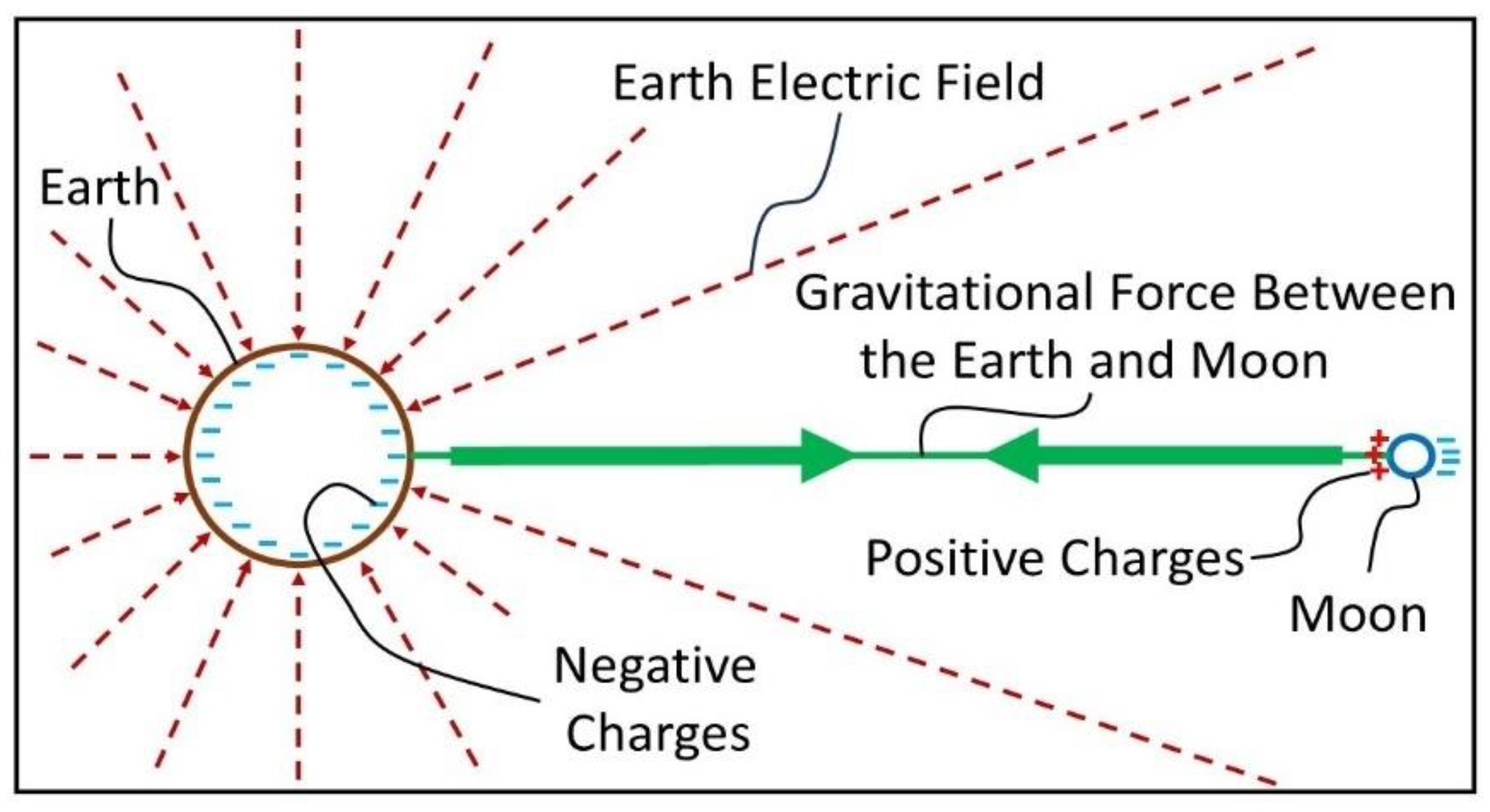
The Moon also has an electric field near its surface. The Moon’s electric field will interact with the Earth’s electric field too. Thus, an interaction electric force is generated between the Earth and the Moon, as shown in Figure 7.

The Moon’s nightside is negatively charged, while its dayside surface is positively charged [10]. Thus, the Moon becomes a typical electric dipole with its moment direction toward Earth. Although the Earth’s entire surface is negatively charged and has a surrounding and centripetal electric field, the Earth may still become a generalized electric dipole. First, the electric charge distribution in Earth’s interior is very complicated and continually changing; thus, there is almost no chance that the Earth’s electric charge distribution is exactly centrally symmetric. In addition, with the Moon’s non-stop rotation around the Earth, the Moon’s electric field will certainly cause Earth’s charge distribution to reform into new equilibrium state continually, that is, driving the net electric charges to flow continually. The Earth’s tides caused by the rotation of the moon are manifestation of the similar interaction. As a result, for example, the net negative charges on the surface of the Earth’s side facing the Moon can be appropriately more than the net negative charges on the surface of the Earth’s side away from the Moon. Due to the conservation of electric charge for the whole Earth, the net positive charges on the surface of the Earth’s side facing the Moon will be correspondingly less than the net positive charges on the surface of the Earth’s side away from the Moon. This will produce a generalized electric dipole in the Earth in response to the Moon’s electric dipole. Thus, even if all of the Earth’s surface is negatively charged, the overall charge distribution of the Earth may still form a generalized electric dipole in response to the Moon. In Figure 7, we can see that the direction of the Moon’s electric dipole moment aligns with the direction of the Earth’s surface electric field and should be the same as the moment direction of the Earth’s generalized electric dipole. Thus, an attractive electric force is generated between the Earth and the Moon, causing the Moon to rotate around the Earth with only its dayside facing the Earth permanently. Because the Earth only attracts the dayside of the Moon, observers on Earth never see the nightside of the Moon.

The peculiarity of the charge distribution on the surface of the Moon is likely caused by its internal electrical structure. However, the influence of the Earth’s electric field on the Moon cannot be ignored. The negative charges distributed on the Earth’s surface can push more negative charges of the Moon to move to the Moon’s far side.

Apart from the Earth, the Moon is affected by other celestial bodies, such as the Sun, Mars, Venus, Mercury, and so on. However, compared to the Earth’s electric field on the Moon, the electric fields of other celestial bodies on the Moon, including the Sun, are weak. Therefore, the Moon can rotate around the Earth, forming an Earth-Moon system.

The observations show that the Sun’s electromagnetic field is complex. It is mainly generated by the movements of charged particles in the Sun’s interior and is also influenced by the Sun’s rotation and temperature. The solar wind is a stream of charged particles released from the Sun’s outermost atmospheric layer, and influence the Earth and the Moon.

These observation results indicate that the charge distribution inside the Sun is extremely non-uniform. As mentioned above, this extremely non-uniform charge distribution is bound to turn the Sun into a massive macroscopic electric dipole or a massive macroscopic generalized electric dipole.

The electric dipole formed by the Sun interacts with the electric dipole formed by the Earth, affecting the electric charge distributions in both the Earth and the Sun. Naturally, the influence of the Earth on the Sun is much smaller than that of the Sun on the Earth, due to the Sun's significantly greater mass and higher temperature. Consequently, the interaction between the Earth and the Sun reaches an equilibrium state at every moment. Please note that when the electrical interaction force between these two dipoles becomes attractive, the equilibrium state is stable. Thus, the Sun and the Earth always attract each other, resulting in the Earth orbiting the Sun. The observed and recorded daily periodic variation curves of the Earth's surface space electric field strength provide clear evidence of the strong electric field interaction between the Earth and the Sun [17].

The author indicates that, within the Earth’s interior, the complex electric charge distribution can form two main separate electric dipoles to respond to the Sun and Moon simultaneously. This charge distribution can also change continually, accompanied by the rotation of the Moon around the Earth and the Earth around the Sun. In other words, the Earth is capable of attracting a variety of small objects attached to its surface in all directions, as well as two particularly large objects in two changing directions with attractive electric forces. It may be difficult to understand such a complicated situation, but due to the complexity of the charge distribution and the ease and speed of the charge distribution change, this is entirely possible. It is also one of the difficulties that have long plagued people in understanding nature of the gravitational force.

In this way, the Earth, as a very large generalized electric dipole, is attracted by the Sun which is a much larger electric dipole or generalized electric dipole. Thus, the Earth-Moon system, along with other planet-satellite systems like the Mars, the Venus and the Mercury systems, rotates around the Sun, forming the Solar System.

According to current knowledge, there are hundreds of billions of planetary systems, including our Solar system, in the Milky Way galaxy. These planetary systems are either the same as or different from our Solar system. Because these planetary systems are so far away, we know little about them. But one thing is for sure: based on obtained observation results through spectral analyses until now, these planetary systems all consist of the microscopic and subatomic particles same as those composing our Solar system. These particles include photons, electrons, protons, neutrons, various atoms, and various molecules. Since all of these microscopic and subatomic particles move, combine, and split depending on electric forces [18], and as explained above, the dynamically self-calibrating process can cause multiple electric dipoles, or even multiple groups of electric dipoles, to mutually and continuously attract each other, we can be fully confident that the gravitational force originating from the electric attractive force exists in these planetary systems and plays a fundamental role.

Therefore, apart from that the total Milky Way galaxy is formed based on electric forces, such inferences can be applied to systems with larger scales, such as the galaxy clusters (Local Group) and even whole universe.

2. Causes of Flat Galaxies and Filamentary Nebulae

So far, almost all observed celestial systems, including the Solar system, the Milky Way galaxy, and many other galaxies, have approximately flat spherical shapes. Why do these celestial systems have flat shapes, and how can we explain the formation of these shapes? Now we have the answers. These shapes are caused by the anisotropy of the gravitational field, as expressed by Eqs. (2), (3), (4), and (5). Because most celestial bodies can be regarded as electric dipoles or generalized electric dipoles, and the attractive force of the electric dipole is along the direction of the dipole moment, any two celestial bodies are attracted to each other along a line, or multiple celestial bodies are attracted to each other along a plane. When numerous celestial bodies are attracted to each other and to a stronger attractive center simultaneously, the numerous line-like or plane-like celestial body groups move toward the stronger attractive center along various paths. The various rotational lines and planes will feel anisotropic forces from nearby celestial body groups and the stronger attractive center, tending to form a common plane consisting of various rotational line-like and plane-like celestial body groups. Thus, the numerous celestial bodies will form an approximately flat spherical spatial distribution from their previous random spatial distribution. Of course, the rotation of the stronger attractive center and rotations of the numerous line-like or plane-like celestial body groups will help to form such an approximately flat spherical spatial distribution too. Please note that the previously mentioned seemingly isotropic attraction of the electric dipole, caused by a dynamically self-sustaining process, generally cannot help to form spherical celestial systems, as the gravitational force is not only anisotropic but also linear.

The Hubble Space Telescope has discovered the Filamentary Nebulae (also called as the Veil Nebulae or Cirrus Nebulae) [3]. These nebulae have immense sizes of more than 130 light-years at a distant location of about 2,400 light-years. This is one of the most astonishing discoveries in the universe recently. These nebulae have asymmetric and non-homogeneous structures, including filaments and loops. Remarkably, these structures challenge the consensus of the universe being homogeneous. However, these structures just prove the new understanding about the gravitational force, that is, the gravitational force is anisotropic. Under anisotropic gravitational fields, numerous celestial bodies, including gas, dust, planets, stars, galaxies, and galaxy clusters, are more likely to form asymmetric and non-homogeneous structures like filaments and loops of huge sizes.

3. Strange Trajectories of Some Meteors

Recent astronomical observations have found that the trajectories of some comets entering the solar system are very strange, completely defying Newton’s law of the gravitational force, such as ‘Oumuamua¹ to ‘Oumuamua³, and 3I/ATLAS, etc [19,20]. In fact, according to the gravitational theory based on the electric dipole model, the trajectories of these comets can be reasonably explained.

According to the electric dipole gravitation theory, the attraction or repulsion between celestial bodies is generated by the electric fields they carry. The electric field distribution of each celestial body is determined by its physical characteristics and properties. Generally, ordinary celestial bodies are spherical in shape, and the distribution of non-uniform charges inside has roughly spherical symmetry (but still can be an electric dipole). In this case, the electric dipole moment values and attraction characteristics of these celestial bodies are relatively conventional. When such celestial bodies interact, their trajectories can follow the traditional law of the gravitational force, including forming common circular or elliptical orbits with normal acceleration or deceleration, etc. Generally, the rotation of these celestial bodies does not significantly affect their trajectories.

However, some celestial bodies have special physical characteristics and properties, such as unusual shapes, significant differences in material composition, density, temperature, etc., in different inner regions. This can lead to abnormal charge distribution inside, resulting in an electric field strength distribution that is very different from that of ordinary celestial bodies. When such celestial bodies interact with others, their trajectories cannot be predicted using the traditional law of the gravitational force. Especially when these celestial bodies rotate, their interactions with other celestial bodies may be attractive at some times and repulsive at others. Therefore, their trajectories cannot be calculated according to traditional gravitational theory, including the abnormal rapid acceleration and deceleration.

The observed ‘Oumuamua¹, for instance, has a rod-like shape, and coupled with its rotational flight, this is clearly the reason for its very strange trajectory.

4. Misconception About Dark Matter

At present, dark matter is almost a basic consensus regarding the universe constitution. Otherwise, how can we explain why the faraway spiral arms of the giant galaxy and the galaxies on the outskirts of the galaxy cluster don not collapse when they move at much faster speeds? According to current gravity theory, the celestial bodies including fast-moving stars in the spiral arms and the galaxies on the galaxy cluster outskirts must have much greater masses to produce required attractive forces. Since the predicted matter cannot be found, a large quantity of unseen dark matter must exist in these spiral arms and cluster outskirts. However, despite many attempts, no any sign of dark matter has been found.

The new understanding of gravitational force can solve this difficult problem effectively too. According to the electric dipole model, the gravitational force between two objects can change with object dipole lengths

r_{1}

and

r_{2}

, and net electric charges

q_{1}

and

q_{2}

in the objects as expressed by Eq. (9). The values

r_{1}

,

r_{2}

,

q_{1}

and

q_{2}

are determined by charge distributions in the objects. Many factors, including substance state, temperature, pressure, density, conductivity, and mutual interactional electric field strength, can change the charge distributions in the objects and increase the object attractive forces. Thus, the celestial bodies in the galaxy spiral arms and the galaxies on the galaxy cluster outskirts can have much larger attractive forces than estimated without much greater so-called masses, allowing them to rotate at faster speeds without collapsing.

The calculations regarding the change rate of the so-called mass with distance using Eq. (19), as described above, also provide an additional possible way to solving the mystery of dark matter. When the distance

R

between the attracting bodies exceeds a certain threshold (larger than the “effective” distance), the so-called masses of the attracting objects increase rapidly. This results in additional mass beyond what is estimated, eliminating the need for dark matter.

There are no dark matters in the universe because they are not required to maintain the existence of the evolving universe.

5. Misconception About Dark Energy

Dark energy has almost become a basic consensus regarding the composition of the universe. This is because a special kind of unseen energy is required to explain why distant galaxies are moving away from us at increasing speeds.

First, we must determine if the universe is expanding at an accelerated pace, or even if our universe is expanding with a constant speed. This relates to the question of whether the “Big Bang Theory” is correct.

Many new discoveries made by the Hubble and James Webb telescopes have fundamentally shaken the foundation of the “Big Bang Theory.” For example, many overmature massive galactic structures appear during the so-called early stages of the universe. According to the “Big Bang Theory,” the universe has an age that began with an initial big explosion. Any celestial body and system, including star, galaxy, and galaxy cluster, should grow gradually and in line with the age of the universe. The fact that overmature massive galactic structures appear during the early stages of the universe has challenged the correctness of the “Big Bang Theory.”

The basic foundation of the “Big Bang Theory” is the wavelength “redshift” of the light coming from distant stars. Although the “Doppler Effect” can reduce the photon frequency and cause the light wavelength to redshift, there are also other possible reasons for light wavelength “redshift.”

The author has also proposed a new model of the photon [21]. Inspired by the observed phenomena of a photon appearing after electron-positron annihilation [22], and a photon splitting into an electron and a positron after a collision [23], the author has realized that the photon is composed of a pair of a positron and an electron, making the photon an extremely tiny electric dipole. In addition, since both the positron and electron have angular momentums, every photon is a rapidly rotating electric dipole [21].

In space, there are various electric fields since every celestial body has its own electric field. Compared with the rapid rotation of the photon electric field, most spatial electric fields in space are almost stationary. The directions of these relatively stationary electric fields are not the same as the directions of the photon’s rotation and straight-line motion. Thus, both the speeds of the photon’s rotation and straight-line motion will be reduced, especially the photon rotation.

When the photon’s rotation speed decreases, the photon frequency decreases too [21]. Therefore, the wavelength of the photon will increase, resulting in a light wavelength “redshift.” In addition, for most celestial bodies in space, their moving speeds are much slower than the speed of the photon’s straight-line motion. Thus, most of these celestial bodies will exert towing or resisting electric forces on the photon’s straight-line motion. Due to the “Doppler Effect,” this will also reduce the photon frequency and cause the light wavelength to redshift.

Because the photon’s net electric field is extremely weak and has a very short effective interaction distance, the influences of external electric fields in space on the photon are extremely small. Therefore, only after extremely long-distance traveling from faraway stars the photon wavelength “redshift” can be observed obviously.

The light wavelength “redshift” can be considered a photon fatigue phenomenon, resulting from decreases in the photon’s rotation and straight-line motion speeds. The light wavelength “redshift” cannot be used as key evidence to support the “Big Bang Theory.”

Because the expansion of the universe doesn’t exist, the accelerated expansion of the universe doesn’t either. Of course, perhaps some observations show signs of accelerated “redshift,” but they cannot be used as evidence of the accelerated expansion of the universe too.

In addition, celestial bodies, including planets, stars, galaxies, and galaxy clusters, move in different directions and at different speeds, including at accelerated or decelerated speeds. Thus, some of them move away from each other, while others move closer to each other. However, these diverse movements, including accelerated ones, differ from the concept of universal expansion or accelerated expansion.

Because the expansion and accelerated expansion of the universe don’t exist, the dark energy is not required to explain anything.

Furthermore, even if some parts of the universe are really expanding at accelerated rates, the new understanding of the gravitational force can explain such phenomena perfectly. The new understanding of the gravitational force has indicated that the strength of an object’s gravitational force may change and continually change with the change and continual change of electric charge distribution within the object. Thus, the gravitational force of an object could increase and continually increase more than the estimated. Therefore, even some regions of the universe are moving away from us at accelerated speeds, dark energy is still not required to explain such accelerated expansion. There is no dark energy in the universe.

6. Misconception About Universe’s Explosion

The "Big Bang Theory" is primarily based on the belief that the “redshift” of light from distant stars is caused by the "Doppler Effect”. As mentioned above, the light “redshift” can be considered a photon fatigue phenomenon, and so the light “redshift” cannot be used as key evidence to support the “Big Bang Theory.” Many newly observations have fundamentally broken the foundation of the “Big Bang Theory,” including the discovery of more and more superfast matured massive galactic structures appearing during the so-called early stages of the universe.

Indeed, the idea that a vast and real universe can be born out of nothing is hard to believe. After so many years, some physicists, despite their intelligence, could not explain how a vast and real universe was born from an infinitely small and infinitely empty point, there are still many people believing in this theory.

The universe, in fact, has no so-called age, meaning it has no start and no end. Otherwise, what existed before its start, and what will exist after its end? Similarly, the universe has no boundary. Otherwise, what exists outside the universe’s boundary? Even if what outside the universe boundary is true vacuum, the vacuum is still a part of the universe. The universe being infinite in space and time is indeed difficult to accept, but it is the easiest explanation that can be understood.

Saying that the universe has no age doesn’t mean that the various parts of the universe don’t evolve. Under gravitational force and repulsive forces caused by diverse reasons such as extremely high density, pressure and temperature, these various parts of the universe may evolve in different ways and at different rates, including repeated explosions and reunions. Therefore, finding some superfast matured massive galactic structures in somewhere of the universe and some super-slow growing massive galactic structures, including early-stage stars, elsewhere in the universe is normal.

7. Misconception About General Relativity

People may have begun to believe in General Relativity due to its successful prediction of the bending of light as it passes near a celestial body with a large mass. However, the bending of light might also be explained more naturally in another way.

As explained above, two famous observations have hint that the photon is a tiny electric dipole with a definite electric field but with a very short effect distance [21]. Although the photon’s electric field can be detected just within an extremely small range around it, and so many people regard the photon as an electrically neutral subatomic particle, when the photon passes through a massive celestial body, such as the Sun, the non-uniform electric field of that celestial body will still attract the photon and bend its path, causing light bending. Note that the electric field of almost any celestial body is non-uniform, so even if the photon has rotation, it may still be effectively attracted by a celestial body with great mass. Therefore, the light bending is not caused by “space-time curvature”.

The fact of light bending proves that the photon’s speed can change at least in the tangent direction of its straight-line motion. If the photon’s speed can change in the tangent direction of its straight-line motion, then if a celestial body with huge mass is located in the normal direction of the photon’s straight-line motion, such as a massive black hole, the photon’s speed along the normal direction should be changed too.

The constancy of light speed is a fundamental postulate of special relativity. It is extended and incorporated by general relativity. In this way, the bending of light and the constant speed of light are contradictory, meaning that special relativity and general relativity cannot justify themselves.

Some other phenomena, such as Mercury’s anomalous perihelion, the Shapiro time delay of signals near the Sun, and the gravitational redshift of clocks, are also believed to match general relativity. However, the reasons for the occurrence of an event can be explained in different ways.

Several seemingly reasonable explanations of some physical phenomena cannot be used as evidence that general relativity is correct. Due to length constraint for this paper, it is not possible to explain all these effects based on the introduced electric dipole model here. The author will explain these phenomena at suitable times later and believes that these phenomena can be explained successfully.

8. Compatibility of the Gravitational Force Theory and the Quantum Mechanics

Because the gravitational field is the electric field, the gravitational force can be unified with the electromagnetic force completely. Furthermore, if the electric field can be well described by quantum mechanics, the gravitational field can be described by quantum mechanics as well. Therefore, the new theory of the gravitational force is fully compatible with the quantum mechanics. In addition, the satisfying unification of the gravitational and electromagnetic forces opens a key and hopeful door for the ultimate unification of the four fundamental forces of nature [18].

More Discussions

An important practical application of the electric dipole model of the gravitational force is the possibility of using electric field to change object’s gravitational force, commonly known as anti-gravity, which has been desired for a long time. In fact, the influence of electric field on the weight of object has been observed before, such as the Biefeld-Brown effect [24]. The Biefeld-Brown effect is an electrokinetic phenomenon where a force is generated on an asymmetric capacitor when subjected to a high voltage. This force can push the capacitor towards the thinner electrode.

However, because people have not been able to correctly understand the origin and nature of the gravitational force, the Biefeld-Brown effect was mistakenly believed to be caused by “ion wind” [24]. Furthermore, due to the lack of correct and profound understanding of the gravitational force, technical research on using electric field to change gravity has not been on the right path until now, which seriously hindering development of such technology and preventing its practical applications.

It must be emphasized that since the force between any two electric dipoles always tends to become mutually attractive, this will certainly pose serious difficulties for anti-gravity research, which must be overcome through appropriate technical means. However, there is no doubt that the correct and profound understanding of the gravitational force is beneficial to the progress of anti-gravity research and applications.

Conclusions

This paper introduces the origin of the gravitational force, that is, the gravitational force actually originates from the electric force. Due to unavoidable non-uniform charge distribution within objects, almost any object is an electric dipole or a generalized electric dipole. Thus, any two objects will interact each other and can become attracting each other quickly, which is the true origin of the gravitational force.

The theoretical expression for the gravitational force is given, and the special properties of the gravitational force are described and explained, including the change rate of the strength of the gravitational force which closely follows the inverse square law of the distance under certain condition. This new understanding can effectively solve and explain difficult problems and confusing phenomena, such as flat galaxy, filamentary nebulae, strange trajectories of some comets, formations of the Solar system and Milky Way galaxy, dark matter, dark energy, superfast matured galaxy, slow growing star, Big Band theory, and so on. Based on this new understanding, the gravitational force can naturally unify with the electromagnetic force, and opening a hopeful door for the ultimate unification of the four fundamental forces of nature.

The explained phenomena may be regarded as indirect proofs of this new understanding. The author is confident in this theory and welcomes discussions on it.

Acknowledgments

The author acknowledges Joyce Liu at the University of Rochester School of Medicine and Dentistry for useful discussion and help in writing this article.

Disclosure: This paper is written partially based on the specifications recorded in the following patent applications: 1. Canada patent application titled “Methods of Changing Gravitational Force and Producing Electric Current”, which was filed on August 8, 2024 (Project Publication Date: 02/08/2026) with application number: 3,251,371; 2. USA patent application titled “Methods of Changing Gravitational Force and Producing Electric Current”, which was filed on August 9, 2024 (Project Publication Date: 02/12/2026) with application number: 18/799,600. The author declares no competing interests in this work.

Previous Preprint Versions of This Work

Version 1. Shangqing Liu, (25 December 2024), Origin of the Gravitational Force, www.preprints.org, doi: 10.20944/preprints202412.2082.v1; Version 2. Shangqing Liu, (13 January 2025), Origin of the Gravitational Force, www.preprints.org, doi: 10.20944/preprints202412.2082.v2; Version 3. Shangqing Liu, (25 March 2025), Origin of the Gravitational Force, www.preprints.org, doi: 10.20944/preprints202412.2082.v3; Version 4. Shangqing Liu, (31 March 2025), Origin of the Gravitational Force, www.preprints.org, doi: 10.20944/preprints202412.2082.v4; Version 5. Shangqing Liu, (11 August 2025), Origin of the Gravitational Force–Model of Self-Forming Electric Dipoles with Dynamically Self-Calibrating Constant Mutual Attraction, www.preprints.org, doi: 10.20944/preprints202412.2082.v5. 6. Shangqing Liu, (2 October 2025), Origin of the Gravitational Force–Model of Self-Forming Electric Dipoles with Dynamically Self-Calibrating Constant Mutual Attraction, www.preprints.org, doi: 10.20944/preprints202412.2082.v6.

References

Rubin, V. C, Ford, W.K. Jr. (1970), Rotation of the Andromeda nebula from a spectroscopic survey of emission regions. The Astrophysical Journal. 159, 379-403. doi.org/10.1086/150317. S2CID 122756867.
Frieman, J. A, Turner, M. S, Huterer, D., (2008), Dark Energy and the Accelerating Universe. Annual Review of Astronomy and Astrophysics. 46 (1), 385-432. [CrossRef]
King, B. , (2018), Explore the Veil Nebula. Sky & Telescope. Cygnus Loop. Encyclopaedia Britannica. https://www.britannica.com/place/Cygnus-Loop.
Noble, F.W. , (2023), Surprising and Unexpected Discoveries the James Webb Space Telescope Will Likely Make: Based Upon Our Research. Applied Physics Research. 15 (1). doi.org/10.5539/apr.v15n1p115.
Einstein, A., (1916), Die Grundlage der allgemeinen Relativitätstheorie. Annalen der Physik. 49 (7), 769–822. doi:10.1002/andp.19163540702; (2022), Gravity Probe B. Testing Einstein’s Universe. Special & General Relativity Questions and Answers. [CrossRef]
Wu, S. L, (2014), Brief history for the search and discovery of the Higgs particle - A personal perspective. International Journal of Modern Physics A. 29 (27), 1430062. doi.org/10.1142/S0217751X14300622.
Young, H. D, (2016), Freedman, R.A, Ford, A.L. 2016, University Physics with Modern Physics, 14th edition, pp. 684-690. Pearson Education Inc., USA.
Lanzerotii, L. J, Chave, A.D, (1993), Large-Scale Electric Field Measurements on the Earth’s Surface: A Review. Journal of Geophysical Research. 98 (El2): 23525-23534.
Bates, D.R. , (1972), Physic of the upper atmosphere, Ed. Ratcliffe, J.A., 3rd printing, Academic Press, New York, p.421. doi.org/10.1007/978-3-642-27401-5.
Masaki, N. , et al., (2022), An event study on broadband electric field noises and electron distributions in the lunar wake boundary. Earth, Planets and Space, 74:9.
Lockwood, M., Stamper, R., Wild, M. N., (1999), A Doubling of the Sun’s Coronal Magnetic Field during the Last 100 Years. Nature. 399 (6735): 437–439. [CrossRef]
Griffiths, D.J. , (2012), Introduction to Electrodynamics, pp.158-160. Addison-Wesley, New York, USA.
Laud, B.B. , (1987). Electromagnetics (2nd ed.). New Age International, New York, p. 25. ISBN 978-0-85226-499-7.
W. M. Haynes, Editor-in-Chief, Atomic and Molecular Polarizabilities in Section 10: Atomic, Molecular, and Optical Ph, (pp. 10.188-10.189), Handbook of Chemistry and Physics, 75th ed. CRC Press, Inc. 2014.
Mohr, Peter J., Taylor, Barry N., Newell, David B., (13 November 2012), CODATA recommended values of the fundamental physical constants: 2010, Rev. Mod. Phys., 84 (4): 1527–1605. [CrossRef]
Chalmers, J. A. , (1967), Chapter 9-1: The electric potential gradient of the atmosphere, in Atmospheric Electricity, Pergamon Press, London.
Harrison, R. Giles, The Carnegie Curve, (2013), Surveys in Geophysics, V34, pp. 209–232. [CrossRef]
Shangqing Liu, (January 2025), Origins and Unification of the Four Fundamental Forces of Nature. [CrossRef]
Bergner, Jennifer B., Seligman, Darryl Z., (2023), Acceleration of 1I/’Oumuamua from radiolytically produced H2 in H2O ice, Nature, V615, pp. 610–613 (2023). [CrossRef]
Taylor, Aster; Seligman, Darryl Z., (10 July 2025), The Kinematic Age of 3I/ATLAS and its Implications for Early Planet Formation, The Astrophysical Journal, 990 (1): L14. [CrossRef]
Shangqing Liu, Origin of Light. Preprints.org. 18 October (2024). [CrossRef]
L. Sodickson, W. L. Sodickson, W. Bowman, J. Stephenson, R. Weinstein, 1961, Single-Quantum Annihilation of Positrons, Physical Review, 124 (6): 1851-1861. Bibcode:1961PhRv..124.1851S. [CrossRef]
J.H. Hubbell, June 2006. Electron positron pair production by photons: A historical overview. Radiation Physics and Chemistry. 75 (6): 614–623. [CrossRef]
Bahder, T., Fazi, C., (June 2003), Force on an Asymmetric Capacitor. U.S. Army Research Laboratory.

Figure 1. The positively “charged” amber picks up “uncharged” wool. The induced net positive and net negative charges are distributed in the red and blue regions in wool, respectively.

Figure 2. The electric interaction force between two objects with non-uniform charge distributions. The total net positive charges and total net negative charges in each object are regarded as concentrated in their charge distribution centers, represented by orange and blue circles with charge amounts

q_{1 +}

,

q_{1 -}

,

q_{2 +}

and

q_{2 -}

, respectively.

Figure 2. The electric interaction force between two objects with non-uniform charge distributions. The total net positive charges and total net negative charges in each object are regarded as concentrated in their charge distribution centers, represented by orange and blue circles with charge amounts

q_{1 +}

,

q_{1 -}

,

q_{2 +}

and

q_{2 -}

, respectively.

Figure 3. Two objects that attract each other, like two macroscopic electric dipoles attracting each other.

Figure 4. Interaction forces between two dipoles when dipole moment directions are the same.

Figure 5. The two electric dipoles, equivalent to the two objects, attract each other when one rotates around the other.

Figure 6. Under the Earth’s surface electric field, every object on the Earth’s surface is induced to become an electric dipole. Thus, every object on the Earth’s surface is attracted by the Earth’s electric force, that is, the Earth’s gravitational force.

Figure 7. Figure 7. The Earth’s surface is negatively charged, and the Moon’s dayside surface is positively charged. Thus, an attractive electric force between the Earth and the Moon is generated, which is the origin of the gravitational force between the Earth and the Moon.

Table 1. Relative Change Rate

χ_{1}

of Object So-called Mass with Distance Change

L

（

β = 16

，

γ = 1

）.

Table 1. Relative Change Rate

χ_{1}

of Object So-called Mass with Distance Change

L

（

β = 16

，

γ = 1

）.

L (km)	1.00E-03	1.00E-02	1.00E-01	1.00E+00	1.00E+01	1.00E+02	1.00E+03	1.00E+04
$β$	16	16	16	16	16	16	16	16
$γ$	1	1	1	1	1	1	1	1
$χ_{1}$		3.13E-11	3.44E-10	3.47E-09	3.48E-08	3.48E-07	3.48E-06	3.48E-05
L (km)	1.00E+05	1.00E+06	1.00E+07	1.00E+08	1.00E+09	1.00E+10	1.00E+11	1.00E+12
$β$	16	16	16	16	16	16	16	16
$γ$	1	1	1	1	1	1	1	1
$χ_{1}$	3.48E-04	3.49E-03	3.59E-02	5.15E-01	9.16E-01	2.55E+00	3.39E+01	3.47E+02

Table 2. Relative Change Rate

χ_{1}

of Object So-called Mass with Distance Change

L

（

β = 16

，

γ = 10^{21}

）.

Table 2. Relative Change Rate

χ_{1}

of Object So-called Mass with Distance Change

L

（

β = 16

，

γ = 10^{21}

）.

L (km)	1.00E-03	1.00E-02	1.00E-01	1.00E+00	1.00E+01	1.00E+02	1.00E+03	1.00E+04
$β$	16	16	16	16	16	16	16	16
$γ$	1.00E+05	1.00E+05	1.00E+05	1.00E+05	1.00E+05	1.00E+05	1.00E+05	1.00E+05
$χ_{1}$		2.89E-16	3.47E-15	3.49E-14	3.48E-13	3.48E-12	3.48E-11	3.48E-10
L (km)	1.00E+05	1.00E+06	1.00E+07	1.00E+08	1.00E+09	1.00E+10	1.00E+11	1.00E+12
$β$	16	16	16	16	16	16	16	16
$γ$	1.00E+05	1.00E+05	1.00E+05	1.00E+05	1.00E+05	1.00E+05	1.00E+05	1.00E+05
$χ_{1}$	3.48E-09	3.48E-08	3.48E-07	3.48E-06	3.48E-05	3.48E-04	3.49E-03	3.59E-02

Table 3. Relative Change Rate

χ_{1}

of Object So-called Mass with Distance Change

L

（

β = 16

，

γ = 10^{5}

）.

Table 3. Relative Change Rate

χ_{1}

of Object So-called Mass with Distance Change

L

（

β = 16

，

γ = 10^{5}

）.

L (km)	1.00E+06	1.00E+07	1.00E+08	1.00E+09	1.00E+10	1.00E+11	1.00E+12	1.00E+13
$β$	16	16	16	16	16	16	16	16
$γ$	1.00E+21	1.00E+21	1.00E+21	1.00E+21	1.00E+21	1.00E+21	1.00E+21	1.00E+21
$χ_{1}$		0.00E+00	0.00E+00	0.00E+00	0.00E+00	0.00E+00	0.00E+00	0.00E+00
L (km)	1.00E+14	1.00E+15	1.00E+16	1.00E+17	1.00E+18	1.00E+19	1.00E+20	1.00E+21
$β$	16	16	16	16	16	16	16	16
$γ$	1.00E+21	1.00E+21	1.00E+21	1.00E+21	1.00E+21	1.00E+21	1.00E+21	1.00E+21
$χ_{1}$	3.21E-16	3.53E-15	3.47E-14	3.48E-13	3.48E-12	3.48E-11	3.48E-10	3.48E-09

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Origin of Gravitational Force — Model of Self-Forming Electric Dipoles with Dynamically Self-Calibrating Constant Mutual Attraction

Abstract

Keywords:

Subject:

1. Formation of the Solar System and Milky Way Galaxy

2. Causes of Flat Galaxies and Filamentary Nebulae

3. Strange Trajectories of Some Meteors

4. Misconception About Dark Matter

5. Misconception About Dark Energy

6. Misconception About Universe’s Explosion

7. Misconception About General Relativity

8. Compatibility of the Gravitational Force Theory and the Quantum Mechanics

References

MDPI Initiatives

Important Links

Subscribe