Akash Convolution Distribution with Applications

1. Introduction

A widely used distribution is the Lindley model (see Lindley [1]), we say that a random variable X has a Lindley distribution (L) if its probability density function (pdf) is given by

$$f_X(x;\theta )={\displaystyle \frac{{\theta }^2}{\theta +1}}(1+x)exp(-\theta x),x>0,$$

(1)

where $\theta >0$ is a shape parameter. We denote this by $X\sim L\left(\theta \right)$. The cumulative distribution function (cdf) corresponding to (1) is

$$F_X(x;\theta )=1-\left[1+{\displaystyle \frac{\theta x}{\theta +1}}\right]exp(-\theta x),x>0.$$

(2)

The L distribution has been used in various settings such as engineering, demography, reliability, and medicine, among others. Some researchers who have carried out these studies are: Hussain [2], Ghitany et al. [3], Zakerzadeh and Dolati [4], Gómez-Déniz and Calderin-Ojeda [5], Krishna and Kumar [6], Bakouch et al. [7], Shanker et al. [8], Ghitany et al. [9], Al-Mutairi et al. [10], Oluyede and Yang [11], Shanker et al. [12] and Abouammoh et al. [13], among others.

Shanker [14] introduced the Akash distribution and applied it to real lifetime data sets from medical science and engineering. Thus we say that a random variable Y has an Akash distribution (AK) with shape parameter $\theta$ if its pdf is given by

$$f_Y(y;\theta )={\displaystyle \frac{{\theta }^3}{({\theta }^2+2)}}(1+y^2)exp(-\theta y),y>0,$$

(3)

where $\theta >0$ is a shape parameter, and it is denoted by $Y\sim AK\left(\theta \right)$.

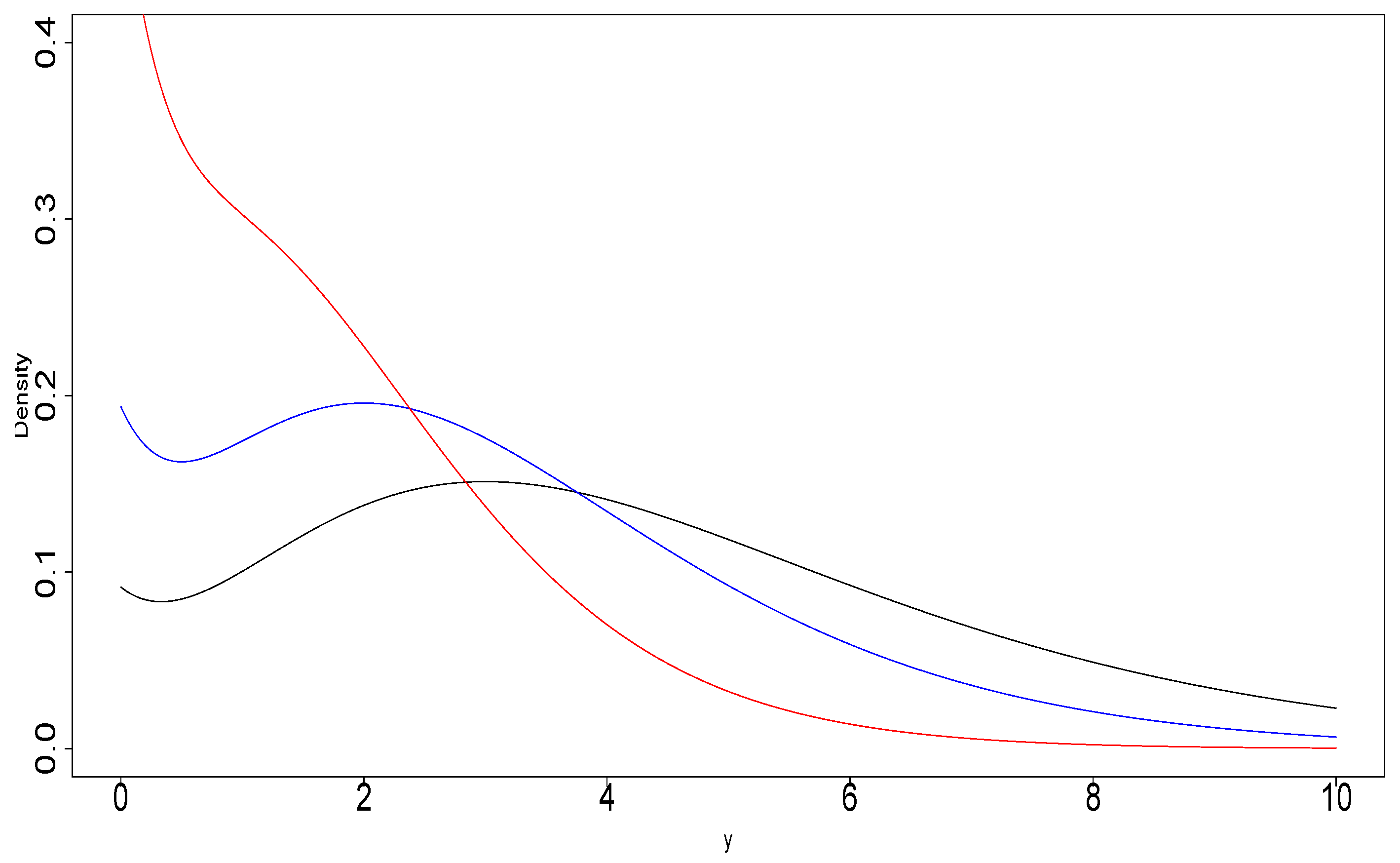
In Figure 1, we show the pdf of the $AK$ distribution for several values of $\theta$.

Some properties of this pdf are:

a)

The cdf of Y is

$$F_Y(y;\theta )=1-\left[1+{\displaystyle \frac{\theta y(\theta y+2)}{{\theta }^2+2}}\right]exp(-\theta y),y>0.$$

(4)

b)

For $r=1,2,3,\dots ,$ the r-th moment of Y is

$${\displaystyle \mathbb{E}\left(Y^r\right)=\frac{r!\left[{\theta }^2+(r+1)(r+2)\right]}{{\theta }^r({\theta }^2+2)}.}$$

(5)

c)

The moment generating function ($M_Y\left(t\right)$) is given by

$$M_Y\left(t\right)=\mathbb{E}\left(exp\left(tY\right)\right)={\displaystyle \frac{{\theta }^3}{{\theta }^2+2}}\left[{\displaystyle \frac{{(\theta -t)}^2+2}{{(\theta -t)}^3}}\right],t<\theta$$

(6)

Extensions $AK$ distribution are given by Shanker and Shukla [15], Shanker and Shukla [16] and Gómez et al. [17], among others.

In this article, we consider two independent $AK$ random variables with the same parameter and study their convolution. We show that the convolution distribution has a closed form and several interesting properties. Applications show that it can be an alternative to the $AK$ and L distributions.

The paper develops as follows: In Section 2, we furnish the $AKC$ distribution and its properties. In Section 3, we perform inference by the methods of moments and maximum likelihood; the Fisher information is obtained, and a simulation study is also carried out. In Section 4, applications are made to two real data sets and compared with the $AK$ and L distributions. In Section 5, we provide some conclusions.

2. AKC Distribution

In this section we introduce the density function properties of the $AKC$ distribution.

2.1. Density Function

Definition 1.

We say that a random variable Z has a $AKC$ distribution with shape parameter θ, $Z\sim AKC\left(\theta \right)$, if it has the following pdf:

$$f_Z(z;\theta )={\displaystyle \frac{{\theta }^{6}z}{30{({\theta }^2+2)}^2}}(30+20z^2+z^4)exp(-\theta z),z>0,$$

(7)

where $\theta >0$.

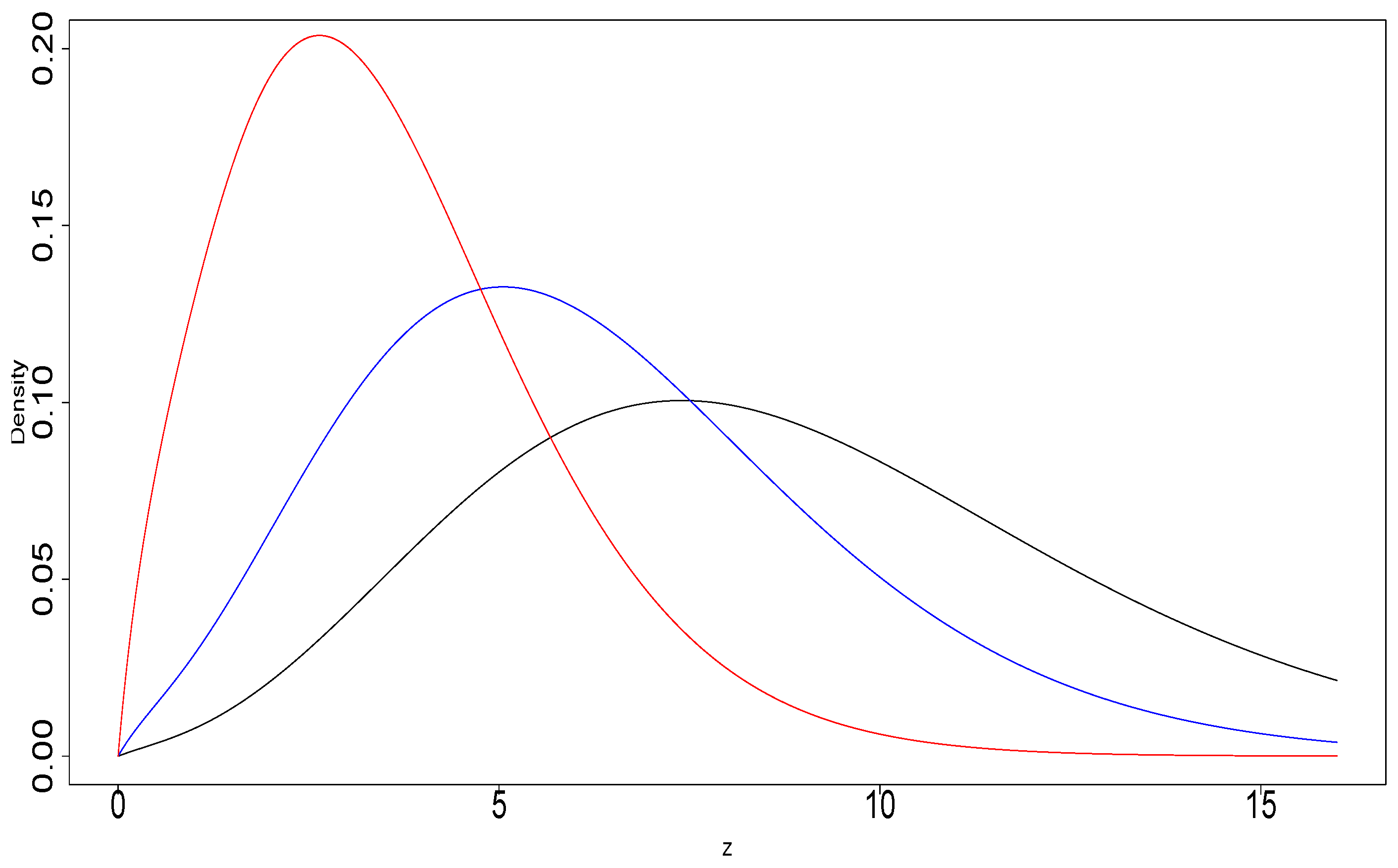
In Figure 2, we show the pdf of the $AKC$ distribution for several values of $\theta$.

2.2. Properties

The following proposition shows that the pdf of the $AKC$ distribution can be obtained from a convolution of two $AK$ distributions.

Proposition 1.

Let $X_1\sim AK\left(\theta \right)$, $X_2\sim AK\left(\theta \right)$ be two independent random variables and define $Z=X_1+X_2$, then $X\sim AKC\left(\theta \right)$.

Proof. 

Since $X_1$ and $X_2$ are independent, the pdf of Z may be obtained from the following convolution product: for $x>0$,

$${\displaystyle f_Z(z;\theta )={\int }_0^z{f}_{X_1}(z-t;\theta )f_{X_2}(t;\theta )dt=\frac{{\theta }^{6}exp(-\theta z)}{{({\theta }^2+2)}^2}{\int }_0^z(1+z^2-2zt+t^2)(1+t^2)dt.}$$

By calculating the right-side integral, the result follows.    □

The following proposition shows the cdf of the $AKC$ distribution.

Proposition 2.

Let $Z\sim AKC\left(\theta \right)$. Then, the cdf of Z is given by

$$F_Z(z;\theta )={\displaystyle \frac{1}{30{({\theta }^2+2)}^2}}\left\{30{\theta }^4\gamma (2,\theta z)+20{\theta }^2\gamma (4,\theta z)+\gamma (6,\theta z)\right\},z>0,$$

(8)

where $\theta >0$ and ${\displaystyle \gamma (a,v)={\int }_0^v{u}^{a-1}exp(-u)du}$ is the incomplete gamma function.

Proof. 

By directly calculating the cdf of Z we have

$$\begin{array}{ccc}{F}_Z(z;\theta )& =& {\displaystyle {\int }_0^z\frac{{\theta }^{6}t}{30{({\theta }^2+2)}^2}(30+20t^2+t^4)exp(-\theta t)dt,}\end{array}$$

and making the following change of variable: $u=\theta t$, the result is obtained.    □

2.3. Reliability Analysis

The reliability function $r\left(t\right)$ and the hazard function $h\left(t\right)$ of the $AKC$ distribution are given in the following corollary.

Corollary 1.

Let $T\sim AKC\left(\theta \right)$. Then, the $r\left(t\right)$ and $h\left(t\right)$ of T are given by

• ${\displaystyle r\left(t\right)=\frac{1}{30{({\theta }^2+2)}^2}\left\{30{({\theta }^2+2)}^2-30{\theta }^4\gamma (2,\theta t)-20{\theta }^2\gamma (4,\theta t)-\gamma (6,\theta t)\right\},}$
• ${\displaystyle h\left(t\right)=\frac{{\theta }^{6}t(30+20t^2+t^4)exp(-\theta t)}{30{({\theta }^2+2)}^2-30{\theta }^4\gamma (2,\theta t)-20{\theta }^2\gamma (4,\theta t)-\gamma (6,\theta t)},}$

where $\theta ,t>0$.

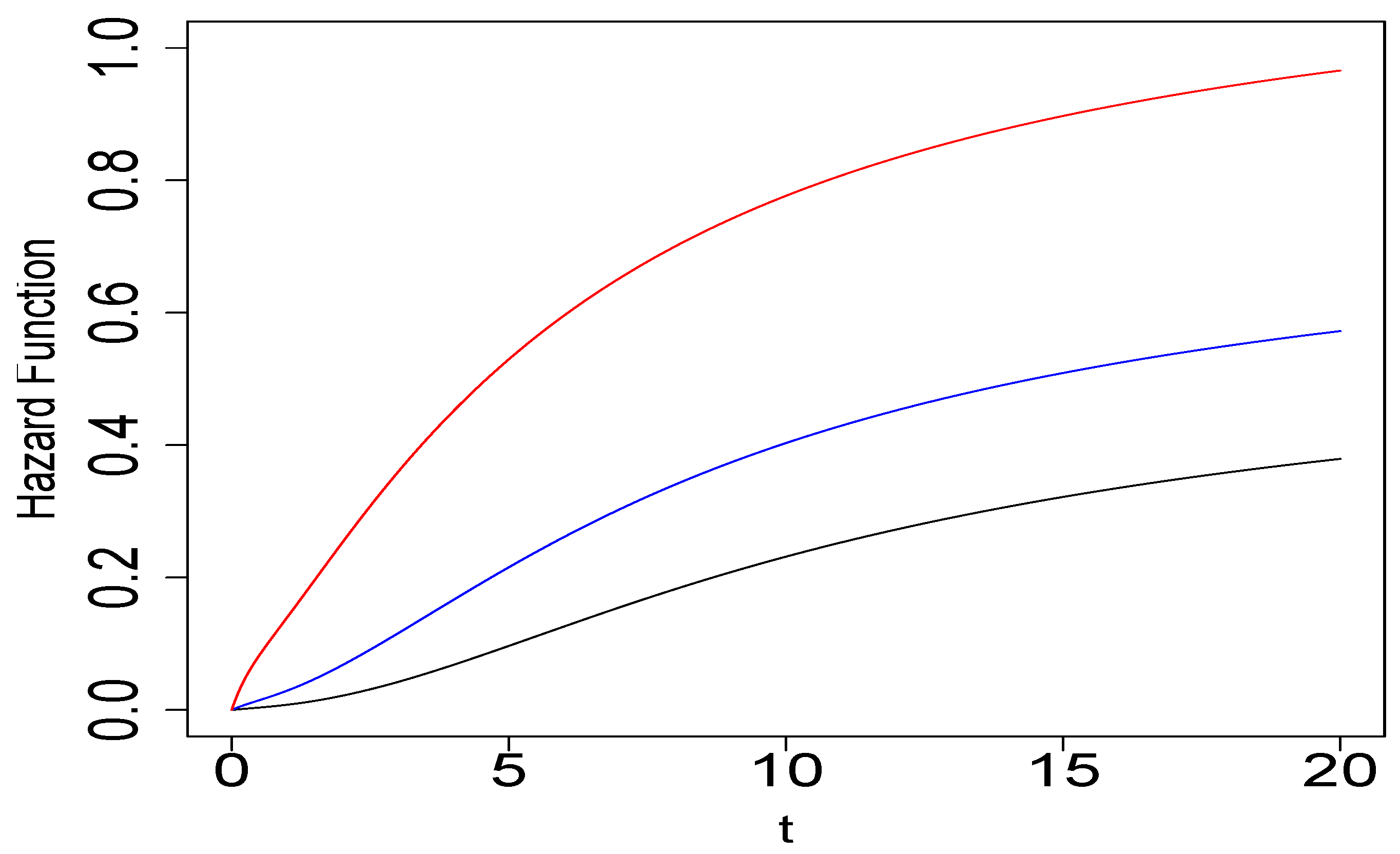
In Figure 3, we show the hazard function of AKC distribution for several values of $\theta$.

Proposition 3.

Let $T\sim AKC\left(\theta \right)$. Then, the hazard function of T is increasing for all $t>0$.

Proof. 

Using item $\left(a\right)$ of a theorem given in Glaser [18] we have that

$$\begin{array}{c}\hfill \eta \left(t\right)=-{\displaystyle \frac{f^{\prime }\left(t\right)}{f\left(t\right)}}=\theta -{\displaystyle \frac{1}{t}}-{\displaystyle \frac{40t+4t^3}{30+20t^2+t^4}},\end{array}$$

where $f\left(t\right)$ is the pdf given in (7). Then differentiating the function $\eta \left(t\right)$ with respect to t

$$\begin{array}{c}\hfill {\eta }^{\prime }\left(t\right)={\displaystyle \frac{900+900t^4+80t^6+5t^8}{t^2{(30+20t^2+t^4)}^2}}>0,\forall t>0,\end{array}$$

the result follows.    □

2.4. Order Statistics

Let $Z_1,...,Z_n$ be a random sample of a random variable $Z\sim AKC\left(\theta \right)$. Let us denote by $Z_{\left(j\right)}$ the $jth-$order statistics, $j\in \{1,\dots ,n\}$.

Proposition 4.

The pdf of $Z_{\left(j\right)}$ is

$$\begin{array}{ccc}\hfill f_{Z_{\left(j\right)}}\left(z\right)& =& {\displaystyle \frac{n!{\theta }^{6}zexp(-\theta z)(30+20z^2+z^4)}{(j-1)!(n-j)!{30}^n{({\theta }^2+2)}^{2n}}}{\left\{30{\theta }^4\gamma (2,\theta z)+20{\theta }^2\gamma (4,\theta z)+\gamma (6,\theta z)\right\}}^{j-1}\hfill \\ & \times & {\left\{30{({\theta }^2+2)}^2-30{\theta }^4\gamma (2,\theta z)-20{\theta }^2\gamma (4,\theta z)-\gamma (6,\theta z)\right\}}^{n-j},\hfill \end{array}$$

where $z>0$ and $\theta >0.$ In particular, the pdf of the minimum, $Z_{\left(1\right)}$, is

$$f_{Z_{\left(1\right)}}\left(z\right)={\displaystyle \frac{n{\theta }^{6}zexp(-\theta z)(30+20z^2+z^4)}{{30}^n{({\theta }^2+2)}^{2n}}}{\left\{30{({\theta }^2+2)}^2-30{\theta }^4\gamma (2,\theta z)-20{\theta }^2\gamma (4,\theta z)-\gamma (6,\theta z)\right\}}^{n-1},$$

and the pdf of the maximum, $Z_{\left(n\right)}$, is

$$f_{Z_{\left(n\right)}}\left(z\right)={\displaystyle \frac{n{\theta }^{6}zexp(-\theta z)(30+20z^2+z^4)}{{30}^n{({\theta }^2+2)}^{2n}}}{\left\{30{\theta }^4\gamma (2,\theta z)+20{\theta }^2\gamma (4,\theta z)+\gamma (6,\theta z)\right\}}^{n-1},$$

Proof. 

Since we are dealing with an absolutely continuous model, the pdf of the $jth-$order statistic is obtained by applying

$$\begin{array}{ccc}\hfill f_{Z_{\left(j\right)}}\left(x\right)& =& {\displaystyle \frac{n!}{(j-1)!(n-j)!}}f\left(z\right){\left[F\left(z\right)\right]}^{j-1}{[1-F\left(z\right)]}^{n-j},,j\in \{1,\dots ,n\}\hfill \end{array}$$

where F and f denote the cdf and pdf of the parent distribution, $Z\sim AKC\left(\theta \right)$ in this case.    □

2.5. Moments

In this subsection we provide the moments, the moment generating function and skewness and kurtosis coefficients.

Proposition 5.

Let $Z\sim AKC\left(\theta \right)$. Then, for $r=1,2,3,\dots ,$ the r-moment of Z is given by

$${\displaystyle \mathbb{E}\left(Z^r\right)=\frac{r!}{{\theta }^r{({\theta }^2+2)}^2}\sum _{k=0}^r\left[{\theta }^2+(k+1)(k+2)\right]\left[{\theta }^2+(r-k+1)(r-k+2)\right].}$$

(9)

Proof. 

Using the representation of Z given in Proposition 1 and the binomial theorem, we have that the r-th moment is

$${\displaystyle \mathbb{E}\left(Z^r\right)=\mathbb{E}\left({(X_1+X_2)}^r\right)=\sum _{k=0}^r\left(\genfrac{}{}{0pt}{}{r}{k}\right)\mathbb{E}\left(X_1^k\right)\mathbb{E}\left(X_2^{r-k}\right),}$$

then using the moments of the $AK$ random variable given in (5), the result is obtained.    □

Proposition 6.

Let $Z\sim AKC\left(\theta \right)$. Then, the moment generating function of the random variable Z is given by

$$M_Z\left(t\right)=\mathbb{E}\left(exp\left(tZ\right)\right)={\displaystyle \frac{{\theta }^6}{{({\theta }^2+2)}^2}}{\left[{\displaystyle \frac{{(\theta -t)}^2+2}{{(\theta -t)}^3}}\right]}^2,t<\theta .$$

(10)

Proof. 

Using the representation given in Proposition 1, we get:

$$M_Z\left(t\right)=\mathbb{E}\left(exp\left(tZ\right)\right)=\mathbb{E}\left(exp\left(t(X_1+X_2)\right)\right)=M_{X_1}\left(t\right)M_{X_2}\left(t\right),$$

and using the moment generating function of the $AK$ random variable given in (6), the result follows.    □

Corollary 2.

Let $Z\sim AKC\left(\theta \right)$. Then, the mean and variance Z are given respectively by:

$$\begin{array}{c}\hfill {\displaystyle \mathbb{E}\left(Z\right)=\frac{2({\theta }^2+6)}{\theta ({\theta }^2+2)}\mathrm{and}Var\left(Z\right)=\frac{2({\theta }^4+16{\theta }^2+12)}{{\theta }^2{({\theta }^2+2)}^2}.}\end{array}$$

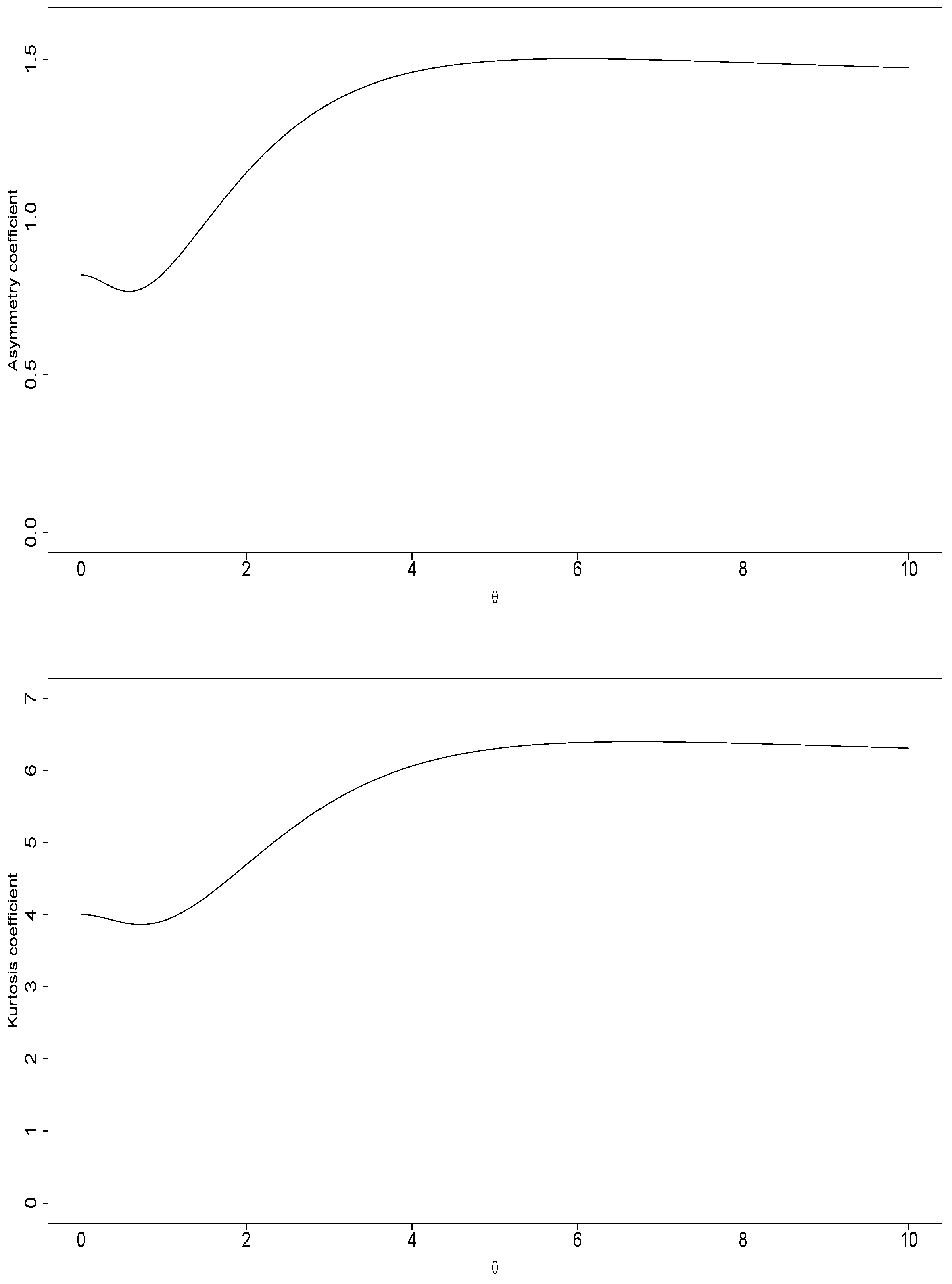
The skewness and kurtosis coefficients are respectively:

$${\displaystyle \sqrt{{\beta }_1}=\frac{\sqrt{2}({\theta }^6+30{\theta }^4+36{\theta }^2+24)}{{({\theta }^4+16{\theta }^2+12)}^{3/2}},}$$

$${\displaystyle {\beta }_2=\frac{6({\theta }^8+40{\theta }^6+172{\theta }^4+240{\theta }^2+96)}{{({\theta }^4+16{\theta }^2+12)}^2}.}$$

Figure 4 depicts plots of skewness and kurtosis coefficients of the $AKC$ distribution.

3. Inference

In this section we estimate the $\theta$ parameter of the $AKC$ model using the method of moments (MM) and the method of maximum likelihood (ML). Asymptotic properties of the ML estimator are discussed and a simulation study is presented.

3.1. Method of Moments

Let $z_1,\dots ,z_n$ be a random sample from $Z\sim AKC\left(\theta \right)$. Let $\overline{z}={\displaystyle \frac{{\sum }_{i=1}^n{z}_i}{n}}$ be the first sample moment.

Proposition 7.

Given $z_1,\dots ,z_n$, a random sample from $Z\sim AKC\left(\theta \right)$, the method of moment estimator of θ (${\widehat{\theta }}_M$) provides the following estimator:

$$\begin{array}{ccc}\hfill {\widehat{\theta }}_M& =& {\displaystyle \frac{2}{3\overline{z}}}+{\displaystyle \frac{-4+6{\overline{z}}^2}{3\times 2^{1/3}\overline{z}{(-4-72{\overline{z}}^2+3\sqrt{6}\sqrt{12{\overline{z}}^2+94{\overline{z}}^4+{\overline{z}}^6})}^{1/3}}}\hfill \\ & & -{\displaystyle \frac{2^{1/3}{(-4-72{\overline{z}}^2+3\sqrt{6}\sqrt{12{\overline{z}}^2+94{\overline{z}}^4+{\overline{z}}^6})}^{1/3}}{3\overline{z}}}.\hfill \end{array}$$

Proof. 

The equation for the method of moments is given by

$$\begin{array}{c}\hfill {\displaystyle \mathbb{E}\left[Z\right]=\frac{2({\theta }^2+6)}{\theta ({\theta }^2+2)}=\overline{z}.}\end{array}$$

(11)

Solving equation (11) for the parameter $\theta$, we obtain the result.    □

3.2. Maximum Likelihood Estimation

For a random sample, $z_1,\dots ,z_n$, derived from the $AKC(\theta$) distribution, the log-likelihood function can be written as

$$\ell \left(\theta \right)=6nlog\left(\theta \right)+\sum _{i=1}^{n}log\left(z_i\right)-2nlog({\theta }^2+2)-n\overline{z}\theta +\sum _{i=1}^{n}log\left(30+20z_i^2+z_i^4\right)-nlog\left(30\right).$$

(12)

The score equation are given by

$$\begin{array}{c}\hfill {\displaystyle \frac{d\ell \left(\theta \right)}{d\theta }}={\displaystyle \frac{6n}{\theta }}-{\displaystyle \frac{4n\theta }{{\theta }^2+2}}-n\overline{z}=0,\end{array}$$

so we get this equation

$$\begin{array}{c}\hfill -\overline{z}{\theta }^3+2{\theta }^2-2\overline{z}\theta +12=0.\end{array}$$

(13)

The ML estimator for $\theta$ ($\widehat{\theta }$) is obtained by solving equation (13). Note that this equation is identical to the equation derived for the method of moments. Consequently, the ML estimator of $\theta$ coincides with the moments estimator given in the Proposition 7.

Hence, for large samples, the ML estimator, $\widehat{\theta }$, is asymptotically normal. That is,

$$\sqrt{n}\left(\widehat{\theta }-\theta \right)\stackrel{\mathcal{L}}{⟶}N(0,I_F^{-1}\left(\theta \right)),$$

where the asymptotic variance of the ML estimator $\widehat{\theta }$ is the inverse of Fisher’s information:

$${\displaystyle Var\left(\widehat{\theta }\right)\approx \frac{{\theta }^2{({\theta }^2+2)}^2}{2n({\theta }^4+16{\theta }^2+12)},I_F\left(\theta \right)=\frac{2({\theta }^4+16{\theta }^2+12)}{{\theta }^2{({\theta }^2+2)}^2}.}$$

3.3. Simulation Study

To examine the performance of the ML estimator of the parameter $\theta$ of the $AKC$ distribution, a simulation study is carried out. An algorithm is available to generate random numbers from the $AKC$ distribution. The simulation analysis is performed generating 1000 samples of sizes $n=20,$ 50 and 100 from the $AKC$ distribution. The algorithm used to generate random numbers from the $AKC$ distribution is shown below. The Algorithm 1 is based on the representation given in Proposition 1.

Algorithm 1:for simulating from the $Z\sim AKC\left(\theta \right)$ can proceed as follows.

Step 1: Generate $S_i\sim Exp\left(\theta \right),i=1,2.$   Step 2: Generate $T_i\sim Gamma(3,\theta ),i=1,2.$   Step 3: Generate $V_i\sim Bernoulli\left({\displaystyle \frac{\theta }{1+\theta }}\right),i=1,2.$   Step 4: Compute $X_i=V_i{S}_i+(1-V_i)T_i,i=1,2.$   Step 5: Compute $Z=X_1+X_2$

Table 1 shows the empirical bias (B), the average of the standard errors (SE), the empirical root mean squared error (RMSE) and the coverage probability (CP). It is to be noted that the CP converge reasonably well to the nominal value used in their construction (95%), suggesting that the normal distribution is a reasonable asymptotic distribution for the the ML estimators in the AKC model. Also, Table 1 shows that, the performance of the estimates is very good even when n is small.

4. Applications

In this Section the $AKC$ distribution is fitted to two engineering science data sets and compared with the $AK$ and L distributions.

4.1. Application 1

In this application the data set consists of the strength of glass of the aircraft window reported by Fuller et al. [19]. The data are shown in Table 2.

Descriptive statistics are given in Table 3, where CS is the sample skewness coefficient and CK is the sample kurtosis coefficient.

Table 4 shows the ML estimates of the parameters of the $AKC$, $AK$ and L models together with their standard errors in parentheses, Also the values of the AIC and BIC criteria are given for each model, (Akaike information criterion (AIC) introduced by Akaike [20] and the Bayesian information criterion (BIC) proposed by Schwarz [21]).

Observe that the smallest AIC and BIC values correspond to the AKC model, meaning that this model produces a better fit than the $AK$ and L models.

For the fitted $AKC$ distribution we calculated the quantile residuals (QR). If the model is appropriate for the data, the QRs should be a sample from the standard normal model (see Dunn and Smyth [22]). This assumption can be validated with traditional normality tests, such as the Anderson-Darling (AD), Cramèr-von Mises (CVM) and Shapiro-Wilkes (SW) tests.

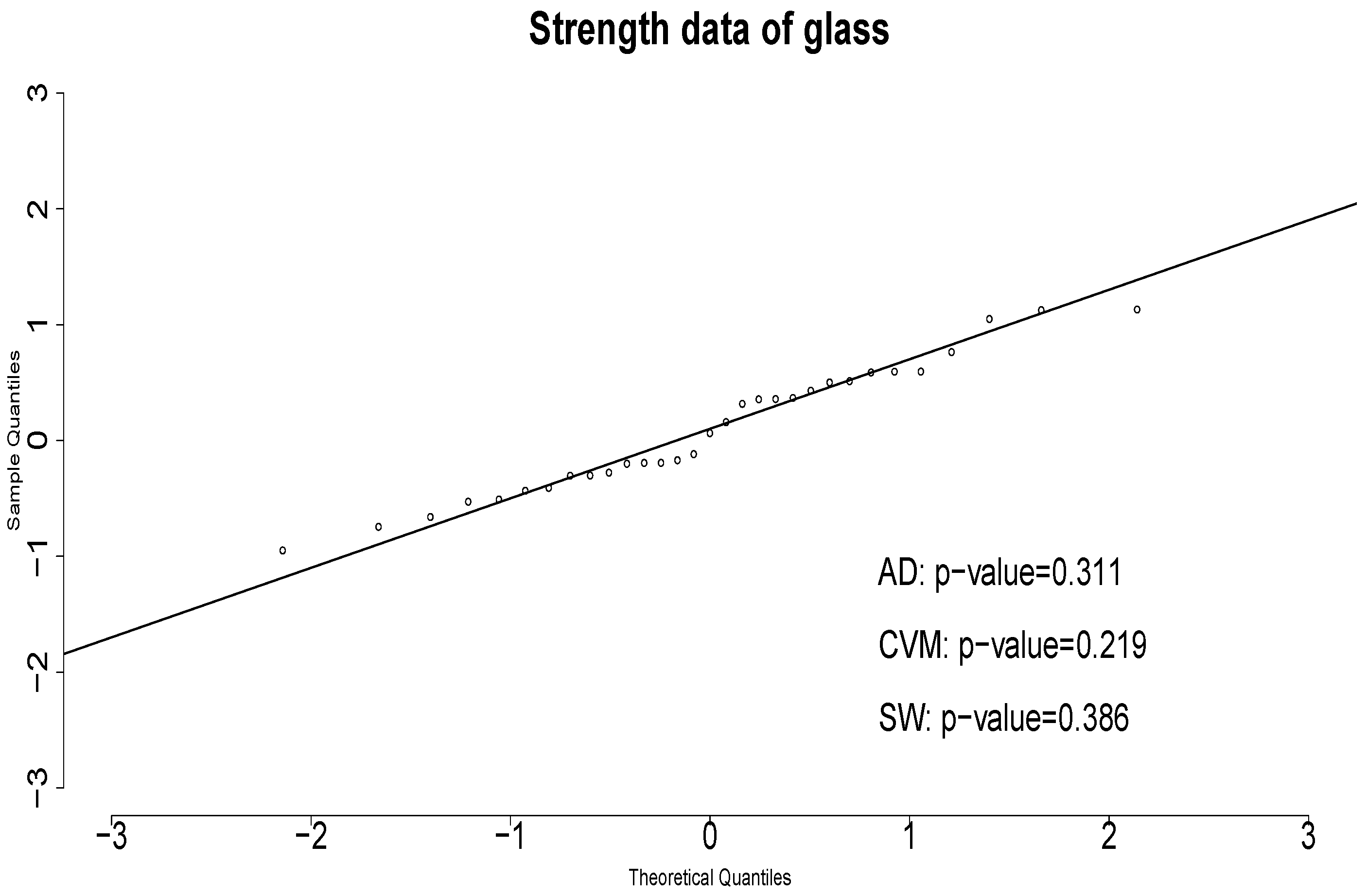
In Figure 5 the QRs for the AKC distribution are shown together with the p-values of the AD, CVM and SW normality tests. It is seen that the AKC distribution verifies the assumption that the QRs come from the standard normal distribution, validating the fit of the $AKC$ distribution to the strength of glass data.

4.2. Application 2

In this application we model a data set collected by the Department of Mines of the University of Atacama, Chile. The data, consisting of Yttrium measurements in 86 samples of mineral, are shown in Table 5.

Summary statistics are reported in Table 6. ML estimates of the parameter of the $AKC$, $AK$ and L models, together with their SE and the values of the AIC and BIC are given in Table 7.

We observe that the smallest values of the AIC and BIC criteria correspond to the AKC model, meaning that the AKC model fits the data better than the AK and L models.

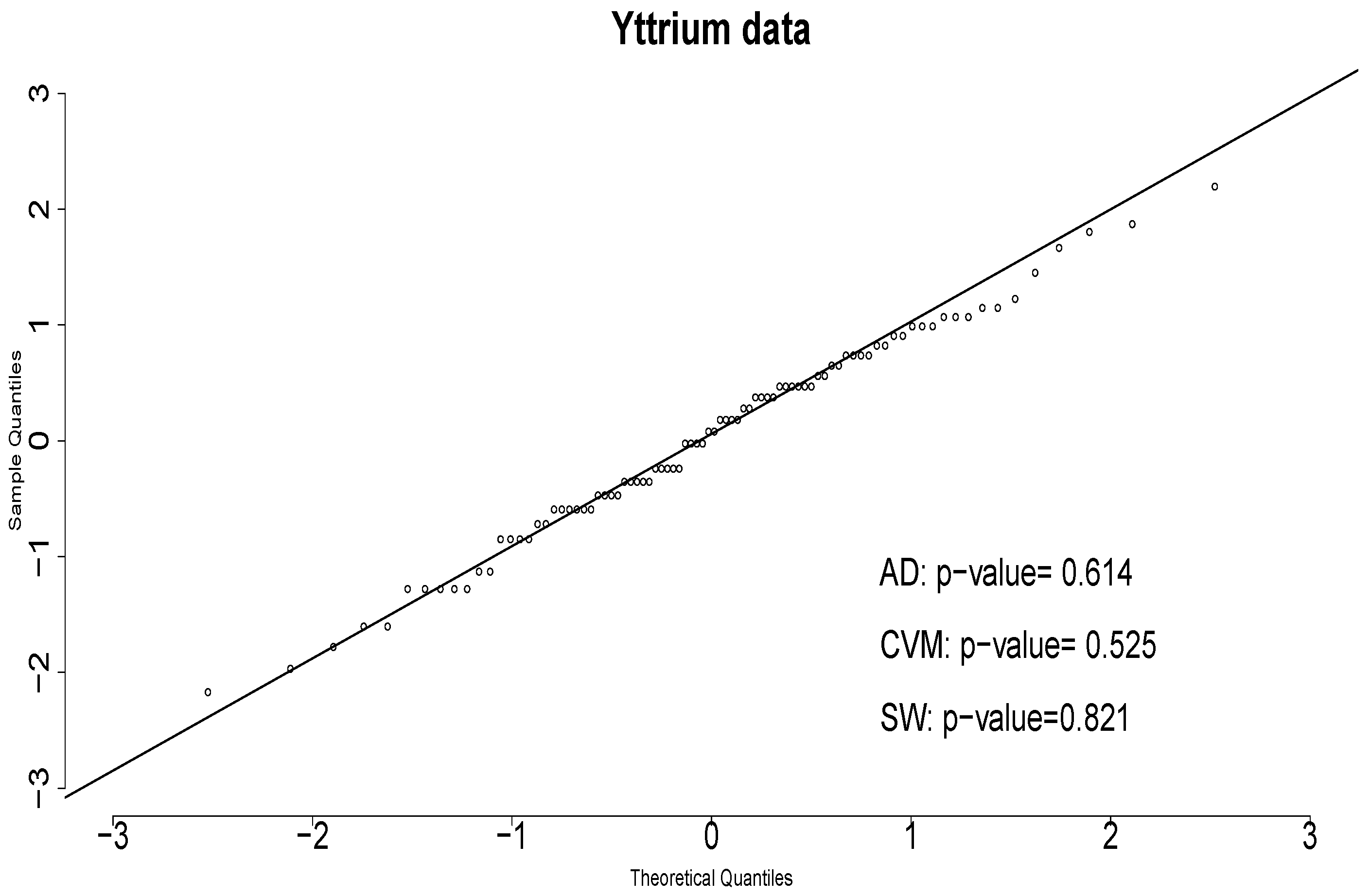
The residual quantiles of the $AKC$ distribution are shown in Figure 6. Also the p-values for the AD, CVM and SW normality tests are given to verify if the QRs come from a standard normal distribution. These indicate that the $AKC$ distribution provides a good fit for the Yttrium data.

5. Conclusions

In this article, we have studied the convolution of two independent $AK$ random variables with a parameter in common. We have given some of the properties of the new $AKC$ distribution and developed parameter estimates by the methods of moments and maximum likelihood. A simulation study is carried out to investigate the performance of the ML estimator. Also, the ability of the $AKC$ distribution is demonstrated in two applications made to real data sets. It consistently produces better fits than the $AK$ and L distributions.

Some additional features of the $AKC$ are:

• The $AKC$ distribution has a simple representation.
• The cumulative distribution and risk functions are explicit and represented by known functions.
• The Moments and Maximum Likelihood estimators coincide and have closed form solutions.
• The Maximun Likelihood estimator performs very well, even when samples are small.
• Applications show that the $AKC$ distribution is a good alternative to model positively skewed data when kurtosis is not too high. This is confirmed by the AIC and BIC model selection criteria and statistical tests such as Anderson-Darling, Cramèr-von Mises and Shapiro-Wilkes.