Submitted:
17 October 2023
Posted:
19 October 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. New density and its properties
2.1. Representation
2.2. Density function
2.3. Properties
2.3.1. Reliability analysis
- 1.
- 2.
2.3.2. Right tail of the SAK distribution
2.3.3. Moments
3. Inference
3.1. Method of moment estimators
3.2. ML estimation
3.3. EM Algorithm
- E-step: Given and , for compute and using equations (20) and (21), respectively.
- M1-step: Update as
- M2-step: Update as the solution for the non-linear equation
3.4. Simulation study
4. Application
5. Discussion
- The distribution has two representations, one based on the quotient of two independent random variables and another based on a scale mixture between the AK and Beta distributions.
- The pdf, cdf and hazard function of the SAK distribution are explicit and are represented by the cdf of the gamma distribution.
- The distribution has a heavy right tail.
- The distribution contains the AK distribution as a limit, that is, when the parameter q tends to infinity in the distribution SAK, the AK distribution is obtained.
- The moments and the coefficients of skewness and kurtosis are explicit.
- In the application, observing the AIC and BIC and the Anderson-Darling, Cramér-von Mises and Shapiro-Wilkes statistical tests, we may conclude that the SAK distribution fits the Betaplasma data set better than the PAD and SMR distributions, which are also extensions of the AK distribution.
References
- Jonhson, N.L., Kotz, S., and Balakrishnan, N.1995.Continuous univariate distributions. Vol 1, 2nd edn. New York: Wiley.
- Rogers, W.H., Tukey, J.W. 1972. Understanding some long-tailed symmetrical distributions. Statist. Neerlandica 26 :211-226. [CrossRef]
- Mosteller, F., Tukey, J.W. 1977. Data analysis and regression. Addison-Wesley, Reading, MA.
- Kafadar, K. 1982. A biweight approach to the one-sample problem. J. Amer. Statist. Assoc. 77 :416-424. [CrossRef]
- Wang, J., Genton, M.G. 2006. The multivariate skew-slash distribution. Journal Statistical Planning and Inference 136 :209-220. [CrossRef]
- Gómez, H.W., Quintana, F.A., Torres, F. J. 2007. A New Family of Slash-Distributions with Elliptical Contours. Statistics and Probability Letters 77(7):717-725. [CrossRef]
- Gómez, H.W., Venegas, O. 2008. Erratum to: A new family of slash-distributions with elliptical contours [Statist. Probab. Lett. 77 (2007) 717-725]. Statistics and Probability Letters 78 (14):2273-2274. [CrossRef]
- Gómez, H.W., Olivares-Pacheco, J.F., Bolfarine, H. 2009. An extension of the generalized birnbaun-saunders distribution. Statistics and Probability Letters 79 (3):331-338. [CrossRef]
- Olmos, N.M., Varela, H., Gómez, H.W. and Bolfarine, H. 2012. An extension of the half-normal distribution. Statistical Papers 53 :875-886. [CrossRef]
- Olmos, N.M., Varela, H., Bolfarine, H., Gómez, H.W. 2014. An extension of the generalized half-normal distribution. Statistical Papers 55:967-981. [CrossRef]
- Astorga, J.M., Reyes, J., Santoro, K.I., Venegas, O., Gómez, H.W. 2020. A Reliability Model Based on the Incomplete Generalized Integro-Exponential Function. Mathematics 8:1537. [CrossRef]
- Rivera P.A., Barranco-Chamorro I., Gallardo D.I., Gómez H.W. 2020. Scale Mixture of Rayleigh Distribution. Mathematics 8(10):1842. [CrossRef]
- Shanker, R. 2015. Akash Distribution and Its Applications. International Journal of Probability and Statistics 4(3):65-75. [CrossRef]
- Shanker, R., Shukla, K.K. 2017a. On Two-Parameter Akash Distribution. Biometrics & Biostatistics International Journal 6(5):00178. [CrossRef]
- Shanker, R., Shukla, K.K. 2017b. Power Akash Distribution and Its Application. Journal of Applied Quantitative Methods 12(3):1-10.
- Rolski, T., H. Schmidli, V. Schmidt, and J. Teugel. 1999. Stochastic Processes for Insurance and Finance. John Wiley & Sons.
- Dempster. A.P.; Laird. N.M.; Rubim. D.B. 1977. Maximum likelihood from incomplete data via the EM algorithm (with discussion). J. R. Stat. Soc. Ser. B, 39, 1–38.
- Akaike, H. 1974. A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6), 716-723. [CrossRef]
- Schwarz, G. 1978. Estimating the dimension of a model. Ann. Statist., 6(2), 461-464. [CrossRef]
- Dunn, P.K., Smyth, G.K. 1996. Randomized Quantile Residuals. Journal of Computational and Graphical Statistics, 5(3), 236-244. [CrossRef]
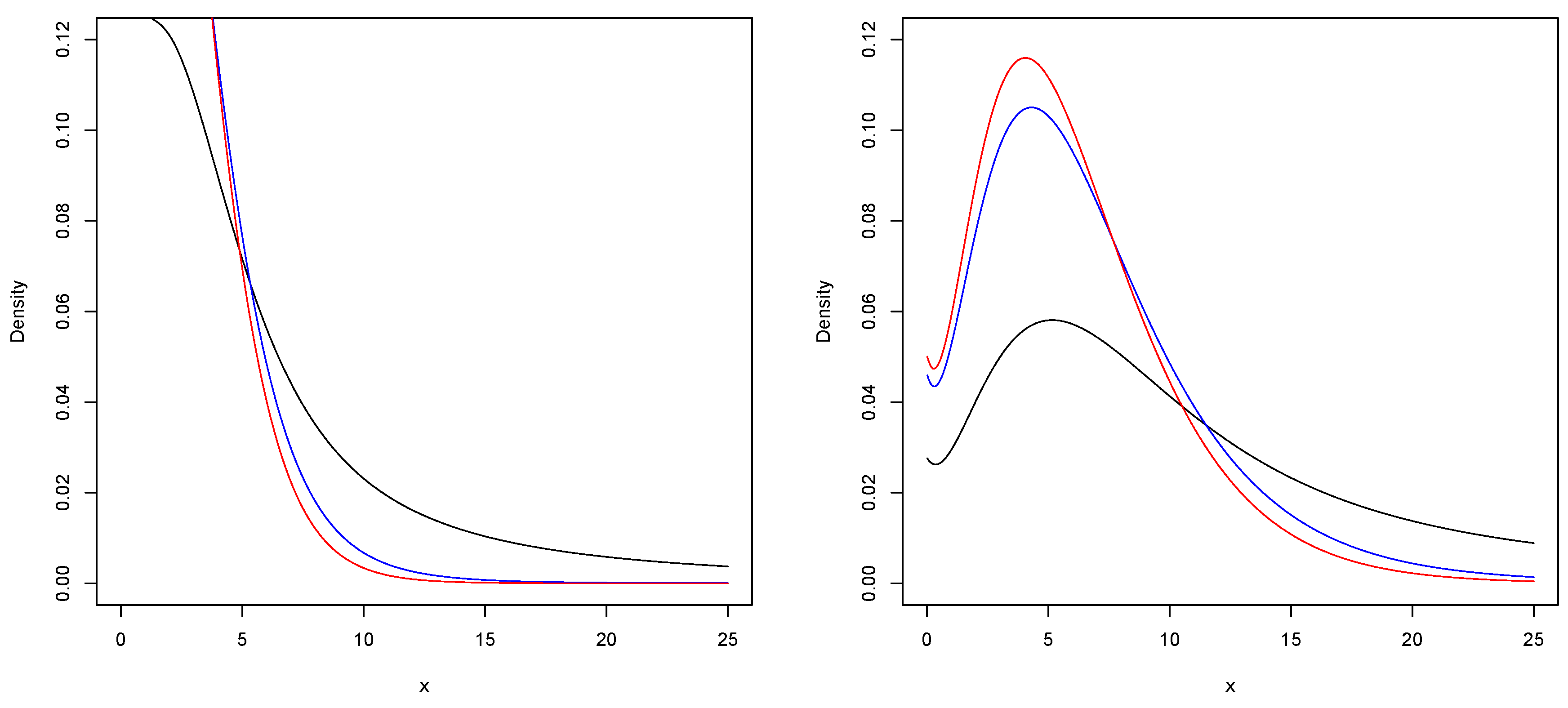
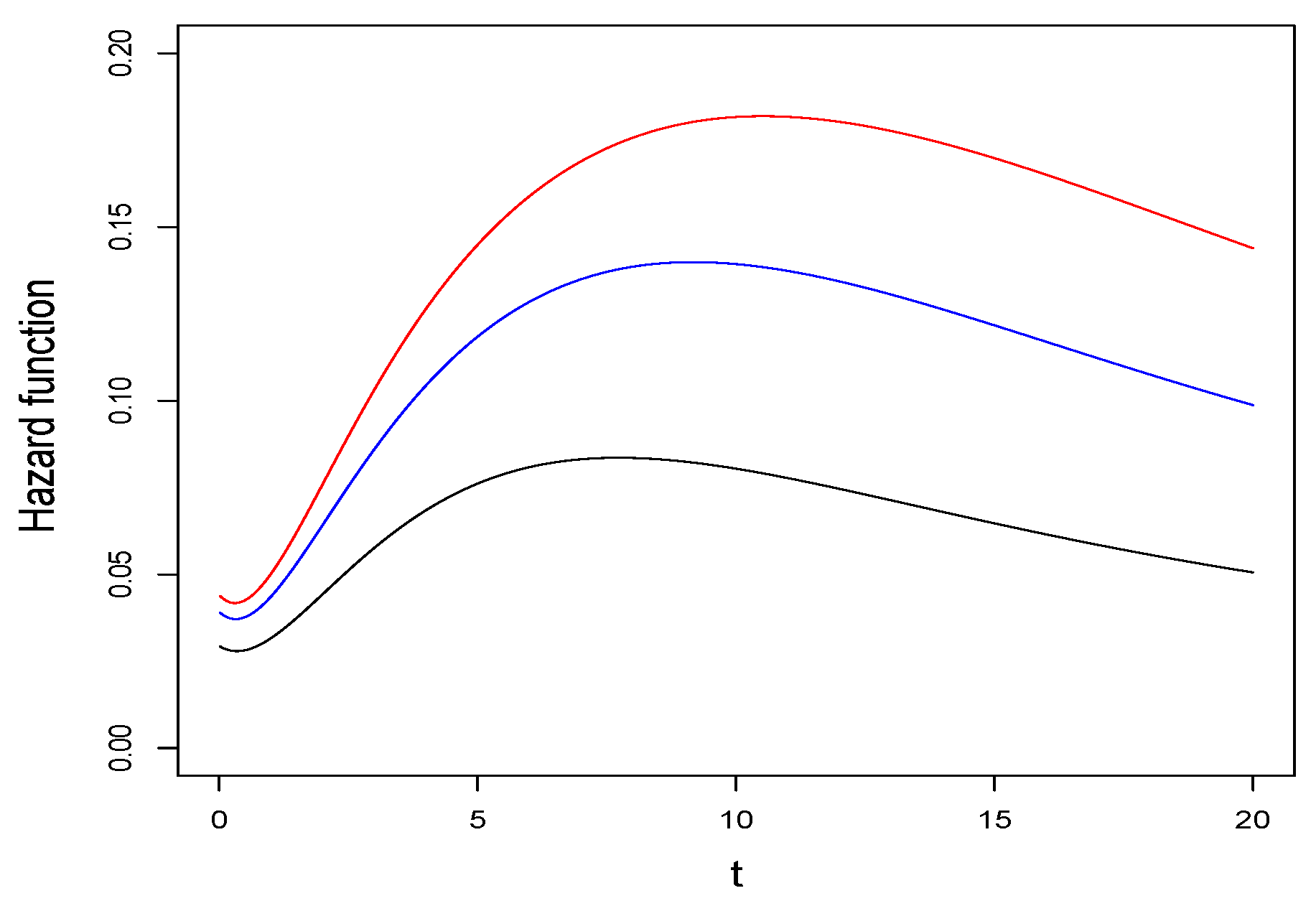
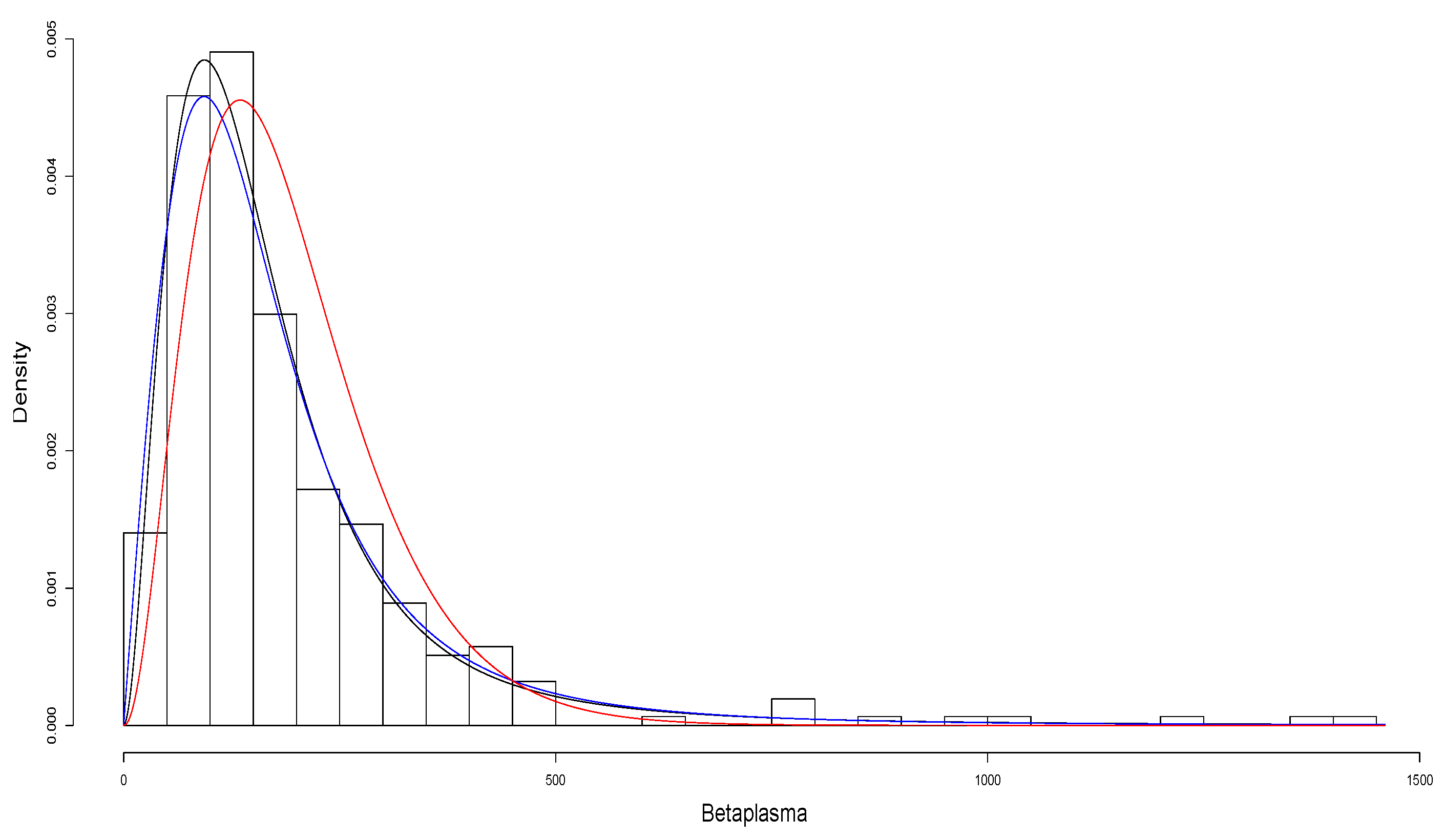
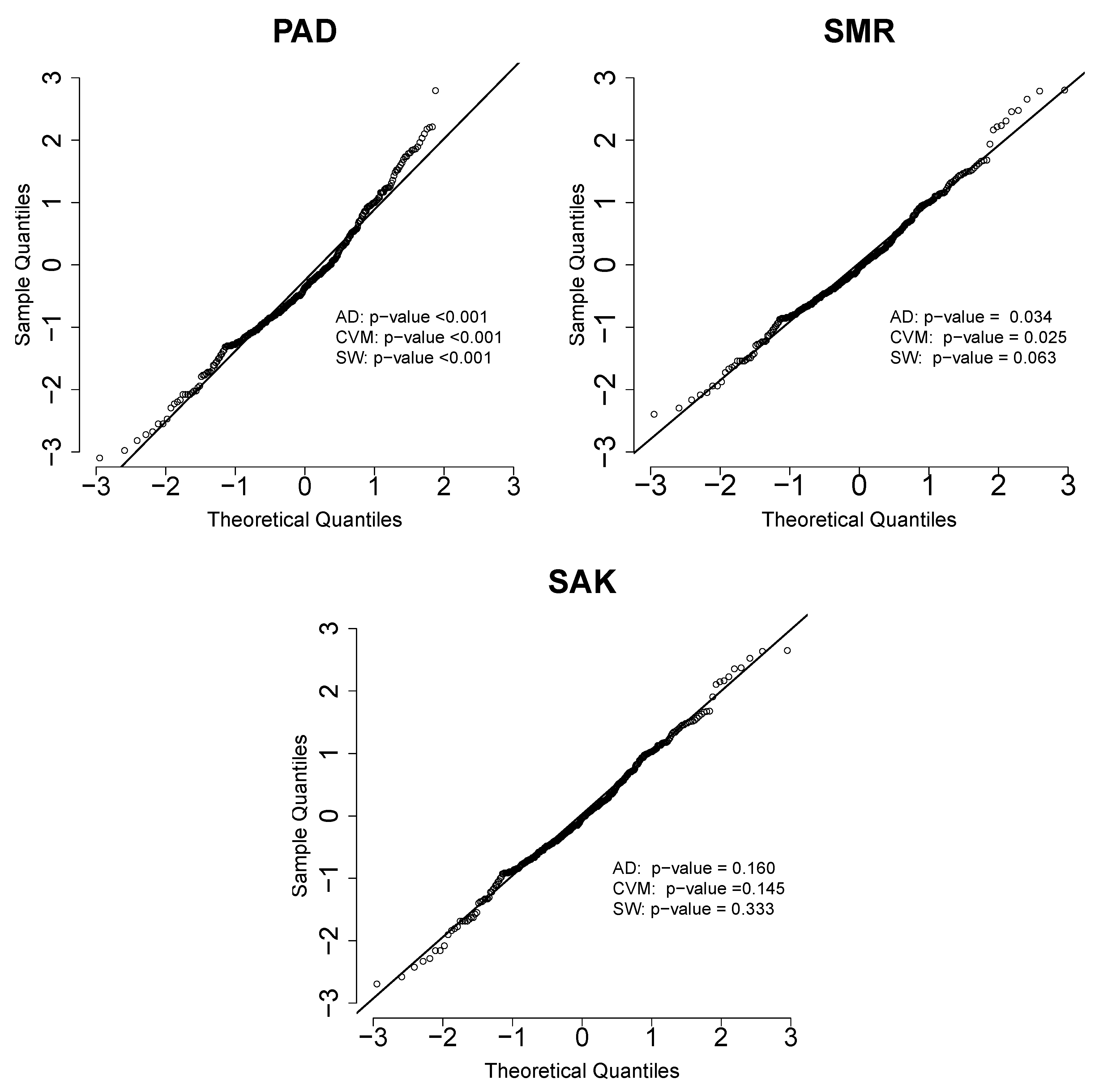
| Distribution | Distribution | ||||
| SAK(1,1) | SAK(0.5,1) | ||||
| SAK(1,5) | SAK(0.5,5) | ||||
| SAK(1,10) | SAK(0.5,10) | ||||
| AK(1) | AK(0.5) |
| q | |||
| 5 | |||
| 1 | |||
| 6 | |||
| 1 | |||
| 7 | |||
| 1 | |||
| 10 | |||
| 1 | |||
| 100 | |||
| 1 | |||
| ∞ | |||
| 1 |
| n = 30 | n = 50 | n = 100 | n = 200 | n = 500 | ||||||||||||||||||
| q | estimator | bias | SE | RMSE | CP | bias | SE | RMSE | CP | bias | SE | RMSE | CP | bias | SE | RMSE | CP | bias | SE | RMSE | CP | |
| 0.5 | 0.5 | -0.002 | 0.119 | 0.124 | 0.914 | -0.004 | 0.092 | 0.094 | 0.930 | -0.001 | 0.065 | 0.066 | 0.937 | 0.000 | 0.046 | 0.046 | 0.946 | 0.000 | 0.029 | 0.029 | 0.947 | |
| 0.036 | 0.122 | 0.139 | 0.961 | 0.025 | 0.092 | 0.100 | 0.958 | 0.012 | 0.063 | 0.065 | 0.952 | 0.005 | 0.043 | 0.044 | 0.952 | 0.001 | 0.027 | 0.027 | 0.951 | |||
| 1.0 | -0.004 | 0.110 | 0.114 | 0.918 | -0.003 | 0.085 | 0.086 | 0.931 | -0.002 | 0.060 | 0.061 | 0.940 | -0.001 | 0.043 | 0.043 | 0.946 | 0.000 | 0.027 | 0.027 | 0.946 | ||
| -0.159 | 0.236 | 0.253 | 0.924 | -0.112 | 0.161 | 0.171 | 0.929 | -0.087 | 0.108 | 0.115 | 0.939 | -0.059 | 0.074 | 0.081 | 0.948 | -0.046 | 0.046 | 0.051 | 0.948 | |||
| 2.0 | -0.003 | 0.105 | 0.107 | 0.931 | -0.003 | 0.081 | 0.082 | 0.939 | -0.002 | 0.057 | 0.058 | 0.940 | -0.001 | 0.040 | 0.041 | 0.945 | 0.000 | 0.025 | 0.026 | 0.947 | ||
| -0.137 | 0.597 | 0.622 | 0.904 | -0.125 | 0.395 | 0.420 | 0.924 | -0.077 | 0.233 | 0.250 | 0.932 | -0.041 | 0.151 | 0.162 | 0.942 | -0.023 | 0.092 | 0.095 | 0.948 | |||
| 3.0 | 0.5 | 0.136 | 1.063 | 1.236 | 0.891 | 0.095 | 0.794 | 0.861 | 0.915 | 0.035 | 0.537 | 0.556 | 0.927 | 0.013 | 0.373 | 0.380 | 0.940 | 0.005 | 0.234 | 0.235 | 0.947 | |
| 0.059 | 0.156 | 0.206 | 0.963 | 0.030 | 0.110 | 0.124 | 0.958 | 0.015 | 0.075 | 0.079 | 0.955 | 0.009 | 0.052 | 0.054 | 0.953 | 0.003 | 0.032 | 0.033 | 0.952 | |||
| 1.0 | 0.104 | 0.982 | 1.112 | 0.896 | 0.060 | 0.729 | 0.786 | 0.912 | 0.028 | 0.499 | 0.517 | 0.929 | 0.012 | 0.347 | 0.354 | 0.941 | 0.003 | 0.218 | 0.219 | 0.948 | ||
| -0.087 | 0.398 | 0.446 | 0.892 | -0.057 | 0.245 | 0.296 | 0.925 | -0.021 | 0.145 | 0.188 | 0.938 | -0.012 | 0.097 | 0.117 | 0.948 | -0.002 | 0.060 | 0.066 | 0.947 | |||
| 2.0 | 0.145 | 0.976 | 1.070 | 0.922 | 0.068 | 0.709 | 0.747 | 0.929 | 0.018 | 0.478 | 0.491 | 0.934 | 0.006 | 0.332 | 0.339 | 0.941 | 0.000 | 0.208 | 0.210 | 0.946 | ||
| -0.105 | 1.025 | 1.090 | 0.915 | -0.084 | 0.724 | 0.790 | 0.924 | -0.069 | 0.440 | 0.485 | 0.935 | -0.048 | 0.255 | 0.282 | 0.942 | -0.008 | 0.140 | 0.155 | 0.948 | |||
| 10.0 | 0.5 | 0.595 | 4.688 | 5.331 | 0.882 | 0.291 | 3.484 | 3.709 | 0.901 | 0.126 | 2.400 | 2.470 | 0.925 | 0.088 | 1.684 | 1.706 | 0.942 | 0.019 | 1.056 | 1.049 | 0.944 | |
| 0.069 | 0.175 | 0.184 | 0.964 | 0.035 | 0.113 | 0.128 | 0.963 | 0.016 | 0.075 | 0.080 | 0.957 | 0.007 | 0.052 | 0.053 | 0.951 | 0.003 | 0.032 | 0.033 | 0.951 | |||
| 1.0 | 0.559 | 4.440 | 4.910 | 0.904 | 0.222 | 3.260 | 3.453 | 0.910 | 0.102 | 2.248 | 2.328 | 0.926 | 0.059 | 1.574 | 1.600 | 0.941 | 0.009 | 0.987 | 0.980 | 0.948 | ||
| -0.097 | 0.508 | 0.631 | 0.899 | -0.051 | 0.284 | 0.389 | 0.903 | -0.031 | 0.152 | 0.199 | 0.939 | -0.023 | 0.098 | 0.117 | 0.948 | -0.012 | 0.060 | 0.080 | 0.948 | |||
| 2.0 | 0.885 | 4.575 | 4.757 | 0.935 | 0.389 | 3.286 | 3.316 | 0.937 | 0.172 | 2.209 | 2.217 | 0.944 | 0.035 | 1.533 | 1.546 | 0.947 | -0.006 | 0.955 | 0.955 | 0.947 | ||
| -0.068 | 1.224 | 1.222 | 0.924 | -0.057 | 0.834 | 0.950 | 0.931 | -0.037 | 0.440 | 0.483 | 0.935 | -0.027 | 0.305 | 0.313 | 0.942 | -0.018 | 0.149 | 0.159 | 0.943 | |||
| n | ||||
| 314 | 190.4968 | 33480.72 | 3.536562 | 16.8145 |
| Parameter estimates | PAD (SE) | SMR (SE) | SAK (SE) |
| 0.012 (0.003) | 16998.167 (3399.076) | 0.027 (0.002) | |
| 1.052 (0.038) | − | − | |
| q | − | 2.926 (0.385) | 2.331 (0.294) |
| Log-likelihood | −1953.632 | −1910.472 | −1908.147 |
| Criterion | PAD | SMR | SAK |
| AIC | 3911.264 | 3824.944 | 3820.294 |
| BIC | 3918.763 | 3832.443 | 3827.793 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





