Single-Step GWAS Multi-Trait Threshold-Linear Model for Growth Rate and Heteroblasty in Eucalyptus globulus

1. Introduction

Most of agronomic traits of interest to breeders are quantitative and polygenic, that is, they are governed by many genes of small effect [1]. Genome-wide association studies (GWAS) are a leading approach for complex trait dissection and identification of genomic segments or superior alleles that underlie phenotypic variation, that can be used for breeding [2].

The first studies on GWAS marked a significant advancement in genetics by enabling researchers to identify genetic variants associated with complex traits and diseases across the entire genome [3,4]. Subsequently, multi-trait models showed that the power to detect QTLs increases [5,6,7]. Bolormaa et al. [8], reported in dairy cattle that the multivariate analyses uncovered SNP associations that were not discovered by the univariate analyses and that the benefit of a multiple-trait analysis increased if the traits were highly correlated. Cappa et al. [7], showed in lodgepole pine that multitrait GWAS provided a substantial increment in the number of significant SNP markers identified and in the potential of identifying pleiotropic effects of individual genes, confirming the statistical power of these models.

Many methods are being developed in GWAS, and a commonly used approach involves converting genomic breeding values from GBLUP into estimated marker effects through a linear transformation, as described by [9]. One limitation of this method is that it only includes phenotypes of genotyped individuals. Particularly in tree breeding populations, but also in crops and livestock populations, only a fraction of individuals are genotyped. Thus, the GBLUP methods were extended to include the information of non-genotyped individuals in prediction analysis, which is known as single-step genomic best linear unbiased prediction (ssGBLUP) [10,65]. Applying this method, marker effects, variance explained by segments and the p-values associated are estimated simultaneously for all markers while accounting for population structure using the pedigree and genomic relationship for all individuals in the population [12,13]. This methodology is based on an infinitesimal model, which assumes equal variance for all single nucleotide polymorphism (SNP) marker-QTL (Quantative Trait loci) associated effects, resulting in an identical genomic relationship matrix for all traits within a population [10].

Several models are used to test the significance of single nucleotide polymorphism (SNP) effects [14], as is the case with EMMAX (Efficient Mixed-Model Association eXpedited). This method fits a mixed model to account for relatedness and population structure while testing SNP associations [15]. However, SNPs within a genomic segment can be highly correlated with each other and jointly influence the phenotype, which makes the effect of a single SNP difficult to be identified [16]. Therefore, GWAS based on testing genomic windows have been proposed to overcome this problem with the use of Bayesian approaches, which include all marker effects simultaneously [13,17]. The advantages of using windows of consecutive SNPs can capture the effect of a QTL better than a single SNP, particularly due that SNPs may be in linkage disequilibrium (LD) with a QTL and are useful to discriminate important effects from statistical noise [18,19]. Several works used windows of different size [8,13,20] but the optimal window size may also be a function of effective population size [21].Fragomeni et al. [22], identified windows of 20 SNP that explained major portions of genetic variance for growth in chicken and showed small individual SNP variances, with just a few SNPs explaining more than 0.5% of the total variance. Sigdel et al. [23] following a Single-step genomic BLUP methodology utilized windows of 2.0 Mb SNP to identify genomic regions and putative candidate genes implicated in milk production under thermoneutral and heat stress conditions and founded genomic regions that explained between 0.6% up to 5.7% of the total variance explained.

In tree breeding, most GWAS models have been applied for quantitative traits, such as volume, categorical traits like forkings, survival, stem straightness, are also analyzed as quantitative traits with or without transformation [24,25], but due to the lack of specific analysis tools, methods designed for binary and quantitative traits have been used to analyze categorical data, which is inappropriate and can result in erroneous results [26]. Wright [27] developed the threshold concept to map a normally distributed underlying variable to the observed ordered categorical phenotypes. Gianola and Foulley [28] developed the threshold mixed effects model, which has become popular for pedigree-based genetic evaluation of ordinal categorical traits. Misztal et al. [29] affirm that threshold models have been applied in animal breeding for traits with categorical data.

In this study, the aim was to identify genomic regions associated with quantitative traits (growth) and categorical traits (heteroblasty) in a multitrait threshold linear model using the single-step GWAS methodology in a tree breeding population of Eucalyptus globulus.

2. Materials and Methods

2.1. Study Population

The study population belongs to the E. globulus tree improvement program of INIA Uruguay. It consists of parents and six progeny tests. The parents consists of two seed orchards that include parents of six progeny test. The two seed orchards that include parents and no selected tree were installed in 1996 at a first generation, and a second generation installed in 2002.

2.2. Phenotypic Information

The phenotypic information comes from progeny tests installed in typical E. globulus plantation areas in southeastern Uruguay, in the departments of Lavalleja and Rocha. The first progeny test is composed by half-sib families, represented by 3853 individuals belonging to 194 open pollinated families (OP), installed in 2011 (see more details in Quezada et al. [30]). The other five progeny tests are composed of full-sib families, represented by 6051 individuals belonging to 137 controlled mattings (CM), installed between 2015 and 2019 (Table 1). The OP comes mainly from the first generation seed orchard and the CM from the second generation seed orchard.

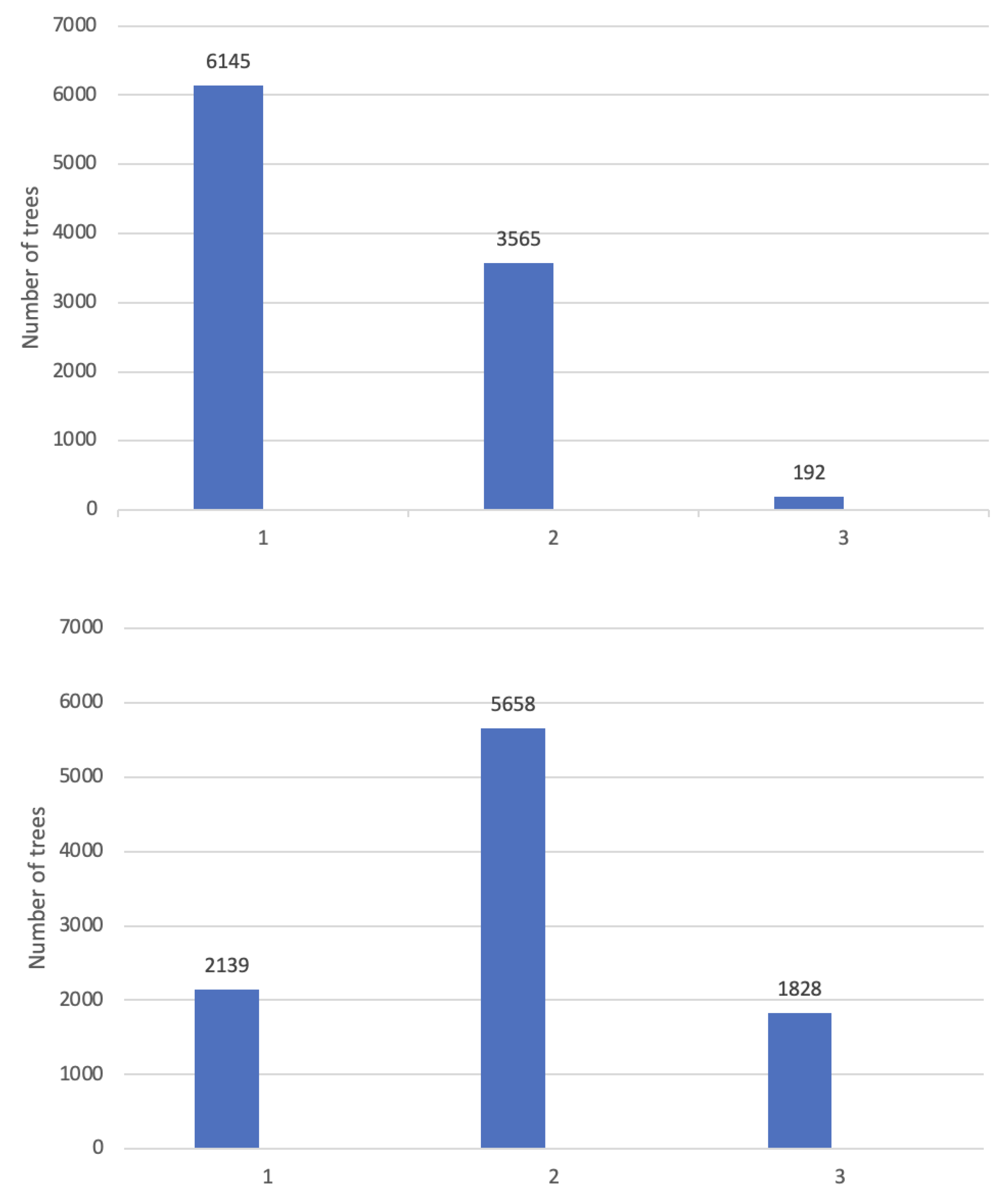
Tree growth was measured as total height (TH) and diameter at breast height (DBH) at 14 and 21 months, respectively. The precocity of change from juvenile to adult foliage (ADFO) was also assessed at 14 and 21 months of age. ADFO was calculated as the percentage of the crown with adult foliage, using a visual scale with percentage intervals of 10%. The distribution of data in the different categories was not uniform and therefore, they were grouped for analysis into three categories:1 = no adult foliage, 2 = up to 50% adult foliage, and 3 = more than 50% adult foliage. The ADFO was considered as a categorical trait, while TH and DBH as quantitative traits. At 14 months, most individuals had only juvenile foliage. At 21 months, most of individuals had up to 50% adult foliage. In both assessments, the proportion of individuals with more than 50% adult foliage was low (Figure 1).

2.3. Genotypic Information

The genotypic information is made up with a total of 2409 individuals including parents and progenies (OP and CM) (Table 1). The genotyping was carried out with the Eucalyptus EUchip60K SNPs chip [31]. The marker data was filtered to select markers with call rate >0.95 and a minor allele frequency (MAF) >0.05, and individuals with call rate >0.80, using PREGSF90 software [32], obtaining 15821 effective markers and 2359 individuals. Pedigree correction was conducted using the seekparent program from the BLUPF90 family [33]. The SNP-density plot was generated using the R package CMPlot [34].

To analyze the genetic diversity of the parents, half-sibs and full-sibs, the principal component analysis (PCA) was carried out using PREGSF90 of BLUPF90 family of programs [32] and the three different groups were represented by different colors using ggplot [35] R package [36]. The PCA was explored based on H matrix [37].

2.4. Single-Step GWAS Model (ssGWAS)

A multi-trait linear-threshold model was developed following the single-step genomic selection methodology [10], using a transformation of the genomic breeding values (a) to estimate SNP effects through equivalent models [38]. The multi-tratit linear threshold ssGWAS model was estimated using variance and covariance matrices between the traits and residual errors specified by Equation (1):

y =Xb+Wp+Za+e

(1)

where y is the vector of phenotypes (TH, ADFO at 14 months, DBH and ADFO at 21 months), b is the vector of fixed effects, including the overall mean of sites and blocks (within site), with incidence matrix X, p is the vector of random plot effects, with incidence matrix W, a is the vector of random genetic additive effects of the individual trees, with incidence matrix Z, and e is the vector of random residuals. The variance structure was defined as:

$$\mathrm{V}\mathrm{a}\mathrm{r}=\left[\begin{array}{c}p\\ a\\ e\end{array}\right]+\left[\begin{array}{ccc}I⨂P_0& 0& 0\\ 0& H⨂G_0& 0\\ 0& 0& I⨂R_0\end{array}\right]$$

where H is the numerator relationship matrix; G₀, P₀ and R₀ are 4 × 4 matrices of (co)variances for additive genetics, plot effects and residual variances corresponding to each trait. I is the identity matrix and ⊗ = the direct matrix product. H is constructed by combining information from markers and pedigree information [37].

The inverse of the relationship matrix that combines pedigree and genomic information (H^-1) was derived by Aguilar et al. [10] defined by Equation (2):

$$H^{-1}=A^{-1}+\left[\begin{array}{cc}0& 0\\ 0& G^{-1}-{A_{22}}^{-1}\end{array}\right]$$

(2)

where A^-1 and A⁻¹₂₂ are the inverse of the pedigree relationship matrices for all individuals and only for the genotyped individuals, respectively, and G^-1, estimated according VanRaden [39], is the inverse of the genomic relationship matrix.

Variance components were estimated using GIBBSF90 [40]. For variance components, the Gibbs sampling process comprised 300000 rounds and 1 every 50th sample was stored. After discarding the first 10000 samples as burn-in, posterior means were calculated.The genetic correlations for all traits was estimated as follows by Equation (3):

$${rg}_{ij}={\displaystyle \frac{{\sigma }_{ij}^2}{\sqrt{{\sigma }_i^2+{\sigma }_j^2}}}$$

(3)

where σ²_i and ${\sigma }_j^2$ are the additive genetic variance for the traits.

The narrow sense heritability for all traits was estimated as follows by Equation (4):

$$h^2={\displaystyle \frac{{\sigma }_a^2}{{\sigma }_a^2+{\sigma }_p^2+{\sigma }_e^2}}$$

(4)

where σ²_a is the additive genetic variance, σ²_p is the plot variance, and σ²_e is the residual variance.

The SNP effects were estimated using the Equation (5):

$$\widehat{u}=F^{\prime }{\displaystyle \frac{1}{2pj\left(1-pj\right)}}{G}^{-1}{\widehat{a}}_{22}$$

(5)

where F is the matrix of gene content adjusted for observed allele frequencies and p_j is the allele frequency of the ith SNP, G^-1 is the inverse of the genomic relationship matrix and ${\widehat{a}}_{22}$ is a vector of genomic breeding values only for genotyped individuals. The variance explained for each QTL were estimated as suggested by [12]. The ssGWAS models were fitted with POSTGF90 of BLUPF90 family software [41].

Windows genetic variance was computed following Peters et al. [42] where breeding values partial for each window were estimated and then the variance of these breeding values was calculated. The size of window used in this study was of 0.2 Mb, this is because the LD for E. globulus, estimated previously by Quezada et al. [43] is the 0.2 Mb, approximately. Only the windows with estimated variance higher than 1% were considered.

3. Results

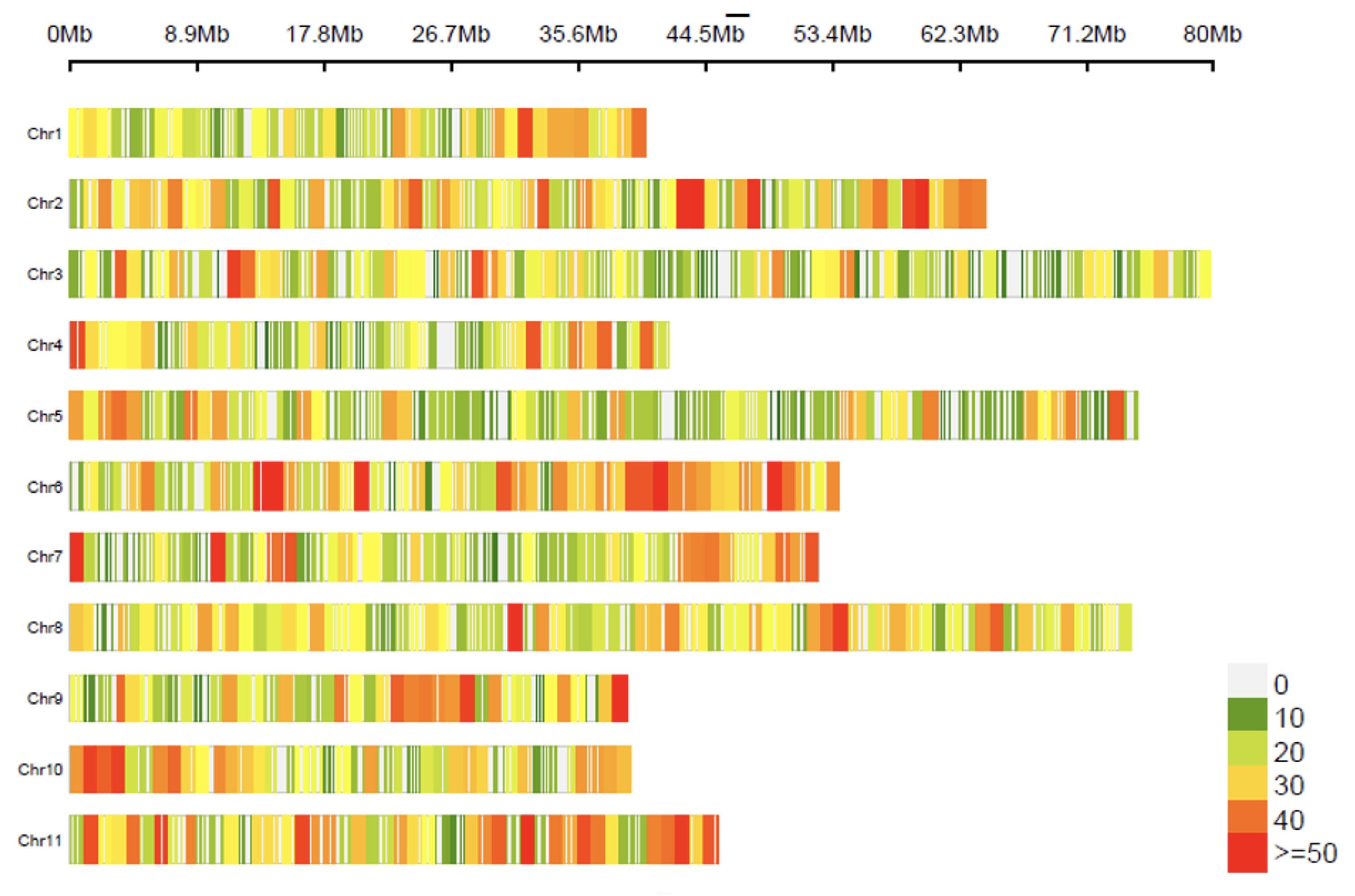
The SNP markers were distributed throughout the 11 chromosomes according to the E. grandis reference genome, where the number of SNPs is summed within adjacent 1 Mb windows (Figure 2). Chromosomes 1, 4, 9 and 10 were those that presented the fewest markers and chromosomes 3, 5 and 8 those that presented the most.

3.1. Genomic Information

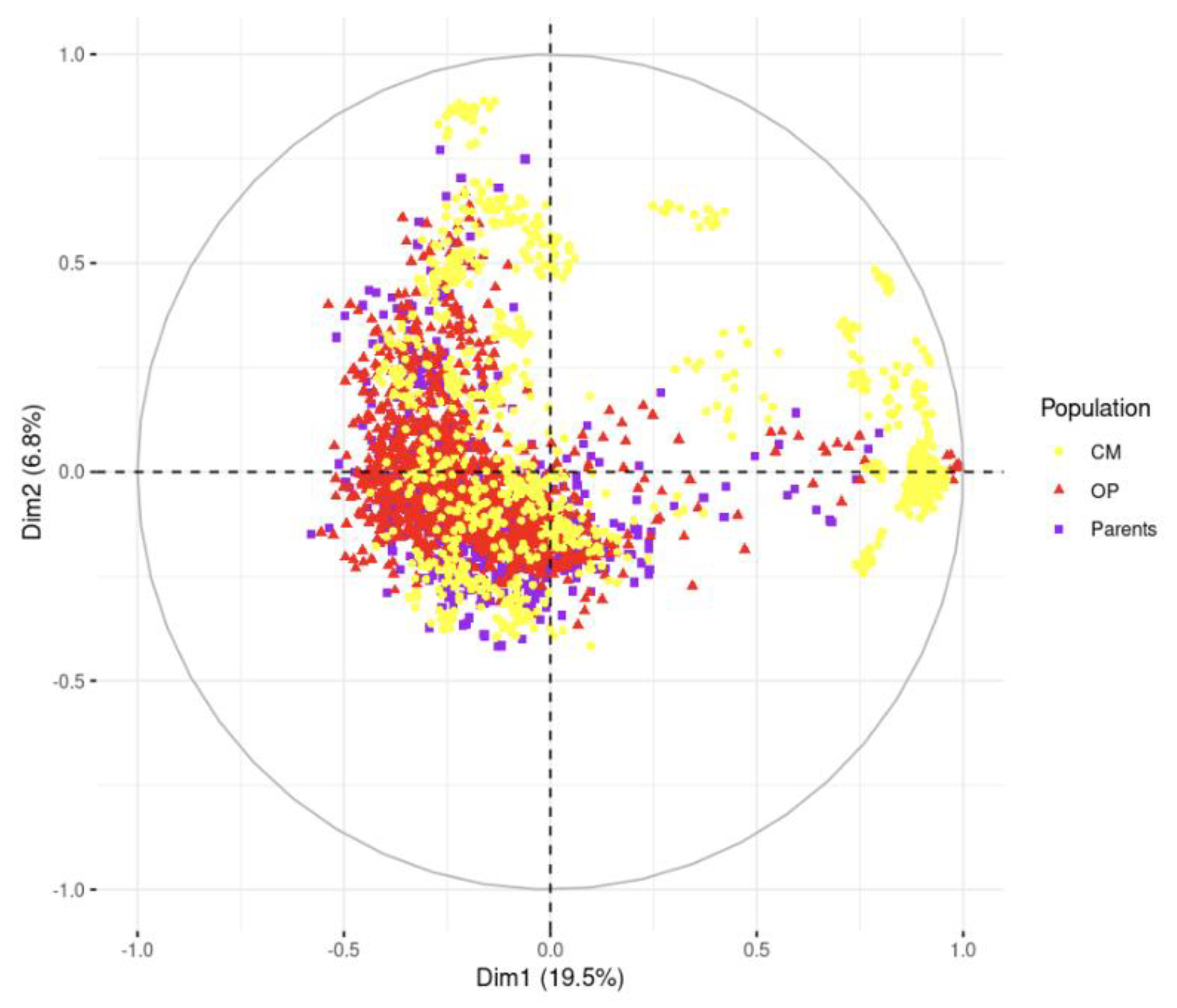
The PCA showed the diversity and population structure present in the studied population (Figure 3). The first two principal components explained 19.5% and 6.8% of the total variation, respectively.

3.2. Multitrait Threshold Linear Model ssGWAS

The genetic correlations for all traits were positive, moderate to high, ranging from 0.51 to 0.97 (Table 2). DBH exhibited the strongest correlation with all traits. The biggest correlation presented ADFO between 14 and 21 months. The heritabilities estimated were high for disease resistance traits (ADFO 14 and ADFO21), and lower for HT and DBH, being DBH moderately higher than HT. The heritability varied from 0.37 to 0.84.

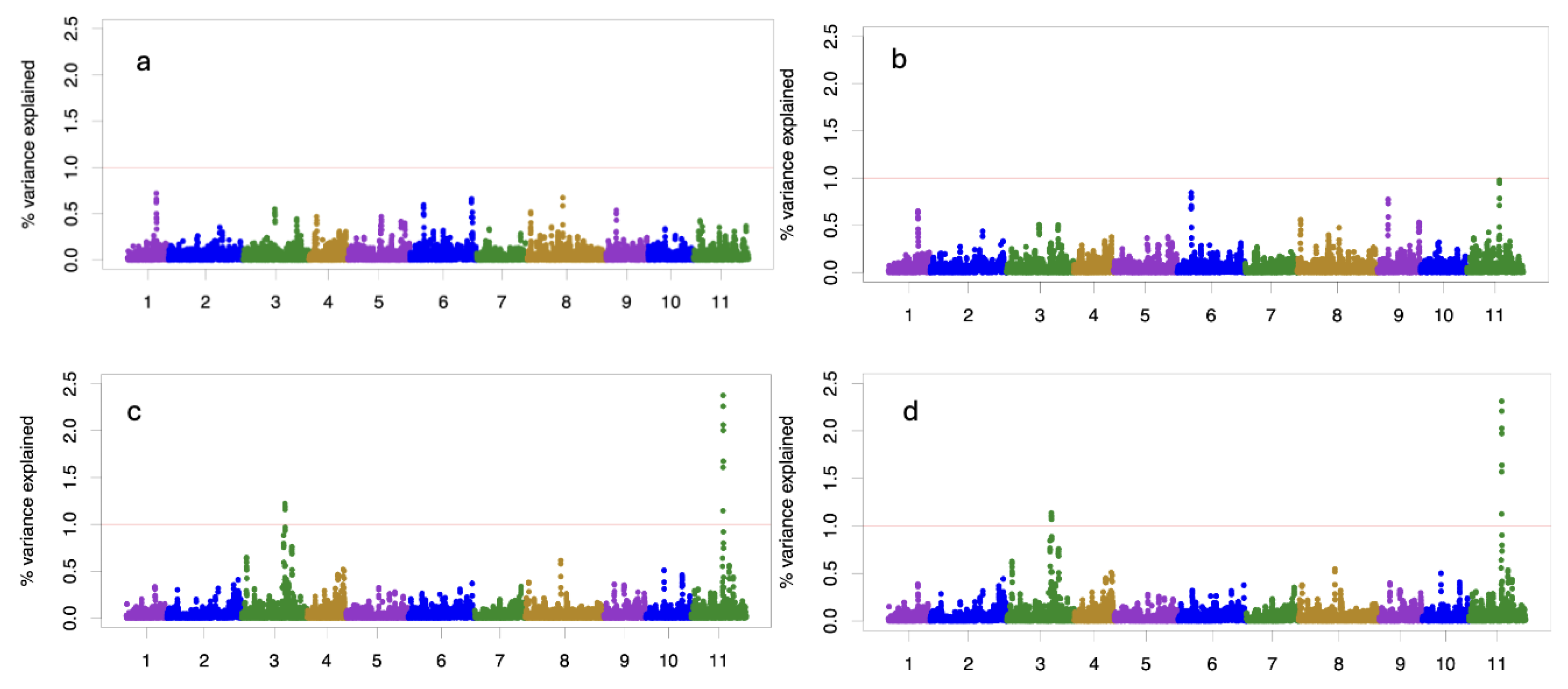
The windows are overlapping with a mean of 12 snps, from 4 to 22 snps per windows 0.2 Mb. The variance explained by 0.2 Mb window for the growth traits (TH and DBH) is less than 1.0% with homogenous distribution across all chromosomes (Figure 4). The variance explained for the windows for ADFO14 and ADFO21 is greater than 1% in chromosomes 3 and 11, reaching 2.5 % of the variance explained in the chromosome 11.

3.3. QTL Identifications

In growth traits, no QTL were found that explained more than 1% of the variance. However, two genomic regions (QTLs) were found related with precocity of vegetative change (ADFO) measured at different ages (14 and 21 months). These genomic regions explained more than 1% of total variance (Table 3). These QTLs are in the chromosome 3 and 11, ranging between 14 to 17 SNPs per window 0.2Mb, respectively.

4. Discussion

In several countries foliar diseases had caused devastating damages in young plantations of E. globulus and the sustainability of this species depends on the rapid development of resistant genetic stock [44]. Some studies have focused on this issue, such as those by Giorello et al.[45] and Quezada et al. [43], evaluating heteroblasty as a form of escape to Teratosphaeria nubilosa. This study represents an additional step toward identifying genomic regions that code for complex traits, such as growth and escape from T. nubilosa, in E. globulus. Despite the population in study is not a diverse panel, associations between SNPs and phenotype were found. Although less genetic variation is available in an operational breeding population, associations found should be considerably more useful to inform practical breeding decision [46,47]. In this work, we were able to evaluate the performance of multi-trait linear-threshold ssGWAS approach by window in operational breeding populations.

The estimation of genetic parameters plays a crucial role in the management of seed orchards and provides valuable guidance for developing the evaluation and selection strategy for the next generation of improvement [48,49]. Positive and high genetics correlations (r_g 0.97) between ADFO measuring in two stages (14 and 21 months) is a strong indicative that is posible evaluate in an early stage (14 months), being ADFO at 14months a good indicative of ADFO at 21 months, reducing time of measuring. The estimated of heritabilities for ADFO suggested a strong genetic control, 0.84 and 0.86 for ADFO14 and ADFO21, respectively. [43] studied the same traits in E.globulus and reported similar results for heritability 0.68, 0.66 and 0.77 for ADFO at 14, 21 and 26 months, respectively. These results confirm the strong genetic control in this trait and suggested that the expected responses to selection for resistance disease are relatively favorable. HT and DBH showed a lower genetic control with h² 0.37 and 0.53, respectively. According with other works in E. globulus that reported similar heredabilities for TH and DBH, varing from 0.20 to 0.43 for TH and 0.20 to 0.50 for DBH [30,50].

The multi-trait threshold ssGWAS was useful for identifying markers contained in genomic regions that explained more than 1% variance for disease resistance traits (ADFO14 and ADFO21). Fernando et al. [51], affirm that most GWA studies are based on inferences involving joint tests on all the SNP markers within a narrow genomic region, recognizing that single SNP marker associations may be fraught by low statistical power, problems with multicollinearity or both. Quezada et al. [43], suggest that ssGWAS is a powerful model in detecting regions associated to the escape to T. nubilosa, showing a greater number of significant SNP associations than Single-SNP and GBLUP-GWAS models. Porter and O’ Reilly [52] reported that multi-trait GWAS can be used to analyze multiple traits simultaneously and was developed to increase statistical power and identify pleiotropic loci. Additionally, Fernandes et al. [53] affirm that multi-trait GWAS is a useful addition to the suite of statistical models that are commonly used to gain insight into the genetic architecture of agronomically important traits. Misztal et al. [54] suggested the ssGWAS is a potentially useful tool for GWAS when the population contains large number of genotypes and especially if models of analyses are complex.

The growth traits (TH and DBH) showed a typical polygenic behavior where the entire genome contributed to their variation, but no genomic region explained more than 1% of the total variation. This result confirms what has been reported in other studies, corroborating the complex architecture of growth traits and the pleiotropic effect among loci for growth traits [55,56]. Rocha et al. [56] found significant associations in E. grandis between DBH, TH and volume measured in different years of data sampling, indicating a strong pleiotropic effect on trait association. ADFO traits showed less polygenic behavior than growth traits, being the genomic regions of chromosomes 3 and 11 which presents the larger effects. These results confirm what was reported in the literature, where chromosomes 3 and 11 are the main responsible for disease traits in Eucalyptus spp [43,45,57]. Therefore, there is strong evidence that studying both chromosomes (3 and 11) we can understand better the control of heteroblasty.Quezada et al. [43] reported QTLs related with ADFO in similar genomic regions studied in this work. The main genes they found linked to most SNPs associated with precocity of vegetative change (ADFO at 14 and 21 months) were in chromosome 3, between position 48526965 and 50801384 Mb. The chromosome 11 contains two genes related to biotic stress resistance, miR157 precursor and Glutathione transferase GST 23, between 29630035 and 29646703 Mb, being these genomic regions relevant to ADFO.

The multi-trait threshold linear ssGWAS allowed the identification of genomic regions (chromosomes 3 and 11) involved in escape to foliar pathogens that coincide with what has been reported in the literature [43,58,59,60]. These regions contain genes that lead the resistance against biotic stresses, including defense responses to fungus infection [61,62]. The miR156 and miR157 has been recognized as the major regulator of vegetative change in plants, promoting juvenility due to high expression in seedlings and decreasing during the development, causing difference in the timing of vegetative phase change [43,45,63,64,65].

5. Conclusions

This study enabled the estimation of genetic correlations and narrow sense heretabilities for disease and growth traits. It also showed that multi-trait threshold linear ssGWAS model allowed the identification of genomic regions that codify for traits related resitance desease, such as adult foliage portion in canopy, as a escape way of infect for T. nubilosa. Allowing for a focus on and deeper exploration of these genomic regions to understand the behavior of these types of traits. In contrast with growth traits (TH and DBH) that showed a typical polygenic behavior, and no genomic region explained more than 1% of the total variation.