Submitted:
12 December 2024
Posted:
14 December 2024
You are already at the latest version
Abstract
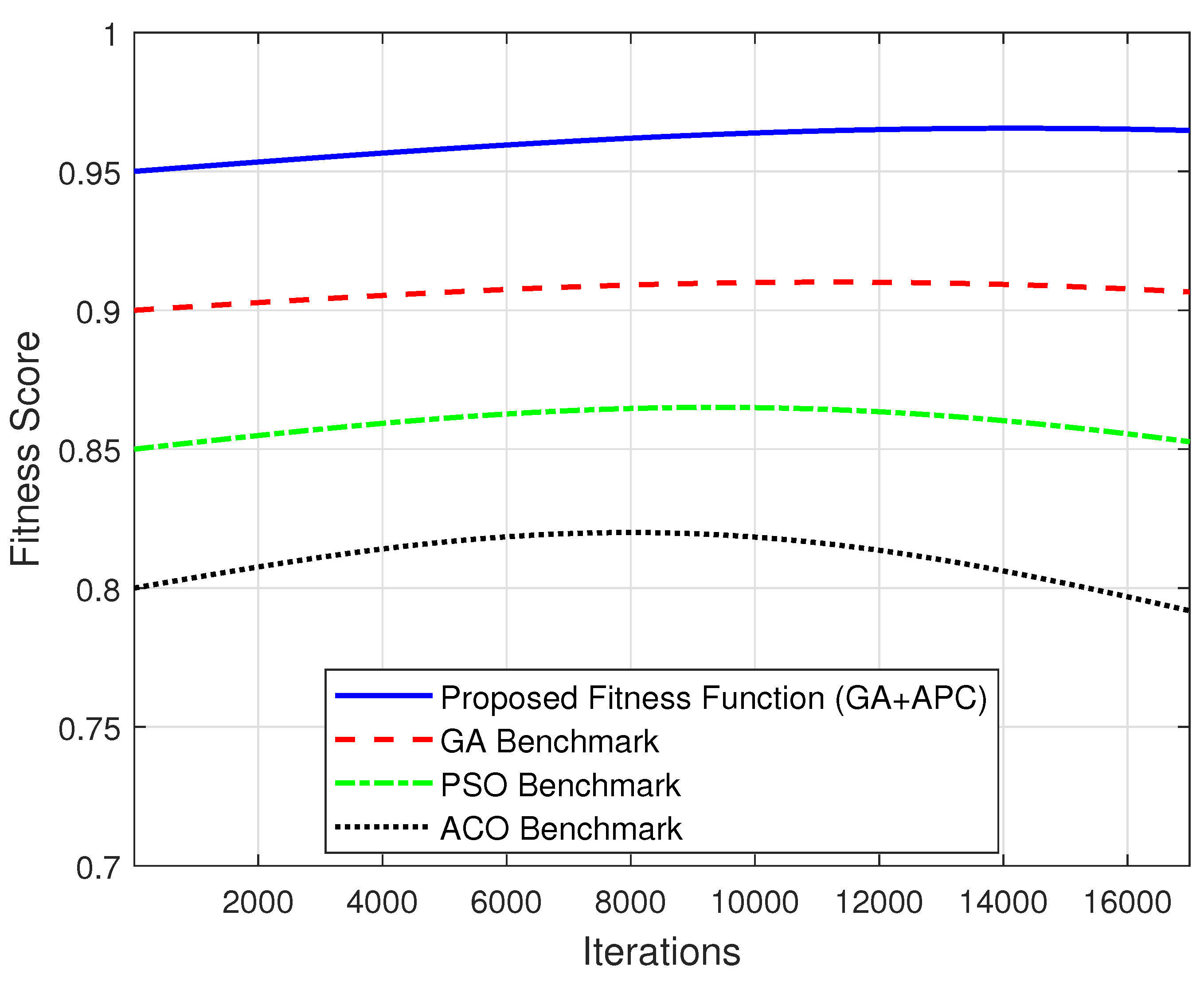
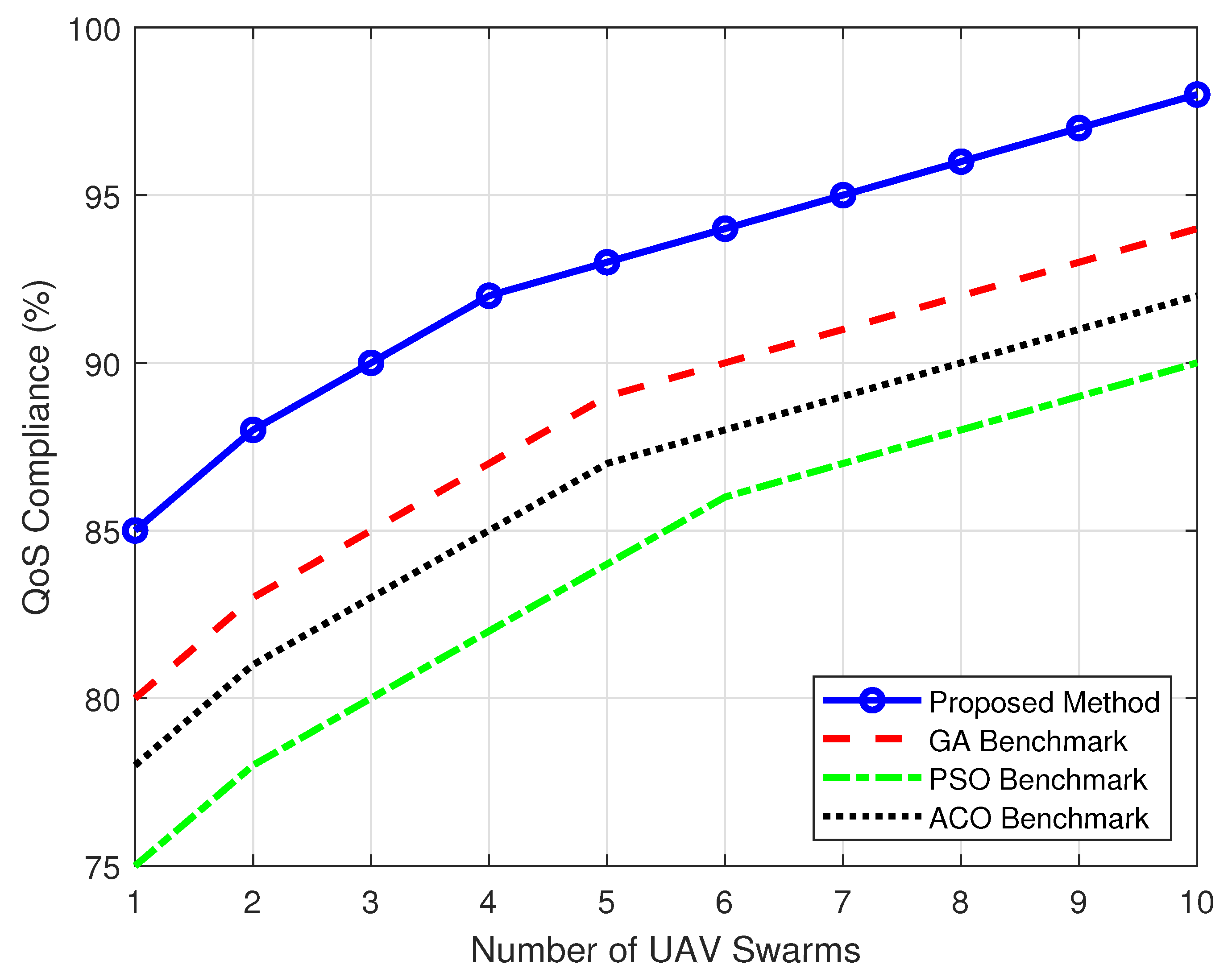
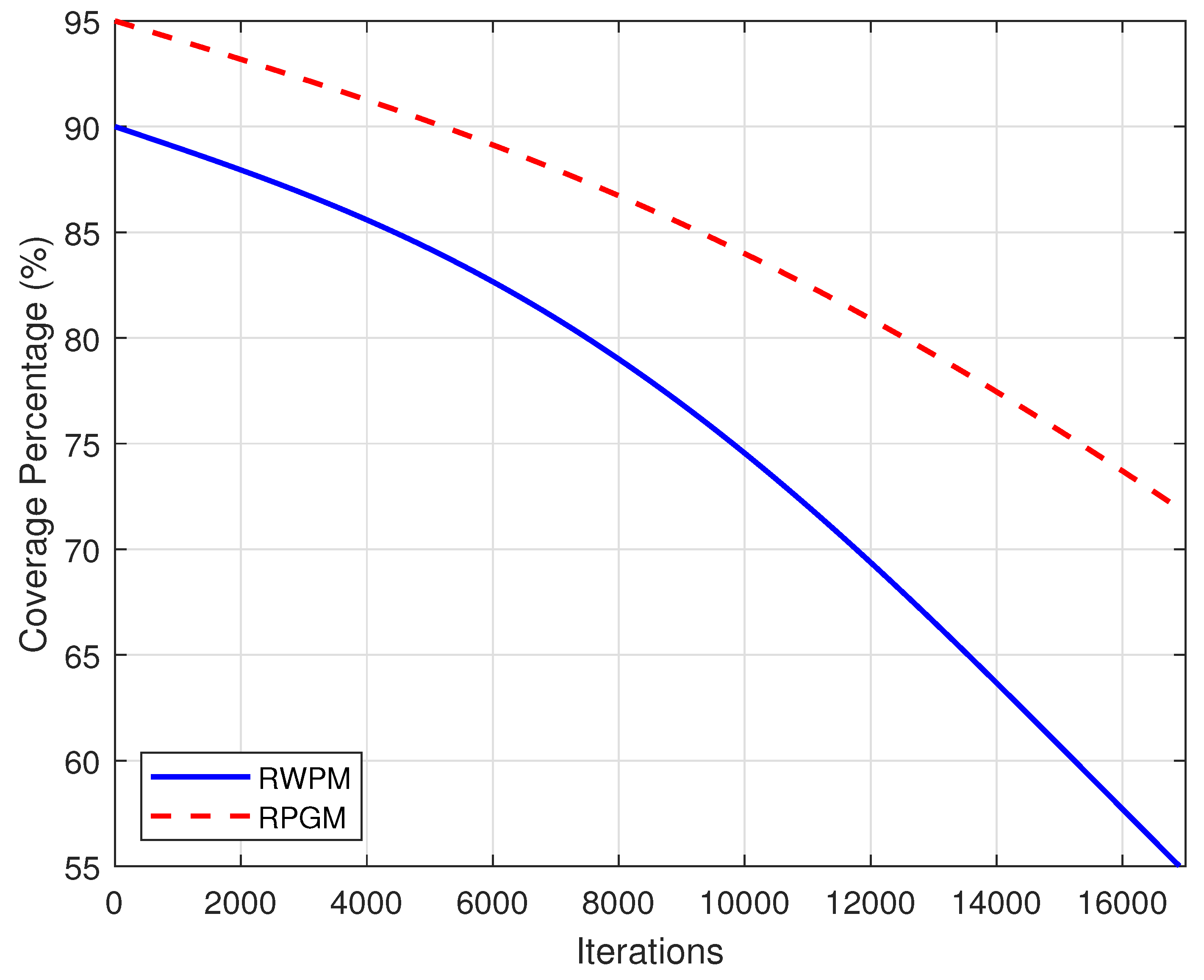
In disaster-stricken areas, rapid restoration of communication infrastructure is critical to ensuring effective emergency response and recovery. Swarm UAVs, operating as mobile aerial base stations (MABS), offer a transformative solution for bridging connectivity gaps in environments where traditional infrastructure has been compromised. This study presents a novel hybrid path-planning approach combining Affinity Propagation Clustering (APC) with Genetic Algorithms (GA), aimed at maximizing coverage, minimizing energy consumption, and ensuring Quality of Service (QoS) compliance across diverse environmental conditions. Comprehensive simulations conducted in suburban, urban, dense urban, and high-rise urban environments demonstrated the efficacy of the APC-GA approach. The proposed method achieves up to 100% coverage in suburban settings with only eight unmanned aerial vehicle (UAV) swarms and maintains superior performance in dense and high-rise urban environments, achieving 97% and 93% coverage, respectively, with 10 UAV swarms. The QoS compliance reached 98%, outperforming benchmarks such as GA (94%), PSO (90%), and ACO (88%). The solution exhibited significant stability, maintaining an average fitness score of 0.95 over 17,000 iterations, highlighting its robustness under dynamic disaster scenarios. The mobility model analysis further underscores the adaptability of the proposed approach. The Reference Point Group Mobility (RPGM) model consistently achieved higher coverage rates (95%) compared to Random Waypoint Model (RWPM) (90%), demonstrating the importance of group-based mobility patterns in enhancing UAV deployment efficiency. The findings reveal that the APC-GA adaptive clustering and path-planning mechanisms effectively navigate propagation challenges, interference, and NLOS conditions, ensuring reliable connectivity in the most demanding environments. This research establishes the APC-GA hybrid as a scalable and QoS-compliant solution for UAV deployment in disaster response scenarios. By dynamically adapting to environmental complexities and user mobility patterns, it advances state-of-the-art emergency communication systems, offering a robust framework for real-world applications in disaster resilience and recovery.
Keywords:
1. Introduction
1.1. Problem Identification and Novelty
- Seamless User Allocation: In disaster zones, users frequently move between service areas, creating challenges for maintaining uninterrupted connectivity. Optimized UAV paths are required to dynamically adapt to user transitions.
- Coverage Maximization: Traditional UAV routing strategies often focus on cluster centroids, potentially neglecting users located in peripheral areas. This study emphasizes a routing approach that ensures complete coverage while maintaining energy efficiency.
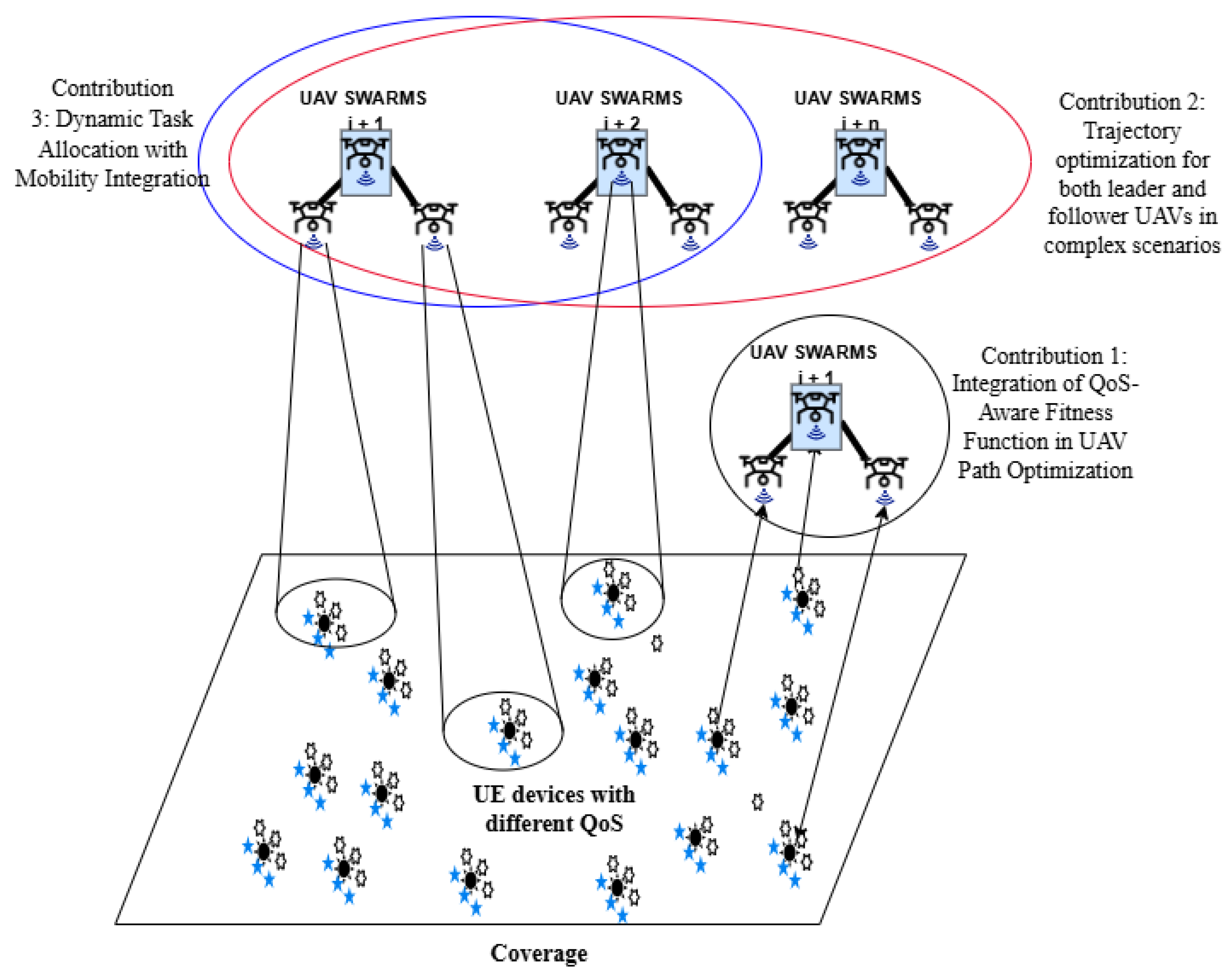
1.2. Novel Contributions and Approach
- A QoS-Aware Fitness Function for UAV Swarm Optimization: A multi-metric fitness function is proposed, integrating path length, energy consumption, and Signal-to-Interference-plus-Noise Ratio (SINR-based) QoS compliance. This ensures that UAVs maintain efficient and interference-free communication while minimizing resource consumption.
- An APC-GA Hybrid Framework for UAV Path Planning: The paper introduces a novel hybrid algorithm that utilizes APC for dynamic user grouping and customized mutation operators for UAV-specific optimization. These enhancements improve adaptability and efficiency in complex environments.
- Real-Time Mobility Integration: The proposed framework incorporates user mobility into the clustering and optimization process, enabling UAV swarms to dynamically adjust their paths and maintain consistent coverage as user distributions change.
1.3. Organization of This Paper
2. Related Works
2.1. UAV Swarm Optimization Techniques
2.2. Clustering Methods in UAV Applications
2.3. Metaheuristic Algorithms for Disaster Response
2.4. Recent Advances in UAV-Assisted Communication
2.5. Research Gap and Contribution
- Integration of Mobility Prediction with Clustering: Most studies fail to incorporate predictive mobility models into clustering algorithms, essential for proactive UAV positioning and resource allocation.
- QoS-Aware Decision-Making: Few approaches consider real-time QoS metrics, such as latency, throughput, and reliability, during UAV deployment and trajectory planning.
- Dynamic Adaptability in Disaster Environments: Traditional optimization methods often rely on static assumptions or offline training, limiting their ability to adapt to rapidly changing disaster conditions.
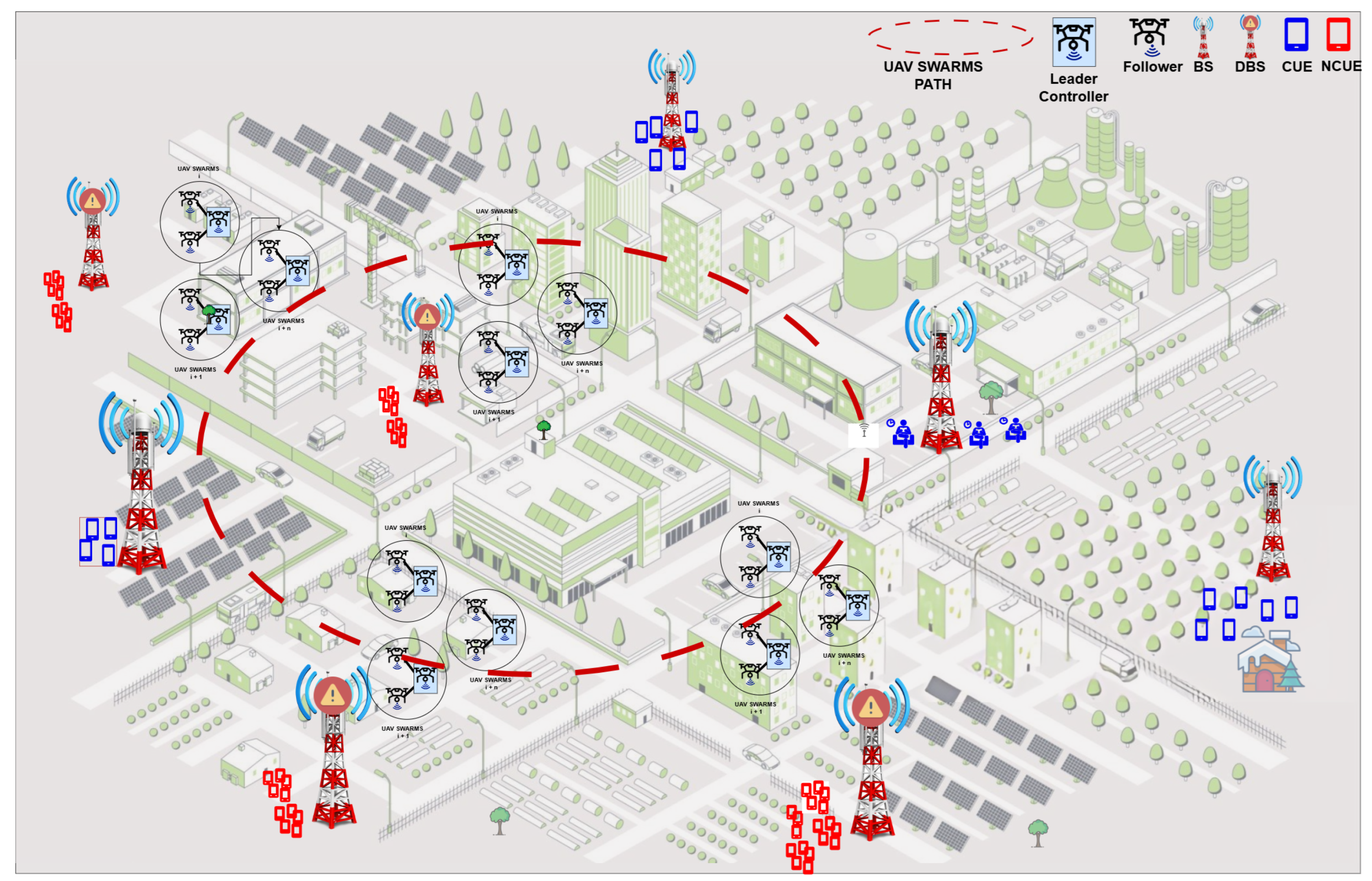
3. Environment Modelling
- In urban areas, UAVs navigate through dense building structures, avoiding obstructions and optimizing communication links for effective service delivery.
- In suburban settings, UAVs utilize clustering techniques to distribute coverage efficiently, addressing the broader spacing between UEs.
- For dense urban regions, the swarm handles high UE densities, managing interference and ensuring consistent data rates even in congested zones.
- In high-rise urban environments, the system dynamically adjusts UAV altitudes, enabling vertical coverage for multi-story buildings and skyscrapers.
- Transmission Power Levels: The UAV transmission power () is configured at 30 dBm to balance coverage and energy efficiency. In comparison, the BSs are assumed to transmit at 46 dBm for a more extensive reach. The UE power is capped at 10 dBm to conserve device energy without sacrificing communication quality.
- Interference Management: By incorporating interference from other UAVs, the SINR model reflects realistic swarm dynamics, where overlapping coverage areas may degrade communication quality.
- MIMO Configurations: Leveraging multiple-input, multiple-output (MIMO) technology, the system can support simultaneous connections to multiple UEs, enhancing data throughput and spectral efficiency. This is particularly critical in high-density, highly mobile environments.
3.1. Path Loss Modeling
3.1.1. General Path Loss Model
3.1.2. Calculation of Parameter A
3.1.3. Calculation of Parameter B
- Random Waypoint Mobility:where is the distance travelled by the UE once and step R is the UAV’s communication range.
- Reference Point Group Mobility:where denotes the group-specific deviation factor.
3.2. Problem Definition
3.3. Parameter Settings
4. Proposed Optimal Path Planning for Uav Swarms
4.1. Integration of Proposed Fitness Function and Swarm Mutation Strategies
| Algorithm 1:Swarm Initialization and UE Clustering |
|
Data: : Number of UAVs, : UE distribution, : UE mobility speed, M: Mobility model, E: Environment parameters.
Result: Cluster assignments V, initial paths .
Step 1: Swarm Role Assignment
Define swarm UAV roles:
Step 2: UE Initialization
Initialise the UE positions:
Mobility model M is applied to compute the UE movement:
Step 3: UE Clustering using APC
Compute the cluster centres .
Step 4: Path Initialization
Assign tasks to UAVs from cluster centre V.
Step 5: Cluster Re-Evaluation and Mobility Integration
Update the cluster centres V dynamically if the UE positions change.
Recompute paths for all UAVs.
Step 6: Output Results
returnV, .
|

4.2. Integration of the Proposed Advanced Fitness Function with QoS, Capacity Constraints, and Mutation for Optimization

5. Performance Evaluation of Proposed Solution
5.1. Evaluation Criteria and Experimental Setup
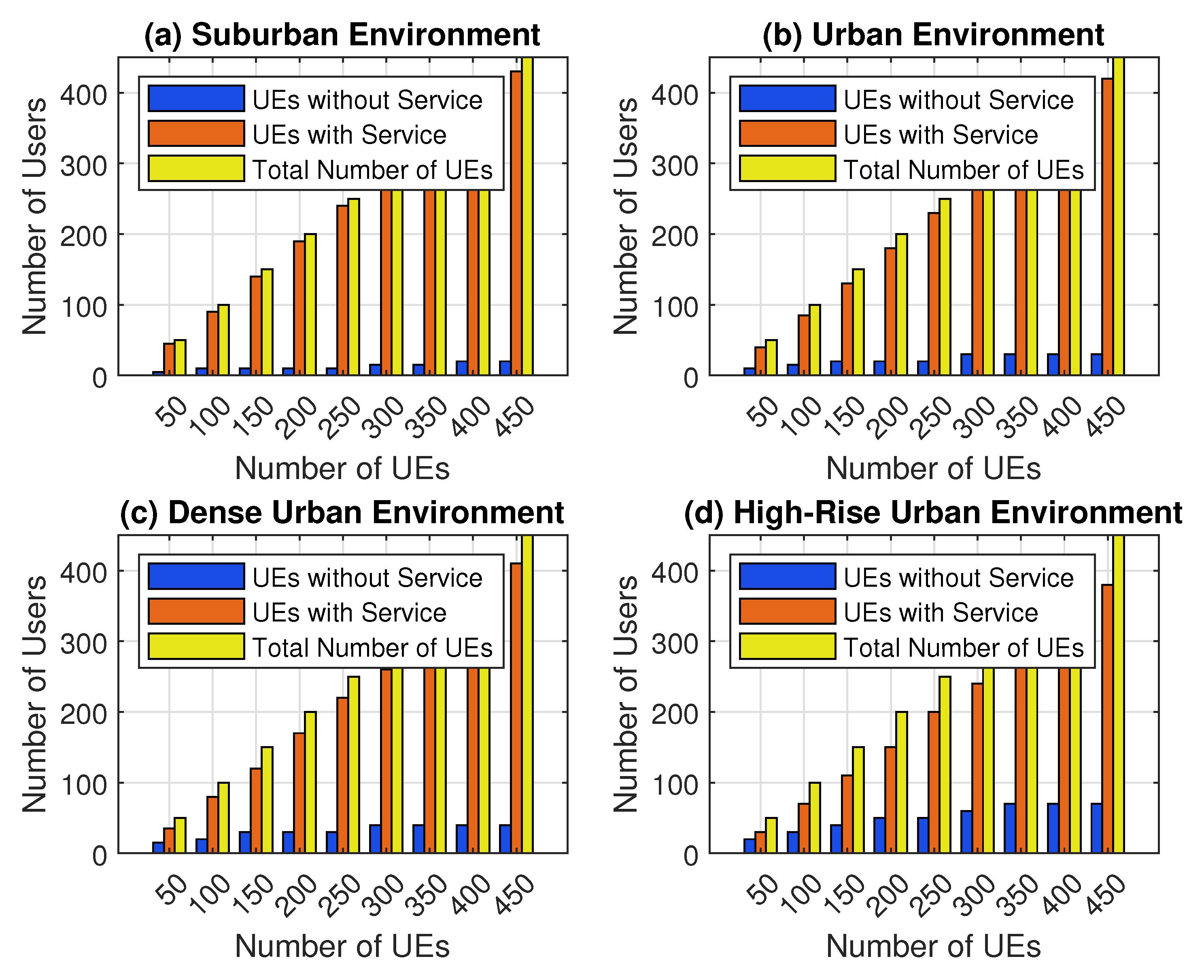
5.2. Coverage Ratio vs Number of UAV Swarms
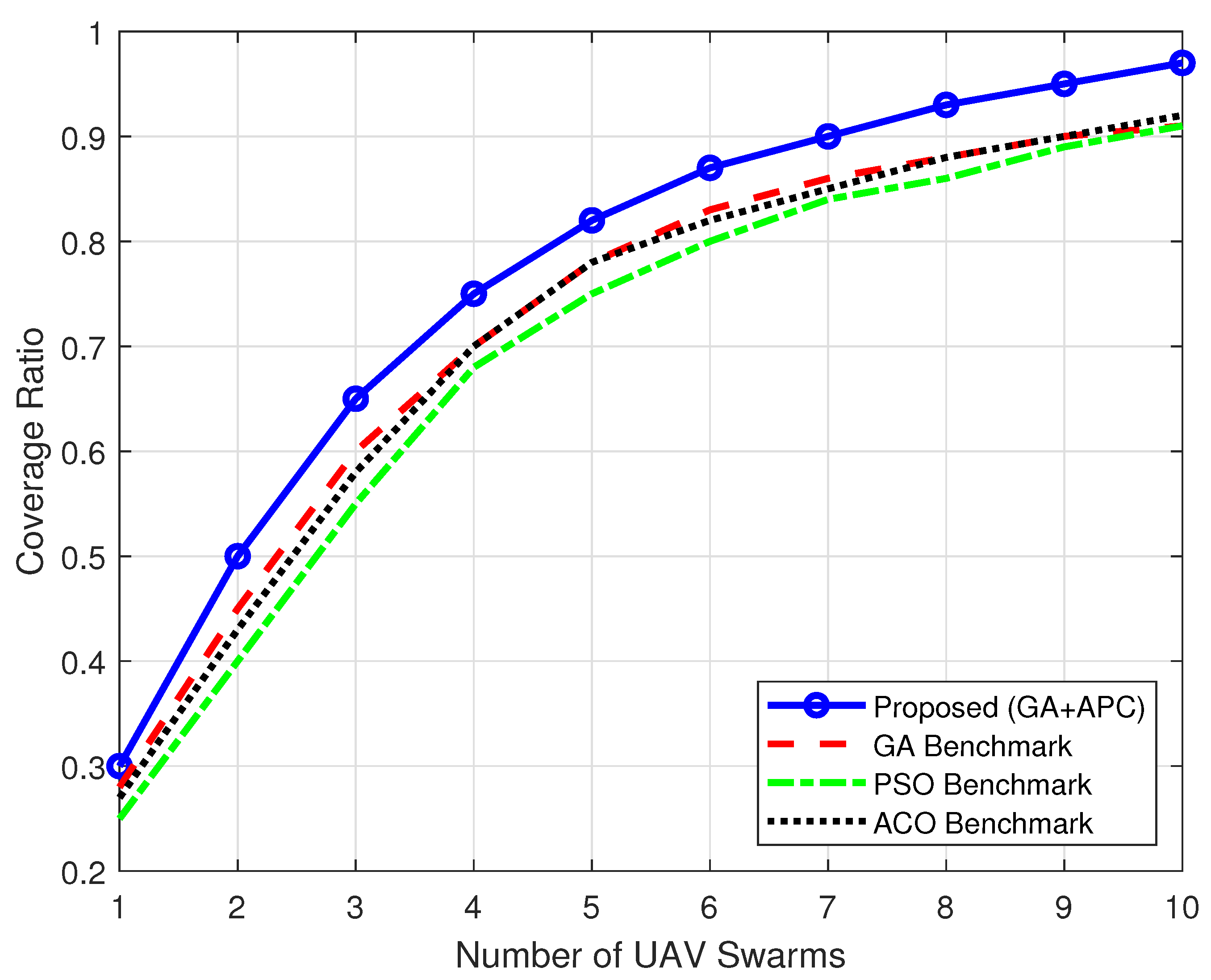
5.2.1. Dense Urban Environment
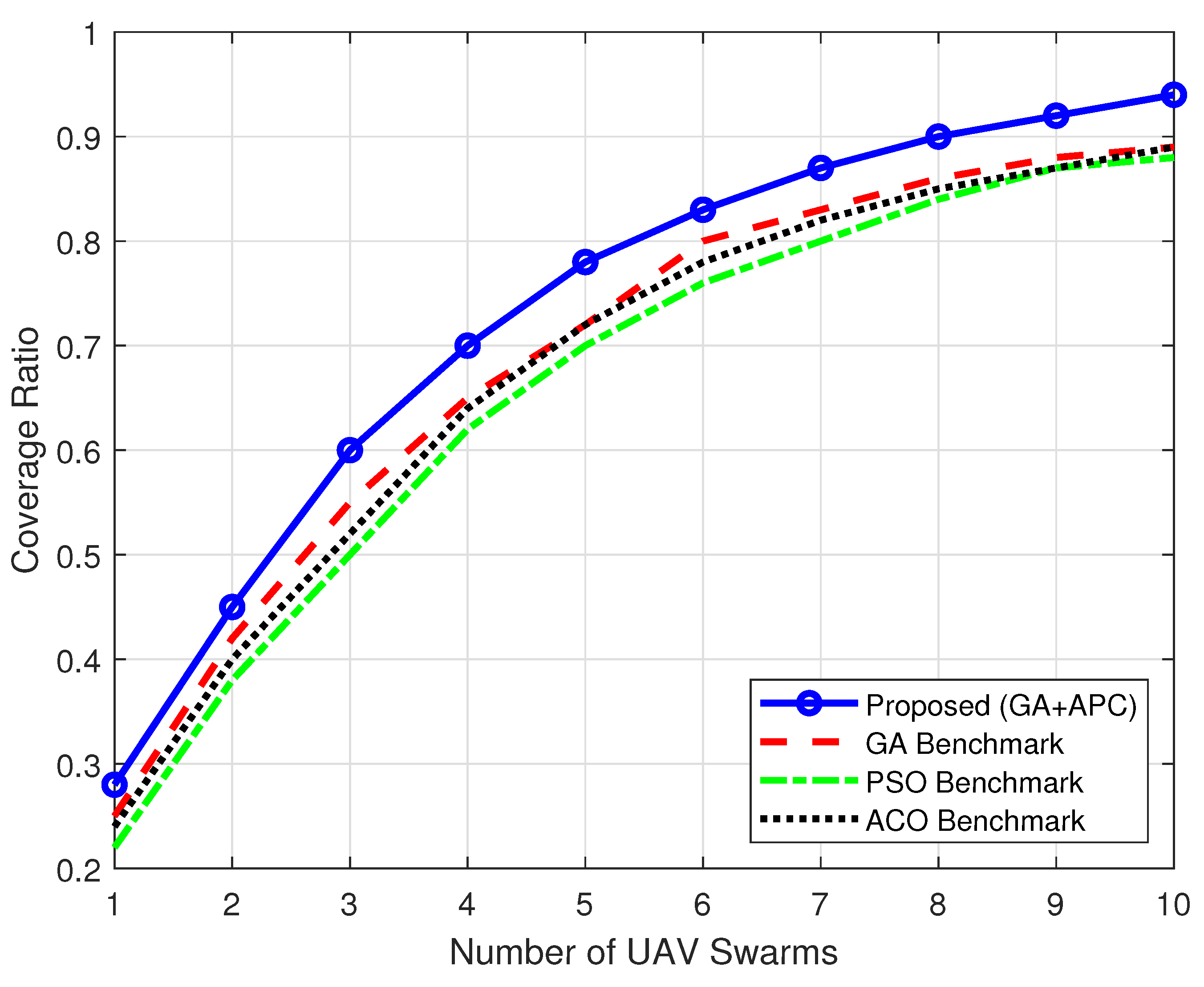
5.2.2. Urban Environment
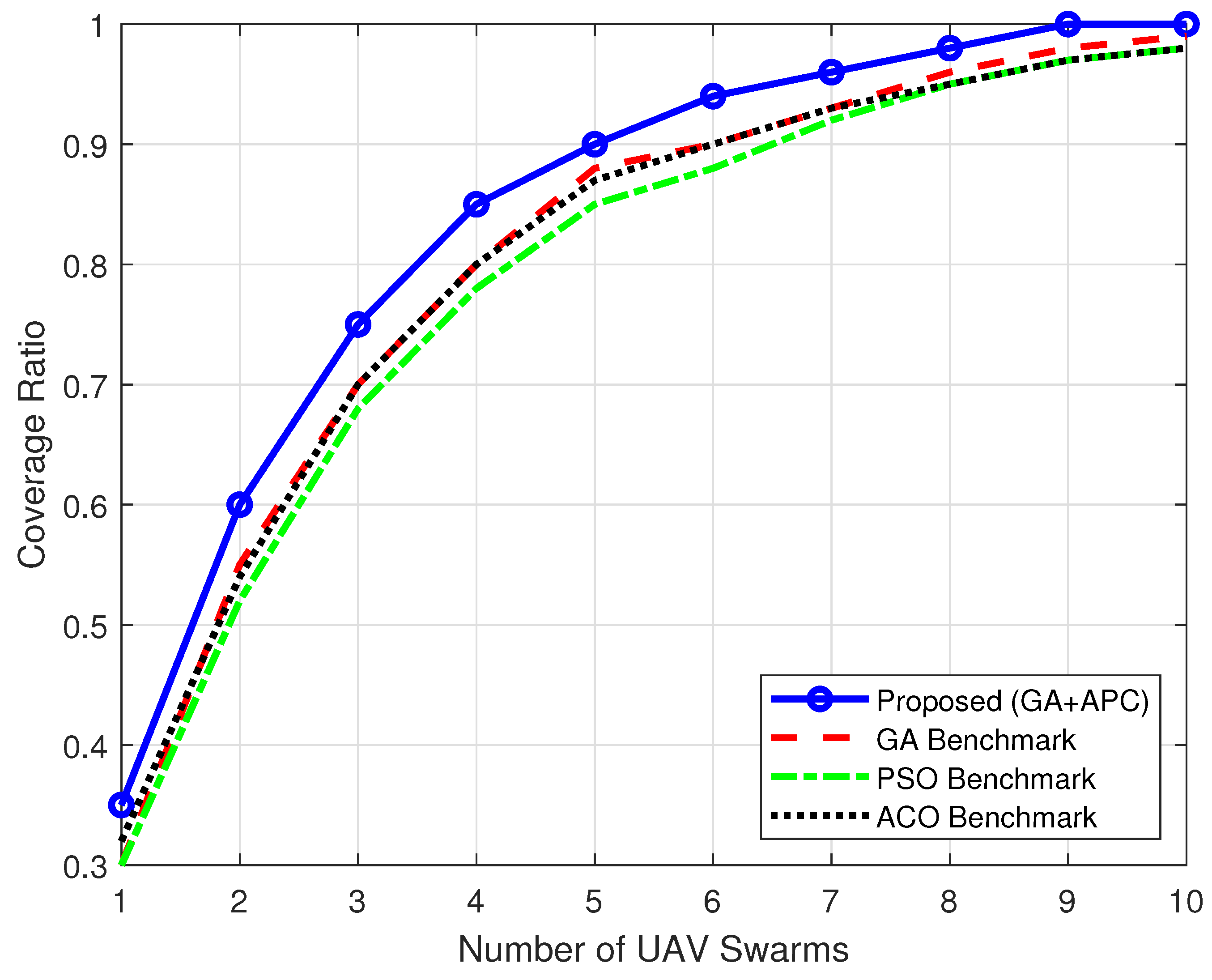
5.2.3. Suburban Environment
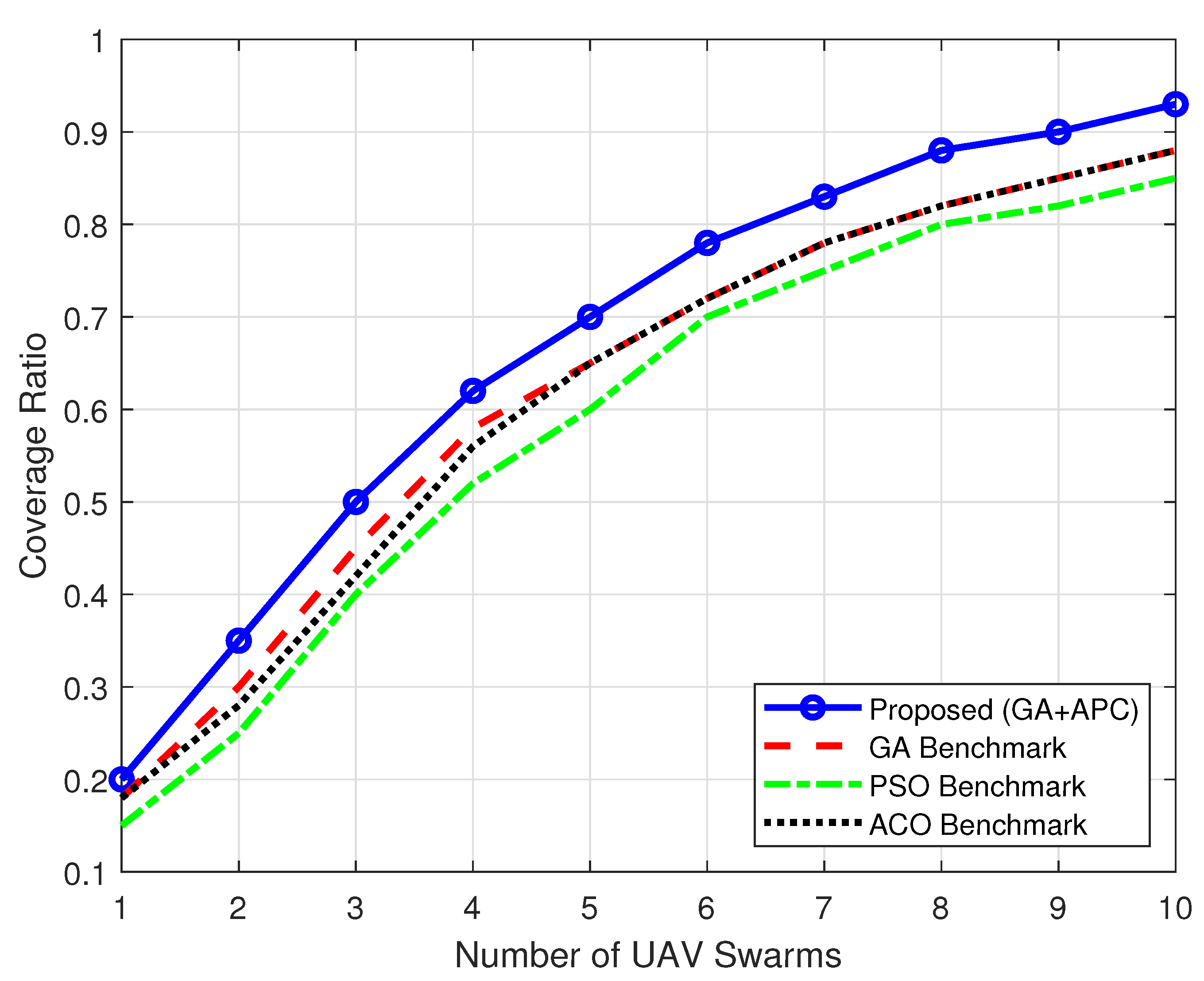
5.2.4. High-Rise Urban Environment
5.3. Fitness Score vs. Iterations
5.4. QoS Compliance vs. Number of UAV Swarms
5.5. Mobility Impact on Coverage
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACO | Ant Colony Optimization |
| AGA | Adaptive Genetic Algorithms |
| A | Frequency Incidence factor |
| AR | Angle Ratio |
| and Env | Environment Correction factors |
| B | Base Station Antenna Height factor |
| BS | Base Station |
| BPS | Bits Per Second |
| bps | Bits Per Second |
| Bw | Bandwidth for a channel in Hz |
| C | Capacity |
| C | Capacity in bps |
| CHs | Cluster Heads |
| COW | Cell on Wings |
| CSV | Comma-Separated Values |
| D2D | Device-to-Device |
| DCUD | Distributed Clustering for User Devices |
| DDQN | Double Deep Q-Networks |
| DR | Distance Ratio |
| DRN | Disaster Response Networks |
| EH | Energy Harvesting |
| ƒ | Frequency in MHz |
| FPA | Flower Pollination Algorithm |
| GA | Genetic Algorithm |
| GHO | Grasshopper Optimization |
| hb | Height of the Base Station |
| hm | Height of the Mobile Aerial Base Station |
| HZ | Hertz |
| ILP | Integer Linear Programming |
| IMSIA | Improved Multiobjective Swarm Intelligence Algorithm |
| IoT | Internet of Things |
| IQR | Interquartile Range |
| IR | Intersection Ratio |
| KBPS | Kilobits Per Second |
| LOS | Line of Sight |
| LTE | Long-Term Evolution |
| mMTC | massive Machine-Type Communications |
| MABS | Mobile Aerial Base Stations |
| Mbps | Megabits per second |
| MHZ | Megahertz |
| MIMO | Multiple-Input Multiple-Output |
| PL | Path Loss |
| PSO | Particle Swarm Optimization |
| PSR | Path Smoothness Ratio |
| QoS | Quality of Service |
| RoI | Region of Interest |
| RPGM | Reference Point Group Mobility |
| RWPM | Random Waypoint Model |
| SFOA | Smart Flower Optimization Algorithm |
| SILC | Swarm Intelligence-based Localization and Clustering |
| SNR | Signal-to-Noise Ratio |
| SINR | Signal-to-Interference-plus-Noise Ratio |
| SR | Service Ratio |
| UE | User Equipment |
| UAVs | Unmanned Aerial Vehicles |
| URLLC | Ultra-Reliable, Low-Latency Communication |
| VD | Voronoi Diagram |
| VDG | Voronoi Diagram Graph |
| WPT | Wireless Power Transfer |
| Density value for Poisson Distribution |
References
- Behjati, M.; Zulkifley, M.A.; Alobaidy, H.A.; Nordin, R.; Abdullah, N.F. Reliable aerial mobile communications with RSRP & RSRQ prediction models for the Internet of Drones: A machine learning approach. Sensors 2022, 22, 5522. [Google Scholar] [CrossRef] [PubMed]
- Behjati, M.; Nordin, R.; Zulkifley, M.A.; Abdullah, N.F. 3D global path planning optimization for cellular-connected UAVs under link reliability constraint. Sensors 2022, 22, 8957. [Google Scholar] [CrossRef]
- Qadir, Z.; Ullah, F.; Munawar, H.S.; Al-Turjman, F. Addressing disasters in smart cities through UAVs path planning and 5G communications: A systematic review. Computer Communications 2021, 168, 114–135. [Google Scholar] [CrossRef]
- Sánchez-García, J.; Reina, D.G.; Toral, S. A distributed PSO-based exploration algorithm for a UAV network assisting a disaster scenario. Future Generation Computer Systems 2019, 90, 129–148. [Google Scholar] [CrossRef]
- Hydher, H.; Jayakody, D.N.K.; Hemachandra, K.T.; Samarasinghe, T. Intelligent UAV deployment for a disaster-resilient wireless network. Sensors 2020, 20, 6140. [Google Scholar] [CrossRef]
- Liu, H.; Ge, J.; Wang, Y.; Li, J.; Ding, K.; Zhang, Z.; Guo, Z.; Li, W.; Lan, J. Multi-UAV optimal mission assignment and path planning for disaster rescue using adaptive genetic algorithm and improved artificial bee colony method. Actuators 2021, 11, 4. [Google Scholar] [CrossRef]
- Li, J.; Lu, D.; Zhang, G.; Tian, J.; Pang, Y. Post-disaster unmanned aerial vehicle base station deployment method based on artificial bee colony algorithm. IEEE Access 2019, 7, 168327–168336. [Google Scholar] [CrossRef]
- Demir, K.; Tumen, V.; Kosunalp, S.; Iliev, T. A Deep Reinforcement Learning Algorithm for Trajectory Planning of Swarm UAV Fulfilling Wildfire Reconnaissance. Electronics 2024, 13, 2568. [Google Scholar] [CrossRef]
- Montero, E.; Rocha, C.; Oliveira, H.; Cerqueira, E.; Mendes, P.; Santos, A.; Rosário, D. Proactive radio-and QoS-aware UAV as BS deployment to improve cellular operations. Computer Networks 2021, 200, 108486. [Google Scholar] [CrossRef]
- Wan, Y.; Zhong, Y.; Ma, A.; Zhang, L. An accurate UAV 3-D path planning method for disaster emergency response based on an improved multiobjective swarm intelligence algorithm. IEEE Transactions on Cybernetics 2022, 53, 2658–2671. [Google Scholar] [CrossRef] [PubMed]
- Masroor, R.; Naeem, M.; Ejaz, W. Efficient deployment of UAVs for disaster management: A multi-criterion optimization approach. Computer Communications 2021, 177, 185–194. [Google Scholar] [CrossRef]
- Liu, J.; Liao, X.; Ye, H.; Yue, H.; Wang, Y.; Tan, X.; Wang, D. UAV swarm scheduling method for remote sensing observations during emergency scenarios. Remote Sensing 2022, 14, 1406. [Google Scholar] [CrossRef]
- Zhou, P.; Xie, Z.; Zhou, W.; Tan, Z. A Heuristic Integrated Scheduling Algorithm Based on Improved Dijkstra Algorithm. Electronics 2023, 12, 4189. [Google Scholar] [CrossRef]
- Arafat, M.Y.; Moh, S. Localization and clustering based on swarm intelligence in UAV networks for emergency communications. IEEE Internet of Things Journal 2019, 6, 8958–8976. [Google Scholar] [CrossRef]
- Hamid, H.; Begh, G. Clustering based strategic 3D deployment and trajectory optimization of UAVs with A-star algorithm for enhanced disaster response. Physical Communication 2024, 102536. [Google Scholar] [CrossRef]
- Saif, A.; Dimyati, K.; Noordin, K.A.; Shah, N.S.M.; Alsamhi, S.; Abdullah, Q.; Farah, N. Distributed clustering for user devices under UAV coverage area during disaster recovery. 2021 IEEE International Conference in Power Engineering Application (ICPEA). IEEE, 2021, pp. 143–148.
- Javed, S.; Hassan, A.; Ahmad, R.; Ahmed, W.; Alam, M.M.; Rodrigues, J.J. UAV trajectory planning for disaster scenarios. Vehicular Communications 2023, 39, 100568. [Google Scholar] [CrossRef]
- Kamyabniya, A.; Sauré, A.; Salman, F.S.; Bénichou, N.; Patrick, J. Optimization models for disaster response operations: a literature review. OR Spectrum 2024, 1–47. [Google Scholar] [CrossRef]
- Kumar, P.A.; Manoj, N.; Sudheer, N.; Bhat, P.P.; Arya, A.; Sharma, R. UAV Swarm Objectives: A Critical Analysis and Comprehensive Review. SN Computer Science 2024, 5, 764. [Google Scholar] [CrossRef]
- Jain, S.; Bharti, K.K. A combinatorial optimization model for post-disaster emergency resource allocation using meta-heuristics. Soft Computing 2023, 27, 13595–13611. [Google Scholar] [CrossRef]
- Elnabty, I.A.; Fahmy, Y.; Kafafy, M. A survey on UAV placement optimization for UAV-assisted communication in 5G and beyond networks. Physical Communication 2022, 51, 101564. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, G. A survey on UAV-assisted wireless communications: Recent advances and future trends. Computer Communications 2023, 208, 44–78. [Google Scholar] [CrossRef]
- Mao, K.; Zhu, Q.; Wang, C.X.; Ye, X.; Gomez-Ponce, J.; Cai, X.; Miao, Y.; Cui, Z.; Wu, Q.; Fan, W. A survey on channel sounding technologies and measurements for UAV-assisted communications. IEEE Transactions on Instrumentation and Measurement 2024. [Google Scholar] [CrossRef]
- Pandey, G.K.; Gurjar, D.S.; Yadav, S.; Jiang, Y.; Yuen, C. UAV-Assisted Communications With RF Energy Harvesting: A Comprehensive Survey. IEEE Communications Surveys & Tutorials 2024. [Google Scholar]
- Li, Y.; Zhou, X.; Gu, J.; Guo, K.; Deng, W. A novel K-means clustering method for locating urban hotspots based on hybrid heuristic initialization. Applied Sciences 2022, 12, 8047. [Google Scholar] [CrossRef]
- Latifi-Pakdehi, A.; Daneshpour, N. DBHC: A DBSCAN-based hierarchical clustering algorithm. Data & Knowledge Engineering 2021, 135, 101922. [Google Scholar]
- Alshaibani, W.; Shayea, I.; Caglar, R.; Din, J.; Daradkeh, Y.I. Mobility management of unmanned aerial vehicles in ultra–dense heterogeneous networks. Sensors 2022, 22, 6013. [Google Scholar] [CrossRef] [PubMed]
- Reina, D.; Camp, T.; Munjal, A.; Toral, S.; Tawfik, H. Evolutionary deployment and hill climbing-based movements of multi-UAV networks in disaster scenarios. Applications of big data analytics: trends, issues, and challenges 2018, 63–95. [Google Scholar]
- Madridano, Á.; Al-Kaff, A.; Martín, D.; de la Escalera, A. 3d trajectory planning method for uavs swarm in building emergencies. Sensors 2020, 20, 642. [Google Scholar] [CrossRef] [PubMed]
- Pasandideh, F. Providing an energy-efficient UAV Base Station positioning mechanism to improve wireless connectivity 2024.
- Aloqaily, M.; Bouachir, O.; Al Ridhawi, I.; Tzes, A. An adaptive UAV positioning model for sustainable smart transportation. Sustainable Cities and Society 2022, 78, 103617. [Google Scholar] [CrossRef]
- Majeed, A.; Hwang, S.O. A multi-objective coverage path planning algorithm for UAVs to cover spatially distributed regions in urban environments. Aerospace 2021, 8, 343. [Google Scholar] [CrossRef]
- Nafees, M.; Huang, S.; Thompson, J.; Safari, M. Backhaul-Aware UAV-Aided Capacity Enhancement in Mixed FSO-RF Network. IEEE Open Journal of the Communications Society 2024. [Google Scholar] [CrossRef]
- Kuru, K. Planning the future of smart cities with swarms of fully autonomous unmanned aerial vehicles using a novel framework. IEEE Access 2021, 9, 6571–6595. [Google Scholar] [CrossRef]
- Adam, M.S.; Nordin, R.; Abdullah, N.F.; Abu-Samah, A.; Amodu, O.A.; Alsharif, M.H. Optimizing Disaster Response through Efficient Path Planning of Mobile Aerial Base Station with Genetic Algorithm. Drones 2024, 8, 272. [Google Scholar] [CrossRef]
- Zhong, X.; Huo, Y.; Dong, X.; Liang, Z. QoS-compliant 3-D deployment optimization strategy for UAV base stations. IEEE Systems Journal 2020, 15, 1795–1803. [Google Scholar] [CrossRef]
- Beegum, T.R.; Idris, M.Y.I.; Ayub, M.N.B.; Shehadeh, H.A. Optimized routing of UAVs using bio-inspired algorithm in FANET: A systematic review. IEEE access 2023, 11, 15588–15622. [Google Scholar] [CrossRef]
- Matamoros Vargas, J.A. Aerial Base Station Deployment for Post-Disaster Public Safety Applications 2019.
- Altay, C.; Koca, M. Design and analysis of energy efficient inter-tier interference coordination in heterogeneous networks. Wireless Networks 2021, 27, 3857–3872. [Google Scholar] [CrossRef]
- Gannapathy, V.R.; Nordin, R.; Abu-Samah, A.; Abdullah, N.F.; Ismail, M. An adaptive TTT handover (ATH) mechanism for dual connectivity (5G mmWave—LTE advanced) during unpredictable wireless channel behavior. Sensors 2023, 23, 4357. [Google Scholar] [CrossRef] [PubMed]
- Zulkifley, M.A.; Subki, M.G.; Behjati, M.; Nordin, R.; Abdullah, N.F. Mobile Communications and Parachute Systems for Safe Beyond Visual Line of Sight (BVLoS) UAV Operation. 2022 IEEE 6th International Symposium on Telecommunication Technologies (ISTT). IEEE, 2022, pp. 22–27.
- Lama, A.; Ray, S.; Biswas, T.; Narsimhaiah, L.; Raghav, Y.S.; Kapoor, P.; Singh, K.; Mishra, P.; Gurung, B. Python code for modeling ARIMA-LSTM architecture with random forest algorithm. Software Impacts 2024, 20, 100650. [Google Scholar] [CrossRef]
- Das, S.K.; Roy, S.K.; Weber, G.W. Heuristic approaches for solid transportation-p-facility location problem. Central European Journal of Operations Research 2020, 28, 939–961. [Google Scholar] [CrossRef]

| Study | UE Mobility Modeled | Types of Mobility | Environment Covered | Mobility Prediction | Trajectory Optimization | Clustering Technique | QoS Awareness | Energy Efficiency |
|---|---|---|---|---|---|---|---|---|
| [25] | Static UE | None | Urban | No | PSO-based optimization | K-means | No | Moderate |
| [7] | Static UE | None | Post-disaster | No | ABC Algorithm | None | No | Low |
| [26] | Quasi-stationary | Directional | Suburban, Rural | Yes | Proactive UAV adjustments | DBSCAN | Limited | Low |
| [27] | Random mobility | Random Walk | Disaster zones | No | Behavioral Imitation Learning | None | Yes | Moderate |
| [28] | Controlled mobility | Directional | Rural | Yes | Optimal transport theory | None | Yes | High |
| [29] | Controlled mobility | Directional | Urban | Yes | 3D trajectory optimization | None | Yes | High |
| [30] | Random mobility | Random Walk | Urban | Yes | Machine learning-based optimization | None | Yes | Moderate |
| [31] | Static UE | None | Urban | No | Heuristic placement | None | No | Low |
| [32] | Random mobility | Random Walk | Urban | No | Heuristic placement | None | No | Low |
| [33] | Static UE | None | Urban | No | FSO-based backhaul | None | No | Moderate |
| [34] | Static UE | None | Urban | No | Self-organizing architecture | None | No | Moderate |
| [35] | Static UE | None | Urban | No | Air-ground integrated network | K-means | No | Moderate |
| [36] | Static UE | None | Urban, Suburban, Dense Urban, High-rise Urban | Yes | Genetic Algorithm-based 3D deployment | K-means | High | Moderate |
| Proposed Work | Dynamic UE | RWPM, RPGM | Urban, Suburban, Dense Urban, High-Rise Urban | Yes | GA+APC Hybrid for real-time paths | APC | High QoS metrics | High energy optimization for hover and travel |
| Category | Parameter | Notation/Value | Description |
|---|---|---|---|
| Environment | Simulation Area | Total area for UE and BS placement. | |
| UE Distribution (UED) | Number of UEs tested at different densities, incremented by 50, represented as a finite set of Poisson-distributed users. | ||
| BS Distribution | Poisson-distributed BSs. | ||
| UE Mobility Speed | Range of UE mobility speeds. | ||
| Environments | Urban (), Suburban (), Dense Urban (), High-Rise Urban (). | ||
| Environment Parameters | (Urban) | , , , | Path loss parameters for urban environments. |
| (Suburban) | , , , | Suburb-specific signal-propagation characteristics. | |
| (Dense Urban) | , , , | Parameters for densely populated urban environments. | |
| (High-Rise Urban) | , , , | Parameters of high-rise urban areas. | |
| Mobility Models | Mobility Model 1 | RWPM | Random Waypoint Mobility for individual users. |
| Mobility Model 2 | RPGM | Reference Point Group Mobility for groups of users. | |
| UE Speed | UE movement speed in both models. | ||
| Path Variation | Pause probability for RWPM. | ||
| Group Deviation | Maximum deviation in the RPGM. | ||
| Time Step | Discrete time step for mobility updates. | ||
| UAV Swarm Parameters | UAV Swarm | Number of UAVs swarms. | |
| UAV Capacity | Max UEs per UAV. | ||
| Trajectory Optimization | Algorithms for swarm path planning. | ||
| Communication Range | Max UAV communication range. | ||
| Coordination Protocol | Distributed | Swarm communication strategy. | |
| QoS Parameters | Data Rate | Different data rate requirements for all UEs. | |
| Base Station Failures | BS Failures | Number of failed base stations considered. | |
| Failure Distribution | Uniform | Distribution pattern of failed base stations. | |
| Recovery Priority | Highest UE density | Priority given to areas with the densest unconnected UEs. |
| Environment | GA+APC Coverage Ratio | Best Benchmark Coverage Ratio | Key Observations |
|---|---|---|---|
| Dense Urban Environment | 97% | 91% (GA) | GA+APC excels in managing severe interference and NLOS conditions through adaptive path planning, achieving significant improvement over traditional methods. |
| Urban Environment | 94% | 89% (GA,ACO) | Moderate performance gap owing to less complex propagation conditions; GA+APC maintains consistent superiority and resource efficiency. |
| Suburban Environment | 100% | 99% (GA) | Favourable conditions allow all methods to perform well, but GA+APC achieves complete coverage with fewer UAVs, emphasising resource efficiency. |
| High-Rise Urban Environment | 93% | 88% (GA,ACO) | GA + APC effectively navigate vertical obstacles and severe NLOS challenges, demonstrating strong adaptability in complex environments. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





