Neural-Guided Adaptive Clustering for UAV-Based User Grouping in 5G/6G Post-Disaster Networks

1. Introduction

The deployment of Mobile Aerial Base Stations (MABSs) has been instrumental in supplementing terrestrial infrastructure, especially in post-disaster environments where ground-based communication is disrupted. MABSs provide rapid, flexible, and cost-effective coverage, leveraging aerial mobility and line-of-sight (LOS) communication to serve dispersed User Equipment (UE) over large geographic areas. In disaster scenarios, such as the 2017 Hurricane Maria in Puerto Rico, aerial solutions, such as cell-on-wings (COW) drones, were deployed to re-establish LTE cellular connectivity, demonstrating the critical role of Unmanned Aerial Vehicles (UAVs) in mission-critical communication recovery. Their ability to operate at varying altitudes, dynamically reposition, and form network topologies on the fly renders them essential components of modern Disaster Response Networks (DRNs).

A key enabler of effective MABS deployment is the intelligent clustering of UEs to guide UAV path planning. Traditional clustering algorithms, such as Affinity Propagation Clustering (APC), are well-suited for this task because of their non-parametric nature and ability to adapt to varying UE numbers. However, APC and similar static methods may not always produce optimal centroids under highly variable UE densities, geographical dispersions, or uneven BS failure rates. These limitations are more pronounced in DRNs where user mobility and environmental uncertainties are common.

To address these issues, this study proposes a hybrid clustering framework that dynamically selects between APC and Density-Based Spatial Clustering of Applications with Noise (DBSCAN), guided by a lightweight neural network classifier. The model is trained to recognise spatial distribution patterns and choose a clustering strategy that is best suited to the environment of interest. By integrating this adaptive mechanism with a Genetic Algorithm (GA) for multi-objective path optimisation, the proposed method enhances the resilience and adaptability of MABS deployment. This approach supports faster convergence, fewer drones, and improved UE coverage in heterogeneous and evolving disaster scenarios.

1.1. Problem Identification and Novelty

This study investigated the limitations of static UE clustering methods in disaster-stricken communication environments and introduced a neural-assisted clustering control framework that enhances UAV path planning in DRNs. Specifically, the challenge addressed is how to dynamically adapt clustering strategies (APC or DBSCAN) based on the spatial characteristics of the affected users while preserving path efficiency and coverage constraints. The proposed model replaces the rigid, one-size-fits-all approach with an adaptive mechanism capable of learning from historical data distributions and making intelligent decisions during operation.

Compared with prior studies (see Section 2), this study introduces a hybrid clustering selector that leverages pattern recognition via machine learning, allowing UAVs to switch clustering strategies in real time. This results in better centroid placement, fewer missed UEs, and more optimal coverage, especially when the UE distribution varies drastically because of evacuation behaviour or terrain obstacles. The system was validated under BS failure rates ranging from 10% to 90%, emphasising its performance in macro-scale service zones rather than in micro hotspots.

The key challenges addressed include the following:

• Choosing the optimal clustering method based on the current UE distribution without human intervention.
• Avoiding centroid overlap or outliers by balancing APC’s adaptability with DBSCAN’s density-awareness.
• Optimising UAV paths over dynamically selected centroids with a multi-objective fitness function considering distance, angle smoothness, intersection count, and service ratio.

1.2. Novel Contributions and Approach

This study makes several contributions to the literature.

• A hybrid clustering architecture combining APC and DBSCAN with a neural selector trained on UE spatial distributions, enabling real-time adaptive centroid generation.
• An integrated multi-objective path planning algorithm using a GA that balances service coverage, and route smoothness.
• Simulation of diverse disaster scenarios, demonstrating improved performance in terms of fitness score, UE coverage, and number of UAVs required compared to conventional APC-based approaches.

1.3. Organization of This Paper

The remainder of this paper is organised as follows: Section 2 reviews related studies on UAV clustering and learning-based path planning. Section 3 presents the environmental modelling and assumptions used in this study. Section 4 details the proposed hybrid clustering framework and GA-based optimisation. Section 5 presents a performance evaluation and discussion of the results. Section 6 concludes the study and outlines future research directions.

2. Related Works

RQ1: What clustering algorithms have been used in UAV-assisted wireless coverage, and how do they perform in disaster scenarios?

Clustering algorithms are vital for optimising UAV-assisted wireless coverage, particularly in disaster scenarios. Among these, K-means and K-means++ have been widely adopted for clustering ground users and UAV deployment. K-means++ enhances the initial centroid selection, significantly improving the user throughput and satisfaction ratio [1,2,3]. The Hybrid K-means PSO approach combines K-means with PSO, achieving a more balanced performance in terms of coverage, energy efficiency, and reliability [4]. Particle swarm optimization (PSO) is another widely used technique for optimising cluster coverage and 3D UAV placement problems. It exhibits faster convergence and requires fewer UAVs than K-means [5,6]. The Ellipse Clustering Algorithm further contributes by adjusting the UAV antenna parameters to maximise the user coverage probability while minimizing the transmission power [7]. Fuzzy Logic and Fuzzy C-Means (FCM) offer dynamic solutions such as cluster head selection based on sensor node energy and storage levels [2]. An enhanced version, Fit-FCM, integrates additional factors such as energy, distance, and trust to improve cluster head selection in UAV-based wireless sensor networks [8]. DBSCAN, a density-based clustering algorithm, has been used in conjunction with convex optimisation for UAV trajectory planning and charger allocation. This integration reduces the number of chargers required while boosting the overall throughput [9]. Meanwhile, Log Linear Learning has proven effective for UAV deployment in disaster-stricken regions by using a UAV coverage utility function to ensure comprehensive network coverage [10]. These algorithms have different strengths and weaknesses in disaster scenarios. K-means is effective for initial coverage and user satisfaction, although its performance can vary based on the centroid initialisation and distance metrics used [1,3]. It supports user association, optimal UAV placement, and altitude selection to maximise data rates in emergencies [11]. PSO-based algorithms not only reduce the number of UAVs required, but also outperform GA and artificial bee colony (ABC) methods in terms of execution time and energy efficiency [6,12]. Fuzzy logic and fit fuzzy c-means clustering improve the lifetime of the network and reduce packet loss, which are crucial for reliable communication in WSNs assisted by UAVs [2,8].

DBSCAN minimises charger use and increases throughput, offering a cost-effective disaster response solution [9]. Finally, log-linear learning has demonstrated both generality and the best performance compared with optimal selection algorithms in emergency deployments [10].

Clustering algorithms, such as K-means, PSO, fuzzy logic, FCM, DBSCAN, and log-linear learning, are critical for enhancing the effectiveness of UAV-assisted wireless coverage. These methods contribute significantly to improving coverage, energy efficiency, and system reliability, particularly when the terrestrial communication infrastructure is compromised by the environment. While K-means and PSO offer robust overall performance, algorithms such as Fuzzy Logic and DBSCAN provide specialised advantages in terms of energy conservation and operational cost, making them indispensable in emergency and disaster response scenarios. Table 1 compares eight clustering methods, K-means, K-means++, PSO, FCM, DBSCAN, and log-linear learning, used in UAV-assisted disaster scenarios. It highlights each method’s type, disaster support capability, optimisation goals, and respective strengths and limitations. For instance, K-means++ offers simplicity and fast convergence but is sensitive to centroid initialisation, whereas DBSCAN is cost-effective in sparse networks but struggles with scalability. This comparison sets the foundation for why a hybrid adaptive clustering method is needed in post-disaster UAV networks (see Table 1).

RQ2: How have machine learning or neural models been used to guide clustering or adapt path planning in dynamic environments?

Machine learning and neural models have been increasingly applied to guide clustering and adapt path planning in dynamic environments. One notable approach is the Two-Stage Learning-Based Model, where the first stage extracts features of the surrounding environment and predicts the trajectories of dynamic obstacles, and the second stage utilises reinforcement learning to plan a feasible and efficient path based on those predictions. This model demonstrates high predictability and processing capacity for dynamic obstacles and successfully executes planning tasks in various dynamic scenarios [13]. In the realm of Neural Network-Guided Path Planning, methods such as NST-PRM and NST-RRT employ neural networks trained on datasets generated through probabilistic roadmaps (PRM) and rapidly exploring random trees (RRT). These techniques notably reduce the dataset generation time and enhance path-planning efficiency in environments with numerous obstacles [14]. A Graph Neural Network (GNN)-Based Planner, further improves planning by leveraging prior exploration experience and minimising replanning costs under unpredictable conditions. This results in a high planning performance with fast speeds and low path costs, outperforming both traditional and other learning-based methods [15]. Another advancement is the Dynamic Distance Transform Algorithm, in which a neural model adapts the distance transform method for dynamic contexts, forming a dynamically updating potential field. This ensures an effective local adaptation and optimal path planning in dynamic environments [16].

In terms of Clustering for Path Planning, cluster-based routing for UAVs integrates online path planning, clustering-based network topology, reinforcement-learning-driven cluster management, and data routing. The outcomes include improved coverage, better adaptation to changing environments, enhanced packet delivery ratios, and reduced communication delays [17]. Furthermore, combining clustering and neural networks for trajectory prediction, such as the use of DBSCAN and multicell neural networks (MCNN), produces accurate short-term 4D trajectory predictions, demonstrating their robustness and effectiveness in dynamic settings [18,19].

Among Hybrid and Reinforcement Learning Approaches, Q-Learning-Based Local Planning considers factors such as path length, safety, and energy consumption and shows reliable performance in both static and dynamic environments by avoiding the typical pitfalls of conventional algorithms [20]. When Artificial Neural Networks (ANNs) are combined with Q-learning, the ANN serves as a path-planning controller, whereas Q-learning generates training samples. This hybrid strategy is more effective than using either technique alone to find optimal paths [21]. In practical applications, Multi-Robot Systems (MRS) benefit from improved neural dynamics approaches that incorporate territorial mechanisms, resulting in robust and fair path planning in complex and changing environments [22]. Similarly, Autonomous Vehicles leverage deep reinforcement learning and clustering-based strategies to develop both theoretical models and practical solutions for effectively navigating dynamic surroundings [23,24].

The integration of machine learning and neural models has significantly improved path planning and clustering performance in dynamic environments. By enhancing efficiency, adaptability, and accuracy, these methods, particularly those involving reinforcement learning, neural networks, and clustering, effectively address the challenges posed by dynamic obstacles and varying conditions. Table 2 lists various ML- and NN-based frameworks that assist in UAV path planning and clustering in dynamic environments. It spans methods such as Two-Stage ML+RL models, GNN, neural potential fields, and hybrid RL-routing systems. The table clarifies their roles in clustering, path planning, adaptability to environmental changes, and trade-offs between complexity and data dependency. This provides the motivation for integrating ANN-guided clustering into the proposed model ( see Table 2).

RQ3: What hybrid clustering or dynamic strategy selection methods exist, and how do they affect trajectory or resource efficiency?

Hybrid clustering and dynamic strategy selection methods have been introduced to enhance trajectory planning and resource efficiency in various applications. One of such approach is the Hybrid Selection Multi-Objective Evolutionary Algorithm (HSMEA), which combines angle and distance metrics for clustering individuals, followed by a hybrid selection mechanism. This method strikes an effective balance between convergence and diversity, making it suitable for complex multi-objective optimisation tasks [25]. Another notable method, the Density-based K-means (DKGK) approach, utilises Differential Evolution (DE) to promote diversification, K-means for refinement, and a GA enhanced with heuristic crossover to ensure fast convergence. This combination outperforms conventional approaches, such as DE, GA, DE-K-means, and GA-K-means, by significantly reducing intra-cluster distances, leading to better clustering accuracy and efficiency [26].

The hybrid grasshopper and differential evolution-based optimisation algorithm (HGDEOA) integrates adaptive strategies into DE, thereby enhancing its global search ability and reducing the risk of premature convergence. This results in improved energy stability, higher throughput, and extended network lifetime in Wireless Sensor Networks (WSNs) [27]. Similarly, the Hybrid Deep Fixed K-Means (HDF-KMeans) approach merges Deep K-Means++ for advanced feature extraction and centroid initialisation with Fixed Centered K-Means to improve stability. This hybrid model enhances clustering accuracy and consistency, particularly in critical domains such as healthcare [28].

Among the Dynamic Strategy Selection Methods, the Dynamic Genetic Algorithm (DGA) improves the automatic calculation of the number of clusters (k) and improves the population initialisation, genetic operators, and fitness functions. These improvements lead to more accurate clustering outcomes and better estimation of the cluster numbers [29]. The Gaussian Mutation Adaptive Artificial Fish Swarm Algorithm (GAAFSA) incorporates Gaussian mutation and adaptive strategies to avoid local optima and early convergence, which boosts the network lifespan, increases packet reception rates, and reduces packet loss in Industrial Wireless Sensor Networks (IWSNs) [30]. Meanwhile, adaptive density peak clustering with Fisher linear discriminant (ADPC-FLD) employs kernel density estimation and weighted Euclidean distances, along with adaptive strategies for selecting cluster centres. This significantly enhances the clustering accuracy and efficiency, particularly in high-dimensional data scenarios [31].

Regarding the effects on trajectory and resource efficiency, methods such as HGDEOA and GAAFSA contribute significantly to energy efficiency and network longevity by optimising cluster head selection and data transmission in WSNs and IWSNs [27,30]. In terms of convergence and diversity, HSMEA and DKGK provide robust clustering solutions that enhance system performance [25,26]. For applications demanding high precision, such as healthcare and complex data analysis, techniques such as HDF-KMeans and ADPC-FLD deliver notable improvements in precision and consistency [28,31]. Hybrid clustering and dynamic strategy selection methods offer meaningful advancements in trajectory optimisation and resource efficiency. By enhancing energy stability, promoting balanced convergence and diversity, and increasing clustering accuracy, these techniques are valuable in a wide array of technical domains. Table 3 compares hybrid approaches, such as HSMEA, DKGK, HGDEOA, and adaptive clustering methods. Each combines different algorithms (e.g., DE+GA+K-means) to optimize clustering accuracy, convergence, and resource use. The strengths of these models include improved energy stability and accuracy; however, their limitations often involve parameter tuning or domain-specific constraints. The discussion in this paper leverages this to justify the hybrid APC–DBSCAN + ANN framework (see Table 3).

RQ4: What fitness functions or multi-objective optimisation approaches are most effective for UAV path planning in DRNs?

To identify the most effective fitness functions or multi-objective optimisation approaches for UAV path planning in DRNs, various insights have emerged from recent research. Several fitness functions are typically used in this context. One core focus is on minimising both distance and risk, as seen in methods that apply the Bézier theory and impose constraints such as turning angle and flight altitude [32]. Similarly, another study incorporated travelling distance and risk along with height, angle, and slope limitations to guide UAV navigation [33].

Energy efficiency is another critical criterion. Some models aim to reduce fuel consumption, altitude costs, and threat exposure during flights [34]. In particular, Bézier curve-guided paths optimised via GAs and multi-objective swarm-based strategies are effective in improving energy use [35]. In multi-UAV systems, utility-based objectives such as maximising the number of people rescued are coupled with collision avoidance to ensure operational safety [36]. Additionally, Quality of Service (QoS) is emphasised in UAV-assisted Mobile Edge Computing (MEC) frameworks, where path planning considers geometric distance, risk level, and terminal user demand [37]. Several techniques have been proposed for textbfmulti-objective approaches. A knee-guided differential evolution algorithm directs the search toward optimal UAV paths with smooth trajectory generation [32], whereas another variant incorporates an adaptive selection mutation to improve refinement while preserving exploration [33]. Reinforcement learning (RL) methods are effective in dynamic urban settings, optimising UAV paths under conditions of mobile obstacles and variable threats [37].

GAs remain widely used for path optimization due to their versatility in complex optimisation. One approach normalizes the fitness criteria and employs swarm-based enhancements for energy efficiency [35]. Another study combined an adaptive GA for mission assignment with an improved artificial bee colony method for optimal path planning [38]. The Hybrid Equilibrium Optimizer (HEO) uses techniques such as Gaussian distribution estimation and Lévy flight to divide populations and balance exploration and exploitation [34]. Moreover, Ant Colony Optimisation (ACO) has been improved for accurate 3D path planning, minimising flight path length, and terrain threats [39]. Table 4 outlines the fitness criteria, such as distance, risk, energy, and QoS, alongside the optimisation technique used (e.g., DE, RL, GA, hybrid metaheuristics, ACO). This emphasises that effective UAV path planning must balance efficiency, safety, and adaptability. This reinforces why the proposed GA-based framework incorporates multiple weighted objectives ( see Table 4).

Effective UAV path planning in DRNs using GA depends on fitness functions that measure distance, risk, energy consumption, and mission utility. Multi-objective optimisation techniques, such as differential evolution, reinforcement learning, GAs, hybrid optimisation, and ant colony optimisation, exhibit strong capabilities in navigating complex dynamic environments. Each technique offers unique strengths, ranging from convergence speed to adaptability, making it appropriate for different operational requirements. Expanding Table 4, Table 5 details the scope, strengths, and limitations of specific optimisation approaches, such as knee-guided DE, RL-based planning, GA+swarm hybrids, and enhanced ACO. It shows how each method addresses constraints such as smoothness, collision avoidance, and threat minimisation, further supporting the design choices in the hybrid framework (see Table 5).

RQ5: How do clustering and optimisation approaches handle varying BS loss, user densities, or terrain constraints in DRNs?

Clustering and Optimisation Approaches in DRNs

To handle varying BS losses, clustering approaches often face challenges due to interference from nodes outside the cluster. To address this, some frameworks allow clusters to exchange optimisation parameters through low-rate backhauls, approaching near-global optimisation performance [40]. In the case of BS failures, delay-tolerant networks (DTNs) offer resilience by enabling user devices to self-organise and relay messages through multihop connections to functional BSs or nearby users, thereby improving load balancing [41]. Under sparse BS deployment, users may rely on others who are willing to relay messages to an accessible BS. Optimized beaconing policies are used to maximise message delivery success while minimising power usage [42]. In high-density scenarios, clustering algorithms such as K-means, DBSCAN, and Agglomerative Clustering were evaluated to determine the most efficient choice. Machine learning (ML) methods can also predict optimal BS parameters, thereby reducing the computational overhead [43].

The optimization of irregular terrain requires sophisticated modelling. For instance, the Longley-Rice model enables accurate path-loss estimation using high-resolution topographic data [44]. In urban vehicular DTNs, geographic complexity is managed by segmenting maps into adjacent regions to aid delay analysis and trajectory prediction [45]. Energy-saving strategies include optimising the activation and deactivation of BS transmissions. Clustering and timed activation approaches help minimise energy use while fulfilling traffic demands [46]. Battery-aware techniques, such as Improved Lifetime Optimization Clustering (ILCK), apply Kruskal’s minimal spanning tree heuristic and monitor battery health to extend the network lifetime [47]. Analytical methods, such as convex optimisation, are used to minimise the total transmit power under QoS constraints and are often extended to multi-BS scenarios using iterative algorithms [48]. Metaheuristic approaches, such as chaotic gorilla troop optimization, enhance energy-aware clustering by considering the neighbor distance, BS proximity, and energy ratio [49]. Table 6 summarises the strategies for dealing with BS loss, varying user densities, and terrain constraints. Approaches range from DTN routing and ML-based parameter tuning to terrain-aware propagation models and energy-saving BS scheduling. The relevance of the proposed work lies in showing how adaptability to these challenges is crucial (see Table 6).

These clustering and optimisation techniques collectively address the challenges related to BS loss, varying user densities, and complex terrain in disaster relief networks. By leveraging analytical models, adaptive routing, and energy-aware clustering, these methods can significantly improve the reliability and efficiency of DRNs. The strategies compared in Table 7 further illustrate how clustering and optimisation methods address BS loss, varying user densities, and terrain constraints in DRNs. By juxtaposing their benefits and limitations, the table highlights that adaptability and energy-awareness are the most critical enablers for post-disaster UAV deployments.

To provide a broader perspective, Table 8 consolidates the methods examined across all five research questions (RQ1–RQ5). This summary highlights how clustering, learning-based optimisation, and hybrid strategies collectively contribute to improving UAV service coverage, path efficiency, and resilience in disaster response networks.

3. Environment Modelling

This section outlines the key assumptions and system architecture of the studied UAV-assisted emergency network deployment in post-disaster scenarios. The objective is to provide resilient and rapid connectivity to UEs through the deployment of MABSs using a newly proposed hybrid clustering-based optimisation framework. The proposed solution enhances the previous work [50] by dynamically selecting between APC and a learned clustering strategy that combines DBSCAN with an ANN. This hybrid model enables more flexible and adaptive UAV path planning depending on the network density, terrain, and disaster impact levels.

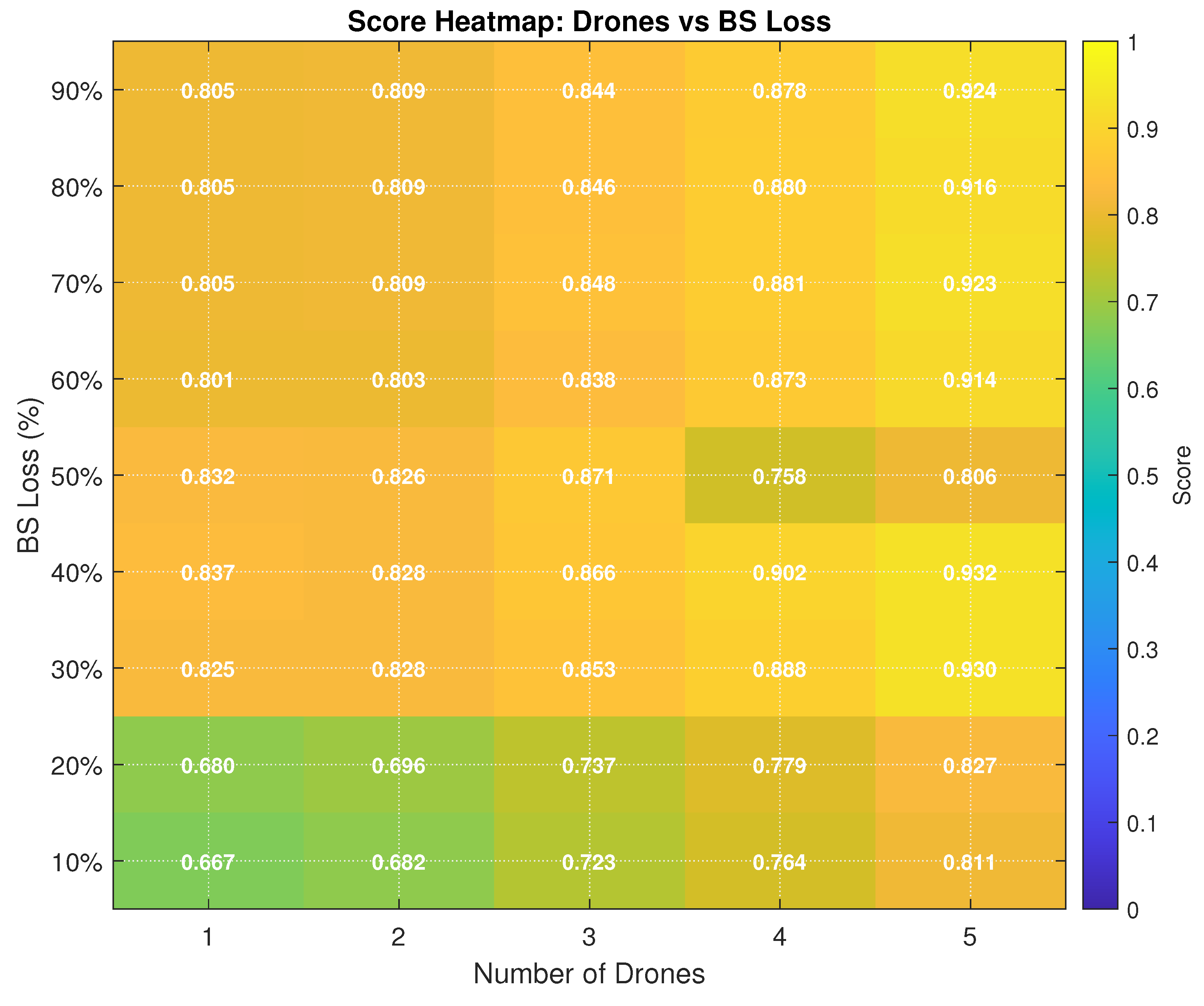
Figure 1 illustrates the proposed system model, which offers an intelligent and resilient solution for restoring wireless connectivity in post-disaster environments in which conventional base stations have failed. UAVs are used as MABSs to provide temporary coverage to disconnected UEs. The green markers indicate UEs with active services, whereas the red markers indicate UEs that have lost connectivity and require temporary MABS coverage. Each MABS follows an optimised trajectory to visit the centroid of the user clusters.

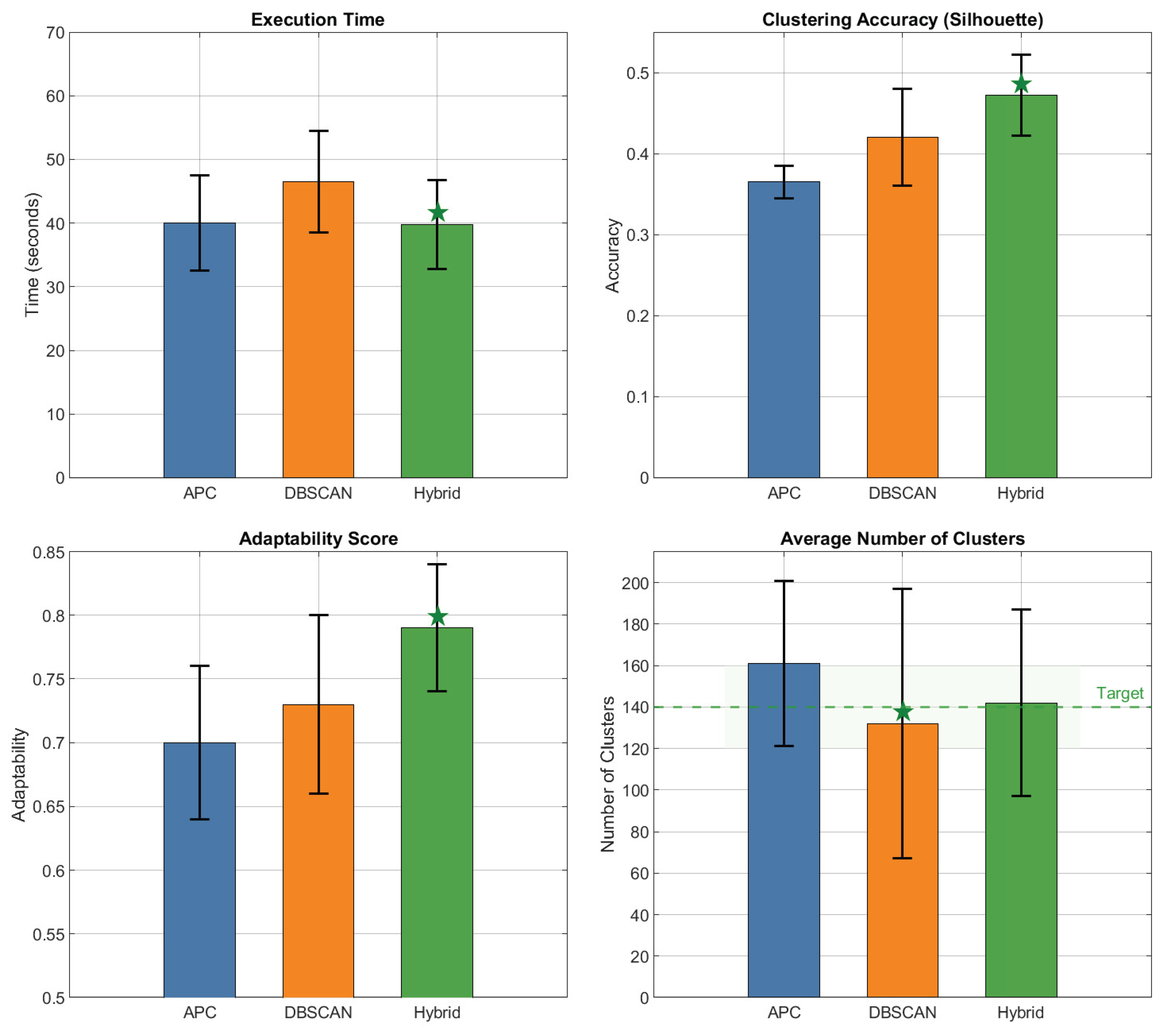
The process begins with the identification of failed base station zones and the classification of the UEs as either connected or disconnected. Spatial features, such as UE density, base station outage levels, and distribution spread, are then extracted and fed into a lightweight neural classifier. This classifier dynamically selects the optimal clustering method by choosing either APC for dense, structured regions or DBSCAN with ANN-guided parameter tuning for sparse or irregular topologies. This hybrid selection process enables more accurate and adaptive clustering, thereby ensuring efficient centroid placement. These centroids serve as UAV visitation points and are further processed by a GA that optimises the UAV trajectories based on multi-objective criteria, including service ratio, smoothness, and overlap avoidance.

The hybrid model’s ability to adapt to varying UE distributions and disaster intensities, combined with machine-learning-driven decision-making, makes it a robust and scalable framework for real-time UAV-assisted communication restoration. The adaptability of the system was further enhanced by incorporating real-time data updates, allowing for dynamic reclustering and trajectory adjustments as the post-disaster scenario evolved. This continuous optimisation ensures that the UAV network remains responsive to changing ground conditions, such as shifting UE concentrations or newly restored BSs.

In this extended model, the cluster centroids were computed using a decision layer selected between APC and DBSCAN+ANN, depending on the real-time conditions. Moreover, the framework includes a predictive component that anticipates potential changes in the UE distribution based on historical patterns and current movement trends, enabling proactive UAV positioning for improved service continuity.

3.1. Clustering Mode Selection

The novel contribution of this study is the dynamic selection of a clustering method for identifying UAV visitation centroids. This logic is defined as follows:

Table 9. Clustering selection logic based on UE distribution.

Condition	Selected Clustering Method
High UE density	APC
Low UE density or sparse regions	DBSCAN with ANN-guided parameter tuning
Unstructured or mixed topology	ANN-only centroid prediction

Table 9. Clustering selection logic based on UE distribution.

Condition	Selected Clustering Method
High UE density	APC
Low UE density or sparse regions	DBSCAN with ANN-guided parameter tuning
Unstructured or mixed topology	ANN-only centroid prediction

The ANN model was pretrained on synthetic post-disaster UE distributions to predict the optimal clustering configurations. When used with DBSCAN, the ANN adjusts the clustering parameters (e.g., $\epsilon$ and MinPts) or refines the centroid locations to minimize misclustering in sparse environments.

3.2. Simulation Setup and Parameters

Table 10. Simulation Parameters and Settings.

Notation	Description	Value
U	Number of UEs	2500
$BSD$	BS Distribution (Poisson)	$\lambda =10\times 25$
A	Area	25 km × 25 km
D	Number of MABS	1 to 5
S	GA Population Size	50
P	GA Iterations	100
$CLM$	Clustering Logic Mode	Hybrid (APC, DBSCAN+ANN)
ANNmodel	Neural Model Enabled	True
$Loss$	BS Outage Percentage	10% to 90%

Table 10. Simulation Parameters and Settings.

Notation	Description	Value
U	Number of UEs	2500
$BSD$	BS Distribution (Poisson)	$\lambda =10\times 25$
A	Area	25 km × 25 km
D	Number of MABS	1 to 5
S	GA Population Size	50
P	GA Iterations	100
$CLM$	Clustering Logic Mode	Hybrid (APC, DBSCAN+ANN)
ANNmodel	Neural Model Enabled	True
$Loss$	BS Outage Percentage	10% to 90%

The simulation emulates a $25\times 25$ km² area, representing a mid-sized town. The UE and BS locations follow a Poisson distribution with $\lambda =100\times 25$ and $\lambda =10\times 25$, respectively. Each UE requires a minimum bandwidth of 200 kbps. The signal-to-noise ratio (SNR) and link capacity are estimated using the Shannon–Hartley theorem as follows:

$$C=Bw·{log}_2(1+\mathrm{SNR})$$

(1)

$$\mathrm{SNR}={\displaystyle \frac{P_i}{{\sum }_{j\ne i}{P}_j+\eta }}$$

(2)

$P_i$ and $P_j$ represent the desired and interfering signal powers, respectively. $\eta$ is the noise set to $-112$ dBm. The transmission powers were 46 dBm (BS), 30 dBm (MABS), and 10 dBm (UE). Path loss was calculated using the Okumura–Hata model as follows:

$$PL=A+B·log\left(d\right)+\mathrm{Env}$$

(3)

$$A=69.55+26.16·log\left(f\right)-13.82·log\left(h_b\right)-a\left(h_m\right)$$

(4)

$$a\left(h_m\right)=(1.1·log\left(f\right)-0.7)·h_m-(1.56·log\left(f\right)-0.8)$$

(5)

3.3. Clustering Algorithm Integration

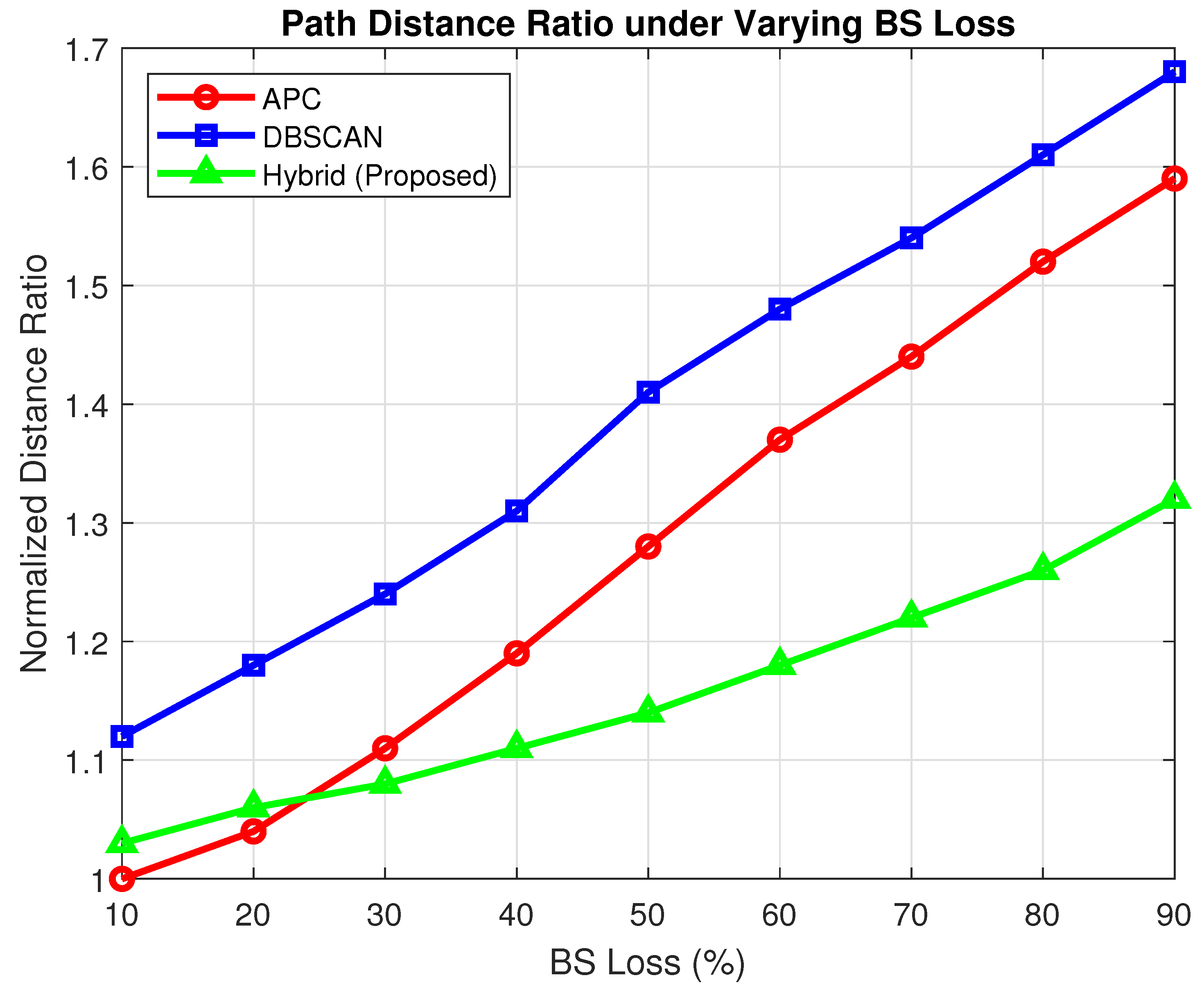
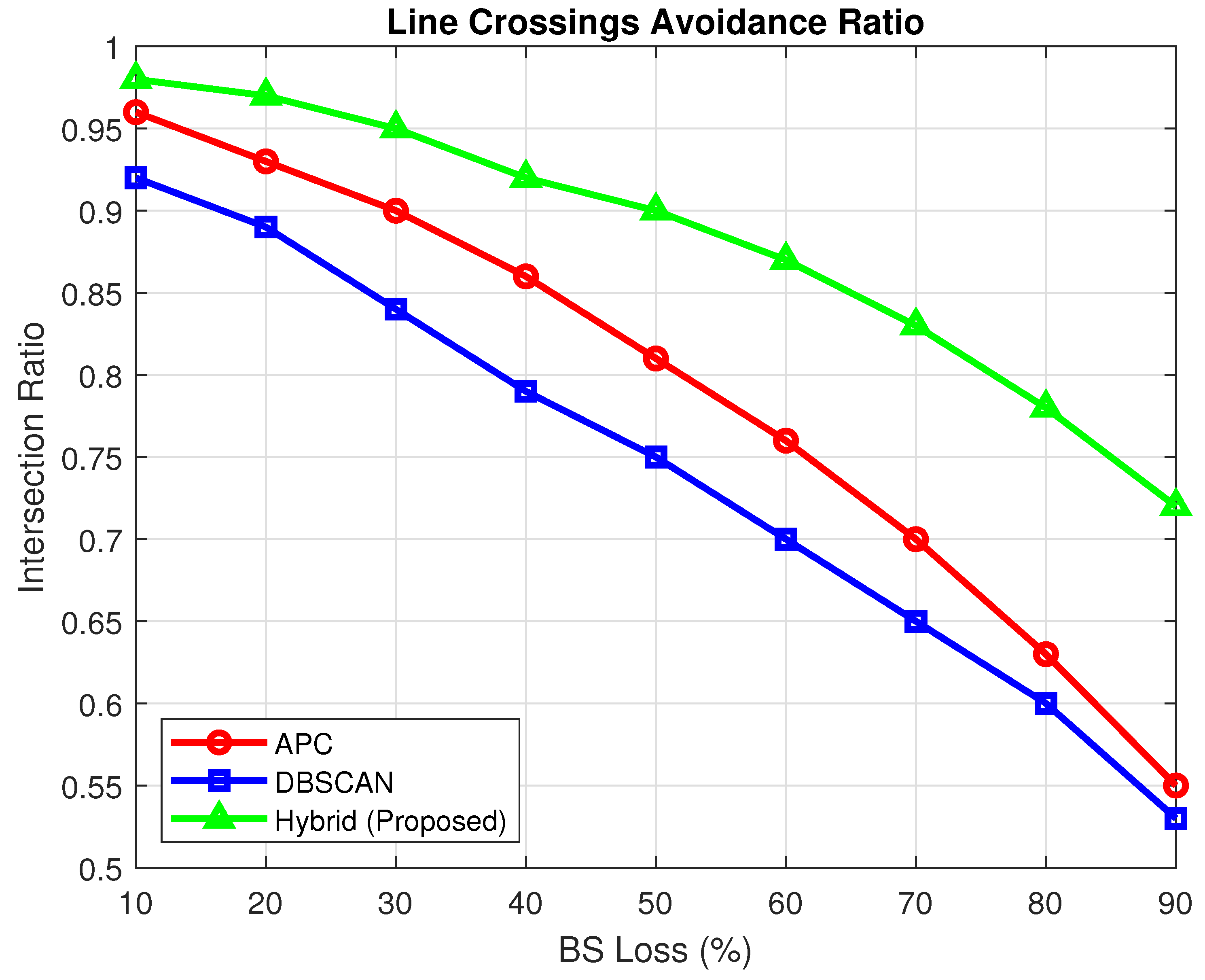
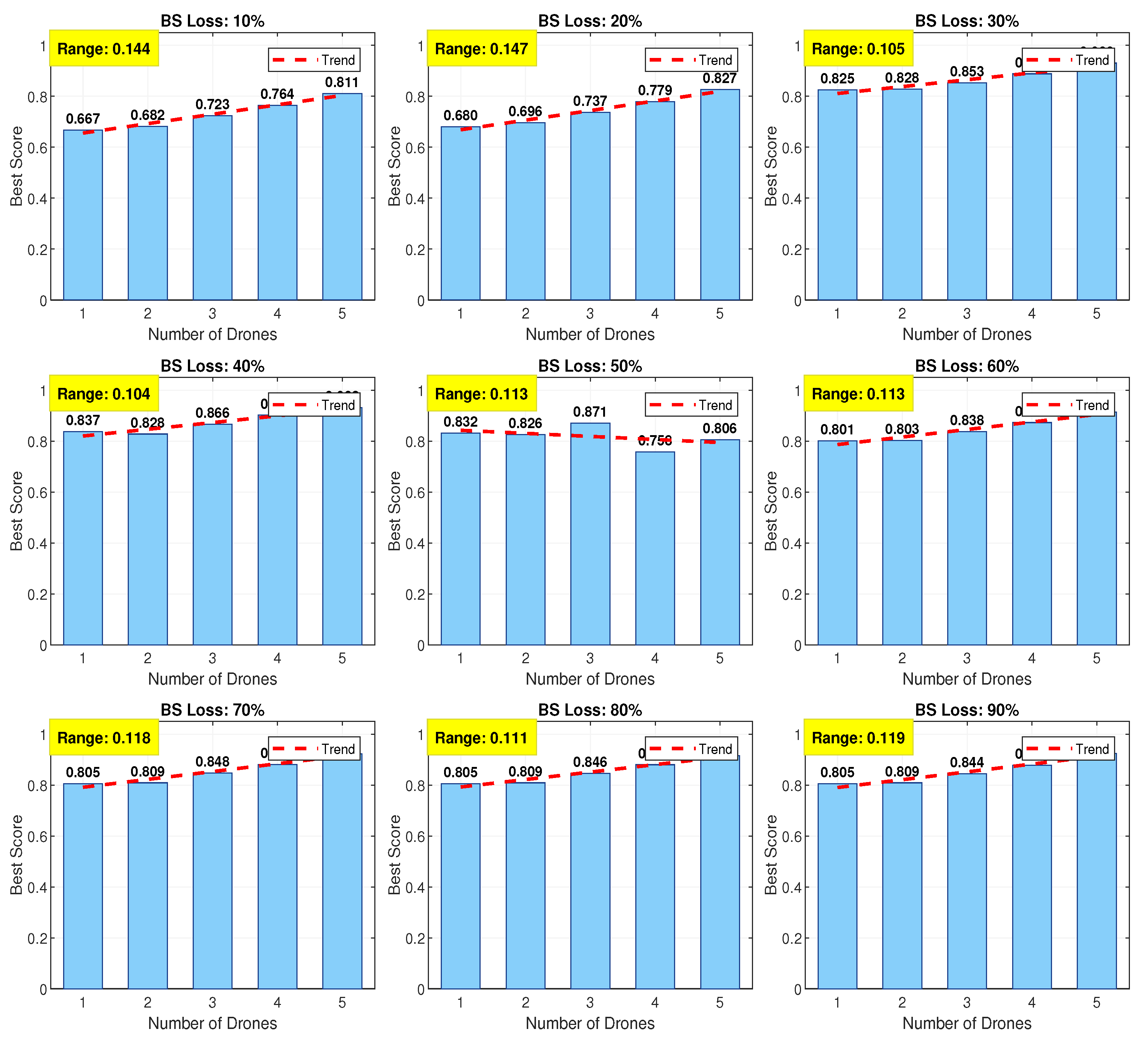
For each level of BS outage (10% to 90%), the hybrid clustering model selectes the most suitable strategy. If the ANN recommends an APC, traditional cluster propagation is applied; otherwise, DBSCAN with ANN-guided parameter tuning generates adaptive centroids. These centroids act as waypoints for UAVs during subsequent genetic optimisation.

A damping factor of 0.6 was used for APC, whereas $\epsilon$ and MinPts in DBSCAN were adapted dynamically. The output centroids vary according to the sparsity of the network, the distribution of services, and the distance traveled.

3.4. Hybrid Clustering Strategy for UAV-Based UE Grouping

The hybrid clustering strategy described in this study is a neural-guided adaptive framework that dynamically selects between APC and DBSCAN based on the spatial characteristics of the UE distributions. This decision was driven by a lightweight neural network classifier.

Stage 1: Spatial Feature Extraction of UE Distribution

The spatial pattern of UEs is quantified to inform the clustering choice. Key features: Local density of UE ${\rho }_i$, statistics of distance between users (e.g., mean, variance), percentage of BS outage ${\eta }_{BS}$, and topological spread ${\sigma }_{xy}$. For a set of UE coordinates $\mathcal{U}=\{(x_1,y_1),\dots ,(x_N,y_N)\}$, the following:

• Local density around point i:

  $${\rho }_i=\sum _{j=1}^N\mathbb{I}(d_{ij}<ϵ)$$

  (6)
  where $d_{ij}$ is the Euclidean distance, and $\mathbb{I}$ is the indicator function.
• Global density:

  $$\overline{\rho }={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\rho }_i$$

  (7)
• Spread (spatial variance):

  $${\sigma }_{xy}^2={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left({(x_i-\overline{x})}^2+{(y_i-\overline{y})}^2\right)$$

  (8)

These features form the input vector $\mathbf{f}$ for the classifier.

$$\mathbf{f}=[\overline{\rho },{\sigma }_{xy},{\eta }_{BS}]$$

(9)

Stage 2: Neural Classifier-Based Clustering Selection

Objective: Use a trained neural model to decide between APC and DBSCAN.

Classifier structure:

$$y=\mathrm{softmax}(W_2·\mathrm{ReLU}(W_1\mathbf{f}+b_1)+b_2)$$

(10)

where: $\mathbf{f}$ is the input feature vector, $W_1,W_2$, $b_1,b_2$ are trainable weights and biases, and $y\in \{0,1\}$: 0 = APC, 1 = DBSCAN (possibly with ANN refinement).

Stage 3: Clustering Execution

Case A: If APC is selected

Similarity matrix:

$$s(i,j)=-\parallel {\mathbf{x}}_i-{\mathbf{x}}_j{\parallel }^2$$

Update equations:

$$\begin{array}{cc}\hfill r(i,j)& \leftarrow s(i,j)-\underset{j^{\prime }\ne j}{max}\left\{a(i,j^{\prime })+s(i,j^{\prime })\right\}\hfill \\ \hfill a(i,j)& \leftarrow min\left(0,r(j,j)+\sum _{i^{\prime }\notin \{i,j\}}max(0,r(i^{\prime },j))\right)\hfill \end{array}$$

Exemplar selection:

$$j^{*}=arg\underset{j}{max}\left\{a(i,j)+r(i,j)\right\}$$

Case B: If DBSCAN is selected

Parameters:$ϵ$: neighborhood radius, and MinPts: minimum number of points to form a cluster. Definitions: Core point: $|{\mathcal{N}}_{ϵ}\left(p\right)|\ge \mathrm{MinPts}$ and Directly density-reachable: $q\in {\mathcal{N}}_{ϵ}\left(p\right)$.

An ANN can refine the centroid locations or tune the clustering parameters $ϵ$ and MinPts dynamically.

Stage 4: Centroid Generation for UAV Routing

Cluster centroids are computed as:

$$\mathcal{C}=\{{\mathbf{c}}_1,{\mathbf{c}}_2,\dots ,{\mathbf{c}}_K\},{\mathbf{c}}_k={\displaystyle \frac{1}{|U_k|}}\sum _{{\mathbf{u}}_i\in U_k}{\mathbf{u}}_i$$

where $U_k\subset \mathcal{U}$ is the kth cluster.

Table 11. Summary of the hybrid clustering process for UAV deployment.

Stage	Description	Output
1	Extract UE spatial features	Feature vector $\mathbf{f}$
2	Neural classifier decision	APC or DBSCAN
3	Apply selected clustering	Cluster centroids
4	Generate centroids	$\mathcal{C}=\{{\mathbf{c}}_1,\dots \}$
5	Feed into GA path planning	Optimized UAV routes

Table 11. Summary of the hybrid clustering process for UAV deployment.

Stage	Description	Output
1	Extract UE spatial features	Feature vector $\mathbf{f}$
2	Neural classifier decision	APC or DBSCAN
3	Apply selected clustering	Cluster centroids
4	Generate centroids	$\mathcal{C}=\{{\mathbf{c}}_1,\dots \}$
5	Feed into GA path planning	Optimized UAV routes

4. Proposed Hybrid Solution

4.1. Hybrid Clustering-Driven Genetic Algorithm Framework for MABS Path Planning

This section introduces a novel hybrid clustering-driven optimisation framework that combines APC with a learned clustering mechanism to guide UAV-based MABS path planning in disaster-response scenarios. The objective is to enhance the flexibility and robustness of dynamic UE distributions caused by varying disaster severities.

Overview of the Framework: The proposed MABS path-planning algorithm is built on a GA foundation. Unlike previous models that rely solely on APC, the proposed hybrid system uses a clustering selector that switches between the APC and DBSCAN guided by ANN hybrid models, depending on the scenario. APC is preferred under sparse conditions, whereas DBSCAN paired with a pre-trained ANN is utilised under dense or highly disrupted networks, where APC fails to stabilise.

Each specimen in the GA represents a candidate solution composed of multiple drone-path chromosomes, each containing a set of clustered UE. Chromosomes undergo mutation, crossover, and selection operations during evolutionary cycles.

Clustering Switch Module A scenario-dependent clustering strategy is introduced.

• For low-density UE distributions and minimal BS loss (<50%), APC is used.
• For high-density clusters or when BS loss exceeds 50%, DBSCAN groups the UEs, and a pre-trained ANN predicts optimised centroids.

This selection is based on input metrics, such as UE density, BS outage percentage, and spatial variance.

4.2. Chromosome Representation and Mutation Operators

Each chromosome is represented as a directed graph $G=(V,E)$ where V is the set of centroids from clustering and E is the set of Euclidean distances between centroids:

$$E_{ij}=\sqrt{{(x_i-x_j)}^2+{(y_i-y_j)}^2},\forall i,j\in V$$

(11)

The GA incorporates multiple mutation operators to enhance search diversity and improve solution quality. One such operator is the in-chromosome point swap, which exchanges two nodes within the same path to generate alternative route configurations. Another is the cross-chromosome merge/split, which either combines or separates UAV paths depending on the resulting impact on fitness, thereby balancing workload distribution. Finally, the insertion operator repositions nodes within a path according to capacity thresholds, ensuring that service constraints are respected while exploring new trajectory options. Together, these operators promote adaptability and prevent premature convergence, enabling the GA to evolve more efficient and resilient UAV deployment strategies. These operators encourage genetic diversity and adaptability across generations.

4.3. Scenario-Aware Fitness Function Integration

The enhanced UAV-assisted communication framework incorporates a scenario-aware fitness function that evaluates UAV deployment strategies across multiple realistic operational dimensions. This multi-objective fitness evaluation addresses the complex trade-offs inherent in post-disaster network restoration scenarios.

4.3.1. Multi-Dimensional Fitness Components

The fitness function integrates seven key performance metrics as follows:

• Distance Efficiency ($d_{total}$): Total path length optimization for fuel conservation
• Path Quality (${\theta }_{ratio}$): Angular smoothness to minimize mechanical stress
• Intersection Avoidance ($I_{cross}$): Self-intersection prevention for safe navigation
• Service Coverage ($S_{ratio}$): Fraction of unserved users covered by UAV routes
• Communication Coverage ($C_{score}$): Effective coverage accounting for interference
• Environmental Robustness ($R_{env}$): Weather condition adaptability

4.3.2. Scenario-Adaptive Parameterization

The fitness evaluation dynamically adapts to the operational scenarios as follows:

$$F_{enhanced}=[d_{total},{\theta }_{ratio},I_{cross},S_{ratio},C_{score},R_{env}]$$

(12)

Each component of the fitness function is normalised to the range $[0,1]$, where higher values indicate better performance. The system dynamically adjusts these parameters in response to environmental and operational factors, including weather conditions such as wind speed, visibility, and temperature; UAV specifications, including communication range, energy efficiency, and payload capacity; and network topology characteristics, such as user density and interference patterns. This adaptive parameterisation ensures that the optimisation framework remains robust and context-aware, allowing UAVs to maintain efficient and reliable performance under diverse disaster scenarios.

4.3.3. Integration with Genetic Algorithm Framework

This section provides a comprehensive overview of how the scenario-aware fitness function integrates multiple realistic factors to guide the genetic algorithm toward practical UAV deployment strategies. The multidimensional approach ensures that solutions balance technical performance with operational constraints, making the framework suitable for real-world disaster-response scenarios. The enhanced fitness function is seamlessly integrated into the genetic algorithm as follows:

Multi-Objective Selection: Pareto dominance comparison for solution ranking, Scenario-Aware Mutation: Parameter adjustments based on environmental conditions, and Adaptive Crossover: Route optimisation considering energy and coverage constraints. This integration ensures that the GA evolves solutions that are operationally feasible under realistic post-disaster network conditions.

5. Performance Evaluation of Proposed Solution

5.1. Evaluation Criteria and Experimental Setup

This section presents a comprehensive evaluation of the proposed hybrid clustering-based MABS path-planning method. The system is assessed in various disaster scenarios that involve different levels of BS outages and UE distributions.

5.2. Evaluation Metrics

To thoroughly evaluate the effectiveness of the proposed solution compared with the baseline methods, a series of well-defined metrics was employed. The service ratio (SR) metric quantifies the percentage of previously unconnected UEs that were successfully linked after the implementation of MABS. The distance ratio (DR) serves as a normalised measure of the total UAV flight path length relative to the shortest possible route, thereby indicating path efficiency. The intersection ratio (IR) metric records the number of path intersections, with lower values indicating smoother and less tangled trajectories. Similarly, angle ratio (AR) assesses the average angular deviation along the UAV paths, where higher values suggest more continuous and navigable routes. The PSR further enhances this by evaluating the geometric fluidity of UAV paths to minimise sharp turns and associated power losses. To account for network resilience, the CS metric evaluates the consistency of UE coverage as the BS outage levels increase. From a computational standpoint, the Clustering Time refers to the processing time required to perform user clustering using APC, DBSCAN, or the proposed hybrid model. Finally, the Computation Time indicates the total duration required to complete the entire genetic optimisation process. Collectively, these metrics provide a comprehensive view of the effectiveness, efficiency, and adaptability of a system in dynamic post-disaster scenarios.

5.3. Simulation Results and Analysis

The performance of each approach was analysed for different levels of BS outage. The key performance indicators are presented as line plots, histograms, and coverage maps. It also evaluated the efficiency of path planning, clustering accuracy, and computational efficiency of the proposed hybrid method.

5.3.1. UAV Deployment Performance (Extended with Heatmap)

The heatmap visualisation of drone scores against BS loss percentages provides further evidence of the interplay between outage severity and UAV deployment size. Along the horizontal axis, as the number of drones increases, the scores improve consistently, showing that multi-UAV deployments can compensate for service gaps more effectively than single UAVs. Along the vertical axis, higher BS loss values (70–90%) reduce the baseline score achievable with one or two UAVs, but the addition of more drones restores the performance to near-optimal levels. A particularly interesting feature of the heatmap is the nonlinear nature of the improvements. For example, under moderate BS loss conditions (40–60%), deploying three drones already produces scores above 0.85, with four or five drones pushing performance over 0.90 in most cases. In contrast, at a 20% loss, the jump from one drone (score $approx$ 0.68) to three drones (score $approx$ 0.74) is modest, but the increase to four drones ($approx$ 0.78) and five drones ($approx$ 0.83) represents a stronger recovery. This suggests that there are “sweet spots” in UAV deployment, where the marginal benefit of adding drones becomes especially valuable. At the extreme of 90% BS loss, even one UAV achieves a score above 0.80, but five UAVs boost the performance to approximately 0.93, showing that coordinated multi-UAVs can mitigate nearly catastrophic failures. This shows that while the system is inherently resilient, maintaining service above a baseline threshold even with minimal UAVs, adding drones improves coverage and capacity, ensuring that users are not only reconnected but also experience acceptable service quality.

Figure 2. Score heatmap of Drones vs BS Loss.

Figure 2. Score heatmap of Drones vs BS Loss.

5.3.2. Path Efficiency and Smoothness

The efficiency of the route quality of the UAV trajectories using the intersection and path smoothness ratios is assessed.

Figure 3 presents the normalised path distance ratio ($\delta /{\delta }_{min}$) for the three clustering approaches, APC, DBSCAN, and the proposed hybrid model, under increasing levels of BS loss ranging from 10% to 90%. The x-axis reflects the percentage of BS infrastructure failure, whereas the y-axis represents the normalised path distance ratio, which quantifies the deviation of the UAV flight paths from the shortest possible trajectories. This metric is critical for evaluating the efficiency of UAV route planning, particularly under post-disaster conditions.

As shown, all methods exhibited an upward trend in the path-distance ratio with increasing BS loss, indicating a greater deviation from the optimal paths as the network conditions degraded. However, the magnitude of this deviation varied significantly across the three methods. DBSCAN consistently incurs the highest path distance ratios across all BS loss levels, reaching nearly 1.7 at 90% BS loss. APC performs moderately better, although its path lengths grow rapidly as infrastructure degradation intensifies. In contrast, the hybrid model maintained the lowest path distance ratio throughout, starting just above 1.0 at 10% BS loss and rising modestly to approximately 1.3 at 90% BS loss.

The best performance of the hybrid method is attributed to its ability to generate more strategically located centroids through adaptive clustering selection and ANN-guided parameter tuning. This leads to more coherent cluster structures and shorter and smoother UAV trajectories. In contrast, DBSCAN often produces fragmented clusters in sparse or noisy environments (UE spatial distributions with irregular, scattered, or outlier-heavy patterns), leading to suboptimal path planning. Similarly, APC’s rigid propagation mechanics can result in inefficient centroid placement when faced with irregular UE distributions.

The results underscore the importance of clustering quality in downstream UAV trajectory optimisation. Poor clustering leads to scattered centroids and erratic paths, increasing energy consumption and mission time, which are vital constraints in post-disaster scenarios. The Hybrid model mitigates these challenges by combining the structural strengths of APC with the density awareness of DBSCAN, reinforced by neural network-based decision logic.

Figure 3 confirms that the hybrid clustering approach not only improves service coverage but also delivers more efficient path planning. Its ability to minimise path elongation under severe BS failure scenarios makes it a compelling choice for real-time UAV deployment in disaster-stricken environments.

Figure 4 presents the Intersection Ratio, also referred to as the Line Crossing Avoidance Ratio, across different clustering strategies under increasing levels of BS loss. The x-axis represents the percentage of BS infrastructure failures, whereas the y-axis quantifies the intersection ratio, where higher values indicate smoother UAV trajectories with fewer path crossings. A high intersection ratio is desirable because it implies better path planning, reduced aerial traffic complexity, and lower energy consumption due to fewer abrupt direction changes.

From the graph, it is observe that all three methods, APC, DBSCAN, and the proposed hybrid model, experience a decline in the intersection ratio as the BS loss increases. This reflects the growing difficulty in maintaining smooth UAV routes when the underlying UE clustering becomes more fragmented due to network degradation. However, the extent of degradation varies substantially between the different methods. The Hybrid model consistently achieved the highest intersection ratios across all BS loss levels, maintaining values above 0.9, up to 60% BS loss, and declining modestly to approximately 0.72, at 90% BS loss. In contrast, APC performs moderately with a more pronounced downward trend, whereas DBSCAN exhibits the lowest intersection ratios, falling below 0.55 at the highest BS loss level.

These results highlight the robustness of the hybrid clustering approach in generating non-overlapping centroid paths, which directly contributes to UAV trajectory smoothness. The integrated use of a neural classifier enables context-aware centroid placement, which avoids spatial overlap and cluster crowding in the Figure 4. Although APC is effective in denser regions, it struggles to maintain centroid separation in dispersed UE topologies, leading to more frequent UAV path intersections. Because DBSCAN is density sensitive, it often forms irregular and disjointed clusters, exacerbating path overlaps, especially in environments with uneven UE distributions.

From a critical perspective, the intersection ratio is a vital metric for operational efficiency in disaster response. Frequent path crossings can lead to UAV collision risks, increased communication latency, and energy inefficiencies due to abrupt manoeuvring. The performance of the hybrid method in this regard underscores its ability to produce coordinated and scalable UAV flight plans, even under harsh network conditions. Figure 4 shows that the proposed hybrid model significantly outperforms traditional clustering methods in minimising UAV path intersections. By maintaining high intersection ratios despite increasing the BS loss, the hybrid approach enhances the reliability, safety, and energy efficiency of UAV-assisted communication restoration in post-disaster environments.

5.3.3. UAV Deployment Performance

The Figure 5 shows the results of the drone score analysis highlight the effectiveness of the genetic algorithm in optimising UAV deployments under different levels of BS loss. When only a small proportion of BSs fail (10–20% loss), even a single UAV achieves satisfactory coverage, and the incremental gains from deploying additional drones are limited. In these low-loss cases, one UAV provides a cost-efficient solution because it can service most of the unserved users without excessive path overlap or resource waste. However, as the scale of the BS loss increases, particularly beyond 50%, the advantages of multi-UAV deployment become much more pronounced. In severe outage conditions (70–90% BS loss), the score improvements from adding drones were substantial. A single UAV is unable to cover the dispersed unserved users effectively, whereas multiple UAVs can share the workload, reduce overall travel distances, and ensure that service coverage remains acceptable. The heatmap results confirm that the best performance is consistently achieved when four or five UAVs are deployed in high-loss scenarios, with scores approaching 0.9 in some cases. These findings demonstrate that while minimal deployment is sufficient for localized failures, coordinated multi-UAV swarms are indispensable for maintaining service continuity under catastrophic disruptions.

5.3.4. Clustering Benchmark Performance

Figure 6 shows the clustering benchmark with 2,500 UEs provides further insight into the comparative performance of APC, DBSCAN, and the Hybrid clustering framework. APC, being deterministic and free of parameter tuning, consistently achieved the lowest execution times. However, its rigidity limits its adaptability to non-uniform user distributions, and it often produces an excessive number of clusters. In contrast, DBSCAN adapts more effectively to irregular and noisy distributions, but its performance is sensitive to parameter settings and is computationally more demanding. The Hybrid method combines the strengths of both approaches. By leveraging a neural classifier to dynamically select between APC and DBSCAN based on extracted spatial features, the hybrid clustering framework consistently matches or outperforms the best of the two single methods (seen in Figure 6). Accuracy metrics, such as the silhouette score and the Calinski–Harabasz index, confirm its performance, particularly in scenarios with heterogeneous or mixed-density user distributions. Furthermore, the Hybrid method generates a number of clusters that align more closely with UAV deployment requirements, avoiding the over-fragmentation of APC and the occasional under-clustering of DBSCAN. In terms of adaptability, hybrid clustering clearly outperforms both single methods, as it adjusts intelligently to the underlying spatial distribution without manual parameter tuning.

5.3.5. Discussion

Taken together, the UAV deployment results and clustering benchmarks demonstrate the complementary strength of the proposed framework. The genetic algorithm provides a robust mechanism for differentiating multi-UAV configurations, showing that additional drones bring diminishing returns in lightly disrupted networks, but are crucial under large-scale failures. At the same time, hybrid clustering ensures that the UAV deployment process is guided by high-quality centroids that accurately reflect user demand. This synergy between adaptive clustering and multi-UAV optimisation enables the system to maintain service continuity efficiently across a wide range of outage scenarios, outperforming both single-clustering methods and fixed-UAV strategies. These findings underline the importance of coupling adaptive clustering with multi-UAV optimisation for resilient wireless networks. By intelligently selecting clustering strategies and tailoring UAV deployments according to the severity of disruptions, the proposed framework provides a scalable and robust solution for service restoration. Such an approach holds significant promise for next-generation 5G and 6G systems, where maintaining seamless connectivity during infrastructure failures is a critical requirement for reliability, disaster recovery, and future smart city applications.

The results highlight the strengths of integrating learned clustering with evolutionary path planning. The hybrid model maintained high service and low overlap with relatively shorter paths. It adapts well to sudden topology changes and uneven UE distributions, making it ideal for post-disaster deployments in which the conditions are dynamic and unpredictable.

6. Conclusions

This study presents a neural-guided hybrid clustering framework for UAV-assisted communication recovery in post-disaster networks. By integrating a lightweight neural classifier with APC and DBSCAN, the proposed method dynamically selects the most suitable clustering strategy according to the spatial distribution of users and the extent of base-station outages. Coupled with a genetic-algorithm-based path optimiser, this approach enables multi-UAV to achieve robust, efficient, and adaptive service restoration under heterogeneous and highly dynamic disaster conditions.

The simulation results demonstrate that the hybrid framework consistently outperforms single clustering methods in terms of service coverage, path efficiency, and adaptability. Even under extreme BS outage scenarios, the hybrid model maintained higher service ratios, smoother UAV trajectories, and reduced path intersections compared with APC- or DBSCAN-only strategies. These results highlight the importance of adaptive centroid generation for guiding UAV deployments, particularly when user distributions are sparse, irregular, or rapidly evolving. The findings of this study emphasize the need for flexible, learning-driven solutions in the design of UAV-assisted disaster response systems.

By fusing machine learning with evolutionary optimisation, the proposed approach not only enhances immediate post-disaster connectivity but also lays a foundation for scalable and resilient UAV deployments in future 5G and 6G networks. Future work will extend this framework by incorporating real-time mobility prediction, cross-layer optimisation with energy-aware routing, and reinforcement learning for adaptive swarm coordination. These extensions will further strengthen the ability of UAVs to provide reliable, low-latency, and autonomous connectivity in complex, large-scale disaster environments.