Broadband Dielectric Spectroscopy Insight Into Compressed ODIC-Forming Neopentyl Glycol (NPG)

1. Introduction

Neopentyl glycol (NPG) has a wide range of applications, from the textiles, plastics, and coatings industries to pharmaceuticals and foods processing [1,2]. It is also important for cognitive fundamentals. Namely, it can exist in orientationally disordered crystal (ODIC) mesophase between liquid and solid crystal, matched with a discontinuous transition. ODIC-forming materials are in the plastic crystals family, with free orientational or rotational motions of molecules translationally ‘trapped’ in the crystalline network [3,4,5,6,7]. Two decades ago, the concept of the barocaloric effect, related to ‘exploration’ of the discontinuous phase transition latent heat on compressing and decompressing, was introduced [8]. However, only in 2019 the colossal barocaloric effect (CBE) in NPG, yielding hopes for groundbreaking applications, was found [9,10]. As the phenomenon metric the entropy change at the transition is used. For NPG the colossal value $\Delta S\approx 400 J{K}^{-1}{kg}^{-1}$was obtained when compressing up to $~450MPa$ [9].

Since then, NPG is considered the reference basis for new generations of thermal energy storage facilities, refrigerators, chillers, air-conditioners, and related technological solutions [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. CBE-based devices can be wholly environment-friendly and more energy efficient than the omnipresent devices based on the circulation of special fluids and their almost continuous adiabatic decompression.

BCE is related to hidden heat ($L$) coupled to the discontinuous phase transition, explored during compressing and decompressing. Clapeyron-Clausius (C-C) relation [27], constitutes the essential interpretative tool [9,14,15,16,19,22,23,24,25,28]:

$${\displaystyle \frac{d{T}_m}{dP}}=T_m{\displaystyle \frac{\Delta V}{L}}={\displaystyle \frac{\Delta V}{\Delta S}}$$

(1)

where $T_m$ denotes the melting temperature under given pressure $P$; $V$, $S$ are for the volume and entropy changes at the discontinuous transition.

Fundamental BCE research, yielding essential support for applications and new materials searching, follows the path set in discontinuous phase transition related studies, particularly melting/freezing between liquid and solid crystal states [28,29,30,31,32,33]. The phenomenon is intensively studied since the 19th century [33], but it remains a challenge. The cognitve situation is in contrast to the continuous, critical phase transitions, with the grand universalistic success of Critical Phenomena Physics [34,35,36,37].

To a large extent, cognitive problem in ultimate explanation of dicontinuous phase transitions can be related to the apparent absence of long-range pretransitional effects [28,29,30,31,32,33]. Generally, fundamental studies on melting/freezing transitiona BCE phenomenon are focused on magnitudes in C-C Eq. (1) and comparison of structural and spectroscopic properties in adjacent phases [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. A hope for a cognitive breakthrough can suggest recent findings of critical-like premelting effects appearing when using dielectric methods [38,39,40,41]. The second cognitive problem, is the still limited evidence for high pressure studies [28,29,30,31,32,33]. Notable, that the high temperature ODIC phase can be considered a specific model liquid, where the ‘freedom’ is related solely to orientations. Hence, the broadband dielectric spectroscopy (BDS) [42], inherently coupled to the electric field action, is the primary primary method for testing the ODIC mesophase [3,4,5,6,43].

When commenting on the importance of high pressure and dielectric studies for NPG worth noting is the recent model analyses of entropy changes $S$ for discontinuous phase transitions.leading to the following output relation [44]:

$$\Delta S={\Delta s}_1+{\Delta s}_2+{\Delta s}_3={\int }_{T_{ref.}}^T{\displaystyle \frac{C_{P,E}}{T}}dT+\underset{P_{ref.}}{\overset{P}{\int }}vdP+{\varepsilon }_0{\int }_0^{E}v{\left({\displaystyle \frac{d}{dE}}\right)}_{P}EdE$$

(2)

where $C_{P,E}$ is the heat capacity related to constant pressure and/or electric field, $v$ is the specific volume per unit mass, and α is the isobaric thermal expansion concerning subsequent pressures.

The first term ${\Delta s}_1$, can be related to the general internal energy change. The second term ${\Delta s}_2$ can be retrieved as follows at the transition: indicates the significance of compressibility change at the Δχ_T discontinuous transition and the pressure dependence of the phase transition, namely: $\alpha =\left(1/V\right){\left(\partial V/\partial T\right)}_{P }={\left(\partial V\partial P/\partial T\partial P\right)}_{T_{m,}{P}_m}=\left(1/V\right){\left(\partial V/\partial P\right)}_{T_{m,}{P}_m}{\left(d{T}_m/dP\right)}^{-1}$⇒$\alpha =\Delta {\chi }_T{\left(d{T}_m/dP\right)}^1$. It explicitly shows the importance of the compressibilities difference for adjacent phases. It is particularly impressive impressive fo NPG, due to the ductility of the high-temperature plastic crystal ODIC mesophase and the ‘hardness’ of the solid state crystal. Notable is also the significance of the discontinuous phase transition $T_m\left(P\right)$ patten. The last term in Eq. (2), ${\Delta s}_3$, directly recalls the significance of dielectric constant change when passing the transition.

This report shows the first multi-aspect broadband dielectric spectroscopy insight for neopentyl glycol (NPG) on compressing, in the broad surrounding of the discontinuous phase transition between the ‘soft’ ODIC’ phase and the ‘hard’ crystal phase. The report introduce new evidences regarding properties of the ODIC mesophase, the ODIC- crystal or even melting/freezing discontinuous phase transition, and the colossal barocaloric effect in NPG and related materials [45,46].

3. Materials and Methods

Neopentyl glycol, with the highest available purity, was purchased from Sigma-Aldrich NPG Glycol (CAS 126-30-7). It shows the following phase sequence under atmospheric pressure: $\mathit{L}\mathit{i}\mathit{q}\mathit{u}\mathit{i}\mathit{d}\to \left({\mathit{T}}_{\mathit{L}-\mathit{O}}=\mathbf{403.6}\mathit{K}\right)\to \mathit{O}\mathit{D}\mathit{I}\mathit{C}\to \left({\mathit{T}}_{\mathit{O}-\mathit{C}}=\mathbf{315.6}\mathit{K}\right)\to \mathit{S}\mathit{o}\mathit{l}\mathit{i}\mathit{d} \mathit{C}\mathit{r}\mathit{y}\mathit{s}\mathit{t}\mathit{a}\mathit{l}.$

High-pressure measurements were carried out using two setups. The first one was used to study up to 700 MPa. It is shown in Figure 1. For this facility, the pressure pump supports the pressure chamber, where Plexol is used to transmit the pressure. It consists of a pressure chamber linked to the pressure pump. The chamber was surrounded by a jacket, linked to the large volume ($V=25L$) thermostat with external circulation. Both temperature and pressure were computer-controlled. Temperature was measured by the copper-constant thermocouple placed in the pressure chamber and two Pt100 resistors along the chamber to monitor a possible temperature gradient. The pressure was monitored by a tensometric meter, with $\pm 0.1MPa$ precision. Tested samples were placed in the measurement flat-parallel capacitor in the pressure chamber. The pressure was transmitted to the sample inside the capacitor via the deformation of an elastic element. Its design is shown in ref. [50]. The measurement capacitor was made from Invar, with the $d=0.3mm$ gap between capacitor plates.

The second setup focused on extending pressure up to challenging 2 GPa. It consists of a pressure chamber with an internal diameter 12 mm. The capacitor with the tested sample was placed in the Teflon tube with an external diameter only slightly lower than the diameter of the chamber. Inside the Teflon tube, a flat-parallel measuring capacitor was created on the basis of an Invar cylinder cut along the long axis. The distance between the plates was 0.3 mm.

High and very high pressures acting on the tested sample were created by the piston being pressed into the pressure chamber, causing the Teflon tube plastic (reversible) deformation. The pressure chamber was also surrounded by a jacket, allowing the circulation of liquid from a large-volume thermostat with external circulation. The temperature was measured using a thermocouple inside the chamber. Changing the experimental pressure technique from method 1 to method 2 allows us to avoid problems with a strong increase in the viscosity of the medium (liquid) transmitting the pressure in method 1.

Method 2 is associated with limitations in high-pressure values estimations to at least $\pm 5MPa$. It can be calculated from the force acting on the piston, creating pressure by high-pressure press. It has to be calibrated by testing pressure induced using the manganin coil electric resistance placed in the chamber. Consequently, applying the second method for pressures above a few hundred MPa can be advised.

The pressure was transmitted to the sample inside the capacitor via the deformation of an elastic element. Its design is shown in ref. [50]. The measurement capacitor was made from Invar, with the $d=0.3mm$ gap between plates of the capacitor.

BDS measurements were carried out using the Alpha Novocontrol BDS spectrometer, supported by Novocontrol system software, allowing the avoidance of parasitic capacitances and yielding directly the real and imaginary parts of dielectric permittivity or electric conductivity as the output of measurements. The analyzer enables 5 or 6 digits resolution scans. Tests were carried out for $U=1V$ measurement voltage, which guaranteed the optimal measurement resolution. BDS studies under pressure are still limited to a few MHz in frequency because of unsolved technical challenges. NPG was purchased from Aldrich company and placed in the measurement capacitor after heating up to the liquid phase.

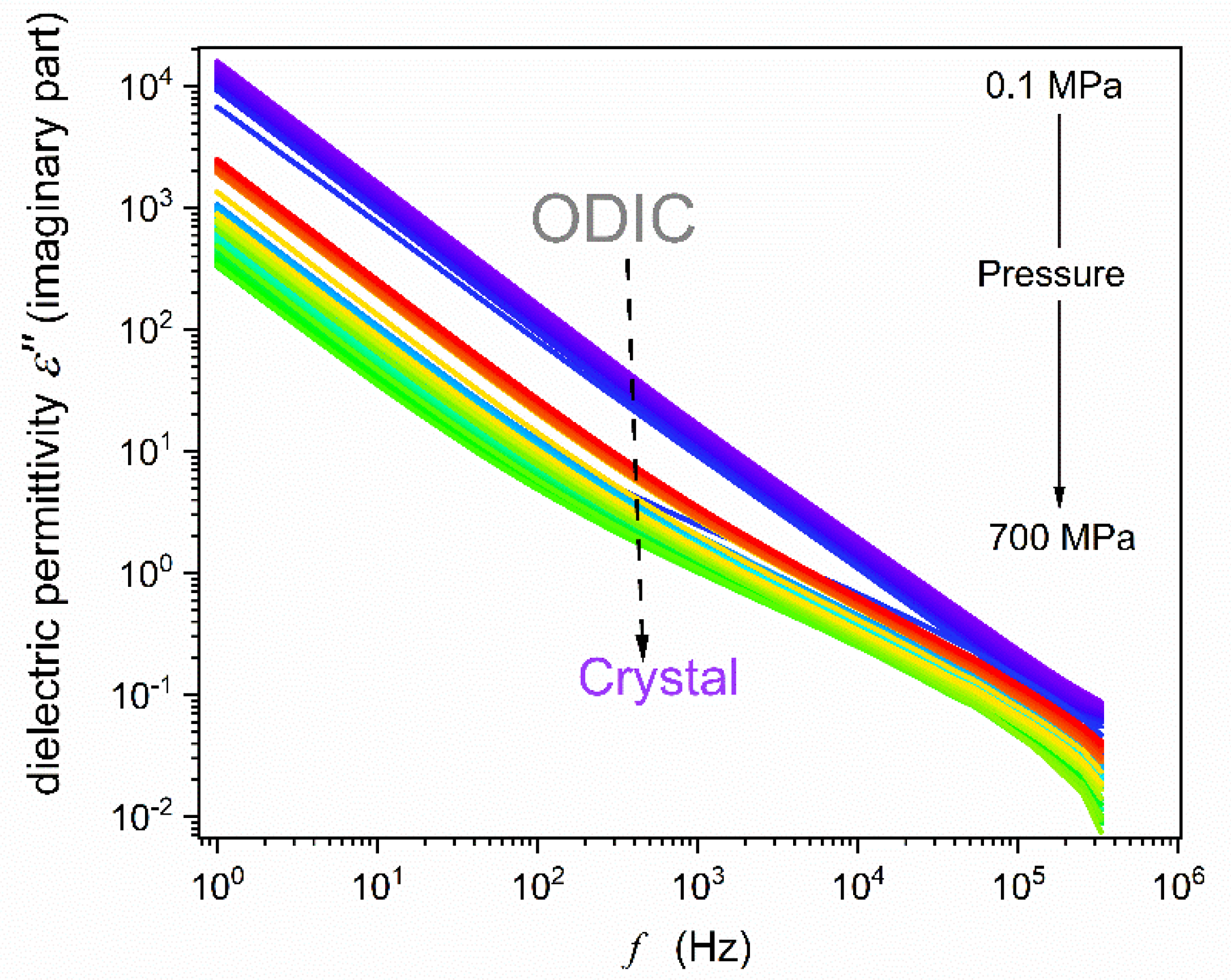
The example of experimental spectra detected in BDS-based scans is presented in Figure 2 and Figure 3 for the real imaginary parts of dielectric permittivity: ${\varepsilon }^{\ast }={\varepsilon }^{\prime }+i{\varepsilon }^{″}$, where ${\varepsilon }^{\prime }=C/C_0$ and ${\varepsilon }^{″}=1/CR$; $C\left(f\right)$ and $C_0$ are detected electric capacitances for the capacitor with the sample and ‘empty’, $R\left(f\right)$ is the resistivity, $=2f$ [42] They were the base for deriving properties discussed in the subsequent section. In Figure 2 important frequency domains are indicated.

4. Results and Discussion

4.1. Real Part of Dielectric Permittivity, Moderate Pressures

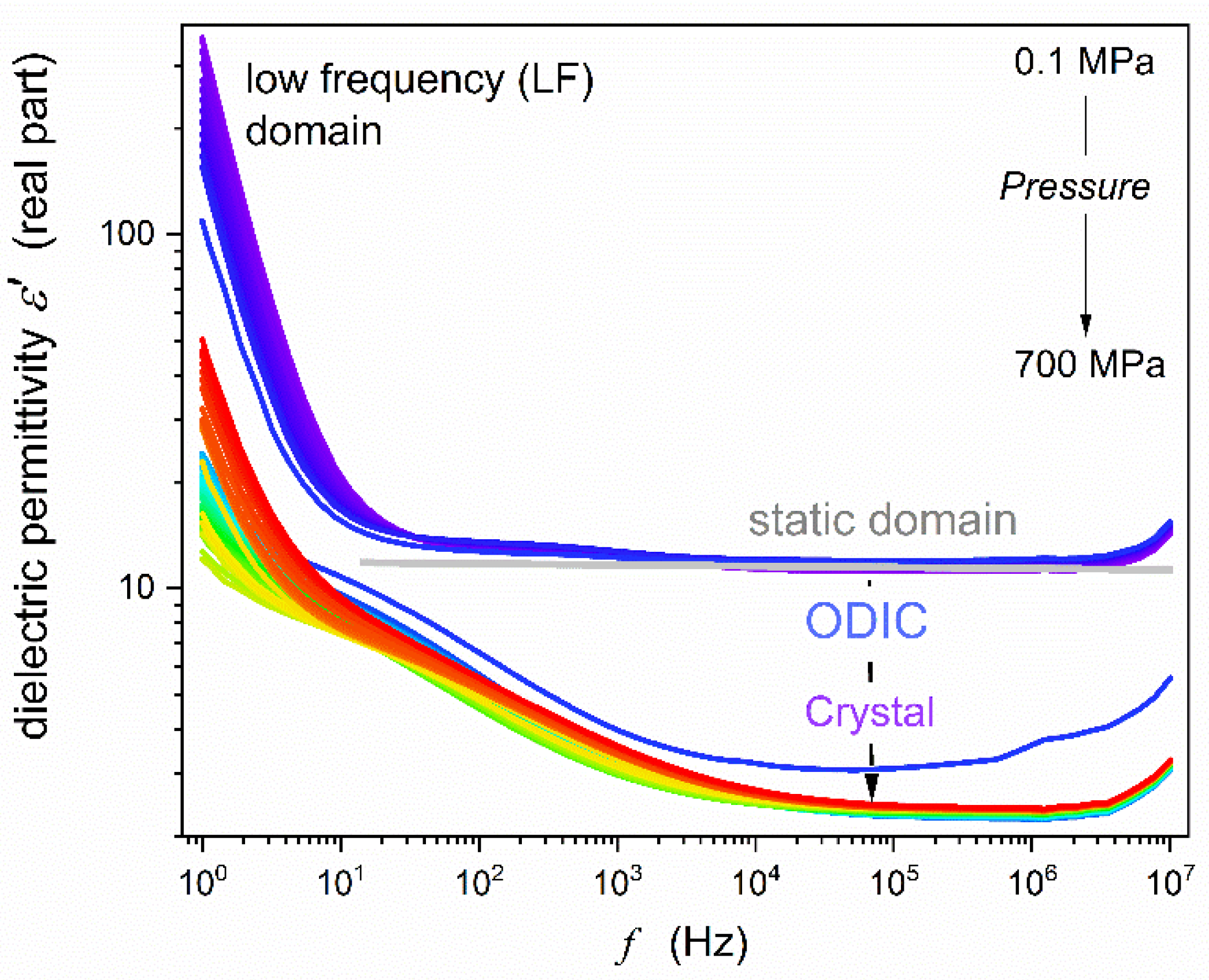
Dielectric constant is the first, and still essential, characterization of dielectric materials, introduced yet by Michel Faraday [67]. It is related to the horizontal ‘static’ domain of the real part of dielectric permittivity ${\varepsilon }^{\prime }\left(f\right)$. For NPG the static domain appears explicitly only in the ODIC phase, for $~2kHz<f<~2MHz$, as shown in Figure 2 by the horizontal line in grey. For the solid crystal phase, the extent of the static domain is qualitatively lesser. For frequencies above the static domain, the relaxation domain with the primary loss curve addresses the reorientations of permanent dipole moments directly. It was not possible to access it in the given experiment because of the frequency range technical limitations in high-pressure studies.

Below the static domain, the boost in ${\varepsilon }^{\prime }\left(f\right)$ and ${\varepsilon }^{″}\left(f\right)$ values are linked to the low frequency (LF) domain. Generally, it is related to ionic species in dielectric material, which can contribute to dielectric materials for low enough frequencies.

The strong rise of dielectric permittivity is essentially linked to ‘generally recalled ‘ionic species’ or ‘contaminations [68,69,70,71,72,73,74,75]. Neverteless, they can also explaine by translational shift, in respect to the average position, for basic molecules of a givan system/material [50].

Worth recalling, is the still existing challenge for dielectric permimittivity parameterization in the LF domain, particularly for ${\varepsilon }^{\prime }\left(f\right)$ [66,67,68,69,70,71,72,73].

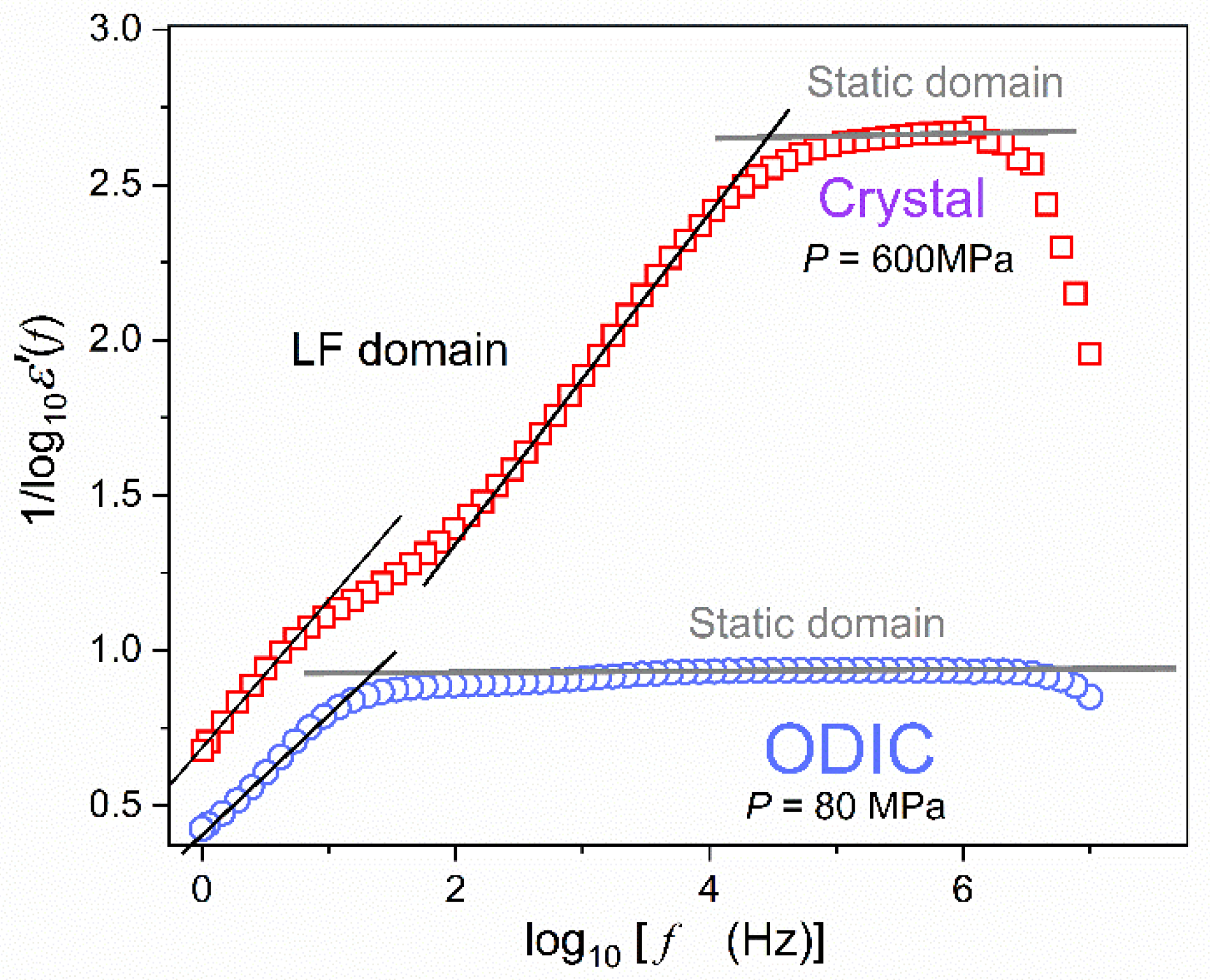
Figure 4 shows an empirical attempt to overcome this problem. It presents the changes of the real part of dielectric permittivity reciprocal, revealing features not explicitly visible in Figure 2. Horizontal lines in grey indicate the static domain, where frequency shifts do not yield changes in ${\varepsilon }^{\prime }\left(f\right)$ values. For LF domain, i.e., frequencies below the static domain. also a simple linear pattern emerges. It leads to the following set of equations:

$$1/ln{\varepsilon }^{\prime }\left(f\right)=a+lnf \Rightarrow ln{\varepsilon }^{\prime }\left(f\right)=1/\left(a+lnf\right) \text{⇒} {\varepsilon }^{\prime }\left(f\right)=exp{\left(a+lnf\right)}^{-1}$$

(9)

where $a, b$ are empirical constants.

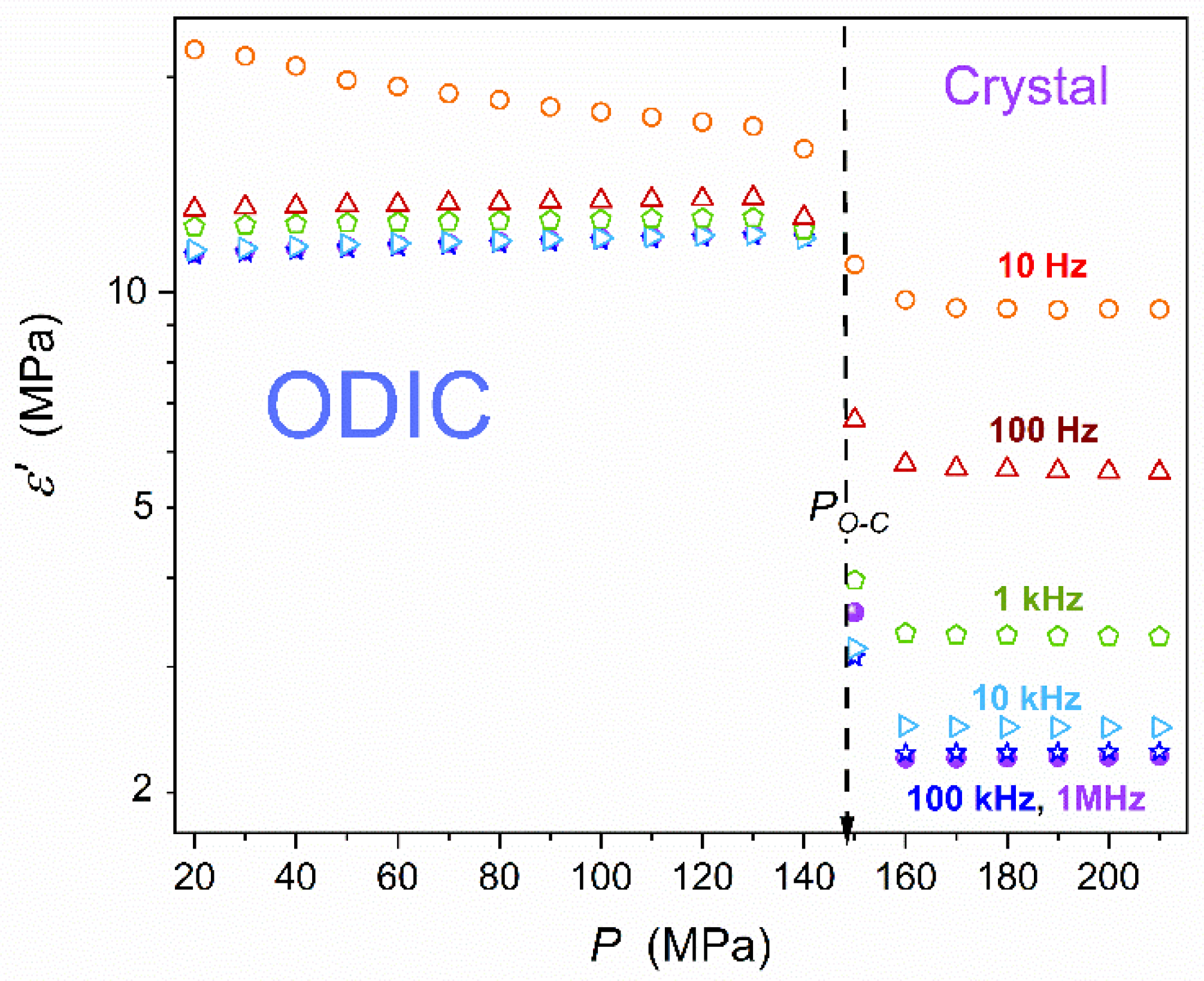
Figure 5 presents isothermal pressure changes of dielectric constant in the surroundings of the discontinuous phase transition. The plot is in the semi-log scale to support the insights both in the ODIC and Crystal phase, despite strong different values. In both phases, the impact of frequency shift to the LF domain is visible. For the static domain, in the frequency range ~100 kHz, changes of $\varepsilon \left(P\right)$ seems to be nearly linear. Visible is a weak pretransitional rise in the solid phase for pressures just above the phase transition.

Studies of temperature changes of dielectric constant in dipolar liquid dielectrics showed that the general tendency in $\varepsilon \left(T\right)$ evolution can indicate the dominant way of permanent dipole arrangements. Namely, for $d\varepsilon \left(T\right)/dT>0$ the preference for their antiparallel arrangement can be expected, and for $d\varepsilon \left(T\right)/dT<0$ the parallel one [61]. A similar ‘rule’ should be expected in the ODIC phase, with a large range of permanent dipole moments orientational freedom. Implementing this reasoning to isothermal changes on compressing, one should expect $d\varepsilon \left(P\right)/dP<0$ as the indicator of the preferable antiparallel arrangement and $d\varepsilon \left(P\right)/dP>0$ for the parallel one.

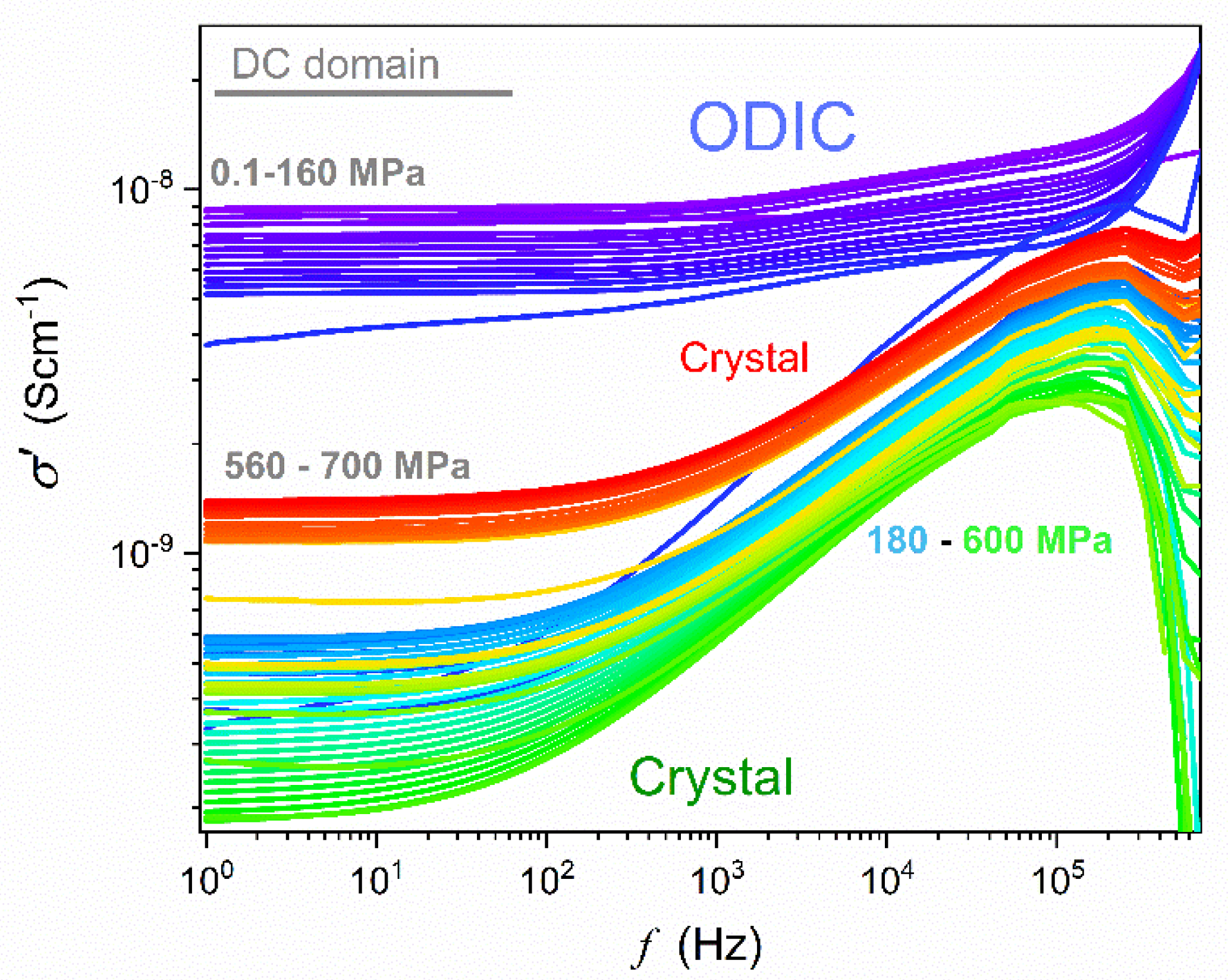
4.2. Electric Conductivity, Moderate Pressures

Figure 6 displays the results of the transformation of experimental data given in Figure 3 to the electric conductivity representation: ${\sigma }^{\prime }={\epsilon }_0\omega {\epsilon }^{″}\left(f\right)$, $\omega =2\pi f$ [61], to enable the insight into dynamic properties overcoming the mentioned frequency range limitations in high-pressure studies . The DC electric conductivity domain, which can be considered as the ‘static domain’ parallel for dynamic properties, is indicated by the gray horizontal line. For this domain, the frequency shift does not change the electric conductivity value: ${\sigma }^{\prime }\left(f\right)=\sigma ={\sigma }_{DC}$. In the ODIC phase, the DC domain covers 3 decades in frequency: $1Hz<f<1kHz.$In the solid crystal phase, such behavior emerges only for $f\text{→}1Hz$. 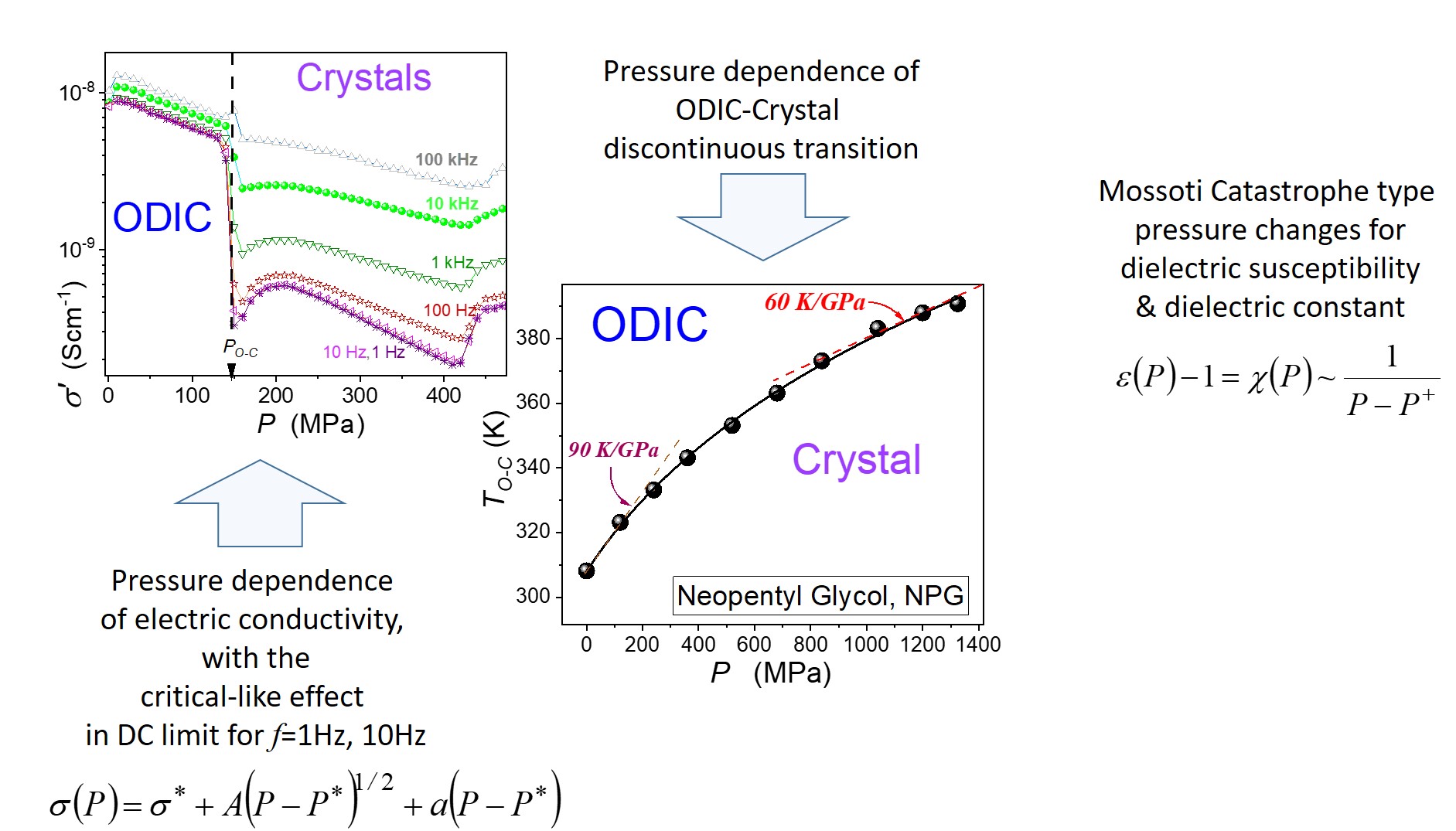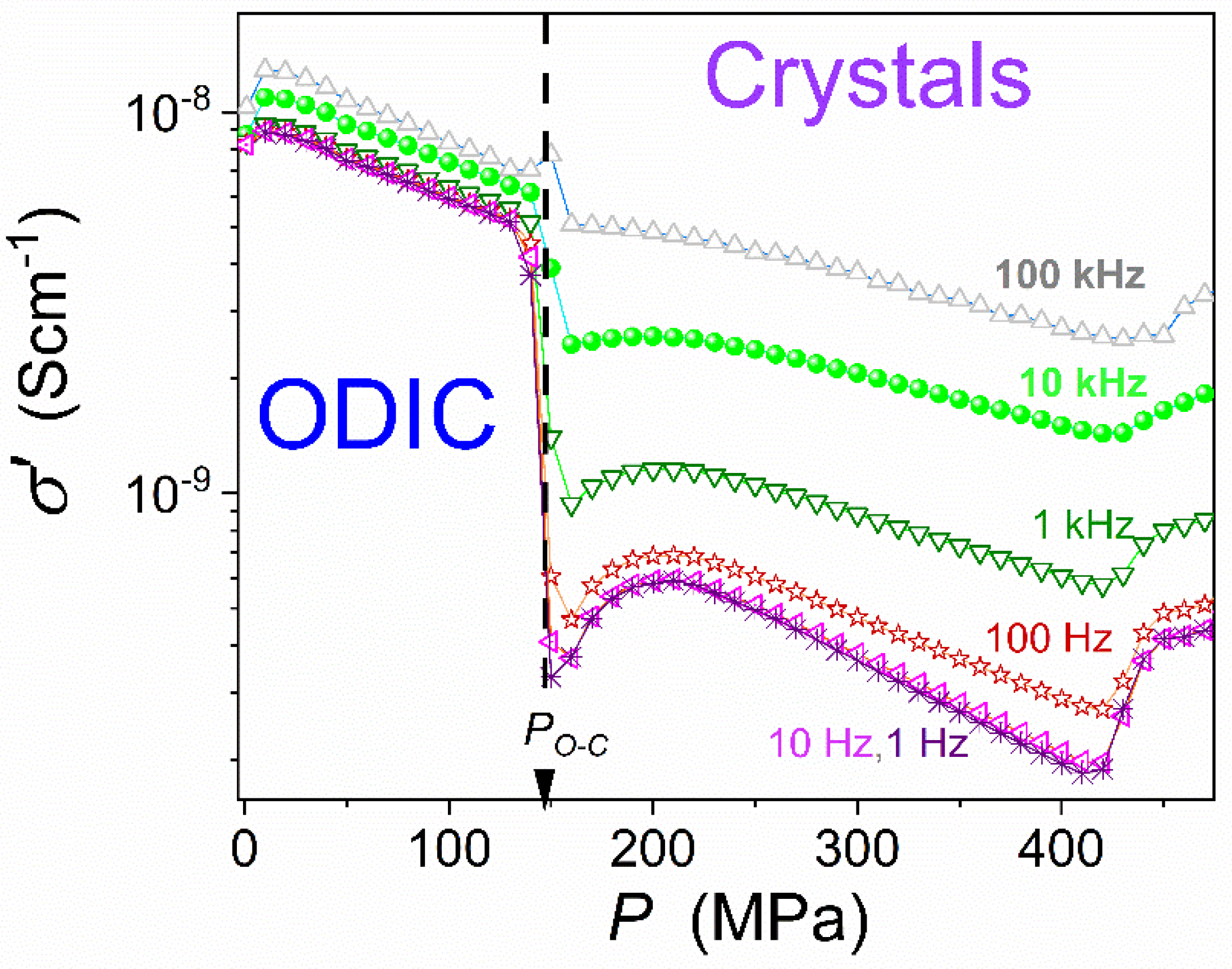Pressure changes of electric conductivity, including the DC domain, are presented in Figure 7. Notable is the complex pattern in the Solid Crystal phase.

Vertical continuous arrows indicate possible phase transitions or transformations in this domain. The first one is for $P_1\approx 510MPa$ . The second one is more complex since its hallmarks are frequency–dependent: $P_2\approx 415-450 MPa$.

The ODIC – Crystal discontinuous transition is explicitly visible at $P_{O-C}=148MPa$, as shown by the ;thick’, dashed arrow. The striking feature is the pretransitional behavior in the Solid Crystal phase and extends up to $P_{O-C}+250MPa$. At least for the first 150 MPa from the transition, it can be approximated by the critical-like relation:

$$\sigma \left(P\right)={\sigma }_C+A{\left(P-P^{\ast }\right)}^{\varphi =1/2}+a\left(P-P^{\ast }\right)$$

(10)

where ${\sigma }_C,A,a$are constant parameters, the exponent $\varphi =1/2$, and the singular pressure $P^{\ast }\approx 144MPa$, note - it is close to the discontinuous transition $P_{O-C}=148MPa$.

The above result is for the DC limited, i.e., $f=1Hz$. The pretransitional effect diminishes when rising the frequency, i.e., shifting away from the DC domain limit.

The results in Figure 6 are presented in the ‘Barus scale’ i.e., $ln{\sigma }^{\prime }\left(P\right)$ vs. $P$, which can be considered as the pressure counterpart of the Arrhenius scale $ln{\sigma }^{\prime }\left(T\right)$ vs. $1/T$ [42] used in temperature studies under atmospheric pressure. For the ‘Barus scale’ the linear dependence validates the simple behavior with the constant activation volume $V_a=const$ in the given pressure range, namely:

$$\sigma \left(P\right)={\sigma }_{0}exp\left(cP\right) \text{⇒}\sigma \left(P\right)={\sigma }_{0}exp\left(P{\displaystyle \frac{V_a}{RT}}\right), T=const$$

(11)

where the left side is for the original Barus report [76] and the right side, with the activation volume $V_a$; in the given case $V_a=const$ and the empirical Barus parameter $c=const$; $R$ means the gas constant.

Notable that the authors of the given report in refs. [50,65] introduced the name Barus scale. to honor the author of refs. [76] who introduced the pressure portrayal via the left side of Eq. (11). It also included names Super-Barus behavior and Super-Barus (SB) equation with the pressure-dependent apparent activation volume${ V}_a\left(P\right)$ [50,65,77].

4.3. Dielectric Loss Factor Changes

The dissipation factor $D$addresses both dynamics and energy-related issues in dielectric materials. It is defined as follows [61,64,78,79,80]:

$$D=tan\delta ={\displaystyle \frac{{\varepsilon }^{″}}{{\varepsilon }^{\prime }}}={\displaystyle \frac{energy loss}{energy stored}}\left(per cycle\right)$$

(12)

It is the crucial parameter in the evaluation of materials used for isolations in electric equipment, from solid covers of cables, capacitors, and some machines to transformers’ oil. Its measurement can indicate the presence of moisture, aging, or other degradation factors. Such tests are essential to predict dielectric materials' life expectancy and maintenance in tested elements [78,79,80]. Surprisingly, this magnitude, commonly used in material engineering, is hardly discussed in fundamental studies of dielectric properties in solids and liquids [42,60,61,62,63,64].

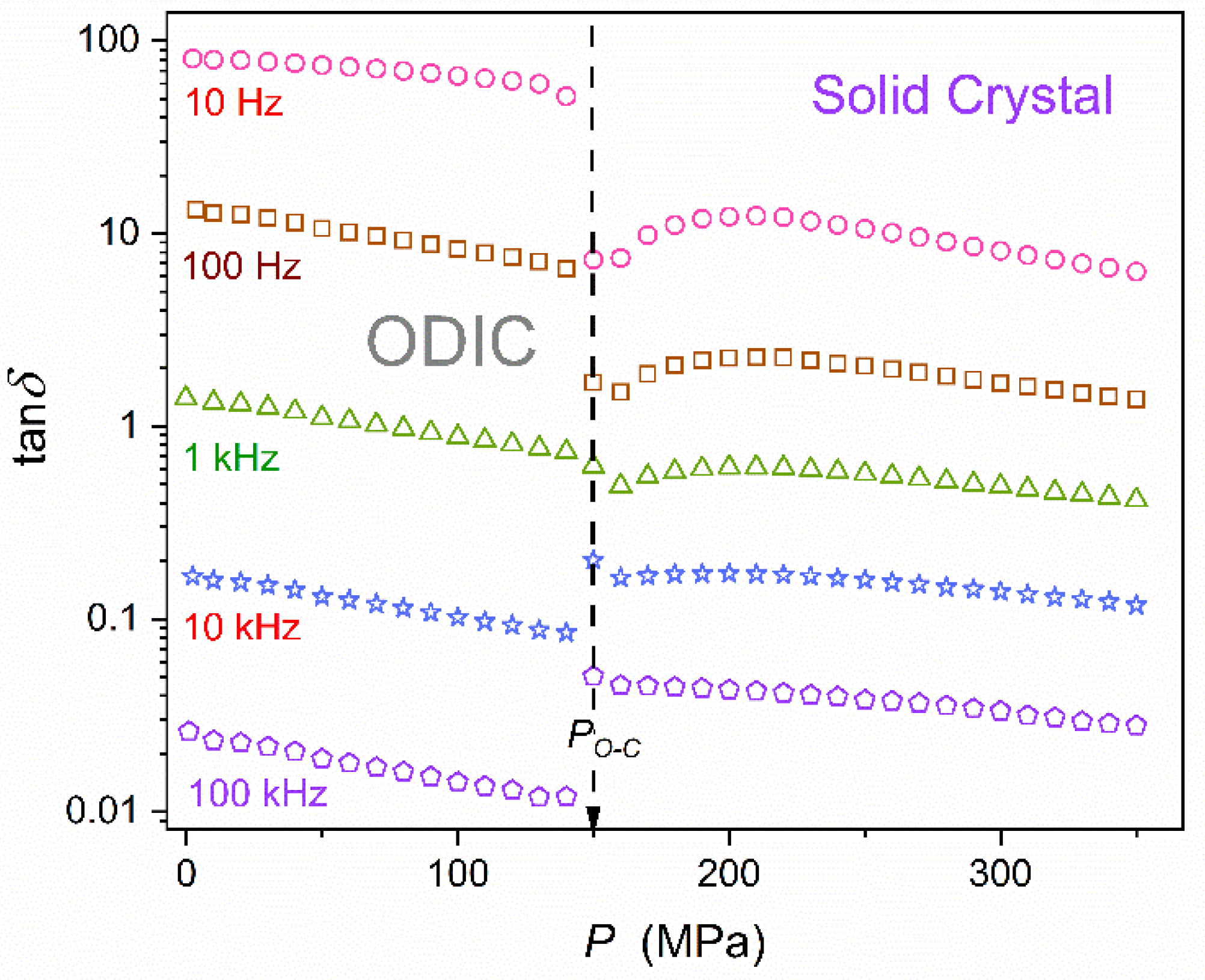
Figure 8 shows pressure changes of the dissipation factor in neopentyl glycol (NPG), derived from experimental data shown in Figure 2 and Figure 3. The linear behavior in the semi-log scale plot 8 suggests the evolution following the parallel of the Barus relation, namely: $tg\delta \left(P\right)=D_{0}exp\left(cP\right)$, $c=const$. Nevertheless, pretransitional effects are visible in the solid phase , particularly for the lowest presented frequency. Notable is the significant change in values from $tg\delta \left(P\right)~0.01$ for $f=100kHz$, which in applications would be classified as an excellent isolator (no energy loss) for $tg\delta \left(P\right)~100$ for $f=10Hz$, i.e., the value linked to extremely poor isolator and substantial energy losses that can be converted to heat.

Figure 9 supplements the above discussion by showing $tan\delta \left(f\right)$ frequency-related spectrum. In the ODIC phase, the plot suggests the evolution $tan\delta \left(f\right)\propto f^{-1}$ for $30Hz<f<300kHz$. Such behavior is considered as a pattern for a non-ideal capacitor in an AC circuit when the ratio of resistive power loss to reactive power loss is considered [78,79,80]. When commenting such behavior for NPG, one can recall Figure 3, where ion the ODIC phase ${\epsilon }^{\prime }\left(f\right)=\epsilon \approx const$ in the static domain, and ${\epsilon }^{″}\left(f\right)\propto f^{-1}$. The latter is related to DC electric conductivity domain in Figure 6. Although the ‘canonic’ static domain terminates at $f~10kHz$, it remains only slightly distorted down to $50-100Hz$ in the ODIC phase. It is notable that usually, in molecular liquid dielectrics, $f~1kHz$ is the definitive onset of the LF domain boost of dielectric permittivity. These feature of spectra presented in Figure 2, Figure 3 and Figure 6 , confronted with the definition of the disipation factore (Eq. 12) one obtaines ${\epsilon }^{\prime } \left(f\right)\approx const$, even down to ~100Hz. In same domain the DC electric conductivity ‘horizontal evolution is equivalent to ${\epsilon }^{″}\left(f\right)\propto f^{-1}$. 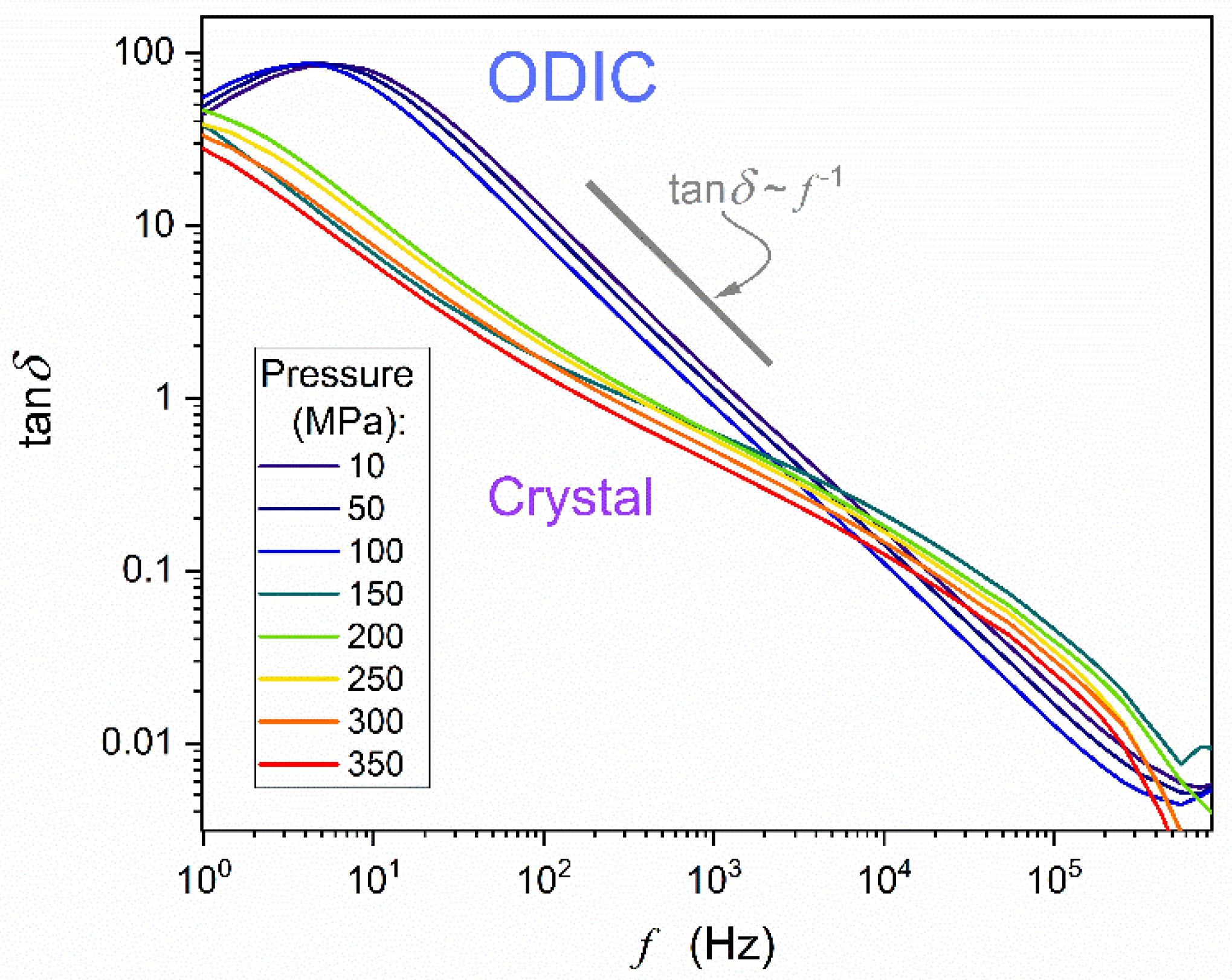Hence, for the ODIC phase in NPG the appearing model-relation $tg\delta \left(f\right)~f^{-1}$ can be linked to the dominance of translational processes.

The crossover $d{log}_{10}\left(tan\delta \right)/d{log}_{10}>0\text{←} d{log}_{10}\left(tan\delta \right)/d{log}_{10}<0$ for low frequencies is associated with the definitive leave by ${\epsilon }^{\prime }\left(f\right)$ near static domain domain and LF domain strong boost in values.

4.4. Dielectric Constant: Extreme Pressures Tests

The above evidence suggests linear changes of dielectric constant and simple Barus-type evolution for electric conductivity. However, it can also be linked to the relatively small pressure range: $P\left(ODIC\right)~150MPa$ . To test this hypothesis, challenging studies for isotherms reaching T = 110 °C, where the ODIC phase extends up to $P=1.2GPa$.were carried out.

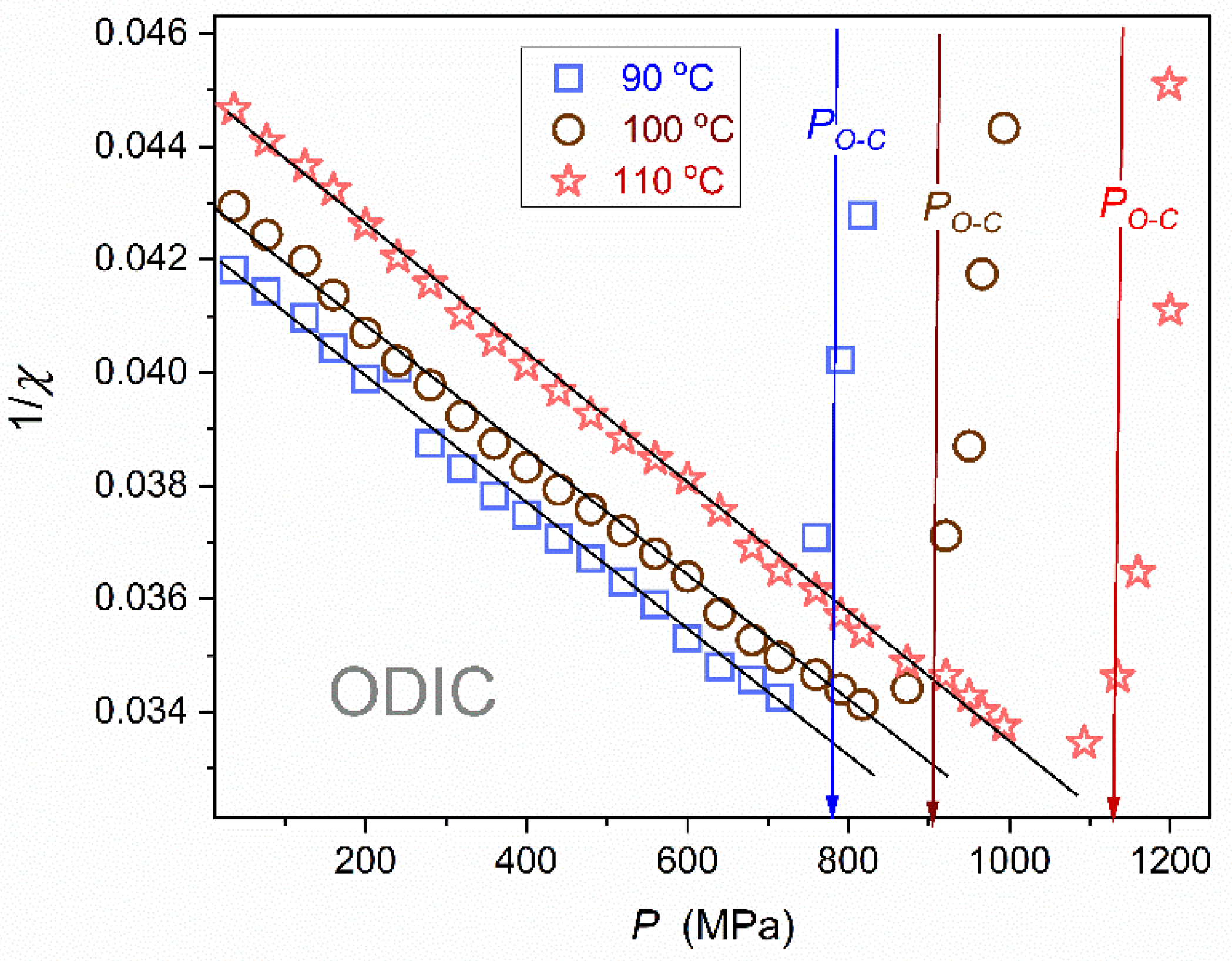
The mentioned extreme pressure tests reveal slight distortion from the linear behavior in $\epsilon \left(P\right)$ changes. Figure 10 presents the results of these data via the analysis of the dielectric susceptibility $\chi =\epsilon -1$ reciprocal. The explicit linear behavior suggests the following scaling pattern:

$$\epsilon \left(P\right)-1=\chi \left(P\right)={\displaystyle \frac{A}{P^{+}-P}}\text{⇒} {\chi }^{-1}\left(P\right)=a+bP$$

(13)

where $A=const$ and $P^{+}$ is the extrapolated singular pressure; $a=A^{-1}{P}^{+}$ and $b=-A^{-1}P$.

Notable is the similarity of the pressure related Eq. (13) and temperature related Eq. (6) The latter has been just repported in ODIC phase of NPG [43] and earlier in cyclooctanol [66]. In those reports, it was explained via precursors of the Mossotti – Catastrophe behavior and the validation of the Clausius-Mossotti simple local field modeling. The similarity of Eq. (6) for temperature and Eq. (13) for pressure changes in the ODIC phase also recalls the Isomorphism Postulate within the Critical Phenomena Physics [35], suggesting the same critical scaling pattern when a given physical property is tested along two different field variable related paths of approaching continuous phase transition. It is particularly related to values of universal critical exponents for pressure and temperature paths of approaching the critical. For the ODIC phase of NPG, Eq. (13) for $\chi \left(P\right)$ and Eq. (6) $\chi \left(T\right)$ aloso resemble the Curie-Weiss type behavior pattern in the paraelectric phase of ferroelectric materials, coupled to the susceptibility (compressibility) exponent ($\gamma =1$).

2.5. DC Electric Conductivity: Extreme Pressures Test

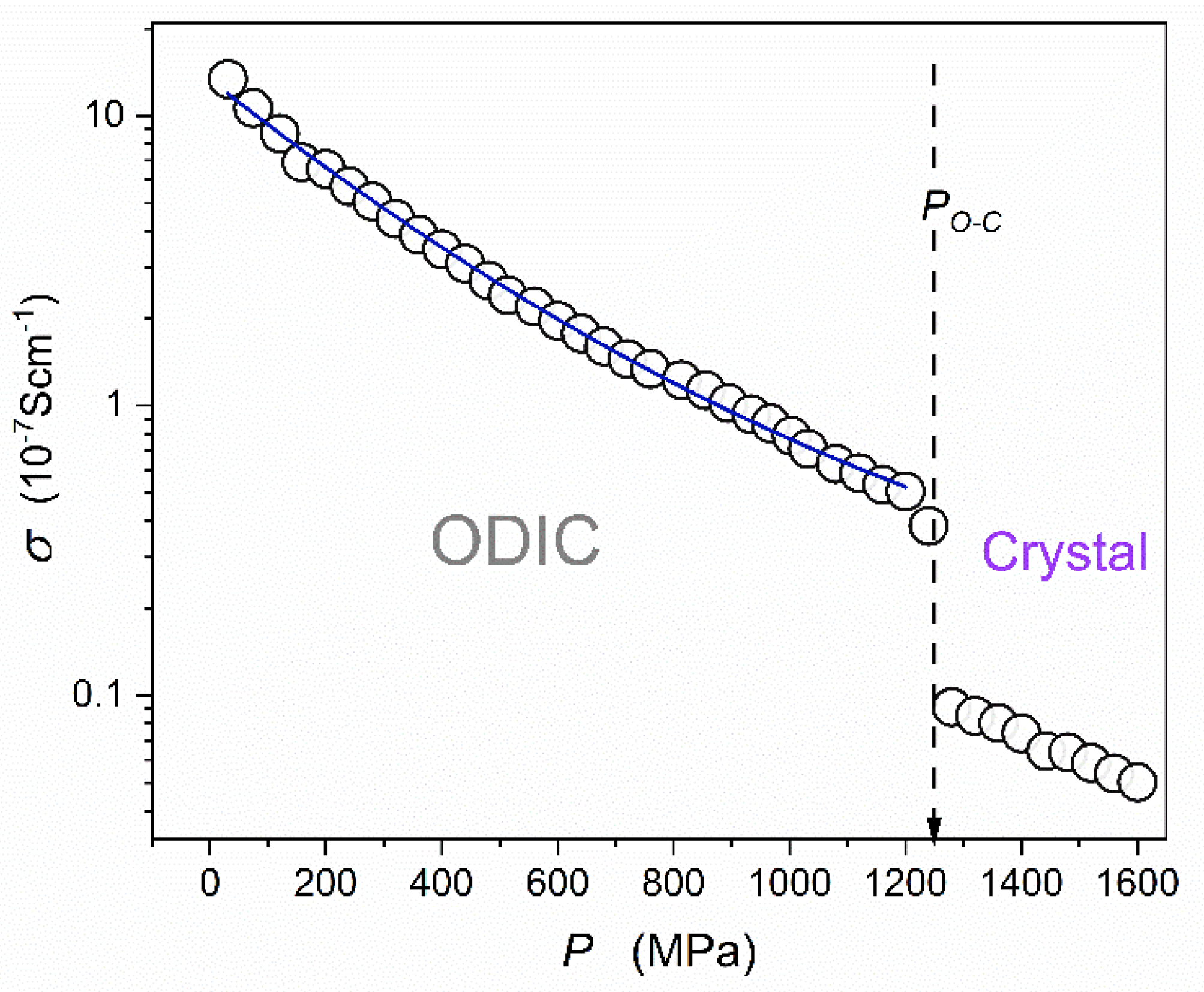
Figure 11 presents the evolution of DC electric conductivity in the ODIC phase extended up to $P=1.2 GPa$ ‘extreme’ pressure. It reveals a slight distortion from the apparent Barus pattern visible in Figure 7, where the ODIC phase covers only $~0.15GPa$. The nonlinear, non-Barus, behavior in Figure 11 is visible but it is too weak for a reliable and decisive fitting by a model equation.

To overcome this problem, the analysis recalling the super-Barus equation, i.e., the extension of Eq. (11) with the pressure-dependent apparent activation energy $V_a\left(P\right)$ can be considered. Generally, such super-Barus equation cannot be used for fitting electric conductivity $\sigma \left(P\right)$, primary relaxation time $\tau \left(P\right)$ or viscosity $\eta \left(P\right)$ data because of the unknown general pattern of $V_a\left(P\right)$ changes. Nevertheless, it is commonly used for estimating the apparent activation via the following relation Eq. (11) [81,82,83,84,85,86,87,88,89,90]:

$$ln\sigma \left(P\right)=ln{\sigma }_0+P{\displaystyle \frac{V_a}{RT}} \text{⇒} RT{\displaystyle \frac{dln\sigma \left(P\right)}{dP}}=V_{\#}\left(P\right)$$

(14)

In the analysis using the above equation it is assumed that the right part of the above relation estimates the apparent activation volume estimation, i.e., $V_{\#}\left(P\right){=V}_a\left(P\right)$. Unfortunately, this assumption is essentially wrong, i.e., $V_{\#}\left(P\right)\ne V_a\left(P\right)$ and $V_{\#}\left(P\right)~dln\left(P\right)/dP$ determine the steepness index for the non-Barus type experimental data presented in the Barus scale plot [50,77]. Namely, the right part of Eq. (14) can be obtained only by assuming $V_a=const$. The proper analysis of the super-Barus relation, gives [50,77]:

$$ln\sigma \left(P\right)=ln{\sigma }_0-P{\displaystyle \frac{V_a\left(P\right)}{RT}} \text{⇒} RT{\displaystyle \frac{dln\sigma \left(P\right)}{dP}}=V_a\left(P\right)-{\displaystyle \frac{d{V}_a\left(P\right)}{dP}}$$

(15)

The term $d{V}_a\left(P\right)/dP=0$ only for the basic Barus equation with $V_a\left(P\right)=V_a=const$.

A protocol overcoming this problem and allowing the determination of the real apparent activation volumes for subsequent pressures was proposed by Drozd-Rzoska [77], where the prevalence of the following extension of the SB relation was also indicated:

$$\sigma \left(P\right)={\sigma }_{0}exp\left(-\Delta P{\displaystyle \frac{V_a\left(P\right)}{RT}}\right)$$

(16)

where $\Delta P=P-P_{Sp}$; $P_{Sp}<0$ is the absolute stability (spinodal) limit for the tested isotherm $T=const$.

Originally in refs. [50,77], the discussion was carried out in frames of the primary relaxation time. Eq.(16) take into account that for real liquids and solids, the pressure $P=0$ does not constitute any specific reference. Such value can be passed without any hallmark into the negative pressures domain, where isotropic stretching until reaching $P_{Sp}<0$ value is possible. $P=0$ is the terminal point only for gases [50,77].

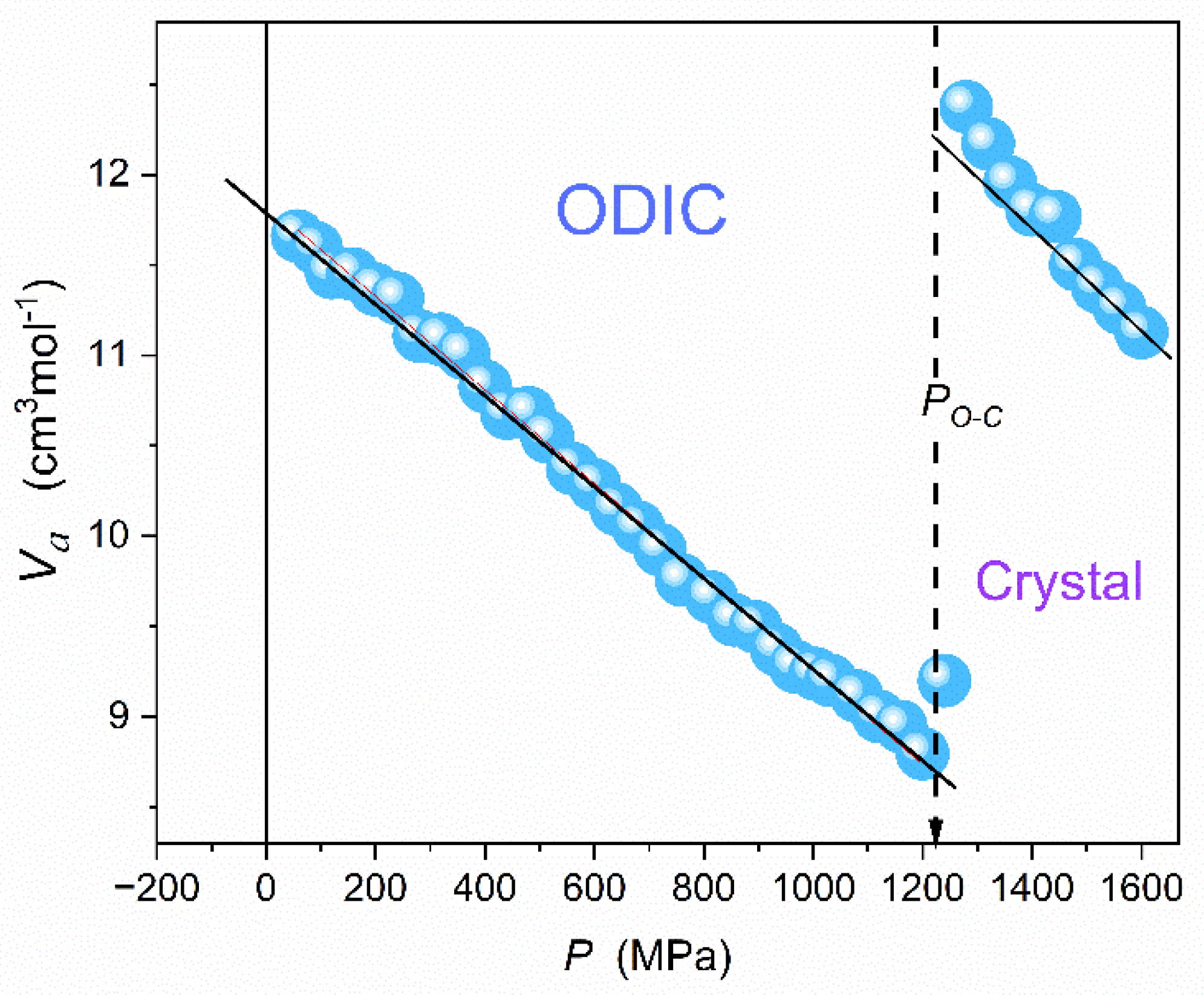
Figure 12 presents pressure changes of the apparent activation volume, related to Eq. (16) and recalling the analysis presented in ref. [77]. Notable that for the basic Barus relation, i.e., Eq. (11) with $V_a=const$, the horizontal line related to $V_a=const$ should appear.

The linear parameterization appearing in Figure 12 can be substituted to Eq. (16), yielding the following dependence portraying experimental data in the ODIC phase of NPG:

$$\sigma \left(P\right)={\sigma }_{0}exp\left(-\Delta P{\displaystyle \frac{a+bP}{RT}}\right)={\sigma }_{0}exp\left(-\Delta P{\displaystyle \frac{a+bP}{RT}}\right)$$

(17)

where $\Delta P=P-P_{Sp}$, and values of $P_{Sp}$,$a,b$ are given in the caption of Figure 12.

The result of such decription is shown by the red curve portraying experimental data in Figure 12: Notably, that the described routine avoids a nonlinear fitting.

4.6. Pressure Dependence of the ODIC-Crystal Discontinuous Phase Transition Temperature

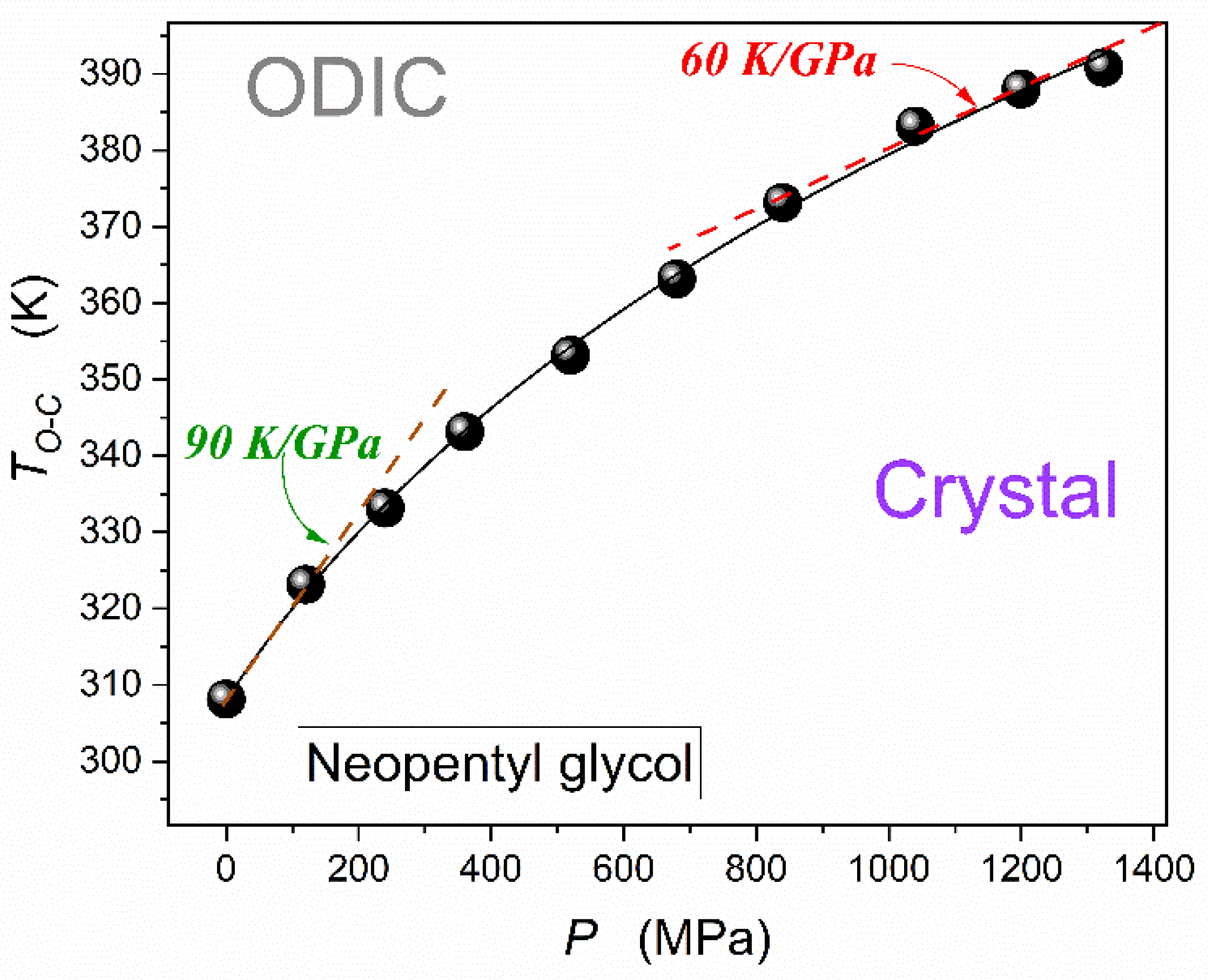
Figure 13 concludes the discussion of NPG pressure-related features presented in the given report by showing the pressure dependence of the discontinuous ODIC – Crystal phase transition. Data were determined by detecting dielectric constant step changes when passing the transition.

Results presented in Figure 13 can be parameterized by the |Simon-Glatzel equation [50,90], as shown by shown by the solid curve in the plot:

$$T_m\left(P\right)=T_0{\left(1+{\displaystyle \frac{P}{\prod }}\right)}^{1/b}$$

(18)

where $T_0=307.9K$ is related to the melting temperature under atmospheric pressure, $=431MPa$ and $b=5.65$ are empirical constants when recalling the original reference of this model relation.

When considering the barocaloric ‘experiment’, related to subsequent isothermal path of approaching $T_{O-C}\left(P\right)$ curve notable is the rise of ${\left[d{T}_{O-C}\left(P\right)/dP\right]}^{-1}$ which has to lead to a similar change in the related contrinution to entropy $s_2$ in Eq. (2).