The Impact of Nanoparticles on the Previtreous Behavior: Glass-Forming Nematogenic E7 Mixture-Based Nanocolloids

1. Introduction

At the turn of the 20th and 21st centuries, the glass transition problem was noted among the grand challenges of 21st-century Science. A cognitive breakthrough was expected in the subsequent decade. The year 2025 has just begun, and the understanding of the glass transition remains puzzling [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. The exceptional interest can be linked to universalistic features observed in the previtreous domain on approaching the glass temperature ($T_g$), for microscopically different systems. One can recall: (i) non-Arrhenius changes of primary relaxation time ($\tau , {\tau }_{\alpha }$), viscosity (η), or DC electric conductivity ($\sigma$); (ii) decoupling between translational and orientational dynamics; (iii) the non-Debye distribution of the primary relaxation time, (iv) the dynamic crossover, often linked to the “magic” time scale $\tau \left(T_B\right)={10}^{-7\pm 1}s$, (v) the secondary relaxation emerging for $T<T_B$, and related to the time-scale ${\tau }_{\beta }<{\tau }_{\alpha }$ [6,7,8,9,11]. Characteristic changes of heat capacity related to the configurational entropy [8,9,17,18], or still puzzling “dynamic heterogeneities” are also noteworthy. The latter is associated with hypothetical multimolecular assemblies, whose direct detection seems to be limited to physical properties related to 4-point correlation function, such as nonlinear dielectric spectroscopy (NDS) or nonlinear dielectric effect (NDE) – methods related to changes of dielectric permittivity under the strong electric field [6,19,20,21,22,23,24].

The glass transition occurring on cooling from the deeply supercooled liquid to the amorphous solid is “diffused” in some temperature range, distinguishing the phenomenon from standard continuous or discontinuous phase transitions occurring at precisely defined temperatures. The conventional metric of the glass temperature $T_g$ is the center of the ‘diffused domain’ between the deeply supercooled liquid and amorphous solid, detected in heat capacity or density scans at a standard cooling rate. It correlates with values determined from primary relaxation time ($\tau$) or viscosity ($\eta$) evolution: $\tau \left(T_g\right)=100s$ or $\eta \left(T_g\right)={10}^{13}Poise$. Notably, in the range $T_g<T<T_B\approx T_g+80K$ changes in the primary relaxation time or viscosity values reach 10 decades [4,5,6,7,8,9,10,11,16,17,18]. Therefore, experimental methods able to record such enormous time scales in single scans can be dedicated to testing previtreous phenomena. This is a generic feature of broadband dielectric spectroscopy (BDS) [6,7,8,9,10,11].

Several models outlining possible glass transition foundations have emerged [4,5,7,8,9,10,11,12]. However, their experimental validation remains problematic. None of them has managed to address quantitatively a set of universalistic properties recalled above. The most common model validation is the reference to Super-Arrhenius (SA) changes of dynamic properties, primarily by deriving its most popular replacement equation – the Vogel-Fulcher-Tamman (VFT) dependence [7,8,9,10,11,12,25,26,27]:

$$\tau \left(T\right)={\tau }_{\infty }exp\left({\displaystyle \frac{E_a\left(T\right)}{RT}}\right) \tau \left(T\right)={\tau }_{\infty }exp\left({\displaystyle \frac{D}{T-T_0}}\right)={\tau }_{\infty }exp\left({\displaystyle \frac{D_T{T}_0}{T-T_0}}\right),$$

(1a)

where the left side is the general SA equation and the right one is the VFT relation; $E_a\left(T\right)$ is the temperature-dependent apparent activation energy, $T>T_g$, $T_0<T_g$ denotes the extrapolated VFT singular temperature; the amplitude $D=D_T{T}_0=const$ ; $D_T$ is the fragility strength coefficient, considered the metric of the discrepancy from the basic Arrhenius description related to $E_a\left(T\right)=E_a=const$.

When comparing the general SA and VFT equations, for the latter one obtains the following activation energy approximation:

$$E_a={\displaystyle \frac{RDT}{T-T_0}}=RD{t}^{-1},$$

(1b)

where $t=\left(T-T_0\right)/T$ is the measure of the relative temperature distance from the VFT singular temperature.

Despite the impressive success of the VFT equation in parameterizing experimental data, up to the status of the universalistic symbol of the previtreous dynamics, it can only be considered the effective parameterization tool, as explicitly shown in refs. [11,28]. Questioning the informal paradigm of the VFT relation “universality” significantly increased the glass transition cognitive impasse. One can expect that inspiration from new experimental results beyond the dominant canon can be essential for progress. It is the case of high-pressure exogenic impact studies, developed mainly via BDS studies for the last decades [11,29,30,31,32,33,34,35,36].

A cognitive counterpoint can be an endogenic impact factor, such as nanoparticles. However, such experimental evidence is minimal. The most in-depth studies were probably carried out for glycerol + silver nanoparticles nanocolloids, focusing on phenomenal dynamics [37].

This report discusses the influence of nanoparticles on previtreous properties in nanocolloids composed of the E7 liquid crystalline (LC) mixture and paraelectric BaTiO₃ nanoparticles. E7 can be supercooled in the nematic phase down to $T_g$, at any cooling rate [38,39]. In 2000, 135 publications related to nematics and nanoparticles appeared. In 2010, it was 847 reports, and 2560 papers in 2020. In 2024: 3026 reports were published [40]. This boosting interest was primarily motivated by expectations that adding nanoparticles to LC compounds can substantially extend and support omnipresent applications of ‘pure’ LC materials. Nowadays, LC-based nanocolloids are considered a new, specific domain of Liquid Crystal Physics and Materials Engineering. [41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60]. However, the evidence regarding previtreous behavior in LC nanocolloids remains lacking.

This report addresses the mentioned research gaps in general glass transition physics and the specific topics of LC nanocolloids.

2. Materials and Methods

E7 is the eutectic mixture composed of rod-like cyanobiphenyl and cyanoterphenol components, at a specific composition, namely (1) 4-cyano-4’-n-pentyl-biphenyl (5CB, 51%), (2) 4-cyano-4’-n-heptyl-biphenyl (7CB, 25%), (3) 4-cyano-4’-n-oxyoctyl-biphenyl (8OCB, 16%), and (4) 4-cyano-4’’-n-pentyl-p-terphenyl (5CT, 8%). E7 was developed for display applications, with an operational range from $-5℃$ to $50℃$ in the nematic phase, supported by convenient dielectric and optical properties. It was first implemented for calculators and watches [61,62,63].

In the given report the E7 mixture was purchased from Synthon, with the top offered quality. Before measurements, it was degassed & purified in subsequent and repeated steps: (i) solidification by freezing, supported by liquid nitrogen, (ii) removal of air and vapors via a vacuum pump, (iii) heating up to ca. $90℃$ i.e., deeply into the isotropic liquid state. The tested samples exhibit the following mesomorphism: Solid Glass - ($211.2 K$) - Nematic - ($332.9 K$) - Isotropic Liquid, in agreement with references [38,62,63]. Each rod-like LC compound in the E7 mixture is associated with a significant permanent dipole moment ($\mu \approx 5 Debye$), approximately parallel to the long molecular axis [38,63].

Tested nanocolloids composed of E7 and BaTiO₃. For nanocolloids, the sedimentation of nanoparticles (NPs) can constitute a problem. One can minimize such a parasitic feature by introducing a macromolecular surface agent. However, it can complicate the spectrum registered in BDS scans and influence phase transition temperature. For nanoparticles applied in the given research, avoiding this parasitic impact factor is possible for mass fraction concentrations $x<1\%$ NPs.

BaTiO₃ nanopowder (paraelectric, globular, diameter $d=50 nm$) was purchased from US Research Nanomaterials, Inc.: see ref. [64]. Mixtures of the liquid crystal and nanoparticles were sonicated at a temperature above the isotropic–nematic phase transition for 4 hours to obtain homogeneous suspensions.

This report discusses nanocolloids with concentrations $x\le 0.5\%$ of NPs. The stability of nanocolloidal samples was tested by measuring the dielectric constant and electric conductivity in a special capacitor with rectangular plates: 20 mm in length and 5 mm in width, with two sections. Tests were conducted in the isotropic liquid and the nematic phase to the ‘longitudinal’ and ‘transverse’ positions. For concentrations $x\le 0.5\%$ no changes in dielectric properties were noted. A small sedimentation effect appeared for $x\to 1\%$ appeared after $t>1hour$. This factor can be removed by sine–wave packages ($U=200V, f=1kHz$) and lasting $10ms$. It is worth noting that for results presented in the given report, BDS-related scans required less than 5 minutes.

Broadband dielectric spectroscopy (BDS) is the essential experimental tool for studies on glass transition and liquid crystals [65]. The previtreous domain of glass-forming systems is associated with 10-12 decades in the process time scale for temperature in the range $T_g<T<T_B\approx T_g+100K$. It correlates with the time/frequency BDS scan range. The sensitivity to even weak electric fields is essential for liquid crystals, and it is also generic for BDS.

In this report BDS Novocontrol spectrometer, enabling the high-resolution complex dielectric permittivity ${\epsilon }^{*}={\epsilon }^{\text{'}}-i{\epsilon }^{\text{'}\text{'}}$ scans with 5 – 6 digits resolution was used. Tests were carried out for $U=1 V$ voltage, offering the optimal resolution. Tested samples were placed in a flat–parallel capacitor made of gold-coated Invar: diameter $2r=20mm,$ and the distance between plates $d=0.15 mm$. All these yielded the intensity of the applied electric field: $E=6.7 kV{m}^{-1}$, located within the low-intensity limit values. The measurement capacitor was placed within the Quattro Novocontrol temperature control unit, which is coupled to the spectrometer. It enabled temperature resolution during tests from 0.02K to 0.05K. The Novocontrol WinDeta software controlled the measurement process. The final analysis was carried out using ORIGIN 2025 software.

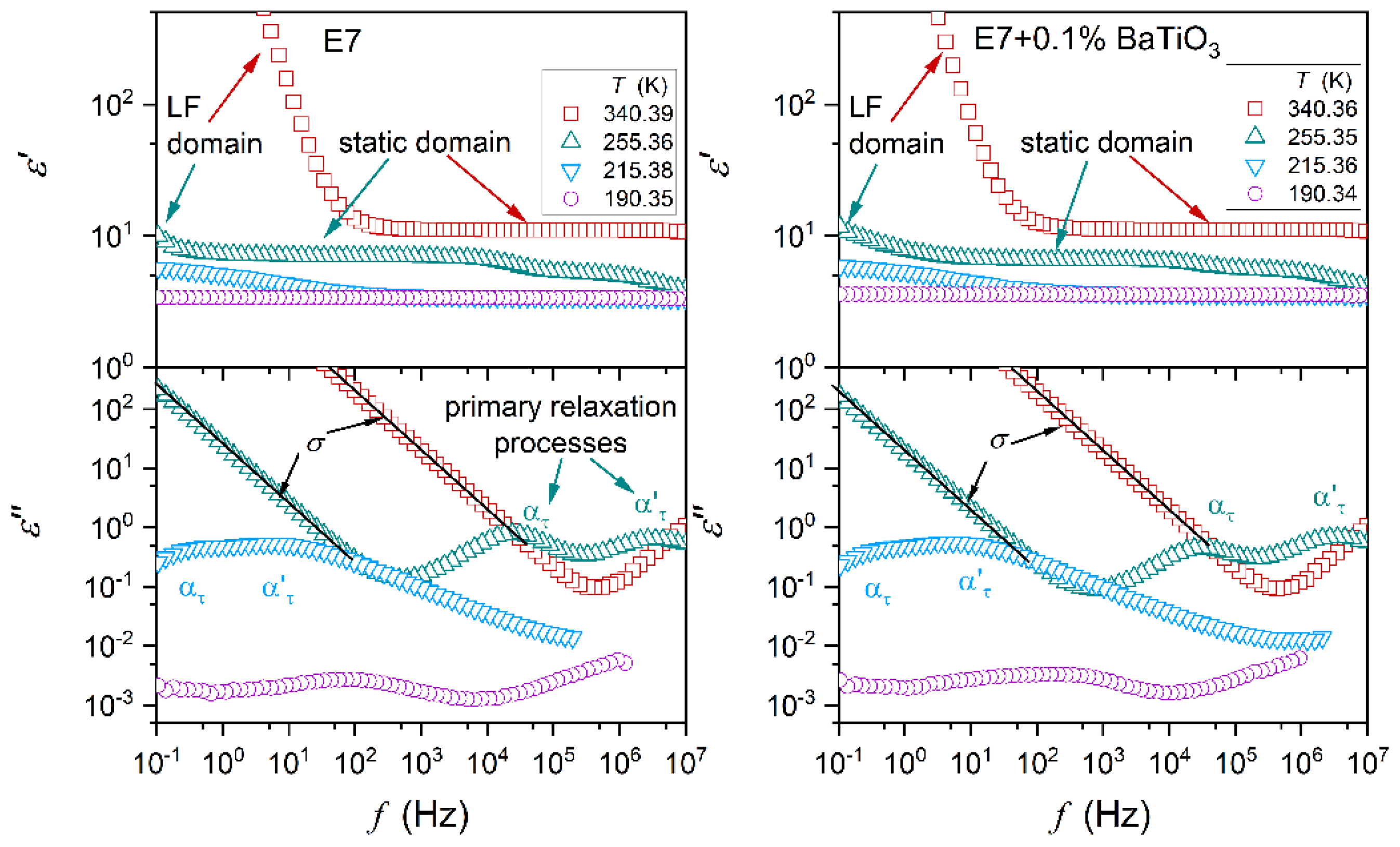
Figure 1 shows master plots presenting dielectric spectra – the real and imaginary parts of dielectric permittivity as a function of frequency. They illustrate the behavior in subsequent phases for E7 and its nanocolloids. Characteristic features and domains are indicated. For ${\epsilon }^{\text{'}}\left(f\right)$ they are (i) the static domain, where ${\epsilon }^{\text{'}}\left(f\right)=\epsilon =const$ in a broad range of frequencies – defining the dielectric constant $\epsilon$, and (ii) the low frequency (LF) domain with the boost of ${\epsilon }^{\text{'}}\left(f\right)$ values. The emerging contribution of ionic contamination is most often cited as an explanation of the latter, but the authors would like to indicate that translational shifts of molecules from their equilibrium positions can yield a similar contribution.

For the imaginary part of dielectric permittivity, primary loss curves, related to the orientation of molecules emerge, are significant, particularly in the nematic phase. Peaks (maxima) of loss curves determine the primary ($alpha, {\alpha }_{\tau }$) relaxation time characterizing the ability to the orientation process: $\tau =1/{\omega }_{peak}$, $\omega =2\pi f$. Branches of the loss curves reflect the distribution of these relaxation times. Jonsher indicated the following scaling of loss curves [66,67]:

$${\epsilon }^{\text{'}\text{'}}\left(f<f_{peak}\right)\propto f^m \Rightarrow {log}_{10}{\epsilon }^{\text{'}\text{'}}\left(f\right)=c+m{log}_{10}f,$$

(2)

$${\epsilon }^{\text{'}\text{'}}\left(f>f_{peak}\right)\propto f^{-n} \Rightarrow {log}_{10}{\epsilon }^{\text{'}\text{'}}\left(f\right)=c^{\text{'}}-n{log}_{10}f,$$

(3)

where $c,c^{\text{'}}=const$ and $m,n\le 1$ are coefficients related to the distribution of relaxation times. For a single relaxation time Debye process $m,n=1$.

The above relations enable a simple way of estimating the peak frequency and then the relaxation time using the derivative of experimental data and the following relation [11]:

$$d{log}_{10}{\epsilon }^{\text{'}\text{'}}\left(f\right)/d{log}_{10}f=0\mathrm{for} f=f_{peak}.$$

(4)

Relations (2), (3) & (4) offer a reliable protocol for determining the primary relaxation times, avoiding the uncertainty associated with the nonlinear fitting. The alternative path is associated with portraying loss curves via the Havriliak-Negami (HN) equation [11,65,68,69]:

$${\epsilon }^{*}\left(\omega \right)={\epsilon }_{\infty }+{\displaystyle \frac{\Delta \epsilon }{{\left[1+{\left(i\omega \tau \right)}^a\right]}^b}}+{\displaystyle \frac{{\sigma }_{DC}}{i{\epsilon }_0{\omega }^{\varphi }}},$$

(5)

where $\omega =2\pi f$, ${\epsilon }_{\infty }$ is the value of permittivity at the high-frequency limit, it is related to the sum of atomic and electronic polarizabilities, $\varphi$ is related to the distortion from the DC conductivity limit related to $\varphi =1$; Parameters $a,b\le 1$ describe the distribution of relaxation times: $a,b=1$ are for the single relaxation time Debye model.

Jonsher and HN distribution parameters can be linked: $m=b$ and $n=ab$ [11,65]. Relaxation time determined via HN equation requires multi-parameter nonlinear fitting, inherently associated with a notable error. Nevertheless, it is the only tool when loss curves overlap, limiting the reliable application of Eqs (2), (3), and (4). The transformation ${{\epsilon }^{\text{'}\text{'}}\left(f\right)\to \sigma }^{\text{'}}\left(f\right)=\omega {\epsilon }^{\text{'}\text{'}}\left(f\right)$ enables determining the DC electric conductivity, manifesting as the horizontal line in the plot ${log}_{10}{\sigma }^{\text{'}}\left(f\right)$ vs. ${log}_{10}f$. In the DC domain: ${{\sigma }^{\text{'}}\left(f\right)=\sigma }_{DC}=\sigma =const.$

3. Results

3.1. Dielectric Constant Changes

The dielectric constant $\epsilon$ is related to the real part of dielectric permittivity ${\epsilon }^{\text{'}}\left(f\right)$ in the static frequency domain, where ${\epsilon }^{\text{'}}\left(f\right)=\epsilon \approx const$. Figure 1 shows that for systems tested in the given report, it ranges between ~1 kHz and $~1 MHz$ in the isotropic phase.

For dipolar liquids $\epsilon \left(T\right)$ pattern of changes can indicate the preferred arrangement of permanent dipolar moments coupled to molecules, namely: (i) ‘antiparallel’ for $d\epsilon \left(T\right)/dT>0$, and (ii) ‘parallel’ for $d\epsilon \left(T\right)/dT<0$, i.e., they mostly follow the external electric field [70].

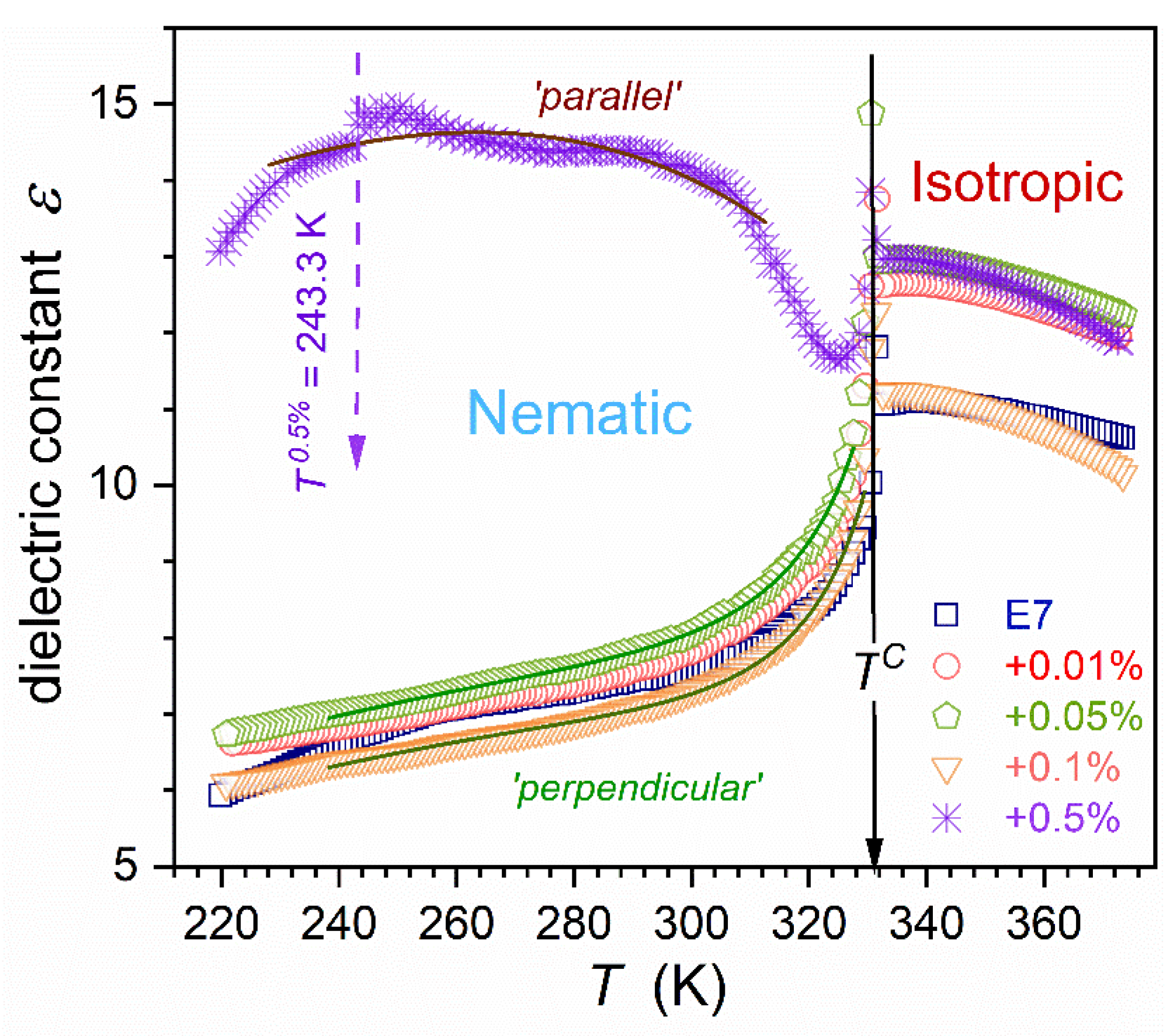
Figure 2 presents changes in the dielectric constant for E7 and related nanocolloids, from the isotropic liquid phase down to the glass temperature vicinity. In the isotropic liquid phase, for each concentration of nanoparticles (NPs), the same pattern of pretransitional changes takes place [71,72,73]:

$$\epsilon \left(T\right)={\epsilon }^{*}+a\left(T-T^{*}\right)+A{\left(T-T^{*}\right)}^{\phi },$$

(6)

where $T^{*}<T^C$ is the extrapolated continuous phase transition temperature, $a,A=const$; the exponent $\phi =1-\alpha$, where $\alpha =1/2$ is the heat capacity critical exponent. The value $\Delta T=T^C-T^{*}$ is the metric of the isotropic – nematic (I-N) transition discontinuity, constituting a significant reference for theoretical models.

Such behavior was noted for rod-like LC compounds with a permanent dipole moment approximately parallel to the long molecular axis, like 5CB or 8OCB [72,73]. In the isotropic liquid phase, the pretransitional/precritical growth of prenematic fluctuations is associated with the weakly discontinuous nature of I-N transition [38,39]:

$$\xi \left(T\right)={\xi }_0{\left(T-T^{*}\right)}^{-\nu =-1/2} V\left(T\right)\propto {\left[\xi \left(T\right)\right]}^3\propto {\left(T-T^{*}\right)}^{-3\nu =-3/2},$$

(7)

where $\xi$ is the correlation length of pretransitional fluctuations related to the critical exponent $\nu$ with the mean-field value in the given case; $V\left(T\right)$ approximates the volume of prenematic fluctuations.

Within prenematic fluctuations, the antiparallel arrangement of permanent dipole moments [38,39], leading to the ‘cancellation’ of permanent dipole moments impact, takes place. Consequently, the dielectric constant within fluctuations is significantly smaller than for the isotropic surrounding. One can consider the Contrast Factor ($CF$), as the metric for the difference between the physical characterization of fluctuations and their isotropic liquid surrounding. In the given case $CF\ne 0$.

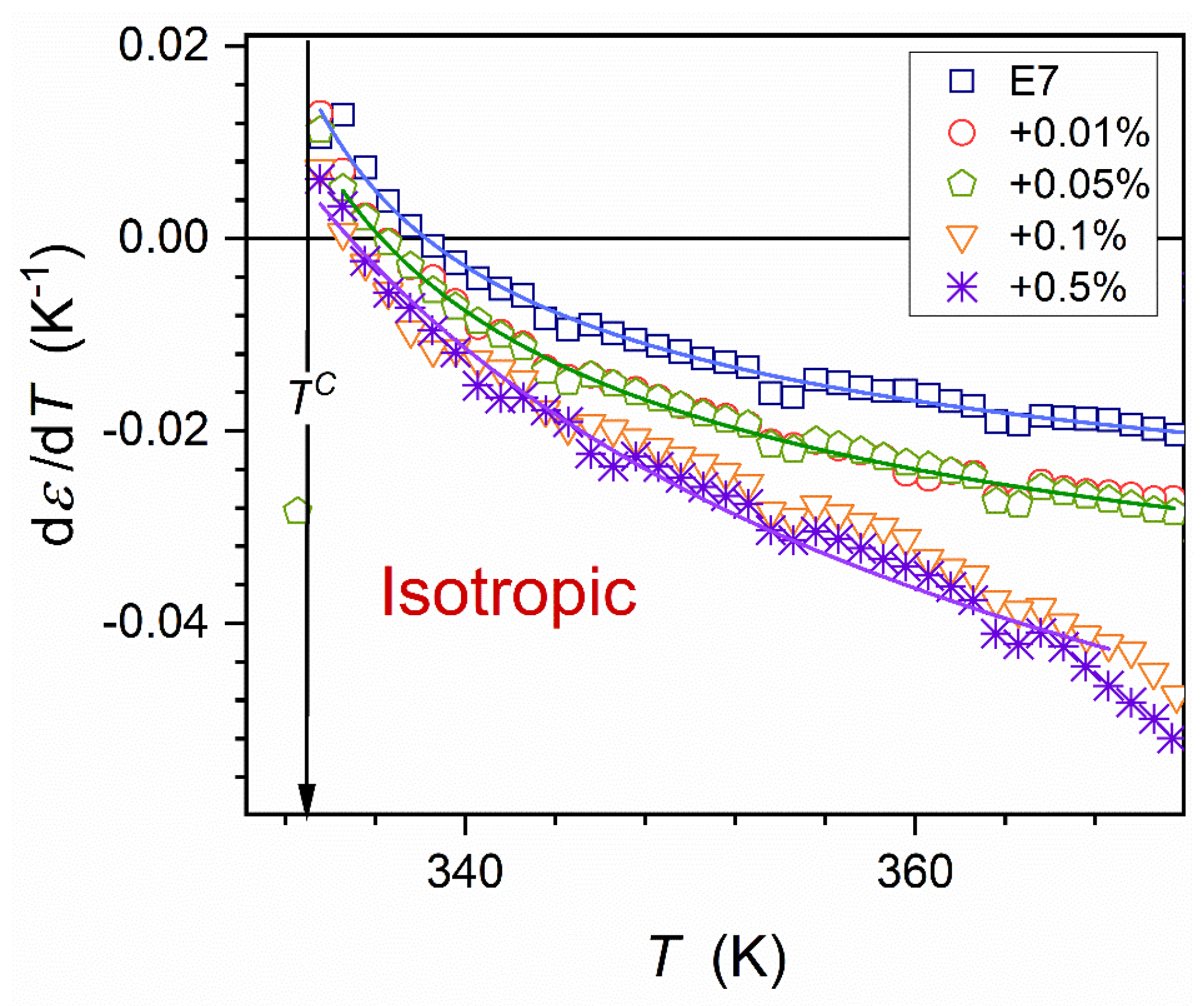
The volume occupied by prenematic fluctuations rapidly grows on approaching phase transition $T\to T^{*}$, as shown in Equation (7). The ‘prenematic’ contribution to the total registered value of the dielectric constant can dominate close to the clearing temperature. It is related to the crossover: $d\epsilon \left(T\right)/dT>0 \leftarrow d\epsilon \left(T\right)/dT<0$. Such behavior and the portrayal by Eq. (6) are validated in Figure 3, where the parameterization via the derivative analysis is also shown [73]:

$$d\epsilon \left(T\right)/dT=a+B{\left(T-T^{*}\right)}^{\phi -1}\propto {\left(T-T^{*}\right)}^{-1/2},$$

(8)

where $B=A\phi =A\left(1-\alpha \right)$ and the exponent $\phi -1=-\alpha$.

Related parameters are given in Table 1. The lack of impact of nanoparticles on values of the clearing temperature ($T^C, T_{I-N}$) and exponent $\alpha$ is notable.

The same behavior was observed in earlier studies in other LC compounds (5CB and 8OCB) based nanocolloids, for which here discussed supercooling is absent [75,76]. A notable influence of nanoparticles on the phase transition discontinuity metric is visible: $\Delta T^{*}=T^C-T^{*}$, from $\Delta T^{*}(x=0\%)\approx 3.4K$ to $T^{*}(x=0.5\%)\approx 17K$.

In the nematic phase of rod-like LC materials, the dielectric constant can be tested for two general paths: (i) in non-oriented samples, which is associated with the spontaneous arrangement of molecules and coupled dipole moments, and (ii) in oriented samples with respect to the long molecular axis. The latter can be realized via the strong magnetic field (a few Tesla) or by covering the capacitor plates with a polymeric layer interacting with LC molecules to yield the desired orientation. The latter is dedicated to thin-layer (micrometric) samples. [38,74,75]. These cases are related to the orientation by exogenic impact factors.

One can consider components of dielectric constant in the nematic phase in frames of the Landau – de Gennes model [38,39], recalling the behavior of the order parameter $\Delta \epsilon \left(T\right)$ and the ‘diameter’ $\delta \left(T\right)$ [76]:

$$\Delta \epsilon \left(T\right)={\epsilon }_{\phantom{­}}-{\epsilon }_{\phantom{­}}\approx {\epsilon }_{op}^{**}+B{\left(T^{**}-T\right)}^{\beta },$$

(9)

$$\delta \left(T\right)={\displaystyle \frac{1}{3}}{\epsilon }_{\phantom{­}}+{\displaystyle \frac{2}{3}}{\epsilon }_{\phantom{­}}\approx {\epsilon }_d^{**}+D{\left(T^{**}-T\right)}^{1-\alpha }+d\left(T^{**}-T\right),$$

(10)

where $T<T^C$, $\Delta \epsilon \left(T\right)$ is the order parameter (op) metric, and $\delta \left(T\right)$ denotes the ‘diameter’, $B,d,D$ are constant amplitudes; $T^{**}$ is the hypothetical continuous transition extrapolated from the nematic phase.

High resolution and distortions – sensitive studies in 5CB and 8OCB yield the order parameter $\beta =1/4$ and $\alpha =1/2$, which indicates tricritical point (TCP) mean-field-type approximation [76].

Linking the above dependencies, one obtains relations modeling the parallel and perpendicular ‘branches’ of the dielectric constant in the nematic phase:

$${\epsilon }_{\phantom{­}}\approx a_1-a_2{\left(T^{**}-T\right)}^{\beta }+a_3{\left(T^{**}-T\right)}^{1-\alpha }+a_4\left(T^{**}-T\right),$$

(11)

$${\epsilon }_{\phantom{­}}=b_1+b_2{\left(T^{**}-T\right)}^{\beta }+b_3{\left(T^{**}-T\right)}^{1-\alpha }+b_4\left(T^{**}-T\right),$$

(12)

where $a_i$ and $b_i$ are empirical parameters related to Eqs. (9) and (10).

In refs. [77,78], in nanocolloids 8OCB+BaTiO₃ and 5CB+ BaTiO₃, the arrangement of molecules controlled solely by NPs concentration was shown. Both ‘parallel’ and ‘perpendicular’ permanent endogenic orientations were obtained. For E7 and its nanocolloids up to $x=0.1\%$ NPs the fair portrayal via Eq. (11) takes place, as shown in Figure 2. Notable that for ‘pure’ E7 ($x=0\%$) the decrease of the capacitor gap distorts such pattern, increasing detected values. It was not observed for nanocolloids. For the concentration $x=0.5\%$ nanocolloid dielectric constant ‘roughly’ follows the ‘parallel’ pattern (Eq. 12), with distortions near I-N transition and a ‘slight’ discontinuous transition at $T=243.3K$.

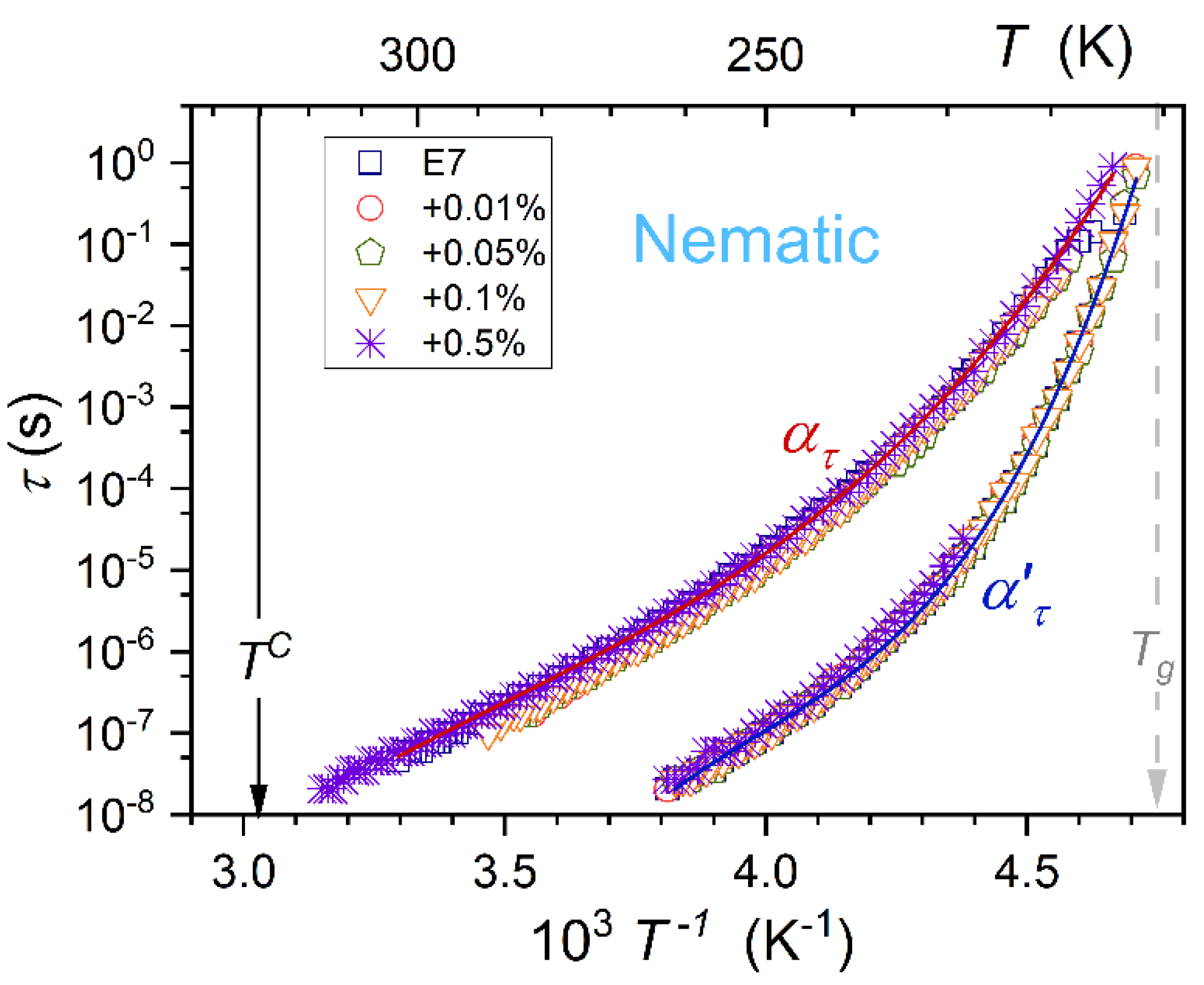
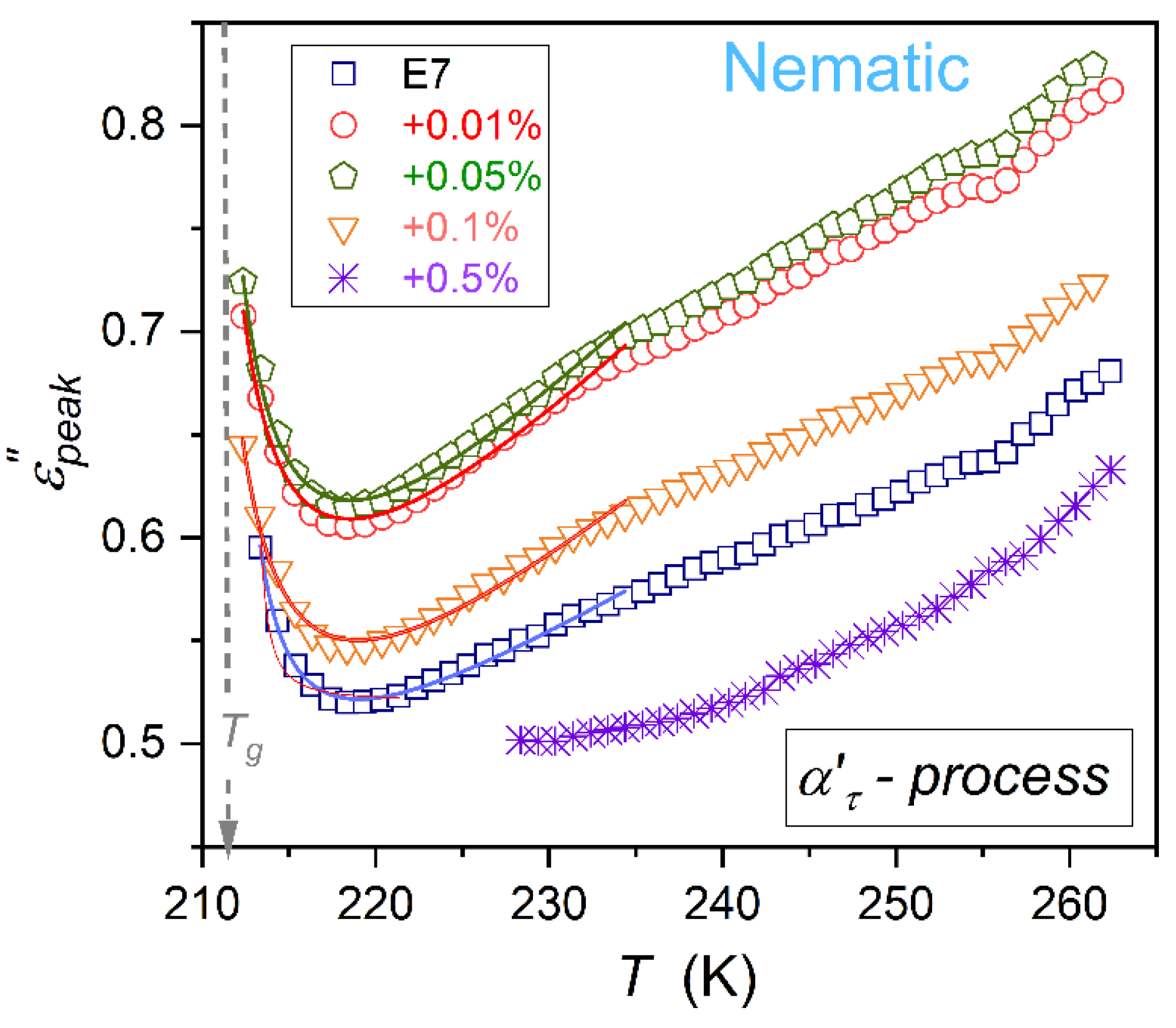
3.2. Primary Relaxation Time in the Previtreous Domain

The dielectric constant is the static (frequency-independent) dielectric property associated with the real part of dielectric permittivity. Dynamic properties explicitly manifest for the imaginary part of dielectric permittivity, as presented in Figure 1. The primary loss curve peak is associated with the ability to re-orient the permanent dipole moment coupled to rod-like molecules. For E7 and related nanocolloids, there are two loss curves (alpha (${\alpha }_{\tau }$) and alpha’ (${\alpha }_{\tau }^{\text{'}}$)) in the nematic phase, as shown in Figure 1. It can be associated with multicomponent E7 composition. The temperature changes of ${\alpha }_{\tau }$ and ${\alpha }_{\tau }^{\text{'}}$ primary relaxation times are presented in Figure 4. Notable is their overlapping, i.e., they are almost non-impacted by nanoparticle concentrations.

In ref. [11], the distortions-sensitive analysis of various model equations portraying previtreous dynamics in glass-forming liquids was carried out. It showed the limited validity of the VFT portrayal (Eq. 1) and indicated the universalistic prevalence of the double-exponential MYEGA equation [79,80]:

$$\tau \left(T\right)={\tau }_{\infty }exp\left({\displaystyle \frac{K}{T}}\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{C}{T}}\right)\right),$$

(13a)

The fair parameterizations via this relation are shown in Figure 4. They are associated with the following sets of parameters ${\tau }_{\infty }=0.34ns, K=120K, C=780K$ for ${\alpha }_{\tau }$ relaxation, and ${\tau }_{\infty }=3.8ns, K=0.1K, C=2250K$ for ${\alpha }_{\tau }^{\text{'}}$ primary relaxations.

The comparison of the above relation and the general SA dependence (the left side of Equation (1)) yields the apparent activation energy for the MYEGA equation:

$$E_a\left(T\right)=RK\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{C}{T}}\right)={\displaystyle \frac{RK}{exp\left(-C/T\right)}} \Rightarrow E_a\left(T\right)\approx {\displaystyle \frac{RK}{1+C/T+\dots }}\approx {\displaystyle \frac{RK}{\left(T-C\right)/T}}=RK{t}^{-1}.$$

(13b)

The right side of Equation (13b) indicates the transformation $MYEGA VFT$, leading to the apparent activation energy given in Equation (1b). The VFT equation emerges when considering limited to the first term Taylor expansion of MYEGA-related apparent activation energy. The comparison of Eqs. (1) and (13) show the link between VFT and MYEGA equation parameters: $C=T_0$, and $K=D=D_T{T}_0$. Notable that the MYEGA equation is not associated with the finite temperature singularity, which is the inherent feature of the VFT dependence. As shown above, it appears due to the ‘nonlinear terms truncation’ in the Taylor expansion of the exponential term in Eq. (13b).

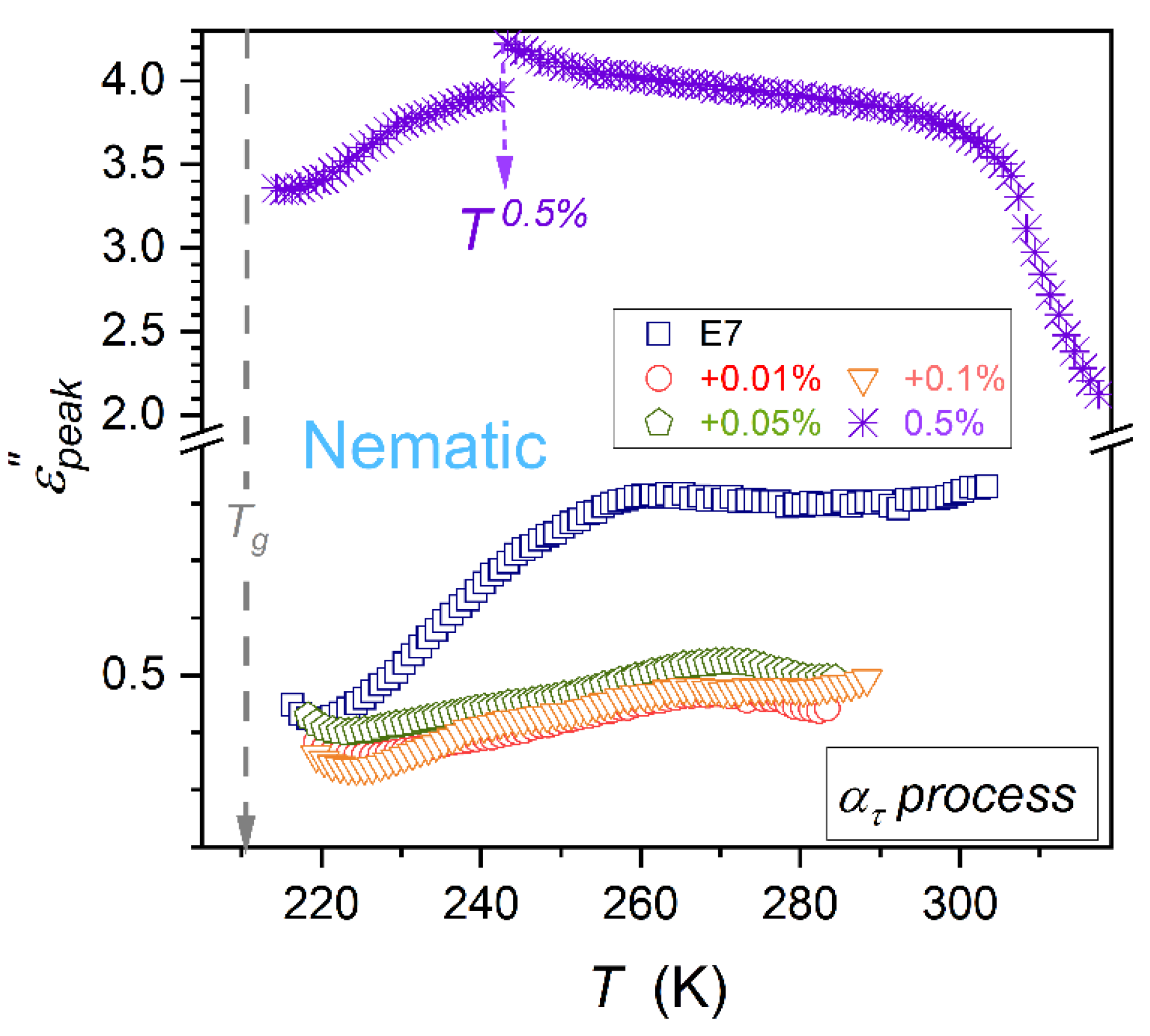
3.3. Primary Loss Curve Maximum Previtreous Changes

Coordinates of the loss curve maximum $\left(\tau ,{\epsilon }_{peak}^{\text{'}\text{'}}\right)$ define the primary relaxation time ($\tau$) discussed above and the metric of the energy related to this process (${\epsilon }_{peak}^{\text{'}\text{'}}$) [78].

Temperature changes of the primary relaxation time $\tau \left(T\right)$ are almost independent from NPs concentration, as visible in Figure 4. The loss curves peaks ${\epsilon }_{peak}^{\text{'}\text{'}}\left(T\right)$ patterns of changes strongly depend on NPs concentration, as shown in Figure 5 and Figure 6, for ${\alpha }_{\tau }$ and ${\alpha }_{\tau }^{\text{'}}$ relaxation processes. For ${\alpha }_{\tau }$ process, the addition of nanoparticles first decreases the values of ${\epsilon }_{peak}^{\text{'}\text{'}}\left(T\right)$, but for the highest tested concentration, $x=0.5\%$, it strongly rises, as presented in Figure 5. Moreover, the discontinuous transition at $T^{0.5\%}=243.3K$ appears both for $\epsilon \left(T\right)$ (Figure 4) and ${\epsilon }_{peak}^{\text{'}\text{'}}\left(T\right)$ (Figure 5). Patterns of ${\epsilon }_{peak}^{\text{'}\text{'}}\left(T\right)$ changes for ${\alpha }_{\tau }$ and ${\alpha }_{\tau }^{\text{'}}$ are notably different. However, for both primary processes, a previtreous ‘bending up’ when approaching $T_g$ appears, suggesting a significant change in the energy required for electric field-related reorientation. The reliable estimations of ${\epsilon }_{peak}^{\text{'}\text{'}}\left(T\right)$ in the immediate vicinity of $T_g$ were possible only for ${\alpha }_{\tau }^{\text{'}}$ processes, due to its explicit manifestation (Figure 6). As shown by solid curves portraying experimental data, the ‘anomaly’ can be parameterized by the following relation:

$${\epsilon }_{peak}^{\text{'}\text{'}}\left(T\right)\approx A{\left({T-T}_g^{*}\right)}^{-\left({\gamma }^{\text{'}}=1\right)}+\left[{\epsilon }_{min}^{\text{'}\text{'}}+a\left({T-T}_g^{*}\right)\right],$$

(14)

where $A, a, {\epsilon }_{min}^{\text{'}\text{'}}$ are constant amplitudes.

Results of the parameterization are shown in Figure 6 and related parameters are given in Table 2.

When recalling Critical Phenomena Physics [81,82], the term in the square bracket (Eq. (14)) can be considered the so-called ‘background effect’, which supports the fact that values of ${\epsilon }_{min}^{\text{'}\text{'}}$ are close to the minimum of ${\epsilon }_{peak}^{\text{'}\text{'}}\left(T\right)$ occurring ca. 8K above $T_g$. Using values given in Table 2 one can estimate the ‘discontinuity’ $\Delta T_g^{*}=T_g-T_g^{*}$, it is in range from $1.7 K$ for E7+0.05% BaTiO₃ nanocolloid to $1.9 K$ for E7+0.1% BaTiO₃ nanocolloid.

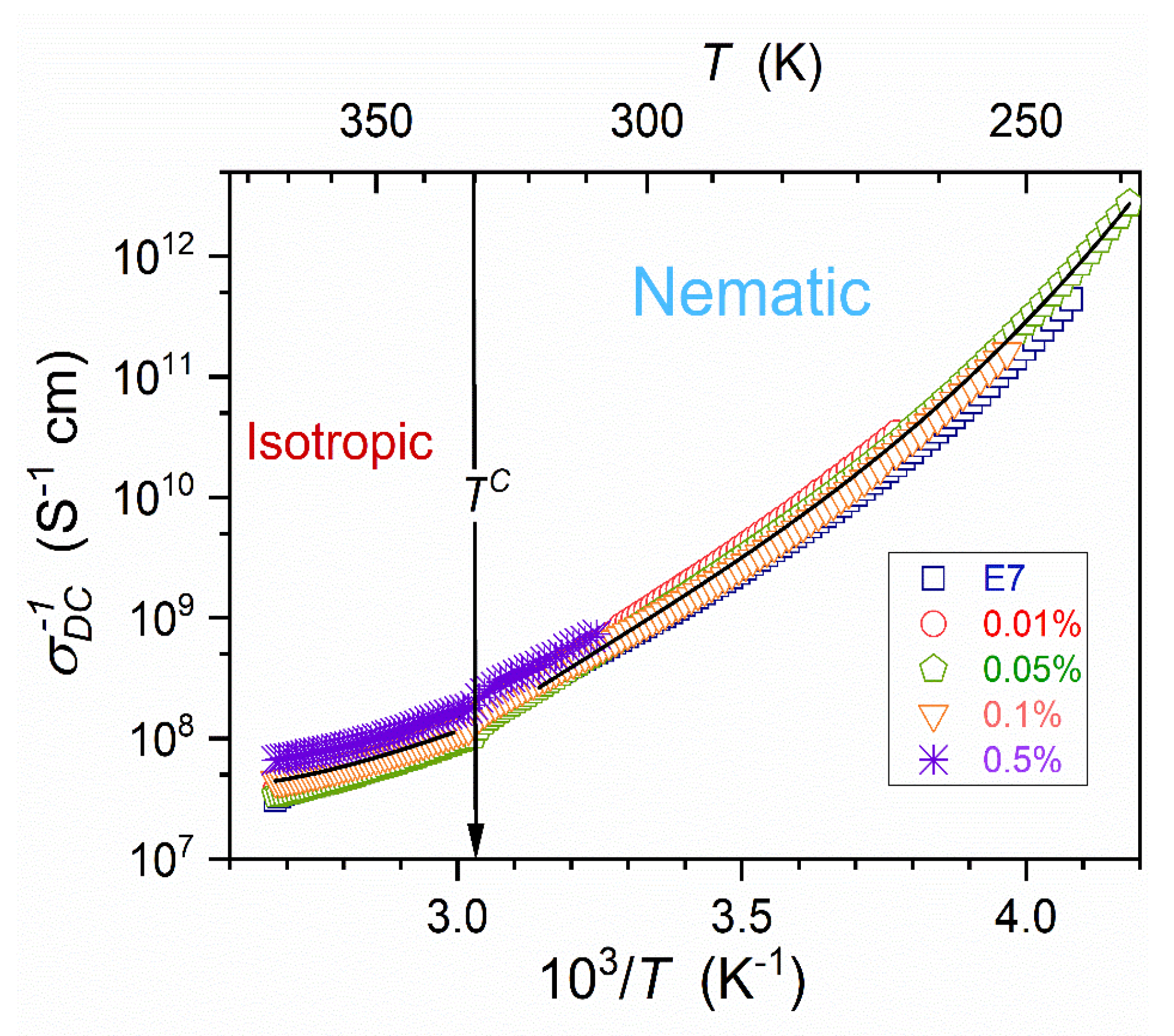
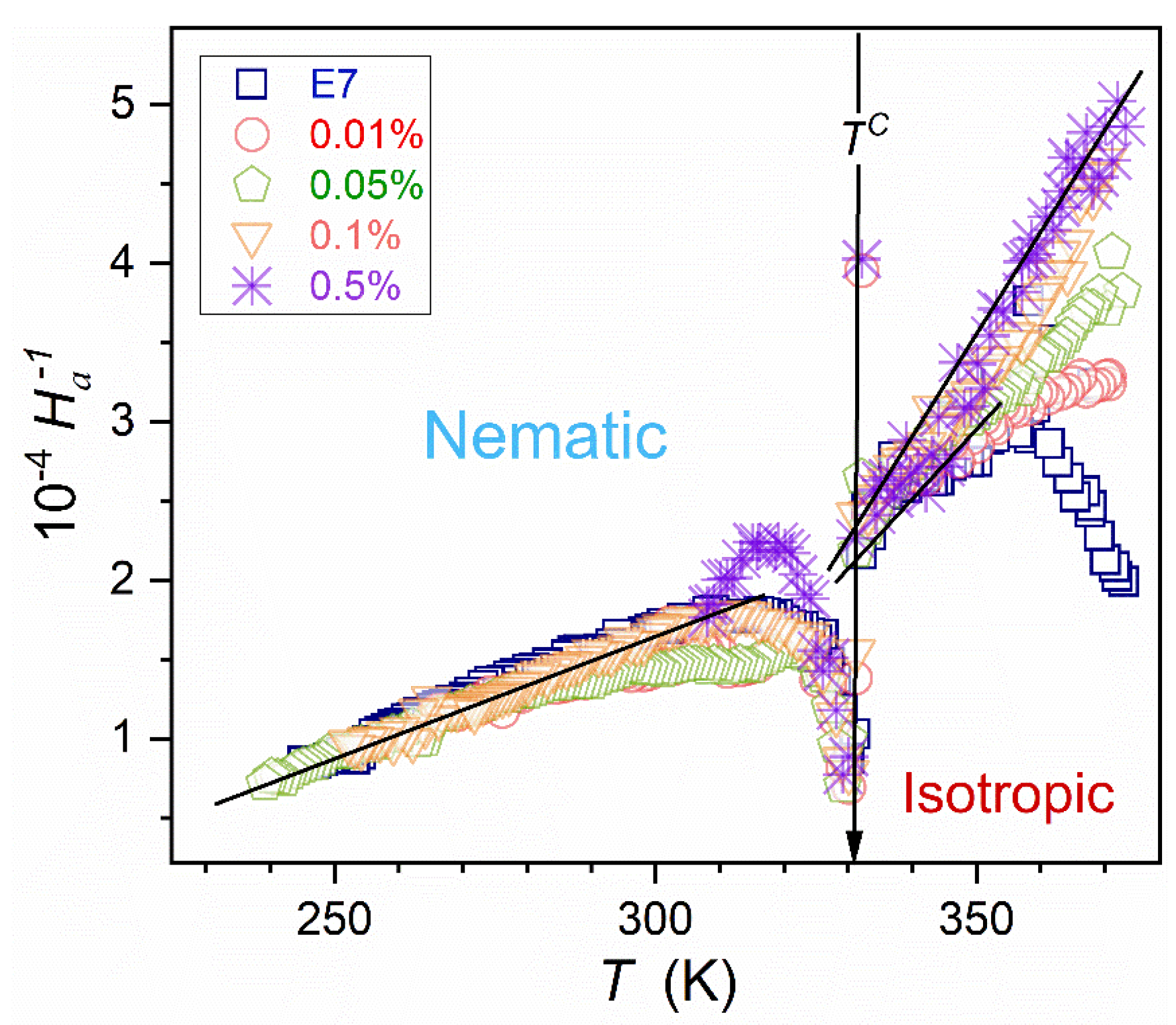
3.4. DC Electric Conductivity in the Isotropic Liquid and Supercooled Nematic

Figure 7 presents the temperature evolution of DC electric conductivity, reflecting translational processes. The non-linear evolution in the Arrhenius scale used in Figure 7 shows the Super-Arrhenius pattern of changes. For all tested NPs concentrations $\mathsf{\sigma }\left(T\right)$ dependencies almost overlap and can be approximated by the counterpart of MYEGA relation [79,80], namely:

$${\left[\mathsf{\sigma }\left(T\right)\right]}^{-1}={\left({\mathsf{\sigma }}_{\mathrm{\infty }}\right)}^{-1}exp\left({\displaystyle \frac{E_a^{\mathsf{\sigma }}\left(T\right)}{RT}}\right)\text{⇒} {\left[\mathsf{\sigma }\left(T\right)\right]}^{-1}={\left({\mathsf{\sigma }}_{\mathrm{\infty }}\right)}^{-1}exp\left({\displaystyle \frac{C}{T}}\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{K^{\mathrm{\text{'}}}}{T}}\right)\right).$$

(15)

Following ref. [83], for vitrifying systems, one can consider the ‘universalistic’ pattern for the steepness index, also representing the apparent activation enthalpy:

$$H_a^{\sigma }\left(T\right)={\displaystyle \frac{1}{R}}{\displaystyle \frac{d{ln\sigma }^{-1}\left(T\right)}{d\left(1/T\right)}}={\displaystyle \frac{1}{R}}{\displaystyle \frac{\left[d{\sigma }^{-1}\left(T\right)/{\sigma }^{-1}\left(T\right)\right]}{d\left(1/T\right)}}\approx {\displaystyle \frac{\varphi }{T-T^{+}}} {\left[H_a^{\sigma }\left(T\right)\right]}^{-1}={\varphi }^{-1}T-\left({\varphi }^{-1}{T}^{+}\right),$$

(16)

where $,\varphi ,T^{+}=const$ and $T^{+}$ is the singular temperature.

The above equation also shows the link to ‘relative changes’ of the considered dynamic property in the given case $d{\sigma }^{-1}\left(T\right)/{\sigma }^{-1}\left(T\right)$.

Figure 8 validates the portrayal of the apparent activation enthalpy by Eq. (16) for E7 and related nanocolloids, with the convergence when approaching $T_g$ and $T^{+}\approx 196K$. Such a description also appears in the isotropic liquid phase, with $T^{+}\approx 298K$ for pure E7 and $T^{+}\approx 287K$ for $x=0.5\%$ nanocolloid. Recalling the discussion presented in ref. [83] the approximation in the isotropic liquid phase can be linked to the dynamic crossover temperature, matched to a hypothetical ‘magic’ time-scale: namely $T^{+}\left(isotropic\right)\approx T_B$.

4. Discussion

A particularly puzzling result of this work is the explicit evidence for the anomalous, critical-like (Eq. (14)) behavior of the loss curve maximum in the immediate vicinity of $T_g$.

Generally, it recalls the long-standing discussion regarding a possible relationship between the glass transition and a hypothetical hidden critical point [9,10,11,84,85,86,87,88,89,90]. The essential problem of these model discussions has been the practical lack of evidence of critical-type pretransitional effects near $T_g$. In Critical Phenomena Physics [81,82], they are the essential inspiration and reference for model validations.

The results for ${\epsilon }_{peak}^{\text{'}\text{'}}\left(T\right)$ changes presented in Figure 6 and parameterized via Equation (14), as well as the very recent communication [90], can be considered the unique evidence of the previtreous ‘critical-type’ effect near $T_g$.

To discuss these results, it is worth recalling the case of Isotropic–Nematic (I-N) weakly discontinuous phase transition, which is also the topic of this report. It is notable, that the isotropic liquid phase above $T_{I-N}$ is considered a specific model-system for the glass transition phenomenon [92,93,94,95,96,97].

Let's recall basic features regarding pretransitional effects in the isotropic liquid phase of nematogenic LC:

• Dynamic properties such as primary relaxation time $\tau$, viscosity $\eta$, or electric conductivity $\sigma$ do not show a pretransitional anomaly, but the long-range Super-Arrhenius changes: see Figure 7 and Eq. (15) above and refs. [38,39,76,77,78,83,90].
• Thermodynamic properties, where heat capacity (specific heat) is the crucial example, show well-evidenced pretransitonal, critical-like ‘anomaly’ [38,39,76].
• Static properties, such as dielectric constant, can show an explicit ‘critical’ anomaly –. However, it appears only for LC systems with the permanent dipole moment approximately parallel to the long molecular axis, yielding contrast factor $CF\ne 0$: see Figure 2 and Figure 3, Equations (6) & (8) above. For LC molecules with the perpendicular (transverse) arrangement of the dipole moment, the pretransitional effect is absent, since $CF=0$ [73,76,77,78,91].
• ‘Nonlinear’ properties, coupled to a 4-point correlation function, such as NDE/NDS or the Kerr effect (KE), the pretransitional, ‘critical’ effects are always observed in the isotropic phase [38,76,81,96,97,98]. NDE, NDS, KE are inherently associated with the strong electric field, which impacts fluctuations, and as their surrounding is different, it yields $CF\ne 0$, and then the contribution related to fluctuations is extracted.

Comparing the previtreous domain of glass-formers for cooling $T_g T$, & the isotropic phase of LC nematogens for $T_{I-N} T$, one obtains:

• Ad. (1) – Similar SA changes of $\tau \left(T\right)$, $\eta \left(T\right)$ or $\sigma \left(T\right)$ [4,5,6,7,8,9,10,11].
• Ad. (2) – Recently, in the previtreous domain, the critical-like behavior of the configurational entropy and the associated contribution of the heat capacity have been evidenced due to the innovative distortions-sensitive analysis. [17]
• Ad. (3) – Recently, hallmarks of dielectric constant pretransitional behavior have been noted for 8*OCB, an LC compound that can be supercooled down to $T_g$ in the isotropic phase [90]. There are extreme problems in such tests since they require ${\epsilon }^{\text{'}}\left(T\right)$ scans for extremely low frequencies.
• Ad. (4) Generally, for 4-point correlation functions related to experimental methods like NDS, the response from ‘heterogeneities’ has been registered. However, obtained data do not allow to consider temperature-related pretransitional effects. It is associated with the ultraviscous/ultraslowed features of the previtreous domain, yielding very challenging experimental requirements [9]. Nevertheless, for plastic crystal forming systems, like the Orientationally Disordered Crystals (ODICs) the ‘ultraviscous’ limitation is minimized: for NDE, the explicit critical-type effects have been obtained [23]. Moreover, its description can be correlated with pretransitional effect modeling for the isotropic phase of nematogens [23].

For supercritical and subcritical domains described by the Critical Phenomena Physics, collective precritical fluctuations are essential, shaping pretransitional effects as the phenomenal hallmark. These fluctuations exhibit features of the subsequent, approaching phase. In case of the isotropic liquid phase of LC nematogens, there are prenematic fluctuations in the isotropic liquid surrounding, i.e., symmetries related to fluctuations and their surrounding are different.

Assuming that ‘dynamical heterogeneities’ are related to precritical/pretransitional fluctuations, they should express characterization of the next, approaching phase – in the given case, amorphous solid. Hence, in the previtreous domain, near $T_g$ one can consider solid amorphous fluctuations/heterogeneities submerged in the isotropic ultraviscous/ultraslowed surrounding. There is no symmetry difference between ‘fluctuations’ and surrounding. Within fluctuations, only some bonding that supports solidification appears.

The latter means that for many standard methods, that scan physical properties, the contrast factor $CF\approx 0$, can explain the slightly puzzling evidence of ‘universalistic effects’ in the previtreous domain. Notable that the contrast factor has no meaning for the primary relaxation time DC electric conductivity detected in BDS studies since these properties are related to the averaged response from individual molecules, whose ability to orientation or translation can be only slightly ‘distorted’ by the ‘frustration’ related to the appearance or disappearance of fluctuations/heterogeneities. This can be linked to the Super-Arrhenius and non-Debye dynamics, which are characteristic of both the isotropic phase of LC nematogens and the previtreous domain of glassformers.

One can expect the appearance of ${\mathsf{\epsilon }}_{peak}^{\text{'}\text{'}}\left(T\right)$ pretransitional effect if the response regarding energy requirement for reorientation is essentially different for fluctuations/heterogeneities and their surroundings. It is the case of supercooled E7 where the solidification/vitrification is related to the translational disorder of the locally orientationally ordered nematic phase. It means previtreous/pretransitional fluctuation with a ‘frozen’ prenematic arrangement supported by intermolecular bondings. Such a mechanism could not be effective for non-anisotropic molecular systems, like glycerol – the most standard glass former.

For E7-based nanocolloids the addition of nanoparticles can influence the arrangement and bonding process, changing the values of ${\mathsf{\epsilon }}_{peak}^{\text{'}\text{'}}\left(T\right)$ but not the general pattern, as shown in Figure 6

5. Conclusions

The aim of this report is to fill the research gap for the previtreous behavior in LC-based nanocolloids. BDS studies were carried out in the E7 glass-forming LC mixture composed of rod-like molecules, and in E7 nanocolloids with BaTiO₃ nanoparticles dispersion. First, pretransitional changes of dielectric constant in the isotropic liquid phase have been presented. They follow the pattern known for nematogenic compounds with the permanent dipole moment approximately parallel to the long molecular axis for E7 and related nanocoloids. This pretransitional effect is related to prenematic fluctuations due to the weakly discontinuous character of the I-N transition.

The dominant part of studies on the previtreous behavior in glass-forming systems is focused on dynamics, tested via the primary relaxation time and DC electric conductivity.

For E7 and related nanocolloids, the fair portrayal of $\tau \left(T\right)$ and $\sigma \left(T\right)$ changes via the super-Arrhenius MYEGA equation have been shown (Eqs. (13) and (15)). The universalistic pattern of changes for the apparent activation enthalpy is notable, which coincides with the steepness index for the Arrhenius scale presentation. Further, this property can be considered the metric of $\tau \left(T\right)$ or $\sigma \left(T\right)$ relative changes in this scale (Eq. (16)). It is worth recalling that these properties are associated with orientational and translational dynamics, respectively [7,11].

The primary relaxation time is related to the time-scale associated with the primary loss curve peak in ${\epsilon }^{\text{'}\text{'}}\left(f\right)$ spectrum [7,11]. The second coordinate of the peak is the loss curve maximum ${\epsilon }_{peak}^{\text{'}\text{'}}\left(T\right)$. It reflects the energy required for the orientation [78]. Surprisingly, the evolution of these properties is hardly, if at all, evidenced in studies on the previtreous dynamics. The results of this report show $\tau \left(T\right)$ changes in supercooling E7-based nanocolloids overlaps. Previtreous changes of ${\epsilon }_{peak}^{\text{'}\text{'}}\left(T\right)$ strongly depend on the concentration of nanoparticles in tested nanocolloids. For this property, the unique critical-like effect near $T_g$, extending up to $~T_g+20K$, has been found. It is shown in Figure 6, with the parameterization via Equation (14).

All these can indicate a possible milestone significance for studying previtreous phenomena in glassformers composed of anisotropic molecules, where the addition of nanoparticles offers a supplementary possibility of testing the impact of local nano-frustrations.