Submitted:
05 December 2024
Posted:
06 December 2024
You are already at the latest version
Abstract

Keywords:
1. Introduction
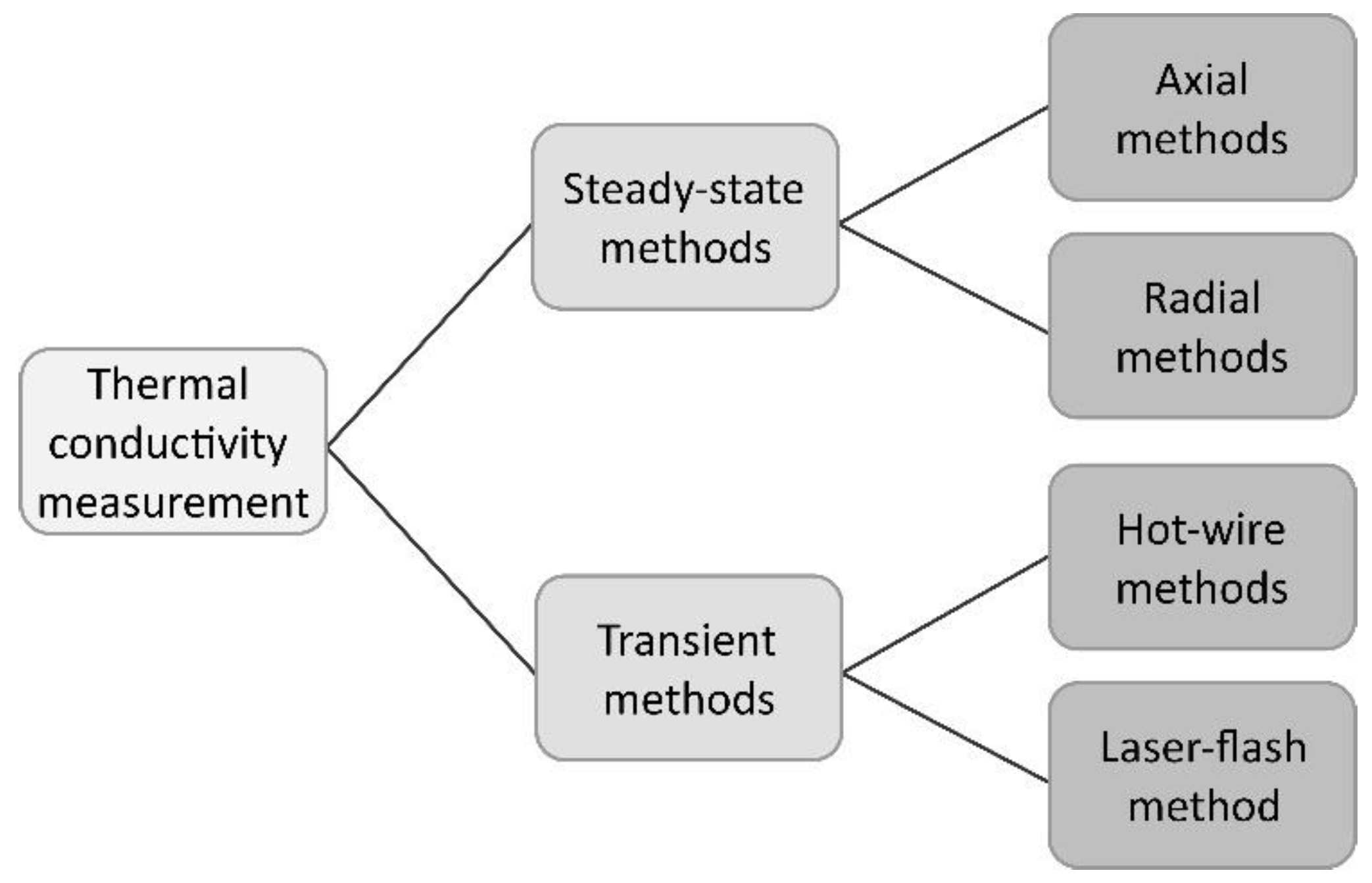
2. On the Overview of the Methods Applied to Measure Thermal Conductivity
- → Time required for the measurements
- → Possibility to measure in a hydrogen atmosphere
- → Possible temperature and pressure range
- → Type of sample
- → Amount of sample
- → Commercial availability
2.1 Steady-State Methods
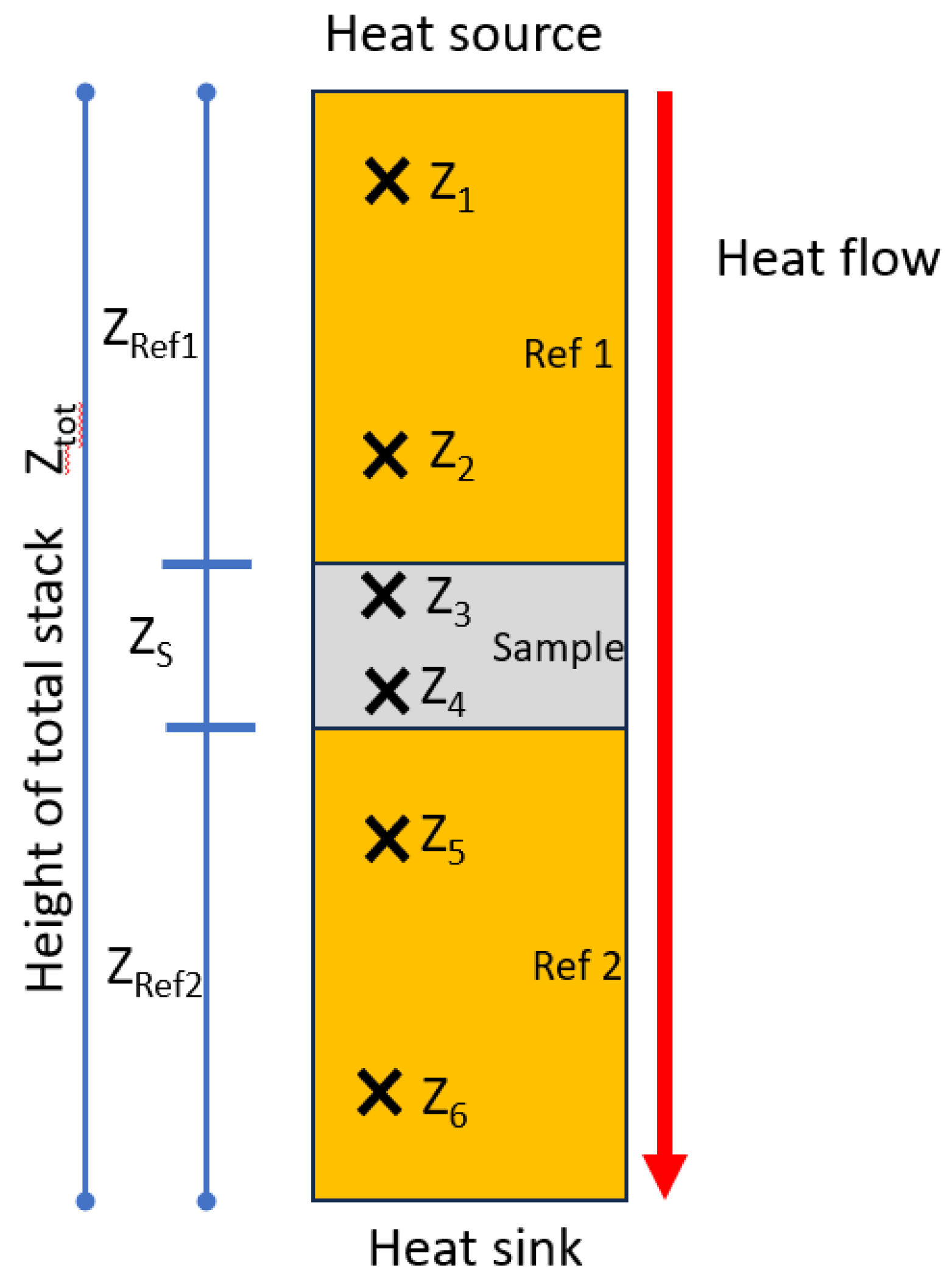
2.1.1 Axial Heat Flow
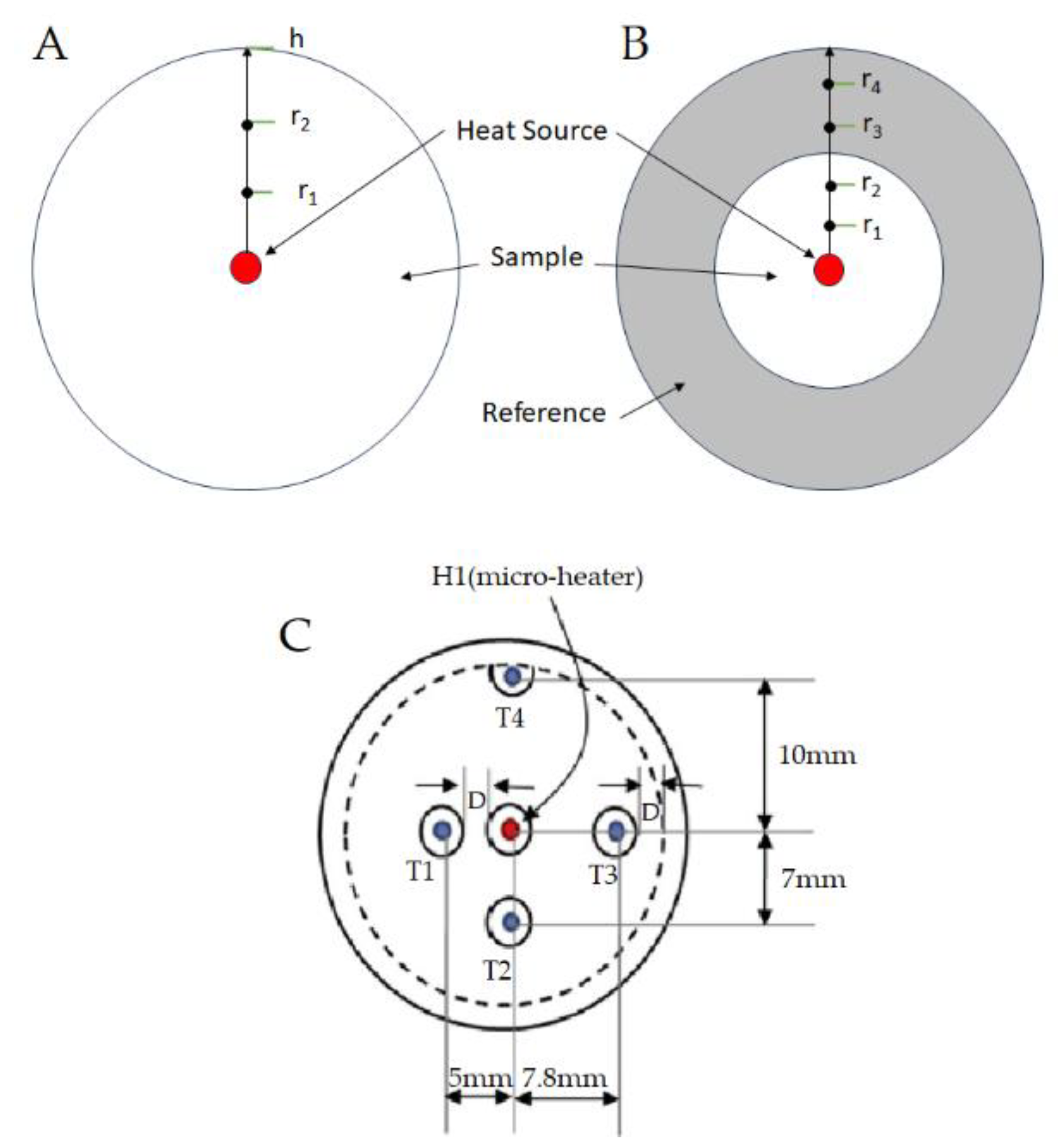
2.1.2 Radial Heat Flow
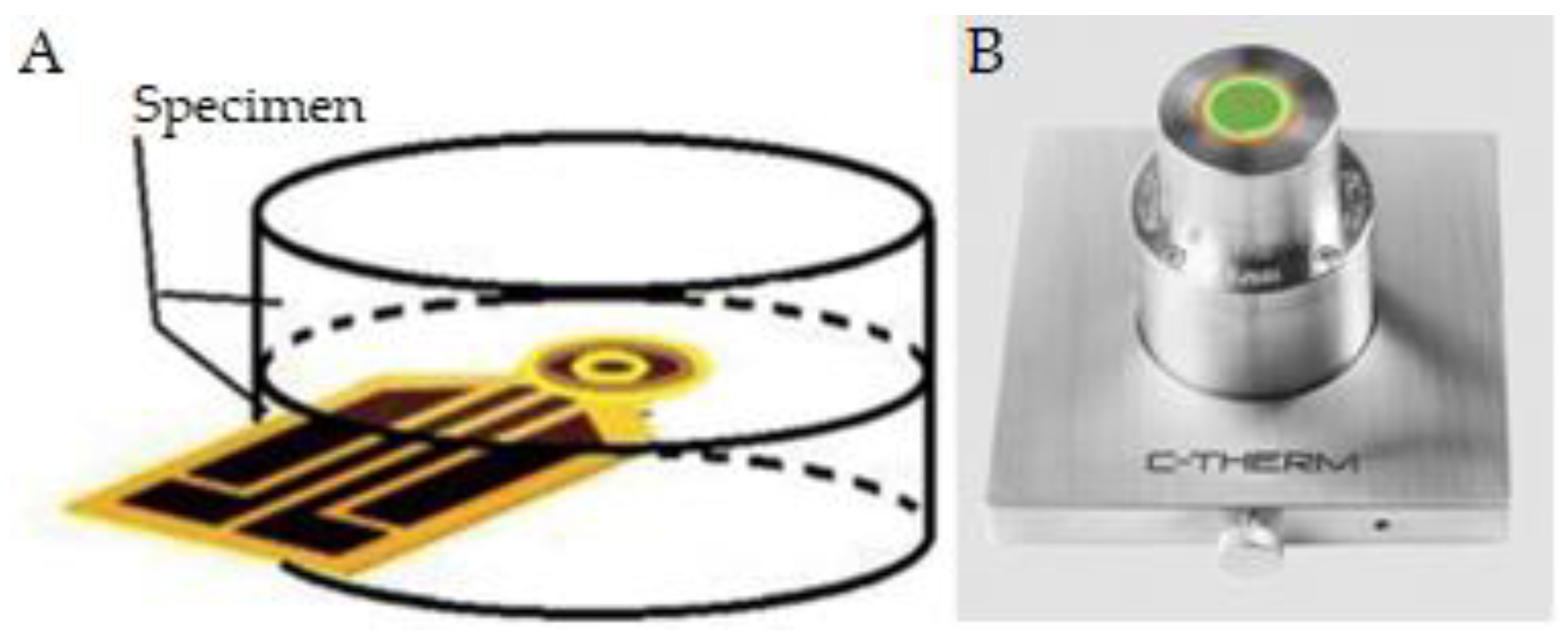
2.2 Transient Methods
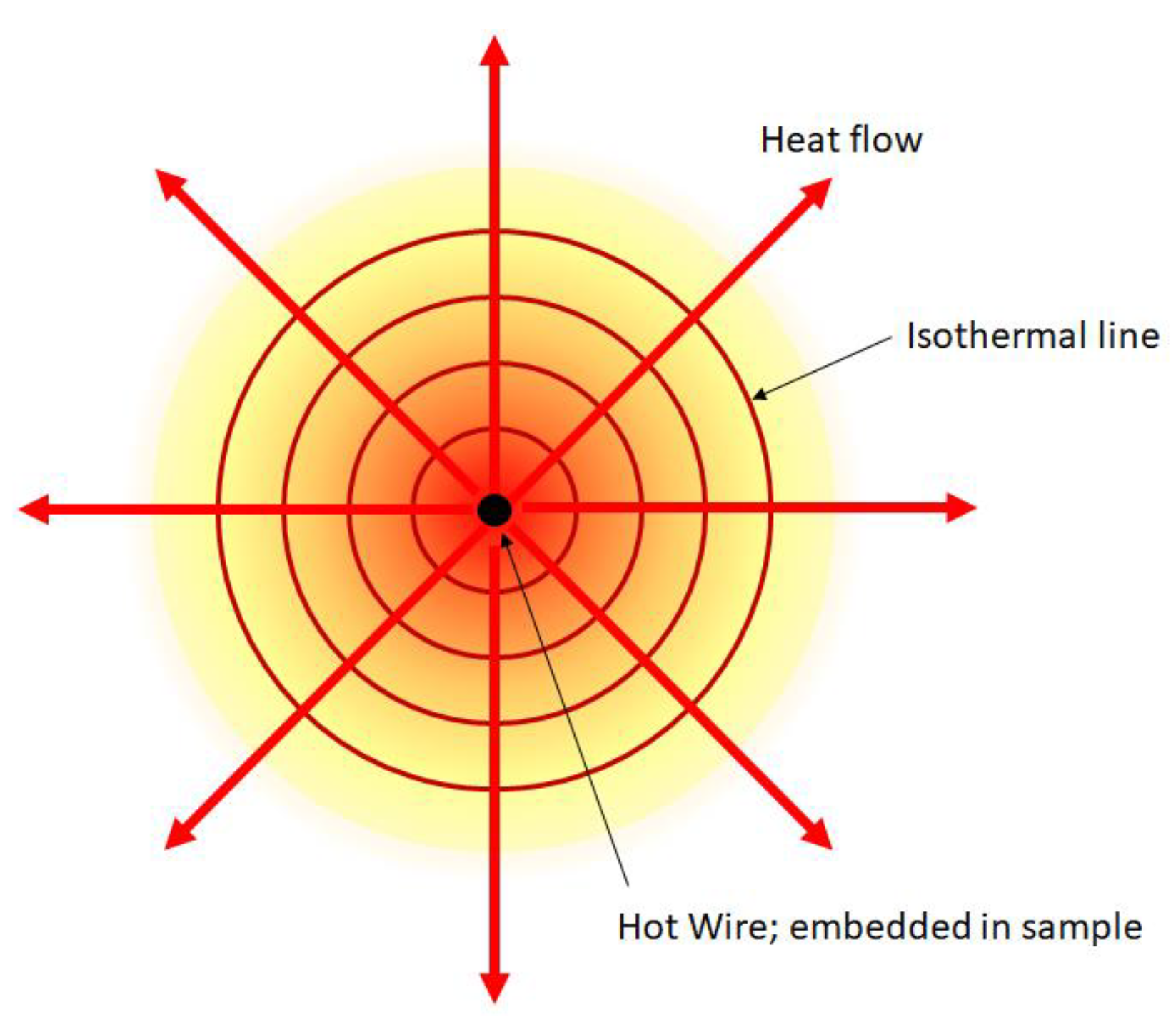
2.2.1 Hot-Wire Method
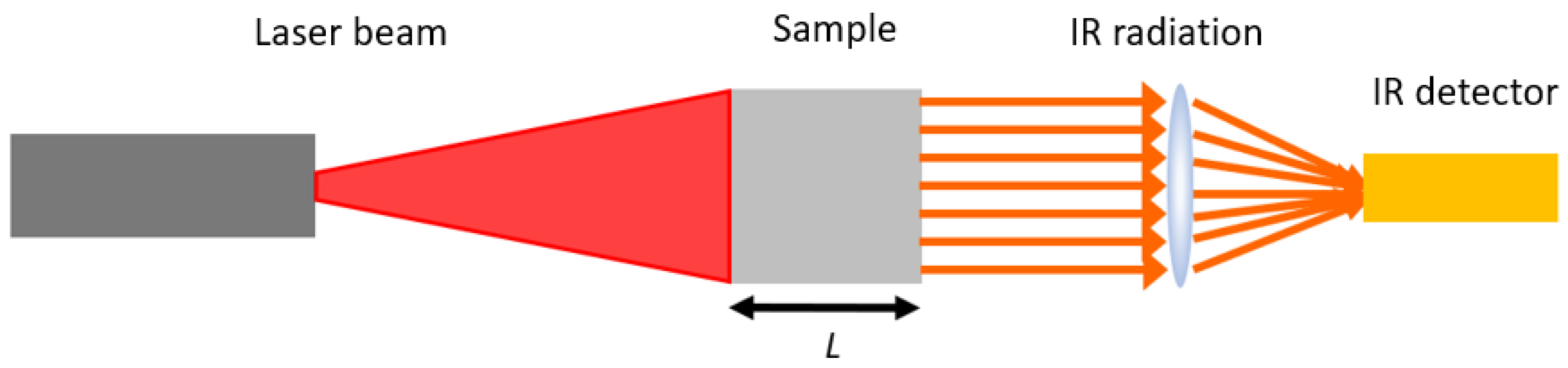
2.2.2 Laser-Flash Method
3. Development of Models for the Effective Thermal Conductivity
3.1. Description of the Models and Parameters to Calculate the ETC (keff)
3.1.1 Maxwell Model (1873)
3.1.2 Yagi and Kunii Model (1957)
3.1.3 Zehner-Schlünder Model (1970)
3.1.4 Zehner-Bauer-Schlünder Model (1978)
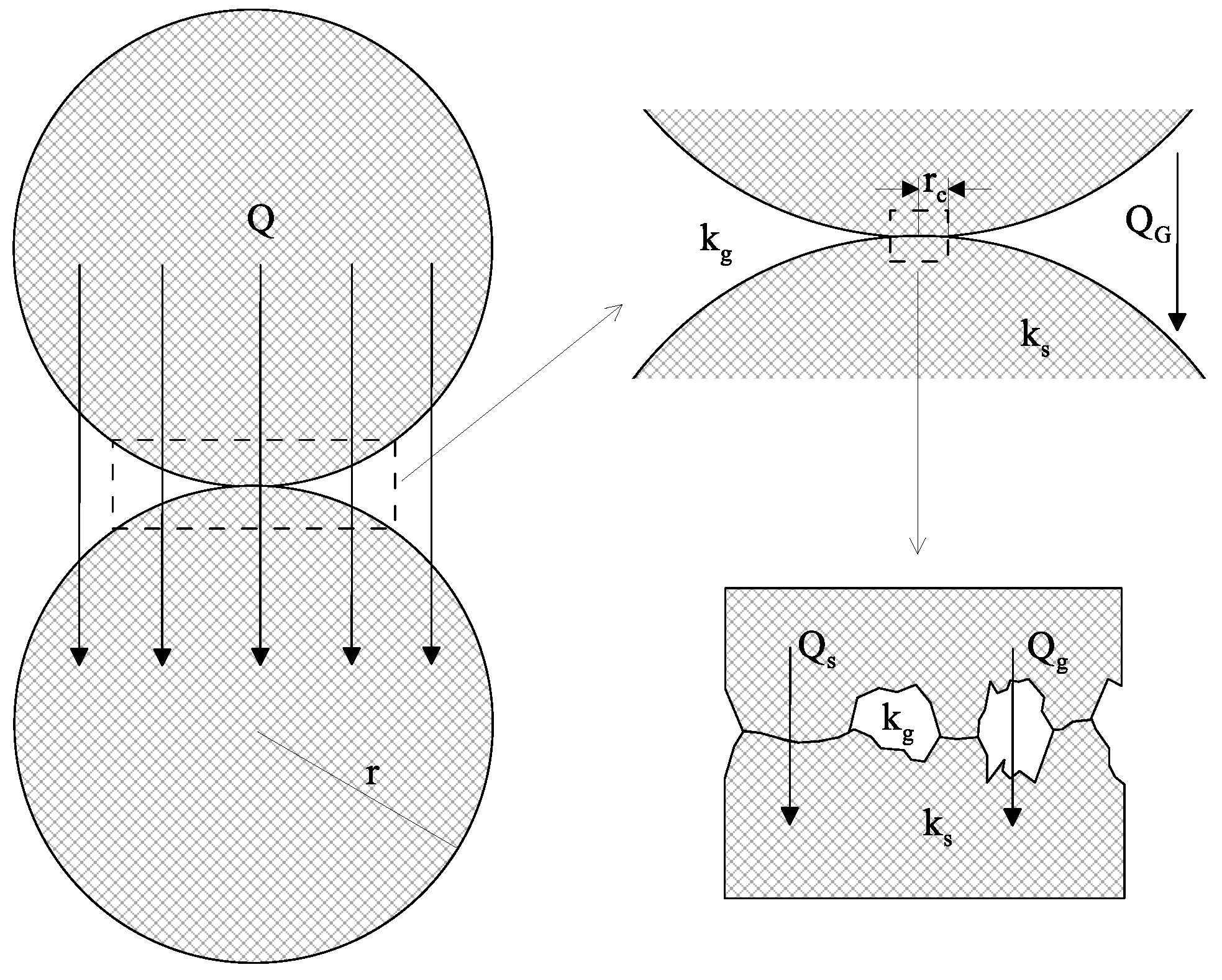
3.1.5 Hayashi Model (1987)
- Conductive and radiative heat transfer in the gaseous phase
- Conductive and radiative heat transfer in series through the gas and the solid in the biphasic region
- Conductive heat transfer through the contact surface of solid particles
3.1.6 Sun and Deng Model (1990)
3.1.7 Extended Zehner-Bauer-Schlünder Model (1994)
3.1.8 Modified Zehner-Schlünder: Area-Contact Model (1994)
3.1.9 Modified Zehner-Schlünder: Phase-Symmetry Model (1994)
3.1.10 Raghavan-Martin Model (1995)
3.1.11 Improved Area-Contact Model (2014)
3.1.12 Abdin-Webb-Gray Model (2018)
3.1.13 Heat Transfer Concentrating Model (2023)
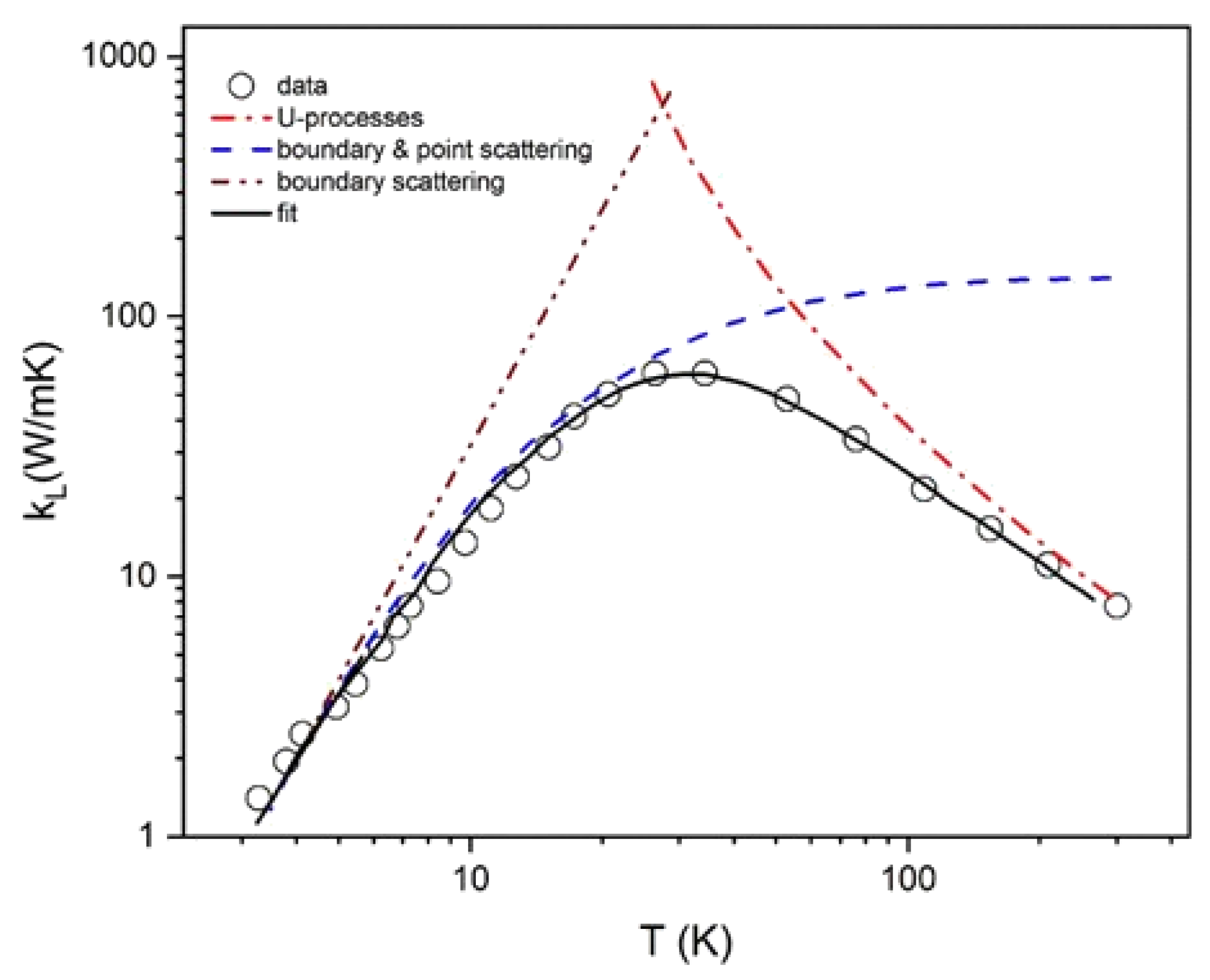
3.2 On the Thermal Conductivity of the Solid
4. Effect of the Pressure, Temperature, and Composition on the ETC
- the ks, kg, ε, and l expressions given by the authors of every keff model are used;
- if the authors did not include any model for ks, a constant value is used for this parameter;
- if no information or model for kg is given, as it can be considered readily available and generally acceptable, it is calculated through data from RefProp v.10.0 (which is available from the free Mini-RefProp v.10.0 too) [168], where a dependence on P and T is present;
- if the authors did not include any model for ε, a constant value is used for this parameter;
- if no information on l is given, it is calculated through Equation (134);
- to analyze the influence of the composition on keff in the improved area-contact model, X, through R, is treated as a variable and not as a parameter.
| Parameter | Value |
| ε | 0.52 |
| μg | 8.8·10-6 Pa·s |
| cp,g | 14300 J kg-1·K-1 |
| γ | 1.4 |
| ks | 8 W m1·K-1 |
| d | 15·10-6 m |
| dkin | 289·10-12 m |
| lv | 0.034·d |
| e | 0.5 |
| Xmax | 1.45 wt % |
| E | 155·109 Pa |
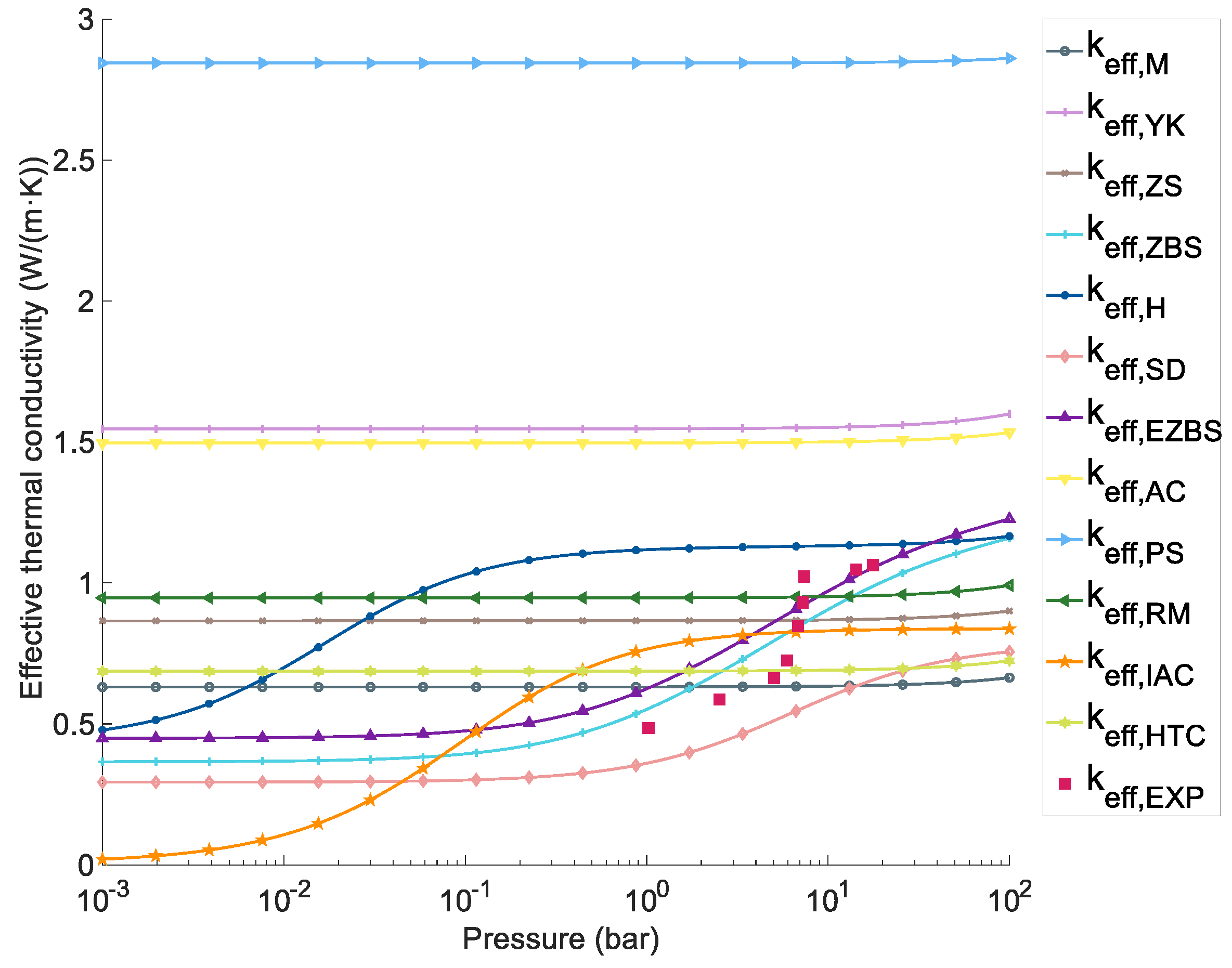
- 3.1.1 Maxwell model [42]: M
- 3.1.2 Yagi and Kunii model [92]: YK
- 3.1.3 Zehner-Schlünder model [44]: ZS
- 3.1.5 Hayashi model [43]: H
- 3.1.7 Extended Zehner-Bauer-Schlünder model [95]: EZBS
- 3.1.8 Area-contact model [45]: AC
- 3.1.9 Phase-symmetry model [45]: PS
- 3.1.10 Raghavan-Martin model [49]: RM
- 3.1.11 Improved area-contact model [50]: IAC
- 3.1.12 Abdin-Webb-Gray [102]: AWG
- 3.1.13 Heat transfer concentrating model [91]: HTC
4.1 Effect of the Pressure on the ETC
4.2 Effect of the Concentration on the ETC
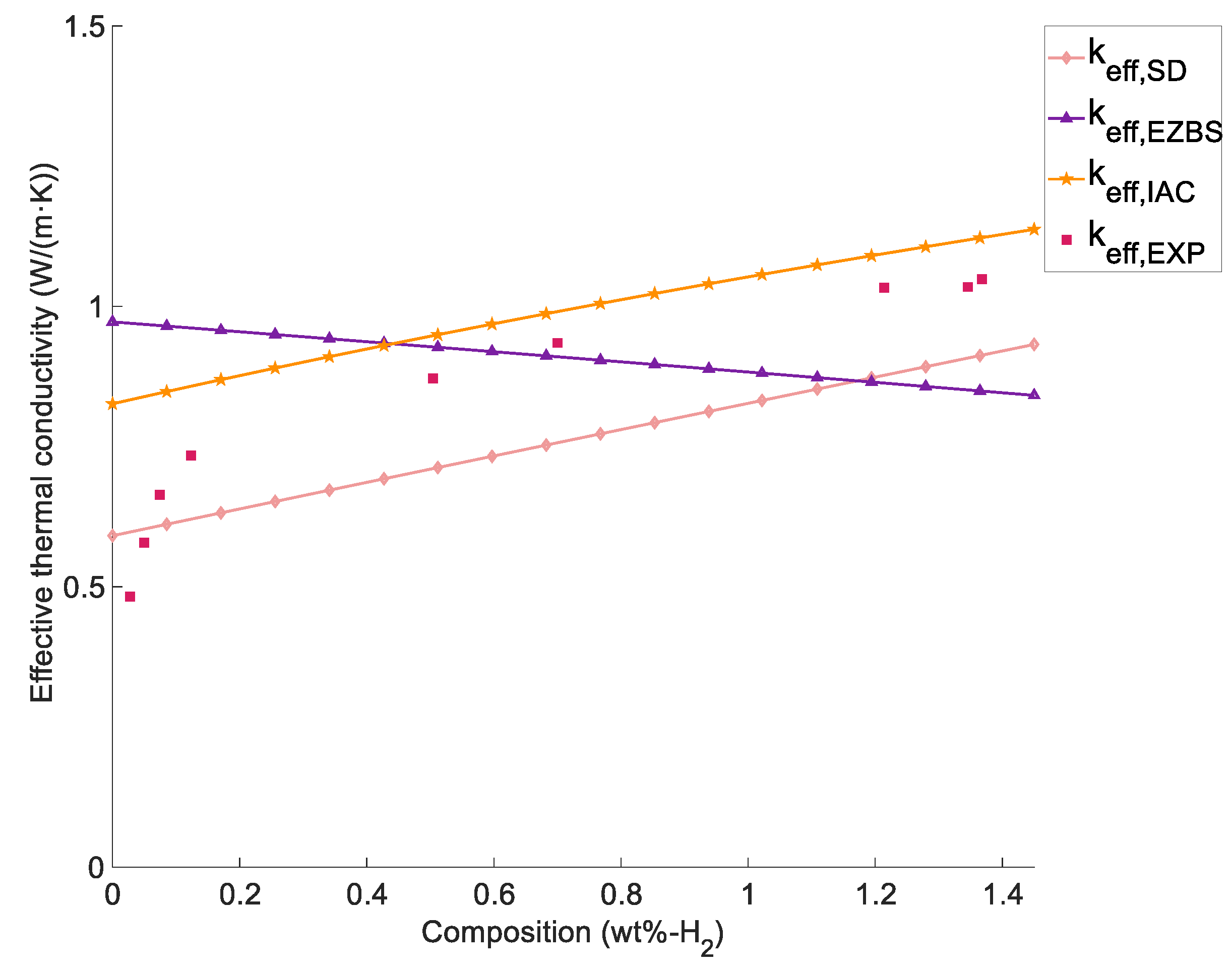
4.3 Effect of the Temperature on the ETC
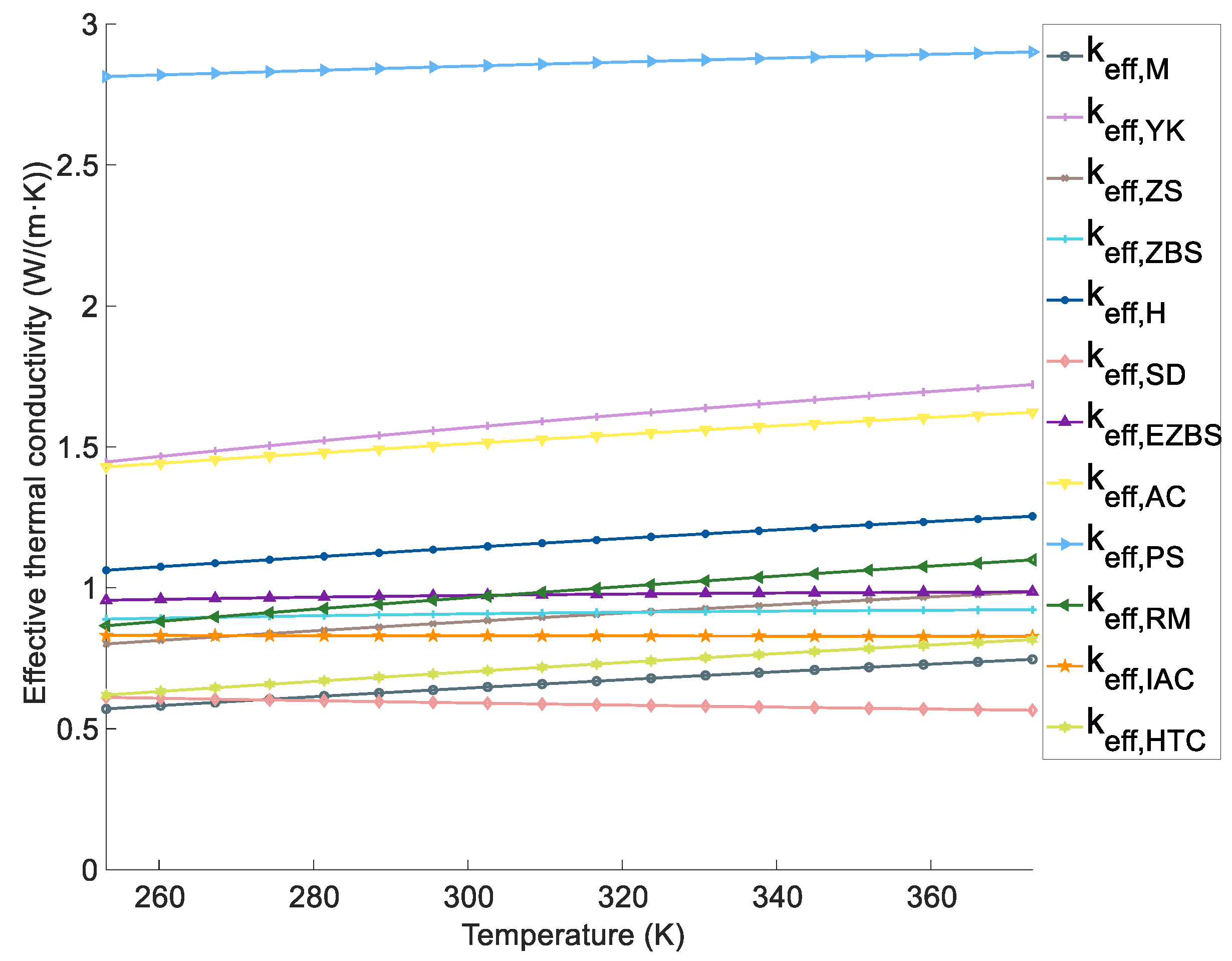
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Abbreviations
| ABS | Absorption |
| Abs. | Hydrogenation |
| DES | Desorption |
| Des. | Dehydrogenation |
| ETC | Effective thermal conductivity |
| GHG | Greenhouse gas |
| HTC | Heat transfer concentration model |
| LFM | Laser-flash method |
| LGHV | Low gravimetric heating value |
| LVHV | Low volumetric heating value of hydrogen |
| MFP | Mean free path |
| MHB | Metal Hydride Bed |
| MHs | Metal hydrides |
| MTPS | Modified transient plane source |
| PCIs | Pressure-Composition-Isotherms |
| RT | Room temperature |
| TLS | Transient line source |
| TPS | Transient plane source |
List of Symbols
| a | Accommodation coefficient |
| A | Cross-Sectional Area |
| A0 | Fitting parameter |
| Aconst | Proportionality constant |
| a1 | Operator to compact equations |
| A1 | Fitting parameter |
| a2 | Operator to compact equations |
| a3 | Operator to compact equations |
| Asf | Solid-fluid interface |
| b | Accommodation coefficient |
| B | Shape factor |
| Bbulk | Bulk modulus |
| B0 | Initial shape factor |
| b1 | Operator to compact equations |
| b2 | Operator to compact equations |
| Ba | Shape factor after the expansion |
| bg | Constant depending on the gas |
| C | Form factor |
| c1 | Operator to compact equations |
| C1 | Vickers microhardness coefficient 1 |
| c2 | Operator to compact equations |
| C2 | Vickers microhardness coefficient 2 |
| cp | Heat capacity at constant pressure |
| cv | Heat capacity at constant volume |
| cve | Volume-specific heat capacity of the electron gas |
| cvp | Volume-specific heat capacity of the phonon gas |
| d | Particle diameter |
| dkin | Kinetic diameter of hydrogen |
| D | Size of the boundary of the solid |
| d0 | Initial particle diameter |
| dc | Contact area diameter |
| de | Equivalent diameter for the void space |
| dv | Mean indentation diagonal depth |
| e | Elementary charge |
| e | Emissivity factor of the solid surface |
| E | Young's modulus |
| E' | Effective Young's modulus |
| F | Force between two particles |
| F0 | Force between two particles for constant area during expansion |
| fF | Force factor |
| Fn | Normal contact force |
| fve | Maximum expansion factor of the particles |
| FX | Force for the expansion of a fully restrained particle |
| G | Effective gas coefficient |
| G | Reciprocal lattice vector |
| h | Dimensionless height |
| Hc | Contact microhardness |
| hMaxwell | Value of h taking to the Maxwell result |
| hrs | Radiative heat transfer coefficients for solid-to-solid |
| hrv | Radiative heat transfer coefficients for void-to-void |
| hsc | Height of the spherical cap |
| hsh | Height of the sample holder |
| H | Hydrogen Atom |
| Hv | Vickers microhardness |
| k | Thermal conductivity |
| kB | Boltzmann constant |
| kbp | Thermal conductivity of the biphasic region in the model 3.1.4 |
| k’ | Thermal conductivity of the biphasic region in the model 3.1.7 |
| ke | Heat conduction in solids owing to electrons |
| ke0 | Effective thermal conductivity at zero pressure |
| keff | Effective thermal conductivity |
| kg | Gas (hydrogen) thermal conductivity |
| kg,Eucken | Gas (hydrogen) thermal conductivity with the Eucken Equation |
| kg,ref | Gas (hydrogen) thermal conductivity at reference pressure |
| kg1 | Gas (hydrogen) thermal conductivity in the gas domain |
| kg2 | Gas (hydrogen) thermal conductivity in the biphasic domain |
| ki | Heat conduction channels i |
| kp | Heat conduction in solids owing to phonons |
| Kn | Knudsen number |
| Kn* | Modified Knudsen number |
| ks | Solid phase (bulk) thermal conductivity |
| ks* | Solid phase thermal conductivity for the metal/alloy to hydride transition |
| kref | Thermal Conductivity of Reference Materials |
| L | Thickness |
| l | Mean free path |
| lp | Effective length between the centers of two adjacent particles |
| ls | Effective length of the solid particles relating to the heat conduction |
| lv | Effective thickness of fluid film adjacent to the contact surface of two solid particles |
| m | Exponential fitting parameter |
| me | Electron mass |
| M | Gas parameter |
| Mav | Average atomic mass |
| Me | Metal |
| MHs | Metal hydrides |
| MexHy | Metal Hydride Compound |
| MW | Molecular weight |
| MWH2 | Molecular weight of molecular hydrogen |
| N | Particle coordination number |
| NA | Avogadro constant |
| Natoms | Number of atoms in the sample |
| Natoms-cell | Number of atoms in the unit cell |
| Ni | Concentration of the impurity in the metal |
| Nur | Nusselt number |
| Nur* | Modified Nusselt number |
| nd | Defects concentration |
| ne | Electrons concentration |
| np | Phonons concentration |
| P | Pressure |
| P0 | Hydrogen mean free path reference pressure |
| Peq | Equilibrium pressure |
| Pload,max | Maximum contact load pressure |
| Pr | Prandtl number |
| q | Heat flow |
| Q | Operator to compact equations |
| Q | Heat flux perpendicular to an area in the solid |
| R | Reacted fraction |
| rn | Radial position of the thermocouple, with n= 1, 2, 3, …, n. |
| r | Particle radius |
| r0 | Initial particle radius |
| rc | Contact area radius |
| Rc | Thermal contact resistance |
| rc,0 | Initial contact area radius |
| Rg | Micro-gap thermal resistance |
| RG | Macro-gap thermal resistance |
| Rgas | Gas constant |
| RL | Macro-contact thermal resistance |
| Rmax | Maximum reacted fraction |
| RP | Reacted fraction at the beginning of the plateau |
| Rs | Micro-contact thermal resistance |
| T | Temperature |
| Teq | Equlibrium temperature |
| ∇T | Temperature gradient |
| tn | Times, n= 1 (initial) and 2 (final) |
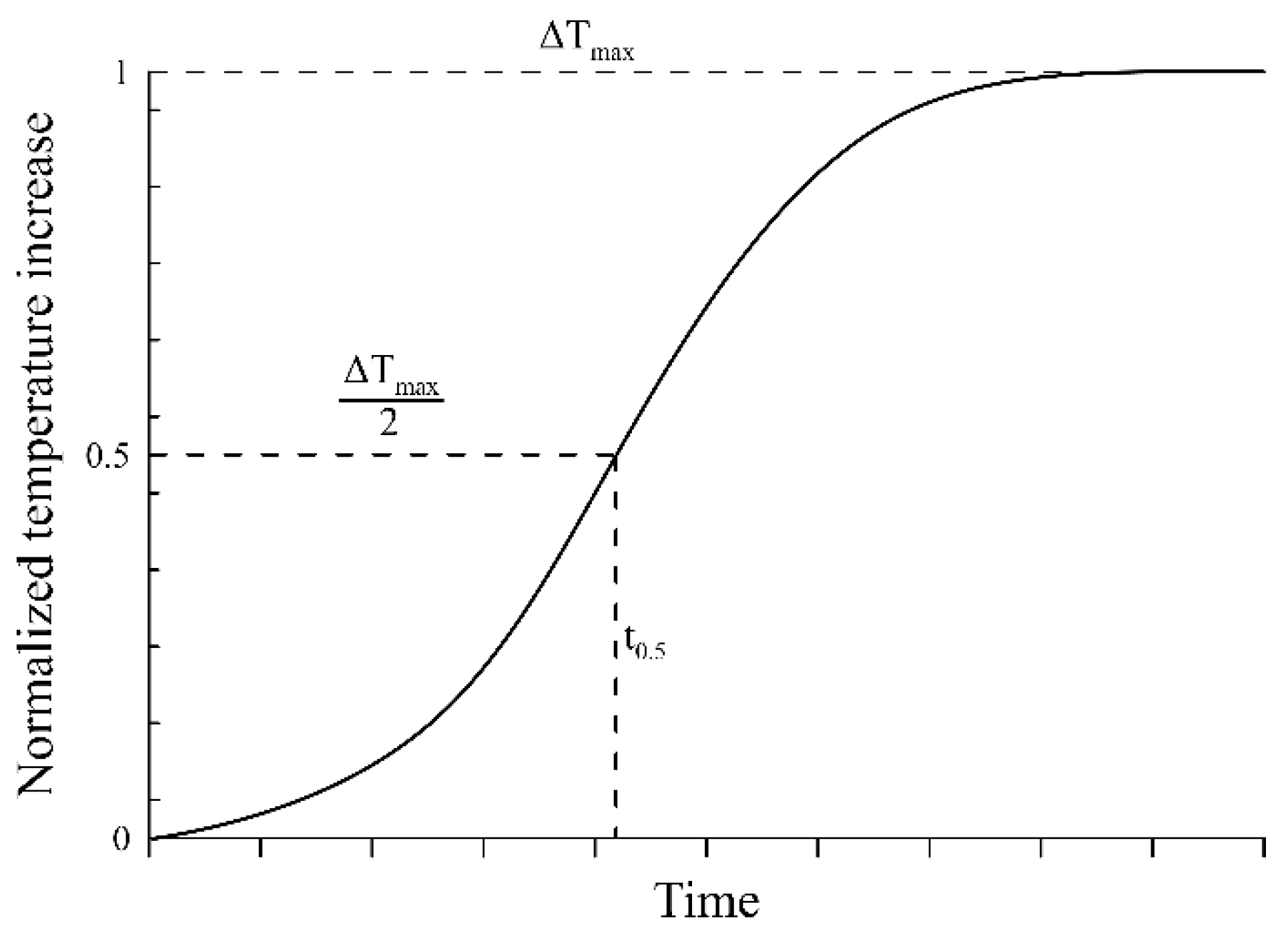
| t0.5 | Time after reaching 50 % of the total temperature increase |
| V | Volume of the metal |
| V0 | Minimum MH bed volume |
| V1 | Maximum MH bed volume |
| V2 | MH bed volume at the end of the cycle |
| vF | Fermi velocity of the conducting electrons at the Fermi surface |
| Vgas,all | Total gas volume in the characteristic cubic unit |
| Vgas,cylinder | Gas volume of the cylinder region |
| Vgas,eff | Effective gas film region |
| vp | Average group velocity of the phonons |
| vs | Speed of sound inside the solid |
| Vs,0 | Initial volume of the solid particle |
| wt% | Weight percentage |
| x | Distance |
| X | Hydrogen to metal concentration (wt%) |
| Xat | Hydrogen to metal atomic ratio |
| Xeq | Equilibrium hydrogen concentration |
| Xmax | Maximum hydrogen to metal concentration |
| Y | Operator to compact equations |
| Z | Operator accounting for geometric distortions |
| Zn | Position of the thermocouple |
List of Greek Symbols
| α | Deformed factor |
| α0 | Initial deformed factor |
| αa | Deformed factor after the expansion |
| αd | Thermal diffusivity |
| αss | Metal solid solution phase |
| αT1 | Thermal accommodation coefficient 1 |
| αT2 | Thermal accommodation coefficient 2 |
| β | Operator to compact equations |
| β' | Factor of the angle between actual and parallel heat flow directions |
| βMH | Metal hydride phase |
| ЄF | Fermi energy |
| Γ | Specific heat ratio |
| γGrü | Grüneisen parameter |
| γSommerfeld | Sommerfeld constant |
| δ | Fractional area associated with the conductive heat transfer through particles |
| δv | Average atomic volume |
| ΔHr | Reaction Enthalpy |
| ΔM | Difference in mass between the two isotopes |
| ΔSr | Reaction Entropy |
| ΔV | Volume variation per hydrogen atom |
| ΔVs | Relative expansion of the solid particle |
| ε | Porosity |
| ε0 | Initial porosity |
| η2 | Heat transferred ratio – "cylinder region": "characteristic cubic unit" |
| η3 | Gas volume ratio – Vgas,eff:Vgas,all |
| θ0 | Contact angle between solid particles at zero pressure |
| θ | Contact angle between solid particles |
| θD | Debye temperature |
| Κ | Wave-vector of the phonons |
| μ | Dynamic viscosity |
| ν | Poisson's ratio |
| ρ | Density |
| ρg | Gas density |
| ρs | Solid material density |
| σ | Stefan-Boltzmann constant |
| σelectrical | Electrical conductivity |
| σe-i | Cross-section for the scattering of the impurity |
| σd | Scattering cross-section for phonons |
| σR | Surface roughness |
| τ | Angle from the centre of the spherical particle to the annular cylinder |
| τe | Relaxation time of an electron |
| τe-e | Relaxation time of the electron-electron scattering processes |
| τe-i | Relaxation time of the electron-impurity scattering |
| τe-p | Relaxation time of electrons scattered by phonons at low temperatures |
| τp | Relaxation time of a phonon |
| τU | Relaxation time for the U-process |
| τp-B | Relaxation time for the phonon-boundary scattering |
| τp-d | Relaxation times for the lattice imperfections of crystals |
| τp-is | Relaxation time for the phonons mean free path |
| τp | Relaxation times of all phononic scattering processes |
| ΔT | Temperature difference |
| ϕ | Flattening factor |
| ϕ* | Dimensionless length |
| ϕ1* | Support parameter for the dimensionless length |
| ϕ2* | Support parameter for the dimensionless length |
| ϕabs | Expansion ratio |
| ϕdes | Contraction ratio |
| ϕp | Particle expansion ratio |
| ϕs | Metal hydride bed expansion ratio |
| ω | Angle of the cylinder region |
| ωf | Angular frequency of the phonons |
| ∇ | Nabla, vector differential operator |
| Ʌ | Characteristic length |
| Λp | Particle mean free path between two collision events for phonons |
| Λe | Particle mean free path between two collision events of electrons |
References
- Allen, M.R., O.P. Dube, W. Solecki, F. Aragón-Durand, W. Cramer, S. Humphreys, M. Kainuma, J. Kala, N. Mahowald, Y. Mulugetta, R. Perez, M. Wairiu, and K. Zickfeld, 2018: Framing and Context Supplementary Material. In: Global Warming of 1.5°C. An IPCC Special Report on the impacts of global warming of 1.5°C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty [Masson-Delmotte, V., P. Zhai, H.-O. Pörtner, D. Roberts, J. Skea, P.R. Shukla, A. Pirani, W. Moufouma-Okia, C. Péan, R. Pidcock, S. Connors, J.B.R. Matthews, Y. Chen, X. Zhou, M.I. Gomis, E. Lonnoy, T. Maycock, M. Tignor, and T. Waterfield (eds.)]. Available from https://www.ipcc.ch/sr15.
- Lambert, M.; Hawkes, A.; Patonia, A.; Poudineh, R.; Moore, B.; Isaac, T.; Lewis, T.; Schöffel, M.; Barnes, A.; Heather, P.; et al. The Role of Hydrogen in the Energy Transition. The Oxford Institute for Energy Studies 2021.
- Dawood, F.; Anda, M.; Shafiullah, G.M. Hydrogen Production for Energy: An Overview. Int J Hydrogen Energy 2020, 45, 3847–3869. [CrossRef]
- Xu, Z.; Zhao, N.; Hillmansen, S.; Roberts, C.; Yan, Y. Techno-Economic Analysis of Hydrogen Storage Technologies for Railway Engineering: A Review. Energies (Basel) 2022, 15, 6467. [CrossRef]
- Yanxing, Z.; Maoqiong, G.; Yuan, Z.; Xueqiang, D.; Jun, S. Thermodynamics Analysis of Hydrogen Storage Based on Compressed Gaseous Hydrogen, Liquid Hydrogen and Cryo-Compressed Hydrogen. Int J Hydrogen Energy 2019, 44, 16833–16840. [CrossRef]
- Zheng, J.; Liu, X.; Xu, P.; Liu, P.; Zhao, Y.; Yang, J. Development of High Pressure Gaseous Hydrogen Storage Technologies. Int J Hydrogen Energy 2012, 37, 1048–1057. [CrossRef]
- Ahluwalia, R.K.; Peng, J.-K.; Hua, T.Q. Cryo-Compressed Hydrogen Storage. In Compendium of Hydrogen Energy; Elsevier, 2016; pp. 119–145.
- Aziz, M. Liquid Hydrogen: A Review on Liquefaction, Storage, Transportation, and Safety. Energies (Basel) 2021, 14. [CrossRef]
- Aceves, S.M.; Petitpas, G.; Espinosa-Loza, F.; Matthews, M.J.; Ledesma-Orozco, E. Safe, Long Range, Inexpensive and Rapidly Refuelable Hydrogen Vehicles with Cryogenic Pressure Vessels. Int J Hydrogen Energy 2013, 38, 2480–2489. [CrossRef]
- Clematis, D.; Bellotti, D.; Rivarolo, M.; Magistri, L.; Barbucci, A. Hydrogen Carriers: Scientific Limits and Challenges for the Supply Chain, and Key Factors for Techno-Economic Analysis. Energies (Basel) 2023, 16, 6035. [CrossRef]
- Cetinkaya, S.A.; Disli, T.; Soyturk, G.; Kizilkan, O.; Colpan, C.O. A Review on Thermal Coupling of Metal Hydride Storage Tanks with Fuel Cells and Electrolyzers. Energies (Basel) 2022, 16, 341. [CrossRef]
- Zhang, F.; Zhao, P.; Niu, M.; Maddy, J. The Survey of Key Technologies in Hydrogen Energy Storage. Int J Hydrogen Energy 2016, 41, 14535–14552. [CrossRef]
- Wijayanta, A.T.; Oda, T.; Purnomo, C.W.; Kashiwagi, T.; Aziz, M. Liquid Hydrogen, Methylcyclohexane, and Ammonia as Potential Hydrogen Storage: Comparison Review. Int J Hydrogen Energy 2019, 44, 15026–15044. [CrossRef]
- Durbin, D.J.; Malardier-Jugroot, C. Review of Hydrogen Storage Techniques for on Board Vehicle Applications. Int J Hydrogen Energy 2013, 38, 14595–14617. [CrossRef]
- Prachi R., P.; Mahesh M., W.; Aneesh C., G. A Review on Solid State Hydrogen Storage Material. Advances in Energy and Power 2016, 4, 11–22. [CrossRef]
- Liu, Y.; Chabane, D.; Elkedim, O. Intermetallic Compounds Synthesized by Mechanical Alloying for Solid-State Hydrogen Storage: A Review. Energies (Basel) 2021, 14. [CrossRef]
- Pasquini, L.; Sakaki, K.; Akiba, E.; Allendorf, M.D.; Alvares, E.; Ares, J.R.; Babai, D.; Baricco, M.; Bellosta von Colbe, J.; Bereznitsky, M.; et al. Magnesium- and Intermetallic Alloys-Based Hydrides for Energy Storage: Modelling, Synthesis and Properties. Progress in Energy 2022, 4, 032007. [CrossRef]
- Bellosta von Colbe, J.; Ares, J.-R.; Barale, J.; Baricco, M.; Buckley, C.; Capurso, G.; Gallandat, N.; Grant, D.M.; Guzik, M.N.; Jacob, I.; et al. Application of Hydrides in Hydrogen Storage and Compression: Achievements, Outlook and Perspectives. Int J Hydrogen Energy 2019, 44, 7780–7808. [CrossRef]
- Puszkiel, J.; Bellosta von Colbe, J.M.; Jepsen, J.; Mitrokhin, S. V.; Movlaev, E.; Verbetsky, V.; Klassen, T. Designing an Ab2-Type Alloy (TIZr-CrMNMO) for the Hybrid Hydrogen Storage Concept. Energies (Basel) 2020, 13. [CrossRef]
- Dreistadt, D.M.; Puszkiel, J.; Bellosta von Colbe, J.M.; Capurso, G.; Steinebach, G.; Meilinger, S.; Le, T.-T.; Covarrubias Guarneros, M.; Klassen, T.; Jepsen, J. A Novel Emergency Gas-to-Power System Based on an Efficient and Long-Lasting Solid-State Hydride Storage System: Modeling and Experimental Validation. Energies (Basel) 2022, 15, 844. [CrossRef]
- Dematteis, E.M.; Barale, J.; Corno, M.; Sciullo, A.; Baricco, M.; Rizzi, P. Solid-State Hydrogen Storage Systems and the Relevance of a Gender Perspective. Energies (Basel) 2021, 14. [CrossRef]
- Scarpati, G.; Frasci, E.; Di Ilio, G.; Jannelli, E. A Comprehensive Review on Metal Hydrides-Based Hydrogen Storage Systems for Mobile Applications. J Energy Storage 2024, 102, 113934. [CrossRef]
- Møller, K.; Sheppard, D.; Ravnsbæk, D.; Buckley, C.; Akiba, E.; Li, H.-W.; Jensen, T. Complex Metal Hydrides for Hydrogen, Thermal and Electrochemical Energy Storage. Energies (Basel) 2017, 10, 1645. [CrossRef]
- Ge, Y.T.; Lang, P.Y. Alloy Selections in High-Temperature Metal Hydride Heat Pump Systems for Industrial Waste Heat Recovery. Energy Reports 2022, 8, 3649–3660. [CrossRef]
- Guo, F.; Jain, A.; Miyaoka, H.; Kojima, Y.; Ichikawa, T. Critical Temperature and Pressure Conditions of Degradation during Thermochemical Hydrogen Compression: A Case Study of V-Based Hydrogen Storage Alloy. Energies (Basel) 2020, 13. [CrossRef]
- Ham, S.; Kang, S.; Kim, K.J. A Numerical Study for Performance Prediction of a Metal Hydride Thermal Energy Conversion System Elaborating the Superadiabatic Condition. Energies (Basel) 2020, 13. [CrossRef]
- Mohammadshahi, S.S.; Gray, E.M.A.; Webb, C.J. A Review of Mathematical Modelling of Metal-Hydride Systems for Hydrogen Storage Applications. Int J Hydrogen Energy 2016, 41, 3470–3484. [CrossRef]
- Bohmhammel, K.; Wolf, U.; Wolf, G.; Königsberger, E. Thermodynamic Optimization of the System Magnesium–Hydrogen. Thermochim Acta 1999, 337, 195–199. [CrossRef]
- Aguey-Zinsou, K.-F.; Ares-Fernández, J.-R. Hydrogen in Magnesium: New Perspectives toward Functional Stores. Energy Environ Sci 2010, 3, 526. [CrossRef]
- Sandrock, G. A Panoramic Overview of Hydrogen Storage Alloys from a Gas Reaction Point of View. J Alloys Compd 1999, 293–295, 877–888. [CrossRef]
- Gray, E.M.A. Alloy Selection for Multistage Metal-Hydride Hydrogen Compressors: A Thermodynamic Model. Int J Hydrogen Energy 2021, 46, 15702–15715. [CrossRef]
- Schwarz, R.B.; Khachaturyan, A.G. Thermodynamics of Open Two-Phase Systems with Coherent Interfaces. Phys Rev Lett 1995, 74, 2523–2526. [CrossRef]
- Ye, J.; Li, Z.; Zhang, L.; Wang, S.; Jiang, L. Measurement and the Improvement of Effective Thermal Conductivity for a Metal Hydride Bed - a Review. RSC Adv 2022, 12, 25722–25743. [CrossRef]
- Wang, D.; Wang, Y.; Huang, Z.; Yang, F.; Wu, Z.; Zheng, L.; Wu, L.; Zhang, Z. Design Optimization and Sensitivity Analysis of the Radiation Mini-Channel Metal Hydride Reactor. Energy 2019, 173, 443–456. [CrossRef]
- Shafiee, S.; McCay, M.H. Different Reactor and Heat Exchanger Configurations for Metal Hydride Hydrogen Storage Systems - A Review. Int J Hydrogen Energy 2016, 41, 9462–9470. [CrossRef]
- Kukkapalli, V.K.; Kim, S. Optimization of Internal Cooling Fins for Metal Hydride Reactors. Energies (Basel) 2016, 9. [CrossRef]
- Nyamsi, S.N.; Tolj, I. The Impact of Active and Passive Thermal Management on the Energy Storage Efficiency of Metal Hydride Pairs Based Heat Storage. Energies (Basel) 2021, 14. [CrossRef]
- Kukkapalli, V.K.; Kim, S.; Thomas, S.A. Thermal Management Techniques in Metal Hydrides for Hydrogen Storage Applications: A Review. Energies (Basel) 2023, 16. [CrossRef]
- Gillia, O. Hydride Breathing and Its Consequence on Stresses Applied to Containers: A Review. Int J Hydrogen Energy 2021, 46, 35594–35640. [CrossRef]
- Warfsmann, J.; Puszkiel, J.A.; Passing, M.; Krause, P.S.; Wienken, E.; Taube, K.; Klassen, T.; Pistidda, C.; Jepsen, J. Applying Wash Coating Techniques for Swelling-Induced Stress Reduction and Thermal Improvement in Metal Hydrides. J Alloys Compd 2023, 950, 169814. [CrossRef]
- Zhao, W.; Yang, Y.; Bao, Z.; Yan, D.; Zhu, Z. Methods for Measuring the Effective Thermal Conductivity of Metal Hydride Beds: A Review. Int J Hydrogen Energy 2020, 45, 6680–6700. [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Macmillan and Co.: London, 1873;
- Hayashi, S.; Kubota, K.; Masaki, H.; Shibata, Y.; Takahashi, K. Theoretical Model for the Estimation of the Effective Thermal Conductivity of a Packed Bed of Fine Particles. Chemical Engineering Journal 1987, 35. [CrossRef]
- Zehner, P.; Schlunder, E.U. Warmeleitfahigkeit von Schuttungen Bei Maßigen Temperaturen. Chemie. Ing. Techn. 1970, 42, 933–941. [CrossRef]
- Hsu, C.T.; Cheng, P.; Wong, K.W. Modified Zehner-Schlunder Models for Stagnant Thermal Conductivity of Porous Media. Int J Heat Mass Transf 1994, 37, 2751–2759. [CrossRef]
- Sun, D.-W.; Deng, S.-J. A Theoretical Model Predicting the Effective Thermal Conductivity in Powdered Metal Hydride Beds. Int Journal of Hydrogen Energy 1990, 15, 3–336. [CrossRef]
- Sun, D.-W.; Deng, S.-J. Theoretical Descriptions and Experimental Measurements on the Effective Thermal Conductivity in Metal Hydride Powder Beds. Journal of the Less-Common Metals 1990, 387–395. [CrossRef]
- Ghafir, M.F.A.; Batcha, M.F.M.; Raghavan, V.R. Prediction of the Thermal Conductivity of Metal Hydrides - The Inverse Problem. Int J Hydrogen Energy 2009, 34, 7125–7130. [CrossRef]
- Raghavan, V.R.; Martin, H. Modelling of Two-Phase Thermal Conductivity. Chemical Engineering and Processing: Process Intensification 1995, 34, 439–446. [CrossRef]
- Matsushita, M.; Monde, M.; Mitsutake, Y. Predictive Calculation of the Effective Thermal Conductivity in a Metal Hydride Packed Bed. Int J Hydrogen Energy 2014, 39, 9718–9725. [CrossRef]
- Yüksel, N. The Review of Some Commonly Used Methods and Techniques to Measure the Thermal Conductivity of Insulation Materials. In Insulation Materials in Context of Sustainability; InTech, 2016.
- Vieira, A.; Alberdi-Pagola, M.; Christodoulides, P.; Javed, S.; Loveridge, F.; Nguyen, F.; Cecinato, F.; Maranha, J.; Florides, G.; Prodan, I.; et al. Characterisation of Ground Thermal and Thermo-Mechanical Behaviour for Shallow Geothermal Energy Applications. Energies (Basel) 2017, 10. [CrossRef]
- Burger, N.; Laachachi, A.; Ferriol, M.; Lutz, M.; Toniazzo, V.; Ruch, D. Review of Thermal Conductivity in Composites: Mechanisms, Parameters and Theory. Prog Polym Sci 2016, 61, 1–28. [CrossRef]
- Asadi, I.; Shafigh, P.; Abu Hassan, Z.F. Bin; Mahyuddin, N.B. Thermal Conductivity of Concrete – A Review. Journal of Building Engineering 2018, 20, 81–93. [CrossRef]
- Palacios, A.; Cong, L.; Navarro, M.E.; Ding, Y.; Barreneche, C. Thermal Conductivity Measurement Techniques for Characterizing Thermal Energy Storage Materials – A Review. Renewable and Sustainable Energy Reviews 2019, 108, 32–52. [CrossRef]
- Arfken, G.B.; Griffing, D.F.; Kelly, D.C.; Priest, J. University Physics; 1984;
- Eaton, E.E.; Olsen, C.E.; Sheinberg, H.; Steyert, W.A. Mechanically Stable Hydride Composites Designed for Rapid Cycling. Int. J. Hydrogen Energy 1981, 6, 609–623.
- Xamán, J.; Esquivel-Ramon, J.; Chávez, Y.; Hernández-Pérez, I. Numerical Simulation of an Instrument to Determine the Thermal Conductivity of Conductive Solids. Mechanics and Industry 2017, 18. [CrossRef]
- Springer Handbook of Materials Measurement Methods; Czichos, H., Saito, T., Smith, L., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2006; ISBN 978-3-540-20785-6.
- Sánchez, A.R.; Klein, H.P.; Groll, M. Expanded Graphite as Heat Transfer Matrix in Metal Hydride Beds. Int J Hydrogen Energy 2003, 28, 515–527. [CrossRef]
- Park, C.S.; Jung, K.; Jeong, S.U.; Kang, K.S.; Lee, Y.H.; Park, Y.-S.; Park, B.H. Development of Hydrogen Storage Reactor Using Composite of Metal Hydride Materials with ENG. Int J Hydrogen Energy 2020, 45, 27434–27442. [CrossRef]
- Yasuda, N.; Tsuchiya, T.; Okinaka, N.; Akiyama, T. Thermal Conductivity and Cycle Characteristic of Metal Hydride Sheet Formed Using Aramid Pulp and Carbon Fiber. Int J Hydrogen Energy 2013, 38, 1657–1661. [CrossRef]
- Anil Kumar, E.; Prakash Maiya, M.; Srinivasa Murthy, S. Measurement and Analysis of Effective Thermal Conductivity of MmNi 4.5Al0.5 Hydride Bed. Ind Eng Chem Res 2011, 50, 12990–12999. [CrossRef]
- Netzsch-Grätebau GmbH. Thermal Insulation Mateirals. Available online: https://analyzing-testing.netzsch.com/en/applications/thermal-insulation (accessed on 10 October 2024).
- Yang, Y.; Mou, X.; Zhu, Z.; Bao, Z. Measurement and Analysis of Effective Thermal Conductivity of LaNi5 and Its Hydride under Different Gas Atmospheres. Int J Hydrogen Energy 2021, 46, 19467–19477. [CrossRef]
- Shim, J.H.; Park, M.; Lee, Y.H.; Kim, S.; Im, Y.H.; Suh, J.Y.; Cho, Y.W. Effective Thermal Conductivity of MgH2 Compacts Containing Expanded Natural Graphite under a Hydrogen Atmosphere. Int J Hydrogen Energy 2014, 39, 349–355. [CrossRef]
- Kapischke, J.; Hapke, J. Measurement of the Effective Thermal Conductivity of a Metal Hydride Bed with Chemical Reaction. Exp Therm Fluid Sci 1994, 9, 337–344. [CrossRef]
- Wang, C.-Y.; Tien, H.-C.; Chyou, S.-D.; Huang, N.-N.; Wang, S.-H. Hydrogen Absorption/Desorption in a Metal Hydride Reactor Accounting for Varied Effective Thermal Conductivity. J Mar Sci Technol 2011, 19, 168–175. [CrossRef]
- Mou, X.; Zhou, W.; Bao, Z.; Huang, W. Measurement and Theoretical Analysis of Effective Thermal Conductivity of Lanthanum Pentanickel Powder Beds for Hydrogen Storage in Different Particle Sizes and Bed Porosities. J Clean Prod 2024, 468, 143098. [CrossRef]
- Madaria, Y.; Anil Kumar, E. Measurement and Augmentation of Effective Thermal Conductivity of La0.8Ce0.2Ni5 Hydride Bed. J Alloys Compd 2017, 691, 442–451. [CrossRef]
- C-Therm Technologies Ltd. Trident Thermal Conductivity Instrument. Available online: https://ctherm.com/thermal-conductivity-instruments/trident/ (accessed on 11 October 2024).
- Salim, S.G.R. Thermal Conductivity Measurements Using the Transient Hot-Wire Method: A Review. Meas Sci Technol 2022, 33, 125022. [CrossRef]
- Sundqvist, B.; Andersson, O. Thermal Conductivity and Phase Diagrams of Some Potential Hydrogen Storage Materials Under Pressure. Int J Thermophys 2009, 30, 1118–1129. [CrossRef]
- Dedrick, D.E.; Kanouff, M.P.; Replogle, B.C.; Gross, K.J. Thermal Properties Characterization of Sodium Alanates. J Alloys Compd 2005, 389, 299–305. [CrossRef]
- Zhang, X.L.; Liu, Y.F.; Zhang, X.; Hu, J.J.; Gao, M.X.; Pan, H.G. Empowering Hydrogen Storage Performance of MgH2 by Nanoengineering and Nanocatalysis. Mater Today Nano 2020, 9, 100064. [CrossRef]
- Zheng, Q.; Kaur, S.; Dames, C.; Prasher, R.S. Analysis and Improvement of the Hot Disk Transient Plane Source Method for Low Thermal Conductivity Materials. Int J Heat Mass Transf 2020, 151, 119331. [CrossRef]
- Julian Jepsen; Chiara Milanese; Julián Puszkiel; Alessandro Girella; Benedetto Schiavo; Gustavo A. Lozano; Giovanni Capurso; José M. Bellosta von Colbe; Amedeo Marini; Stephan Kabelac; et al. Fundamental Material Properties of the 2LiBH4-MgH2 Reactive Hydride Composite for Hydrogen Storage: (II) Kinetic Properties. Energies (Basel) 2018, 11. [CrossRef]
- Albert, R.; Wagner, C.; Urbanczyk, R.; Felderhoff, M. Cycle Stability of the Effective Thermal Conductivity of Nickel-Activated Magnesium Hydride Powder under Operating Conditions. Energy Technology 2020, 8. [CrossRef]
- Jensen, E.H.; Lombardo, L.; Girella, A.; Guzik, M.N.; Züttel, A.; Milanese, C.; Whitfield, P.; Noréus, D.; Sartori, S. The Effect of Y Content on Structural and Sorption Properties of A2B7-Type Phase in the La–Y–Ni–Al–Mn System. Molecules 2023, 28. [CrossRef]
- Pentimalli, M.; Imperi, E.; Zaccagnini, A.; Padella, F. Nanostructured Metal Hydride – Polymer Composite as Fixed Bed for Sorption Technologies. Advantages of an Innovative Combined Approach by High-Energy Ball Milling and Extrusion Techniques. Renew Energy 2017, 110, 69–78. [CrossRef]
- Atalmis, G.; Demiralp, M.; Yelegen, N.; Kaplan, Y. The Effect of Copper Coated Metal Hydride at Different Ratios on the Reaction Kinetics. Int J Hydrogen Energy 2023, 48, 23067–23076. [CrossRef]
- Atalmis, G.; Toros, S.; Timurkutluk, B.; Kaplan, Y. Effect of Expanded Natural Graphite Addition and Copper Coating on Reaction Kinetics and Hydrogen Storage Characteristics of Metal Hydride Reactors. Int J Hydrogen Energy 2024, 53, 647–656. [CrossRef]
- Bock, R.; Hamre, B.; Onsrud, M.A.; Karoliussen, H.; Seland, F.; Burheim, O.S. The Influence of Argon, Air and Hydrogen Gas on Thermal Conductivity of Gas Diffusion Layers and Temperature Gradients in PEMFCS. ECS Trans 2019, 92, 223–245. [CrossRef]
- Albers, A.P.F.; Restivo, T.A.G.; Pagano, L.; Baldo, J.B. Effect of Testing Conditions on the Laser Flash Thermal Diffusivity Measurements of Ceramics. Thermochim Acta 2001, 370, 111–118. [CrossRef]
- Inseis. Die Flash Methode (Temperaturleitfähigkeit). Available online: https://www.linseis.com/methoden/flash-methode/ (accessed on 11 October 2024).
- Lauerer, A.; Lunev, A. Experimental Evidence of Gas-Mediated Heat Transfer in Porous Solids Measured by the Flash Method. International Journal of Thermal Sciences 2023, 184, 107948. [CrossRef]
- Pohlmann, C.; Röntzsch, L.; Heubner, F.; Weißgärber, T.; Kieback, B. Solid-State Hydrogen Storage in Hydralloy-Graphite Composites. J Power Sources 2013, 231, 97–105. [CrossRef]
- Pohlmann, C.; Hutsch, T.; Röntzsch, L.; Weißgärber, T.; Kieback, B. Novel Approach for Thermal Diffusivity Measurements in Inert Atmosphere Using the Flash Method. J Therm Anal Calorim 2013, 114, 629–634. [CrossRef]
- Popilevsky, L.; Skripnyuk, V.M.; Amouyal, Y.; Rabkin, E. Tuning the Thermal Conductivity of Hydrogenated Porous Magnesium Hydride Composites with the Aid of Carbonaceous Additives. Int J Hydrogen Energy 2017, 42, 22395–22405. [CrossRef]
- Lunev, A.; Heymer, R. Decreasing the Uncertainty of Classical Laser Flash Analysis Using Numerical Algorithms Robust to Noise and Systematic Errors. Review of Scientific Instruments 2020, 91. [CrossRef]
- Bai, X.S.; Rong, L.; Yang, W.W.; Yang, F.S. Effective Thermal Conductivity of Metal Hydride Particle Bed: Theoretical Model and Experimental Validation. Energy 2023, 271. [CrossRef]
- Yagi, S.; Kunii, D. Studies on Effective Thermal Conductivities in Packed Beds. A.I.Ch.E. Journal 1957, 3, 373–381. [CrossRef]
- Nozad, I.; Carbonell, R.G.; Whitaker, S. Heat Conduction in Multiphase Systems-I. Theory and Experiment for Two-Phase Systems. Chem Eng Sci 1985, 40, 843–855. [CrossRef]
- Nozad, I.; Carbonell, R.G.; Whitaker, S. Heat Conduction in Multiphase Systems-II. Experimental Method and Results for Three-Phase Systems. Chem Eng Sci 1985, 40, 857–863. [CrossRef]
- Kallweit, J.; Hahne, E. Effective Thermal Conductivity of Metal Hydride Powders: Measurement and Theoretical Modelling. In Proceedings of the International Heat Transfer Conference Digital Library; 1994; pp. 373–378.
- Bauer, R.; Schlünder, E.U. Effective Radial Thermal Conductivity of Packings in Gas Flow. Part II: Thermal Conductivity of the Racking Fraction without Gas Flow. Int. Chem. Eng. 1978, 18, 189–204.
- Kallweit, J. Effektive Wärmeleitfähigkeit von Metallhydrid-Materialien Zur Speicherung von Wasserstoff, Universität Stuttgart : Stuttgart , 1994.
- Masamune, S.; Smith, J. Thermal Conductivity of Beds of Spherical Particles. Industrial & Engineering Chemistry Fundamentals 1963, 2, 136–143.
- Peisl, H. Wasserstoff in Metallen. Physik in unserer Zeit 1978, 9, 37–45.
- Hahne, E.; Kallweit, J. Thermal Conductivity of Metal Hydride Materials for Storage of Hydrogen: Experimental Investigation. Int J Hydrogen Energy 1998, 23, 107–114. [CrossRef]
- Matsushita, M.; Monde, M.; Mitsutake, Y. Experimental Formula for Estimating Porosity in a Metal Hydride Packed Bed. Int J Hydrogen Energy 2013, 38, 7056–7064. [CrossRef]
- Abdin, Z.; Webb, C.J.; Gray, E.M.A. One-Dimensional Metal-Hydride Tank Model and Simulation in Matlab–Simulink. Int J Hydrogen Energy 2018, 43, 5048–5067. [CrossRef]
- Gusarov, A. V.; Kovalev, E.P. Model of Thermal Conductivity in Powder Beds. Phys Rev B Condens Matter Mater Phys 2009, 80. [CrossRef]
- Van de Lagemaat, J.; Benkstein, K.D.; Frank, A.J. Relation between Particle Coordination Number and Porosity in Nanoparticle Films: Implications to Dye-Sensitized Solar Cells. Journal of Physical Chemistry B 2001, 105, 12433–12436. [CrossRef]
- Bahrami, M.; Yovanovich, M.M.; Culham, J.R. Effective Thermal Conductivity of Rough Spherical Packed Beds. Int J Heat Mass Transf 2006, 49, 3691–3701. [CrossRef]
- Song, S.; Yovanovich, M. Explicit Relative Contact Pressure Expression - Dependence upon Surface Roughness Parameters and Vickers Microhardness Coefficients. In Proceedings of the AlAA 25th Aerospace Sciences Meeting; American Institute of Aeronautics and Astronautics (AIAA), March 24 1987.
- Valentin L. Popov Contact Mechanics and Friction - Physical Principles and Applications; Second.; Springer, 2017;
- Ueoka, K.; Miyauchi, S.; Asakuma, Y.; Hirosawa, T.; Morozumi, Y.; Aoki, H.; Miura, T. An Application of a Homogenization Method to the Estimation of Effective Thermal Conductivity of a Hydrogen Storage Alloy Bed Considering Variation of Contact Conditions between Alloy Particles. Int J Hydrogen Energy 2007, 32, 4225–4232. [CrossRef]
- Pons, M.; Dantzer, P. Determination of Thermal Conductivity and Wall Heat Transfer Coefficient of Hydrogen Storage Materials. Int J Hydrogen Energy 1994, 19, 611–616. [CrossRef]
- Pons, M.; Dantzer, P.; Guilleminot, J.J. A Measurement Technique and a New Model for the Wall Heat Transfer Coefficient of a Packed Bed of (Reactive) Powder without Gas Flow. 1993, 36, 2635–2646. [CrossRef]
- Asakuma, Y.; Miyauchi, S.; Yamamoto, T.; Aoki, H.; Miura, T. Homogenization Method for Effective Thermal Conductivity of Metal Hydride Bed. Int J Hydrogen Energy 2004, 29, 209–216. [CrossRef]
- Abyzov, A.M.; Goryunov, A. V.; Shakhov, F.M. Effective Thermal Conductivity of Disperse Materials. I. Compliance of Common Models with Experimental Data. Int J Heat Mass Transf 2013, 67, 752–767. [CrossRef]
- Dirac, P.A.M. The Quantum Theory of the Emission and Absorption of Radiation. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 1927, 114, 243–265. [CrossRef]
- Schrödinger, E. Quantisierung Als Eigenwertproblem. Ann Phys 1926, 386, 109–139. [CrossRef]
- Hund, F. Allgemeine Quantenmechanik Des Atom- Und Molekelbaues. In Quantentheorie.; Bethe, H., Hund, F., Mott, N.F., Pauli, W., Rubinowicz, A., Wentzel, G., Smekal, A., Eds.; Springer Berlin Heidelberg: Berlin, 1933; pp. 561–694 ISBN 978-3642525650.
- Mayer, I. Perturbational Methods. In Simple Theorems, Proofs, and Derivations in Quantum Chemistry.; Springer US: Boston, 2003; pp. 69–120 ISBN 0306474093.
- Löwdin, P.-O. A Note on the Quantum-Mechanical Perturbation Theory. J Chem Phys 1951, 19, 1396–1401. [CrossRef]
- Born, M. Zur Quantenmechanik Der Stoßvorgänge. Zeitschrift für Physik 1926, 37, 863–867. [CrossRef]
- Born, M.; Oppenheimer, R. Zur Quantentheorie Der Molekeln. Ann Phys 1927, 389, 457–484. [CrossRef]
- Phillips, P. Advanced Solid State Physics.; 2nd ed.; Cambridge University Press: Cambridge, 2012; ISBN 978-0-521-19490-7.
- Sutcliffe, B.T. The Born-Oppenheimer Approximation. In Methods in Computational Molecular Physics; Springer US: Boston, 1992; pp. 19–46.
- Baer, M. Born-Oppenheimer Approach: Diabatization and Topological Matrix. In Beyond Born–Oppenheimer; Wiley, 2006; pp. 26–57 ISBN 9780471778912.
- Baer, M. Degeneracy Points and Born-Oppenheimer Coupling Terms as Poles. In Beyond Born–Oppenheimer; Wiley, 2006; pp. 105–138 ISBN 9780471778912.
- Baer, M. Extended Born-Oppenheimer Approximations. In Beyond Born–Oppenheimer; Wiley, 2006; pp. 197–223 ISBN 9780471778912.
- Born, M. Das Adiabatenprinzip in Der Quantenmechanik. Zeitschrift für Physik 1927, 40, 167–192. [CrossRef]
- Born, M.; Fock, V. Beweis Des Adiabatensatzes. Zeitschrift für Physik 1928, 51, 165–180. [CrossRef]
- Ehrenfest, P. Adiabatische Invarianten Und Quantentheorie. Ann Phys 1916, 356, 327–352. [CrossRef]
- Ho-Kim, Q.; Pham, X.-Y. Elementary Particles and Their Interactions; Springer Berlin Heidelberg: Berlin Heidelberg, 2010; ISBN 978-3-642-08349-5.
- Kleinert, H. Gauge Fields in Condensed Matter; WORLD SCIENTIFIC, 1989; ISBN 978-9971-5-0210-2.
- Fradkin, E. Field Theories of Condensed Matter Physics; Cambridge University Press, 2013; ISBN 9780521764445.
- Rammer, J. Quantum Field Theory of Non-Equilibrium States; Cambridge University Press, 2007; ISBN 9780521874991.
- Haken, H. Quantum Field Theory of Solids, an Introduction; North-Holland, 1976;
- Lannoo, M.; Bescond, M. Non-Equilibrium Green’s Function Formalism. In Simulation of Transport in Nanodevices.; Triozon, F., Dollfus, P., Eds.; Wiley-ISTE, 2016; pp. 223–259.
- Eucken, A. Allgemeine Gesetzmäßigkeiten Für Das Wärmeleitvermögen Verschiedener Stoffarten Und Aggregatzustände. Forschung auf dem Gebiete des Ingenieurwesens 1940, 11, 6–20. [CrossRef]
- Planck, M.; Debye, P.; Nernst, W.; Smoluchowski, M.; Sommerfeld, A.; Lorentz, H.A. Vorträge Über Die Kinetische Theorie Der Materie Und Der Elektrizität : Gehalten in Göttingen Auf Einladung Der Kommission Der Wolfskehlstiftung; Teubner, B.G.: Leipzig and Berlin, 1914;
- Born, M.; von Kármán, T. Uber Schwingungen Im Raumgittern. Physikalishe Zeitschrift 1912, 13, 297–309.
- Born, M. Atomtheorie Des Festen Zustandes (Dynamik Der Kristallgitter). In Encyklopädie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen; Vieweg+Teubner Verlag: Wiesbaden, 1926; pp. 527–781.
- Schrödinger, E. Zur Dynamik Elastisch Gekoppelter Punktsysteme. Ann Phys 1914, 349, 916–934. [CrossRef]
- Ornstein, L.; Zernike, F. Bemerkung Zur Arbeit von Herrn KC Kar: Die Molekularzerstreuung Des Lichtes Beim Kritischen Zustande. Physikalische Zeitschrift 1926, 27, 761–763.
- Ross, R.G.; Andersson, P.; Sundqvist, B.; Backstrom, G. Thermal Conductivity of Solids and Liquids under Pressure. Reports on Progress in Physics 1984, 47, 1347–1402. [CrossRef]
- Debye, P. Zur Theorie Der Spezifischen Wärmen. Ann Phys 1912, 344, 789–839. [CrossRef]
- Ziman, J.M. Electrons and Phonons: The Theory of Transport Phenomena in Solids; Oxford University Press, 2001; ISBN 9780198507796.
- Klemens, P.G. Theory of the Thermal Conductivity of Amorphous Solids. In Thermal Conductivity 18; Springer US: Boston, MA, 1985; pp. 307–314.
- Ashcroft, N.W.; Mermin, N.D.; Wi, D. Solid State Physics; Cengage Learning, 2016;
- Peierls, R. Zur Kinetischen Theorie Der Wärmeleitung in Kristallen. Ann Phys 1929, 395, 1055–1101. [CrossRef]
- Callaway, J. Model for Lattice Thermal Conductivity at Low Temperatures. Physical Review 1959, 113, 1046–1051. [CrossRef]
- Tritt, T.M. Thermal Conductivity; Tritt, T.M., Ed.; Springer US: New York, 2004; ISBN 978-0-306-48327-1.
- Frankl, D.; Campisi, G.J. Boundary Scattering of Phonons in Germanium and Silicon; 1972;
- Holland, M.G. Analysis of Lattice Thermal Conductivity. Physical Review 1963, 132, 2461–2471. [CrossRef]
- Klemens, P.G. The Scattering of Low-Frequency Lattice Waves by Static Imperfections. Proceedings of the Physical Society. Section A 1955, 68, 1113–1128. [CrossRef]
- Nabarro, F.R.N.; Peierls, R.E. The Interaction of Screw Dislocations and Sound Waves. Proc R Soc Lond A Math Phys Sci 1951, 209, 278–290. [CrossRef]
- Pohl, R.O. Thermal Conductivity and Phonon Resonance Scattering. Phys Rev Lett 1962, 8, 481–483. [CrossRef]
- Blatt, F.J. Matthiessen’s Rule.; McGraw Hill, 2020;
- Yang, J.; Morelli, D.T.; Meisner, G.P.; Chen, W.; Dyck, J.S.; Uher, C. Influence of Electron-Phonon Interaction on the Lattice Thermal Conductivity of Co1-XNixSb3. Phys Rev B 2002, 65, 094115. [CrossRef]
- Kittel, C.; Fong, C.Y. Quantum Theory of Solids.; Second revised ed.; John Wiley & Sons: NewYork, 1987;
- Newell, D.B.; Tiesinga, E. The International System of Units (SI); Gaithersburg, MD, 2019;
- Leibfried, G.; Schlömann, E. Wärmeleitung in Elektrisch Isolierenden Kristallen; Vandenhoeck & Ruprecht, 1954;
- Slack, G.A. The Thermal Conductivity of Nonmetallic Crystals. In; 1979; pp. 1–71.
- Inyushkin, A. V. Thermal Conductivity of Group IV Elemental Semiconductors. J Appl Phys 2023, 134. [CrossRef]
- Carruthers, J.A.; Geballe, T.H.; Rosenberg, H.M.; Ziman, J.M. The Thermal Conductivity of Germanium and Silicon between 2 and 300° K. Proc R Soc Lond A Math Phys Sci 1957, 238, 502–514. [CrossRef]
- Slack, G.A. Thermal Conductivity of Pure and Impure Silicon, Silicon Carbide, and Diamond. J Appl Phys 1964, 35, 3460–3466. [CrossRef]
- Glassbrenner, C.J.; Slack, G.A. Thermal Conductivity of Silicon and Germanium from 3°K to the Melting Point. Physical Review 1964, 134, A1058–A1069. [CrossRef]
- Ravichandran, N.K.; Broido, D. Phonon-Phonon Interactions in Strongly Bonded Solids: Selection Rules and Higher-Order Processes. Phys Rev X 2020, 10, 021063. [CrossRef]
- Klemens, P.G.; Williams, R.K. Thermal Conductivity of Metals and Alloys. International Metals Reviews 1986, 31, 197–215. [CrossRef]
- Pundt, A.; Wagner, S. Hydrogen Interactions with Defects in Materials. Chemie Ingenieur Technik 2024, 96, 182–191. [CrossRef]
- Yoshida, A.; Naka, Y.; Ohkita, T. Experimental Study on Thermophysical and Kinetic Properties of the LaNi5-H2 System. Transactions of the Japan Society of Mechanical Engineers, Part B 1990, 56, 536–540. [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; Revised 2nd edition.; John Wiley & Sons Inc, 2007; ISBN 978-0470115398.
- Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 10.0, National Institute of Standards and Technology 2018.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).