Research on the Production of Hydrogen Fluoride from Silicon Tetrafluoride Using 2.45 GHz Microwave Plasma

1. Introduction

The traditional process to prepare anhydrous hydrogen fluoride (AHF) is to react fluorite ore with sulfuric acid, and then to purify the gaseous hydrogen fluoride by multiple distillation and recrystallization [1]. This method is not only time-consuming and energy-intensive but also emits harmful gases, necessitating rigorous process management. Moreover, the raw material fluorite ore is a kind of scare and nonrenewable mineral resources [2]. Hence, this traditional method of producing AHF from fluorite ore bears the problems of unsustainability and environmental concerns [3]. In the phosphate fertilizer industry, fluorosilicic acid is produced as a byproduct during the preparation of phosphoric acid from phosphorus ore [4]. This acid, abundant in fluorine and silicon resources, is often regarded as industrial waste from the phosphate fertilizer industry [5]. However, it can also serve as a crucial raw material for the production of AHF [6]. The methods of producing AHF from fluorosilicic acid can be divided into direct methods and indirect methods. The direct methods include the direct pyrolysis of fluorosilicic acid and the decomposition of fluorosilicic acid by concentrated sulfuric acid [7,8]. These methods face the challenges of high energy consumption, limited AHF purity and emissions of the toxic gas silicon tetrafluoride. The indirect methods involve utilizing fluorosilicic acid to react with a metal or metal oxide to yield fluorosilicate, followed by the application of the direct method to produce AHF from the resultant fluorosilicate [9-11]. The indirect methods can improve the purity of AHF, but the handling process is complicated and they still bear the drawbacks of the direct methods.

During the process of preparing AHF from fluorosilicic acid, the toxic gaseous silicon tetrafluoride (SiF₄) is generated as a byproduct. Noteworthily, this gas contains valuable fluorine and silicon resources that possess potential for recycling. This realization motivates us to explore the direct conversion of SiF₄ into HF. As the fourth state of matter, the plasma is widely used in gas conversion applications, such as nitrogen fixation [12-14], CO₂ conversion [15-17] and methane reforming [18-20]. The electron impact reactions within the plasma have the ability to transform gas molecules into atoms, ions, and radicals under gentle conditions (without the need for high temperatures or high pressures), thereby achieving the desired gas conversion. Due to this advantage, many scholars investigate the plasma treatment on SiF₄. For example, Vodopyanov A. V. and colleagues studied for the first time the decomposition of SiF₄ in electron cyclotron resonance (ECR) microwave plasma for the purpose of depositing silicon [21]. They utilized the mass-spectrometry method to measure the composition of the decomposition products of SiF₄ as a function of various process parameters. Notably, they successfully obtained silicon films with excellent adhesion on both silicon and molybdenum wafers. Sennikov P. G. et al. used a radiofrequency (RF) discharge to convert SiF₄ [22]. They achieved silicon deposition in an H₂/SiF₄ plasma, with a maximum silicon yield of 60% operated at a pressure of 0.2 Torr. Dornstetter J-C et al. also used RF plasma to grow silicon films from the dissociation of SiF₄/H₂/Ar gas mixtures [23]. By control the gas molar ratio, gas flow rate and RF power, the amorphous silicon could transfer into microcrystalline silicon. Gaiaschi S. et al. conducted research on the deposition of hydrogenated microcrystalline silicon–carbon alloy within a SiF₄/CH₄ plasma that was generated by RF power [24]. Their findings revealed that the RF power density, CH₄ flow rate and the amount of SiF₄ significantly influenced the microstructure of the resultant film. Kornev R. A. et al. developed a highly efficient inductively coupled plasma (ICP) method for obtaining silicon from SiF₄ in the presence of argon [25]. This method achieved a silicon production rate of 0.9 g/h with an energy cost of 0.56 kWh/g.

All the aforementioned investigations have exhibited that SiF₄ can be dissociated within the plasma, ultimately yielding the valuable product silicon under appropriate process parameters. However, most of these investigations primarily focus on obtaining the solid silicon from SiF₄ using RF plasma, with a lack of reports detailing the conversion of SiF₄ into HF. Therefore, this paper presents an experimental investigation on producing HF from SiF₄ using microwave plasma. On the one hand, microwave plasma has the advantages of being electrodeless, possessing high electron density and electron energy, and having long lifespan compared to RF plasma. On the other hand, the HF product is valuable for industrial applications due to its expanding utilities across diverse sectors such as fluororubbers [26], pharmaceuticals [27], aerospace [28], semiconductors [29], fuels [30], and fluorocarbons [31].

2. Materials and Methods

2.1. Experimental Setup

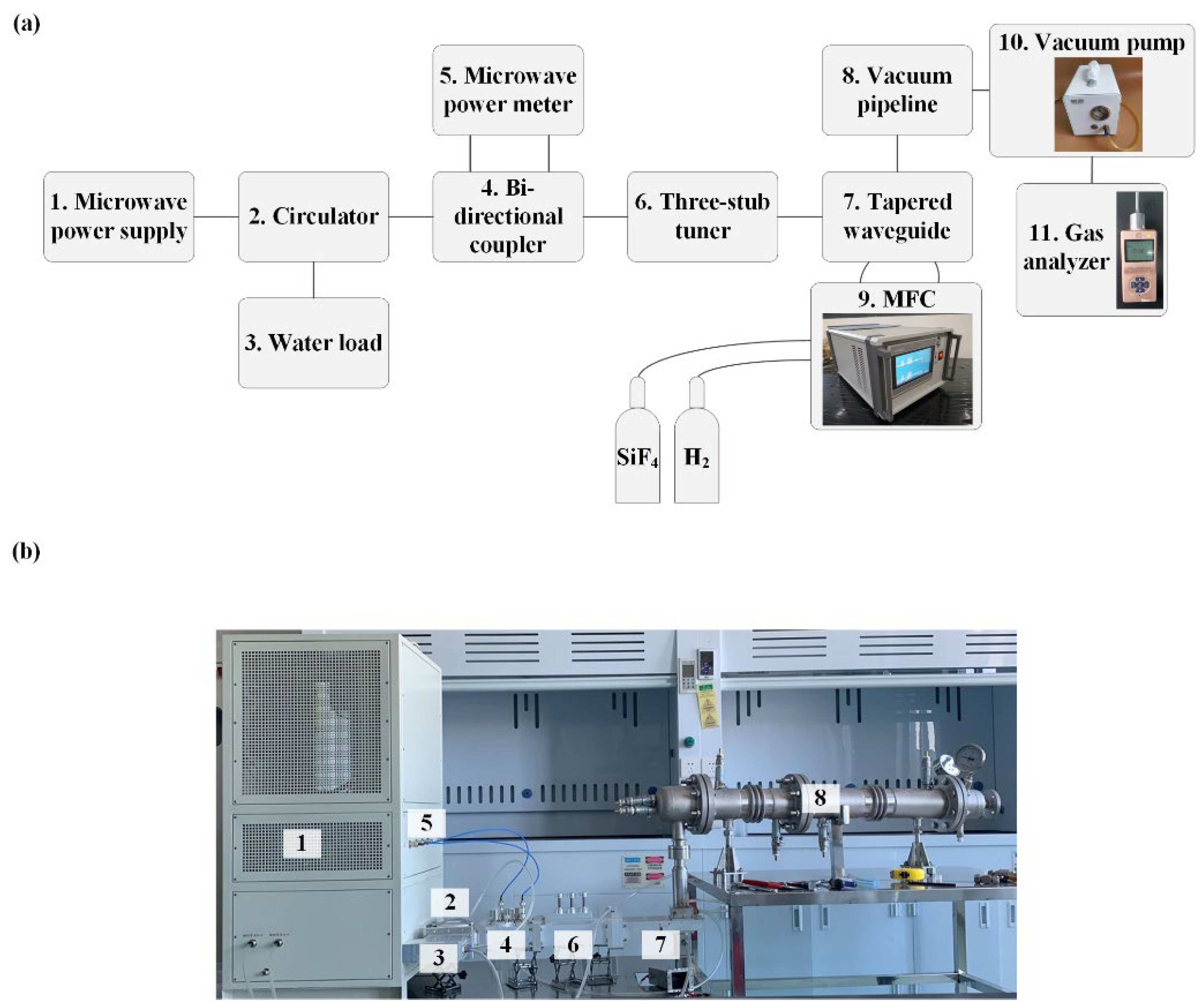
A 2.45 GHz microwave plasma system based on the WR-430 waveguide was built for the HF production from SiF₄ in this paper. The experimental system comprised four components: microwave transmission, gas intake, vacuum pumping, and gas composition measurement. Figure 1 shows the schematic and photograph of the system. The microwave was generated by a microwave power supply based on a magnetron (2M265, MUEGGE, Reichelsheim, Germany) cooled by water. The center frequency and maximum output power of the magnetron were 2.45 GHz and 3 kW, respectively. The circulator (MPWG22CIA01, Mapingtec, Chengdu, China) acted as the magnetron protection device, ensuring that the reflected power was absorbed by the water load (MPWG22WLA01, Mapingtec, Chengdu, China). The bi-directional coupler (MPWG22CPA01, Mapingtec, Chengdu, China) coupled the incident and reflected microwave power which was then measured by the microwave power meter (KC9532, Measall Technology, Chengdu, China). The three-stub tuner (MPWG22THTA01P10KW, Mapingtec, Chengdu, China) was used to adjust the impedance match between the plasma and the WR-430 waveguide system. The electric field was concentrated within the tapered waveguide where the plasma was generated. The specific dimensions of this tapered waveguide have been detailed in our previous research [32].

The working gas used in this paper consisted of SiF₄ and H₂, both of which were stored in the gas cylinder and introduced into the discharge area of the tapered waveguide in a swirling motion. The gas flow rate was controlled by the mass flow controller (MFC, KT-C4Z, Ketanyiqi, Zhengzhou, China) with a range from 0 to 5 standard cubic centimeter per minute (sccm). Since the entire experiment needed to be conducted under a low pressure at about 0.7 atmospheres, a vacuum pump (FUJ-V3, Fujiwara, Taizhou, China) capable of achieving a vacuum up to 0.3 atmospheres was used and connected to the vacuum pipeline. The output gas was measured by the gas analyzer capable of detecting HF concentrations within a range of 0 to 10,000 parts per million (ppm). This device necessitated that the gas being measured be maintained at room temperature; hence, a vacuum pipeline equipped with water cooling was utilized to chill the output gas.

2.2. Electron Density Measurement

The electron density can influence the electron-neutral particle impact reaction rate in the plasma, thereby affecting the gas conversion rate. This parameter depends on both the gas flow rate and gas composition. Therefore, this paper measured the electron density of the microwave plasma under different gas flow rates and gas compositions to analyze its effect on the production of HF. The measurement method in [32] was adopted to determine the electron density of the microwave plasma in this paper. The microwave power reflection ratio in the experiment was obtained initially, which was defined by the following formula:

$$\Gamma ={\displaystyle \frac{P_{re}}{P_{in}}}\times 100\%=10^{-\left|S_{11}\right|/10}$$

(1)

where P_re and P_in represent the reflected and incident microwave power, respectively; |S₁₁| refers to the S parameter calculated by the simulation of microwave-plasma interaction. The governing equation of this simulation is written as the Helmholtz equation,

$$\nabla \times ({\displaystyle \frac{1}{{\mu }_r}}\nabla \times E)-{\displaystyle \frac{{\omega }^2}{c_0}}{\epsilon }_{p}E=0$$

(2)

where μ_r indicates the permeability; E denotes the electric field vector; ω is the angular frequency of microwave; c₀ is the light speed; ε_p refers to the relative complex permittivity of the plasma which can be derived as the Appleton formula [33],

$${\epsilon }_p=1-{\displaystyle \frac{{{\omega }_p}^2}{{{\omega }_{co}}^2}}-j{\displaystyle \frac{{{\omega }_p}^2}{{{\omega }_{co}}^2}}{\displaystyle \frac{{\upsilon }_m}{\omega }}$$

(3)

where ω_p is the plasma angular frequency with ω_p = [n_e∙e²/(ε₀∙m_e)]^1/2, here n_e denotes the electron density and m_e refers to the electron mass; υ_m refers to the electron-neutral particle collision frequency; ω_co represents the combination frequency which can be derived as follows:

$${\omega }_{co}=\sqrt{{\omega }^2+{{\upsilon }_m}^2}$$

(4)

From the above equations, the electron density n_e determines the relative complex permittivity of the plasma. Here, a Gaussian model is assumed to describe the electron density distribution which is written as

$$\begin{array}{l}{n}_e=N_e\times \exp [-a_r\times {({\displaystyle \frac{r-r_0}{R_p}})}^2]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \exp [-a(z)\times {({\displaystyle \frac{z-h_0}{L_p}})}^2]\end{array}$$

(5)

where N_e indicates the maximum electron density number; a_r and a(z) are radial and axial fitting parameters, respectively, for adjusting the spatial electron density profile; r₀ and h₀ are the radial and axial coordinates of the plasma core in cylindrical coordinates, respectively; R_p is the radius of plasma and L_p is the plasma length; The fitting parameter a(z) is a function of z-axis written as

$$a(z)=\{\begin{array}{c}{a}_{z1},\\ {\displaystyle \frac{a_{z2}-a_{z1}}{2\Delta h}}\cdot z+{\displaystyle \frac{a_{z2}+a_{z1}}{2}}-{\displaystyle \frac{a_{z2}-a_{z1}}{2\Delta h}}\cdot h,\\ a_{z2},\end{array}\begin{array}{c}0\le z<h-\Delta h\\ h-\Delta h\le z<h+\Delta h\\ h+\Delta h\le z<L\end{array}$$

(6)

where a_z1 and a_z2 are used to adjust the lower and upper axial electron density profile, respectively; ∆h is the small step size in the z-axis direction with ∆h = 0.01 mm.

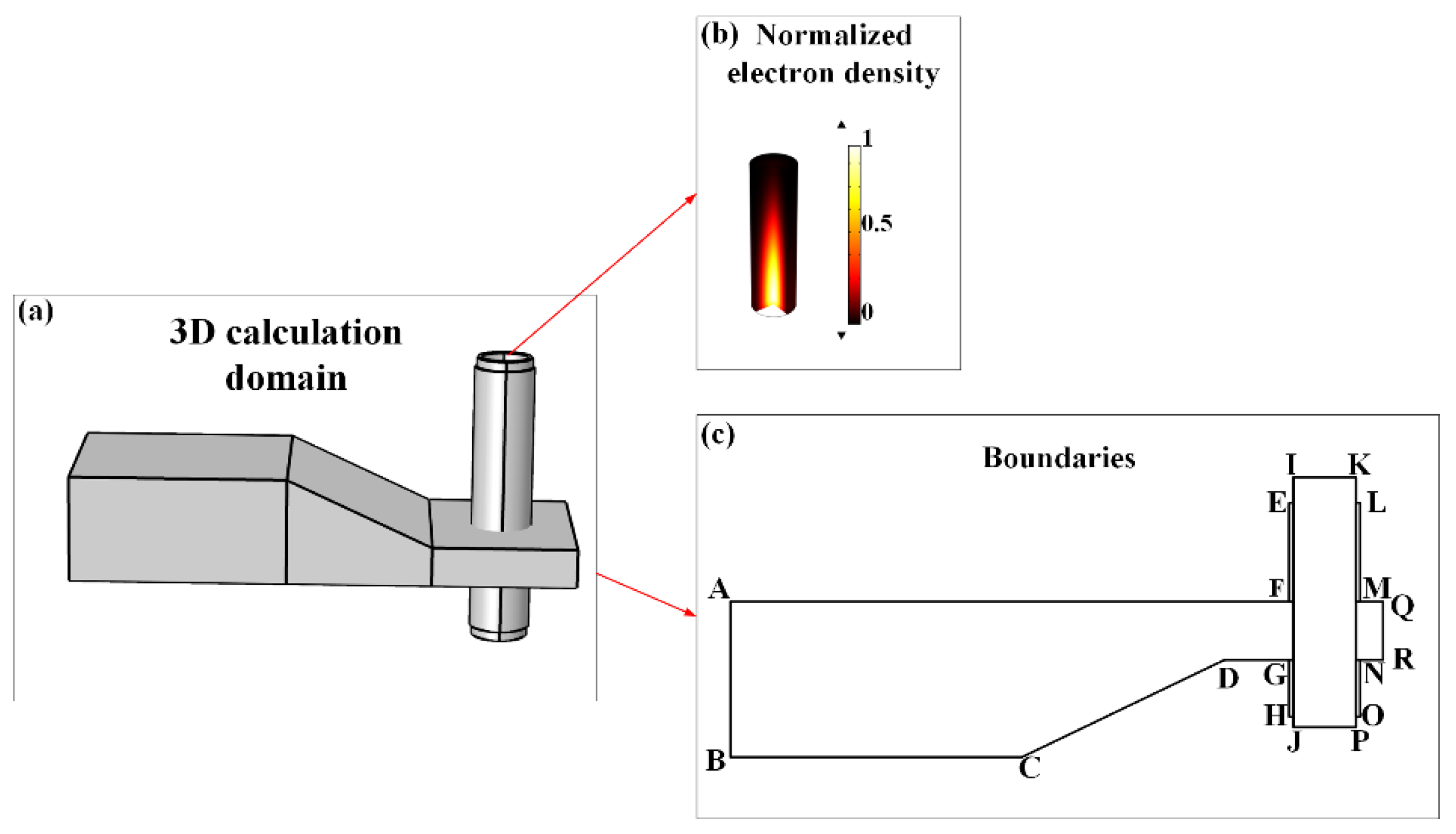
Figure 2 shows the calculation domain of the microwave-plasma interaction. In Figure 2(a), microwaves were incident from the left port of the waveguide (labeling as boundary AB in Figure 2(c)) and transmitted through the tapered waveguide into the quartz tube for the purpose of generating discharges. Two metal sleeves EFLM and GHNO were surrounding the quartz tube to prevent the microwave power leakage. Figure 2(b) shows a normalized electron density distribution derived from the above Gaussian model. The boundary conditions for both the waveguide wall and metal sleeve wall were designated as perfect electric conductors (PECs), as specified by

$$n\times E=0$$

(7)

where n is the unit normal vector perpendicular to the boundary. The top and bottom boundaries of the quartz tube IK and JP were assigned as the scattering boundary conditions (SBCs), as expressed in

$$n\times (\nabla \times E)-j{k}_{0}n\times (E\times n)=0$$

(8)

where k₀ is the wave number in vacuum. The materials and boundary conditions for the pertinent domain are listed in Table 1.

The commercial software COMSOL Multiphysics was utilized to perform the microwave-plasma interaction simulation. Free tetrahedral meshes were generated for the calculation domain, resulting in a total of 683,846 meshes and 10,820,613 unknowns in the simulation. The computing platform was a workstation with the CPU of Intel (R) Core (TM) CPU i5-12400 @ 2.5 GHz and RAM of 128 GHz based on the 64-bit Windows 10 operating system.

3. Results and Discussion

During the experimental process, the pressure in the discharge area was initially fixed at approximately 0.68 atmospheres using a vacuum pump, prior to plasma ignition. Subsequently, the H₂ was introduced into the quartz tube, and the microwave power supply was activated to excite the plasma. Once the plasma was ignited, the SiF₄ was introduced into the quartz tube for conversion. The incident and reflected power values were recorded to calculate the power reflection ratio, which was then used to obtain the plasma electron density based on the method described in Section 2.2. Therewith, the output HF was measured at the outlet of the vacuum pump. In this work, the microwave power range varied from 400 W to 1100 W, and the flow rate of SiF₄ ranged from 0.2 sccm to 2 sccm. The H₂ flow rate varied at four levels: 1 sccm, 1.5 sccm, 2.0 sccm, and 2.5 sccm.

3.1. Power Reflection Ratio and Electron Density

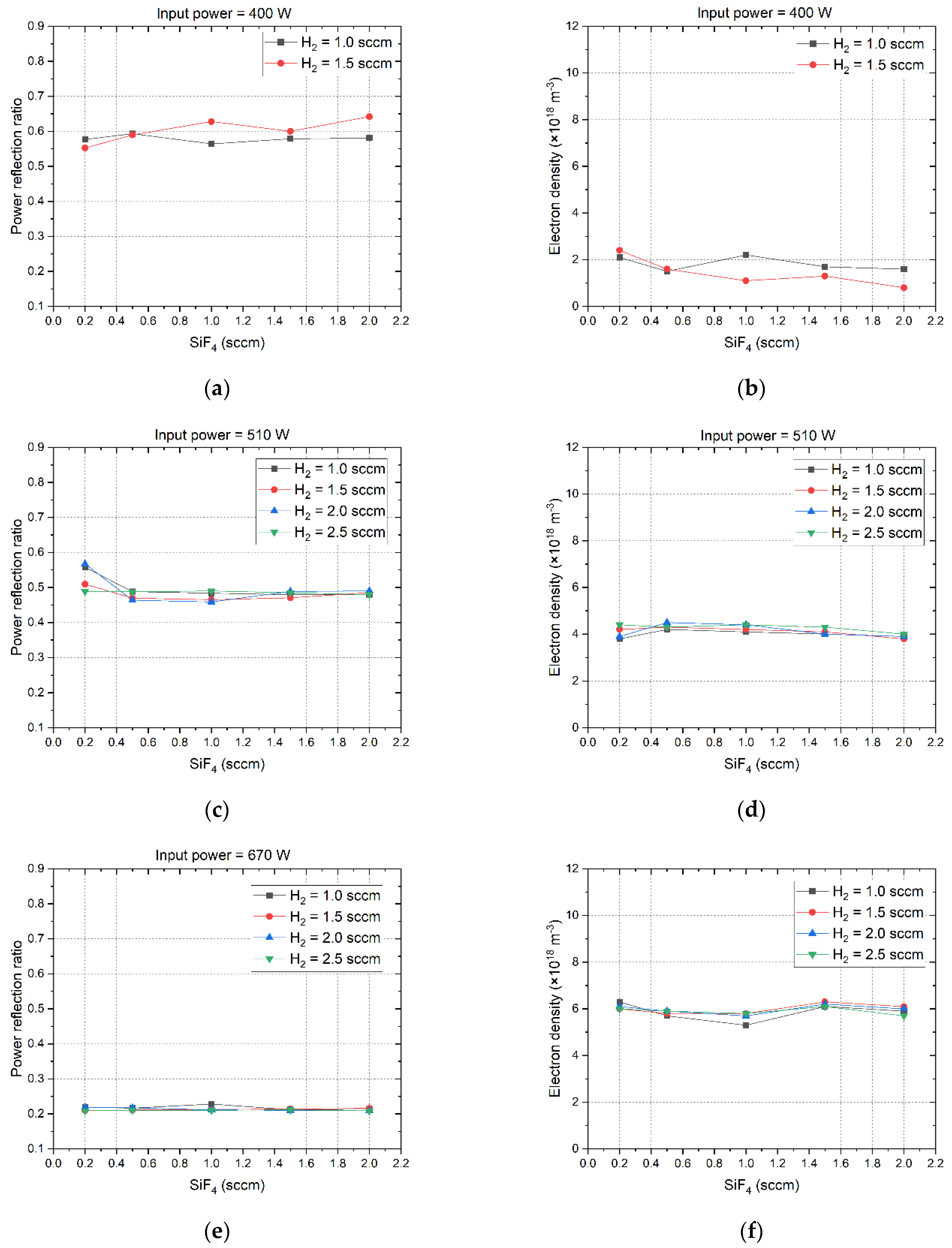
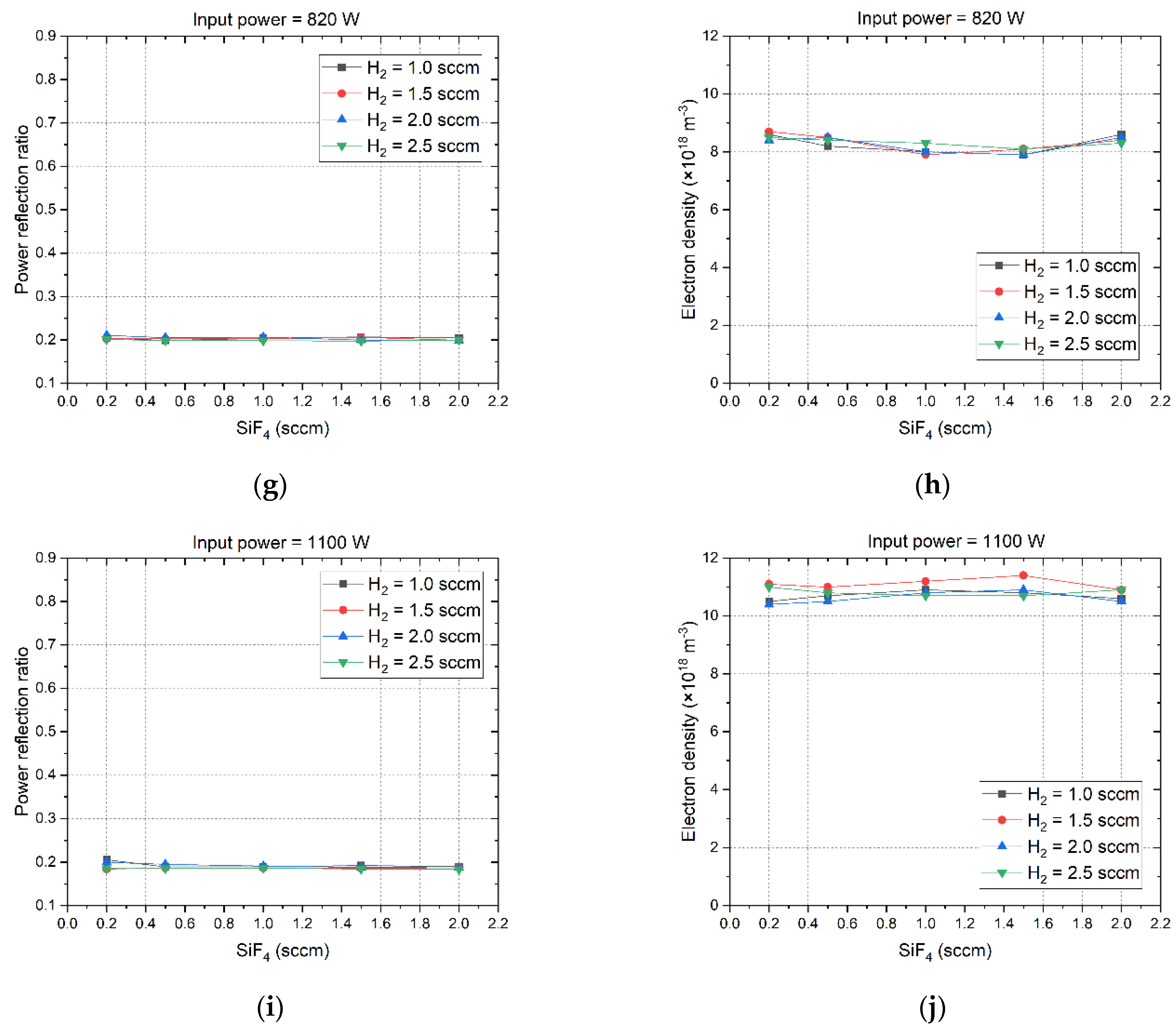
Figure 3 illustrates the microwave power refection ratio and the corresponding electron density as they vary with the flow rates of SiF₄ and H₂. At the microwave power of 400 W, the H₂ flow rate must not exceed 1.5 sccm in order to guarantee the ignition of plasma. At other microwave power levels, the H₂ flow rate can be set up to 2.5 sccm. There exists a notable negative correlation between the power reflection ratio and electron density when they are compared. That means a high power reflection ratio corresponds to a low electron density. The flow rates of SiF₄ and H₂ induce merely minor fluctuations in the power reflection ratio and electron density, and as the microwave power increases, these fluctuations progressively diminish. This is attributable to the fact that the plasma morphology and electron density remain relatively unaffected by the low gas flow rate in low-pressure environments [33]. At the microwave power level of 400 W, the power reflection ratio reaches its maximum value at about 0.6. The corresponding electron density is as low as about 1.5×10¹⁸ m^-3. As the microwave power increases gradually to 1100 W, the power reflection ratio will decrease to around 0.2, and the electron density reaches up to 11.5×10¹⁸ m^-3. These results indicate that increasing the microwave power can enhance the absorption of microwave power by the plasma, because the volume of the plasma is directly proportional to the microwave power it absorbs, meaning that a larger plasma volume results in higher microwave power absorption [32]. As the microwave power is increased from 400 W to 670 W, the power reflection ratio undergoes a notable decrement, dropping from 0.6 to approximately 0.2. Subsequently, further augmentation of the microwave power results in the power reflection ratio remaining virtually stable. This result demonstrates that as the microwave power rises to 670W or higher, the dielectric properties of the plasma will become stabilized.

3.2. HF Production

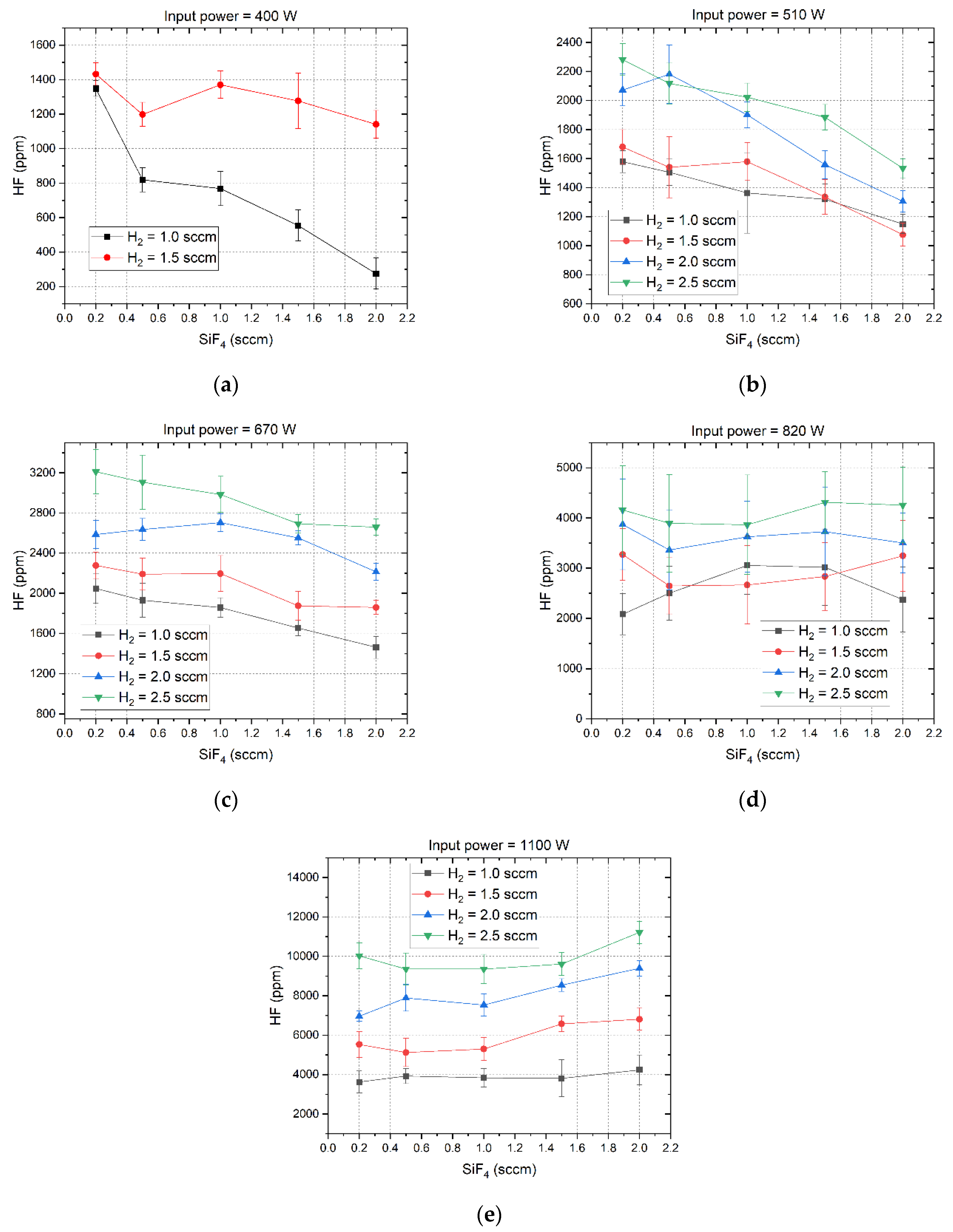
The measured HF concentrations of the output gases under different microwave power levels are shown in Figure 4. It is known that the concentration of the produced HF depends on the feeding gas flow rates and the microwave power. At 400 W, the HF concentration decreases with the SiF₄ flow rate but increases with the H₂ flow rate. Moreover, the decrement rate of HF concentration with the SiF₄ flow rate is larger when the H₂ flow rate is set to 1 sccm compared to when it is set to 1.5 sccm. Increasing the microwave power to either 510 W or 670 W does not change this trend; however, it results in a higher HF concentration and a smaller decrement rate. Additionally, the decrement rate of HF concentration remains nearly consistent across various H₂ flow rates. At a microwave power level of 820 W, the HF concentrations under different H₂ flow rates remain relatively stable with varying SiF₄ flow rates. As the microwave power increases to 1100 W, the HF concentrations across varying H₂ flow rates gradually increase with the SiF₄ flow rate, achieving a maximum concentration of approximately 11200 ppm at an H₂ flow rate of 2.5 sccm and a SiF₄ flow rate of 2 sccm.

It is reasonable that the increment in microwave power leads to an increment in HF concentration, because at a constant gas volume, an increment in the energy obtained per unit volume of the input gas leads to a more vigorous plasma impact reaction and a higher probability of SiF₄ and H₂ conversion to HF. This can be quantified by the specific energy input (SEI) written as

$$\mathrm{SEI} [\mathrm{kJ}/\mathrm{mL}]={\displaystyle \frac{P [W]\times {10}^{-3} [\mathrm{kJ}/J]\times 60 [s/\min ]}{\mathrm{Flow} \mathrm{rate} \left[\mathrm{sccm}\right]}}$$

(9)

where P is the input microwave power.

The key reaction pathway of the conversion process of SiF₄ and H₂ into HF is analyzed herein to facilitate a deeper understanding of the HF concentration curves presented in Figure 4. The dissociation of H₂ into H atoms within the plasma can be summarized in one reaction formula as:

$$e+{\mathrm{H}}_2\stackrel{4.5 eV}{\to }2\mathrm{H}+e$$

(10)

where the dissociation energy is 4.5 eV. In low-pressure plasma, this reaction can occur with a reduced energy of 3 eV [25]. The dissociation process of SiF₄ in the plasma is more complex than that of H₂, its reaction formulas are shown as follows [34]:

$$e+\mathrm{S}\mathrm{i}{\mathrm{F}}_4\stackrel{5.6 \mathrm{e}\mathrm{V}}{\to }\mathrm{S}\mathrm{i}{\mathrm{F}}_3+\mathrm{F}+e$$

(11)

$$e+\mathrm{S}\mathrm{i}{\mathrm{F}}_4\stackrel{11.2 \mathrm{e}\mathrm{V}}{\to }\mathrm{S}\mathrm{i}{\mathrm{F}}_2+2\mathrm{F}+e$$

(12)

$$e+\mathrm{S}\mathrm{i}{\mathrm{F}}_4\stackrel{16.8 \mathrm{e}\mathrm{V}}{\to }\mathrm{S}\mathrm{i}\mathrm{F}+3\mathrm{F}+e$$

(13)

$$e+\mathrm{S}\mathrm{i}{\mathrm{F}}_4\stackrel{22.4 \mathrm{e}\mathrm{V}}{\to }\mathrm{S}\mathrm{i}+4\mathrm{F}+e$$

(14)

Obviously, the dissociation of SiF₄ needs more energy compared to that of H₂. The generated H atom and F atom can be combined to form HF molecules as [35]:

$$\mathrm{H}+\mathrm{F}\stackrel{-2.7 \mathrm{e}\mathrm{V}}{\to }\mathrm{H}\mathrm{F}$$

(15)

In the gas conversion process, H₂ is firstly dissociated in the plasma following by the dissociation of SiF₄ because H₂ is initially introduced in the discharge area to form plasma. From Equation (10) to (15) we can deduce that, upon ignition of the H₂ plasma, almost all the H₂ molecules involved in the reaction can be dissociated into H atoms due to the low dissociation energy. Consequently, this results in the production of a greater number of H atoms compared to F atoms. In this case, if the microwave power remains at a low level and keeps constant, an increment in the SiF₄ flow rate will lead to a reduction in the SEI, which will impede the dissociation of a significant portion of SiF₄ into F atoms. Therefore, the produced HF concentration drops with the SiF₄ gas flow rate as illustrated in Figure 4(a) through 4(c). When the microwave is at a high level, such as 820 W or 1100 W, the SEI is high enough to guarantee the dissociation of SiF₄ in high gas flow rates. As a result, increasing the SiF₄ flow rates can increase slightly the produced HF concentrations as evidenced by the trends depicted in Figure 4(d) and 4(e).

3.3. Energy Cost

The energy cost (EC) for producing HF by microwave plasma can be calculated by the following formula [36]

$$\mathrm{E}\mathrm{C} [\mathrm{G}\mathrm{J}/\mathrm{mol}]={\displaystyle \frac{\mathrm{SEI} [\mathrm{kJ}/\mathrm{mL}]\times {\mathrm{V}}_{\mathrm{mol}} [\mathrm{L}/\mathrm{mol}]\times {10}^3}{\mathrm{H}\mathrm{F} [\mathrm{ppm}]}}$$

(16)

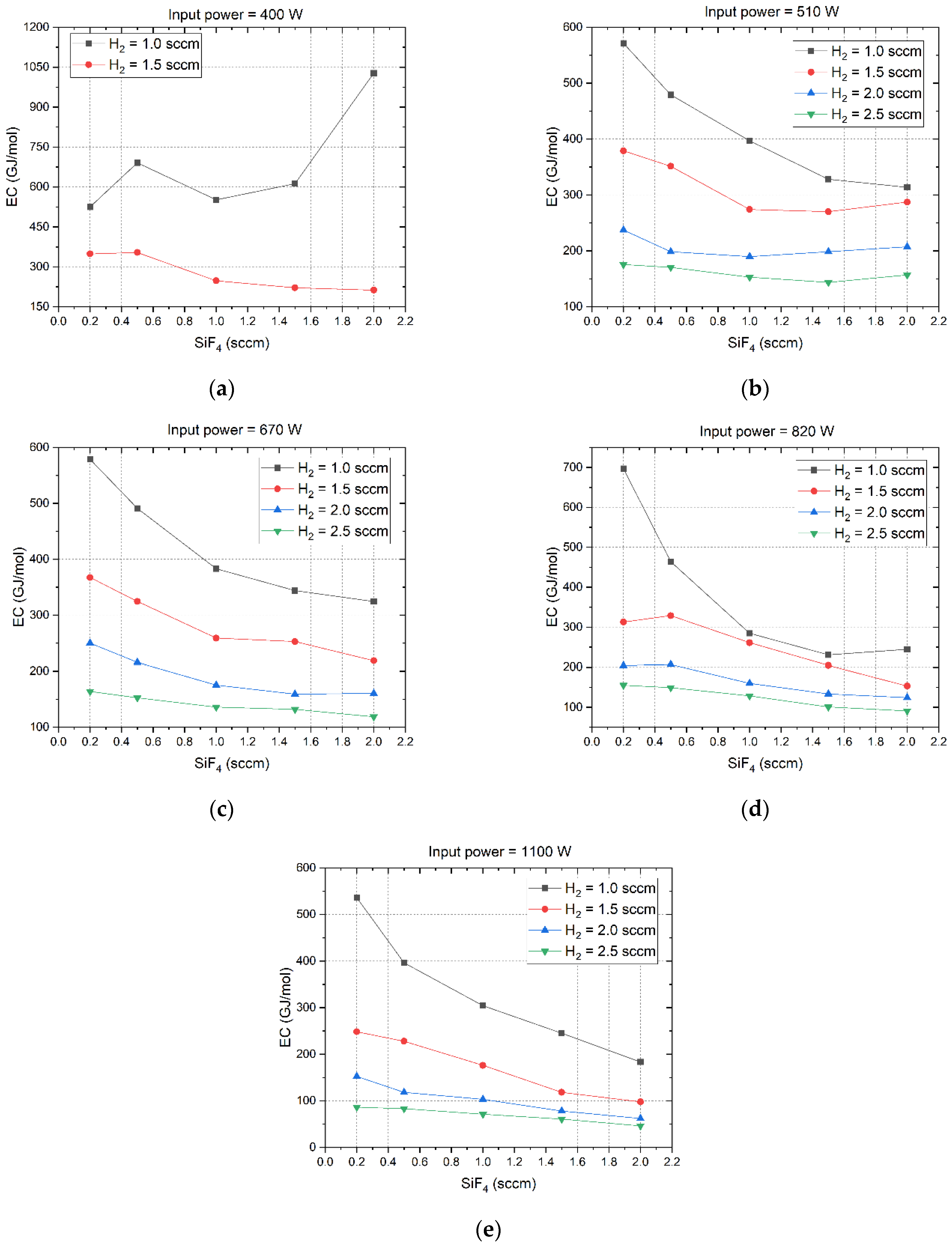
where SEI is derived from Equation (9), V_mol represents the molar volume of ideal gas at room temperature and the pressure of 0.68 atmospheres with V_mol = 35.37 L/mol [14]. Based on the measured results in Figure 4 and Equation (16), the EC under different microwave power and gas flow rates are calculated as presented in Figure 5. Comparing Figure 5(a) through 5(e), it is observed that the EC decreases with the H₂ flow rate. With the exception of the specific condition where the microwave power is set to 400 W and the H₂ flow rate is maintained at 1 sccm, the EC will also drop down with the SiF₄ flow rate. This is attributed to the low HF production in this condition. However, it is worth noting that the rate of decrement in EC with the SiF₄ flow rate slows down when the H₂ flow rate increases in different microwave power levels. Furthermore, when the H₂ flow rate exceeds 1.5 sccm, an increment in microwave power can result in a decrement in EC, regardless of the SiF₄ flow rate.

The EC value for producing HF in this paper is three orders of magnitude (in units of GJ/mol) greater than that reported in other gas conversion applications utilizing plasma (in units of MJ/mol) [12-20]. This discrepancy arises because the gas flow rate employed here (in units of sccm) is three orders of magnitude lower than in those applications (in units of slm). Our future endeavor will be to enhance the gas processing capacity using low-pressure microwave plasmas. The lowest EC of 46.3 GJ/mol is attained with a microwave power setting of 1100 W and flow rates of 2.5 sccm for H₂ and 2 sccm for SiF₄, respectively. This is also the condition of achieving the maximum HF concentration as depicted in Figure 4(e).

4. Conclusions

In this paper, a low-pressure microwave plasma was utilized to produce HF from SiF₄ and H₂ mixtures. An experimental system was built up to study the process parameters influencing the HF production. In the experiments, the microwave power reflection ratio and electron density under different microwave power levels and SiF₄ and H₂ flow rates were acquired. The results revealed that as the microwave power level increased, the power reflection ratio decreased, whereas the electron density increased. The flow rates of SiF₄ and H₂ had merely minimal impact on both the power reflection ratio and electron density. The HF production was also measured in different process conditions. The results demonstrated that, on the one hand, the increment of the microwave power or H₂ flow rate could improve the produced HF concentration. On the other hand, at low microwave power levels ranging from 400 W to 700 W, the HF concentration decreased with the SiF₄ flow rate. Conversely, when the microwave power was above 800 W, the HF concentration slowly increased with the SiF₄ flow rate. The highest HF concentration achieved in this paper was 11200 ppm, which was obtained at the microwave power of 1100 W and flow rates of 2.5 sccm for H₂ and 2 sccm for SiF₄, respectively. Notably, the energy cost at this condition was also the lowest among all the process conditions, which was 46.3 GJ/mol. This work proposes an experimental investigation on the HF production by microwave plasma processing. However, the experimental parameters, particularly the SiF₄ and H₂ flow rates, are still at the laboratory scale. Further research is needed to enhance the gas processing capacity for the potential application of this method at an industrial scale.