Note on Redshift and the Principle of Conservation of Energy

1. Introduction

The energy of a photon is given by Planck’s relation and is dependent on the frequency. As the frequency drops when redshift is observed, the energy drops. This note questions the link redshift – Doppler effect, which doesn’t explain the energy drop, and will present a proposal which maintains energy conservation.

1.1. Speed of Light and Energy

Special relativity and corresponding observations are telling us that, whatever is its frequency, a photon and its attached wave are always travelling at the speed of light [Einstein1905; Michelson1887; de Sitter1913]. The photon being massless shouldn’t have any kinetic energy, its energy is in the wave with the famous relation:

E = hf

E being the energy of the photon, f its frequency and h the Planck constant. If the frequency changes, the energy changes as well.

1.2. Redshift

Redshift (and blueshift) of stars have been predicted by Fizeau in 1848 [Hellemans,1988] then observed as early as 1869 [Huggins]. The mechanics of the redshift were in place before science knew about the existence of a photon (with its energy). Nobody questioned why there was a change of energy. Redshift is often described as a Doppler effect (or relativistic Doppler effect). Although the dissipation of the energy of an acoustic wave is well understood, the Doppler effect doesn’t deal with the energy of the acoustic wave, only the frequency. Redshift is about a photon, so it is different because with a change of frequency, there is a change of energy.

2. Dark Energy, Spacetime and Potential of the Universe

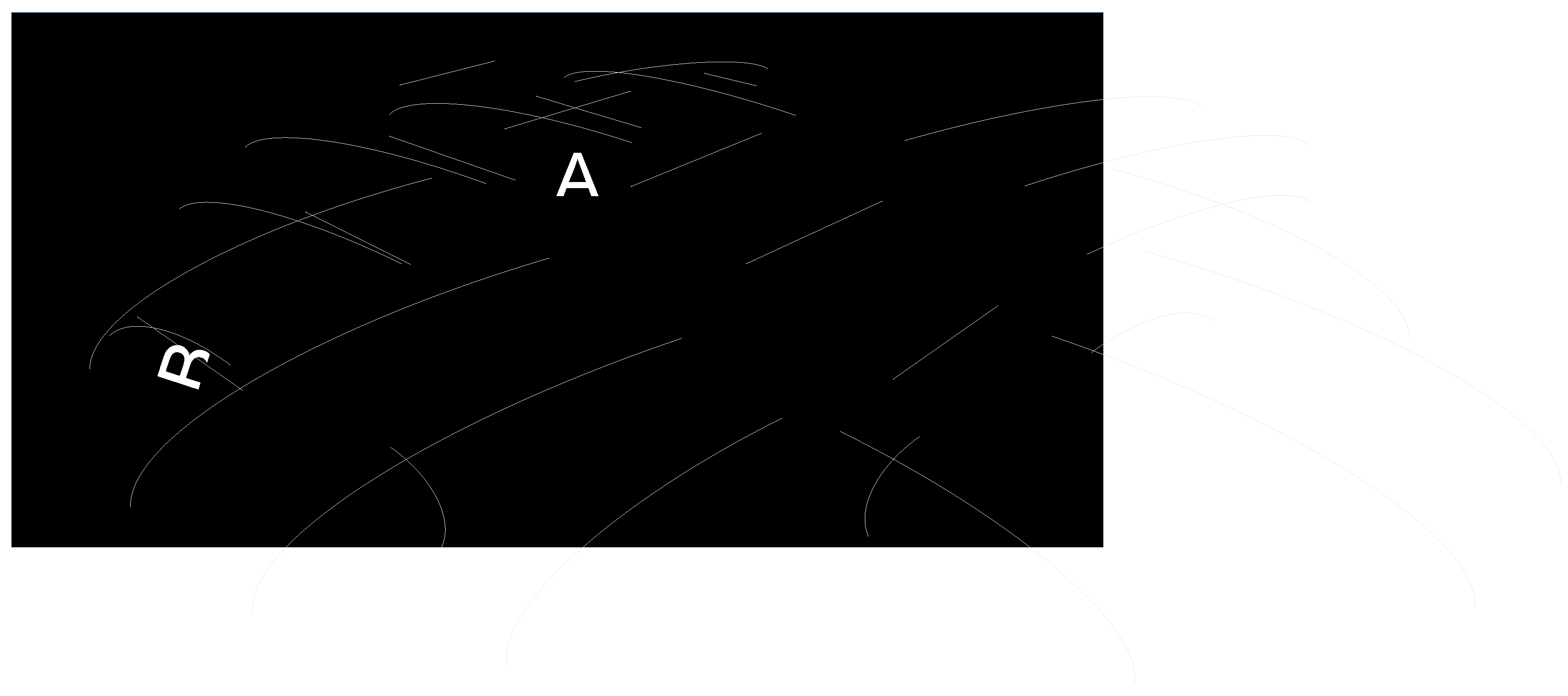
In the universe, we are immobile and the universe is expanding; because of the acceleration of its expansion, there is a fifth-force. With a force there is a potential that deforms spacetime as in Fig.1. This figure was in my mind when I suggested in my previous paper [Danis,2024a] that “speed-force” could explain dark energy. But even if my previous paper is wrong, spacetime should resemble Fig.1 because of the acceleration of the expansion.

One photon is leaving point B with an energy corresponding to a high frequency. Because the frequency is dropping, the energy due to the frequency is dropping as well. But to move from B to A, the potential energy is increasing. I hypothesise that the potential energy is the reason for the difference of energy/frequency; energy would be conserved. If gravitational potential bends light as observed with gravitational lensing, then the potential of Figure 1 should have an effect on the photon.

3. Discussions

The fifth-force gives Fig.1 and Fig.1 explains the fifth-force. It is a circular “argument” and doesn’t explain anything. The reason for the fifth-force/potential has to be found.

If redshift is not a Doppler effect (because the change of energy is not currently explained), then the accepted recessional speeds are wrong. Could this be the origin of Hubble’s crisis [Riess,2022]? Please do leave a comment if I have missed something.

The conservation of energy with redshift is a question that has to be addressed for the reasons above, and it could also help with the identification of the fifth force. This note is a call for such a move.

This idea supposes that a difference of potential would be a function of the speed between the source and the observer. That difference of potential could be measured with the redshift and then the speed could be deduced from that difference of potential. This new speed would be different to the speed obtained with the application of the Doppler effect. One study shows that the application of the “speed-force” would indeed lead to different recessional speeds to Doppler’s speeds [Danis,2024b]. This study is still a work in progress because a- it is not trivial and b- it is a serious claim which would demand a revision of all the speeds obtained with a redshift.

If the idea of Fig.1 is accepted it would mean that the frequency of the photon would seem to increase again when the photon is moving away from us and reaches the opposite end of the visible universe. But do not conclude that a new observer at the opposite end would see no redshift. That observer would see spacetime as in Fig.1. Potential is relative to the observer; one observer cannot judge for another observer, as already stated in the previous paper [Danis,2024a].

Here is another example of the relativity of such potential: the potential of a star in a galaxy will be higher at the place where the rotation is towards us than away from us (because of the redshift). Observing the same star, an observer situated on the other side of the galaxy will conclude the opposite (lower potential for the place where we concluded the higher potential). That difference in potential difference should lead to an identical velocity.