A Testable Hypothesis on the Nature of Dark Matter Based upon Hawking’s Cosmology, A Natural Explanation for Flat Rotation Curves as Well as an Improved Prediction Algorithm for Rotation Velocities

1. Introduction

The hypothesis of dark matter is a way to explain why among other galaxies seem not to obey Newton’s law of gravity. There exist several approaches to account for dark matter or for the additional gravity it yields. Like Modified Newtonian Dynamics (MOND) [1–3] , Bekenstein’s TensorVectorScalar gravity (TeVeS) [4] or Covariant Emergent Gravity (CEG) [5,6] , which assume dark matter does not really exist. But that leaves the statistical distribution of ‘cold’ and ‘hot’ spots in the background radiation unresolved, that would still need the existence of (much) dark matter vs. baryonic matter to be understandable in terms of Big Bang nucleosynthesis, as well as matters like gravitational lensing.

In this paper a hybrid alternative will be presented, which is based upon the existence of dark matter and follows from Hawking’s Cosmology [7,8]. It solves the problem that Lelli and Mistele [9] showed, that the common way to project dark matter halos around galaxies cannot be valid, since the alternative naturally assumes dark matter is distributed like the visible matter in a galaxy. The hypothesis gives a natural explanation for both dark matter and the behaviour of gravity and why it shows behaviour as described by MOND and TeVeS theory. The term naturalness is extensively discussed by Hossenfelder [10] (p. 57). In short it means that a theory is without fine-tuned constants. Since General Relativity (GR) in galaxies would need the said halos too so as to properly include the effect of dark matter, it must be modified with some additional terms to make correct solutions possible without these halos. TeVeS [4] meets this need.

In this paper the Spitzer Space Telescope satellite data of 175 galaxies, as processed and reported by Lelli et al. [11] and Starkman et al [12] are used to test several predictions that follow from this theory. The mass-to-light ratio has been used as the only fitting parameter to fit the baryonic rotation velocity, and hence the baryonic gravitational acceleration in each galaxy to the observed values near the core of the galaxies. After that, the hypothesis in hand is used to predict the additional gravitational acceleration at all radii without any further fitting and to compare the predictions with the observed values.

After a brief introduction of Big Bang theory in chapter 2.1 and Hawking’s cosmology in chapter 2.2 and some other indispensable literature about quantum systems in chapter 2.3, MOND and TeVeS will be discussed in chapter 3. Then, in chapter 4.1, firstly, an interpretation of the MOND like behaviour of dark matter as a sum of two fields will be proposed. Secondly, the natural basis for this will be explored in chapter 4.2 and will stepwise be derived in a logical manner from Hawking’s cosmology in chapter 4.3. In chapter 5, based upon chapter 6, the hypothesis for dark matter will be elaborated and its consequences and behaviour will be explored. In chapter 6 six testable predictions are proposed, five of which are proved, and an improved alternative to MOND for the prediction of rotation velocities will be presented. In chapter 7 TeVeS will be elaborated and used for a relativistic formulation of the hypothesis. In chapter 8 the conclusions and suggestions for further work are presented.

2. Hawking´s Cosmology and Superposition State of Universe

2.1. Big Bang Theory

The line of thought of the universe as a quantum system is an elaboration of The Grand Design, [8] with additions from Van den Heuvel [13] and references to Hartle & Hawking [7] .

The universe, according to the Big Bang theory, comes from an infinitesimal small point in which only elementary particles existed in the form of a plasma, with an extremely high temperature [13] (pp. 127-136).

The originally extremely high temperature is still visible and measurable in the so-called background radiation. Its properties are direct evidence that the universe originated from a hot Big Bang stage. The Big Bang theory is also a logical extrapolation of the expansion of the universe that we observe, among other things due to the redshift of the spectrum of the radiation of stars, but also of the history/evolution of stars and galaxies as visible through our telescopes. In addition, the non-uniform distribution of stellar objects as quasars over the different redshifts proves the universe is not static.

Moreover, Big Bang theory can quantitatively explain many phenomena, such as the distribution over the various elements of the mass in the universe, the cosmic composition, based on nuclear physics. The fact that it is dark at night also proves that the universe cannot be infinitely large and infinitely old, because then the entire sky would be filled with light from stars. So, our universe indeed has a beginning. Moreover, the Big Bang theory forms a well-cohesive whole with astronomy and the rest of physics.

2.2. Hawking´s Cosmology

Somewhere at the beginning, our universe has been in a quantum state, because that's where one ends upon extrapolating the expansion of the universe back to the very smallest starting point, [7,8] have derived solutions to the wave function of the universe as proposed by Everett [14] and further elaborated by DeWitt [15] . As derived and explained by Hartle & Hawking [7] these solutions must satisfy the Wheeler-DeWitt equation.

Hartle & Hawking [7] show the Wheeler-DeWitt equation has the following form:

$$\mathrm{Ĥ}\mathrm{}\left(x\right)\mathrm{}|\mathrm{ѱ}\mathrm{}⟩=0$$

(1)

Where $|\mathrm{}\mathrm{ѱ}⟩$ is the wave function of the universe and where Ĥ(x) is called the Hamiltonian constraint, [7] . The Hamiltonian, in this case derived from General Relativity [7] , describes the total energy of a system and $Ĥ$  is the Hamiltonian operator [16] (p. 27). The so-called constraint described by (1) follows from the total energy of the universe being zero, gravitational energy cancelling out the mass energy.

Hawking’s & Hartle’s solutions of this equation describe a universe that has no beginning, the Hartle-Hawking state, [7] . Hawking [8] explains this in simpler terms as well: time must have been indeterminate there on the smallest scale in that quantum state, because of the extreme gravitational warpage of space-time at that moment, [8] (p. 172). The time t=0 therefore is not precisely defined and at these scales time reduces to a fourth spatial dimension.

So, the universe has no exact measurable beginning. Hawking calls this the ‘no-boundary-condition’, [8] (pp. 172-173). It makes it impossible to trace the development of our universe from the beginning to this time in a deterministic ‘bottom-top’ way and, hence, there is a need for a statistical ‘top-down cosmology’, considering all possible alternative histories of the universe.

He states that as a consequence of this, at the very beginning time acted as a fourth spatial dimension, ”In the early universe-when the universe was small enough to be governed by both general relativity and quantum theory, there were effectively four dimensions of space and none of time”, [8] (p. 172) This is the starting point of the proposal of this paper. String theory, however, suggests as much as eleven dimensions, but using the minimum of four is more economical and easier to understand.

The quantum aspects of the Big Bang become clearer when considering so-called ‘double-slit’ experiments, with a light beam split in two that are directed at a wall with two narrow slits. Especially the variant where only one photon is fired at a time is exciting. The same interference patterns then arise as with continuous beams of photons, so the probability waves of single photons interfere with themselves, as it were. One photon behaves as if it passed through both slits. That can only happen if the photon itself follows all possible alternative paths simultaneously, as it were like a split probability wave. So, the behaviour of the single photon can be seen as a superposition of all possible alternative paths it follows, so alternative histories, [8] (p.104).

Hawking’s and other’s point about the probabilities is that a quantum experiment will only have a certain outcome when it is performed. The Big Bang can be regarded as such an experiment [8] p. 179), where the universe in the quantum state may have had a statistical probability distribution of many ‘alternative histories’, following the interpretation of Feynman. Maybe 10⁵⁰⁰ ones as ‘String-theory’ and the more general ‘M-theory’ suggest, [8] (pp. 152 and 181). At page 77 Hawking states that “the universe does not have a single existence or history, but rather every possible version of the universe exists simultaneously in what is called a quantum superposition”.

This does not a-priori imply we still are in a real a state of superposition between all, or part of these alternative histories now, but this paper will argue that this is indeed the case with our universe, to some extent.

The parameters and hence the quantum state of our universe are known now. Our universe has known single values for the fundamental parameters and constants. Of all the ‘alternative histories’, ours is the one that has come true. It has been performed; we know the outcome. This is only possible when there is an observer to the experiment, [8] (pp. 107 and 179). This where the idea of an ‘observed universe’ of Hawking and others like Wheeler comes from. The assumption is that man or other sentient beings can perform this role of external observer, as Hawking and Wheeler argue, based upon the ‘delayed-choice’ experiment by Wheeler. That shows that the moment of time where the observer enters the history is not relevant [8] p. 106-107).

2.3. Other Relevant Quantum Systems in a State of Superposition

Quantum superposition can be forced by a beam-splitter like in the famous ‘double-slit’ experiment discussed up here. It can be forced as well by a dedicated device like in a Qubit or in an MRI-scanner. A tensor-interaction like in the deuteron may as well yield a superposition state. The latter will be discussed into more depth in the sequel, since it might be very relevant to the behaviour of our universe.

A deuteron Is a bare proton and a neutron, glued together, without electrons. The binding force between the neutron and the proton is the sum of the resulting forces of the superposition of two quantum spin states, see Bethe [17] . This force would not be strong enough if the deuteron were in just one of those states, according to Khalili [18] (p. 20).

This is essential to the following part of this paper: as with the single photon in the double-slit or with the deuteron, our universe could still be in a superposition of multiple histories. The result should be able to interfere with itself very well like the single photon, and forces like gravity might add up like in the deuteron.

This, at its turn, leads to a pair of testable hypotheses of the nature of dark matter. This now is presented as well as the path of thinking that led to it. But firstly, MOND and TeVeS theories are briefly visited in the next chapter.

3. Introduction to MOND and TeVeS Theories

Modified Newtonian Dynamics (MOND) is an empirical alternative to the hypothesis of dark matter to explain why galaxies and open clusters [19] seem not to obey Newton’s law of gravity. It is explored in this chapter and among other described by Schilling [20].

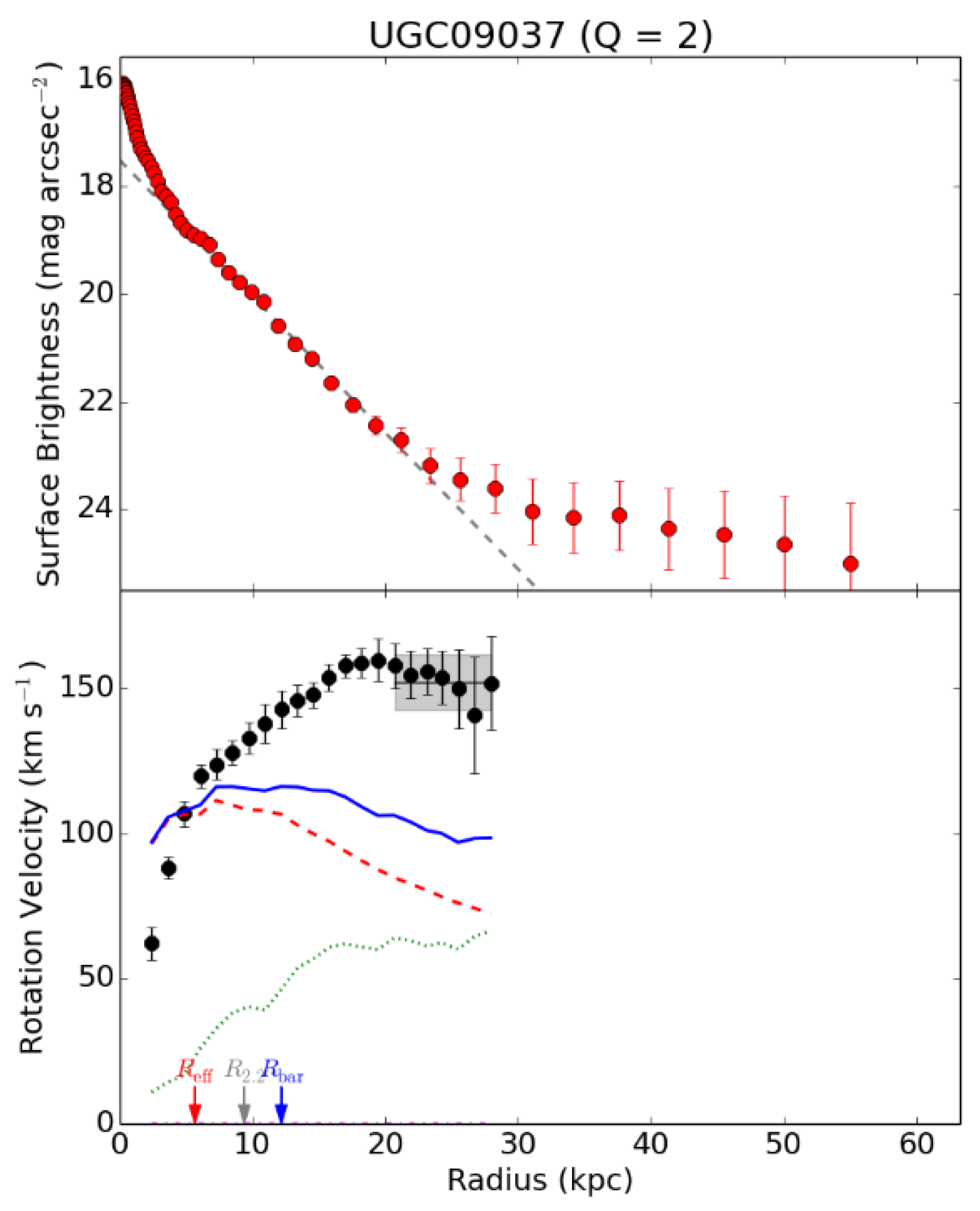
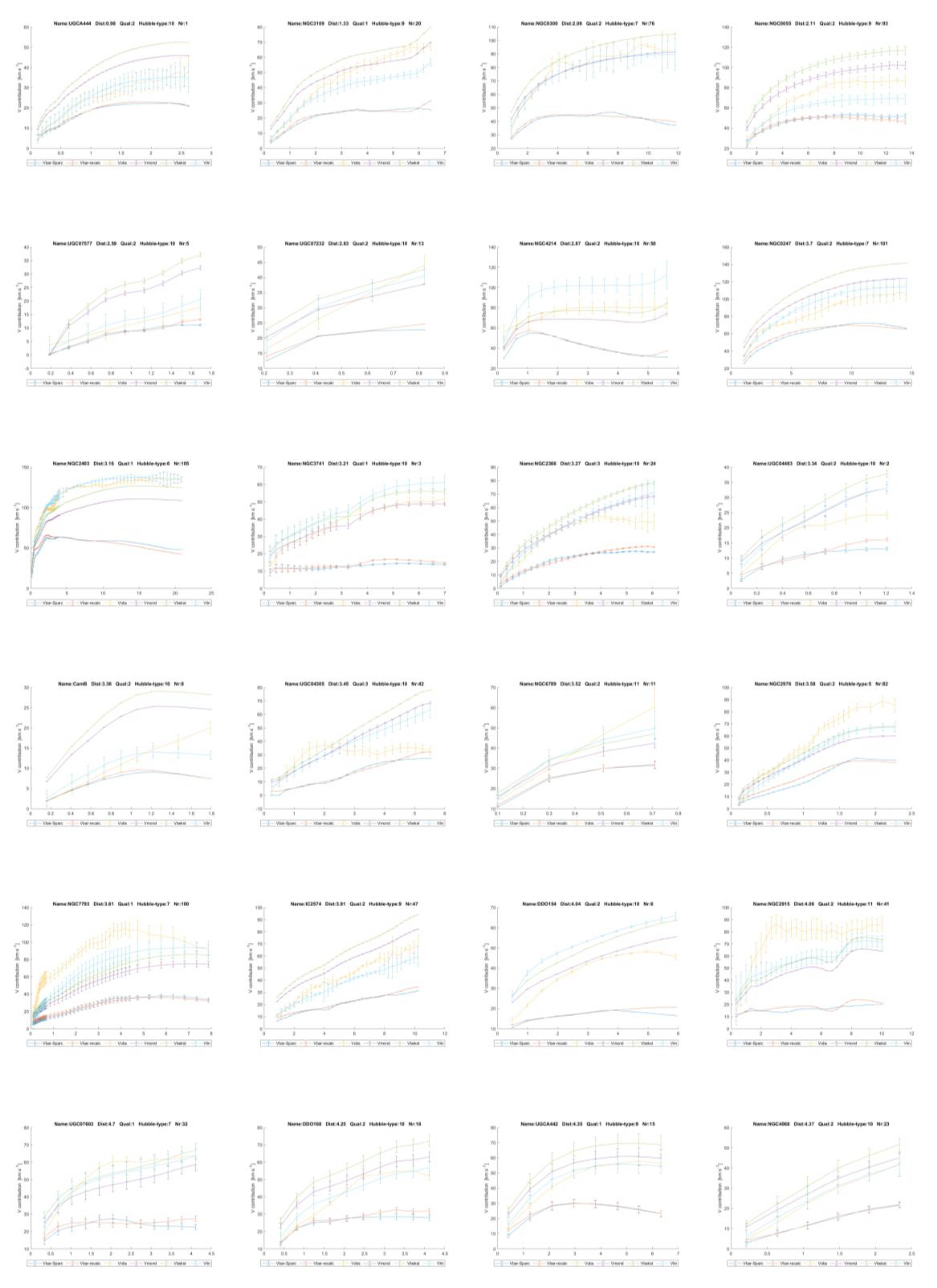
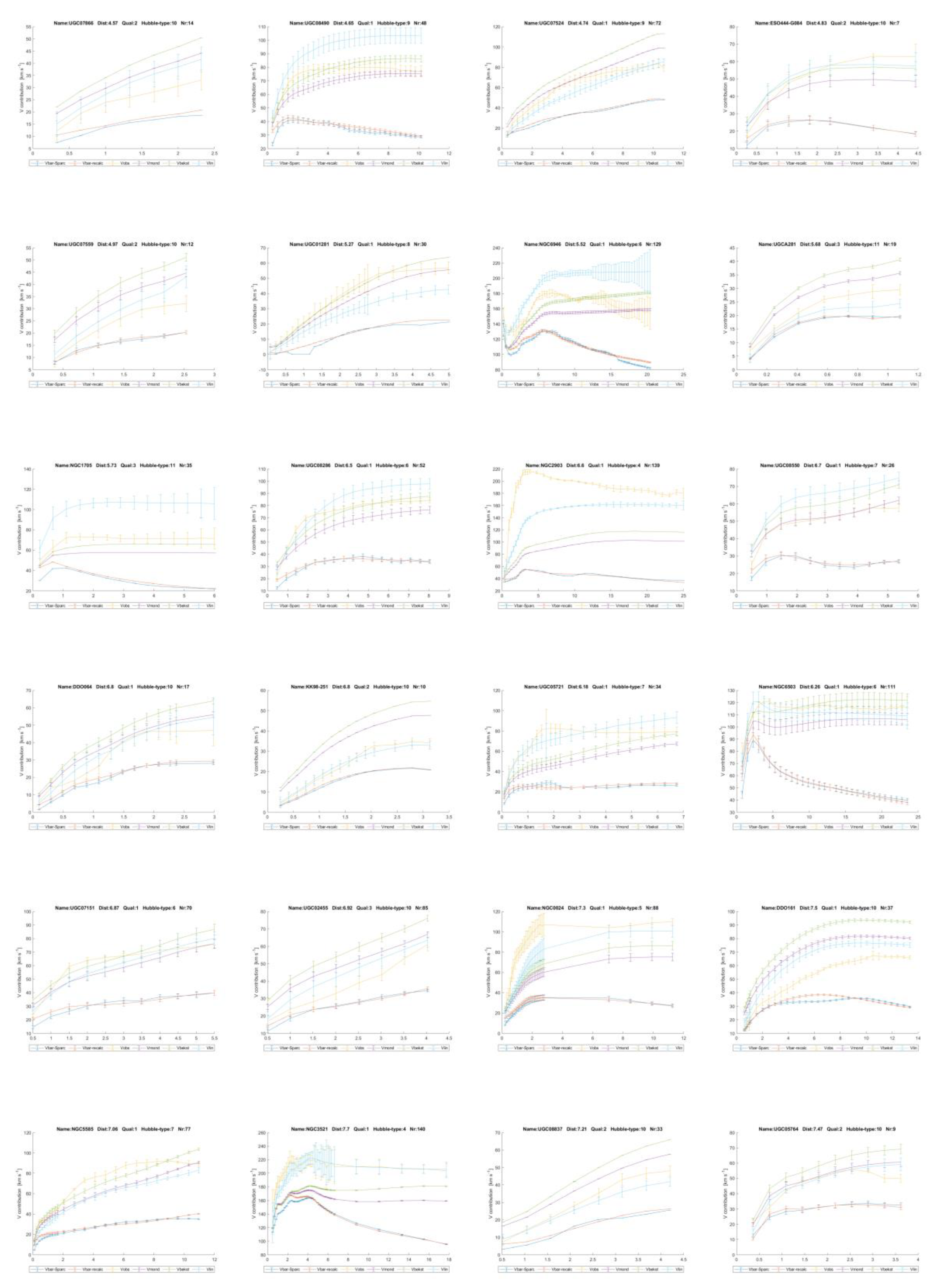
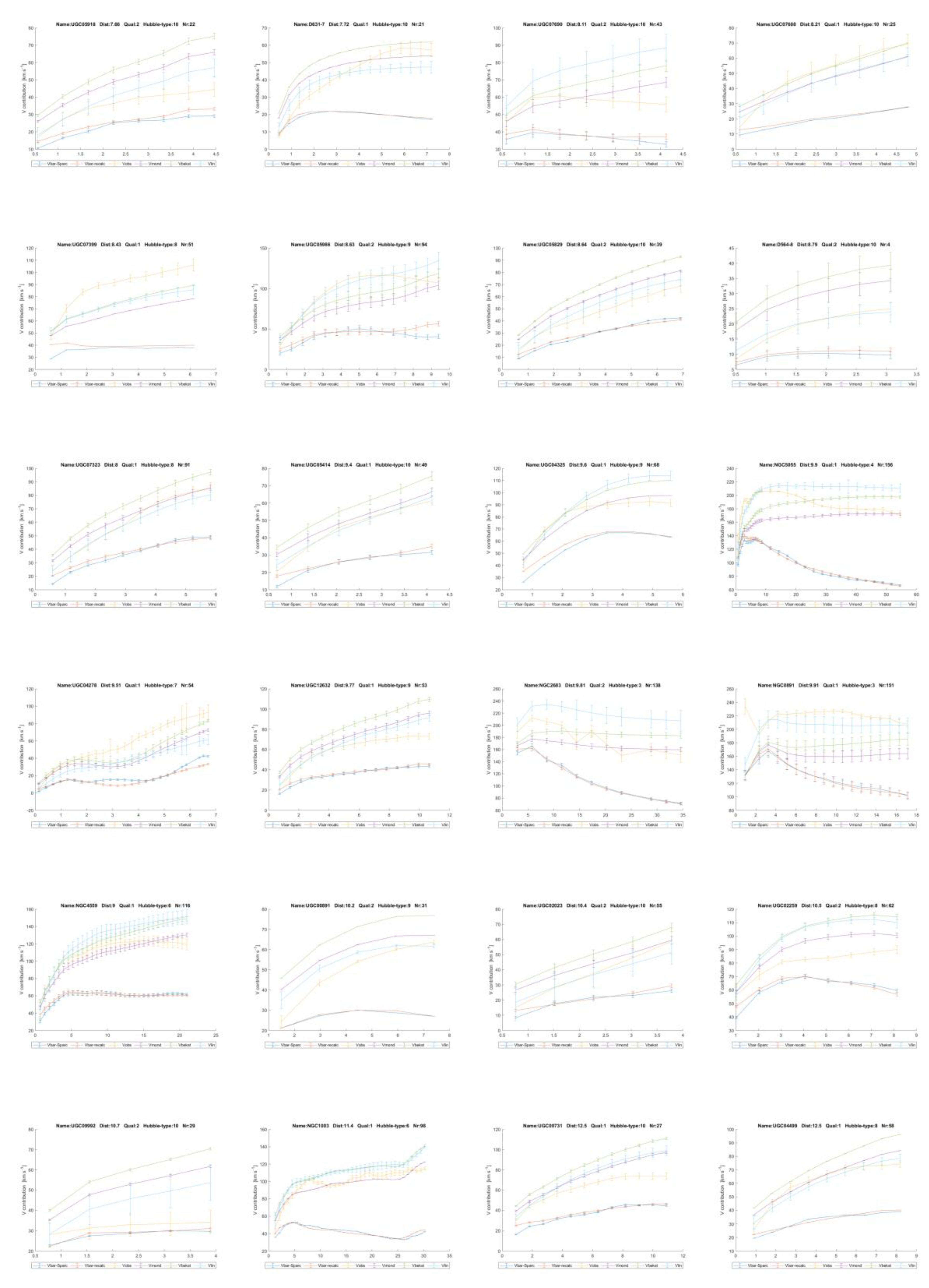
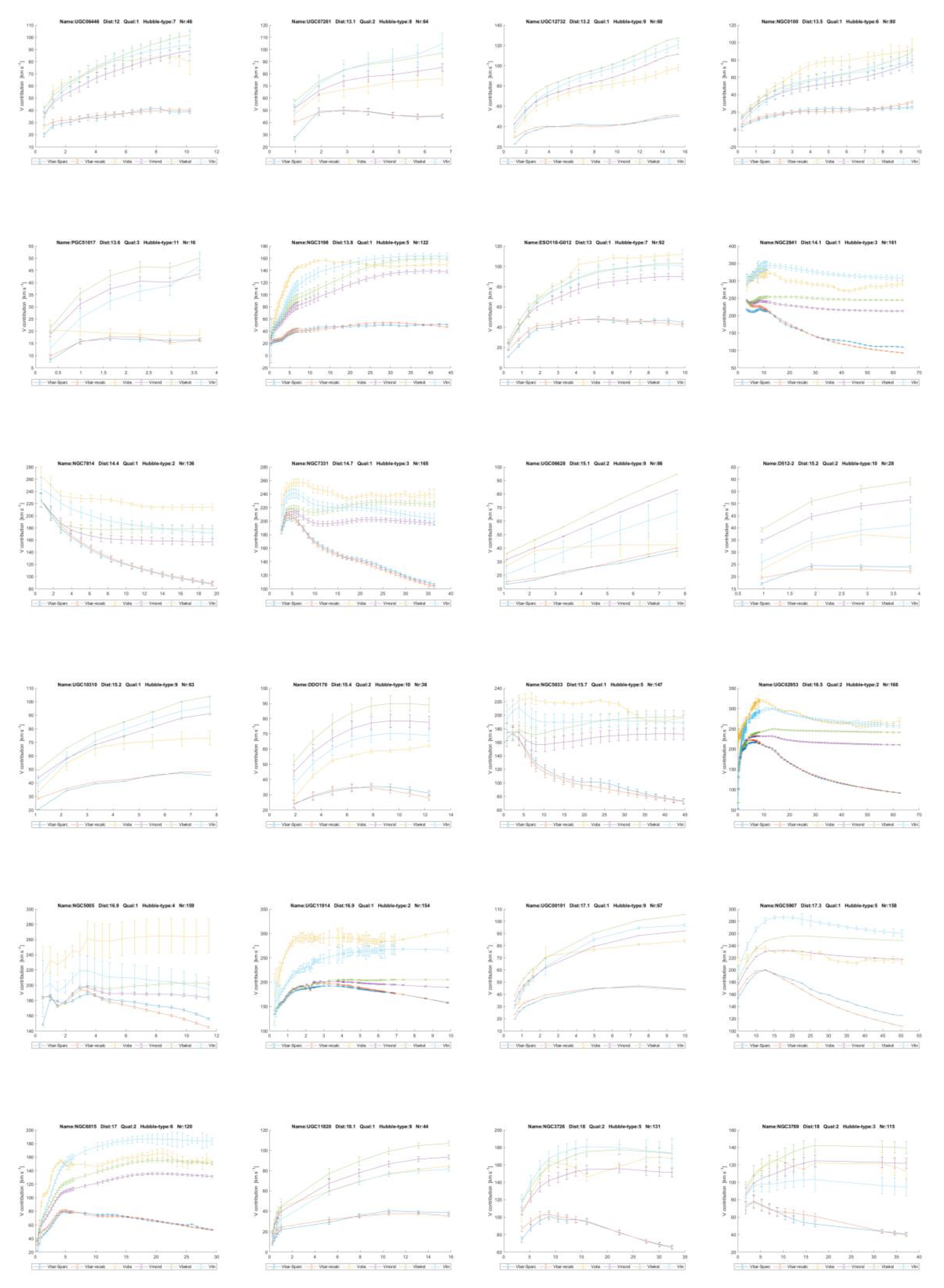
First published in 1983 by Milgrom [1–3], the aim was to explain why the observed velocities of stars in galaxies are larger than expected based on Newtonian gravity. An example of the so-called ‘rotation curves’ discussed down here, is shown below in Figure 1. It shows the rotation velocities as a function of radius from the centre of a galaxy, as well as the logarithmic brightness curve, which is a good measure for radial mass distribution. It comes from Lelli [11]. It is one of the 175 galaxies studied with the SPARC satellite (UCG09037). The black dots are observed velocities, to be called V_obs in the sequel. They are higher than the velocities calculated from gravitational attracting force according to Newton’s law of gravity. Taking this equal to the centrifugal force, results in the theoretically expected velocity, called V_bar, the blue line.

Figure 1. rotation curve sample [11].

Figure 1. rotation curve sample [11].

If at large radii both the total observed gravity decrease linearly with radius, just like the opposing centrifugal force, the observed velocities, V_obs, can remain constant over a long range of radii as can be seen in Figures 1 and 7 and as is shown by Lelli [9,11] for many of the other galaxies with Spitzer photometry. See Annex 3 for all the rotation curves.

Milgrom noted that instead of assuming dark matter to solve this, the discrepancy might be resolved if the gravitational force experienced by a star in the outer regions of a galaxy would vary inversely linearly with radius R (as opposed to the inverse square of the radius, as in Newton’s law of gravity). MOND has been fitted empirically such that it differs from Newton’s laws at extremely small accelerations that are characteristic of the outer regions of galaxies with formula (2). The transition would occur below an acceleration of a_m = 1.2 x 10^-10 m²/s, Milgrom’s constant. The area with lower gravitational acceleration is called the MOND regime. The theory needs an interpolation algorithm for the acceleration beneath a_m in a pragmatic manner. The interpolation depends on the variable µ ($x$) with $x=g/a_m$ , so the predicted total acceleration over Milgrom’s constant, as follows:

$$\mathrm{\mu }\left(x\right)={\displaystyle \frac{x}{\sqrt{1+\mathrm{}{x}^2}}}$$

(2)

and the Newtonian acceleration g_Nis related to the resulting total predicted acceleration a through:

$$g_N=\mathrm{}\mathrm{\mu }\mathrm{}\left(x\right)g\mathrm{}$$

(3)

Since this equation needs to be solved iteratively when it is used to predict the total acceleration from the Newtonian, and since this interpolation formula allows for inversion, it can be rewritten as follows:

$$g=g_N\mathrm{}{({\displaystyle \frac{1}{2}}+\mathrm{}{\displaystyle \frac{1}{2}}\sqrt{1+{\left(2\mathrm{}{\displaystyle \frac{a_m}{g_N}}\right)}^2})}^{1/2}$$

(4)

See for example Platschorre [21]. With back and forth calculating a series of values for $a_0$ and $a$ it can easily be shown that this formula works correctly.

In terms of the Newtonian gravitational potential of the visible matter, $\nabla {\mathsf{\Phi }}_N$, this can be written as follows [4]:

$$\mu \left({\displaystyle \frac{\left|g\right|}{a_m}}\right)g=\mathrm{}-\nabla {\mathsf{\Phi }}_N$$

(5)

Bekenstein uses a parameter y = |$\nabla \mathsf{\Phi }$|²/a_m² which equals x². So: µ($\sqrt{y}$) or simpler µ(y), which will be used in the sequel. He gives an alternative for µ(y) resulting from formula (2).

However, this MOND theory of gravity does improve the calculations on the velocities of stars but does not explain the observed deviations from Newtonian mechanics. Furthermore, as Bekenstein [4] mentions it does not specify how to calculate gravitational lensing by galaxies and clusters of galaxies and it violates conservation of momentum. For the latter, a theory derived from an action principle is needed.

Early attempts to generalise MOND by making a relativistic version of it were relativistic AQUAL [4,22] and Phase Coupled Gravity (PCG) [4,22]. Fascinating is that PCG yields a description of total gravity as a sum of two competing fields, one with quadratic decay of gravity with distance x and one that decays linearly [4] (formula (17) at p. 7). This is consistent with formula (7) in the next chapter. It is interesting to note that Covariant Emergent Gravity (CEG) [5,6] as well yields a sum of two competing fields, as Platschorre [21] shows.

But both AQUAL and PCG attempts had problems like waves propagating faster than light and incorrect light deflection [4]. Bekenstein provided a theory, that accounts for this, TeVeS, in which MOND is reformulated in terms of GR [4]. This will be succesfully applied to the linear gravity hypothesis in chapter 7.

However, the mathematical framework of Bekenstein still does not give an explanation for the source of the additional scalar and vector fields. The paper in hand, presents a hypothesis that provides a natural explanation for it, one that does not need any interpolation algorithm and that significantly can improve the MOND predictions for all galaxies in the database, especially those that are at large distances from our galaxy further. It is presented down here.

4. A Hypothesis on the Nature of Dark Matter

4.1. Interpreting Linear MOND-Like Behaviour of Gravity

When interpreting the linear behaviour of MOND, first thing to realize is, that the dependency of gravitational acceleration g from the radius R can be interpreted as the sum of two contributions. The case for this will be argued in the sequel, but here it suffices just to see how it would work out,

Now, there is no need for an interpolation procedure, like in formulas (2) to (4), above g = 1.2 x 10^-10 m/s², Milgrom’s constant, because taking the sum of the Newtonian gravitational acceleration and the linear one does this naturally at the place where they have the same order of magnitude. This reduces the number of assumptions. Down here it is written as a simple formula, which then is reformulated in the format consistent with MOND, for further use in chapter 7.

$$g=g_N+\mathrm{}{g}_{linear}$$

(6)

With g_linear being proportional to R^-1 instead of R^-2 for the Newtonian gravity.

Thus, the gravitational potential then, upon integrating g, takes the form:

$$\mathsf{\Phi }={\mathsf{\Phi }}_N+\mathrm{}k\ln \left(R\right)+k_2$$

(7)

k being a positive constant that depends on the dark matter distribution, to be discussed in chapter 6 and k₂ being some integration constant. The same potential results from MOND and TeVeS, according to Bekenstein [4] . He concludes that in his theory the additional potential (a term that is greater than zero) of an isolated galaxy is growing logarithmically with distance R, in the case it is not spherically symmetric [4] (p. 19). According to Platschorre [21] (p. 51), it as well follows from CEG in the non-relativistic limit.

Since g_N is proportional to R^-2 and g_linear proportional to R^-1 equation (6) can be rewritten as:

$$g=g_N+\mathrm{}c\mathrm{}\sqrt{g_N}\mathrm{}$$

(8)

Here c is a smooth function of the radial position R, that depends on the different contributions of all masses in the galaxy to the acceleration at a certain R. In fact, g is the sum of an almost infinite amount of contributions, from all masses in the galaxy, each with a varying value of c. This will be elaborated in chapters 6 and 7.

Inverting formula (8) to find g_N as function of g, allows this concept to be reformulated in a way analogue to MOND, so in line with formula (3), in terms of a function µ(y). With y as defined in the previous chapter.

$$\mu \left(y\right)=\mathrm{}{\displaystyle \frac{g_N}{g}}\mathrm{}=1+\mathrm{}{\displaystyle \frac{c^2}{2a_m\sqrt{y}}}-{\displaystyle \frac{1}{2}}\mathrm{}\sqrt{{\displaystyle \frac{c^{2\mathrm{}}(c^2+4\mathrm{}{a}_m\mathrm{}\sqrt{y})}{{a_m}^2\mathrm{}y}}}$$

(9)

But firstly, it must be shown this concept holds, for this natural explanation to be satisfactory. This will be shown in chapters 6 and 7. But firstly, the underlying natural explanation for this concept will be presented in the next section.

4.2. Exploring the Logical Consequences of Hawkings’s Cosmology

In the sequel, the case is argued for a natural explanation for the MOND-like behaviour explained in the previous section, starting from this cosmology and the other elaborations made about superposition. This will not only merge to a natural explanation but yield an improvement of MOND too, in the form of a simple physical model.

The crucial observation of the paper in hand is that if the moment of time where the observer enters the history is not relevant, as discussed in chapter 2.2, this would give all possible observers the same causal status.

Now, it is of paramount importance to realize that there is no natural relationship between the numbers 1, for one universe, and 10⁵⁰⁰ for the number of possibilities, mentioned in chapter 2. Arguing that this number can only lead to one single universe with sentient beings, has created a fine-tuned number, which is not the most economical of explanations, since it would require more explanations itself.

If a universe in which man originated is a realization of 10⁵⁰⁰ possibilities, it is irrational to assume that not at least one more history of the universe, with sentient beings who can also act as observers, has been realized. Who was first or last does not play a role in this, as the 'delayed choice' experiments show. We are then in a multiverse, which state of real superposition, as defined by [8] (p. 77), would result necessarily from the existence of multiple observers. The superposition has then been maintained in the way presented earlier in this essay. The real superposition must necessarily exist if man is the needed observer of our universe. The states will be able to interact with our universe by adding up certain effects, as in the deuteron or the double-slit experiments.

The additional gravity attributed to dark matter can be such an effect. The constants of nature in those universes will have nearly exactly the same value as ours, since the existence of sentient beings does not allow very different values, as explained by [8] (chapter 7 p. 203 in particular) and by Rees in Just Six Numbers [23] .

When one would argue that universes can never get in a superposition state, one ends in a ‘reductio ad absurdum’. There must necessary be a real superposition, but there cannot be one…

But, the values of some of the forces or energies in our universe, like gravity or the cosmological constant, or the mass might be explained as the sum of contributions from different quantum states or histories of the universe if it still would be in real superposition. Then their value should match the sum of two or more allowed values conforming to their probability distribution, as defined by for instance Weinberg regarding the cosmological constant, see Hossenfelder [10] (p. 155). Cosmic forces would then act on the sum of all mass in this superposed universe. The necessary existence of sentient beings in more than one universe, will then be the mechanism that maintains part of the original superposition. Because the ‘delayed-choice’ experiment by Wheeler shows that the moment of time where the observer enters the history is not relevant [8] (p. 106), the observers in the parallel universes possess exactly the same causal status, so they must necessarily all act as observers then. That might be the natural and necessary cause of such a maintained superposition state.

This is a logical way of creating a multiverse from one Big Bang that results inevitably from Hawking’s cosmology if 10⁵⁰⁰ is not a fine-tuned number, and it is presented in chapter 4.3 in steps. The result should interfere with itself very well, as the single photon in a double-slit experiment and yield a sum of binding forces (each with their own amplitude) like in the deuteron.

For there is nothing outside our universe that could disturb the superposition state, it could be in that state forever, without de-coherence effects disturbing it. Since a universe has one history as defined by Feynman, so a common, shared, set of values of nature’s constants, its size is not a reason to disturb it either. And that is why Hawking and others [7,14] can speak of the wave function of the universe in the first place.

4.3. The Argument in Steps

The thoughts leading to the hypothesis can be logically summarized as follows:

• Hawking’s cosmology is a logical combination of two well proven theories, quantum mechanics and Big Bang theory, and thus, it is a good description of the earliest stages of our universe.
• Our universe results from a Big Bang that was in a quantum superposition state at its start, that can be interpreted as 10⁵⁰⁰ alternative histories in an 11-dimensional space, using the Feynman interpretation of quantum mechanics and M-theory.
• The realization of our universe from the 10⁵⁰⁰ alternative histories cannot have occurred without a sentient observer.
• Our universe has been realized.
• At least one sentient observer exists, which can have come into being in the universe following the conclusion of Wheeler’s delayed choice experiments.
• Since it is not economical to consider 10⁵⁰⁰ a fine-tuned number, aimed at creating exactly one universe with sentient being, there still remains a superposition state of more than one alternative histories of the universe. This makes it a multiverse, each universe with sentient beings. This multiverse still exists by means of a state of superposition, which must not necessarily be disturbed by de-coherence, since nothing exists outside the multiverse.
• The other universes in superposition can follow a history comparable with ours that leads to sentient beings, but do not necessarily share all our spatial dimensions in the 11-dimensional space, but do have nearly exactly the same constants of nature. From the delayed choice experiment it follows they all have the same causal status.
• The gravity of these superposed 11-dimensional universes acts together just like the binding force in a deuteron.
• Since there are more ways to yield partly overlapping universes in an 11-dimensional space than fully overlapping, the odds are that there exist multiple universes that share only one or two dimensions with our universe.
• Gravity acting in our universe resulting from the 2-dimensional projection of another one, leads to a linear decrease of the gravitational acceleration as a function of distance from a mass.
• The existence of multiple universes that share two dimensions with our universe in a state of superposition, forms a natural explanation for the linear MOND-like behaviour of gravity at large distances from the core of galaxies.

An argument like this is as strong as its premises. Therefore, the word proof or evidence is avoided here and it is called an argument. In the sequel, this path of thinking will be further worked out.

5. An Elaborated Proposal for Dark Matter

Here it is important to recall that mathematically, a linear gravity field, following an inversed linear law, can only occur in a 2-dimensional universe. Or in a 2-dimensional projection or intersection of a higher dimensional universe that is proposed here. This is analogue to the fact that mathematically in our 3-dimensional universe gravity must follow an inversed square law. That is the starting point for the line of thought to be pursued in the sequel.

The intersection of these universes one would appear to one another as a series of mutually unconnected planar cross sections of the same higher dimensional galaxy, so with one dimension less. Together the 2-dimensional projections fill the volume like a stack of papers. This will be elaborated further in the sequel.

It is vital to note, that to get from one intersection of a galaxy to another, can take an exceedingly long distance in the 2-dimensional universe. With one dimension more, as discussed in the previous, this would even concern different galaxies. But what would the expansion of space dot to this? This is explored in chapter 6.3.

Taking a side-step about the number of dimensions in a universe within the framework of String-theory i.e., eleven is important here. Our 3-dimensional universe does have eight other dimension that are curled up in the strings of which all matter and energy is made. This means they are not zero but have the Planck-length Lp. But, for the sake of economy it suffices to work with four dimensions instead of eleven.

All the universes could fill the higher dimensional multiverse in exactly the same manner, but orthogonally to each other. In the multiverse, what in a 3-dimensional universe seem independent galaxies at huge distances from another, might be part of one larger structure in 4-dimensional space, analogue to the 4-dimensional representation of the bookshelves towards the end of the motion picture Interstellar at 2 h: 16 m.

Now, the proposed natural explanation for dark matter comes from the line of thought set in motion with Hawkings’s cosmology and the investigation of MOND-like behaviour in the above. It is that the universe consists of four 3-dimensional universes, existing as four states of a superposed 4-dimensional space. ‘Our’ third dimension will be curled up in the strings of the others, just like ours is in the four others, according to String-theory. At the very start, the diameter of our 3-dimensional universe Lp, would exactly match the thickness in the other three universes, being Lp too. Thus, they can all be represented by the same particle. This could be Lemaitre’s ‘primeval atom’ [24]. And this was in a state of superposition.

At the very beginning, ‘ours’ and the superposed universes, a multiverse in a sense, would then have a perfect geometrical and physical match, without any internal contradiction. All would be perfectly overlapping and thus be causally coupled entirely, since they all exist the same underlying 4-dimensional space, with, say dimensions w, x, y and z. All the constants of nature could be the same or differ only very slightly and just the distribution of the dimensions that are not curled up, would differ. Then, when the universe starts expanding, the thickness of the other as seen from our universe would remain Lp. The four expanding universes fill the higher dimensional multiverse each in the same way, but mutually orthogonal. The four dimensions will be distributed over the universes as follows: xyz, wxy, wxz and wyz.

Galaxies that in our 3-dimensional universe seem independent galaxies at huge distances from another, might be part of one larger structure in 4-dimensional space. In the other superposed universes this will be different structures, but the structures will attract each other by 4-dimensional gravity and tend to overlap in 4-dimensional space. As a result, on the scale of a galaxy the mass would be located at globally the same positions as in our universe, but on the scale of individual stars or solar systems not, since on these smaller scales Newtonian gravity fully dominates.

As a result, our 3-dimensional universe would from the start be totally keep filled with three additional linear gravity fields. Linear because it comes from a two-dimensional projection of the others in our universe.

Formula 1 can then be rewritten as follows for the fourfold multiverse:

$$\mathrm{Ĥ}\left(x\right)\mathrm{}({\mathrm{}a}_{xyz}\left|{\mathrm{ѱ}}_{xyz}\mathrm{}⟩+\mathrm{}{a}_{wxy}\right|{\mathrm{ѱ}}_{wxy}\mathrm{}⟩+a_{wxz}\left|{\mathrm{ѱ}}_{wxz}\mathrm{}⟩+a_{wyz}\right|{\mathrm{ѱ}}_{wyz}\mathrm{}⟩\mathrm{})\mathrm{}=0$$

(1*)

In a sense (1*) says the total energy of the multiverse is zero.

A variant with only three of those would as well give linear gravity in all directions, but then one of the coordinates would be in the set three times and the other only twice, yielding an anisotropy of sorts. Such an anisotropy would as well occur if the amplitudes a_ijk in formula (1*) would not all have equal values. Since the said SPARC data give no clue to this option, it is not further elaborated in this paper.

The same applies to universes that overlap in one dimension; this gravity would remain constant with distance and hence, along a closed loop through the universe, this gravity from both sides would cancel out. Three overlapping dimensions would just yield additional gravity with an inverse square law. The said SPARC data gives no indication for that either, since its effects will remain hidden upon fitting the mass-to-light ratios but contributing to the variation in these ratios between different galaxies.

The additional gravity field, i.e. the sum of three 2- dimensional fields, will then naturally be a field with linear decrease of gravity with distance r between two objects.

The dark matter would be there in the Big Bang at the time it was needed to come to the cosmic composition as we know it and create the ‘hot’ and ‘cold’ spots in the background radiation, see Darling [25] (p. 204), Schilling [20] (p. 225).

The orientation of the sets of two overlapping dimensions in relation to a galaxy still is an issue. Han in 2023 [26] showed that the outer disk of the Milky Way Galaxy is warped and flared. Several mechanisms have been proposed to explain these phenomena, but none have quantitatively reproduced both features. Han demonstrated that the Galactic stellar halo is tilted with respect to the disk plane, suggesting that at least some component of the dark matter halo may also be tilted. The origin of this misalignment of the dark halo, of approximately 25°, can be explained by the linear gravity theory in the paper in hand, since the orientation of the two dimensions of another superposition state overlapping with ours can deviate from the orientation of a galaxy. There is no reason s galaxy should be in line with these dimensions and hence with the linear gravity field. But a tilting will cause a moment acting on the galaxy, because linear gravity will give a force acting in its own plane, which will act to rotate the galaxy in the direction of the 2-dimensional linear gravity, but that will take time. In the meanwhile, the apparent dark matter halo can be tilted.

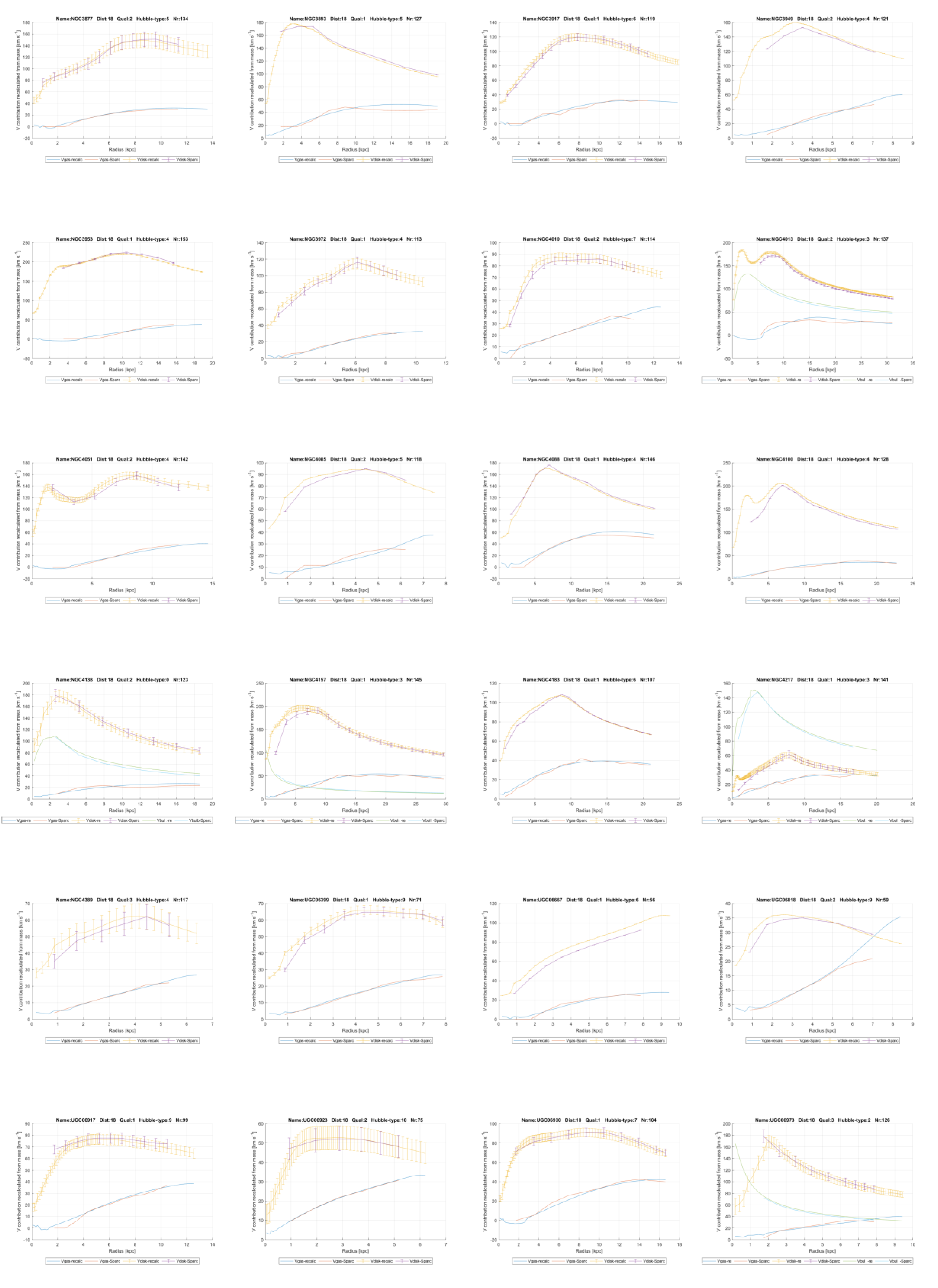
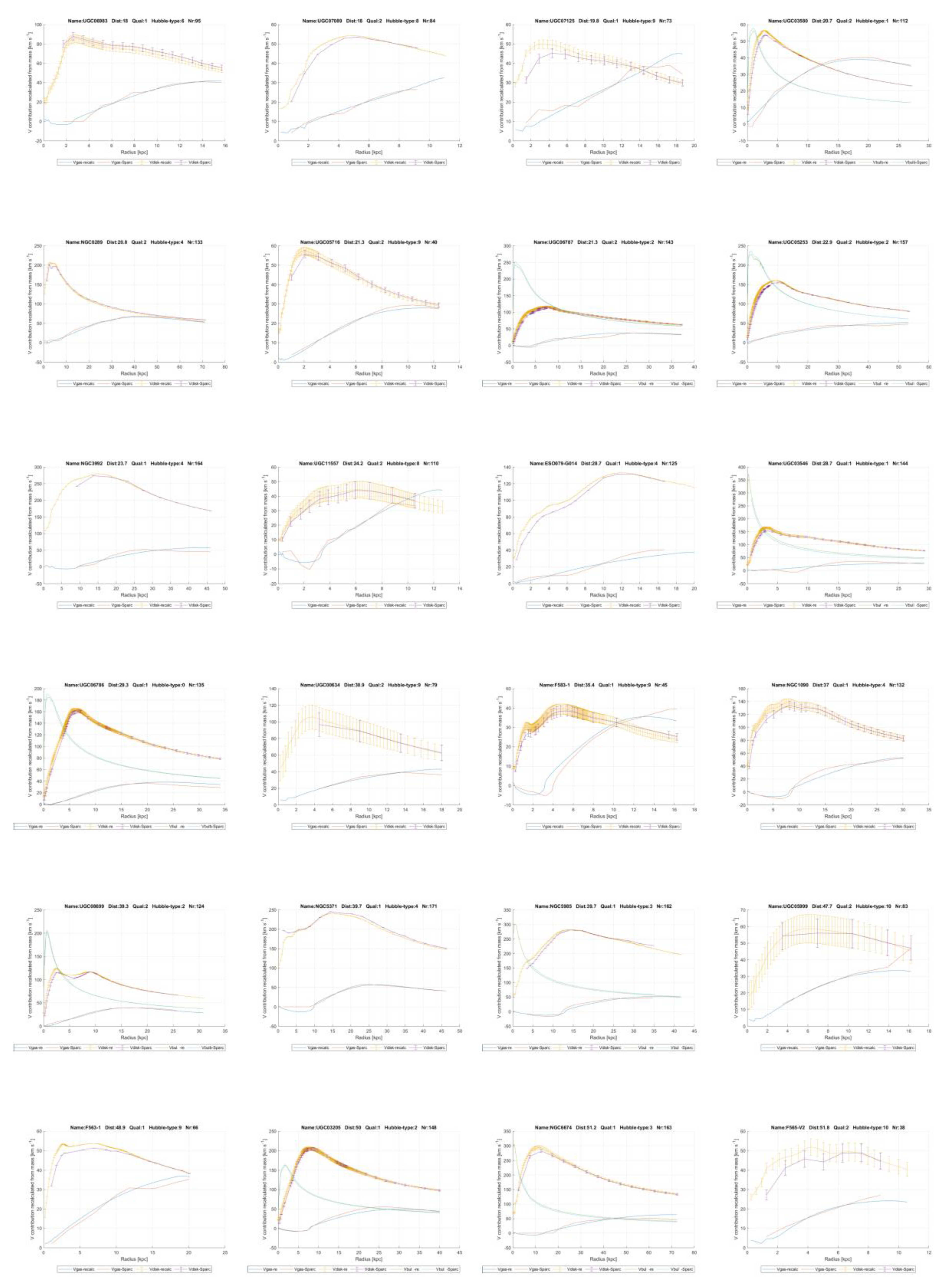
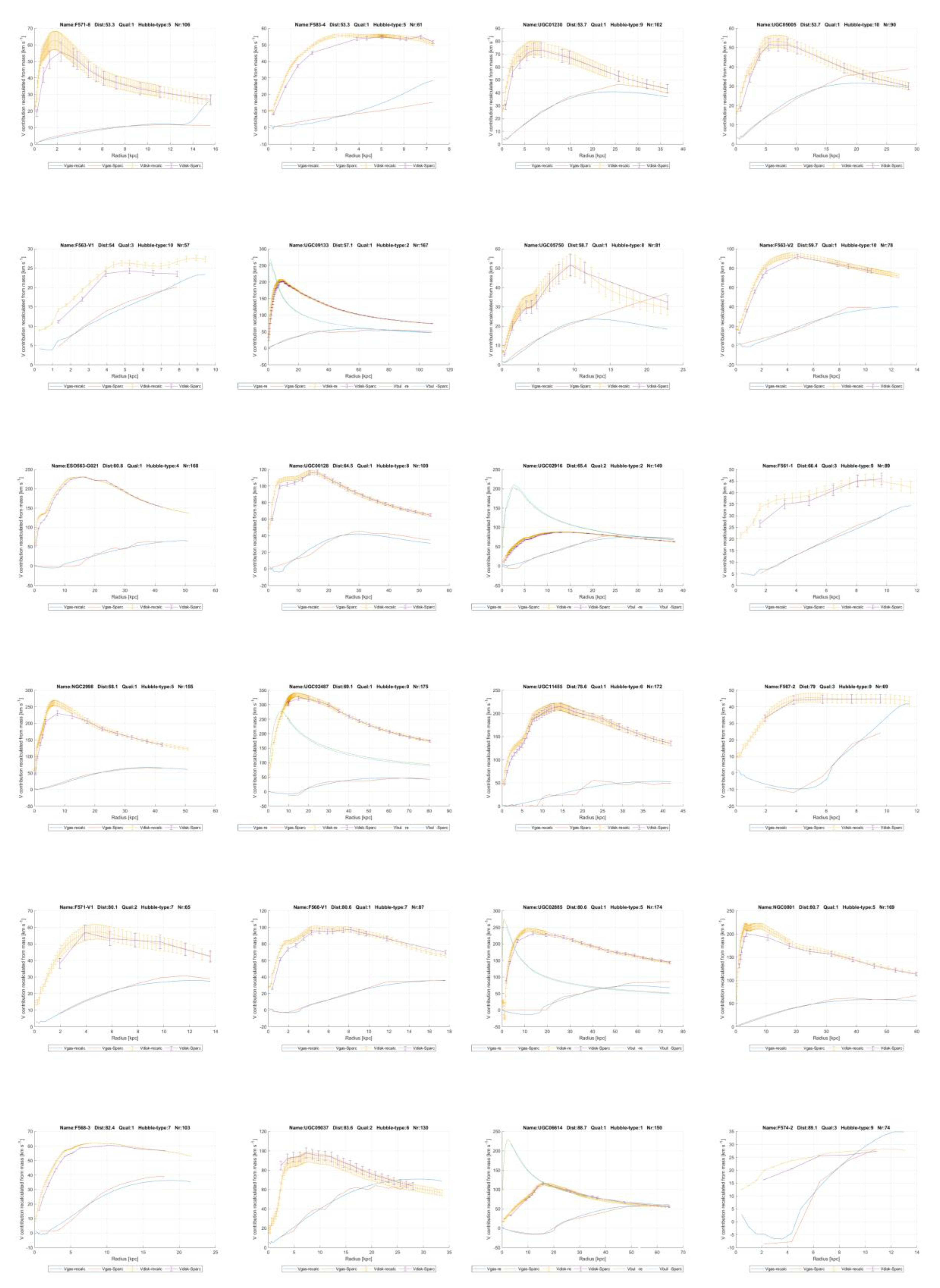
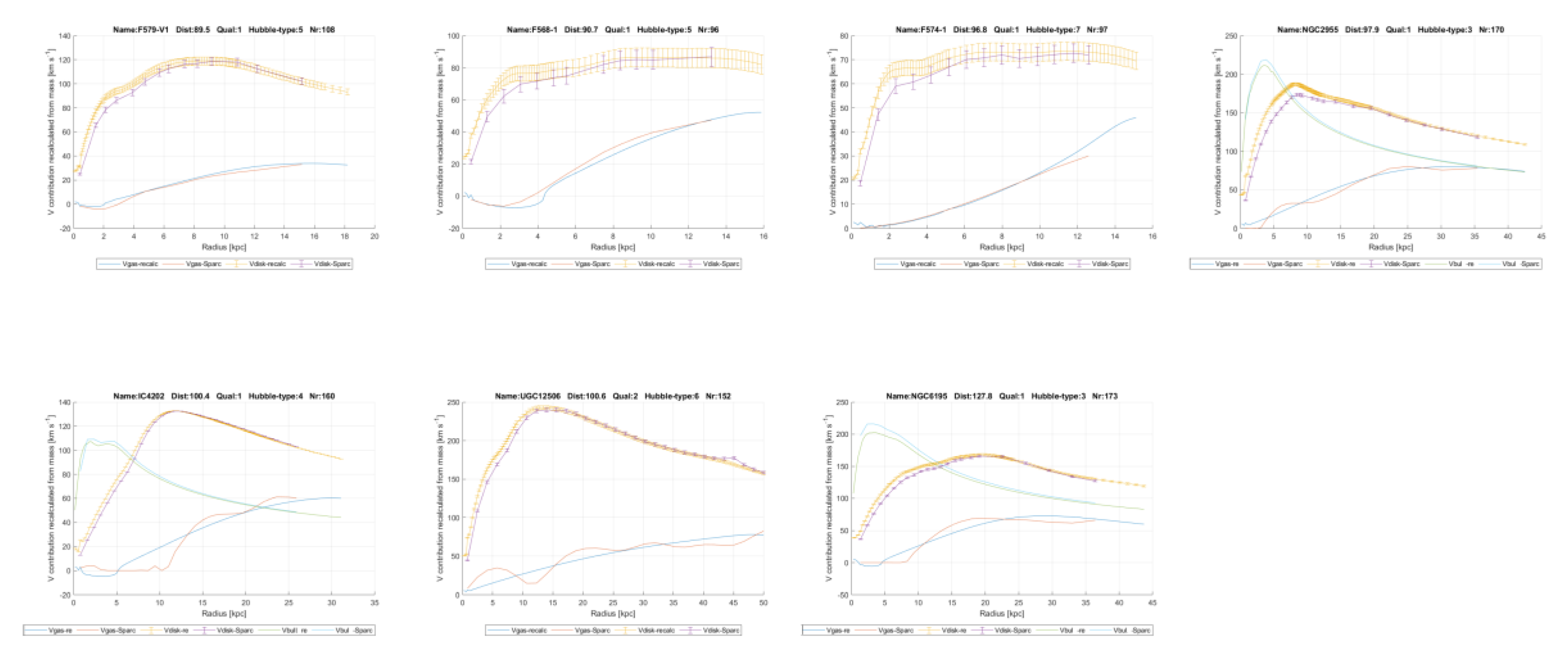
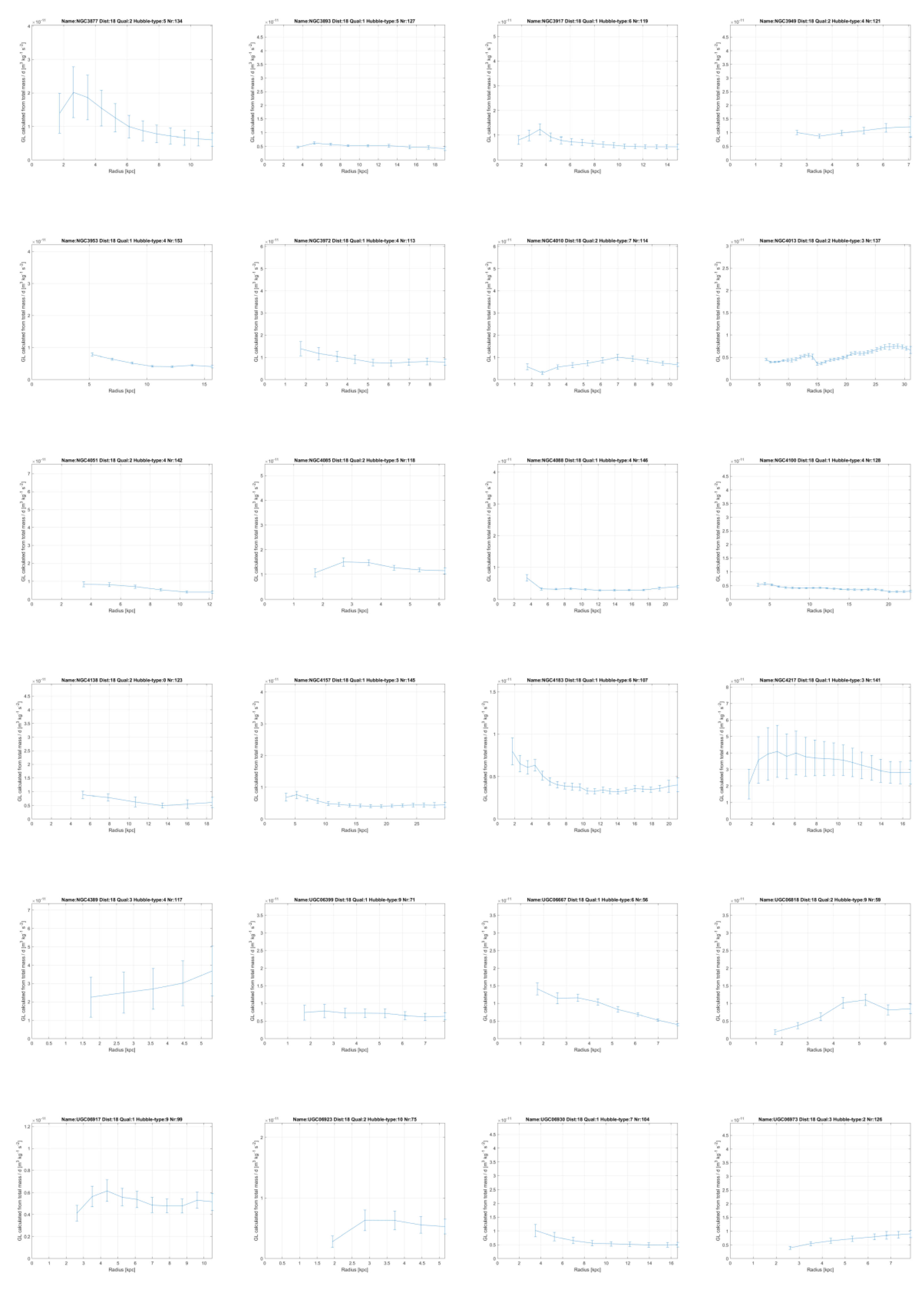
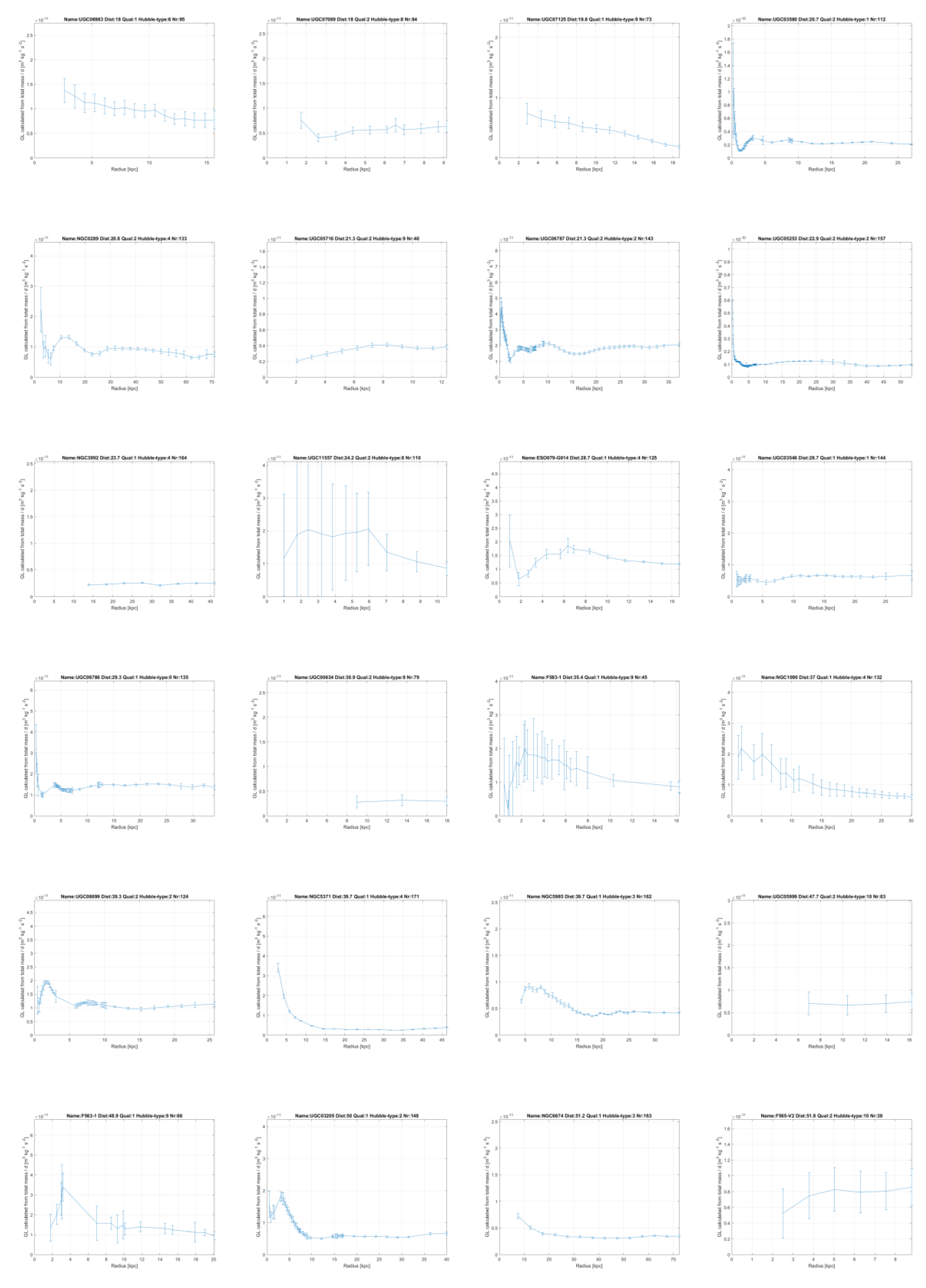
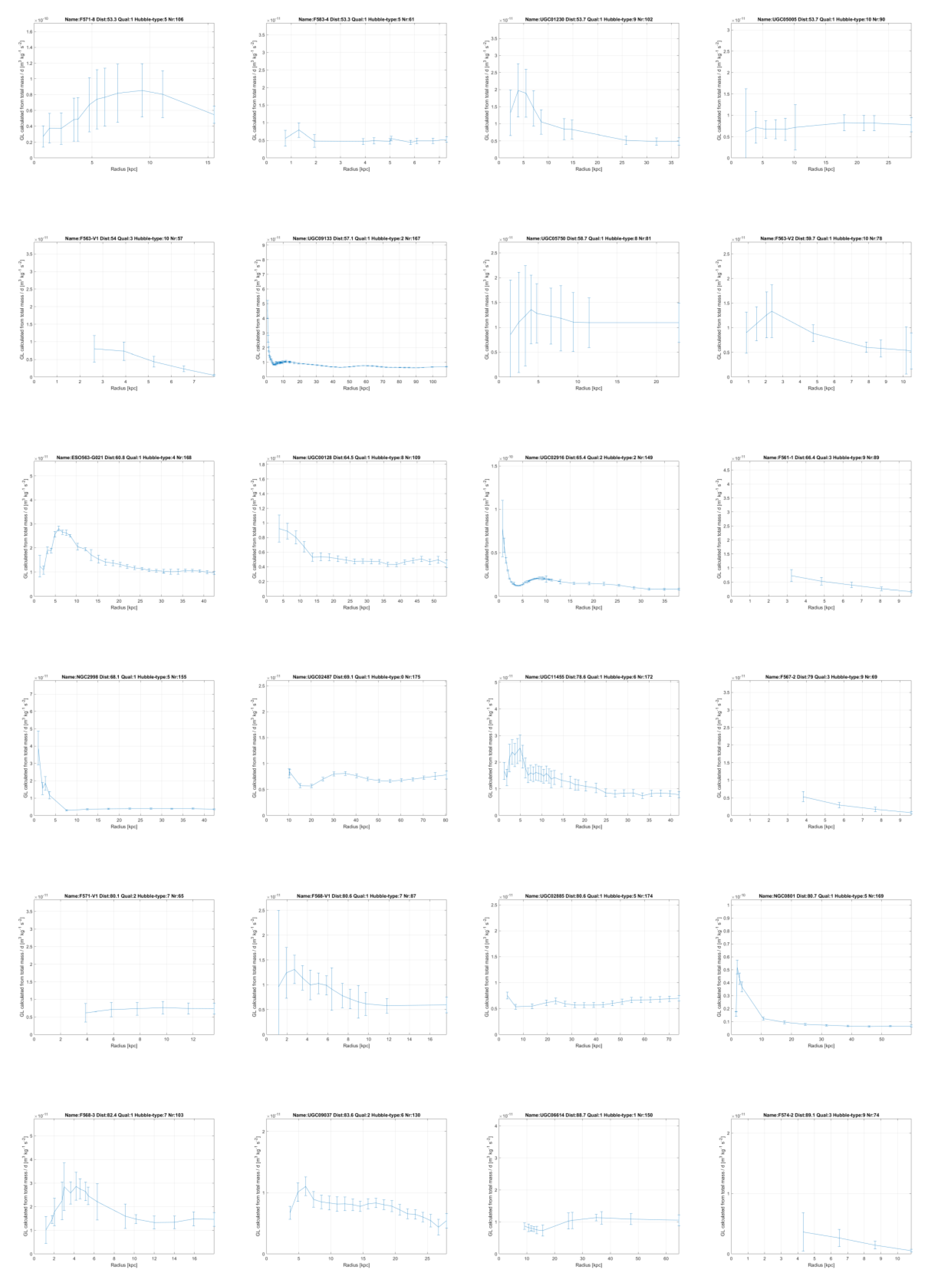
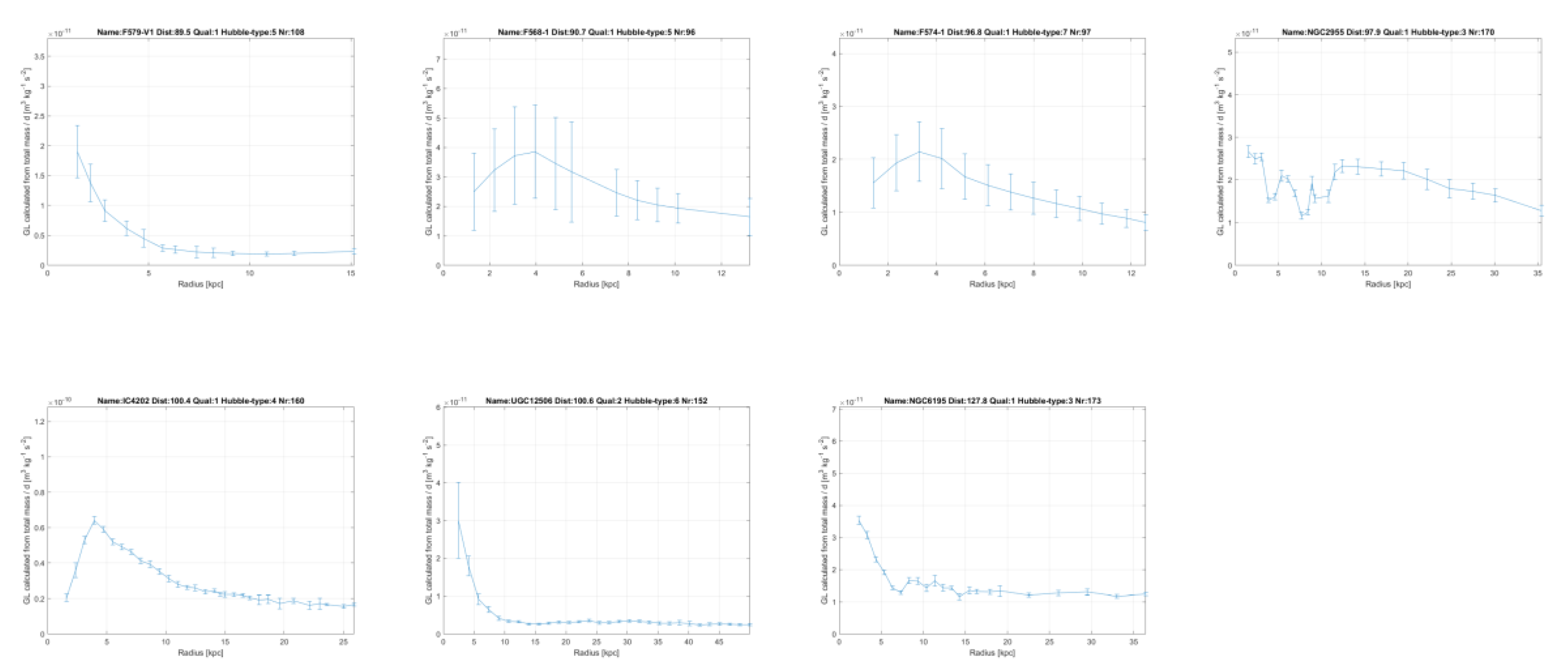
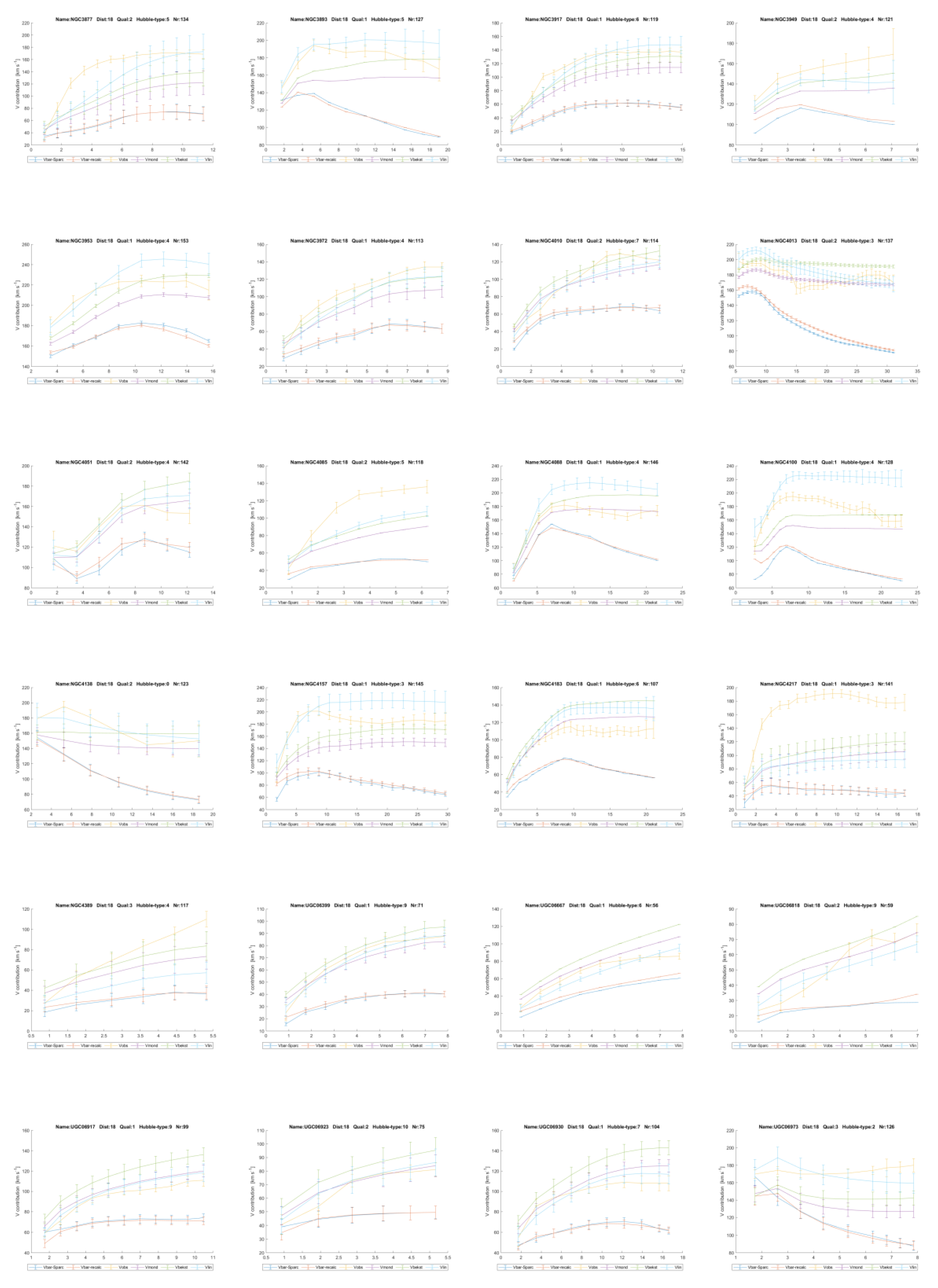
In chapter 6 it will be shown this linear gravity proposal indeed works and leads to a good description of the contribution of dark matter to gravity in galaxies. To get there, firstly for all 175 galaxies in the SPARC database as reported by Lelli et al. [11] and Starkman et al. [12], the contributions of the visible ‘baryonic’ matter distribution to the gravitational acceleration and from the invisible gas have been recalculated.

The resulting matter distribution has been derived from the brightness profiles and HI gas concentrations as reported by Lelli et al. [11] and Starkman et al. [12] and then compared with their results. This has done so as to be sure that the author has performed the conversion from brightness to mass distribution correctly, for gas, disk and bulges, see Figure 2 and annex 1 where the variables V_gas, V_disk and V_bulge of the SPARC team and the author are mutually compared. In chapter 6.1 this is all explained in depth.

6. Testable Predictions

In the sequel, six predictions that follow from the hypothesis and support for them will be presented.

6.1. First Prediction

The first prediction that follows from the above considerations is that this superposed particle fits in the mathematics of M-theory. It will be a valid solution of the equations of M-theory. They can then be exactly solved for the superposed ‘primeval atom’ depicted earlier.

Now, the boundary condition for this solution would be the existence of ‘our’ multiverse, following the ‘top-down’ way as Hawking argues, since our observed multiverse is the realized one in the ‘cosmic double-slit’ experiment. This would need to be done with a quantum gravity theory based upon this superposition. In line with this, Einstein’s field equations, with some added fields, will have a solution that matches with this hypothesis. This will be studied in chapter 7.

6.2. Second Prediction

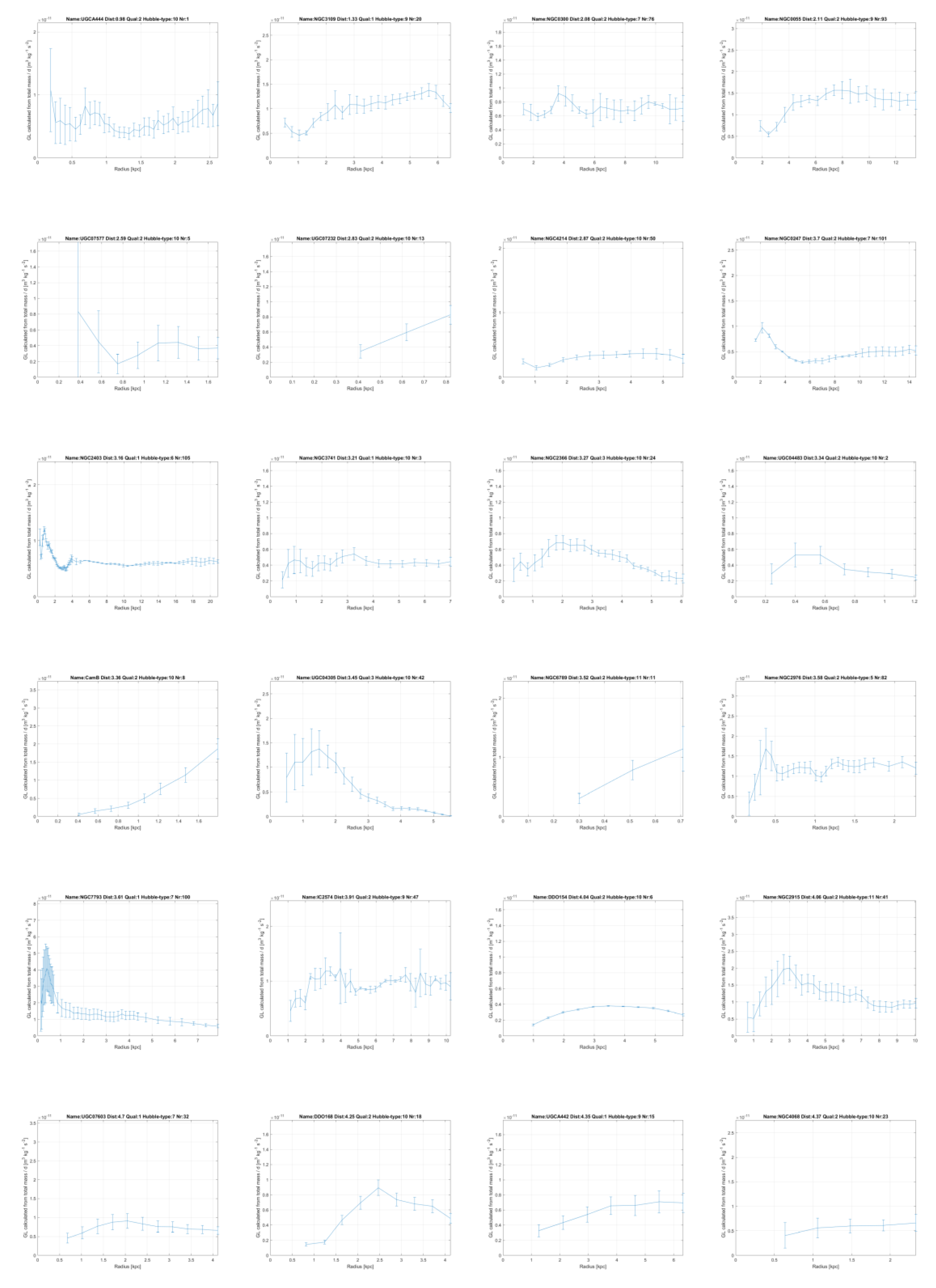
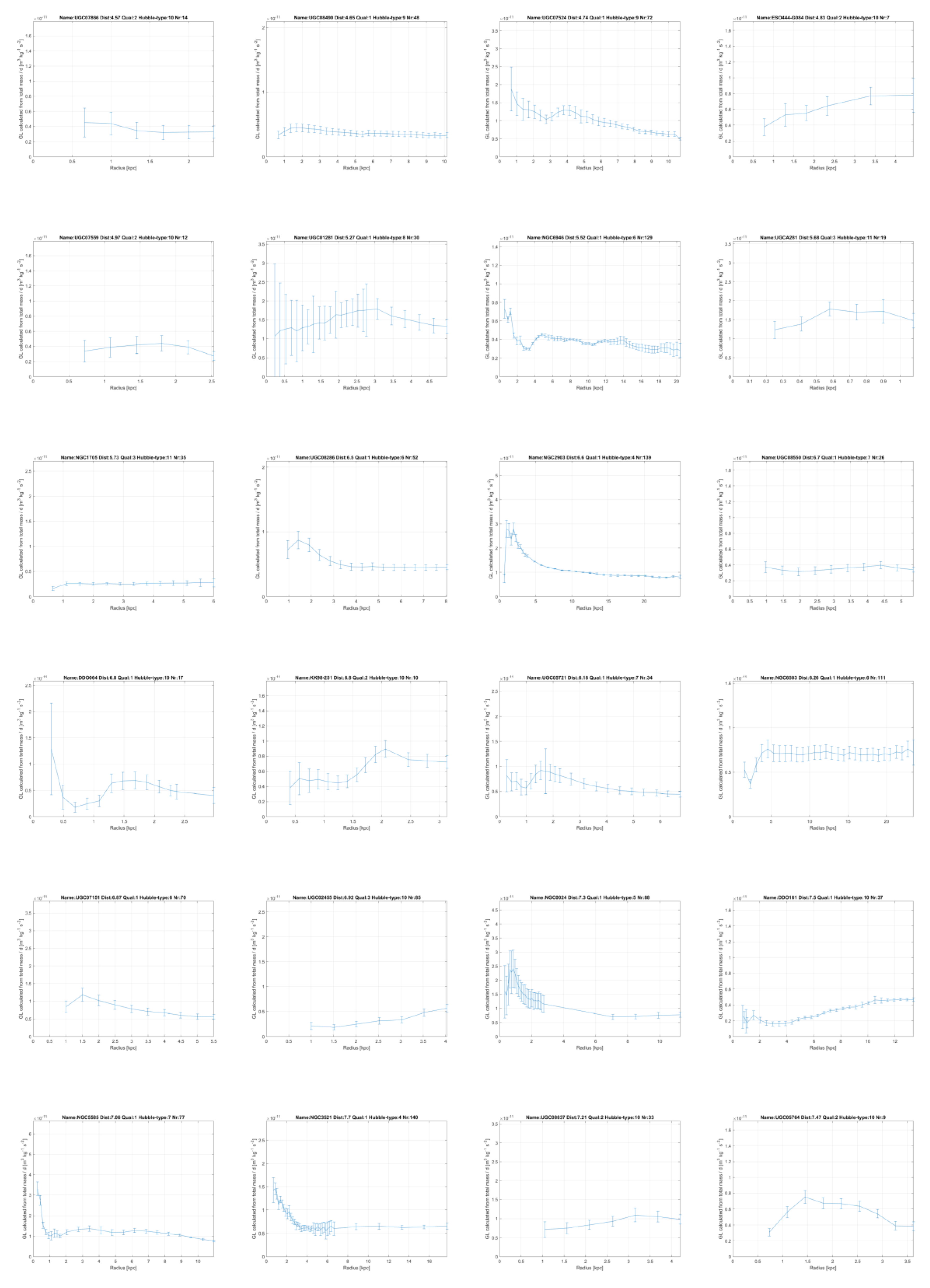
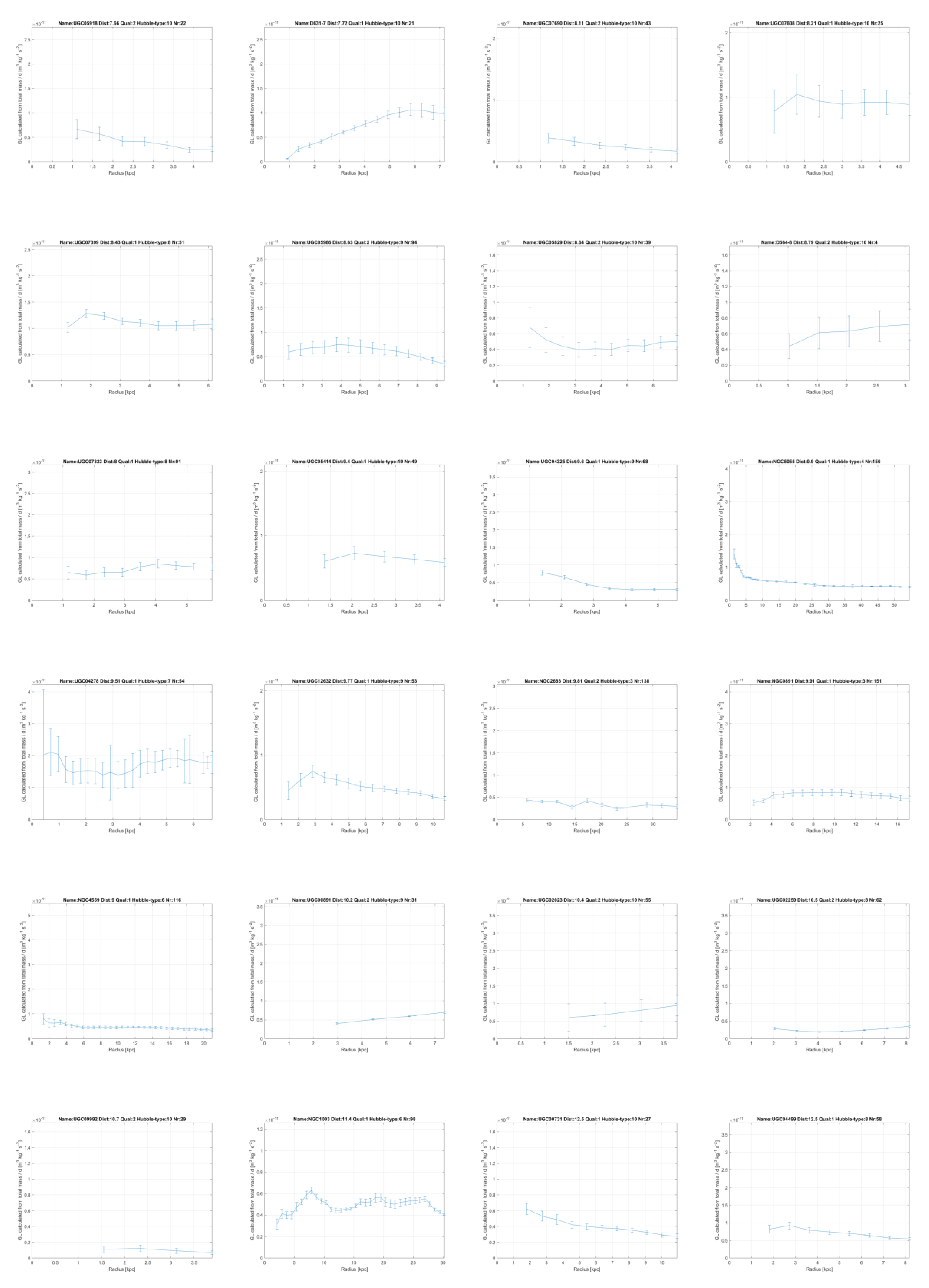
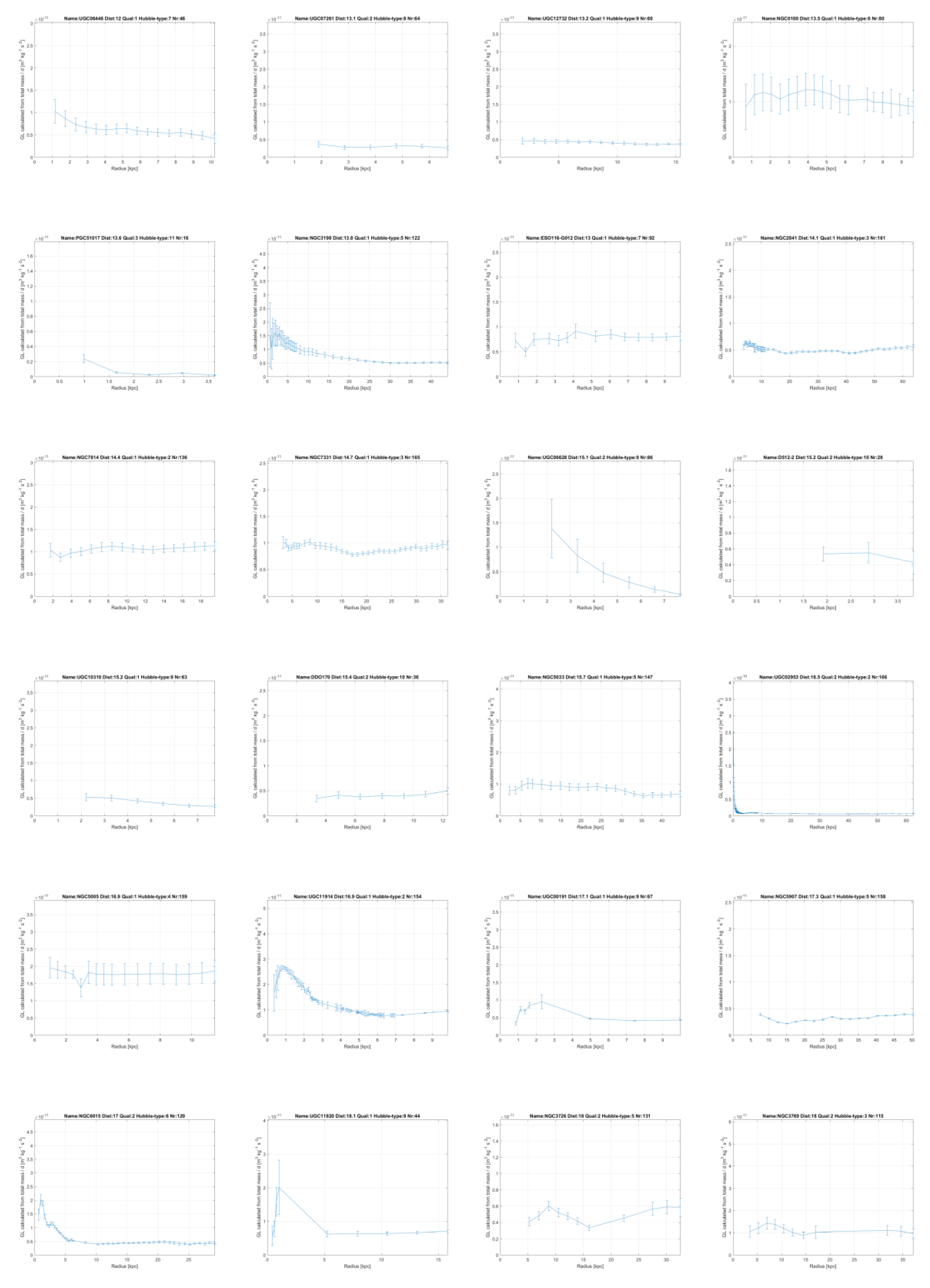
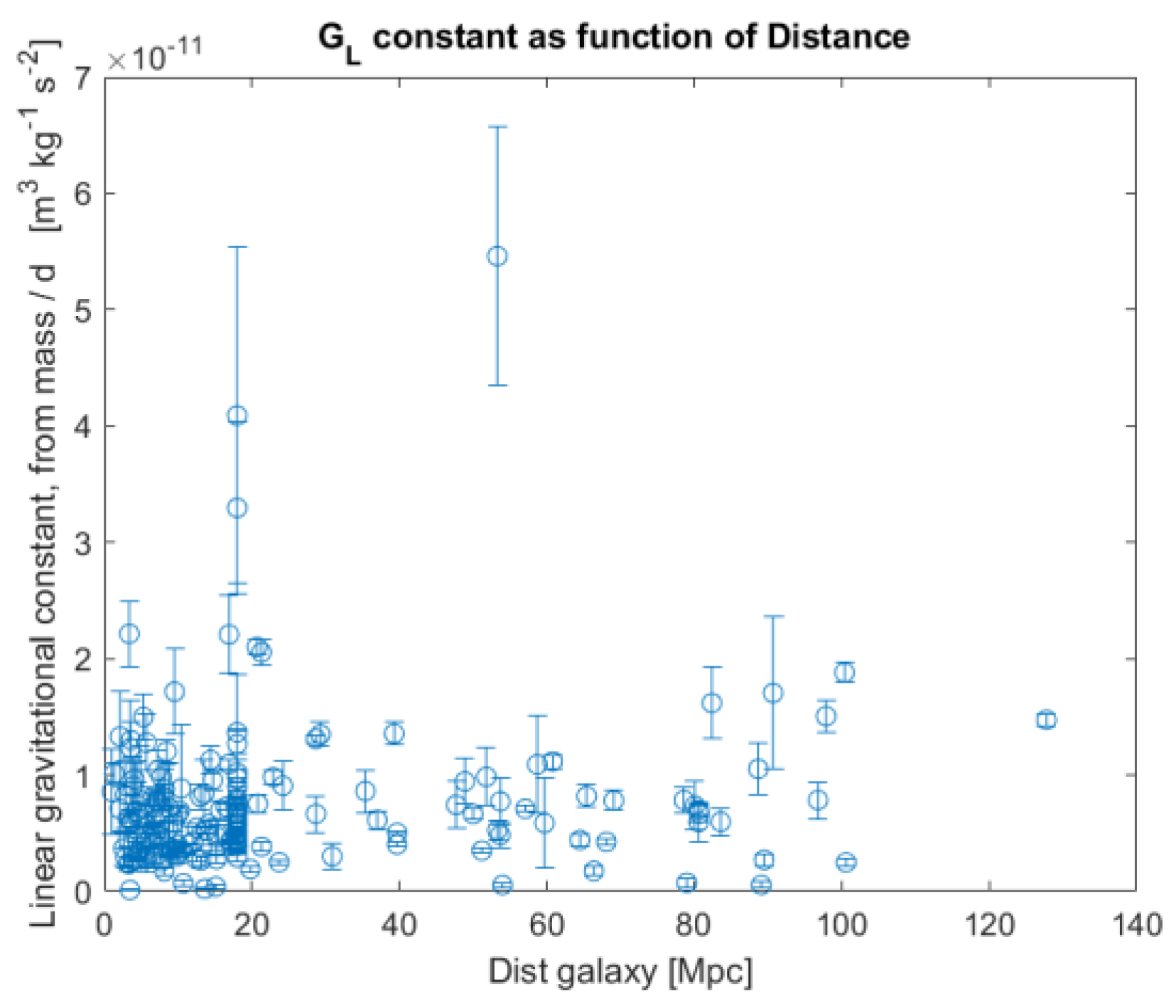
The second prediction is that the additional acceleration can be expressed in the form of a linear constant of gravity G_L, which is constant within each galaxy and will be proportional to the amount of dark matter in a galaxy, which will vary between different galaxies, but to a limited extent. In the annex this linear constant of gravity G_L, has been plotted for all 175 galaxies from the SPARC database measured with the Spitzer Space Telescope [11,12] and it is mainly seen to be constant.

The core assumption, as mentioned, is that the distribution of dark matter closely resembles the that of the visible matter, since they attract each other through linear gravity in the 4-dimensional space. This is consistent with the findings of Lelli and Mistele [9] mentioned in the introduction. They used a new deprojection formula to infer the gravitational potential around isolated galaxies from weak gravitational lensing with the said SPARC data. With these data, they showed circular velocity curves that remain flat for hundreds of kpc, greatly extending the classic result from 21 cm observations. Indeed, they state there is no clear hint of a decline out to 1 Mpc, well beyond the expected virial radii of dark matter halos. This means the common way to project dark matter halos around galaxies cannot be valid. The hypothesis in the paper in hand clearly does not have this problem, since it models dark matter as existing at the same location as the visible matter because of the mutual gravitational attraction.

To assess the validity of this constant for linear gravity, firstly for all 175 galaxies the contributions of the visible ‘baryonic’ matter distribution to the gravitational acceleration and from the invisible gas have been recalculated from the brightness profiles and HI-gas concentrations as reported by Starkman et al. [12]. This has been expressed in the form of velocity contributions, as the SPARC team did too. For the visible disk contribution, it is called V_disk and for the HI gas V_gas. This done in order to verify and show that the author has interpreted the brightness profiles from the visible disk, from the bulges and the gas mass distributions correctly.

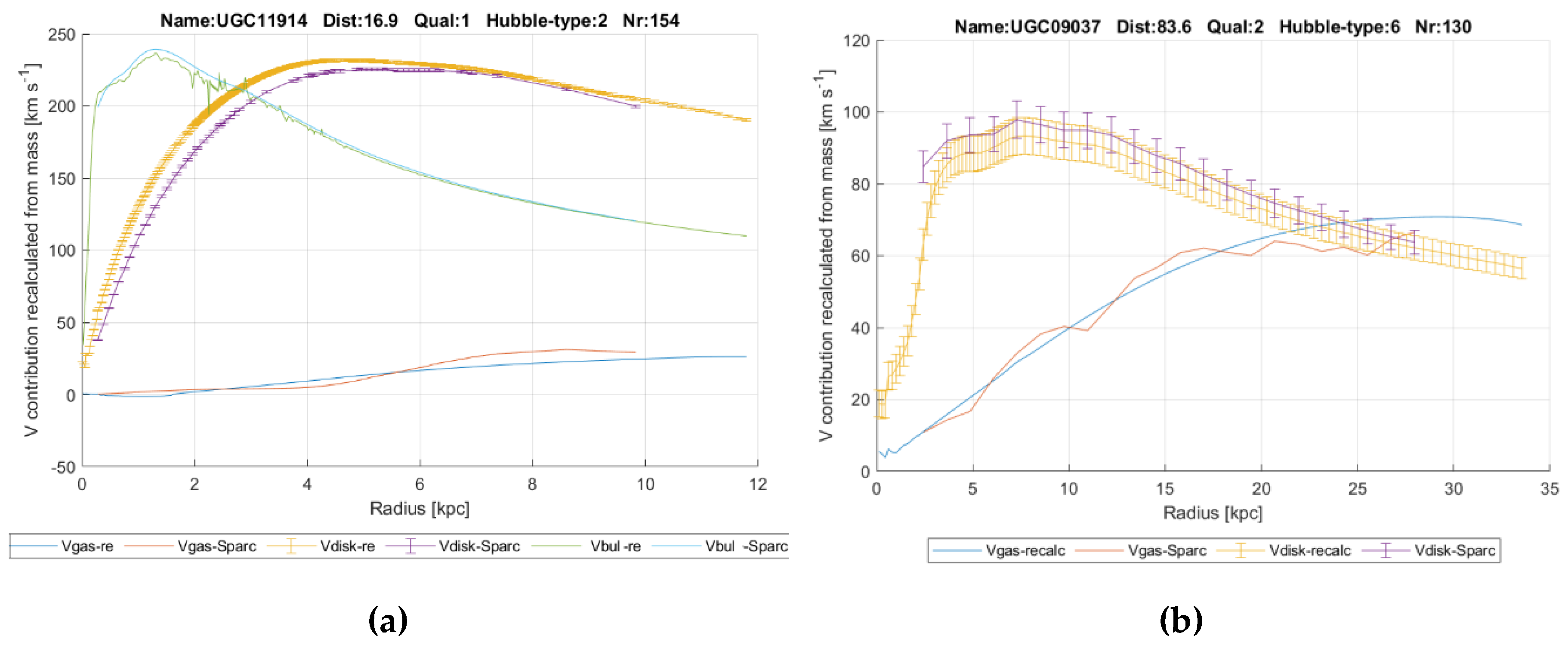
Figure 2 shows the contributions to gravitational acceleration as a function of radius distance. It is plotted for the galaxies UGC11914 and UCG09037, the first of which with a bulge contribution, called V_bulge. The ‘recalc’ subscripts refer to the values as calculated by the author, The ‘SPARC’ indications refer to the values as reported by Starkman [12] at the website, in the file MaximumDisk_Mass_Models_mrt.txt. This is the file produced by [12]. It contains disk brightness profiles as well as observed rotation velocities, V_obs and bulge brightness profiles as well as the theoretical velocities as calculated by the SPARC team with Newton’s law of gravity. It also contains error estimates, except for V_bulge and for the HI gas V_gas. As a consequence, for those variables, no error bars will be shown in the graphs down here and in the Annexes.

The squared theoretical velocities can be added and then result in the total Newtonian or baryonic gravitational acceleration, which can as well be expressed as a velocity contribution V_bar. But the contribution of V_disk and V_buls depend on the mass-light-ratio Y_ml, as follows:

$$V_{bar}=\sqrt{Y_{ml}\left(V_{disk}^2+V_{bul}^2\right)+\left|V_{gas}\right|V_{gas}}$$

(10)

V_gas in particular can have a significant negative contribution from gas outside the observed radius. Therefore, it is multiplied with its absolute value here to maintain the correct sign.

The mass-light-ratio, Y_ml is assumed 1 at this stage and will later act as the single fitting parameter.

The contributions are calculated from the brightness profiles under the assumption that in thin disks the latter directly represent a distribution of the mass density. In the bulges this is not true; here brightness represents a cumulative mass density distribution since all observations of brightness run through the entire bulge and each layer adds brightness to the inward layers. So, it must be converted to a distributive mass distribution first, by subsequently subtracting the brightness contributions from larger radii at each observed radius, the part between two radii considered as a slice of a sphere. A complication with this is that the integration path length through each slice of the bulge is dependent on the radius observed. For example, at the most inner radius the brightness contribution from the outmost slice is much smaller than at the second outmost radius, since there one looks a long way perpendicularly through the outmost slice.

The HI-gas densities have been retrieved from the reported total HI mass and from the reported HI-radius by fitting the reported V_gas to the formula from Martinsson [27], see formula (11). Three of the parameters that were fixed by Martinsson have been replaced by fitted parameters a, b and $\sum _{HI}.$ The latter is fitted to match the total reported HI mass of the galaxy. Multivariate regression has been used to find the optimal values in:

$${\sum }_{R}HI\left(R\right)={\sum }_{\mathit{HI}}{e}^{-{\left({\displaystyle \frac{R-a{R}_{\mathit{HI}}}{0.36R_{\mathit{HI}}}}\right)}^b}$$

(11)

Following Lelli [11], the total gas mass has been multiplied by a factor of 1.33 to account for helium gas as well.

Since, as mentioned, the goal of the calculations in the above merely is to verify and show that the author has interpreted the brightness profiles from the visible disk, from the bulges and the gas mass distributions correctly and not to obtain an improved mass-model, for some galaxies interpolations and extrapolations of the brightness profiles have been made to come closer to the SPARC graphs. In some cases, the extrapolations have been performed based upon the logarithm of brightness, which more or less is linear, but sometimes manual adaption to this profile have been made to, again, come closer to the SPARC graphs.

The centrifugal force F_c is linearly decreasing with radius R and proportional to the square of rotation velocity. Thus, the contribution of each mass component to the velocity can be calculated from the respective gravitational acceleration contribution g_c = F_c/m with:

$$F_c=m{\displaystyle \frac{V^2}{R}} [\mathsf{N}]$$

(12)

Then gravitational acceleration for each particle at each radius and each angle of it’s orbit can be calculated by summing up masses in each part of the galaxy disk and bulge with (13) for the disk and with (14) for the 3-dimensional bulge:

$$g_c\left(R\right)=G{\sum }_i{\sum }_{\mathrm{\varnothing }}{m}_i/\left(X_{i,\mathrm{\varnothing }}^2\right) [\mathsf{m}/{\mathsf{s}}^2]$$

(13)

$$g_c\left(R\right)=G{\sum }_i{\sum }_{\mathrm{\varnothing }}{\sum }_{\beta }{m}_i/\left(X_{i,\mathrm{\varnothing },\beta }^2\right) [\mathsf{m}/{\mathsf{s}}^2]$$

(14)

G is Newtons constant of gravity. Mass outside the orbit of each particle as far as it is not at the side of the centre of rotation as seen from the particle has a negative sign. It has a negative contribution to the centrifugal force after all.

Gravitational acceleration as observed in each galaxy, is calculated from the observed velocities V_obs i.e. from the centrifugal force. This V_obs is plotted in Figure 3, as well as the baryonic contribution to the acceleration expressed as V_bar, see its definition in formula (10). The lines Vmond and Vrecalc will be discussed in chapter 6.4.

The mass-to-light ratio has been used as the only fitting parameter to fit the baryonic rotation velocity, and hence the baryonic gravitational acceleration in each galaxy to the observed values near the core of the galaxies. After that, the hypothesis in hand is used to predict the additional gravitational acceleration at all radii without any further fitting.

The Newtonian gravitational accelerations, expressed by V_bar, are now calculated with a fitted mass-to-light ratio, Y_ml. It has for each galaxy simply be fitted such that V_bar < 0.85 V_obs, at all radii, so following the sub-maximum disk hypothesis. This assumes that the contribution from the Newtonian gravity never can be larger than the observed value, with some margin at all radii, so assuming there always is some contribution of dark matter at the smallest radii where Newtonian gravity will dominate too.

The error bars have been computed from the error estimates provided by the SPARC team, which concern eV_disk, eV_bar, eV_obs and the error of the disk surface brightness eSB_disk. But eV_disk is already entailed in eV_bar, so it is ignored in the following. It has been assumed that deviations occurring in the measurements of the surface brightness at each radius are independent from each other and that those measurements are independent from the measurements of the rotation velocities and from the calculated velocities. The latter means that the correlation between eV_bar and individual errors of eSB_disk, each occurring at one radius, is negligible. Furthermore, the contributions of eSB_disk. at specific radii have been weighted with the inverse of the squared distance $X_{i,\varnothing ,\beta }^2$ of each mass m_i as defined in formulas (13) and (14) to the observed point. $X_{i,\varnothing ,\beta }^2$. The errors in the variables computed in formulas (13) and (14) can then be combined at each radius R, after Ku [28] (p. 265) as follows:

$${\displaystyle \frac{\sigma g_c\left(R\right)}{g_c\left(R\right)}}=\sqrt{({\displaystyle \frac{e_{V_{obs}\left(R\right)}}{V_{obs}\left(R\right)}}{)}^2+({\displaystyle \frac{e_{V_{bar}\left(R\right)}}{V_{bar}\left(R\right)}}{)}^2+({\displaystyle \frac{\sum e_{{SB}_{disk}\left(R\right)/X_{i,\mathrm{\varnothing },\beta }^2}}{\sum {SB}_{disk}\left(R\right)/X_{i,\mathrm{\varnothing },\beta }^2}}{)}^2}$$

(15)

The case for linear gravity from dark matter being a 2-dimensional projection of other 3-dimensional universes, makes the additional gravity g_linear dependent on the mass density in the plane of rotation since this gravity only can work in a 2-dimensional plane.

It thus depends on the mass density in the plane of rotation M/d. For the disks the thickness d must be estimated, for the bulges this can be exactly calculated. Please note, for the bulges all mass in the bulge outside the plane of rotation is ignored and only the mass density in that plane contributes to the observed rotation velocities. It will be shown this holds very well.

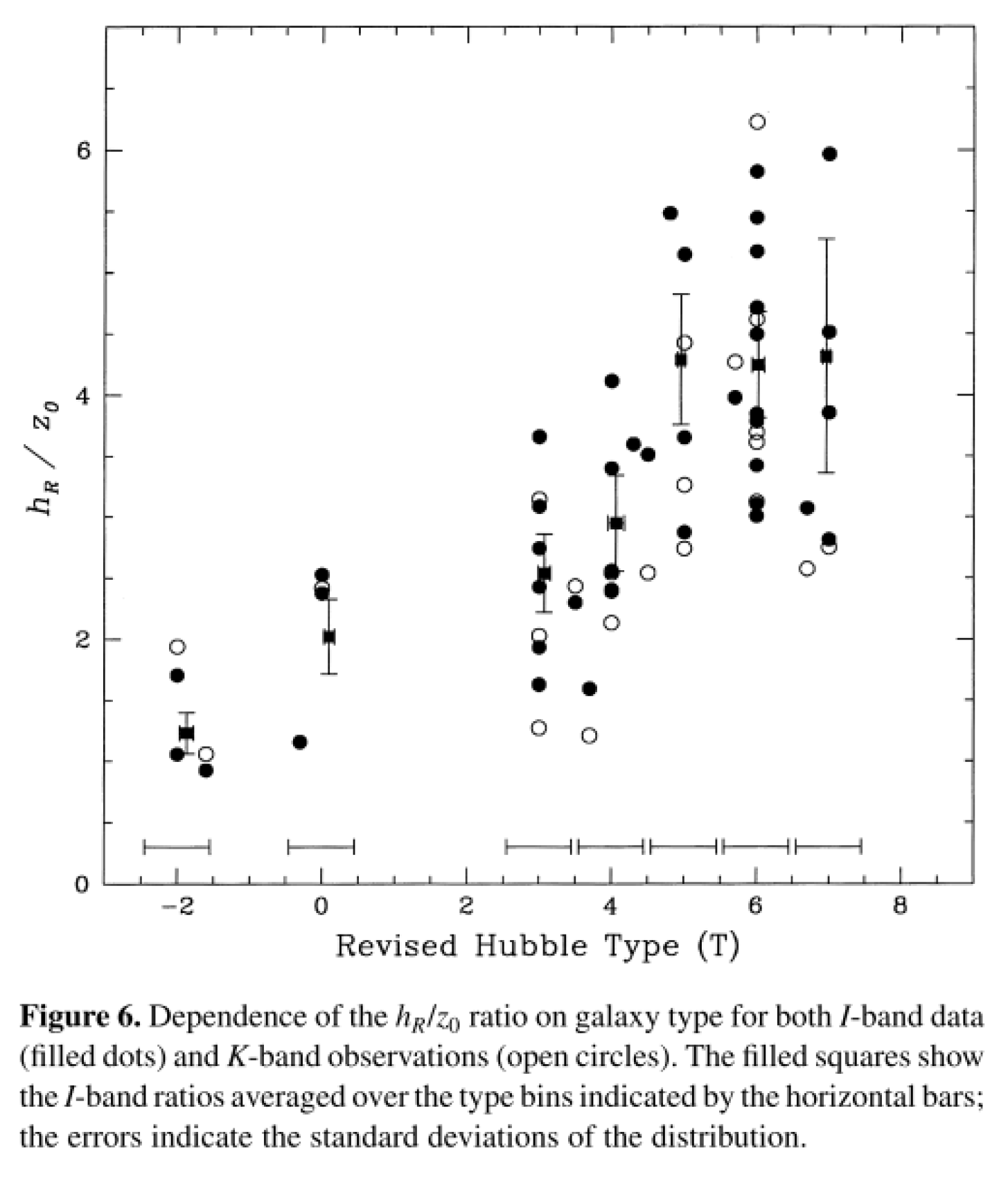
The thickness d has been taken equal to the vertical scale length z_o as calculated from the disk scale length ratio h_r /z_o, defined after Kruijt [29] (p. 11) and Sparke and Gallagher [30] (p. 202). The latter reference states at that page that typically the disk is about 10 % as thick as it is wide, so h_r /z_o ≈ 0.1. But, calculations by the author show that better predictions can be made if this ratio is made dependent of the Hubble type of a galaxy. The ratio h_r /z_o depends on the galaxies’ Hubble type after De Grijs [31], see Figure 4.

The definition is as follows:

$$g_{linear}={\displaystyle \frac{G_{L}M/d}{X}} [\mathsf{m} {\mathsf{s}}^{-2}]$$

(16)

G_L is the linear constant of gravity. From which follows:

$$G_L={\displaystyle \frac{g_{linear}X}{M/d}} [{\mathsf{m}}^3 {\mathrm{kg}}^{-1} {\mathsf{s}}^{-2}]$$

(17)

The mass density M/d is calculated over the full two dimensions of the disk and the rotation plane through the bulge and the gas cloud, comparable with the procedure in formulas (13) and (14) so over all other particles i at radii within the observed radius and outside, for all azimuths. This has been done in a numerical manner in patches, so with a limited resolution of radial distances and for 24 azimuth angles and using one mean value for d, the disk vertical scale length, in a galaxy.

$${\displaystyle \frac{M/d}{X}}={\sum }_i{m}_i/{(X}_{i}d) [\mathrm{kg} {\mathsf{m}}^{-2}]$$

(18)

In the bulge, the 3-dimensional distribution of the bulge mass is exactly known, so no assumption for d is needed. Here m’ is the mass density in the plane of rotation:

$${\displaystyle \frac{M/d}{X}}={\sum }_i{m\mathrm{\text{'}}}_i/X_i [\mathrm{kg} {\mathsf{m}}^{-2}]$$

(19)

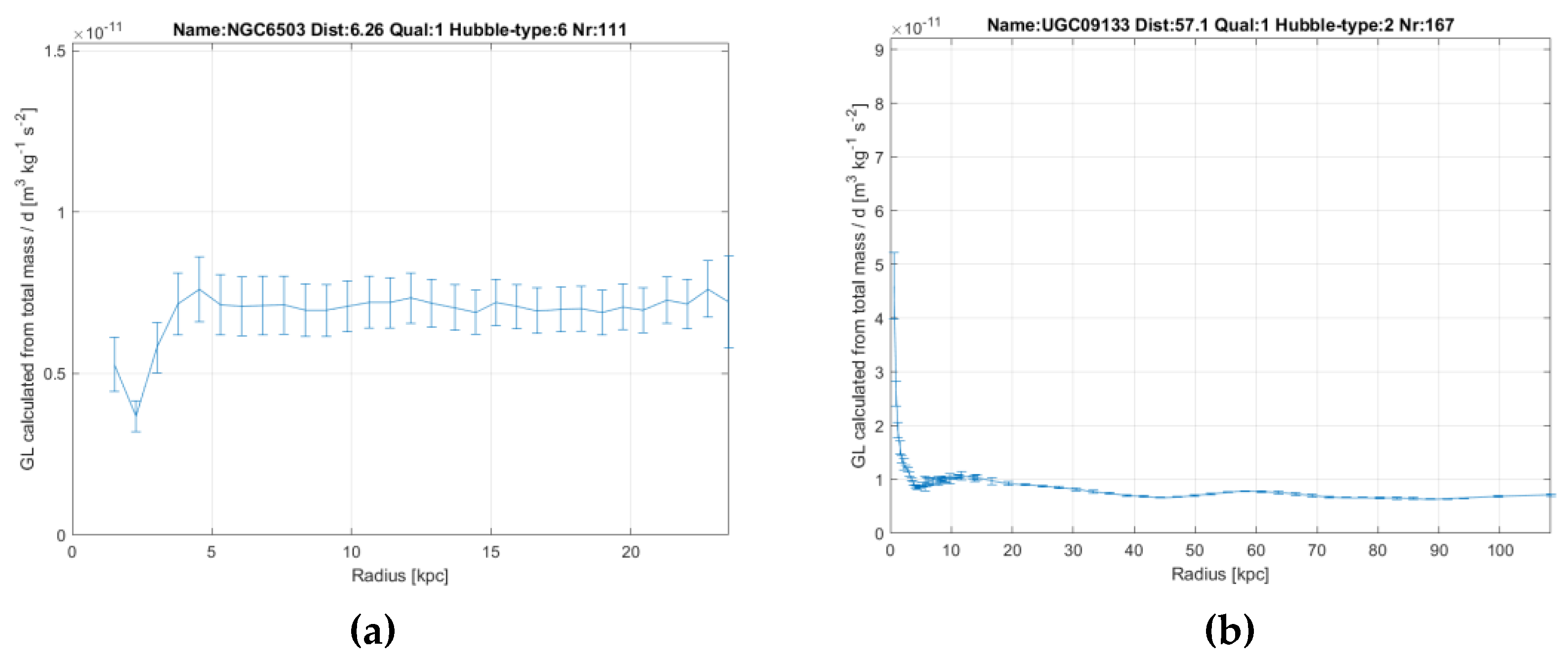
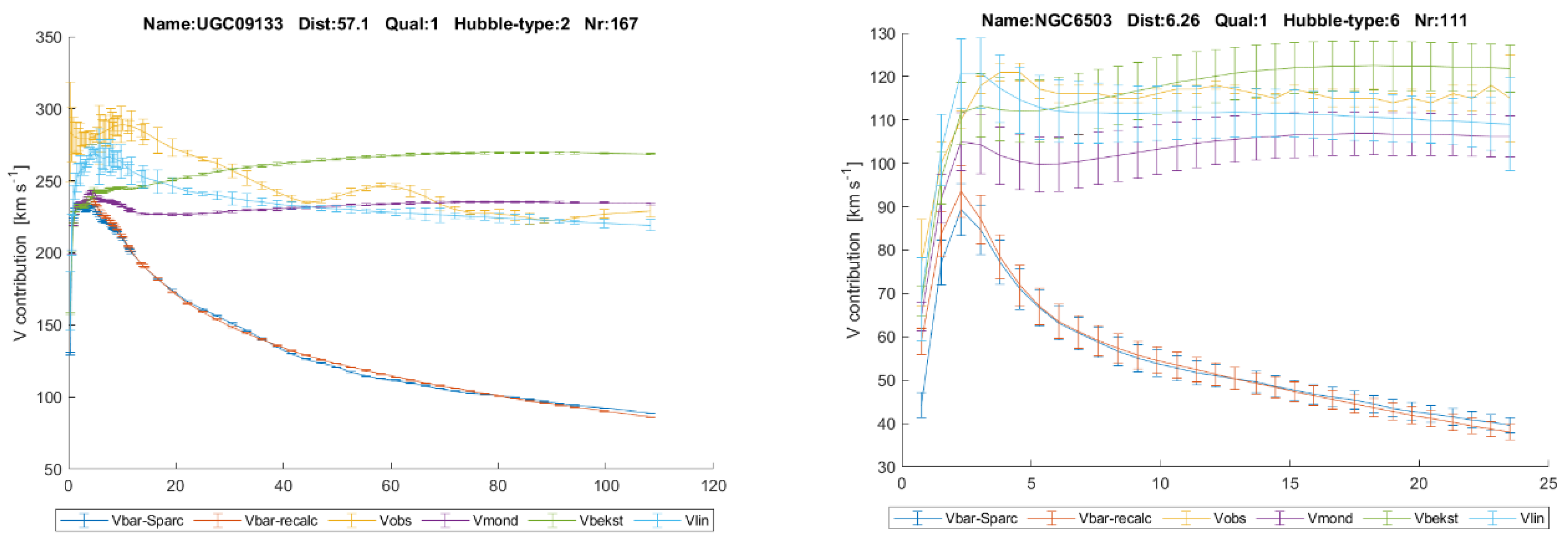
Since no assumption for d is needed in a bulge, they typically show more constant values. In Figure 5 two typical examples are depicted: NGC6503 and UGC09133. UGC09133 is a huge galaxy and has a significant bulge. The constant value of G_L extents over more than 100 kpc (!). The great majority of the galaxies show this constant value, or a clear convergence to a constant value at higher radii.

It should, however, be noted that in the disk and gas cloud a certain amount of ‘viscosity’ because of magnetism occurs, see Begelman & Rees [32] (pp. 66 and 67), This yields an exchange of angular momentum over the disks cross dimension. As a result, still one value of V_bar and V_obs can be attributed to or measured at each radius in the galaxy.

The reformulation of the linear gravity concept in line with MOND in formulas (8) and (9) in chapter 6, so gravity modified by µ(y), led to a factor c. The meaning of this factor becomes clear now: for every mass patch m_i at a position X_i it is some ratio of the mass m_i and the thickness d and it contains G_L over G. It becomes (the subscript i added to stress it has a dedicated value for all patches m_i):

$$c_i={\displaystyle \frac{G_L}{d}}\sqrt{{\displaystyle \frac{m_i}{G}}}$$

(20)

The size chosen for a patch, i.e.. the resolution of the calculation, does not affect µ a priori, since, for instance, doubling m_i doubles g_N and that makes the term $c\sqrt{g_N}$ double as well, and so g in formula (9). For this reason, this formulation is free from the violation of conservation of momentum and the paradox Bekenstein mentions regarding MOND [4] (p. 2) and can be used to predict gravitational acceleration from a given mass distribution.

All the values of G_L at the highest reported radii of each galaxy have been plotted in Figure 6. They show a certain bandwidth, which indicates that the amount of dark matter can vary between different galaxies and have a different proportion to the visible matter. After all, the values of G_L represent the effect of the matter in the superposed universes as observed in our galaxies. The amount of matter in the galaxies in the superposed universes can vary according to their history, since there is no fundamental reason why it should be exactly distributed as in our universe. However, in the sequel it will be shown that assuming one mean value for G_L nevertheless can yield better predictions for the rotation curves, starting from the visible matter, as compared with MOND, formula (4).

6.3. Third Prediction

The third prediction is mentioned already: the 2-dimensional matter density will be slowly decaying, strongly correlated to the expansion of the radius of our universe i.e. expansion of space-time, as described by the Hubble constant, see Riess [33].

This affects the 2-dimensional projections of universes in one another in the proposed 4-dimensional multiverse. The 2-dimensional projections of other 3-dimensional universes that expand at the same rate as ours, will be stretched, at the same rate as the radius of the 3-dimensional universe, to remain consistent geometrically. Now, to fill the expanding space in all dimensions, additional note papers must be added. This occurs since a 2-dimensional plane with a fixed thickness, i.e. The Planck-length L_p, will have to increase its number of surfaces at the same rate as the other increases its volume to still fill that volume.

The expansion of space will not enlarge a galaxy as such, since gravity and angular momentum will resist to that. It is only the space in between galaxies that expands [8] (p. 160). Now the projections, i.e. the intersections of the corresponding galaxies from the other 2-dimensional universe, are separate objects with continuously more planes added between them, more and more space appearing between the intersections. But as noted in chapter 5, the distance to cover to get from one intersection to another a plane may be very large. An intersection of a galaxy cannot just hop from one plane to another, not even when the higher dimensional gravity attracts them to another in the cross-dimension.

Therefore, its projections and hence its gravity contribution in the other universe will be diluted and decrease strongly correlated with the expansion rate of the radius of the universes.

The test of this prediction must come from a solution of Einstein’s equations, with an added term to describe dark matter well, as provided by TeVeS [4], which is elaborated in chapter 7. In chapter 7.2 it will be shown this indeed is consistent with these equations, and that a vast decay must have occurred since the start of the matter dominated era. Bekenstein himself concluded that too [4] (section E p. 21). Since in equation (32) the time derivative of the potential in this equation will be multiplied by the value of µ, which is inversely proportional to the potential, this gives a change proportional to the value, which is exactly what you would expect for a dilution as described up here.

Besides this, from this prediction, it logically follows that in the past, when the universe was much smaller, the additional gravity must have been much larger. In the small universe of the beginning, it has been larger than Newtonian gravity. The effect of this must be traceable in the initial stages of the evolution of the universe.

Recently a paper published in Nature by Labbé et al. [34] confirmed this. The James Webb telescope showed there is a very rapid development of large galaxies already at 600 million years after the Big Bang [34]. Figure 7 is a compilation of photographs from that paper. Following Heuvel [13] (p. 236), the diameter of the universe over this timespan expands with time^2/3. Thus, the diameter of our universe was roughly 7 times smaller than now. As a result, linear gravity according to our hypothesis was significantly stronger too.

This rapid development of large galaxies is much sooner than the current theories predict. But a much larger gravitational acceleration can account for this, since that will greatly accelerate the contraction of gas clouds and the development of stars and galaxies.

Another prediction, that logically follow from this, is that because of this extra gravity, the rotation velocities of these early galaxies will be shown to be exceedingly higher than what we observe in nearby galaxies. This prediction can eventually be tested.

The question remains to what extent this can be extrapolated back in time into the smaller universe that existed then. Looking back in time, the ratio of linear gravity over Newtonian will not increase anymore when the distances over which it can work at all, start to decrease as well. From that moment the density of dark matter will continue to increase, but the square distance term in the Newtonian gravity will increase more rapidly than the linear one. This perfectly compensates each other at small sizes of our universe.

6.4. Fourth Prediction

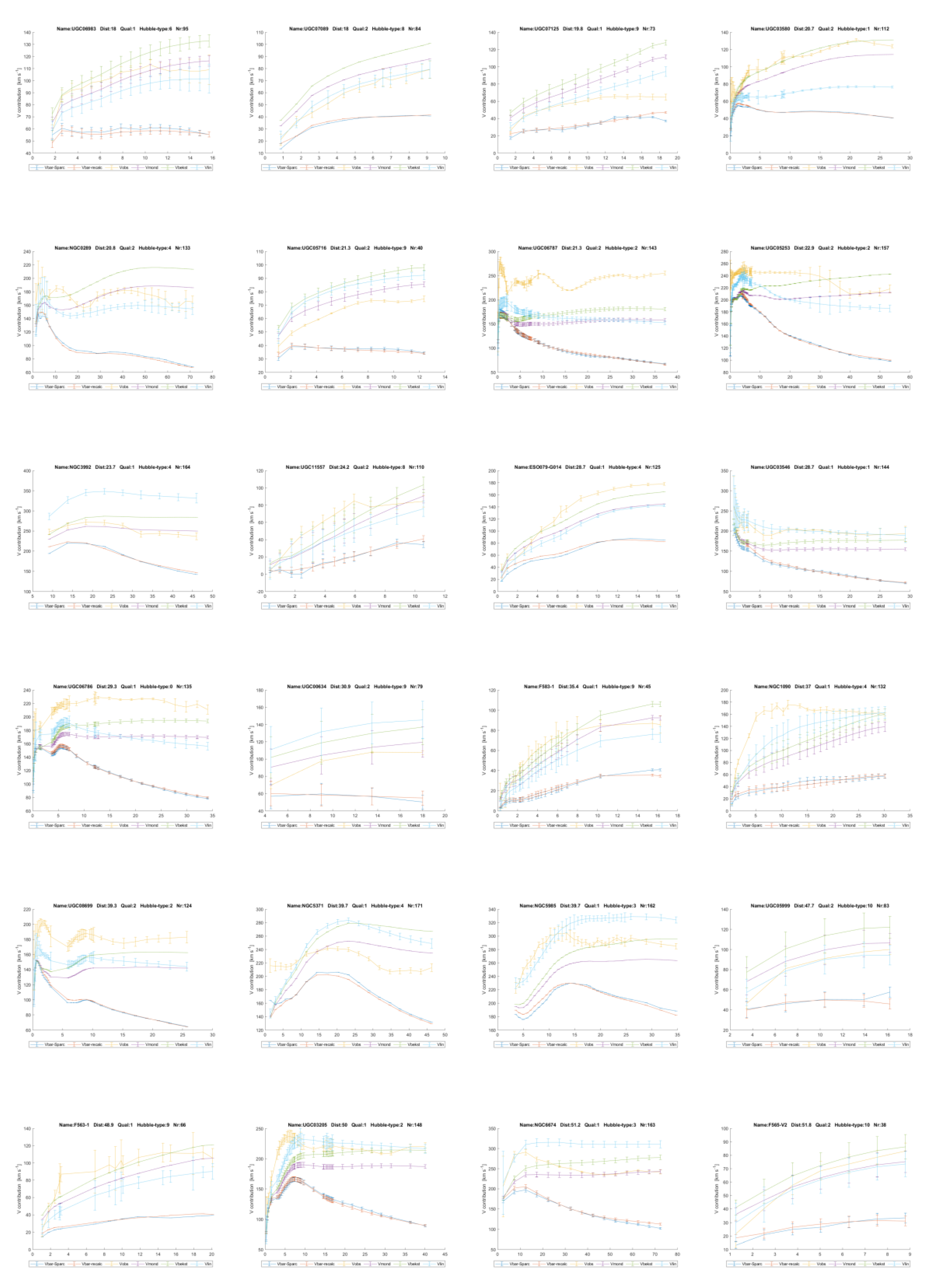
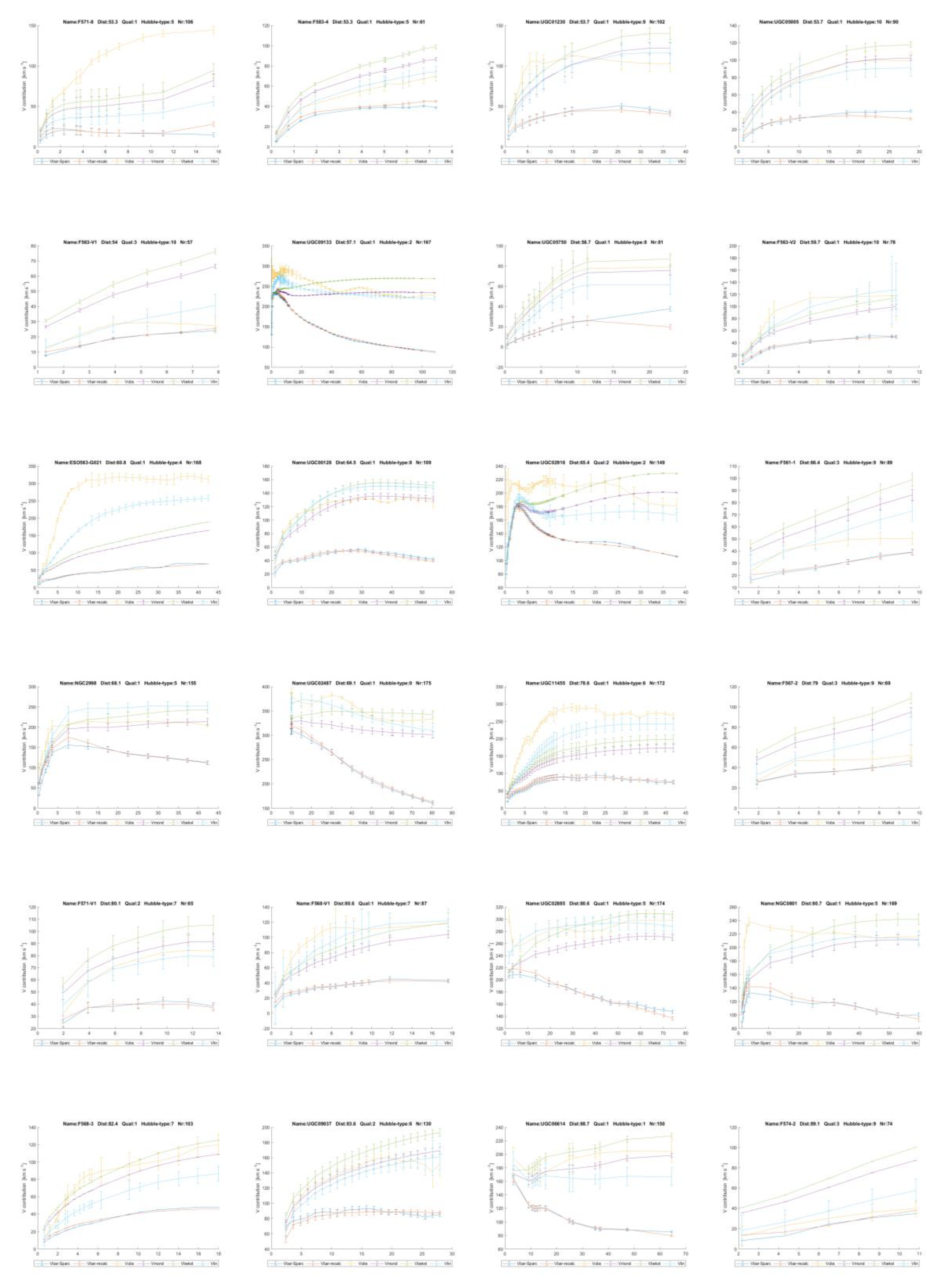
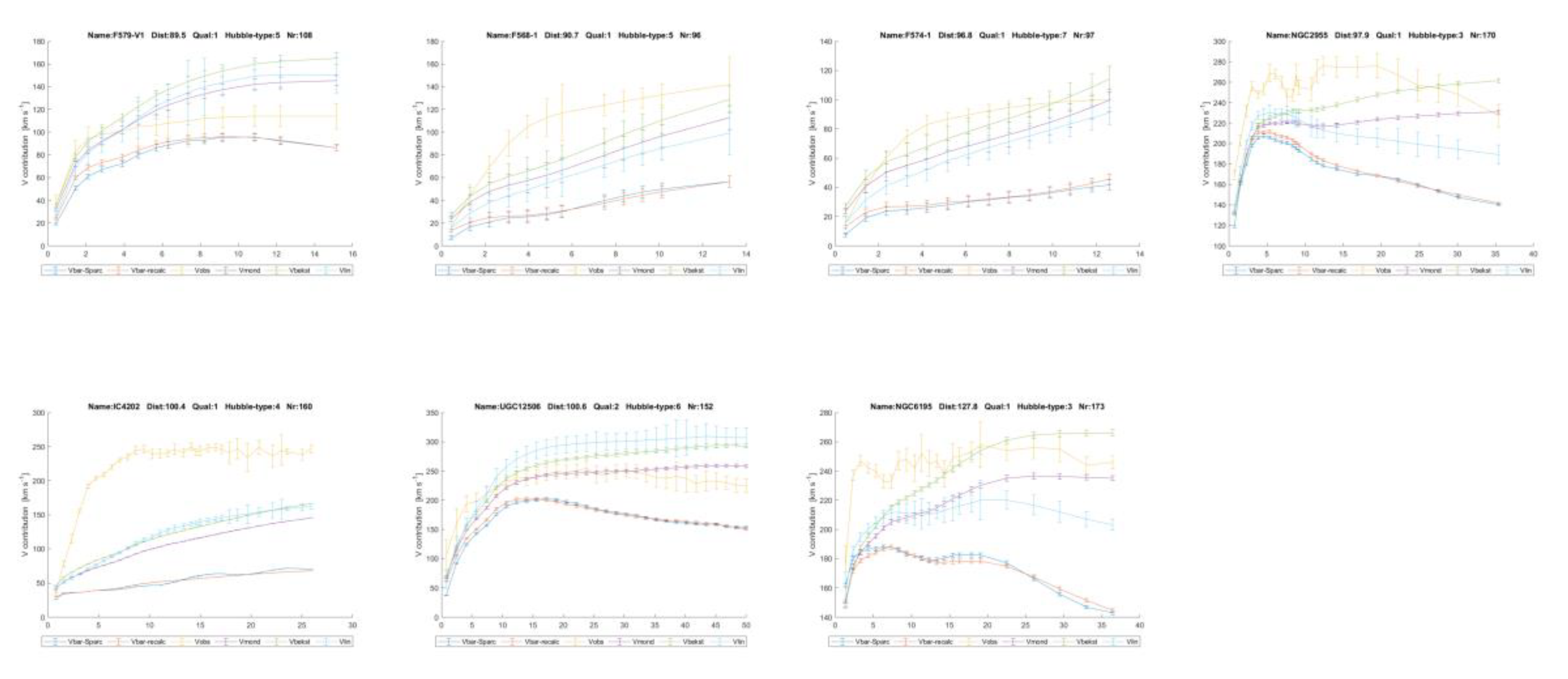
The fourth prediction is that with this natural explanation and the formula’s (16) to (19) a prediction model for the total acceleration, g_linear + g_bar (as defined in formula (6)) can be made that is more accurate than MOND and TeVeS, upon employing one optimised value of G_L ≈ 6.4 ± 0.2 x 10^-12 [m³ kg^-1 s^-2].

The proof of this prediction comes from the same 175 measurements with SPARC. To this end, The observed Newtonian gravitational accelerations, corrected with MOND or TeVeS using formula (4) are divided by the observed gravitational acceleration V_obs²/R. Firstly, this was done with observed velocity V_obs at the highest reported radius R at which it was measured. Optimisation of G_L has been done such that the r.m.s. error value of the deviations of g_linear + g_bar from g_obs over all radii is minimised. The said error estimate of ± 0.2 [m³ kg^-1 s^-2] directly follows from testing the sensitivity of this optimisation. It is consistent with the integer values of the % improvement compared with MOND. In practical terms, a step of ± 0.2 reduces the improvement from 24 % to 23 %.

As a confirmation of this, following Ku [28] (p. 265) the error estimate has as well been calculated as the r.m.s. value of the 175 error estimates of G_L over $\sqrt{175}$ (175 the number of SPARC galaxies). This gives an error estimate of ± 0.14 [m³ kg^-1 s^-2].

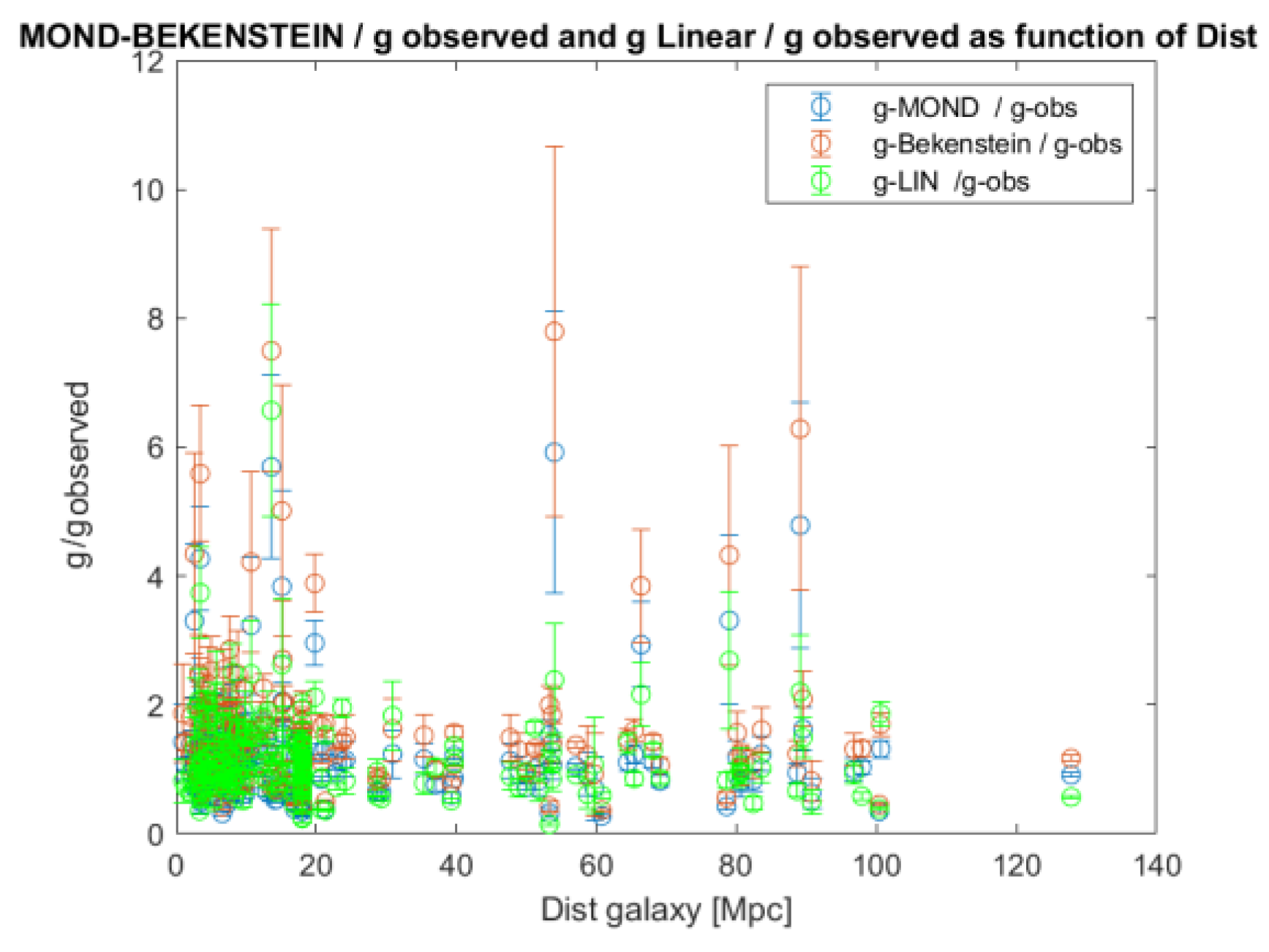
Both the predictions following from MOND and the µ(y) variant used by Bekenstein [4] have been plotted as function of the distance Dist of the galaxy to ourselves in Figure 8. This can be done, since in galaxies, because of the low velocities and the weak field, the non-relativistic limit of TeVeS is applicable and that is equivalent to MOND, only with a different function µ(y) [4]. The ratio to the observed value g_obs has been plotted in Figure 8 for all 175 galaxies as function of distance to ourselves. For linear gravity it shows the smallest scatter from the target value of unity.

As well the ratio of values predicted with the linear model presented in this paper and the observed accelerations, (g_linear + g_bar) / g_obs have been compared for all 175 galaxies. The predictions lie 24 % closer to the observed values than MOND and 26 % closer than TeVeS, when the square root of the deviations of g_MOND and (g_linear + g_bar) compared to g_obs are added for all radii of all 175 galaxies. To get here, the function µ(y) from TeVeS had to be solved in an iterative manner at each radius, since it has an implicit form, see chapter 7, and it cannot be inverted.

But this was based upon fitting the mass-to-light ratio Y_ml based upon the sub-maximal disk hypothesis. As well it is computed what happens when a constant value is assumed, for example Y_ml = 0.5 for all galaxies, like Lelli [11] suggests as the best overall approximation. Then the predictions lie 23 to 27 % closer to the observed values. The overall performance of MOND is again slightly better than that of TeVeS.

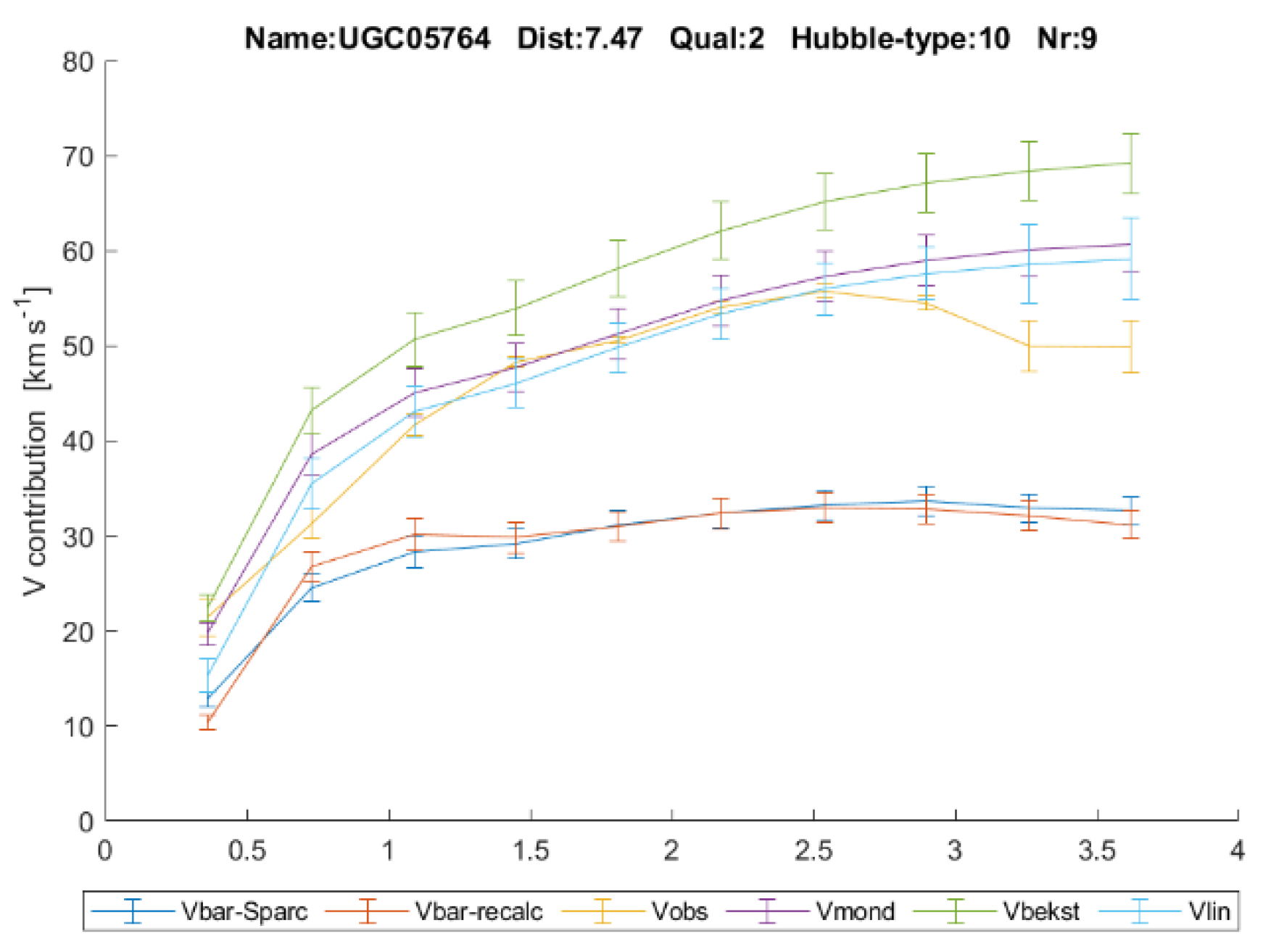
This is based upon the velocities V_gas and V_disk as calculated by the SPARC team from the detailed density distributions they measured, resulting in V_bar. The Newtonian gravitational accelerations as calculated by that team were corrected with MOND as well as Bekenstein’s TeVeS. In Annex 3 all the 175 rotation curves with the predictions are depicted. Some show that the predictions with linear gravity, Vlin, reproduce little more details of the observed rotation curves too, see for example Figure 9 down here. In the legend TeVeS is indicated as Vbekst in the graphs.

The error-bars in the graphs have again been calculated with formula (15) from the error margins as reported by the SPARC team with the assumption that the different quantities are independent.

The question is what this brings in terms of improving calculation methods for galaxies or simulation models for the evolution of galaxies. The linear gravity is the best way to proceed, but should be extended with a transient term, implementing the decay of linear gravity in proportion with the expansion of space, which is rather straightforward. The application of this calculation scheme, alternative to MOND, would take the following steps for a given radius R in a galaxy:

• Calculate the Newtonian gravitational acceleration at R, from the baryonic mass distribution with formula (13), for bulges with formula (14).
• From the same baryonic mass distribution, already available from step 1), calculate the sum of mass/distance at R, only taking the mass density in the rotation plane into account.
• Assuming a value G_L ≈ 6.4 x 10^-12 [m³ kg^-1 s^-2], calculate the additional linear gravitational acceleration with formula (16).
• Correct the computed linear gravitational acceleration at time t with the ratio current radius of the universe / radius at time t.
• Add the Newtonian gravitational acceleration to the linear gravitational acceleration and compute the rotation velocity with formula (12).

It works at all radii, without the need for a distinction between two regimes, and without an interpolation scheme between the two regimes, as with MOND.

6.5. Fifth Prediction

A fifth prediction is that the dark matter is undetectable in any way, since it cannot interact with visible matter, except by gravity, which deforms space and time. The effect of this non-interacting is directly visible in the Bullet cluster [13]. In the plot down here, Figure 10, depicting the Bullet Cluster, the calculated distribution of dark matter is coloured blue. It is shown the dark matter acts like the heaviest visible matter and just flows through the other galaxy, because of its momentum, whereas the ionized HI gas cloud, coloured pink, interacts and stays behind. It may be expected that when the halos are recomputed based upon the linear gravity proposal, this behaviour will still be visible in the Bullet Cluster.

Now, according to the hypothesis in hand, there is a fundamental reason dark matter is undetectable. That is orthogonality, see Griffiths & Schroeter [16] (p. 98 and 151) in terms of quantum mechanics. It follows from the definition of a superposition state, namely as a linear combination of independent quantum states, i.e. orthogonal states. They are per definition not accessible to each other. For the superposition of 3-dimensional universes in a 4-dimensioanl space with two overlapping dimensions, the meaning of this is evident, because one of the dimensions is orthogonal to that of the other universes. But it is in all cases necessary to maintain a superposed state. For instance, Zeilinger [35] states about the double-slit experiment: “The superposition of amplitudes .. is only valid if there is no way to know, even in principle, which path the particle took. It is important to realize that this does not imply that an observer actually takes note of what happens. It is sufficient to destroy the interference pattern, if the path information is accessible in principle from the experiment or even if it is dispersed in the environment and beyond any technical possibility to be recovered, but in principle still ‘‘out there.’’ The absence of any such information is the essential criterion for quantum interference to appear”.

That is why we can never perform any measurement on the properties of dark matter. This information must be and remain absent for the superposition at the earliest stage of the Big Bang to have been possible at all. Otherwise, the quantum states are not independent anymore. But gravity differs greatly from the other forces and interactions, deforming space and time. the question, however, may be asked whether gravity itself, would make a sort of information exchange between the universes possible, for instance like the manipulation of the seconds hand of the wristwatch in the said motion picture Interstellar at 2 h: 21 m. Fortunately, our entire history can never be transmitted, i.e. it cannot even be known in its entirety.

6.6. Sixth Prediction

As mentioned in chapter 5, Han [26] shows that the Milky Way galactic stellar halo is tilted with respect to the disk plane, suggesting that at least some component of the dark matter halo may also be tilted, see Figure 11 in the sequel. The origin of this misalignment of the dark halo, of approximately 25°, can be explained by the linear gravity hypothesis in the paper in hand, since the orientation of the two dimensions of another superposition state overlapping with ours, can deviate from the orientation of a galaxy and can be anisotropic if the amounts of matter in overlapping galaxies differ. The sixth prediction is that the orientations of the halos of different galaxies will reveal a deep underlying structure in the universe, i.e. will display the direction of the pair of two dimensions overlapping with our universe. In other words, the orientations of the halos will, when compared with each other on a large scale, display the underlying coordinate system, of sorts, of the universe.

7. General Relativity and TeVeS Theory

Bekenstein [4] provided a theory, TeVeS, in which MOND is reformulated in terms of GR. TeVeS was developed on the basis of the action principle, with two additional actions and a free function added to the geometric action of GR and varying those actions with respect to the metric and to the scalar and vector fields added by Bekenstein in those actions. This yields a differential equation for the free function F, which then is shown to reproduce MOND. The differential equation of Bekenstein is used here to show the theory of linear gravity as well is a valid solution of this. And it is shown that the mentioned decay with time inevitably follows from these equations.

His work resulted in a general theory: TeVeS, so as to provide for a relativistic formulation of gravity without the assumption of dark matter. Then Bekenstein shows that MOND is well incorporated in TeVeS, so that it is a relativistic formulation of MOND. He applies different metrics in his actions for different applications and solves them for those situations, like for instance non-spherical symmetric cases like galaxies and to study the evolution in time using the Friedmann-Robertson-Walker (FRW) metric in his added actions. In this chapter it will be shown that this framework as well allows for the hypothesis of linear gravity to be entered into TeVeS, so the mathematics of TeVeS as well can incorporate linear gravity perfectly. And hence that linear gravity yields a consistent relativistic formulation.

As with MOND, in TeVeS a function µ is introduced, that modifies the total gravitational acceleration to obtain the Newtonian acceleration. It thus acts on the sum of all contributions to the total gravitational acceleration and not on the contributions from different masses in a galaxy separately. The application of TeVeS in this chapter will, however, do so. Like in chapter 6.3 formulas (13) and (14), the contributions all masses in a galaxy have to be summed up. Here this will be done after modification with µ for each contribution separately.

7.1. Introducing and Applying TeVeS

Conservation of momentum is not satisfied by MOND, but is automatically satisfied in physical theories that are derived using an action principle [4]. To that end, in AQUAL, his starting point, the following Lagrangian was formulated under the assumption of and additional real scalar field ψ:

$${\mathcal{L}}_{\psi }=-{\displaystyle \frac{1}{8\pi G{L}^2}}f\left(L^2{g}^{\alpha \beta }{\psi }_{,\alpha }{\psi }_{,\beta }\right)$$

(21)

Where f is some function, not known a priori. The same recipe is followed in TeVeS: define and additional scalar field as well as a free function, the exact form of which at a later stage follows from constraints that come with solving the linearized GR equations. MOND formula (5) then follows from (21) under spherical symmetry and static conditions. But, as mentioned in chapter 3, AQUAL failed to describe light deflection.

TeVeS [4] is based on three dynamical gravitational fields: and Einstein metric g_µυ with a well-defined inverse g^µυ and a time-like 4-vector field Џ_µ as well as a dynamic scalar field ϕ and a non-dynamical scalar field σ. The physical metric is obtained by stretching the Einstein metric in space-time directions orthogonal to Џ^α _{= g}^αβ Џ_β by a factor e^-2ϕ while shrinking it by the same factor in the direction parallel to it. As becomes clear from [4] (p. 21 formulas (52), (53) and (58)) the scalar field ϕ is to be interpreted as the additional gravitational potential. So, in TeVeS this ϕ is added to the Newtonian potential.

Then the total action resulting from the scalar fields contains a geometric part just as in GR, the Einstein-Hilbert action S_g, the matter action S_m and two extra actions, S_s and S_v, including two positive parameters k (dimensionless) and l (a length scale) and a free dimensionless function F, which is related to an additional gravitational potential [4] (p. 8). The shape and behaviour of F must be consistent with the theory and yield a valid solution of the equations, so effectively it is not entirely free. In the hypothesis in hand, it directly will follow from the acceleration being the sum of two components, so from formula (8). The extra action for the pair of scalar fields is as follows [4]:

$$S_s=-{\displaystyle \frac{1}{2}}\int \left[{\sigma }^2{h}^{\alpha \beta }{\varphi }_{,\alpha }{\varphi }_{,\beta }+{\displaystyle \frac{1}{2}}G{l}^{-2}{\sigma }^{4}F\left(kG{\sigma }^2\right)\right]{(-g)}^{1/2}{d}^{4}x$$

(22)

where h^αβ = g^αβ - Џ^α Џ^β. The extra term for the action of the vector Џ^α has the form:

$$S_V=-{\displaystyle \frac{K}{32\pi G}}\int \left[g^{\mu \nu }{g}^{\alpha \beta }{\mathrm{Џ}}_{[\alpha ,\mu ]}{\mathrm{Џ}}_{[\beta ,\nu ]}-2{\displaystyle \frac{\lambda }{K}}(g^{\mu \nu }{\mathrm{Џ}}_{\mu }{\mathrm{Џ}}_{\nu }+1)\right]{(-g)}^{1/2}{d}^{4}x$$

(23)

The square brackets around pairs of indices indicate anti-symmetrisation in that pair. The factor λ is a spacetime dependent Lagrange multiplier to enforce normalisation. This action of the vector field by Bekenstein introduces the parameter K, but does not contain F, so is left unaltered by the hypothesis in hand and therefore it is not further discussed here. But the value of the dimensionless parameter K was determined by fitting to cosmological effects, with µ > 1, which is not necessary anymore in the hypothesis of linear gravity. So it is free to be determined again, which might be a favourable to solve some reported problems with TeVeS, see the discussion in the sequel.

Then, varying those three actions with respect to the metric and to the scalar and vector fields added by Bekenstein in those actions gives a general solution for spherically symmetric situations. Variation of σ in S_s gives the relation between σ and ϕ_,α and F, where per definition [4] F’ = dF(µ)/dµ:

$$-kG{\sigma }^{2}F-{\displaystyle \frac{1}{2}}{\left(kG{\sigma }^2\right)}^2{F}^{\mathrm{\text{'}}}=k{l}^2{h}^{\alpha \beta }{\varphi }_{,\alpha }{\varphi }_{,\beta }$$

(24)

Now [4] defines the function µ(y) such that equation (24) takes the following shape:

$$-\mu F\left(\mu \right)-{\displaystyle \frac{1}{2}}{\mu }^2{F}^{\mathrm{\text{'}}}\left(\mu \right)=y$$

(25)

so that $kG{\sigma }^2=\mu \left(k{l}^2{h}^{\alpha \beta }{\varphi }_{,\alpha }{\varphi }_{,\beta }\right)$.

This differential equation can be solved when the function µ(y) is specified, so as to yield the function F(µ). If µ(y) yields a solution for F(µ) and the solution shows proper behaviour, i.e. consistent with the theory, then the theory incorporates relativity consistently. This now is done for the hypothesis of linear gravity.

Bekenstein has firstly derived his free function F(µ) for relativity in quasistatic systems. He does not calculate it for MOND separately, but explores the behaviour in different limits, for example the non-relativistic limit, to show it just reproduces MOND in those cases. This, for example leads to an equation [4] (p. 13 formula (58)) that closely resembles equation (7), so the potential being the sum of Newtonian and an additional potential. This, again, hints at the strong relationship between MOND, TeVeS and linear gravity.

As a starting point to determine F(µ) for linear gravity, so as to predict gravitational acceleration from a given mass distribution including relativistic effects, inverting formula (9) yields:

$$y={\displaystyle \frac{c^4}{{a_m}^2{(1-\mu )}^4}}$$

(26)

This follows directly from the theory of linear gravity as outlined in chapters 4 and 6 and it can be used instead of Bekenstein’s free function y(µ) from [4] (Bekenstein’s formula (50) to predict gravitational acceleration from a given mass distribution. Bekenstein states that there is great freedom in choosing y(µ) and hence F(µ), but here it directly follows from the theory that the gravitational acceleration in a galaxy is the sum of two contributions, see chapter 4, formula’s (6) to (9).

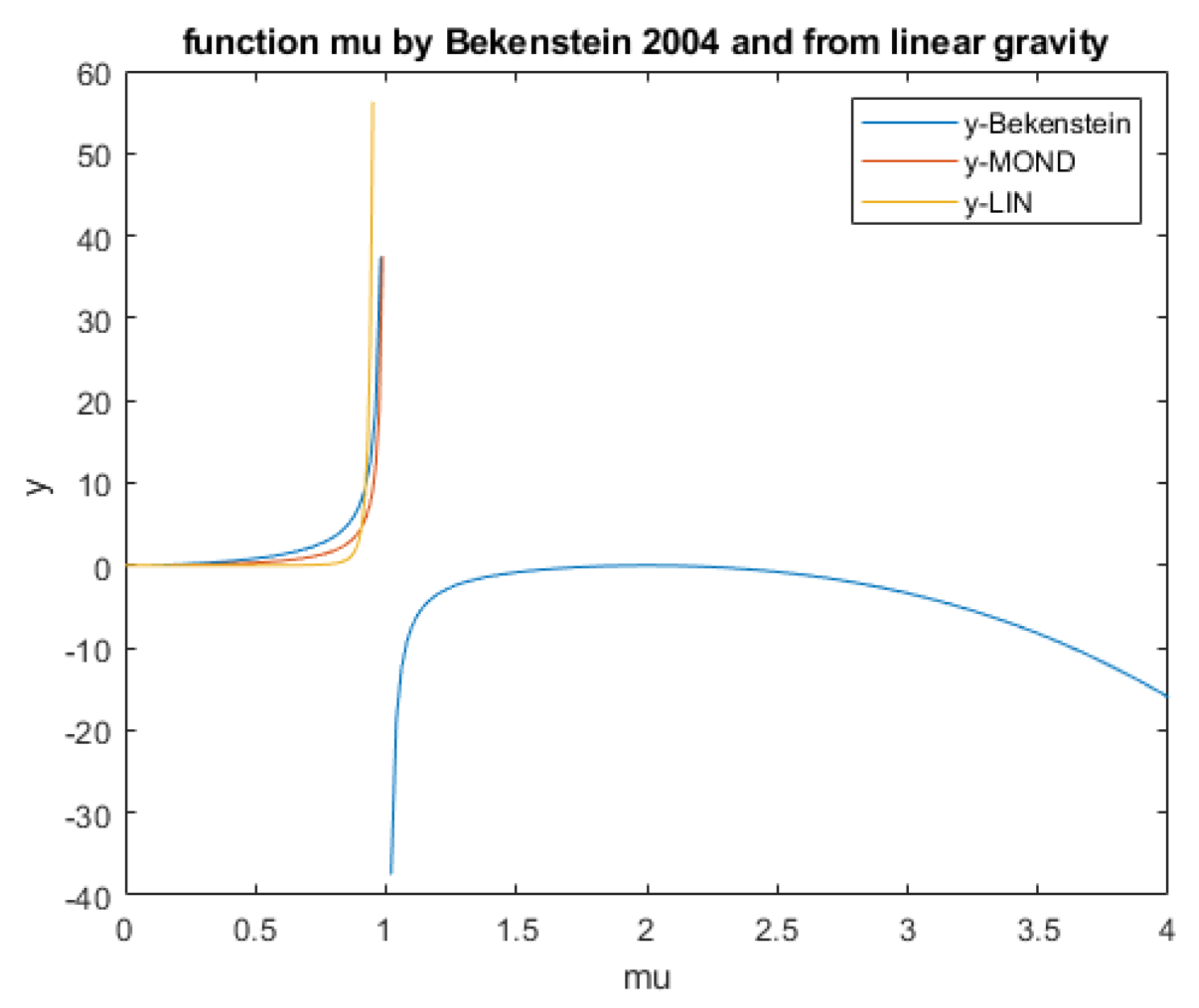
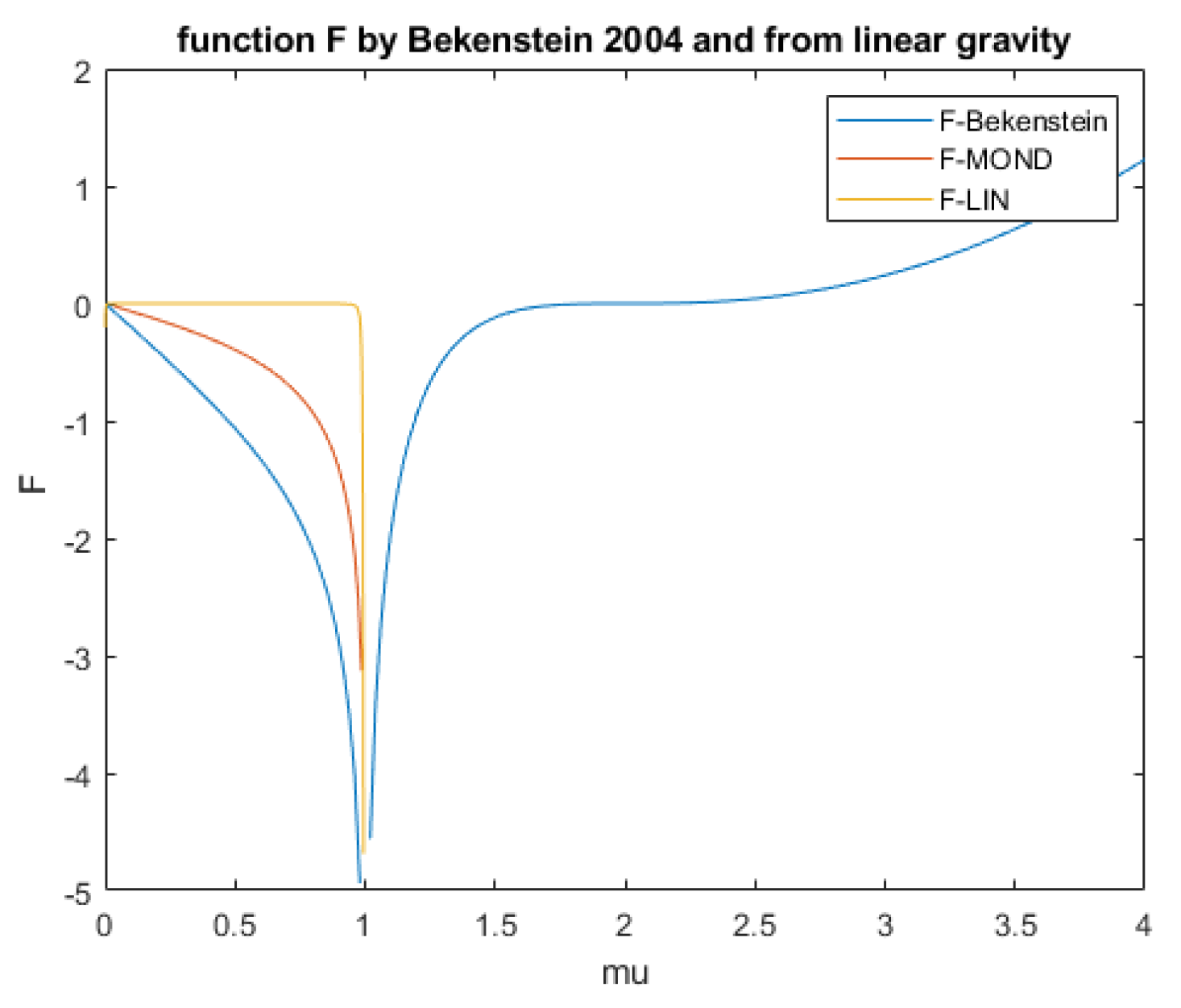
Figure 12 shows it gives a somewhat steeper increase towards µ = 1, but the trend as well as the sign and magnitude are of the same order as MOND and TeVeS. And no values for µ > 1 to account for cosmological effects are needed now, since dark matter is part of this hypothesis, opposed to MOND and TeVeS. The most left part, with µ << 1 is the deep MOND-regime. µ = 1 is the case where Newtonian gravity fully dominates.

However, c is not a constant but depends on the mass m_i in a certain position in the galaxy now as discussed in chapter 6.3 formula (20). But, on using a linearised metric as in Bekenstein [4] (p. 18, section B) the sum is a valid solution when each contribution to the sum is a valid solution.

As explained in Schutz [36] (p. 200) this is only valid for low gravitational acceleration where space-time is nearly flat, but comparing Milgrom’s constant with the Earth’s gravitational acceleration in one glance shows that this is the case in galaxies. And Bekenstein as well does it in his section B to study systems wit no particular symmetry.

For stronger fields, the accelerations due to the different masses in a galaxy should be added to each other using the acceleration addition formula for GR, based upon the Lorentz factor, to obtain a relativistic solution for the sum.

So, in galaxies, y may be treated the sum of many contributions from all mass in the galaxy, each with their own value of c, i.e conforming to formula (20). c_i. And in galaxies with a bulge, in line with chapter 6, the bulge and the disk can be treated separately and the results added to yield a solution for the galaxy with bulge as a whole. The same applies to all different masses in a galaxy. So, if at one radial position R for one contribution from mass at another position X, agreement is proved, it is valid for the total acceleration g at a point.

Integration of (25) with use of (26), with c* = c⁴/a_m², gives:

$$F\left(\mu \right)={\displaystyle \frac{2c^{\mathrm{*}}}{3{(\mu -1)}^3{\mu }^2}}+{\displaystyle \frac{k_1}{{\mu }^2}}$$

(27)

k₁ is an integration constant, which can be chosen small compared to c* such that the function F(µ) at small values of µ, i.e. in the outer regions of the galaxy, is not dominated by the most right quadratic term in (27) but continues to converge steadily when µ, goes to zero. µ is limited to the range [0-1) in galaxies and when µ = 1 Newtonian acceleration is the only contribution to the acceleration, so in the centre of the galaxy and y would go to infinity. Bekenstein applies his function F to values of µ > 1 for cosmology and gravitational lensing, but that is not necessary if dark matter is used to explain those effects.

Again, as Figure 13 shows, the function F by linear gravity towards µ = 1 is steeper, but the trend and the sign are as well as the orders of magnitude are the same. The same applies to the function derived from MOND, what Bekenstein did not do, but is done here in the same way equation (27) was derived. As can be seen in Figure 9 and in chapter 6.4 as well as Annex 3, the impact of the differences in F on the predicted rotation velocities are small. And again, no values for µ > 1 to account for cosmological effects are needed here.

This latter restriction, valid since dark matter is not excluded here, as well cures some of the reported problems of TeVeS like the incompatibility with the value of the quantity E_g at cosmological scales reported by Zhang [37]. Since linear gravity is an explanation of dark matter and not designed to do without it, it unlike TeVeS, does not have to account for gravitational lensing effects and cosmological dark matter. The function µ introduced in chapter 4 and used up here now, like in MOND, only is applied in the range µ =[0-1), so with a positive contribution of dark matter to gravity, as it happens in galaxies. And since it is only applied for very weak fields, determining the motions of stars and gas in galaxies, the TeVeS problem with instability in stars reported by Seifert [38] does not apply here either.

7.2. Evolution in Time

Bekenstein [4] also explores the dynamic, time-dependent, behaviour in his section E for, among other, the matter ara in the evolution of our universe. Please note, the elaboration in the sequel fully applies to his theory and MOND as well, since in the outer regions of galaxies, i.e. the deep MOND regime, the theories behave the same with respect to the function y(µ) and F(µ). And they are still free in Bekenstein’s scalar equation [4] (Bekenstein’s equation (37)) that is applied down here again.

Recall that µ is the ratio of Newtonian acceleration over total acceleration. Hence it is a decreasing function of the radial position in a galaxy and a supposed decay of the additional gravity by dark matter would make it grow towards unity. To explore this, Bekenstein uses the Friedmann-Robertson-Walker (FRW) cosmology [4] (p. 10) in which a(t) is the scale factor of the expanding universe.

$$g_{\alpha \beta }d{x}^{\alpha }d{x}^{\beta }=-d{t}^2+a({t)}^2[d{\chi }^2+f\left(\chi {)}^2\right(d{\theta }^2+si{n}^2\theta d{\phi }^2)]$$

(28)

Bekenstein uses (28) to a obtain a modified, now time-dependent scalar equation, (31) in the sequel, as well as a modified Friedmann equation (29) in TeVeS. Then he uses a combination of both to study the resulting evolution of F in time.

His modified Friedmann equation, obtained from variation of his additional action S with respect to this metric, with ρ being the proper energy density and p the pressure and ϕ the additional gravitational potential caused by the added scalar field (ϕ > 0), is:

$$\left({{\displaystyle \frac{1da}{adt}}}^2\right)={\displaystyle \frac{8\pi G}{3}}\rho e^{-2\varphi }+{\displaystyle \frac{4\pi }{3k^2{l}^2}}⌊-\mu y\left(\mu \right)+{\displaystyle \frac{1}{2}}{\mu }^{2}F\left(\mu \right)⌋$$

(29)

Please note, that all variables are scaled such way by Bekenstein that ϕ << 1 and that is it dimensionless [4] (pp. 8, 12 and 20). Later on he will argue that the left term of the right-hand-side in (29) dominates over the right term, which he then ignores.

Now Bekentein wants to find a relation between the time derivatives of a(t) and ϕ(t) by combining this, as said, with a time dependent scalar equation. Applying his scalar equation (Bekenstein’s formula (37)) to the FRW metric yields Bekenstein’s formula (45) copied down here [4] (p. 10):

$$\mu (-2k{l}^2\left({d\varphi /dt)}^2\right)){\displaystyle \frac{d\varphi }{dt}}={\displaystyle \frac{-k}{2a^3}}{\int }_0^{t}G(\rho +3p)e^{-2\varphi }{a}^{3}dt$$

(30)

Since the function F(µ) was part of the definitions of Bekenstein’s additional action S_s and hence of formula (24), the function µ reappears here as part of a differential equation, but, as said, with F still free.

In the matter era $p\approx 0$and ρ varies as a^-3 [4] (p. 21). Then integrating equation (30) from the start of this era gives:

$${\displaystyle \frac{\mu d\varphi }{dt}}={\displaystyle \frac{-k}{2a^3}}{\int }_{t_r}^{t}G\rho e^{-2\varphi }{a}^{3}dt+{\displaystyle \frac{{\mu }_r{d\varphi }_r}{dt}}{\left({\displaystyle \frac{a_r}{a}}\right)}^3$$

(31)

The time t_r is the time at the end of the radiation era and the start of the matter era, where a = a_r. Now Bekenstein explicitly evaluated this integral from t_r to t to let (31) become the following equation:

$${\displaystyle \frac{\mu d\varphi }{dt}}={\displaystyle \frac{-1}{2}}kG\rho (t-t_r)+{\displaystyle \frac{{\mu }_r{d\varphi }_r}{dt}}{\left({\displaystyle \frac{a_r}{a}}\right)}^3$$

(32)

Now equation (29) is used to express the left term in the right-hand-side in as a function of ${\displaystyle \frac{1da}{adt}}$.

After that, Bekenstein argues that after the start of the matter era, after the first e-folding of a, the first term of the right-hand side becomes dominant, so over most of the matter era up to the present. Ignoring the second term in the right hand makes (32) a simple differential equation. This is elaborated down here following Bekenstein.

Bekenstein [4] (p. 22) only elaborates on the situation that µ > 2, so for application in cosmology and then states the evolution in time is small. But it is important to note that if µ << 1, like in the flat rotation region of a galaxy (typically in the order of O (0.1) in the 175 galaxies studied with a deep MOND regime) dϕ/dt might become very large indeed in this equation. For it then is multiplied with a very small µ in the left-hand side, which is relevant in the sight of the third prediction of this paper. So, this case is elaborated in the sequel.

Bekenstein does solve this equation with the help of (29) and ends with the following inequality, which in galaxies gets a < sign, since now F < 0 and y > 0:

$${\displaystyle \frac{\mu d\varphi }{dt}}<\left({\displaystyle \frac{k}{8\pi }}\right)({\displaystyle \frac{da}{dt}}/a)$$

(33)

But, he argues that this inequality is nearly saturated, since the scalar field contributions to his modified version of the Friedmann’s equations (29) are small compared to the left term in the right-hand-side [4] (pp. 20 and 21) as mentioned earlier after equation (29). Since in galaxies the absolute values of µ, y and F, are all smaller than in cosmology (µ > 2) this is even much truer in galaxies as can be seen upon comparing the left and right parts of Figure 12 with each other, and the same with Figure 13.

Then he integrates his equation from t_r to the current time t, But this can only be an approximation since µ actually is a function of time too, so this is valid only for a certain value of µ. With µ = O (0.1) instead of 2 this gives:

$$\varphi \left(t\right)-{\varphi }_r\approx -\left({\displaystyle \frac{5.6k}{8\pi }}\right)\ln \left({\displaystyle \frac{a}{a_r}}\right)$$

(34)

With k = 0.03 as determined by Bekenstein, it follows that this decay $\varphi \left(t\right)-{\varphi }_r$amounts to -0.11 approximately. In his work, Bekenstein [4] (pp. 20-22) scaled his variables such that during the entire cosmological evolution ϕ << 1 (i.e. e^ϕ≈ 1). His initial value was 0.007 < ϕ₀ << 1 [4] (p. 22). This simply means that the predicted decay of -0.11 in a typical galaxy, dominates the current value of the gravitational potential by linear gravity, so in the past it must have been much stronger than nowadays. Comparing Milgrom’s constant with Earth’s gravitational acceleration, confirms it is a very weak field now in galaxies, so ϕ << 1 now. Bekenstein [4] (pp. 10,11,12) gives another estimate of ϕ in cosmology and in localised systems like galaxies, and states that ϕ as defined in his theory nowadays typically has a value of order O (k). The actual value 0.03 evidently is much smaller than 0.11.

And for galaxies the inequality (33) gives an lower limit on the decay, so it’s magnitude may be larger even than 0.11, but as stated up here, Bekenstein argues the inequality is nearly saturated and therefore close to an equality in galaxies, so the real decay will be very close to -0.11 in galaxies, if µ were constant, what is discussed in the sequel. And, as can be seen in equation (33), there will always be a decay as long as there is linear gravity, except when k would be zero, but that would mean no linear gravity, so no dark matter.

But all this is only relevant when the decay of the additional potential affects the additional gravitational acceleration. So, the radial derivatives of the potential must be affected by this in a galaxy. µ being a decreasing function of the radial position, as stated earlier, ensures this. It decreases with increasing radial position and hence increases ${\displaystyle \frac{d\varphi }{dt}}$ as function of the radial position, cf. formulas (31) to (33). So the additional acceleration in a galaxy decreases as well. It must have undergone a vast decay since the start of the matter dominated era, since through the lower µ values then, ϕ varied much more with the radial position than it does now, so it’s radial derivative must have been huge compared to nowadays.

As a consequence, the lower values of µ in the past made the magnitude of the decay much larger than 0.11 in the past. The decay getting smaller and smaller as time proceeds is exactly what you would expect for a dilution as described in Chapter 6.3.

This can be made explicit by solving (33) again, but now assuming µ is a function of time t as well, so as to check whether the predicted additional acceleration in the past as well decreased linearly with radial position, so consistent with the hypothesis.

This can be checked by modifying equation (7) analogue to the approach leading to the FRW metric and see if the equation has a solution. Bekenstein follows exactly the same approach [4] p. 10) to obtain his equations [4] (Bekenstein’s equations (44) and (45) and the text above his equation (44)). So equation (7) is modified as follows:

$$\mathsf{\Phi }={\mathsf{\Phi }}_N+f\left(t\right)\mathrm{l}\mathrm{n}\left(R\right)$$

(35)

Then, differentiating (35) with respect to R gives a gravitational acceleration that is as well proportional to f(t). Hence, if one defines a function f(t) that decreases or increases the potential ϕ with time t, so that ϕ(t) = f(t-tr) ϕ_r, then it follows logically that µ(t) =

f^-1(t-t_r) µ_r. In the sequel it will be verified this has a solution.

Inserting the above in equation (33) and as argued, considering (33) nearly saturated and assuming ${\displaystyle \frac{a}{a_r}}={\left({\displaystyle \frac{t}{t_r}}\right)}^{{\displaystyle \frac{2}{3}}}$ [4] (p. 21), [13] (p. 236) makes it a simple differential equation in f(t-tr) with the following solution:

$$f(t-t_r)={\left({\displaystyle \frac{t+t_r}{2t_r}}\right)}^{-c}$$

(36)

With c = k/(12π ϕ_r µ_r.) and t_r the time at the start of the matter era. Rewriting this in terms of ${\displaystyle \frac{a}{a_r}}$ makes it possible to extrapolate as well to the current era with accelerating expansion, where t_r in the denominator of the fraction can be ignored:

$$f(t-t_r)={\left({\displaystyle \frac{a}{2a_r}}\right)}^{-c}$$

(37)

With c = k/(8π ϕ_r µ_r). The exact speed of the decay is unknown, but clearly depends on the product ϕ_r µ_r. But ϕ_r and µ_r are unknown, and their values, at the start of the matter dominated era, cannot be determined directly from the current values using equation (37). For the galaxies have undergone an evolution in this long period. But it can be showed, the assumption made up here, ϕ(t) = f(t-tr) ϕ_r etc_,, in this derivation, beneath equation (35), are not a limitation, since f(t) is eliminated in the product ϕ_rµ_r, for it appears in both the numerator and the denominator. And during the largest period of the matter dominated era galaxies as studied here did already exist, from 300 million years after the Big Bang [13] (p. 141), and before that already localised and rotating clouds of matter so formula (35) may hold over the very largest part of this period [13] (p. 150).

It can be shown, this as well holds when the most right term in the right-hand side of equation (32) is not ignored; then the right-hand side of (37) only will be multiplied with a power of e, that in the product ϕ_r µ_r still drops out. But the current value of the product ϕ µ clearly is not a constant, and will be a function of radial position R in a galaxy, so it does not have a unique value now, but it does not vary with an order of magnitude, since it varies only with ln(R)/R (less than a factor 8 from 2 to even 100 kpc). Given this small range, the deviation from the assumptions made in equation (35) in the first period of this era may be limited. So, using actual values, some constraints and an estimation can be given to find the order of magnitude of c.

A constraint on µ_r for c to be unity, so the power of a/a_r is minus unity, the most simple form of a dilution of ϕ, can be derived. Given the lowest value for ϕ_r estimated in the above ϕ_r > 0.11, the value of c could be unity when µ_r < 0.012. This is realistic when compared with the current typical value of µ = O (0.1), and a pair of values for ϕ and µ that obeys to this and to equation (37) can exist.

As mentioned, Bekenstein [4] (pp. 10,11,12) gives an estimate of ϕ in cosmology and in localised systems like galaxies, and states that ϕ as defined in his theory currently typically has a value of order O (k). Combining this with the current typical value of µ = O (0.1) in the deep MOND regime gives an estimate of the order of magnitude of the power: c = O (1). So the dilution of ϕ goes with a power of a/a_r that is of order O (-1). So, the power law (37) is typical for a case of simple dilution of a physical quantity with the scale of space a.

The exact value hopefully can be determined by simulating the evolution of galaxies through this era or by using the SPARC data with the aid of machine learning or by extending the SPARC measurements to much more distant galaxies.

To summarize: since the function F was part of the definition of Bekenstein’s additional action S_s and hence of formula (24), the function µ reappears as part of a differential equation for ϕ(t) when Bekenstein’s actions are combined with the, time-dependent, FRW metric. It is shown there is a decay of the additional gravitational potential by linear gravity with time, that the decay till now has been vast, that it follows a power law typical for simple dilution of a physical quantity with time and that the power has a value in the order of minus unity.

This all confirms the third prediction of this paper and this significant time evolution of ϕ in TeVeS gives a possible explanation for the rapid evolution of large galaxies in the early universe.

7.3. Application

Applying this in line with the hypothesis of linear gravity, reduces the range of values of µ to the range [0-1).

As stated at the top of this chapter, with MOND, in TeVeS the function µ only modifies the total gravitational acceleration to obtain the Newtonian acceleration at a certain position. So, in TeVeS it does not act on the contributions from different masses at different distances in a galaxy m_i separately. Application of TeVeS with the function µ from linear gravity, however, forces one to do so. Like in chapter 6.2 formulas (13) and (14), the contributions all masses in a galaxy must be summed up afterwards. This means, a linearised metric can be applied in combination with the scalar and vector fields as developed by Bekenstein in TeVeS, but with the function F from formula (35). As well the function f(t) can be used as a modifier, if wished so. This latter modifier can as well be applied to MOND and TeVeS if wished so, since it follows from TeVeS.

But, as stated in the top of this chapter, the above is only valid for linearised GR, which is applicable to weak fields. Now it is shown that the contribution of dark matter will decrease with time, it becomes clear that somewhere in the past this will break down, since then the field was much stronger. So, for calculations of the gravitational acceleration by dark matter in the far past, the accelerations due to the different masses in a galaxy should be added to each other using the acceleration addition, based upon the Lorentz factor, to obtain a relativistic solution in stronger fields too.

8. Conclusions and Suggestions for Further Work

The conclusion is that the universe consists of four 3-dimensional universes, existing as at least four states of a superposed 4-dimensional multiverse, which each have two overlapping dimensions with the observed universe. For there is nothing outside it that could disturb the superposition state, it could be in that state forever, without de-coherence effects ending it. That is why Hawking and others can speak of the wave function of the universe in the first place.

Gravity from dark matter and visible matter is very well interpreted as the sum of two gravitational accelerations. In each galaxy, one constant value for the ratio between the surplus acceleration and the sum of all mass-density over distance can be determined. This will be called the ‘linear constant of gravity’, G_L. From the values of the calculated baryonic and the observed velocities in galaxies in the SPARC data, an average value for the gravitational constant G_l of the 2-dimensional gravity is deduced: G_L ≈ 6.4 ± 0.2 x 10^-12 [m³ kg^-1 s^-2]. This is not a fine-tuned number as meant in (Hossenfelder 2019), but an empirical value that represents the average effect of the matter in the superposed universes as observed in our galaxies. The amount of matter in the galaxies in the superposed universes can vary according to their history, which becomes visible values of G_L that vary from galaxy to galaxy.

The mass-to-light ratio has been used as the only fitting parameter to fit the baryonic rotation velocity, and hence the baryonic gravitational acceleration in each galaxy to the observed values near the core of the galaxies. After that, the above-mentioned value for G_L is used to predict the additional gravitational acceleration at all radii without any further fitting. Applying this value to predict rotation velocities from the baryonic matter distribution in a galaxy, upon using the mass density in the plane of rotation, will yield predictions that are on average 25 % closer to observation than MOND or Bekenstein’s work, TeVeS. Implementing the decay of linear gravity argued in this paper might further improve the predictions for galaxies at larger distances than the SPARC data set.

Further investigation of the shapes and orientations of dark matter halos based upon the linear gravity hypothesis, will yield halos with comparable orientation as the ones currently calculated by many researchers, but more concentrated at the centre of galaxies. This avoids the fundamental problems with the current view of halos surrounding galaxies as recently reported by Mistele and Lelli based upon the SPARC data.

Using TeVeS, it is shown a consistent relativistic formulation of the hypothesis can be constructed. This has been done following the same steps Bekenstein took with MOND and GR. The solution based upon TeVeS and the FRW metric confirms the prediction of decaying linear gravity from a decreasing concentration of dark matter in time, by the expansion of space in accordance with the hypothesis. But then, it becomes clear that somewhere in the past linearised calculations will break down, since then the field was much stronger. So, for calculations of the gravitational acceleration by dark matter in the far past, the accelerations caused by different masses in a galaxy should be added with the addition formula based upon the Lorentz transformations. And, perhaps, the said models of Mistele and Lelli used to analyse the SPARC data are accurate enough to falsify or confirm the predicted decay, probably with the aid of machine-learning algorithms, taking into account the evolution of galaxies in time. And, to check whether G_L stays constant over the huge distances, out to 1 Mpc, they analysed.

More future work is to implement the linear gravity approach, including the transient term, in existing simulation software for the evolution of galaxies to verify whether that will yield better agreement with the observed trends, in particular the rapid evolution of large galaxies in the early universe as well as to study how linear gravity can be applied to gravitational lensing, including dark matter as a source.

Supporting material like figure sets, machine-readable tables including all the numerical data presented in the graphs in this paper, Matlab ® .m code will be made available on-line. The SPARC files that have been employed, have been converted to Matlab ® .mat files [39] and added as well.

The author looks forward to receiving responses to this hypothesis from the field.

G.M. van Uffelen MSc

Wageningen, The Netherlands, 2024-11-22

Supporting Material: figure sets, machine-readable tables, Matlab ® code [39].