Submitted:
11 November 2024
Posted:
14 November 2024
Read the latest preprint version here
Abstract
An analytical solution to arbitrarily loaded isotropic rectangular Kirchhoff plates supported at three corner points, having two adjacent edges free and the other edges being simply supported, clamped or free, was presented. Analytical methods such as the single trigonometric series of Lévy or the double trigonometric series of Navier are not applicable here because of the adjacent free edges. In this paper the deflection surface was approximated with the sum of a particular solution to the governing differential equation (GDE) and two single series. The terms of the single series were the product of an unknown function of an independent variable and a trigonometric function of the other independent variable, whereby the trigonometric functions were consistent with the deflection-related boundary conditions (zero deflection or not along an edge). On the one hand the terms of the series were required to satisfy the homogeneous GDE, leading to two uncoupled differential equations, one for each unknown function, and so the approximate solution satisfied exactly the GDE. On the other hand the boundary conditions were satisfied only at selected collocation points along the boundary, the number of collocation points in each direction corresponding to the number of terms of the associated series. The results obtained showed a reasonable agreement with the exact results, the accuracy increasing the more terms of series were considered. So a powerful computation tool is needed to consider higher number of terms of the series and so to approach the exact results. Cantilevered plates will be analyzed using this approach in future research.
Keywords:
1. Introduction
2. Materials and Methods
2.1. Governing Equations of the Plate
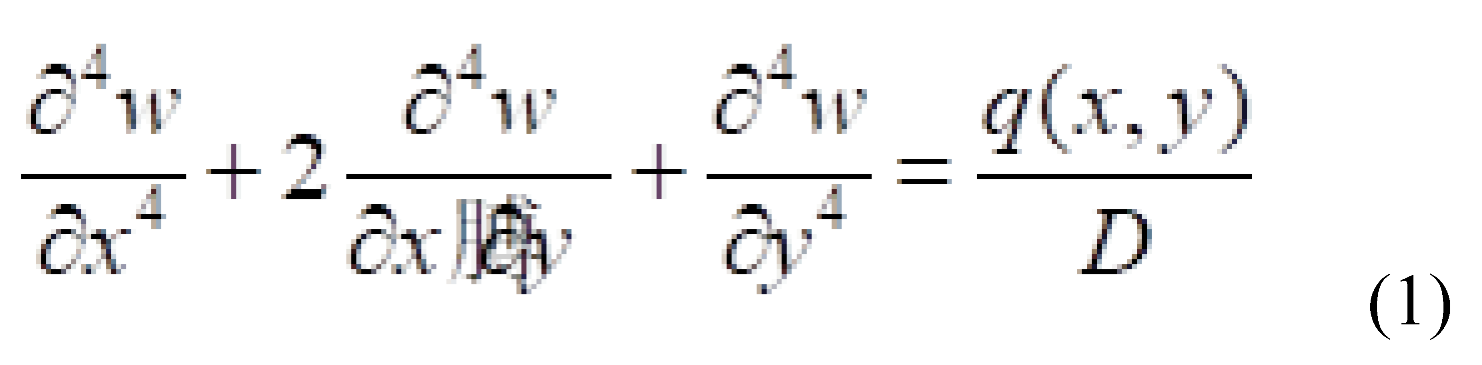
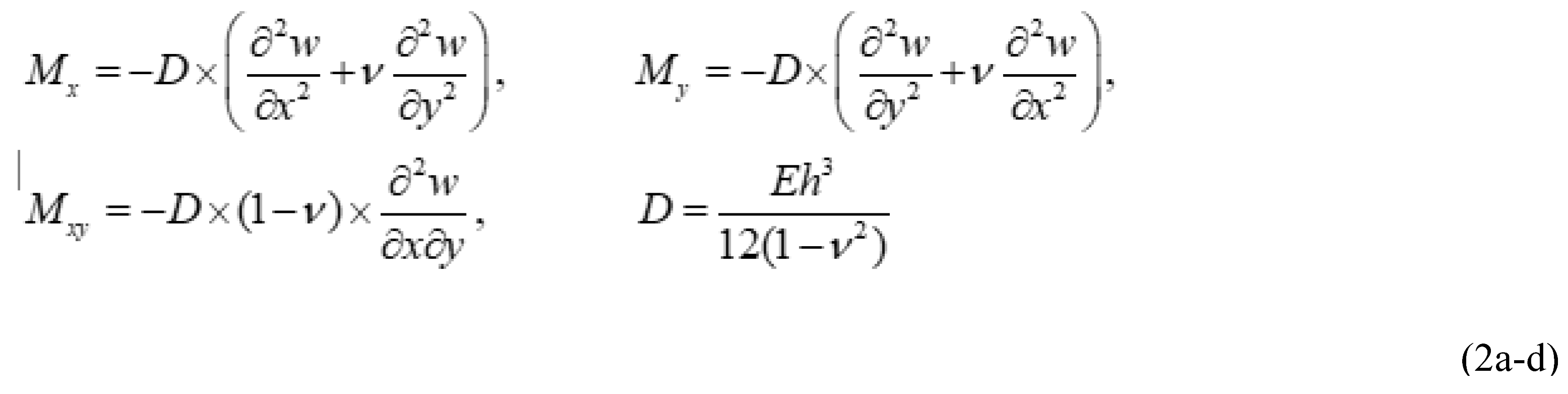
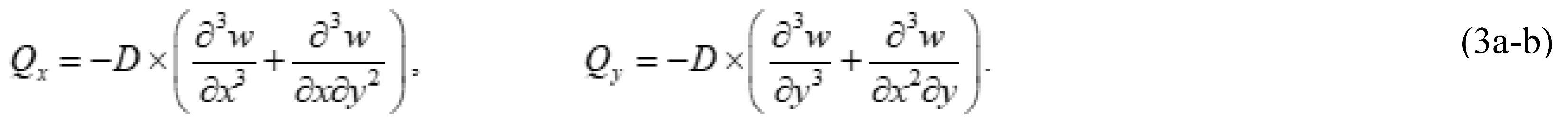
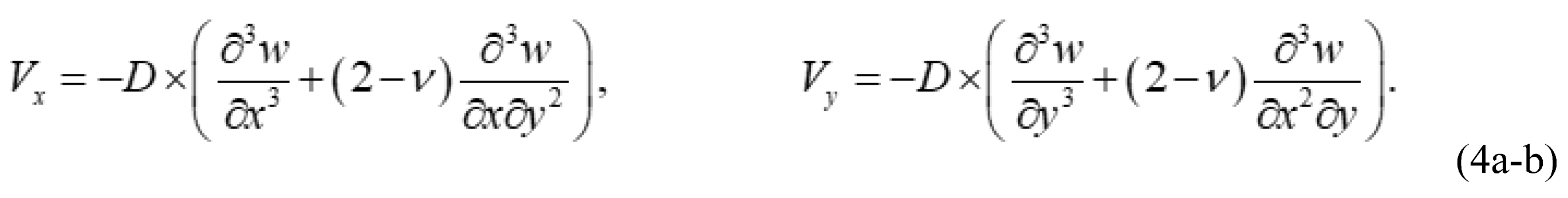
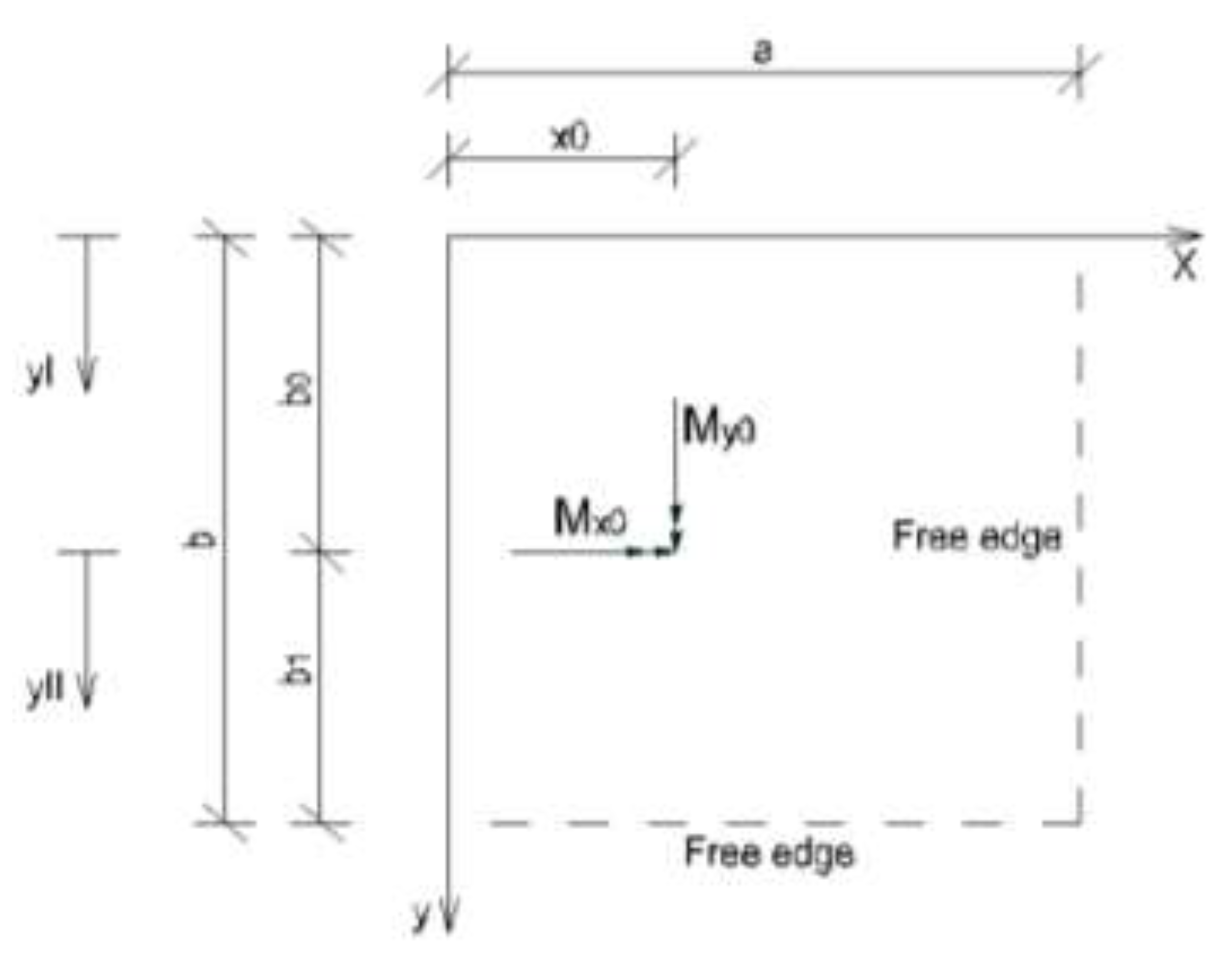
2.2. Plate Having Two Adjacent Edges Free And Supported At Three Corner Points
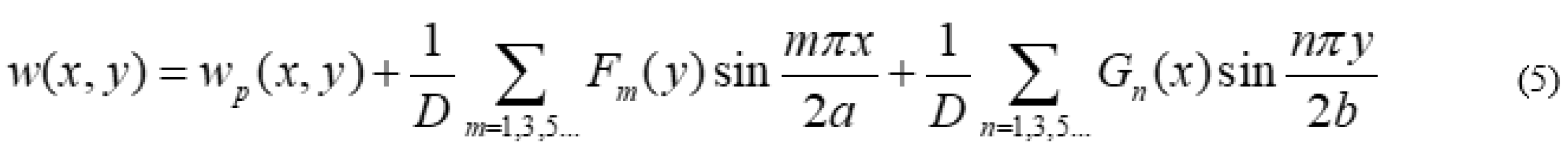
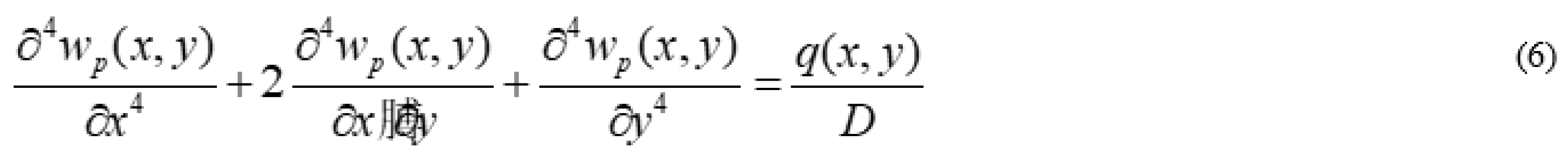
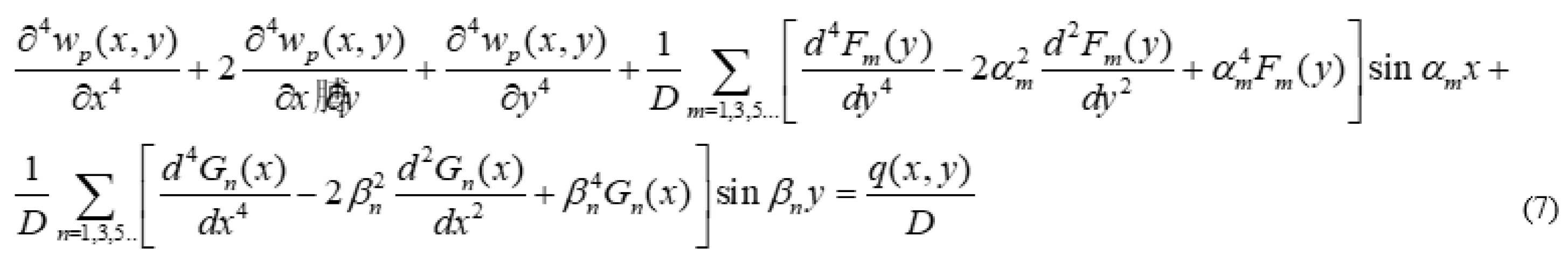
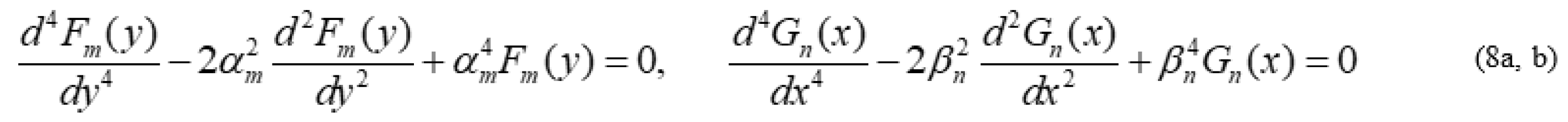
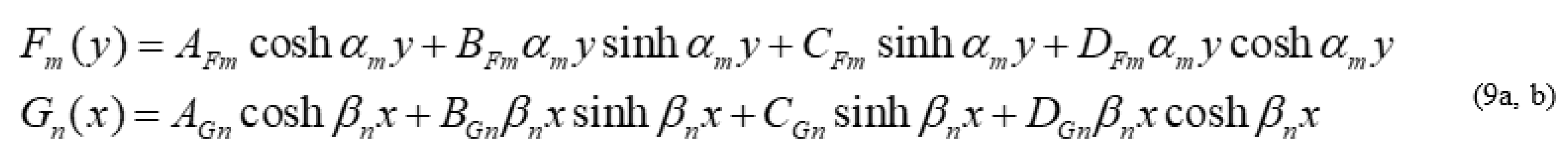

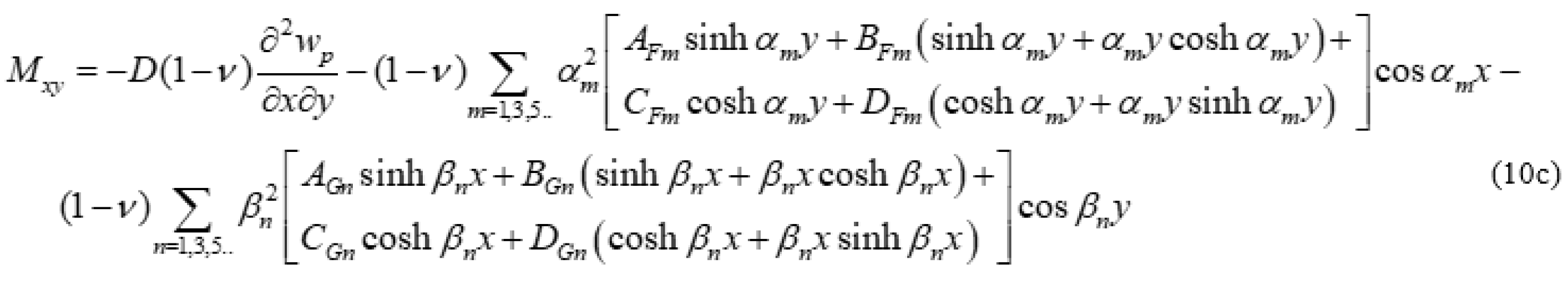

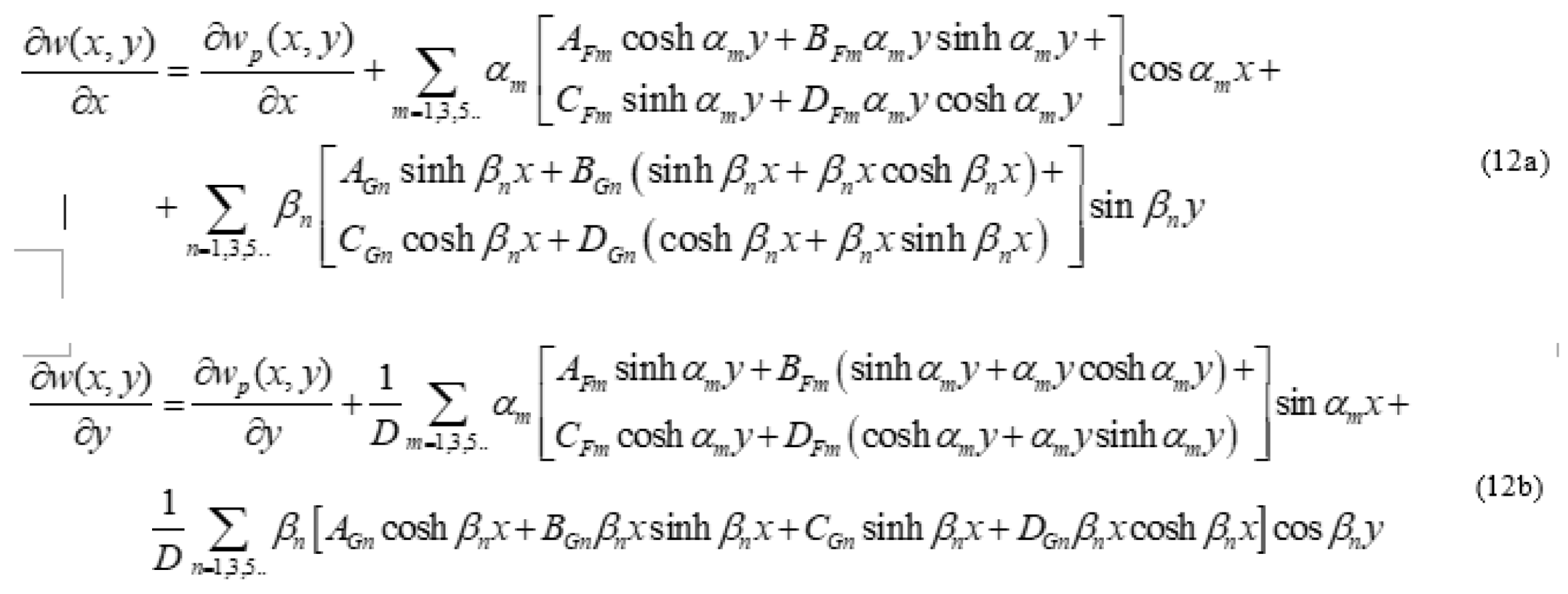
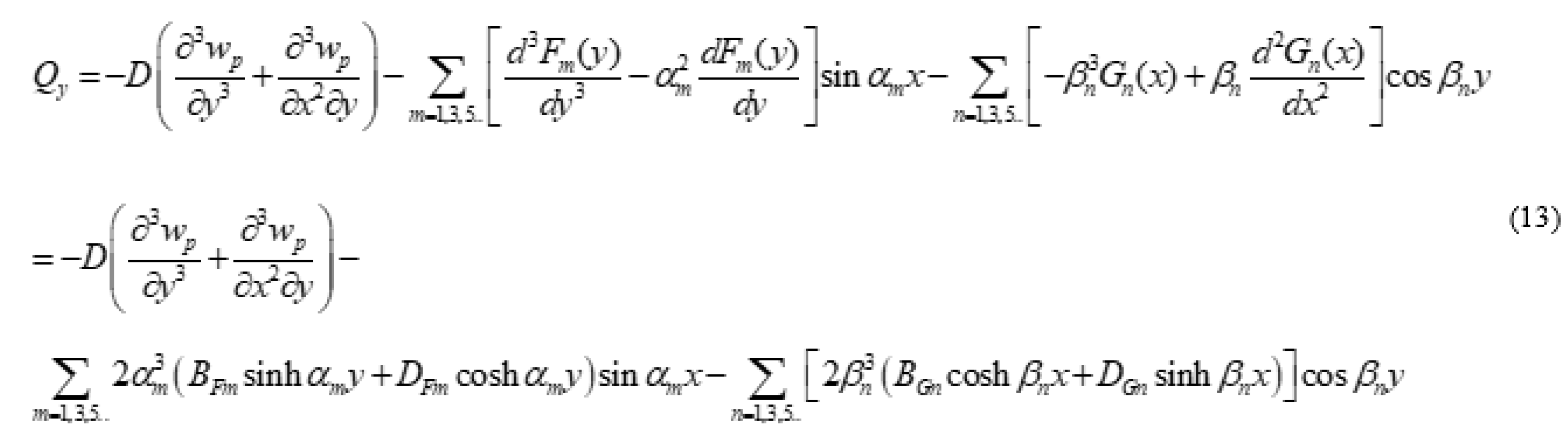
Analysis of Special Cases
a) Concentrated load acting at the unsupported angle

b) Concentrated force and moment applied at the interior of the plate
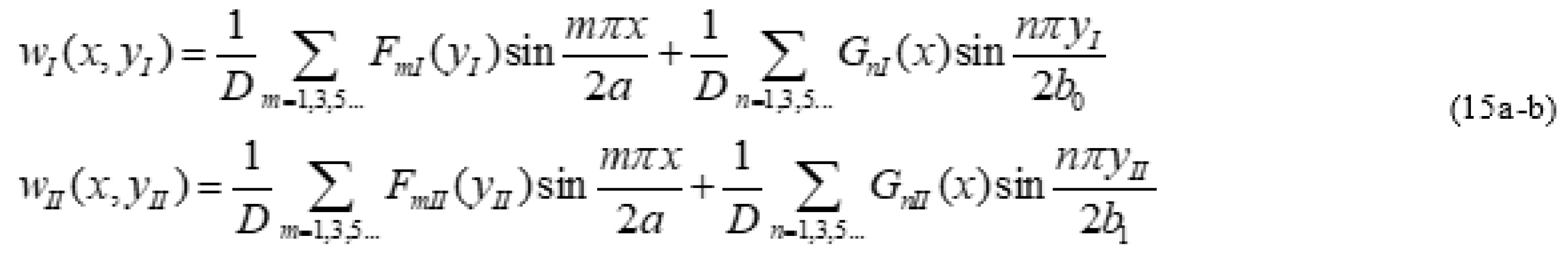
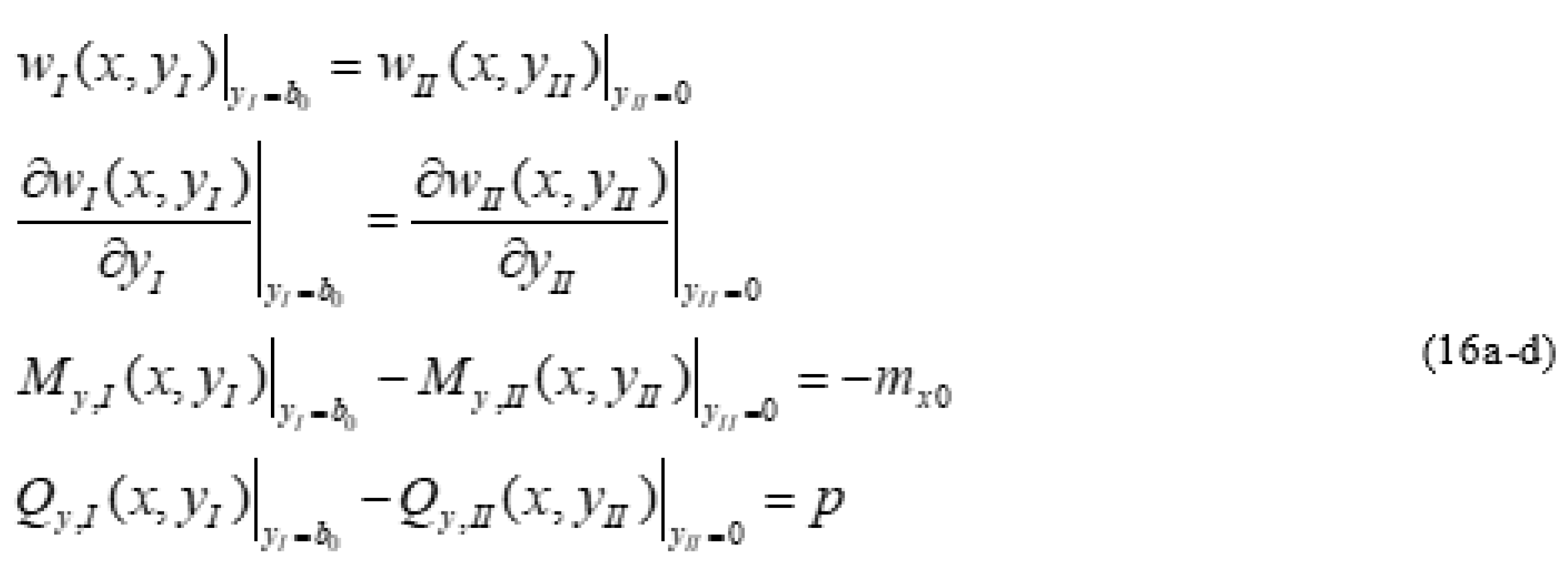
- Plate zone I: 2NI equations at each of the edges x = 0 and x = a and 2M equations at yI = 0
- Plate zone II: 2NII equations at each of the edges x = 0 and x = a and 2M equations at yII = b1
- 4M continuity equations at yI = b0 (or yII = 0)
a) Plate resting on three corner points with all edges free
3 Results and discussion
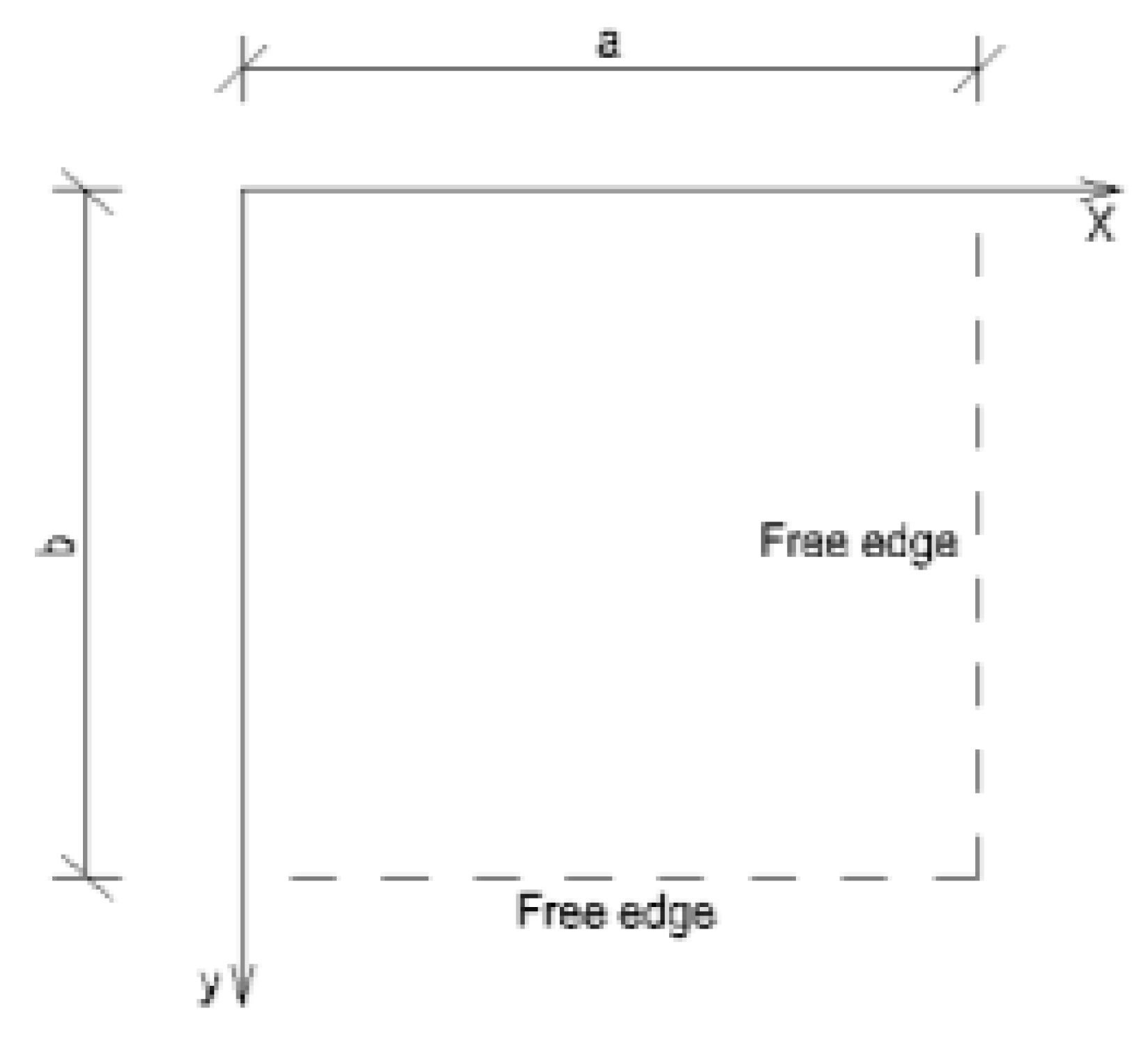
3.1. Rectangular Plate Having Two Adjacent Edges Free, Simply Supported Along The Other Edges And Subjected To A Uniformly Distributed Loading
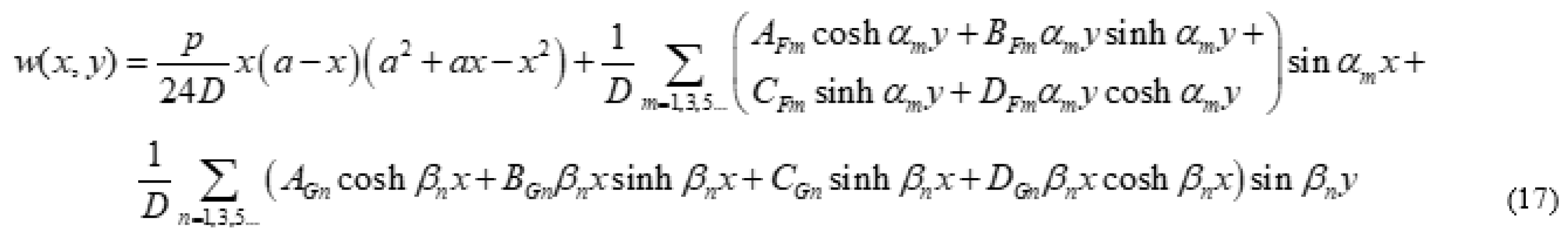
- Case M = 1 N = 1: yj = b along the edges x = 0 and x = a and xj = a along the edges y = 0 and y = b
- Case M = 2 N = 2: yj = b/2 and b along the edges x = 0 and x = a and xj = a/2 and a along the edges y = 0 and y = b
4. Conclusions
Supplementary Materials
Conflicts of Interest
References
- Fogang, V. An Analytical Solution to Rectangular Kirchhoff Plates Supported at All Corner Points Using Two Single Series and the Boundary Collocation Method. Preprints 2024, 2024102244. [Google Scholar] [CrossRef]
- Kirchhoff, G. Über das Gleichgewicht und die Bewegung einer elastischen Scheibe. J. für die Reine und Angew. Math.; vol. 18, no. 40, pp. 51-88, 1850.
- Trefftz, E. Ein Gegenstück zum Ritzschen Verfahren (An alternative to the Ritz method). Proceedings, 2nd International Congress of Applied Mechanics, Zurich, pp。131-137. 1926. [Google Scholar]
- Herrera, I. (2000), Trefftz method: A general theory. Numer. Methods Partial Differential Eq., 16: 561-580. [CrossRef]
- R. Piltner. Some remarks on Trefftz type approximations. Engineering Analysis with Boundary Elements, Volume 101, Pages 102-112. 2019. [CrossRef]
- R. Li, H. R. Li, H. Wang, X. Zheng, S. Xiong, Z. Hu, X. Yan, Z. Xiao, H. Xu, P. Li. New analytic buckling solutions of rectangular thin plates with two free adjacent edges by the symplectic superposition method. European Journal of Mechanics - A/Solids, Volume 76, 2019, Pages 247-262. [CrossRef]
- Q. Gao. Analytical Bending Solutions of Orthotropic Rectangular Thin Plates with Two Adjacent Edges Free and the Others Clamped or Simply Supported Using Finite Integral Transform Method. Advances in Civil Engineering. 2020. [CrossRef]
- B. Babu, B.P. B. Babu, B.P. Patel. Analytical solution for strain gradient elastic Kirchhoff rectangular plates under transverse static loading. European Journal of Mechanics - A/Solids, Volume 73, 2019, Pages 101-111. [CrossRef]
- E. Ramm. Lecture notes. Flächentragwerke, Platten. 1993. Institut für Baustatik, Universität Stuttgart. In German.

| b/a = | 1.00 | 1.20 | 1.50 | 2.00 | ||||
|---|---|---|---|---|---|---|---|---|
| Nxm | Nym | Nxm | Nym | Nxm | Nym | Nxm | Nym | |
| Lecture notes [9] | ||||||||
| 0.0508 | 0.0508 | 0.0547 | 0.0669 | 0.0598 | 0.0878 | 0.0703 | 0.1117 | |
| Present study | ||||||||
| M = 1 N = 1 | 0.1073 | 0.0177 | 0.1008 | 0.0314 | 0.0933 | 0.0497 | 0.0857 | 0.0724 |
| M = 2 N = 2 | 0.0635 | 0.0558 | 0.0733 | 0.0664 | 0.0840 | 0.0805 | 0.0957 | 0.0978 |
| M = 3 N = 3 | 0.0583 | 0.0615 | 0.0703 | 0.0720 | 0.0826 | 0.0867 | 0.0964 | 0.1049 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





