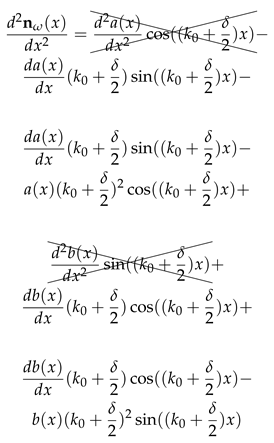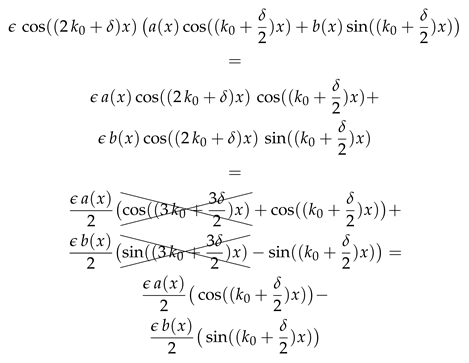Spatially Modulated Plasma Profile for Turbulence and Instabilities Mitigation in Fusion Plasma

1. Mathematical Formalism

Let us consider the mathematical formalism of this process. As a test-bed in our discussion we choose drift waves, although on the place of drift waves can be any other type of plasma waves (interchange-type turbulence or MHD waves). Without delving into details, we write the wave equation for drift waves.

The phase velocity of these waves, as can be seen, is determined by the electron diamagnetic drift velocity, i.e., it is inversely proportional to the magnetic field strength and plasma density. Thus, a spatial periodic variation of these quantities is equivalent to a spatial variation of the phase velocity.

The equation descibing the propagation of the drift wave in the magnetized plasma can be written as follows:

$${\displaystyle \frac{d^2\mathbf{n}}{d{t}^2}}=u_p^2{\displaystyle \frac{d^2\mathbf{n}}{d{x}^2}}$$

(1)

here $u_p$ is the wave phase velocity. The drift wave phase velocity represent the electron diamagnetic drift velocity:

$$u_p={\displaystyle \frac{\nabla p\times \mathbf{B}}{ne{\mathbf{B}}^2}},$$

where $p=n{T}_e$ is the plasma pressure.

First, we take the time Fourier transform of both sides of the Eq.1.

$$\mathcal{F}\left\{{\displaystyle \frac{{\partial }^2\mathbf{n}}{\partial x^2}}\right\}={\displaystyle \frac{{\partial }^2{\mathbf{n}}_{\omega }\left(x\right)}{\partial x^2}}$$

(2)

$$\mathcal{F}\left\{{\displaystyle \frac{d^2\mathbf{n}}{d{t}^2}}\right\}=-{\omega }^2{\mathbf{n}}_{\omega }$$

Combining both parts we rewrite the equation above in the Fourier space.

$$u_p^2{\displaystyle \frac{{\partial }^2{\mathbf{n}}_{\omega }\left(x\right)}{\partial x^2}}=-{\omega }^2{\mathbf{n}}_{\omega }$$

(3)

Let us rewrite this equation as a traditional equation for a harmonic oscillator.

$${\displaystyle \frac{{\partial }^2{\mathbf{n}}_{\omega }\left(x\right)}{\partial x^2}}=-{\displaystyle \frac{{\omega }^2}{u_p^2}}{\mathbf{n}}_{\omega }=-k^2{\mathbf{n}}_{\omega }$$

(4)

The drift wave favorably develops in the conditions where $u_p$ is constant on the wavelength scale.

Let’s now consider the opposite situation, the development in the plasma where $u_p$ has a periodical spatial dependence.

Specifically, we will determine the conditions for wave development in a case where $u_p$ slightly differs from some constant value and is a simple spatially periodic function $u_p\left(x\right)$.

$$u_p\left(x\right)=u_p^0(1-\epsilon cos\left(\beta x\right))$$

(5)

where the constant $\epsilon \ll 1$ and $\beta$ designates the wave number of the spatial modulation. The sign of $\epsilon$ is not that important since we can always change this sign by the corresponding choice of the reference frame. Substituting this expression (5) in the Equation (4) gives

$${\displaystyle \frac{{\partial }^2{\mathbf{n}}_{\omega }\left(x\right)}{\partial x^2}}=-{\displaystyle \frac{{\omega }^2}{{\left(u_p^0(1-\epsilon cos\left(\beta x\right))\right)}^2}}{\mathbf{n}}_{\omega }\approx -({\displaystyle \frac{\omega }{u_p^0}}{)}^2(1+2\epsilon cos\left(\beta x\right)){\mathbf{n}}_{\omega }$$

(6)

or, designating

$$k_0={\displaystyle \frac{\omega }{u_p^0}}$$

(7)

$${\displaystyle \frac{{\partial }^2{\mathbf{n}}_{\omega }\left(x\right)}{\partial x^2}}=-k_0^2(1+2\epsilon cos\left(\beta x\right)){\mathbf{n}}_{\omega }$$

(8)

We will see later that the effect of modulation is strongest if the wavenumber $\beta$ is close to the doubled wavenumber of drift wave $k_0$. Therefore we will assume

$$\beta =2k_0+\delta$$

(9)

where $\delta$ is a small deviation of $\beta$ from $2k_0$.

$${\displaystyle \frac{{\partial }^2{\mathbf{n}}_{\omega }\left(x\right)}{\partial x^2}}=-k_0^2(1+2\epsilon cos\left((2k_0+\delta )x\right)){\mathbf{n}}_{\omega }$$

(10)

For the simplification we introduce the new designation

$$ϵ=2\epsilon$$

(11)

and rewrite the equation

$${\displaystyle \frac{{\partial }^2{\mathbf{n}}_{\omega }\left(x\right)}{\partial x^2}}=-k_0^2(1+ϵcos\left((2k_0+\delta )x\right)){\mathbf{n}}_{\omega }$$

(12)

The equations of this type are called in mathematics the Mathieu equation.

Using the method of variation of parameters, the solution ${\mathbf{n}}_{\omega }\left(x\right)$ to our transformed equation may be written as

$${\mathbf{n}}_{\omega }\left(x\right)=a\left(x\right)cos\left((k_0+{\displaystyle \frac{\delta }{2}})x\right)+b\left(x\right)sin\left((k_0+{\displaystyle \frac{\delta }{2}})x\right)$$

(13)

where the rapidly varying components, $cos\left((k_0+{\displaystyle \frac{\delta }{2}})x\right)$ and $sin\left((k_0+{\displaystyle \frac{\delta }{2}})x\right)$ have been factored out to isolate the slowly varying amplitudes $a\left(x\right)$ and b(x).

Where (a(x)) and (b(x)) are slowly (compared to the factors cos and sin) changing functions of time. Such a solution, of course, is not exact. We proceed by substituting this form of the solution (13) into the differential Equation (12) and considering that both the coefficients in front of $cos\left((k_0+{\displaystyle \frac{\delta }{2}})x\right)$ and $sin\left((k_0+{\displaystyle \frac{\delta }{2}})x\right)$ must be zero to satisfy the differential equation identically. We also omit the second derivatives of $a\left(x\right)$ and $b\left(x\right)$ on the grounds that $a\left(x\right)$ and $b\left(x\right)$ are slowly varying functions.

$$\begin{array}{c}-2{\displaystyle \frac{da\left(x\right)}{dx}}(k_0+{\displaystyle \frac{\delta }{2}})-b\left(x\right){(k_0+{\displaystyle \frac{\delta }{2}})}^2+k_0^{2}b\left(x\right)\left(1-{\displaystyle \frac{ϵ}{2}}\right)=0\\ 2{\displaystyle \frac{db\left(x\right)}{dx}}(k_0+{\displaystyle \frac{\delta }{2}})-a\left(x\right){(k_0+{\displaystyle \frac{\delta }{2}})}^2+k_0^{2}a\left(x\right)\left(1+{\displaystyle \frac{ϵ}{2}}\right)=0\end{array}$$

(14)

A more detailed derivation is provided in the Appendix A. Neglecting all terms above the first order in $\delta$, we can simplify

$$\begin{array}{c}2{\displaystyle \frac{da\left(x\right)}{dx}}+b\left(x\right)\delta +{\displaystyle \frac{k_{0}b\left(x\right)ϵ}{2}}=0\\ 2{\displaystyle \frac{db\left(x\right)}{dx}}-a\left(x\right)\delta +{\displaystyle \frac{k_{0}a\left(x\right)ϵ}{2}}=0\end{array}$$

(15)

We got the system of two first-order linear differential equations. To find the general solution of a system, the system can be expressed in matrix form as:

$$\begin{array}{c}{\displaystyle \frac{d\mathbf{Y}}{dx}}=A\mathbf{Y},\end{array}$$

(16)

where

$$\begin{array}{c}\mathbf{Y}=\left[\begin{array}{c}a\left(x\right)\\ b\left(x\right)\end{array}\right]=c_1{\overrightarrow{V}}_1{e}^{{\lambda }_{1}x}+c_2{\overrightarrow{V}}_2{e}^{{\lambda }_{2}x},\end{array}$$

(17)

${\lambda }_1$ and ${\lambda }_2$ are the eigenvalues of the matrix A

$$\begin{array}{c}A={\displaystyle \frac{1}{2}}\left[\begin{array}{cc}0& \delta +{\displaystyle \frac{ϵk_0}{2}}\\ -\delta +{\displaystyle \frac{ϵk_0}{2}}& 0\end{array}\right],\end{array}$$

(18)

${\overrightarrow{V}}_1$ and ${\overrightarrow{V}}_2$ are corresponding eigenvectors, and $c_1$ and $c_2$ are some constants.

The eigenvalues are given by the expression

$$\begin{array}{c}{\lambda }_{1,2}=\pm {\displaystyle \frac{1}{2}}\sqrt{{\left({\displaystyle \frac{ϵk_0}{2}}\right)}^2-{\delta }^2}\end{array}$$

(19)

The condition for the occurrence of a wave attenuation is that $\lambda$ is real (i.e., ${\lambda }^2\ge 0$). The parameter $\lambda$ characterizes the spatial attenuation (or amplification) of the wave. Thus, it occurs in the interval of

$$\begin{array}{c}-{\displaystyle \frac{ϵk_0}{2}}<\delta <{\displaystyle \frac{ϵk_0}{2}}\end{array}$$

(20)

around the wavenumber $2k_0$ of the $u_p\left(x\right)$ spatial modulation.

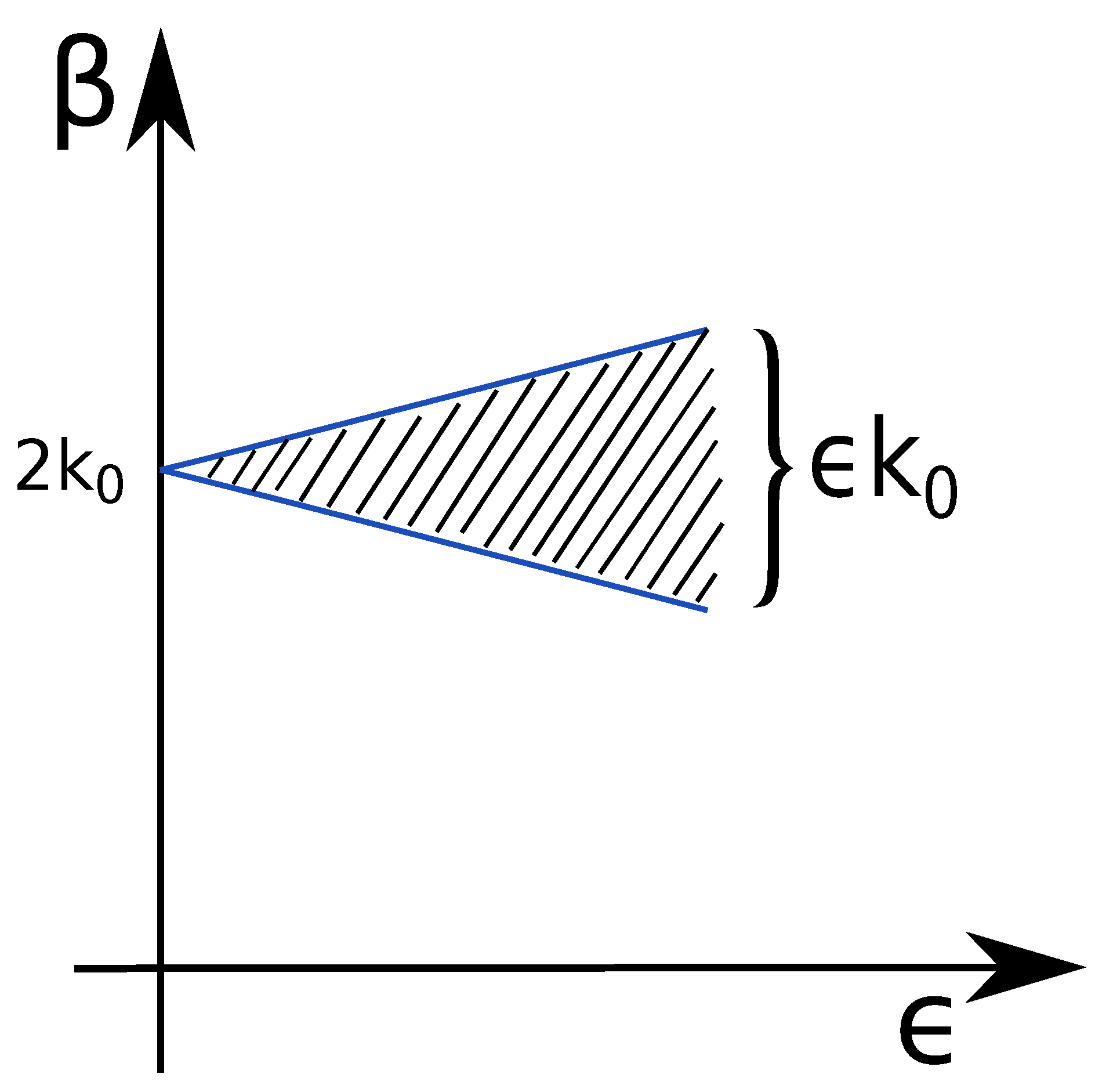
The chart in Figure 1 presents the graphical illustration of the mathematical results above. The effective damping of turbulent or instability waves occurs within a range defined by $ϵk_0$ around the spatial modulation wavenumber $\beta =2k_0$.

2. Practical Significance

2.1. Modulation Approach

The obtained result indicates that by creating a spatially modulated phase velocity profile, one establishes conditions to suppress drift waves. The main issue lies in finding a rational and feasible method for a modulation of plasma parameters. Here are some technical ways to implement this approach:

• RF electromagnetic waves (Alfvén waves), which lead to perturbations in the plasma’s magnetic field and, therefore, drift wave phase velocity $u_p$.
• Amplitude modulation of the microwave electromagnetic waves, which lead to perturbations in the plasma density due to ponderomotive force and, therefore, drift wave phase velocity $u_p$.
• Externally driving an another plasma instability leading to the perturbation of the plasma magnetic field or density.
• A static magnetic field perturbation created by external currents.
• A spatially-modulated neutral particle beam.

In this paper we are not aiming to discuss the technical details on the implementation of these approach, this is the subject of separate works.

2.2. Amplification vs. Damping

As seen in the Equation (20), the parameter $\lambda$ can be either positive or negative. From a purely mathematical perspective, this implies that the observed resonance can result in either amplification or decay of the propagating wave.

Whether the propagating wave instability is amplified or damped is a complex question that depends on numerous factors and the specific plasma modulation approach. The amplification or damping of the wave is determined by the specific physical mechanisms that facilitate or inhibit energy and momentum exchange between the plasma instability wave and the imposed modulation.

For instance, the steady state static magnetic field $\mathbf{B}$ spatial modulation created by an external currents (if this is feasible at all) will lead to the dumping since it is not the subject of the energy exchange with plasma waves. The low-frequency plasma modulation created by an externally launched wave have a more complex wave-wave interaction physics and can lead to both amplification and dumping, depending on the features of dispersion relations of both imposed modulation (on the one hand) and plasma instability waves (on the other hand).

Summarizing the results obtained above, it can be said that waves propagating in such a medium will experience attenuation. This result is well-known in many areas of physics that deal with oscillations or waves, and is therefore quite predictable.

3. Conclusion

This work has demonstrated that introducing a spatially modulated phase velocity profile in plasma holds promising potential for mitigating turbulence, specifically drift wave instabilities, in fusion plasma environments. The framework established here illustrates that spatial modulation creates conditions akin to bandgaps in solid-state physics, where specific frequencies are inhibited, thus attenuating wave propagation. This principle could serve as an alternative approach to current turbulence suppression methods, which frequently encounter practical limitations and challenges in implementation.

The practical feasibility of applying spatial modulation was also explored, offering several methods for implementing these profiles in plasma, such as using RF waves, modulated microwave electromagnetic waves, or static magnetic perturbations. These methods provide a foundation for further investigation into the optimal means of achieving effective modulation in various fusion device configurations. The study underscores the dual potential of modulation, highlighting that careful tuning of the parameters can either amplify or dampen wave instabilities, depending on specific interactions between imposed modulation and instability waves. Future work should focus on feasibility study of these specific approaches, assessing their practicality, and testing their effectiveness in experimental settings to advance toward stable, high-performance fusion plasmas.