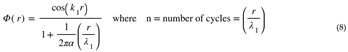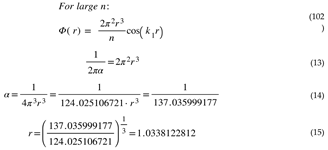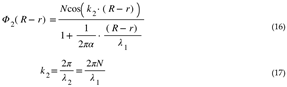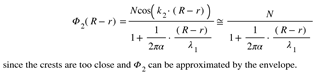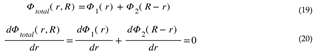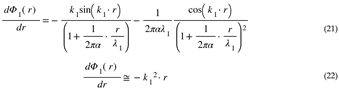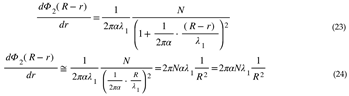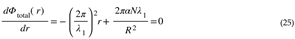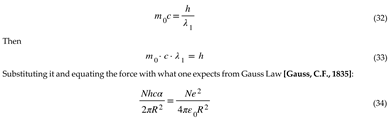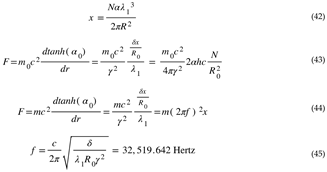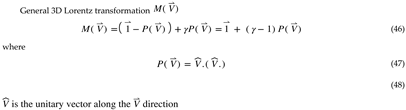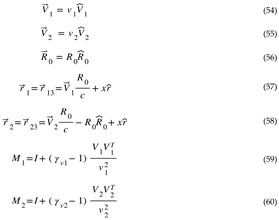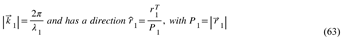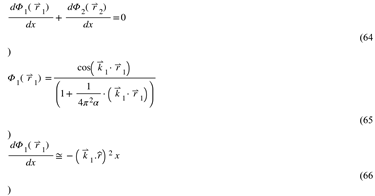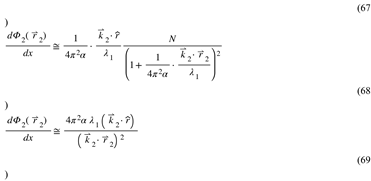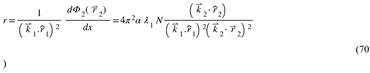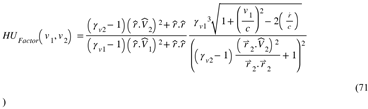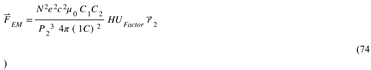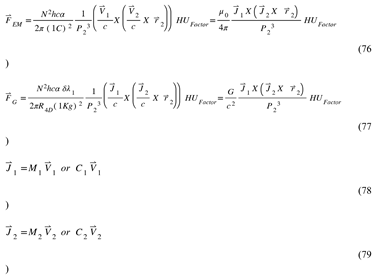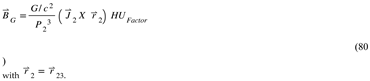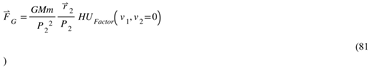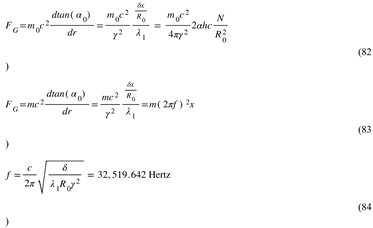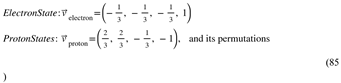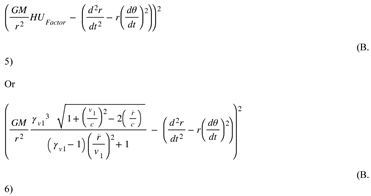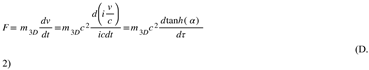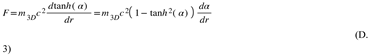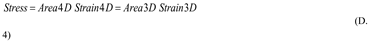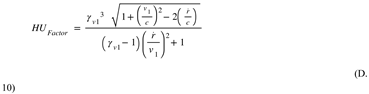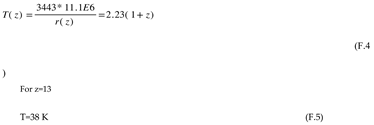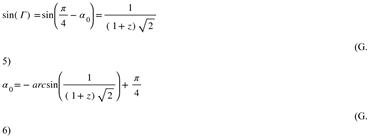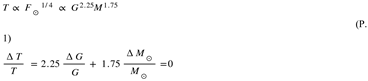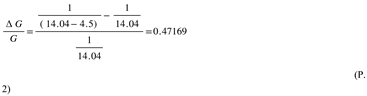1. Introduction
In the early days of scientific inquiry into the nature of matter, two prominent figures, Sir Isaac Newton and Christiaan Huygens, presented contrasting views. Newton described particles as discrete entities, essentially small, hard objects interacting through forces. On the other hand, Huygens proposed that particles exhibit wave-like properties, a perspective that laid the groundwork for the wave theory of light.
A parallel debate regarding the nature of light, specifically photons, mirrored the historical debate between Newton and Huygens on the nature of matter.
HU introduced the 4D metric waves or dilaton field. What we call Lights are waving on the top of these metric waves. The Dilaton Field has a wavelength equal to the Hydrogen Atom Compton Wavelength. The whole field is a quantum system; energy is added or extracted from it in quantized packets.
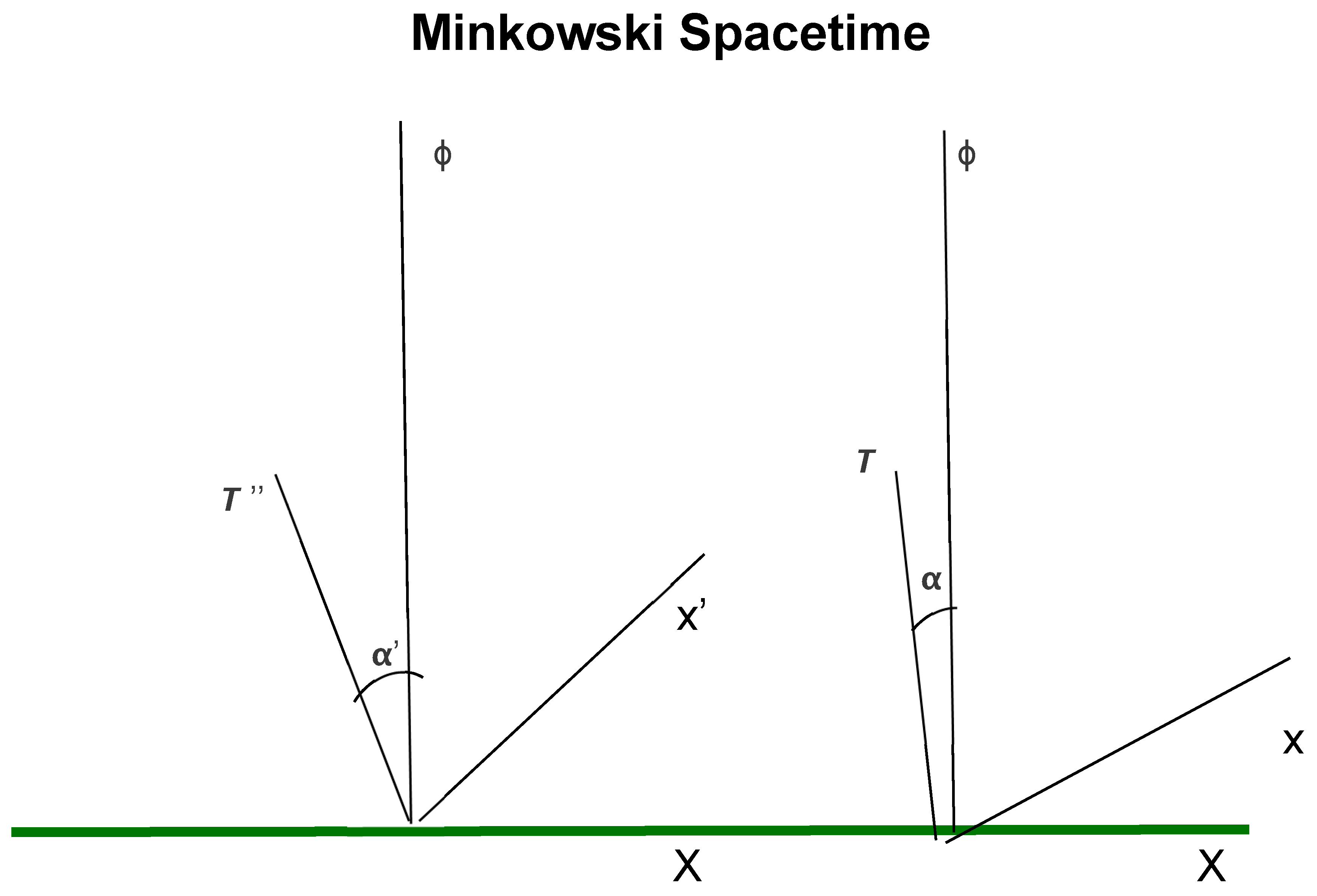
The concept of the Absolute Reference Frame (ARF) is central to HU and is first visualized through the depiction of Minkowski Spacetime in
Figure 1. In HU, the ARF comprises a vertical vector perpendicular to the Minkowski hyperplane and any three orthogonal vectors within that hyperplane. When HU replaces the Minkowski hyperplane with the Lightspeed Expanding Hyperspherical Universe (LEHU), the vertical vector becomes the Radial Direction, reflecting the expansion and structure of the universe. This transition from the conventional Minkowski interpretation to the LEHU model emphasizes HU’s view that the universe operates within a 4D spatial manifold, challenging traditional perceptions of space and time
[Einstein, A., 1905].
The Hypergeometrical Universe Theory (HU) fundamentally redefines our understanding of matter, physics, and quantum mechanics. HU introduces a new model for matter as shapeshifting deformations of space, moving beyond traditional particle concepts. This model operates under the Quantum Lagrangian Principle (QLP), a unifying principle that replaces all existing physical laws. Furthermore, HU corrects the limitations of the particle-wave dualism by proposing a Quantum Trinity consisting of the Fundamental Dilator (FD), the dilaton field, and the QLP, providing a complete and consistent framework for describing physical reality
Newton's contributions to physics are monumental, particularly his four laws of dynamics, which have been foundational to our understanding of motion and forces:
Newton's First Law (Law of Inertia) [Newton, I., 1687]: An object will remain at rest or in uniform motion in a straight line unless acted upon by an external force.
Newton's Second Law (Law of Acceleration): The acceleration of an object is directly proportional to the net force acting upon it and inversely proportional to its mass (F = ma).
Newton's Third Law (Action and Reaction): For every action, there is an equal and opposite reaction.
Newton's Law of Universal Gravitation: Every particle attracts every other particle in the universe with a force directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers.
HU Replaces Mass and Force by 3D Displacement Volume and Acceleration as Fundamental Constructs
The Hypergeometrical Universe Theory (HU) introduces a new perspective on this foundational concept. Instead of focusing on mass and force, HU considers 3D displacement-volume and acceleration as the primary concepts. From these, mass and force can be derived.
HU Replaces Particle-Wave Dualism with Fundamental Dilator-Dilaton Field-Quantum Lagrangian Principle Trinity
At the core of HU is the Fundamental Dilator (FD), a wave generator that serves as the monomer of particles. All particles are polymers of the Fundamental Dilator, and these FDs generate metric waves as they interact with the fabric of space. Displacement Volume is the volume a phase of the Fundamental Dilator has at a given time.
The debate between Newton and Huygens continued to evolve, and with the advent of quantum mechanics, a new understanding emerged: the wave-particle duality. This principle posits that particles like electrons and photons exhibit wave-like and particle-like properties, depending on the experimental setup.
Instead of particle-wave duality, HU introduced wave-generator (FDs), wave (dilaton field or metric waves created by FD shapeshifting and spinning in 4D), and the connection between wave-generators and waves - the Quantum Lagrangian Principle or QLP.
The Quantum Lagrangian Principle states that FDs will move at the speed of light radially and within the 3D hypersurface such that they always land in a position where they dilate space in phase with the local dilaton field.
This is a Quantum Trinity - or three intertwined concepts. QLP is the connecting tissue between the wave and the particle in the wave-particle dualism. It is the ONLY Law of Nature and replaces Newton’s Four Laws of Dynamics.
HU Replaces Newton’s Laws of Dynamics with the Quantum Lagrangian Principle (QLP) and a Single Field - The Dilaton Field
HU derives the laws of Nature from first principles using a single field - the Dilaton Field. The Dilaton Field is the interference pattern from the metric waves generated in all Fundamental Dilators. QLP is a Lagrangian Principle because it postulates that a particle (Fundamental Dilator Polymer) will not do work against or receive energy from its constraint (Space). It is “Quantum” because the Fundamental Dilator is a Quantum Mechanical Construct. In other words, HU is a Quantum Mechanical Theory because its fundamental construct is a Quantum Object.
HU Replaces Indistinguishable 3D Reference Frames with an Absolute 4D Reference Frame
HU assigns absolute velocity to be used in Lorentz transformations[Jackson, J.D., 1998], fundamentally changing how we understand these transformations. In traditional physics, Lorentz transformations are applied to time and space. In HU, they are applied both to spacetime and to the 4D spatial manifold.
HU Changes the Domain of Lorentz Transformation from Spacetime to the Reciprocal Space (Wavelength, Period, and 4D K-Vectors)
In 1905, Einstein looked at Physics and recognized these items:
- (a)
Electromagnetism evolved to a point where it became codified into Maxwell’s equations.
- (b)
Maxwell's equations allowed you to derive a wave equation coupling electric and magnetic fields, thus indicating that light is an electromagnetic wave.
- (c)
The coupled wave equation wasn’t covariant to Galilean Reference Frame transformations; it was only covariant to Lorentz transformations.
- (d)
As we know, a wave is defined by the position of its peaks and troughs, and those are defined not by (x,t) only but by (k.x, w.t). In other words, the wave nature of electromagnetism wouldn’t change if one considers that Maxwell’s equations are written for the Absolute Reference Frame.
- (e)
HU considers Lorentz transformations effect upon the reciprocal space (λ, T) to derive the Laws of Nature on the Absolute Reference Frame.
HU expanded space to include a fourth spatial dimension and instead applied Lorentz Rotation to dilaton field 4D k-vectors and frequencies. The addition of the extra spatial dimension allows for the identification of an Absolute Reference Frame.
In other words, Lorentz transformations dilate the Period of the Fundamental Dilator Coherence instead of dilating Time. The Fundamental Dilator coherence is the Cosmological Clock. If one dilates the period of the clock, one is effectively dilating time and more importantly slowing down dynamics. The latter is HU’s interpretation of events. By keeping track of the existence of an Absolute Time and a Cosmological Clock, HU avoids the pitfalls of “Dilating Time without a Clock”. Currently, that kind of reasoning leads to absurd conclusions like “A person falling into a Black Hole will see the end of times” or “there is an accumulation layer of things falling into a Black Hole.”
Similarly, Lorentz transformations dilate the Wavelength of the Fundamental Dilator Coherence instead of dilating length.
This is a requirement for the Fundamental Dilator always be at the Lightspeed Expanding Hyperspherical Locus of our 3D Universe. In other words, the period and wavelength adjust to remain traveling with our universe. That is expected if one considers the Conservation of Linear Momentum along the radial direction.
All forces are carried by the dilaton field (metric waves) and indirectly through space elasticity.
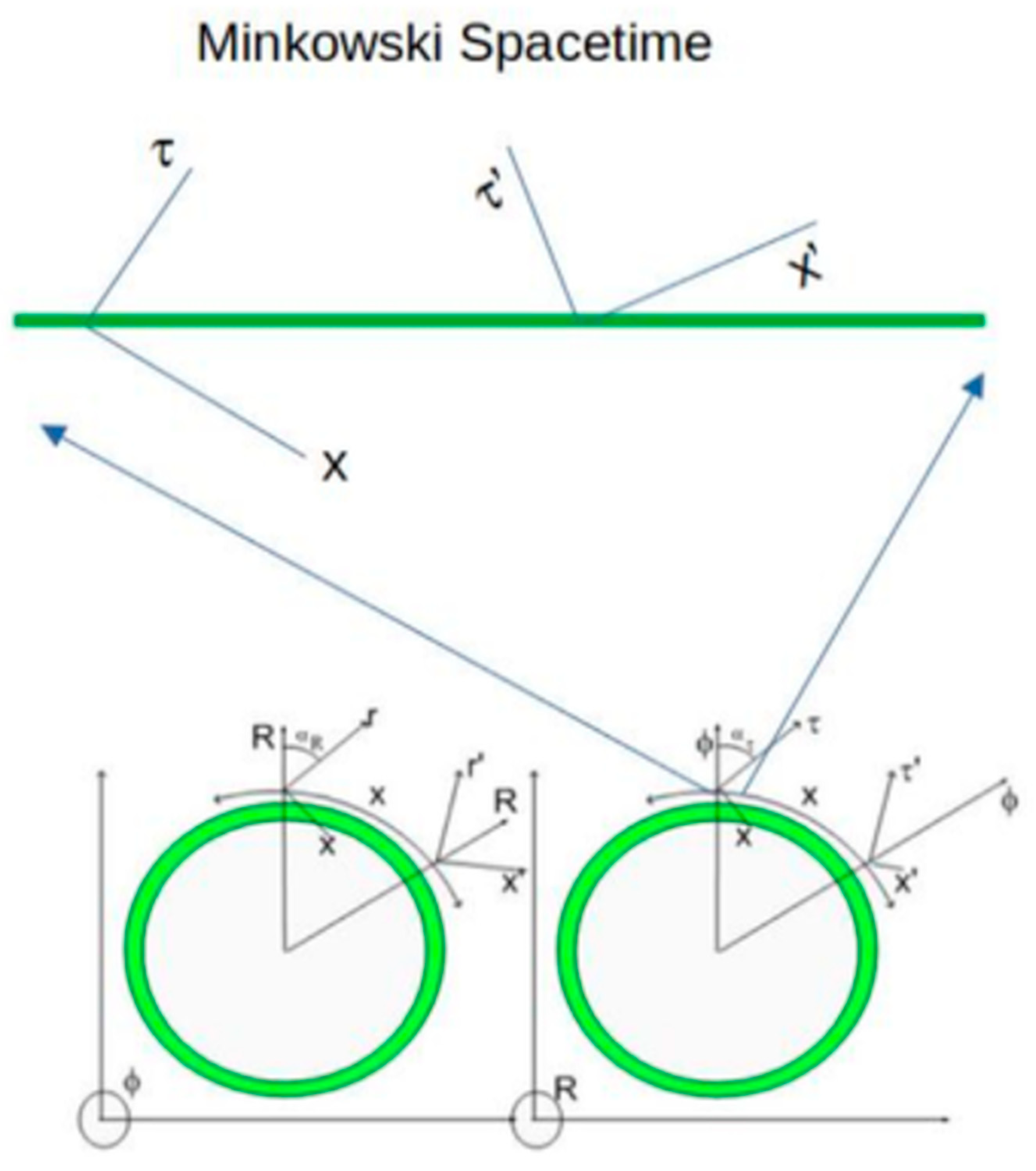
Figure 2.
Here, it shows how the Fundamental Dilator wavelength stretches with time dilation. This is a requirement because everything is regulated by the elasticity of space. Notice that the diagonal green line represents the proper r or τ,depending if you are considering this cross-section to be in the 4D spatial manifold or in the 4D spacetime.
Figure 2.
Here, it shows how the Fundamental Dilator wavelength stretches with time dilation. This is a requirement because everything is regulated by the elasticity of space. Notice that the diagonal green line represents the proper r or τ,depending if you are considering this cross-section to be in the 4D spatial manifold or in the 4D spacetime.
Figure 3.
Here, you see the cross-sections of the 4D spatial manifold and 4D spacetime. You can identify the unperturbed Fabric of Space, represented by the circles and the Radial direction R, perpendicular to our 3D spatial manifold at every point. Notice that for short distances (local phenomenon), the circle on the right becomes the familiar Minkowski Spacetime Hyperplane.
Figure 3.
Here, you see the cross-sections of the 4D spatial manifold and 4D spacetime. You can identify the unperturbed Fabric of Space, represented by the circles and the Radial direction R, perpendicular to our 3D spatial manifold at every point. Notice that for short distances (local phenomenon), the circle on the right becomes the familiar Minkowski Spacetime Hyperplane.
One can see that Minkowski Spacetime (on the right panel) is just a local homology to what happens in the actual universe, represented by the circle in the left panel. In other words, everything exists in a 4D Spatial Manifold.
When one considers that HU applies it to the wavelength and period, it is straightforward to understand why the speed of light is constant, irrespective of which inertial frame one uses. Light Velocity is the ratio between wavelength and period, and these are modified by the same cosh(α). This means that HU recognized that Lorentz transformations govern not space and time or spacetime but the reciprocal space to spacetime (wavelength and period).
In other words, HU disavowed all later developments in metrics and geodesics. To be 100% clear, HU retakes Physics to the point before Einstein and Minkowski drove into spacetime and differential geometry. In HU, the Universe exists in a 4D Spatial Manifold. Time is there just to time processes.
HU Provides the Fundamental Process, the Timepiece for the Whole Universe. This Process Is the Fundamental Dilator Tunneling Process and the Generated Metric Waves
Unlike Relativity (current Physics), HU has an underlying process (the tunneling of the Fundamental Dilator) that provides Time with meaning. Lorentz transformations dilate wavelength and period for this process, assuring that the Fundamental Dilator, the dilaton field, and the electromagnetic field (waves on the top of a finer wave) keep pace with the Lightspeed Expanding Hyperspherical Universe.
This approach highlights the true essence of Lorentz transformations: ensuring that the laws of physics remain consistent across all reference frames when expressed in terms of the Absolute Reference Frame.
HU Creates Covariance by Making the Force in all Inertial Reference Frames Equal to the Force in the Absolute Reference Frame
The relationship between force and acceleration in HU is given by:
is the time dilation interpretation.
What Is the Kinetic Energy of a Body of Mass m Driven from Absolute Velocity 0 to v0?
Minkowski Diagram
For that, one needs to calculate dW = F.dr and integrate it for velocities 0 to v0.
HU predicts interaction to diminish with Absolute Velocity and that resembles the Shield a Spacecraft needs when traveling at Relativistic speeds.
HU Changes the Concept of Time Dilation to Absolute-Velocity-Dependence of Forces Vanishing When the Absolute Velocity Approaches C
Here, v, dr, and α are all defined in the Absolute Reference Frame. This consistency ensures that all reference frames obey the same HU laws, emphasizing that time dilation is an artifact. It arises because forces approach zero as absolute velocity approaches the speed of light c, as equation (2) demonstrates. That is expected since, in HU, forces are carried by the dilaton field, metric waves that travel at the speed of light.
2. Hypergeometrical Universe Theory Hypotheses
Spacetime Is just a Proxy of What Happens in the 4D Spatial Manifold
Not unlike and representation as a straight line for the linear motion of a car along a straight road.
Dimensionality Reduction and Particle Dynamics
A key aspect of the Hypergeometrical Universe (HU) theory is the concept of dimensionality reduction. This concept is similar to surfers riding circular waves in a pond.
Likewise, in the lightspeed-expanding 4D hyperspherical universe, particles are restricted in their radial motion because they surf the Inner Dilation Layer, effectively experiencing a reduction in their degrees of freedom.
To elaborate, imagine being inside a lightspeed expanding 4D hypersurface. This hypersurface is analogous to the 3D surface of a sphere but exists in a higher dimension. Particles within this universe move along the Inner Dilation Layer, a negative energy 4D dilation wave. This process is similar to the behavior of a Prince Rupert Drop, where particles are ejected because of the Entropic Explosion resulting from dilation in its inner layers and contraction in the outer layers. Consequently, they do not perceive the existence of the fourth spatial dimension, leading to an apparent reduction in dimensionality from their perspective.
The Stroboscopic Universe concept within HU illustrates how the perception of time and motion is fundamentally tied to the quantization of Absolute Time. This quantization arises from the discrete nature of the tunneling process of the Fundamental Dilator and the resulting intermittent interaction. Unlike metric waves, which are continuous, the interaction and enforcement of the Quantum Lagrangian Principle (QLP) occur only at specific phases of the Fundamental Dilator's coherence. Similar to how a strobe light creates the illusion of continuous motion by flashing at intervals, the Stroboscopic Universe reflects how interactions happen only during discrete phases of tunneling. These phases vary depending on the Inertial Reference Frame (see Fig.2), creating differences in how time quatization is perceived across reference frames. This approach ties the dynamics of the Quantum Trinity directly to the QLP, illustrating that our perception of continuous time is an effect of the discrete and intermittent nature of these fundamental interactions.
The Lightspeed Expanding Hyperspherical Universe (Lehu Topology)
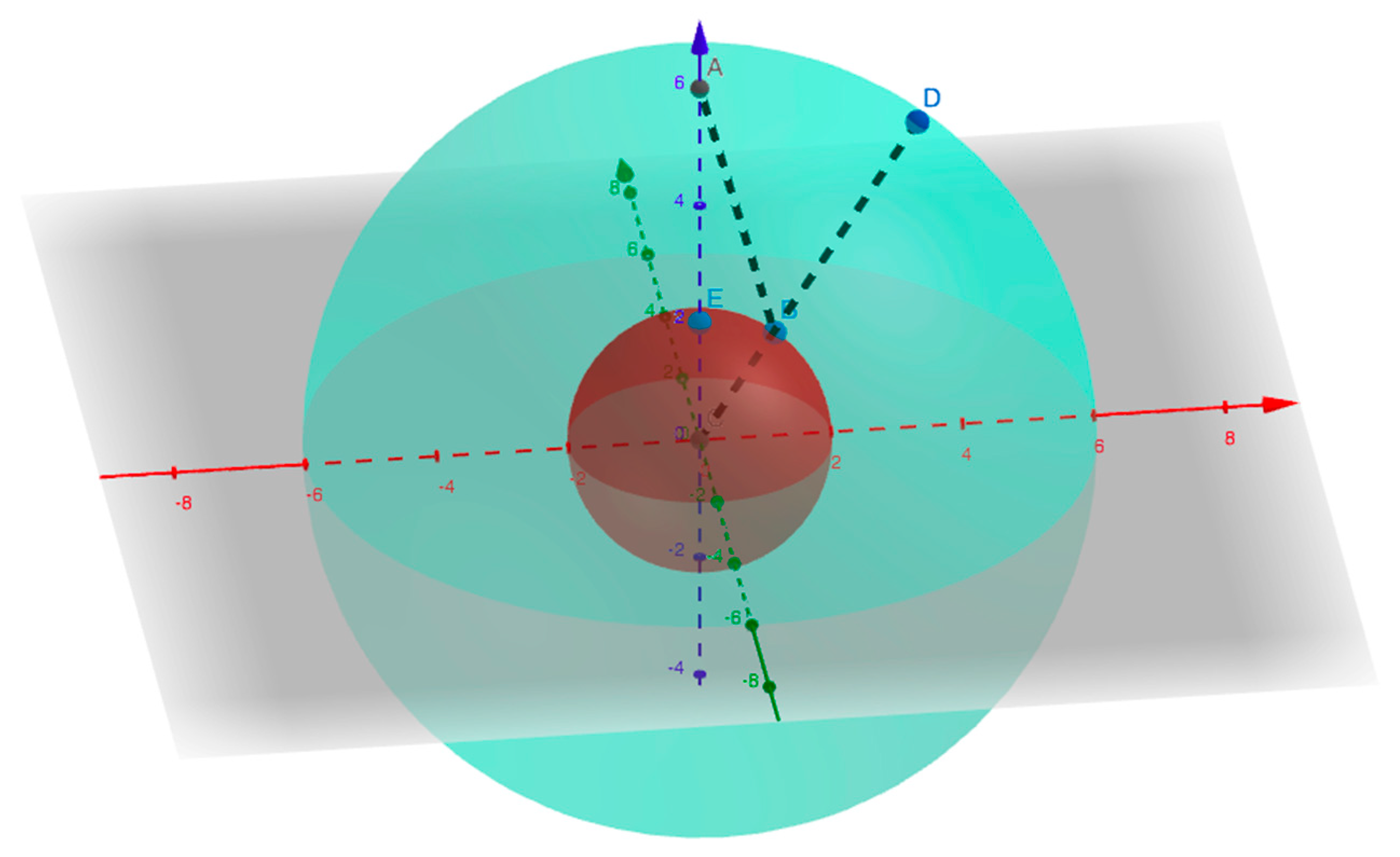
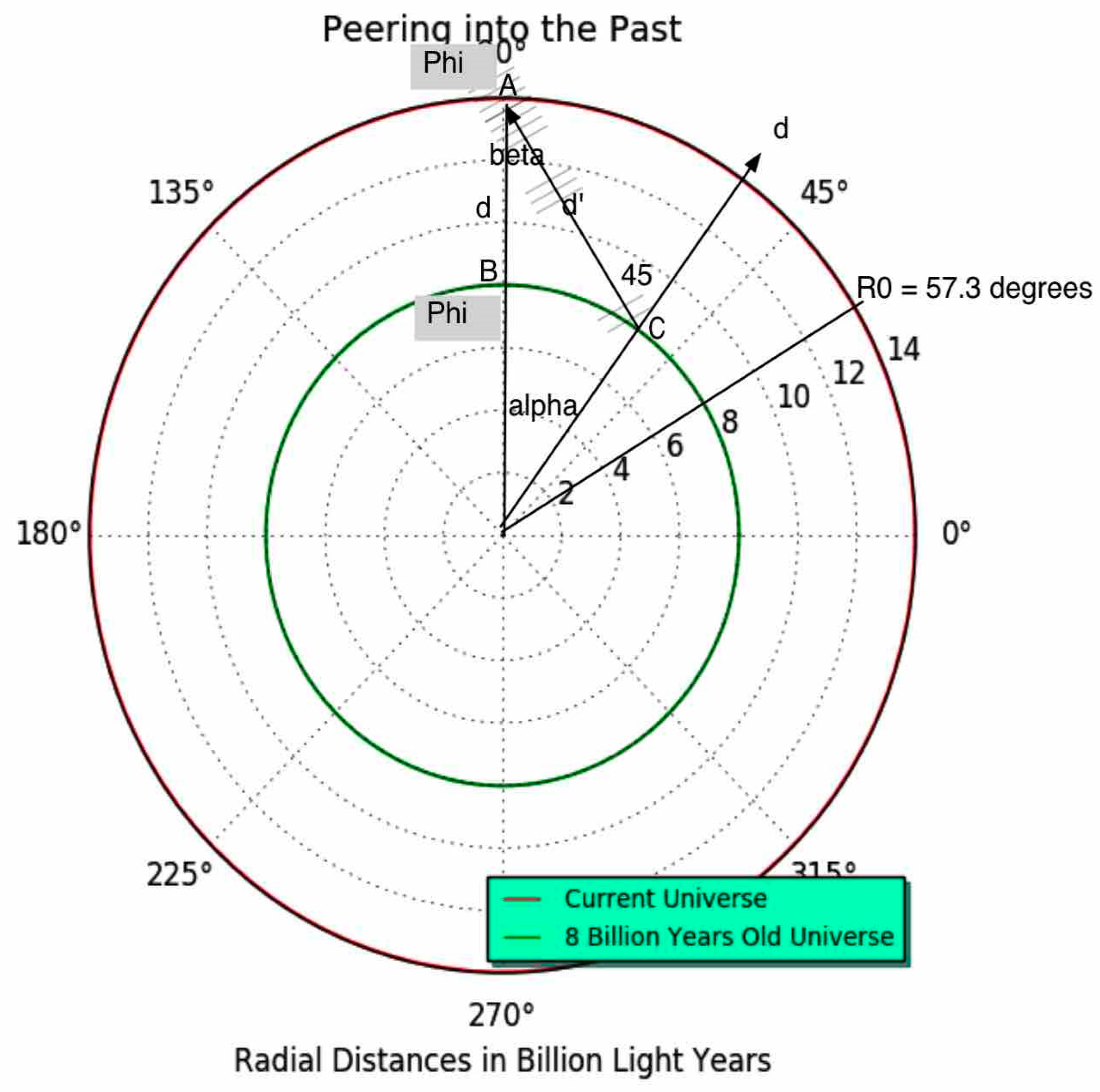
Figure 5.
LEHU: This figure shows yourself at position A, looking into the sky and seeing the light of a Type 1a Supernova (SN1a) at position B when the universe was smaller, denser, and more homogeneous. The SN1 and the host galaxy will travel radially to point D. This means that HU provides the mechanism to predict the current map of the universe from what we see in the sky.
Figure 5.
LEHU: This figure shows yourself at position A, looking into the sky and seeing the light of a Type 1a Supernova (SN1a) at position B when the universe was smaller, denser, and more homogeneous. The SN1 and the host galaxy will travel radially to point D. This means that HU provides the mechanism to predict the current map of the universe from what we see in the sky.
The Fundamental Dilator Paradigm
The Fundamental Dilator and the Quantum Lagrangian Principle expand the concept of particle-wave dualism. Instead of an immutable particle connected to a de Broglie or Compton wave - without any connecting logic between them [Compton, A.H., 1923], HU introduced particles as Wave-Generators (coherence between stationary states of deformation of space) that both generate metric waves and interact with those waves in a way as never exchange any energy with the elastic space medium. Notice that elastic space is not Aether. Aether is a material medium that has been debunked by the Michelson-Morley experiment. Space has no mass and cannot be dragged by gravitational fields.
This figure depicts the Fundamental Dilator coherence. Each ball represents a localized deformation of space. The phases are relative to each other after the initial phase following the recombination of the Initial Metric Fluctuation (see
Appendix N). In other words, after the Universe executed its first step in the hyperspherical expansion, being positively or negatively charged became a relative matter. In the figure, I depicted yellow as positive and green as negative.
The orientation of the letters indicates the orientation of the phase with respect to our 3D hypersurface. The phases are modeled as pizza-like objects (with a small height with respect to the Radial Direction).
Four Phases of the Fundamental Dilator
Here are the four phases of the Fundamental Dilator:
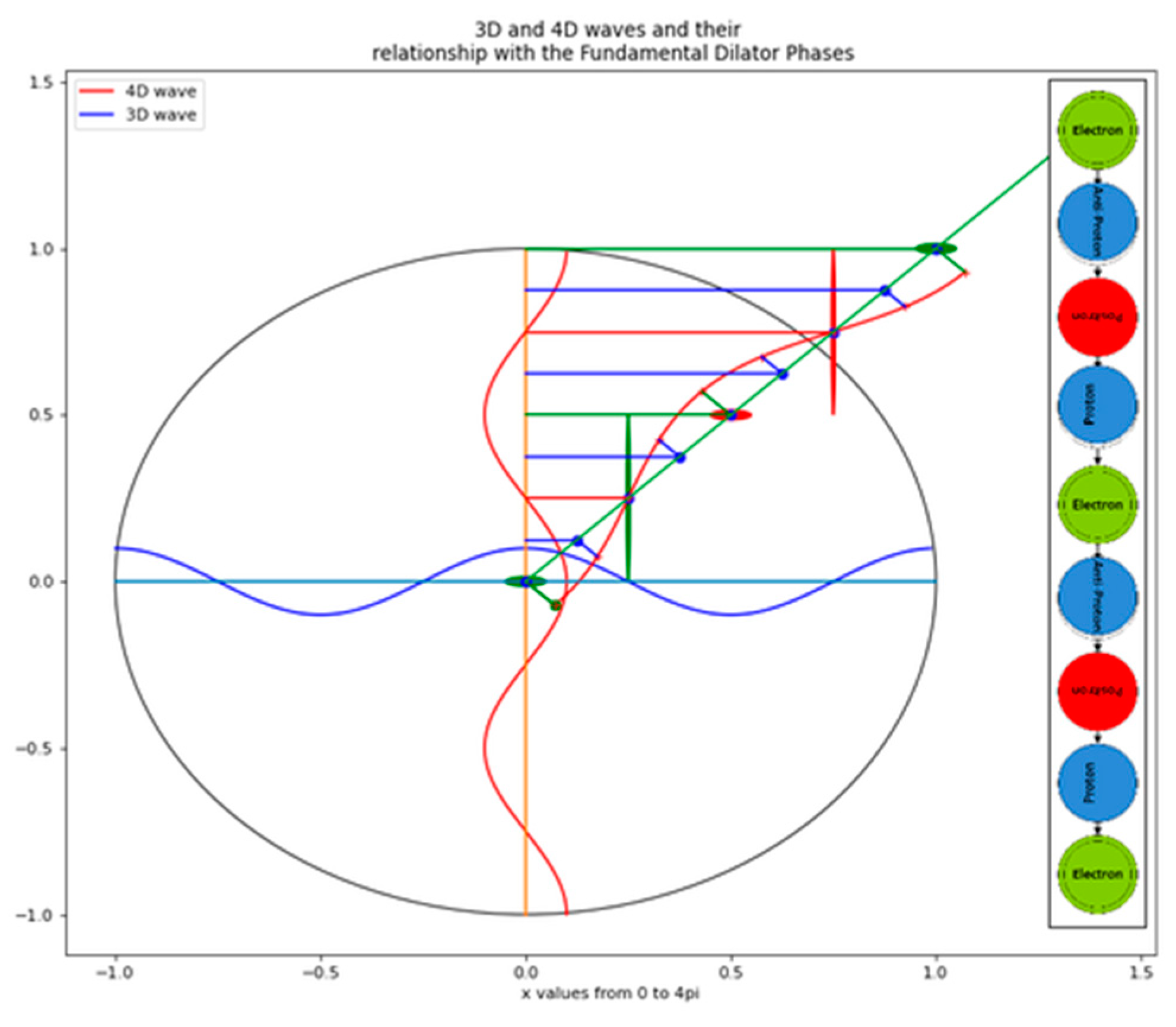
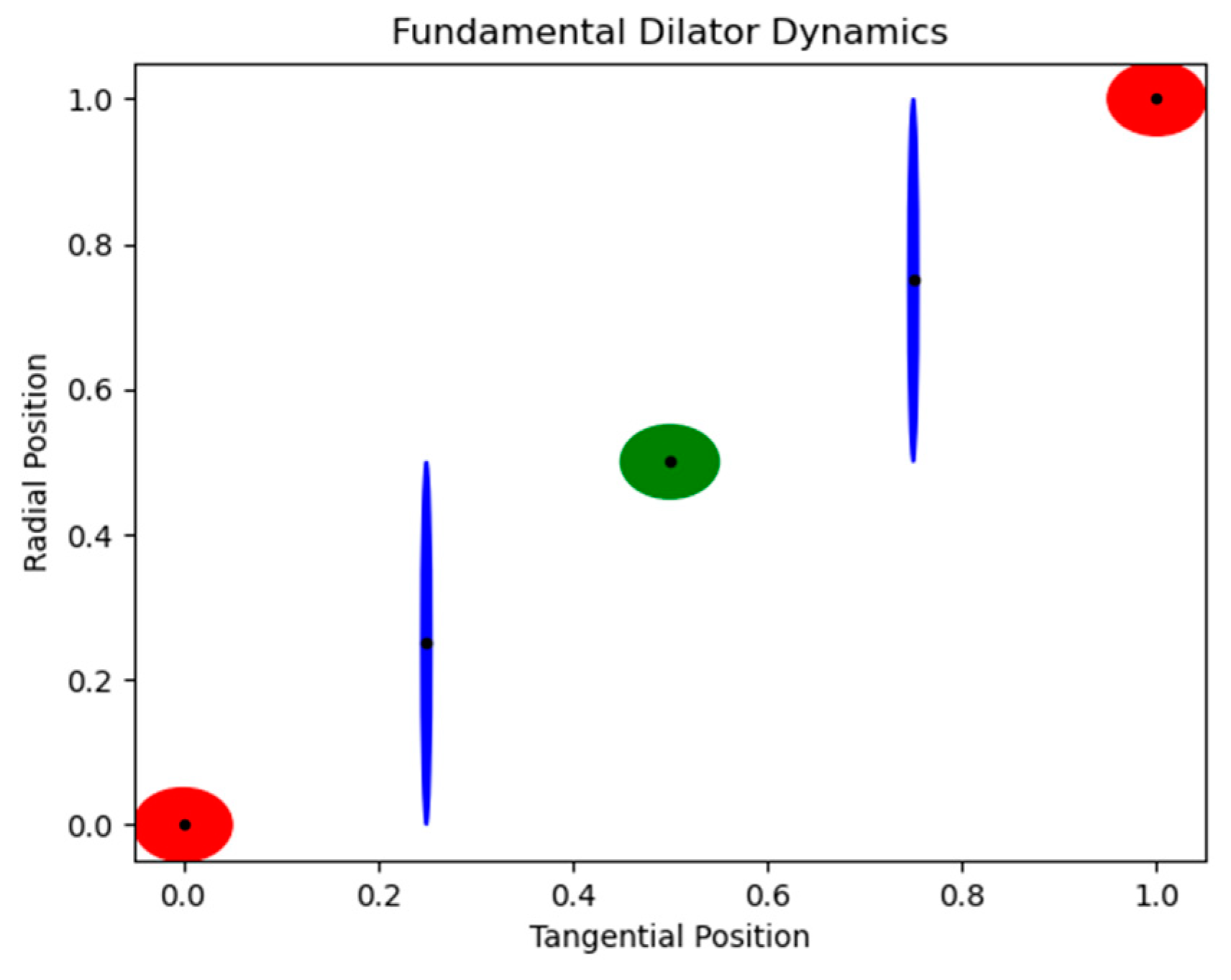
Figure 6.
Fundamental Dilator Phases: The second and third images show the four phases of the fundamental dilator, corresponding to the four fundamental particles (electron, positron, proton, and antiproton). Other fundamental particles are due to subcoherences between orientationally distinct states within the 3D hypersurface. Intermediate phases are perpendicular to our 3D Universe and don’t interact. That is results in an Absolute Time Quantization or the Stroboscopic Universe.
Figure 6.
Fundamental Dilator Phases: The second and third images show the four phases of the fundamental dilator, corresponding to the four fundamental particles (electron, positron, proton, and antiproton). Other fundamental particles are due to subcoherences between orientationally distinct states within the 3D hypersurface. Intermediate phases are perpendicular to our 3D Universe and don’t interact. That is results in an Absolute Time Quantization or the Stroboscopic Universe.
Figure 7.
The phase sequence of an electron. Colors are used to express dilation or contraction. Notice that the perpendicular phases with respect to the 3D hypersurface (our 3D Universe) do not interact and have zero cross-section.
Figure 7.
The phase sequence of an electron. Colors are used to express dilation or contraction. Notice that the perpendicular phases with respect to the 3D hypersurface (our 3D Universe) do not interact and have zero cross-section.
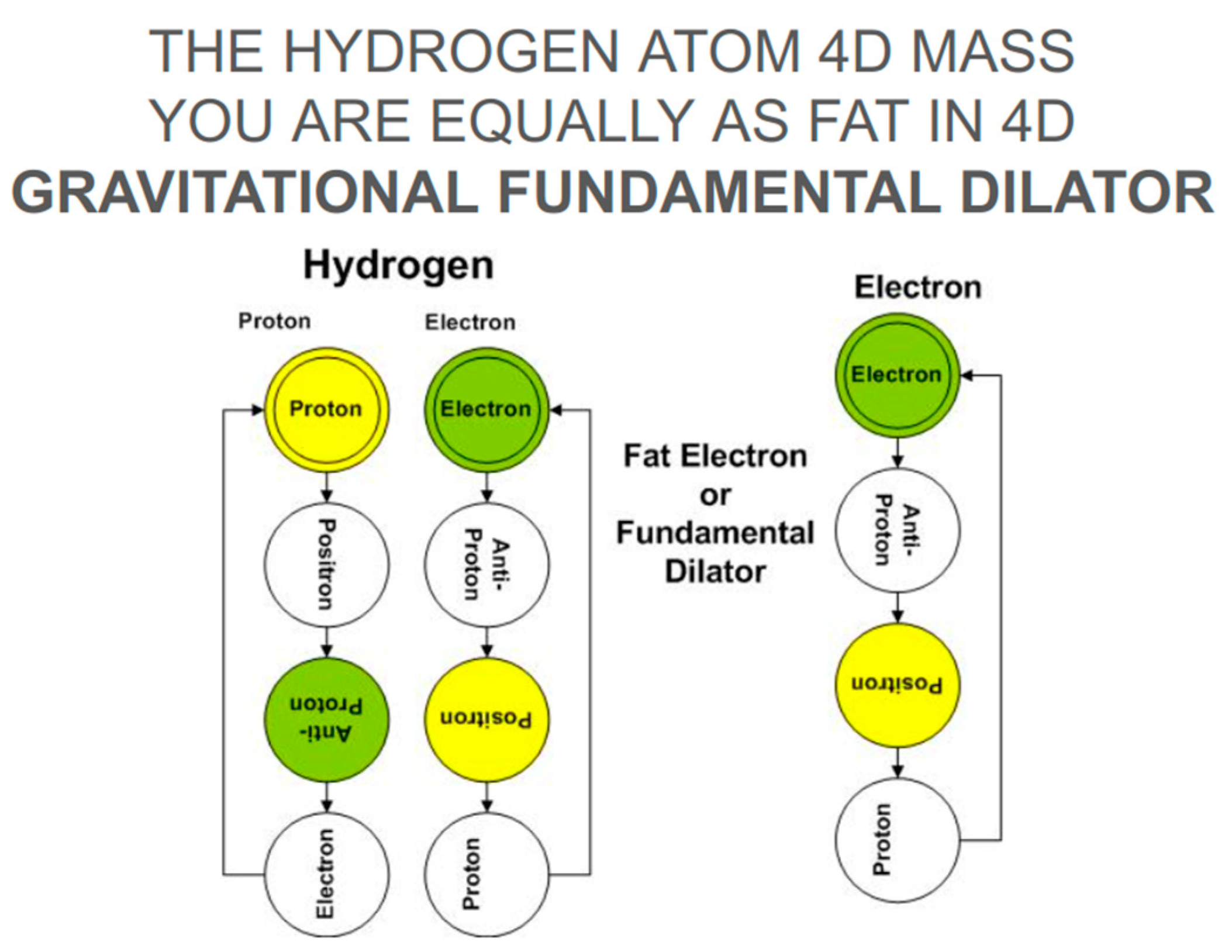
Figure 8.
The Gravitational Fundamental Dilator is a Hydrogen Atom. This means the Electromagnetic Fundamental Dilator is mapped to a 4D Mass equal to half of a Hydrogen Atom. When you join two FDs, you get a Hydrogen Atom with a 4D Mass equal to the mass of a Hydrogen Atom. In other words, the 3D and 4D masses of a Hydrogen Atom are the same. The 4D mass is used to calculate the Compton Wavelength of the dilaton field. It is straightforward to see that both phases (Proton-Electron and Antiproton-Positron are neutral and indistinguishable). That does not happen for a single dilator since electron and positron phases will differ in dilation or contraction. Hence, the electromagnetic FD has a wavelength that is twice that of the gravitational FD.
Figure 8.
The Gravitational Fundamental Dilator is a Hydrogen Atom. This means the Electromagnetic Fundamental Dilator is mapped to a 4D Mass equal to half of a Hydrogen Atom. When you join two FDs, you get a Hydrogen Atom with a 4D Mass equal to the mass of a Hydrogen Atom. In other words, the 3D and 4D masses of a Hydrogen Atom are the same. The 4D mass is used to calculate the Compton Wavelength of the dilaton field. It is straightforward to see that both phases (Proton-Electron and Antiproton-Positron are neutral and indistinguishable). That does not happen for a single dilator since electron and positron phases will differ in dilation or contraction. Hence, the electromagnetic FD has a wavelength that is twice that of the gravitational FD.
It will be shown that the forces are not dependent on the dilaton field's wavelength or the dilator's mass.
Electron and Proton states are expected to be narrow along the radial direction. This means that when they rotate 90 degrees, their overlap (footprint or 3D volume) with the 3D hypersurface goes to zero. Zero 3D-volume implies that those phases do not interact. This allows for this shapeshifting, spinning in 4D construct to keep particles’ nature (charge, inertial mass, dipole, multipole moments, and 3D-volume).
If one assumes that mass is some density multiplied by a displacement volume, it should be clear that the 4D mass of the Fundamental Dilator is equal to half the mass of a Hydrogen Atom. This simple model competes with the Higgs Model.
QUANTUM LAGRANGIAN PRINCIPLE (QLP)
QLP is a replacement for Newton’s Laws of Dynamics. It states that FDs will move into positions where they dilate space in phase with the local dilaton field. The Dilaton field is the interference pattern from the traveling metric waves generated by the shapeshifting metric deformations (a.k.a. particles). This Lagrangian Principle describes the interaction of the dilator (matter) with its boundaries (space). Particles are not supposed to gain or lose energy to space just by existing. Particles don’t dissipate, which explains the need for QLP.
In other words, HU materializes metric waves in a 4D spatial manifold [Dirac, P.A.M., 1928]. HU distinguishes four kinds of metric waves:
- (a)
Hypersuperficial. These metric waves are created by the Fundamental Dilator 3D footprint onto the traveling surface of the Universe. They are sensitive only to the FD phases in phase with the Universe, and thus, they are sensitive only to the characteristic mass of the FD phase. They are mapped to de Broglie Waves.
- (b)
Hypervolumetric. These metric waves travel through the 4D space and are responsible for Gravitation and Electromagnetism. Later, we will show that other forces (strong and weak) are also due to these metric waves.
- (c)
Shear. Shear Metric Waves are the reason for entanglement [Aspect, A., 1982]. At this time, it is not clear if they are Shear Metric Waves of spatial or spacetime nature. That will become clearer when we have data on the speed of entanglement. If instantaneous, the shear metric waves would have a spacetime nature and travel through time. If entanglement is just really fast, then shear metric waves of a spatial nature would suffice.
- (d)
Tsunami Metric Waves - These are long wavelength metric waves similar to those that carry all particles in the Universe (the Inner Dilation Layer). Being carried by these waves means maximum acceleration (0 to c in one Compton Wavelength). The energy associated with an instantaneous acceleration is mc2. This explains the at-rest energy of a particle since all particles are surfing the Inner Dilation Layer. This also explains the energy component of particles subject to non-instantaneous accelerations( mv2/2).
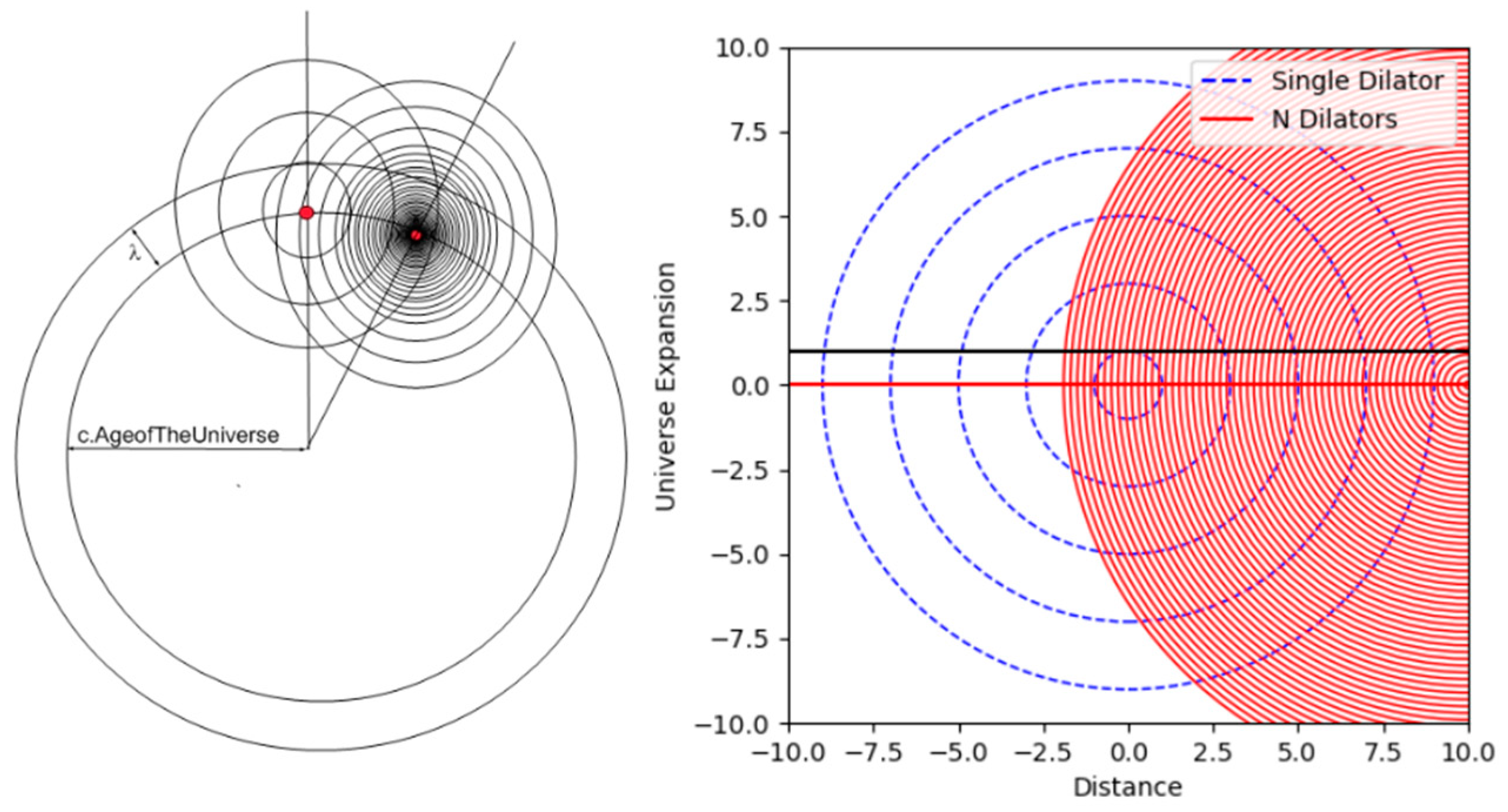
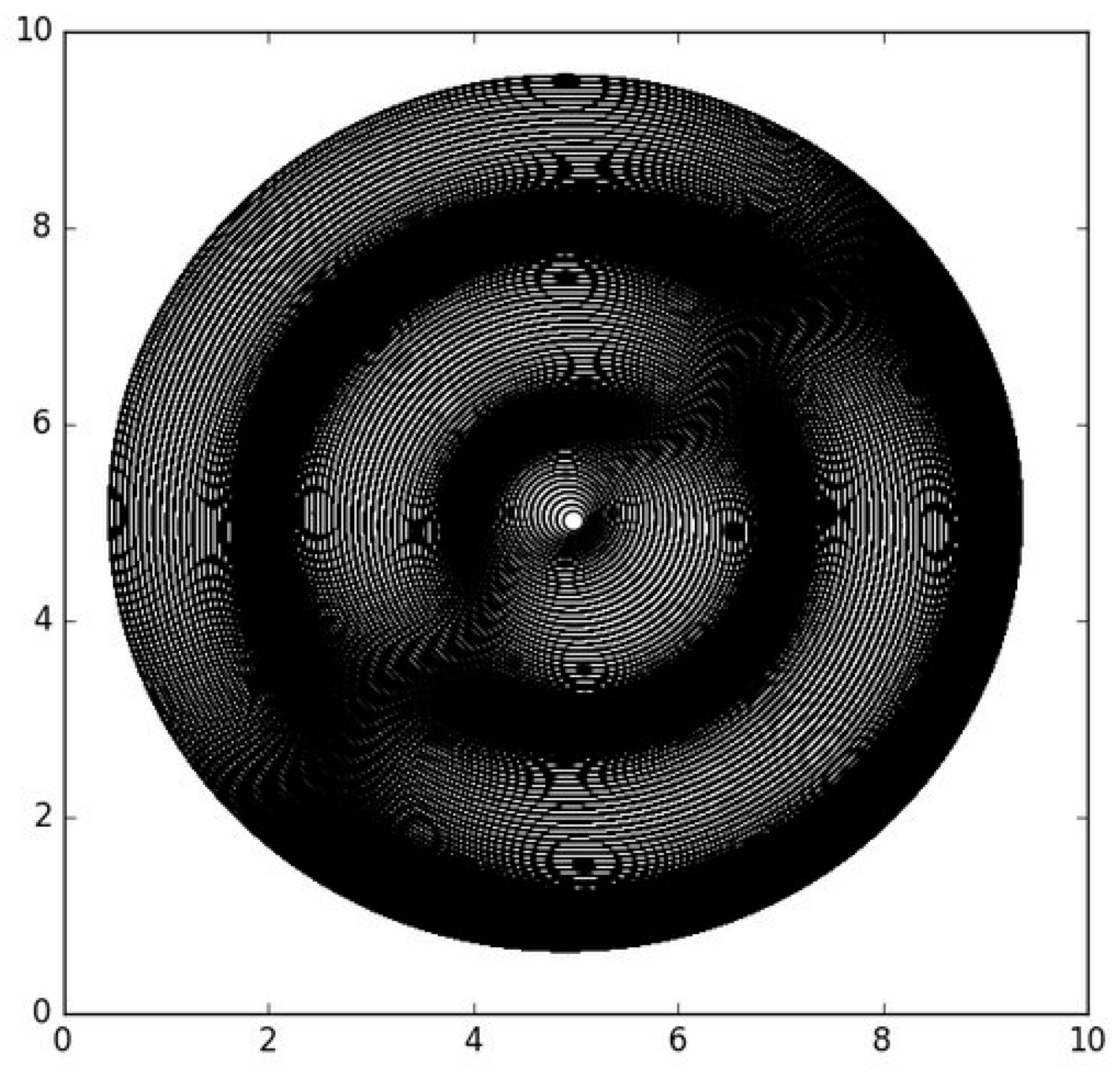
Figure 9.
Interaction of Dilators: This image depicts a probe dilator and a large mass of dilators interacting as the universe executes its lightspeed stepwise expansion. Notice the metric waves or dilaton field. The interference pattern on the metric waves created by the large dilator mass simulates a dilaton field with a much finer wavelength (λ/N where N is the number of dilators and λ is the Compton Wavelength of a Hydrogen Atom).
Figure 9.
Interaction of Dilators: This image depicts a probe dilator and a large mass of dilators interacting as the universe executes its lightspeed stepwise expansion. Notice the metric waves or dilaton field. The interference pattern on the metric waves created by the large dilator mass simulates a dilaton field with a much finer wavelength (λ/N where N is the number of dilators and λ is the Compton Wavelength of a Hydrogen Atom).
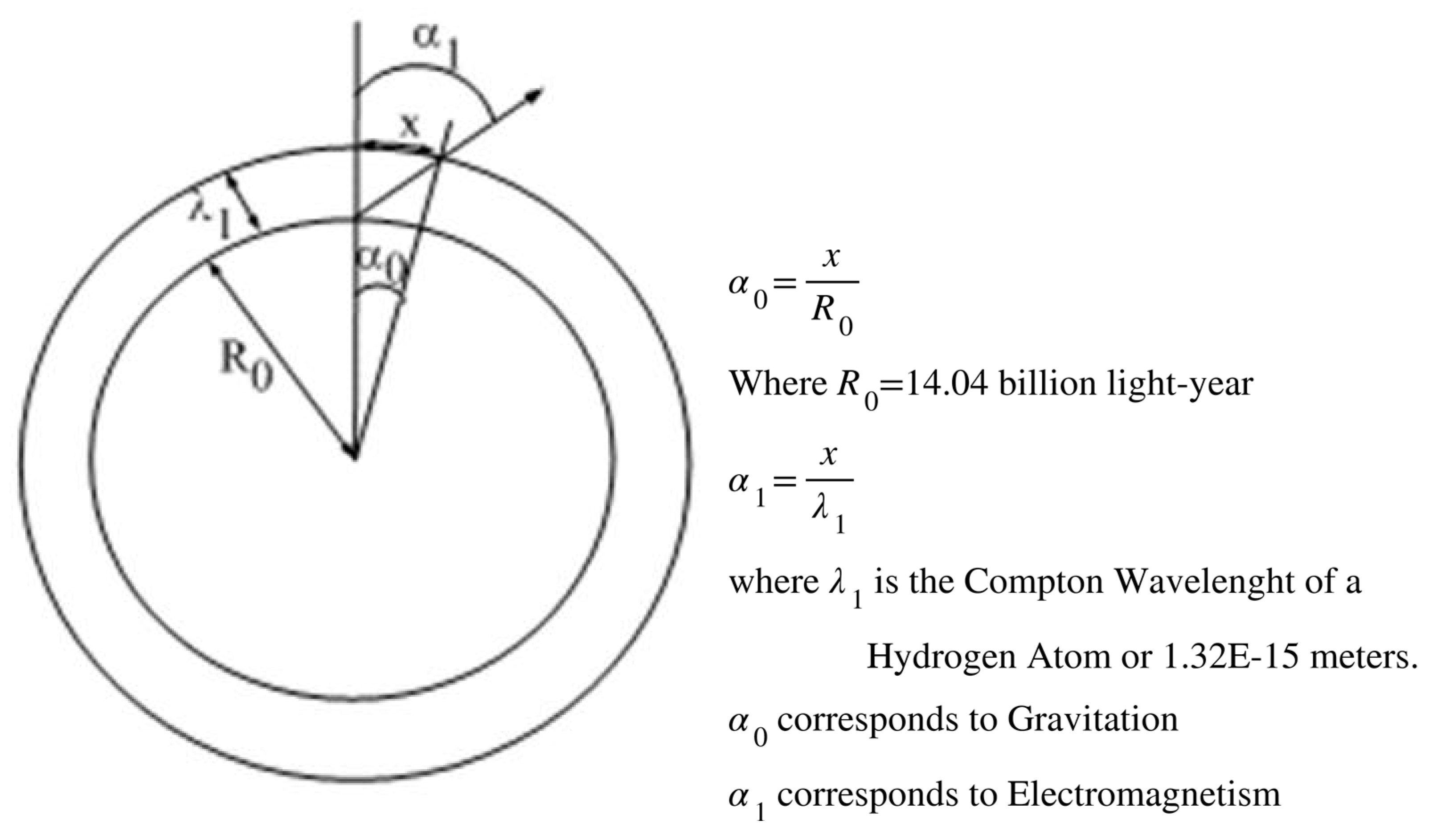
Figure 10.
Space Stress-Strain Relationship: The dilaton field has a wavelength equal to the Compton Wavelength of a Hydrogen Atom or 1.32 femtometers. The 4D radius of the Univers is 14.04 billion light-years—their ratio maps to the ratio between Gravitational and Electromagnetic forces. From the ratio between HU-derived G and the observed Newton’s Gravitational Constant G, HU derives the natural frequency of metric/gravitational waves.
Figure 10.
Space Stress-Strain Relationship: The dilaton field has a wavelength equal to the Compton Wavelength of a Hydrogen Atom or 1.32 femtometers. The 4D radius of the Univers is 14.04 billion light-years—their ratio maps to the ratio between Gravitational and Electromagnetic forces. From the ratio between HU-derived G and the observed Newton’s Gravitational Constant G, HU derives the natural frequency of metric/gravitational waves.
Particle-Wave Dualism Is Replaced by Wave-Generator, Wave, and QLP
The HU model for matter replaces the particle-wave description of matter with the recognition that particles create metric waves and interact with them through the QLP. Wavefunctions become the loci for FD 3D footprints as they obey the non-deterministic QLP. The final result is the same.
HU Wavefunction Interpretation [Schrödinger, E., 1926]
HU explains the motion of particles using the Fundamental Dilator Paradigm. QLP defines where the Fundamental Dilator will land in the 3D Hypersurface. In other words, particle motions are subject to the interference pattern created by their dilaton fields. That results in an inherent uncertainty in particle motion. If you add the frequency at which these jumps occur (1E24 Hertz), it is easy to understand that the locus on 3D (our moving 3D hypersurface) of the solution to QLP is what we call Wavefunction. It is a seemingly random distribution of points created by a single particle (electron in the case of the Hydrogen Atom) following QLP. It contains information about its momentum imprinted in the shape of the dilaton field.
Observation is any interaction with the moving dilator, which modifies its momentum and future trajectory.
Hence, HU provides a much more mundane interpretation of Quantum Mechanics and Wavefunctions. Those are inconsistent with Multiverse, Many World Interpretation of Quantum Mechanics [Everett, H., 1957], which is a good thing since there is no evidence whatsoever of a Multiverse, and the idea of splitting timelines every time one makes an arbitrary decision is ludicrous.
Conclusions
The Hypergeometrical Universe Theory (HU) proposes a transformative perspective on the structure of the universe, unifying cosmology, quantum mechanics, and classical physics. The theory introduces the Fundamental Dilator (FD), a quantum wave generator that interacts with the dilaton field and follows the Quantum Lagrangian Principle (QLP) [Feynman, R.P., and Hibbs, A.R., 1965], forming the basis for all matter and forces. This trinity replaces the traditional particle-wave dualism [Dirac, P.A.M., 1928][Feynman, R.P., and Hibbs, A.R., 1965] and shifts the foundational constructs of physics from mass and force to displacement volume and acceleration, providing a unified framework for describing nature.
HU’s redefinition of the universe as a lightspeed-expanding hyperspherical hypersurface eliminates the need for concepts like dark matter, dark energy [Riess, A.G., et al., 1998], and inflation. By introducing an absolute 4D reference frame, HU provides a new interpretation of Lorentz transformations as rotations in 4D space, fundamentally altering our understanding of time dilation as an artifact rather than a physical reality.
HU resolves longstanding issues in cosmology, such as the need for dark matter, dark energy, and inflation, by addressing the horizon problem and galaxy dynamics using simple idiosyncratic exponential mass distributions. The theory also introduces an absolute 4D reference frame, reinterpreting Lorentz transformations and establishing a new understanding of time dilation as an artifact rather than a physical reality.
A major contribution of HU is its derivation of the Laws of Gravitation and Electromagnetism, showing that both forces follow the same Lorentz force format. The theory’s interpretation of gravitation as a Van der Waals force, with the dilaton field oscillating at 1E24 Hertz, unifies it with electromagnetism and provides insights into why gravitation appears weaker than electromagnetic forces. This framework suggests revolutionary advancements in technologies such as magnetic confinement systems and space propulsion.
The Absolute Reference Frame (ARF) model provides a kinetic energy formulation that diverges from traditional relativistic expectations, adhering to a mass-dependent energy cap as velocity approaches lightspeed. The formula for HU Kinetic Energy is the same as the Classical Mechanics formula. This contrasts with relativistic predictions and suggests novel experimental approaches, such as temperature-sensitive calorimeters, which could isolate thermal energy deposition without relying on relativistic calibration assumptions. If validated, this approach would not only affirm the ARF model but also reinforce the Hypergeometrical Universe Theory (HU), challenging the framework of General Relativity and indicating that particle dynamics and kinetic energy may need reevaluation within the ARF model. Such insights reinforce HU's foundation and underscore the theory's implications for future explorations in particle dynamics and aerospace applications.
One of HU's pivotal contributions is the creation of a Cosmological Clock. The coherence of the Fundamental Dilator and the dilaton field (metric waves) keep track of Absolute Time, providing a one-to-one relationship between any inertial reference frame and the absolute time measured within it. This feature bridges the gap between relative motion and absolute timing, offering a clear framework for understanding time in the universe.
Crucially, HU derives the laws of gravitation and electromagnetism, showing that both have the same format as Lorentz forces. The radial dependence of gravitational forces is explained by reference frame selection, particularly in cases where symmetry, such as centering the frame on the Sun, dictates the radial nature of the force. This derivation challenges conventional interpretations and promises revolutionary advancements in electrodynamics, including the design of magnetic confinement systems (magnetic bottles, stellarators, tokamaks), as well as space propulsion technologies.
Moreover, HU interprets gravitation as a Van der Waals force [Van der Waals, J.D., 1873], with a carrier dilaton field oscillating at a frequency of 1E24 Hertz. This interpretation offers a unified view of gravitation and electromagnetism and explains the dynamic screening that makes gravitation appear weaker than electromagnetic forces.
The Hypergeometrical Universe Theory presents a compelling framework that aligns with the Pati-Salam Model through its SU(4) representation and decomposition into SU(3)C and U(1)B-L symmetries. By modeling spin as a physical rotation in four-dimensional space and explaining fermionic behavior through phase sequences, HU provides a physical basis for chirality and the behavior of fermions. This approach naturally incorporates SU(2)L × SU(2)R symmetries, making HU compatible with the weak interaction's left-right structure.
The compatibility of HU with the Pati-Salam Model, particularly its SU(4) representation and decomposition into SU(3)C and U(1)B-L symmetries, highlights its robustness.
Moreover, HU offers a physical explanation for the antisymmetric nature of fermionic wavefunctions and the Pauli Exclusion Principle, enhancing our understanding of these fundamental concepts. By bridging the gap between physical phenomena and mathematical descriptions, HU complements quantum mechanics and provides new insights into the nature of matter and the universe.
The elimination of the need for an integral functional in the Lagrangian Principle, combined with the mapping of HU to the Pati-Salam SU(4) model, opens the door to non-perturbative Quantum Chromodynamics (HU-QCD). This approach avoids the complexities of Lattice Quantum Chromodynamics and sets the stage for a new understanding of quantum forces.
Finally, HU provides a solution to the Faint Sun Paradox, further solidifying its role as a comprehensive framework capable of addressing key challenges in modern physics. This paradox, along with other cosmological phenomena, will be discussed in future work.
The introduction of HU’s model for matter as deformations of space not only redefines our perception of particles but aligns with observable physical phenomena, offering a coherent explanation for complex dynamics. The Quantum Lagrangian Principle (QLP) demonstrates its capability as the singular governing law, unifying various aspects of physics traditionally described by multiple, distinct laws. Finally, the replacement of the particle-wave dualism with HU’s Quantum Trinity resolves inconsistencies in quantum mechanics, showcasing a complete framework that aligns theory with experimental results and advances our understanding of fundamental forces and particles.
The Hypergeometrical Universe Theory (HU) derives the laws of nature from first principles using the Quantum Lagrangian Principle (QLP), which states that no particle should perform or receive work from the constraints (the space itself). In HU, with the correct universe topology (LEHU) and a model for matter where particles are coherences between stationary states of deformation of space, all laws of nature emerge from a single field—the dilaton field. HU shows that both electromagnetism and gravitation are governed by simple absolute-velocity-dependent forces, demonstrating that gravitation is a Van der Waals electromagnetic interaction with a 1E-24 second relaxation time. This approach offers a more straightforward and practical framework for relativistic calculations in multi-body systems than deforming spacetime and deriving geodesics. HU’s derivations also explain why gravitation appears as a radial force when, in fact, it is a Lorentz force, resolving a longstanding question in physics. HU provides a means to derive gravitational magnetic fields, gravitational Poynting vectors, and gravitational irradiation power—concepts not accessible through traditional GR. The gravitational lensing and perihelion precession rates are derived using classical and quantum mechanics without the need for relativity (see Appendices C and B respectively), showcasing HU’s capability to reproduce Einstein’s successes using force-based dynamics.
The Hypergeometrical Universe Theory (HU) introduces an epoch-dependent gravitational constant (G)
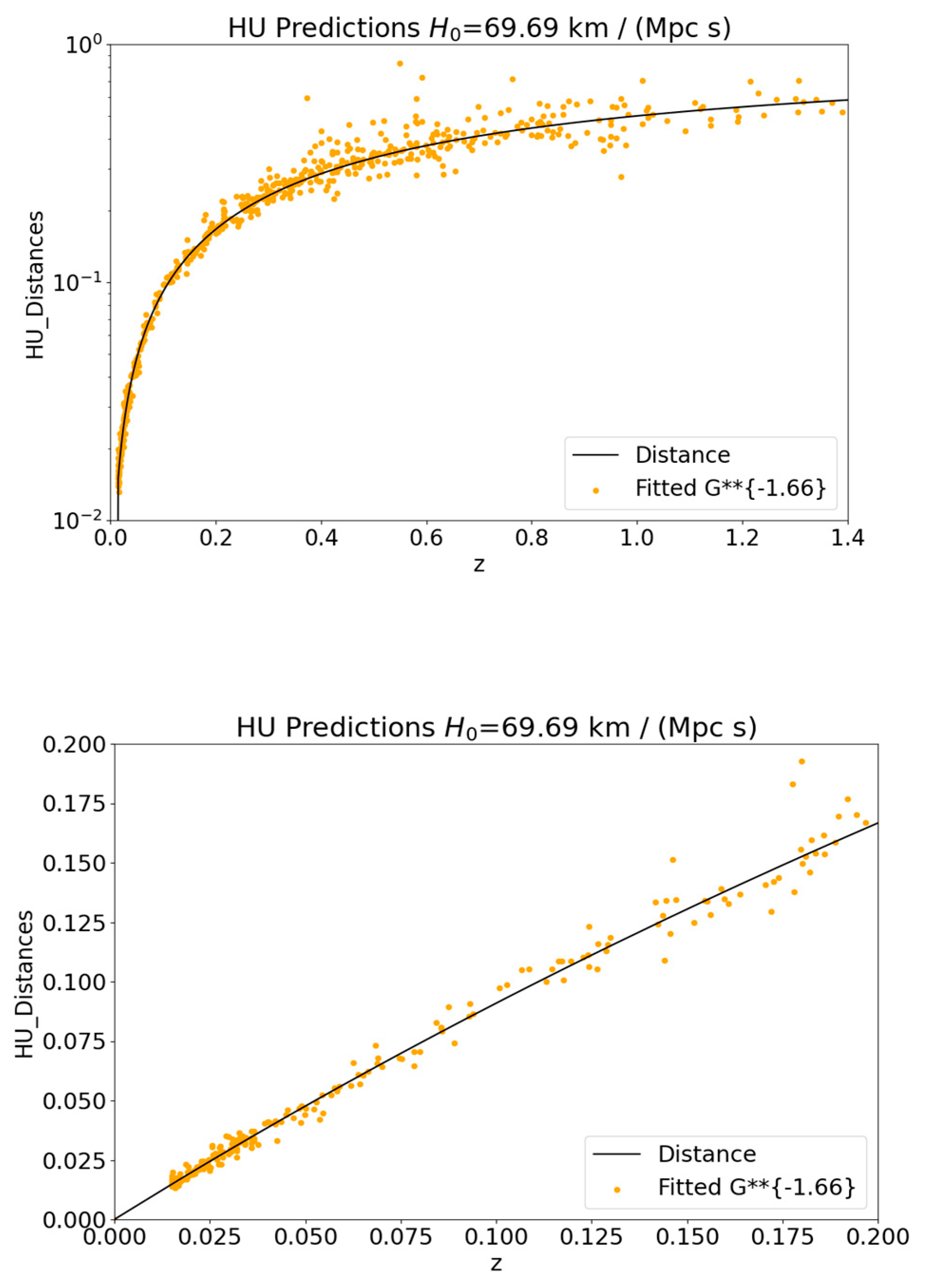
[Teller, E., 1948] [Sahni, V., and Shtanov, Y., 2014] that fundamentally reshapes our understanding of cosmological distances. This dependency implies that Type Ia Supernovae (SN1a), traditionally considered standard candles based on their detonation at the Chandrasekhar mass limit, should be reinterpreted, as their photometric distances depend on the epoch’s value of G (G
(-3/2)). HU's approach corrects the Cosmic Distance Ladder, removing the need for dark matter or dark energy to explain supernova data (see
Appendix L). Additionally, HU explains spiral galaxy rotation curves through idiosyncratic radially exponentially decaying densities rather than distant light-mass density estimates, further eliminating the need for dark matter. These adjustments not only remove the need for space stretching and inflation but also address the issue of absurd distances that exceed what is possible at the speed of light. By creating the universe from an energy-neutral initial metric fluctuation, HU bypasses the need for a Big Bang explosion or false vacuum decay. In essence, HU simplifies the cosmological model and unifies phenomena without resorting to speculative constructs.
HU shows that it doesn’t take an infinite amount of energy to bring a massive body to the speed of light. In fact, the amount is the same as in the classical case. This is supportive of possible applications of the theory in Instantaneous Lightspeed Accelerators.
The Hypergeometrical Universe Theory (HU) fundamentally redefines our understanding of cosmic and stellar evolution, unifying diverse phenomena through an absolute 4D framework and epoch-dependent forces. HU’s solutions to the faint young Sun paradox and the Fermi Paradox illustrate its broader implications for astrophysics and the potential for interstellar travel, marking HU as a comprehensive model that bridges theoretical physics with observable phenomena.
The appendices play a crucial role in demonstrating the robustness and applicability of this theory. Below is an analysis of the key contributions from the appendices and their significance:
The appendices collectively validate HU's theoretical constructs through computational and empirical means, strengthening its claims and illustrating its applicability in classical and modern physics scenarios. By incorporating these insights, HU offers a cohesive and comprehensive alternative to current cosmological and quantum models, pointing the way toward future advancements in theoretical physics and technology development.
In conclusion, the Hypergeometrical Universe Theory lays the foundation for a new era in physics. It replaces outdated paradigms with a cohesive, quantum mechanical framework that unifies forces, reinterprets cosmological events, and reshapes the understanding of the fundamental nature of matter and the universe.
GitHub Repositories provided on CMB_HU,, HU_GalaxyPackage, .HU_Papers.
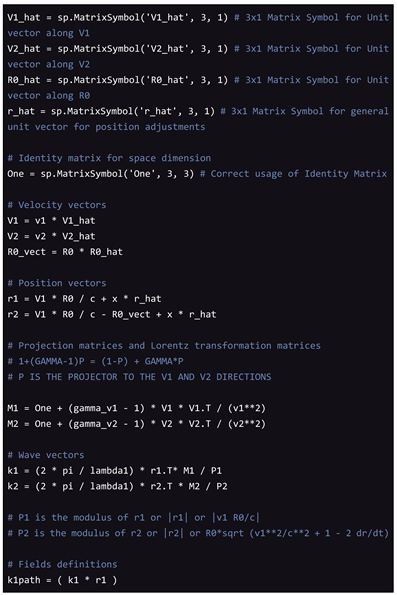
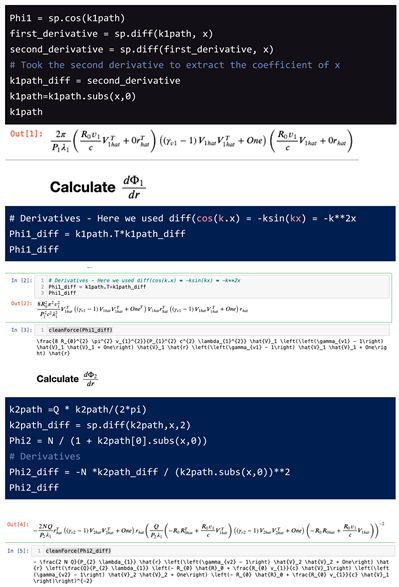
Appendix A - Deriving Natural Laws Using Python Sympy
Here we use the standard definition of the dilaton field and the Quantum Lagrangian Principle. Since Fundamental Dilators are moving, one has to modify k-vectors back into the Absolute Reference Frame before applying QLP.
Defining Symbols and Unit Vectors
Projection Matrices or Lorentz transformations
- -
Projection or Rotation Matrices M1 and M2 are the corresponding Lorentz transformations:
- -
For Lorentz transformations, defined as:
- -
Wave Vectors k1 and k2:
Appendix B - Planets Perihelion Precession Rate - Results
For the calculator of Perihelion Precession, one used an ansatz for the orbit:
The radial acceleration was calculated using HU FG
Around the trajectory, the prediction should be equal to

Error Minimization
We adjusted σ such as to minimize the quadratic error:
Below are the results for all planets in the Solar System.
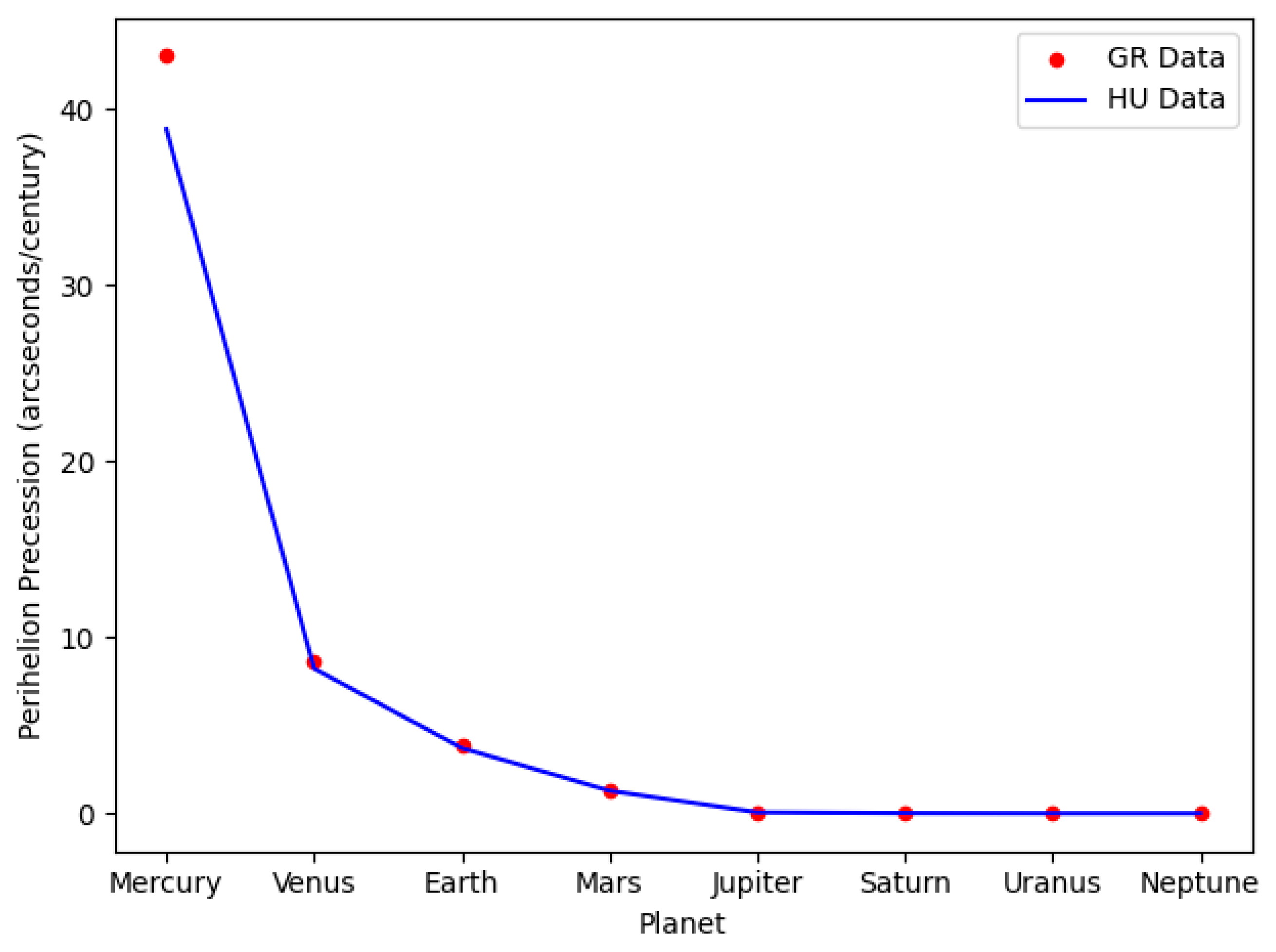
Figure B1.
Perihelion Precession Rate Predictions compared with General Relativity Predictions. GR uses linearization. HU does not. This indicates that the GR prediction for Mercury is off by 2 arcseconds.
Figure B1.
Perihelion Precession Rate Predictions compared with General Relativity Predictions. GR uses linearization. HU does not. This indicates that the GR prediction for Mercury is off by 2 arcseconds.
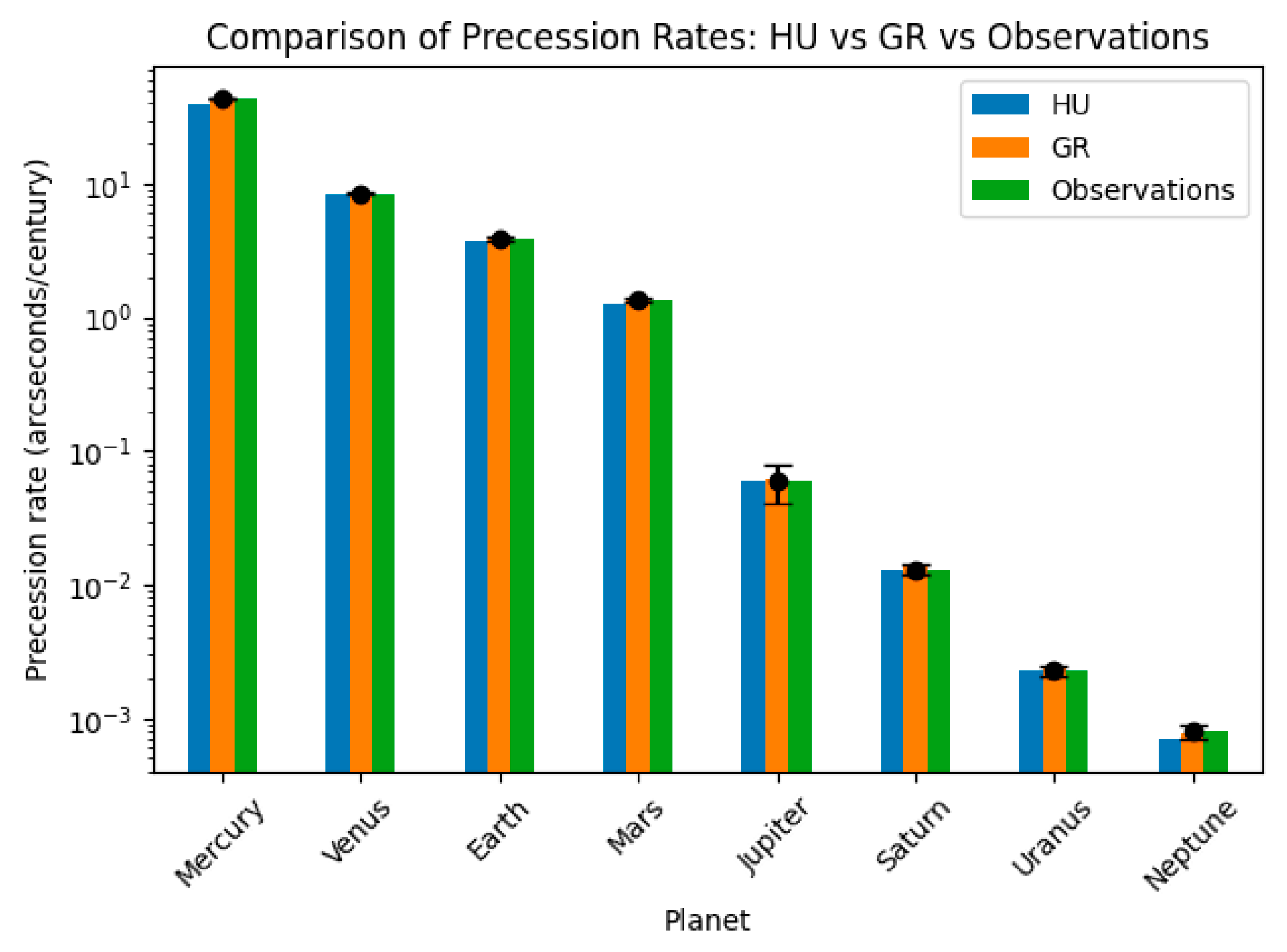
Figure B2.
Comparison of predicted and observed Perihelion Precession Rates. Notice that the actual observed rates are around ten times larger than the GR or HU predictions. The reason is that the “unexplained” perihelion precession rate is the observed rate (550 arcseconds in the case of Mercury) minus the modeled contribution of all other planets (550-43=507 arcseconds). The error in this simulation is larger than 2 arcseconds. Hence, the HU prediction is very likely the correct one.
Figure B2.
Comparison of predicted and observed Perihelion Precession Rates. Notice that the actual observed rates are around ten times larger than the GR or HU predictions. The reason is that the “unexplained” perihelion precession rate is the observed rate (550 arcseconds in the case of Mercury) minus the modeled contribution of all other planets (550-43=507 arcseconds). The error in this simulation is larger than 2 arcseconds. Hence, the HU prediction is very likely the correct one.
Appendix C - Gravitational Lensing
To explore the deflection of light by gravity using classical mechanics, this approach involves assigning a hypothetical mass to the photon. This enables the application of classical gravitational dynamics to a massless particle, providing a conceptual bridge to more complex theories. Here, the focus is on energy conservation and the geometrical configuration of gravitational forces.
How does that compare with General Relativity? Does GR assign an arbitrary mass to photons? Yes. It is implicit in the Schwarzschild Metric. The boost is given by:
So, the characterization of a massive photon is part of the General Relativity derivation despite not being explicitly declared.
The same goes for Quantum Mechanical or Ondulatory Mechanics properties of light. GR derivation might use Fermat’s Principle. HU derivation uses the fact that the Energy of a photon is proportional to its momentum. HU also uses the fact the linear momentum of a particle at c is given by: mc2/2.
Energy Conservation
In both classical mechanics and General Relativity, energy conservation is a pivotal concept. For the classical approach, we assume:
- -
G is the gravitational constant.
- -
M is the mass of the Sun.
- -
b is the radius of the Sun.
Using these parameters, the kinetic energy gained by a photon due to gravitational attraction can be expressed as:
The maximum possible Kinetic Energy by interaction in 3D is mc2/2. Analogously, the maximum linear momentum is mc.
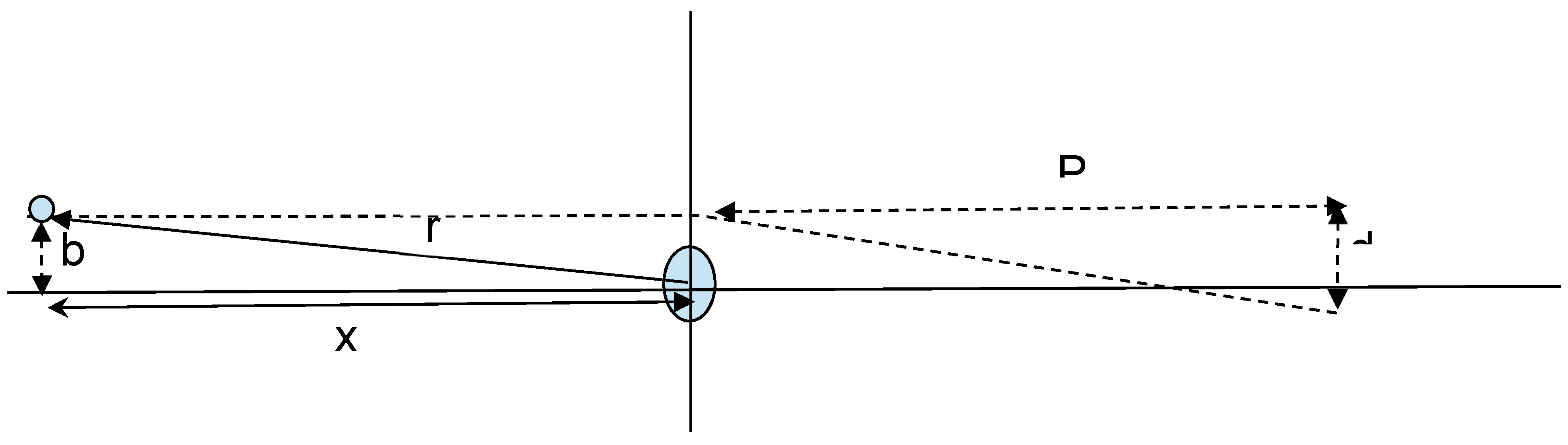
Figure C1.
Diagram for calculating light deflection. Show are the impact parameter b, the distance, and the change in momentum dP. The Sun is shown at the center of the diagram.
Figure C1.
Diagram for calculating light deflection. Show are the impact parameter b, the distance, and the change in momentum dP. The Sun is shown at the center of the diagram.
The deviation angle is given by:
In General Relativity, this principle of conservation is embedded within the coefficients of the Schwarzschild metric, ensuring that the energy remains constant for a particle traversing a gravitational field.
Integral Calculation of Gravitational Influence
The integral that quantifies the gravitational potential experienced by the photon as it passes near the Sun is given by:
Deflection Angle Calculation
This classical estimation, when calculated with the defined values for G , M , and b , yields a deflection angle close to 1.75 arcseconds. This result remarkably aligns with the values observed during solar eclipses and predicted by General Relativity. This demonstration of classical calculations mirroring relativistic outcomes highlights the fundamental role of energy conservation and geometric alignments in gravitational light deflection.
Appendix D - Space Stress-Strain Paradigm and the Silver Surfer Paradigm for Motion
Newton’s First Law of Motion
An object at rest stays at rest, and an object in motion stays in motion at the same speed and in the same direction unless acted upon by an unbalanced force.
HU’S Newton’s First Law
Motion occurs to relax the Fabric of Space. In the absence of forces, a body will travel in a straight line across a 4D spatial manifold while traveling at lightspeed along the radial direction. All matter will asymptotically reach rest with respect to the Fabric of Space.
No object is ever at rest. All particles in the Universe travel radially at the speed of light. Tangentially, objects not subject to net forces (inertial motion in 4D) will asymptotically try to reach their Hubble Position d, where they would stay at rest with respect to the Fabric of Space while moving at a receding velocity equal to H0*d. H0 is the Hubble Constant, and d is the Hubble distance.
where R0 is the 4D radius of the Universe. For our Universe, at this current time, R0 is 14.03 billion light-years, and the Universe age is 14.03 billion years.
Why Do Things Move?
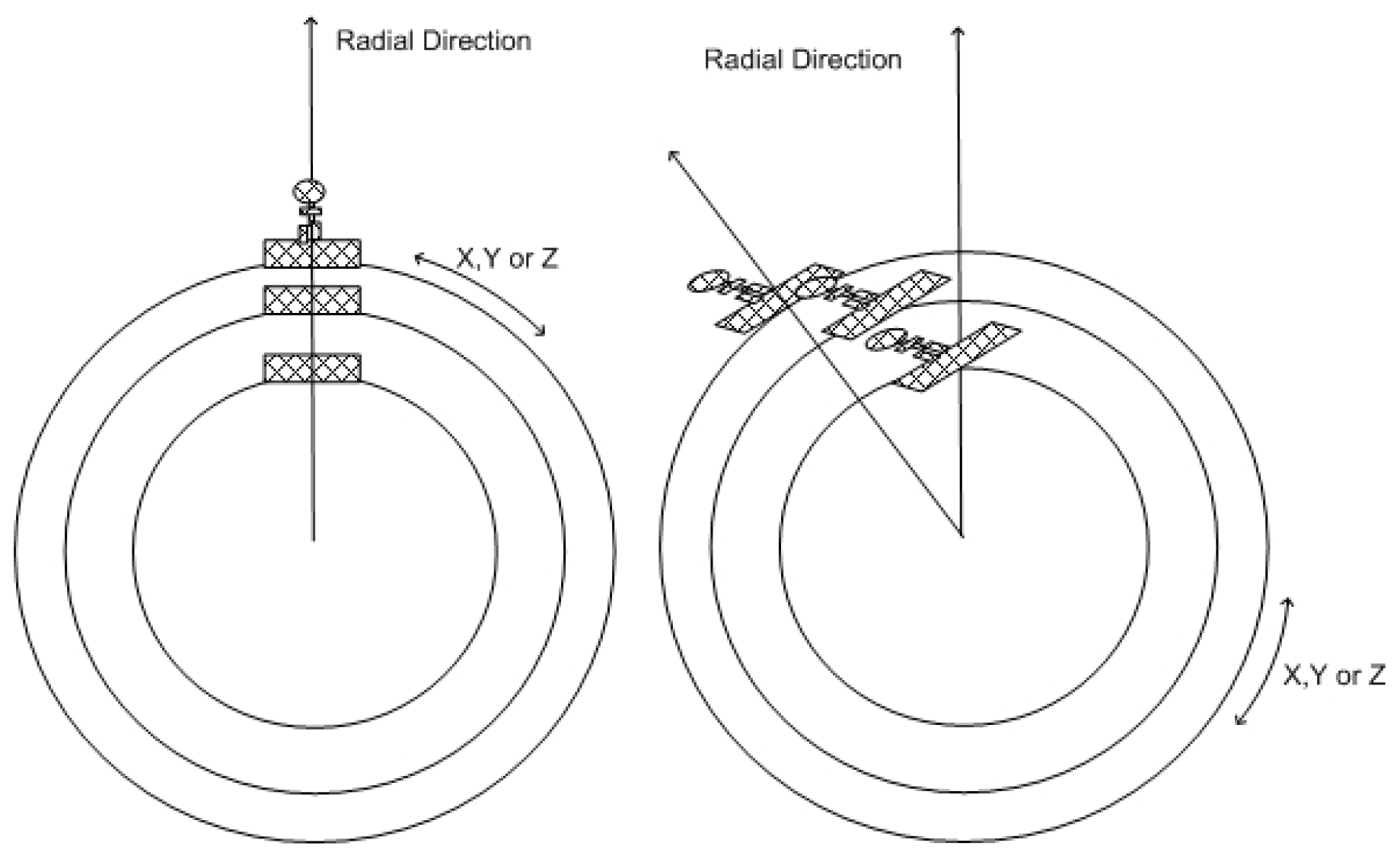
Figure D1.
Here, we show the path of a material body traveling inertially in 4D. The Strain (hyperbolic tangent of the angle between the Fabric of Space and the radial direction) diminishes as motion occurs.
Figure D1.
Here, we show the path of a material body traveling inertially in 4D. The Strain (hyperbolic tangent of the angle between the Fabric of Space and the radial direction) diminishes as motion occurs.
The first thing to notice is that the angle decreases as 4D inertial motion occurs, and the Universe 4D radius R(t) increases.
Newton’s Second Law
From
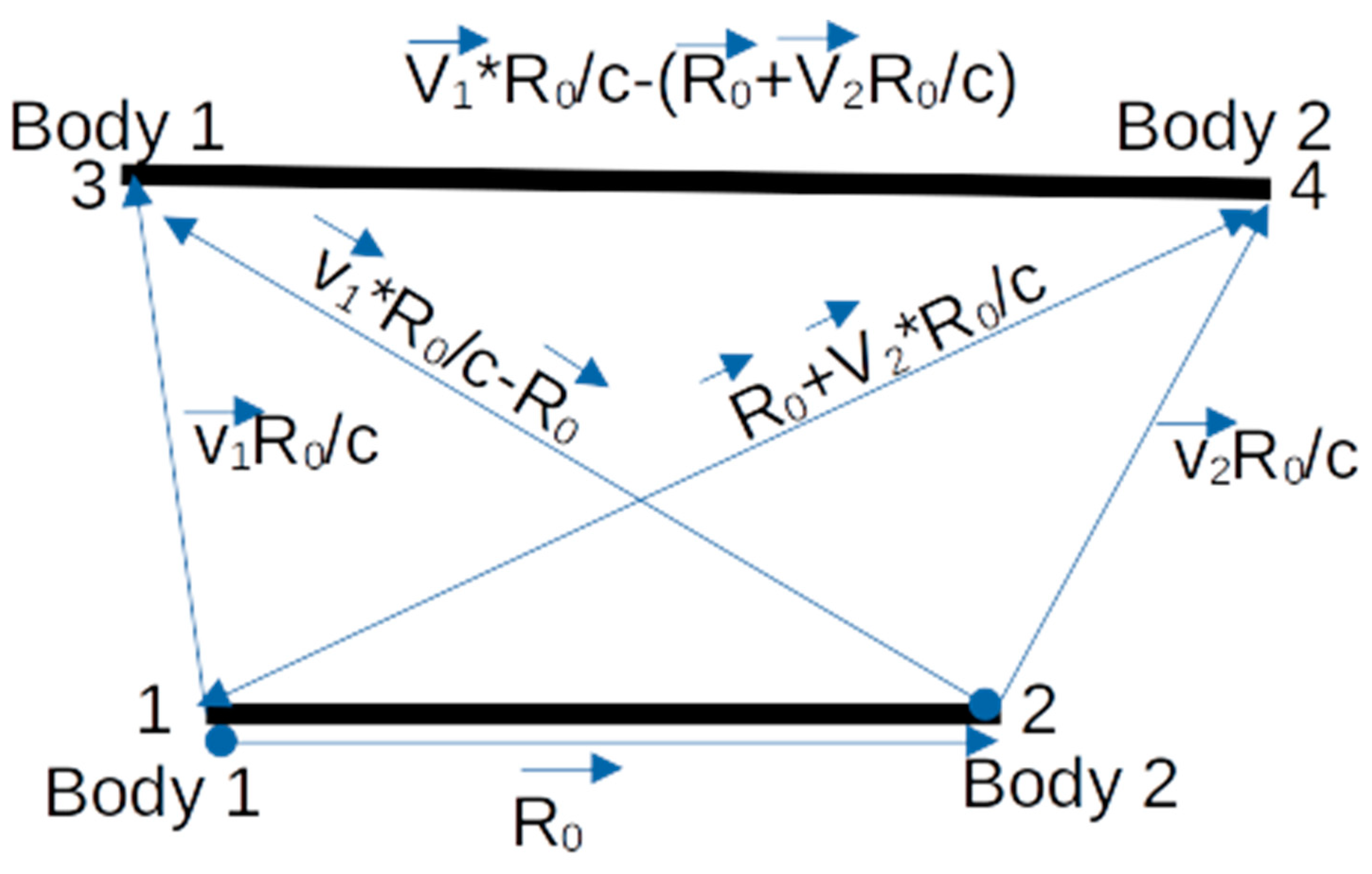
Figure 4, the rate of torsion of the local FS is proportional to the force (Hypergeometrical Universe interpretation of Newton’s Second Law is given by:
Adding the extra spatial dimension implies that:
where is the dimensionalized proper time (c*Proper Time). Notice that it is related to the dimensionalized Absolute Time by a rotation. Of course, again, the rotation will be trigonometric or hyperbolic, depending on whether the time is real or imaginary. We will use imaginary r and τ .
So, Force is given by the product of an “area” times the rate of variation of Strain (tanh(r) or tanh() ). So, force would be the driving force for a variation in space stress.
In a geometrical theory, the only relevant constructs are space, time, dilators, dilaton fields (dependent upon dilators position, velocity, and space properties). A theory about the Universe based on those constructs would recast equation (8) as:
The force between dilators can be calculated using the RXYZ frame. That force would then be used in equation (7) to determine dynamics in a 4D Spacetime.
From the modeling of the Fundamental Dilator (FD)[
9,
13], it becomes evident the reason why the 4D Mass of the Fundamental Dilator is to be mapped to the mass of a hydrogen atom. If one knows where the FD will be and its mass, one knows the Force acting upon it.
Newton’s Third Law
Newton’s Third Law is also represented within this theory. The stress on interacting dilators (bodies) is also the same as that of opposing signs; this is equivalent to saying that the force felt on each other is equal to that of opposite signs. This law connects the RXYZ and ΦXYZ cross-sections.
Newton’s Fourth Law
Newton’s fourth law is the Natural Law of Gravitation, which will be derived later from the first principles. The equations above are the basis for this theory's more fundamental theoretical development. The first analysis is just an extrapolation of Newton’s Law, which only covers the 3D space and introduces an unknown quantity F (Force). The introduction of a fourth spatial dimension allows for the creation of a purely geometric identity relating to Stresses on the two cross-sections shown in Fig. 4. These are HU’s Laws of Nature:
Notice that the Absolute Law of Nature uses the distance between epochs instead of a metric distance. This doesn’t change anything, but it is there to emphasize the Optical Path of Ancient Photons[
12] and its extension to Gravity.
Appendix E - The Silver Surfer Paradigm For Motion
Here, we see the Surfer. If the Fabric of Space (FS) is twisted to the left (the Surfer always travels along the normal to FS), the Surfer will travel to the Left. Notice that the highest torsional angle is 45 degrees, corresponding to a tangential motion at the speed of light.
Figure E1.
These figures are self-explanatory if you ever saw anyone surfing. HU claims that we are surfing a 4D metric deformation shockwave. That is the simplest model consistent with the HU Laws of Nature, The Fundamental Dilator Model for Matter, and the Big Pop Cosmogenesis.
Figure E1.
These figures are self-explanatory if you ever saw anyone surfing. HU claims that we are surfing a 4D metric deformation shockwave. That is the simplest model consistent with the HU Laws of Nature, The Fundamental Dilator Model for Matter, and the Big Pop Cosmogenesis.
The particle footprint (surfboard) on the Fabric of Space is its 3D volume.
This paradigm is what allows for the Space Stress-Strain Paradigm.
Appendix F - When Was It First Possible for Galaxies to Form?
This means that the hot gas clouds at the surface of the last scattering would have traveled many multiples of the initial 4D radius by the time the first galaxy was born. This inertial traveling is what cools down the Universe. In HU, the CMB was released when the Universe was 11.1 million years old and had an 11 million light-year 4D radius. The gas was 3443 K hot [Saha, M.N., 1921]. The earliest galaxies started forming when the universe was 200 million years old.
This means that the temperature had lowered adiabatically to:
with
For any redshift z, the 4D radius is given by:
The CMB (surface of last scattering) took place when the Universe was 11.1 million years old:
Appendix G - The Optical Path of Ancient Photons -Results
Figure G1.
Inertial Motion and Cooling of Gases: This figure explains how inertial motion in the 4D spatial manifold cools down gases. As bodies and gases travel in straight lines in 4D, the amount of space stress diminishes (the angle between the normal to the particle’s 3D volume’s normal and the radial direction). The diminished absolute velocities indicate that bodies will reach their “Hubble Points,” defined as the point where they will only move radially (perpendicularly to our universe) asymptotically as they travel through the 4D spatial manifold. This explains why Hubble realized that Galaxies are like dots on an expanding balloon. That only can happen if they are static in an Absolute Reference Frame. This figure explains WHY they are sitting still on the Fabric of Space.
Figure G1.
Inertial Motion and Cooling of Gases: This figure explains how inertial motion in the 4D spatial manifold cools down gases. As bodies and gases travel in straight lines in 4D, the amount of space stress diminishes (the angle between the normal to the particle’s 3D volume’s normal and the radial direction). The diminished absolute velocities indicate that bodies will reach their “Hubble Points,” defined as the point where they will only move radially (perpendicularly to our universe) asymptotically as they travel through the 4D spatial manifold. This explains why Hubble realized that Galaxies are like dots on an expanding balloon. That only can happen if they are static in an Absolute Reference Frame. This figure explains WHY they are sitting still on the Fabric of Space.
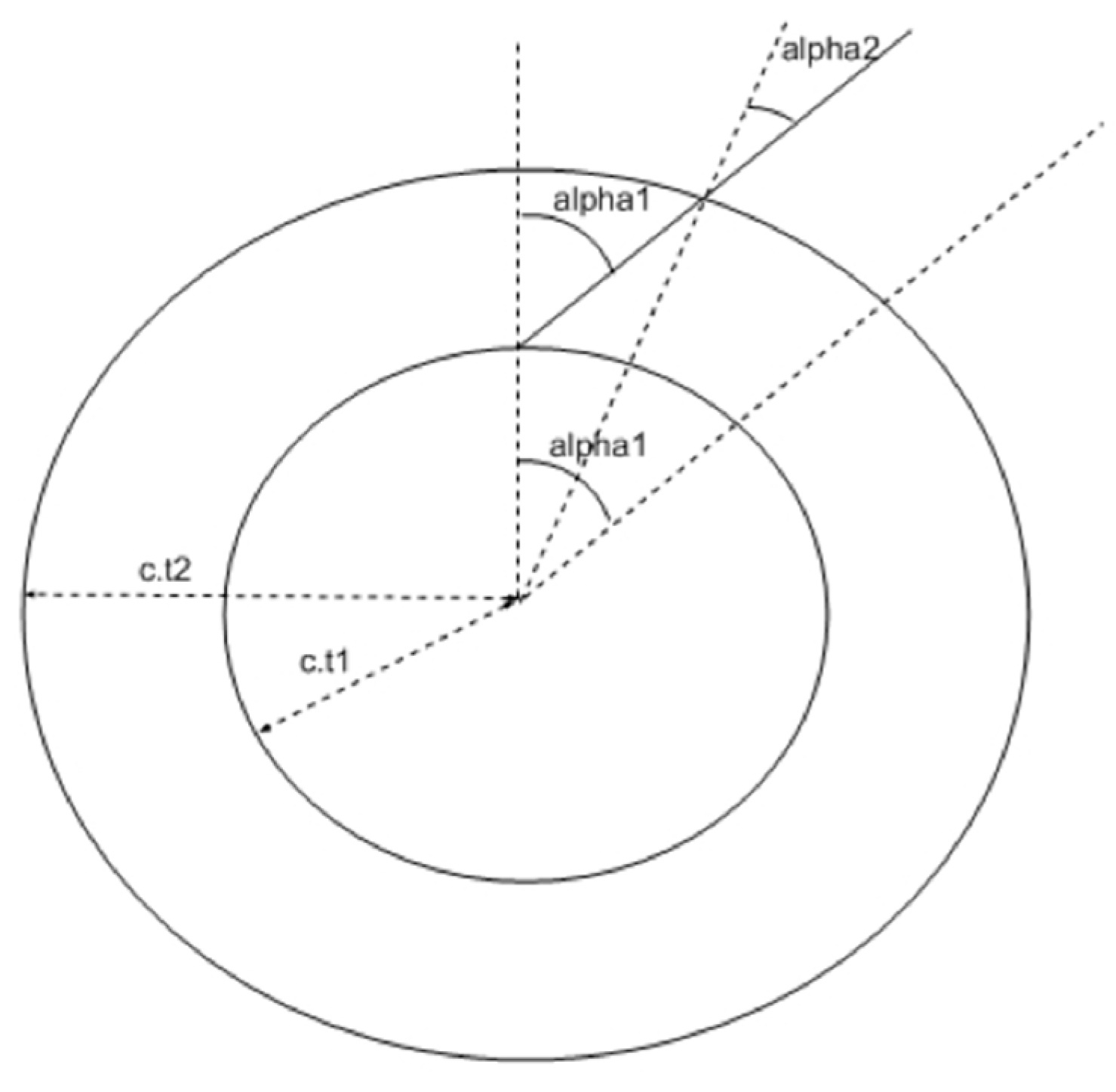
Figure G2.
Relationship between the Cosmological Angle Alpha and redshift z. This figure shows the redshift as a function of cosmological angle alpha. Notice that when Gamma is equal to 45 degrees, one recovers the initial wavelength (zero redshift).
Figure G2.
Relationship between the Cosmological Angle Alpha and redshift z. This figure shows the redshift as a function of cosmological angle alpha. Notice that when Gamma is equal to 45 degrees, one recovers the initial wavelength (zero redshift).
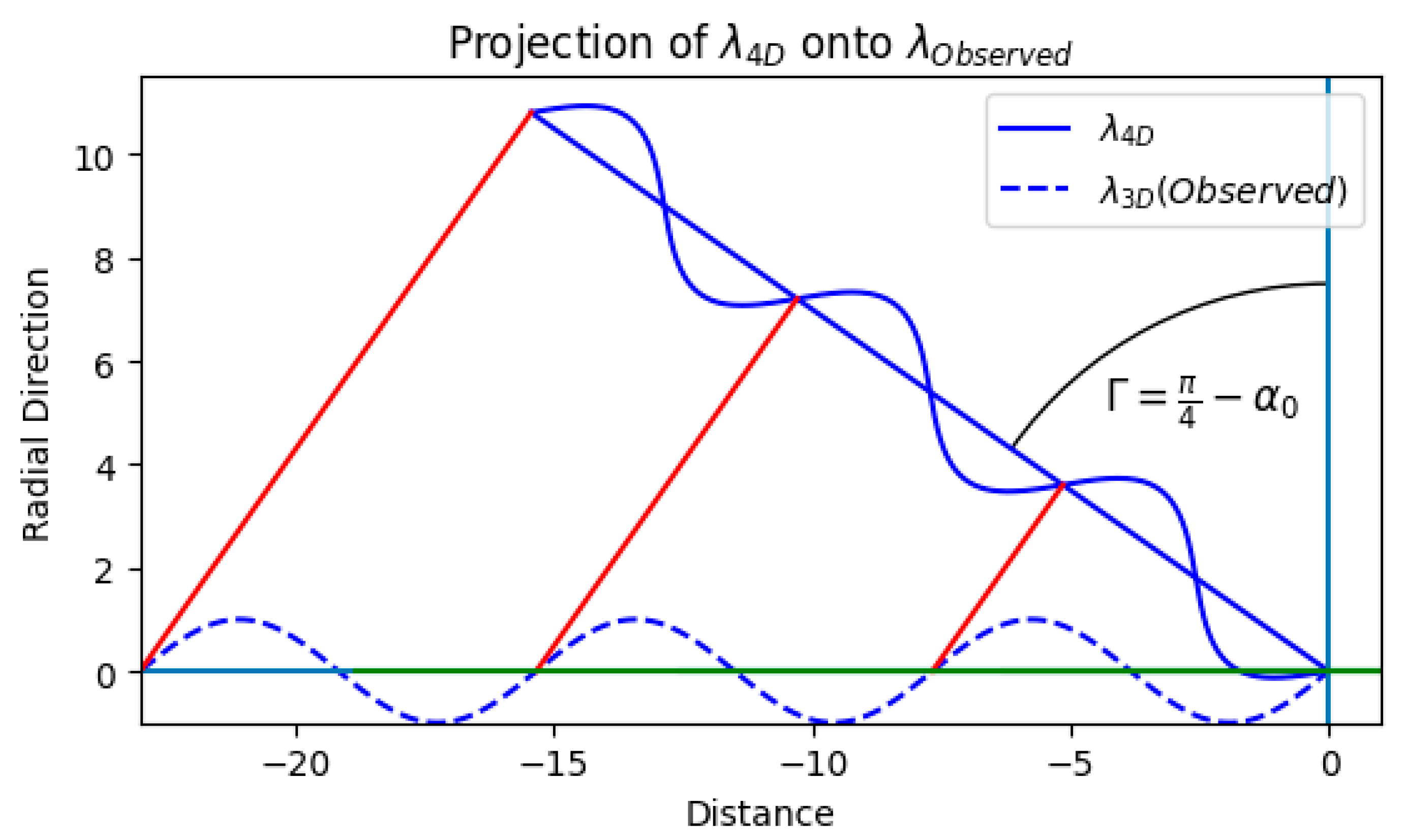
Figure G3.
Momentum Representation of the Light Path of Ancient Photons. This figure shows the momentum conservation as a function of cosmological angle alpha.
Figure G3.
Momentum Representation of the Light Path of Ancient Photons. This figure shows the momentum conservation as a function of cosmological angle alpha.
Applying the Law of Sines on the on the triangle OAB, one get:
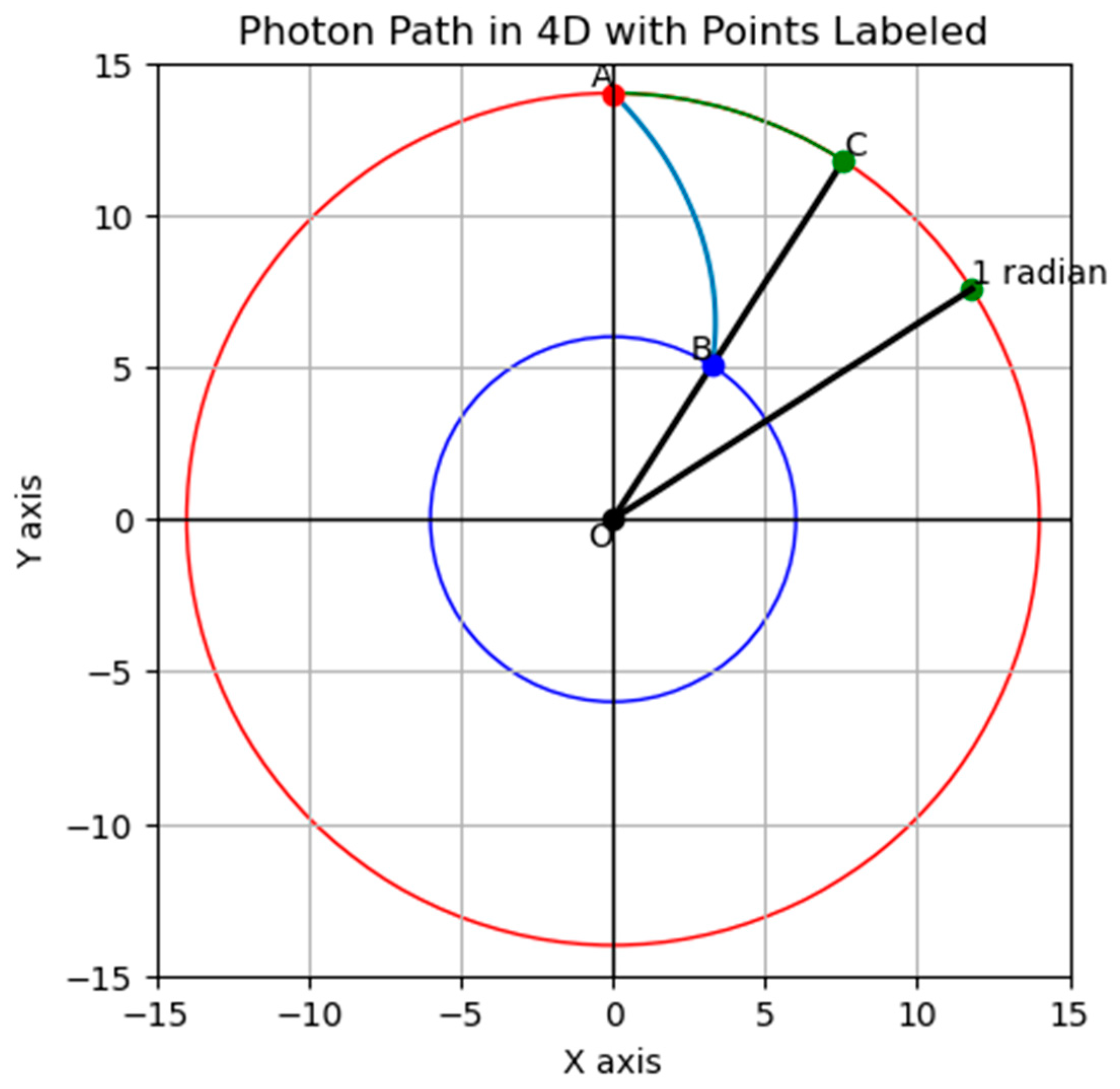
Figure G4.
The optical path of ancient photons. The angle alpha is given by 1 - R(z)/R0.
Figure G4.
The optical path of ancient photons. The angle alpha is given by 1 - R(z)/R0.
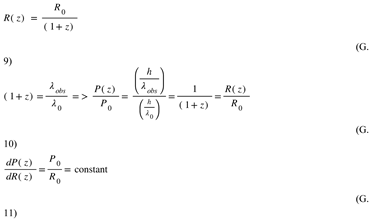
Since R(z) = R0/(1+z), we get alpha= z/(1+z).
P(z) is the observed photon moment. P0 is the original photon momentum. R0 is the 4D radius of the epoch of observation. That means that today, the 4D radius is 14.04 billion light-years.
This optical path produces a trajectory where the photon momentum loss is constant, and no step is distinct from the other, as one would expect.
The Supernova Data Analysis
Figure G5.
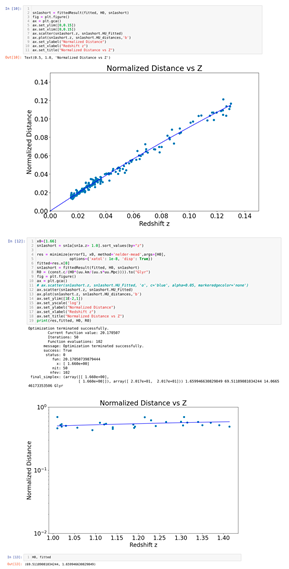
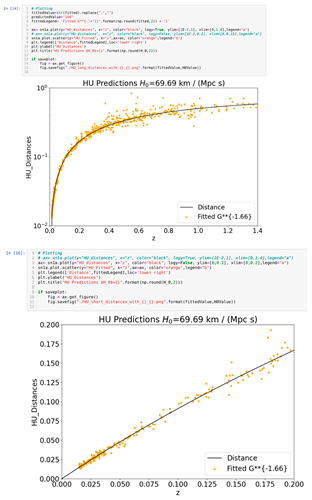
Here we present the fitting of the corrected Supernova Data (Supernova Cosmology Project) to accommodate the epoch-dependent G. This is a two-parameter model that eliminates the Hubble Tension, and the need for Dark Matter and Dark Energy [Riess, A.G., et al., 1998].
Figure G5.
Here we present the fitting of the corrected Supernova Data (Supernova Cosmology Project) to accommodate the epoch-dependent G. This is a two-parameter model that eliminates the Hubble Tension, and the need for Dark Matter and Dark Energy [Riess, A.G., et al., 1998].
Notice that these results explain the Supernova Cosmology Project data without the need for Dark Matter or Dark Energy, while eliminating “observations” of bodies farther that it would be possible had their emitted light traveled at the speed of light for the age of the universe (a preposterous observation). Hence, HU eliminates the need for Space-Stretching, Inflation, False Vacuum Decay, Massless Particles, and the Higgs Mechanism for Inertia.
Appendix H - Revisiting the Twin Paradox - Quantifying the Non-Inertial Section’s Time Dilation
Hermann Minkowski, a mathematician known for his work developing the geometric interpretation of the theory of relativity, saw the Lorentz boost—a transformation used to describe how the observed properties of an object change when it moves at a constant velocity—as a kind of rotation in spacetime.
Minkowski’s insight was to treat time as a geometric dimension similar to the dimensions of space, allowing spacetime to be expressed as a four-dimensional manifold.
He conceptualized the Lorentz boost as a rotation in this four-dimensional space, but with a crucial twist: the "angle" of this rotation was imaginary, which aligns with the mathematical properties of hyperbolic functions.
Specifically, Minkowski used the idea that the hyperbolic tangent of this imaginary angle, denoted as alpha, is equal to the ratio of the velocity of the moving object v to the speed of light c, such that
Where a is a constant.
This relationship directly ties the velocity to a hyperbolic angle, reflecting the non-Euclidean geometry of spacetime under special relativity. We have already shown that this is an artifact.
So
Evaluating the integral for the ramping up velocity section:
with
That is, an infinite acceleration would result in no aging for the short non-inertial sections of the trip. That said, an infinite acceleration would result in those sections lasting zero seconds.
LAB FRAME IS ALWAYS AT REST WITH RESPECT TO THE ABSOLUTE REFERENCE FRAME OR FABRIC OF SPACE
It is estimated that the Milky-Way Galaxy itself moves at about 600 km/s with respect to the Cosmic Microwave Background (CMB) rest frame (0.2% of c). So, the Milky Way and all galaxies have small idiosyncratic Absolute Velocities and can be a good approximation for the Absolute Reference Frame.
Since:
The whole Twin trip comprises of:
Four accelerated sections of no importance and two Coasting Sections at full speed v.
The Time Delay Associated With The Accelerated Sections Of The Twin Trip Can Be Minimized, Leaving Only The Time Dilation From The Coasting Sections.
If these two inertial sections are equivalent to the Earthly Twin reference frame, the aging should be the SAME. According to Minkowski, the standard explanation that acceleration makes the Traveling Twin age is nonsensical.
Since They Are Not (We Know That Time Dilation Is Real From The Dilation Of Subatomic Particle Lifetimes), The Basic Principle Of Relativity Is Wrong: Inertial Frames Are Not Equivalent.
We know that Earth is very close to the Absolute Reference frame since the Milky Way's Absolute Velocity with respect to the Cosmic Microwave Background is only 0.2% c.
The velocity in Lorentz transformations and Minkowski Spacetime is the ABSOLUTE VELOCITY. THAT IS HOW ONE LIFTS THE TWIN PARADOX!
Appendix I - Revisiting the Twin Paradox and Refuting the Equivalence of Inertial Frames
The Twin Paradox has long been a thought experiment used to illustrate the effects of time dilation as predicted by Einstein’s theory of special relativity. The paradox is simple: one twin embarks on a journey through space at relativistic speeds, while the other remains on Earth. Upon the traveler’s return, they find that less time has passed for them compared to the twin who stayed behind.
According to special relativity, this differential aging is due to the time dilation experienced by the traveling twin, whose clock runs slower as observed from Earth. However, this explanation implicitly relies on the equivalence of all inertial frames—a core postulate of special relativity that asserts no preferred reference frame exists. Yet, careful scrutiny of this postulate reveals fundamental inconsistencies, particularly when non-inertial phases of the journey (acceleration and deceleration) are factored in.
1. Absolute Reference Frame and Cosmic Microwave Background (CMB)
The Absolute Reference Frame Hypothesis (ARF) challenges the equivalence of inertial frames by proposing the existence of a preferred reference frame: the one in which the Cosmic Microwave Background (CMB) is at rest. Observations show that our galaxy, and consequently the Earth, move at approximately 0.3% of the speed of light relative to this background. Given this low velocity, it is reasonable to approximate the Earth-bound twin as being nearly at rest in this Absolute Reference Frame. This distinction has profound implications for interpreting time dilation and the twin paradox.
In this framework, the Earth-bound twin’s clock ticks at the "true" proper time, unaffected by relativistic time dilation, while the traveling twin’s velocity, measured relative to this Absolute Reference Frame, induces significant time dilation. The velocity of the traveling twin must be treated as an absolute velocity with respect to this frame, not merely a relative velocity between two inertial frames.
2. Non-Inertial Sections of the Trip and Their Impact
Special relativity struggles to explain the large differential aging between the twins, particularly since the non-inertial sections of the trip—where the twin accelerates or decelerates—are brief. The conventional explanation suggests that these short acceleration periods account for the majority of the time dilation. However, this cannot hold, as the observed aging difference vastly exceeds what would be expected from such short phases of non-inertial motion.
Let us quantify this more rigorously:
Acceleration Periods Are Insignificant: If we restrict the non-inertial sections of the journey (acceleration and deceleration) to a small duration (say, four days), the time dilation induced by these segments would also be minimal—on the order of four days. In this case, if the principle of inertial frame equivalence were correct, the differential aging should likewise be small. The maximum difference in aging due to acceleration should be only the amount of time spent in these accelerated sections.
Inertial Sections Should Yield Equivalence: The paradox intensifies when considering the inertial sections of the trip. If the equivalence of inertial frames holds, the traveling twin should experience time similarly to the Earth-bound twin during the periods of uniform motion. Since the inertial sections comprise the bulk of the trip, the total aging difference should be close to zero if the principle were valid.
3. Time Dilation and Subatomic Particles
Experimental evidence from subatomic particles, whose lifetimes extend significantly when accelerated to relativistic speeds, provides a clear refutation of the inertial frame equivalence postulate. These particles experience real time dilation, indicating that time dilation is not limited to non-inertial motion. It affects the traveling twin continuously throughout the journey, particularly during inertial motion at high velocity relative to the Absolute Reference Frame.
5. Conclusion: Refutation of Inertial Frame Equivalence
The Absolute Reference Frame resolves the twin paradox by recognizing that the Earth-bound twin experiences proper time in the Absolute Frame, while the traveling twin’s clock is slowed due to their motion relative to this frame. The differential aging is primarily a result of the traveling twin's absolute velocity during the inertial sections of the trip, not the brief periods of acceleration. This leads to the conclusion that inertial frames are not equivalent, refuting a foundational postulate of special relativity.
The implications of this are profound. If all inertial frames were truly equivalent, the twin paradox would yield minimal differential aging. Instead, the large observed difference in aging, corroborated by experiments on subatomic particles, supports the hypothesis that time dilation depends on absolute motion relative to the Cosmic Microwave Background.
Appendix J - Code for Gravitational Lensing Prediction
Appendix K - Code for Planets Perihelion Precession Rate Prediction
Appendix L - Code for SN1a Data Analysis
Appendix M - Quantum Gravity and the Maximum Acceleration in the Universe
Does HU Provided Quantum Gravity!
Inside Black Holes, we have the strongest forces in the Universe. The maximum force (acceleration) possible would be such that one would move from zero absolute velocity to c in a single Compton Step. In other words, the angle would have to move from 0 to 45 (using trigonometric projection to make it simpler) in a single step (the step is Compton Wavelength of a Hydrogen Atom).
That means that each Fundamental Dilator (Flat Hydrogen) will be compacted such that the lattice length is equal to the Compton Wavelength of a Hydrogen Atom.
That defines the maximum density inside a Black Hole. At that density, the Gravitational Force goes to zero.
The maximum density is around 3.63E18 kg per cubic meter. There might be some variation if you choose one or another lattice (CFC, CCC, etc).
Appendix N - Initial 4D Radius of the Universe
My theory calculated the total mass of the Universe and used this density to calculate the initial 4D radius of the Universe (662 light-seconds).
Appendix O: The Big Pop Cosmogenesis - Phenomenology
1. Introduction
The Hypergeometrical Universe Theory (HU) proposes a novel cosmogenesis model, termed The Big Pop, as a paradigm shift from traditional cosmological models like the Big Bang. In contrast to singularities and inflationary models, HU offers a cohesive and simplified approach to the universe’s creation and evolution. This appendix outlines the principles, logic, and sequence of events that led to the formation and development of the universe under HU.
2. Hypotheses
HU’s Big Pop Cosmogenesis is based on three core hypotheses:
- -
The universe exists as a lightspeed expanding hyperspherical hypersurface (LEHU).
- -
Matter is composed of polymers of the Fundamental Dilator (FD), which are coherences between stationary states of deformation of space.
- -
FDs obey the Quantum Lagrangian Principle (QLP), which dictates that no particle should perform or receive work from the constraints of space itself. This principle replaces all other physical laws within HU.
These hypotheses imply that HU creates Matter directly and simply from deformed space, resulting in a simplified universe where only Space, Deformed Space, and Time exist. This is the simplest possible model for the Universe, and one can use Occam’s Razor to assign it as the Theory of Everything.
3. Stages of the Big Pop Cosmogenesis
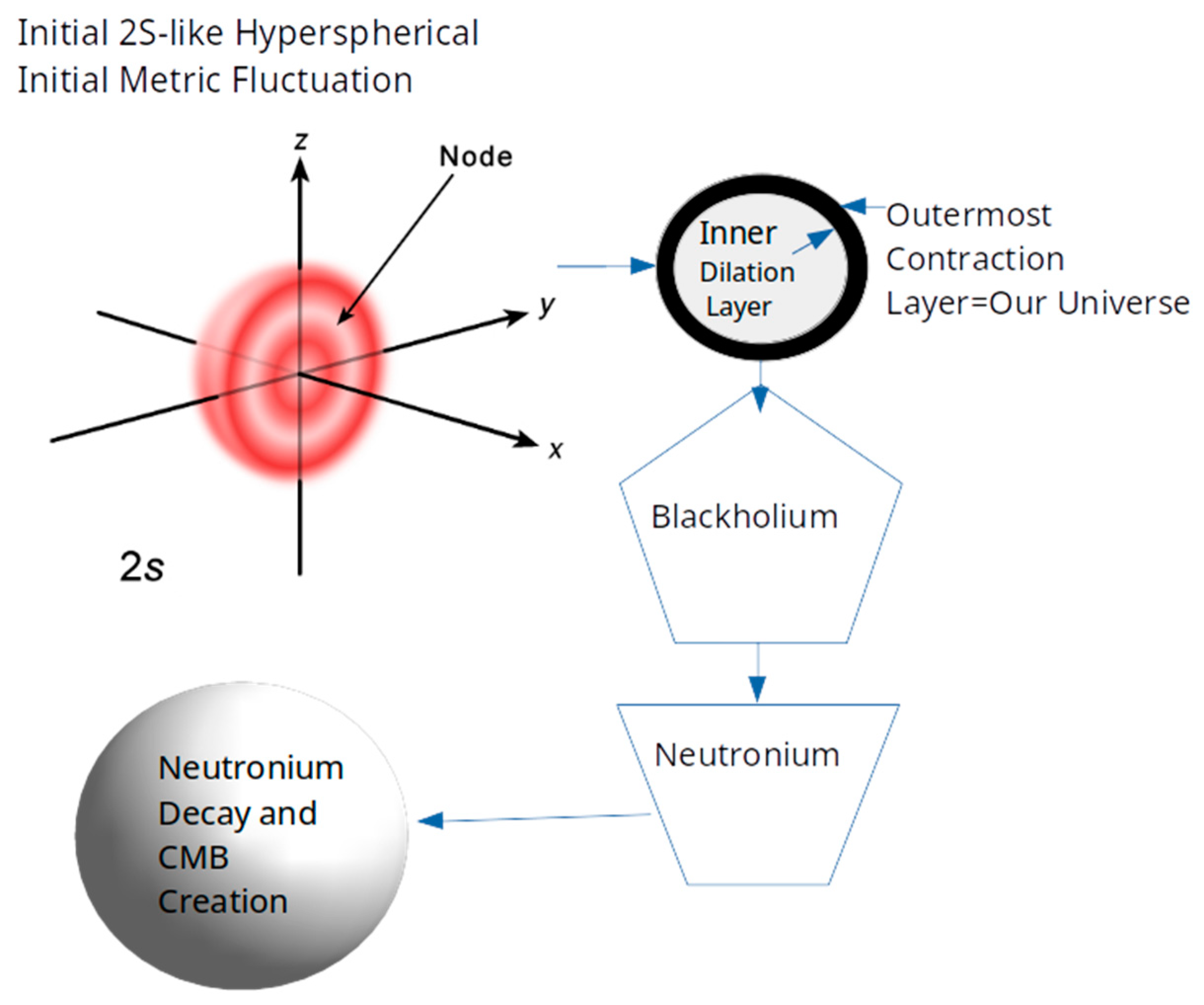
Figure O1.
The Big Pop Cosmogenesis. HU proposes that the Universe started with a simple Heisenberg Principle Driven Hyperspherical Metric Fluctuation of 662 light-seconds 4D radius.
Figure O1.
The Big Pop Cosmogenesis. HU proposes that the Universe started with a simple Heisenberg Principle Driven Hyperspherical Metric Fluctuation of 662 light-seconds 4D radius.
The Big Pop model describes the universe’s formation through a series of stages:
- -
Initial Metric Fluctuation: HU proposes that the universe began as a 4D hyperspherical metric fluctuation around 14 billion years ago. This fluctuation featured dilation at the core and contraction at the outer layers. Without the infinite potential well typically associated with a singularity, the universe started with a temperature of zero Kelvin, containing all the matter it would ever have.
- -
Big Pop: The Heisenberg principle dictates the Initial Metric Fluctuation. This fluctuation led to the formation of the Inner Dilation Layer (IDL) and the Outermost Contraction Layer (OCL), which eventually became the expanding universe’s Matter. No energy is required to create the universe. Matter, the positive energy contained in the OCL, is countered by the negative energy contained in the IDL.
- -
The Big Pop (partial recombination of dilation and contraction layers) is analogous to a Prince Rupert’s Drop, the outermost contraction layer set into motion at lightspeed, forming a hyperspherical black hole to be known as Blackholium.
- -
Blackholium-Neutronium Phase Transition: As the universe continued expanding, a phase transition occurred, converting Blackholium into Neutronium. This phase triggered Neutronium Acoustic Oscillations (NAO), a key process that influenced the features observed in the Cosmic Microwave Background (CMB).
- -
Neutronium Acoustic Freezing: As the universe expanded further, the speed of sound in Neutronium matter [Kragh, H., 2016] dropped significantly, freezing the NAOs. These oscillations are modeled as hyperspherical harmonics, influencing the CMB’s low-frequency components.
- -
HU Big Bang: Neutronium eventually decayed, leading to the release of energy at the end of the first day, and the formation of a hot hydrogen plasma, marking the HU equivalent of the Big Bang. The Neutronium evaporation lasted three days. Continued expansion led to the cooling of the Universe. This process leads to the Transparency Epoch when the universe cooled enough for light to propagate freely.
The neutronium acoustic oscillations are sensitive to the speed of sound in the neutron matter.
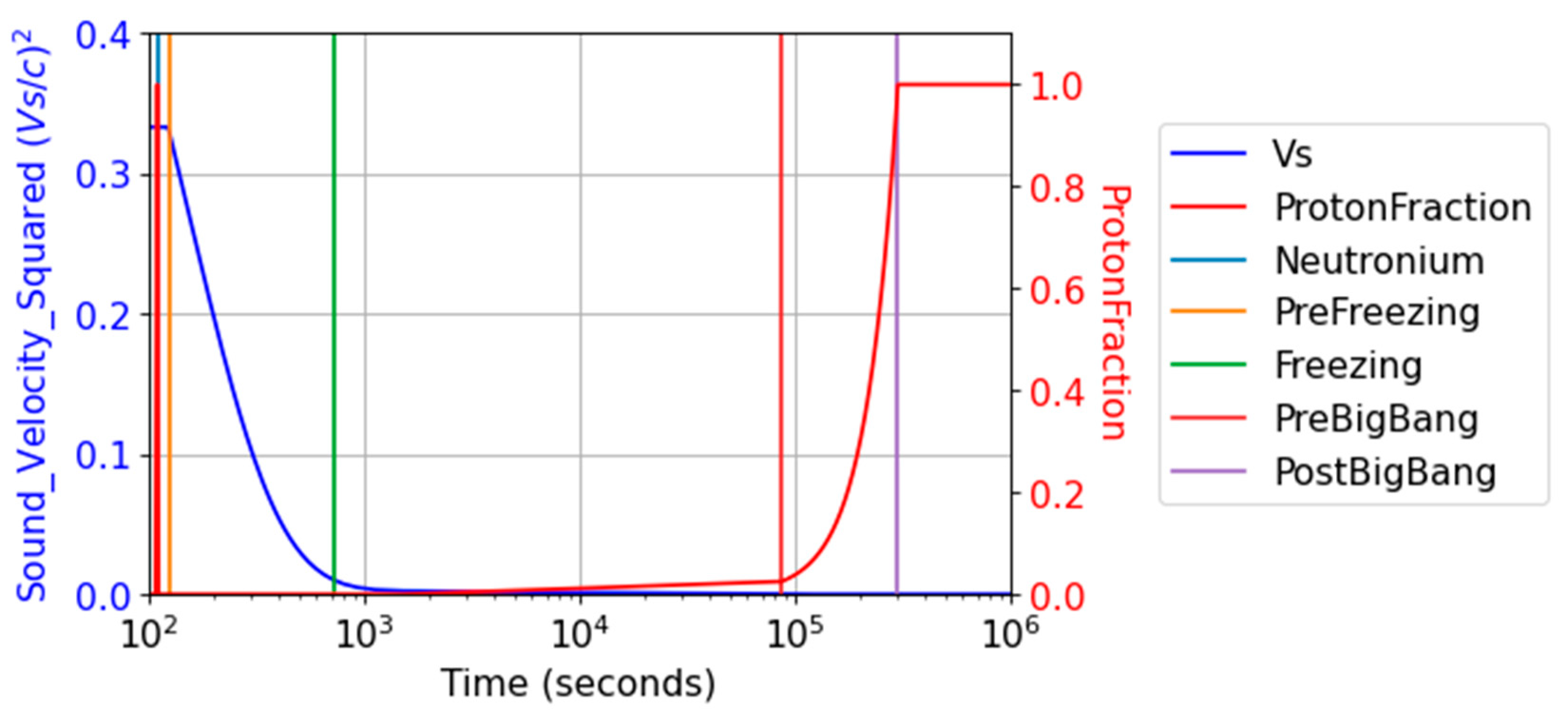
Figure O2.
Plotting showing the square of the speed of sound inside a Neutron Star. Around 300 MeV/fm3 (around 100 seconds after the Big Pop), the speed of sound changes abruptly, freezing in place neutronium acoustic oscillations. NAOs are construed to be the reason for the observed features of the cosmic microwave background. They are modeled as hyperspherical harmonics. This figure also shows the Neutronium Decay and the rise of the Proton Fraction, which is the reason for the heating up of the Universe in the HU Big Bang.
Figure O2.
Plotting showing the square of the speed of sound inside a Neutron Star. Around 300 MeV/fm3 (around 100 seconds after the Big Pop), the speed of sound changes abruptly, freezing in place neutronium acoustic oscillations. NAOs are construed to be the reason for the observed features of the cosmic microwave background. They are modeled as hyperspherical harmonics. This figure also shows the Neutronium Decay and the rise of the Proton Fraction, which is the reason for the heating up of the Universe in the HU Big Bang.
4. Cosmological Implications
The Big Pop model offers several insights and implications:
- -
Baryonic Acoustic Oscillations (BAO): The decay of Neutronium initiated Baryonic Acoustic Oscillations, distinct from the Neutronium Acoustic Oscillations. HU models these as hyperspherical harmonics, matching the observed features in the CMB as recorded by satellites like Planck.
- -
Epoch-Dependent G and SN1a Reinterpretation: HU’s model includes an epoch-dependent gravitational constant (G). This implies that Type Ia Supernovae (SN1a), traditionally used as standard candles, should have their photometric distances recalculated based on the epoch’s value of G (G
-3/2). This adjustment eliminates the need for dark matter and dark energy to explain the data (see
Appendix L for details). It also corrects the Cosmic Distance Ladder, removing inconsistencies related to distances exceeding the speed of light.
- -
Simplification of Cosmogenesis: The Big Pop eliminates the need for speculative constructs like inflation, false vacuum decay, and singularities. By positing that the universe formed from a neutral initial metric fluctuation, HU provides a coherent and less parameterized model that adheres to Occam’s Razor.
5. The Birth of Blackholium: The Prince Rupert’s Drop Analogy
As the outermost contraction layer expanded, propelled by the inner dilation layer, it formed Blackholium, a hyperspherical black hole. This process can be analogized with a Prince Rupert’s Drop, where the smooth outer layer undergoes rapid expansion. At this moment, the universe was born with zero entropy—no internal degrees of freedom existed initially.
Further expansion led to the phase transition from Blackholium to Neutronium, where the emission of electron neutrinos enabled neutrons to form. These transitions played a critical role in the subsequent evolution of the universe’s structure.
6. Modeling and Observations
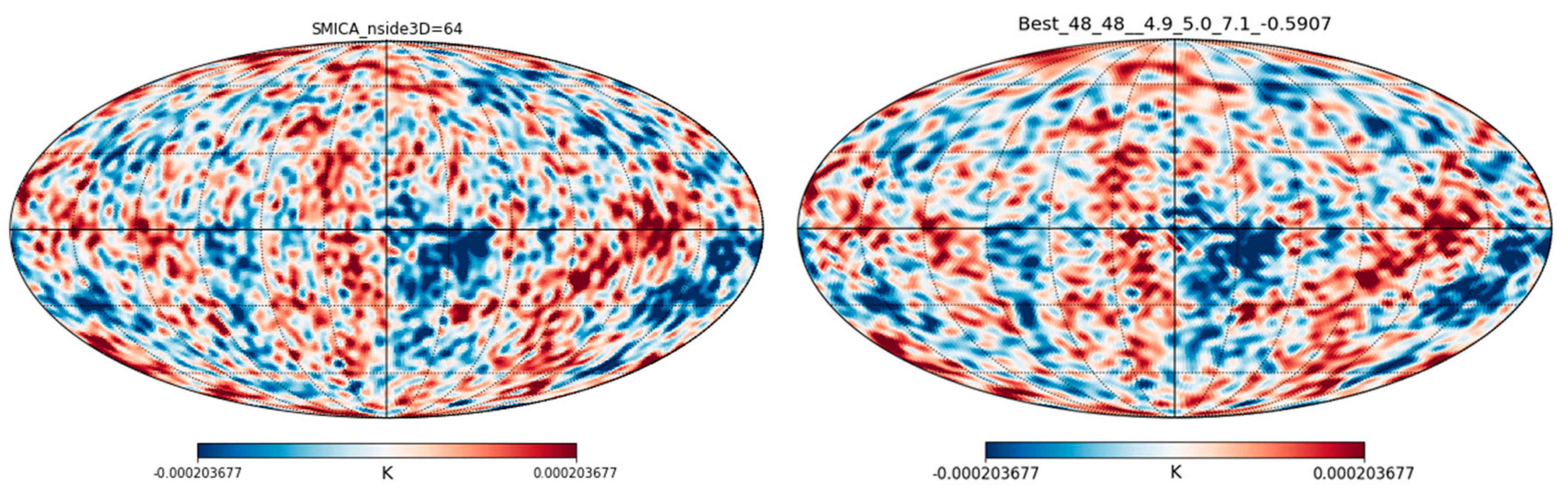
The Neutronium phase and its transitions are modeled using hyperspherical harmonics and acoustic oscillations. By filtering the CMB’s low-frequency components (up to k=48), HU identifies and simulates the features observed by the Planck Satellite. The alignment of these simulations with observed data supports HU’s Big Pop model as a viable alternative to the inflationary Big Bang paradigm.
7. The modeling of the Neutronium Acoustic Oscillations
Since the Blackholium-Neutronium-phase-transition-induced sound waves take place in 4D, the natural basis to represent them is Hyperspherical Harmonics[
15]. Hyperspherical Harmonics are defined by three quantum numbers (k, l, m).
The modeling of the CMB required filtering the CMB low-frequency components (up to k=9) and a grid-search to find the proximity of our locus (Earth location).
After the localization of our neighborhood, I increased the maximum value of k to 48 and performed further refining of our position. That was the limit that I could achieve using my available computing power.
Earth’s Location
The 4D radius is 14.03 billion light-years. The best site for Earth is shown below:
χ= 339.46 degrees
θ = 341.1 degrees
ϕ= 104.08 degrees
Here are the Cosmic Microwave Background observations by the Planck Satellite and HU simulation using Hyperspherical Harmonics:
Figure O3.
This figure shows Planck Satellite CMB observation filtered to show the low-frequency components and the simulation using hyperspherical harmonics (up to k=48).
Figure O3.
This figure shows Planck Satellite CMB observation filtered to show the low-frequency components and the simulation using hyperspherical harmonics (up to k=48).
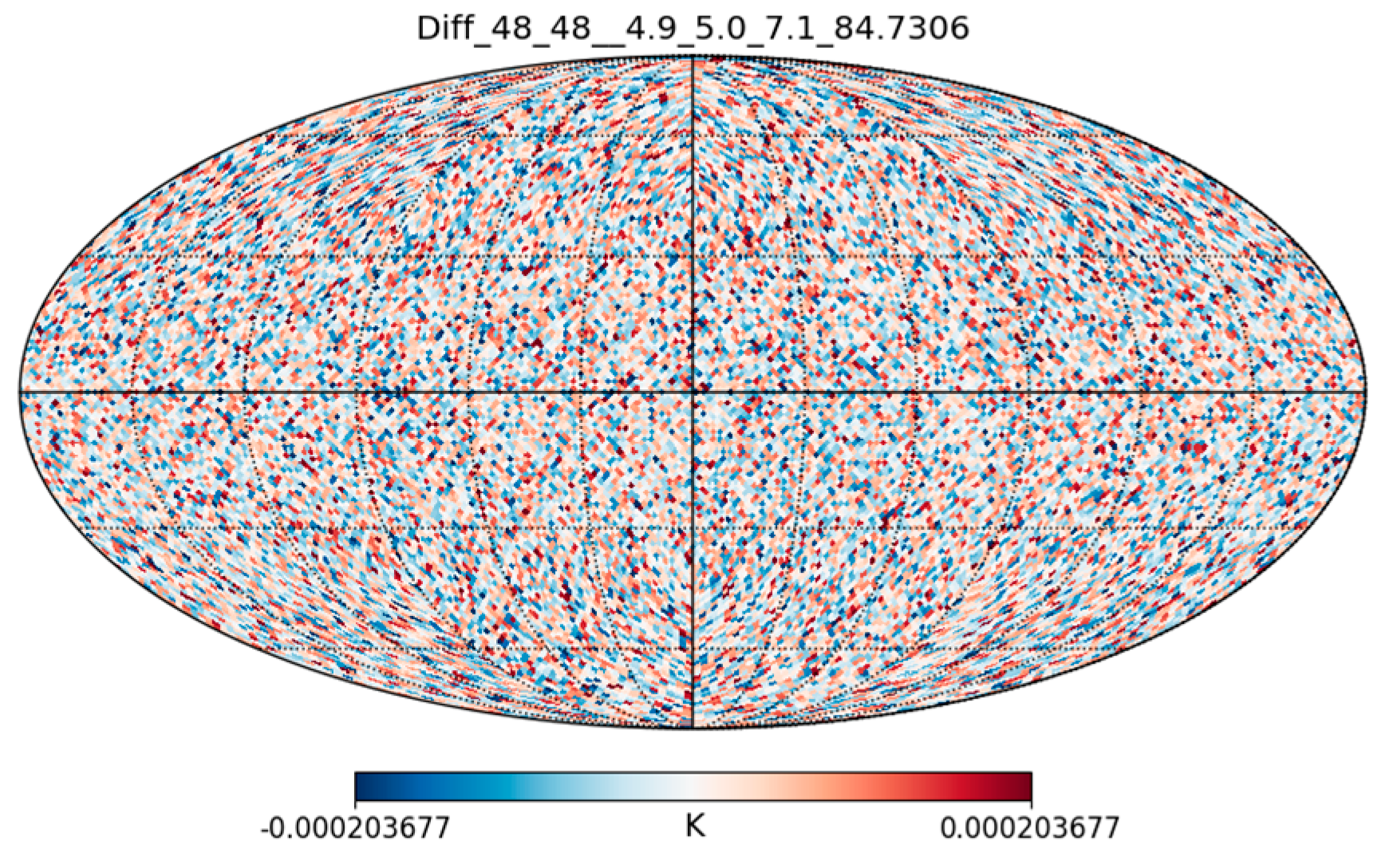
The Neutronium decay results in the Baryonic Acoustic Oscillations and corresponds to the difference between these two images:
Figure O4.
Baryonic Acoustic Oscillations related to Neutronium decay.
Figure O4.
Baryonic Acoustic Oscillations related to Neutronium decay.
8. Conclusions
The Big Pop Cosmogenesis offers a simplified and consistent model for the creation and evolution of the universe. By eliminating the need for singularities, dark matter, dark energy, and inflation, HU adheres to the principles of simplicity and consistency. It aligns with observable phenomena, such as the CMB and supernova data, providing a cohesive framework that stands as a viable alternative to the current cosmological models.
Appendix P: HU Solution to the Young Faint Sun’s Paradox
DOES HYDROGEN CONSTANTLY RAINS ON THE SUN?
In the code provided in the Additional Resources, I created a Gravitational Drude Model to explain the slow deposition of hydrogen onto our Sun.
Here I present just a simple calculation of rates.
From Sahni, V., & Shtanov, Y. (2014):
Since G is inversely proportional to the 4D radius (or epoch) of the universe and the Sun was born 4.5 billion years ago:
This means that the accreted mass onto the Sun that would keep Earth temperature constant would be:
Every year, the Sun would accrete a net mass equal 0.003491% to of Earth’s mass (5.972e+24 kg).
That would correspond to a drizzle of 1.08 micrograms per second per square meter.
The Kinetic Energy from the Sun as a Gravitational Accelerator would be:
The velocity corresponding to a kinetic energy of 900 keV for a hydrogen atom is approximately:
This means that if one accelerates a spacecraft to 13,136 km/s (4.37% c), one can use existing hydrogen rain to drive simple fusion reactors.
This result together with the shielding effect of relativistic velocities could provide the path to interstellar travel.
The rain would come mostly from the direction of propagation, as the solar system travels around the galactic center. The ecliptic is almost perpendicular to that path and that would explain why we are not as well informed about the space environment and haven’t discovered this hydrogen rain.
Since the rain travels along the sun’s path, that points toward the direction of future interstellar travel. To make use of the hydrogen rain as fuel, travel should be done forward, along the path of the sun.
Omuhamuha unexpected behavior can be explained by the asteroid interacting with a denser region of space, basically skipping in the undiscovered “sea of hydrogen”.