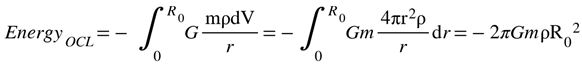1. Introduction
The Universe’s expansion is oftentimes explained in terms of a balloon, where galaxies are mapped to dots. As the balloon expands, the dots move farther apart.
For almost a hundred years, this analogy has been used, and that begs the question: Why isn’t the Universe an expanding balloon? The expanding balloon analogy clearly explains short-distance redshifting.
The reason lies in larger distances. Currently, scientists claim to have measured distances up to 46 billion light-years. Prior to my work, the hyperspherical hypersuperficial Universe was proposed by Richard Feynman and others and failed because of these large distance data. Solutions with light traveling in a log spiral or with a variable velocity [
9,
10] were proposed and failed. The reasons for their failure include the fact that a log-spiral wouldn’t produce any redshift, Gravitation and Radial Expansion are orthogonal degrees of freedom and General Relativity. None of the solutions complied with General Relativity [
11,
12], and when they complied, they were just versions of L-CDM where the placeholders Dark Matter and Dark Energy were replaced by other placeholders (e.g., negative surface tension in an m-brane). Of course, “failure” also means: They were not adopted by mainstream academia, where the bulk of the papers are produced.
The reason is simple. Lightspeed means constant speed, irrespective of the inner contents of the hyperspherical hypersurface (the Stress Tensor). Einstein’s equations describe a Universe that is analogous to a stone thrown upward under a gravitational field. LEHU is akin to a circular pond wave expanding at a constant speed. HU introduced the Silver Surfer Paradigm for Motion and placed all particles in the Universe surfing the Inner Dilation Layer. This leads to Dimensionality Reduction since surfing particles have no control over their radial position or velocity. This aspect of the theory is unique to the Hypergeometrical Universe Theory.
The goal of this article is to replace Special and General Relativity with HU’s laws of Nature shown below and the current model for matter with HU’s Fundamental Dilator Paradigm.
Interaction in the 4D Spatial Manifold
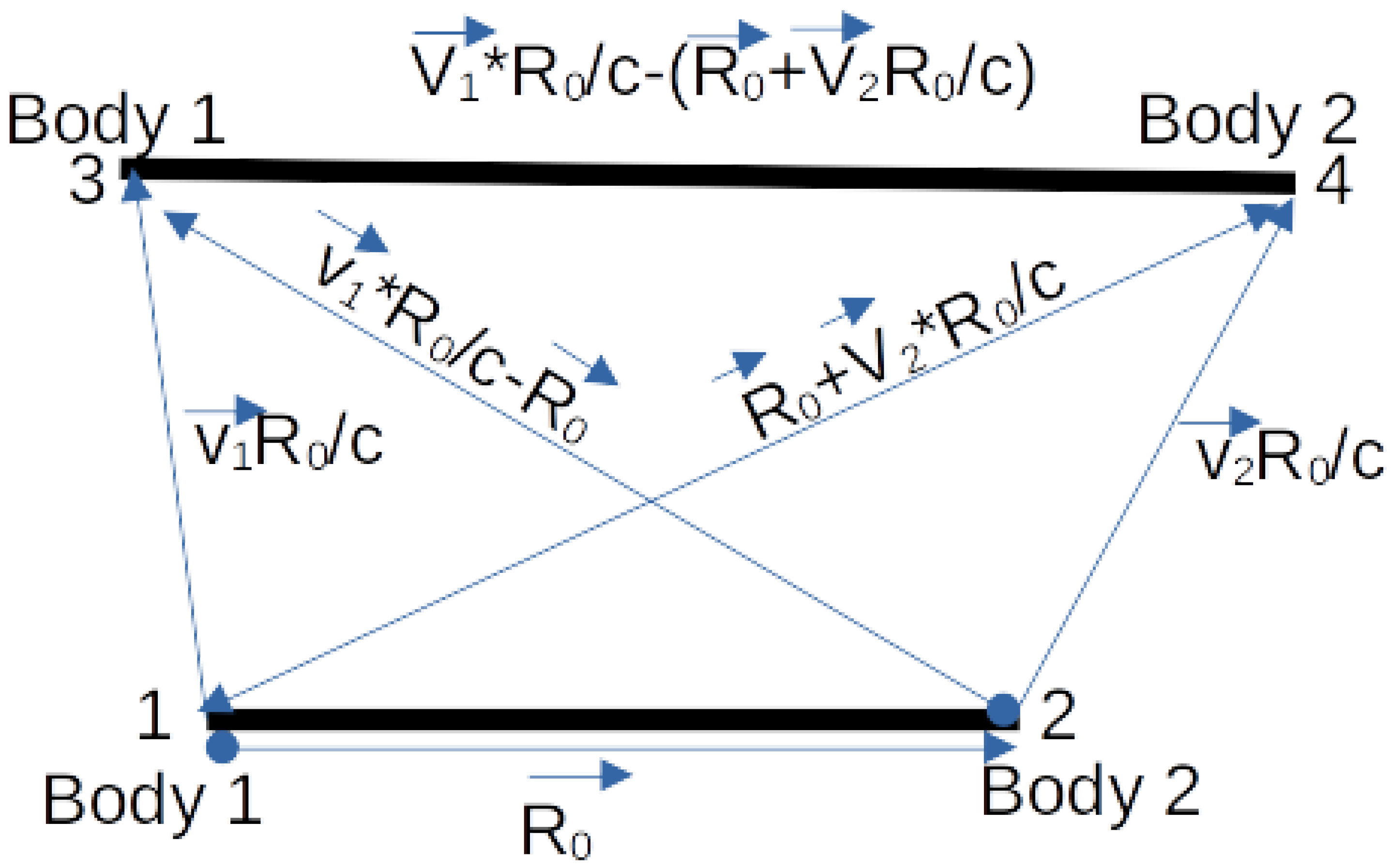
Figure 1.
This is a side view of a 4D diagram. The Projection Plane is defined by R0 and the Radial Direction (perpendicular to our 3D Universe). The horizontal lines show two epochs differing in Absolute Time by R0/c. The observation of body 1 happens across r13. Notice that distances are normalized on R0. That will become relevant when choosing which 3D vector to use in the Laws of Nature.
Figure 1.
This is a side view of a 4D diagram. The Projection Plane is defined by R0 and the Radial Direction (perpendicular to our 3D Universe). The horizontal lines show two epochs differing in Absolute Time by R0/c. The observation of body 1 happens across r13. Notice that distances are normalized on R0. That will become relevant when choosing which 3D vector to use in the Laws of Nature.
Notice that the two values for N are different. For Electromagnetism, N is the number of electrons in one Coulomb, and for Gravity, N is the number of hydrogen atoms in one kilogram. δ is 81489.699. Also, notice that G is epoch-dependent and not a Constant.
The derivation of the Laws of Nature will be presented elsewhere.
To do so, HU will have to show that it can actually replicate GR and SR accomplishments and succeed where General Relativity fails.
Appendix B contains the derivation of the lightspeed-expanding hyperspherical universe total mass.
Appendix C contains the Big Pop Cosmogenesis model. It models the Neutronium’s speed of sound as a function of density, showcasing the freezing of the hyperspherical harmonic acoustic oscillations. These oscillations are responsible for the low-frequency (long wavelength) components of the Cosmic Microwave Background (CMB). It also models of the Neutronium decay and the heating of the Universe, which resulted in the short-wavelength plasma acoustic oscillations or baryonic acoustic oscillations. Notice that both processes have a beginning and are windowed by the continued slowing down of the sound velocity.
Appendix D contains extra pictures and figures.
Table A1 summarizes all results.
The Big Bang Model
The current view of creation is that the Universe was born out of Singularity. This is supported by Hubble’s observation of receding galaxies (redshift light from galaxies not connected gravitationally to our local cluster) and from the observation of the Cosmic Microwave Background.
The Horizon Problem is how to explain the Cosmic Microwave Background [
13] homogeneity where opposing areas in the sky have the same temperature. Dr. Guth’s [
14] Inflation theory and Dr. Higgs’ Model [
15,
16,
17] for Inertial mass are the basis of the current Big Bang’s eight-step Universe creation:
A False Vacuum decayed and released infinite amounts of energy which created matter and antimatter massless particles AND spacetime. Everything was inside a Singularity.
Matter and antimatter particles annihilate each other, leaving just a sliver of matter particles.
Thermal Equilibrium is achieved.
Inflation takes place and expands the Universe into infinity. Inflation is driven by a postulated Inflaton Field. Notice that I chose to describe the Big Bang as creating an infinite universe because the explanation of a finite Universe inside a 3D non-embedded spatial manifold makes no sense. They would introduce edges in the Universe. Hence, the Big Bang has to propose infinite energy, infinite mass, and infinite Universe size.
At some point, the Higgs’ Mechanism for Mass creation kicks in and massless particles become massive.
Dark Matter and Dark Energy are created at some point. Dark Energy drives the supposed Universe’s accelerated-expansion, once the Inflaton Field is turned off.
Undefined “Quantum Fluctuations” modulate space and seed galaxies.
The gas cools down after 380,000 years of adiabatic expansion to over 3000 Kelvin when recombination makes the Universe transparent and allows the CMB to escape. The temperature of the microwave radiation is 2.725 Kelvin, and fluctuations are 1 in 100,000 in amplitude.
That is an utterly convoluted process, and this complexity is part of the argument against the Big Bang Model.
Before we can talk quantitatively about the Universe, we need to find out its mass and number of particles. We will do that, but first, we have to review the Big Pop Cosmogenesis since one cannot derive the total mass of the Universe from General Relativity or from the Big Bang Theory.
HU Cosmogenesis distinguishes it from the prior 5D [
18,
19,
20,
21,
22,
23,
24,
25] Big Bang model and from the one proposed by Vilenking [
26] because the initial fluctuation is dictated by the Heisenberg Principle and the creation of the Universe is both reversible and dynamic. Vilenkin proposed that “It is possible in principle that the big bang was a
quantum tunneling event from nothing into 4D de Sitter space
”. Quantum Tunneling requires the existence of a prior potential and the predecessor to our Universe to be already in an excited state (e.g., False Vacuum). A spontaneous metric fluctuation requires nothing like that. It is dynamic and continuous in time.
Vilenkin’s model of a phase transition or quantum transition is a precursor to the current False Vacuum Decay model, where one assigns a state for a vacuum that has higher energy than the actual lowest vacuum state. Because of the higher energy, it is called a False Vacuum. That is a requirement because scientists see the Universe as having positive energy and that energy has to come from something, thus the False Vacuum.
HU initial Metric Fluctuation happens in space, which, in HU, is not distinguished from a physical vacuum. The metric fluctuation has to have dilation in the inner layers and contraction in the outer layers for obvious reasons. It is clear that both the creation and the recombination of the contraction and dilation layers require no energy, and that the combined energy of both types of layers has to be zero. Notice that one can change the paradigm from Energy to metric deformation. It is easier to see that the metric deformation in the two regions balances each other if the distance between points outside the deformation is not affected (radially opposing points).
So, HU sees both layers, and because of that, there is no need to invoke a phase transition or a quantum transition from states. Of course, introducing those states requires further explanation, which the current view does not provide.
The introduction of an extra spatial dimension always brings about these two questions:
- a)
Dimensional Leakage—Why don’t Gravitation and Electromagnetism decay with cubic distance?
- b)
Dimensional Containment—Why doesn’t Matter wander off from the hypersurface?
Banerjee [
18] replaced Dark Matter and Dark Energy with a hyperspherical hypersuperficial m-brane dotted with negative surface tension. Needless to say, that is the replacement of unsupported (never detected) Dark Matter and Dark Energy by another never detected construct. It brings nothing new and it just changes names. Since HU explains particles without the complexity of an m-brane (with just elasticity), Occam’s Razor does not support Bannerjee’s model.
Banerjee just postulated that Gravitation and Electromagnetism are ‘superficial modes” without providing a physical model or deriving the corresponding natural laws. HU derives natural laws without an equivalent postulate. In fact, the observed light redshifts wouldn’t be possible without considering the 4D nature of space in the propagation of ancient photons through them. The same would go for gravitation if one could create oscillating gravitational dipoles or monopoles. The Dimensional Confinement question is addressed by the fact that the m-brane carries matter as excitations of its inner structure and that is distinct from plain space outside the m-brane, hence matter cannot wander around.
Paul Wesson, from the 5D Consortium, proposed that the Big Bang could be an explosion in a higher dimensionality spatial manifold [
21], while the universe would be a standing 4D hyperplane. Wesson developed his model using Einstein’s equations, hence it could never produce LEHU topology.
Dr. Suntola [
9,
10] proposes the model Dynamic Universe (DU) where the Universe is the hyperspherical hypersurface of an expanding hypersphere. The present value of the 4-radius is about 14 billion light-years, but the age of expanding space is 9.3 billion years because the expansion velocity, and the speed of light, have been higher in the past. DU relies on a zero-energy principle which allows solving the contraction/expansion speed as the function of the 4-radius. The problem in that approach is that the degrees of freedom are perpendicular to each other and thus not coupled. In other words, gravitational energy cannot flow into kinetic energy along the radial direction (perpendicular to our 3D Universe). In addition, the work relies on a log-spiral path for ancient photons and that cannot produce any redshift. The reason is that in a log-spiral, the EM field would always travel at a fixed angle with respect to the 3D hypersurface. Of course, that coupling, if it existed, it would make matter to wander out from the hypersurface.
In
Appendix B, I use his derivation of the hyperspherical Universe’s mass. Unlike Dr. Suntola, I didn’t use nonlocal gravitational interaction to calculate the mass of the universe.
HU proposed that the Universe SURFS the inner dilation layer, which is the actual 4D Entropic Explosion. The entropic explosion is analogous to Prince Rupert Drop [
27,
28,
29], in many ways.
Section 2 will present the Fundamental Dilator’s model for matter, where Matter is proposed to be made directly and simply from deformed space (not spacetime).
Section 3 contains the Big Pop Cosmogenesis, the simplest possible explanation for how our Universe came into existence. The reason it is the simplest possible is that it relies just on the Heisenberg Principle and the created universe contains only space, deformed space, and time.
2. New Model for Matter
HU proposed in its three hypotheses that the Universe was a Lightspeed Expanding Hyperspherical Hypersurface (LEHU topology) and that Matter is composed of coherences between stationary states of deformation. The Fundamental Dilator (FD) is the monomeric unit. Isotopes and subatomic particles are polymers of that monomeric unit. FDs obey the Quantum Lagrangian Principle (QLP). Later we will learn that particles SURF the Inner Dilation Layer.
The paradigm change for the definition of Matter is what allows HU to propose the Universe creation in terms of metric deformations. There is no underlying complexity (confinement potentials, compact spaces, Inflation Fields, Dark energy, quantum fields, etc). Matter is created just using space elasticity.
All other models have Mass as the main actor in their plays since that is a requirement by Einstein’s Relativity where one has to have Mass to deform Spacetime.
Four Phases of the Fundamental Dilator
Here are the four phases of the Fundamental Dilator:
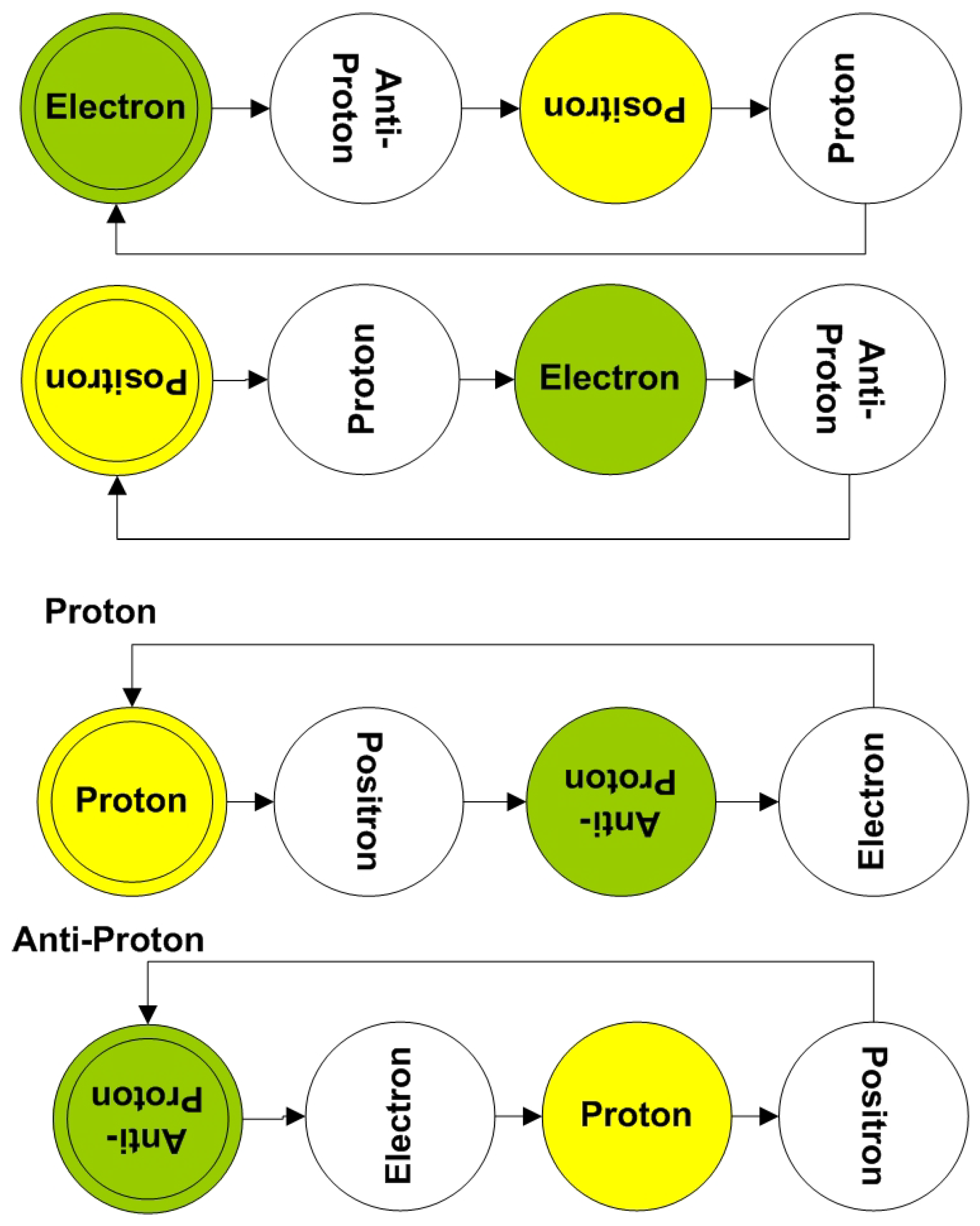
Figure 1.
This figure depicts the Fundamental Dilator coherence. Each ball represents a localized deformation of space. The phases are relative to each other after the initial phase following the recombination of the Initial Metric Fluctuation. In other words, after the Universe executed its first step in the hyperspherical expansion, being positively charged or negatively charged became a relative matter. In the figure, I depicted yellow as positive and green as negative. The orientation of the letters indicates the orientation of the phase with respect to the 3D hypersurface (our 3D Universe). Electron and Proton states are expected to be narrow along the radial direction. This means that when they rotate 90 degrees, their overlap (footprint or 3D volume) with the 3D hypersurface goes to zero. Zero 3D volume implies that those phases do not interact. This allows for this shapeshifting, spinning in 4D construct to keep particles’ nature (charge, inertial mass, dipole, multipole moments, and 3D volume).
Figure 1.
This figure depicts the Fundamental Dilator coherence. Each ball represents a localized deformation of space. The phases are relative to each other after the initial phase following the recombination of the Initial Metric Fluctuation. In other words, after the Universe executed its first step in the hyperspherical expansion, being positively charged or negatively charged became a relative matter. In the figure, I depicted yellow as positive and green as negative. The orientation of the letters indicates the orientation of the phase with respect to the 3D hypersurface (our 3D Universe). Electron and Proton states are expected to be narrow along the radial direction. This means that when they rotate 90 degrees, their overlap (footprint or 3D volume) with the 3D hypersurface goes to zero. Zero 3D volume implies that those phases do not interact. This allows for this shapeshifting, spinning in 4D construct to keep particles’ nature (charge, inertial mass, dipole, multipole moments, and 3D volume).
If one assumes that mass is some density multiplied by a displacement volume, it should be obvious that the 4D mass of the Fundamental Dilator is equal to the mass of a Hydrogen Atom.
The Quantum Lagrangian Principle
QLP is a replacement for Newton’s Laws of Dynamics. It states simply that FDs will move into positions where they dilate space in phase with the local dilaton field. Dilaton field is the interference pattern resulting from the traveling metric waves generated by the shapeshifting metric deformations (a.k.a. particles).
In other words, HU materializes metric waves in a 4D spatial manifold. HU distinguishes three kinds of metric waves:
- a)
Dilaton Field. HU Force Carrier. These metric waves travel through the 4D space and are responsible for Gravitation and Electromagnetism. Later we will show that other forces (strong and weak) are also due to these metric waves.
- b)
Shear Dilaton Field. HU Explanation for Quantum Entanglement. Shear Metric Waves are the reason for entanglement. The Quantum Object is normally the 4D Metric Wave or Dilaton Field. For entangled particles the Quantum Object is not just two particles or two photons. Instead, the Quantum Object would be the two particles and the 4D Dilaton Field. If a particle polarisation is determined, the polarizer becomes part of the quantum system
- c)
Self-Interacting Field. HU Explanation for de Broglie Waves. When one considers the interaction of the Fundamental Dilator (wave generator) and the waves it creates, that immediately replicates de Broglie waves. To understand this, consider that the direction of particle propagation in the 4D Spatial Manifold is perfectly aligned with the 4D k-vector of the created dilaton field and the k-vector projection onto the hypersurface immediately becomes the de Broglie waves.
HU Gravitation
HU Gravitation will be explained properly later. It should be said here that Gravitation is just a van der Waals force not distinct from electromagnetism. In other words, the same dilaton field generated by charged particles (e.g., electron and proton), also generates gravitation when the neutral moiety (hydrogen) is created. The reason we couldn’t see this is that we didn’t know about the Fundamental Dilator, Quantum Lagrangian Principle, and the extremely fast relaxation process (1E24 Hertz). In other words, extremely fast relaxation of charge distribution is what makes gravitation so weak. The extremely fast relaxation is what is shown in wavefunctions (the loci of FDs as they touch our Universe).
Particle-Wave Dualism Is Replaced by Wave-Generator and Qlp
The HU model for matter replaces the particle-wave description of matter with the recognition that particles create metric waves and they interact with these metric waves through the QLP. Wavefunctions become the loci for FD footprints as they obey the non-deterministic QLP. The final result is the same.
3. The Big Pop Cosmogenesis Model
Now let’s delve into the model
Figure 1depicts the Big Pop Cosmogenesis proposed by the Hypergeometrical Universe Theory (HU).
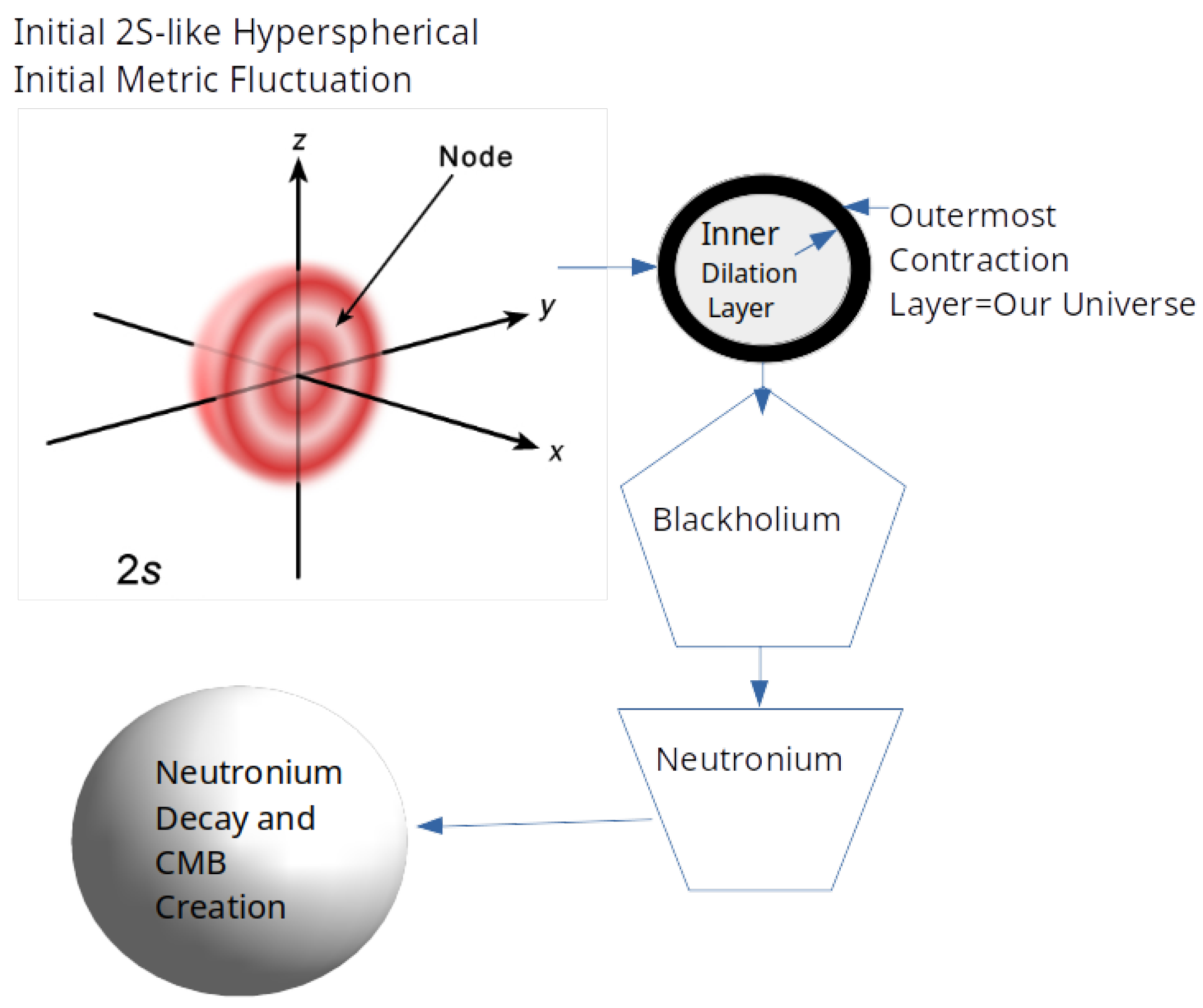
Figure 2.
The Big Pop Cosmogenesis. HU proposes that the Universe started with a simple Heisenberg Principle Driven Hyperspherical Metric Fluctuation of 421 light-second 4D radius. The Universe starts from a Heisenberg-Principle dictated metric fluctuation having a contraction in the outer layers and dilation in the inner layers, which partially recombines. The recombination process is called the Big Pop. After the partial recombination, the remaining layers are the Inner Dilation Layer and the Outermost Contraction Layer (our Universe).
Figure 2.
The Big Pop Cosmogenesis. HU proposes that the Universe started with a simple Heisenberg Principle Driven Hyperspherical Metric Fluctuation of 421 light-second 4D radius. The Universe starts from a Heisenberg-Principle dictated metric fluctuation having a contraction in the outer layers and dilation in the inner layers, which partially recombines. The recombination process is called the Big Pop. After the partial recombination, the remaining layers are the Inner Dilation Layer and the Outermost Contraction Layer (our Universe).
Blackholium is a hyperspherical hypersuperficial Black Hole. Neutronium is a similarly shaped Neutron Star. Notice that as the Universe expands, density decreases in a predictable manner.
HU Big Pop
Immediately after the Initial Metric Fluctuation appeared, a partial recombination followed. Dilation layers annihilated contraction layers until there was only one inner dilation layer and one outermost contraction layer. This process is the Big Pop.
The assignment of contraction for the outermost layer and dilation for the inner layer are essential since the opposite assignment wouldn’t result in a Universe.
HU Explains the Lack of Antimatter Using Simple Symmetry
Since the outermost layer is contraction and since the proton 3D volume is larger than the electron 3D volume, the initial phase associated with a positive charge was also contraction. HU assigns the Universe as starting with just electrons and protons (all electrons and protons it will ever have) from the very beginning.
This explains why there were never anti-particles in the Universe, in other words, HU eliminates any initial anti-matter using the spatial symmetry of the hyperspherical initial metric fluctuation. Without this, the current view fails to account for the ratio between photons and protons. The photon density is not consistent with having billions of universe masses of matter and antimatter mutually annihilating and converting the energy into photons.
HU Explains the Horizon Problem Using Simple Symmetry
While Dr. Guth has to invent a convoluted process to explain why the Universe is homogeneous, HU explains the same just using homogeneous initial conditions in all directions. In other words, since the Universe was hyperspherical Blackholium at Zero Kelvin when expanded homogeneously and isotropically, it resulted in a homogeneous density and temperature distribution.
Due to symmetry, all 3D forces (gravitation and electromagnetism) play no role in the Universe’s expansion. The Universe was driven to expand by the remaining inner dilation layer. The Inner Dilation Layer (IDL) lags behind our 3D Universe and all particles SURF that wave. This is called the Silver Surfer Paradigm for Motion [
14] and will be covered in another article of the series.
According to HU, the Universe goes through seven milestones:
Big Pop—The end of the Initial Hyperspherical Metric Fluctuation. This is also the instant when the Universe started moving at the speed of light and the smooth outermost contraction layer became the Blackholium (hyperspherical hypersuperficial Black Hole containing Flat Hydrogen).
Blackholium-Neutronium Phase-Transition, which triggered the hyperspherical harmonic acoustic oscillations, a.k.a. Neutronium Acoustic Oscillations or N.A.O.
Pre-Freezing. The moment before the velocity of sound decays suddenly within the superfluid neutron matter of the Neutronium phase. This happens around 300 MeV/fm3 density.
Post-Freezing. The moment when the velocity of the sound becomes insignificant when compared with the speed of light.
Pre-Big Bang. The moment before the Neutronium starts to decay (the proton fraction is still zero but will start moving up soon).
Post-Big Bang. The moment after the proton fraction reaches 1, that is, all the energy from the Neutronium is released and we have hot hydrogen plasma.
The Birth of Blackholium and Prince Rupert Drop Analogy
At that moment the Outermost Contraction Layer initiated its expansion at the speed of light propelled by the inner dilation layer. The conversion from a smooth (no internal degrees of freedom and thus zero entropy) contraction layer into a fragmented layer containing Flat Hydrogen occurred. This process has a physical analogy in Prince Rupert Drop.
Flat Hydrogen is the electron and proton state with a spin degree of freedom but without the orbital degree of freedom. That is the HU model for the composition of a Black Hole. HU shows that 3D Forces go to zero at a maximum acceleration (maximum density) and at maximum velocity (lightspeed). The maximum density happens when particles are sitting at a Compton Wavelength of a Hydrogen atom distance from each other. That replaces the Planck Length in the current literature. Needless to say, there is no physics that would constrain interaction at the Planck Length since the current view relies on Newton’s Empirical Law of Gravitation.
In that instance, the Universe was born with Zero Entropy (no internal degrees of freedom). Further expansion broke the smooth contraction layer into Flat Hydrogen. So, HU has the Universe starting as a Zero Kelvin Blackholium.
That is the first instant when the Fundamental Dilator representation for Matter has become valid since there was no Matter before that.
The expanding contraction layer is now a Blackholium or a hyperspherical hypersuperficial Black Hole. So, it is a Black Hole spanning the whole Universe, and it has a hyperspherical hypersuperficial shape. Symmetry alone will tell you that Gravitation doesn’t matter. Gravitation will only become locally relevant when density decays much further.
Neutronium Phase
Further expansion leads to the Blackholium-Neutronium phase transition where an orbital degree of freedom is gained with the emission of electron neutrinos. At that instant, Flat Electrons combined to form neutrons, and the Blackholium became a Neutronium.
The Blackholium-Neutronium Phase Transition also triggers Hyperspherical Harmonic Acoustic Oscillations (a.k.a. Neutronium Acoustic Oscillations or N.A.O.). They are distinct from the sound waves triggered when the Neutronium decayed and released the 0.782343 MeV per neutron. Those correspond to the Baryonic Acoustic Oscillations and have a much shorter wavelength. The reason for the shorter wavelength is the much slower sound velocity. Incidentally, a shorter wavelength in the CMB spherical harmonic decomposition corresponds to a higher frequency or higher L.
The Freezing of Hyperspherical Acoustic Oscillations and Neutronium Decay Dynamics
The neutronium acoustic oscillations are sensitive to the speed of sound in the neutron matter.
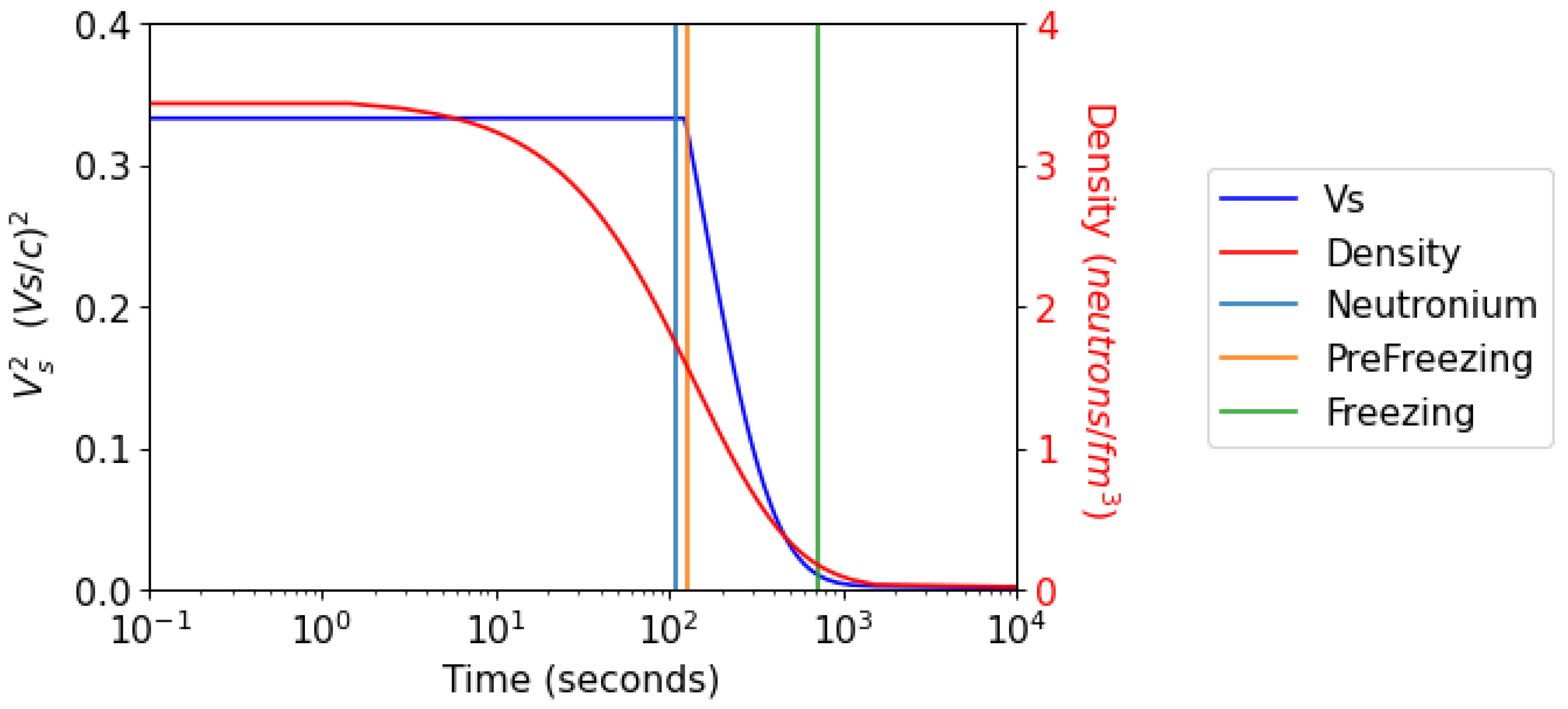
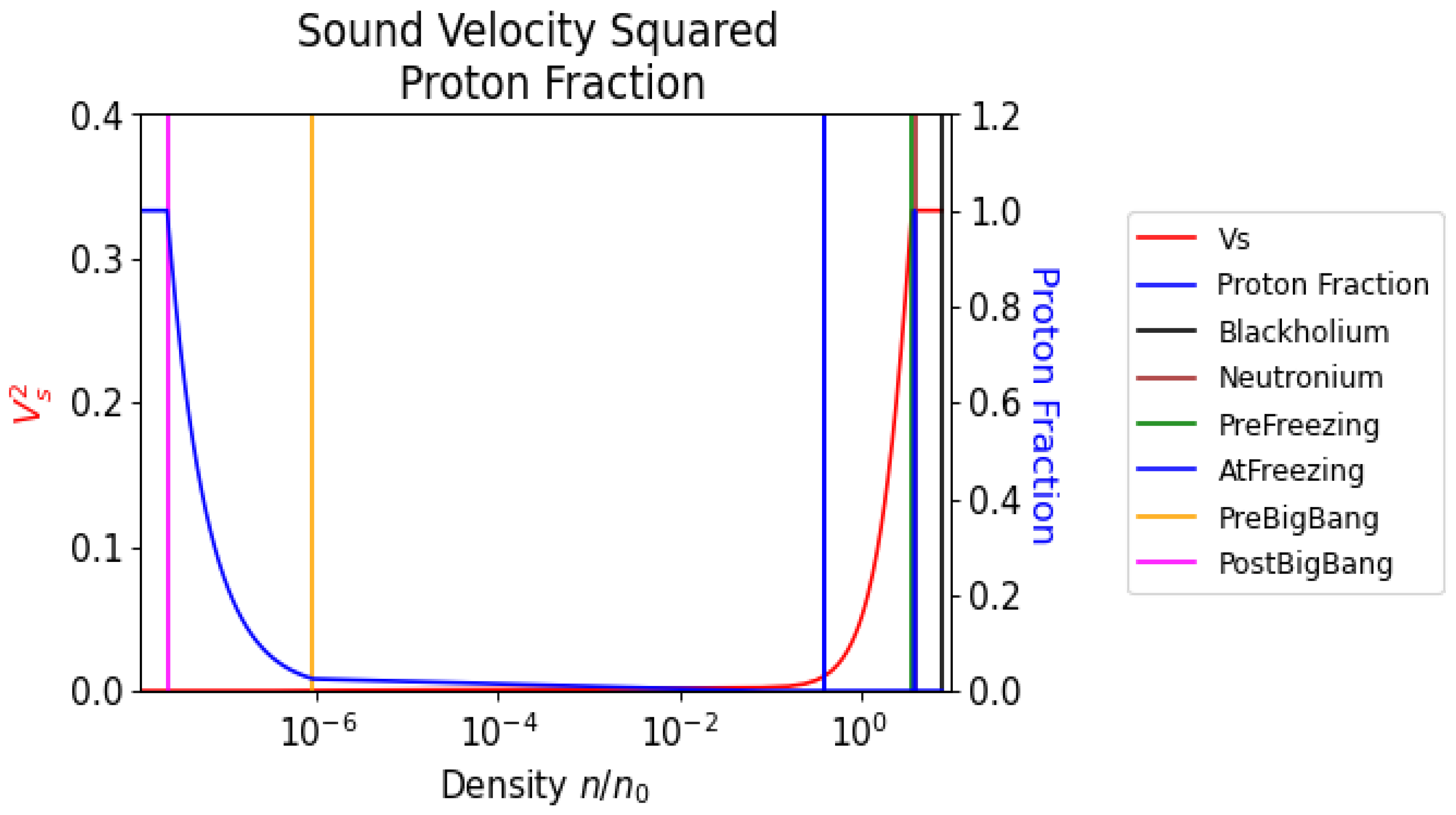
Figure 3.
This figure shows the slow down of the velocity of sound inside the Neutronium as a function of time t. Since density is known at any given time, it is possible to calculate when the hyperspherical harmonic acoustic oscillations, triggered by the Blackholium-Neutronium phase transition, freeze.
Figure 3.
This figure shows the slow down of the velocity of sound inside the Neutronium as a function of time t. Since density is known at any given time, it is possible to calculate when the hyperspherical harmonic acoustic oscillations, triggered by the Blackholium-Neutronium phase transition, freeze.
Hebeler
[30], Bedaque, and Steiner
[31] use the calculated nuclear saturation density as a reference density. HU predicts the density at the Blackholium to be 8 hydrogen atoms per cubic cell, with cell length equal to the Compton Wavelength of a hydrogen atom, or 1.32 femtometers. The density is 8/(1.32
3) per femtometer or 3.48/fm
3. For neutrons, we consider that 4 neutrons occupy the cell or 1.74/fm
3. HU assigns n
0 to 0.43/fm
3 or 1 neutron per cell.
In principle, Bedaque states that the properties of matter at densities comparable to the nuclear saturation density (n0 ≈ 0.16/fm3) are determined by QCD. In practice, it has been very difficult to extract the QCD predictions for dense matter except at extremely high densities where asymptotic freedom allows for perturbative calculations. In other words, the actual value of n0 is approximate and HU’s assignment is within reason.
Hence we will be using n0 which is around three times more diluted. This has no influence on the conclusions. In fact, even the assignment of the maximum density as having 8 neutrons per cell, has no influence. It would just affect HU’s prediction of the Initial Radius and nothing else. So, 8, or 4 or 2 neutrons per cell for the Neutronium wouldn’t affect the conclusions. The exact density will only be known when we precisely measure the actual radius of a Black Hole.
Below are the results of modeling the freezing of hyperspherical acoustic oscillations and the modeling of the Neutronium decay (both shown in
Appendix C).
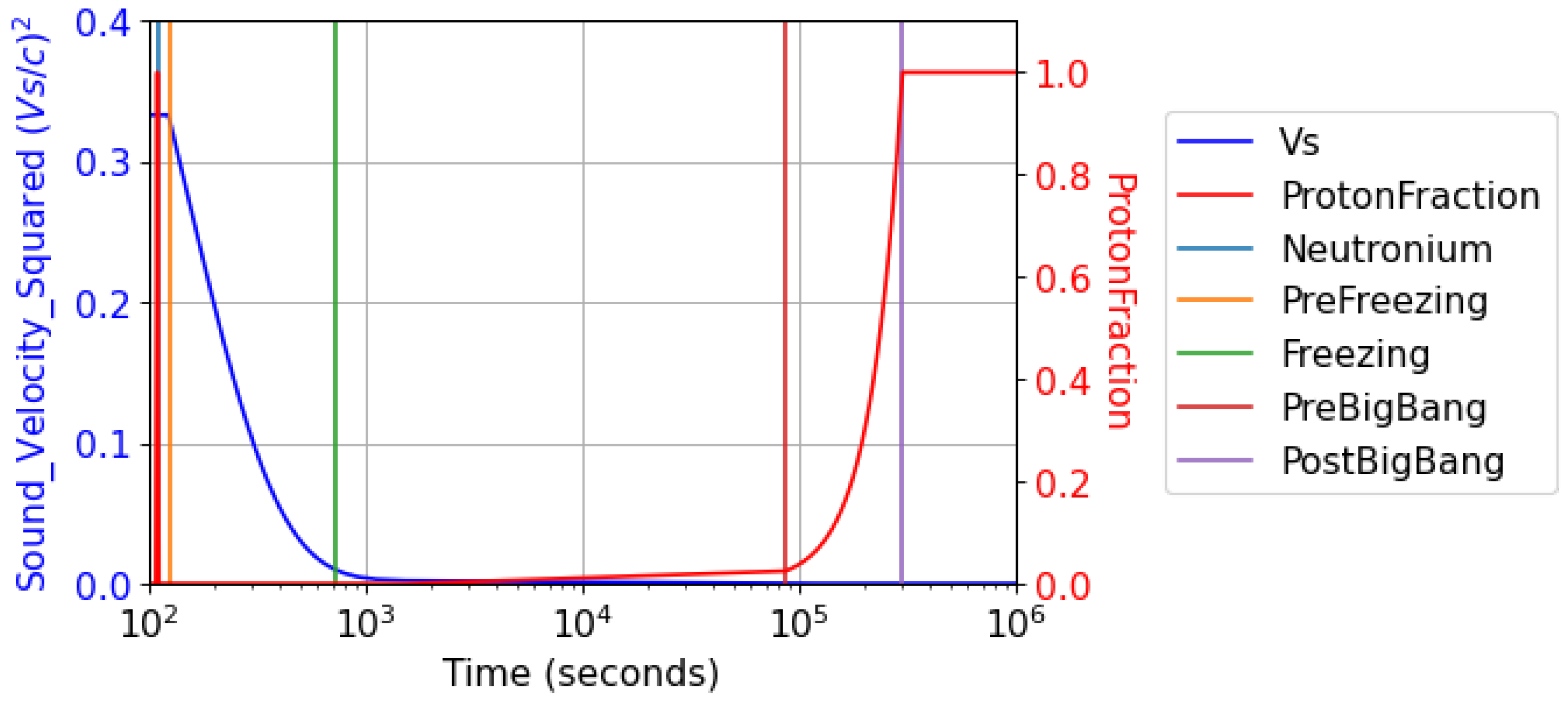
Figure 4.
This figure depicts the Cs2 = for the Neutronium phase and the evolution of the proton fraction during the HU Big Bang. This speed of sound transition is responsible for freezing the hyperspherical harmonic Neutronium Acoustic Oscillations. The evolution of the proton fraction maps the release of energy during the Neutronium decay.
Figure 4.
This figure depicts the Cs2 = for the Neutronium phase and the evolution of the proton fraction during the HU Big Bang. This speed of sound transition is responsible for freezing the hyperspherical harmonic Neutronium Acoustic Oscillations. The evolution of the proton fraction maps the release of energy during the Neutronium decay.
The Big Pop Cosmogenesis was used to replicate the Cosmic Microwave Background observation by the Planck Satellite. Details will be discussed in another article of this series
[10].
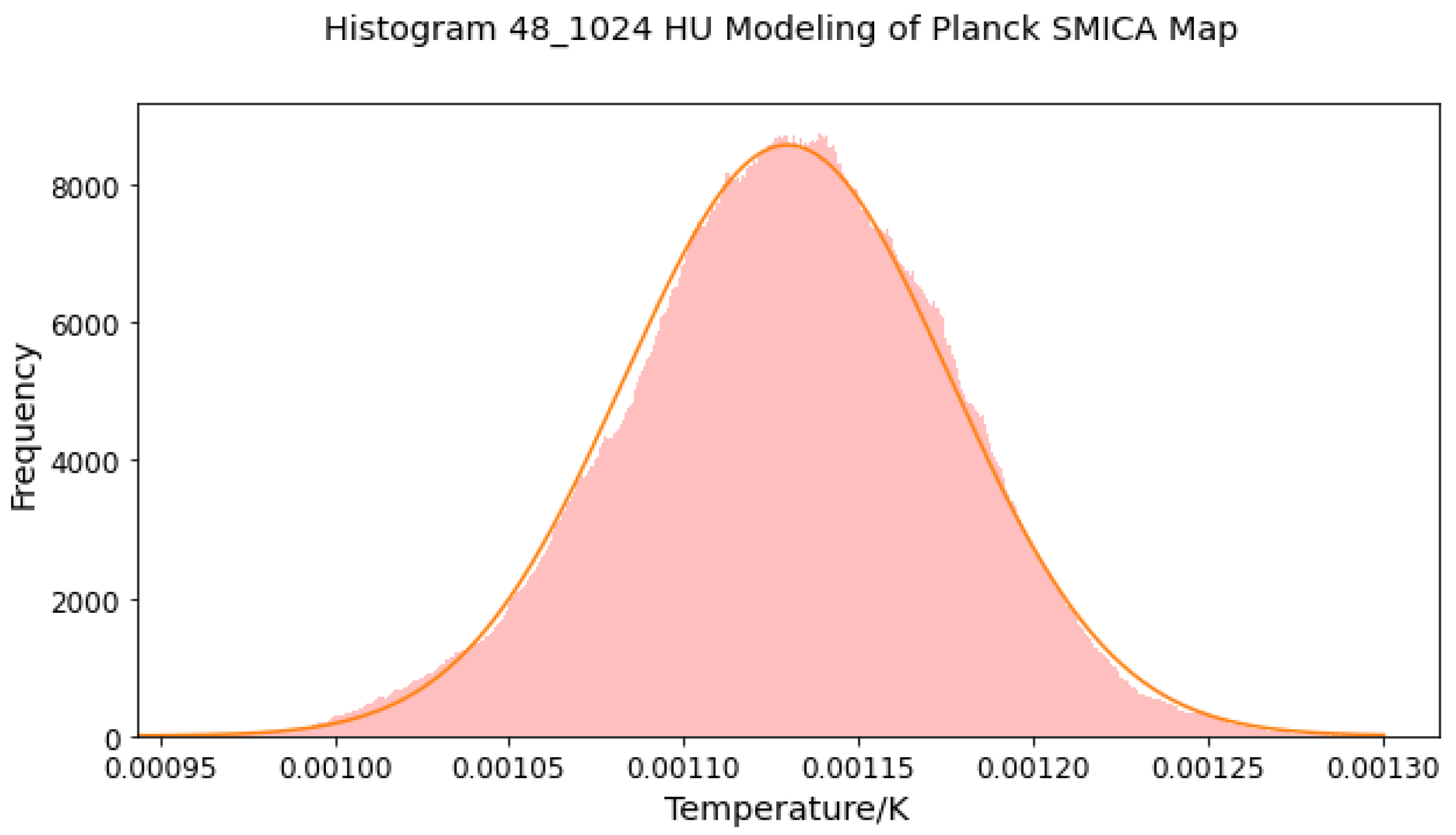
Here is the Cosmic Microwave Background observation by the Planck Satellite and HU simulation using Hyperspherical Harmonics:
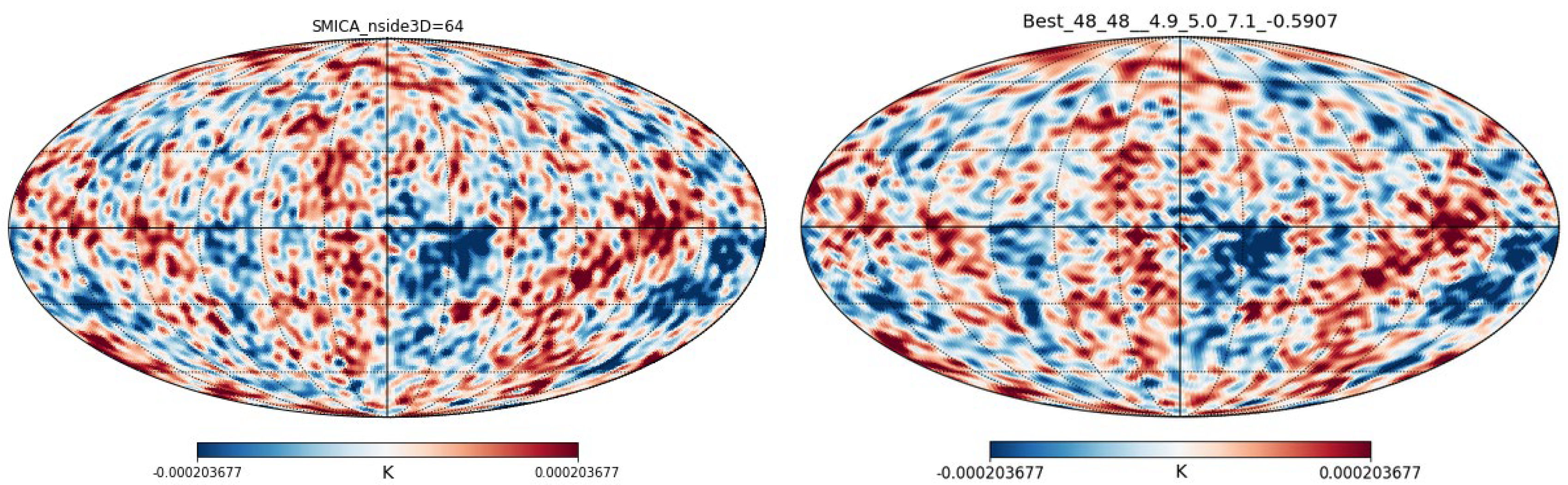
Figure 5.
This figure shows Planck Satellite CMB observation filtered to show the low-frequency components and the simulation using hyperspherical harmonics (up to k=49). .
Figure 5.
This figure shows Planck Satellite CMB observation filtered to show the low-frequency components and the simulation using hyperspherical harmonics (up to k=49). .
This was used to pinpoint the location of Earth as
χ= 339.46 degrees
θ = 341.1 degrees
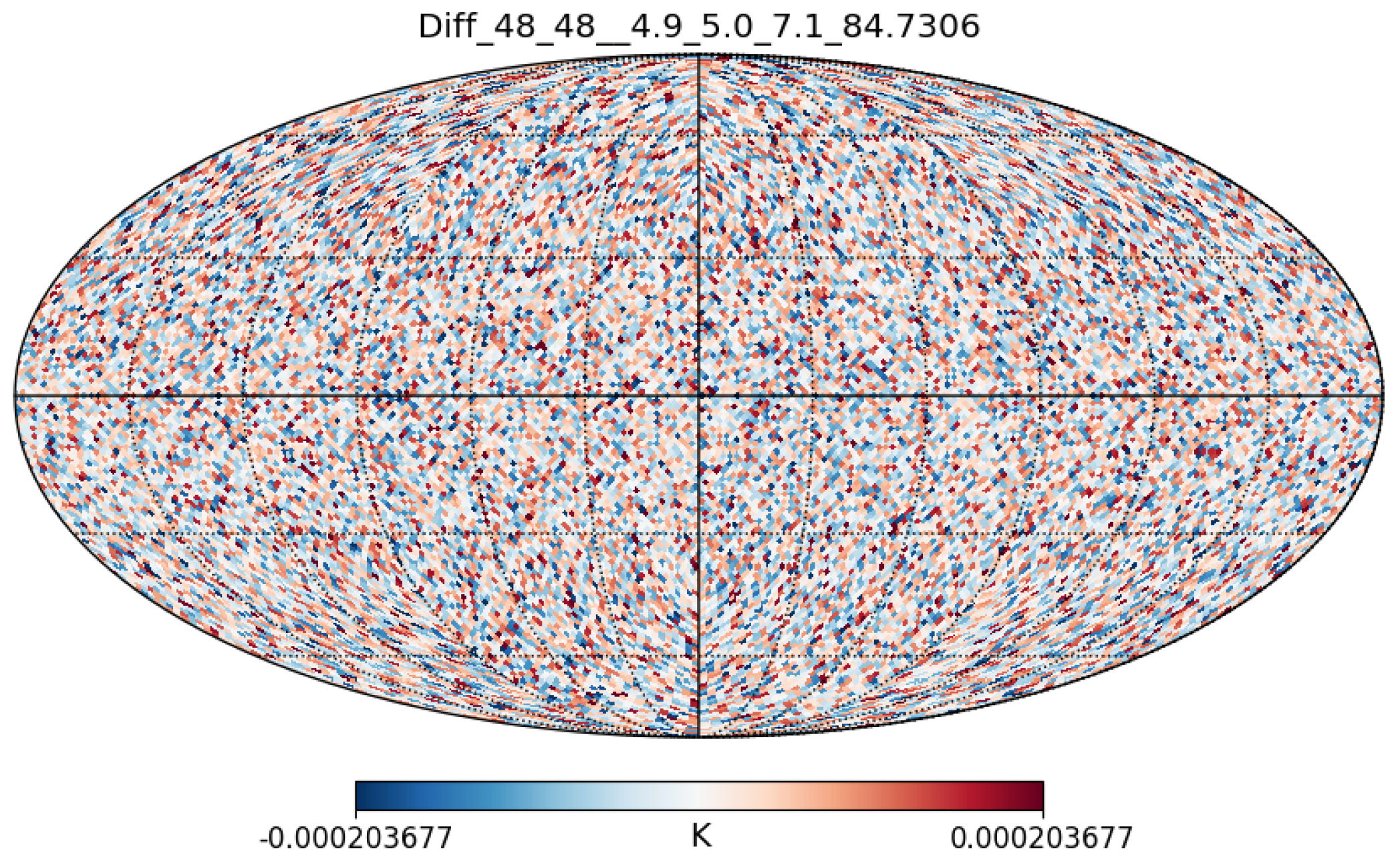
ϕ= 104.08 degreesThe Neutronium decay results in the Baryonic Acoustic Oscillations and corresponds to the difference between these two images:
Figure 6.
Simulated and Observed CMB difference. Baryonic Acoustic Oscillations related to Neutronium decay.
Figure 6.
Simulated and Observed CMB difference. Baryonic Acoustic Oscillations related to Neutronium decay.
HU fitted Hyperspherical Harmonic Spectrum Composition by minimizing quadratic error to the CMB observation to parameterless predict the galaxy density distribution across the whole universe, including the unobservable part.
3D Galaxy Density Map
Before optimizing the hyperspherical harmonic components, I had to find Earth’s location within the 4D Hyperpherical Hypersurface. Below is that search done with a smaller resolution:
Walking around in the Hyperspherical Universe
HU shows that simple idiosyncratic initial gas cloud exponential mass distribution is enough to explain the flat rotation curves observed in spiral galaxies. HU fitted the exponential to a local M33 spiral galaxy and were able to show that that mass distribution would replicate the same rotation curve irrespective of the value of G (Newton’s Gravitation Constant). HU shows that G is inversely proportional to the 4D radius of the Universe (or equivalently, to the Age of the Universe).
M33Evolution
In other words, HU predicts how M33 would fare from its formation.
The Heating Up of the Universe - Neutronium Decay
Table 1 shows some figures associated with the Neutronium Decay (a.k.a. HU Big Bang).
The energy density is colossal because the Neutronium decay occurred very early in the life of the Universe.
All the energy was released between 8.7E4 seconds (24.16 hours) and 3E5 seconds (83.3 hours) after the Big Pop. Hence the HU Big Bang happened for 59 hours and started at the end of the first day in the life of this Universe.
Table 2.
This table shows the conditions during the HU Big Bang.
Table 2.
This table shows the conditions during the HU Big Bang.
| |
Pressure N/m2 |
Time (s) |
Radius (lyr) |
Density (kg/m3) |
Temp
K
|
Time (year) |
Radius (l-s) |
Obs. Volume (lyr3) |
HU Volume (lyr3) |
Neutron
Density (1/m3)
|
Pre
BB
|
2.43E+23 |
8.69E+04 |
2.77E-03 |
6.51E+11 |
1.000E-04 |
2.8E-03 |
8.7E+04 |
8.9E-08 |
4.2E-07 |
3.9E+38 |
Post
BB
|
5.35E+20 |
3.01E+05 |
9.54E-03 |
1.59E+10 |
2.746E+09 |
9.5E-03 |
3.0E+05 |
3.6E-06 |
1.7E-05 |
9.5E+36 |
Adiabatic Cooling Model for the Universal Gas
In the vast expanse of our universe, a fundamental question arises concerning the thermal history of cosmic gas. This adiabatic cooling model seeks to address the intricate temperature evolution of the predominant gases in the universe, particularly in relation to the Cosmic Microwave Background (CMB).
Assumptions
Neutral Gas Dominance: This model operates on the presumption that a significant portion of the gas in the universe remains neutral and shielded from ionizing radiation sources. This assumption is derived from the large optical path of the CMB photons, suggesting that an extensive part of the Intergalactic Medium (IGM) remains neutral.
Equilibrium with CMB: Given the universe’s age, it is hypothesized that gas, if left undisturbed by other energy sources like stars and supernovae, would tend towards a thermal equilibrium with the CMB over cosmic time.
Model Description
Tracing back to the epoch of recombination, the universe was a dense soup of charged particles with a gas temperature around 3443 Kelvin. As the universe expanded, both the CMB and the gas began cooling. The model postulates that, in the absence of significant energy input from other sources, the gas would continue cooling in tandem with the CMB. Thus, by the present epoch, both would approach a temperature close to 2.725 Kelvin.
This model is anchored in the principle of adiabatic expansion. As the universe expands, its volume increases, leading to a drop in pressure and temperature, a natural consequence of the adiabatic process. By integrating over the universe’s entire history, the model seeks to derive an average adiabatic index, γ, for the cosmic gas. Initial findings suggest a γ value leaning towards a radiation-dominated universe, γ=4/3.
Implications and Predictions
A core implication of this model is that regions of the universe distant from the influence of ionizing sources might display temperatures closely mirroring the CMB. Furthermore, this model underscores the importance of the neutral gas’s role in the universe’s thermal narrative, potentially offering an alternative perspective to current paradigms that emphasize ionized gas and associated processes.
During and after the Neutronium decay, one considers that an adiabatic process is taking place. Since the density is still high, the gamma is fitted. y is the normalized density n/n0
During the Neutroniun decay, energy is injected into the plasma due to neutron decaying into proton, electron, and antineutrino with a release of 0.782343 MeV per neutron, while adiabatic cooling was taking place according to an average gamma of 1.22.
As
neutrons are converted into protons, electrons, and antineutrinos, energy is released corresponding to an electron temperature jump
. That happens concomitantly with adiabatic cooling from the continuous expansion.
Where x is the proton fraction, M
N, M
P, and M
E are the masses of the neutron, proton, and electron respectively and k
B is the Boltzmann Constant.
The adiabatic cooling is expressed by the equation below:
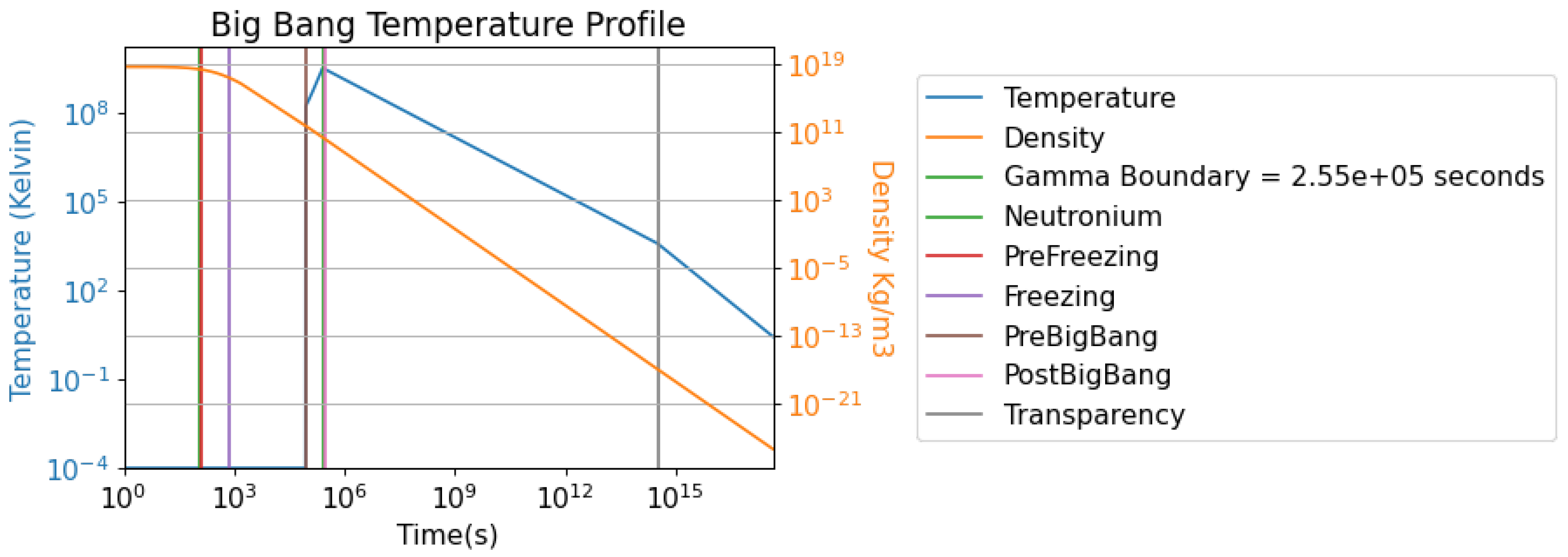
Figure 7 below shows the temperature profile resulting from this process. The maximum temperature was 3.05E9 Kelvin. Notice that the cooling of the CMB radiation and of the hot hydrogen have the same density dependency. In other words, gas and photons cool down at the same rate although through different processes.
Nucleosynthesis
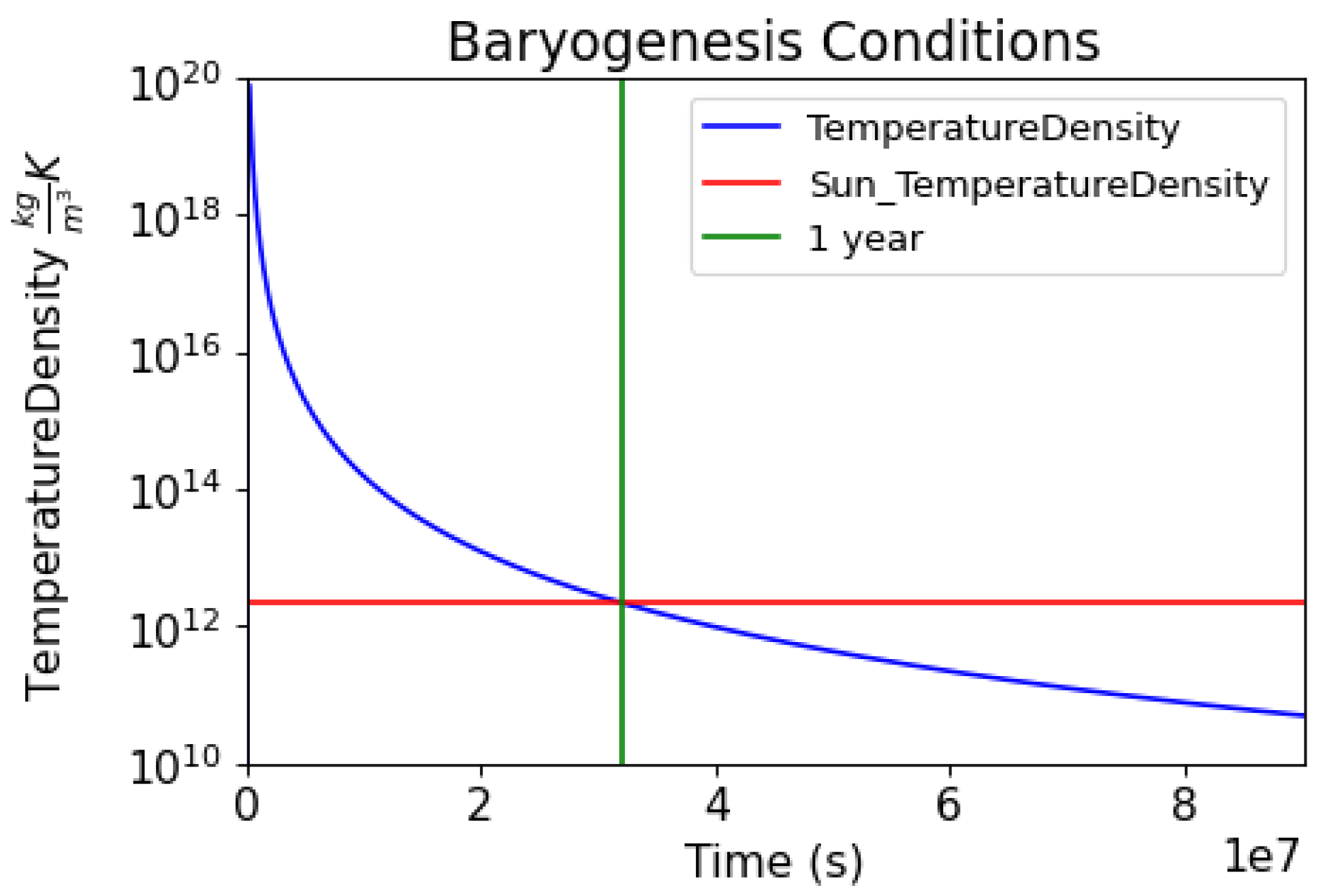
For the first year, the Universe was denser and hotter than the Sun, but unlike the Sun, the antineutrinos produced cannot escape. The antineutrino density is the same as the proton or electron density. These are HU’s predicted conditions for nucleosynthesis.
Figure 8.
This figure depicts the product of temperature times density. The red line is the temperature density product at the core of the Sun. At its peak, the product calculated for the Neutronium Decay was 100 million times higher than the Sun’s core. Maximum temperature 3.05E9 Kelvin. These conditions are consistent with the observed nucleosynthesis. The quantitative nature of this modeling will allow for a better understanding of nucleosynthesis.
Figure 8.
This figure depicts the product of temperature times density. The red line is the temperature density product at the core of the Sun. At its peak, the product calculated for the Neutronium Decay was 100 million times higher than the Sun’s core. Maximum temperature 3.05E9 Kelvin. These conditions are consistent with the observed nucleosynthesis. The quantitative nature of this modeling will allow for a better understanding of nucleosynthesis.
The Adiabatic Expansion and the Transparency Epoch
Here we used an equilibrium condition as defined by the Saha equation instead of using a more sophisticated non-equilibrium model because this is not the core of this article and the better models are implemented entangled with other models (e.g., COSMOREC).
Better estimates of the exact time of recombination are not as relevant as it might seem given the fact that HU is proposing a distinct Cosmic Distance Ladder, which introduces a distinct expansion profile. So, it is pointless polishing the modeling of the fraction of atomic hydrogen if the time of the recombination changed from 380,000 to 11.1 million years after the Big Pop.
The recombination epoch is defined by the Saha equation [
32]:
is the density of atoms in the i-th state of ionization, that is with i electrons removed.
is the degeneracy of states for the i-ions
is the energy required to remove i electrons from a neutral atom, creating an i-level ion.
is the electron density
is the thermal de Broglie wavelength of an electron
is the mass of an electron
T is the temperature of the gas
h is Planck’s constant
From the Saha equation for a single ionization:
Where x is the ionized fraction. So, one solves this equation for z and the boundary where gamma switches using the current temperature T=2.725 K, x=½, and gamma=4/3
We allow the gamma to be piecewise constant with a moving adiabatic boundary. The fitting results are presented in
Table 3.
Location of the Transparency Zone
Starting from our current CMB temperature and the knowledge that the cooling process since the transparency epoch was adiabatic(, HU calculated what is the density and corresponding z that produces ionization fraction= 0.5.
Table 4.
HU tells us that recombination occurred at 11.1 million years after the Big Pop and that the temperature of the plasma was 3443 Kelvin.
Table 4.
HU tells us that recombination occurred at 11.1 million years after the Big Pop and that the temperature of the plasma was 3443 Kelvin.
| Recombination Data |
| z |
1262 |
| TransparencyRadius |
11,105,550 light-year |
| TransparencyTime |
11.1 million years after the Big Pop |
| Density At Recombination |
1.0E−17 kg/m3 or 9.51e-18 atm |
| T at Recombination |
3443 K |
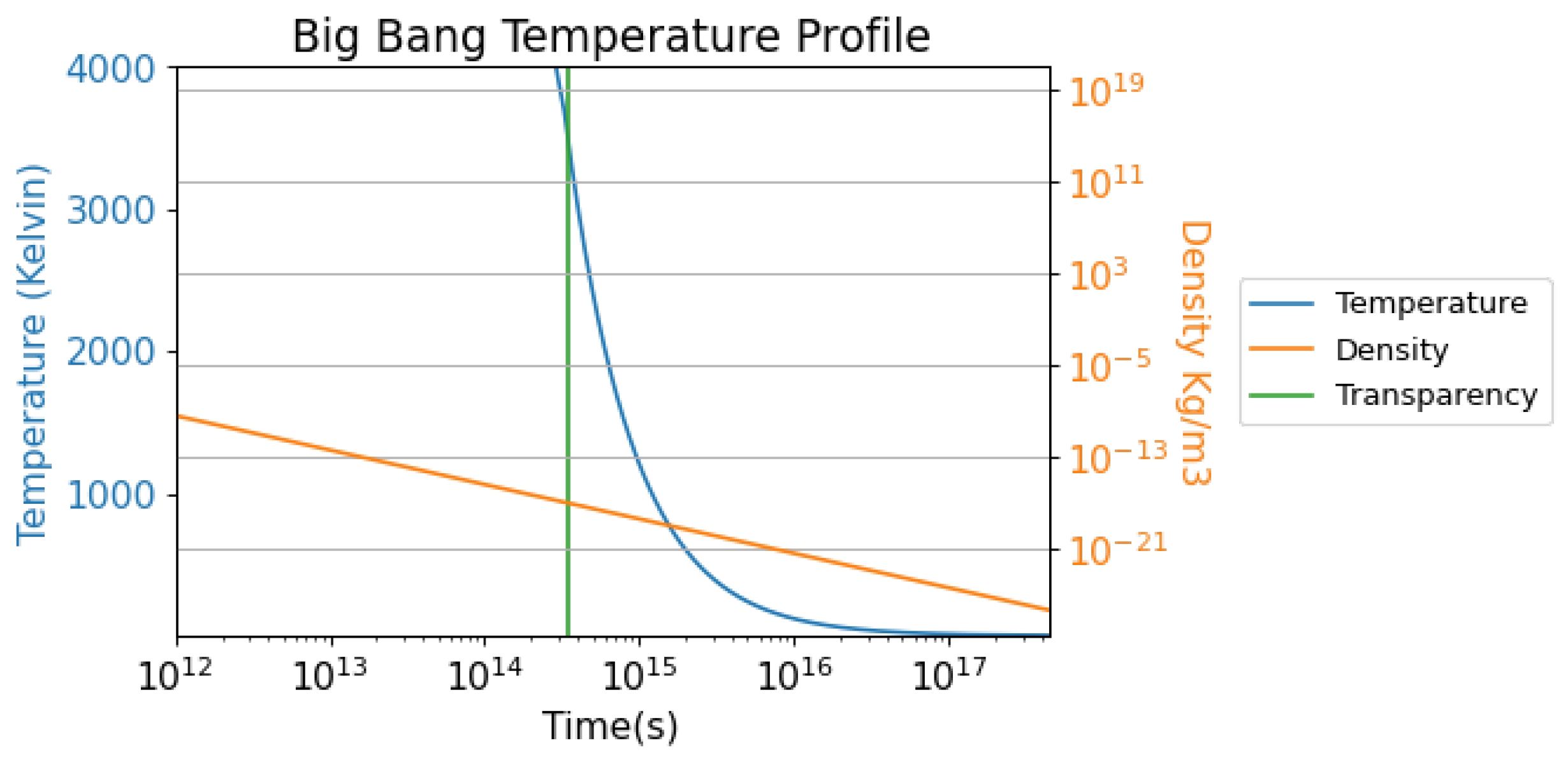
Figure 9.
This figure depicts the temperature and density from the Transparency epoch (11.1 million years old Universe) to the current epoch.
Figure 9.
This figure depicts the temperature and density from the Transparency epoch (11.1 million years old Universe) to the current epoch.
The Current Universe
Table 5.
Properties associated with the current Universe, both observable and hyperspherical. The number of Supernovae or the number of neutrons is the value for the corresponding partitions. They correspond to the number of Supernovae (standard SN=1E51 ergs) to the energy released in the Neutronium Decay Event.
Table 5.
Properties associated with the current Universe, both observable and hyperspherical. The number of Supernovae or the number of neutrons is the value for the corresponding partitions. They correspond to the number of Supernovae (standard SN=1E51 ergs) to the energy released in the Neutronium Decay Event.
| Current Observable Universe |
| Observable Universe Volume |
1.16E+31 |
lyr3 |
| Observable Universe Mass |
4.89E+52 |
kg |
| Number of Neutrons |
2.92E+79 |
|
| BigBangEnergy |
3.66E+66 |
J |
| BB Number of Supernovae |
3.66E+22 |
|
| Current Hyperspherical Universe |
| HU Volume |
5.45E+31 |
lyr3 |
| HU Mass |
2.31E+53 |
kg |
| Number of Neutrons HU |
1.38E+80 |
|
| BigBangEnergy HU |
1.73E+67 |
J |
| BB Number of Supernovae HU |
1.73E+23 |
|
4. Discussion
Against the Big Bang Theory, there is the fact that there has been no actual observation of Dark Matter, Dark Energy, Inflaton Field. Even the Higgs Boson hasn’t been shown to give mass to anything.
I mentioned that because there was a precedent in Particle Physics when pion zero was assigned certain abilities (carry the Strong Force) and later the theory was recanted.
In other words, just because a theory tells you something, that doesn’t mean it is true. The multiple steps (creating massless particles and then adding mass to them) are unnecessarily complex if you consider HU’s alternative. HU just creates all the mass in the Universe as a zero Kelvin Blackholium. A single step for the Universe’s creation is better, according to Occam’s Razor, than multiple steps without a single observation to support them.
LEHU is not a solution to Einstein’s equations and HU’s Laws of Nature are a full replacement for General and Special Relativity. HU explains something as fantastic as the receding motion of all galaxies in the Universe as a simple case of inertial motion in 4D.This is only possible because of both the LEHU topology and the epoch-dependent G in HU’s Law of Gravitation.
HU uses the equation of state for the neutron star [45,46] for the period during and after the Neutronium decay. This is just an acceptable approximation, in the same way, adiabatic expansion of monoatomic hydrogen is an approximation to the dynamics the Universe went through, which includes star and galaxy formation, star deaths, etc.
This means that the perfect adiabatic cooling of the intergalactic gas might deviate from the theoretical predictions. That said, the equilibrium between the 21-cm hydrogen line and the CMB radiation bath might help the gas to follow our predictions. Data on the evolution of the intergalactic gas [47] is not precise enough at this moment for us to draw any conclusion.
5. Conclusions
HU provides a simple picture of the Universe’s creation and a trivial energy source to heat up the Universe: Neutron Decay. It creates the Universe as a Zero Kelvin Blackholium as the final product of the Big Pop. Blackholium is a perfectly homogeneous isotropic initial condition that is also consistent with the Second Law of Thermodynamics and does so using simply the Heisenberg Principle. In a single scoop, it solves the inexistence of Anti-Matter in the Universe and the homogeneity and isotropy of the Cosmic Microwaves Background.
The driving “force” for the expansion of the Universe is Inertial Motion or Natural Propagation of Information within the 4D spatial Manifold [
10].
HU explains Hubble’s Observations using simply Inertial Motion in 4D [48]. No forces are required. This is only possible because of the Silver Surfer Paradigm for Motion [
14].
HU creates the Universe without breaking a single law of physics and using the simplest possible model. HU’s Universe contains only space, deformed space, and time. Those are the Fundamental Concepts and because of that HU is a Fundamental Theory.
The proton-fraction is shown in
Figure 4. Its value is used to calculate the heating of the Universe during the Neutronium decay.
This is the HU Big Bang, which started at the end of the first day and lasted 59 hours.
The Universe goes through seven milestones:
Big Pop - The end of the Initial Hyperspherical Metric Fluctuation. This is also the instant when the Universe started moving at the speed of light and the smooth outermost contraction layer became the Blackholium (hyperspherical hypersuperficial Black Hole).
Blackholium-Neutronium Phase-Transition which triggered the hyperspherical harmonic acoustic oscillations, a.k.a. Neutronium Acoustic Oscillations or N.A.O.
Pre-Freezing. The moment before the velocity of sound decays suddenly within the superfluid neutron matter of the Neutronium phase. This happens around 300 MeV/fm3 density.
Pos-Freezing. The moment when the velocity of the sound becomes insignificant when compared with the speed of light.
Pre-Big Bang. The moment before the Neutronium starts to decay (the proton fraction is still zero but will start moving soon.
Post-Big Bang. The moment after the proton fraction reaches 1, that is, all the energy from the Neutronium is released and we have a hot hydrogen plasma.
Transparency Epoch or Event is the moment when density and temperature allow for light to propagate. HU has both density and temperature. Temperature is dependent both on density and redshift. HU does not postulate either.
Since the Universe density is prescribed by the lightspeed expansion, HU can calculate the density and temperature at any time. This precise modeling is required to calculate the precise moment of transparency (recombination).
During the first year of this Universe’s existence, the nucleosynthesis conditions were better than the core of the Sun. This is shown in
Figure 8, where the initial Temperature-Density product was 100 million times higher than at the core of the Sun.
HU places recombination at 11.1 million years after the Big Pop (the creation of the Universe). The CMB plasma temperature was 3443 Kelvin and the redshift was 1262. The pressure was 9.5E-18 atm with a density of 1E-17 kg/m3.
Where n0 is given by 1 particle per unit cell. The unit cell has a side with a length equal to the Compton wavelength of a hydrogen atom. The maximum concentration has eight Flat Hydrogen units (one in each vertex) and represents the Blackholium phase. The Neutronium phase is assigned to half of that density or four Neutrons per cell.
Black Hole Density (BHD=1.6735575E-27*8/(1.32E-15**3)=5.8211506e+18 kg/m3)
Symmetry alone eliminates Antimatter. The Horizon Problem is solved by symmetric and isotropic homogeneous initial conditions. This is possible because HU creates matter out of deformed space, instead of using the current paradigm of undefined massless particles that acquire inertia through a rigamarole process involving Higgs bosons. In the initial states, protons are large contractions (large contracted 3D displacement volume) and electrons are small dilations (smaller dilated 3D displacement volume). Under these conditions, the net effect is contraction and that is consistent with OCL (Outermost Contraction Layer).
Epoch-dependent G and LEHU topology eliminates the need for Dark Matter and Dark Energy [48] and
Appendix A.
HU offers a new model for the creation of the Universe which requires less speculation and that is consistent with the Laws of Nature. HU’s model for Matter allows for Matter to be spontaneously created from a metric fluctuation. The current paradigm focuses on Energy, a non-fundamental construct. The fundamental constructs of HU’s Universe are time, space, and deformed space. In other words, HU’s goal is to explain all physics in terms of time and space, whereby space one should include metric and dimensionality as variables.
HU allows for a new level of detail in the understanding of the Universe, which includes the recalibration of our Cosmic Distance Ladder (because of G being epoch-dependent) and the materialization of the Expanding Balloon Analogy.
Notice that the realization of an otherwise theoretical construct was what Einstein did when he realized Minkowski’s spacetime.
LEHU is not compatible with Einstein’s equations. HU doesn’t shy away from that part of the controversy. During the current series of articles, HU will make the case to replace GR and SR and the current Standard Model of Particle Physics and Cosmology.
GitHub Repositories provided on CMB_HU,, HU_GalaxyPackage, .HU_Papers.
Appendix A - Energy Conservation and the Total Mass of the Universe
HU presents an actual argument for Energy Conservation that starts with a set of constructs that reduces to zero (flat metric). In the section on the Big Pop Cosmogenesis, I will explain that after the partial recombination of a 4D hyperspherical metric fluctuation, there were only two layers left - one Inner Dilation Layer (IDL) and the Outermost Contraction Layer (OCL).
If those layers were to interact, they would recombine and space would recover flatness (a Cartesian 4D Spatial Manifold with nothing inside). So, starting from this initial condition and two constructs (IDL and our Universe as the OCL), one can create an Energy Conservation Equation.
After the push, the energy balance can be written as:
Mc2 is added to The left side of the equation to reflect the change in the reference frame. The right side is not affected because now the OCL reference frame is traveling at the speed of light.
After billions of years, the expansion of the Universe would minimize EnergyIDL and the absolute velocity (Galaxies are at rest with respect to the Fabric of Space or no tangential kinetic energy). So, we approximate KineticEnergy3D to zero, and EnergyIDL to the energy contained in the mass of particles to derive the mass of the Universe. The two quantities left are the initial gravitational energy and the final radial kinetic energy.
Hubble observations are consistent with zero KineticEnergy3D. Galaxies can be thought as having kinetic and gravitational energies nullifying each other.
IDL is not gone and all particles surf it.
MASS of the Universe
The derivation of the Universe’s mass follows the work of Dr. Suntola without the assumption of non-local gravitation.
Equation (10) can be rewritten to calculate the total mass of the Universe as:
The implicit approximation is that Galaxies have Zero Transversal Kinetic Energy and only travel perpendicularly with respect to the 3D Hypersurface.
Where the 3D volume of the Observable Universe is there to emphasize that Gravitation is a local force and that we can only send the Gravitational pull from masses without our Observable Universe.
So, HU solves this equation:
Summing m over all particles, you get M.
Energy conservation between these two states, results:
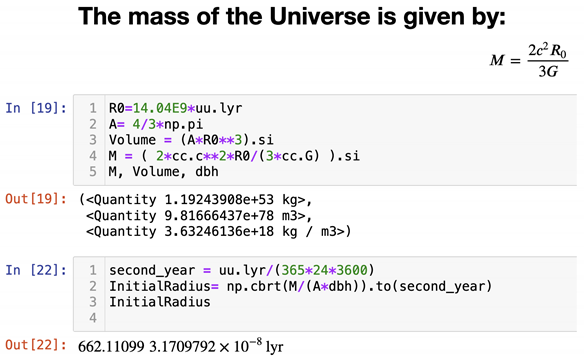
Mass of the Embedded Sphere (Observable Universe)
M= 1.192E53 kg
Initial Density = 3.632E18 kg/m3
Density calculation: 8 x 1/8 + 6*1/2+1=5 FD per 1.32 femtometer cell
Initial Volume = 9.816E78 m3
Initial 4D Radius = 662 light-seconds
Notice that there is uncertainty on how many Flat-Hydrogens one would have per cell. The cell length is 1.32 femtometers. This has no bearing on the dynamics of the Universe proposed in this article. It only affects one prediction: The Initial 4D radius of the Universe.
That Energy Conservation Law is exactly what we expected, with the caveat that the breaking of the smooth contraction layer creates a Blackholium with Black Hole density but no gravitational pressure (due to symmetry). So, the Universe starts like a wing toy, with pent-up inner tension that eventually is released when the pressure allows it (during the Neutronium Decay).
So, in HU energy conservation among orthogonal degrees of freedom does not modulate the Universe’s expansion. There is no need for the Inflaton Field, Dark Matter, or Dark Energy. The Universe expansion starts because of the Big Pop and proceeds unabated through INERTIA AND NATURAL VELOCITY OF THE INNER DILATION LAYER.
A model that requires no forces (e.g., Dark Energy or Zero Point Energy) and no interconnection between orthogonal degrees of freedom is more easily defensible. HU requires none of that and explains Hubble Observations as Inertial Motion in 4D.
I derived HU’s Laws of Nature where Newton’s Gravitational Constant is epoch-dependent (inversely proportional to the 4D radius of the Universe) and derived the Supernova Absolute Luminosity G-dependence to be G-3.33. Since SN1a detonates at the Chandrasekhar Mass Limit and that has a G-3/2 dependence, SN1a distances have to be corrected by the epoch-dependent Absolute Luminosity (not a Stellar Candle). So, HU is compliant with modified SN1a distances and has an epoch-dependent Law of Gravitation and 4D Laws of Nature.
Appendix B Derivation of Sound Speed and Neutron Decay
Here we follow Hebeler et al.l work on modeling neutron matter [44,45]
To calculate the proton fraction within the Neutronium as a function of time or density we used the following equations for pressure and Energy for the neutronium matter.
Where n
0 is the Nuclear Density of o.434/fm
3 and:
The proton-neutron equilibrium equation is given by:
Where x is the proton fraction and:
During the Neutronium decay the equilibrium equation becomes:
Where n is determined just by the Mass of the Universe and the 4D radius of the Universe at any given time.
Equilibrium Conditions within the Neutronium:

Table A1. This table contains the conditions for the nuclear parameters and the explicit solutions to the parameters.
Appendix C Extra Figures
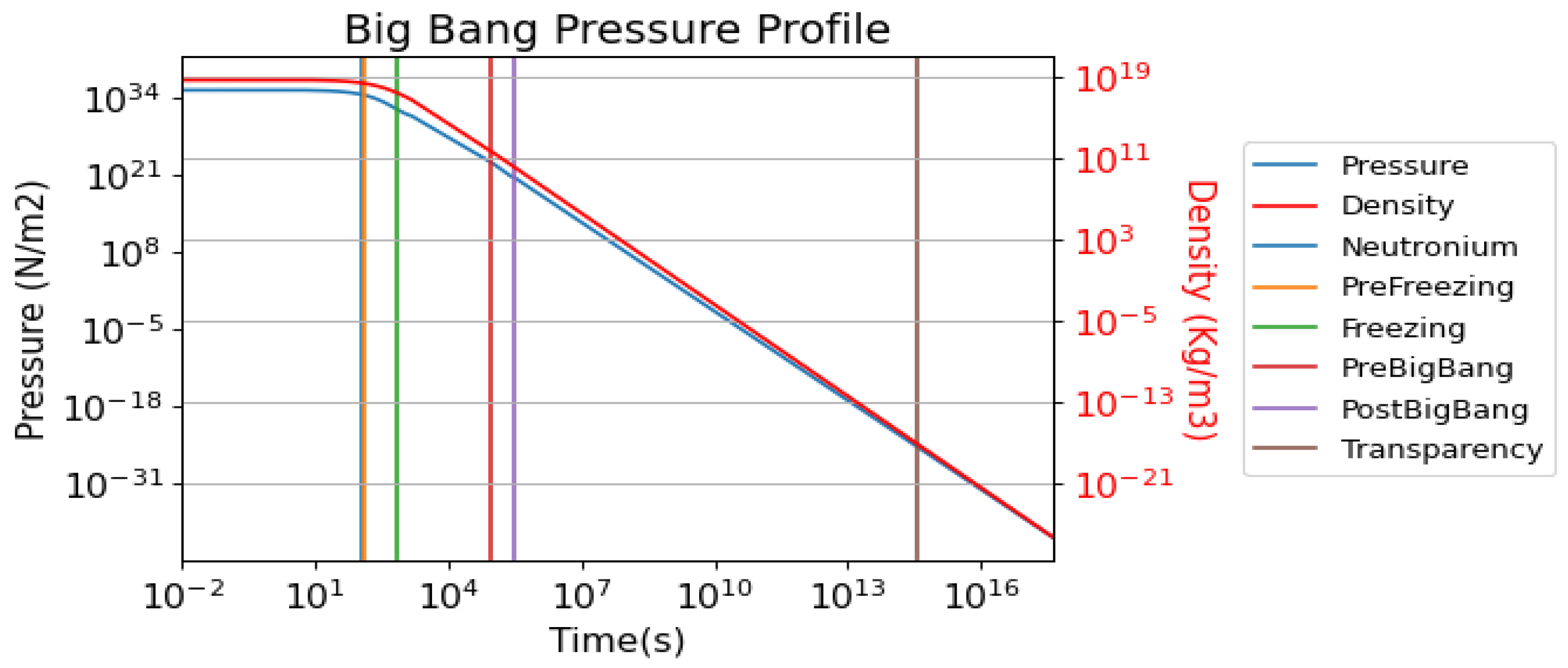
Figure A1.
This figure depicts the pressure and density of the Universe since the Big Pop.
Figure A1.
This figure depicts the pressure and density of the Universe since the Big Pop.
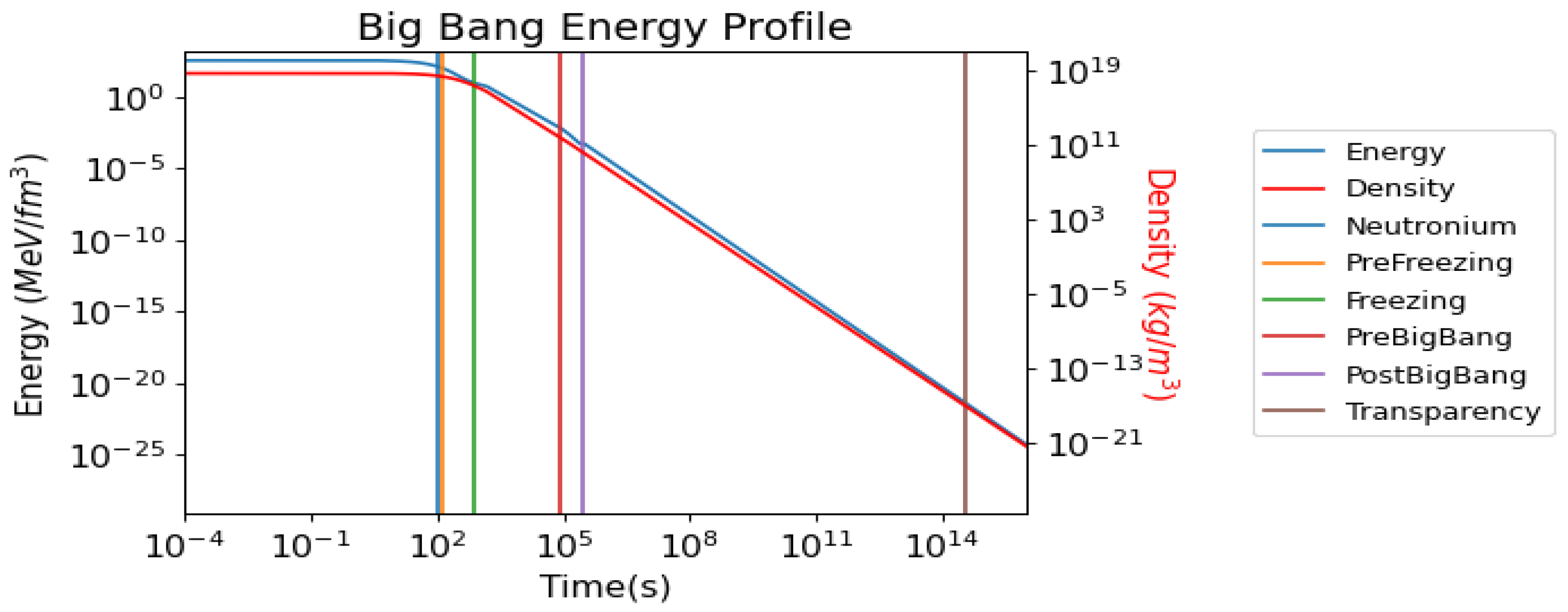
Figure A2.
This figure depicts the energy and density of the Universe since the Big Pop. Energy excludes the rest energy of the particles.
Figure A2.
This figure depicts the energy and density of the Universe since the Big Pop. Energy excludes the rest energy of the particles.
Figure A3.
This figure depicts the temperature distribution of the simulated Cosmic Microwave Background. The temperature presented here is the result of modeling the hyperspherical acoustic oscillations, and it has nothing to do with the CMB temperature, which is the electronic plasma blackbody radiation redshifted temperature. The Neutronium Acoustic Oscillations occurred before any energy was released in the Universe, and the temperature was expected to be very close to Zero Kelvin.
Figure A3.
This figure depicts the temperature distribution of the simulated Cosmic Microwave Background. The temperature presented here is the result of modeling the hyperspherical acoustic oscillations, and it has nothing to do with the CMB temperature, which is the electronic plasma blackbody radiation redshifted temperature. The Neutronium Acoustic Oscillations occurred before any energy was released in the Universe, and the temperature was expected to be very close to Zero Kelvin.
Figure A4.
This figure depicts the Cs2 = for the Neutronium phase. It shows the abrupt speed of sound change around 300 MeV/fm3. This transition is responsible for freezing the hyperspherical harmonic Neutronium Acoustic Oscillations.
Figure A4.
This figure depicts the Cs2 = for the Neutronium phase. It shows the abrupt speed of sound change around 300 MeV/fm3. This transition is responsible for freezing the hyperspherical harmonic Neutronium Acoustic Oscillations.
Appendix D Extra Tables
Table A1.
A.
| |
Density n/n0 |
Density
MeV/fm3
|
Density (Kg/m3) |
Neutron
Density
(1/m3)
|
Pressure
N/m2
|
Time (s) |
| Blackholium |
8.00E+00 |
3.29E+02 |
5.82E+18 |
3.5E+45 |
2.81E+35 |
0.00E+00 |
| Neutronium |
4.00E+00 |
1.13E+02 |
2.91E+18 |
1.7E+45 |
4.83E+34 |
1.09E+02 |
| PreFreezing |
3.64E+00 |
9.77E+01 |
2.64E+18 |
1.6E+45 |
3.77E+34 |
1.26E+02 |
| Freezing |
4.04E-01 |
8.98E+00 |
2.94E+17 |
1.8E+44 |
1.25E+32 |
7.18E+02 |
| PreBB |
8.95E-07 |
5.93E-03 |
6.51E+11 |
3.9E+38 |
2.43E+23 |
8.69E+04 |
| PostBB |
2.19E-08 |
5.30E-04 |
1.59E+10 |
9.5E+36 |
5.35E+20 |
3.01E+05 |
| Transparency |
1.38E-35 |
3.93E-22 |
1.01E-17 |
6.0E+09 |
2.52E-25 |
3.51E+14 |
| Today |
6.87E-45 |
2.46E-28 |
4.99E-27 |
3.0E+00 |
7.85E-41 |
4.43E+17 |
Table A1.
B. These tables contain the Universe’s properties at the Universe’s milestones: Blackholium, Neutronium, PreFreezing, Freezing, PreBigBang, PostBigBang, Transparency, Today. The initial radius of the Universe was 421 light-seconds. n0 is the Nuclear Matter Density parameter. HU considers it to be the inverse of the volume of a minimum cell (cell side equal to the Compton Wavelength of a Hydrogen Atom). Universe peak temperature was 3 billion degrees Kelvin.
Table A1.
B. These tables contain the Universe’s properties at the Universe’s milestones: Blackholium, Neutronium, PreFreezing, Freezing, PreBigBang, PostBigBang, Transparency, Today. The initial radius of the Universe was 421 light-seconds. n0 is the Nuclear Matter Density parameter. HU considers it to be the inverse of the volume of a minimum cell (cell side equal to the Compton Wavelength of a Hydrogen Atom). Universe peak temperature was 3 billion degrees Kelvin.
| |
Density (Kg/m3) |
Time (s) |
Radius (lyr) |
Temp
K
|
Time (year) |
Radius (light-seconds) |
Observable
Volume
(lyr3)
|
HU Volume (lyr3) |
| Blackholium |
5.82E+18 |
0.00E+00 |
1.33E-05 |
1.000E-04 |
0.0E+00 |
421 |
9.9E-15 |
4.7E-14 |
| Neutronium |
2.91E+18 |
1.09E+02 |
1.68E-05 |
1.000E-04 |
3.5E-06 |
5.3E+02 |
2.0E-14 |
9.4E-14 |
| PreFreezing |
2.64E+18 |
1.26E+02 |
1.73E-05 |
1.000E-04 |
4.0E-06 |
5.5E+02 |
2.2E-14 |
1.0E-13 |
| Freezing |
2.94E+17 |
7.18E+02 |
3.61E-05 |
1.000E-04 |
2.3E-05 |
1.1E+03 |
2.0E-13 |
9.3E-13 |
| PreBB |
6.51E+11 |
8.69E+04 |
2.77E-03 |
1.000E-04 |
2.8E-03 |
8.7E+04 |
8.9E-08 |
4.2E-07 |
| PostBB |
1.59E+10 |
3.01E+05 |
9.54E-03 |
2.746E+09 |
9.5E-03 |
3.0E+05 |
3.6E-06 |
1.7E-05 |
| Transparency |
1.01E-17 |
3.51E+14 |
1.11E+07 |
3.443E+03 |
1.1E+07 |
3.5E+14 |
5.7E+21 |
2.7E+22 |
| Today |
4.99E-27 |
4.43E+17 |
1.40E+10 |
2.725E+00 |
1.4E+10 |
4.4E+17 |
1.2E+31 |
5.5E+31 |
Table A2.
This table summarizes the general conditions of the Universe. The initial 4D radius of the Blackholium was 421 light-seconds 4D radius. This radius is connected with what is considered to be the Black Hole density. The Fundamental Cell has a side length equal to the Compton Wavelength of a Hydrogen Atom or 1.32 femtometers. If that cell contains a single neutron, the density is called the Nuclear Matter Density (1/1.323)=0.435 fm-3. I assigned Blackholium density to have 8 neutrons per cell. The choice of Black Hole density just changes the initial 4D radius, but it doesn’t change the dynamics of the Universe. The current average density is 2.98 atoms per cubic meter.
Table A2.
This table summarizes the general conditions of the Universe. The initial 4D radius of the Blackholium was 421 light-seconds 4D radius. This radius is connected with what is considered to be the Black Hole density. The Fundamental Cell has a side length equal to the Compton Wavelength of a Hydrogen Atom or 1.32 femtometers. If that cell contains a single neutron, the density is called the Nuclear Matter Density (1/1.323)=0.435 fm-3. I assigned Blackholium density to have 8 neutrons per cell. The choice of Black Hole density just changes the initial 4D radius, but it doesn’t change the dynamics of the Universe. The current average density is 2.98 atoms per cubic meter.
| Initial Properties |
| Initial 4D Radius of the Universe |
421 |
ls |
| Initial Volume of the Observable Universe |
2.65E+56 |
m3 |
| Current Properties |
| rho |
4.99E-27 |
kg / m3 |
| rho_atoms |
2.98 |
Hydrogen Atoms per m3 |
| Cell Length (m) |
1.32E-15 |
m |
| EnergyPerSupernova |
1.00E+51 |
ergs |
Table A3.
This table summarizes the general conditions of the Universe.
Table A3.
This table summarizes the general conditions of the Universe.
| Initial Properties |
| Initial 4D Radius of the Universe |
421 |
ls |
| Blackholium Density |
5.82E+18 |
kg/m3 |
| Neutronium Density |
2.91E+18 |
kg/m3 |
| EnergyPerSupernova |
1.00E+51 |
ergs |
| Initial Observable Universe |
| Initial Volume of the Observable Universe |
9.9E-15
8.38E33 |
Lyr3
m3 |
| Mass of the Observable Universe |
4.89E52 |
kg |
| Initial Hyperspherical Universe |
| Initial Volume of the Hyperspherical Universe |
4.7E-14
3.98E34 |
Lyr3
m3 |
| Mass of the Hyperspherical Universe |
2.3E53 |
kg |
| Current Properties |
| rho |
4.99E-27 |
kg / m3 |
| rho_atoms |
2.98 |
Hydrogen Atoms per m3 |
| EnergyPerSupernova |
1.00E+51 |
ergs |
References
- Smarandache, F. (2007). Hadron Models and related New Energy issues. “Hadron models and related New Energy issues” by Florentin Smarandache.
- Smarandache, F., & Christianto, V. (2007). Quantization in Astrophysics, Brownian Motion, and Quantization in Astrophysics, Brownian Motion, and Supersymmetry Supersymmetry. “Quantization in Astrophysics, Brownian Motion, and Supersymmetry” by Florentin Smarandache and Victor Christianto.
- Pereira, M. (2017). The Hypergeometrical Universe: Cosmogenesis, Cosmology and Standard Model. World Scientific News, 82, 1–96.
- Pereira, M. (2018). The Case for a Fourth Spatial Dimension and the Hyperspherical Force. World Scientific News, 98, 127–139.
- Pereira, M. (2018). The Hypergeometrical Force: The Coma Cluster without Dark Matter. World Scientific News, 101, 222–228.
- Pereira, M. (2019). The Optical Path of Ancient Photons and the Supernova Project. World Scientific News, 130, 195–215. [CrossRef]
- Pereira, M. (2017). The Hypergeometrical Universe: Cosmogenesis, Cosmology and Standard Model. Global Journal of Science Frontier Research, 17(5).
- Pereira, M. A. (2010). The Hypergeometrical Universe: Cosmology and Standard Model. AIP Conference Proceedings, 1316(1). [CrossRef]
- Suntola, T. (2005). Observations support spherically closed dynamic space without dark energy. In C. Roychoudhuri & K. Creath (Eds.), The Nature of Light: What Is a Photon? (Vol. 5866, p. 160). [CrossRef]
- Suntola, T., & Day, R. (2004). Supernova observations fit Einstein-deSitter expansion in 4-sphere. Available online: https://arxiv.org/abs/astro-ph/0412701v2.
- Einstein, A. (1905). {Zur Elektrodynamik bewegter K{ö}rper}. ({German}) [{On} the electrodynamics of moving bodies]. Annalen Der Physik, 322(10), 891–921.
- Available online: https://einsteinpapers.press.princeton.edu/.
- Planck Collaboration, Aghanim, N., Akrami, Y., Ashdown, M., Aumont, J., Baccigalupi, C., Ballardini, M., Banday, A. J., Barreiro, R. B., Bartolo, N., Basak, S., Battye, R., Benabed, K., Bernard, J.-P., Bersanelli, M., Bielewicz, P., Bock, J. J., Bond, J. R., Borrill, J., … Zonca, A. (2018). Planck 2018 results. VI. Cosmological parameters. Available online: http://arxiv.org/abs/1807.06209.
- Guth, A. H. (1981). Inflationary universe: A possible solution to the horizon and flatness problems. Physical Review D, 23(2), 347–356. [CrossRef]
- Higgs, P. W. (1964). Broken Symmetries, Massless Particles, and Gauge Fields. Physics Letters, 12(2), 132–133. [CrossRef]
- Higgs, P. W. (1964). Broken Symmetries and the Masses of Gauge Bosons. Physical Review Letters, 13(16), 508–509. [CrossRef]
- Higgs, P. W. (1966). Spontaneous Symmetry Breakdown without Massless Bosons. Physical Review, 145(4), 1156–1163. [CrossRef]
- Banerjee, S., Danielsson, U., Dibitetto, G., Giri, S., & Schillo, M. (2018). Emergent de Sitter Cosmology from Decaying Anti–deSitter Space. Physical Review Letters, 121(26), 261301. [CrossRef]
- Kaluza, Theodor (1921). “Zum Unitätsproblem in der Physik”. Sitzungsber. Preuss. Akad. Wiss. Berlin. (Math. Phys.): 966–972.
- Klein, Oskar (1926). “Quantentheorie und fünfdimensionale Relativitätstheorie”. Zeitschrift für Physik A. 37 (12): 895–906. [CrossRef]
- Wesson, P. S., Liu, H., & Seahra, S. S. (2000). The big bang as a higher-dimensional shock wave. [CrossRef]
- Wesson, P. S. (2014). The Status of Modern Five-Dimensional Gravity. International Journal of Modern Physics D, 24(1), 1530001. [CrossRef]
- Liko, T., & Wesson, P. S. (2005). The big bang as a phase transition. International Journal of Modern Physics A, 20(10), 2037–2045. [CrossRef]
- Wesson, P. S., & Liu, H. (2001). The cosmological constant problem and Kaluza-Klein theory. International Journal of Modern Physics D, 10(6), 905–912. [CrossRef]
- Seahra, S. S., & Wesson, P. S. (2003). Universes encircling five-dimensional black holes. Journal of Mathematical Physics, 44(12), 5664–5680. [CrossRef]
- Vilenkin A., 1982, Phys. Lett. B 117, 25.
- Prince Rupert’s Drops. (1876). Popular Science Monthly, 8.
- Bochkov, M., Gusenkova, D., Glushkov, E., Zotova, J., & Zhabin, S. N. (2016). Resistive method for measuring the disintegration speed of Prince Rupert’s drops. European Journal of Physics, 37(5). [CrossRef]
- Prince Rupert Drop video -. Available online: https://www.youtube.com/watch?v=xe-f4gokRBs.
- Hebeler, K., Lattimer, J. M., Pethick, C. J., & Schwenk, A. (2013). Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophysical Journal, 773(1). [CrossRef]
- Bedaque, P. F., & Steiner, A. W. (2015). Sound velocity bound and neutron stars. Physical Review Letters, 114(3), 031103. [CrossRef]
- Saha, M. N. (1921). On a Physical Theory of Stellar Spectra. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 99(697), 135–153. [CrossRef]
- Riess, A. G., Filippenko, A. v, Challis, P., Clocchiatti, A., Diercks, A., Garnavich, P. M., Gilliland, R. L., Hogan, C. J., Jha, S., Kirshner, R. P., Leibundgut, B., Phillips, M. M., Reiss, D., Schmidt, B. P., Schommer, R. A., Smith, R. C., Spyromilio, J., Stubbs, C., Suntzeff, N. B., & Tonry, J. (1998). Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant To Appear in the Astronomical Journal. [CrossRef]
- Gaztañaga, E., García-Berro, E., Isern, J., Bravo, E., & Domínguez, I. (2002). Bounds on the possible evolution of the gravitational constant from cosmological type-Ia supernovae. Physical Review D, 65(2). [CrossRef]
- Garcia-Berro, E., Kubyshin, Y., Loren-Aguilar, P., & Isern, J. (2006). The variation of the gravitational constant inferred from the Hubble diagram of type Ia supernovae. International Journal of Modern Physics D, 15(8), 1163–1174. [CrossRef]
- Swaczyna, P., McComas, D. J., Zirnstein, E. J., Sokół, J. M., Elliott, H. A., Bzowski, M., Kubiak, M. A., Richardson, J. D., Kowalska-Leszczynska, I., Stern, S. A., Weaver, H. A., Olkin, C. B., Singer, K. N., Spencer, J. R., Swaczyna, P., McComas, D. J., Zirnstein, E. J., Sokół, J. M., Elliott, H. A., … Spencer, J. R. (2020). Density of Neutral Hydrogen in the Sun’s Interstellar Neighborhood. ApJ, 903(1), 48. [CrossRef]
- Pereira, M. (2024). CMB_HU: Cosmic Microwave Background and assorted Hypergeometrical Universe Notebooks [Code repository]. GitHub. Available online: https://github.com/ny2292000/CMB_HU.
- Pereira, M. (2024). HU_GalaxyPackage: HU_Galaxy Package for Hypergeometrical Universe Theory [Code repository]. GitHub. Available online: https://github.com/ny2292000/HU_GalaxyPackage.
- Pereira, M. (2024). HU_Papers: Collection of Papers on Hypergeometrical Universe Theory [Code repository]. GitHub. Available online: https://github.com/ny2292000/HU_Papers.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).