3.1. Face-Centered Central Composite Design
As the experimental design chosen was the Face-Centered Central Composite, a total of 19 experiments were obtained, including 8 cubic points, 6 axial points, and 5 central points, which were run in random order. The responses evaluated were retention factor (k), tailing factor, and resolution of the critical pairs (Rs) of the three curcuminoids: BMC, DMC, and CUR (a total of 8 responses). These chromatographic parameters are directly affected by experimental conditions and therefore are important in the development of liquid chromatographic methods. The experimental matrix with the measured response values is shown in
Table 2.
The DOE experimental data (
Table 2) were then submitted to regression analysis for the construction of mathematical models that express the relationship between the factors (CMPs) and the responses (CMAs) in the Fusion QbD and Design Expert software. For each response monitored a model was generated, so this study provided eight models. The least squares method (LS) was the used approach in regression analysis for estimating regression coefficients (β). This method is widely employed for modeling data, aiming to determine coefficients by minimizing the sum of the squares of the residuals (SSr) [
20]. The general solution for fitting a least squares model, in matrix notation, is given by
In optimization design or response surface designs, polynomial models are most often built (2), which includes an intercept (β
0), the main effects terms (βi), the interactions terms (βij), and the quadratic terms (βii) [
6]. The complexity of the model depends on the design chosen and the number of factors studied. Therefore, a CCD can generate up to a second-order polynomial or quadratic model and the equation for k factors can be represented by:
Where y represents the experimental response, xi, …, xj, are the factors studied and ε is the random error.
However, usually, not all coefficients are statistically significant, the significant ones can be identified by applying model selection techniques, which will be described in the subsequent sections. Model fitting, model inference, and validation are critical procedures that must be carried out before using the model for interpretation and prediction. Regarding model inference, hypothesis tests may be used to evaluate the utility of the fitted model and the significance of the estimated parameters [
21]. The first step in model inference is to assess the significance of the regression, i.e., to check whether the factors
x influence
y. To do this, a hypothesis test based on the F distribution (F-test) is performed. The appropriate hypothesis for the overall test of model significance is
The null hypothesis (H
0) (3) states that the regression coefficients are equal to zero, which means that a variation in
x does not influence
y. In this case, there is no model relating
y to any
x variable. On the other hand, the alternative hypothesis (H
a) (4) assumes that at least one coefficient is different from zero, indicating that at least one factor has a significant effect on the evaluated response. After postulating the hypotheses, the F-test is used to compare two sources of variation provided by ANOVA, the mean square of the regression (MS
R) and the mean square of the residuals (MS
r) (5). These sources of the variation come from decomposing the sum of the total squares (SS
T) into the sum of the squares of the regression (SS
R) and the sum of the squares of the residuals (SS
r), which can be written as SS
T = SS
R + SS
r. These mean squares are obtained by dividing the sum of the squares by their respective degrees of freedom
(p – 1) and
(n – p) as shown in Equation (5).
where p is the number of parameters in the model and n is the number of experiments.
When the calculated F value (F
0) from equation (5) exceeds the tabulated F value (F
tab) at the desired confidence level, the null hypothesis can be rejected, and the regression is significant. The higher the calculated F value, the more significant the regression. Alternatively, the p-value can also be used for hypothesis testing and reject H
0 if the p-value for the F
0 is lower than the chosen significance level (α = 0.05). This means that the probability of the H
0 being correct is lower than 5%. For example, based on the design with a single solution, the five-parameter BMC retention factor regression model is significant as the F-value = 1825.11 is greater than the Ftab = 3.11 (F-distribution table) and the p-value < 0.05 at a 95% level of confidence (
Table 3). The BMC retention factor model is shown in equation (6). Consequently, the number of degrees of freedom for the model is four (
Table 3), calculated as the number of parameters minus one (p – 1). For the residuals, the number of degrees of freedom is fourteen, as it is calculated by (n – p) the number of experiments (n) minus the number of parameters (p).
After establishing the significance of the regression model through the F-test or p-value, the next step is to evaluate the explanatory power of the model, using the coefficient of multiple determination (R²) parameter as a metric. The R² is used to assess the model's overall adequacy which shows how much of the variation related to the response can be explained by the coefficients (7)
The closer the R² values are to 1, the higher the amount of experimental variation of the response that is described by the model. However, a high R² value does not always indicate that the regression model is adequate for its intended use. Adding a new coefficient to the model will increase the R² value regardless of whether it is statistically significant or not. Thus, the adjusted R² (R
2adj) and the predicted R
2 (R
2pred) can be used to obtain additional information on the explanatory power of the regression model [
22]. The adjusted R² indicates the percentage of variation explained by the significant coefficients (8) [
23], this means that the adjusted R² only increases when the added coefficient improves the model and decreases if the added coefficient does not improve the model or if the improvement is lower than expected [
24].
where
p is the number of parameters in the model.
The predicted R² indicates the predictive capability of the regression model and can be computed by equation (9) which involves the Predicted Residual Sum of Squares for the model (PRESS) (10)
Where
e-i is the residual calculated by fitting a model without the
i-th run and then predicting the
i-th observation using the resulting model.
As shown in
Table 4, the models with the higher number of coefficients, including the non-significant ones have the highest R² values. However, the predicted R² for the model with ten coefficients (0.9736) is lower than that for the model with five coefficients (0.9925), indicating the superior predictive capacity of the model with fewer coefficients. This aligns with the model obtained for the BMC retention factor, with 5 parameters. When choosing the most suitable model, it is important to consider the concept of parsimony, favoring simpler models with fewer coefficients over complex models when they fit the data similarly. As a result, models with high R
2 values may produce inaccurate predictions of future observations or estimates of the mean response, i.e., smaller predicted R
2 values due to model overfitting [
24]. This happens because non-significant coefficients are actually describing random variation, which is not reproducible in future predictions. Ideally, a model should have both high R² and high predicted R², which suggests that the model not only explains the data well but also has the potential to make accurate predictions in future observations.
Furthermore, when the R² and the adjusted R² diverge more than 0.2, non-significant terms have likely been included in the model [
25]. Thus, by considering both R² and predicted R² along with adjusted R², a more complete evaluation of the regression model can be performed, ensuring that it not only explains the data well but also has the potential to make accurate predictions in future observations.
3.2. Model Selection
Using a model selection technique helps evaluate and compare possible model coefficients. Several methods have been developed to assess small subsets of regression models by adding or removing a single coefficient at a time. These methods are generally called stepwise procedures and can be classified into forward selection, backward elimination, and stepwise regression [
20].
Forward selection starts by including only the intercept as a coefficient in the model. The coefficients are included in the model one at a time until the optimal subset is found. The first coefficient to be selected for the model is the one with the largest simple correlation with the response, and it also provides the largest statistic to test the significance of the regression. The model will include the coefficient if the F-statistic is greater than the preselected F value, also called F
IN or F-to-enter (F-to-add in Fusion QbD). The next coefficient chosen for inclusion in the model will be the one with the highest correlation after adjusting for the effect of the first coefficient added to the response. This procedure will continue until the partial F-statistic (12) at a certain step is smaller than the F
IN or until the last coefficient is added to the model [
20,
26].
Where SSRp is the sum of squares for the complete model, and SSRp-1 is the sum of squares for the model with the coefficients removed. This partial F-statistic (F-ratio) is similar to the F-value calculated in the regression significance phase. However, in this case, MSR is obtained from a partial sum of squares, and MSr comes from the full model with all parameters (SSEp). The terms (p – 1) and (n – p) are the degrees of freedom of the MSR and MSr, respectively.
Some software, such as Fusion QbD, can also report the t-statistic for adding or removing a variable because it can be considered a variation of the F-statistic, given that t
2α/2,υ = F
α,1,υ [
26]. Where
α is the significance level and
υ is the degrees of freedom.
Conversely, backward elimination seeks to find the best-fitting model from the full model, including all K candidate factors. Then the partial statistical F is calculated for each regressor as if it were the last variable to enter the model and the smallest F value is compared to the preselected F
OUT (or F-to-Remove in Fusion QbD). Suppose F-ratio < F
OUT, the regressor is removed from the model. This procedure is then repeated for a regression model with K-1 regressors. The backward elimination algorithm terminates when the smallest partial value F-ratio > F
OUT. Stepwise regression is a modification of the forward selection procedure, where at every step all the coefficients that entered the model are reevaluated by their partial F-tests or t-tests. Stepwise regression, therefore, requires two cut-off values, F
IN and F
OUT. The choice of the F
IN/OUT cut-off value can be conceived as a stopping rule for the above procedures [
27].
In Fusion QbD, data analysis can be performed through the model regression (Stepwise Regression) with the options Backward Elimination - Design Model and Extended Model, Forward Selection, or Combined. All of these regression modes use the F to Add/Remove to select the model coefficients with the default value of F to Add/Remove being equal to 4, which corresponds to a 5% in the F-distribution and is equivalent to a probability p-value of 0.05 used in a t-test [
26].
Design Expert also uses model selection using stepwise regression in both forward and backward modes, which are performed in the same way as in Fusion QbD. However, the criteria used in Design Expert are the p-value and the adjusted R². In addition, the Design Expert provides options for selecting model terms based on information theory, demonstrating the relationship between likelihood and the amount of information lost when approximating the data with a model. Design Expert has two algorithms for model selection, the corrected Akaike's Information Criterion (AICc), which provides an estimate of the information lost when a specific model is used to represent the process that generated the data, i.e., the best model will be the one that approximates the data with the least loss of information and is best for small designs. Mathematically, the AICc is calculated by the equation
where
p is the number of terms in the model including the intercept, random effects, and fixed effects,
n is the number of lines in the plan and the term (L[M│Data]) is the model fit measure, the larger this term is the better the fit.
Bayesian Information Criterion (BIC) is another algorithm option in Design Expert and is similar to AICc but tends to favor models with fewer parameters. The equation 14 expresses BIC:
The smaller AICc or BIC values represent a parsimonious model with a higher quality of fit. Thus, for model selection of the responses, the p-value (backward mode and α=0.05) in Design Expert and the backward elimination-design model option (F=4.0) in Fusion QbD were used as selection criteria.
Table 5 shows that the selected model factors for BMC retention factor were quite similar for both software. However, since the Fusion QbD selection criterion is not based only on the p-value but considers that the F
0 value must be greater than 4, the AC term was included in the model since it had an F
0 = 4.069. This value is very close to 4 and, considering the AC p-value = 0.0648, this coefficient should be removed from the model. A confidence interval (CI) at a 95% level of confidence can also be used to establish whether a coefficient is significant. If the CI passes through zero, that is, one of the limits is positive and the other is negative. The coefficient may be zero indicating that the coefficient is not significant. As seen in
Table 5, the confidence interval of the AC term includes zero and agrees with the p-value that this coefficient is not significant and should be removed from the model.
Another difference observed in
Table 5 is that Fusion QbD does not include the term A, unlike Design Expert, which retains it to maintain model hierarchy. Non-hierarchical models, like the one suggested by Fusion QbD, are advantageous in optimization-focused experiments because excluding non-significant terms reduces model variance, resulting in narrower confidence intervals for the mean response. On the other hand, the principle of hierarchy dictates that if an interaction term is included, its main effects must also be included, even if their p-values are not significant [
28].
While hierarchical models retain non-significant terms, which can increase prediction variance, this often leads to wider confidence intervals, particularly when the inclusion of non-significant terms increases the residual mean square (MSr). In optimization studies, preserving hierarchy can yield an inferior model because it affects the empirical response surface and predicted values, both of which are critical for optimization. Therefore, when the primary goal is prediction, model parsimony becomes more important [
20,
29]. Since the AC interaction really is non-significant and will be removed from the model, this content will not be further developed. For more information on hierarchical and non-hierarchical models and their implications, see [
20,
28,
29,
30,
31].
3.4. Residual Analysis and Diagnostic Plots
The t and F-statistics, as well as R², reflect global model properties and the evaluation of only these parameters does not guarantee that the model is adequate. In general, examining the model fit is essential to ensure that it provides an acceptable approximation of the true system and that none of the least squares regression assumptions are violated [
32].
Residual analysis is the basis of most diagnostic procedures to detect failures of basic assumptions of the regression model [
7,
20]. Normality, homoscedasticity, and independence are the major assumptions about the residuals that need to be verified. It is also useful for identifying concerning data points by leverage and influence point analysis. The residuals are defined as the difference between the observed (y
i) and the estimated value by the model
Thus, the residuals are a measure of the variability in the response variable that the regression model does not describe, and the analysis of the residual plots is also a key step in evaluating the model adequacy and is an effective way to determine how well the regression model is adjusted to the data [
20]. To build these plots, scaled residuals (Externally and Internally Studentized Residuals, Standardized Residuals, or Residuals, ...) are used to aid the visualization of points [
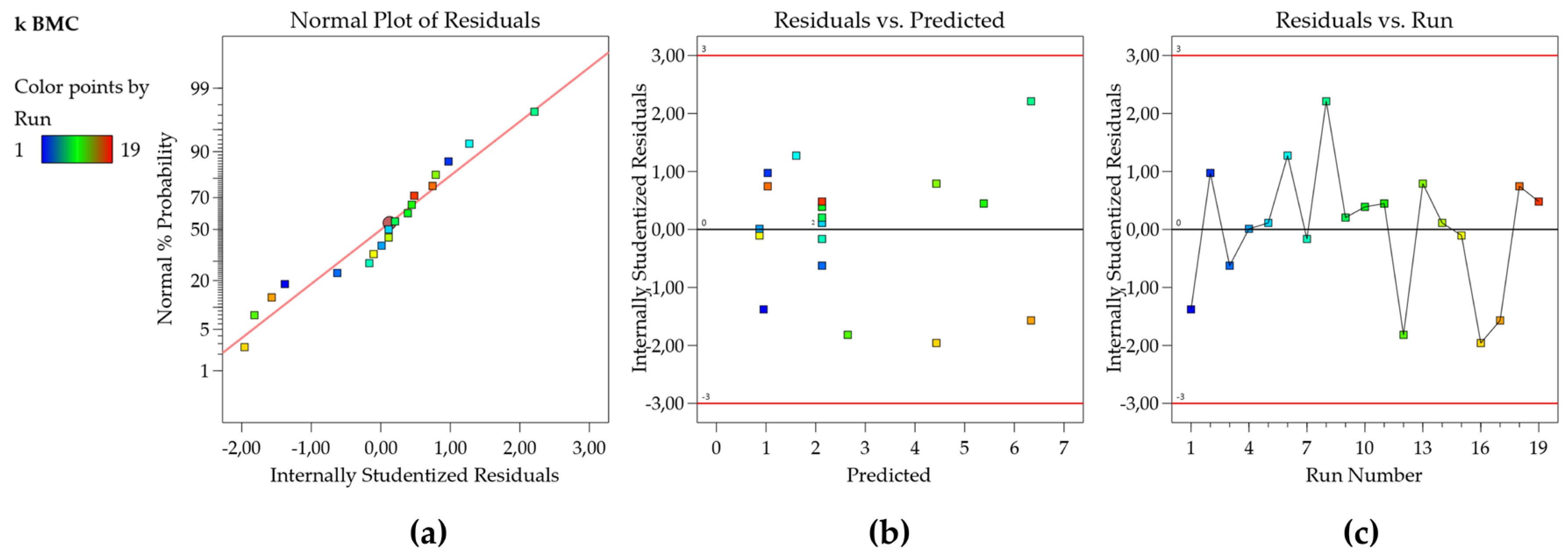
33]. The F and t statistics, along with confidence and prediction intervals, all rely on the assumption that the residuals have a normal distribution. To check this assumption, a normal probability plot of the residuals is used to visualize if the residuals follow a straight line with emphasis on the central values, as seen in
Figure 1a. Some scattering is expected even for Normal data (represented by a soft ‘S-shaped’ curve) but the presence of defined patterns such as a strongly well-defined S-shaped curve suggests that the response needs to be transformed to improve the model fit [
33].
The plot of residuals as a function of the predicted response values is used to test the assumption of constant variance (homoscedasticity). The plot should present a random scatter, which means, a constant range of the residuals across the graph (
Figure 1b) [
33]. If the scatter expands following a ‘megaphone pattern’, this suggests that the data may need a transformation, or the range of experimental design should be decreased. The independence (uncorrelation) of the residuals can be verified using the plot of the residuals as a function of the experiment run order. This plot should present a random pattern, indicating that there is no influence of an external factor or an error during the execution of the experiment (
Figure 1c) [
33]. Also, in
Figure 1b,c, the points should be within the limits ± 2 studentized residuals (residuals/regression standard deviation) for a 95% confidence level (Fusion QbD default) and ± 3 studentized residues for a 99,7% confidence level 99,7% (Design Expert default). Points outside or near these boundaries should be checked as possible outliers (transcription errors should be verified and a new experiment carried out, if possible). The external standardized residuals present a similar metric; however, the residuals are calculated using a model where the point was not included [
34], therefore they are more sensitive to outliers.
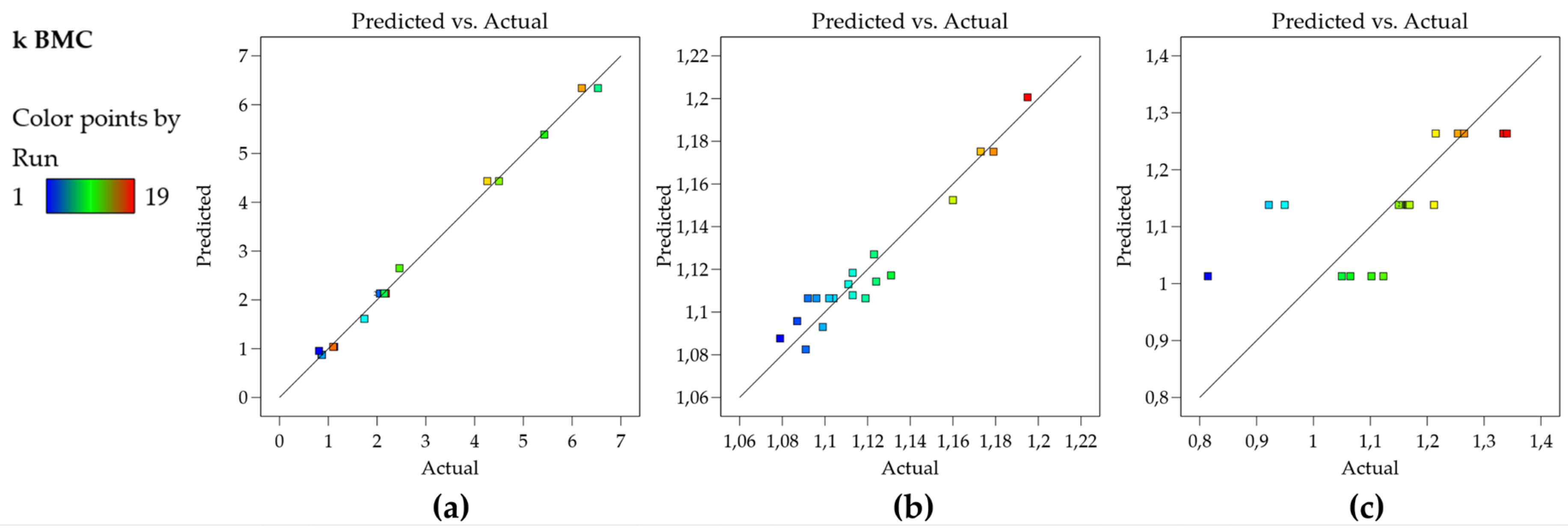
The residual plots have shown normality, homoscedasticity, and independence, indicating that the model is appropriate to describe the experimental responses obtained. Finally, the plot of observed versus predicted values is very useful as a diagnostic for model prediction capability [
35]. In
Figure 2a, the plot shows that the residuals are close to the straight line, which means that the predicted values are in good agreement with the experimental values, therefore, the model for the k BMC can be used for prediction.
Figure 2b,c bring graphs for other data sets for an illustrative purpose.
Figure 2b shows residuals of a model that presents R
2 of 0.938 and still presents a good predictive capability (there is no indication of lack of fit, but rather the experimental error is high, therefore cannot be described by the model which leaves higher residuals than the ones shown in
Figure 2a).
Figure 2c shows an inadequate model (R
2 of 0.48) and a poor prediction capability observe that for a broad range of the experimental data, the predicted value is the same, therefore the corresponding model cannot be used either for prediction or the construction of Design Space/MODR.
Other residual graphs that should be analyzed are influential plots such as Leverage and Cook’s distance, due to their ability to detect influential points—data points that significantly impact the regression coefficients and predictions. Even though influential points significantly impact the regression results, they are not necessarily outliers and they can be identified by assessing both leverage and the residuals graphs. Leverage measures how far an individual predictor value deviates from the mean of the predictor values, points with high leverage have a greater potential to affect the regression model’s estimates [
20,
36]. For instance, a single influential point with high leverage and a large residual can alter the slope and intercept of the regression line, leading to misleading conclusions. Leverage is calculated using the hat matrix, denoted as
H. For a given data point
i, leverage
hi is derived from the diagonal elements of this matrix (17) [
20,
34].
Specifically,
H is obtained as:
Where X is the design matrix, with a row for each execution in the project (n) and a column for each term in the model (p).
Leverage values range from 0 to 1, with higher values indicating that the corresponding data point has a greater potential to influence the regression model’s parameter estimates. Points with leverage substantially larger than the average leverage (
), are considered high leverage points and require closer examination [
34,
36].
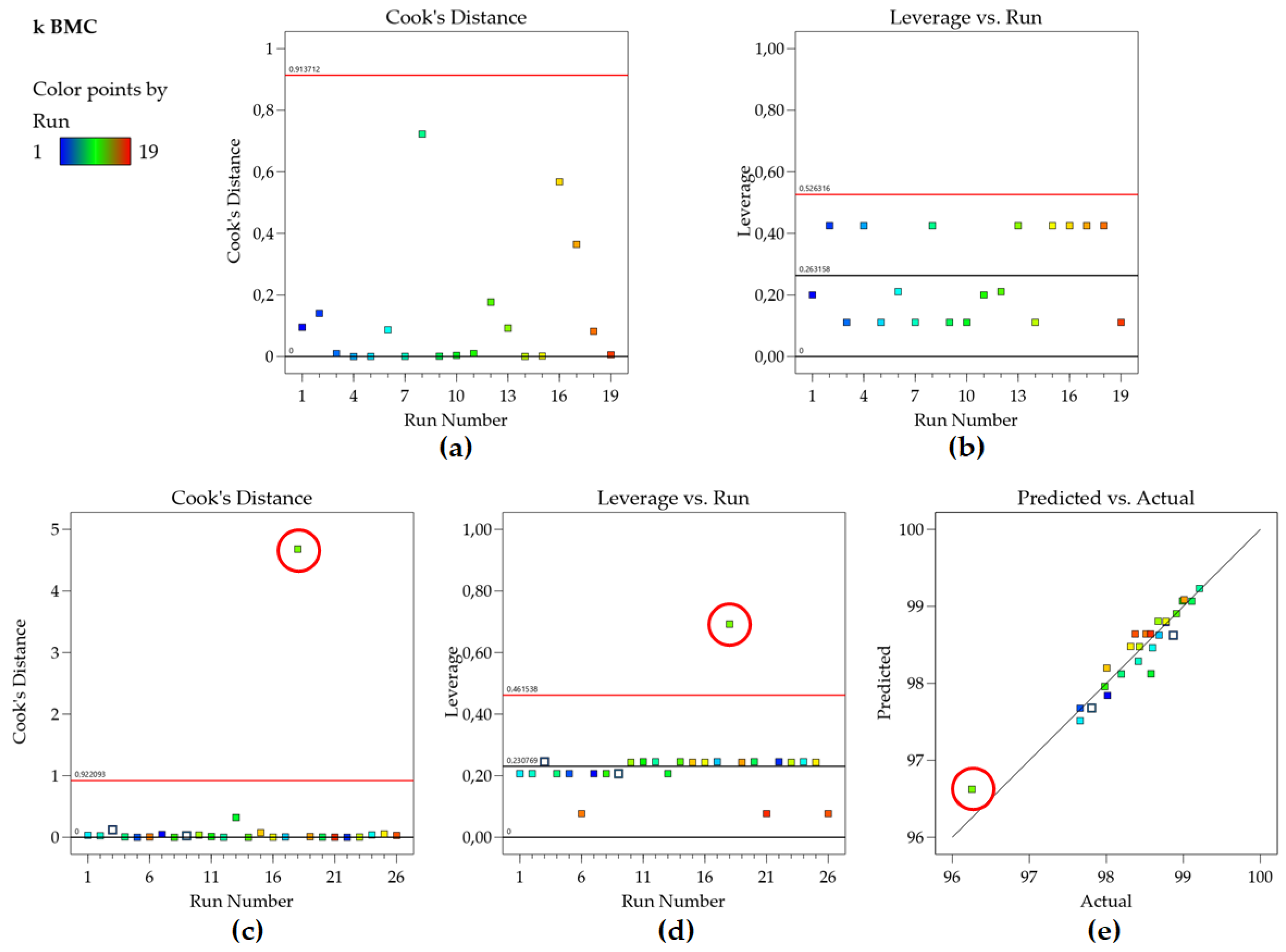
Figure 2B shows that no point in the k BMC model has high leverage since all points are located below the calculated average leverage value (red line).
Cook’s Distance (D
i,) described by equation (19) is another important diagnostic that combines the information from leverage and residuals to quantify the influence of each data point on the fitted regression model [
36]. Cook’s Distance is a summary of how much a regression model changes when the ith observation is removed.
Cook’s Distance plot visually represents this influence, where points with a large Cook’s Distance value (typically greater than 1) are considered influential and may have a negative impact on the model’s predictions [
34]. Evaluating the Cook’s Distance graph for the retention factor of BMC (
Figure 3a) confirms this, as no point exceeds the calculated threshold. Therefore, no outlier or influential point is present in the data set. Identifying such points is crucial for ensuring the robustness and reliability of the regression model, as influential points can distort the model’s outcomes and lead to misleading conclusions.
Attention should be paid not to exclude a given point with high Cook’s Distance interpreting it as an outlier, when it is actually a high leverage point but that is well described by the model, as shown in
Figure 3 c–e (another data set of our group). Another metric sometimes used is DFFITS, and although the raw values resulting from the equations are different, Cook’s distance and DFFITS are conceptually identical and there is a closed-form formula to convert one value to the other [
34,
36].
All eight models, equation (3) and equations (20 – 26), obtained in this study went through all the evaluation steps described so far. The ANOVA tables, fit statistics, and residual plots for these models are available in the supplementary material.
3.6. MODR Construction
From DOE-derived models, knowledge is acquired, allowing access to a region where the behavior of analytical responses and method performance can be understood based on variations in the analytical parameters [
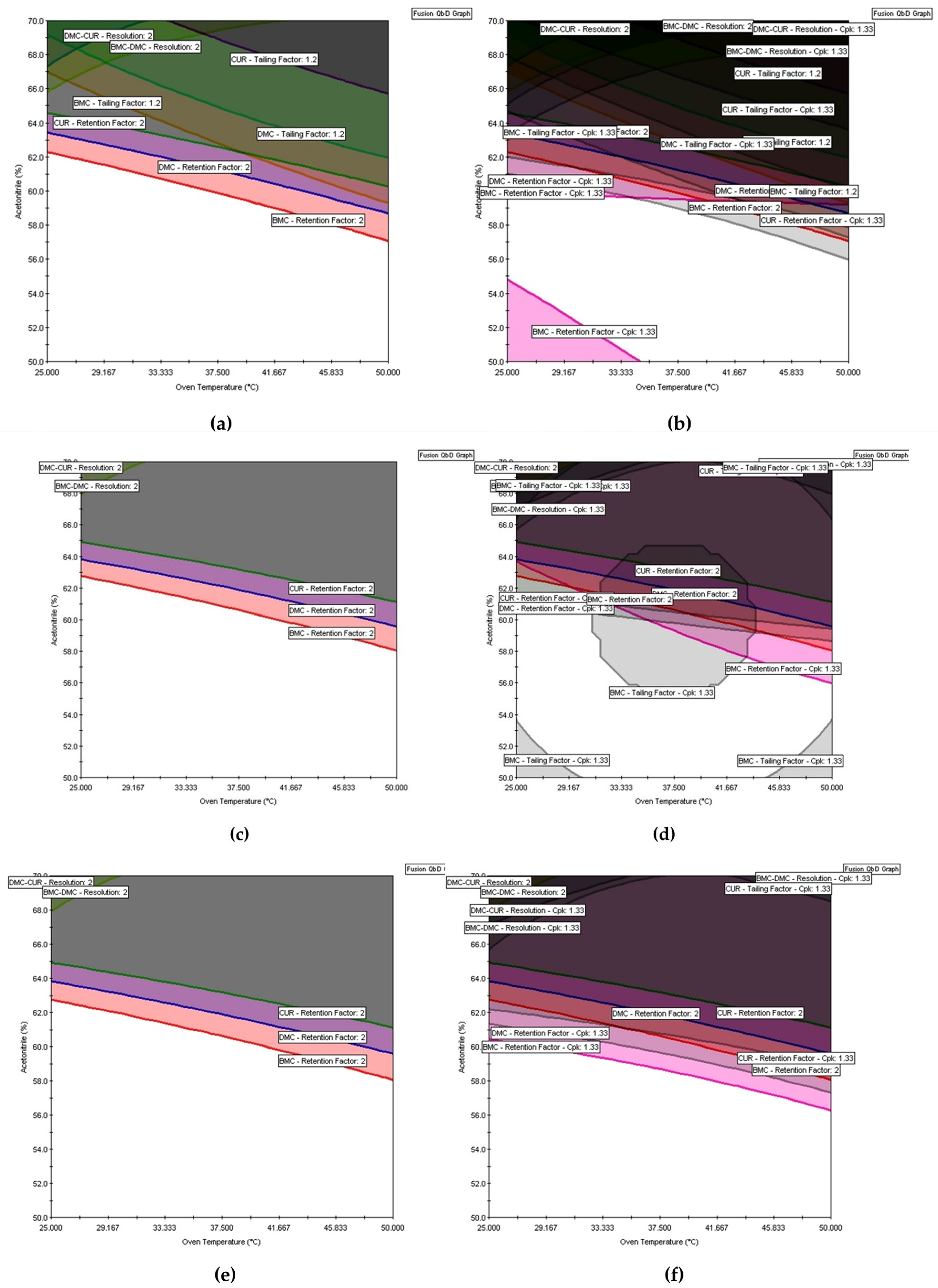
8]. This region, known as the knowledge space, is confined to the experimental domain in the context of empirical models. In
Figure 4 and
Figure 5, the knowledge space is represented by the entire region of the graph. Within the knowledge space, areas where analytical parameters and their ranges fail to meet specifications, termed as the “non-acceptable performance region,” and areas where mean responses meet specifications, referred to as the “acceptable mean performance region” can be identified [
9].
Multiple response optimization tools are used to find the acceptable mean performance region when several responses are studied simultaneously. There are two primary methods for multiple response optimization. The first is graphical optimization, often referred to as overlay graphs, where the contour plots of each response model are superimposed to estimate the region of intersection, thereby providing a region of optimal conditions or an acceptable performance region. The second method is based on the desirability functions (often called ‘numeric optimization’ or Derringer and Suich desirability) [
10]. Initially, individual desirability functions di(ŷi) for each ŷi must be created using fitted models and establishing the optimization criteria. Desirability values always range from 0 to 1, with desirability equal to zero representing an undesired response and di(ŷi) = 1 for the optimal response. Desirability functions can be customized to suit the chosen optimization criteria. These criteria typically fall into the following categories:
Maximize: The objective is to elevate the response variable to its maximum potential. Desirability increases as the response approaches its highest value.
Minimize: This criterion minimizes the response variable, striving for the lowest achievable value. Desirability increases as the response approaches its minimum value.
Target: The focus is on achieving a specific target value for the response variable. Desirability decreases as the response deviates from this target, emphasizing alignment with the desired outcome.
In range: which specifies a range (lower limit - upper limit) for acceptable results.
Cpk: the process capability index, which calculates the number of standard errors of the predicted response that are within the specification limits.
By tailoring desirability functions according to these criteria, the optimization process can effectively pursue the desired objectives for the analytical method. Once all n variables are transformed into desirability functions, they are combined into a single function called overall desirability (D), employed to discover the best combinations of responses. In mathematical terms, the overall desirability is given by the geometric mean of the n individual desirability shown by equation (27) [
10]
In Design Expert, Graphical and Numerical (desirability) optimizations are available, whereas Fusion QbD uses only desirability to find the best overall answer. In Design Expert, the graphical optimization criteria are defined by the values specified by the analyst for the lower and upper limits, or sometimes just one of these limits.
All eight models (3, 20 – 26) were used to find the acceptable mean performance region. In Fusion QbD the responses k BMC, k DMC, and k CUR were maximized with a lower bond of 2 in order to provide adequate retention. To ensure that the peaks were symmetrical, the Tailing BMC, Tailing DMC, and Tailing CUR responses were minimized with the upper bound equal to 1.2. To ensure that adjacent peaks have adequate separation and avoid coelution, the response Rs (BMC, DMC) and Rs (DMC, CUR) were maximized with a lower bound equal to 2. The same criteria were adopted for graphical optimization in Design Expert. The results of the multiple response optimization are shown in Figures 5a and 6a.
In
Figure 5a of Fusion QbD, the white regions indicate areas of acceptable mean performance, while the colored regions denote areas of non-acceptable mean performance. Similarly, in Design Expert’s graphical optimization shown in
Figure 6a, the bright-yellow regions imply acceptable mean performance, and the grey regions indicate unacceptable performance. However, like the mean response surfaces, these regions only represent the average performance and do not guarantee that the method will meet the requirements of its intended use. Furthermore, these regions cannot be referred to MODR because according to GC USP <1220>, MODR is defined as a “multivariate space of analytical procedure parameters that ensure the ATP is fulfilled and therefore provide assurance of the quality of the measured value” [
3]. Moreover, the MODR should ensure quality, which implies that it should represent a robust region as described in ICH Q14 [
37]. Therefore, the design of MODR should incorporate the method uncertainties to determine whether the analytical procedure will assure quality. If a method is robust “on average” but exhibits excessive variation, it may fail to meet its robustness criteria [
26]. Robustness incorporation includes estimating the variability of analytical measurements related to the CMAs. Also, each source of error is identified to increase analytical performance by reducing the variability associated with the analytical parameters.
Fusion QbD uses Monte Carlo simulations to include the measurement uncertainty of model parameters and estimate the probability of meeting CMA specifications. To start the simulations, the maximum expected variation (± 3σ value) of each CMP must be entered. Then, the robustness indices should be selected, and the lower and upper specification limits (LSL and ULS, respectively) (26) defined for each CMA. These specification limits represent the MODR boundaries for each response and are also known as Edges of Failure. In Fusion QbD, process capability indices such as C
p, C
pk, C
pm, and C
pkm are implemented as robustness capability metrics to quantify system robustness [
26]. These are standard Statistical Process Control (SPC) metrics widely used to quantify and evaluate method variation in critical quality and performance characteristics. The C
p index measures the potential capability of a process and is used when the response has a specified maximum allowable variation and symmetrical upper and lower specification limits (USL and LSL). It can be calculated as
where 6σ represents the inherent variation in the average response value, constrained within the limits of a 3σ confidence interval. The C
pk index measures the actual capability of a process accounting for how centered the process is between the specification limits. If the goal of the response is to maximize, only the LSL is established (29). If the objective is to minimize, then only the USL is established (30).
The C
pm index is used when the response has a target value, and the specification limits are symmetrical (31). When the specification limits are asymmetrical the C
pkmindex is used (32)
A Cp = 1.00 indicates that the process variation exactly matches the specification limits, meaning the process spread (±3σ) is equal to the distance between the upper and lower specification limits (USL and LSL). This implies that approximately 99.7% of the process output falls within the specified limits, but it also suggests there is no room for error or drift in the process mean. When Cp = 1.33, the specification limits are four standard deviations (±4σ) away from the process mean, compared to three standard deviations in the case of Cp = 1.00. This allows for greater assurance that the process outputs will remain within the specified limits, even if there are minor variations or shifts in the process. This value suggests that approximately 99.99% of the process output will meet the specified limits A Cp = 2.00 reflects an exceptionally capable process, where the process spread is only half of the specification range. This indicates that almost all output will be within the specification limits, demonstrating a highly robust and reliable process with substantial tolerance for variations in process parameters [
38]. Higher Cp values, therefore, indicate better process capability and reduced risk of producing out-of-specification products. Subsequently, the Monte Carlo simulations method begins by modeling the system, including input factors CMAs and their variability, characterized by probability distributions. The simulation generates numerous sets of input values through random sampling, each representing a possible scenario. The model calculates the corresponding analytical response for each set, repeating this process thousands to millions of times to produce a distribution of outcomes. This distribution reflects the combined measurement uncertainty of the analytical response, accounting for the variability of all input factors. By analyzing the outcomes, Monte Carlo simulations estimate the likelihood that the analytical method meets specified performance criteria under different conditions.
The desired levels of robustness for each study factor computed for the MU estimation were inserted as (A) flow rate ± 0.024 mL/min, (B) % of organic solvent in the mobile phase ±1.5%, and (C) column temperature ± 1.5 °C. The Cpk was the robustness index chosen for all responses. For the k BMC, k DMC, and k CUR responses, the goal was to maximize and the Cp, lower was calculated by setting up the LSL at 2.00 so the compounds have a minimal retention factor of 2. To obtain symmetrical peaks for all compounds, the Tailing responses were minimized and the Cp, upper was calculated setting the ULS of 1.2. For adequate separation of the critical pairs, the Rs (BMC, DMC) and Rs (DMC, CUR) responses were maximized and Cp, lowerwas calculated by setting up the LSL at 2.00. In this study, the risk control strategy involved selecting conditions that achieve Cpk≥ 1.33 for all the responses.
Figure 5b,d,f show that after the robustness assessment using Monte Carlo simulations and the insertion of uncertainties into the MODR, the white region is smaller than that obtained without the robustness assessment. It is also possible to see how authentic replicates impact the MODR by comparing
Figure 5a,b (results of the DOE without authentic replicates) to
Figure 5e,f (results of the DOE with authentic replicates for all the runs). The importance of selecting the models that will be used to build the MODR can also be demonstrated. In
Figure 5c,d, for example, the plots were constructed based on the DOE with authentic replicates using the value of F= 4, which resulted in the inclusion of a non-significant term in the Tailing BMC model with, as explained in the model selection section. When removing this term by increasing the F value to 5, the MODR changes again (
Figure 5e,f).
On the other hand, Design Expert uses the Propagation of Error (POE) method to identify factor settings that minimize the variation transmitted to a response from factors that are not fully controllable, thereby making the process more robust to input variations. This approach involves applying partial derivatives to locate flat areas on the response surface, which are less sensitive to variations. POE methods require a second-order hierarchical response surface model and estimated standard deviations for the numeric factors. These standard deviations can be inputted for all factors on the Column Info Sheet or individually by selecting specific columns or cells and adjusting them in the Design Properties tool. The same uncertainty values used in Fusion QbD were applied in Design Expert. Using this information, the software constructs a response surface map that shows how factor variations affect each response. By employing multiple response optimization, including objectives to minimize the POE, optimal factor settings can be determined to achieve desired response goals with minimal variation [
11]. Robustness assessment in Design Expert utilizes interval estimation to quantify variability and uncertainty in CMAs and CMPs. Interval estimates, including confidence, prediction, and tolerance intervals, can be added to graphical optimization plots (
Figure 6) by selecting the "Show Interval" box and specifying the type and confidence level [
39]
. Unlike confidence intervals (CI) [
40], which quantify the uncertainty of an estimated population variable (such as the mean or standard deviation), prediction and tolerance intervals address the uncertainty of future observations. A CI provides a range that is likely to contain the unknown population value, indicating the precision of a sample estimate (33). Therefore, it is worth emphasizing that the use of CI is not recommended for evaluating robustness.
Where SE is the standard error of the design at x0 and x0 is the expanded point vector. In a predictive model, the expanded point vector is a list of values and their interactions and is a way to represent the settings of the factors for a particular location for purposes of prediction. It can be seen as a single-row matrix, with one element for every term in the model, it resembles a row of the expanded model matrix (X). The elements of the point vector and the terms represented by the model matrix's columns must be in the same order. At last, s is the estimated standard deviation.
In contrast, a prediction interval (PI) [
40] accounts for both the uncertainty in estimating the population mean and the random variation of individual values, thus offering a range within which the average of a future sample is expected to fall (35).
Being SEpred the predicted error for one future response measurement at x0.
Consequently, PIs are always wider than Cs (
Figure 6b,c). Tolerance intervals (TI) [
40] are even broader, as they include a specified proportion of all individual outcomes, accounting for observed and unobserved variability within the population (
Figure 6d). In mathematical terms, TI is represented as
Where p is the number of terms in the model, P the proportion of the population contained in the tolerance interval, φ is the inverse normal function to convert the proportion to a normal score and X
2 is the chi-square critical value [
40]
Estimating prediction and tolerance intervals is crucial for evaluating total analytical error (TAE) and assessing robustness in the Analytical Quality by Design (AQbD) framework. For robustness studies and procedure qualification in the AQbD framework, determining the range where future response values are likely to be found is critical for proper risk assessment. Using wider prediction and tolerance intervals can more accurately resolve this issue. In contrast, confidence intervals are less suitable for quantifying uncertainty in future observations and may not adequately support the design of the MODR [
9]. By incorporating interval estimates, the graphical optimization (
Figure 5) becomes a more powerful tool for visualizing and managing the uncertainty associated with process optimization, thereby enhancing decision-making and process robustness. As shown in
Figure 6, the pale yellow represents the region where the point estimate fulfills the criteria requirements but a portion of its interval estimate does not. This region becomes wider when moving from CI (
Figure 6b) to PI (
Figure 6c) and TI (
Figure 6d).
Despite the differences in the software calculations and insertion of uncertainties, the regions delimited as MODR in Design Expert (
Figure 6d) and Fusion QbD (
Figure 5f) were the same. Once the MODR has been established, verification runs can be carried out to evaluate performance and provide additional evidence that the MODR is valid. Since the MODR is an irregular and multidimensional space, validating or qualifying the entire MODR can be challenging. Therefore, selecting a portion of the MODR for the verification runs is often practical. Fusion QbD verification runs can be performed by inserting the proven acceptable range (PARs), a rectangle added to the overlay graph within the MODR [
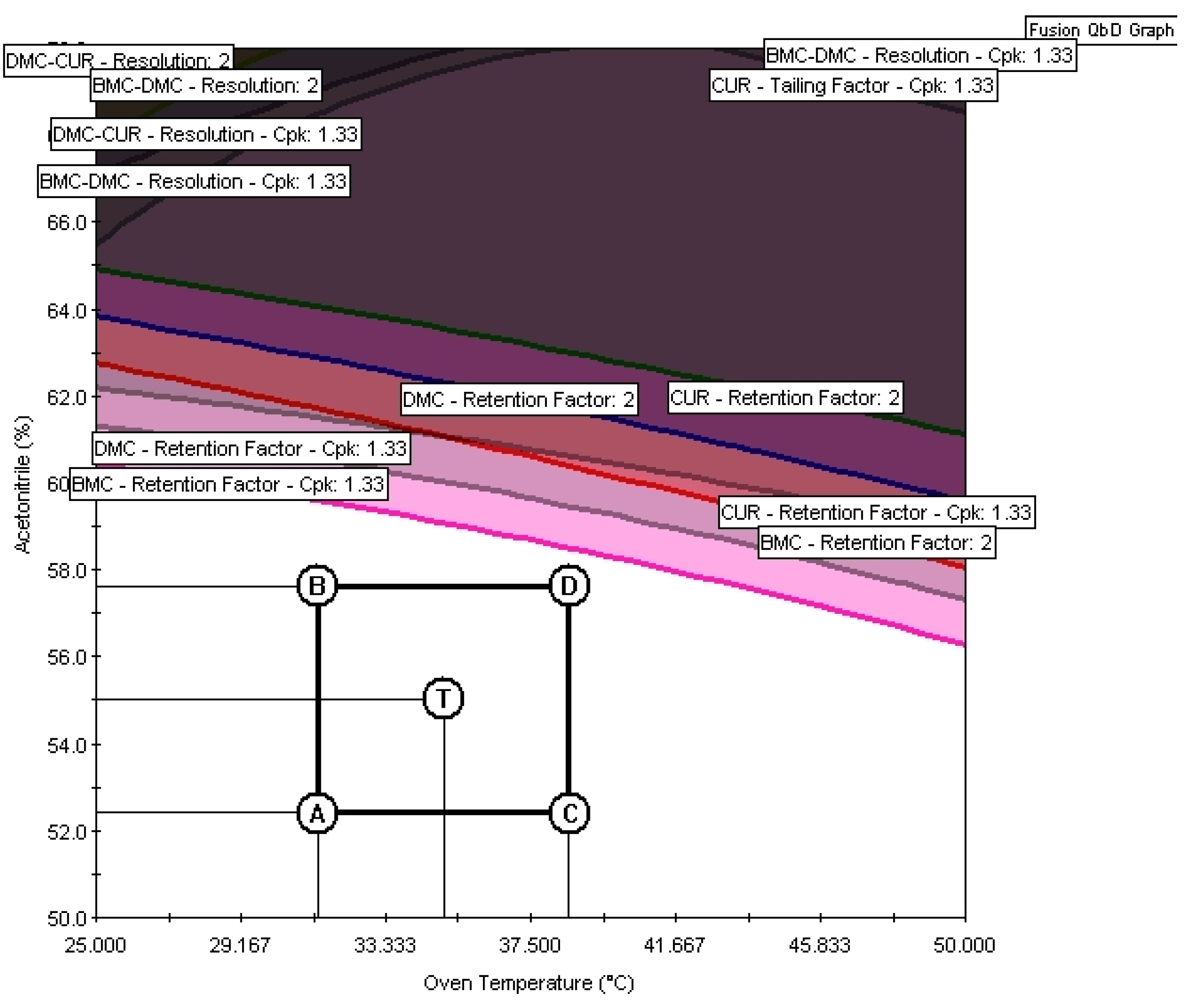
26], as shown in
Figure 7.
The conditions chosen for method validation were a flow rate of 0.825 ml min
-1, a temperature of 35° C, and 55 % acetonitrile in the mobile phase, represented by point T in
Figure 7. To check the method's performance, the predicted values of the evaluated responses were compared with the experimental ones (
Table 9).
The Fusion QbD provides the predicted value and a corresponding lower and upper limit of the 2-sigma confidence interval. According to
Table 9, all the experimental results were close to the predicted value and within the 2-sigma confidence interval, ensuring that under these conditions the method meets the quality performance requirements.
It is important to note that if verification runs were conducted after a prolonged time of column use of the column, the experimental values may deviate from the predicted values due to column degradation and a loss of separation efficiency. This is illustrated in
Table 10, where verification runs were performed after a prolonged time of column use. While the retention factor values remained close to the predicted ones and within the confidence interval, the tailing factor values were higher than the predicted, and the resolution values were lower. This indicates a decrease in the column’s efficiency.
In this way, the experimental results must be compared to the acceptance criteria of the CMAs. In this case, the acceptance criteria for the resolution between the critical pairs are met since the resolution values in
Table 10 are greater than 2 at all points. However, the experimental results for tailing are at or slightly above the acceptance criterion of tailing less than 1.2. Although the tailing values are slightly above the acceptance criterion, the resolution values above 2 guarantee the separation of the compounds.