A System of Tensor Equations over the Dual Split Quaternion Algebra with an Application

1. Introduction

Irish mathematician W.R. Hamilton pioneered the related research about the concept of quaternions in 1843 [1]. There has been a rapid development in quaternions during recent years. There exist various kinds of related work about quaternions that achieve valuable results [2,3]. Most recently, researchers focus on the theories of solving quaternion matrix equations, i.e., general and special solutions of quaternion matrix equations [4]. Quaternions and quaternion matrices have been comprehensively applied to multiple areas including algebra, analysis, topology, and physics. In particular, they are crucial in several fields, such as signal processing [5], image processing [6], and quantum physics [7].

In 1849, building upon Hamilton’s work, James Cockle further introduced "split quaternions" [8]. The set of split quaternions is denoted as:

$$\begin{array}{c}\hfill {\mathbb{H}}_S=\{q=q_0+q_{1}i+q_{2}j+q_{3}k:q_0,q_1,q_2,q_3\in \mathbb{R}\},\end{array}$$

where

$$\begin{array}{c}\hfill i^2=-j^2=-k^2=-1,ij=-ji=k,jk=-kj=-i,ki=-ik=j.\end{array}$$

As a derivative version of quaternions, its form is similar to the original definition of quaternions, but they are indeed two different algebras. The definition proposed by James Cockle has a more complex algebraic structure. Split quaternions play a significant role in various fields, e.g., physics, quantum mechanics, signal processing, and deep learning. Split quaternions have been applied to denote Lorentz rotations, and Lorentz transformations can be represented as $2\times 2$ unitary matrices of split quaternions, which reveals the geometric and physical importance of split quaternions [10,11,12,13,14,38,39].

Clifford [42] later proposed dual numbers and dual quaternions in 1873 and they have already become the basis of handling some typical engineering problems [15]. Dual split quaternions, like dual quaternions, expand the idea of dual numbers to include split quaternions. Building on the principles of split quaternions, dual split quaternions have been applied to diverse disciplines including algebra, geometry, and physics [9,16,17,18].

Below is a typical matrix equation system that this paper mainly focuses on. There exists some related work providing solutions to it, while this paper will explore this equation system defined in the domain of dual split quaternion tensor.

$$\left\{\begin{array}{c}AX=B,\hfill \\ XC=D.\hfill \end{array}\right.$$

(1)

Due to its wide applications in fields such as biology, inverse problems in vibration theory and linear programming, system (1) has been extensively studied. Rao and Mitra [19] established the criteria for the solvability of the system (1). They also presented their general solutions. Khatri and Mitra [20] examined their Hermitian solutions within the complex field. Wang [21] derived conditions for solvability and provided solutions for bi-symmetric cases of system (1) in the quaternion skew field. Li and others [22] examined generalized reflexive solutions for complex system (1). Yuan [23] used spectral decomposition to investigate least squares solutions for system (1). Xie [24] applied the M-P inverse as well as the rank of quaternion matrices to determine the equivalent conditions when there exist solutions and then propose the general solution. Si and others [39] used real representations to establish various solutions of system (1) and their equivalent conditions over split quaternion field.

It is revealed that tensors are useful in engineering and science, and there are some papers focusing on the solutions of tensor equations [25,26,27,28,29,35]. Based on the extensive applications of tensors, this paper focuses on solving system (1) defined on the space of dual split quaternion tensors. To the best of our knowledge, it is the first exploration of the above system within the dual split quaternion tensor algebra. Specifically, it aims to solve the following system of dual split quaternion tensor equations:

$$\left\{\begin{array}{c}\mathcal{A}{*}_N\mathcal{X}=\mathcal{B},\hfill \\ \mathcal{X}{*}_S\mathcal{C}=\mathcal{D}.\hfill \end{array}\right.$$

(2)

This paper is designed with such structure: Section 2 describes essential definitions and corollaries that are essential to our subsequent analysis. Section 3 investigates the conditions that are equivalent for system (2) when there exist solutions. In this section, We further demonstrate its general solution in cases where solutions are attainable. Furthermore, we present the sufficient and necessary criteria when system (2) have $\eta$-Hermitian solutions. Based on these results, we will introduce the equivalent condition for the Hermitian solution, along with the general expressions of solutions for two specific dual split quaternion tensor equations. Ultimately, we will present a specific numerical example and an encryption and decryption algorithm as an application.

In this paper, the dual number field, quaternion field, split quaternion field, dual quaternion field, and dual split quaternion field are represented by $\mathbb{D}$, $\mathbb{H}$, ${\mathbb{H}}_s$, $\mathbb{DQ}$, and ${\mathbb{DQ}}_s$ respectively. All $I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N$ tensors over ${\mathbb{DQ}}_s$ are represented using ${\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$.

2. Preliminary

In this section, there are three parts to provide fundamental knowledge for the subsequent demonstration of this paper. In the first part, we will give the definition of dual split quaternion tensors. The second part will cover some definitions and propositions about tensors. Lastly, we will present various real representations of split quaternion tensors.

2.1. Dual Split Quaternion Tensors

$\mathcal{A}={\left(a_{j_1\cdots j_M}\right)}_{1\le j_k\le J_k(k=1,\dots ,M)}$ is a multidimensional array tensor with $J_1\times J_2\times \cdots \times J_M$ entries. Let ${\mathbb{R}}^{J_1\times \cdots \times J_M}$, ${\mathbb{H}}^{J_1\times \cdots \times J_M}$, and ${\mathbb{H}}_s^{J_1\times \cdots \times J_M}$ respectively represent the sets of the order M tensors with $J_1\times \cdots \times J_M$ dimensions over the real field $\mathbb{R}$, real quaternion algebra $\mathbb{H}$, and real split quaternion algebra ${\mathbb{H}}_s$.

For $\mathcal{A}=\left(a_{i_1\cdots i_M{l}_1\cdots l_N}\right)\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_N}$, $\mathcal{B}=\left(b_{l_1\cdots l_N{i}_1\cdots i_M}\right)\in {\mathbb{H}}_s^{L_1\times \cdots \times L_N\times I_1\times \cdots \times I_M}$. When $b_{l_1\cdots l_N{i}_1\cdots i_M}=a_{i_1\cdots i_M{l}_1\cdots l_N}$, $\mathcal{B}$ is referred to as the transpose of $\mathcal{A}$ and is denoted by ${\mathcal{A}}^T$. When $b_{l_1\cdots l_M{i}_1\cdots i_N}={\overline{a}}_{i_1\cdots i_N{l}_1\cdots l_M}$, $\mathcal{B}$ is the conjugate transpose of $\mathcal{A}$, represented as ${\mathcal{A}}^{*}$. A diagonal tensor $\mathcal{D}=\left(d_{t_1\cdots t_M{t}_1\cdots t_M}\right)\in {\mathbb{H}}_s^{T_1\times \cdots \times T_M\times T_1\times \cdots \times T_M}$ has all zero entries except for the elements $d_{t_1\cdots t_M{t}_1\cdots t_M}$. When all diagonal elements of $\mathcal{D}$ are equal to 1, $\mathcal{D}$ is referred to as a unit tensor, expressed as $\mathcal{I}$. Specifically, if $\mathcal{I}\in {\mathbb{H}}_s^{T_1\times \cdots \times T_M\times T_1\times \cdots \times T_M}$, it is expressed as ${\mathcal{I}}_M$. $\mathcal{O}$ denotes the zero tensor whose elements are all zero.

Definition 1

([30,42]). The field of dual numbers is expressed as: 

$$\mathbb{D}=\{q=q_0+q_1ϵ:q_0,q_1\in \mathbb{R},ϵ\ne 0,{ϵ}^2=0\},$$

where ϵ is the infinitesimal unit.

By extending quaternions and split quaternions to include dual numbers, we derive the definitions of dual quaternions and dual split quaternions:

$$\mathbb{DQ}=\{q=q_0+q_1ϵ:q_0,q_1\in \mathbb{H},ϵ\ne 0,{ϵ}^2=0\},$$

$${\mathbb{DQ}}_s=\{q=q_0+q_1ϵ:q_0,q_1\in {\mathbb{H}}_s,ϵ\ne 0,{ϵ}^2=0\}.$$

The sets of dual quaternion tensors and dual split quaternion tensors [9,30] are represented as follows:

$$\begin{array}{cc}\hfill & {\mathbb{DQ}}^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}=\{Q=Q_0+Q_1ϵ:Q_0,Q_1\in {\mathbb{H}}^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N},ϵ\ne 0,{ϵ}^2=0\},\hfill \\ \hfill & {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}=\{Q=Q_0+Q_1ϵ:Q_0,Q_1\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N},ϵ\ne 0,{ϵ}^2=0\}.\hfill \end{array}$$

For $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_1ϵ,\mathcal{Y}={\mathcal{Y}}_0+{\mathcal{Y}}_1ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_N}$, $\mathcal{X}=\mathcal{Y}$ means that ${\mathcal{X}}_0={\mathcal{Y}}_0$ and ${\mathcal{X}}_1={\mathcal{Y}}_1$, and vice versa. ${\mathcal{X}}^{*}={\mathcal{X}}_0^{*}+{\mathcal{X}}_1^{*}ϵ$ is called the conjugate transpose of $\mathcal{X}$. ${\mathcal{X}}^{\eta *}={\mathcal{X}}_0^{\eta *}+{\mathcal{X}}_1^{\eta *}ϵ$ are called the $\eta$-conjugate transposes of $\mathcal{X}$, where $\eta =\{i,j,k\}$.

For $\mathcal{X}\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_N}$, $\mathcal{X}$ is uniquely identified as $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_{1}i+{\mathcal{X}}_{2}j+{\mathcal{X}}_{3}k$, where ${\mathcal{X}}_0,{\mathcal{X}}_1,{\mathcal{X}}_2$ and ${\mathcal{X}}_3\in {\mathbb{R}}^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_N}$. The conjugate transpose of $\mathcal{X}$ satisfies ${\mathcal{X}}^{*}={\mathcal{X}}_0^T-{\mathcal{X}}_1^{T}i-{\mathcal{X}}_2^{T}j-{\mathcal{X}}_3^{T}k$. Additionally, for $\eta \in \{i,j,k\}$, the $\eta$-conjugates and $\eta$-conjugate transposes [36] of $\mathcal{X}$ have following forms:

$$\begin{array}{cc}\hfill {\mathcal{X}}^i& =i^{-1}\mathcal{X}i={\mathcal{X}}_0+{\mathcal{X}}_{1}i-{\mathcal{X}}_{2}j-{\mathcal{X}}_{3}k,\hfill \\ \hfill {\mathcal{X}}^j& =j^{-1}\mathcal{X}j={\mathcal{X}}_0-{\mathcal{X}}_{1}i+{\mathcal{X}}_{2}j-{\mathcal{X}}_{3}k,\hfill \\ \hfill {\mathcal{X}}^k& =k^{-1}\mathcal{X}k={\mathcal{X}}_0-{\mathcal{X}}_{1}i-{\mathcal{X}}_{2}j+{\mathcal{X}}_{3}k,\hfill \end{array}$$

and

$$\begin{array}{c}{\mathcal{X}}^{i*}=i^{-1}{\mathcal{X}}^{*}i={\mathcal{X}}_0^T-{\mathcal{X}}_1^{T}i+{\mathcal{X}}_2^{T}j+{\mathcal{X}}_3^{T}k,\\ {\mathcal{X}}^{j*}=j^{-1}{\mathcal{X}}^{*}j={\mathcal{X}}_0^T+{\mathcal{X}}_1^{T}i-{\mathcal{X}}_2^{T}j+{\mathcal{X}}_3^{T}k,\\ {\mathcal{X}}^{k*}=k^{-1}{\mathcal{X}}^{*}k={\mathcal{X}}_0^T+{\mathcal{X}}_1^{T}i+{\mathcal{X}}_2^{T}j-{\mathcal{X}}_3^{T}k.\end{array}$$

Definition 2.

Let $\mathcal{X}\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_N\times I_1\times \cdots \times I_N}$. Provided that $\mathcal{X}$ fulfills subsequent criteria: 

$$\mathcal{X}={\mathcal{X}}^{\eta *}:={\eta }^{-1}{\mathcal{X}}^{*}\eta ,\eta \in \{i,j,k\},$$

we refer to $\mathcal{X}$ as a η-Hermitian tensor.

For $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_1ϵ,\mathcal{Y}={\mathcal{Y}}_0+{\mathcal{Y}}_1ϵ\in {\mathbb{DQ}}_s^{T_1\times \cdots \times T_M\times J_1\times \cdots \times J_N}$, then we can derive that ${(\mathcal{X}+\mathcal{Y})}^{\eta *}={\mathcal{X}}^{\eta *}+{\mathcal{Y}}^{\eta *}$ and ${\left({\mathcal{X}}^{\eta *}\right)}^{\eta *}=\mathcal{X}$. And $\mathcal{X}=\mathcal{Y}$ means that ${\mathcal{X}}_0^{\eta *}={\mathcal{Y}}_0^{\eta *}$ and ${\mathcal{X}}_1^{\eta *}={\mathcal{Y}}_1^{\eta *}$, and vice versa.

2.2. Basic theory with Einstein product

Definition 3

([31]). Let $\mathcal{X}\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_N}$ and $\mathcal{Y}\in {\mathbb{DQ}}_s^{L_1\times \cdots \times L_N\times K_1\times \cdots \times K_S}$, then we can define the Einstein product of tensors $\mathcal{X}$ and $\mathcal{Y}$ through the operation ${*}_N$ as follows: 

$$\begin{array}{c}\hfill {\left(\mathcal{X}{*}_N\mathcal{Y}\right)}_{i_1\cdots i_M{k}_1\cdots k_S}=\sum _{l_1\cdots l_N}{x}_{i_1\cdots i_M{l}_1\cdots l_N}{y}_{l_1\cdots l_N{k}_1\cdots k_S}\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times K_1\times \cdots \times K_S}.\end{array}$$

Proposition 1.

Let $\mathcal{X}\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_S}$ and $\mathcal{Y}\in {\mathbb{DQ}}_s^{L_1\times \cdots \times L_S\times K_1\times \cdots \times K_T}$, then

• ${\left(\mathcal{X}{*}_S\mathcal{Y}\right)}^{*}={\mathcal{Y}}^{*}{*}_S{\mathcal{X}}^{*}$;
• ${\mathcal{I}}_S{*}_S\mathcal{Y}=\mathcal{Y}$ and $\mathcal{Y}{*}_T{\mathcal{I}}_T=\mathcal{Y}$.

Definition 4

([32,35]). Let $\mathcal{A}\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_T}$ and $\mathcal{Y}\in {\mathbb{H}}_s^{L_1\times \cdots \times L_T\times I_1\times \cdots \times I_M}$. $\mathcal{Y}$ is referred to as the Moore-Penrose inverse of $\mathcal{A}$, expressed as ${\mathcal{A}}^{†}$, if the subsequent conditions are all fulfilled: 

• $\mathcal{A}{*}_T\mathcal{Y}{*}_M\mathcal{A}=\mathcal{A}$;
• $\mathcal{Y}{*}_M\mathcal{A}{*}_T\mathcal{Y}=\mathcal{Y}$;
• ${\left(\mathcal{A}{*}_T\mathcal{Y}\right)}^{*}=\mathcal{A}{*}_T\mathcal{Y}$;
• ${\left(\mathcal{Y}{*}_M\mathcal{A}\right)}^{*}=\mathcal{Y}{*}_M\mathcal{A}$.

Furthermore, projectors ${\mathcal{L}}_{\mathcal{A}}$ and ${\mathcal{R}}_{\mathcal{A}}$ have following forms: 

$${\mathcal{L}}_{\mathcal{A}}=\mathcal{I}-{\mathcal{A}}^{†}{*}_M\mathcal{A},{\mathcal{R}}_{\mathcal{A}}=\mathcal{I}-\mathcal{A}{*}_T{\mathcal{A}}^{†}.$$

Similar to block matrices, reference [32] provides the definition of block tensors and reference [33] provides the definition of block tensors when their sizes are same. Next, we extend the definitions from references [32,33] to split quaternion tensors to give the definition of block tensors with the same size.

Definition 5.

Let $\mathcal{X}=\left(x_{l_1\cdots l_T{k}_1\cdots k_N}\right)$ and $\mathcal{Y}=\left(y_{l_1\cdots l_T{k}_1\cdots k_N}\right)\in {\mathbb{H}}_s^{L_1\times \cdots \times L_T\times K_1\times \cdots \times K_N}$, then

• The ’row block tensor’ formed by $\mathcal{X}$ and $\mathcal{Y}$ is $\left[\mathcal{X}\mathcal{Y}\right]\in {\mathbb{H}}_s^{L_1\times \cdots \times L_T\times K_1\times \cdots \times K_{N-1}\times 2K_N}$, and

  $$\begin{array}{cc}\hfill & {\left[\mathcal{X}\mathcal{Y}\right]}_{l_1\cdots l_T{k}_1\cdots k_N}\hfill \\ & =\left\{\begin{array}{cc}{x}_{l_1\cdots l_T{k}_1\cdots k_N},\hfill & l_1\cdots l_T\in \left[L_1\right]\times \cdots \times \left[L_T\right],k_1\cdots k_N\in \left[K_1\right]\times \cdots \times \left[K_N\right];\hfill \\ y_{l_1\cdots l_T{k}_1\cdots (k_N-K_N)},\hfill & l_1\cdots l_T\in \left[L_1\right]\times \cdots \times \left[L_T\right],k_1\cdots k_N\in \left[K_1\right]\times \cdots \times \Gamma ,\hfill \end{array}\right.\hfill \end{array}$$
  where $\Gamma =\{K_N+1,K_N+2\dots ,2K_N\}$.
• The ’column block tensor’ formed by $\mathcal{X}$ and $\mathcal{Y}$ is $\left[\begin{array}{c}\mathcal{X}\\ \mathcal{Y}\end{array}\right]\in {\mathbb{H}}_s^{L_1\times \cdots \times L_{T-1}\times 2L_T\times K_1\times \cdots \times K_N}$, and

  $$\begin{array}{cc}\hfill & {\left[\begin{array}{c}\mathcal{X}\\ \mathcal{Y}\end{array}\right]}_{l_1\cdots l_T{k}_1\cdots k_N}\hfill \\ & =\left\{\begin{array}{cc}{x}_{l_1\cdots l_T{k}_1\cdots k_N},\hfill & l_1\cdots l_T\in \left[L_1\right]\times \cdots \times \left[L_T\right],k_1\cdots k_N\in \left[K_1\right]\times \cdots \times \left[K_N\right];\hfill \\ y_{l_1\cdots (l_T-L_T)k_1\cdots k_N},\hfill & l_1\cdots l_T\in \left[L_1\right]\times \cdots \times \Gamma ,k_1\cdots k_N\in \left[K_1\right]\times \cdots \times \left[K_N\right],\hfill \end{array}\right.\hfill \end{array}$$
  where $\Gamma =\{L_T+1,L_T+2\dots ,2L_T\}$.

In particular, let ${\mathcal{X}}_{11}$, ${\mathcal{X}}_{12}$, ${\mathcal{X}}_{21}$ and ${\mathcal{X}}_{22}\in {\mathbb{H}}_s^{L_1\times \cdots \times L_T\times K_1\times \cdots \times K_N}$, then

$$\begin{array}{c}\hfill \left[\begin{array}{c}{\mathcal{X}}_{11}{\mathcal{X}}_{12}\\ {\mathcal{X}}_{21}{\mathcal{X}}_{22}\end{array}\right]\in {\mathbb{H}}_s^{L_1\times \cdots \times L_{T-1}\times 2L_T\times K_1\times \cdots \times K_{N-1}\times 2K_N}.\end{array}$$

Remark 1.

${\mathcal{X}}_{ij}$ is the tensor located at row i, column $j(i,j=1,2)$ in the aforementioned block tensor and it will be used in the following statement.

Lemma 1

([32]). Let ${\mathcal{X}}_i\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N},i=\{1,2,3,4\}$, ${\mathcal{Y}}_j\in {\mathbb{H}}_s^{J_1\times \cdots \times J_N\times T_1\times \cdots \times T_S}$, $j=\{1,2\}$, and ${\mathcal{Z}}_k\in {\mathbb{H}}_s^{S_1\times \cdots \times S_N\times I_1\times \cdots \times I_M}$, $k=\{1,2\}$, then

• $$\begin{array}{c}\hfill \left[\begin{array}{cc}{\mathcal{X}}_1& {\mathcal{X}}_3\\ {\mathcal{X}}_2& {\mathcal{X}}_4\end{array}\right]{*}_N\left[\begin{array}{c}{\mathcal{Y}}_1\\ {\mathcal{Y}}_2\end{array}\right]=\left[\begin{array}{c}{\mathcal{X}}_1{*}_N{\mathcal{Y}}_1+{\mathcal{X}}_3{*}_N{\mathcal{Y}}_2\\ {\mathcal{X}}_2{*}_N{\mathcal{Y}}_1+{\mathcal{X}}_4{*}_N{\mathcal{Y}}_2\end{array}\right];\end{array}$$
• $$\begin{array}{c}\hfill \left[\begin{array}{cc}{\mathcal{Z}}_1& {\mathcal{Z}}_2\end{array}\right]{*}_M\left[\begin{array}{cc}{\mathcal{X}}_1& {\mathcal{X}}_3\\ {\mathcal{X}}_2& {\mathcal{X}}_4\end{array}\right]=\left[\begin{array}{cc}{\mathcal{Z}}_1{*}_M{\mathcal{X}}_1+{\mathcal{Z}}_2{*}_M{\mathcal{X}}_2& {\mathcal{Z}}_1{*}_M{\mathcal{X}}_3+{\mathcal{Z}}_2{*}_M{\mathcal{X}}_4\end{array}\right].\end{array}$$

Next, we will introduce the definition of the transformation t between a tensor and a matrix within split quaternion algebra [34,35]. Under this definition, we can simplify the tensor into a matrix.

Definition 6.

The transformation $t:{\mathbb{T}}_{I_1,I_2,\dots ,I_M,L_1,L_2,\dots ,L_N}\left({\mathbb{H}}_s\right)\to {\mathbb{M}}_{I_1·I_2\cdots I_M,L_1·L_2\cdots L_N}\left({\mathbb{H}}_s\right)$ with $t\left(\mathcal{X}\right)=X$ is defined as follows: 

$$\begin{array}{c}\hfill {\left(\mathcal{X}\right)}_{i_1{i}_2\cdots i_M{l}_1{l}_2\cdots l_N}\stackrel{t}{\to }{\left(X\right)}_{[i_1+{\sum }_{k=2}^M(i_k-1){\prod }_{s=1}^{k-1}{I}_s][l_1+{\sum }_{k=2}^N(l_k-1){\prod }_{s=1}^{k-1}{L}_s]},\end{array}$$

where $\mathcal{X}\in {\mathbb{T}}_{I_1,I_2,\dots ,I_M,L_1,L_2,\dots ,L_N}\left({\mathbb{H}}_s\right)$ and $X\in {\mathbb{M}}_{I_1·I_2\cdots I_M,L_1·L_2\cdots L_N}\left({\mathbb{H}}_s\right)$.

Lemma 2

([35]). Let $\mathcal{X}\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_N}$ and $\mathcal{Y}\in {\mathbb{H}}_s^{L_1\times \cdots \times L_N\times K_1\times \cdots \times K_S}$. Then t satisfies following properties: 

• The map t is bijective and its inverse map $t^{-1}$ exists as follows: 

  $$\begin{array}{c}\hfill {\mathbb{M}}_{I_1·I_2\cdots I_{M-1}·I_M,L_1·L_2\cdots L_{N-1}·L_N}\left({\mathbb{H}}_s\right)\stackrel{t^{-1}}{\to }{\mathbb{T}}_{I_1,I_2,\cdots ,I_{M-1},I_M,L_1,L_2,\cdots ,L_{N-1},L_N}\left({\mathbb{H}}_s\right);\end{array}$$
• t satisfies: $t\left(\mathcal{X}{*}_N\mathcal{Y}\right)=t\left(\mathcal{X}\right)·t\left(\mathcal{Y}\right)$ and $t\left({\mathcal{X}}^{†}\right)=t{\left(\mathcal{X}\right)}^{†}$.

Example 1.

Let $\mathcal{A}\in {\mathbb{H}}_s^{2\times 2\times 2\times 2}$ is defined by

$$\begin{array}{cc}\hfill & {\left(\mathcal{A}\right)}_{1111}=i+2k,{\left(\mathcal{A}\right)}_{1121}=k,{\left(\mathcal{A}\right)}_{1112}=3i,{\left(\mathcal{A}\right)}_{1122}=2,\hfill \\ \hfill & {\left(\mathcal{A}\right)}_{2111}=0,{\left(\mathcal{A}\right)}_{2121}=i+j,{\left(\mathcal{A}\right)}_{2112}=2k,{\left(\mathcal{A}\right)}_{2122}=i+2j,\hfill \\ \hfill & {\left(\mathcal{A}\right)}_{1211}=-i+2j,{\left(\mathcal{A}\right)}_{1221}=4k,{\left(\mathcal{A}\right)}_{1212}=0,{\left(\mathcal{A}\right)}_{1222}=3j,\hfill \\ \hfill & {\left(\mathcal{A}\right)}_{2211}=4i+2k,{\left(\mathcal{A}\right)}_{2221}=i+3j,{\left(\mathcal{A}\right)}_{2212}=2+3i+j,{\left(\mathcal{A}\right)}_{2222}=1+2j+5k.\hfill \end{array}$$

Then

$$\begin{array}{cc}\hfill A=t\left(\mathcal{A}\right)& =\left(\begin{array}{cccc}{\left(\mathcal{A}\right)}_{1111}& {\left(\mathcal{A}\right)}_{1121}& {\left(\mathcal{A}\right)}_{1112}& {\left(\mathcal{A}\right)}_{1122}\\ {\left(\mathcal{A}\right)}_{2111}& {\left(\mathcal{A}\right)}_{2121}& {\left(\mathcal{A}\right)}_{2112}& {\left(\mathcal{A}\right)}_{2122}\\ {\left(\mathcal{A}\right)}_{1211}& {\left(\mathcal{A}\right)}_{1221}& {\left(\mathcal{A}\right)}_{1212}& {\left(\mathcal{A}\right)}_{1222}\\ {\left(\mathcal{A}\right)}_{2211}& {\left(\mathcal{A}\right)}_{2221}& {\left(\mathcal{A}\right)}_{2212}& {\left(\mathcal{A}\right)}_{2222}\end{array}\right)\hfill \\ \hfill & =\left(\begin{array}{cccc}i+2k& k& 3i& 2\\ 0& i+j& 2k& i+2j\\ -i+2j& 4k& 0& 3j\\ 4i+2k& i+3j& 2+3i+j& 1+2j+5k\end{array}\right).\hfill \end{array}$$

Consequently, there is a one-to-one correspondence between the elements of the split quaternion matrix and the split quaternion tensor. Thus, we can make use of the above definition to transform the tensor into a matrix for further calculations.

2.3. Real Representations of Split Quaternion Tensors

In this section, we will provide various real representations using the definition of block tensors in the above section.

Let $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_{1}i+{\mathcal{X}}_{2}j+{\mathcal{X}}_{3}k\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, where ${\mathcal{X}}_i\in {\mathbb{R}}^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, $i=\{0,1,2,3\}$. We will define three kinds of real representations of $\mathcal{X}$ based on the real representation in [12]:

$${\mathcal{X}}^{{\sigma }_i}:=\left[\begin{array}{cccc}{\mathcal{X}}_0& {\mathcal{X}}_1& {\mathcal{X}}_2& {\mathcal{X}}_3\\ -{\mathcal{X}}_1& {\mathcal{X}}_0& -{\mathcal{X}}_3& {\mathcal{X}}_2\\ {\mathcal{X}}_2& -{\mathcal{X}}_3& {\mathcal{X}}_0& -{\mathcal{X}}_1\\ {\mathcal{X}}_3& {\mathcal{X}}_2& {\mathcal{X}}_1& {\mathcal{X}}_0\end{array}\right]\in {\mathbb{R}}^{I_1\times \cdots \times 4I_M\times J_1\times \cdots \times 4J_N}.$$

Definition 7

([36,39]). Let $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_{1}i+{\mathcal{X}}_{2}j+{\mathcal{X}}_{3}k\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, where ${\mathcal{X}}_0$, ${\mathcal{X}}_1$, ${\mathcal{X}}_2$, ${\mathcal{X}}_3\in {\mathbb{R}}^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, ${\mathcal{I}}_M\in {\mathbb{R}}^{I_1\times \cdots \times I_M\times I_1\times \cdots \times I_M}$. Then we define

$$\begin{array}{cc}\hfill {\mathcal{X}}^{{\sigma }_j}:={\mathcal{V}}_M{*}_M{\mathcal{X}}^{{\sigma }_i}=\left[\begin{array}{cccc}{\mathcal{X}}_0& {\mathcal{X}}_1& {\mathcal{X}}_2& {\mathcal{X}}_3\\ {\mathcal{X}}_1& -{\mathcal{X}}_0& {\mathcal{X}}_3& -{\mathcal{X}}_2\\ -{\mathcal{X}}_2& {\mathcal{X}}_3& -{\mathcal{X}}_0& {\mathcal{X}}_1\\ {\mathcal{X}}_3& {\mathcal{X}}_2& {\mathcal{X}}_1& {\mathcal{X}}_0\end{array}\right],& {\mathcal{V}}_M=\left[\begin{array}{cccc}{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& -{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& -{\mathcal{I}}_M& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& \mathcal{O}& {\mathcal{I}}_M\end{array}\right];\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathcal{X}}^{{\sigma }_k}:={\mathcal{W}}_M{*}_M{\mathcal{X}}^{{\sigma }_i}=\left[\begin{array}{cccc}{\mathcal{X}}_0& {\mathcal{X}}_1& {\mathcal{X}}_2& {\mathcal{X}}_3\\ {\mathcal{X}}_1& -{\mathcal{X}}_0& {\mathcal{X}}_3& -{\mathcal{X}}_2\\ {\mathcal{X}}_2& -{\mathcal{X}}_3& {\mathcal{X}}_0& -{\mathcal{X}}_1\\ -{\mathcal{X}}_3& -{\mathcal{X}}_2& -{\mathcal{X}}_1& -{\mathcal{X}}_0\end{array}\right],& {\mathcal{W}}_M=\left[\begin{array}{cccc}{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& -{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& {\mathcal{I}}_M& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& \mathcal{O}& -{\mathcal{I}}_M\end{array}\right];\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathcal{X}}^{{\sigma }_1}:={\mathcal{P}}_M{*}_M{\mathcal{X}}^{{\sigma }_i}=\left[\begin{array}{cccc}{\mathcal{X}}_0& {\mathcal{X}}_1& {\mathcal{X}}_2& {\mathcal{X}}_3\\ -{\mathcal{X}}_1& {\mathcal{X}}_0& -{\mathcal{X}}_3& {\mathcal{X}}_2\\ -{\mathcal{X}}_2& {\mathcal{X}}_3& -{\mathcal{X}}_0& {\mathcal{X}}_1\\ -{\mathcal{X}}_3& -{\mathcal{X}}_2& -{\mathcal{X}}_1& -{\mathcal{X}}_0\end{array}\right],& {\mathcal{P}}_M=\left[\begin{array}{cccc}{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& {\mathcal{I}}_M& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& -{\mathcal{I}}_M& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& \mathcal{O}& -{\mathcal{I}}_M\end{array}\right],\hfill \end{array}$$

where ${\mathcal{V}}_M,{\mathcal{W}}_M$ and ${\mathcal{P}}_M\in {\mathbb{R}}^{I_1\times \cdots \times 4I_M\times I_1\times \cdots \times 4I_M}$.

As shown in the next proposition, we present the relevant characteristics of real representations discussed previously. These properties will play a crucial role in subsequent sections and can be easily obtained through simple calculations. Let

$$\begin{array}{c}\hfill {\mathcal{R}}_M=\left[\begin{array}{cccc}\mathcal{O}& -{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}\\ {\mathcal{I}}_M& \mathcal{O}& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& \mathcal{O}& -{\mathcal{I}}_M\\ \mathcal{O}& \mathcal{O}& {\mathcal{I}}_M& \mathcal{O}\end{array}\right],{\mathcal{S}}_M=\left[\begin{array}{cccc}\mathcal{O}& \mathcal{O}& {\mathcal{I}}_M& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& \mathcal{O}& -{\mathcal{I}}_M\\ {\mathcal{I}}_M& \mathcal{O}& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& -{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}\end{array}\right],{\mathcal{T}}_M=\left[\begin{array}{cccc}\mathcal{O}& \mathcal{O}& \mathcal{O}& {\mathcal{I}}_M\\ \mathcal{O}& \mathcal{O}& {\mathcal{I}}_M& \mathcal{O}\\ \mathcal{O}& {\mathcal{I}}_M& \mathcal{O}& \mathcal{O}\\ {\mathcal{I}}_M& \mathcal{O}& \mathcal{O}& \mathcal{O}\end{array}\right].\end{array}$$

Proposition 2.

For $\eta =\{i,j,k\}$, let $\mathcal{X},\mathcal{Y}\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N},\mathcal{P}\in {\mathbb{H}}_s^{J_1\times \cdots \times J_N\times K_1\times \cdots \times K_T}$, and $\lambda \in \mathbb{R}$. Then

• $\mathcal{X}=\mathcal{Y}\iff {\mathcal{X}}^{\eta *}={\mathcal{Y}}^{\eta *}$;
• ${(\mathcal{X}+\mathcal{Y})}^{{\sigma }_{\eta }}={\mathcal{X}}^{{\sigma }_{\eta }}+{\mathcal{Y}}^{{\sigma }_{\eta }},{\left(\lambda \mathcal{X}\right)}^{{\sigma }_{\eta }}=\lambda {\mathcal{X}}^{{\sigma }_{\eta }};$
• ${\left(\mathcal{X}{*}_N\mathcal{P}\right)}^{{\sigma }_i}={\mathcal{X}}^{{\sigma }_i}{*}_N{\mathcal{P}}^{{\sigma }_i},{\left(\mathcal{X}{*}_N\mathcal{P}\right)}^{{\sigma }_j}={\mathcal{X}}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{P}}^{{\sigma }_j},{\left(\mathcal{X}{*}_N\mathcal{P}\right)}^{{\sigma }_k}={\mathcal{X}}^{{\sigma }_k}{*}_N{\mathcal{W}}_N{*}_N{\mathcal{P}}^{{\sigma }_k},{\left(\mathcal{X}{*}_N\mathcal{P}\right)}^{{\sigma }_1}={\mathcal{X}}^{{\sigma }_1}{*}_N{\mathcal{P}}_N{*}_N{\mathcal{P}}^{{\sigma }_1}$;
• • ${\mathcal{R}}_M^T{*}_M{\mathcal{X}}^{{\sigma }_i}{*}_N{\mathcal{R}}_N={\mathcal{X}}^{{\sigma }_i},{\mathcal{S}}_M^T{*}_M{\mathcal{X}}^{{\sigma }_i}{*}_N{\mathcal{S}}_N={\mathcal{X}}^{{\sigma }_i},{\mathcal{T}}_M^T{*}_M{\mathcal{X}}^{{\sigma }_i}{*}_N{\mathcal{T}}_N={\mathcal{X}}^{{\sigma }_i}$;
  • ${\mathcal{R}}_M^T{*}_M{\mathcal{X}}^{{\sigma }_j}{*}_N{\mathcal{R}}_N=-{\mathcal{X}}^{{\sigma }_j},{\mathcal{S}}_M^T{*}_M{\mathcal{X}}^{{\sigma }_j}{*}_N{\mathcal{S}}_N=-{\mathcal{X}}^{{\sigma }_j},{\mathcal{T}}_M^T{*}_M{\mathcal{X}}^{{\sigma }_j}{*}_N{\mathcal{T}}_N={\mathcal{X}}^{{\sigma }_j}$;
  • ${\mathcal{R}}_M^T{*}_M{\mathcal{X}}^{{\sigma }_k}{*}_N{\mathcal{R}}_N=-{\mathcal{X}}^{{\sigma }_k},{\mathcal{S}}_M^T{*}_M{\mathcal{X}}^{{\sigma }_k}{*}_N{\mathcal{S}}_N={\mathcal{X}}^{{\sigma }_k},{\mathcal{T}}_M^T{*}_M{\mathcal{X}}^{{\sigma }_k}{*}_N{\mathcal{T}}_N=-{\mathcal{X}}^{{\sigma }_k}$;
• ${\left({\mathcal{X}}^{*}\right)}^{{\sigma }_1}={\left({\mathcal{X}}^{{\sigma }_1}\right)}^T,{\left({\mathcal{X}}^{\eta *}\right)}^{{\sigma }_{\eta }}={\left({\mathcal{X}}^{{\sigma }_{\eta }}\right)}^T$;
• • $\mathcal{X}={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_M& i{\mathcal{I}}_M& j{\mathcal{I}}_M& k{\mathcal{I}}_M\end{array}\right]{*}_M{\mathcal{X}}^{{\sigma }_i}{*}_N\left[\begin{array}{c}{\mathcal{I}}_N\\ i{\mathcal{I}}_N\\ j{\mathcal{I}}_N\\ k{\mathcal{I}}_N\end{array}\right]$;
  • $\mathcal{X}={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_M& -i{\mathcal{I}}_M& -j{\mathcal{I}}_M& k{\mathcal{I}}_M\end{array}\right]{*}_M{\mathcal{X}}^{{\sigma }_j}{*}_N\left[\begin{array}{c}{\mathcal{I}}_N\\ i{\mathcal{I}}_N\\ j{\mathcal{I}}_N\\ k{\mathcal{I}}_N\end{array}\right]$;
  • $\mathcal{X}={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_M& -i{\mathcal{I}}_M& j{\mathcal{I}}_M& -k{\mathcal{I}}_M\end{array}\right]{*}_M{\mathcal{X}}^{{\sigma }_k}{*}_N\left[\begin{array}{c}{\mathcal{I}}_N\\ i{\mathcal{I}}_N\\ j{\mathcal{I}}_N\\ k{\mathcal{I}}_N\end{array}\right]$;
• ${\left({\mathcal{X}}^i\right)}^{{\sigma }_1}={\mathcal{P}}_M{*}_M{\mathcal{X}}^{{\sigma }_1}{*}_N{\mathcal{P}}_N,{\left({\mathcal{X}}^k\right)}^{{\sigma }_j}={\mathcal{V}}_M{*}_M{\mathcal{X}}^{{\sigma }_j}{*}_N{\mathcal{V}}_N,{\left({\mathcal{X}}^j\right)}^{{\sigma }_k}={\mathcal{W}}_M{*}_M{\mathcal{X}}^{{\sigma }_k}{*}_N{\mathcal{W}}_N$.

3. The General Solution to System (2)

Using the definitions and lemmas outlined above, this part will examine the solutions to system (2). At the beginning of this section, we present two lemmas. Utilizing Definition (6), we can transform tensors into matrices. Consequently, the subsequent lemmas can be readily proven using matrix proof techniques found in references [24,37], so this paper will not delve into the details. Building on these lemmas, split quaternion tensors’ real representations are used for obtaining the necessary and sufficient criteria when system (2) exists solutions as well as the general solution expression.

Lemma 3

([37]). Let ${\mathcal{A}}_1,{\mathcal{A}}_2\in {\mathbb{H}}^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, ${\mathcal{B}}_1,{\mathcal{B}}_2\in {\mathbb{H}}^{L_1\times \cdots \times L_S\times K_1\times \cdots \times K_T}$, and ${\mathcal{C}}_1,{\mathcal{C}}_2\in {\mathbb{H}}^{I_1\times \cdots \times I_M\times K_1\times \cdots \times K_T}$. Set

$$\begin{array}{cc}\hfill \mathcal{K}& ={\mathcal{A}}_2{*}_N{\mathcal{L}}_{{\mathcal{A}}_1},\mathcal{F}={\mathcal{R}}_{{\mathcal{B}}_1}{*}_S{\mathcal{B}}_2,\mathcal{G}={\mathcal{C}}_2-{\mathcal{A}}_2{*}_N{\mathcal{A}}_1^{†}{*}_M{\mathcal{C}}_1{*}_T{\mathcal{B}}_1^{†}{*}_S{\mathcal{B}}_2,\mathcal{H}={\mathcal{R}}_{\mathcal{K}}{*}_M{\mathcal{A}}_2,\hfill \\ \hfill \mathcal{Q}& ={\mathcal{A}}_1^{†}{*}_M{\mathcal{C}}_1{*}_T{\mathcal{B}}_1^{†}+{\mathcal{L}}_{{\mathcal{A}}_1}{*}_N{\mathcal{K}}^{†}{*}_M\mathcal{G}{*}_T{\mathcal{B}}_2^{†}-{\mathcal{L}}_{{\mathcal{A}}_1}{*}_N{\mathcal{K}}^{†}{*}_M{\mathcal{A}}_2{*}_N{\mathcal{H}}^{†}{*}_M{\mathcal{R}}_{\mathcal{K}}{*}_M\mathcal{G}{*}_T{\mathcal{B}}_2^{†}\hfill \\ & +{\mathcal{H}}^{†}{*}_M{\mathcal{R}}_{\mathcal{K}}{*}_M\mathcal{G}{*}_T{\mathcal{F}}^{†}{*}_S{\mathcal{R}}_{{\mathcal{B}}_1}.\hfill \end{array}$$

Then

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathcal{A}}_1{*}_N\mathcal{X}{*}_S{\mathcal{B}}_1& ={\mathcal{C}}_1,\hfill \\ \hfill {\mathcal{A}}_2{*}_N\mathcal{X}{*}_S{\mathcal{B}}_2& ={\mathcal{C}}_2\hfill \end{array}\right.\end{array}$$

(3)

is consistent if and only if

$$\begin{array}{c}\hfill {\mathcal{R}}_{{\mathcal{A}}_1}{*}_M{\mathcal{C}}_1=0,{\mathcal{C}}_1{*}_T{\mathcal{L}}_{{\mathcal{B}}_1}=0,{\mathcal{R}}_{{\mathcal{A}}_2}{*}_M{\mathcal{C}}_2=0,{\mathcal{C}}_2{*}_T{\mathcal{L}}_{{\mathcal{B}}_2}=0,{\mathcal{R}}_{\mathcal{K}}{*}_M\mathcal{G}{*}_T{\mathcal{L}}_{\mathcal{F}}=0.\end{array}$$

Building on this, the general solution for system (3) is stated in the following form: 

$$\begin{array}{c}\hfill \mathcal{X}=\mathcal{Q}+{\mathcal{L}}_{{\mathcal{A}}_1}{*}_N{\mathcal{L}}_{\mathcal{K}}{*}_N{\mathcal{W}}_1+{\mathcal{W}}_2{*}_S{\mathcal{R}}_{\mathcal{F}}{*}_S{\mathcal{R}}_{{\mathcal{B}}_1}+{\mathcal{L}}_{{\mathcal{A}}_1}{*}_N{\mathcal{W}}_3{*}_S{\mathcal{R}}_{{\mathcal{B}}_2}+{\mathcal{L}}_{{\mathcal{A}}_2}{*}_N{\mathcal{W}}_4{*}_S{\mathcal{R}}_{{\mathcal{B}}_1},\end{array}$$

where ${\mathcal{W}}_i(i=\overline{1,4})$ are arbitrary tensors of appropriate size defined on $\mathbb{H}$.

Lemma 4

([24]). Suppose that $\mathcal{A}={\mathcal{A}}_0+{\mathcal{A}}_1ϵ\in {\mathbb{DQ}}^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, $\mathcal{B}={\mathcal{B}}_0+{\mathcal{B}}_1ϵ\in {\mathbb{DQ}}^{I_1\times \cdots \times I_M\times K_1\times \cdots \times K_S}$, $\mathcal{C}={\mathcal{C}}_0+{\mathcal{C}}_1ϵ\in {\mathbb{DQ}}^{K_1\times \cdots \times K_S\times L_1\times \cdots \times L_T}$, and $\mathcal{D}={\mathcal{D}}_0+{\mathcal{D}}_1ϵ\in {\mathbb{DQ}}^{J_1\times \cdots \times J_N\times L_1\times \cdots \times L_T}$. Set

$$\begin{array}{cc}\hfill {\mathcal{A}}_2& ={\mathcal{A}}_1{*}_N{\mathcal{L}}_{{\mathcal{A}}_0},{\mathcal{C}}_2={\mathcal{R}}_{{\mathcal{C}}_0}{*}_S{\mathcal{C}}_1,{\mathcal{B}}_2={\mathcal{B}}_1-{\mathcal{A}}_1{*}_N\left({\mathcal{A}}_0^{†}{*}_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N{\mathcal{D}}_0{*}_T{\mathcal{C}}_0^{†}\right),\hfill \\ \hfill {\mathcal{A}}_3& ={\mathcal{R}}_{{\mathcal{A}}_0}{*}_M{\mathcal{A}}_2,{\mathcal{B}}_3={\mathcal{R}}_{{\mathcal{C}}_0},{\mathcal{D}}_2={\mathcal{D}}_1-\left({\mathcal{A}}_0^{†}{*}_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N{\mathcal{D}}_0{*}_T{\mathcal{C}}_0^{†}\right){*}_S{\mathcal{C}}_1,\hfill \\ \hfill {\mathcal{C}}_3& ={\mathcal{R}}_{{\mathcal{A}}_0}{*}_M{\mathcal{B}}_2,{\mathcal{A}}_4={\mathcal{L}}_{{\mathcal{A}}_0},{\mathcal{B}}_4={\mathcal{C}}_2{*}_T{\mathcal{L}}_{{\mathcal{C}}_0},{\mathcal{C}}_4={\mathcal{D}}_2{*}_T{\mathcal{L}}_{{\mathcal{C}}_0},{\mathcal{A}}_5={\mathcal{A}}_4{*}_N{\mathcal{L}}_{{\mathcal{A}}_3},\hfill \\ \hfill {\mathcal{B}}_5& ={\mathcal{R}}_{{\mathcal{B}}_3}{*}_S{\mathcal{B}}_4,{\mathcal{C}}_5={\mathcal{C}}_4-{\mathcal{A}}_4{*}_N{\mathcal{A}}_3^{†}{*}_M{\mathcal{C}}_3{*}_S{\mathcal{B}}_3^{†}{*}_S{\mathcal{B}}_4,{\mathcal{D}}_5={\mathcal{R}}_{{\mathcal{A}}_5}{*}_N{\mathcal{A}}_4,\hfill \\ \hfill \mathcal{F}& ={\mathcal{A}}_3^{†}{*}_M{\mathcal{C}}_3{*}_S{\mathcal{B}}_3^{†}+{\mathcal{L}}_{{\mathcal{A}}_3}{*}_N{\mathcal{A}}_5^{†}{*}_N{\mathcal{C}}_5{*}_T{\mathcal{B}}_4^{†}-{\mathcal{L}}_{{\mathcal{A}}_3}{*}_N{\mathcal{A}}_5^{†}{*}_N{\mathcal{A}}_4{*}_N{\mathcal{D}}_5^{†}{*}_N{\mathcal{R}}_{{\mathcal{A}}_5}{*}_N{\mathcal{C}}_5{*}_T{\mathcal{B}}_4^{†}\hfill \\ \hfill & +{\mathcal{D}}_5^{†}{*}_N{\mathcal{R}}_{{\mathcal{A}}_5}{*}_N{\mathcal{C}}_5{*}_T{\mathcal{B}}_5^{†}{*}_S{\mathcal{R}}_{{\mathcal{B}}_3}.\hfill \end{array}$$

Then the subsequent descriptions are equivalent: 

• The system (2) is solvable.
• $$\begin{array}{cc}\hfill & {\mathcal{R}}_{{\mathcal{A}}_0}{*}_M{\mathcal{B}}_0=0,{\mathcal{D}}_0{*}_T{\mathcal{L}}_{{\mathcal{C}}_0}=0,{\mathcal{A}}_0{*}_N{\mathcal{D}}_0={\mathcal{B}}_0{*}_S{\mathcal{C}}_0,\hfill \\ \hfill & {\mathcal{A}}_0{*}_N{\mathcal{D}}_1-{\mathcal{B}}_0{*}_S{\mathcal{C}}_1={\mathcal{B}}_1{*}_S{\mathcal{C}}_0-{\mathcal{A}}_1{*}_N{\mathcal{D}}_0,{\mathcal{R}}_{{\mathcal{A}}_3}{*}_M{\mathcal{C}}_3=0,\hfill \\ \hfill & {\mathcal{C}}_3{*}_S{\mathcal{L}}_{{\mathcal{B}}_3}=0,{\mathcal{R}}_{{\mathcal{A}}_4}{*}_N{\mathcal{C}}_4=0,{\mathcal{C}}_4{*}_T{\mathcal{L}}_{{\mathcal{B}}_4}=0,{\mathcal{R}}_{{\mathcal{A}}_5}{*}_N{\mathcal{C}}_5{*}_T{\mathcal{L}}_{{\mathcal{B}}_5}=0.\hfill \end{array}$$

Based on these, the general solution for the system (2) is represented as $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_1ϵ$, where

$$\begin{array}{cc}\hfill {\mathcal{X}}_0& ={\mathcal{A}}_0^{†}{*}_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N{\mathcal{D}}_0{*}_T{\mathcal{C}}_0^{†}+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N\mathcal{W}{*}_S{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill {\mathcal{X}}_1& ={\mathcal{A}}_0^{†}{*}_M({\mathcal{B}}_2-{\mathcal{A}}_2{*}_N\mathcal{W}{*}_S{\mathcal{R}}_{{\mathcal{C}}_0})+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N({\mathcal{D}}_2-{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N\mathcal{W}{*}_S{\mathcal{C}}_2){*}_T{\mathcal{C}}_0^{†}\hfill \\ \hfill & +{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N{\mathcal{W}}_1{*}_S{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill \mathcal{W}& =\mathcal{F}+{\mathcal{L}}_{{\mathcal{A}}_3}{*}_N{\mathcal{L}}_{{\mathcal{A}}_5}{*}_N{\mathcal{W}}_2+{\mathcal{W}}_3{*}_S{\mathcal{R}}_{{\mathcal{B}}_5}{*}_S{\mathcal{R}}_{{\mathcal{B}}_3}+{\mathcal{L}}_{{\mathcal{A}}_3}{*}_N{\mathcal{W}}_4{*}_S{\mathcal{R}}_{{\mathcal{B}}_4}+{\mathcal{L}}_{{\mathcal{A}}_4}{*}_N{\mathcal{W}}_5{*}_S{\mathcal{R}}_{{\mathcal{B}}_3},\hfill \end{array}$$

and ${\mathcal{W}}_i(i=\overline{1,5})$ are random tensors with suitable dimensions.

Remark 2.

Note that the set of real tensors is included within the set of quaternion tensors since real numbers are special cases of quaternions with all imaginary parts set to 0. Thus, the conclusions above also hold in the field of real tensors.

Theorem 1.

Suppose that $\mathcal{A}={\mathcal{A}}_{00}+{\mathcal{A}}_{01}ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, $\mathcal{B}={\mathcal{B}}_{00}+{\mathcal{B}}_{01}ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times K_1\times \cdots \times K_S}$, $\mathcal{C}={\mathcal{C}}_{00}+{\mathcal{C}}_{01}ϵ\in {\mathbb{DQ}}_s^{K_1\times \cdots \times K_S\times L_1\times \cdots \times L_T}$, and $\mathcal{D}={\mathcal{D}}_{00}+{\mathcal{D}}_{01}ϵ\in {\mathbb{DQ}}_s^{J_1\times \cdots \times J_N\times L_1\times \cdots \times L_T}$. Set

$$\begin{array}{cc}\hfill & {\mathcal{A}}_0={\mathcal{A}}_{00}^{{\sigma }_i},{\mathcal{A}}_1={\mathcal{A}}_{01}^{{\sigma }_i},{\mathcal{B}}_0={\mathcal{B}}_{00}^{{\sigma }_i},{\mathcal{B}}_1={\mathcal{B}}_{01}^{{\sigma }_i},{\mathcal{C}}_0={\mathcal{C}}_{00}^{{\sigma }_i},{\mathcal{C}}_1={\mathcal{C}}_{01}^{{\sigma }_i},{\mathcal{D}}_0={\mathcal{D}}_{00}^{{\sigma }_i},{\mathcal{D}}_1={\mathcal{D}}_{01}^{{\sigma }_i},\hfill \\ \hfill & {\mathcal{A}}_{11}={\mathcal{A}}_1{*}_N{\mathcal{L}}_{{\mathcal{A}}_0},{\mathcal{C}}_{11}={\mathcal{R}}_{{\mathcal{C}}_0}{*}_S{\mathcal{C}}_1,{\mathcal{B}}_{11}={\mathcal{B}}_1-{\mathcal{A}}_1{*}_N\left({\mathcal{A}}_0^{†}{*}_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N{\mathcal{D}}_0{*}_T{\mathcal{C}}_0^{†}\right),\hfill \\ \hfill & {\mathcal{D}}_{11}={\mathcal{D}}_1-\left({\mathcal{A}}_0^{†}{*}_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N{\mathcal{D}}_0{*}_T{\mathcal{C}}_0^{†}\right){*}_S{\mathcal{C}}_1,{\mathcal{A}}_2={\mathcal{R}}_{{\mathcal{A}}_0}{*}_M{\mathcal{A}}_{11},{\mathcal{B}}_2={\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill & {\mathcal{C}}_2={\mathcal{R}}_{{\mathcal{A}}_0}{*}_M{\mathcal{B}}_{11},{\mathcal{A}}_3={\mathcal{L}}_{{\mathcal{A}}_0},{\mathcal{B}}_3={\mathcal{C}}_{11}{*}_T{\mathcal{L}}_{{\mathcal{C}}_0},{\mathcal{C}}_3={\mathcal{D}}_{11}{*}_T{\mathcal{L}}_{{\mathcal{C}}_0},{\mathcal{A}}_4={\mathcal{A}}_3{*}_N{\mathcal{L}}_{{\mathcal{A}}_2},\hfill \\ \hfill & {\mathcal{B}}_4={\mathcal{R}}_{{\mathcal{B}}_2}{*}_S{\mathcal{B}}_3,{\mathcal{C}}_4={\mathcal{C}}_3-{\mathcal{A}}_3{*}_N{\mathcal{A}}_2^{†}{*}_M{\mathcal{C}}_2{*}_S{\mathcal{B}}_2^{†}{*}_S{\mathcal{B}}_3,{\mathcal{D}}_4={\mathcal{R}}_{{\mathcal{A}}_4}{*}_N{\mathcal{A}}_3,\hfill \\ \hfill & \mathcal{F}={\mathcal{A}}_2^{†}{*}_M{\mathcal{C}}_2{*}_S{\mathcal{B}}_2^{†}+{\mathcal{L}}_{{\mathcal{A}}_2}{*}_N{\mathcal{A}}_4^{†}{*}_N{\mathcal{C}}_4{*}_T{\mathcal{B}}_3^{†}-{\mathcal{L}}_{{\mathcal{A}}_2}{*}_N{\mathcal{A}}_4^{†}{*}_N{\mathcal{A}}_3{*}_N{\mathcal{D}}_4^{†}{*}_N{\mathcal{R}}_{{\mathcal{A}}_4}{*}_N{\mathcal{C}}_4{*}_T{\mathcal{B}}_3^{†}\hfill \\ \hfill & +{\mathcal{D}}_4^{†}{*}_N{\mathcal{R}}_{{\mathcal{A}}_4}{*}_N{\mathcal{C}}_4{*}_T{\mathcal{B}}_4^{†}{*}_S{\mathcal{R}}_{{\mathcal{B}}_2}.\hfill \end{array}$$

Then the subsequent descriptions are equivalent: 

• The system of dual split quaternion tensor equations (2) is solvable.
• The system of real tensor equations

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{*}_N{\mathcal{X}}_0={\mathcal{B}}_0,\hfill \\ {\mathcal{X}}_0{*}_S{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{A}}_0{*}_N{\mathcal{X}}_1+{\mathcal{A}}_1{*}_N{\mathcal{X}}_0={\mathcal{B}}_1,\hfill \\ {\mathcal{X}}_0{*}_S{\mathcal{C}}_1+{\mathcal{X}}_1{*}_S{\mathcal{C}}_0={\mathcal{D}}_1\hfill \end{array}\right.\end{array}$$

  (4)
  is consistent.
• $$\begin{array}{cc}\hfill & {\mathcal{R}}_{{\mathcal{A}}_0}{*}_M{\mathcal{B}}_0=0,{\mathcal{D}}_0{*}_T{\mathcal{L}}_{{\mathcal{C}}_0}=0,\hfill \\ \hfill & {\mathcal{A}}_0{*}_N{\mathcal{D}}_0={\mathcal{B}}_0{*}_S{\mathcal{C}}_0,{\mathcal{A}}_0{*}_N{\mathcal{D}}_1-{\mathcal{B}}_0{*}_S{\mathcal{C}}_1={\mathcal{B}}_1{*}_S{\mathcal{C}}_0-{\mathcal{A}}_1{*}_N{\mathcal{D}}_0,\hfill \\ \hfill & {\mathcal{R}}_{{\mathcal{A}}_2}{*}_M{\mathcal{C}}_2=0,{\mathcal{C}}_2{*}_S{\mathcal{L}}_{{\mathcal{B}}_2}=0,{\mathcal{R}}_{{\mathcal{A}}_3}{*}_N{\mathcal{C}}_3=0,{\mathcal{C}}_3{*}_T{\mathcal{L}}_{{\mathcal{B}}_3}=0,{\mathcal{R}}_{{\mathcal{A}}_4}{*}_N{\mathcal{C}}_4{*}_T{\mathcal{L}}_{{\mathcal{B}}_4}=0.\hfill \end{array}$$

Based on these circumstances, the general solution of the system (2) can be represented as $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$, where

$$\begin{array}{cc}\hfill {\mathcal{X}}_{00}& ={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{*}_N({\mathcal{X}}_0+{\mathcal{R}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{T}}_S^T){*}_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],\hfill \\ \hfill {\mathcal{X}}_{01}& ={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{*}_N({\mathcal{X}}_1+{\mathcal{R}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{T}}_S^T){*}_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],\hfill \\ \hfill {\mathcal{X}}_0& ={\mathcal{A}}_0^{†}{*}_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N{\mathcal{D}}_0{*}_T{\mathcal{C}}_0^{†}+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N\mathcal{W}{*}_S{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill {\mathcal{X}}_1& ={\mathcal{A}}_0^{†}{*}_M({\mathcal{B}}_{11}-{\mathcal{A}}_{11}{*}_N\mathcal{W}{*}_S{\mathcal{R}}_{{\mathcal{C}}_0})+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N({\mathcal{D}}_{11}-{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N\mathcal{W}{*}_S{\mathcal{C}}_{11}){*}_T{\mathcal{C}}_0^{†}\hfill \\ & +{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N{\mathcal{W}}_1{*}_S{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill \mathcal{W}& =\mathcal{F}+{\mathcal{L}}_{{\mathcal{A}}_2}{*}_N{\mathcal{L}}_{{\mathcal{A}}_4}{*}_N{\mathcal{W}}_2+{\mathcal{W}}_3{*}_S{\mathcal{R}}_{{\mathcal{B}}_4}{*}_S{\mathcal{R}}_{{\mathcal{B}}_2}+{\mathcal{L}}_{{\mathcal{A}}_2}{*}_N{\mathcal{W}}_4{*}_S{\mathcal{R}}_{{\mathcal{B}}_3}+{\mathcal{L}}_{{\mathcal{A}}_3}{*}_N{\mathcal{W}}_5{*}_S{\mathcal{R}}_{{\mathcal{B}}_2},\hfill \end{array}$$

and ${\mathcal{W}}_i(i=\overline{1,5})$ are random tensors with proper dimensions.

Proof. (1)⇔ (2)

If condition (1) holds, it indicates that the system (2) possesses a solution. Thus, we can express the solution for the system (2) as $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ\in {\mathbb{DQ}}_s^{J_1\times \cdots \times J_N\times K_1\times \cdots \times K_S}$, where ${\mathcal{X}}_{00},{\mathcal{X}}_{01}\in {\mathbb{H}}_s^{J_1\times \cdots \times J_N\times K_1\times \cdots \times K_S}$. By substituting $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$ into system (2), we obtain the following split quaternion tensor equations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_{00}{*}_N{\mathcal{X}}_{00}={\mathcal{B}}_{00},\hfill \\ {\mathcal{X}}_{00}{*}_S{\mathcal{C}}_{00}={\mathcal{D}}_{00},\hfill \\ {\mathcal{A}}_{00}{*}_N{\mathcal{X}}_{01}+{\mathcal{A}}_{01}{*}_N{\mathcal{X}}_{00}={\mathcal{B}}_{01},\hfill \\ {\mathcal{X}}_{00}{*}_S{\mathcal{C}}_{01}+{\mathcal{X}}_{01}{*}_S{\mathcal{C}}_{00}={\mathcal{D}}_{01}.\hfill \end{array}\right.\end{array}$$

(5)

Let ${\mathcal{X}}_0={\mathcal{X}}_{00}^{{\sigma }_i},{\mathcal{X}}_1={\mathcal{X}}_{01}^{{\sigma }_i}$. Apply the real representation to the system, and by (b), (c) of Proposition (2), then we have

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_{00}^{{\sigma }_i}{*}_N{\mathcal{X}}_{00}^{{\sigma }_i}={\mathcal{B}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_i}{*}_S{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{A}}_{00}^{{\sigma }_i}{*}_N{\mathcal{X}}_{01}^{{\sigma }_i}+{\mathcal{A}}_{01}^{{\sigma }_i}{*}_N{\mathcal{X}}_{00}^{{\sigma }_i}={\mathcal{B}}_{01}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_i}{*}_S{\mathcal{C}}_{01}^{{\sigma }_i}+{\mathcal{X}}_{01}^{{\sigma }_i}{*}_S{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{01}^{{\sigma }_i}.\hfill \end{array}\right.\end{array}$$

(6)

i.e.,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{*}_N{\mathcal{X}}_0={\mathcal{B}}_0,\hfill \\ {\mathcal{X}}_0{*}_S{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{A}}_0{*}_N{\mathcal{X}}_1+{\mathcal{A}}_1{*}_N{\mathcal{X}}_0={\mathcal{B}}_1,\hfill \\ {\mathcal{X}}_0{*}_S{\mathcal{C}}_1+{\mathcal{X}}_1{*}_S{\mathcal{C}}_0={\mathcal{D}}_1.\hfill \end{array}\right.\end{array}$$

(7)

Thus, $({\mathcal{X}}_0,{\mathcal{X}}_1)$ is a pair of solutions to the system (4).

On the other hand, let $({\mathcal{X}}_0,{\mathcal{X}}_1)$ be the solutions to the system (4). By (da) of Proposition (2), we have

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{R}}_M^T{*}_M{\mathcal{A}}_0{*}_N{\mathcal{R}}_N{*}_N{\mathcal{X}}_0={\mathcal{R}}_M^T{*}_M{\mathcal{B}}_0{*}_S{\mathcal{R}}_S,\hfill \\ {\mathcal{X}}_0{*}_S{\mathcal{R}}_S^T{*}_S{\mathcal{C}}_0{*}_T{\mathcal{R}}_T={\mathcal{R}}_N^T{*}_N{\mathcal{D}}_0{*}_T{\mathcal{R}}_T,\hfill \\ {\mathcal{R}}_M^T{*}_M{\mathcal{A}}_0{*}_N{\mathcal{R}}_N{*}_N{\mathcal{X}}_1+{\mathcal{R}}_M^T{*}_M{\mathcal{A}}_1{*}_N{\mathcal{R}}_N{*}_N{\mathcal{X}}_0={\mathcal{R}}_M^T{*}_M{\mathcal{B}}_1{*}_S{\mathcal{R}}_S,\hfill \\ {\mathcal{X}}_0{*}_S{\mathcal{R}}_S^T{*}_S{\mathcal{C}}_1{*}_T{\mathcal{R}}_T+{\mathcal{X}}_1{*}_S{\mathcal{R}}_S^T{*}_S{\mathcal{C}}_0{*}_T{\mathcal{R}}_T={\mathcal{R}}_N^T{*}_N{\mathcal{D}}_1{*}_T{\mathcal{R}}_T.\hfill \end{array}\right.\end{array}$$

(8)

i.e.,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{*}_N{\mathcal{R}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{R}}_S^T={\mathcal{B}}_0,\hfill \\ {\mathcal{R}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{R}}_S^T{*}_S{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{A}}_0{*}_N{\mathcal{R}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{R}}_S^T+{\mathcal{A}}_1{*}_N{\mathcal{R}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{R}}_S^T={\mathcal{B}}_1,\hfill \\ {\mathcal{R}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{R}}_S^T{*}_S{\mathcal{C}}_1+{\mathcal{R}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{R}}_S^T{*}_S{\mathcal{C}}_0={\mathcal{D}}_1.\hfill \end{array}\right.\end{array}$$

(9)

Thus, $({\mathcal{R}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{R}}_S^T,{\mathcal{R}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{R}}_S^T)$ represent solutions to the system of real tensor equations. Likewise, $({\mathcal{S}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{S}}_S^T,{\mathcal{S}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{S}}_S^T)$ and $({\mathcal{T}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{T}}_S^T,{\mathcal{T}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{T}}_S^T)$ are also solutions to the system. Then, we define

$${\mathcal{Y}}_0:={\displaystyle \frac{1}{4}}({\mathcal{X}}_0+{\mathcal{R}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{T}}_S^T),$$

$${\mathcal{Y}}_1:={\displaystyle \frac{1}{4}}({\mathcal{X}}_1+{\mathcal{R}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{T}}_S^T).$$

Set

$${\mathcal{X}}_0=\left[\begin{array}{cccc}{\mathcal{V}}_{11}& {\mathcal{V}}_{12}& {\mathcal{V}}_{13}& {\mathcal{V}}_{14}\\ {\mathcal{V}}_{21}& {\mathcal{V}}_{22}& {\mathcal{V}}_{23}& {\mathcal{V}}_{24}\\ {\mathcal{V}}_{31}& {\mathcal{V}}_{32}& {\mathcal{V}}_{33}& {\mathcal{V}}_{34}\\ {\mathcal{V}}_{41}& {\mathcal{V}}_{42}& {\mathcal{V}}_{43}& {\mathcal{V}}_{44}\end{array}\right]\in {\mathbb{R}}^{J_1\times \cdots \times 4J_N\times K_1\times \cdots \times 4K_S},$$

$${\mathcal{X}}_1=\left[\begin{array}{cccc}{\mathcal{W}}_{11}& {\mathcal{W}}_{12}& {\mathcal{W}}_{13}& {\mathcal{W}}_{14}\\ {\mathcal{W}}_{21}& {\mathcal{W}}_{22}& {\mathcal{W}}_{23}& {\mathcal{W}}_{24}\\ {\mathcal{W}}_{31}& {\mathcal{W}}_{32}& {\mathcal{W}}_{33}& {\mathcal{W}}_{34}\\ {\mathcal{W}}_{41}& {\mathcal{W}}_{42}& {\mathcal{W}}_{43}& {\mathcal{W}}_{44}\end{array}\right]\in {\mathbb{R}}^{J_1\times \cdots \times 4J_N\times K_1\times \cdots \times 4K_S}.$$

By direct computation, we have

$${\mathcal{Y}}_0=\left[\begin{array}{cccc}{\mathcal{B}}_0& {\mathcal{B}}_1& {\mathcal{B}}_2& {\mathcal{B}}_3\\ -{\mathcal{B}}_1& {\mathcal{B}}_0& -{\mathcal{B}}_3& {\mathcal{B}}_2\\ {\mathcal{B}}_2& -{\mathcal{B}}_3& {\mathcal{B}}_0& -{\mathcal{B}}_1\\ {\mathcal{B}}_3& {\mathcal{B}}_2& {\mathcal{B}}_1& {\mathcal{B}}_0\end{array}\right]$$

and

$${\mathcal{Y}}_1=\left[\begin{array}{cccc}{\mathcal{D}}_0& {\mathcal{D}}_1& {\mathcal{D}}_2& {\mathcal{D}}_3\\ -{\mathcal{D}}_1& {\mathcal{D}}_0& -{\mathcal{D}}_3& {\mathcal{D}}_2\\ {\mathcal{D}}_2& -{\mathcal{D}}_3& {\mathcal{D}}_0& -{\mathcal{D}}_1\\ {\mathcal{D}}_3& {\mathcal{D}}_2& {\mathcal{D}}_1& {\mathcal{D}}_0\end{array}\right],$$

where

$${\mathcal{B}}_0={\displaystyle \frac{1}{4}}({\mathcal{V}}_{11}+{\mathcal{V}}_{22}+{\mathcal{V}}_{33}+{\mathcal{V}}_{44}),{\mathcal{B}}_1={\displaystyle \frac{1}{4}}({\mathcal{V}}_{12}-{\mathcal{V}}_{21}-{\mathcal{V}}_{34}+{\mathcal{V}}_{43}),$$

$${\mathcal{B}}_2={\displaystyle \frac{1}{4}}({\mathcal{V}}_{13}+{\mathcal{V}}_{24}+{\mathcal{V}}_{31}+{\mathcal{V}}_{42}),{\mathcal{B}}_3={\displaystyle \frac{1}{4}}({\mathcal{V}}_{14}-{\mathcal{V}}_{23}-{\mathcal{V}}_{32}+{\mathcal{V}}_{41}),$$

and

$${\mathcal{D}}_0={\displaystyle \frac{1}{4}}({\mathcal{W}}_{11}+{\mathcal{W}}_{22}+{\mathcal{W}}_{33}+{\mathcal{W}}_{44}),{\mathcal{D}}_1={\displaystyle \frac{1}{4}}({\mathcal{W}}_{12}-{\mathcal{W}}_{21}-{\mathcal{W}}_{34}+{\mathcal{W}}_{43}),$$

$${\mathcal{D}}_2={\displaystyle \frac{1}{4}}({\mathcal{W}}_{13}+{\mathcal{W}}_{24}+{\mathcal{W}}_{31}+{\mathcal{W}}_{42}),{\mathcal{D}}_3={\displaystyle \frac{1}{4}}({\mathcal{W}}_{14}-{\mathcal{W}}_{23}-{\mathcal{W}}_{32}+{\mathcal{W}}_{41}).$$

Then, we let

$${\mathcal{X}}_{00}={\mathcal{B}}_0+{\mathcal{B}}_{1}i+{\mathcal{B}}_{2}j+{\mathcal{B}}_{3}k={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{*}_N{\mathcal{Y}}_0{*}_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right]$$

and

$${\mathcal{X}}_{01}={\mathcal{D}}_0+{\mathcal{D}}_{1}i+{\mathcal{D}}_{2}j+{\mathcal{D}}_{3}k={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{*}_N{\mathcal{Y}}_1{*}_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],$$

where ${\mathcal{X}}_{00}$ and ${\mathcal{X}}_{01}\in {\mathbb{H}}_s^{J_1\times \cdots \times J_N\times K_1\times \cdots \times K_S}$.

Due to (fa) of Proposition (2), ${\mathcal{Y}}_0={\mathcal{X}}_{00}^{{\sigma }_i}$, ${\mathcal{Y}}_1={\mathcal{X}}_{01}^{{\sigma }_i}$. Thus, due to

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_{00}^{{\sigma }_i}{*}_N{\mathcal{X}}_{00}^{{\sigma }_i}={\mathcal{B}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_i}{*}_S{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{A}}_{00}^{{\sigma }_i}{*}_N{\mathcal{X}}_{01}^{{\sigma }_i}+{\mathcal{A}}_{01}^{{\sigma }_i}{*}_N{\mathcal{X}}_{00}^{{\sigma }_i}={\mathcal{B}}_{01}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_i}{*}_S{\mathcal{C}}_{01}^{{\sigma }_i}+{\mathcal{X}}_{01}^{{\sigma }_i}{*}_S{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{01}^{{\sigma }_i},\hfill \end{array}\right.\end{array}$$

(10)

we can obtain $({\mathcal{X}}_{00},{\mathcal{X}}_{01})$ as the solution of system (5). And it is clear that system (2) and system (5) are equivalent. Therefore, when system (2) has solutions, system (4) also has solutions, and vice versa. In addition, we can deduce the general solution of system of dual split quaternion tensor equations by Lemma (4) as $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$, where

$$\begin{array}{cc}\hfill & {\mathcal{X}}_{00}={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{*}_N({\mathcal{X}}_0+{\mathcal{R}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{T}}_S^T){*}_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],\hfill \\ \hfill & {\mathcal{X}}_{01}={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{*}_N({\mathcal{X}}_1+{\mathcal{R}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{T}}_S^T){*}_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],\hfill \\ \hfill & {\mathcal{X}}_0={\mathcal{A}}_0^{†}{*}_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N{\mathcal{D}}_0{*}_T{\mathcal{C}}_0^{†}+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N\mathcal{W}{*}_S{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill & {\mathcal{X}}_1={\mathcal{A}}_0^{†}{*}_M({\mathcal{B}}_{11}-{\mathcal{A}}_{11}{*}_N\mathcal{W}{*}_S{\mathcal{R}}_{{\mathcal{C}}_0})+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N({\mathcal{D}}_{11}-{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N\mathcal{W}{*}_S{\mathcal{C}}_{11}){*}_T{\mathcal{C}}_0^{†}\hfill \\ \hfill & +{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N{\mathcal{W}}_1{*}_S{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill & \mathcal{W}=\mathcal{F}+{\mathcal{L}}_{{\mathcal{A}}_2}{*}_N{\mathcal{L}}_{{\mathcal{A}}_4}{*}_N{\mathcal{W}}_2+{\mathcal{W}}_3{*}_S{\mathcal{R}}_{{\mathcal{B}}_4}{*}_S{\mathcal{R}}_{{\mathcal{B}}_2}+{\mathcal{L}}_{{\mathcal{A}}_2}{*}_N{\mathcal{W}}_4{*}_S{\mathcal{R}}_{{\mathcal{B}}_3}+{\mathcal{L}}_{{\mathcal{A}}_3}{*}_N{\mathcal{W}}_5{*}_S{\mathcal{R}}_{{\mathcal{B}}_2},\hfill \end{array}$$

and ${\mathcal{W}}_i(i=\overline{1,5})$ are random tensors with suitable size.

Besides, (2) and (3) are equivalent to each other that can be easily proven using Lemma (3) and Lemma (4). We will not elaborate further on these points here.    □

In the following part, we will propose equivalent conditions required when system (2) have $\eta$-Hermitian solutions.

Theorem 2.

Suppose that $\mathcal{A}={\mathcal{A}}_{00}+{\mathcal{A}}_{01}ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, $\mathcal{B}={\mathcal{B}}_{00}+{\mathcal{B}}_{01}ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, $\mathcal{C}={\mathcal{C}}_{00}+{\mathcal{C}}_{01}ϵ\in {\mathbb{DQ}}_s^{J_1\times \cdots \times J_N\times K_1\times \cdots \times K_T}$, and $\mathcal{D}={\mathcal{D}}_{00}+{\mathcal{D}}_{01}ϵ\in {\mathbb{DQ}}_s^{J_1\times \cdots \times J_N\times K_1\times \cdots \times K_T}$.

Set

$$\begin{array}{cc}\hfill {\mathcal{A}}_0& =\left\{\begin{array}{cc}{\mathcal{A}}_{00}^{{\sigma }_i},\hfill & \eta =i,\hfill \\ {\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j},\hfill & \eta =j,\hfill \\ {\left({\mathcal{A}}_{00}^j\right)}^{{\sigma }_k},\hfill & \eta =k,\hfill \end{array}\right.{\mathcal{A}}_1=\left\{\begin{array}{cc}{\mathcal{A}}_{01}^{{\sigma }_i},\hfill & \eta =i,\hfill \\ {\left({\mathcal{A}}_{01}^k\right)}^{{\sigma }_j},\hfill & \eta =j,\hfill \\ {\left({\mathcal{A}}_{01}^j\right)}^{{\sigma }_k},\hfill & \eta =k,\hfill \end{array}\right.\hfill \\ \hfill {\mathcal{B}}_0& ={\mathcal{B}}_{00}^{{\sigma }_i},{\mathcal{B}}_1={\mathcal{B}}_{01}^{{\sigma }_i},{\mathcal{C}}_0={\mathcal{C}}_{00}^{{\sigma }_i},{\mathcal{C}}_1={\mathcal{C}}_{01}^{{\sigma }_i},\eta =\{i,j,k\}\hfill \\ \hfill {\mathcal{D}}_0& ={\mathcal{D}}_{00}^{{\sigma }_{\eta }},{\mathcal{D}}_1={\mathcal{D}}_{01}^{{\sigma }_{\eta }},\eta =\{i,j,k\}.\hfill \end{array}$$

Then the system (2) have η-Hermitian solutions $\mathcal{X}={\mathcal{X}}^{\eta *}\in {\mathbb{DQ}}_s^{J_1\times \cdots \times J_N\times J_1\times \cdots \times J_N},\eta =\{i,j,k\}$, and this means that the system (4) possesses a pair of solutions $({\mathcal{X}}_0,{\mathcal{X}}_1)$ that satisfies ${\mathcal{X}}_0={\mathcal{X}}_0^T,{\mathcal{X}}_1={\mathcal{X}}_1^T$, and vice versa.

Proof. 

It is only necessary to demonstrate the situation for $\eta =j$, the other situations are identical to it, so we omit them. Let’s assume that $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ\in {\mathbb{DQ}}_s^{J_1\times \cdots \times J_N\times J_1\times \cdots \times J_N}$ is a j-Hermitian solution of system (2), where $\mathcal{X}={\mathcal{X}}^{j*}$. Then we have

$$\begin{array}{c}\hfill {\mathcal{X}}_{00}={\mathcal{X}}_{00}^{j*},{\mathcal{X}}_{01}={\mathcal{X}}_{01}^{j*}.\end{array}$$

By substituting $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$ into system (2), then system (2) corresponds to the subsequent system:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_{00}{*}_N{\mathcal{X}}_{00}=B_{00},\hfill \\ {\mathcal{X}}_{00}{*}_N{\mathcal{C}}_{00}={\mathcal{D}}_{00},\hfill \\ {\mathcal{A}}_{00}{*}_N{\mathcal{X}}_{01}+{\mathcal{A}}_{01}{*}_N{\mathcal{X}}_{00}=B_{01},\hfill \\ {\mathcal{X}}_{00}{*}_N{\mathcal{C}}_{01}+{\mathcal{X}}_{01}{*}_N{\mathcal{C}}_{00}={\mathcal{D}}_{01}.\hfill \end{array}\right.\end{array}$$

(11)

Let ${\mathcal{X}}_0={\mathcal{X}}_{00}^{{\sigma }_j},{\mathcal{X}}_1={\mathcal{X}}_{01}^{{\sigma }_j}$. Apply the real representation to the system, and by (b), (c) of Proposition (2), then we have

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_{00}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{B}}_{00}^{{\sigma }_j},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{D}}_{00}^{{\sigma }_j},\hfill \\ {\mathcal{A}}_{00}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{X}}_{01}^{{\sigma }_j}+{\mathcal{A}}_{01}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{B}}_{01}^{{\sigma }_j},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{C}}_{01}^{{\sigma }_j}+{\mathcal{X}}_{01}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{D}}_{01}^{{\sigma }_j}.\hfill \end{array}\right.\end{array}$$

(12)

i.e.,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{V}}_M{*}_M{\mathcal{A}}_{00}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{V}}_M{*}_M{\mathcal{B}}_{00}^{{\sigma }_j},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{D}}_{00}^{{\sigma }_j},\hfill \\ {\mathcal{V}}_M{*}_M{\mathcal{A}}_{00}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{X}}_{01}^{{\sigma }_j}+{\mathcal{V}}_M{*}_M{\mathcal{A}}_{01}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{V}}_M{*}_M{\mathcal{B}}_{01}^{{\sigma }_j},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{C}}_{01}^{{\sigma }_j}+{\mathcal{X}}_{01}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{D}}_{01}^{{\sigma }_j}.\hfill \end{array}\right.\end{array}$$

(13)

According to (g) of Proposition (2) and the definition of real representation, we have

$$\begin{array}{cc}\hfill & {\mathcal{V}}_M{*}_M{\mathcal{A}}_{00}^{{\sigma }_j}{*}_N{\mathcal{V}}_N={\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j},{\mathcal{V}}_M{*}_M{\mathcal{A}}_{01}^{{\sigma }_j}{*}_N{\mathcal{V}}_N={\left({\mathcal{A}}_{01}^k\right)}^{{\sigma }_j},\hfill \\ \hfill & {\mathcal{V}}_M{*}_M{\mathcal{B}}_{00}^{{\sigma }_j}={\mathcal{B}}_{00}^{{\sigma }_i},{\mathcal{V}}_M{*}_M{\mathcal{B}}_{01}^{{\sigma }_j}={\mathcal{B}}_{01}^{{\sigma }_i},{\mathcal{V}}_N{*}_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{C}}_{00}^{{\sigma }_i},{\mathcal{V}}_N{*}_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{C}}_{00}^{{\sigma }_i}.\hfill \end{array}$$

Thus, the above system can be expressed as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j}{*}_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{B}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{*}_N{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{00}^{{\sigma }_j},\hfill \\ {\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j}{*}_N{\mathcal{X}}_{01}^{{\sigma }_j}+{\left({\mathcal{A}}_{01}^k\right)}^{{\sigma }_j}{*}_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{B}}_{01}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{*}_N{\mathcal{C}}_{01}^{{\sigma }_i}+{\mathcal{X}}_{01}^{{\sigma }_j}{*}_N{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{01}^{{\sigma }_j},\hfill \end{array}\right.\end{array}$$

(14)

i.e.,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{*}_N{\mathcal{X}}_0={\mathcal{B}}_0,\hfill \\ {\mathcal{X}}_0{*}_N{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{A}}_0{*}_N{\mathcal{X}}_1+{\mathcal{A}}_1{*}_N{\mathcal{X}}_0={\mathcal{B}}_1,\hfill \\ {\mathcal{X}}_0{*}_N{\mathcal{C}}_1+{\mathcal{X}}_1{*}_N{\mathcal{C}}_0={\mathcal{D}}_1.\hfill \end{array}\right.\end{array}$$

(15)

By (e) in Proposition (2), we have

$${\left({\mathcal{X}}_{00}^{j*}\right)}^{{\sigma }_j}={\left({\mathcal{X}}_{00}^{{\sigma }_j}\right)}^T,{\left({\mathcal{X}}_{01}^{j*}\right)}^{{\sigma }_j}={\left({\mathcal{X}}_{01}^{{\sigma }_j}\right)}^T.$$

Consequently,

$$\begin{array}{c}\hfill {\mathcal{X}}_{00}^{{\sigma }_j}={\left({\mathcal{X}}_{00}^{j*}\right)}^{{\sigma }_j}={\left({\mathcal{X}}_{00}^{{\sigma }_j}\right)}^T,{\mathcal{X}}_{01}^{{\sigma }_j}={\left({\mathcal{X}}_{01}^{j*}\right)}^{{\sigma }_j}={\left({\mathcal{X}}_{01}^{{\sigma }_j}\right)}^T,\end{array}$$

i.e.,

$${\mathcal{X}}_0={\mathcal{X}}_0^T,{\mathcal{X}}_1={\mathcal{X}}_1^T.$$

On the other hand, if system (4) has a pair of solutions $({\mathcal{X}}_0,{\mathcal{X}}_1)$ that satisfies ${\mathcal{X}}_0={\mathcal{X}}_0^T,{\mathcal{X}}_1={\mathcal{X}}_1^T$, then the system (4) can be denoted as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j}{*}_N{\mathcal{X}}_0={\mathcal{B}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_0{*}_N{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{00}^{{\sigma }_j},\hfill \\ {\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j}{*}_N{\mathcal{X}}_1+{\left({\mathcal{A}}_{01}^k\right)}^{{\sigma }_j}{*}_N{\mathcal{X}}_0={\mathcal{B}}_{01}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_0{*}_N{\mathcal{C}}_{01}^{{\sigma }_i}+{\mathcal{X}}_1{*}_N{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{01}^{{\sigma }_j}\hfill \end{array}\right.\end{array}$$

(16)

and

$$\begin{array}{c}\hfill {\mathcal{X}}_0={\mathcal{X}}_0^T,{\mathcal{X}}_1={\mathcal{X}}_1^T.\end{array}$$

As indicated by (db) in Proposition (2),

$$\begin{array}{cc}\hfill & (-{\mathcal{R}}_N{*}_N{\mathcal{X}}_0{*}_N{\mathcal{R}}_N^T,-{\mathcal{R}}_N{*}_N{\mathcal{X}}_1{*}_N{\mathcal{R}}_N^T),\hfill \\ & (-{\mathcal{S}}_N{*}_N{\mathcal{X}}_0{*}_N{\mathcal{S}}_N^T,-{\mathcal{S}}_N{*}_N{\mathcal{X}}_1{*}_N{\mathcal{S}}_N^T),\hfill \\ & ({\mathcal{T}}_N{*}_N{\mathcal{X}}_0{*}_N{\mathcal{T}}_N^T,{\mathcal{T}}_N{*}_N{\mathcal{X}}_1{*}_N{\mathcal{T}}_N^T)\hfill \end{array}$$

are also solutions to the system. Next, we define

$${\mathcal{Y}}_0:={\displaystyle \frac{1}{4}}({\mathcal{X}}_0-{\mathcal{R}}_N{*}_N{\mathcal{X}}_0{*}_N{\mathcal{R}}_N^T-{\mathcal{S}}_N{*}_N{\mathcal{X}}_0{*}_N{\mathcal{S}}_N^T+{\mathcal{T}}_N{*}_N{\mathcal{X}}_0{*}_N{\mathcal{T}}_N^T),$$

$${\mathcal{Y}}_1:={\displaystyle \frac{1}{4}}({\mathcal{X}}_1-{\mathcal{R}}_N{*}_N{\mathcal{X}}_1{*}_N{\mathcal{R}}_N^T-{\mathcal{S}}_N{*}_N{\mathcal{X}}_1{*}_N{\mathcal{S}}_N^T+{\mathcal{T}}_N{*}_N{\mathcal{X}}_1{*}_N{\mathcal{T}}_N^T).$$

Set

$${\mathcal{X}}_0=\left[\begin{array}{cccc}{\mathcal{V}}_{11}& {\mathcal{V}}_{12}& {\mathcal{V}}_{13}& {\mathcal{V}}_{14}\\ {\mathcal{V}}_{21}& {\mathcal{V}}_{22}& {\mathcal{V}}_{23}& {\mathcal{V}}_{24}\\ {\mathcal{V}}_{31}& {\mathcal{V}}_{32}& {\mathcal{V}}_{33}& {\mathcal{V}}_{34}\\ {\mathcal{V}}_{41}& {\mathcal{V}}_{42}& {\mathcal{V}}_{43}& {\mathcal{V}}_{44}\end{array}\right]\in {\mathbb{R}}^{J_1\times \cdots \times 4J_N\times J_1\times \cdots \times 4J_N},$$

$${\mathcal{X}}_1=\left[\begin{array}{cccc}{\mathcal{W}}_{11}& {\mathcal{W}}_{12}& {\mathcal{W}}_{13}& {\mathcal{W}}_{14}\\ {\mathcal{W}}_{21}& {\mathcal{W}}_{22}& {\mathcal{W}}_{23}& {\mathcal{W}}_{24}\\ {\mathcal{W}}_{31}& {\mathcal{W}}_{32}& {\mathcal{W}}_{33}& {\mathcal{W}}_{34}\\ {\mathcal{W}}_{41}& {\mathcal{W}}_{42}& {\mathcal{W}}_{43}& {\mathcal{W}}_{44}\end{array}\right]\in {\mathbb{R}}^{J_1\times \cdots \times 4J_N\times J_1\times \cdots \times 4J_N}.$$

By direct computation, we have

$${\mathcal{Y}}_0=\left[\begin{array}{cccc}{\mathcal{B}}_0& {\mathcal{B}}_1& {\mathcal{B}}_2& {\mathcal{B}}_3\\ {\mathcal{B}}_1& -{\mathcal{B}}_0& {\mathcal{B}}_3& -{\mathcal{B}}_2\\ -{\mathcal{B}}_2& {\mathcal{B}}_3& -{\mathcal{B}}_0& {\mathcal{B}}_1\\ {\mathcal{B}}_3& {\mathcal{B}}_2& {\mathcal{B}}_1& {\mathcal{B}}_0\end{array}\right]$$

and

$${\mathcal{Y}}_1=\left[\begin{array}{cccc}{\mathcal{D}}_0& {\mathcal{D}}_1& {\mathcal{D}}_2& {\mathcal{D}}_3\\ {\mathcal{D}}_1& -{\mathcal{D}}_0& {\mathcal{D}}_3& -{\mathcal{D}}_2\\ -{\mathcal{D}}_2& {\mathcal{D}}_3& -{\mathcal{D}}_0& {\mathcal{D}}_1\\ {\mathcal{D}}_3& {\mathcal{D}}_2& {\mathcal{D}}_1& {\mathcal{D}}_0\end{array}\right],$$

where

$${\mathcal{B}}_0={\displaystyle \frac{1}{4}}({\mathcal{V}}_{11}-{\mathcal{V}}_{22}-{\mathcal{V}}_{33}+{\mathcal{V}}_{44}),{\mathcal{B}}_1={\displaystyle \frac{1}{4}}({\mathcal{V}}_{12}+{\mathcal{V}}_{21}+{\mathcal{V}}_{34}+{\mathcal{V}}_{43}),$$

$${\mathcal{B}}_2={\displaystyle \frac{1}{4}}({\mathcal{V}}_{13}-{\mathcal{V}}_{24}-{\mathcal{V}}_{31}+{\mathcal{V}}_{42}),{\mathcal{B}}_3={\displaystyle \frac{1}{4}}({\mathcal{V}}_{14}+{\mathcal{V}}_{23}+{\mathcal{V}}_{32}+{\mathcal{V}}_{41}),$$

and

$${\mathcal{D}}_0={\displaystyle \frac{1}{4}}({\mathcal{W}}_{11}-{\mathcal{W}}_{22}-{\mathcal{W}}_{33}+{\mathcal{W}}_{44}),{\mathcal{D}}_1={\displaystyle \frac{1}{4}}({\mathcal{W}}_{12}+{\mathcal{W}}_{21}+{\mathcal{W}}_{34}+{\mathcal{W}}_{43}),$$

$${\mathcal{D}}_2={\displaystyle \frac{1}{4}}({\mathcal{W}}_{13}-{\mathcal{W}}_{24}-{\mathcal{W}}_{31}+{\mathcal{W}}_{42}),{\mathcal{D}}_3={\displaystyle \frac{1}{4}}({\mathcal{W}}_{14}+{\mathcal{W}}_{23}+{\mathcal{W}}_{32}+{\mathcal{W}}_{41}).$$

Then, we let

$$\begin{array}{c}\hfill {\mathcal{X}}_{00}={\mathcal{B}}_0+{\mathcal{B}}_{1}i+{\mathcal{B}}_{2}j+{\mathcal{B}}_{3}k={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_N& -i{\mathcal{I}}_N& -j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{*}_N{\mathcal{Y}}_0{*}_N\left[\begin{array}{c}{\mathcal{I}}_N\\ i{\mathcal{I}}_N\\ j{\mathcal{I}}_N\\ k{\mathcal{I}}_N\end{array}\right]\end{array}$$

and

$${\mathcal{X}}_{01}={\mathcal{D}}_0+{\mathcal{D}}_{1}i+{\mathcal{D}}_{2}j+{\mathcal{D}}_{3}k={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_N& -i{\mathcal{I}}_N& -j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{*}_N{\mathcal{Y}}_1{*}_N\left[\begin{array}{c}{\mathcal{I}}_N\\ i{\mathcal{I}}_N\\ j{\mathcal{I}}_N\\ k{\mathcal{I}}_N\end{array}\right],$$

where ${\mathcal{X}}_{00}$ and ${\mathcal{X}}_{01}\in {\mathbb{H}}_s^{J_1\times \cdots \times J_N\times J_1\times \cdots \times J_N}$.

Due to (fb) of Proposition (2), ${\mathcal{Y}}_0={\mathcal{X}}_{00}^{{\sigma }_j}$, ${\mathcal{Y}}_1={\mathcal{X}}_{01}^{{\sigma }_j}$. Thus,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j}{*}_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{B}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{*}_N{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{00}^{{\sigma }_j},\hfill \\ {\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j}{*}_N{\mathcal{X}}_{01}^{{\sigma }_j}+{\left({\mathcal{A}}_{01}^k\right)}^{{\sigma }_j}{*}_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{B}}_{01}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{*}_N{\mathcal{C}}_{01}^{{\sigma }_i}+{\mathcal{X}}_{01}^{{\sigma }_j}{*}_N{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{01}^{{\sigma }_j}.\hfill \end{array}\right.\end{array}$$

(17)

That is, $({\mathcal{X}}_{00}^{{\sigma }_j},{\mathcal{X}}_{01}^{{\sigma }_j})$ is a pair of solutions of system (4). Then,

$$\begin{array}{cc}\hfill {\mathcal{X}}_{00}^{{\sigma }_j}& ={\left({\mathcal{X}}_{00}^{{\sigma }_j}\right)}^T={\left({\mathcal{X}}_{00}^{j*}\right)}^{{\sigma }_j},\hfill \\ \hfill {\mathcal{X}}_{01}^{{\sigma }_j}& ={\left({\mathcal{X}}_{01}^{{\sigma }_j}\right)}^T={\left({\mathcal{X}}_{01}^{j*}\right)}^{{\sigma }_j}.\hfill \end{array}$$

The above system is equivalent to

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{V}}_M{*}_M{\mathcal{A}}_{00}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{V}}_M{*}_M{\mathcal{B}}_{00}^{{\sigma }_j},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{D}}_{00}^{{\sigma }_j},\hfill \\ {\mathcal{V}}_M{*}_M{\mathcal{A}}_{00}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{X}}_{01}^{{\sigma }_j}+{\mathcal{V}}_M{*}_M{\mathcal{A}}_{01}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{V}}_M{*}_M{\mathcal{B}}_{01}^{{\sigma }_j},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{C}}_{01}^{{\sigma }_j}+{\mathcal{X}}_{01}^{{\sigma }_j}{*}_N{\mathcal{V}}_N{*}_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{D}}_{01}^{{\sigma }_j},\hfill \end{array}\right.\end{array}$$

(18)

i.e.,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_{00}{*}_N{\mathcal{X}}_{00}={\mathcal{B}}_{00},\hfill \\ {\mathcal{X}}_{00}{*}_N{\mathcal{C}}_{00}={\mathcal{D}}_{00},\hfill \\ {\mathcal{A}}_{00}{*}_N{\mathcal{X}}_{01}+{\mathcal{A}}_{01}{*}_N{\mathcal{X}}_{00}={\mathcal{B}}_{01},\hfill \\ {\mathcal{X}}_{00}{*}_N{\mathcal{C}}_{01}+{\mathcal{X}}_{01}{*}_N{\mathcal{C}}_{00}={\mathcal{D}}_{01}\hfill \end{array}\right.\end{array}$$

(19)

and

$$\begin{array}{c}\hfill {\mathcal{X}}_{00}={\mathcal{X}}_{00}^{j*},{\mathcal{X}}_{01}={\mathcal{X}}_{01}^{j*}.\end{array}$$

It is obvious that system (19) and system (2) are equivalent. Consequently, $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ={\mathcal{X}}_{00}^{j*}+{\mathcal{X}}_{01}^{j*}ϵ={\mathcal{X}}^{j*}$ is a j-Hermitian solution of system (2).    □

Based on above theorems and lemmas, we will next present the equivalent condition when system (2) possesses a Hermitian solution. Additionally, we will put forward the equivalent criteria when two specific equations $\mathcal{A}{*}_N\mathcal{X}=\mathcal{B}$ and $\mathcal{X}{*}_M\mathcal{C}=\mathcal{D}$ have solutions, along with their general solution expressions.

Corollary 1.

Let $\mathcal{A}={\mathcal{A}}_{00}+{\mathcal{A}}_{01}ϵ$ and $\mathcal{B}={\mathcal{B}}_{00}+{\mathcal{B}}_{01}ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times K_1\times \cdots \times K_S}$, $\mathcal{C}={\mathcal{C}}_{00}+{\mathcal{C}}_{01}ϵ$ and $\mathcal{D}={\mathcal{D}}_{00}+{\mathcal{D}}_{01}ϵ\in {\mathbb{DQ}}_s^{K_1\times \cdots \times K_S\times S_1\times \cdots \times S_T}$. Set

$$\begin{array}{cc}\hfill {\mathcal{A}}_0& ={\left({\mathcal{A}}_{00}^i\right)}^{{\sigma }_1},{\mathcal{A}}_1={\left({\mathcal{A}}_{01}^i\right)}^{{\sigma }_1},{\mathcal{B}}_0={\mathcal{B}}_{00}^{{\sigma }_i},{\mathcal{B}}_1={\mathcal{B}}_{01}^{{\sigma }_i},\hfill \\ \hfill {\mathcal{C}}_0& ={\mathcal{C}}_{00}^{{\sigma }_i},{\mathcal{C}}_1={\mathcal{C}}_{01}^{{\sigma }_i},{\mathcal{D}}_0={\mathcal{D}}_{00}^{{\sigma }_1},{\mathcal{D}}_1={\mathcal{D}}_{01}^{{\sigma }_1}.\hfill \end{array}$$

Then the system (2) has a Hermitian solution $\mathcal{X}={\mathcal{X}}^{*}\in {\mathbb{DQ}}_s^{K_1\times \cdots \times K_S\times K_1\times \cdots \times K_S}$, and it means that the system of real tensor equations

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{*}_S{\mathcal{X}}_0={\mathcal{B}}_0,\hfill \\ {\mathcal{X}}_0{*}_S{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{A}}_0{*}_S{\mathcal{X}}_1+{\mathcal{A}}_1{*}_S{\mathcal{X}}_0={\mathcal{B}}_1,\hfill \\ {\mathcal{X}}_0{*}_S{\mathcal{C}}_1+{\mathcal{X}}_1{*}_S{\mathcal{C}}_0={\mathcal{D}}_1\hfill \end{array}\right.\end{array}$$

has a pair of symmetric solutions $({\mathcal{X}}_0,{\mathcal{X}}_1)$, and vice versa.

Corollary 2.

Let $\mathcal{A}\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times T_1\times \cdots \times T_N}$ and $\mathcal{B}\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times K_1\times \cdots \times K_S}$, where $\mathcal{A}={\mathcal{A}}_{00}+{\mathcal{A}}_{01}ϵ,\mathcal{B}={\mathcal{B}}_{00}+{\mathcal{B}}_{01}ϵ$. Set

$$\begin{array}{cc}\hfill & {\mathcal{A}}_0={\mathcal{A}}_{00}^{{\sigma }_i},{\mathcal{A}}_1={\mathcal{A}}_{01}^{{\sigma }_i},{\mathcal{B}}_0={\mathcal{B}}_{00}^{{\sigma }_i},{\mathcal{B}}_1={\mathcal{B}}_{01}^{{\sigma }_i},{\mathcal{B}}_2={\mathcal{B}}_1-{\mathcal{A}}_1{*}_N{\mathcal{A}}_0^{†}{*}_M{\mathcal{B}}_0,\hfill \\ \hfill & {\mathcal{A}}_2={\mathcal{A}}_1{*}_N{\mathcal{L}}_{{\mathcal{A}}_0},{\mathcal{A}}_3={\mathcal{R}}_{{\mathcal{A}}_0}{*}_M{\mathcal{A}}_2,{\mathcal{C}}_3={\mathcal{R}}_{{\mathcal{A}}_0}{*}_M{\mathcal{B}}_2.\hfill \end{array}$$

Then the subsequent descriptions correspond to each other: 

• Dual split quaternion tensor equation $\mathcal{A}{*}_N\mathcal{X}=\mathcal{B}$ is solvable.
• The following system of real tensor equations is consistent,

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{*}_N{\mathcal{X}}_0={\mathcal{B}}_0,\hfill \\ {\mathcal{A}}_0{*}_N{\mathcal{X}}_1+{\mathcal{A}}_1{*}_N{\mathcal{X}}_0={\mathcal{B}}_1.\hfill \end{array}\right.\end{array}$$

  (20)
• ${\mathcal{R}}_{{\mathcal{A}}_0}{*}_M{\mathcal{B}}_0=0,{\mathcal{R}}_{{\mathcal{A}}_3}{*}_M{\mathcal{C}}_3=0$.

Based on these circumstances, the general solution of tensor equation $\mathcal{A}{*}_N\mathcal{X}=\mathcal{B}$ is represented as $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$, where

$$\begin{array}{cc}\hfill & {\mathcal{X}}_{00}={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{*}_N({\mathcal{X}}_0+{\mathcal{R}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{*}_N{\mathcal{X}}_0{*}_S{\mathcal{T}}_S^T){*}_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],\hfill \\ \hfill & {\mathcal{X}}_{01}={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{*}_N({\mathcal{X}}_1+{\mathcal{R}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{*}_N{\mathcal{X}}_1{*}_S{\mathcal{T}}_S^T){*}_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\mathcal{X}}_0& ={\mathcal{A}}_0^{†}{*}_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N\mathcal{V},\hfill \\ \hfill {\mathcal{X}}_1& ={\mathcal{A}}_0^{†}{*}_M({\mathcal{B}}_2-{\mathcal{A}}_2{*}_N\mathcal{V})+{\mathcal{L}}_{{\mathcal{A}}_0}{*}_N{\mathcal{V}}_1,\hfill \\ \hfill \mathcal{V}& ={\mathcal{A}}_3^{†}{*}_M{\mathcal{C}}_3+{\mathcal{L}}_{{\mathcal{A}}_3}{*}_N{\mathcal{V}}_2,\hfill \end{array}$$

and ${\mathcal{V}}_1,{\mathcal{V}}_2$ are arbitrary real tensors with appropriate dimensions.

Corollary 3.

Suppose that $\mathcal{C}={\mathcal{C}}_0+{\mathcal{C}}_1ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$ and $\mathcal{D}={\mathcal{D}}_0+{\mathcal{D}}_1ϵ\in {\mathbb{DQ}}_s^{K_1\times \cdots \times K_T\times J_1\times \cdots \times J_N}$. Let

$$\begin{array}{cc}\hfill & {\mathcal{C}}_0={\mathcal{C}}_{00}^{{\sigma }_i},{\mathcal{C}}_1={\mathcal{C}}_{01}^{{\sigma }_i},{\mathcal{D}}_0={\mathcal{D}}_{00}^{{\sigma }_i},{\mathcal{D}}_1={\mathcal{D}}_{01}^{{\sigma }_i},{\mathcal{D}}_2={\mathcal{D}}_1-{\mathcal{D}}_0{*}_N{\mathcal{C}}_0^{†}{*}_M{\mathcal{C}}_1,\hfill \\ & {\mathcal{C}}_2={\mathcal{R}}_{{\mathcal{C}}_0}{*}_M{\mathcal{C}}_1,{\mathcal{B}}_3={\mathcal{C}}_2{*}_N{\mathcal{L}}_{{\mathcal{C}}_0},{\mathcal{C}}_3={\mathcal{D}}_2{*}_N{\mathcal{L}}_{{\mathcal{C}}_0}.\hfill \end{array}$$

Then the descriptions below correspond to each other: 

• Dual split quaternion tensor equation $\mathcal{X}{*}_M\mathcal{C}=\mathcal{D}$ is solvable.
• The following system of real tensor equations is consistent.

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{X}}_0{*}_M{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{X}}_0{*}_M{\mathcal{C}}_1+{\mathcal{X}}_1{*}_M{\mathcal{C}}_0={\mathcal{D}}_1.\hfill \end{array}\right.\end{array}$$

  (21)
• ${\mathcal{D}}_0{*}_N{\mathcal{L}}_{{\mathcal{C}}_0}=0,{\mathcal{C}}_3{*}_N{\mathcal{L}}_{{\mathcal{B}}_3}=0$.

Based on these situations, the general solution of tensor equation $\mathcal{X}{*}_M\mathcal{C}=\mathcal{D}$ can be expressed as $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$, where

$$\begin{array}{cc}\hfill & {\mathcal{X}}_{00}={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_T& i{\mathcal{I}}_T& j{\mathcal{I}}_T& k{\mathcal{I}}_T\end{array}\right]{*}_T({\mathcal{X}}_0+{\mathcal{R}}_T{*}_T{\mathcal{X}}_0{*}_M{\mathcal{R}}_M^T+{\mathcal{S}}_T{*}_T{\mathcal{X}}_0{*}_M{\mathcal{S}}_M^T+{\mathcal{T}}_T{*}_T{\mathcal{X}}_0{*}_M{\mathcal{T}}_M^T){*}_M\left[\begin{array}{c}{\mathcal{I}}_M\\ i{\mathcal{I}}_M\\ j{\mathcal{I}}_M\\ k{\mathcal{I}}_M\end{array}\right],\hfill \\ \hfill & {\mathcal{X}}_{01}={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_T& i{\mathcal{I}}_T& j{\mathcal{I}}_T& k{\mathcal{I}}_T\end{array}\right]{*}_T({\mathcal{X}}_1+{\mathcal{R}}_T{*}_T{\mathcal{X}}_1{*}_M{\mathcal{R}}_M^T+{\mathcal{S}}_T{*}_T{\mathcal{X}}_1{*}_M{\mathcal{S}}_M^T+{\mathcal{T}}_T{*}_T{\mathcal{X}}_1{*}_M{\mathcal{T}}_M^T){*}_M\left[\begin{array}{c}{\mathcal{I}}_M\\ i{\mathcal{I}}_M\\ j{\mathcal{I}}_M\\ k{\mathcal{I}}_M\end{array}\right],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\mathcal{X}}_0& ={\mathcal{D}}_0{*}_N{\mathcal{C}}_0^{†}+\mathcal{W}{*}_M{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill {\mathcal{X}}_1& =({\mathcal{D}}_2-\mathcal{W}{*}_M{\mathcal{C}}_2){*}_N{\mathcal{C}}_0^{†}+{\mathcal{W}}_1{*}_M{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill \mathcal{W}& ={\mathcal{C}}_3{*}_N{\mathcal{B}}_3^{†}+{\mathcal{W}}_2{*}_M{\mathcal{R}}_{{\mathcal{B}}_3},\hfill \end{array}$$

and ${\mathcal{W}}_1,{\mathcal{W}}_2$ denote random tensors over $\mathcal{R}$ with suitable dimensions.

4. Numerical Example

This segment will show an example to substantiate Theorem (1) and an example as an application of Theorem (1).

Example 2.

Let $\mathcal{A}={\mathcal{A}}_{00}+{\mathcal{A}}_{01}ϵ$, $B=B_{00}+B_{01}ϵ$, $\mathcal{C}={\mathcal{C}}_{00}+{\mathcal{C}}_{01}ϵ$ and $\mathcal{D}={\mathcal{D}}_{00}+{\mathcal{D}}_{01}ϵ$, where

$$\begin{array}{cc}\hfill & {\left({\mathcal{A}}_{00}\right)}_{1111}=i,{\left({\mathcal{A}}_{00}\right)}_{1121}=j,{\left({\mathcal{A}}_{00}\right)}_{1112}=k,{\left({\mathcal{A}}_{00}\right)}_{1122}=1,\hfill \\ \hfill & {\left({\mathcal{A}}_{00}\right)}_{2111}=0,{\left({\mathcal{A}}_{00}\right)}_{2121}=k,{\left({\mathcal{A}}_{00}\right)}_{2112}=i,{\left({\mathcal{A}}_{00}\right)}_{2122}=i+j,\hfill \\ \hfill & {\left({\mathcal{A}}_{00}\right)}_{1211}=-i,{\left({\mathcal{A}}_{00}\right)}_{1221}=1,{\left({\mathcal{A}}_{00}\right)}_{1212}=0,{\left({\mathcal{A}}_{00}\right)}_{1222}=j,\hfill \\ \hfill & {\left({\mathcal{A}}_{00}\right)}_{2211}=0,{\left({\mathcal{A}}_{00}\right)}_{2221}=i,{\left({\mathcal{A}}_{00}\right)}_{2212}=j,{\left({\mathcal{A}}_{00}\right)}_{2222}=1,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{A}}_{01}\right)}_{1111}=j,{\left({\mathcal{A}}_{01}\right)}_{1121}=k,{\left({\mathcal{A}}_{01}\right)}_{1112}=i,{\left({\mathcal{A}}_{01}\right)}_{1122}=0,\hfill \\ \hfill & {\left({\mathcal{A}}_{01}\right)}_{2111}=1+j,{\left({\mathcal{A}}_{01}\right)}_{2121}=i-k,{\left({\mathcal{A}}_{01}\right)}_{2112}=0,{\left({\mathcal{A}}_{01}\right)}_{2122}=j\hfill \\ \hfill & {\left({\mathcal{A}}_{01}\right)}_{1211}=i,{\left({\mathcal{A}}_{01}\right)}_{1221}=i-2k,{\left({\mathcal{A}}_{01}\right)}_{1212}=1,{\left({\mathcal{A}}_{01}\right)}_{1222}=j,\hfill \\ \hfill & {\left({\mathcal{A}}_{01}\right)}_{2211}=2,{\left({\mathcal{A}}_{01}\right)}_{2221}=i,{\left({\mathcal{A}}_{01}\right)}_{2212}=j,{\left({\mathcal{A}}_{01}\right)}_{2222}=k\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{B}}_{00}\right)}_{1111}=1,{\left({\mathcal{B}}_{00}\right)}_{1121}=-1,{\left({\mathcal{B}}_{00}\right)}_{1112}=j,{\left({\mathcal{B}}_{00}\right)}_{1122}=i,\hfill \\ \hfill & {\left({\mathcal{B}}_{00}\right)}_{2111}=0,{\left({\mathcal{B}}_{00}\right)}_{2121}=1,{\left({\mathcal{B}}_{00}\right)}_{2112}=-1-i-k,{\left({\mathcal{B}}_{00}\right)}_{2122}=0,\hfill \\ \hfill & {\left({\mathcal{B}}_{00}\right)}_{1211}=j-k,{\left({\mathcal{B}}_{00}\right)}_{1221}=1,{\left({\mathcal{B}}_{00}\right)}_{1212}=-i,{\left({\mathcal{B}}_{00}\right)}_{1222}=0,\hfill \\ \hfill & {\left({\mathcal{B}}_{00}\right)}_{2211}=-j+k,{\left({\mathcal{B}}_{00}\right)}_{2221}=-i+j,{\left({\mathcal{B}}_{00}\right)}_{2212}=-2,{\left({\mathcal{B}}_{00}\right)}_{2222}=1+i-j,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{B}}_{01}\right)}_{1111}=1-j,{\left({\mathcal{B}}_{01}\right)}_{1121}=-k,{\left({\mathcal{B}}_{01}\right)}_{1112}=-1+2j-k,{\left({\mathcal{B}}_{01}\right)}_{1122}=1+i-j+k,\hfill \\ \hfill & {\left({\mathcal{B}}_{01}\right)}_{2111}=1-i+j,{\left({\mathcal{B}}_{01}\right)}_{2121}=1,{\left({\mathcal{B}}_{01}\right)}_{2112}=i+2j,{\left({\mathcal{B}}_{01}\right)}_{2122}=-1-j-k,\hfill \\ \hfill & {\left({\mathcal{B}}_{01}\right)}_{1211}=-2-3i+3k,{\left({\mathcal{B}}_{01}\right)}_{1221}=-i+2k,{\left({\mathcal{B}}_{01}\right)}_{1212}=i-j,{\left({\mathcal{B}}_{01}\right)}_{1222}=-3-k,\hfill \\ \hfill & {\left({\mathcal{B}}_{01}\right)}_{2211}=-j+k,{\left({\mathcal{B}}_{01}\right)}_{2221}=-1+2i+j+k,{\left({\mathcal{B}}_{01}\right)}_{2212}=2+i,{\left({\mathcal{B}}_{01}\right)}_{2222}=2-i,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{C}}_{00}\right)}_{1111}=k,{\left({\mathcal{C}}_{00}\right)}_{1121}=0,{\left({\mathcal{C}}_{00}\right)}_{1112}=i,{\left({\mathcal{C}}_{00}\right)}_{1122}=1+j,\hfill \\ \hfill & {\left({\mathcal{C}}_{00}\right)}_{2111}=1,{\left({\mathcal{C}}_{00}\right)}_{2121}=j,{\left({\mathcal{C}}_{00}\right)}_{2112}=i-k,{\left({\mathcal{C}}_{00}\right)}_{2122}=i,\hfill \\ \hfill & {\left({\mathcal{C}}_{00}\right)}_{1211}=j,{\left({\mathcal{C}}_{00}\right)}_{1221}=-k,{\left({\mathcal{C}}_{00}\right)}_{1212}=0,{\left({\mathcal{C}}_{00}\right)}_{1222}=i,\hfill \\ \hfill & {\left({\mathcal{C}}_{00}\right)}_{2211}=1+i,{\left({\mathcal{C}}_{00}\right)}_{2221}=1,{\left({\mathcal{C}}_{00}\right)}_{2212}=-j,{\left({\mathcal{C}}_{00}\right)}_{2222}=k,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{C}}_{01}\right)}_{1111}=0,{\left({\mathcal{C}}_{01}\right)}_{1121}=i,{\left({\mathcal{C}}_{01}\right)}_{1112}=-k,{\left({\mathcal{C}}_{01}\right)}_{1122}=1,\hfill \\ \hfill & {\left({\mathcal{C}}_{01}\right)}_{2111}=j,{\left({\mathcal{C}}_{01}\right)}_{2121}=2,{\left({\mathcal{C}}_{01}\right)}_{2112}=-i,{\left({\mathcal{C}}_{01}\right)}_{2122}=0,\hfill \\ \hfill & {\left({\mathcal{C}}_{01}\right)}_{1211}=k,{\left({\mathcal{C}}_{01}\right)}_{1221}=i,{\left({\mathcal{C}}_{01}\right)}_{1212}=j,{\left({\mathcal{C}}_{01}\right)}_{1222}=-k,\hfill \\ \hfill & {\left({\mathcal{C}}_{01}\right)}_{2211}=1,{\left({\mathcal{C}}_{01}\right)}_{2221}=k,{\left({\mathcal{C}}_{01}\right)}_{2212}=0,{\left({\mathcal{C}}_{01}\right)}_{2222}=j,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{D}}_{00}\right)}_{1111}=j,{\left({\mathcal{D}}_{00}\right)}_{1121}=0,{\left({\mathcal{D}}_{00}\right)}_{1112}=-1+j-k,{\left({\mathcal{D}}_{00}\right)}_{1122}=i+j,\hfill \\ \hfill & {\left({\mathcal{D}}_{00}\right)}_{2111}=-1-i+j+2k,{\left({\mathcal{D}}_{00}\right)}_{2121}=k,{\left({\mathcal{D}}_{00}\right)}_{2112}=-2i,\hfill \\ \hfill & {\left({\mathcal{D}}_{00}\right)}_{2122}=1-i+j,{\left({\mathcal{D}}_{00}\right)}_{1211}=-1+j-k,{\left({\mathcal{D}}_{00}\right)}_{1221}=-i+2j,\hfill \\ \hfill & {\left({\mathcal{D}}_{00}\right)}_{1212}=-1-i,{\left({\mathcal{D}}_{00}\right)}_{1222}=-2-i-j+k,{\left({\mathcal{D}}_{00}\right)}_{2211}=-1+2i+j,\hfill \\ \hfill & {\left({\mathcal{D}}_{00}\right)}_{2221}=i,{\left({\mathcal{D}}_{00}\right)}_{2212}=i-2k,{\left({\mathcal{D}}_{00}\right)}_{2222}=-k,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{D}}_{01}\right)}_{1111}=4k,{\left({\mathcal{D}}_{01}\right)}_{1121}=3i+j-k,{\left({\mathcal{D}}_{01}\right)}_{1112}=1+2i+j,{\left({\mathcal{D}}_{01}\right)}_{1122}=2j-k,\hfill \\ \hfill & {\left({\mathcal{D}}_{01}\right)}_{2111}=1+k-2j,{\left({\mathcal{D}}_{01}\right)}_{2121}=-3+i,{\left({\mathcal{D}}_{01}\right)}_{2112}=-1+2i+3j+k,\hfill \\ \hfill & {\left({\mathcal{D}}_{01}\right)}_{2122}=-1+2i+2j-k,{\left({\mathcal{D}}_{01}\right)}_{1211}=1+j-k,{\left({\mathcal{D}}_{01}\right)}_{1221}=-2i+2j+k,\hfill \\ \hfill & {\left({\mathcal{D}}_{01}\right)}_{1212}=-2+i+k,{\left({\mathcal{D}}_{01}\right)}_{1222}=-i,{\left({\mathcal{D}}_{01}\right)}_{2211}=2+2i+j+k,\hfill \\ \hfill & {\left({\mathcal{D}}_{01}\right)}_{2221}=i+2j-k,{\left({\mathcal{D}}_{01}\right)}_{2212}=-1+i+j+2k,{\left({\mathcal{D}}_{01}\right)}_{2222}=-2+i+k.\hfill \end{array}$$

From MATLAB 7.0, it can be proven that part (3) of the Theorem (1) in this paper holds: 

$$\begin{array}{cc}\hfill & {\mathcal{R}}_{{\mathcal{A}}_0}{*}_M{\mathcal{B}}_0=0,{\mathcal{D}}_0{*}_T{\mathcal{L}}_{{\mathcal{C}}_0}=0,{\mathcal{R}}_{{\mathcal{A}}_2}{*}_M{\mathcal{C}}_2=0,{\mathcal{C}}_2{*}_S{\mathcal{L}}_{{\mathcal{B}}_2}=0,\hfill \\ \hfill & {\mathcal{R}}_{{\mathcal{A}}_3}{*}_N{\mathcal{C}}_3=0,{\mathcal{C}}_3{*}_T{\mathcal{L}}_{{\mathcal{B}}_3}=0,{\mathcal{R}}_{{\mathcal{A}}_4}{*}_N{\mathcal{C}}_4{*}_T{\mathcal{L}}_{{\mathcal{B}}_4}=0,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & t\left({\mathcal{A}}_0{*}_N{\mathcal{D}}_0\right)=t\left({\mathcal{B}}_0{*}_S{\mathcal{C}}_0\right)=\hfill \\ \hfill & \left[\begin{array}{cccccccccccccccc}-1& 0& 0& 1& 1& 2& 0& -1& 0& -1& 0& 0& 1& 0& 0& -1\\ 1& 1& 0& 1& -1& 0& 1& 0& -1& 0& 0& -1& -1& 1& -1& 0\\ 0& 0& 0& 2& -1& 0& 1& 0& 0& 0& -1& 1& -1& 0& -2& -1\\ 1& 2& 2& 0& 2& 1& 1& 0& -2& -1& -1& -2& 1& 1& -1& 1\\ -1& -2& 0& 1& -1& 0& 0& 1& -1& 0& 0& 1& 0& -1& 0& 0\\ 1& 0& -1& 0& 1& 1& 0& 1& 1& -1& 1& 0& -1& 0& 0& -1\\ 1& 0& -1& 0& 0& 0& 0& 2& 1& 0& 2& 1& 0& 0& -1& 1\\ -2& -1& -1& 0& 1& 2& 2& 0& -1& -1& 1& -1& -2& -1& -1& -2\\ 0& -1& 0& 0& -1& 0& 0& 1& -1& 0& 0& 1& -1& -2& 0& 1\\ -1& 0& 0& -1& 1& -1& 1& 0& 1& 1& 0& 1& 1& 0& -1& 0\\ 0& 0& -1& 1& 1& 0& 2& 1& 0& 0& 0& 2& 1& 0& -1& 0\\ -2& -1& -1& -2& -1& -1& 1& -1& 1& 2& 2& 0& -2& -1& -1& 0\\ 1& 0& 0& -1& 0& -1& 0& 0& 1& 2& 0& -1& -1& 0& 0& 1\\ -1& 1& -1& 0& -1& 0& 0& -1& -1& 0& 1& 0& 1& 1& 0& 1\\ -1& 0& -2& -1& 0& 0& -1& 1& -1& 0& 1& 0& 0& 0& 0& 2\\ 1& 1& -1& 1& -2& -1& -1& -2& 2& 1& 1& 0& 1& 2& 2& 0\end{array}\right],\hfill \end{array}$$

$$\begin{array}{cc}\hfill & t({\mathcal{A}}_0{*}_N{\mathcal{D}}_1-{\mathcal{B}}_0{*}_S{\mathcal{C}}_1)=t({\mathcal{B}}_1{*}_S{\mathcal{C}}_0-{\mathcal{A}}_1{*}_N{\mathcal{D}}_0)=\hfill \\ \hfill & \left[\begin{array}{cccccccccccccccc}-1& 0& 0& -1& 2& 2& 0& 1& -1& -1& 1& -1& 2& 0& 0& 0\\ 1& 0& 0& -2& 0& 2& 0& -1& 0& 2& -1& 0& 2& 0& 0& -3\\ 2& -1& 1& -1& -1& 2& -1& 1& 2& 0& 2& -1& -1& -1& 0& -3\\ 1& 1& -1& -3& 3& 0& 0& 0& 2& 0& 0& 1& 2& -1& 3& 0\\ -2& -2& 0& -1& -1& 0& 0& -1& -2& 0& 0& 0& -1& -1& 1& -1\\ 0& -2& 0& 1& 1& 0& 0& -2& -2& 0& 0& 3& 0& 2& -1& 0\\ 1& -2& 1& -1& 2& -1& 1& -1& 1& 1& 0& 3& 2& 0& 2& -1\\ -3& 0& 0& 0& 1& 1& -1& -3& -2& 1& -3& 0& 2& 0& 0& 1\\ -1& -1& 1& -1& -2& 0& 0& 0& -1& 0& 0& -1& -2& -2& 0& -1\\ 0& 2& -1& 0& -2& 0& 0& 3& 1& 0& 0& -2& 0& -2& 0& 1\\ 2& 0& 2& -1& 1& 1& 0& 3& 2& -1& 1& -1& 1& -2& 1& -1\\ 2& 0& 0& 1& -2& 1& -3& 0& 1& 1& -1& -3& -3& 0& 0& 0\\ 2& 0& 0& 0& -1& -1& 1& -1& 2& 2& 0& 1& -1& 0& 0& -1\\ 2& 0& 0& -3& 0& 2& -1& 0& 0& 2& 0& -1& 1& 0& 0& -2\\ -1& -1& 0& -3& 2& 0& 2& -1& -1& 2& -1& 1& 2& -1& 1& -1\\ 2& -1& 3& 0& 2& 0& 0& 1& 3& 0& 0& 0& 1& 1& -1& -3\end{array}\right],\hfill \end{array}$$

i.e.,

$${\mathcal{A}}_0{*}_N{\mathcal{D}}_0={\mathcal{B}}_0{*}_S{\mathcal{C}}_0,{\mathcal{A}}_0{*}_N{\mathcal{D}}_1-{\mathcal{B}}_0{*}_S{\mathcal{C}}_1={\mathcal{B}}_1{*}_S{\mathcal{C}}_0-{\mathcal{A}}_1{*}_N{\mathcal{D}}_0.$$

Then, it can be deduced that the system of dual split quaternion tensor equations (2) is solvable and a solution of this system can be expressed as $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$, where

$$\begin{array}{cc}\hfill & {\left({\mathcal{X}}_{00}\right)}_{1111}=j,{\left({\mathcal{X}}_{00}\right)}_{1121}=i,{\left({\mathcal{X}}_{00}\right)}_{1112}=1,{\left({\mathcal{X}}_{00}\right)}_{1122}=0,\hfill \\ \hfill & {\left({\mathcal{X}}_{00}\right)}_{2111}=j,{\left({\mathcal{X}}_{00}\right)}_{2121}=-1,{\left({\mathcal{X}}_{00}\right)}_{2112}=i,{\left({\mathcal{X}}_{00}\right)}_{2122}=k,\hfill \\ \hfill & {\left({\mathcal{X}}_{00}\right)}_{1211}=-1,{\left({\mathcal{X}}_{00}\right)}_{1221}=0,{\left({\mathcal{X}}_{00}\right)}_{1212}=i-j,{\left({\mathcal{X}}_{00}\right)}_{1222}=j,\hfill \\ \hfill & {\left({\mathcal{X}}_{00}\right)}_{2211}=0,{\left({\mathcal{X}}_{00}\right)}_{2221}=j,{\left({\mathcal{X}}_{00}\right)}_{2212}=k,{\left({\mathcal{X}}_{00}\right)}_{2222}=i,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\left({\mathcal{X}}_{01}\right)}_{1111}=1,{\left({\mathcal{X}}_{01}\right)}_{1121}=0,{\left({\mathcal{X}}_{01}\right)}_{1112}=i,{\left({\mathcal{X}}_{01}\right)}_{1122}=0,\hfill \\ \hfill & {\left({\mathcal{X}}_{01}\right)}_{2111}=k,{\left({\mathcal{X}}_{01}\right)}_{2121}=i,{\left({\mathcal{X}}_{01}\right)}_{2112}=j,{\left({\mathcal{X}}_{01}\right)}_{2122}=-1,\hfill \\ \hfill & {\left({\mathcal{X}}_{01}\right)}_{1211}=0,{\left({\mathcal{X}}_{01}\right)}_{1221}=1,{\left({\mathcal{X}}_{01}\right)}_{1212}=-k,{\left({\mathcal{X}}_{01}\right)}_{1222}=j,\hfill \\ \hfill & {\left({\mathcal{X}}_{01}\right)}_{2211}=-j,{\left({\mathcal{X}}_{01}\right)}_{2221}=k,{\left({\mathcal{X}}_{01}\right)}_{2212}=1,{\left({\mathcal{X}}_{01}\right)}_{2222}=0.\hfill \end{array}$$

Example 3.

In this section, we propose a method for video encryption and decryption using Theorem (1) and provide a specific example to demonstrate this method.

Similar to quaternions [6], it has been demonstrated that split quaternions can represent color images [40]. Split quaternion tensors can represent color videos, as long as the video is segmented into multiple image slices. Then, the dual split quaternion tensor can represent two color videos.

We can encrypt two color videos through system (2) and the following model is the encryption process based on system (2): 

Figure 1. The model of encrypting two videos.

Figure 1. The model of encrypting two videos.

It is clear that system (2) and the following system are equivalent, so we can use system (22) to encrypt and decrypt videos.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{*}_S{\mathcal{X}}_0={\mathcal{B}}_0,\hfill \\ {\mathcal{X}}_0{*}_S{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{A}}_0{*}_S{\mathcal{X}}_1+{\mathcal{A}}_1{*}_S{\mathcal{X}}_0={\mathcal{B}}_1,\hfill \\ {\mathcal{X}}_0{*}_S{\mathcal{C}}_1+{\mathcal{X}}_1{*}_S{\mathcal{C}}_0={\mathcal{D}}_1\hfill \end{array}\right.\end{array}$$

(22)

We use two original videos ${\mathcal{X}}_0$ and ${\mathcal{X}}_1$, each composed of 51 slices of color images of size $540\times 540$ pixels, represented as ${\mathbb{H}}_s^{540\times 540\times 51}$[41]. That is, $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_1ϵ\in {\mathbb{DQ}}_s^{540\times 540\times 51}$. $\mathcal{A}={\mathcal{A}}_0+{\mathcal{A}}_1ϵ$ and $\mathcal{C}={\mathcal{C}}_0+{\mathcal{C}}_1ϵ\in {\mathbb{DQ}}_s^{540\times 540}$ are the system coefficients. For simplicity, we select all ${\mathcal{A}}_0$, ${\mathcal{A}}_1$, ${\mathcal{C}}_0$ and ${\mathcal{C}}_1$ as real matrices and they are invertible. And we represent ${\mathcal{B}}_0$ and ${\mathcal{B}}_1\in {\mathbb{H}}_s^{540\times 540\times 51}$ as keys. ${\mathcal{D}}_0$ and ${\mathcal{D}}_1\in {\mathbb{H}}_s^{540\times 540\times 51}$ represent two encrypted videos. The process of encryption is described below: 

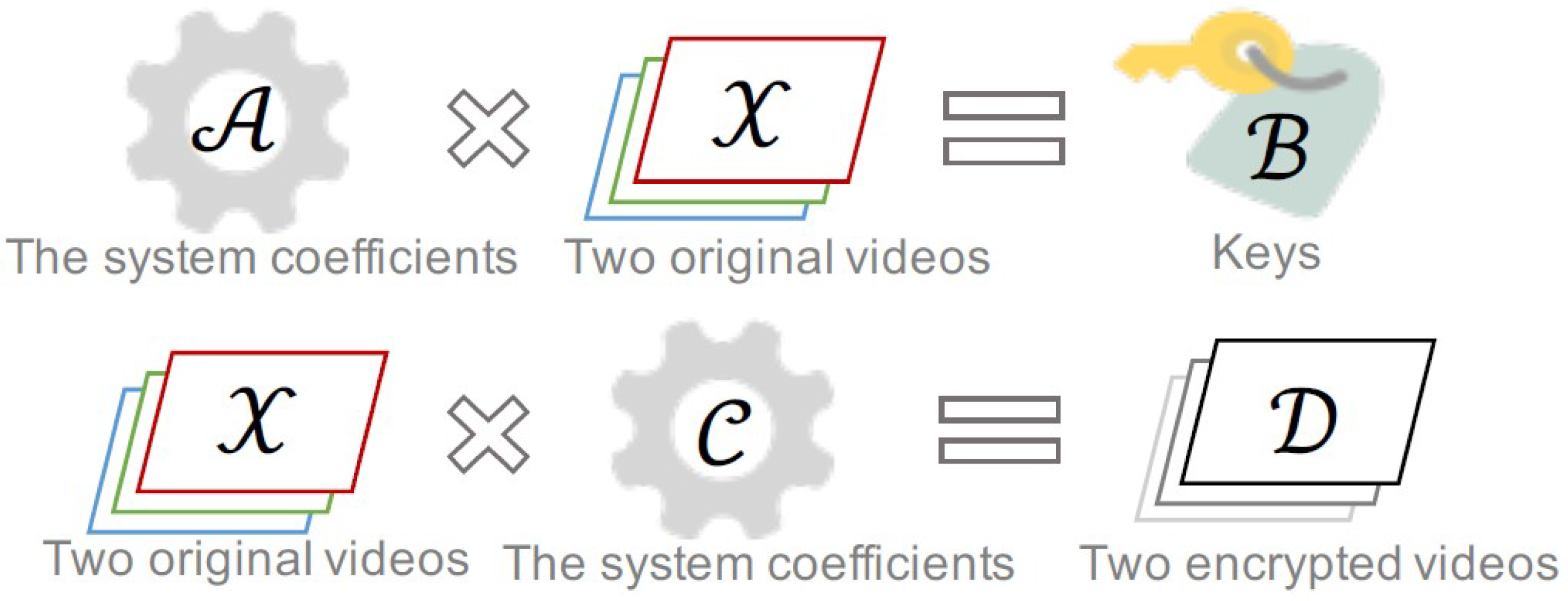
Algorithm 1 Encryption process

1:  Input:Two original videos and system coefficients. 2:  Let ${\mathcal{X}}_0$ and ${\mathcal{X}}_1$ represent the first original video and the second original video. Then $X_{0i}$ and $X_{1i}$ represent i-th slice of video ${\mathcal{X}}_0$ and ${\mathcal{X}}_1$, where $i=1,\cdots ,51$. The system coefficients are ${\mathcal{A}}_0$, ${\mathcal{A}}_1$, ${\mathcal{C}}_0$ and ${\mathcal{C}}_1$. 3:  Encrypt ${\mathcal{X}}_0$ and ${\mathcal{X}}_1$ by the system (22). 4:  ${\mathcal{B}}_{0i}$ and ${\mathcal{B}}_{1i}$ denote keys. ${\mathcal{D}}_{0i}$ and ${\mathcal{D}}_{1i}$ represent i-th slice of the two encrypted videos, where $i=1,\cdots ,51$. So we have obtained two encrypted videos ${\mathcal{D}}_0$ and ${\mathcal{D}}_1$. 5:  Output:Two encrypted videos and keys.

For the decryption process, we use two encrypted videos, ${\mathcal{D}}_0$ and ${\mathcal{D}}_1$, obtained from the encryption process, along with keys ${\mathcal{B}}_0$ and ${\mathcal{B}}_1$, as well as system coefficients ${\mathcal{A}}_0$, ${\mathcal{A}}_1$, ${\mathcal{C}}_0$, and ${\mathcal{C}}_1$, to recover the two original color videos. The decryption algorithm is represented as follows: 

Algorithm 2 Decryption process

1:  Input:System coefficients, keys and two encrypted videos. 2:  ${\mathcal{B}}_0$ and ${\mathcal{B}}_1$ represent keys. ${\mathcal{D}}_0$ and ${\mathcal{D}}_1$ denote the encrypted videos. ${\mathcal{A}}_0$, ${\mathcal{A}}_1$, ${\mathcal{C}}_0$, and ${\mathcal{C}}_1$ are the system coefficients and they are reversible. 3:  Using the real representation, we obtain ${\mathcal{A}}_p^{{\sigma }_i}$, ${\mathcal{B}}_p^{{\sigma }_i}$, ${\mathcal{C}}_p^{{\sigma }_i}$, and ${\mathcal{D}}_p^{{\sigma }_i}$, where $p=1,2$. 4:  By Theorem (1), we obtain ${\mathcal{XD}}_0$ and ${\mathcal{XD}}_1$. 5:  Convert ${\mathcal{XD}}_0$ and ${\mathcal{XD}}_1$ into ${\mathcal{XD}}_{00}$ and ${\mathcal{XD}}_{01}$ using Theorem (1), respectively. 6:  Two decrypted videos are ${\mathcal{XD}}_{00}$ and ${\mathcal{XD}}_{01}$, respectively. 7:  Output:Two decrypted videos.

Figure 2. The original, encrypted, and decrypted images of randomly selected slices from color videos ${\mathcal{X}}_0$ and ${\mathcal{X}}_1$.

Figure 2. The original, encrypted, and decrypted images of randomly selected slices from color videos ${\mathcal{X}}_0$ and ${\mathcal{X}}_1$.

The encryption’s CPU time is 59.2300 seconds and the decryption’s CPU time is 145.9600 seconds. The figure below illustrates a portion of slices from the encrypted and decrypted videos results: 

To assess the quality of the encryption and decryption algorithm for color videos, we utilize the Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index Measure (SSIM) and Feature Similarity Index Measure (FSIM), with the results presented in Table 1 and Table 2. A higher PSNR value usually indicates smaller errors, meaning that the quality of the processed image is higher. The results show that the PSNR values are all greater than 30 and all SSIM and FSIM values are equal to 1, indicating a high degree of similarity between the decrypted videos and the original videos. This further demonstrates the effectiveness of our encryption and decryption algorithm.

5. Conclusions

We use the real representations of split quaternions to simplify the system of dual split quaternion tensor equations $(\mathcal{A}{*}_N\mathcal{X},\mathcal{X}{*}_S\mathcal{C})=(\mathcal{B},\mathcal{D})$ into real tensor equations. Based on this, we put forward the equivalent conditions for this system’s solvability and the general expression of solutions. Subsequently, this proposed theorem is applied to two specific cases of dual split quaternion tensor equations. Furthermore, the paper presents the equivalent conditions when the Hermitian solution (denoted as $\mathcal{X}={\mathcal{X}}^{*}$) and $\eta$-Hermitian solutions (denoted as $\mathcal{X}={\mathcal{X}}^{\eta *}$) of the system (2) exist, using various real representations. Additionally, we provide a numerical example using MATLAB to validate the correctness of the key theorem presented in this paper. In the end, we use Theorem (1) to present a method for encrypting and decrypting two color videos, along with a specific example. The algorithm’s efficacy is demonstrated by PSNR, SSIM and FSIM.