The BiCG Algorithm for Solving the Minimal Frobenius Norm Solution of Generalized Sylvester Tensor Equation over the Quaternions

1. Introduction

An order N tensor $\mathcal{A}={\left(a_{i_1\dots i_N}\right)}_{1⩽i_j⩽I_j}(j=1,\dots ,N)$ over a field $\mathbb{F}$ is a multidimensional array with $I_1{I}_2\dots I_N$ entries in $\mathbb{F}$, where N is a positive integer ([27,44]). The set of all such N tensors is denoted by ${\mathbb{F}}^{I_1\times \dots \times I_N}$. In the past decades, there have been active researches on tensors due to various applications in many areas such as physics, computer vision, data mining, etc. (see, e.g., [9,11,15,16,17,21,25,26,27,29,30,31,32,33,35,36,37,41,42,43,54,56]).

In this paper, we investigate the solvability of some tensor equations over quaternions. This is motivated by the recent researches on tensor equations as well as a long research history of solving matrix equations, which are briefly outlined as follows. It is well-known that the following Sylvester matrix equation

$$AX+YB=C$$

(1)

and its generalized forms have been widely investigated and found numerous applications in many areas.

During the past decades, many methods have been developed for solving Sylvester-type matrix equation over the quaternion algebra. For example, Kyrchei [28] gave explicit determinantal representation formulas of solutions to the Equation (1). Heyouni et al. [20] presented the SGl-CMRH method and preconditioned framework of this method to solve matrix Equation (1) when $X=Y$. Zhang [53] investigated the general system of generalized Sylvester quaternion matrix equations. Ahmadi-Asl and Beik [1,2,7] presented effective iterative algorithms for solving different quaternion matrix equations. Song [47] investigated the general solution to a system of quaternion matrix equation by Cramer’s rule. Wang et al. [48] considered the solvability of a system of constrained two-sided coupled generalized Sylvester quaternion matrix equations. Zhang et al. [52] obtained some special least squares solutions of the quaternion matrix equation $AXB+CXD=E$. Huang et al. [22] considered the modified conjugate gradient method to solve the generalized coupled Sylvester conjugate matrix equations.

Quaternions offer greater versatility and flexibility compared to real and complex numbers, particularly in addressing multidimensional problems. This unique property has attracted growing interest among scholars, leading to numerous valuable achievements in quaternion-related research (see, e.g., [13,19,23,34,38,50,51]). The tensor equation is a natural extension of the matrix equation.

In this paper, we consider the following generalized Sylvester tensor equation over $\mathbb{H}$:

$$\mathcal{X}\times { }_1{A}^{\left(1\right)}+\mathcal{X}\times { }_2{A}^{\left(2\right)}+\dots +\mathcal{X}{\times }_N{A}^{\left(N\right)}+\mathcal{Y}\times { }_1{B}^{\left(1\right)}+\mathcal{Y}\times { }_2{B}^{\left(2\right)}+\dots +\mathcal{Y}{\times }_N{B}^{\left(N\right)}=\mathcal{C},$$

(2)

where the tensors $A^{\left(n\right)}$, $B^{\left(n\right)}\in {\mathbb{H}}^{I_n\times I_n}(n=1,2,\dots ,N)$, $\mathcal{C}\in {\mathbb{H}}^{I_1\times \dots \times I_N}$ are given, and the tensors $\mathcal{X}$, $\mathcal{Y}\in {\mathbb{H}}^{I_1\times \dots \times I_N}$ are unknown. The n-mode product of a tensor $\mathcal{X}\in {\mathbb{H}}^{I_1\times \dots \times I_N}$ with a matrix $A\in {\mathbb{H}}^{I_n\times I_n}$ is defined as

$${\left(\mathcal{X}\times { }_{n}A\right)}_{i_1\dots i_{n-1}j{i}_{n+1}\dots i_N}=\sum _{i_n=1}^{I_n}{a}_{j{i}_n}{x}_{i_1\dots i_{n-1}{i}_n{i}_{n+1}\dots i_N}.$$

Note that the n-mode product can also be expressed in terms of unfolded quaternion tensors:

$$\mathcal{Y}=\mathcal{X}{\times }_{n}A⟺{\mathcal{Y}}_{\left[n\right]}=A{\mathcal{X}}_{\left[n\right]},$$

where ${\mathcal{X}}_{\left[n\right]}$ is the mode-n unfolding of $\mathcal{X}$ ([27]). We consider the following problems corresponding to (2):

Problem 1.1: For given the tensor $\mathcal{C}\in {\mathbb{H}}^{I_1\times I_2\times \dots \times I_N}$, the matrices $A^{\left(n\right)},B^{\left(n\right)}\in {\mathbb{H}}^{I_n\times I_n}(n=$$1,2,\dots ,N)$, find the tensors $\tilde{\mathcal{X}},\tilde{\mathcal{Y}}\in {\mathbb{H}}^{I_1\times I_2\times \dots \times I_N}$ such that

$$∥\sum _{k=1}^N\tilde{\mathcal{X}}\times { }_k{A}^{\left(k\right)}+\tilde{\mathcal{Y}}\times { }_k{B}^{\left(k\right)}-\mathcal{C}∥=\underset{\mathcal{X}}{min}∥\sum _{k=1}^N\mathcal{X}{\times }_k{A}^{\left(k\right)}+\mathcal{Y}{\times }_k{B}^{\left(k\right)}-\mathcal{C}∥.$$

Problem 1.2: Let the solution set of Problem 1.1 be denoted by $S_{XY}$. For a given tensor ${\mathcal{X}}_0,{\mathcal{Y}}_0\in {\mathbb{H}}^{I_1\times I_2\times \dots \times I_N}$, find the tensor $\check{\mathcal{X}},\check{\mathcal{Y}}\in {\mathbb{H}}^{I_1\times I_2\times \dots \times I_N}$ such that

$$∥\check{\mathcal{X}}-{\mathcal{X}}_0∥+∥\check{\mathcal{Y}}-{\mathcal{Y}}_0∥=\underset{\mathcal{X}\in S_L}{min}∥\mathcal{X}-{\mathcal{X}}_0∥+∥\mathcal{Y}-{\mathcal{Y}}_0∥.$$

It is worth emphasizing that the tensor equation (2) includes several well-studied matrix/tensor equations as special cases. For example, if $\mathcal{X}$ and $\mathcal{Y}$ in (2) are order 2 tensors, i.e., matrices, then Equation (2) can be reduced to the following extended Sylvester matrix equation

$$A^{\left(1\right)}\mathcal{X}+\mathcal{X}{\left(A^{\left(2\right)}\right)}^{\mathrm{T}}+B^{\left(1\right)}\mathcal{Y}+\mathcal{Y}{\left(B^{\left(2\right)}\right)}^{\mathrm{T}}=\mathcal{C}.$$

In the case of $B^{\left(n\right)}=0(n=1,2\dots ,N)$, Equation (2) becomes the following equation

$$\mathcal{X}{\times }_1{A}^{\left(1\right)}+\mathcal{X}\times { }_2{A}^{\left(2\right)}+\dots +\mathcal{X}{\times }_N{A}^{\left(N\right)}=\mathcal{C},$$

(3)

which has been studied extensively in recent years. For instance, Saberi et al. [45,46] investigated the SGMRES-BTF method and SGCRO-BTF method to solve Equation (3) over $\mathbb{R}$. Wang et al. [49] gave the conjugate gradient least squares method to solve Equation (3) over $\mathbb{H}$. Zhang and Wang [55] presented the tensor forms of the bi-conjugate gradient (BiCG-BTF) and bi-conjugate residual (BiCR-BTF) methods for solving tensor Equation (3) over real number field $\mathbb{R}$. Chen and Lu [10] considered a projection method with a Kronecker product preconditioner to solve Equation (3) over $\mathbb{R}$. Karimi and Dehghan [24] presented the tensor form of global least squares method for finding an approximate solution of (3). Furthermore, Najafi-Kalyani et al. [39] derived some iterative algorithms on global Hessenberg process in their tensor forms to solve Equation (3). Considering Equation (3) over $\mathbb{R}$ and $N=3$, that is,

$$\mathcal{X}{\times }_1{A}^{\left(1\right)}+\mathcal{X}\times { }_2{A}^{\left(2\right)}+\mathcal{X}{\times }_3{A}^{\left(3\right)}=\mathcal{C}.$$

(4)

It has been shown that Equation (4) plays an important role in finite difference [3], thermal radiation [29], information retrieval [33], finite elements [14], and microscopic heat transport problem [37]. Therefore, our study on Equation (2) will provide a unified treatment for these matrix/tensor equations.

The rest of this paper is organized as follows. In Section 2, we recall some definitions and notations, and prove several lemmas for changing Equation (2). In Section 3, we develop the BiCG iterative algorithm for solving the quaternion tensor Equation (2), and prove that our algorithm is correct. We also show that the minimal Frobenious norm solution can be obtained by choosing special kinds of initial tensors. Some numerical examples are presented in Section 4 for illustrating the efficiency and applications of the proposed algorithm. Finally, we summarize our contributions in Section 5.

2. Preliminaries

We first recall some notations and definitions. For two complex matrices $U=\left(u_{ij}\right)\in {\mathbb{C}}^{m\times n},V=\left(v_{ij}\right)\in {\mathbb{C}}^{p\times q}$, the symbol $U\otimes V=\left(u_{ij}V\right)\in {\mathbb{C}}^{mp\times nq}$ denotes the Kronecker product of U and V.

The operator $vec(·)$ is defined as: for a matrix A and a tensor $\mathcal{X}$,

$$\mathrm{vec}\left(A\right)={\left(a_1^{\mathrm{T}},a_2^{\mathrm{T}},\dots ,a_n^{\mathrm{T}}\right)}^{\mathrm{T}},\mathrm{and}\mathrm{vec}\left(\mathcal{X}\right)=\mathrm{vec}\left({\mathcal{X}}_{\left[1\right]}\right),$$

respectively, where $a_k$ is the kth column of A and ${\mathcal{X}}_{\left[1\right]}$ is the mode-1 unfolding of the tensor $\mathcal{X}$. The inner product of two tensors $\mathcal{X},\mathcal{Y}\in {\mathbb{H}}^{I_1\times \dots \times I_N}$ is defined by

$$\langle \mathcal{X},\mathcal{Y}\rangle =\sum _{i_1=1}^{I_1}\sum _{i_2=1}^{I_2}\dots \sum _{i_N=1}^{I_N}{x}_{i_1{i}_2\dots i_N}{\overline{y}}_{i_1{i}_2\dots i_N},$$

where ${\overline{y}}_{i_1{i}_2\dots i_N}$ represents the quaternion conjugate of $y_{i_1{i}_2\dots i_N}$. If $\langle \mathcal{X},\mathcal{Y}\rangle =0$, then we say that tensors $\mathcal{X}$ and $\mathcal{Y}$ are orthogonal. The Frobenius norm of tensor $\mathcal{X}$ is defined as $\parallel \mathcal{X}\parallel =\sqrt{\langle \mathcal{X},\mathcal{X}\rangle }.$

For any $\mathcal{X}\in {\mathbb{H}}^{I_1\times \dots \times I_N}$, it is well-known that $\mathcal{X}$ can be uniquely expressed as $\mathcal{X}={\mathcal{X}}_1+{\mathcal{X}}_2\mathbf{i}+{\mathcal{X}}_3\mathbf{j}+{\mathcal{X}}_4\mathbf{k}$, where ${\mathcal{X}}_i\in {\mathbb{R}}^{I_1\times \dots \times I_N},i=1,2,3,4$. Next we define n-mode operators for ${\mathcal{X}}_i$.

Let $A^{\left(n\right)}=A_1^{\left(n\right)}+A_2^{\left(n\right)}\mathbf{i}+A_3^{\left(n\right)}\mathbf{j}+A_4^{\left(n\right)}\mathbf{k},B^{\left(n\right)}=B_1^{\left(n\right)}+B_2^{\left(n\right)}\mathbf{i}+B_3^{\left(n\right)}\mathbf{j}+B_4^{\left(n\right)}\mathbf{k}\in {\mathbb{H}}^{I_n\times I_n}$, where $A_i^{\left(n\right)},B_i^{\left(n\right)}\in {\mathbb{R}}^{I_n\times I_n},i=1,2,3,4$. For $\mathcal{W}\in {\mathbb{R}}^{I_1\times \dots \times I_N}$, we define

$$\begin{array}{cc}\hfill & {\mathcal{L}}_{A_i^{\left(n\right)}}\left(\mathcal{W}\right)=\mathcal{W}\times { }_1{A}_i^{\left(1\right)}+\mathcal{W}{\times }_2{A}_i^{\left(2\right)}+\dots +\mathcal{W}{\times }_N{A}_i^{\left(N\right)},i=1,2,3,4,\hfill \\ \hfill & {\mathcal{L}}_{B_i^{\left(n\right)}}\left(\mathcal{W}\right)=\mathcal{W}\times { }_1{B}_i^{\left(1\right)}+\mathcal{W}{\times }_2{B}_i^{\left(2\right)}+\dots +\mathcal{W}{\times }_N{B}_i^{\left(N\right)},i=1,2,3,4.\hfill \end{array}$$

Next, replacing $\mathcal{W}$ in above equations by ${\mathcal{X}}_i$’s, we define the following notations:

$$\begin{array}{cc}\hfill & {\Gamma }_1[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]={\mathcal{L}}_{A_1^{\left(n\right)}}\left({\mathcal{X}}_1\right)-{\mathcal{L}}_{A_2^{\left(n\right)}}\left({\mathcal{X}}_2\right)-{\mathcal{L}}_{A_3^{\left(n\right)}}\left({\mathcal{X}}_3\right)-{\mathcal{L}}_{A_4^{\left(n\right)}}\left({\mathcal{X}}_4\right),\hfill \\ \hfill & {\Gamma }_2[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]={\mathcal{L}}_{A_2^{\left(n\right)}}\left({\mathcal{X}}_1\right)+{\mathcal{L}}_{A_1^{\left(n\right)}}\left({\mathcal{X}}_2\right)+{\mathcal{L}}_{A_4^{\left(n\right)}}\left({\mathcal{X}}_3\right)-{\mathcal{L}}_{A_3^{\left(n\right)}}\left({\mathcal{X}}_4\right),\hfill \\ \hfill & {\Gamma }_3[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]={\mathcal{L}}_{A_3^{\left(n\right)}}\left({\mathcal{X}}_1\right)-{\mathcal{L}}_{A_4^{\left(n\right)}}\left({\mathcal{X}}_2\right)+{\mathcal{L}}_{A_1^{\left(n\right)}}\left({\mathcal{X}}_3\right)+{\mathcal{L}}_{A_2^{\left(n\right)}}\left({\mathcal{X}}_4\right),\hfill \\ \hfill & {\Gamma }_4[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]={\mathcal{L}}_{A_4^{\left(n\right)}}\left({\mathcal{X}}_1\right)+{\mathcal{L}}_{A_3^{\left(n\right)}}\left({\mathcal{X}}_2\right)-{\mathcal{L}}_{A_2^{\left(n\right)}}\left({\mathcal{X}}_3\right)+{\mathcal{L}}_{A_1^{\left(n\right)}}\left({\mathcal{X}}_4\right),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & {\Phi }_1[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]={\mathcal{L}}_{B_1^{\left(n\right)}}\left({\mathcal{X}}_1\right)-{\mathcal{L}}_{B_2^{\left(n\right)}}\left({\mathcal{X}}_2\right)-{\mathcal{L}}_{B_3^{\left(n\right)}}\left({\mathcal{X}}_3\right)-{\mathcal{L}}_{B_4^{\left(n\right)}}\left({\mathcal{X}}_4\right),\hfill \\ \hfill & {\Phi }_2[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]={\mathcal{L}}_{B_2^{\left(n\right)}}\left({\mathcal{X}}_1\right)+{\mathcal{L}}_{B_1^{\left(n\right)}}\left({\mathcal{X}}_2\right)+{\mathcal{L}}_{B_4^{\left(n\right)}}\left({\mathcal{X}}_3\right)-{\mathcal{L}}_{B_3^{\left(n\right)}}\left({\mathcal{X}}_4\right),\hfill \\ \hfill & {\Phi }_3[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]={\mathcal{L}}_{B_3^{\left(n\right)}}\left({\mathcal{X}}_1\right)-{\mathcal{L}}_{B_4^{\left(n\right)}}\left({\mathcal{X}}_2\right)+{\mathcal{L}}_{B_1^{\left(n\right)}}\left({\mathcal{X}}_3\right)+{\mathcal{L}}_{B_2^{\left(n\right)}}\left({\mathcal{X}}_4\right),\hfill \\ \hfill & {\Phi }_4[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]={\mathcal{L}}_{B_4^{\left(n\right)}}\left({\mathcal{X}}_1\right)+{\mathcal{L}}_{B_3^{\left(n\right)}}\left({\mathcal{X}}_2\right)-{\mathcal{L}}_{B_2^{\left(n\right)}}\left({\mathcal{X}}_3\right)+{\mathcal{L}}_{B_1^{\left(n\right)}}\left({\mathcal{X}}_4\right),\hfill \end{array}$$

(6)

The following lemma shows that the quaternion tensor Equation (2) is equivalent to a system of four real tensor equations.

Lemma 1.

In Equation (2), we assume that $A^{\left(n\right)}=A_1^{\left(n\right)}+A_2^{\left(n\right)}\mathbf{i}+A_3^{\left(n\right)}\mathbf{j}+A_4^{\left(n\right)}\mathbf{k},B^{\left(n\right)}=B_1^{\left(n\right)}+B_2^{\left(n\right)}\mathbf{i}+B_3^{\left(n\right)}\mathbf{j}+B_4^{\left(n\right)}\mathbf{k}\in {\mathbb{H}}^{I_n\times I_n},n=1,2,\dots ,N$, and $\mathcal{C}=$ ${\mathcal{C}}_1+{\mathcal{C}}_2\mathbf{i}+{\mathcal{C}}_3\mathbf{j}+{\mathcal{C}}_4\mathbf{k},\mathcal{X}={\mathcal{X}}_1+{\mathcal{X}}_2\mathbf{i}+{\mathcal{X}}_3\mathbf{j}+{\mathcal{X}}_4\mathbf{k},\mathcal{Y}={\mathcal{Y}}_1+{\mathcal{Y}}_2\mathbf{i}+{\mathcal{Y}}_3\mathbf{j}+{\mathcal{Y}}_4\mathbf{k}\in {\mathbb{H}}^{I_1\times \dots \times I_N}$. Then the quaternion Sylvester tensor Equation (2) is equivalent to the following system of real tensor equations

$$\begin{array}{cc}\hfill {\Gamma }_1[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]+{\Phi }_1[{\mathcal{Y}}_1,{\mathcal{Y}}_2,{\mathcal{Y}}_3,{\mathcal{Y}}_4]& ={\mathcal{C}}_1,\hfill \\ \hfill {\Gamma }_2[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]+{\Phi }_2[{\mathcal{Y}}_1,{\mathcal{Y}}_2,{\mathcal{Y}}_3,{\mathcal{Y}}_4]& ={\mathcal{C}}_2,\hfill \\ \hfill {\Gamma }_3[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]+{\Phi }_3[{\mathcal{Y}}_1,{\mathcal{Y}}_2,{\mathcal{Y}}_3,{\mathcal{Y}}_4]& ={\mathcal{C}}_3,\hfill \\ \hfill {\Gamma }_4[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]+{\Phi }_4[{\mathcal{Y}}_1,{\mathcal{Y}}_2,{\mathcal{Y}}_3,{\mathcal{Y}}_4]& ={\mathcal{C}}_4,\hfill \end{array}$$

(7)

where ${\Gamma }_i[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]$, ${\Phi }_i[{\mathcal{Y}}_1,{\mathcal{Y}}_2,{\mathcal{Y}}_3,{\mathcal{Y}}_4](i=1,2,3,4)$ are defined by (5) and (6). Furthermore, the system of real tensor Equations (7) is equivalent to the following linear system

$$[{\mathcal{M}}_A,{\mathcal{M}}_B]z=c,$$

(8)

where

$$\begin{array}{c}\hfill {\mathcal{M}}_A=\left(\begin{array}{cccc}Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}\right)\hfill \\ Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}\right)\hfill & +Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}\right)\hfill & +Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}\right)\hfill \\ Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}\right)\hfill & +Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}\right)\hfill & +Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}\right)\hfill \\ Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}\right)\hfill & +Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}\right)\hfill & +Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}\right)\hfill \end{array}\right),\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{M}}_B=\left(\begin{array}{cccc}Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}\right)\hfill \\ Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}\right)\hfill & +Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}\right)\hfill & +Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}\right)\hfill \\ Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}\right)\hfill & +Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}\right)\hfill & +Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}\right)\hfill \\ Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}\right)\hfill & +Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}\right)\hfill & +Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}\right)\hfill \end{array}\right),\end{array}$$

$$z=\left(\begin{array}{c}\mathrm{vec}\left({\mathcal{X}}_1\right)\\ \mathrm{vec}\left({\mathcal{X}}_2\right)\\ \mathrm{vec}\left({\mathcal{X}}_3\right)\\ \mathrm{vec}\left({\mathcal{X}}_4\right)\\ \mathrm{vec}\left({\mathcal{Y}}_1\right)\\ \mathrm{vec}\left({\mathcal{Y}}_2\right)\\ \mathrm{vec}\left({\mathcal{Y}}_3\right)\\ \mathrm{vec}\left({\mathcal{Y}}_4\right)\end{array}\right),c=\left(\begin{array}{c}\mathrm{vec}\left({\mathcal{C}}_1\right)\\ \mathrm{vec}\left({\mathcal{C}}_2\right)\\ \mathrm{vec}\left({\mathcal{C}}_3\right)\\ \mathrm{vec}\left({\mathcal{C}}_4\right)\end{array}\right),$$

$$\begin{array}{c}\hfill Kro\left({\mathcal{L}}_{A_i^{\left(n\right)}}\right)=\sum _{n=1}^N{I}^{\left(I_N\right)}\otimes \dots \otimes I^{\left(I_{n+1}\right)}\otimes A_i^{\left(n\right)}\otimes I^{\left(I_{n-1}\right)}\otimes \dots \otimes I^{\left(I_1\right)},i=1,2,3,4,\\ \hfill Kro\left({\mathcal{L}}_{B_i^{\left(n\right)}}\right)=\sum _{n=1}^N{I}^{\left(I_N\right)}\otimes \dots \otimes I^{\left(I_{n+1}\right)}\otimes B_i^{\left(n\right)}\otimes I^{\left(I_{n-1}\right)}\otimes \dots \otimes I^{\left(I_1\right)},i=1,2,3,4,\end{array}$$

and $I^{\left(n\right)}$ stands for the identity matrix of order n.

Proof of Lemma 1.

We apply the definition of n-mode product of the quaternion tensor for (2).

$$\begin{array}{cc}\hfill & \sum _{n=1}^N\left(\mathcal{X}{\times }_n{A}^{\left(n\right)}+\mathcal{Y}{\times }_n{B}^{\left(n\right)}\right)\hfill \\ \hfill =& \sum _{n=1}^N\left(\left({\mathcal{X}}_1+{\mathcal{X}}_2\mathbf{i}+{\mathcal{X}}_3\mathbf{j}+{\mathcal{X}}_4\mathbf{k}\right){\times }_n\left(A_1^{\left(n\right)}+A_2^{\left(n\right)}\mathbf{i}+A_3^{\left(n\right)}\mathbf{j}+A_4^{\left(n\right)}\mathbf{k}\right)\right.\hfill \\ \hfill & \left.+\left({\mathcal{Y}}_1+{\mathcal{Y}}_2\mathbf{i}+{\mathcal{Y}}_3\mathbf{j}+{\mathcal{Y}}_4\mathbf{k}\right){\times }_n\left(B_1^{\left(n\right)}+B_2^{\left(n\right)}\mathbf{i}+B_3^{\left(n\right)}\mathbf{j}+B_4^{\left(n\right)}\mathbf{k}\right)\right)\hfill \\ \hfill =& \sum _{n=1}^N\left({\mathcal{X}}_1{\times }_n{A}_1^{\left(n\right)}-{\mathcal{X}}_2{\times }_n{A}_2^{\left(n\right)}-{\mathcal{X}}_3{\times }_n{A}_3^{\left(n\right)}-{\mathcal{X}}_4{\times }_n{A}_4^{\left(n\right)}\right.\hfill \\ \hfill & \left.+{\mathcal{Y}}_1{\times }_n{B}_1^{\left(n\right)}-{\mathcal{Y}}_2{\times }_n{B}_2^{\left(n\right)}-{\mathcal{Y}}_3{\times }_n{B}_3^{\left(n\right)}-{\mathcal{Y}}_4{\times }_n{B}_4^{\left(n\right)}\right)\hfill \\ \hfill & +\sum _{n=1}^N\left({\mathcal{X}}_1{\times }_n{A}_2^{\left(n\right)}+{\mathcal{X}}_2{\times }_n{A}_1^{\left(n\right)}+{\mathcal{X}}_3{\times }_n{A}_4^{\left(n\right)}-{\mathcal{X}}_4{\times }_n{A}_3^{\left(n\right)}\right.\hfill \\ \hfill & \left.+{\mathcal{Y}}_1{\times }_n{B}_2^{\left(n\right)}+{\mathcal{Y}}_2{\times }_n{B}_1^{\left(n\right)}+{\mathcal{Y}}_3{\times }_n{B}_4^{\left(n\right)}-{\mathcal{Y}}_4{\times }_n{B}_3^{\left(n\right)}\right)\mathbf{i}\hfill \\ \hfill & +\sum _{n=1}^N\left({\mathcal{X}}_1{\times }_n{A}_3^{\left(n\right)}-{\mathcal{X}}_2{\times }_n{A}_4^{\left(n\right)}+{\mathcal{X}}_3{\times }_n{A}_1^{\left(n\right)}+{\mathcal{X}}_4{\times }_n{A}_2^{\left(n\right)}\right.\hfill \\ \hfill & \left.+{\mathcal{Y}}_1{\times }_n{B}_3^{\left(n\right)}-{\mathcal{Y}}_2{\times }_n{B}_4^{\left(n\right)}+{\mathcal{Y}}_3{\times }_n{B}_1^{\left(n\right)}+{\mathcal{Y}}_4{\times }_n{B}_2^{\left(n\right)}\right)\mathbf{j}\hfill \\ \hfill & +\sum _{n=1}^N\left({\mathcal{X}}_1{\times }_n{A}_4^{\left(n\right)}+{\mathcal{X}}_2{\times }_n{A}_3^{\left(n\right)}-{\mathcal{X}}_3{\times }_n{A}_2^{\left(n\right)}+{\mathcal{X}}_4{\times }_n{A}_1^{\left(n\right)}\right.\hfill \\ \hfill & \left.+{\mathcal{Y}}_1{\times }_n{B}_4^{\left(n\right)}+{\mathcal{Y}}_2{\times }_n{B}_3^{\left(n\right)}-{\mathcal{Y}}_3{\times }_n{B}_2^{\left(n\right)}+{\mathcal{Y}}_4{\times }_n{B}_1^{\left(n\right)}\right)\mathbf{k}\hfill \\ \hfill =& {\mathcal{C}}_1+{\mathcal{C}}_2\mathbf{i}+{\mathcal{C}}_3\mathbf{j}+{\mathcal{C}}_4\mathbf{k}.\hfill \end{array}$$

By the definitions of ${\Gamma }_i$ and ${\Phi }_i$, the Equations (7) hold. To show (8), we make use of operator “vec” to ${\Gamma }_1[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]$ and ${\Phi }_1[{\mathcal{Y}}_1,{\mathcal{Y}}_2,{\mathcal{Y}}_3,{\mathcal{Y}}_4]$, that is,

$$\begin{array}{cc}\hfill & vec\left({\Gamma }_1[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]\right)\hfill \\ \hfill =& vec\left({\mathcal{L}}_{A_1^{\left(n\right)}}\left({\mathcal{X}}_1\right)-{\mathcal{L}}_{A_2^{\left(n\right)}}\left({\mathcal{X}}_2\right)-{\mathcal{L}}_{A_3^{\left(n\right)}}\left({\mathcal{X}}_3\right)-{\mathcal{L}}_{A_4^{\left(n\right)}}\left({\mathcal{X}}_4\right)\right)\hfill \\ \hfill =& vec\left({\mathcal{L}}_{A_1^{\left(n\right)}}\left({\mathcal{X}}_1\right)\right)-vec\left({\mathcal{L}}_{A_2^{\left(n\right)}}\left({\mathcal{X}}_2\right)\right)-vec\left({\mathcal{L}}_{A_3^{\left(n\right)}}\left({\mathcal{X}}_3\right)\right)-vec\left({\mathcal{L}}_{A_4^{\left(n\right)}}\left({\mathcal{X}}_4\right)\right)\hfill \\ \hfill =& Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}\right)vec\left({\mathcal{X}}_1\right)-Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}\right)vec\left({\mathcal{X}}_2\right)-Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}\right)vec\left({\mathcal{X}}_3\right)-Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}\right)vec\left({\mathcal{X}}_4\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & vec\left({\Phi }_1[{\mathcal{Y}}_1,{\mathcal{Y}}_2,{\mathcal{Y}}_3,{\mathcal{Y}}_4]\right)\hfill \\ \hfill =& vec\left({\mathcal{L}}_{B_1^{\left(n\right)}}\left({\mathcal{Y}}_1\right)-{\mathcal{L}}_{B_2^{\left(n\right)}}\left({\mathcal{Y}}_2\right)-{\mathcal{L}}_{B_3^{\left(n\right)}}\left({\mathcal{Y}}_3\right)-{\mathcal{L}}_{B_4^{\left(n\right)}}\left({\mathcal{Y}}_4\right)\right)\hfill \\ \hfill =& vec\left({\mathcal{L}}_{B_1^{\left(n\right)}}\left({\mathcal{Y}}_1\right)\right)-vec\left({\mathcal{L}}_{B_2^{\left(n\right)}}\left({\mathcal{Y}}_2\right)\right)-vec\left({\mathcal{L}}_{B_3^{\left(n\right)}}\left({\mathcal{Y}}_3\right)\right)-vec\left({\mathcal{L}}_{B_4^{\left(n\right)}}\left({\mathcal{Y}}_4\right)\right)\hfill \\ \hfill =& Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_1\right)-Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_2\right)-Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_3\right)-Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_4\right).\hfill \end{array}$$

Similarly, we have the following results for the rest of ${\Gamma }_i$’s and ${\Phi }_i$’s:

$$\begin{array}{cc}\hfill & vec\left({\Gamma }_2[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]\right)\hfill \\ \hfill =& Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}\right)vec\left({\mathcal{X}}_1\right)+Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}\right)vec\left({\mathcal{X}}_2\right)+Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}\right)vec\left({\mathcal{X}}_3\right)-Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}\right)vec\left({\mathcal{X}}_4\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & vec\left({\Phi }_2[{\mathcal{Y}}_1,{\mathcal{Y}}_2,{\mathcal{Y}}_3,{\mathcal{Y}}_4]\right)\hfill \\ \hfill =& Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_1\right)+Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_2\right)+Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_3\right)-Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_4\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & vec\left({\Gamma }_3[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]\right)\hfill \\ \hfill =& Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}\right)vec\left({\mathcal{X}}_1\right)-Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}\right)vec\left({\mathcal{X}}_2\right)+Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}\right)vec\left({\mathcal{X}}_3\right)+Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}\right)vec\left({\mathcal{X}}_4\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & vec\left({\Phi }_3[{\mathcal{Y}}_1,{\mathcal{Y}}_2,{\mathcal{Y}}_3,{\mathcal{Y}}_4]\right)\hfill \\ \hfill =& Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_1\right)-Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_2\right)+Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_3\right)+Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_4\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & vec\left({\Gamma }_4[{\mathcal{X}}_1,{\mathcal{X}}_2,{\mathcal{X}}_3,{\mathcal{X}}_4]\right)\hfill \\ \hfill =& Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}\right)vec\left({\mathcal{X}}_1\right)+Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}\right)vec\left({\mathcal{X}}_2\right)-Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}\right)vec\left({\mathcal{X}}_3\right)+Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}\right)vec\left({\mathcal{X}}_4\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & vec\left({\Phi }_4[{\mathcal{Y}}_1,{\mathcal{Y}}_2,{\mathcal{Y}}_3,{\mathcal{Y}}_4]\right)\hfill \\ \hfill =& Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_1\right)+Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_2\right)-Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_3\right)+Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}\right)vec\left({\mathcal{Y}}_4\right),\hfill \end{array}$$

By writing up above equations, we obtain the system (8). □

Lemma 2.

[21,40] Suppose that $A\in {\mathbb{R}}^{m\times n},b\in {\mathbb{R}}^m$ and the linear matrix equation $Ax=b$ has a solution $\tilde{x}\in \mathcal{R}\left(A^{\top }\right)$, then, $\tilde{x}$ is the unique minimum norm solution of $Ax=b$.

From Lemma 1 and 2, it is easy to see that the uniqueness of the solution of equation (2) can be described as follows:

Theorem 1.

The tensor Equation (2) has the unique minimal Frobenius norm solution if and only if the matrix Equation (8) has a solution $\tilde{z}\in \mathcal{R}\left({[{\mathcal{M}}_A,{\mathcal{M}}_B]}^{\top }\right)$, then, $\tilde{z}$ is the unique minimum norm solution of matrix Equation (8).

Given fixed matrices $A^{\left(n\right)}\in {\mathbb{R}}^{I_n\times I_n},n=1,2,\dots ,N$, we define the following linear operators

$${\mathcal{L}}_{A^{\left(n\right)}}\left(\mathcal{X}\right)=\mathcal{X}\times { }_1{A}^{\left(1\right)}+\mathcal{X}\times { }_2{A}^{\left(2\right)}+\dots +\mathcal{X}{\times }_N{A}^{\left(N\right)},forany\mathcal{X}\in {\mathbb{R}}^{I_1\times I_2\times \dots \times I_N}.$$

Using the property $〈\mathcal{X},\mathcal{Y}{\times }_n{A}^{\left(n\right)}〉=〈\mathcal{X}{\times }_n{\left(A^{\left(n\right)}\right)}^{\mathrm{T}},\mathcal{Y}〉$ in [26], it is easy to prove the following lemma.

Lemma 3.

Let $A^{\left(n\right)}\in {\mathbb{R}}^{I_n\times I_n},n=1,2,\dots ,N,\mathcal{X},\mathcal{Y}\in {\mathbb{R}}^{I_1\times I_2\times \dots \times I_N}$. Then

$$\langle {\mathcal{L}}_{A^{\left(n\right)}}\left(\mathcal{X}\right),\mathcal{Y}\rangle =〈\mathcal{X},{\mathcal{L}}_{A^{\left(n\right)}}^{*}\left(\mathcal{Y}\right)〉,$$

where

$${\mathcal{L}}_{A^{\left(n\right)}}^{*}\left(\mathcal{Y}\right)=\mathcal{Y}{\times }_1{\left(A^{\left(1\right)}\right)}^{\mathrm{T}}+\mathcal{Y}\times { }_2{\left(A^{\left(2\right)}\right)}^{\mathrm{T}}+\dots +\mathcal{Y}\times { }_N{\left(A^{\left(N\right)}\right)}^{\mathrm{T}}.$$

Clearly, ${\mathcal{L}}_{A^{\left(n\right)}}$ defined above is a linear mapping. The following lemma provides the uniqueness of the dual mapping for these kinds of linear mappings.

Lemma 4.

([49]) Let $\mathcal{N}$ be a linear mapping from tensor space ${\mathbb{R}}^{I_1\times \dots \times I_N}$ to tensor space ${\mathbb{R}}^{J_1\times \dots \times J_N}.$ For any tensors $\mathcal{X}\in {\mathbb{R}}^{I_1\times \dots \times I_N}$ and $\mathcal{Y}\in {\mathbb{R}}^{J_1\times \dots \times J_N}$, there exists a unique linear mapping $\mathcal{M}$ from tensor space ${\mathbb{R}}^{J_1\times \dots \times J_N}$ to tensor space ${\mathbb{R}}^{I_1\times \dots \times I_N}$ such that

$$\langle \mathcal{N}\left(\mathcal{X}\right),\mathcal{Y}\rangle =\langle \mathcal{X},\mathcal{M}\left(\mathcal{Y}\right)\rangle .$$

Finally, we use linear operators $\mathcal{L}$ and ${\mathcal{L}}^{*}$ to describe the inner products involving ${\Gamma }_i$ and ${\Phi }_i$, which we will use in next sections.

Lemma 5.

Let ${\Gamma }_i[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4]$, ${\Phi }_i[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4](i=1,2,3,4)$ be defined by (5) and (6), ${\mathcal{W}}_i\in {\mathbb{R}}^{I_1\times \dots \times I_N}(i=1,2,3,4)$. Then

$$\begin{array}{cc}\hfill & \sum _{i=1}^4〈{\Gamma }_i[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4],{\mathcal{W}}_i〉=\sum _{i=1}^4\langle {\mathcal{Z}}_i,{\Gamma }_i^{*}[{\mathcal{W}}_1,{\mathcal{W}}_2,{\mathcal{W}}_3,{\mathcal{W}}_4]\rangle ,\hfill \\ \hfill & \sum _{i=1}^4〈{\Phi }_i[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4],{\mathcal{W}}_i〉=\sum _{i=1}^4\langle {\mathcal{Z}}_i,{\Phi }_i^{*}[{\mathcal{W}}_1,{\mathcal{W}}_2,{\mathcal{W}}_3,{\mathcal{W}}_4]\rangle ,\hfill \end{array}$$

(9)

where

$$\begin{array}{cc}& {\Gamma }_1^{*}[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4]={\mathcal{L}}_{A_1^{\left(n\right)}}^{*}\left({\mathcal{Z}}_1\right)+{\mathcal{L}}_{A_2^{\left(n\right)}}^{*}\left({\mathcal{Z}}_2\right)+{\mathcal{L}}_{A_3^{\left(n\right)}}^{*}\left({\mathcal{Z}}_3\right)+{\mathcal{L}}_{A_4^{\left(n\right)}}^{*}\left({\mathcal{Z}}_4\right),\hfill \\ \hfill & {\Gamma }_2^{*}[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4]=-{\mathcal{L}}_{A_2^{\left(n\right)}}^{*}\left({\mathcal{Z}}_1\right)+{\mathcal{L}}_{A_1^{\left(n\right)}}^{*}\left({\mathcal{Z}}_2\right)-{\mathcal{L}}_{A_4^{\left(n\right)}}^{*}\left({\mathcal{Z}}_3\right)+{\mathcal{L}}_{A_3^{\left(n\right)}}^{*}\left({\mathcal{Z}}_4\right),\hfill \\ \hfill & {\Gamma }_3^{*}[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4]=-{\mathcal{L}}_{A_3^{\left(n\right)}}^{*}\left({\mathcal{Z}}_1\right)+{\mathcal{L}}_{A_4^{\left(n\right)}}^{*}\left({\mathcal{Z}}_2\right)+{\mathcal{L}}_{A_1^{\left(n\right)}}^{*}\left({\mathcal{Z}}_3\right)-{\mathcal{L}}_{A_2^{\left(n\right)}}^{*}\left({\mathcal{Z}}_4\right),\hfill \\ \hfill & {\Gamma }_4^{*}[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4]=-{\mathcal{L}}_{A_4^{\left(n\right)}}^{*}\left({\mathcal{Z}}_1\right)-{\mathcal{L}}_{A_3^{\left(n\right)}}^{*}\left({\mathcal{Z}}_2\right)+{\mathcal{L}}_{A_2^{\left(n\right)}}^{*}\left({\mathcal{Z}}_3\right)+{\mathcal{L}}_{A_1^{\left(n\right)}}^{*}\left({\mathcal{Z}}_4\right),\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & {\Phi }_1^{*}[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4]={\mathcal{L}}_{B_1^{\left(n\right)}}^{*}\left({\mathcal{Z}}_1\right)+{\mathcal{L}}_{B_2^{\left(n\right)}}^{*}\left({\mathcal{Z}}_2\right)+{\mathcal{L}}_{B_3^{\left(n\right)}}^{*}\left({\mathcal{Z}}_3\right)+{\mathcal{L}}_{B_4^{\left(n\right)}}^{*}\left({\mathcal{Z}}_4\right),\hfill \\ \hfill & {\Phi }_2^{*}[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4]=-{\mathcal{L}}_{B_2^{\left(n\right)}}^{*}\left({\mathcal{Z}}_1\right)+{\mathcal{L}}_{B_1^{\left(n\right)}}^{*}\left({\mathcal{Z}}_2\right)-{\mathcal{L}}_{B_4^{\left(n\right)}}^{*}\left({\mathcal{Z}}_3\right)+{\mathcal{L}}_{B_3^{\left(n\right)}}^{*}\left({\mathcal{Z}}_4\right),\hfill \\ \hfill & {\Phi }_3^{*}[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4]=-{\mathcal{L}}_{B_3^{\left(n\right)}}^{*}\left({\mathcal{Z}}_1\right)+{\mathcal{L}}_{B_4^{\left(n\right)}}^{*}\left({\mathcal{Z}}_2\right)+{\mathcal{L}}_{B_1^{\left(n\right)}}^{*}\left({\mathcal{Z}}_3\right)-{\mathcal{L}}_{B_2^{\left(n\right)}}^{*}\left({\mathcal{Z}}_4\right),\hfill \\ \hfill & {\Phi }_4^{*}[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4]=-{\mathcal{L}}_{B_4^{\left(n\right)}}^{*}\left({\mathcal{Z}}_1\right)-{\mathcal{L}}_{B_3^{\left(n\right)}}^{*}\left({\mathcal{Z}}_2\right)+{\mathcal{L}}_{B_2^{\left(n\right)}}^{*}\left({\mathcal{Z}}_3\right)+{\mathcal{L}}_{B_1^{\left(n\right)}}^{*}\left({\mathcal{Z}}_4\right),\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & {\mathcal{L}}_{A_i^{\left(n\right)}}^{*}\left(\mathcal{X}\right)=\mathcal{X}\times { }_1{\left(A_i^{\left(1\right)}\right)}^{\mathrm{T}}+\mathcal{X}{\times }_2{\left(A_i^{\left(2\right)}\right)}^{\mathrm{T}}+\dots +\mathcal{X}{\times }_N{\left(A_i^{\left(N\right)}\right)}^{\mathrm{T}},i=1,2,3,4,\hfill \\ \hfill & {\mathcal{L}}_{B_i^{\left(n\right)}}^{*}\left(\mathcal{X}\right)=\mathcal{X}\times { }_1{\left(B_i^{\left(1\right)}\right)}^{\mathrm{T}}+\mathcal{X}{\times }_2{\left(B_i^{\left(2\right)}\right)}^{\mathrm{T}}+\dots +\mathcal{X}{\times }_N{\left(B_i^{\left(N\right)}\right)}^{\mathrm{T}},i=1,2,3,4.\hfill \end{array}$$

Proof of Lemma 5.

For the first part of the equalities, we divide ${\sum }_{i=1}^4〈{\Gamma }_i[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4],{\mathcal{W}}_i〉$ into 4 parts by i, and then apply Lemma 3 to each part, that is,

$$\begin{array}{cc}& 〈{\Gamma }_1[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4],{\mathcal{W}}_1〉\hfill \\ & =\langle {\mathcal{L}}_{A_1^{\left(n\right)}}\left({\mathcal{Z}}_1\right),{\mathcal{W}}_1\rangle -\langle {\mathcal{L}}_{A_2^{\left(n\right)}}\left({\mathcal{Z}}_2\right),{\mathcal{W}}_1\rangle -\langle {\mathcal{L}}_{A_3^{\left(n\right)}}\left({\mathcal{Z}}_3\right),{\mathcal{W}}_1\rangle -\langle {\mathcal{L}}_{A_4^{\left(n\right)}}\left({\mathcal{Z}}_4\right),{\mathcal{W}}_1\rangle \hfill \\ & =\langle {\mathcal{Z}}_1,{\mathcal{L}}_{A_1^{\left(n\right)}}^{*}\left({\mathcal{W}}_1\right)\rangle -\langle {\mathcal{Z}}_2,{\mathcal{L}}_{A_2^{\left(n\right)}}^{*}\left({\mathcal{W}}_1\right)\rangle -\langle {\mathcal{Z}}_3,{\mathcal{L}}_{A_3^{\left(n\right)}}^{*}\left({\mathcal{W}}_1\right)\rangle -\langle {\mathcal{Z}}_4,{\mathcal{L}}_{A_4^{\left(n\right)}}^{*}\left({\mathcal{W}}_1\right)\rangle ,\hfill \end{array}$$

$$\begin{array}{cc}& 〈{\Gamma }_2[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4],{\mathcal{W}}_2〉\hfill \\ & =\langle {\mathcal{L}}_{A_2^{\left(n\right)}}\left({\mathcal{Z}}_1\right),{\mathcal{W}}_2\rangle +\langle {\mathcal{L}}_{A_1^{\left(n\right)}}\left({\mathcal{Z}}_2\right),{\mathcal{W}}_2\rangle +\langle {\mathcal{L}}_{A_4^{\left(n\right)}}\left({\mathcal{Z}}_3\right),{\mathcal{W}}_2\rangle -\langle {\mathcal{L}}_{A_3^{\left(n\right)}}\left({\mathcal{Z}}_4\right),{\mathcal{W}}_2\rangle \hfill \\ & =\langle {\mathcal{Z}}_1,{\mathcal{L}}_{A_2^{\left(n\right)}}^{*}\left({\mathcal{W}}_2\right)\rangle +\langle {\mathcal{Z}}_2,{\mathcal{L}}_{A_1^{\left(n\right)}}^{*}\left({\mathcal{W}}_1\right)\rangle +\langle {\mathcal{Z}}_3,{\mathcal{L}}_{A_3^{\left(n\right)}}^{*}\left({\mathcal{W}}_2\right)\rangle -\langle {\mathcal{Z}}_4,{\mathcal{L}}_{A_4^{\left(n\right)}}^{*}\left({\mathcal{W}}_2\right)\rangle ,\hfill \end{array}$$

$$\begin{array}{cc}& 〈{\Gamma }_3[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4],{\mathcal{W}}_3〉\hfill \\ & =\langle {\mathcal{L}}_{A_3^{\left(n\right)}}\left({\mathcal{Z}}_1\right),{\mathcal{W}}_3\rangle -\langle {\mathcal{L}}_{A_4^{\left(n\right)}}\left({\mathcal{Z}}_2\right),{\mathcal{W}}_3\rangle +\langle {\mathcal{L}}_{A_1^{\left(n\right)}}\left({\mathcal{Z}}_3\right),{\mathcal{W}}_3\rangle +\langle {\mathcal{L}}_{A_2^{\left(n\right)}}\left({\mathcal{Z}}_4\right),{\mathcal{W}}_3\rangle \hfill \\ & =\langle {\mathcal{Z}}_1,{\mathcal{L}}_{A_3^{\left(n\right)}}^{*}\left({\mathcal{W}}_3\right)\rangle -\langle {\mathcal{Z}}_2,{\mathcal{L}}_{A_4^{\left(n\right)}}^{*}\left({\mathcal{W}}_3\right)\rangle +\langle {\mathcal{Z}}_3,{\mathcal{L}}_{A_1^{\left(n\right)}}^{*}\left({\mathcal{W}}_2\right)\rangle +\langle {\mathcal{Z}}_4,{\mathcal{L}}_{A_2^{\left(n\right)}}^{*}\left({\mathcal{W}}_3\right)\rangle ,\hfill \end{array}$$

$$\begin{array}{cc}& 〈{\Gamma }_4[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4],{\mathcal{W}}_4〉\hfill \\ & =\langle {\mathcal{L}}_{A_4^{\left(n\right)}}\left({\mathcal{Z}}_1\right),{\mathcal{W}}_4\rangle +\langle {\mathcal{L}}_{A_3^{\left(n\right)}}\left({\mathcal{Z}}_2\right),{\mathcal{W}}_4\rangle -\langle {\mathcal{L}}_{A_2^{\left(n\right)}}\left({\mathcal{Z}}_3\right),{\mathcal{W}}_4\rangle +\langle {\mathcal{L}}_{A_1^{\left(n\right)}}\left({\mathcal{Z}}_4\right),{\mathcal{W}}_4\rangle \hfill \\ & =\langle {\mathcal{Z}}_1,{\mathcal{L}}_{A_4^{\left(n\right)}}^{*}\left({\mathcal{W}}_4\right)\rangle +\langle {\mathcal{Z}}_2,{\mathcal{L}}_{A_3^{\left(n\right)}}^{*}\left({\mathcal{W}}_4\right)\rangle -\langle {\mathcal{Z}}_3,{\mathcal{L}}_{A_2^{\left(n\right)}}^{*}\left({\mathcal{W}}_4\right)\rangle +\langle {\mathcal{Z}}_4,{\mathcal{L}}_{A_1^{\left(n\right)}}^{*}\left({\mathcal{W}}_4\right)\rangle .\hfill \end{array}$$

By adding up the above four parts, we have

$$\sum _{i=1}^4〈{\Gamma }_i[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4],{\mathcal{W}}_i〉=\sum _{i=1}^4\langle {\mathcal{Z}}_i,{\Gamma }_i^{*}[{\mathcal{W}}_1,{\mathcal{W}}_2,{\mathcal{W}}_3,{\mathcal{W}}_4]\rangle ,$$

where ${\Gamma }_i^{*}[{\mathcal{W}}_1,{\mathcal{W}}_2,{\mathcal{W}}_3,{\mathcal{W}}_4]$’s are defined by (10). Using a similar process, we can get the second equality

$$\sum _{i=1}^4〈{\Phi }_i[{\mathcal{Z}}_1,{\mathcal{Z}}_2,{\mathcal{Z}}_3,{\mathcal{Z}}_4],{\mathcal{W}}_i〉=\sum _{i=1}^4\langle {\mathcal{Z}}_i,{\Phi }_i^{*}[{\mathcal{W}}_1,{\mathcal{W}}_2,{\mathcal{W}}_3,{\mathcal{W}}_4]\rangle ,$$

where ${\Phi }_i^{*}[{\mathcal{W}}_1,{\mathcal{W}}_2,{\mathcal{W}}_3,{\mathcal{W}}_4]$’s are defined by (11). □

3. An Iterative Algorithm For Solving The Problem 1.1 And 1.2

The purpose of this section is to propose an iterative algorithm for obtaining the solution of Sylvester tensor Equation (2). As well known that the classical bi-conjugate gradient (BiCG) methods for solving nonsymmetric linear system of equations are feasible and efficient, one may refer to [5,6,12,18,55]. We extend the BiCG method based on tensor format (BTF) for solving Equation (2) and discuss its convergence. Clearly, the tensor Equation (2) and (8) have the same solution from Lemma 1. However, the size of $[{\mathcal{M}}_A,{\mathcal{M}}_B]$ in Equation (8) is usually too large to save computation time and memory space. Beik et al. [8] showed that the algorithms based on tensor format are more efficient than their classical forms in general. Inspired by these issues, we develop the following least squares algorithm based on tensor format for solving tensor Equation (2):

Note that ${\Gamma }_i,{\Phi }_i$ and ${\Gamma }_i^{*},{\Phi }_i^{*}$ are defined by (5), (6) and (10), (11), respectively. Next, we discuss some bi-orthogonality properties of Algorithm 1.

Theorem 2.

Assume that iterative sequences $\left\{{\mathcal{R}}_i\left(k\right)\right\}$, $\left\{{\mathcal{R}}_i^{*}\left(k\right)\right\}$, $\left\{{\mathcal{P}}_i\left(k\right)\right\}$, $\left\{{\mathcal{P}}_i^{*}\left(k\right)\right\}$$\left\{{\mathcal{Q}}_{ix}\left(k\right)\right\}$ and $\left\{{\mathcal{Q}}_{iy}\left(k\right)\right\}(i=1,2,3,4)$ are generated by Algorithm 1. Then we have

$$\sum _{i=1}^4\langle {\mathcal{R}}_i\left(l\right),{\mathcal{R}}_i^{*}\left(m\right)\rangle =0,l\ne m,$$

(12)

$$\sum _{i=1}^4\langle {\mathcal{Q}}_{ix}\left(l\right)+{\mathcal{Q}}_{iy}\left(l\right),{\mathcal{P}}_i^{*}\left(m\right)\rangle =0,l\ne m,$$

(13)

$$\sum _{i=1}^4\langle {\mathcal{R}}_i\left(l\right),{\mathcal{P}}_i^{*}\left(m\right)\rangle =0,l>m.$$

(14)

Proof of Theorem 2.

We apply mathematics induction on k. Let’s consider $1\le m<l\le k$ first.

When $k=2$. The conclusion holds as the following calculations show:

$$\begin{array}{cc}\hfill & \sum _{i=1}^4〈{\mathcal{R}}_i\left(2\right),{\mathcal{R}}_i^{*}\left(1\right)〉\hfill \\ \hfill =& \sum _{i=1}^4〈{\mathcal{R}}_i\left(1\right)-{\alpha }_1\left({\mathcal{Q}}_{ix}\left(1\right)+{\mathcal{Q}}_{iy}\left(1\right)\right),{\mathcal{R}}_i^{*}\left(1\right)〉\hfill \\ \hfill =& \sum _{i=1}^4〈{\mathcal{R}}_i\left(1\right),{\mathcal{R}}_i^{*}\left(1\right)〉-{\displaystyle \frac{{\sum }_{i=1}^4〈{\mathcal{R}}_i\left(1\right),{\mathcal{R}}_i^{*}\left(1\right)〉}{{\sum }_{i=1}^4\langle {\mathcal{P}}_i^{*}\left(1\right),{\mathcal{Q}}_{ix}\left(1\right)+{\mathcal{Q}}_{iy}\left(1\right)\rangle }}\sum _{i=1}^4\langle {\mathcal{P}}_i^{*}\left(1\right),{\mathcal{Q}}_{ix}\left(1\right)+{\mathcal{Q}}_{iy}\left(1\right)\rangle \hfill \\ \hfill =& 0,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \sum _{i=1}^4\langle {\mathcal{Q}}_{ix}\left(2\right)+{\mathcal{Q}}_{iy}\left(2\right),{\mathcal{P}}_i^{*}\left(1\right)\rangle \hfill \\ \hfill =& \sum _{i=1}^4〈{\Gamma }_i[{\mathcal{P}}_1\left(2\right),{\mathcal{P}}_2\left(2\right),{\mathcal{P}}_3\left(2\right),{\mathcal{P}}_4\left(2\right)],{\mathcal{P}}_i^{*}\left(1\right)〉+\sum _{i=1}^4〈{\Phi }_i[{\mathcal{P}}_1\left(2\right),{\mathcal{P}}_2\left(2\right),{\mathcal{P}}_3\left(2\right),{\mathcal{P}}_4\left(2\right)],{\mathcal{P}}_i^{*}\left(1\right)〉\hfill \\ \hfill =& \sum _{i=1}^4〈{\mathcal{P}}_i\left(2\right),{\Gamma }_i^{*}[{\mathcal{P}}_1^{*}\left(1\right),{\mathcal{P}}_2^{*}\left(1\right),{\mathcal{P}}_3^{*}\left(1\right),{\mathcal{P}}_4^{*}\left(1\right)]〉+\sum _{i=1}^4〈{\mathcal{P}}_i\left(2\right),{\Phi }_i^{*}[{\mathcal{P}}_1^{*}\left(1\right),{\mathcal{P}}_2^{*}\left(1\right),{\mathcal{P}}_3^{*}\left(1\right),{\mathcal{P}}_4^{*}\left(1\right)]〉\hfill \\ \hfill =& \sum _{i=1}^4\left[\langle {\mathcal{R}}_i\left(2\right),{\mathcal{Q}}_{ix}^{*}\left(1\right)\rangle +\beta \left(1\right)\langle {\mathcal{P}}_i\left(1\right),{\mathcal{Q}}_{ix}^{*}\left(1\right)\rangle \right]+\sum _{i=1}^4\left[\langle {\mathcal{R}}_i\left(2\right),{\mathcal{Q}}_{iy}^{*}\left(1\right)\rangle +\beta \left(1\right)\langle {\mathcal{P}}_i\left(1\right),{\mathcal{Q}}_{iy}^{*}\left(1\right)\rangle \right]\hfill \\ \hfill =& \sum _{i=1}^4\left[\langle {\mathcal{R}}_i\left(2\right),{\mathcal{Q}}_{ix}^{*}\left(1\right)\rangle +{\displaystyle \frac{{\sum }_{i=1}^4\langle {\mathcal{R}}_i\left(2\right),{\mathcal{R}}_i^{*}\left(1\right)-\alpha \left(1\right)({\mathcal{Q}}_{ix}^{*}\left(1\right)+{\mathcal{Q}}_{iy}^{*}\left(1\right))\rangle }{{\sum }_{i=1}^4\langle {\mathcal{R}}_i\left(1\right),{\mathcal{R}}_i^{*}\left(1\right)\rangle }}\langle {\mathcal{P}}_i\left(1\right),{\mathcal{Q}}_{ix}^{*}\left(1\right)\rangle \right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +\sum _{i=1}^4\left[\langle {\mathcal{R}}_i\left(2\right),{\mathcal{Q}}_{iy}^{*}\left(1\right)\rangle +{\displaystyle \frac{{\sum }_{i=1}^4\langle {\mathcal{R}}_i\left(2\right),{\mathcal{R}}_i^{*}\left(1\right)-\alpha \left(1\right)({\mathcal{Q}}_{ix}^{*}\left(1\right)+{\mathcal{Q}}_{iy}^{*}\left(1\right))\rangle }{{\sum }_{i=1}^4\langle {\mathcal{R}}_i\left(1\right),{\mathcal{R}}_i^{*}\left(1\right)\rangle }}\langle {\mathcal{P}}_i\left(1\right),{\mathcal{Q}}_{iy}^{*}\left(1\right)\rangle \right]\hfill \\ \hfill =& \sum _{i=1}^4\left[\langle {\mathcal{R}}_i\left(2\right),{\mathcal{Q}}_{ix}^{*}\left(1\right)\rangle -{\displaystyle \frac{{\sum }_{i=1}^4\langle {\mathcal{R}}_i\left(2\right),{\mathcal{Q}}_{ix}^{*}\left(1\right)+{\mathcal{Q}}_{iy}^{*}\left(1\right)\rangle }{{\sum }_{i=1}^4\langle {\mathcal{P}}_i^{*}\left(1\right),{\mathcal{Q}}_{ix}\left(1\right)+{\mathcal{Q}}_{iy}\left(1\right)\rangle }}\langle {\mathcal{P}}_i\left(1\right),{\mathcal{Q}}_{ix}^{*}\left(1\right)\rangle \right]\hfill \\ \hfill & +\sum _{i=1}^4\left[\langle {\mathcal{R}}_i\left(2\right),{\mathcal{Q}}_{iy}^{*}\left(1\right)\rangle -{\displaystyle \frac{{\sum }_{i=1}^4\langle {\mathcal{R}}_i\left(2\right),{\mathcal{Q}}_{ix}^{*}\left(1\right)+{\mathcal{Q}}_{iy}^{*}\left(1\right)\rangle }{{\sum }_{i=1}^4\langle {\mathcal{P}}_i^{*}\left(1\right),{\mathcal{Q}}_{ix}\left(1\right)+{\mathcal{Q}}_{iy}\left(1\right)\rangle }}\langle {\mathcal{P}}_i\left(1\right),{\mathcal{Q}}_{iy}^{*}\left(1\right)\rangle \right]\hfill \\ \hfill =& \sum _{i=1}^4\langle {\mathcal{R}}_i\left(2\right),{\mathcal{Q}}_{ix}^{*}\left(1\right)+{\mathcal{Q}}_{iy}^{*}\left(1\right)\rangle -{\displaystyle \frac{{\sum }_{i=1}^4\langle {\mathcal{R}}_i\left(2\right),{\mathcal{Q}}_{ix}^{*}\left(1\right)+{\mathcal{Q}}_{iy}^{*}\left(1\right)\rangle }{{\sum }_{i=1}^4\langle {\mathcal{P}}_i^{*}\left(1\right),{\mathcal{Q}}_{ix}\left(1\right)+{\mathcal{Q}}_{iy}\left(1\right)\rangle }}\sum _{i=1}^4\langle {\mathcal{P}}_i^{*}\left(1\right),{\mathcal{Q}}_{ix}\left(1\right)+{\mathcal{Q}}_{iy}\left(1\right)\rangle \hfill \\ \hfill =& 0.\hfill \end{array}$$

It has been found ${\sum }_{i=1}^4\langle {\mathcal{R}}_i\left(2\right),{\mathcal{P}}_i^{*}\left(1\right)\rangle =0$ clearly. Now, assume that (12) and (13) hold for $1\le m<l\le k$ ($k>2$). Then

$$\begin{array}{cc}\hfill \sum _{i=1}^4\langle {\mathcal{R}}_i(k+1),{\mathcal{P}}_i^{*}\left(m\right)\rangle =& \sum _{i=1}^4\langle {\mathcal{R}}_i\left(k\right)-\alpha \left(k\right)\left({\mathcal{Q}}_{ix}\left(k\right)+{\mathcal{Q}}_{iy}\left(k\right)\right),{\mathcal{P}}_i^{*}\left(m\right)\rangle \hfill \\ \hfill =& \sum _{i=1}^4\left[\langle {\mathcal{R}}_i\left(k\right),{\mathcal{P}}_i^{*}\left(m\right)\rangle -\alpha \left(k\right)\langle {\mathcal{Q}}_{ix}\left(k\right)+{\mathcal{Q}}_{iy}\left(k\right),{\mathcal{P}}_i^{*}\left(m\right)\rangle \right]\hfill \\ \hfill =& 0,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \sum _{i=1}^4\langle {\mathcal{R}}_i(k+1),{\mathcal{P}}_i^{*}\left(k\right)\rangle =& \sum _{i=1}^4\langle {\mathcal{R}}_i\left(k\right)-\alpha \left(k\right)\left({\mathcal{Q}}_{ix}\left(k\right)+{\mathcal{Q}}_{iy}\left(k\right)\right),{\mathcal{P}}_i^{*}\left(k\right)\rangle \hfill \\ \hfill =& \sum _{i=1}^4\left[\langle {\mathcal{R}}_i\left(k\right),{\mathcal{P}}_i^{*}\left(k\right)\rangle -\alpha \left(k\right)\langle {\mathcal{Q}}_{ix}\left(k\right)+{\mathcal{Q}}_{iy}\left(k\right),{\mathcal{P}}_i^{*}\left(k\right)\rangle \right]\hfill \\ \hfill =& \sum _{i=1}^4\left[{\mathcal{R}}_i\left(k\right),{\mathcal{R}}_i^{*}\left(k\right)+\beta (k-1)\langle {\mathcal{R}}_i\left(k\right),{\mathcal{P}}_i^{*}(k-1)\rangle \right]\hfill \\ \hfill & -{\displaystyle \frac{{\sum }_{i=1}^4\langle {\mathcal{R}}_i\left(k\right),{\mathcal{R}}_i^{*}\left(k\right)\rangle }{{\sum }_{i=1}^4\langle {\mathcal{P}}_i^{*}\left(k\right),{\mathcal{Q}}_{ix}\left(k\right)+{\mathcal{Q}}_{iy}\left(k\right)\rangle }}\sum _{i=1}^4\langle {\mathcal{P}}_i^{*}\left(k\right),{\mathcal{Q}}_{ix}\left(k\right)+{\mathcal{Q}}_{iy}\left(k\right)\rangle \hfill \\ \hfill =& 0.\hfill \end{array}$$

The equality (14) holds for all $l>m$. Next, we will prove that the equalities (12) and (13) hold for all $l>m$.

$$\begin{array}{cc}\hfill \sum _{i=1}^4\langle {\mathcal{R}}_i(k+1),{\mathcal{R}}_i^{*}\left(m\right)\rangle =& \sum _{i=1}^4\langle {\mathcal{R}}_i(k+1),{\mathcal{P}}_i^{*}\left(m\right)-\beta (m-1){\mathcal{P}}_i^{*}(m-1)\rangle \hfill \\ \hfill =& \sum _{i=1}^4\left[\langle {\mathcal{R}}_i(k+1),{\mathcal{P}}_i^{*}\left(m\right)\rangle -\beta (m-1)\langle {\mathcal{R}}_i(k+1),{\mathcal{P}}_i^{*}(m-1)\rangle \right]\hfill \\ \hfill =& 0,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \sum _{i=1}^4\langle {\mathcal{R}}_i(k+1),{\mathcal{R}}_i^{*}\left(k\right)\rangle =& \sum _{i=1}^4\langle {\mathcal{R}}_i(k+1),{\mathcal{P}}_i^{*}\left(m\right)-\beta (m-1){\mathcal{P}}_i^{*}(m-1)\rangle \hfill \\ \hfill =& \sum _{i=1}^4\left[\langle {\mathcal{R}}_i(k+1),{\mathcal{P}}_i^{*}\left(m\right)\rangle -\beta (m-1)\langle {\mathcal{R}}_i(k+1),{\mathcal{P}}_i^{*}(m-1)\rangle \right]\hfill \\ \hfill =& 0,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \sum _{i=1}^4\langle {\mathcal{Q}}_{ix}(k+1)+{\mathcal{Q}}_{iy}(k+1),{\mathcal{P}}_i^{*}\left(m\right)\rangle \hfill \\ \hfill =& \sum _{i=1}^4\langle {\mathcal{Q}}_{ix}(k+1),{\mathcal{P}}_i^{*}\left(m\right)\rangle +\sum _{i=1}^4\langle {\mathcal{Q}}_{iy}(k+1),{\mathcal{P}}_i^{*}\left(m\right)\rangle \hfill \\ \hfill =& \sum _{i=1}^4\left[\langle {\mathcal{R}}_i(k+1),{\Gamma }_i^{*}[{\mathcal{P}}_1^{*}\left(m\right),{\mathcal{P}}_2^{*}\left(m\right),{\mathcal{P}}_3^{*}\left(m\right),{\mathcal{P}}_4^{*}\left(m\right)]\rangle \right.\hfill \\ \hfill & \left.+\beta \left(k\right)\langle {\mathcal{P}}_i\left(k\right),{\Gamma }_i^{*}[{\mathcal{P}}_1^{*}\left(m\right),{\mathcal{P}}_2^{*}\left(m\right),{\mathcal{P}}_3^{*}\left(m\right),{\mathcal{P}}_4^{*}\left(m\right)]\rangle \right]\hfill \\ \hfill & +\sum _{i=1}^4\left[\langle {\mathcal{R}}_i(k+1),{\Phi }_i^{*}[{\mathcal{P}}_1^{*}\left(m\right),{\mathcal{P}}_2^{*}\left(m\right),{\mathcal{P}}_3^{*}\left(m\right),{\mathcal{P}}_4^{*}\left(m\right)]\rangle \right.\hfill \\ \hfill & \left.+\beta \left(k\right)\langle {\mathcal{P}}_i\left(k\right),{\Phi }_i^{*}[{\mathcal{P}}_1^{*}\left(m\right),{\mathcal{P}}_2^{*}\left(m\right),{\mathcal{P}}_3^{*}\left(m\right),{\mathcal{P}}_4^{*}\left(m\right)]\rangle \right]\hfill \\ \hfill =& \sum _{i=1}^4\left[〈{\mathcal{R}}_i(k+1),{\mathcal{Q}}_{ix}^{*}\left(m\right)〉+\beta \left(k\right)\langle {\mathcal{P}}_i\left(k\right),{\mathcal{Q}}_{ix}^{*}\left(m\right)\rangle \right.\hfill \\ \hfill & \left.+\langle {\mathcal{R}}_i(k+1),{\mathcal{Q}}_{iy}^{*}\left(m\right)\rangle +\beta \left(k\right)\langle {\mathcal{P}}_i\left(k\right),{\mathcal{Q}}_{iy}^{*}\left(m\right)\rangle \right]\hfill \\ \hfill =& \sum _{i=1}^4\left[〈{\mathcal{R}}_i(k+1),-{\displaystyle \frac{1}{\alpha \left(m\right)}}({\mathcal{R}}_i^{*}(m+1)-{\mathcal{R}}_i\left(m\right))〉\right.\hfill \\ \hfill & \left.+\beta \left(k\right)〈{\mathcal{P}}_i\left(k\right),-{\displaystyle \frac{1}{\alpha \left(m\right)}}({\mathcal{R}}_i^{*}(m+1)-{\mathcal{R}}_i\left(m\right))〉\right]\hfill \\ \hfill =& 0,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \sum _{i=1}^4\langle {\mathcal{Q}}_{ix}(k+1)+{\mathcal{Q}}_{iy}(k+1),{\mathcal{P}}_i^{*}\left(k\right)\rangle \hfill \\ \hfill =& \sum _{i=1}^4\langle {\mathcal{Q}}_{ix}(k+1),{\mathcal{P}}_i^{*}\left(k\right)\rangle +\sum _{i=1}^4\langle {\mathcal{Q}}_{iy}(k+1),{\mathcal{P}}_i^{*}\left(k\right)\rangle \hfill \\ \hfill =& \sum _{i=1}^4\left[\langle {\mathcal{R}}_i(k+1),{\Gamma }_i^{*}[{\mathcal{P}}_1^{*}\left(k\right),{\mathcal{P}}_2^{*}\left(k\right),{\mathcal{P}}_3^{*}\left(k\right),{\mathcal{P}}_4^{*}\left(k\right)]\rangle \right.\hfill \\ \hfill & \left.+\beta \left(k\right)\langle {\mathcal{P}}_i\left(k\right),{\Gamma }_i^{*}[{\mathcal{P}}_1^{*}\left(k\right),{\mathcal{P}}_2^{*}\left(k\right),{\mathcal{P}}_3^{*}\left(k\right),{\mathcal{P}}_4^{*}\left(k\right)]\rangle \right]\hfill \\ \hfill & +\sum _{i=1}^4\left[\langle {\mathcal{R}}_i(k+1),{\Phi }_i^{*}[{\mathcal{P}}_1^{*}\left(k\right),{\mathcal{P}}_2^{*}\left(k\right),{\mathcal{P}}_3^{*}\left(k\right),{\mathcal{P}}_4^{*}\left(k\right)]\rangle \right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \left.+\beta \left(k\right)\langle {\mathcal{P}}_i\left(k\right),{\Phi }_i^{*}[{\mathcal{P}}_1^{*}\left(k\right),{\mathcal{P}}_2^{*}\left(k\right),{\mathcal{P}}_3^{*}\left(k\right),{\mathcal{P}}_4^{*}\left(k\right)]\rangle \right]\hfill \\ \hfill =& \sum _{i=1}^4\left[〈{\mathcal{R}}_i(k+1),{\mathcal{Q}}_{ix}^{*}\left(k\right)〉+\beta \left(k\right)\langle {\mathcal{P}}_i\left(k\right),{\mathcal{Q}}_{ix}^{*}\left(k\right)\rangle +\langle {\mathcal{R}}_i(k+1),{\mathcal{Q}}_{iy}^{*}\left(k\right)\rangle +\beta \left(k\right)\langle {\mathcal{P}}_i\left(k\right),{\mathcal{Q}}_{iy}^{*}\left(k\right)\rangle \right]\hfill \\ \hfill =& \sum _{i=1}^4\left[〈{\mathcal{R}}_i(k+1),{\mathcal{Q}}_{ix}^{*}\left(k\right)+{\mathcal{Q}}_{iy}^{*}\left(k\right)〉\right.\hfill \\ \hfill & \left.-{\displaystyle \frac{{\sum }_{i=1}^4〈{\mathcal{R}}_i(k+1),{\mathcal{Q}}_{ix}^{*}\left(k\right)+{\mathcal{Q}}_{iy}^{*}\left(k\right)〉}{{\sum }_{i=1}^4〈{\mathcal{P}}_i\left(k\right),{\mathcal{Q}}_{ix}^{*}\left(k\right)+{\mathcal{Q}}_{iy}^{*}\left(k\right)〉}}+〈{\mathcal{P}}_i\left(k\right),{\mathcal{Q}}_{ix}^{*}\left(k\right)+{\mathcal{Q}}_{iy}^{*}\left(k\right)〉\right]\hfill \\ \hfill =& 0.\hfill \end{array}$$

Similarly, the equalities (12) and (13) also hold for the case $1\le m<l\le k.$ Therefore, the facts illustrate that (12) and (13) are satisfied for $l\ne m$. □

Corollary 1.

Assume the conditions in Theorem 2 are satisfied. Then

$$\begin{array}{c}\hfill \sum _{i=1}^4\langle {\mathcal{R}}_i\left(k\right),{\mathcal{P}}_i^{*}\left(k\right)\rangle =\sum _{i=1}^4\langle {\mathcal{R}}_i\left(k\right),{\mathcal{R}}_i^{*}\left(k\right)\rangle ,\end{array}$$

(15)

$$\sum _{i=1}^4\langle {\mathcal{Q}}_{ix}\left(k\right)+{\mathcal{Q}}_{iy}\left(k\right),{\mathcal{R}}_i^{*}\left(k\right)\rangle =\sum _{i=1}^4\langle {\mathcal{Q}}_{ix}\left(k\right)+{\mathcal{Q}}_{iy}\left(k\right),{\mathcal{P}}_i^{*}\left(k\right)\rangle .$$

(16)

Proof of Corollary 1.

From Algorithm 1 and Theorem 2, we have

$$\begin{array}{cc}\hfill \sum _{i=1}^4\langle {\mathcal{R}}_i\left(k\right),{\mathcal{P}}_i^{*}\left(k\right)\rangle =& \sum _{i=1}^4\langle {\mathcal{R}}_i\left(k\right),{\mathcal{R}}_i^{*}\left(k\right)+\beta (k-1){\mathcal{P}}_i^{*}(k-1)\rangle \hfill \\ \hfill =& \sum _{i=1}^4\langle {\mathcal{R}}_i\left(k\right),{\mathcal{R}}_i^{*}\left(k\right)\rangle ,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \sum _{i=1}^4\langle {\mathcal{Q}}_{ix}\left(k\right)+{\mathcal{Q}}_{iy}\left(k\right),{\mathcal{R}}_i^{*}\left(k\right)\rangle =& \sum _{i=1}^4〈{\mathcal{Q}}_{ix}\left(k\right)+{\mathcal{Q}}_{iy}\left(k\right),{\mathcal{P}}_i^{*}\left(k\right)-\beta (k-1){\mathcal{P}}_i^{*}(k-1)〉\hfill \\ \hfill =& \sum _{i=1}^4\langle {\mathcal{Q}}_{ix}\left(k\right)+{\mathcal{Q}}_{iy}\left(k\right),{\mathcal{P}}_i^{*}\left(k\right)\rangle .\hfill \end{array}$$

□

Theorem 3.

Let tensor sequences $\left\{{\mathcal{X}}_i\left(k\right)\right\}$, $\left\{{\mathcal{Y}}_i\left(k\right)\right\}(i=1,2,3,4)$ be generated by Algorithm . If Algorithm 1 does not break down, then the tensor sequences

$$\begin{array}{cc}\hfill \left\{\right[\mathcal{X}\left(k\right),\mathcal{Y}\left(k\right)]\mid \mathcal{X}(k)& ={\mathcal{X}}_1\left(k\right)+{\mathcal{X}}_2\left(k\right)\mathbf{i}+{\mathcal{X}}_3\left(k\right)\mathbf{j}+{\mathcal{X}}_4\left(k\right)\mathbf{k},\hfill \\ \hfill \mathcal{Y}\left(k\right)& ={\mathcal{Y}}_1\left(k\right)+{\mathcal{Y}}_2\left(k\right)\mathbf{i}+{\mathcal{Y}}_3\left(k\right)\mathbf{j}+{\mathcal{Y}}_4\left(k\right)\mathbf{k},k=1,2,\dots \}\hfill \end{array}$$

converge to the solution of Equation (2) within a finite iteration steps in the absence of round-off errors.

Proof of Theorem 3.

We will prove that there exists a $k\le 4S_N$ such that ${\mathcal{R}}_i\left(k\right)=0$. By contradiction, assume that ${\mathcal{R}}_i\left(k\right)\ne 0,i=1,2,3,4,$ for all $k\le 4S_N$, and thus we can compute ${\mathcal{R}}_i(4S_N+1)$. Suppose that ${\mathcal{R}}_i\left(1\right),{\mathcal{R}}_i\left(2\right),\dots ,{\mathcal{R}}_i\left(4S_N\right)$ is a dependent sequence, then there exist real numbers ${\lambda }_{i,1},\dots ,{\lambda }_{i,4S_N}$, not all zero, such that

$${\lambda }_{i,1}{\mathcal{R}}_i\left(1\right)+\dots +{\lambda }_{i,4S_N}{\mathcal{R}}_i\left(4S_N\right)=0,$$

for $i=1,2,3,4.$ Then

$$\begin{array}{cc}\hfill \sum _{i=1}^4\langle {\mathcal{R}}_i\left(l\right),0\rangle =& \sum _{i=1}^4\langle {\mathcal{R}}_i\left(l\right),{\lambda }_{i,1}{\mathcal{R}}_i\left(1\right)+\dots +{\lambda }_{i,4S_N}{\mathcal{R}}_i\left(4S_N\right)\rangle \hfill \\ \hfill =& \sum _{i=1}^4{\lambda }_{i,l}\langle \langle {\mathcal{R}}_i\left(l\right),\langle {\mathcal{R}}_i\left(l\right)\rangle \hfill \\ \hfill =& 0,\hfill \end{array}$$

which implies ${\sum }_{i=1}^4\langle \langle {\mathcal{R}}_i\left(l\right),\langle {\mathcal{R}}_i\left(l\right)\rangle =0$. This is a contradiction since we can not calculate ${\mathcal{R}}_i(4S_N+1)$ in this case. Therefore, there must exists a $k\le 4S_N$ such that ${\mathcal{R}}_i\left(k\right)=0$, that is, the exact solution of tensor Equation (2) can be computed by Algorithm 1 within a finite iteration steps in the absence of round-off errors. □

In the following theorem, we show that if we choose special kinds of initial tensor, then Algorithm 1 can yield the unique minimal Frobenius norm solution of the tensor Equation (2).

Theorem 4.

If we choose the initial tensors as

$$\begin{array}{c}\hfill {\mathcal{X}}_j\left(1\right)={\Gamma }_j^{*}[{\mathcal{H}}_1\left(1\right),{\mathcal{H}}_2\left(1\right),{\mathcal{H}}_3\left(1\right),{\mathcal{H}}_4\left(1\right)],{\mathcal{Y}}_j\left(1\right)={\Phi }_j^{*}[{\mathcal{H}}_1\left(1\right),{\mathcal{H}}_2\left(1\right),{\mathcal{H}}_3\left(1\right),{\mathcal{H}}_4\left(1\right)],\end{array}$$

(17)

where ${\Gamma }_j^{*},{\Phi }_j^{*}(j=1,2,3,4)$ are defined by (10) and (11), ${\mathcal{H}}_i\left(1\right)\in {\mathbb{R}}^{I_1\times I_2\times \dots \times I_N},(i=1,2,3,4)$ are arbitrary tensors (in particular, we take $\left.{\mathcal{X}}_j\left(1\right)=\mathcal{O},{\mathcal{Y}}_j\left(1\right)=\mathcal{O},j=1,2,3,4\right)$, then the solution group $\widetilde{\mathcal{X}{ }_j},\widetilde{\mathcal{Y}{ }_j}(j=1,2,3,4)$ given by Algorithm 1 is the unique minimal Frobenius norm solution of the tensor Equations (2).

Proof of Theorem 4.

If we choose the initial tensors as (17), it is not difficult to verify that $\widetilde{{\mathcal{X}}_j},\widetilde{{\mathcal{Y}}_j}(j=1,2,3,4)$ obtained by Algorithm 1 have the following form

$$\begin{array}{c}\hfill \widetilde{{\mathcal{X}}_j}={\Gamma }_j^{*}[{\mathcal{H}}_1,{\mathcal{H}}_2,{\mathcal{H}}_3,{\mathcal{H}}_4],\widetilde{{\mathcal{Y}}_j}={\Phi }_j^{*}[{\mathcal{H}}_1,{\mathcal{H}}_2,{\mathcal{H}}_3,{\mathcal{H}}_4],\end{array}$$

where tensors ${\mathcal{H}}_i\in {\mathbb{R}}^{I_1\times I_2\times \dots \times I_N}(i=1,2,3,4)$. Now, we show that $\tilde{\mathcal{X}}=\widetilde{{\mathcal{X}}_1}+\widetilde{{\mathcal{X}}_2}\mathbf{i}+\widetilde{{\mathcal{X}}_3}\mathbf{j}+\widetilde{{\mathcal{X}}_4}\mathbf{k}$, $\tilde{\mathcal{Y}}=\widetilde{{\mathcal{Y}}_1}+\widetilde{{\mathcal{Y}}_2}\mathbf{i}+\widetilde{{\mathcal{Y}}_3}\mathbf{j}+\widetilde{{\mathcal{Y}}_4}\mathbf{k}$ is the unique minimal Frobenius norm solution of tensor Equation (2). Let

$$\begin{array}{cc}\hfill \tilde{z}& =\left(\begin{array}{c}\mathrm{vec}\left(\widetilde{{\mathcal{X}}_1}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{X}}_2}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{X}}_3}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{X}}_4}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{Y}}_1}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{Y}}_2}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{Y}}_3}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{Y}}_4}\right)\end{array}\right)=\left(\begin{array}{cccc}Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}^T\right)\hfill \\ -Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}^T\right)\hfill & -Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}^T\right)\hfill \\ -Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}^T\right)\hfill & -Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}^T\right)\hfill \\ -Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}^T\right)\hfill & -Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}^T\right)\hfill \\ Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}^T\right)\hfill \\ -Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}^T\right)\hfill & -Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}^T\right)\hfill \\ -Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}^T\right)\hfill & -Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}^T\right)\hfill \\ -Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}^T\right)\hfill & -Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}^T\right)\hfill & +Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}^T\right)\hfill \end{array}\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \times \left(\begin{array}{c}\mathrm{vec}\left(\widetilde{{\mathcal{H}}_1}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{H}}_2}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{H}}_3}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{H}}_4}\right)\end{array}\right),\hfill \\ \hfill & =\left(\begin{array}{cccc}Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}\right)\hfill \\ Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}\right)\hfill & Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}\right)\hfill & Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}\right)\hfill \\ Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}\right)\hfill & Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}\right)\hfill & Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}\right)\hfill \\ Kro\left({\mathcal{L}}_{A_4^{\left(n\right)}}\right)\hfill & Kro\left({\mathcal{L}}_{A_3^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{A_2^{\left(n\right)}}\right)\hfill & Kro\left({\mathcal{L}}_{A_1^{\left(n\right)}}\right)\hfill \end{array}\right.\hfill \\ \hfill & {\left.\begin{array}{cccc}Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}\right)\hfill \\ Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}\right)\hfill & Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}\right)\hfill & Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}\right)\hfill \\ Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}\right)\hfill & Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}\right)\hfill & Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}\right)\hfill \\ Kro\left({\mathcal{L}}_{B_4^{\left(n\right)}}\right)\hfill & Kro\left({\mathcal{L}}_{B_3^{\left(n\right)}}\right)\hfill & -Kro\left({\mathcal{L}}_{B_2^{\left(n\right)}}\right)\hfill & Kro\left({\mathcal{L}}_{B_1^{\left(n\right)}}\right)\hfill \end{array}\right)}^T\times \left(\begin{array}{c}\mathrm{vec}\left(\widetilde{{\mathcal{H}}_1}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{H}}_2}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{H}}_3}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{H}}_4}\right)\end{array}\right),\hfill \\ \hfill & ={[{\mathcal{M}}_A,{\mathcal{M}}_B]}^T\times \left(\begin{array}{c}\mathrm{vec}\left(\widetilde{{\mathcal{H}}_1}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{H}}_2}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{H}}_3}\right)\\ \mathrm{vec}\left(\widetilde{{\mathcal{H}}_4}\right)\end{array}\right)\in \mathcal{R}\left({[{\mathcal{M}}_A,{\mathcal{M}}_B]}^T\right).\hfill \end{array}$$

According to Theorem 1, we can conclude that $\tilde{\mathcal{X}}=\widetilde{{\mathcal{X}}_1}+\widetilde{{\mathcal{X}}_2}\mathbf{i}+\widetilde{{\mathcal{X}}_3}\mathbf{j}+\widetilde{{\mathcal{X}}_4}\mathbf{k}$, $\tilde{\mathcal{Y}}=\widetilde{{\mathcal{Y}}_1}+\widetilde{{\mathcal{Y}}_2}\mathbf{i}+\widetilde{{\mathcal{Y}}_3}\mathbf{j}+\widetilde{{\mathcal{Y}}_4}\mathbf{k}$ generated by Algorithm 1 is the unique minimal Frobenius norm solution of the tensor Equations (2). □

Now, we solve Problem 1.2. If the tensor Equation (2) is consistent, the solution pair set $S_{XY}$ of Problem 1.1 is non-empty, for given tensors $\overline{\mathcal{X}},\overline{\mathcal{Y}}\in {\mathbb{H}}^{I_1\times I_2\times \dots \times I_N}$, we have

$$\begin{array}{cc}& \underset{\mathcal{X},\mathcal{Y}\in {\mathbb{H}}_1\times I_2\times \dots \times I_N}{min}∥\sum _{k=1}^N\mathcal{X}{\times }_k{A}^{\left(k\right)}+\mathcal{Y}{\times }_k{B}^{\left(k\right)}-\mathcal{C}∥\hfill \\ & =\underset{\mathcal{X},\mathcal{Y}\in {\mathbb{H}}^{I_1\times I_2\times \dots \times I_N}}{min}∥\sum _{k=1}^N\left(\mathcal{X}-\overline{\mathcal{X}}\right){\times }_k{A}^{\left(k\right)}+\left(\mathcal{Y}-\overline{\mathcal{Y}}\right){\times }_k{B}^{\left(k\right)}\hfill \\ & -\left(\mathcal{C}-\sum _{k=1}^N\overline{\mathcal{X}}{\times }_k{A}^{\left(k\right)}-\overline{\mathcal{Y}}{\times }_k{B}^{\left(k\right)}\right)∥.\hfill \end{array}$$

Let $\tilde{\mathcal{X}}=\mathcal{X}-\overline{\mathcal{X}},\tilde{\mathcal{Y}}=\mathcal{Y}-\overline{\mathcal{Y}}$, and $\tilde{\mathcal{C}}=\mathcal{C}-{\sum }_{k=1}^N\overline{\mathcal{X}}{\times }_k{A}^{\left(k\right)}-\overline{\mathcal{Y}}{\times }_k{B}^{\left(k\right)}$, then the tensor nearness Problem 1.2 is equivalent to first finding the minimal Frobenius norm sulution of tensor equation

$$\sum _{k=1}^N\tilde{\mathcal{X}}{\times }_k{A}^{\left(k\right)}+\tilde{\mathcal{Y}}{\times }_k{B}^{\left(k\right)}=\mathcal{C}.$$

(18)

By using Algorithm 1, and letting the initial tensors be $\tilde{\mathcal{X}}=\widetilde{{\mathcal{X}}_1}+\widetilde{{\mathcal{X}}_2}\mathbf{i}+\widetilde{{\mathcal{X}}_3}\mathbf{j}+\widetilde{{\mathcal{X}}_4}\mathbf{k}$, $\tilde{\mathcal{Y}}=\widetilde{{\mathcal{Y}}_1}+\widetilde{{\mathcal{Y}}_2}\mathbf{i}+\widetilde{{\mathcal{Y}}_3}\mathbf{j}+\widetilde{{\mathcal{Y}}_4}\mathbf{k}$, where ${\mathcal{X}}_j\left(1\right)={\Gamma }_j^{*}[{\mathcal{H}}_1\left(1\right),{\mathcal{H}}_2\left(1\right),{\mathcal{H}}_3\left(1\right),{\mathcal{H}}_4\left(1\right)],$${\mathcal{Y}}_j\left(1\right)={\Phi }_j^{*}[{\mathcal{H}}_1\left(1\right),{\mathcal{H}}_2\left(1\right),{\mathcal{H}}_3\left(1\right),$${\mathcal{H}}_4\left(1\right)](j=1,2,3,4)$, where ${\mathcal{H}}_i\left(1\right)\in {\mathbb{R}}^{I_1\times I_2\times \dots \times I_N}(i=1,2,3,4)$ are arbitrary tensors (in particular, we take $\left.{\mathcal{X}}_j\left(1\right)=\mathcal{O},{\mathcal{Y}}_j\left(1\right)=\mathcal{O},j=1,2,3,4\right)$, we can obtain the unique minimal Frobenius norm solution ${\tilde{\mathcal{X}}}^{*},{\tilde{\mathcal{Y}}}^{*}$ of Equation (18). Once the above tensor ${\tilde{\mathcal{X}}}^{*},{\tilde{\mathcal{Y}}}^{*}$ are achieved, the unique solution $\check{\mathcal{X}},\check{\mathcal{Y}}$ of Problem 1.2 can be computed. In this case, $\check{\mathcal{X}},\check{\mathcal{Y}}$ can be expressed as $\check{\mathcal{X}}={\tilde{\mathcal{X}}}^{*}+\overline{\mathcal{X}}$, $\check{\mathcal{Y}}={\tilde{\mathcal{Y}}}^{*}+\overline{\mathcal{Y}}$.

4. Numerical Examples

In this section, we will give some numerical examples to support the efficiency and applications of Algorithm 1. The codes in our computation are written in Matlab R2018a with 2.3 GHz central processing unit (Intel(R) Core(TM) i5), 8GB memory. Moreover, we implemented all the operations based on tensor toolbox (version 3.2.1) proposed by Bader and Kolda [27]. For all of the examples, the iterations begin with the initial values ${\mathcal{X}}_i={\mathcal{Y}}_i=0,i=1,2,3,4$ in Algorithm 1, and the stopping criteria is Res $\le {10}^{-5}$ or the number of iteration steps exceeding 2000. We describe some notations that appear in the following examples in Table 1.

Example 1.

We consider the tensor Equation (2) with:

$$\begin{array}{cc}\hfill A^{\left(1\right)}& =\left(\begin{array}{ccc}2+4\mathbf{i}+4\mathbf{j}+5\mathbf{k}& 1-\mathbf{i}+\mathbf{j}+2\mathbf{k}& -2\mathbf{i}-2\mathbf{j}+\mathbf{k}\\ -2+\mathbf{j}& 3+2\mathbf{i}+5\mathbf{j}+\mathbf{k}& 1-2\mathbf{j}+\mathbf{k}\\ 2+2\mathbf{i}+\mathbf{j}& 1-2\mathbf{i}+2\mathbf{j}-\mathbf{k}& 3+4\mathbf{i}+4\mathbf{j}+\mathbf{k}\end{array}\right),\hfill \\ \hfill A^{\left(2\right)}& =\left(\begin{array}{ccc}3+4\mathbf{j}& -1+\mathbf{j}& -1-2\mathbf{j}\\ -2+\mathbf{j}& 4+3\mathbf{j}& -\mathbf{j}\\ -\mathbf{j}& 1& 2+\mathbf{j}\end{array}\right),A^{\left(3\right)}=\left(\begin{array}{ccc}2\mathbf{i}+3\mathbf{j}& \mathbf{i}& 1+\mathbf{j}\\ -2\mathbf{i}-\mathbf{j}& 5\mathbf{i}+3\mathbf{j}& -\mathbf{i}\\ 2\mathbf{i}-\mathbf{j}& -\mathbf{i}-\mathbf{j}& 5\mathbf{i}+4\mathbf{j}\end{array}\right),\hfill \\ \hfill B^{\left(1\right)}& =\left(\begin{array}{ccc}3+3\mathbf{i}& 2+\mathbf{i}& -2\mathbf{i}\\ -2+\mathbf{i}& 4+4\mathbf{i}& -2-2\mathbf{i}\\ 2+2\mathbf{i}& 2& 6+4\mathbf{i}\end{array}\right),B^{\left(2\right)}=\left(\begin{array}{ccc}3\mathbf{i}+5\mathbf{j}& 2\mathbf{i}& 2\mathbf{i}+2\mathbf{j}\\ 0& 2\mathbf{i}+3\mathbf{j}& \mathbf{j}\\ -2\mathbf{i}+2\mathbf{j}& -2\mathbf{i}-2\mathbf{j}& 6\mathbf{i}+6\mathbf{j}\end{array}\right),\hfill \\ \hfill B^{\left(3\right)}& =\left(\begin{array}{ccc}1+3\mathbf{i}+3\mathbf{k}& -1-2\mathbf{i}& \mathbf{i}+2\mathbf{k}\\ -\mathbf{i}& 2+4\mathbf{i}+2\mathbf{k}& 2+2\mathbf{i}\\ 2+\mathbf{i}+2\mathbf{k}& 2+\mathbf{i}-2\mathbf{k}& 5+4\mathbf{i}+6\mathbf{k}\end{array}\right),\hfill \\ \hfill \mathcal{C}(:,:,1)& =\left(\begin{array}{ccc}3-11\mathbf{i}+31\mathbf{j}+19\mathbf{k}& 6-8\mathbf{i}+\mathbf{j}+28\mathbf{k}& 2-6\mathbf{i}+20\mathbf{j}+24\mathbf{k}\\ 4+36\mathbf{j}+8\mathbf{k}& 7+3\mathbf{i}+27\mathbf{j}+17\mathbf{k}& 3+5\mathbf{i}+25\mathbf{j}+13\mathbf{k}\\ 24-2\mathbf{i}+52\mathbf{j}+22\mathbf{k}& 27+\mathbf{i}+43\mathbf{j}+31\mathbf{k}& 23+3\mathbf{i}+41\mathbf{j}+27\mathbf{k}\end{array}\right),\hfill \\ \hfill \mathcal{C}(:,:,2)& =\left(\begin{array}{ccc}11-13\mathbf{i}+31\mathbf{j}+13\mathbf{k}& 14-10\mathbf{i}+22\mathbf{j}+22\mathbf{k}& 10-8\mathbf{i}+20\mathbf{j}+18\mathbf{k}\\ 12-2\mathbf{i}+36\mathbf{j}+2\mathbf{k}& 15+\mathbf{i}+27\mathbf{j}+11\mathbf{k}& 11+3\mathbf{i}+25\mathbf{j}+7\mathbf{k}\\ 32-4\mathbf{i}+52\mathbf{j}+16\mathbf{k}& 35-\mathbf{i}+43\mathbf{j}+25\mathbf{k}& 31+\mathbf{i}+41\mathbf{j}+21\mathbf{k}\end{array}\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathcal{C}(:,:,3)& =\left(\begin{array}{ccc}9-9\mathbf{i}+45\mathbf{j}+25\mathbf{k}& 12-6\mathbf{i}+36\mathbf{j}+34\mathbf{k}& 8-4\mathbf{i}+34\mathbf{j}+30\mathbf{k}\\ 10+2\mathbf{i}+50\mathbf{j}+14\mathbf{k}& 13+5\mathbf{i}+41\mathbf{j}+23\mathbf{k}& 9+7\mathbf{i}+39\mathbf{j}+19\mathbf{k}\\ 30+66\mathbf{j}+28\mathbf{k}& 33+3\mathbf{i}+57\mathbf{j}+3\mathbf{k}& 29+5\mathbf{i}+55\mathbf{j}+33\mathbf{k}\end{array}\right).\hfill \end{array}$$

Applying for Algorithm 1, the IT is 46, the costed CPU time is 3.9496s and the Res is 1.2885e-06. Besides that, the Figure 1 reported here illustrates Algorithm 1 is feasible.

Example 2

(Test matrices from [1]). In this example, we consider the quaternion tensor Equation (2) such that

$$A^{\left(m\right)}=A_{m1}+A_{m2}\mathbf{i}+A_{m3}\mathbf{j}+A_{m4}\mathbf{k},B^{\left(m\right)}=B_{m1}+B_{m2}\mathbf{i}+B_{m3}\mathbf{j}+B_{m4}\mathbf{k},m=1,2,3,$$

where

$$\begin{array}{cc}& A_{11}=triu\left(hilb\left(n\right)\right),A_{12}=triu\left(ones(n,n)\right),A_{13}=eye\left(n\right),A_{14}=ones\left(n\right),\hfill \\ & A_{21}=zeros\left(n\right),A_{22}=zeros\left(n\right),A_{23}=tridiag(-1,2,-1,n),A_{24}=zeros\left(n\right),\hfill \\ & A_{31}=zeros\left(n\right),A_{32}=tridiag(0.5,6,-0.5,n),A_{33}=eye\left(n\right),A_{34}=zeros\left(n\right),\hfill \end{array}$$

$$\begin{array}{cc}& B_{11}=eye\left(n\right),B_{12}=ones\left(n\right),B_{13}=zeros\left(n\right),B_{14}=zeros\left(n\right),\hfill \\ & B_{21}=zeros\left(n\right),B_{22}=tridiag(0.5,6,-0.5,n),B_{23}=eye\left(n\right),B_{24}=zeros\left(n\right),\hfill \\ & B_{31}=tridiag(0.5,6,-0.5,n),B_{32}=eye\left(n\right),B_{33}=zeros\left(n\right),B_{34}=ones\left(n\right).\hfill \end{array}$$

$$\mathcal{C}=tenrand(n,n,n)+tenrand(n,n,n)\mathbf{i}+tenrand(n,n,n)\mathbf{j}+tenrand(n,n,n)\mathbf{k}.$$

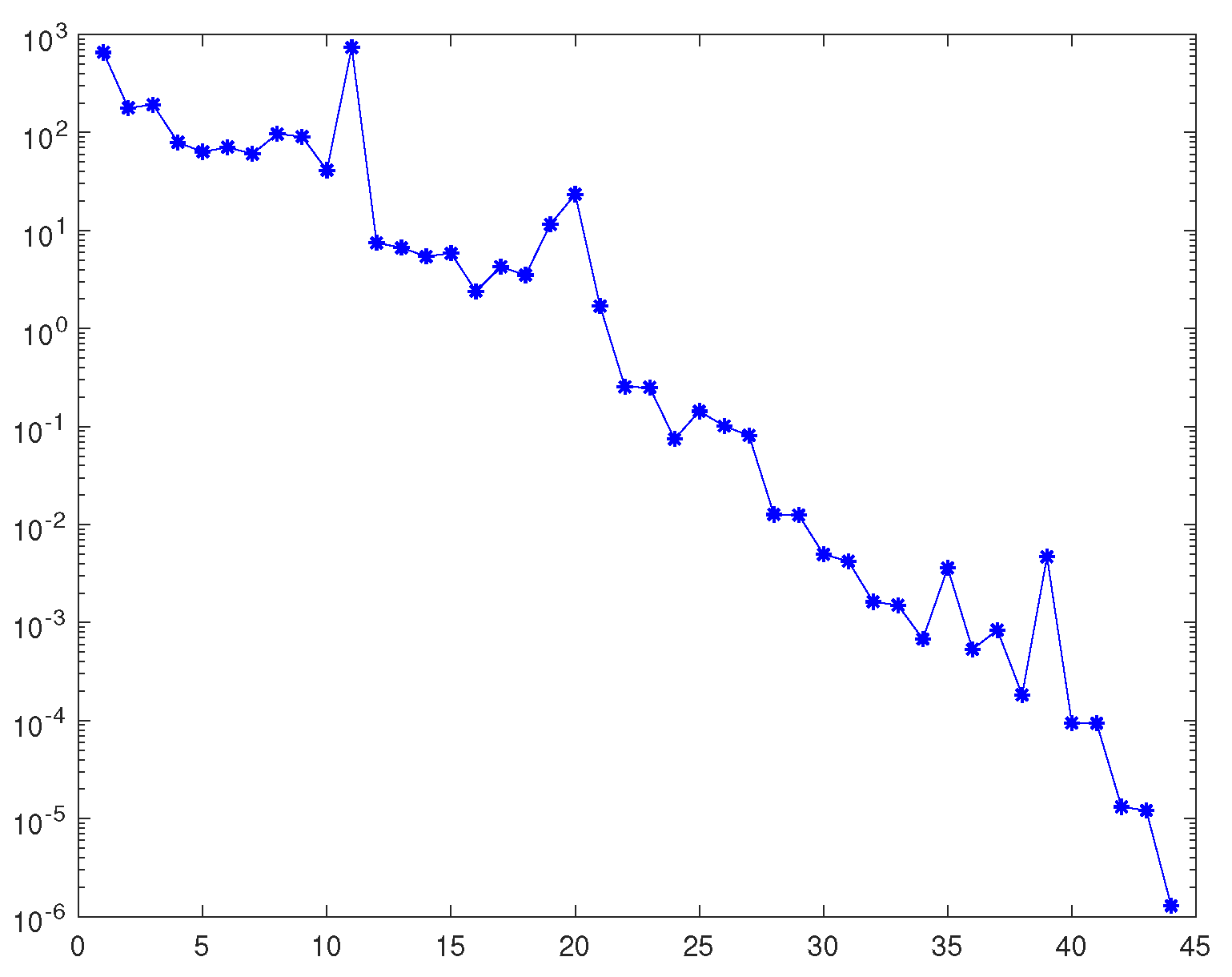
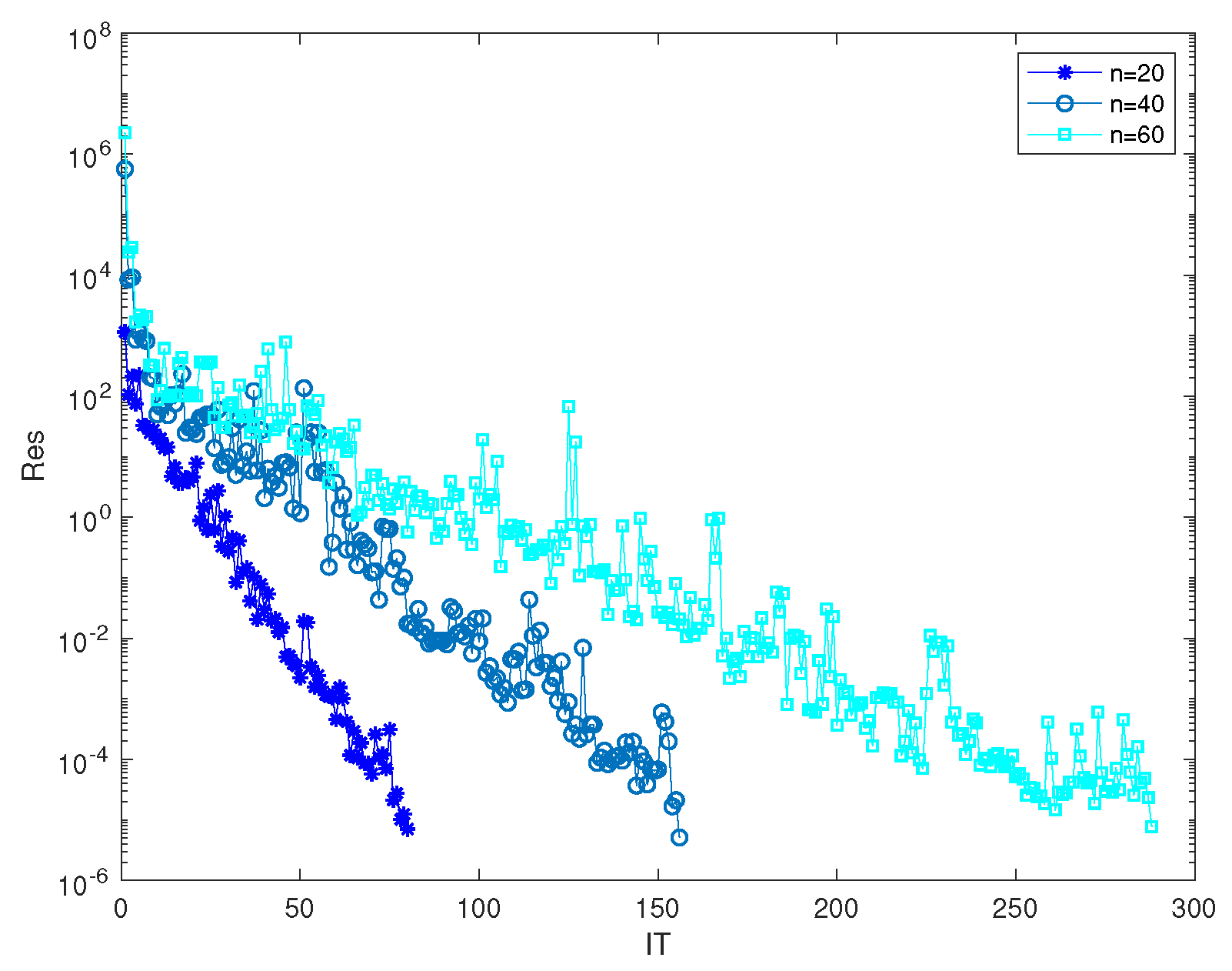
Choosing the initial tensor $\mathcal{X}=\mathcal{Y}=0$, we depict the convergence curves of Algorithm 1 for different n in Figure 2. For $n=20,$$n=40$ and $n=60$, we list the costed CPU time, residual norms after finite steps and the relative errors of approximate solutions by Algorithm 1 in Table 2.

Example 3.

We consider the solution of the following convection-diffusion equation over the quaternion algebra [4]

$$\begin{array}{cc}\hfill -v\Delta u+c^T\nabla u& =f\mathrm{in}\Gamma =[0,1]\times [0,1]\times [0,1]\hfill \\ \hfill u& =0\mathrm{on}\partial \Gamma .\hfill \end{array}$$

Based on a standard finite difference discretization on a uniform grid for the diffusion term and a second-order convergent scheme (Fromm’s scheme) for the convection term with the mesh-size $h={\displaystyle \frac{1}{p+1}}$, we solve the quaternion tensor Equation (3) with

$$A^{\left(n\right)}=A_1^{\left(n\right)}+A_2^{\left(n\right)}\mathbf{i}+A_3^{\left(n\right)}\mathbf{j}+A_4^{\left(n\right)}\mathbf{k},n=1,2,3,$$

where

$$\begin{array}{c}\hfill A_i^{\left(n\right)}={\displaystyle \frac{v_i^{\left(n\right)}}{h^2}}{\left[\begin{array}{ccccc}2& -1& & & \\ -1& 2& -1& & \\ & \ddots & \ddots & \ddots & \\ & & -1& 2& -1\\ & & & -1& 2\end{array}\right]}_{p\times p}+{\displaystyle \frac{c_i^{\left(n\right)}}{4h}}{\left[\begin{array}{ccccc}3& -5& 1& & \\ 1& 3& -5& & \\ & \ddots & \ddots & \ddots & 1\\ & & 1& 3& -5\\ & & & 1& 3\end{array}\right]}_{p\times p},i=1,2,3,4.\end{array}$$

The right hand side tensor $\mathcal{C}$ is contructed such that the exact solution of Equation (3) is ${\mathcal{X}}^{*}={\mathcal{X}}_1^{*}+{\mathcal{X}}_2^{*}\mathbf{i}+{\mathcal{X}}_3^{*}\mathbf{j}+{\mathcal{X}}_4^{*}\mathbf{k}=tenones(p,p,p)+tenones(p,p,p)\mathbf{i}+tenones(p,p,p)\mathbf{j}+tenones(p,p,p)\mathbf{k}$.

We consider two cases in order to compare Algorithm 1 with the CGLS algorithm in [49]. In case I, we choose different $v_i^{\left(n\right)}$ and $c_i^{\left(n\right)}$ to obtain the results. In Table 3, we set

$$\begin{array}{c}\hfill v_i^{\left(1\right)}=1,c_i^{\left(1\right)}=1;v_i^{\left(2\right)}=1,c_i^{\left(2\right)}=2;v_i^{\left(3\right)}=1,c_i^{\left(2\right)}=3,i=1,2,3,4\end{array}$$

(19)

to get ${\mathcal{A}}^{\left(n\right)}(n=1,2,3)$ with same real part and imaginary part. In Table 4, we set

$$\begin{array}{cc}\hfill & v_i^{\left(1\right)}=1,c_1^{\left(1\right)}=1,c_2^{\left(1\right)}=-1,c_3^{\left(1\right)}=0,c_4^{\left(1\right)}=1;\hfill \\ \hfill & v_i^{\left(2\right)}=0.1,c_1^{\left(2\right)}=-1,c_2^{\left(2\right)}=-1,c_3^{\left(2\right)}=1,c_4^{\left(2\right)}=0;\hfill \\ \hfill & v_i^{\left(3\right)}=0.01,c_1^{\left(3\right)}=1,c_2^{\left(3\right)}=1,c_3^{\left(3\right)}=0,c_4^{\left(3\right)}=0,i=1,2,3,4\hfill \end{array}$$

(20)

to get ${\mathcal{A}}^{\left(n\right)}(n=1,2,3)$ with different real parts and imaginary parts.

In case II, we set $c_i^{\left(1\right)}=1;c_i^{\left(2\right)}=2;c_i^{\left(2\right)}=3,i=1,2,3,4$, we apply Algorithm 1 and the CGLS algorithm in [49] with $v_i^{\left(j\right)}=1e-03,1,100,i=1,2,3,4,j=1,2,3$ for grid $10\times 10\times 10$. The corresponding relative errors of approximate solution ${\sum }_{i=1}^{i=4}\parallel {\mathcal{X}}_i\left(k\right)-{\mathcal{X}}_i^{*}\parallel /\parallel {\mathcal{X}}_i^{*}\parallel$ computed by these methods are presented in Table 5.

The previous results show that Algorithm 1 has faster convergent rates than the CGLS algorithm in [49] as p increases.

Example 4.

In this example, we employ Algorithm 1 to compare its performance with the CGLS algorithm in restoring a color video comprised of a sequence of RGB images (slices). The video, named `rhinos’, is sourced from Matlab and stored in AVI format. Each frontal slice of this color video is depicted by a pure quaternion matrix measuring $240\times 320$ pixels. For $\mathcal{C}=\widehat{\mathcal{C}}+\mathcal{N}=\mathcal{X}{\times }_{1}A$, we consider $\mathcal{X}$ to represent the orginal colour video, A as the blurred matrix, and $\mathcal{N}$ as a noise tensor. When $\mathcal{N}=0$, $\mathcal{C}$ is referred to as the blurred and noise-free color video. In this scenario, we select a blurred matrix $A=A_1\otimes A_2\in {\mathbb{R}}^{240\times 320}$, where $A_1={\left(a_{ij}^{\left(1\right)}\right)}_{1\le i,j\le 16}$ and $A_2={\left(a_{ij}^{\left(2\right)}\right)}_{1\le i\le 15,1\le j\le 20}$ are Toeplitz matrices with entries defined as:

$$a_{ij}^{\left(1\right)}=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}exp\left({\displaystyle \frac{{(i-j)}^2}{2{\sigma }^2}}\right),\hfill & |i-j|\le r,\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array};a_{ij}^{\left(2\right)}=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2s-1}},\hfill & |i-j|\le s,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\right.$$

We denote ${\mathcal{X}}_{\mathrm{restored}}$ as the resulting restored color video. The algorithm’s performance is assessed using the peak signal-to-noise ratio (PSNR) measured in decibels (dB):

$$PSNR\left(\mathcal{X}\right)=10{log}_{10}\left({\displaystyle \frac{I_1{I}_2{d}^2}{{∥\mathcal{X}-{\mathcal{X}}_{\mathrm{restored}}∥}^2}}\right),$$

where d represents the maximum possible pixel value of the image. $RE\left(\mathcal{X}\right)$ represents the relative error defined as

$$RE\left(\mathcal{X}\right)={\displaystyle \frac{∥\mathcal{X}-{\mathcal{X}}_{\mathrm{restored}}∥}{\parallel \mathcal{X}\parallel }}.$$

Here, we set $d=255$ and the variance $\sigma =1$. The peak signal-to-noise ratio (PSNR) and the relative error (RE) of Algorithm 1 and the CGLS algorithm with different parameters are presented in Table 6. As indicated, the PSNR and the relative error of our algorithms are significantly superior to those of CGLS. For the case where $r=6$ and $s=6$ with slice No. 7 of the color video, we illustrate the original image, blurred image, and the restored image by CGLS and Algorithm 1 in Figure 3. This figure demonstrates that our algorithm can effectively restore blurred and noise-free color video with high quality.

5. Conclusions

The main goal of this paper is to solve the generalized quaternion tensor Equation (2). We herewith develop a BiCG iterative algorithm based on the tensor format to solve Equation (2) efficiently, and we also prove the convergence of our proposed method. Moreover, we demonstrate that the solution with minimal Frobenius norm can be achieved by initializing specific types of tensors. We present several examples to effectively demonstrate the efficiency of our algorithm. Furthermore, our algorithm is successfully applied to the restoration of color videos. This contribution significantly advances the current understanding of quaternion tensor equations by introducing a practical iterative approach.