Submitted:
14 October 2024
Posted:
14 October 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Method
2.1. Hydrodinamic Equations
2.2. Lattice Boltzmann Method
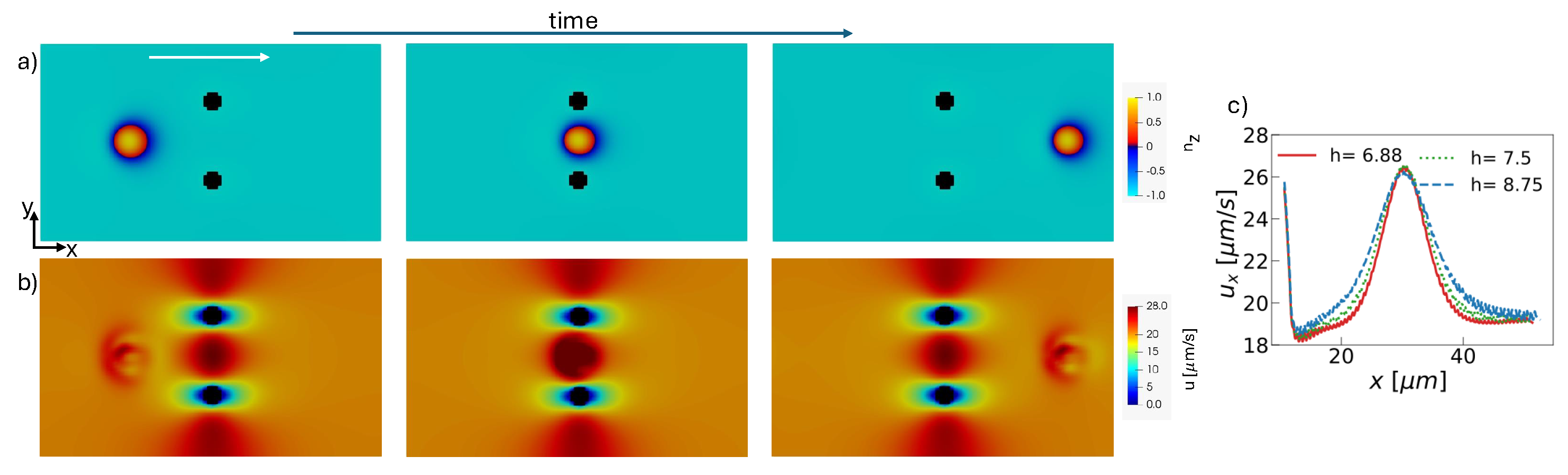
3. Results
4. Conclusion
Acknowledgments
References
- Chen, H.W.; Lee, J.H.; Lin, B.Y.; Chen, S.; Wu, S.T. Liquid crystal display and organic light-emitting diode display: present status and future perspectives. Light Sci. Appl. 2018, 7, 17168–17168. [Google Scholar] [CrossRef] [PubMed]
- Smalyukh, I.I.; Lansac, Y.; Clark, N.A.; Trivedi, R.P. Three-dimensional structure and multistable optical switching of triple-twisted particle-like excitations in anisotropic fluids. Nat. Mater. 2010, 9, 139–145. [Google Scholar] [CrossRef]
- Ackerman, P.J.; Trivedi, R.P.; Senyuk, B.; van de Lagemaat, J.; Smalyukh, I.I. Two-dimensional skyrmions and other solitonic structures in confinement-frustrated chiral nematics. Phys. Rev. E 2014, 90, 012505. [Google Scholar] [CrossRef] [PubMed]
- Ackerman, P.J.; Boyle, T.; Smalyukh, I.I. Squirming motion of baby skyrmions in nematic fluids. Nat. Commun. 2017, 8, 673. [Google Scholar] [CrossRef]
- Sohn, H.R.O.; Smalyukh, I.I. Electrically powered motions of toron crystallites in chiral liquid crystals. Proc. Nat. Acad. Sci. U.S.A 2020, 117, 6437–6445. [Google Scholar] [CrossRef]
- Fukuda, J.i.; Žumer, S. Quasi-two-dimensional Skyrmion lattices in a chiral nematic liquid crystal. Nat. Commun. 2011, 2, 246. [Google Scholar] [CrossRef]
- Posnjak, G.; Čopar, S.; Muševič, I. Points, skyrmions and torons in chiral nematic droplets. Sci. Rep. 2016, 6, 26361. [Google Scholar] [CrossRef]
- Ackerman, P.J.; Smalyukh, I.I. Static three-dimensional topological solitons in fluid chiral ferromagnets and colloids. Nat. Mater. 2017, 16, 426–432. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Afghah, S.; Xiang, J.; Lavrentovich, O.D.; Selinger, R.L.B.; Wei, Q.H. Cholesteric liquid crystals in rectangular microchannels: skyrmions and stripes. Soft Matter 2016, 12, 6312–6320. [Google Scholar] [CrossRef]
- Tai, J.S.B.; Smalyukh, I.I. Three-dimensional crystals of adaptive knots. Science 2019, 365, 1449–1453. [Google Scholar] [CrossRef]
- Zhao, H.; Tai, J.S.B.; Wu, J.S.; Smalyukh, I.I. Liquid crystal defect structures with Möbius strip topology. Nat. Phys 2023, 19, 451–459. [Google Scholar] [CrossRef]
- Sohn, H.R.O.; Ackerman, P.J.; Boyle, T.J.; Sheetah, G.H.; Fornberg, B.; Smalyukh, I.I. Dynamics of topological solitons, knotted streamlines, and transport of cargo in liquid crystals. Phys. Rev. E 2018, 97, 052701. [Google Scholar] [CrossRef] [PubMed]
- Dkhar, D.S.; Kumari, R.; Malode, S.J.; Shetti, N.P.; Chandra, P. Integrated lab-on-a-chip devices: Fabrication methodologies, transduction system for sensing purposes. Journal of Pharmaceutical and Biomedical Analysis 2023, 223, 115120. [Google Scholar] [CrossRef] [PubMed]
- Coelho, R.C.V.; Tasinkevych, M.; da Gama, M.M.T. Dynamics of flowing 2D skyrmions. J. Phys. Cond. Mat. 2021, 34, 034001. [Google Scholar] [CrossRef]
- Coelho, R.C.V.; Zhao, H.; Amaral, G.N.C.; Smalyukh, I.I.; da Gama, M.M.T.; Tasinkevych, M. "Hall" transport of liquid crystal solitons in Couette flow, 2024, [arXiv:cond-mat.soft/2405.10850].
- Coelho, R.C.V.; Zhao, H.; Tasinkevych, M.; Smalyukh, I.I.; Telo da Gama, M.M. Sculpting liquid crystal skyrmions with external flows. Phys. Rev. Res. 2023, 5, 033210. [Google Scholar] [CrossRef]
- Amaral, G.N.C.; Zhao, H.; Sedahmed, M.; Campante, T.; Smalyukh, I.I.; Tasinkevych, M.; da Gama, M.M.T.; Coelho, R.C.V. Liquid crystal torons in Poiseuille-like flows, 2024, [arXiv:cond-mat.soft/2409.09486].
- Duzgun, A.; Saxena, A.; Selinger, J.V. Alignment-induced reconfigurable walls for patterning and assembly of liquid crystal skyrmions. Phys. Rev. Res. 2021, 3, L012005. [Google Scholar] [CrossRef]
- Duzgun, A.; Nisoli, C.; Reichhardt, C.J.O.; Reichhardt, C. Directed motion of liquid crystal skyrmions with oscillating fields. New J. of Phys. 2022, 24, 033033. [Google Scholar] [CrossRef]
- Duzgun, A.; Nisoli, C.; Reichhardt, C.J.O.; Reichhardt, C. Commensurate states and pattern switching via liquid crystal skyrmions trapped in a square lattice. Soft Matter 2020, 16, 3338–3343. [Google Scholar] [CrossRef]
- Alvim, T.; Gama, M.M.T.d.; Tasinkevych, M. Collective variable model for the dynamics of liquid crystal skyrmions. Communications Physics 2024, 7. [Google Scholar] [CrossRef]
- Long, C.; Selinger, J.V. Coarse-grained theory for motion of solitons and skyrmions in liquid crystals. Soft Matter 2021, 17, 10437–10446. [Google Scholar] [CrossRef]
- Teixeira, A.W.; Tasinkevych, M.; Dias, C.S. Particle-based model of liquid crystal skyrmion dynamics. Soft Matter 2024, 20, 2088–2099. [Google Scholar] [CrossRef]
- Ericksen, J.L. Hydrostatic theory of liquid crystals. Archive for Rational Mechanics and Analysis 1962, 9, 371–378. [Google Scholar] [CrossRef]
- Leslie, F.M.; Green, A.E. Some thermal effects in cholesteric liquid crystals. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 1968, 307, 359–372. [Google Scholar] [CrossRef]
- Stewart, I.W. The static and dynamic continuum theory of liquid crystals: a mathematical introduction; Crc Press, 2019.
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method - Principles and Practice; Springer International Publishing, 2016.
- Succi, S. The Lattice Boltzmann Equation: For Complex States of Flowing Matter; Numerical Mathematics and Scientific Computation Series, Oxford University Press, 2018.
- Turk, J.; Svenšek, D. Backflow-mediated domain switching in nematic liquid crystals. Phys. Rev. E 2014, 89, 032508. [Google Scholar] [CrossRef]
- Kirk, D.B.; Hwu, W.m.W. Programming Massively Parallel Processors: A Hands-on Approach, 1st ed.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2010. [Google Scholar]
- Guo, Z.; Zheng, C.; Shi, B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 046308. [Google Scholar] [CrossRef]
- Doi, M. Soft Matter Physics; Oxford University Press, 2013. [CrossRef]
 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





