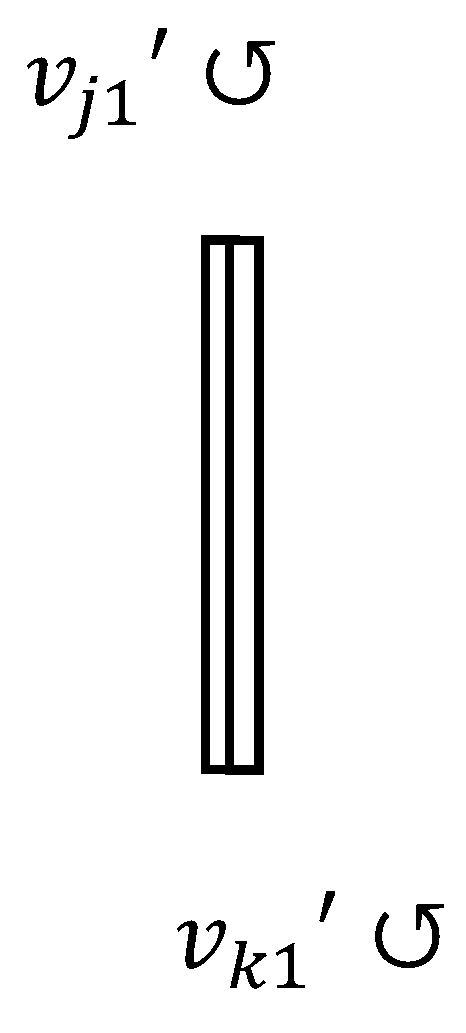Movement and Uncertainty of the Center of Relativistic Energy in an Isolated Frame of Reference

1. Introduction

It is regarded as one of the most fundamental principles of physics that the location of center of mass in an IFR is always constant. From this principle, Einstein has derived the equivalence of mass and energy in special relativity (SR) [1,2]. According to it, the location of the center of energy (CE) is always constant in an IFR [3,4,5]. This is called the CE theorem in SR [3,4,5]. The concept of CE is the relativistic generalization of center of mass because it includes not only rest energy or mass but also all forms of energy [3]. A research demonstrates, using the CE theorem, that relativistic effects appear in rotational motion which results from cutting superposed parts of mechanical transverse waves on a medium traveling at non-relativistic speeds [6]. On the other hand, we cannot find any previous researches that refute the CE theorem.

Nevertheless, we consider the existence of physical phenomena in which the CE theorem does not hold, i.e., those in which the CRE in the IFR is not necessarily constant. We examine whether such physical phenomena occur in a MIFR and when a MO comes to rest.

First, we set up a physical phenomenon in which two objects approach parallel to a coordinate axis from opposite directions in the MIFR. When they are perfectly symmetric with respect to the coordinate axis, the forces perpendicular to the direction of travel of the objects are applied to each CRE. Then a perfectly inelastic collision between them occurs on the coordinate axis, and the CO begins to rotate due to each momentum of the objects before the combination. We examine whether the LCRE of the CO in rotational motion is different from that of the two objects in an initial condition.

Second, suppose a process in which a force causes a negative acceleration on a MO and thereafter the MO eventually comes to rest. Here it is important to pay attention to the position of the force applied to the MO. This is because the TTF inside the MO may vary depending on the position where the force is applied. We examine whether, when the MO comes to rest, its LCRE differs depending on the position of it to which the force is applied, considering the TTF inside each MO.

2. Movement of the LCRE in a MIFR

We presuppose two inertial frames of reference, $S\prime$ and $S$, that are in a state of uniform relative motion to each other. $S\prime$ moves with constant velocity $V$ in the positive direction of the $x$axis in $S$. Moreover, assume that the two objects having the same rest mass (RM) and the same size, in $S\prime$, move parallel to the $x\prime$-axis from opposite directions and with the same speed as shown in Figure 1. Those velocities are $v\prime$ and $-v\prime$, respectively. The two objects are symmetrical to the $x\prime$-axis, and they are located very close to it. Each length in the direction of travel of the objects is much longer than that perpendicular to the direction of travel of them, and moreover the latter is negligibly extremely short. Here let $y\prime$-axis be the axis perpendicular to the $x\prime$-axis. In addition, assume that the origin of the $y\prime$-axis is on the $x\prime$-axis.

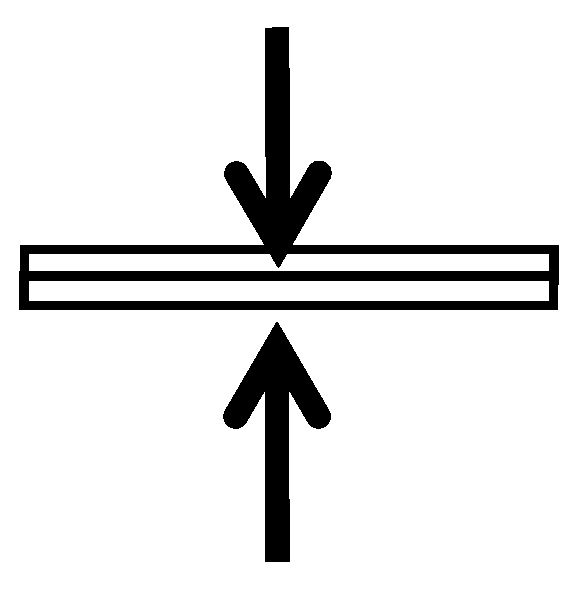
When the objects become perfectly symmetric with respect to the $x\prime$-axis, as shown in Figure 2, the forces perpendicular to the direction of travel of them are applied to the CRE of each object in the MIFR. The forces result in a perfectly inelastic collision between the objects and thereby they combine. Here, as shown in Figure 2, the length in the direction of the $y\prime$-axis of the CO is negligibly extremely short.

After the objects combine, the translational motion of each object stops, and a recoilless rotational motion of the CO occurs counterclockwise. The reason for this is that each momentum of the objects before the combination between them acts like the moment of force on the CO. Suppose that this rotational motion takes place around $y\prime =0$. When the CO rotates and becomes perpendicular to the $x\prime$-axis, it can be considered a rod with negligible width as shown in Figure 3. The distribution of RM of the CO is symmetric with respect to the $x\prime$-axis. Here let $v_{j1}\prime$ be a velocity of a minute portion (MP) of the CO that lies in the range where $y\prime >0$. Similarly, let $v_{k1}\prime$ be a velocity of a MP of the CO that exists in the range where $y\prime <0$. Suppose that a MP with $v_{j1}\prime$ and one with $v_{k1}\prime$ are symmetrical with respect to the $x\prime$-axis. When observed from $S\prime$, $v_{j1}\prime$ and $v_{k1}\prime$ of each MP symmetrical with respect to the $x\prime$-axis are opposite in direction but equal in magnitude, i.e., $\left|v_{j1}\prime \right|=\left|v_{k1}\prime \right|$. Hence, the energy of each MP is equal because the RM and magnitude of velocity of each are the same. In sum, in $S\prime$, the LCRE of the CO is on the $x\prime$-axis.

We will observe these phenomena from $S$. Here assume that, when observed from $S$, $\left|V\right|=\left|-v\prime \right|$. Then, as shown in Figure 4, the object on the right is stationary, and that on the left moves at a speed $v_R$ parallel to the $x$-axis.

Here relativistic velocity, $v_R$, is expressed as $\left(v\prime +V\right)/\left(1+v\prime V/c^2\right)$ based on the law of velocity addition in SR.

After a perfectly inelastic collision between the objects occurs, the CO starts rotating around $y=0$. When the CO rotates and becomes perpendicular to the $x$-axis, the length in the direction of the $x$-axis of the CO is negligibly extremely short as shown in Figure 5. On the other hand, the center of RM of the CO moves at $V$ in the positive direction of the $x$-axis in $S$ since its center of RM is stationary in $S\prime$. This is also shown in Figure 5. Here let $v_{j1}$ be a velocity of a MP of the CO in the range where $y>0$. This corresponds to $v_{j1}\prime$ in $S\prime$. In addition, let $v_{k1}$ be a velocity of a MP of the CO in the range where $y<0$. This corresponds to $v_{k1}\prime$ in $S\prime$. Suppose that a MP with $v_{j1}$ and one with $v_{k1}$ are symmetrical with respect to the $x$-axis. When observed from $S$, $v_{j1}$ and $v_{k1}$ of each MP symmetrical with respect to the $x$-axis are opposite in direction and furthermore different in magnitude.

Based on the thought experiment described above, we consider the LCRE before and after the combination of two objects. First, we confirm the LCRE of the two objects before the combination between them. The formula for relativistic energy (RE) is expressed by the following formula:

$$E(v)={\displaystyle \frac{m{c}^2}{\sqrt{1-v^2/c^2}}}$$

(1)

where $E$, $m$ and $v$ denote energy, RM and velocity, for an object, and $c$ is speed of light. Then the energy of the object stationary, $E\left(0\right)$, by substituting 0 for $v$ in Equation (1), is expressed as follows:

$$E(0)={\displaystyle \frac{m{c}^2}{\sqrt{1-0^2/c^2}}}=m{c}^2.$$

(2)

By contrast, the energy of the object having $v_R=\left(v\prime +V\right)/\left(1+v\prime V/c^2\right)$ , $E\left(v_R\right)$, by substituting $\left(v\prime +V\right)/\left(1+v\prime V/c^2\right)$ for $v$ in Equation (1), is as follows:

$$E(v_R)={\displaystyle \frac{m{c}^2}{\sqrt{1-{\left\{\left(v\prime +V\right)/\left(1+v\prime V/c^2\right)\right\}}^2/c^2}}}.$$

(3)

Since $\left|\left(v\prime +V\right)/\left(1+v\prime V/c^2\right)\right|>0$, $\sqrt{1-{\left\{\left(v\prime +V\right)/\left(1+v\prime V/c^2\right)\right\}}^2/c^2}<1$. Hence, since $E\left(v_R\right)>m{c}^2$, we get the following inequality:

$$E\left(v_R\right)>E\left(0\right).$$

(4)

The center of RM of the two objects is on the $x$-axis since the distribution of RM of them is symmetric to the $x$-axis. By contrast, since $E\left(v_R\right)>E\left(0\right)$ from inequality (4), the distribution of RE of the two objects is not symmetric to the $x$-axis, and the LCRE of them is located near the object having $v_R$. Even so, the LCRE of the two objects is located at the vicinity of $y=0$ on the $x$-axis because they are located very close to the $x$-axis, and each length perpendicular to the $x$-axis is almost negligible.

Second, we consider the LCRE of the two objects after the combination between them. For simplicity, we examine the energy distribution when the CO resulting from the perfectly inelastic collision begins to rotate counterclockwise and thereafter it become perpendicular to the $x$-axis in $S$. The distribution of RM of the CO, since the rotational motion of it takes place around $y=0$, is symmetric to the origin of the $y$-axis on the $x$-axis, in other words, to the $x$-axis.

The velocity of each MP of the CO in the range where $y>0$, since the CO rotates counterclockwise in $S$, is the sum of its negative rotational velocity and the positive translational one of $S\prime$. By contrast, the velocity of each MP of the CO in the range where $y<0$ is the sum of its positive rotational velocity and the positive translational one of $S\prime$ since the CO rotates counterclockwise in $S$.

We compare the RE of each MP of the CO located symmetrically to the $x$-axis. The value of numerator in Equation 1, $m{c}^2$ is equal with respect to every MP since the RM of each MP is the same and $c$ is the constant. Hence, the difference in RE of each MP is determined by $\sqrt{1-v^2/c^2}$ which is the value of denominator in Equation (1).

Let $E_{j1}$ be the RE of a MP having $v_{j1}$ that lies in the range where $y>0$. Similarly, let $E_{k1}$ be the RE of a MP having $v_{k1}$ that exists in the range where $y<0$. First, we calculate the values of $v_{j1}$ and $v_{k1}$ based on the law of velocity addition in SR. Since the direction of $v_{j1}$ is opposite to the direction of translational movement of the CO and that of $v_{k1}$ is the same as that of translational movement of it, each value becomes as follows:

$$v_{j1}={\displaystyle \frac{-v_{j1}\prime +V}{1-\frac{v_{j1}\prime \mathrm{}V}{c^2}}}\mathrm{},\mathrm{}{v}_{k1}={\displaystyle \frac{v_{k1}\prime +V}{1+\frac{v_{k1}\prime \mathrm{}V}{c^2}}}\mathrm{}.\mathrm{}$$

(5)

Here we can assume that the values of $\left|V\right|/c$, $\left|v_{j1}\prime \right|/c$ and $\left|v_{k1}\prime \right|/c$ are extremely small, in other words, $\left(1-v_{j1}\prime V/c^2\right)\cong 1$ and $\left(1+v_{k1}\prime V/c^2\right)\cong 1$. Hence, since the values $v_{j1}$ and $v_{k1}$ are almost determined by each numerator. Then$v_{j1}$ and $v_{k1}$ is approximately equal to $\left(-v_{j1}\prime +V\right)$ and $\left(v_{k1}\prime +V\right)$, respectively. Furthermore, since $\left(-v_{j1}\prime +V\right)<\left(v_{k1}\prime +V\right)$, we obtain the following inequality:

$$v_{j1}<v_{k1}.$$

(6)

Second, substituting $v_{j1}$ in Equation (5) for $v$ in Equation (1) and $v_{k1}$ in Equation (5) for $v$ in Equation (1) gives $\sqrt{1-{v_{j1}}^2/c^2}$ and $\sqrt{1-{v_{k1}}^2/c^2}$, respectively. Since from inequality (6), we get the following inequality:

$$\sqrt{1-{v_{j1}}^2/c^2}>\sqrt{1-{v_{k1}}^2/c^2}$$

(7)

Furthermore, since from inequality (7), for $E_{j1}$ and $E_{k1}$, we find the following expression:

$$E_{j1}={\displaystyle \frac{m{c}^2}{\sqrt{1-{v_{j1}}^2/c^2}}}<E_{k1}={\displaystyle \frac{m{c}^2}{\sqrt{1-{v_{k1}}^2/c^2}}}.\mathrm{}$$

(8)

Let $E_{Tj}$ be the total RE of all minute portions in the range where $y>0$. Similarly, let $E_{Tk}$ be the total RE of all minute portions in the range where $y<0$. $E_{Tj}$ is given by the following expression:

$$E_{Tj}=E_{j1}+E_{j2}+E_{j3}+\cdots =\sum _{i=1}^n{E}_{ji}.$$

(9)

Likewise, $E_{Tk}$ is expressed by the following expression:

$$E_{Tk}=E_{k1}+E_{k2}+E_{k3}+\cdots =\sum _{i=1}^n{E}_{ki}.$$

(10)

Here it is assumed that each term in Equation (9) and the corresponding one in Equation (10) are symmetrical with respect to the $x$-axis. Since Equation (8) holds true for all minute portions symmetrical with respect to the $x$-axis, the RE of each term in Equation (10) is always greater than that of the corresponding one in Equation (9). As a result, we can find the following inequality:

$$E_{Tj}<E_{Tk}.$$

(11)

Here the length of the CO when it becomes perpendicular to the $x$-axis is assumed to be sufficiently long. Then, from inequality (11), the LCRE of the CO consisting of the two objects lies in the range where $y<0$ and which is far away from the vicinity of $y=0$, in other words, that of the $x$-axis. This means that, by change in the distribution of energy, the LCRE of two objects moves from the vicinity of $y=0$. Therefore, we conclude that the LCRE in a MIFR can change.

The above conclusion, of course, also holds when the CO is not perpendicular to the $x$-axis. Suppose that, in $S\prime$, the rotating CO with negligible width overlaps the $x\prime$-axis, and hence its LCRE is on it. When observing this from $S$, we need to consider the relativity of simultaneity in SR. The time at each point in the rear in the CO’s traveling direction is advancing faster than those in the front in its traveling direction because the former is located behind the CO’s traveling direction compared to the latter. Hence, the rotating CO does not overlap the $x$-axis completely. A MP in the rear in its traveling direction is already in the range of $y<0$ even though that in the front in its traveling direction is on the $x$-axis, in other words, on the point of $y=0$. Here the former RE of including the rest energy shifts to the range of $y<0$ since its RM also shifts to there. In the realm where Newtonian mechanics applies, we are usually unable to observe such physical phenomenon because the difference in the locations of each MP are extremely small.[6]

3. Uncertainty of the LCRE When a MO Comes to Rest

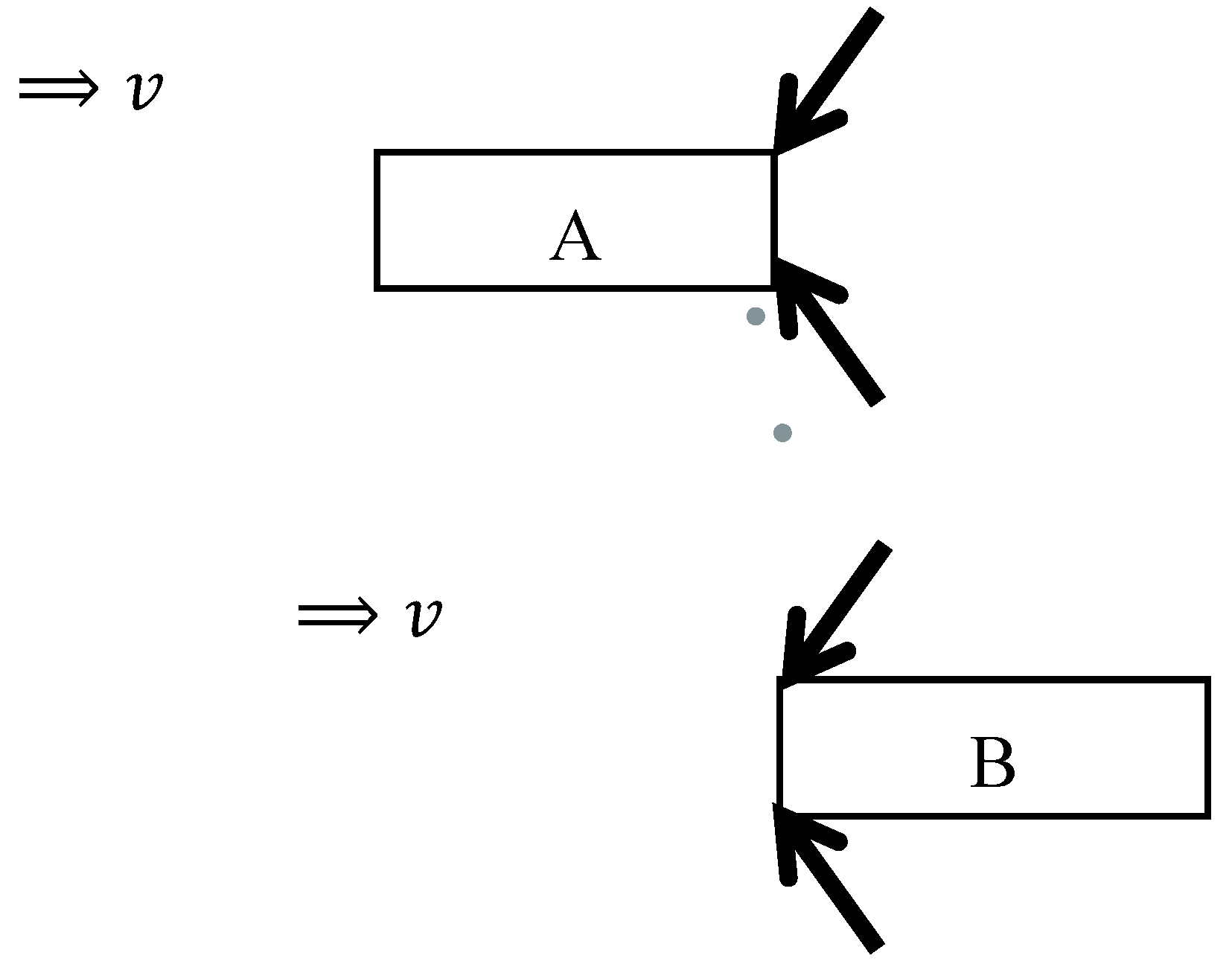
We presuppose that two objects A and B with the same RM and the same size are moving parallel to the positive direction of the $x$-axis with the same velocity $v$.

We simultaneously, to each MO, apply the forces of the same magnitude that act in the direction opposite to the traveling direction of them. Let the $y$-axis be the axis perpendicular to the $x$-axis. 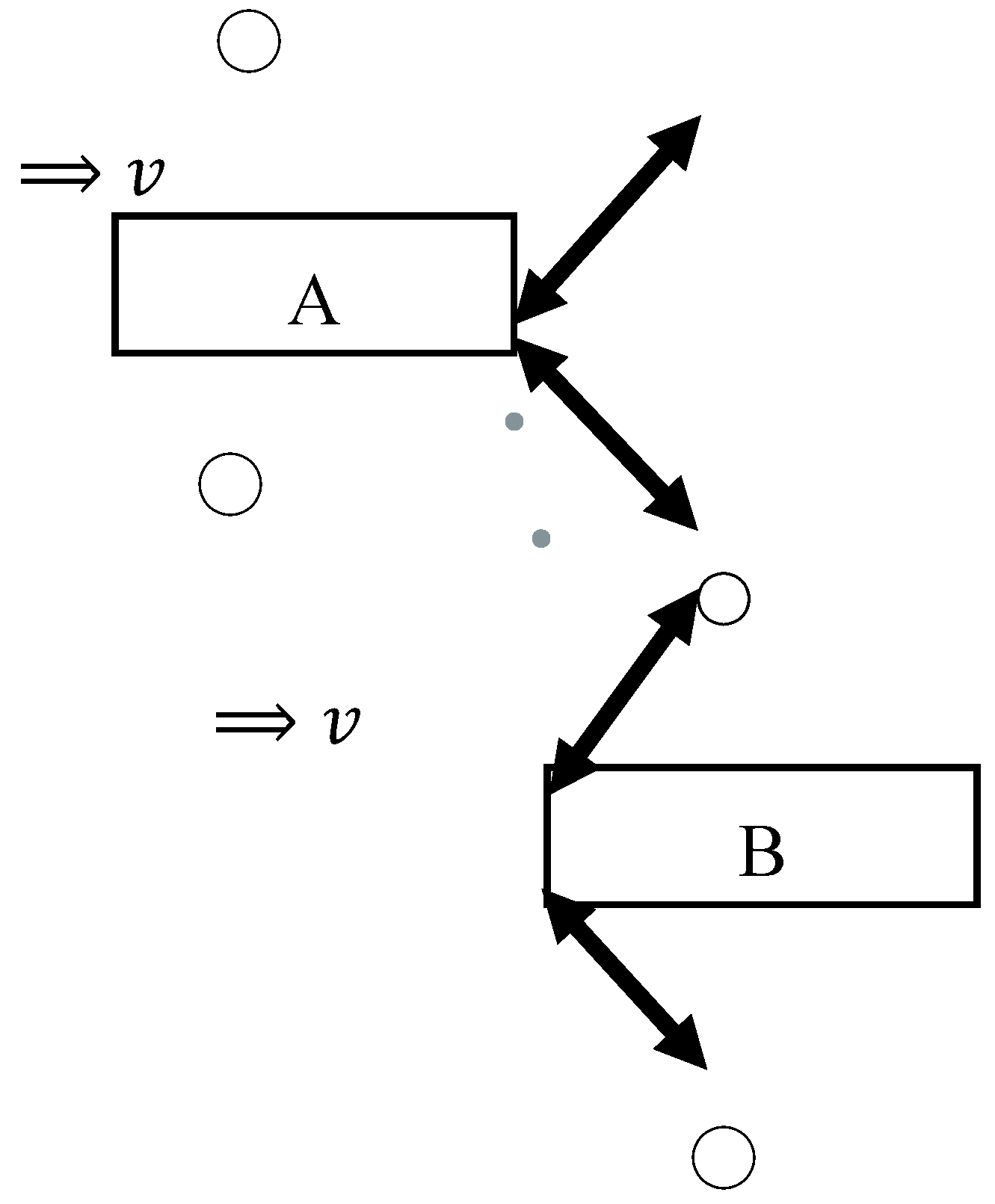To A from the positions $\left(x_2,y_2\right)$ and $\left(x_2,y_1\right)$, and to B from the positions $\left(x_2,y_{-1}\right)$ and $\left(x_2,y_{-2}\right)$, the forces are applied simultaneously in the direction of the arrow in Figure 6.

The forces on A are applied from the front in the traveling direction of it. By contrast, the forces on B are applied from the rear in the traveling direction of it. These are also shown in Figure 6. Each force is simultaneously applied from the point on the same $x$ coordinate and acts on each object at the same time. Here, for component of force, each component perpendicular to the traveling direction of A is cancelled out since the directions of the two components are opposite. The same is true for B. Hence, the resultant force applied to A from two positions is parallel to the $x$-axis. The same is true for the resultant force applied to B from two positions.

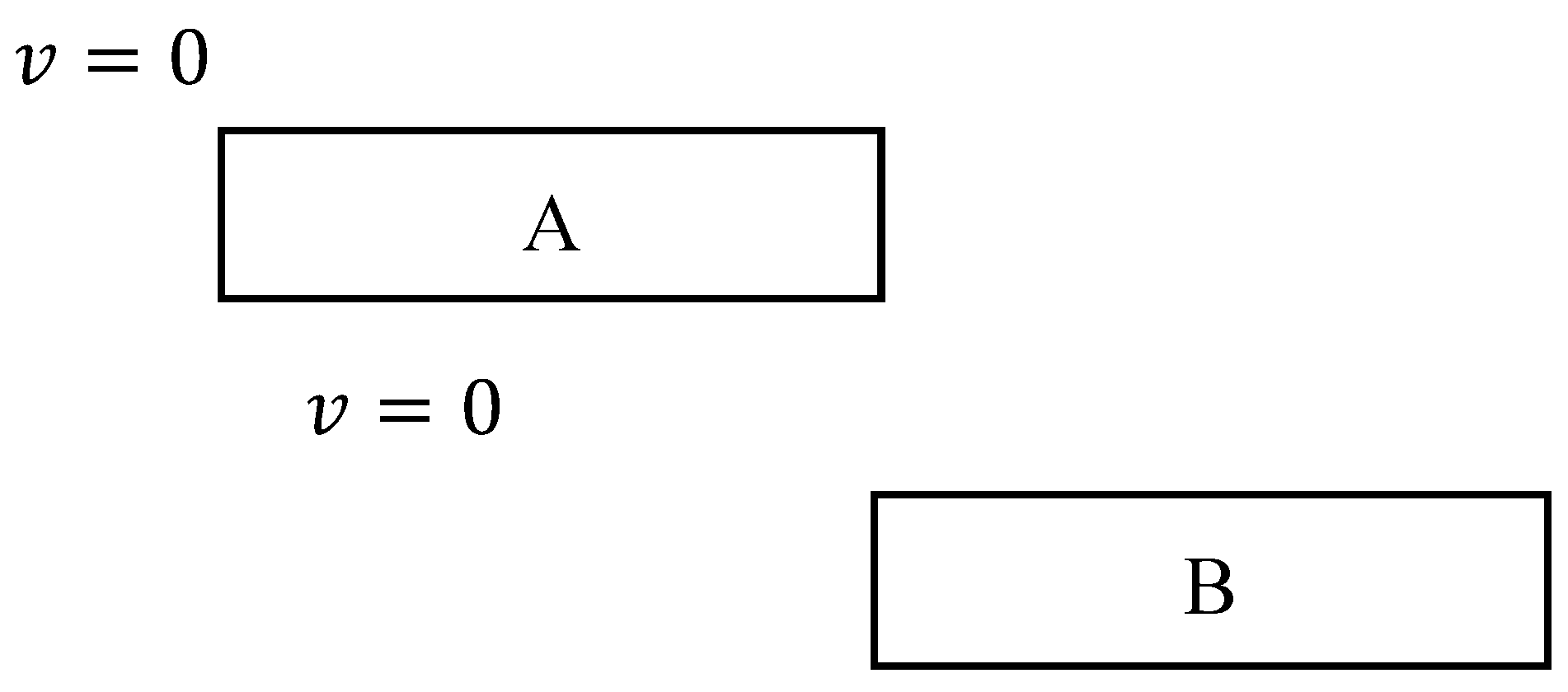
After the force applied to A is transmitted to the rear of it, the velocity of it decreases and finally it comes to rest. By contrast, the force applied to B is transmitted to the front of it, and then the velocity of it decreases and finally it comes to rest. The time at each point in A is advancing faster than that at each point in B because the former is located behind the traveling direction compared to the latter. This is due to the relativity of simultaneity in SR. Therefore, the forces on A are transmitted throughout the object faster than those on B even if, when observed from the frame of reference where A and B are stationary, each force is simultaneously transmitted throughout each object. This means that the TTF inside each MO differs. As a result, as shown in Figure 7, A comes to rest faster than B. In other words, B continues to move after A comes to rest, so it moves forward in the positive direction of the $x$-axis and then comes to rest. The effect of LC disappears when the MO comes to rest due to negative acceleration motion. The length of an object at rest becomes longer than one when it is in motion, and its length becomes proper length.

We try to quantify the above process. Let $x_0$, $x_1$, $x_2$ and so on be the points spaced in order at equal intervals on the $x$-axis. Suppose that the rear end of A advances from $x_0$ to $x_1$ and comes to rest, and its tip advances from $x_2$ to $x_4$ and comes to rest. In other words, A at the position between $x_0$ and $x_2$ is located between $x_1$ and $x_4$ after coming to rest. On the other hand, the rear end of B advances from $x_2$ to $x_4$ and comes to rest, and its tip advances from $x_4$ to $x_7$ and comes to rest. In other words, B at the position between $x_2$ and $x_4$ is located between $x_4$ and $x_7$ after coming to rest.

We examine the movement of the CRE of A (${CRE}_A$) and that of the CRE of B (${CRE}_B$). Each CRE equals to the center of rest energy if each object comes to rest. The ${CRE}_A$ moves from $\left(x_2+x_0\right)/2=x_1$ to $\left(x_4+x_1\right)/2=x_{2.5}$ on the $x$-axis until A completely comes to rest. Therefore, the movement distance of the ${CRE}_A\left(MD{CRE}_A\right)$ is as follows:

$$\left(2.5-1.0\right)=1.5.$$

(12)

On the other hand, the ${CRE}_B$ moves from $\left(x_4+x_2\right)/2=x_3$ to $\left(x_7+x_4\right)/2=x_{5.5}$on the $x$-axis until B completely comes to rest. Therefore, the movement distance of the ${CRE}_B\left(MD{CRE}_B\right)$ is as follows:

$$(5.5-3.0)=2.5.$$

(13)

We find that the difference in $MD{CRE}_B$ and $MD{CRE}_A$ on the $x$-axis is as follows:

$$MD{CRE}_B-MD{CRE}_A=2.5-1.5=1.0.$$

(14)

As a result, the ${CRE}_B$ moves further in the positive direction of the $x$-axis compared with the ${CRE}_A$ even though, to the objects with the same RM and the same size, we simultaneously apply the forces of the same magnitude and direction.

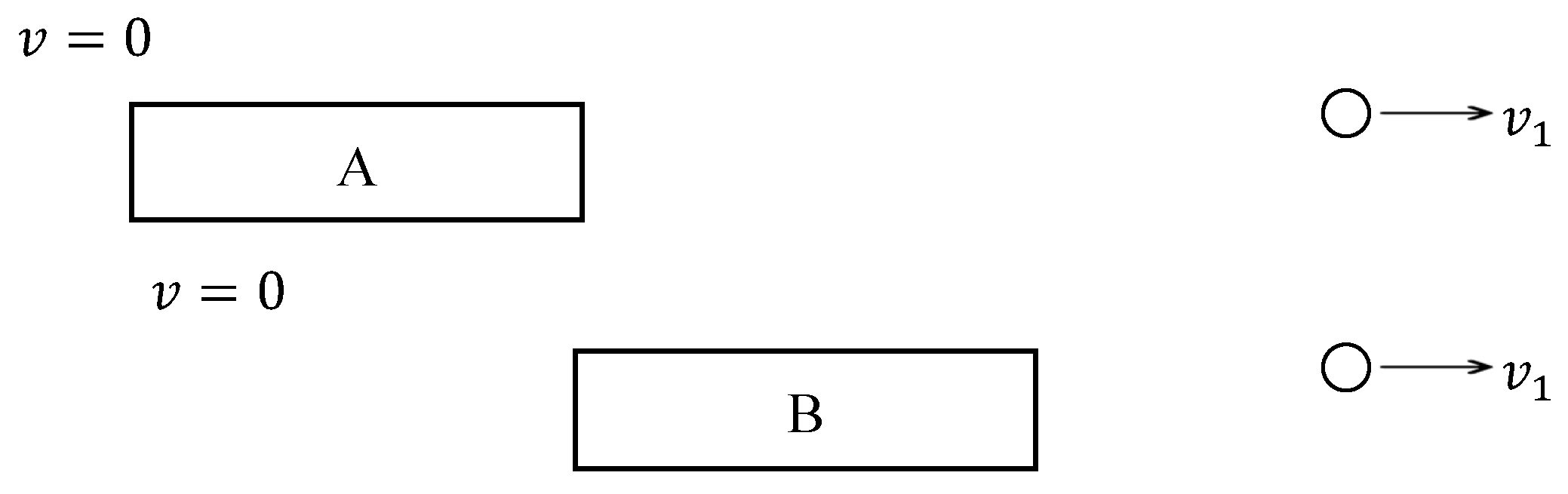
Here, using the case in Figure 6, we assume that two particles at the ends of the double arrow lines, which have the same RM, begin to move due to the reaction of the forces applied to A as shown in Figure 8. The sum of momentums of their particles is equal in magnitude and opposite in the direction compared to the momentum of A. This is also true if two particles at the ends of the double arrow lines start moving due to the reaction of the forces applied to B. Here let ${PS}_A$ be the particle system that interacts with A. Similarly, let ${PS}_B$ be the particle system having the interaction with B. Then, since A and B move in the negative direction of the $x$-axis, each CRE in ${PS}_A$ and ${PS}_B$ moves in the positive direction of it. In addition, each CRE of ${PS}_A$ and ${PS}_B$ always exists at $\left(y_2+y_1\right)/2=y_{1.5}$ and $\left\{\left(y_{-2}+\left(y_{-1}\right)\right)\right\}/2=y_{-1.5}$ since they move parallel to the $x$-axis like A and B. Each CRE of ${PS}_A$ and ${PS}_B$ is originally at the point with the same $x$-coordinate. Each reaction of the forces applied to A and B occurs at the same time and at the above point. Hence, the $x$-coordinate of each CRE of ${PS}_A$ and ${PS}_B$ at the same time is always the same. Figure 9 shows that each CRE of ${PS}_A$ and ${PS}_B$ represented by a circle is moving at the same velocity, and the $x$-coordinate of each CRE at the same time is the same.

We already demonstrate that $MD{CRE}_A$ and $MD{CRE}_B$ are not equal even though the movement distance of CRE of ${PS}_A$ having the interaction with ${CRE}_A$ and that of CRE of ${PS}_B$ having the interaction with ${CRE}_B$ are the same. The LCRE, as shown in Figs. 8 and 9, differs depending on where the forces are applied to the MO, such as when the forces are applied to the front end of the MO, or when the forces are applied to the rear end of it. The thought experiment here can be regarded as that in an IFR. Hence, we find that the LCRE in an IFR is not necessarily uniquely determined.

4. Conclusions

First, we assumed that two objects approach parallel to a coordinate axis from opposite directions in an MIFR. The two objects, when they become perfectly symmetric with respect to the coordinate axis, begin to rotate as one CO after perfectly inelastic collision between them resulting from the application of forces perpendicular to the direction of travel of them. We examined the physical phenomenon resulting from the rotational motion of the CO in the MIFR. When the CO begins to rotate, its LCRE lying very close to the coordinate axis moves to a location away from the coordinate axis because its energy moves in the direction perpendicular to it. Therefore, we concluded that the LCRE in the MIFR is not necessarily invariant.

Second, we supposed a process in which a force causes a negative acceleration on a MO and thereafter the MO eventually comes to rest. Here we paid attention to the position of the force applied to the MO because the TTF inside the MO may vary depending on the position where the force is applied. As a result, we found that the LCRE in an IFR differs depending on the position of the force applied to the MO. This means that the LCRE in an IFR is not necessarily uniquely determined.

We propose that the CE theorem in an IFR does not necessarily hold.