Hydrogen Yield Enhancement in Biogas Dry Reforming with Ni/Cr Catalyst: A Numerical Study

1. Introduction

The production of H₂ as a clean energy carrier has attracted considerable attention in recent years because of its potential to address climate change and decrease reliance on fossil fuels. Among the different methods for generating H₂, biogas dry reforming (BDR) stands out as a promising approach to utilize a renewable feedstock and create a valuable product. A biogas is a fuel consisting of CH₄ (55 vol% - 75 vol%) and CO₂ (25 vol% - 45 vol%) [1] generally. It is produced from fermentation by the action of anaerobic microorganisms on raw materials, e.g. garbage, livestock excretion, and sewage sludge. 1.46 EJ of produced biogas was obtained around the world in 2020 [2]. It was five times larger than that production in 2020 [2]. We can expect the amount of produced biogas will increase more and more in the near future. Consequently, this study thinks a biogas is a promising source to produce H₂.

While a biogas is commonly utilized as a fuel for gas engines and micro gas turbines [3], its lower heating value due to a significant CO₂ content can limit power generation efficiency. To overcome this limitation, the authors propose a synergistic system integrating BDR reactor with a solid oxide fuel cell (SOFC) [4,5,6]. CO, which is by-product from BDR, as well as H₂ can be used as a fuel for SOFC. This approach allows for the valorization of biogas dry converting its CO₂ and CH₄ components into valuable syngas, which can then be efficiently utilized as a fuel in the SOFC. Consequently, this study thinks this system can be used for a wider operation application compared to the existing system.

Many researchers on biogas dry reforming (BDR) have been reported [7,8,9,10,11,12,13,14,15,16,17]. To decide the performance of BDR reactor, this study thinks the selection of catalyst is important. According to the literature survey, Ni-based catalysts have emerged as promising candidates due to their high superiority performance in converting biogas into valuable syngas for BDR [7,8,9,10,11,12,13,14,15,16,17]. Researches have investigated various Ni-based catalysts, including Ni/Co/TiO₂, Ni-promoted pyrochlore, Ni/Al/LDH with Mg and Zn, and Ni-Ce/TiO₂-ZrO₂, Ni/Ru etc. to optimize BDR performance. These studies have demonstrated the influence of catalyst composition, reaction temperature, and molar ratio of CH₄:CO₂ on conversion rates, H₂ yield, and product selectivity. While Ni-based catalyst has shown promising results, challenges such as catalyst deactivation, carbon formation, and H₂/CO ratio control remain to be addressed. Recent advancements in catalyst design and process engineering have aimed to mitigate these issues and enhance the overall efficiency of BDR. For example, the incorporation of promoters or supports can improve catalyst stability and selectivity, while advanced reactor configurations can optimize heat and mass transfer.

At 900 ℃, Ni/Co/TiO₂ catalyst performed CH₄ conversion of 87.13 %, CO₂ conversion of 92.6 % and H₂ production of 41.1 % [7]. In this study [7], the optimum ratio of Ni and Cr was 7 wt% and 4 wt%, respectively. Ni with hollow silica spheres performed CH₄ conversion of 94.4 % and CO₂ conversion of 95 % [8]. Ni-promoted pyrochlore showed that the highest CH₄ conversion and CO₂ conversion were obtained in case of CH₄:CO₂ = 1.1 and 1.85:1, respectively [9]. BDR experiment was carried out using a Ni/Al/LDH with Mg and Zn in case of CH₄:CO₂:N₂ = 1.5:1:7.5 at the temperature range from 500 ℃ to 700 ℃ [10]. This catalyst performed CH₄ conversion of 73 %, CO₂ conversion of 90 % and H₂/CO ratio of approximately 2. Ni-Ce/TiO₂-ZrO₂ performed the highest CH₄ conversion of approximately 98 % at 750 ℃ and the highest H₂/CO ratio of approximately 0.71 and 800 ℃ [11]. Ni/Ru catalyst was investigated, exhibiting the performance that CH₄ and CO₂ conversions were 70 % and 78 %, respectively at 750 ℃ [12]. In case of CH₄ rich condition, i.e. CH₄:CO₂ = 2:1, low Ni loading (2.5 wt%) modified with Gd, Sc or La showed the highest CH₄ conversion of 49 %, the highest CO₂ conversion of 95 % and the highest H₂/CO ratio of 1.0 at 750 ℃ [13]. Kaviani et al investigated the effect of Ni loading on the performance of Ni/SiO₂/SiO₂ core-shell for BDR [14]. As a result, when Ni content increased from 2.5 wt % to 15 wt%, the Ni loading of 15 wt% performed the highest CH₄ conversion of 75 %, the highest CO₂ conversion of 90 % and the highest H₂/CO ratio of 0.9. Ni-SiO₂ sandwiched core-shell catalyst performed the highest CH₄ conversion of 71.5 % and CO₂ conversion of 91.5 % in case of CH₄:CO₂ = 1.5:1 at 700 ℃ [15]. SiO₂ layer in sandwiched catalyst prevented the agglomeration of metal particles and minimized carbon deposition. Ni/LnOx (Ln = La, Ce, Sm or Pr) – type catalyst was developed for the investigation of the characteristics of BDR [16]. As a result, CH₄ and CO₂ conversions increased with the increase in reaction temperature from 600 ℃ to 750 ℃ irrespective of catalyst type, while the temperature change of H₂/CO ratio depended on catalyst type. According to the review paper on Ni-based catalyst [17], CH₄ and CO₂ conversions increased with the increase in reaction temperature from 300 ℃ up to 1000 ℃ irrespective of the molar ratio of CH₄:CO₂. On the other hand, H₂/CO ratio decreased with the increase in reaction temperature from 300 ℃ to 500 ℃ and kept the constant value, i.e. approximately 0 over 500 ℃.

Though several Ni alloy catalysts have been investigated, few Ni/Cr were reported except for experimental studies using membrane reactor, which was carried out by the authors of this paper [18,19]. These previous studies reported that Ni/Cr exhibited the better performance compared to Ni catalyst due to preventing a carbon deposition [18,19]. H₂ yield obtained by Ni/Cr catalyst was approximately 10 – 100 times as large as that of Ni catalyst, which depended on experimental condition. H₂ yield increased with the increase in temperature from 400 ℃ to 600 ℃ irrespective of molar ratio of CH₄:CO₂. The highest H₂ yield which was 12.8 % was obtained using Ni/Cr in case of CH₄:CO₂ = 1.5:1 at 600 ℃ and the differential pressure between the reaction chamber and the sweep chamber of 0.010 MPa without sweep gas. In addition, CO selectivity is much larger than H₂ selectivity within the temperature range from 400 ℃ to 600 ℃, which was over 90 %. According to the previous studies [18,19], it was thought that not only dry reforming (DR) but also the other reactions conducted. However, the numerical analysis on the characteristics of Ni/Cr alloy catalyst used for BDR including the other reactions has not been investigated, which means that the reaction mechanisms has not been clarified. In addition, a catalyst porosity (ε_p) which influences the performance of catalyst as well as reactor has not been investigated numerically and experimentally.

While Ni/Cr catalyst has shown a promising performance in previous experimental studies for BDR [18,19], its reaction mechanisms and the influence of ε_p on performance remain unclear. Therefore, this study aims to address these knowledge gaps through the numerical simulation using CFD software COMSOL Multiphysics. By investigating the impact of reaction temperature, molar ratio of CH₄:CO₂, and ε_p, the study seeks to elucidate the reaction characteristics and optimize H₂ yield in BDR using Ni/Cr catalyst. Since there are more previous studies using COMSOL Multiphysics for numerical analysis on BDR and reports the reaction characteristics as well as heat and mass transfer [20,21,22,23], we have adopted COMSOL Multiphysics for the numerical analysis in this study. To investigate the impact of reaction temperature, molar ratio of CH₄:CO₂ and ε_p on the characteristics of BDR including the other reactions, the following reactions are considered:

<Dry reforming (DR)>

CH₄ + CO₂ ↔ 2H₂ + 2CO + 247 kJ/mol

(1)

<Steam reforming (SR)>

CH₄ + H₂O ↔ CO + 3H₂ + 206 kJ/mol

(2)

<Reverse water gas shift reaction (RWGS)>

CO₂ + H₂ ↔ CO + H₂O + 41 kJ/mol

(3)

<Methanation reaction (MR)>

CO₂ + 4H₂ ↔ CH₄ + 2H₂O - 165.0 kJ/mol

(4)

<Methane decomposition reaction (MDR)>

CH₄ ↔ C + 2H₂ + 74 kJ/mol

(5)

<Boudouard reaction (BD)>

2CO ↔ C + CO₂ - 172 kJ/mol

(6)

In this study, the reaction temperature is changed to 400 ℃, 500 ℃, 600 ℃ and 700 ℃. The molar ratio of CH₄:CO₂ is also changed as 1.5:1, 1:1 and 1:1.5. ε_p is also changed as 0.95, 0.7, 0.4 and 0.1.

2. Numerical Simulation of BDR over Ni/Cr Catalyst

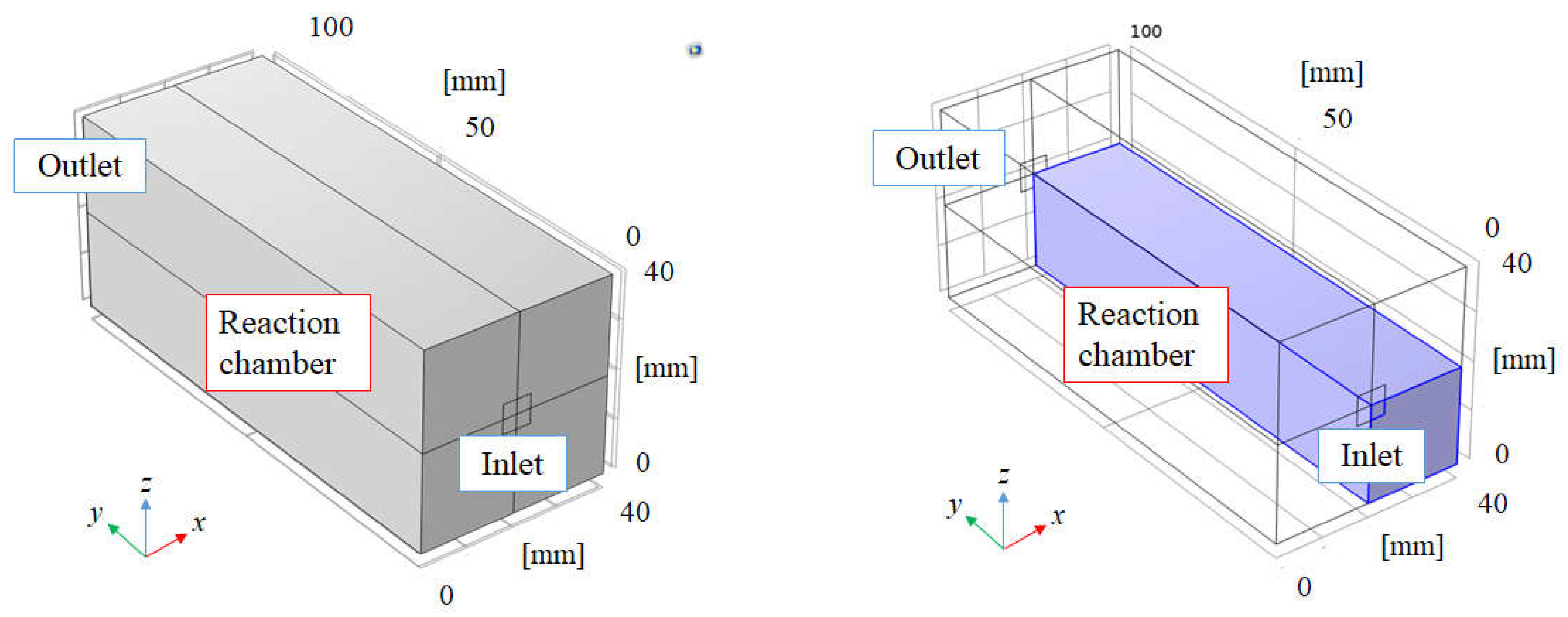
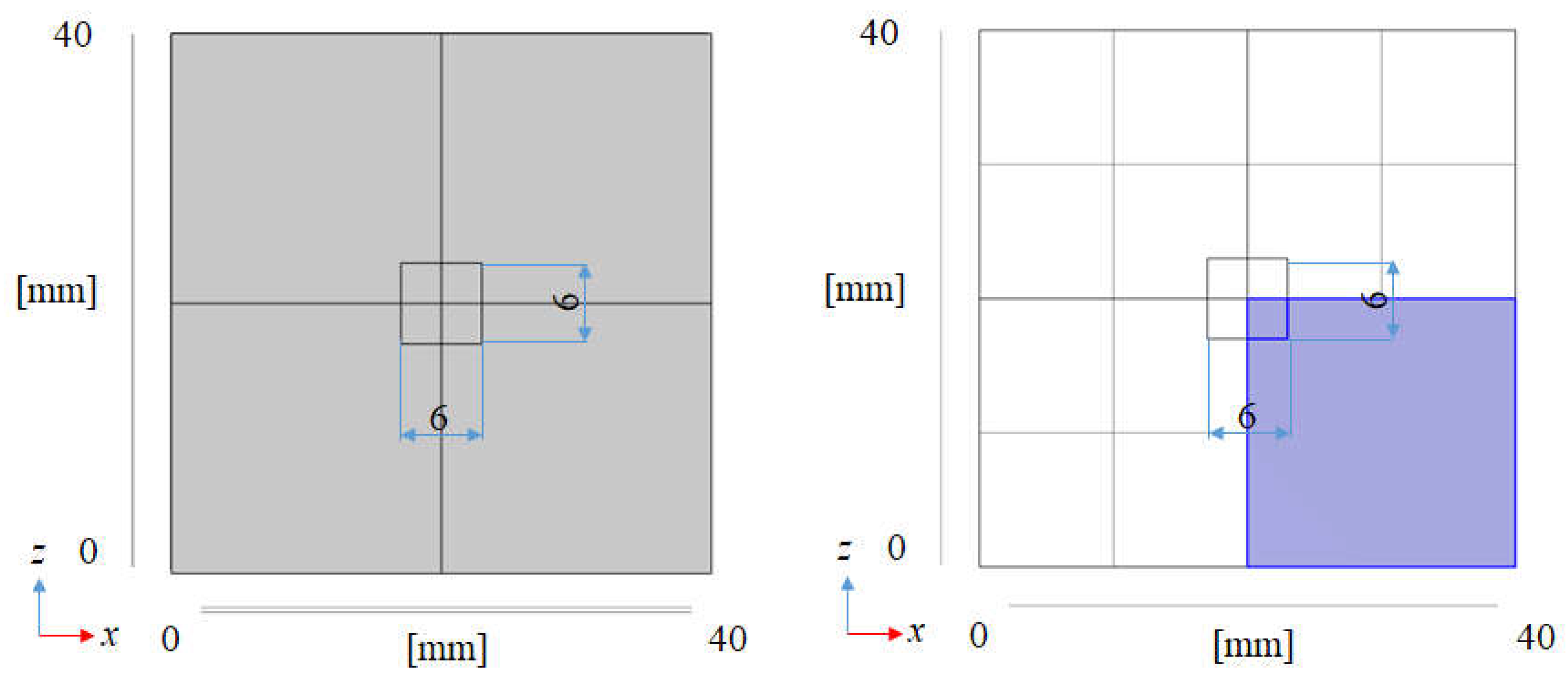
2.1. A Mathematical Formulation

The numerical simulation conducted by a multi-physics software, COMSOL Multiphysics, ver. 6.2. In COMSOL Multiphysics, users could select or customize various partial differential equations and combine them to achieve direct coupled multi-physics field analysis easily [24]. The COMSOL Multyphysics has a simulation function codes. The following governing equations are involved in COMSOL Multiphysics.

The equations of mass conservation in porous material can be defined, as following:

$$\overrightarrow{u}=-{\displaystyle \frac{\kappa }{\mu }}\left(\nabla p+\rho g\nabla D\right)$$

(7)

$$\nabla \cdot \left(\rho \overrightarrow{u}\right)=Q_m$$

(8)

$$\nabla \cdot \rho \left[-{\displaystyle \frac{\kappa }{\mu }}\left(\nabla p\right)\right]=Q_m$$

(9)

where $\overrightarrow{u}$ is a velocity vector [m/s], κ is a permeability [m²], μ is a viscosity [Pa・s], p is a pressure [Pa], ρ is a density [kg/m³], g is a gravitational acceleration [m²/s], D is a height [m] and Q_m is a mass source term [kg/(m³・s)].

The equation of momentum conservation in porous material can be defined by Brinkmann equation, as following:

$$\begin{gathered} {\displaystyle \frac{\rho }{{\epsilon }_p}}\left(\overrightarrow{u}\cdot \nabla \right){\displaystyle \frac{\overrightarrow{u}}{{\epsilon }_p}}= \\ -\nabla p+\nabla \cdot \left[{\displaystyle \frac{1}{{\epsilon }_p}}\left\{\mu \left(\nabla \overrightarrow{u}+{\left(\nabla \overrightarrow{u}\right)}^T\right)-{\displaystyle \frac{2}{3}}\mu \left(\nabla \cdot \overrightarrow{u}\right)\overrightarrow{I}\right\}\right]-\left({\kappa }^{-1}\mu +{\displaystyle \frac{Q_m}{{\epsilon }_p^2}}\right)\overrightarrow{u}+\overrightarrow{F} \end{gathered}$$

(10)

where ε_p is a porosity [-], $\overrightarrow{I}$ is a unit vector [-] and $\overrightarrow{F}$ is a force vector [kg/(m³・s)].

The equation of mass transfer in porous material can be defined by Maxell-Stefan

equation, as following:

$$\nabla \cdot \left(\rho {\omega }_i\overrightarrow{u}-\rho {\omega }_i{\displaystyle \sum _{k=1}^n{\epsilon }_p^{\frac{3}{2}}\widetilde{D_{ik}}\left(\nabla x_k+\left(x_k-{\omega }_k\right)\frac{\nabla p}{p}\right)-{\epsilon }_p^{\frac{3}{2}}{D}_i^T\frac{\nabla T}{T}}\right)=R_{i,tot}$$

(11)

where ${\omega }_i$, ${\omega }_k$ is a mass ratio of chemical i and k, respectively [-], $\widetilde{D_{ik}}$ is a Fick’s diffusion coefficient of effective multi components [m²/s], $D_i^T$ is a thermal diffusion coefficient [kg/(m・s)] and $R_{i,tot}$ is a reaction rate of chemical species [mol/(m³・s)].

The equations of heat transfer in porous material can be defined, as following:

$${\rho }_f{C}_{p,f}\overrightarrow{u}\cdot \nabla T+\nabla \cdot \overrightarrow{q}=Q+Q_p+Q_{vd}$$

(12)

$$\overrightarrow{q}=-k_{eff}\nabla T$$

(13)

where f is a physical quantity on fluid [-], C_p is the constant pressure specific heat [J/(kg・K)], $\overrightarrow{q}$ is a thermal flux vector [W/m²], Q is a thermal source [W/m³], Q_p is a thermal source due to pressure loss [W/m³], Q_vd is a thermal source due to viscosity dissipation [W/m³] and k_eff is an effective thermal conductivity [W/(m・K)].

2.2. 3D Numerical Modeling of BDR

Figure 1 illustrates the overview of 3D model. Figure 2 illustrates the front view of 3D model. The 3D model simulates the experimental apparatus of reaction chamber used for the previous experimental studies carried out by the authors [18,19]. Though the biogas dry reforming experiment was carried out using membrane reactor in the previous studies [18,19], this study focuses on the reaction chamber only without H₂ separation to clarify the reaction characteristics of biogas dry reforming including the other reactions. The dimension of 3D model is 40 mm × 40 mm × 100 mm. The both inlet and outlet area is 6 mm × 6 mm.

In this study, the numerical simulation is carried out by the one-fourth sized model cut with the dimension of 10 mm × 10 mm × 100 mm, which are also shown in Figure 1 and Figure 2, since the similarity of the results toward horizontal and vertical have been confirmed by this study.

2.3. Kinetic Modeling of BDR

This study considers the reaction shown by Equations (1) – (5) for the numerical simulation. Reaction rates of these equations are defined as follows [25,26,27]:

<Dry reforming (DR)>

$$r_1=k_1\cdot \left[{\displaystyle \frac{K_{C{O}_2,1}{K}_{C{H}_4,1}{P}_{C{O}_2}{P}_{C{H}_4}}{{\left(1+K_{C{O}_{2,1}}{P}_{C{O}_2}+K_{C{H}_4,1}{P}_{CH4}\right)}^2}}\right]\cdot \left[1-{\displaystyle \frac{{\left(P_{CO}{P}_{H_2}\right)}^2}{K_1{P}_{C{O}_2}{P}_{C{H}_4}}}\right]$$

(14)

where $k_1=1290\times 5000e^{{\displaystyle \frac{-102065}{RT}}}$, $K_{C{O}_2,1}=2.64\times {10}^{-2}{e}^{{\displaystyle \frac{37641}{RT}}}$, $K_{C{H}_4,1}=2.63\times {10}^{-2}{e}^{{\displaystyle \frac{40684}{RT}}}$, $K_1=e^{34.011}\cdot e^{{\displaystyle \frac{-258598}{RT}}}$.

<Steam reforming (SR)>

$$r_2={\displaystyle \frac{\frac{k_2}{P_{H_2}^{2.5}}\left(P_{C{H}_4}{P}_{H_{2}O}-\frac{P_{CO}{P}_{H_2}^3}{K_2}\right)}{{\left(1+\frac{P_{H_{2}O}{K}_{H_{2}O,2}}{P_{H_2}}+K_{CO,2}{P}_{CO}+K_{H_2,2}{P}_{H_2}+K_{C{H}_4,2}{P}_{C{H}_4}\right)}^2}}$$

(15)

where $k_2=2.636\times {10}^{12}{e}^{{\displaystyle \frac{-240100}{RT}}}$, $K_2=1.198\times {10}^{17}{e}^{{\displaystyle \frac{-26830}{RT}}}$, $K_{C{O}_2,2}=8.23\times {10}^{-5}{e}^{{\displaystyle \frac{70650}{RT}}}$, $K_{C{H}_4,2}=6.65\times {10}^4{e}^{{\displaystyle \frac{38280}{RT}}}$, $K_{H_2,2}=6.12\times {10}^{-9}{e}^{{\displaystyle \frac{82900}{RT}}}$, $K_{H_{2}O,2}=1.77\times {10}^5{e}^{{\displaystyle \frac{-88680}{RT}}}$.

<Reverse water gas shift reaction (RWGS)>

$$r_3=k_3{P}_{C{O}_2}\left(1-{\displaystyle \frac{P_{CO}{P}_{H_{2}O}}{K_3{P}_{C{O}_2}{P}_{H_2}}}\right)$$

(16)

where$k_3=9.28\times {10}^3{e}^{{\displaystyle \frac{-73105}{RT}}}$, $K_3=68.78e^{{\displaystyle \frac{-37500}{RT}}}$.

<Methanation reaction (MR)>

$$r_4={\displaystyle \frac{\frac{k_4}{P_{H_2}^{3.5}}\left(P_{C{H}_4}{P}_{H_{2}O}^2-\frac{P_{C{O}_2}{P}_{H_2}^4}{K_4}\right)}{{\left(1+\frac{P_{H_{2}O}{K}_{H_{2}O,4}}{P_{H_2}}+K_{CO,4}{P}_{CO}+K_{H_2,4}{P}_{H_2}+K_{C{H}_4,4}{P}_{C{H}_4}\right)}^2}}$$

(17)

where $k_4=6.364\times {10}^{11}{e}^{{\displaystyle \frac{-24390}{RT}}}$, $K_4=2.117\times {10}^{15}{e}^{{\displaystyle \frac{-22430}{RT}}}$, $K_{C{H}_4,4}=6.65\times {10}^{-4}{e}^{{\displaystyle \frac{38280}{RT}}}$,

$K_{CO,4}=8.23\times {10}^{-5}{e}^{{\displaystyle \frac{70650}{RT}}}$, $K_{H_2,4}=6.12\times {10}^{-9}{e}^{{\displaystyle \frac{82900}{RT}}}$, $K_{H_{2}O,4}=1.77\times {10}^5{e}^{{\displaystyle \frac{-88680}{RT}}}$.

<Methane decomposition reaction (MDR)>

$$r_5={\displaystyle \frac{k_5{K}_{C{H}_4,5}\left(P_{C{H}_4}-\frac{P_{H_2}^2}{K_5}\right)}{{\left(1+K_{C{H}_4,5}{P}_{C{H}_4}+\frac{P_{H_2}^{1.5}}{K_{H_2,5}}\right)}^2}}$$

(18)

where $k_5=6.95\times {10}^3{e}^{{\displaystyle \frac{-58983}{RT}}}$, $K_5=2.95\times {10}^5{e}^{{\displaystyle \frac{-84440}{RT}}}$, $K_{C{H}_4,5}=0.21e^{{\displaystyle \frac{-567}{RT}}}$, $K_{H_2,5}=5.18\times {10}^7{e}^{{\displaystyle \frac{-133210}{RT}}}$.

<Boudouard reaction (BD)>

$$r_6={\displaystyle \frac{\frac{k_6}{K_{CO,6}{K}_{C{O}_2,6}}\left(\frac{P_{CO}}{K_6}-\frac{P_{C{O}_2}}{P_{CO}}\right)}{{\left(1+K_{CO,6}{P}_{CO}+\frac{1}{K_{CO,6}{K}_{C{O}_2,6}}\frac{P_{C{O}_2}}{P_{CO}}\right)}^2}}$$

(19)

where $k_6=1.34\times {10}^{15}{e}^{{\displaystyle \frac{-243835}{RT}}}$, $K_6=1.9393\times {10}^9{e}^{{\displaystyle \frac{-168527}{RT}}}$, $K_{C{O}_2,6}=2.81\times {10}^7{e}^{{\displaystyle \frac{-104085}{RT}}}$, $K_{CO,6}=7.34\times {10}^{-6}{e}^{{\displaystyle \frac{100395}{RT}}}$. In addition, $r_n$ is a kinetic rate (n = 1, 2, 3, 4, 4, 6) [mol/(kg・s)], $k_n$is a kinetic constant (n = 1, 2, 3, 4, 5, 6) [mol/(kg・s)], $P_i$ is a particle pressure of chemical species i [Pa], $K_n$ is an equilibrium constant (n = 1, 2, 3, 4, 5, 6) [-] and $K_i$ is an absorption equilibrium constants of chemical species i [-].

2.4. Numerical Simulation Parameters and Conditions for BDR

In this study, the molar ratio of CH₄:CO₂ is changed by 1.5:1, 1:1 and 1:1.5. The initial reaction temperature is changed by 400 ℃, 500 ℃, 600 ℃ and 700 ℃. Ni/Cr alloy is assumed to be the catalyst, which was used for the previous experimental studies [18,19].

The weight ratio of Cr to the whole weight of Ni/Cr alloy is 20 wt%. The porosity, permeability, constant pressure specific heat and thermal conductivity of Ni/Cr alloy catalysts are estimated considering the weight ratio of Cr. ε_p is changed by 0.95, 0.7, 0.4 and 0.1. Table 1 lists the main physical properties and parameters for the numerical simulation in this study.

In this study, the following assumptions are set:

(i)

Catalyst is a porous material. The porosity, permeability, constant pressure specific heat and thermal conductivity and isotropic.

(ii)

Wall temperature is isothermal.

(iii)

Gas is a Newton fluid and an ideal gas.

(iv)

Wall of reactor excluding inlet and outlet is no-slip.

(v)

The pressure of outlet is atmosphere (gauge pressure = 0 Pa).

(vi)

The temperature of inflow gas is same as the initial reaction temperature.

(vii)

The produced carbon is treated as a gas.

2.5. Evaluaion Factors and Reaction Pathways in BDR

In this study, the following evaluation factors are considered:

CH₄ conversion = ${\displaystyle \frac{C_{C{H}_4,in}-C_{C{H}_4,out}}{C_{C{H}_4,in}}}\times 100$[%] (20)

where $C_{C{H}_4,in}$ is a molar concentration of CH₄ at the inlet [mol], $C_{C{H}_4,out}$ is a molar concentration of CH₄ at the outlet [mol].

CO₂ conversion = ${\displaystyle \frac{C_{C{O}_2,in}-C_{C{O}_2,out}}{C_{C{O}_2,in}}}\times 100$[%] (21)

where $C_{C{O}_2,in}$ is a molar concentration of CO₂ at the inlet [mol], $C_{C{O}_2,out}$ is a molar concentration of CO₂ at the outlet [mol].

H₂ yield = ${\displaystyle \frac{\frac{1}{2}{C}_{H_2,out}}{C_{C{H}_4,in}}}\times 100$ [%] (22)

where $C_{H_2,out}$ is a molar concentration of H₂ at the outlet [mol].

H₂ selectivity = ${\displaystyle \frac{C_{H_2,out}}{C_{H_2,out}+C_{CO,out}}}\times 100$ [%] (23)

where $C_{CO,out}$ is a molar concentration of CO at the outlet [mol].

CO selectivity = ${\displaystyle \frac{C_{CO,out}}{C_{H_2,out}+C_{CO,out}}}\times 100$ [%] (24)

3. Results and Discussion

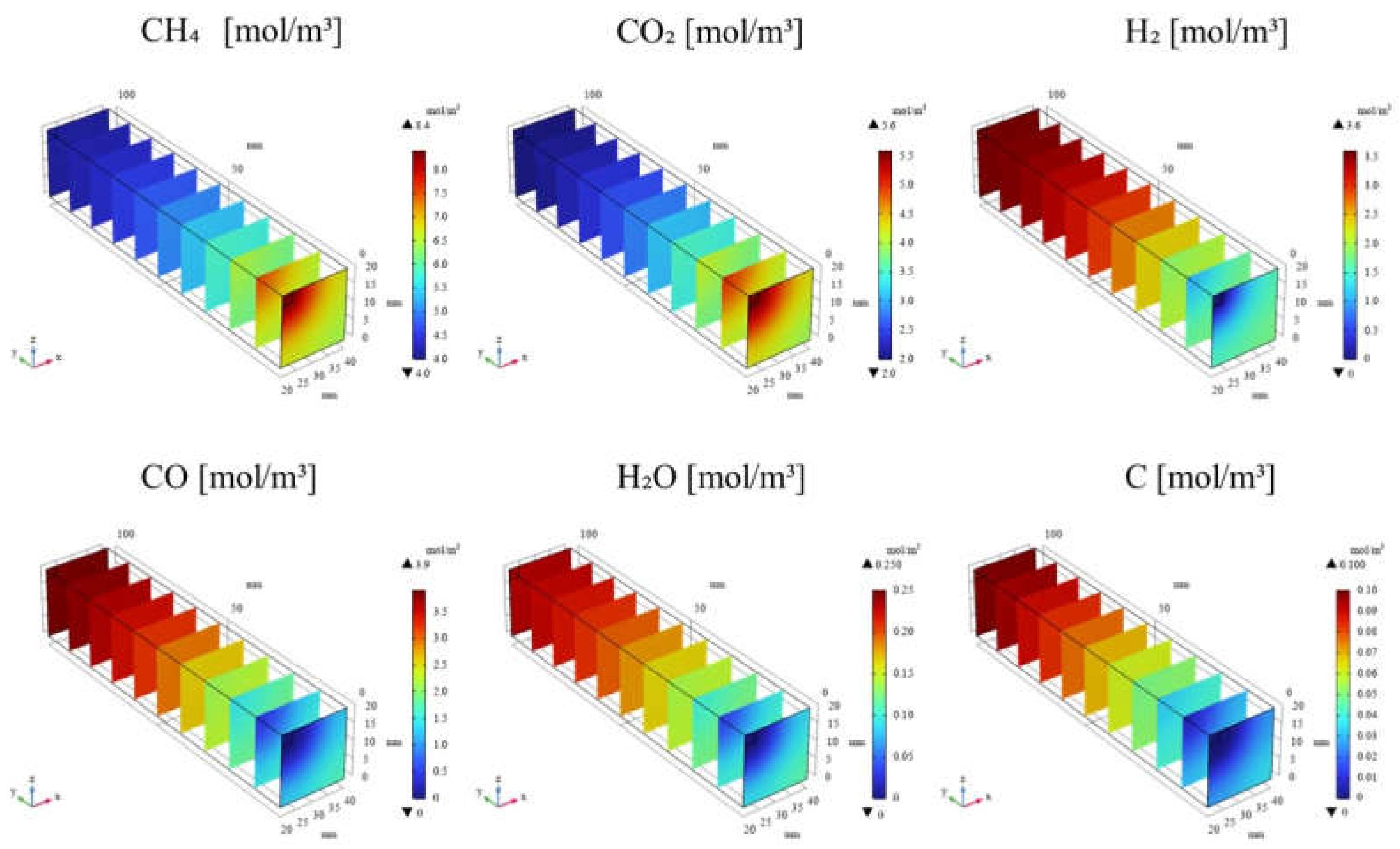
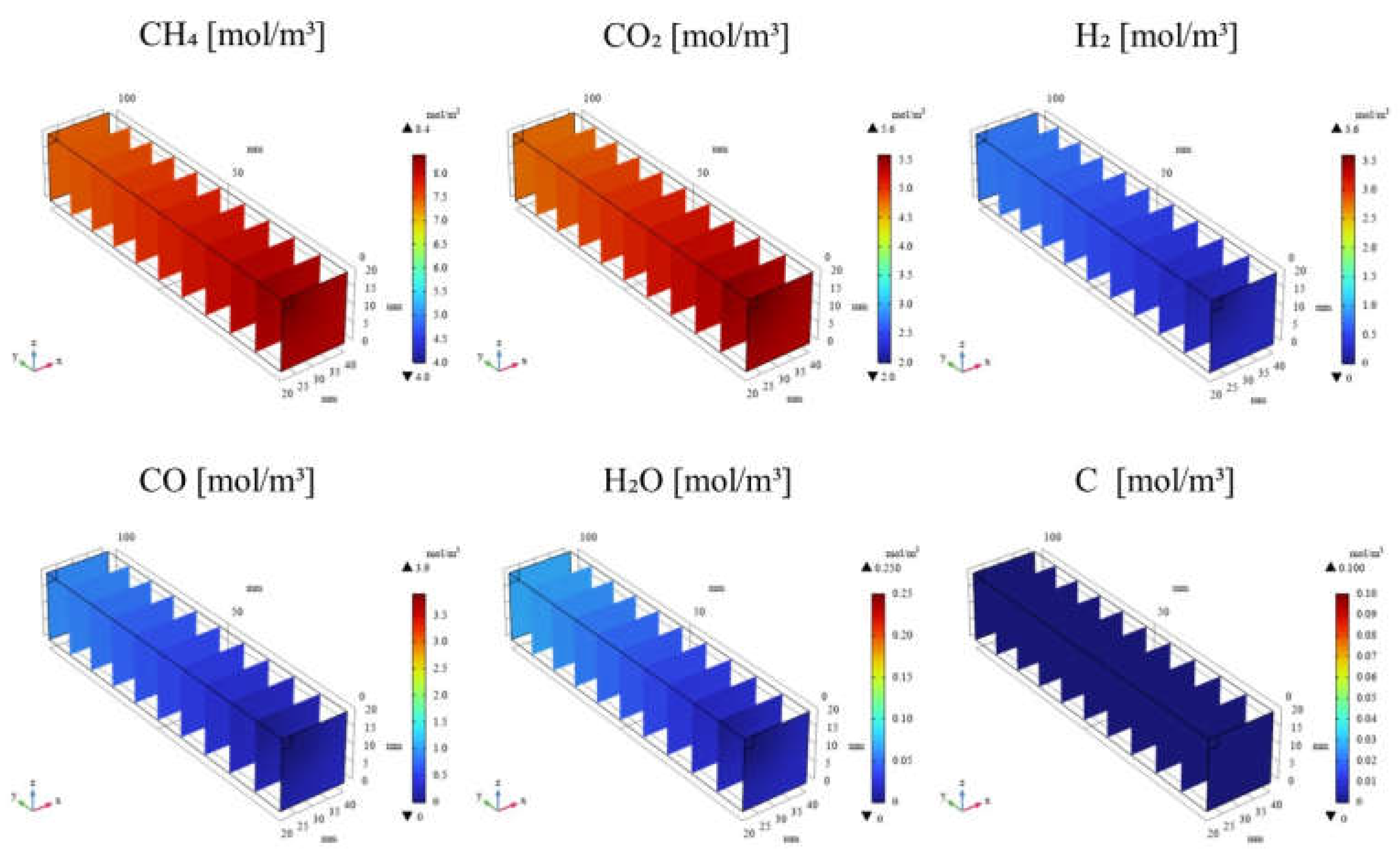
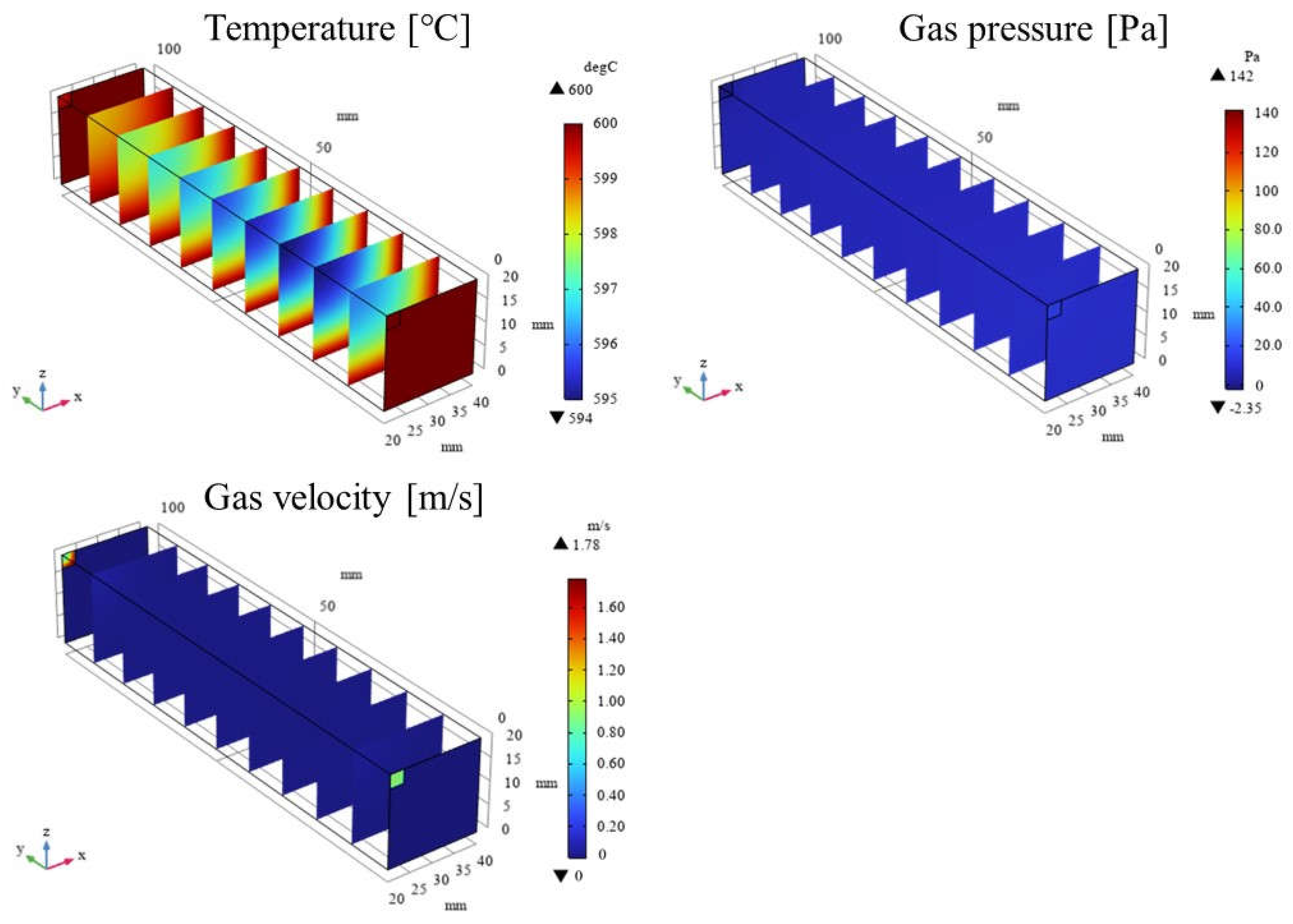
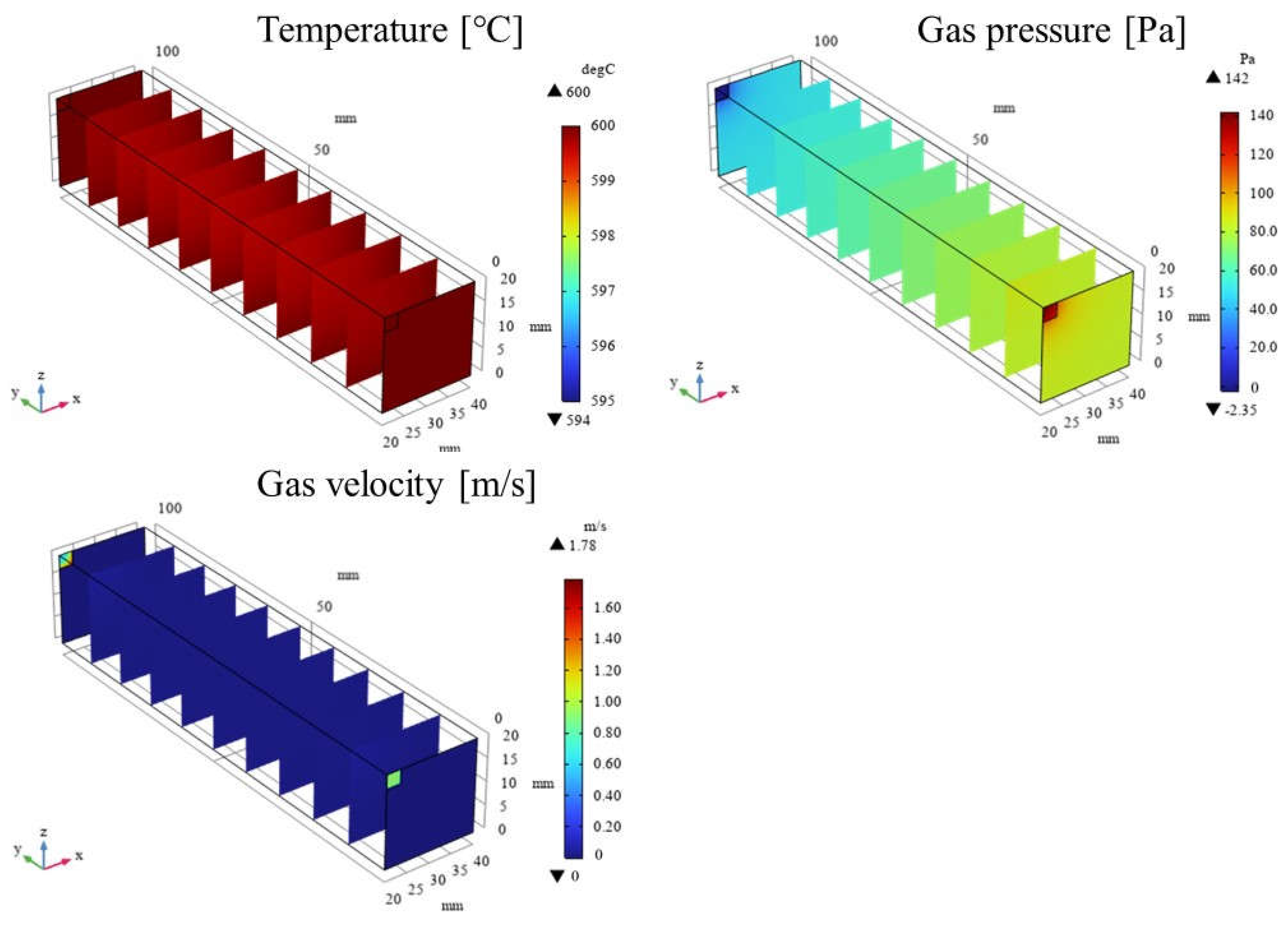
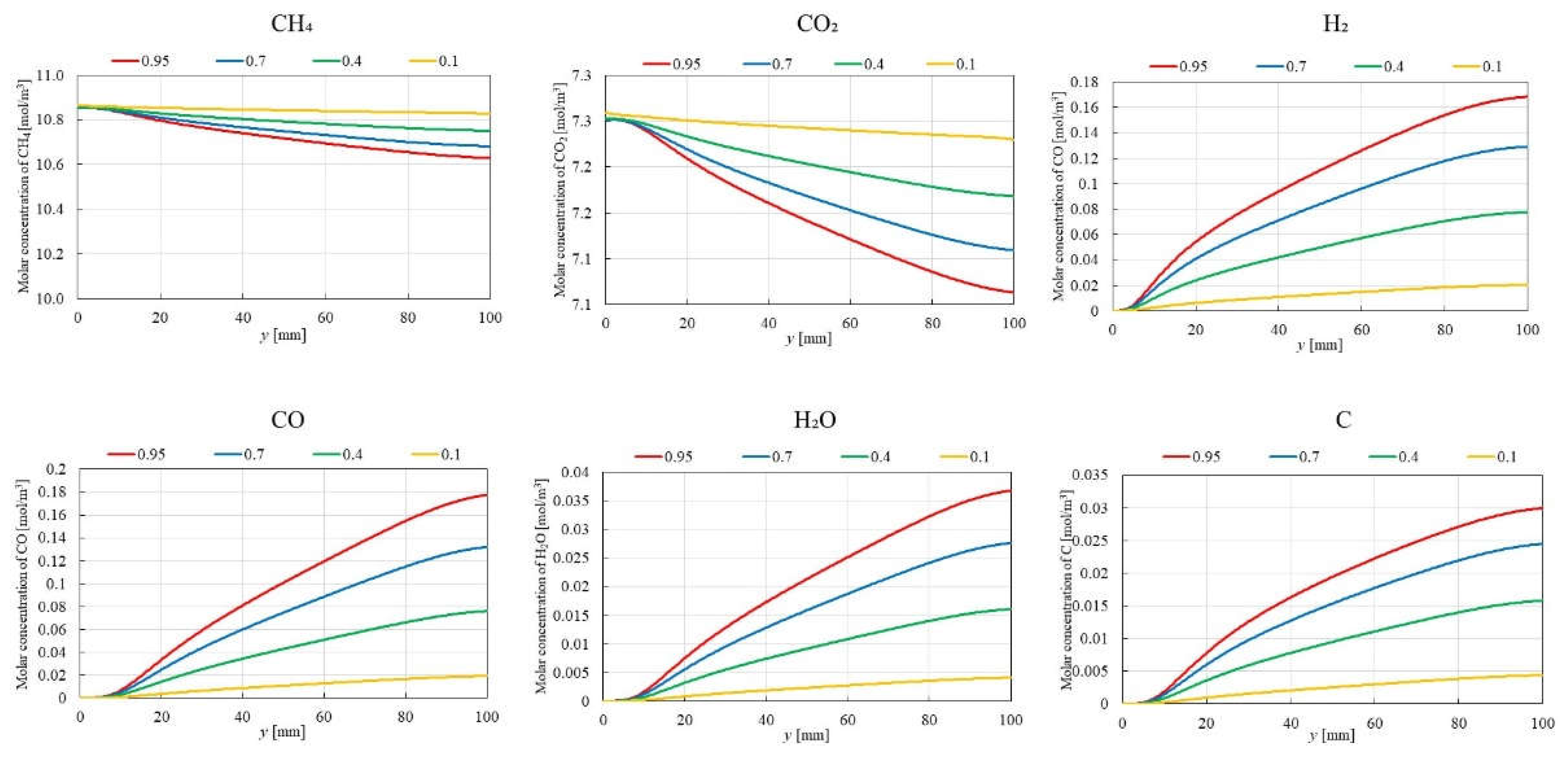
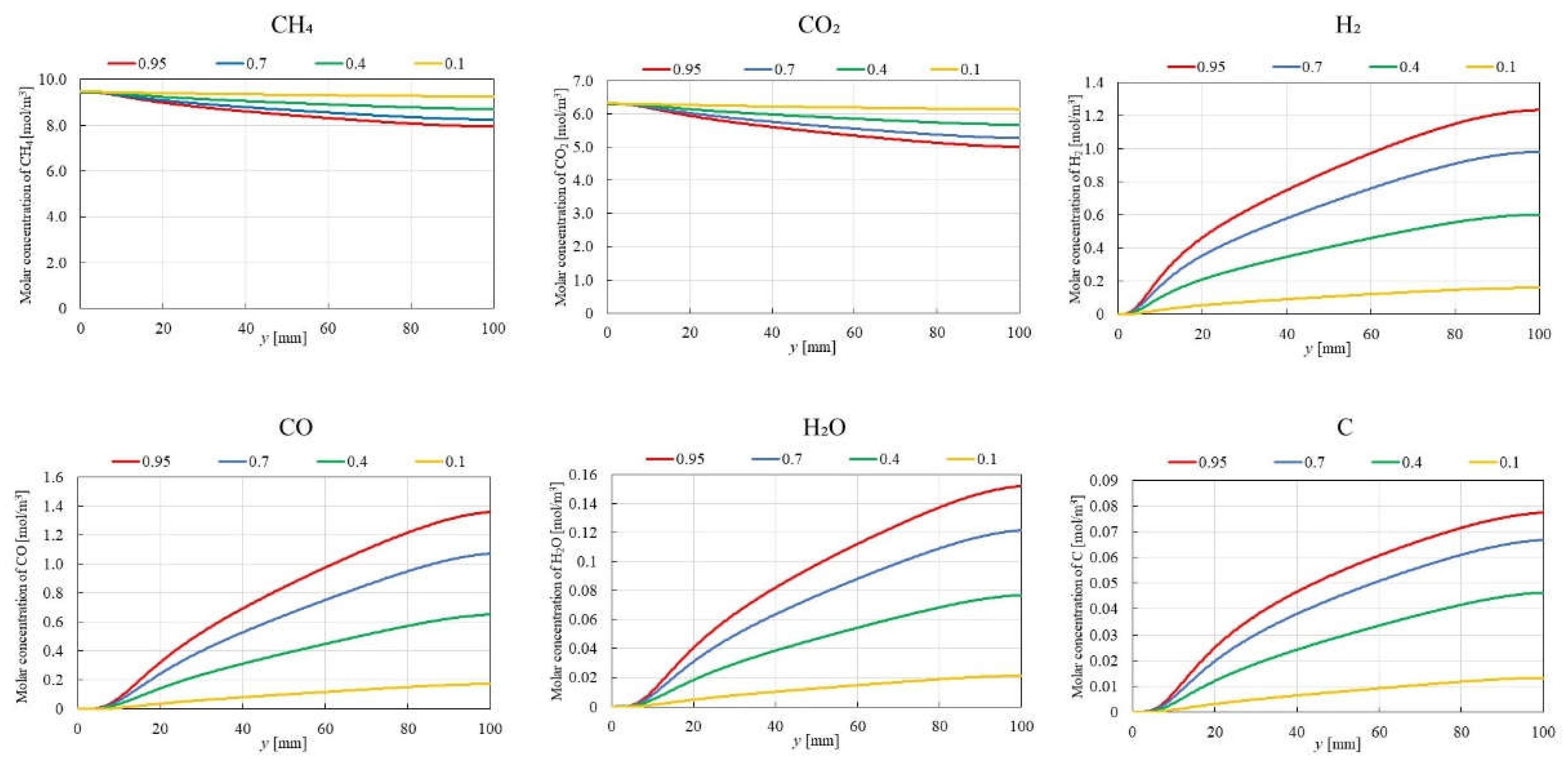
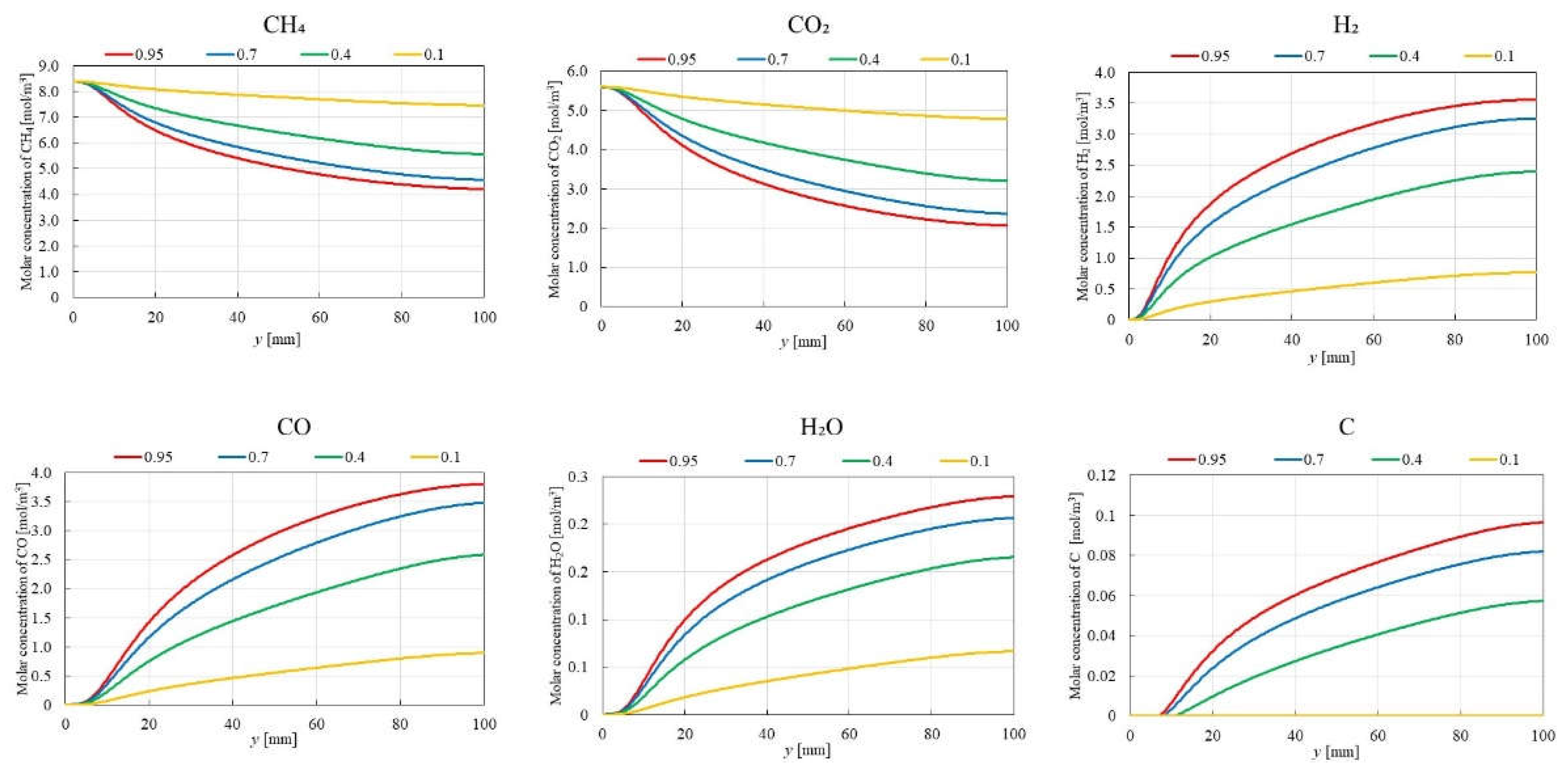
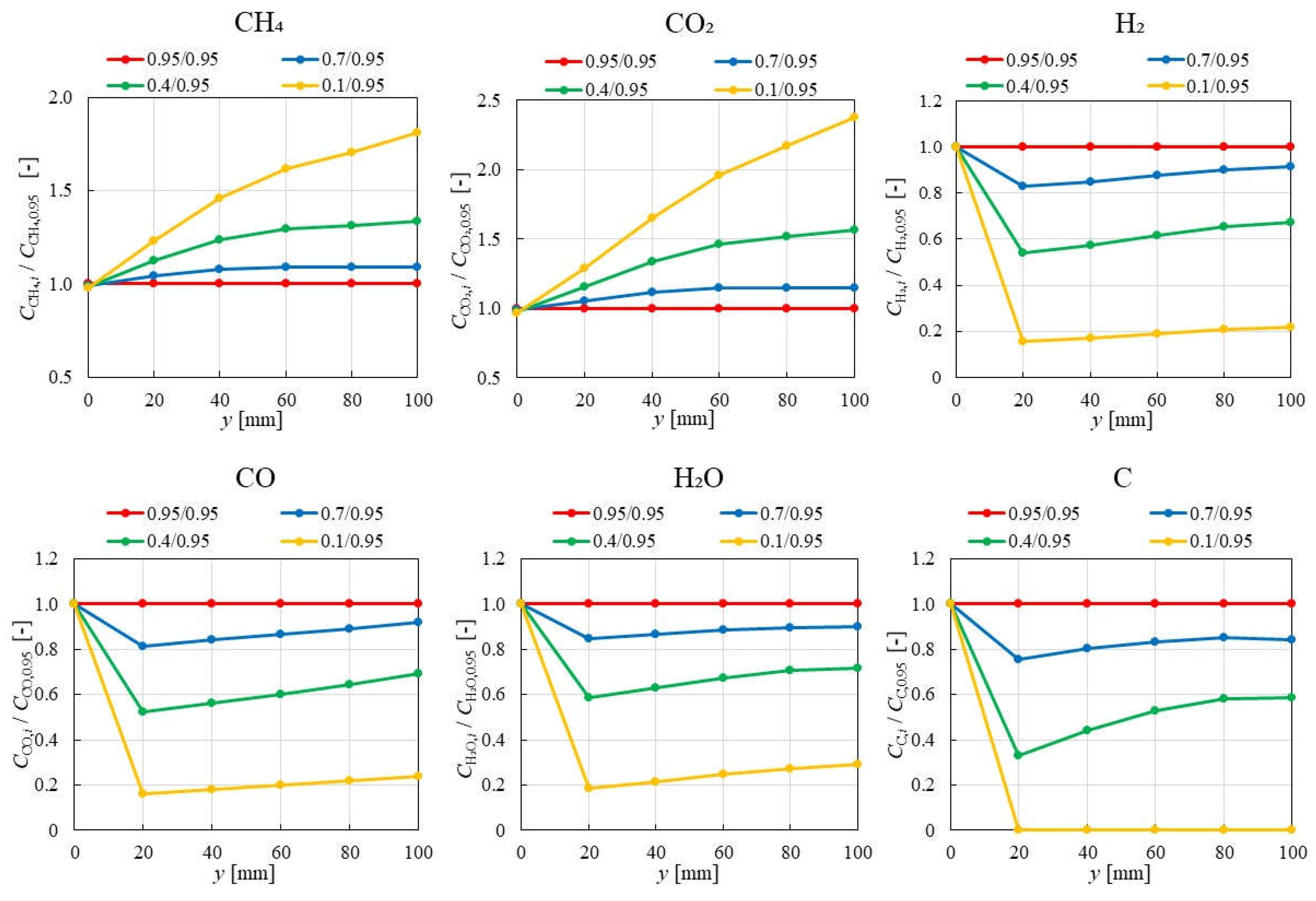
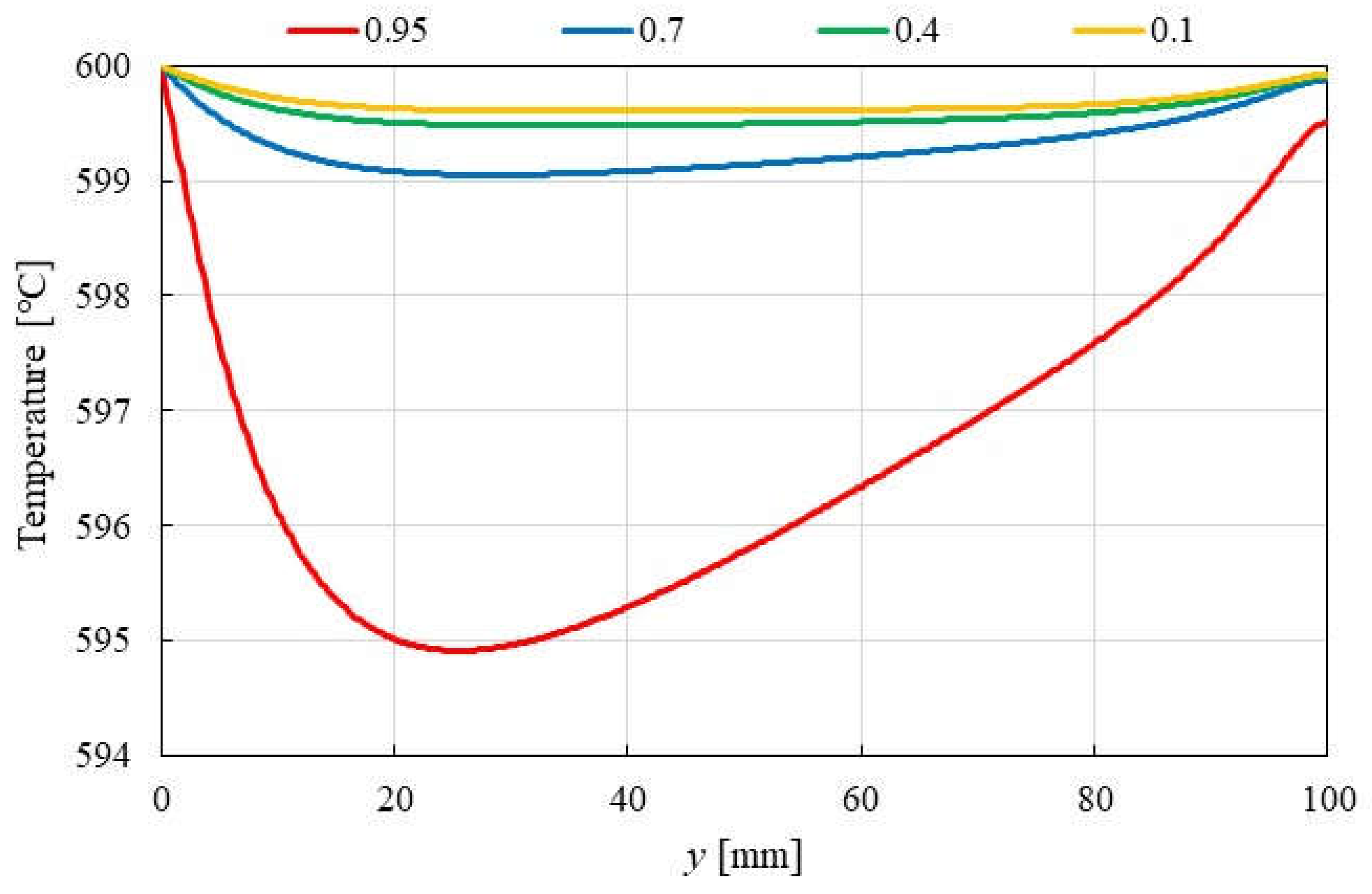
3.1. Impact of Catalyst Porosity on Reaction, Heat, and Mass Transfer Phenomena in BDR

Figure 3, Figure 4, Figure 5 and Figure 6. Illustrate the 3D distributions of molar concentrations (CH₄, CO₂, H₂, CO₂, H₂O and C), temperature, gas pressure, and gas velocity within the reactor. To exemplify the numerical simulation results, Figure 3 and Figure 5 present the data for the CH₄:CO₂ ratio of 1.5:1 at 600 ℃ with ε_p of 0.95, while Figure 4 and Figure 6 show the corresponding data for the same conditions but with a lower ε_p of 0.1.

As depicted in Figure 3 and Figure 4, the molar concentrations of CH₄ and CO₂ (reactants) decrease progressively along the gas flow from the inlet to the outlet, regardless of ε_p. In the initial section (0 mm≤y≤20 mm), the molar concentrations of CH₄ and CO₂ exhibit a radial gradient, with higher values near the center and lower values near the wall. However, this radial distribution becomes less pronounced or disappears in the downstream region (30 mm≤y≤100 mm). This behavior can be attributed to the high gas velocity near the inlet, which promotes preferential axial flow and limits radial diffusion. As the gas progresses through the reactor, the diffusion becomes more significant, leading to a more uniform distribution. In addition, the molar concentrations of H₂, CO, H₂O and C, which are products, increase along the gas flow direction from the inlet to the outlet, regardless of ε_p. Conversely, the temperature profiles depicted in Figure 5 and Figure 6 demonstrate a decrease from the initial reaction temperature of 600 ℃, except near the inlet and the outlet regions. This temperature reduction is attributed to the endothermic nature of reactions described by Equations (1) – (6). These observations validate the accuracy of the simulated reaction model. Furthermore, the gas velocity is notably higher near the inlet and the outlet compared to the central reaction of the reactor. This is due to the larger cross sectional area in these regions. However, away from the inlet and the outlet, the gas velocity stabilizes as a result of sufficient gas diffusion towards the reactor walls.

As illustrated in Figure 3 and Figure 4, a higher ε_p leads to lower molar concentrations of CH₄ and CO₂ and conversely, higher molar concentrations of H₂, CO, H₂O and C. This enhancement in product formation and reactant consumption can be attributed to the improved mass transfer within the porous catalyst structure at higher ε_p values. The enhanced diffusivity within the catalyst facilitates reactant diffusion to active sites and product diffusion away from the catalyst surface, thereby promoting the reaction kinetics. Further analysis of Figure 5 and Figure 6 reveals that the temperature for ε_p = 0.95 is lower than that for ε_p = 0.1. This observation can be attributed to the enhanced diffusion within the catalyst bed at higher porosities, facilitating the progress of the endothermic reactions (Equations (1), (2), (3) and (5)). Additionally, the pressure near the inlet is lower for ε_p = 0.95 compared to ε_p = 0.1, which is directly related to the increased catalyst permeability at higher porosities as indicated in Table 1.

Figure 7, Figure 8, Figure 9 and Figure 10 illustrate the influence of ε_p on the distribution of molar concentrations along the reactor centerline for CH₄:CO₂ = 1.5:1 at various reaction temperature (400 ℃, 500 ℃, 600 ℃ and 700 ℃). ε_p is changed by 0.95, 0.7, 0.4 and 0.1. The results demonstrate that increasing ε_p leads to a decrease in the molar concentrations of CH₄ and CO₂, while simultaneously enhancing the concentrations of H₂, CO, H₂O and C. This enhancement is attributed to the improved mass diffusion within the porous catalyst structure, facilitating the progress of the reforming reactions. Moreover, elevating the reaction temperature promotes the formation of H₂ and CO, as evidenced by the increased molar concentrations of these species. The enhanced performance of DR, SR, RWGS and MR, as described by Equations (1) – (4), at higher reaction temperature contributes to the observed H₂ and CO production.

Figure 11 quantitatively evaluates the influence of ε_p on the distribution of molar concentration ratios for each gas along the reactor centerline under the condition of CH₄:CO₂ = 1.5:1 at 600 ℃. The analysis reveals that the impact of ε_p on the molar concentration distribution becomes more pronounced as ε_p increases, regardless of the gas species. Notably, the effect of ε_p on the products species (H₂, CO, H₂O and C) is more significant near the inlet (y = 20 m), while the influence on the reactant species (CH₄ and CO₂) is more pronounced near the outlet (y > 60 m). This observation can be attributed to the gradual consumption of CH₄ and CO₂ through the various reaction (Equations (1) – (5)) along the gas flow. The enhanced diffusivity within the porous catalyst at higher ε_p values contributes to the more significant impact on reactant concentrations near the outlet.

Figure 12 illustrates the influence of ε_p on the distribution of temperature for CH₄:CO₂ = 1.5:1 at 600 ℃. As depicted in the figure, a larger temperature drop is observed near the inlet (y = 20 m) with increasing ε_p. This phenomenon is attributed to the dominance of the endothermic reactions represented by Equations (1), (2), (2) and (5), which absorbs heat from the surrounding, leading to a localized temperature decrease.

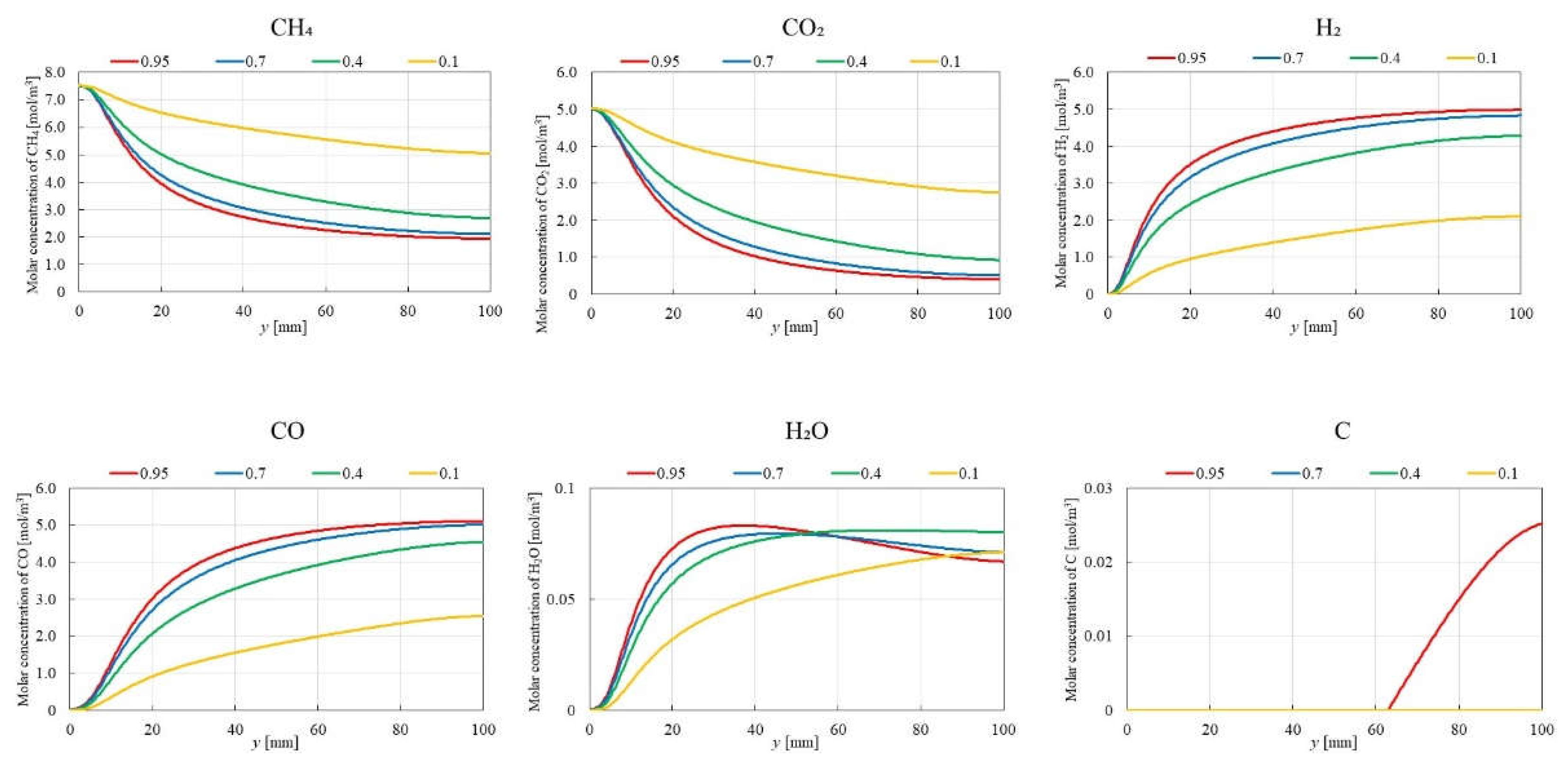
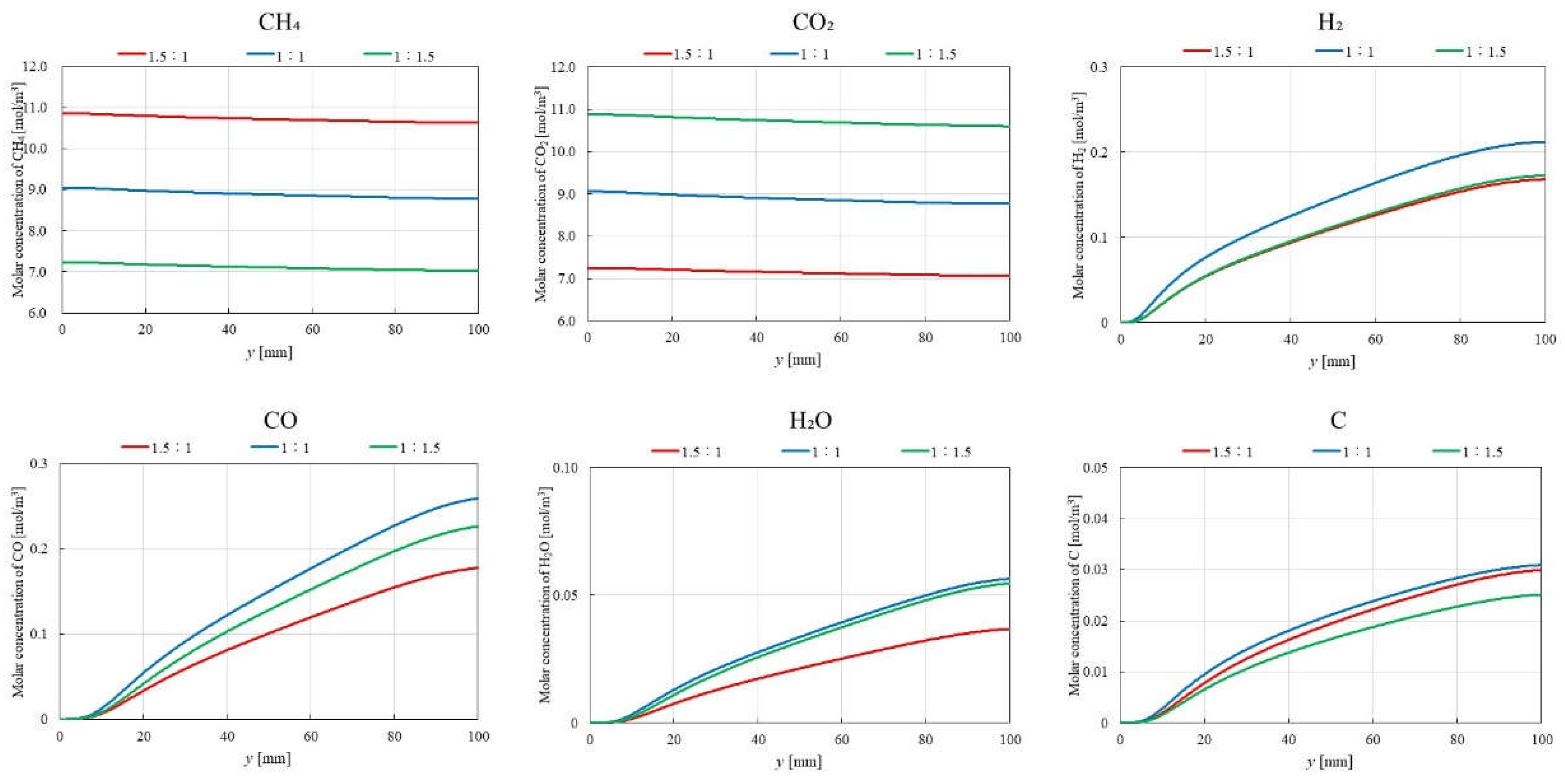
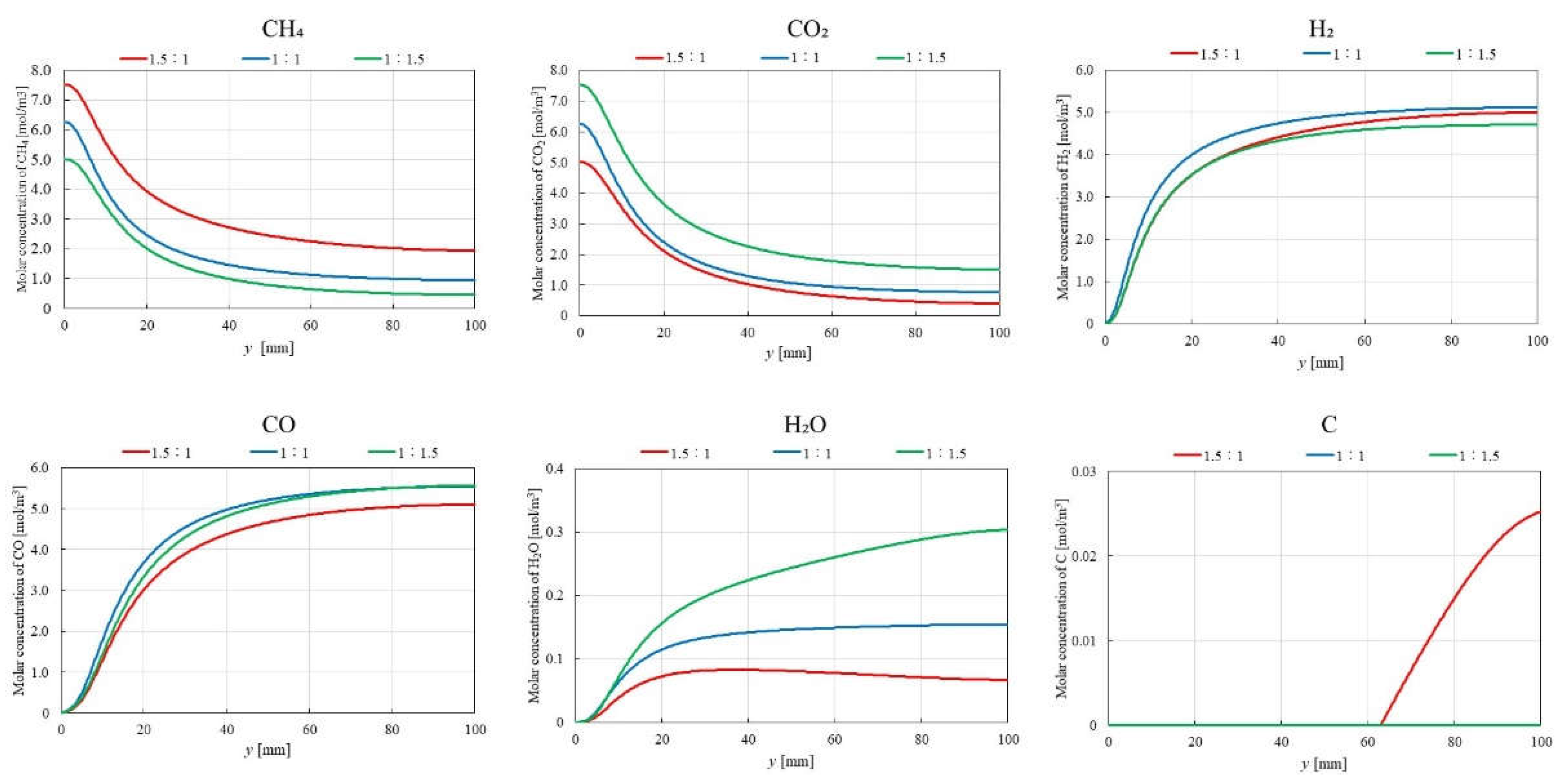
3.2. Influence of Molar Ratio of CH₄:CO₂ on BDR over Ni/Cr Catalyst

Figure 13 and Figure 14 compare the distribution of molar concentration for different molar ratios of CH₄:CO₂ at 400 ℃ and 700 ℃, respectively with ε_p = 0.95. The results indicate that the highest molar concentrations of CH₄ and CO₂ are achieved at CH₄:CO₂ = 1.5:1 and 1:1.5, respectively, regardless of the reaction temperature. This is primarily attributed to the higher inflow rates associated with these ratios. Additionally, the highest molar concentration of H₂ and CO₂ are consistently observed at CH₄:CO₂ = 1:1 irrespective of reaction temperature, aligning with the theoretical molar ratio for DR.

Regarding H₂O production, the highest molar concentration of H₂O is obtained for CH₄:CO₂ = 1:1.5 at 700 ℃. This is due to the favorable conditions for MR, which consumes CO₂ to produce H₂O. In contrast, at 400 ℃, the highest H₂O concentration occurs at CH₄:CO₂ = 1:1 and 1:1.5. Under these conditions, RWGS, which also produces H₂O, is more favored due to its exothermic nature. The lower molar concentration of H₂O at 400 ℃ for CH₄:CO₂ = 1.5:1 can be attributed to the reduced availability of CO₂ for RWGS. Moreover, the molar concentration of C is lower at 700 ℃ compared to 400 ℃, suggesting a decreased contribution of BD at higher temperatures.

3.3. Comparison of Numerical Simulation and Experimental Results for BDR

To comprehensively evaluate the performance of BDR including the other reactions, this study employs the evaluation merits defined by Equations (20) – (24). Table 2 presents a comparative analysis of CH₄ conversion, CO₂ conversion, H₂ yield, H₂ selectivity and CO selectivity for various ε_p at CH₄:CO₂ = 1.5:1 and the reaction temperature of 600 ℃.

As shown in Table 2, increasing ε_p leads to enhanced CH₄ conversion, CO₂ conversion, H₂ yield and H₂ selectivity. Conversely, CO selectivity decreases with rising ε_p. The improved performance can be attributed to enhanced mass diffusion within the porous catalyst structure. This facilitates the progress of the reaction, particularly those consuming CH₄ and CO₂ as reactants.

Table 3 presents a comparative analysis of CH₄ conversion, CO₂ conversion, H₂ yield, H₂ selectivity and CO selectivity among various reaction temperatures for CH₄:CO₂ = 1.5:1 and ε_p = 0.95. Table 4 provides a similar comparison based on experimental data for ε_p 0.95 obtained from the previous experimental study conducted by the authors using membrane reactor [18]. Due to the experimental limitations, data for 700 ℃ were not available in the experimental study [18]. The data presented in Table 4 correspond to the specific condition of 0 MPa of pressure difference between the reaction chamber and the sweep chamber, without the use of a sweep gas. This condition aligns with the numerical simulation setup, which does not consider H₂ separation.

As expected from the endothermic nature of H₂ production reactions (Equations (1), (2) and (5)), Table 3 and Table 4 reveal a positive correlation between the reaction temperature and both H₂ yield and H₂ selectivity. However, a discrepancy exists between the numerical simulation results (Table 3) and the experimental data (Table 4). While the simulation predicts the positive CO₂ conversion and high CO selectivity, the experimental results indicate the negative CO₂ conversion and a very high CO selectivity. This suggests that additional reactions beyond those included in the current model (Equations (1) – (6)) might be occurring in the experiment. To reconcile this discrepancy, a re-evaluation of the reaction scheme employed in the numerical simulations is planned for future investigations.

Furthermore, the previous experimental study by the authors utilized a membrane reactor for H₂ separation [18]. The current simulations do not account for reactions involving H₂ separation. Therefore, a future work will explore the development of numerical simulations specially tailored to BDR in a membrane reactor setting.

4. Conclusion

This study employed numerical simulations using COMSOL Multiphysics to elucidate the reaction characteristics of a Ni/Cr catalyst employed for BDR. By systematically varying reaction temperature, molar ratio of CH₄:CO₂, and ε_p, the study aimed to comprehensively understand the impact of these parameters on the BDR process. The findings of this investigation are summarized as follows:

• The results indicate that increasing ε_p leads to a decrease in the molar concentrations of CH₄ and CO₂, while simultaneously enhancing the molar concentrations of H₂, CO, H₂O and C. This enhancement is attributed to the improved mass diffusion within the porous catalyst structure, while facilitates the progress of the reforming reactions.
• A positive correlation is observed between the reaction temperature and the molar concentrations of H₂ and CO. The enhancement of H₂ and CO production is attributed to the promotion of DR, SR, RWGS and MR at elevated reaction temperatures.
• The results indicate that the influence of ε_p on the distribution of molar concentration of all gases increases with rising ε_p. Notably, the impact of ε_p on the product species (H₂, CO, H₂O and C) is more pronounced near the inlet (y = 20 m), whereas the effect of ε_p on reactant species (CH₄ and CO₂) is more significant near the outlet (y > 60 m).
• A more pronounced temperature drop near the inlet (y = 20 m) is observed with increasing ε_p. This phenomenon is attributed to the dominance of the endothermic reactions in this region, which absorb heat from the surroundings, leading to a localized temperature decrease.
• The highest molar concentration of H₂ and CO₂ are consistently obtained for CH₄:CO₂ = 1:1, regardless of the reaction temperature. This finding aligns with the theoretical stoichiometry of DR, where equal molar amounts of CH₄ and CO₂ are converted to H₂ and CO₂. Therefore, the optimal CH₄:CO₂ for maximizing product yields in BDR is 1:1.
• The highest molar concentration of H₂O is observed at 700 ℃ for CH₄:CO₂ = 1:1.5, whereas the highest molar concentration of H₂O at 400 ℃ occurred with CH₄:CO₂ = 1:1 and 1:1.5. Additionally, the molar concentration of C is found to be lower at 700 ℃ compared to 400 ℃, suggesting a reduced contribution of BD at higher reaction temperatures.
• The results indicate that increasing ε_p leads to higher CH₄ conversion, CO₂ conversion, H₂ yield and H₂ selectivity. Conversely, CO selectivity decreases with increasing ε_p. Furthermore, both numerical simulations’ and experiments’ data demonstrate a positive correlation between the reaction temperature and H₂ yield and H₂ selectivity. This enhancement is attributed to the endothermic nature of the reactions producing H₂, which are favored at higher reaction temperatures.