Submitted:
20 September 2024
Posted:
23 September 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Normalization as a Consequence of Unboundedness
2.1. Why Is Not Always Unitary?
What about Stone’s Theorem?
2.2. How to Unitarize ?
2.3. Classification of Quantum Evolution
2.3.1. The bounded self-adjoint evolution
2.3.2. The Unbounded Evolution
3. The Properties of the Pitaron
3.1. Satisfying the Initial Conditions
3.2. Solving the Schrödinger Equation
4. Examples
4.1. The Free Particle
4.2. The Coulomb Potential
4.3. The Dirac Comb Potential
5. Conclusions
- ⊛
- The currently widely used solution should be regarded as a unitary everywhere operator only when working with a self-adjoint Hamiltonian on a Hilbert space (each state has a defined norm). On infinitely dimensional Hilbert spaces Hermiticity and self-adjoint are not equivalent properties, and Hermiticity is insufficient condition to guarantee a unitary evolution.
- ⊛
- The Liouville part of the evolution is dormant for bounded Hamiltonians and become activated for unbounded Hamiltonians on a measure-0 set. It acts as a "probability conservation regulator," and produces a correction for the discontinuous evolution that is involved in the dynamics of .
- ⊛
- For the proposed solution unitary is maintained manifestly, at all orders and at any given moment of the evolution, rather than asymptotically. The ordinary probabilistic interpretation is applicable even for unbounded Hamiltonians: the modulus of transitions amplitudes are always given by a defined expressions (up to regularization).
- ⊛
- The dynamics of quantum systems with unbounded Hamiltonian is non-Markovian. The typical approach wrongly assumes that the space is suitable to study these problems. However, a more faithful approach would be to assume no knowledge of space or "indefinite norm spaces" such as Krein space, such that a becomes non-trivial operator.
- ⊛
- The solution provided will hopefully pave the way for a better understanding of various quantum systems in which unitarity is currently assumed to be broken. As such are systems with a non-Hermitian Hamiltonians, field theories on non-commutative spaces [46], field theories on factional dimensions [47], or open quantum systems [48].
- ⊛
- The reason which has initiated this study and was not mentioned is scattering amplitudes for entangled states. In this setup, unlike that where fully on-shell states are involved, strangely the JIMWLK equation [45] is no longer applicable. That happens since the normalization of the WF via simple overall factor breaks down and a convolution is required. The analysis of the time evolution of entangled states is a key for experimental verification of our proposed idea.
Data Availability Statement
Acknowledgments
Open Access:
Conflicts of Interest
Appendix A. Why May the Iterative Method Fail?
Appendix B. The Dynamics of N ^
References
- Schrödinger, "An undulatory theory of the mechanics of atoms and molecules," Physical review, 28(6), 1049. [CrossRef]
- Landau, L. D., & Lifshitz, E. M. (2013). Quantum mechanics: non-relativistic theory (Vol. 3). Elsevier.Böhm, A. (2013). Quantum mechanics: foundations and applications. Springer Science & Business Media.
- Peskin, M. E. (2018). An introduction to quantum field theory. CRC press.Kaiser, D. (2018). Lectures of Sidney Coleman on Quantum Field Theory: Foreword by David Kaiser. World Scientific Publishing. [CrossRef]
- Dyson, Freeman J. "The radiation theories of Tomonaga, Schwinger, and Feynman." Physical Review 75.3 (1949): 486.Dyson, Freeman J. "The S matrix in quantum electrodynamics." Physical Review 75.11 (1949): 1736. [CrossRef]
- Robinson, J. C. (2020). An introduction to functional analysis. Cambridge University Press.Yosida, K. (2012). Functional analysis. Springer Science & Business Media.
- Gitman, D. M., Tyutin, I. V., & Voronov, B. L. (2012). Self-adjoint extensions in quantum mechanics: general theory and applications to Schrödinger and Dirac equations with singular potentials (Vol. 62). Springer Science & Business Media.
- Gieres, F. (2000). Mathematical surprises and Dirac’s formalism in quantum mechanics. Reports on Progress in Physics, 63(12), 1893.Bonneau, G., Faraut, J., & Valent, G. (2001). Self-adjoint extensions of operators and the teaching of quantum mechanics. American Journal of physics, 69(3), 322-331. [CrossRef]
- A. Mariani and U. J. Wiese (2023). "Self-adjoint Momentum Operator for a Particle Confined in a Multi Dimensional Cavity".M. H. Al-Hashimi and U.-J. Wiese (2021). "Alternative momentum concept for a quantum mechanical particle in a box," Phys. Rev. Research, vol. 3, p. L042008.
- Apelian, C., & Surace, S. (2009). Real and complex analysis. CRC press.Simon, B. (2015). Real analysis. American Mathematical Soc..
- Teschl, G. Mathematical methods in quantum mechanics. Vol. 157. American Mathematical Soc., 2014.Dimock, J. Quantum mechanics and quantum field theory: a mathematical primer. Cambridge University Press, 2011.
- Schmüdgen, K. Unbounded self-adjoint operators on Hilbert space. Vol. 265. Springer Science Business Media, 2012.Goldberg, S. (2006). Unbounded linear operators: Theory and applications. Courier Corporation.
- Hall, B. C. (2013). Quantum theory for mathematicians. springer publication..Neumann, J. V. (1932). Uber einen satz von herrn mh stone. Annals of Mathematics, 567-573.
- Hall, B. C., & Hall, B. C. (2013). Lie groups, Lie algebras, and representations (pp. 333-366). Springer New York.Lipschutz, S., & Lipson, M. L. (2018). Schaum’s Outline of Linear Algebra. McGraw-Hill Education.
- Lindelöf, E. (1894). "Sur l’application de la méthode des approximations successives aux équations différentielles ordinaires du premier ordre". Comptes rendus hebdomadaires des séances de l’Académie des sciences. 118: 454–7.
- Seifert, C., Trostorff, S., & Waurick, M. (2022). Evolutionary Equations: Picard’s Theorem for Partial Differential Equations, and Applications (p. 317). Springer Nature. [CrossRef]
- Lax, P. D., & Richtmyer, R. D. (1956). Survey of the stability of linear finite difference equations. Communications on pure and applied mathematics, 9(2), 267-293. [CrossRef]
- Byron, Frederick W., and Robert W. Fuller. Mathematics of classical and quantum physics. Courier Corporation, 2012.
- Lighthill, M.J. An Introduction to Fourier Analysis and Generalised FunctionsJ C. Ferreira, R. F. Hoskins, J. Sousa-Pinto, Introduction to the Theory of Distributions.
- Schwartz, L. (1954). Sur l’impossibilité de la multiplication des distributions. CR Acad. Sci. Paris, 239(847-848), 6.
- Kanwal, R. P. (2004). Generalized functions: theory and applications. Springer Science & Business Media.Johnson, S. G. “When functions have no value(s)”.
- Bilenky, S. M. (2013). Introduction to Feynman Diagrams: International Series of Monographs in Natural Philosophy (Vol. 65). Elsevier.
- Stroock, D. W. (2013). An introduction to Markov processes (Vol. 230). Springer Science & Business Media.Dynkin, E. B. (2012). Theory of Markov processes. Courier Corporation.
- Trotter, H. F. (1958). Approximation of semi-groups of operators.
- Moretti, V. (2017). Spectral theory and quantum mechanics. UNITEXT, Italy: Springer International Publishing AG.Prugovecki, E. (1982). Quantum mechanics in Hilbert space. Academic Press.
- S. Albeverio, F. Gesztesy, R. Hoegh-Krohn, H. Holden, Solvable Models in Quantum Mechanics,2012.
- Flugge, S. (1999). Practical quantum mechanics (Vol. 177). Springer Science & Business Media.Galitskii, V. M., Karnakov, B., Galitski, V., & Kogan, V. I. (2013). Exploring quantum mechanics: A collection of 700+ solved problems for students, lecturers, and researchers. Oxford University Press, USA.
- Prugovecki, E. (1982). Quantum mechanics in Hilbert space. Academic Press.Gallone, F. (2014). Hilbert Space and Quantum Mechanics. World Scientific Publishing Company.
- Berezanskiĭ, I. M. (1968). Expansions in eigenfunctions of selfadjoint operators (Vol. 17). American Mathematical Soc..
- Gelfand, I. M., Graev, M. I., & Vilenkin, N. Y. (1962). Generalized Functions, Vol. 1-5, Gos. Izd. Fiz. Mat. Lit., Moscow.De la Madrid, R. (2005). The role of the rigged Hilbert space in quantum mechanics. European journal of physics, 26(2), 287. [CrossRef]
- Bender, C. M. (2007). Making sense of non-Hermitian Hamiltonians. Reports on Progress in Physics, 70(6), 947. [CrossRef]
- Moiseyev, N. (2011). Non-Hermitian quantum mechanics. Cambridge University Press.Bountis, T., & Skokos, H. (2012). Complex hamiltonian dynamics (Vol. 10). Springer Science & Business Media.
- Mostafazadeh, A. (2010). Pseudo-Hermitian representation of quantum mechanics. International Journal of Geometric Methods in Modern Physics, 7(07), 1191-1306.Ashida, Y., Gong, Z., & Ueda, M. (2020). Non-hermitian physics. Advances in Physics, 69(3), 249-435.
- N. N. Bogolubov, and N. N. Bogolubov Jr. "Introduction to quantum statistical mechanics," World Scientific Publishing Company, 2009.
- J. von Neumann, "Wahrscheinlichkeitstheoretischer Aufbau der Quantenmechanik," Nachr. Ges. Wiss. Göttingen, 1, 245-272, 1927.
- Sylvester, J. (1884). "Sur l’equations en matrices px = xq". C. R. Acad. Sci. Paris. 99 (2): 67–71, 115–116.Bartels, R. H.; Stewart, G. W. (1972). "Solution of the matrix equation AX + XB=C". Comm. ACM. 15 (9): 820–826. doi:10.1145/361573.361582. S2CID 12957010.
- Parks, P. C. (1992). AM Lyapunov’s stability theory—100 years on. IMA journal of Mathematical Control and Information, 9(4), 275-303.
- Hannesdottir, H. S., Mizera, S. (2023). What is the iε for the S-matrix?. Springer.Collins, J. C. (1984). Renormalization: an introduction to renormalization, the renormalization group and the operator-product expansion. Cambridge university press.
- Halmos, P. R. (2013). Measure theory (Vol. 18). Springer.Tao, T. (Ed.). (2011). An introduction to measure theory (Vol. 126). American Mathematical Soc..
- Dumitru, Adrian, and Risto Paatelainen. "Sub-femtometer scale color charge fluctuations in a proton made of three quarks and a gluon." Physical Review D 103.3 (2021): 034026.
- M. Born: Zur Quantenmechanik der Stoßvorg¨ange. Z. f. Phys. 37, 863–867 (1926). M. Born: Quantenmechanik der Stoßvorg¨ange. Z. f. Phys. 38, 803–827 (1926).
- Feynman, R. P., Hibbs, A. R., & Styer, D. F. (2010). Quantum mechanics and path integrals. Courier Corporation.Feynman, R. P. (1948). Space-time approach to non-relativistic quantum mechanics. Reviews of modern physics, 20(2), 367. [CrossRef]
- Z. Chen, and A. H. Mueller. "The dipole picture of high energy scattering, the BFKL equation and many gluon compound states," Nuclear Physics B 451.3 (1995): 579-604.C. Marquet, "Forward inclusive dijet production and azimuthal correlations in pA collisions." Nuclear Physics A 796.1-4 (2007): 41-60. [CrossRef]
- Kovner, A., & Wiedemann, U. A. (2001). Eikonal evolution and gluon radiation. Physical Review D, 64(11), 114002. [CrossRef]
- E. Iancu, Y. Mulian. "Forward trijet production in proton–nucleus collisions." Nuclear Physics A 985 (2019): 66-127.E. Iancu, and Y. Mulian. "Forward dijets in proton-nucleus collisions at next-to-leading order: the real corrections." Journal of High Energy Physics 2021.3 (2021): 1-67.
- M. Lublinsky, and Y. Mulian. "High Energy QCD at NLO: from light-cone wave function to JIMWLK evolution." Journal of High Energy Physics 2017.5 (2017): 1-80. [CrossRef]
- Gomis, Jaume, and Thomas Mehen. "Space–time noncommutative field theories and unitarity." Nuclear Physics B 591.1-2 (2000): 265-276. Bahns, D. (2003). Unitary quantum field theory on the noncommutative Minkowski space. Fortschritte der Physik: Progress of Physics, 51(7-8), 658-663. Morita, K., Okumura, Y., & Umezawa, E. (2003). Lorentz invariance and the unitarity problem in non-commutative field theory. Progress of theoretical physics, 110(5), 989-1001. [CrossRef]
- Hogervorst, M., Rychkov, S., & van Rees, B. C. (2016). Unitarity violation at the Wilson-Fisher fixed point in 4-ϵ dimensions. Physical Review D, 93(12), 125025. Jin, Q., Ren, K., Yang, G., & Yu, R. (2023). Is Yang-Mills Theory Unitary in Fractional Spacetime Dimensions?. arXiv preprint arXiv:2301.01786. [CrossRef]
- Rivas, A., & Huelga, S. F. (2012). Open quantum systems (Vol. 10, pp. 978-3). Berlin: Springer.Breuer, H. P., & Petruccione, F. (2002). The theory of open quantum systems. Oxford University Press, USA.
- Higham, N. J. (2008). Functions of matrices: theory and computation. Society for Industrial and Applied Mathematics.Horn, R. A., & Johnson, C. R. (2012). Matrix analysis. Cambridge university press.
- R. Salem, "On some singular monotonic functions which are strictly increasing." Transactions of the American Mathematical Society 53.3 (1943): 427-439.Feder, J., & Feder, J. (1988). Cantor Sets. Fractals, 62-65.
- Hardy, G. H. (1901). The Elementary Theory of Cauchy’s Principal Values. Proceedings of the London Mathematical Society, 1(1), 16-40. [CrossRef]
- Estrada, R., & Kanwal, R. P. (2000). Singular integral equations. Springer Science & Business Media.Mandal, B. N., & Chakrabarti, A. (2016). Applied singular integral equations. CRC press.
- Sebestyén, Zoltán, and Zsigmond Tarcsay. "Adjoint of sums and products of operators in Hilbert spaces." Acta Scientiarum Mathematicarum 82 (2016): 175-191. [CrossRef]
| 1 | A linear operator is called bounded if and only if for any where the notation denotes the norm of on the space [5]. |
| 2 | An operator on the Hilbert space is called self-adjoint if it is operatorically identical to its adjoint, . The equivalence between two operators implies two conditions: for , and additionally the domains are identical,
|
| 3 | The action of this operator, known as the time-ordering operator, is defined by , where is the Heaviside theta function. |
| 4 | We denote the exact solution by from the word pitaron which means solution in Hebrew. |
| 5 | The definition of this component is later provided in Equation (53). |
| 6 | Note that an operator is called a square root of operator if it satisfies . |
| 7 | Therefore, it is clear that the original terms in the perturbative series involving integrations in the iterative form , and not the productive form . |
| 8 | The integration over an operator is defined as where the inner integration includes any . Note that exchanging of the ordering of integrations, , is generally permitted only if is a bounded operator. |
| 9 | At first sight, the solution (9) seems to satisfy the Schrodinger equation. Indeed, by applying the derivative term-by-term based on , it seems that we arrive at
|
| 10 | Essentially, we assume that both and . These non-trivial simplifications can only be guaranteed for bounded self-adjoint Hamiltonians integrted over a proper domain. |
| 11 | An additional operation that is not listed is the Fubini theorem, as mentioned in (14). However, it can be shown that this operation is redundant in terms of the mathematical requirements, as its validity is ensured if (17) is satisfied. In any case, it is clear that applying simplification (14) is not universal, and cannot be guaranteed to yield a correct transition if the integrand is conditionally convergent. |
| 12 | Contrary to the case of bounded operators, unbounded operators on a given space do not form an algebra, nor even a complete linear space [5]. Each unbounded operator is defined on its own domain, so that if and are two unbounded operators defined on the domains and respectively, then the domain of operator is . Note that two operators which act in the same way are to be considered as different if they are not defined on the same subspace of Hilbert space. According to Hellinger-Toeplitz theorem [5], if a self-adjoint operator is well defined on the entire Hilbert space it has to be bounded. |
| 13 | It is worth mentioning that one can ’save additivity’ by replacing the standard Riemann integral with a modified definition of integral, but obviously, this will not cure the fundamental problem, but rather just hide it inside the integrals definitions. |
| 14 | Otherwise, by tracing both sides of the relation, an illogical result is obtained [7]. |
| 15 | Similarly, . |
| 16 | The approximation is used. |
| 17 | The notation is introduced. Notice the difference with the definition of the norm: the outcome of is another operator, while the operation includes an additional tracing operation, and therefore, leaves us with just a number. |
| 18 | More generally, such a choice of Hamiltonian can be expressed by using a complete orthonormal Hilbert space , , where , with for any value of t. |
| 19 | Stating that if , then f is Riemann integrable if and only if f is bounded and the set of discontinuities of f has measure 0. |
| 20 | The notation of a broken arrow ↛ signifies here an invalid transition |
| 21 | For example, the value of is undefined. |
| 22 | Note that differentiation and conjugation are not commutative operations, , with equivalence only when using a self-adjoint Hamiltonian. |
| 23 | The simplification is used. |
| 24 | In order for operators and to represent an eligible decomposition of a diagonalizible Hamiltonian, they need to share a common set of eigenvectors. In that case they are simultaneously diagonalizable, which implies the relations . |
| 25 | In that case only the leading order term dominates the expansion of , . |
| 26 | So that, (A1) is essentially replaced by solving the system , that leads to . |
| 27 | Generally, if the signs of a and x are unknown, . |
| 28 | These are typically of the form with . For example, as discussed in [20], if the obtained result is given by for which approximate expressions cannot be found. |
| 29 | These are equtions of the type where is a self-adjoint operator. |
| 30 | By using the identity along with the observation that since the operator is fully expressible based on the operator they shares a common basis and domain,
|
| 31 | More explicitly, . |
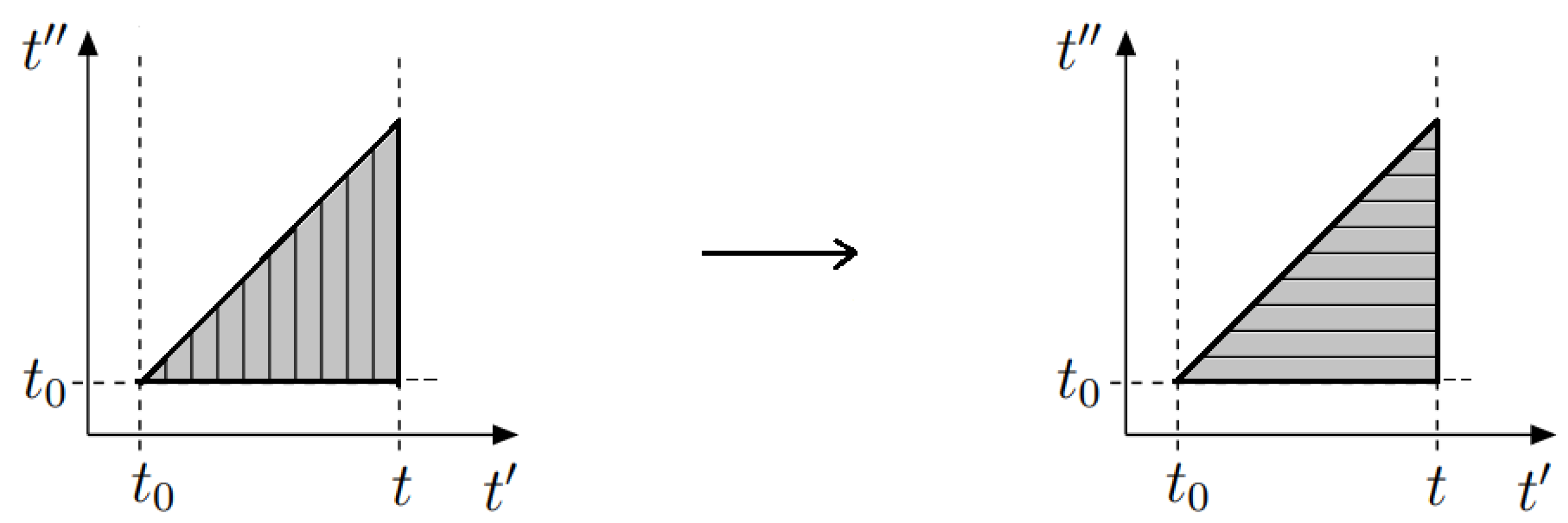
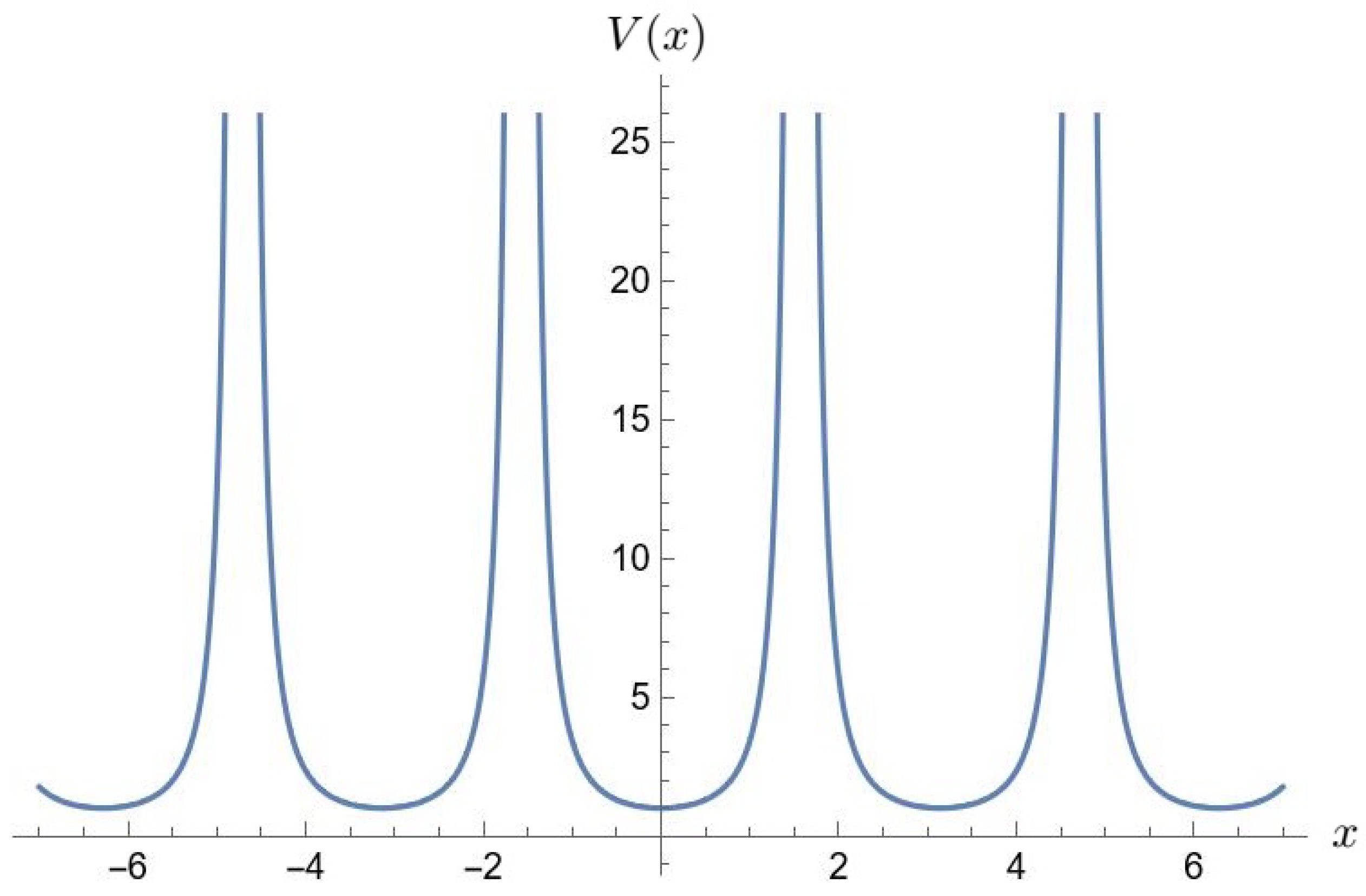
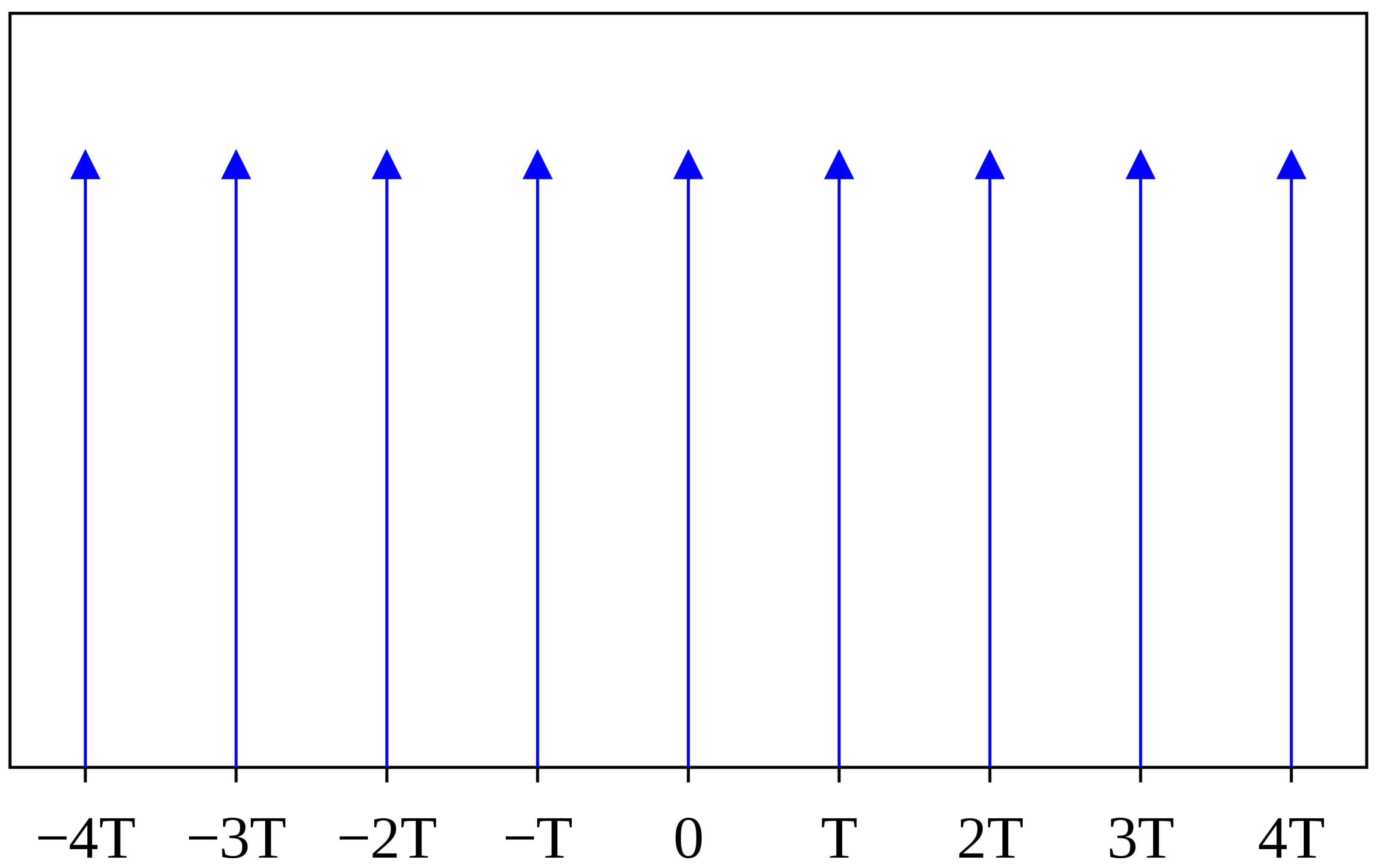
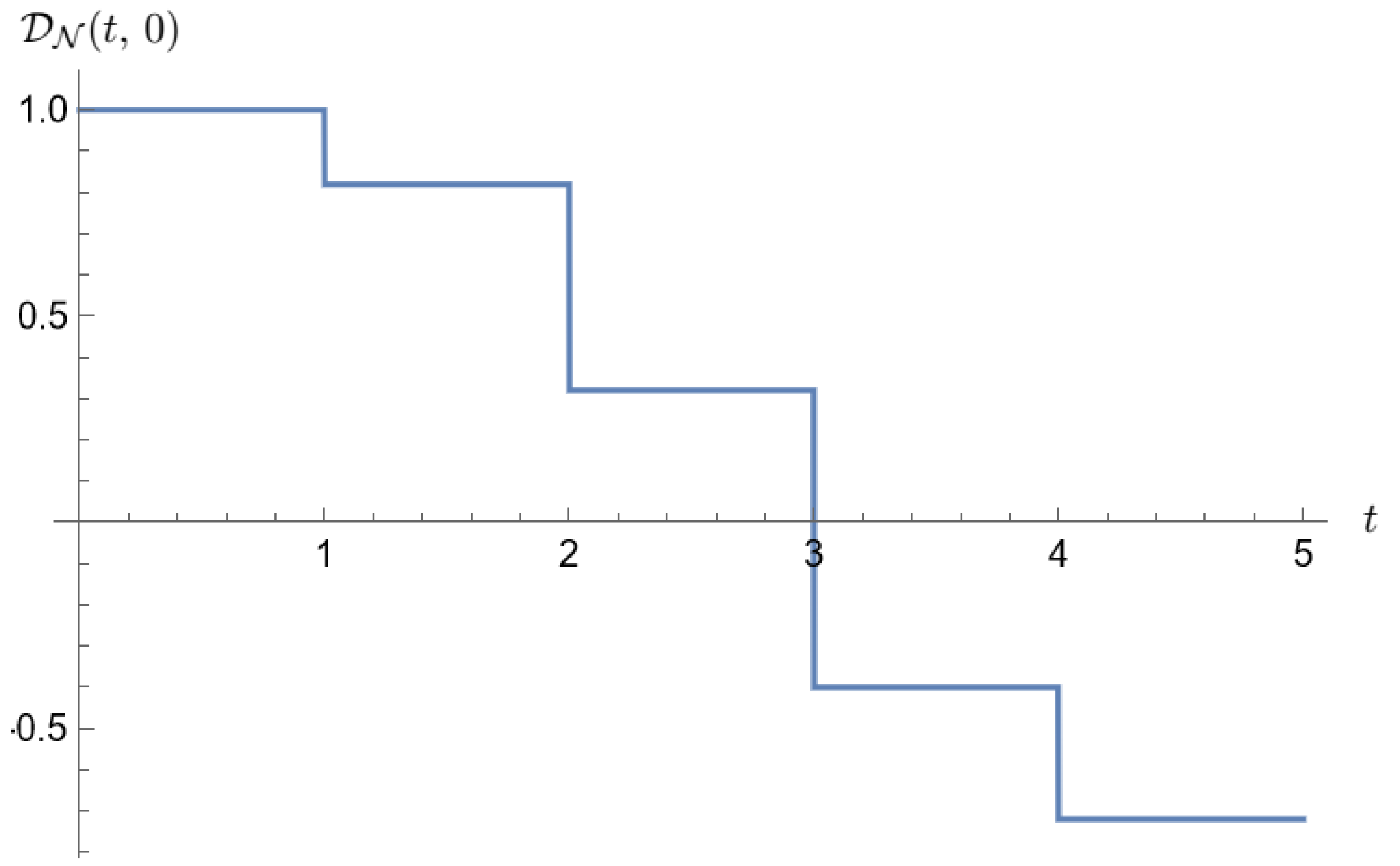
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



