Closed Form Solution to the Hubble Tension Based on Rh = Ct Cosmology

1. The Haug-Tatum Cosmological Model

The Haug and Tatum [1,2] cosmological model that we will discuss is unique in that it provides an exact mathematical relation between the CMB temperature, the Hubble constant and the cosmological red-shift. The Haug-Tatum cosmological model has developed over time in multiple stages. It is consistent with the $R_h=ct$ principle, which describes a universe expanding at the speed of light without accelerated expansion. There are several $R_h=ct$-type cosmological models, and these models are still actively discussed in recent literature, see for example [3,4,5,6]. Melia [7] has recently demonstrated that $R_h=ct$ cosmology seems more in line with recent observations from the James Webb Space Telescope than the $\Lambda$-CDM model. The question of which cosmological model best fits different observed properties of the universe will undoubtedly be an ongoing discussion in the years to come. This paper offers additional evidence in favor of $R_h=ct$ cosmology, as it seems that even with a closed-form solution, we can resolve the Hubble tension within such a cosmological model.

In 2015, Tatum et al. [8] presented the following formula for the Cosmic Microwave Background (CMB) temperature, which was later formally derived based on the Stefan-Boltzmann law [9,10] by Haug and Wojnow [11,12]:

$$T_{CMB,0}={\displaystyle \frac{\hslash c^3}{k_{b}8\pi G\sqrt{M_c{m}_p}}}={\displaystyle \frac{\hslash c}{k_{b}4\pi \sqrt{R_{H}2l_p}}}$$

(1)

It has also recently been derived using a geometric mean approach, see [13]. Additionally, Haug and Tatum [1] have demonstrated that to be consistent with the observed relation $T_t=T_0(1+z)$, the predicted redshift must be given by:

$$z=\sqrt{{\displaystyle \frac{R_h}{R_t}}}-1$$

(2)

Haug and Tatum has also show that the distance relation must be:

$$R_H-R_t={\displaystyle \frac{c}{H_0}}\left(1-{\displaystyle \frac{1}{{(1+z)}^2}}\right)$$

(3)

Solving for $H_0$ gives:

$$H_0={\displaystyle \frac{c\left(1-\frac{1}{{(1+z)}^2}\right)}{D}}$$

(4)

Here, $D=R_H-R_t$ represents the distance between us and the object emitting the observed photons. Haug and Tatum then show that the first term of the Taylor expansion yields:

$$H_0\approx {\displaystyle \frac{2zc}{D}}.$$

(5)

and since $D=2d$, where d is the distance in the $\Lambda$-CDM model one get the standard relation $H_0\approx {\displaystyle \frac{2zc}{D}}={\displaystyle \frac{zc}{d}}$ for $z\ll 1$.

Furthermore, Haug and Tatum demonstrate that the predicted redshift must satisfy:

$$z_{pre}=\sqrt{{\displaystyle \frac{R_h}{R_t}}}-1=\sqrt{{\displaystyle \frac{\frac{c}{H_0}}{{\left(\frac{\hslash c}{T_0(1+z_{obs,i})k_{b}4\pi }\right)}^2\frac{1}{2l_p}}}}-1.$$

(6)

They then use a smart trial-and-error algorithm, such as the Newton-Raphson method or the bisection method, to find the value of $H_0$ that minimizes the sum of the prediction errors ${\sum }_{i=1}^n{\displaystyle \frac{z_{pre,i}-z_{obs,i}}{z_{obs,i}}}$. They demonstrate that this approach leads to a single $H_0$ value that perfectly matches the model with the full observed distance ladder, something that seems to solve the Hubble tension.

However, here we simply solve equation (2) for $H_0$, which yields:

$$H_0=T_0^2{\displaystyle \frac{k_b^{2}32{\pi }^2{l}_p}{{\hslash }^{2}c}}{\displaystyle \frac{{(1+z_{obs,i})}^2}{{(1+z_{pre,i})}^2}}$$

(7)

In the case where the predicted redshift $z_{pre,i}$ is exactly equal to the observed redshift $z_{obs,i}$, we must have ${\displaystyle \frac{{(1+z_{obs,i})}^2}{{(1+z_{pre,i})}^2}}=1$. Substituting ${\displaystyle \frac{{(1+z_{obs,i})}^2}{{(1+z_{pre,i})}^2}}=1$ back into equation (7) gives:

$$H_0=T_0^2{\displaystyle \frac{k_b^{2}32{\pi }^2{l}_p}{{\hslash }^{2}c}}=T_0^2\mathsf{\mho }$$

(8)

The last part, the Greek upsilon: $\mathsf{\mho }={\displaystyle \frac{k_b^{2}32{\pi }^2{l}_p}{{\hslash }^{2}c}}={\displaystyle \frac{k_b^{2}32{\pi }^2\sqrt{G}}{{\hslash }^{3/2}{c}^{5/2}}}$, is a composite constant made up of well-known constants (which we [14,15] have coined $\mathsf{\mho }$). This is the same formula as given by [14], but here we have just demonstrated that this formula is strictly valid only when the predicted redshift exactly matches the observed redshift, or as we soon will see we can use equation (7) to match the full distance ladder of observed supernova redshifts by simply finding this one $H_0$ value directly from the current measured CMB temperature.

This means that we only need to know $T_0$ and this constant to closely match all observed cosmological redshifts. The reason we say "close to perfect" rather than "perfect" is due to small measurement errors in both the measured CMB temperature and in G, and that is the only uncertainty in this method. The Boltzmann constant, the speed of light, and the reduced Planck constant have no uncertainty, as they have been exactly defined since the 2019 NIST CODATA standard.

2. Predictions Relative to the Observations Using the Full Distance Ladder of the Union 2 Database

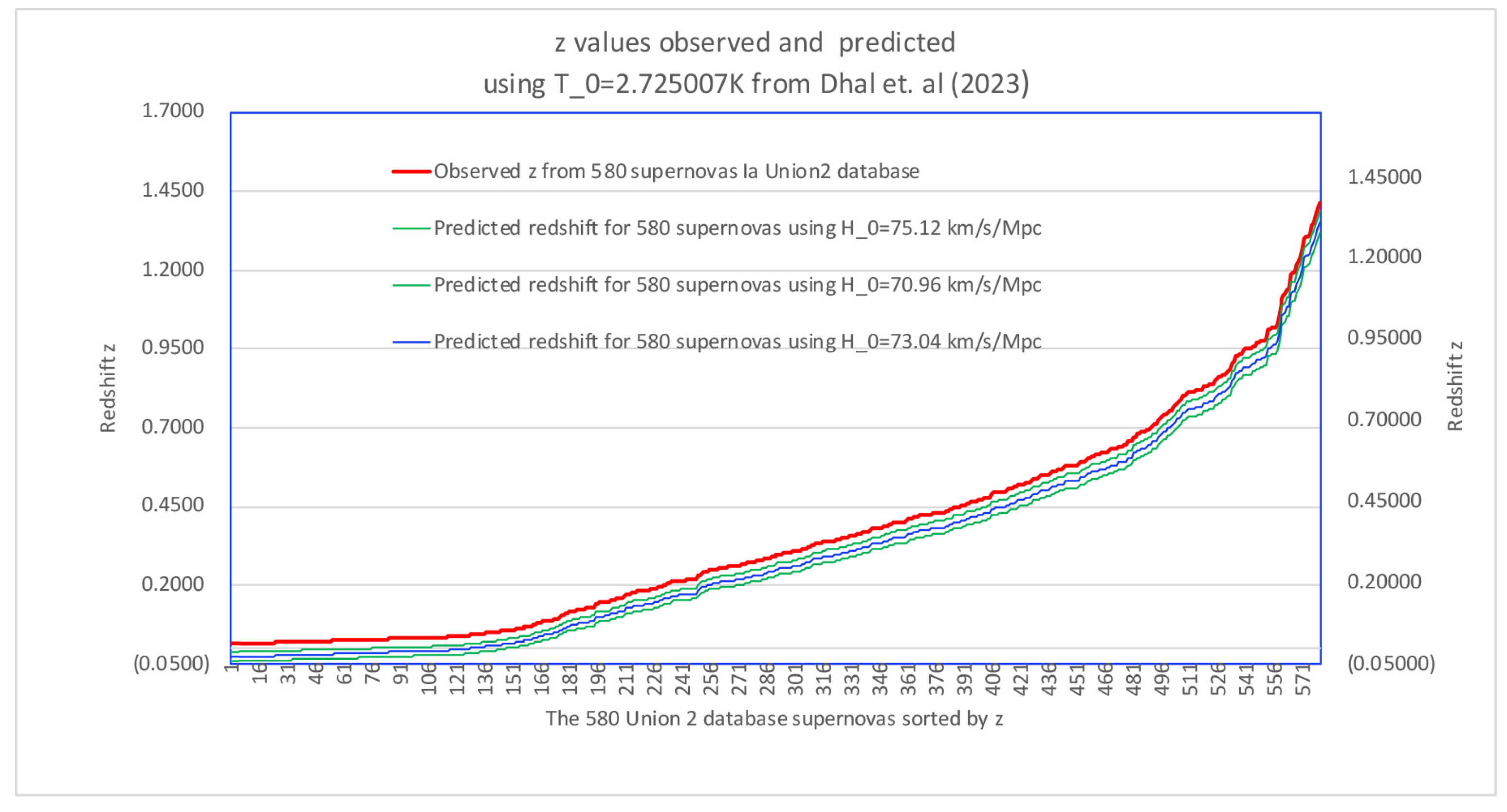
Here, we will see if our model can match all the observed cosmological redshifts by simply determining the $H_0$ constant from equation (8). However to demonstrate the superiority of equation (8), we will first instead use the predicted value for $H_0$ by for example Riess et al. [16] of $H_0=73.04\pm 1.04$ km/s/Mpc. We plot the Riess et al. value, accounting for 2 standard deviations (STD), and from this, we get Figure 1. The blue line represents the predicted redshift from $H_0=73.04$ km/s/Mpc, while the green lines represent the 2 STD confidence interval, i.e., $\pm 2\times 1.04$ km/s/Mpc. We can see that even the 95% confidence interval falls outside the observations, meaning that any $H_0$ value within this interval does not come close to matching the observed redshifts in our cosmological model.

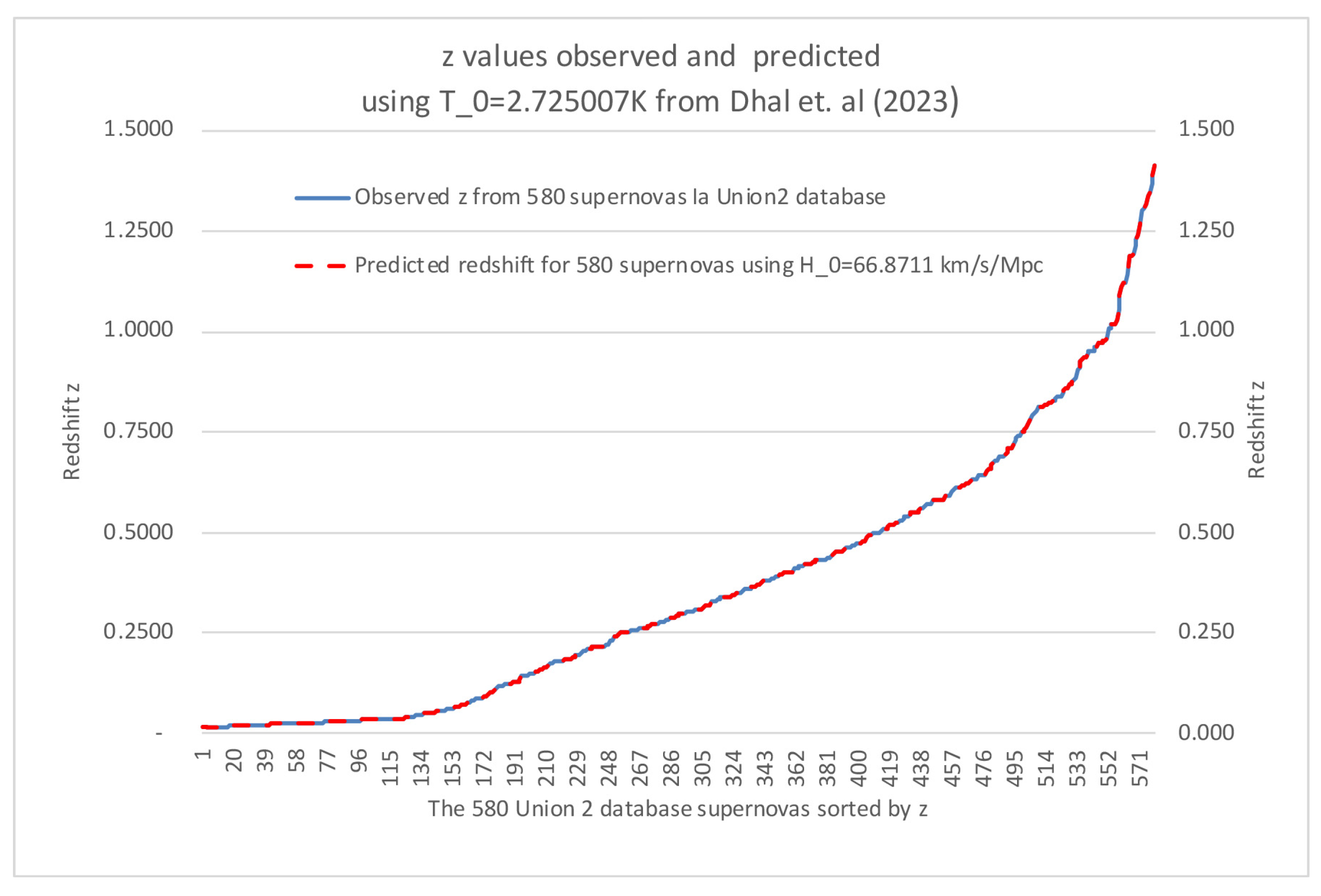
Figure 2 demonstrates the results we get when we instead calculate $H_0$ based on equation (8) when using the Dhal et al [17] measured CMB value of $T_0=2.725007\pm 0.000024K$. According to our theory, this should provide a perfect match between the observed and predicted values, and as we can see, the observed and predicted values lie on top of each other. The confidence interval is now so narrow that even if we plotted it, it would appear to overlap with the observed values.

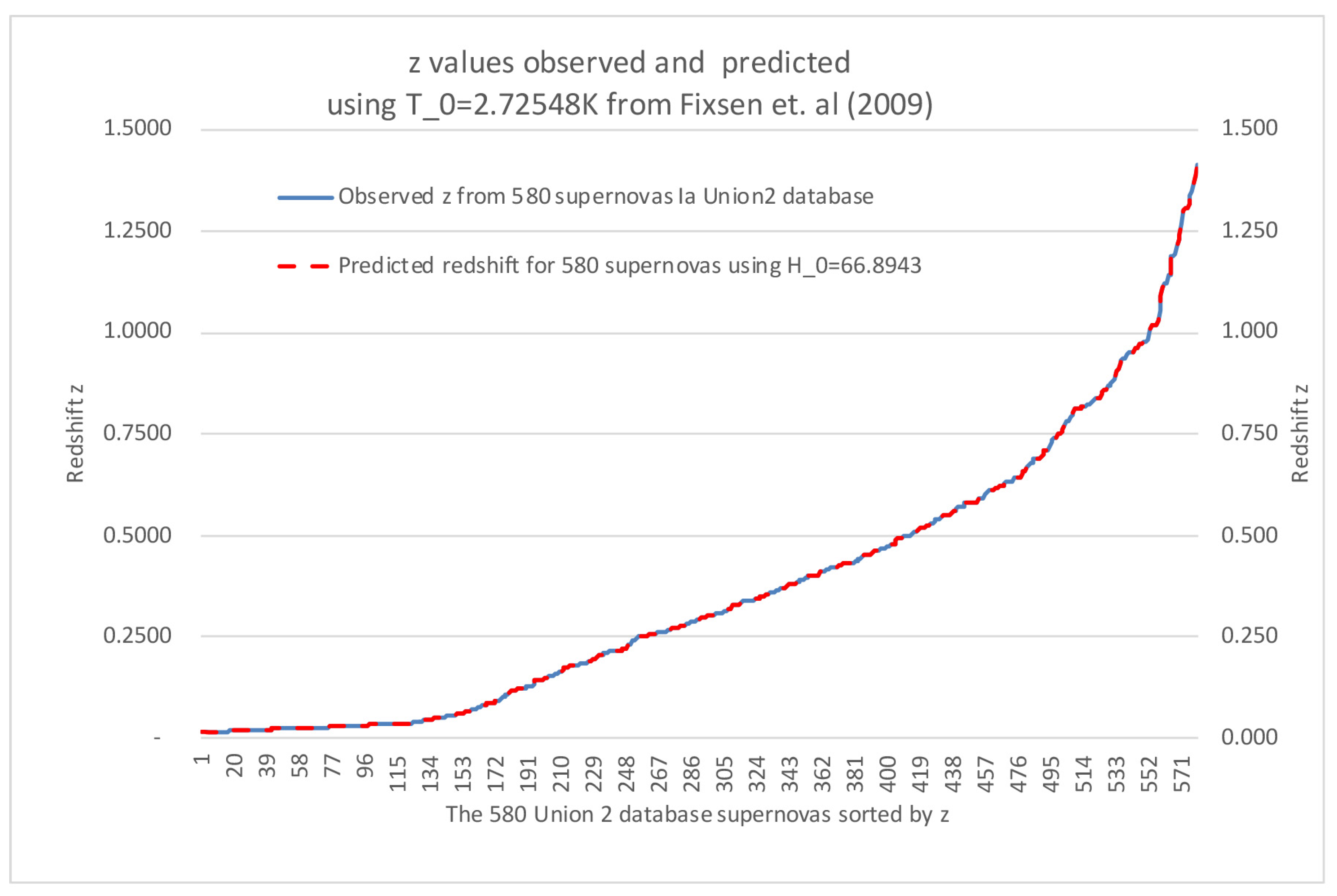
Figure 3 demonstrate the results we get when we calculate $H_0$ based on equation (8) when the measured CMB value of Fixsen [18]: $T_0=2.72548\pm 0.00057K$, this lead to a basically perfect match between predicted and observed SN Ia redshifts with a predicted $H_0=66.8943\pm 0.0287 km/s/Mpc$

3. Conclusion

Haug and Tatum have outlined a way to solve the Hubble tension inside $R_h=ct$ cosmology based on new exact relations between the CMB temperature the Hubble constant and redshift, they however use a numerical search algorithm to do so. Even if their method is intuitive and powerful we here demonstrate one can simply solve one of their equations and further based on logic get to the one single $H_0$ value that make their model matching all observed SN Ia. In other words this leads to a closed form solution of the Hubble tension in side $R_h=ct$ cosmology. We get a $H_0=66.8712\pm 0.0019 km/s/Mpc$ when relying on the very precise Dhal et al measured CMB value matching leading to matching all the observed SN Ia redshifts across the full distance ladder in the Union2 database. This is the same value Haug and Tatum got from their numerical search algorithm solution when solving the Hubble tension. It is basically the same solution, one is using numerical search algorithm while the later used closed form solution. The closed form solution is naturally more elegant as no numerical search rutine with many calculations are needed to find the $H_0$ that matches all the supernovas.