Adaptive Sliding Mode Control for Trajectory Tracking of Quadrotor UAV under Input Saturation and Disturbances

1. Introduction

In recent years, the UAVs has gained widespread applications in areas such as aerial photography [1], emergency communication [2], and agricultural irrigation [3]. Its popularity arises from its small size, affordability, and simple structure. Nevertheless, the demanding task scenarios faced by these quadrotor UAVs improved performance against internal and external disturbances. Moreover, as an underactuated and nonlinear coupled system, traditional control methods face challenges in achieving high-precision control amidst disturbances. Consequently, there is a critical emphasis on developing anti-disturbance methods in control theory and application.

In parallel, the sliding mode control method, known for its robust characteristics, insensitivity to disturbances, and rapid response, offers another avenue for achieving precise control in UAVs [4]. Recent studies, such as [5,6,7,8,9], have explored and demonstrated the effectiveness of sliding mode control algorithms in addressing trajectory tracking challenges and improving the overall robustness of quadrotor UAVs. This control method facilitates system movement along the designated sliding mode surface, with an adjustable convergence rate by selecting the sliding mode surface parameter matrix. Owing to the model’s lower precision, this control method has been user-friendly and widely applied in UAV control [10]. A novel fractional-order non-singular fast terminal sliding mode surface is proposed In [11], specifically designed for precise quadrotor trajectory tracking. Through simulations, the approach demonstrates its enhanced performance in suppressing external disturbances, significantly improving the quadrotor’s stability during flight. Additionally, the method ensures accurate trajectory following, even in the presence of uncertainties, making it an effective solution for high-precision applications. In [12], an iterative learning sliding mode control algorithm was developed, with experimental results confirming its effectiveness in achieving precise trajectory tracking while maintaining robustness against disturbances.

The disturbance observer technique, first introduced in 1987 [13], has proven to be an effective method for suppressing external disturbances in various control systems. Its design involves constructing a dynamic system that estimates unknown disturbances based on known system parameters and behavior. By accurately estimating these disturbances in real-time, the observer allows for the design of a robust compensation term that actively counteracts their effects. This proactive disturbance rejection mechanism greatly enhances the overall performance and stability of control systems, making the technique particularly valuable in environments with significant external disruptions. Due to its clear physical significance and simple design structure, combining disturbance observers with other control methods has become a crucial approach for addressing system uncertainty issues. A comprehensive method and fundamental framework for handling disturbance in nonlinear systems using a disturbance observer were introduced in [14], and the approach extends the traditional disturbance observer-based control strategy, which is typically applied to linear systems, to more complex nonlinear systems. In [15], a composite controller that integrates a disturbance observer with the backstepping method, specifically designed for nonlinear systems subjected to bounded disturbances was developed, enhancing overall system performance and disturbance rejection. An anti-disturbance control strategy was implemented in [16] for an indoor quadrotor UAV system, incorporating a disturbance observer to manage and counteract external disturbances, effectively mitigating the effects of modeling errors and external disturbances to improve system stability and accuracy.

In many cases, the output of an actuator cannot consistently increase due to its physical constraints, resulting in an input saturation problem. Prolonged influence of input saturation accelerates the damage to the actuator, necessitating consideration of this factor in controller design. Currently, there are three primary approaches to address the input saturation problem: The first approach involves using a small gain controller to reduce the amplitude of control inputs, effectively preventing the system from reaching saturation limits [17]. The second approach approximates the nonlinear behavior of input saturation with a smooth function, allowing for a more continuous and manageable control response [18]. Finally, a dynamic auxiliary system can be designed to compensate for saturation effects, actively adjusting the control signals to maintain performance even when inputs are constrained [19]. Based on the boundedness of the hyperbolic tangent function, a quasi-proportion-integral-derivative (PID) control strategy was proposed in [17], ensuring that the sum of the control gains is kept below the saturation upper limit to avoid input saturation. However, determining appropriate control gains remains a highly challenging task. An Nussbaum function was incorporated into the design process of the backstepping method [18], addressing input saturation and avoiding potential singularities during attitude stabilization. Nonetheless, the physical structure and design process of this controller are exceedingly complex. An anti-saturation scheme employing a dynamic auxiliary system that effectively mitigates the impact of input saturation within finite time, ensuring system convergence and stability, was designed in [19]. Moreover, the dynamic auxiliary system does not compromise controller performance when input saturation is absent.

During the flight of quadrotor UAVs, challenges arise not only from wind disturbances and mismatched disturbances but also from model uncertainties, posing a potential threat to overall system stability. Utilizing adaptive control laws offers a solution by approximating unknown upper bounds, enabling compensation for model parameter uncertainties within the controlled system. In [20], an adaptive sliding mode control method that integrated smooth and continuous integrators was explored. This method was specifically crafted for tracking control amid uncertainties and disturbances in aircraft. In [21], a control approach was implemented to enhance the resistance of quadrotor UAVs to wind disturbances. This study implements an adaptive fuzzy PID control system aimed at improving both the stability and tracking performance of the quadrotor UAV. In summary, the adaptive rate provides a promising avenue for UAVs to address model uncertainties.

Building upon the preceding discussions on control methodologies, the present study investigates the trajectory tracking challenges faced by a quadrotor UAV amid input saturation, external disturbances and parametric uncertainty. The key contributions of this article are as follows.

• An adaptive sliding mode trajectory tracking controller is proposed for the uncertain QUAV, ensuring globally uniformly ultimate boundedness(UUB) despite disturbances, input saturation, and parameter uncertainties.
• To address parameter uncertainties, adaptive laws are developed to estimate the quadrotor’s mass and unknown constants related to the moment of inertia. These adaptive laws are integrated into the control scheme, allowing the controller to compensate for external disturbances and input saturation without requiring prior knowledge of the quadrotor’s physical properties.
• The method also incorporates disturbance observers and auxiliary systems, designed to function without prior knowledge of the quadrotor’s mass and moments of inertia. This enables the system to effectively handle unknown disturbances and input saturation, ensuring robust adaptive path tracking performance under uncertain conditions.

The paper is structured as follows: Section 2 lays the foundation by establishing the mathematical model for the quadrotor UAV, providing the necessary framework for control system design. Section 3 develops sliding mode control laws for both position and attitude loops, addressing key challenges such as input saturation, external disturbances, and parametric uncertainties, followed by a subsequent stability analysis. Section 4 presents the simulation results, demonstrating the practical performance of the proposed control strategies in overcoming these challenges, with conclusions drawn in the dedicated section 5.

2. Mathematical Model of Quadrotor

The position of the UAV is represented by the vector $P={\left[\begin{array}{ccc}x& y& z\end{array}\right]}^T$, while the attitude angles are expressed by the vector $\eta ={\left[\begin{array}{ccc}\theta & \varphi & \psi \end{array}\right]}^T$ , where P denotes the spatial coordinates, and $\eta$ represents the pitch, roll, and yaw angles, respectively. Considering the external disturbance, the nonlinear dynamic system of quadrotor can be expressed as follows [22]

$$\begin{array}{c}\left[\begin{array}{c}\ddot{x}\\ \ddot{y}\\ \ddot{z}\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ -g\end{array}\right]+{\displaystyle \frac{1}{m}}\left[\begin{array}{c}cos\varphi sin\theta cos\psi +sin\varphi sin\psi \\ cos\varphi sin\theta sin\psi -sin\varphi cos\psi \\ cos\varphi cos\theta \end{array}\right]U_1+\left[\begin{array}{c}{d}_x\left(t\right)\\ d_y\left(t\right)\\ d_z\left(t\right)\end{array}\right]\hfill \\ \left[\begin{array}{c}\ddot{\varphi }\\ \ddot{\theta }\\ \ddot{\psi }\end{array}\right]=\left[\begin{array}{c}\dot{\theta }\dot{\psi }\left({\displaystyle \frac{J_y-J_z}{J_x}}\right)\\ \dot{\varphi }\dot{\psi }\left({\displaystyle \frac{J_z-J_x}{J_y}}\right)\\ \dot{\varphi }\dot{\theta }\left({\displaystyle \frac{J_x-J_y}{J_z}}\right)\end{array}\right]+\left[\begin{array}{c}{\displaystyle \frac{l{U}_{\varphi }}{J_x}}\\ {\displaystyle \frac{l{U}_{\theta }}{J_y}}\\ {\displaystyle \frac{U_{\psi }}{J_z}}\end{array}\right]+\left[\begin{array}{c}{d}_{\varphi }\left(t\right)\\ d_{\theta }\left(t\right)\\ d_{\psi }\left(t\right)\end{array}\right]\hfill \end{array}$$

(1)

where m is the mass of the UAV, g is the gravitational acceleration, l is the distance of the quadrotor’s center of mass to any of the rotor’s rotation axis, $J_x$, $J_y$, and $J_z$ are airframe inertia of roll, pitch and yaw, respectively, $d_i\left(t\right)$ represents the external disturbances of each channel.

The definition of the virtual control input is provided herewith $U_{\delta }=U_{1}R{e}_3={\left[\begin{array}{ccc}{U}_x& U_y& U_z\end{array}\right]}^T$ for the purpose of facilitating the design of control rates. In practical scenarios, the rotor moment of a quadrotor UAV is subject to physical constraints during flight, limiting the extent to which control inputs can be applied. To accurately reflect these limitations, the following saturation function is used in the control strategy to ensure that the control inputs remain within the feasible range [23]

$$u\left(t\right)=sat\left(U_i\left(t\right)\right)=\left\{\begin{array}{cc}sat\left(U_i\left(t\right)\right)u_{iM},\hfill & \left|U_i\left(t\right)\right|\ge u_{iM}\\ U_i\left(t\right),\hfill & \left|U_i\left(t\right)\right|<u_{iM}\end{array}\right.$$

(2)

where $U_i$ is the ith control input of the system, $u_{iM}$ is the upper bound of the ith control input and $i=x,y,z,\varphi ,\theta ,\psi$.

Define ${\delta }_1={\left[\begin{array}{ccc}x& y& z\end{array}\right]}^T,{\delta }_2={\left[\begin{array}{ccc}\dot{x}& \dot{y}& \dot{z}\end{array}\right]}^T$. Then, the position subsystem of the quadrotor is written as the following affine nonlinear form

$$\left\{\begin{array}{c}{\dot{\delta }}_1={\delta }_2\hfill \\ {\dot{\delta }}_2=f_{\delta }+g_{\delta }{u}_{\delta }+d_{\delta }\hfill \\ y_{\delta }={\delta }_1\hfill \end{array}\right.$$

(3)

where $u_{\delta }={\left[\begin{array}{ccc}sat\left(U_x\left(t\right)\right)& sat\left(U_y\left(t\right)\right)& sat\left(U_z\left(t\right)\right)\end{array}\right]}^T$ represent the saturation input to the position subsystem, $d_{\delta }={\left[\begin{array}{ccc}{d}_x\left(t\right)& d_y\left(t\right)& d_z\left(t\right)\end{array}\right]}^T$ represent the unknown external disturbances in position subsystem, $f_{\delta }={\left[\begin{array}{ccc}0& 0& -g\end{array}\right]}^T$ and $g_{\delta }=1/\phantom{=1m}m$ is the system state vector and the control gain, respectively.

Similarly, define ${\xi }_1={\left[\begin{array}{ccc}\varphi & \theta & \psi \end{array}\right]}^T,{\xi }_2={\left[\begin{array}{ccc}\dot{\varphi }& \dot{\theta }& \dot{\psi }\end{array}\right]}^T$, the attitude subsystem of the quadrotor is written as

$$\left\{\begin{array}{c}{\dot{\xi }}_1={\xi }_2\hfill \\ {\dot{\xi }}_2=f_{\xi }+g_{\xi }{u}_{\xi }+d_{\xi }\hfill \\ y_{\xi }={\xi }_1\hfill \end{array}\right.$$

(4)

where $u_{\xi }={\left[\begin{array}{ccc}sat\left(U_{\varphi }\left(t\right)\right)& sat\left(U_{\theta }\left(t\right)\right)& sat\left(U_{\psi }\left(t\right)\right)\end{array}\right]}^T$ represent the saturation input to the attitude subsystem, $d_{\xi }={\left[\begin{array}{ccc}{d}_{\varphi }\left(t\right)& d_{\theta }\left(t\right)& d_{\psi }\left(t\right)\end{array}\right]}^T$ represent the unknown external disturbances in attitude subsystem. The system state vector is

$$f_{\xi }={\left[\begin{array}{ccc}\dot{\theta }\dot{\psi }{a}_1& \dot{\varphi }\dot{\psi }{a}_2& \dot{\varphi }\dot{\theta }{a}_3\end{array}\right]}^T$$

(5)

Control gain matrix is

$$g_{\xi }=\left[\begin{array}{ccc}{I}_{\varphi }& 0& 0\\ 0& I_{\theta }& 0\\ 0& 0& I_{\psi }\end{array}\right]$$

(6)

And $a_1,a_2,a_3,I_{\varphi },I_{\theta }$ and $I_{\psi }$ are constants in (5) and (6), which are written as follows

$$\begin{array}{c}{a}_1=\left({\displaystyle \frac{J_y-J_z}{J_x}}\right),I_{\varphi }={\displaystyle \frac{l}{J_x}}\hfill \\ a_2=\left({\displaystyle \frac{J_z-J_x}{J_y}}\right),I_{\theta }={\displaystyle \frac{l}{J_y}}\hfill \\ a_3=\left({\displaystyle \frac{J_x-J_y}{J_z}}\right),I_{\psi }={\displaystyle \frac{1}{J_z}}\hfill \end{array}$$

(7)

Due to the difficulty in accurately measuring the mass and inertia moments of a quadrotor UAV, ${\widehat{g}}_{\delta }$ is used in place of $g_{\delta }$ and ${\widehat{g}}_{\xi }$ is used in place of $g_{\xi }$ in the subsequent controller design stages. Meanwhile, the development of adaptive sliding mode tracking controllers for QUAV relies on the following specific lemmas and assumptions.

Lemma 1.

[24] Consider the following equation which describes an affine nonlinear system

$$\begin{array}{c}\dot{x}=f\left(x\right)+{\eta }_1\left(x\right)u+{\eta }_2\left(x\right)d\hfill \\ y=\varpi \left(x\right)\hfill \end{array}$$

(8)

where $x\in R^n$ is the vector of state, $d\in R^l$ is the vector of disturbance, $u\in R^m$ and $y\in R^s$ are the system input and output, respectively. Disturbance observer is designed as

$$\left\{\begin{array}{c}\dot{z}=-\tau \left(x\right){\eta }_2\left(x\right)z-\tau \left(x\right)[{\eta }_2\left(x\right)p\left(x\right)+f\left(x\right)+{\eta }_1\left(x\right)u]\hfill \\ \widehat{d}=z+p\left(x\right)\hfill \end{array}\right.$$

(9)

where z, u, $\widehat{d}$ and $p\left(x\right)$ are auxiliary variable, control input, disturbance estimation, and nonlinear function, respectively. The gain $\tau \left(x\right)$ are calculated as

$$\tau \left(x\right)={\displaystyle \frac{\mathsf{\partial }p\left(x\right)}{\mathsf{\partial }x}}$$

(10)

choosing $p\left(x\right)$ to make it satisfied ${\displaystyle \frac{\mathsf{\partial }p\left(x\right)}{\mathsf{\partial }x}}{g}_2\left(x\right)>0$ , then the disturbance estimation error , as defined below

$$\tilde{d}=d-\widehat{d}$$

(11)

is guaranteed to converge globally exponentially.

Lemma 2.

The command filter is [25]

$$\left\{\begin{array}{c}{\dot{h}}_1=g_n{h}_2\hfill \\ {\dot{h}}_2=-2\varpi g_n{h}_2-g_n\left(h_1-{\alpha }_1\right)\hfill \end{array}\right.$$

(12)

The signal ${\alpha }_1$ satisfies $\left|{\dot{\alpha }}_1\right|\le o_1$ and $\left|{\ddot{\alpha }}_1\right|\le o_2$, where $o_1$,$o_2$ are positive constants and the initial conditions are set as $h_1\left(0\right)={\alpha }_1\left(0\right),h_2\left(0\right)=0$. Under these conditions, for any $\epsilon >0$, there exist $0\le \varpi \le 1,g_n>0$, such that $\left|h_1-{\alpha }_1\right|\le \kappa$ , along with the first and second derivatives $\left|{\dot{h}}_1\right|and\left|{\ddot{h}}_1\right|$ are bounded.

Assumption 1.

[26] Assuming that the external disturbance $d_{\delta }$ and $d_{\xi }$ are slow time-varying signals. They are bounded by positive constant $D_{\delta }$ and $D_{\xi }$, respectively, that is $\left|d_{\delta }\right|\le D_{\delta },\left|d_{\xi }\right|\le D_{\xi }$ for $t\ge 0$, and ${\dot{d}}_{\delta }\approx 0,{\dot{d}}_{\xi }\approx 0$.

Assumption 2.

[27] The reference signals $x_d$, $y_d$, $z_d$ and ${\psi }_d$ , along with their derivatives, are continuous and bounded.

3. Control Design

The quadrotor UAVs are inherently characterized by their high nonlinearity and underactuation. Therefore, it is impossible for quadrotor UAVs to simultaneously track all six degrees of freedom. Accordingly, the primary control objective for the UAV is to accurately track a specified trajectory $P={\left[\begin{array}{ccc}x& y& z\end{array}\right]}^T$ and yaw angle $\psi$, while ensuring the stability of the other two angles.

3.1. Position Subsystem Adaptive Control

For position subsystem described by (4), Its tracking target is designed as $x\to x_d,y\to y_d,z\to z_d$. Assuming that the desired signal are ${\delta }_d={\left[\begin{array}{ccc}{x}_d& y_d& z_d\end{array}\right]}^T,{\dot{\delta }}_d={\left[\begin{array}{ccc}{\dot{x}}_d& {\dot{y}}_d& {\dot{z}}_d\end{array}\right]}^T$. To overcome the adverse effects of external disturbance, it is first necessary to design a DO to compensate for it. A generalized form of DO is designed according to Lemma 1, which requires the calculations for $p\left(x\right)$. Choose

$$p_{\delta }={\lambda }_{\delta }{\delta }_2$$

(13)

where

$${\lambda }_{\delta }=\left[\begin{array}{ccc}{\lambda }_x& 0& 0\\ 0& {\lambda }_y& 0\\ 0& 0& {\lambda }_z\end{array}\right]$$

(14)

is the designed parameter and satisfies ${\lambda }_i>0(i=x,y,z)$ . Then, invoking (4) and (13) in Equation (9), the DO is written as

$$\left\{\begin{array}{c}{\dot{z}}_{\delta }=-{\lambda }_{\delta }(z_{\delta }+p_{\delta }+f_{\delta }+{\widehat{g}}_{\delta }{u}_{\delta })\hfill \\ {\widehat{d}}_{\delta }=z_{\delta }+p_{\delta }\hfill \end{array}\right.$$

(15)

Combining Assumption 1 with Equation (11), the derivative of the disturbance estimation error is derived as

$$\begin{array}{cc}\hfill {\dot{\tilde{d}}}_{\delta }& ={\dot{d}}_{\delta }-{\dot{\widehat{d}}}_{\delta }\hfill \\ \hfill & =-{\dot{z}}_{\delta }-{\displaystyle \frac{\mathsf{\partial }{p}_{\delta }}{\mathsf{\partial }{\delta }_2}}{\dot{\delta }}_2\hfill \\ \hfill & ={\lambda }_{\delta }(z_{\delta }+p_{\delta }+f_{\delta }+{\widehat{g}}_{\delta }{u}_{\delta })-{\lambda }_{\delta }(f_{\delta }+g_{\delta }{u}_{\delta }+d_{\delta })\hfill \\ \hfill & ={\lambda }_{\delta }({\widehat{d}}_{\delta }-d_{\delta }+({\widehat{g}}_{\delta }-g_{\delta })u_{\delta })\hfill \\ \hfill & =-{\lambda }_{\delta }({\tilde{d}}_{\delta }+{\tilde{g}}_{\delta }{u}_{\delta })\hfill \end{array}$$

(16)

To address the issue of input saturation in the uncertain UAV position subsystem (3), the detrimental effects of input saturation are tackled by constructing the following auxiliary systems [28]

$$\left\{\begin{array}{c}{\dot{\beta }}_1=-h_1{\beta }_1+{\beta }_2\hfill \\ {\dot{\beta }}_2=-h_2{\beta }_2-{\beta }_1+{\widehat{g}}_{\delta }\Delta u_{\delta }\hfill \end{array}\right.$$

(17)

where ${\beta }_j\in R^3(j=1,2)$ is the state, $h_j\in R^{3\times 3}$ is the designed positive definite matrix and $\Delta u_{\delta }=u_{\delta }-U_{\delta }$ . In the real world, actuators have finite energy, making it necessary to ensure that $\Delta u_{\delta }$ is constrained by $\left|\Delta u_{\delta }\right|\le \nu$, where $\nu$ is a positive parameter. This finite energy constraint ensures that the control inputs remain within feasible limits, allowing the system to remain controllable while protecting the actuators from excessive load.

A sliding mode surface is proposed as

$${\sigma }_{\delta }=c_{\delta }{e}_{\delta }+{\dot{e}}_{\delta }$$

(18)

where $e_{\delta }={\delta }_1-{\delta }_d-{\beta }_1$ and

$$c_{\delta }=\left[\begin{array}{ccc}{c}_x& 0& 0\\ 0& c_y& 0\\ 0& 0& c_z\end{array}\right]$$

(19)

The designed parameter matrix $c_{\delta }$ satisfies condition $c_{\delta }^T=c_{\delta }>0$. The aim is to get the error $e_{\delta }$ as close to zero as possible. Taking the derivative of Equation (19)

$$\begin{array}{cc}\hfill {\dot{\sigma }}_{\delta }& =c_{\delta }{\dot{e}}_{\delta }+{\ddot{e}}_{\delta }\hfill \\ \hfill & =c_{\delta }{\dot{e}}_{\delta }+{\ddot{\delta }}_1-{\ddot{\delta }}_d-({\dot{\beta }}_2-h_1{\dot{\beta }}_1)\hfill \\ \hfill & =c_{\delta }{\dot{e}}_{\delta }+f_{\delta }+g_{\delta }{u}_{\delta }+d_{\delta }-{\ddot{\delta }}_d-({\widehat{g}}_{\delta }\Delta u_{\delta }-h_2{\beta }_2-{\beta }_1-h_1(-h_1{\beta }_1+{\beta }_2))\hfill \\ \hfill & =c_{\delta }{\dot{e}}_{\delta }+f_{\delta }+{\widehat{g}}_{\delta }{u}_{\delta }+{\tilde{g}}_{\delta }{u}_{\delta }+d_{\delta }-{\ddot{\delta }}_d-{\widehat{g}}_{\delta }\Delta u_{\delta }+h_2{\beta }_2+{\beta }_1+h_1(-h_1{\beta }_1+{\beta }_2)\hfill \\ \hfill & =c_{\delta }{\dot{e}}_{\delta }+f_{\delta }+{\widehat{g}}_{\delta }{U}_{\delta }+d_{\delta }-{\ddot{\delta }}_d+h_2{\beta }_2+{\beta }_1+h_1(-h_1{\beta }_1+{\beta }_2)+{\tilde{g}}_{\delta }{u}_{\delta }\hfill \end{array}$$

(20)

According to (20), the virtual controller is designed as

$$\begin{array}{c}\hfill U_{\delta }={\displaystyle \frac{1}{{\widehat{g}}_{\delta }}}(-c_{\delta }{\dot{e}}_{\delta }+f_{\delta }+{\ddot{\delta }}_d-{\alpha }_{\delta }{\sigma }_{\delta }-{\widehat{d}}_{\delta }-h_2{\beta }_2-{\beta }_1-h_1(-h_1{\beta }_1+{\beta }_2))\end{array}$$

(21)

where ${\alpha }_{\delta }=\left[\begin{array}{ccc}{\alpha }_x& 0& 0\\ 0& {\alpha }_y& 0\\ 0& 0& {\alpha }_z\end{array}\right]$ is the parameter matrix to be designed, ${\widehat{g}}_{\delta }$ and ${\widehat{d}}_{\delta }$ represents the estimate of the inverse of the mass and the output of the DO, respectively. The estimation error of the mass inverse is

$${\tilde{g}}_{\delta }=g_{\delta }-{\widehat{g}}_{\delta }$$

(22)

The adaptive law is designed as [29]

$${\dot{\widehat{g}}}_{\delta }=\mathrm{Pro}{\mathrm{j}}_{[g_{\delta min},g_{\delta max}]}{\gamma }_1({\sigma }_{\delta }^T{u}_{\delta }-{\beta }_2\Delta u_{\delta }-o_1{\widehat{g}}_{\delta })$$

(23)

where ${\gamma }_1>0$ and $o_1>0$ are the constant to be designed. The estimate ${\widehat{g}}_{\delta }$ is projected to the interval $[g_{\delta min},g_{\delta max}]$ using the projection operator, which is expressed as

$$\mathrm{Pro}{\mathrm{j}}_{[g_{\delta min},g_{\delta max}]}{\gamma }_1\left(a\right)=\left\{\begin{array}{cc}{\gamma }_{1}a,\hfill & \mathrm{if}{\widehat{g}}_{\delta }=g_{\delta max}\mathrm{and}a<0\\ 0,\hfill & \mathrm{if}{\widehat{g}}_{\delta }=g_{\delta max}\mathrm{and}a\ge 0\\ {\gamma }_{1}a,\hfill & \mathrm{if}{g}_{\delta min}\le {\widehat{g}}_{\delta }\le g_{\delta max}\hfill \\ 0,\hfill & \mathrm{if}{\widehat{g}}_{\delta }=g_{\delta min}\mathrm{and}a\le 0\\ {\gamma }_{1}a,\hfill & \mathrm{if}{\widehat{g}}_{\delta }=g_{\delta min}\mathrm{and}a>0\end{array}\right.$$

(24)

Redefine a variable ${\Theta }_{\delta }$ that includes the estimation error ${\tilde{d}}_{\delta }$ and ${\tilde{g}}_{\delta }$ as follows

$${\Theta }_{\delta }=\left[\begin{array}{c}{\tilde{d}}_{\delta }\\ {\tilde{g}}_{\delta }\end{array}\right]$$

(25)

And the derivative of (25) can be obtained from (11) and (22) as

$${\dot{\Theta }}_{\delta }=\left[\begin{array}{c}{\dot{\tilde{d}}}_{\delta }\\ -{\dot{\widehat{g}}}_{\delta }\end{array}\right]$$

(26)

Consider the Lyapunov function candidate

$$\begin{array}{cc}\hfill V_{\delta }({\sigma }_{\delta },{\beta }_1,{\beta }_2,{\Theta }_{\delta })=& {\displaystyle \frac{1}{2}}{\sigma }_{\delta }^T{\sigma }_{\delta }+{\displaystyle \frac{1}{2}}{\beta }_1^T{\beta }_1+{\displaystyle \frac{1}{2}}{\beta }_2^T{\beta }_2+{\Theta }_{\delta }^T\left[\begin{array}{cc}{\displaystyle \frac{1}{2}}& 0\\ 0& {\displaystyle \frac{1}{2{\gamma }_1}}\end{array}\right]{\Theta }_{\delta }\hfill \end{array}$$

(27)

Invoking (4), (17), (18), (21), (22) and (24), the time derivative of $V_{\delta }$ is

$$\begin{array}{cc}\hfill {\dot{V}}_{\delta }& ={\sigma }_{\delta }^T{\dot{\sigma }}_{\delta }+{\beta }_1^T{\dot{\beta }}_1+{\beta }_2^T{\dot{\beta }}_2+{\Theta }_{\delta }^T\left[\begin{array}{cc}1& 0\\ 0& {\displaystyle \frac{1}{{\gamma }_1}}\end{array}\right]{\dot{\Theta }}_{\delta }\hfill \\ \hfill & =-{\sigma }_{\delta }^T{\alpha }_{\delta }{\sigma }_{\delta }+{\sigma }_{\delta }^T{\tilde{d}}_{\delta }+{\sigma }_{\delta }^T{\tilde{g}}_{\delta }{u}_{\delta }-{\beta }_1^T{h}_1{\beta }_1-{\beta }_2^T{h}_2{\beta }_2+{\beta }_2^T{\widehat{g}}_{\delta }\Delta u_{\delta }-{\tilde{d}}_{\delta }^T{\lambda }_{\delta }{\tilde{d}}_{\delta }-{\tilde{d}}_{\delta }^T{\lambda }_{\delta }{u}_{\delta }{\tilde{g}}_{\delta }-{\displaystyle \frac{1}{{\gamma }_1}}{\tilde{g}}_{\delta }{\dot{\widehat{g}}}_{\delta }\hfill \\ \hfill & =-{\sigma }_{\delta }^T{\alpha }_{\delta }{\sigma }_{\delta }-{\tilde{d}}_{\delta }^T{\lambda }_{\delta }{\tilde{d}}_{\delta }-{\beta }_1^T{h}_1{\beta }_1-{\beta }_2^T{h}_2{\beta }_2+{\sigma }_{\delta }^T{\tilde{d}}_{\delta }+{\beta }_2^T{g}_{\delta }\Delta u_{\delta }-{\tilde{d}}_{\delta }^T{\lambda }_{\delta }{u}_{\delta }{\tilde{g}}_{\delta }+{\tilde{g}}_{\delta }({\sigma }_{\delta }^T{u}_{\delta }-{\beta }_2^T\Delta u_{\delta }-{\displaystyle \frac{{\dot{\widehat{g}}}_{\delta }}{{\gamma }_1}})\hfill \\ \hfill & \le -{\sigma }_{\delta }^T({\alpha }_{\delta }-{\displaystyle \frac{1}{2}}{I}_{3\times 3}){\sigma }_{\delta }-{\beta }_1^T{h}_1{\beta }_1-{\beta }_2^T(h_2-{\displaystyle \frac{1}{2}}{I}_{3\times 3}){\beta }_2-{\Theta }_{\delta }^T\left[\begin{array}{cc}{\lambda }_{\delta }-{\displaystyle \frac{1}{2}}{I}_{3\times 3}& {\lambda }_{\delta }{u}_{\delta }\\ 0& {\displaystyle \frac{o_1}{2}}\end{array}\right]{\Theta }_{\delta }+{\displaystyle \frac{g_{\delta }^2{\nu }^2}{4}}+{\displaystyle \frac{o_1}{2}}{g}_{\delta }^2\hfill \\ \hfill & \le -{\kappa }_1{V}_{\delta }+C_1\hfill \end{array}$$

(28)

where

$$\begin{array}{cc}\hfill {\kappa }_1=& min\left\{{\lambda }_{min}\left({\alpha }_{\delta }-{\displaystyle \frac{1}{2}}{I}_{3\times 3}\right),\right.{\lambda }_{min}\left(h_1\right),\hfill \\ \hfill & \left.{\lambda }_{min}\left(h_2-{\displaystyle \frac{1}{2}}{I}_{3\times 3}\right),{\lambda }_{min}\left({\lambda }_{\delta }-{\displaystyle \frac{1}{2}}{I}_{3\times 3}\right),{\displaystyle \frac{o_1}{2}}\right\}\hfill \\ \hfill C_1=& {\displaystyle \frac{{\nu }^2}{4m^2}}+{\displaystyle \frac{o_1}{2m^2}}\hfill \end{array}$$

(29)

To ensure system stability, it is essential to ensure that the appropriate design matrices and parameters $\left({\alpha }_{\delta }-{\displaystyle \frac{1}{2}}{I}_{3\times 3}\right)>0,h_1>0,\left(h_2-{\displaystyle \frac{1}{2}}{I}_{3\times 3}\right)>0,\left({\lambda }_{\delta }-{\displaystyle \frac{1}{2}}{I}_{3\times 3}\right)>0,o_1>0$.

In conclusion, the signals ${\sigma }_{\delta }$, the estimate errors ${\tilde{d}}_{\delta }$, ${\tilde{g}}_{\delta }$, the variables of the auxiliary system states ${\beta }_1$, ${\beta }_2$ are all bounded, the drone’s position is able to keep up with the desired signals.

3.2. Attitude Subsystem Adaptive Control

To achieve the desired tracking targets, namely $\theta \to {\theta }_d,\psi \to {\psi }_d,\varphi \to {\varphi }_d$, the actual lift $U_1$ and attitude subsystem intermediate command signals ${\varphi }_d$ and ${\psi }_d$ must first be calculated. The inverse solution according to (2) yields written as follows [27]

$$\left\{\begin{array}{c}{\theta }_d=arctan\left({\displaystyle \frac{U_{x}cos{\psi }_d+U_{y}sin{\psi }_d}{U_z}}\right)\hfill \\ {\varphi }_d=arctan\left({\displaystyle \frac{cos{\theta }_d\left(U_{x}sin{\psi }_d-U_{y}cos{\psi }_d\right)}{U_z}}\right)\hfill \\ U_1={\displaystyle \frac{U_z}{cos{\varphi }_{d}cos{\theta }_d}}\hfill \end{array}\right.$$

(30)

Defining that the desired signal are ${\xi }_d={\left[\begin{array}{ccc}{\varphi }_d& {\theta }_d& {\psi }_d\end{array}\right]}^T$, ${\dot{\xi }}_d={\left[\begin{array}{ccc}{\dot{\varphi }}_d& {\dot{\theta }}_d& {\dot{\psi }}_d\end{array}\right]}^T$. where the derivative of ${\xi }_d$ can be obtain from Lemma 2. According to Lemma 1, we have

$$p_{\xi }={\lambda }_{\xi }{\xi }_2$$

(31)

where

$${\lambda }_{\xi }=\left[\begin{array}{ccc}{\lambda }_{\varphi }& 0& 0\\ 0& {\lambda }_{\theta }& 0\\ 0& 0& {\lambda }_{\psi }\end{array}\right]$$

(32)

is the designed parameter matrix and satisfies ${\lambda }_i>0$$(i=\varphi ,\theta ,\psi )$. Invoking (5) and (30) in (10), the DO is written as

$$\left\{\begin{array}{c}{\dot{z}}_{\xi }=-{\lambda }_{\xi }(z_{\xi }+p_{\xi }+f_{\xi }+{\widehat{g}}_{\xi }{u}_{\xi })\hfill \\ {\widehat{d}}_{\xi }=z_{\xi }+p_{\xi }\hfill \end{array}\right.$$

(33)

where

$${\widehat{g}}_{\xi }=\left[\begin{array}{ccc}{\widehat{I}}_{\varphi }& 0& 0\\ 0& {\widehat{I}}_{\theta }& 0\\ 0& 0& {\widehat{I}}_{\psi }\end{array}\right]$$

(34)

Similarly, the attitude subsystem is susceptible to input saturation, which can be addressed by constructing a system in the same form as the auxiliary system described above. This approach can effectively compensate for the effects of input saturation.[28]

$$\left\{\begin{array}{c}{\dot{\beta }}_3=-h_3{\beta }_3+{\beta }_4\hfill \\ {\dot{\beta }}_4=-h_4{\beta }_4-{\beta }_3+{\widehat{g}}_{\xi }\Delta u_{\xi }\hfill \end{array}\right.$$

(35)

where ${\beta }_j={\left[\begin{array}{ccc}{\beta }_{j\varphi }& {\beta }_{j\theta }& {\beta }_{j\psi }\end{array}\right]}^T$$(j=3,4)$ is the state, $h_j=\left[\begin{array}{ccc}{h}_{j\varphi }& 0& 0\\ 0& h_{j\theta }& 0\\ 0& 0& h_{j\psi }\end{array}\right]$$(j=3,4)$ is the designed positive definite matrix and $\Delta u_{\xi }=u_{\xi }-U_{\xi }$. The sliding mode surface is also defined in the form of (19)

$${\sigma }_{\xi }=c_{\xi }{e}_{\xi }+{\dot{e}}_{\xi }$$

(36)

where $e_{\xi }=\xi -{\xi }_d-{\beta }_3$ and

$$c_{\xi }=\left[\begin{array}{ccc}{c}_{\varphi }& 0& 0\\ 0& c_{\theta }& 0\\ 0& 0& c_{\psi }\end{array}\right]$$

(37)

The designed parameter matrix $c_{\xi }$ satisfies condition $c_{\xi }^T=c_{\xi }>0$. The controller of the attitude subsystem is proposed as

$$\begin{array}{cc}\hfill U_{\xi }=& {\displaystyle \frac{1}{{\widehat{g}}_{\xi }}}(-c_{\xi }{\dot{e}}_{\xi }-f_{\xi }+{\ddot{\xi }}_d-{\alpha }_{\xi }{\sigma }_{\xi }-{\widehat{d}}_{\xi }-h_4{\beta }_4-{\beta }_3-h_3(-h_3{\beta }_3+{\beta }_4))\hfill \end{array}$$

(38)

where ${\alpha }_{\xi }=\left[\begin{array}{ccc}{\alpha }_{\varphi }& 0& 0\\ 0& {\alpha }_{\theta }& 0\\ 0& 0& {\alpha }_{\psi }\end{array}\right]$ is the parameter matrix to be designed, ${\widehat{g}}_{\xi }$ and ${\widehat{d}}_{\xi }$ represents the estimate of the inverse of the inertia matrix and the output of the DO, respectively. In this control rate, the derivatives of the two intermediate control signals ${\varphi }_d$ and ${\psi }_d$ generated by the outer loop can be derived from Lemma 2. The estimation error of the inverse of the inertia are defined as follows

$${\tilde{I}}_i=I_i-{\widehat{I}}_i,i=\varphi ,\theta ,\psi$$

(39)

The adaptive law is designed as [29]

$${\dot{\widehat{I}}}_i=\mathrm{Pro}{\mathrm{j}}_{[{\widehat{I}}_{imin},{\widehat{I}}_{imax}]}{\gamma }_i({\sigma }_i{u}_i-{\beta }_{4i}\Delta u_i-o_i{\widehat{I}}_i)$$

(40)

where ${\gamma }_i$ and $o_i$ are designed positive constants. The estimate ${\widehat{I}}_i$ is projected to the interval $[I_{imin},I_{imax}]$ using the projection operator, which is expressed as

$$\mathrm{Pro}{\mathrm{j}}_{[I_{imin},I_{imax}]}{\gamma }_i\left(a\right)=\left\{\begin{array}{cc}{\gamma }_{i}a,\hfill & \mathrm{if}{\widehat{I}}_i=I_{imax}\mathrm{and}a<0\\ 0,\hfill & \mathrm{if}{\widehat{I}}_i=I_{imax}\mathrm{and}a\ge 0\\ {\gamma }_{i}a,\hfill & \mathrm{if}{I}_{imin}\le {\widehat{I}}_i\le I_{imax}\hfill \\ 0,\hfill & \mathrm{if}{\widehat{I}}_i=I_{imin}\mathrm{and}a\le 0\\ {\gamma }_{i}a,\hfill & \mathrm{if}{\widehat{I}}_i=I_{imin}\mathrm{and}a>0\end{array}\right.$$

(41)

Redefine ${\Theta }_i$ that includes the estimation error ${\tilde{d}}_i$ and ${\tilde{I}}_i$ as follows

$${\Theta }_i=\left[\begin{array}{c}{\tilde{d}}_i\\ {\tilde{I}}_i\end{array}\right],i=\varphi ,\theta ,\psi$$

(42)

For the whole attitude subsystem, taking the following Lyapunov function

$$\begin{array}{cc}\hfill V_{\xi }({\sigma }_{\xi },{\beta }_3,{\beta }_4,{\Theta }_i)=& \sum _{i=\varphi ,\theta ,\psi }({\displaystyle \frac{1}{2}}{\sigma }_i^2+{\displaystyle \frac{1}{2}}{\beta }_{3i}^2+{\displaystyle \frac{1}{2}}{\beta }_{4i}^2+{\Theta }_i^T\left[\begin{array}{cc}{\displaystyle \frac{1}{2}}& 0\\ 0& {\displaystyle \frac{1}{2{\gamma }_i}}\end{array}\right]{\Theta }_i)\hfill \end{array}$$

(43)

Then

$$\begin{array}{cc}\hfill {\dot{V}}_{\xi }& =\sum _{i=\varphi ,\theta ,\psi }(-{\alpha }_i{\sigma }_i^2+{\sigma }_i{\tilde{d}}_i+{\sigma }_i{\tilde{I}}_i{u}_i-h_{3i}{\beta }_{3i}^2-h_{4i}{\beta }_{4i}^2+{\beta }_{4i}{\widehat{I}}_i\Delta u_i-{\lambda }_i{\tilde{d}}_i^2-{\tilde{d}}_i{\lambda }_i{u}_i{\tilde{I}}_i-{\displaystyle \frac{1}{{\gamma }_i}}{\tilde{I}}_i{\dot{\widehat{I}}}_i)\hfill \\ \hfill & =\sum _{i=\varphi ,\theta ,\psi }(-{\alpha }_i{\sigma }_i^2-{\lambda }_i{\tilde{d}}_i^2-h_{3i}{\beta }_{3i}^2-h_{4i}{\beta }_{4i}^2+{\sigma }_i{\tilde{d}}_i+{\beta }_{4i}{I}_i\Delta u_i-{\tilde{d}}_i{\lambda }_i{u}_i{\tilde{I}}_i+{\tilde{I}}_i({\sigma }_i{u}_i-{\beta }_{4i}\Delta u_i-{\displaystyle \frac{1}{{\gamma }_i}}{\dot{\widehat{I}}}_i))\hfill \\ \hfill & \le \sum _{i=\varphi ,\theta ,\psi }(-({\alpha }_i-{\displaystyle \frac{1}{2}}){\sigma }_i^2-h_{3i}{\beta }_{3i}^2-(h_{4i}-{\displaystyle \frac{1}{2}}){\beta }_{4i}^2-{\Theta }_i^T\left[\begin{array}{cc}{\lambda }_i-{\displaystyle \frac{1}{2}}& {\lambda }_i{u}_i\\ 0& {\displaystyle \frac{o_i}{2}}\end{array}\right]{\Theta }_i+{\displaystyle \frac{{\nu }_i^2}{4}}{I}_i^2+{\displaystyle \frac{o_i}{2}}{I}_i^2)\hfill \\ \hfill & \le -{\kappa }_2{V}_{\xi }+C_2\hfill \end{array}$$

(44)

where

$$\begin{array}{cc}\hfill {\kappa }_2=& \underset{i=\varphi ,\theta ,\psi }{min}\left\{{\alpha }_i-{\displaystyle \frac{1}{2}},\right.h_{3i},h_{4i}-{\displaystyle \frac{1}{2}},{\lambda }_i-{\displaystyle \frac{1}{2}},\left.{\displaystyle \frac{o_i}{2}}\right\}\hfill \\ \hfill C_2=& \sum _{i=\varphi ,\theta ,\psi }({\displaystyle \frac{{\nu }_i^2}{4}}{I}_i^2+{\displaystyle \frac{o_i}{2}}{I}_i^2)\hfill \end{array}$$

(45)

Thus, the signal $e_{\xi }$, ${\tilde{d}}_{\xi }$ and ${\tilde{g}}_{\xi }$ are all bounded. To conduct comprehensive stability analysis of the quadrotor, a stability function is defined as

$$V=V_{\delta }+V_{\xi }$$

(46)

Taking derivative of (46), we can obtain

$$\dot{V}={\dot{V}}_{\delta }+{\dot{V}}_{\xi }\le -\kappa V+C$$

(47)

where

$$\begin{array}{c}\kappa =min({\kappa }_1,{\kappa }_2)\hfill \\ C=C_1+C_2\hfill \end{array}$$

(48)

Accordingly, the UAV is able to perform trajectory tracking tasks and achieve control objectives.

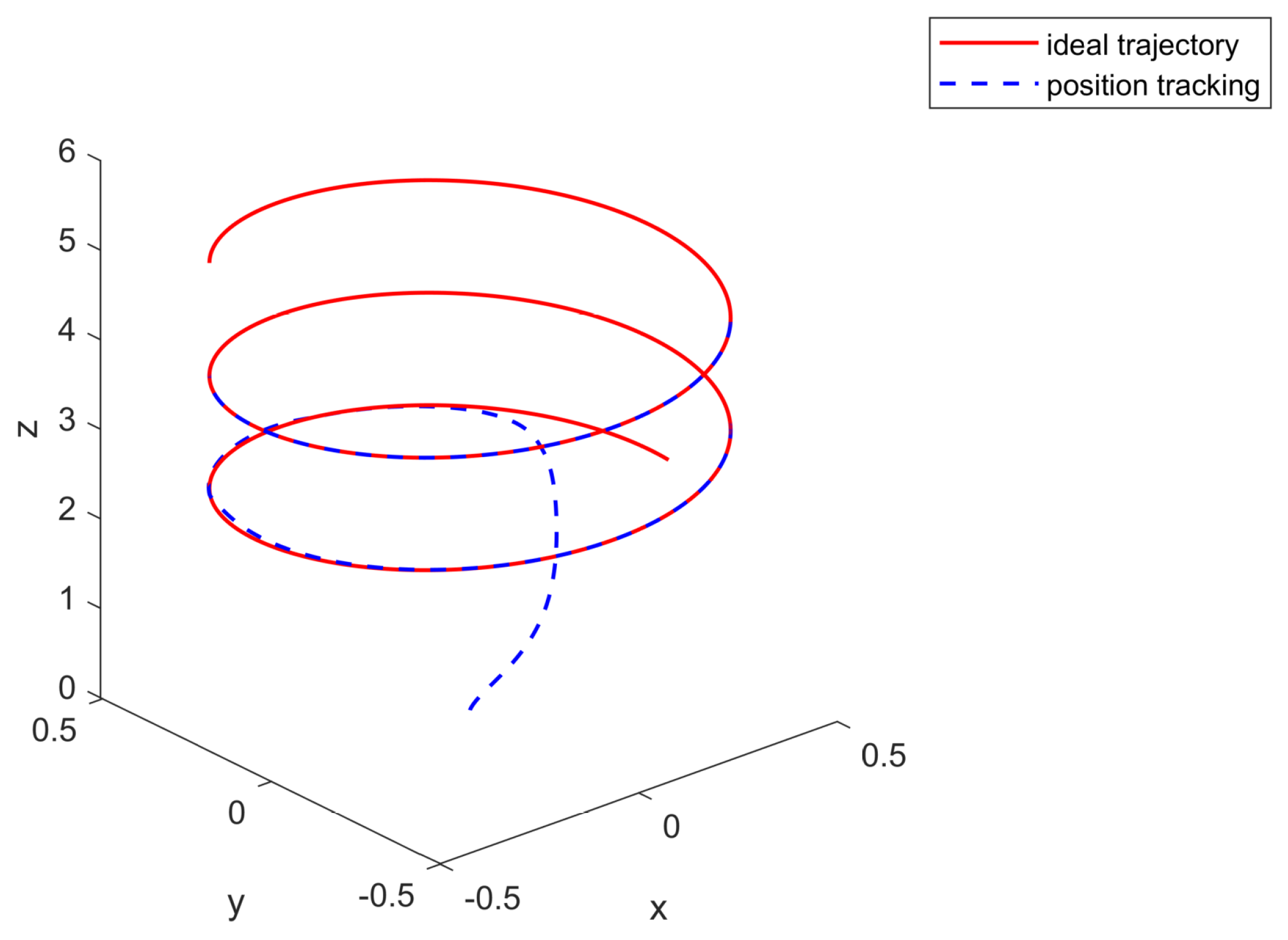
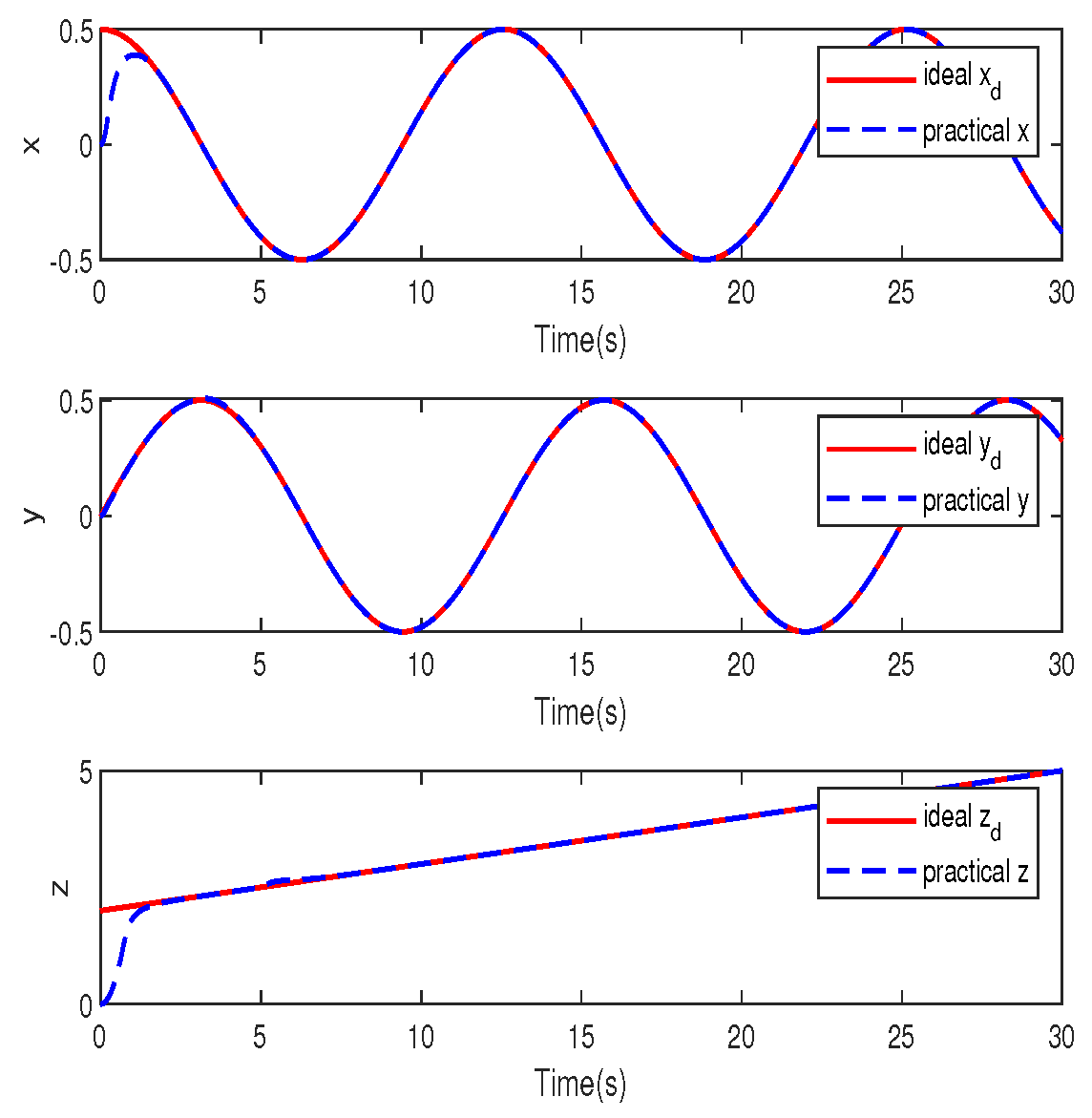
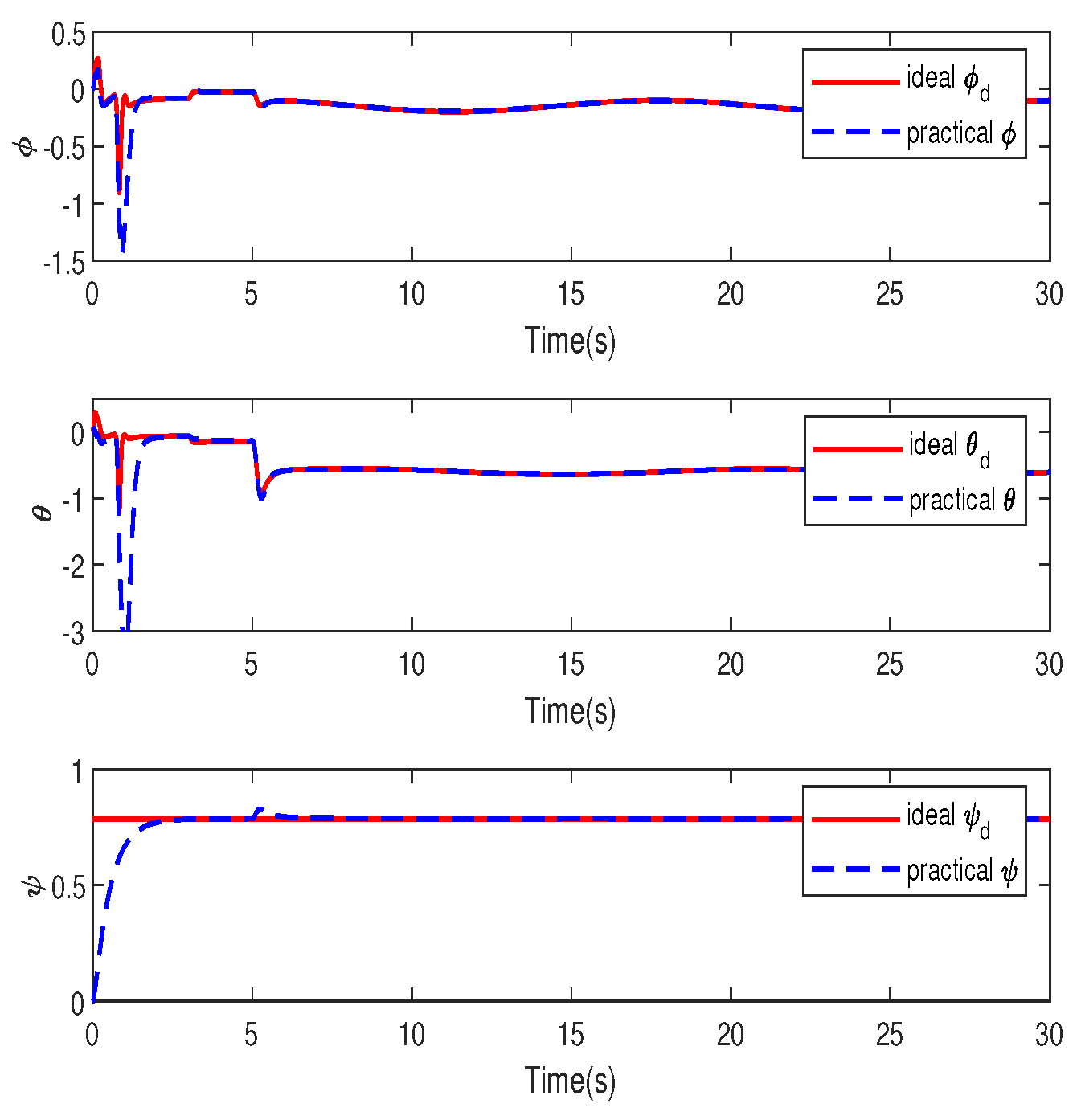
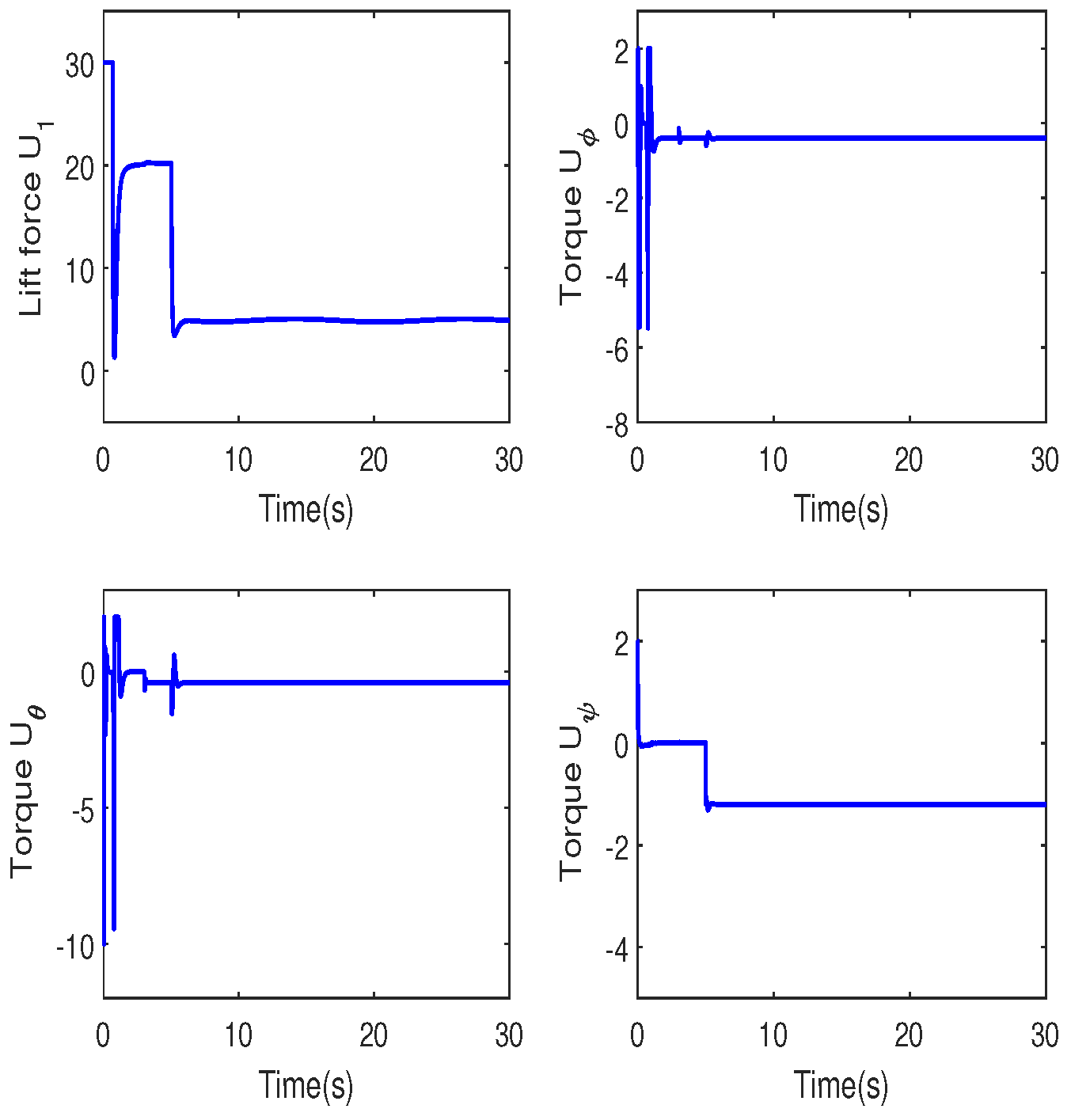
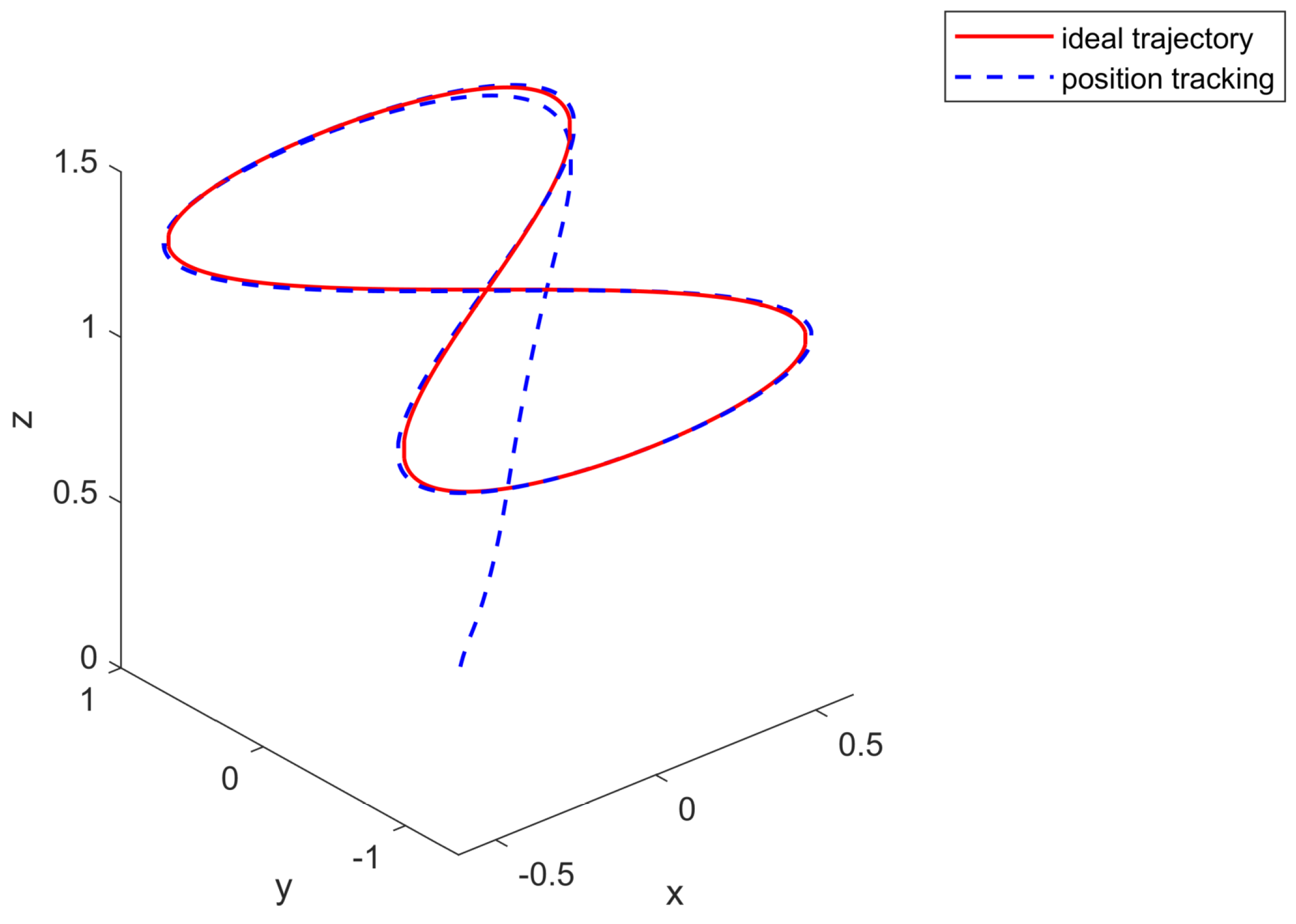
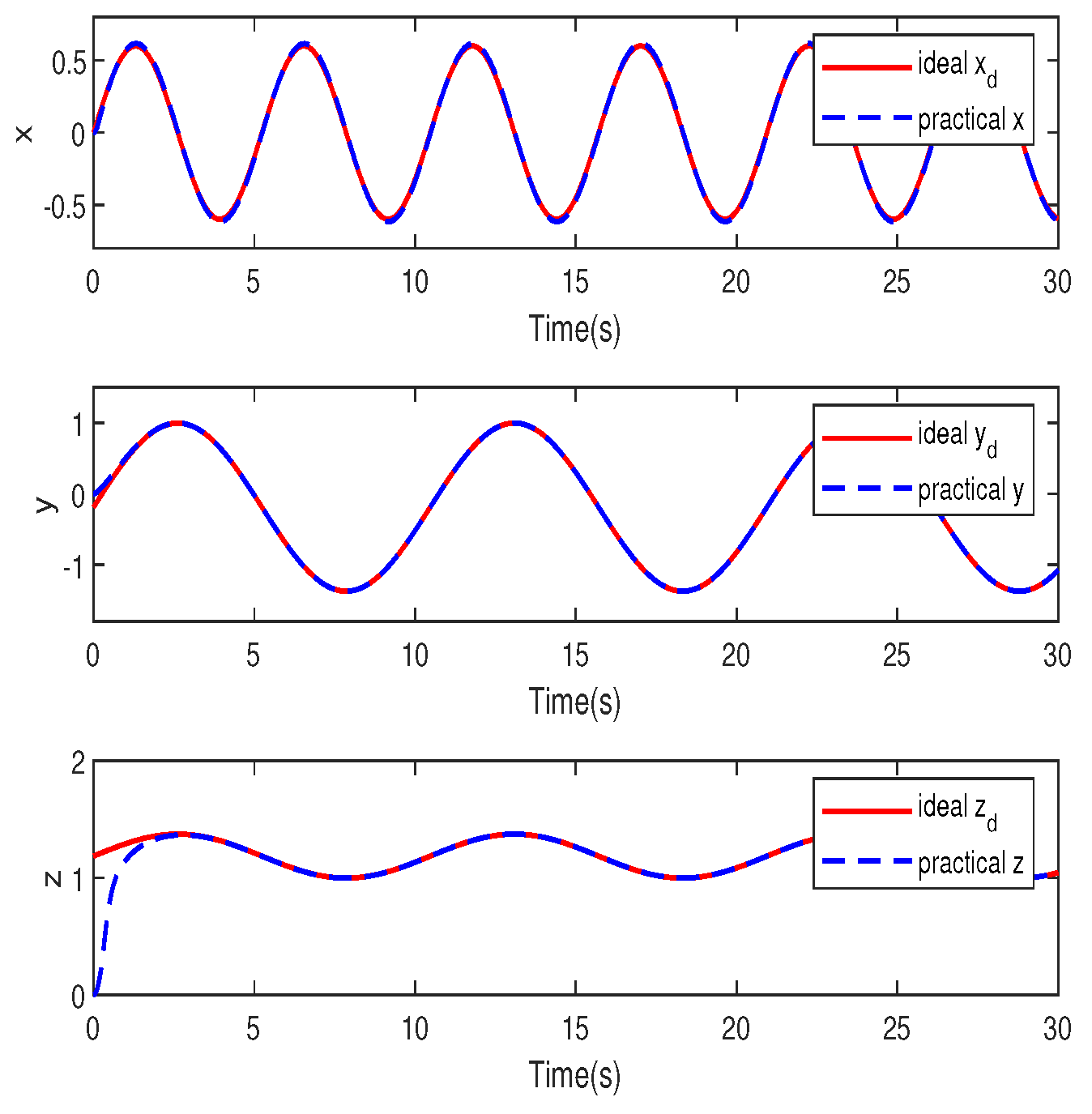
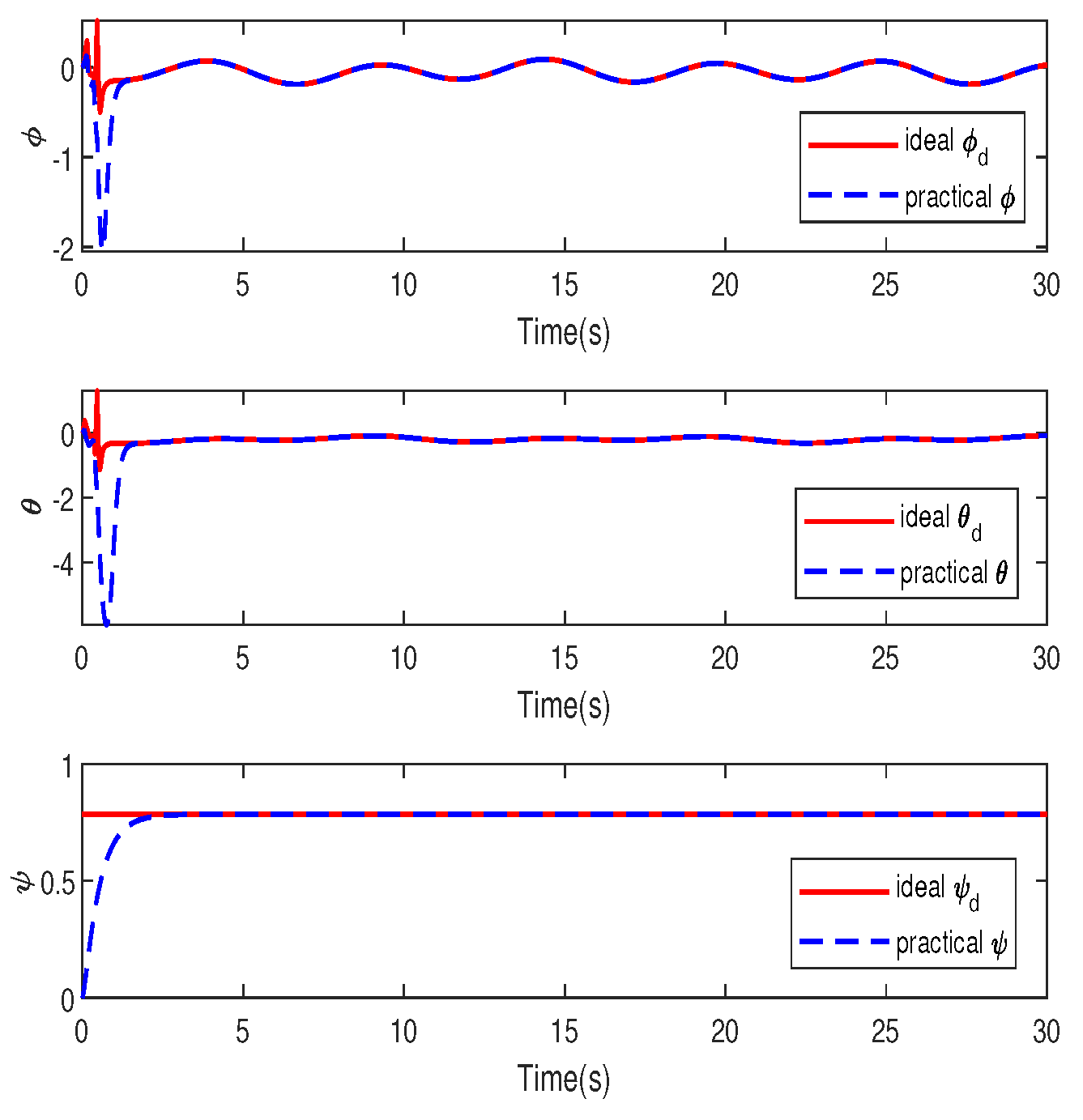
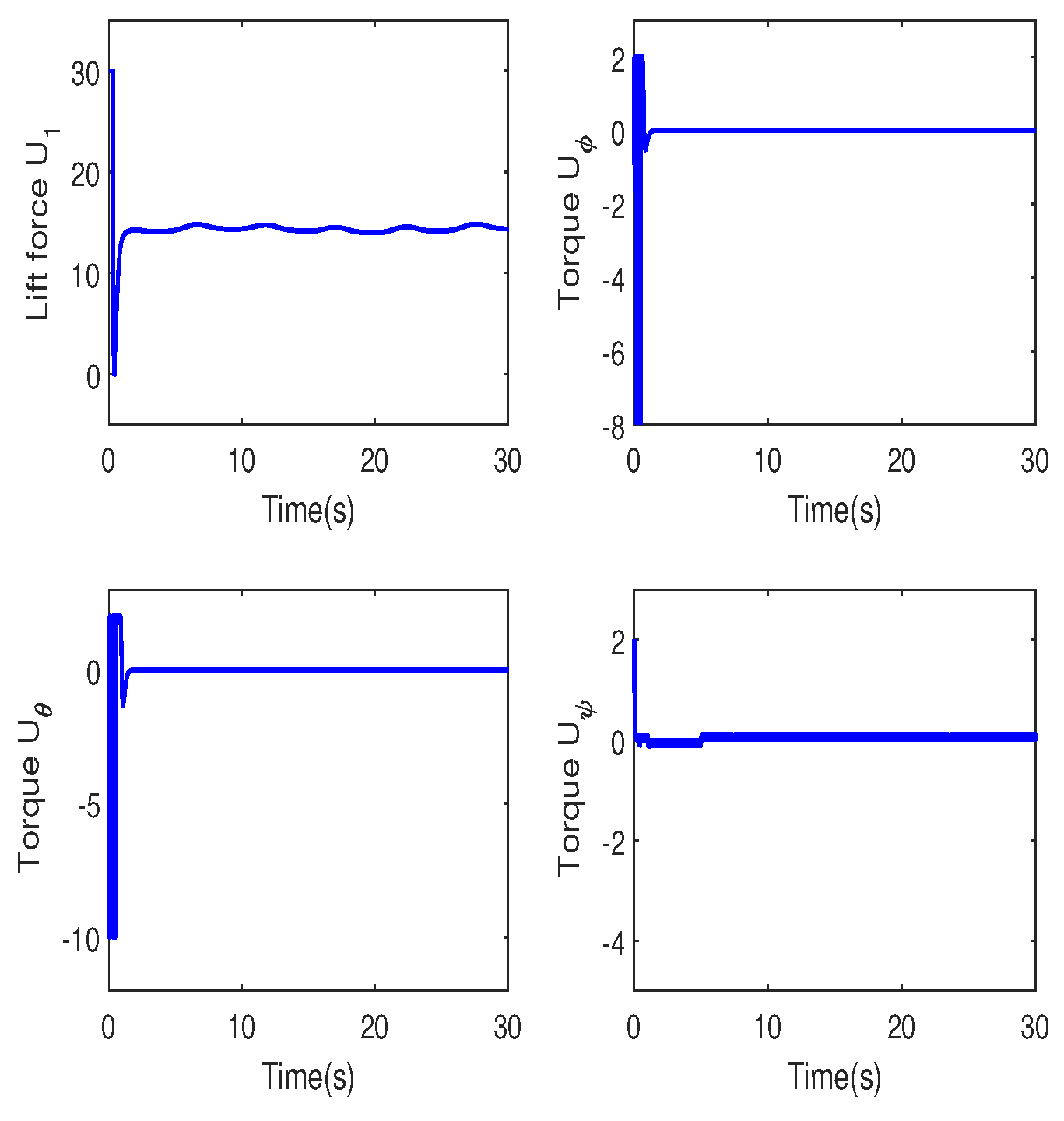
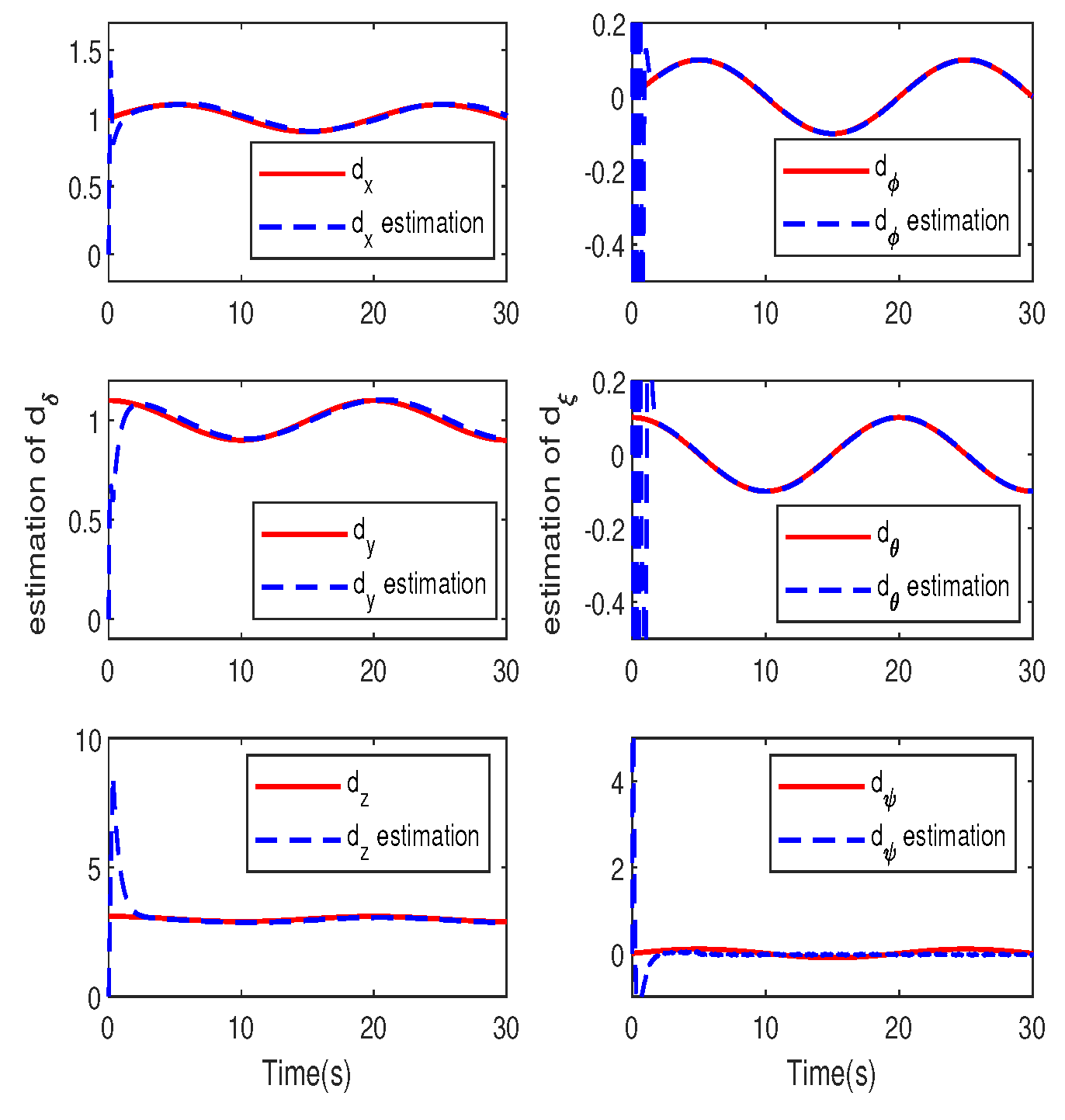
4. Simulation Study

Numerical simulations were performed to validate the proposed control strategy, employing a quadrotor UAV model that was subjected to both input saturation and two distinct types of external disturbances. These simulations provided a rigorous test of the control strategy’s performance under challenging conditions. The UAV and controller parameters used in the simulations are comprehensively detailed in Table 1 and Table 2, respectively. The parameters presented in the table are all expressed in International System of Units.

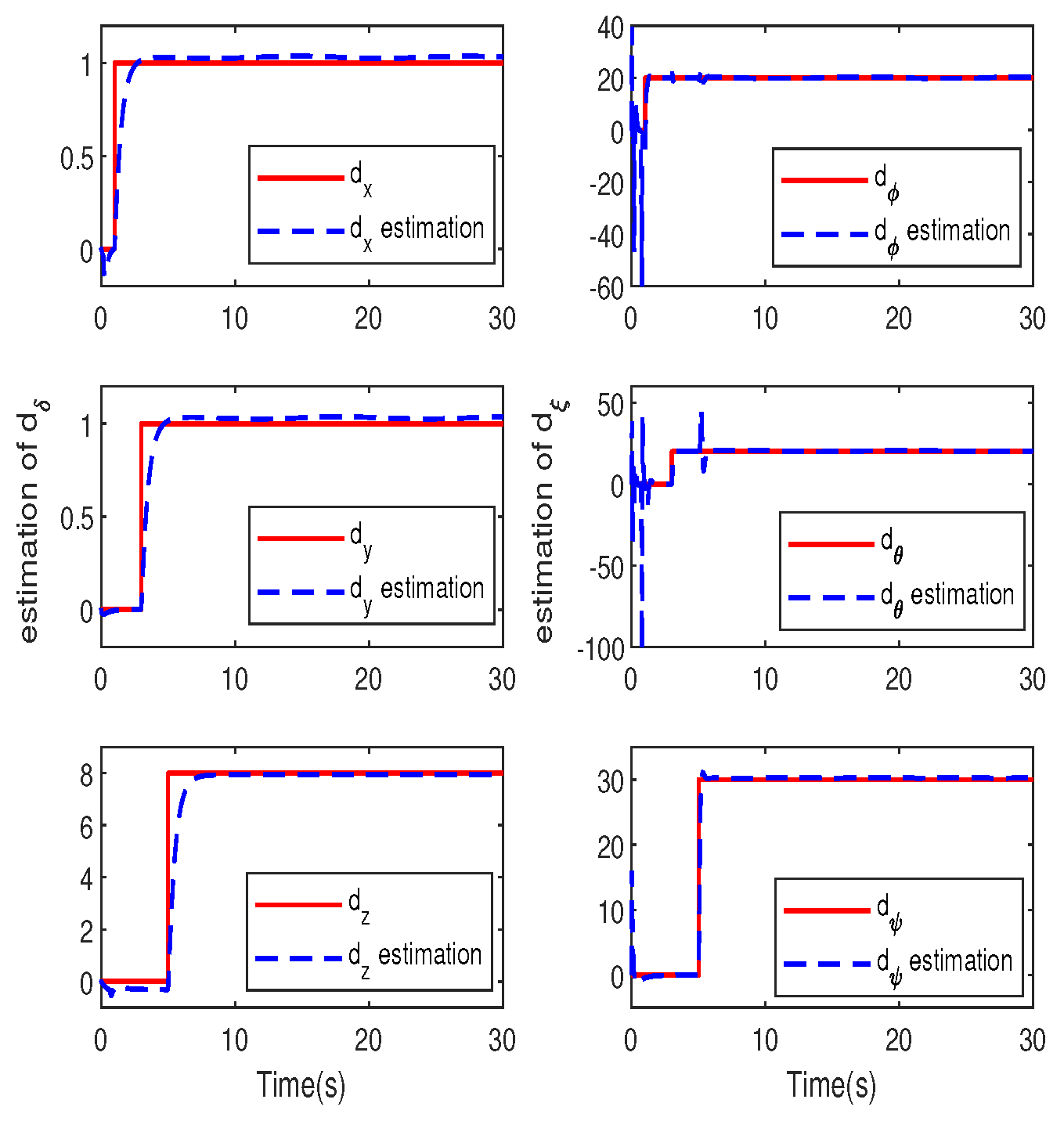
A. Robustness to Constant Disturbances

The reference trajectory signals are expected trajectory $P_d$ and expected yaw Angle ${\psi }_d$ are

$$\left\{\begin{array}{c}{P}_d=\left[\begin{array}{ccc}0.5cos(0.5\ast t)& 0.5sin(0.5\ast t)& 2+0.1\ast t\end{array}\right]\hfill \\ {\psi }_d={\displaystyle \frac{\pi }{4}}\hfill \end{array}\right.$$

The initial position and attitude states of the quadrotor are assumed to be $\delta \left(0\right)=[\begin{array}{ccc}0& 0& 0\end{array}{]}^T,\xi \left(0\right)=[\begin{array}{ccc}0& 0& 0\end{array}{]}^T$. The external disturbances conforming to the hypothesis are: $d_x=1$ at $\mathrm{t}=1\mathrm{s}$; $d_y=1$ at $\mathrm{t}=3\mathrm{s}$; $d_z=8$ at $\mathrm{t}=5\mathrm{s}$; $d_{\varphi }=20$ at $\mathrm{t}=1\mathrm{s}$; $d_{\theta }=20$ at $\mathrm{t}=3\mathrm{s}$;, $d_{\psi }=30\mathrm{N}$ at $\mathrm{t}=5\mathrm{s}$. The thrust $U_1$ and the torque $U_{\xi }$ of the UAV are limited in $\left[0,30\right]$ and $\left[-10,2\right]$, respectively.

Figure 1 presents a three-dimensional plot showing the expected trajectory tracking of the quadrotor UAV in accordance with the methodology proposed in this paper. Figure 2 and Figure 3 depict the position and attitude tracking processes of the UAV, highlighting the controller’s ability to maintain performance even in the presence of disturbances. It can be observed that when the disturbances are small, the tracking performance is not significantly affected. However, under larger disturbances, the UAV’s z and $\psi$ channels deviate noticeably from the desired trajectory but quickly realign. Overall, the designed controller effectively counters external disturbances and achieves the intended tracking objectives, ensuring stable and accurate performance under varying conditions.

Figure 4 presents the input torques of the UAV, while Figure 5 illustrates the outputs of the disturbance observers across the six channels. The disturbance observer is shown to accurately capture the magnitude of the disturbances affecting the system. These observations confirm the effectiveness of the disturbance observer in mitigating the adverse impacts of external disturbances on the quadrotor UAV. As a result, the disturbance observer enhances the UAV’s overall performance and stability, ensuring more reliable and robust operation under challenging conditions. All the results show that the UAV is able to overcome the effects of constant value disturbances and perform the trajectory tracking task with limited inputs.

B. Robustness to Time-Varying Disturbances

In most cases, the external disturbances are variable. Therefore, a second experimental test with the following objectives is designed

$$\left\{\begin{array}{c}{P}_d=R\left(\pi /\phantom{\pi 20}20\right)\left[\begin{array}{c}1.2cos(0.6\ast t)sin(0.6\ast t)\\ 1.2sin(0.6\ast t)\\ 1.2\end{array}\right]\hfill \\ {\psi }_d={\displaystyle \frac{\pi }{4}}\hfill \end{array}\right.$$

(49)

where

$$R\left(\pi /\phantom{\pi 20}20\right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& sin\left(\pi /\phantom{\pi 20}20\right)& cos\left(\pi /\phantom{\pi 20}20\right)\\ 0& -cos\left(\pi /\phantom{\pi 20}20\right)& sin\left(\pi /\phantom{\pi 20}20\right)\end{array}\right]$$

(50)

And

$$\left\{\begin{array}{c}{d}_{\delta }={\left[\begin{array}{c}1+0.1sin(0.1\pi \ast t)\\ 1+0.1cos(0.1\pi \ast t)\\ 3+0.1cos(0.1\pi \ast t)\end{array}\right]}^T\hfill \\ d_{\xi }=\left[\begin{array}{ccc}0.1sin(0.1\pi \ast t)& 0.1cos(0.1\pi \ast t)& 0.1sin(0.1\pi \ast t)\end{array}\right]\hfill \end{array}\right.$$

(51)

The initial position and input limits of the UAV in this experiment are consistent with those used in previous tests. The experimental outcomes, illustrated in Figure 6, Figure 7 and Figure 8, highlight the UAV’s ability to maintain accurate trajectory tracking even in the presence of time-varying disturbances. Despite these dynamic disturbances, the UAV successfully maintains accurate tracking of the target path. The conclusions drawn from this experiment confirm the robustness and stability of the UAV’s control strategy, demonstrating its effectiveness in managing external disturbances while ensuring precise and reliable trajectory tracking.

The output of the drone torque is also well limited to the preset range as seen in Figure 9. Additionally, Figure 10 highlights the capability of the disturbance observer to accurately estimate both the amplitude and frequency of time-varying disturbances, despite their dynamic nature. These findings confirm that the control system successfully maintains the drone’s torque within specified limits and that the disturbance observer provides precise estimations of dynamic disturbances. As a result, the overall robustness and performance of the UAV are significantly enhanced, demonstrating the effectiveness ofthe integrated control and estimation strategies.

The combination of the two aforementioned cases leads to the conclusion that, in the absence of knowledge regarding the mass and moment of inertia of the UAV, and in the presence of input saturation, the force and torque required by the UAV remain within a reasonable range, irrespective of whether the disturbance in question is constant or time-varying. Furthermore, the DO is capable of accurately estimating the magnitude of external disturbances and compensating for them in a manner that is relayed to the controller. This ultimately renders the UAV both robust and capable of excelling in the completion of trajectory tracking tasks.

5. Conclusions

The paper presents a tracking control method for quadrotor UAVs that effectively handles parametric uncertainties, external disturbances, and input saturation, without requiring prior knowledge of the UAV’s mass or moments of inertia. This adaptability allows the control system to perform well under various conditions. Simulations validate the effectiveness of the proposed approach and demonstrate its robustness to various disturbances and uncertainties. Furthermore, the method offers significant advantages over existing control techniques by addressing multiple factors simultaneously, providing a more comprehensive solution for ensuring reliable and accurate trajectory tracking in real-world applications.