Submitted:
12 September 2024
Posted:
14 September 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
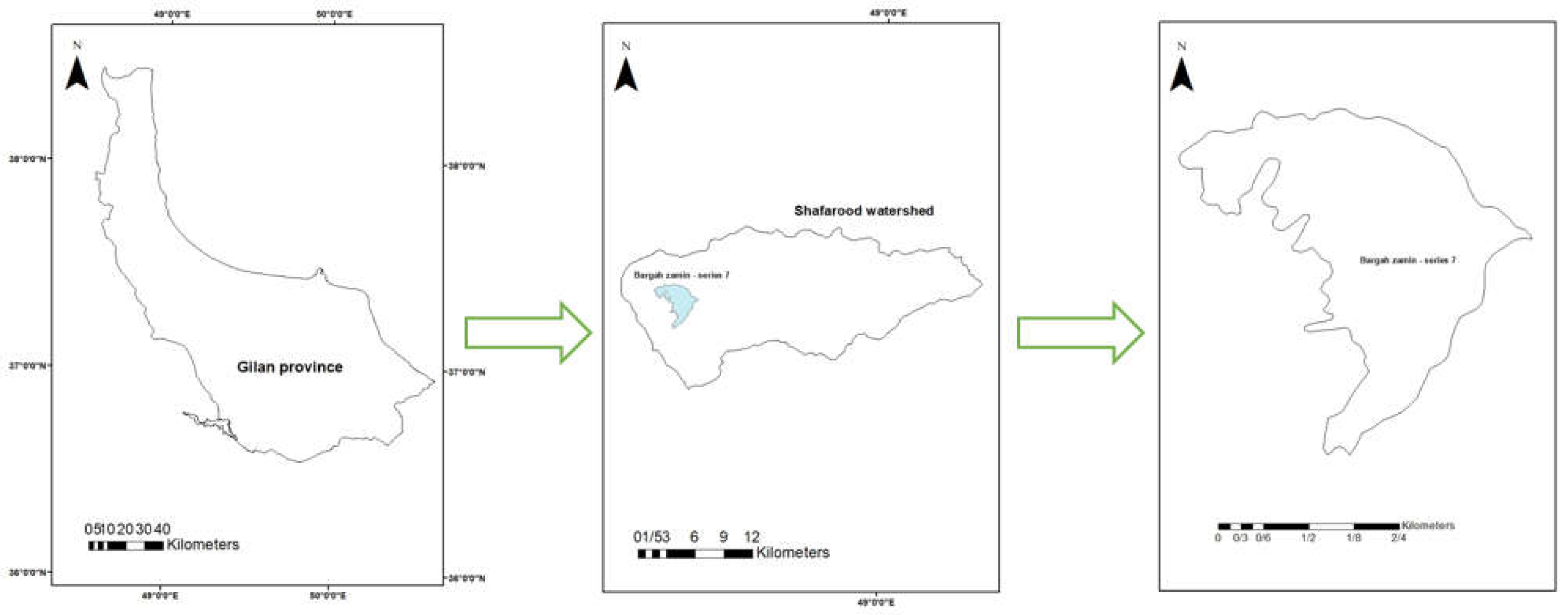
2. Materials and Methods
2.1. Determination of the Volume per ha Relationship
2.2. Growth Model
2.3. Carbon Sequestration Rate
2.4. Stumpage Price
2.5. Determining the Number of Labour
2.6. Sensitivity Analysis
2.7. Questionnaire Design
2.8. Multi-Objective Model
2.9. ε-epsilon Constraint Method
2.10. Lexicographic Optimization Method
2.11. Multi-Objective Game Theory Model (MOGM)
2.12. Sensitivity Analysis
2.13. Objective Functions and Input Parameters
3. Results
3.1. Determining the Volume per ha for Different Tree Species
3.2. The Amount of Carbon Stored in the Optimal Biomass
| Species Name | Carbon model | Predicted volume (m3/ha) | Predicted carbon (tons/ha) | Coefficients |
| Beech | 0.0000004 + X =0.335 Y | 251.4 | 84.22 | 0.335 |
| Hornbeam | 0.000008 + X 0.3501 = Y | 59.4 | 20.8 | 0.3501 |
| Oak | 0.0003 + X =0.32 Y | 73.1 | 23.39 | 0.32 |
| Alder | 0.000004 + X =0.29 Y | 41.1 | 11.92 | 0.29 |
| Other industrial species | 0.0002 + X =0.3107 Y | 32 | 19.88 | 0.3107 |
| - | - | 457 | 160.21 | - |
3.2.1. The Net Present Value of Carbon Sequestration
3.3. Growth Prediction
3.4. Determining the Relationship for the Number of Labour
3.4.1. Labour Income
3.5. Stumpage Price for Various Tree Species
3.5.1. Net Present Value of Harvestable Volume
3.6. Multi-Objective Model
3.7. Game Theory Model
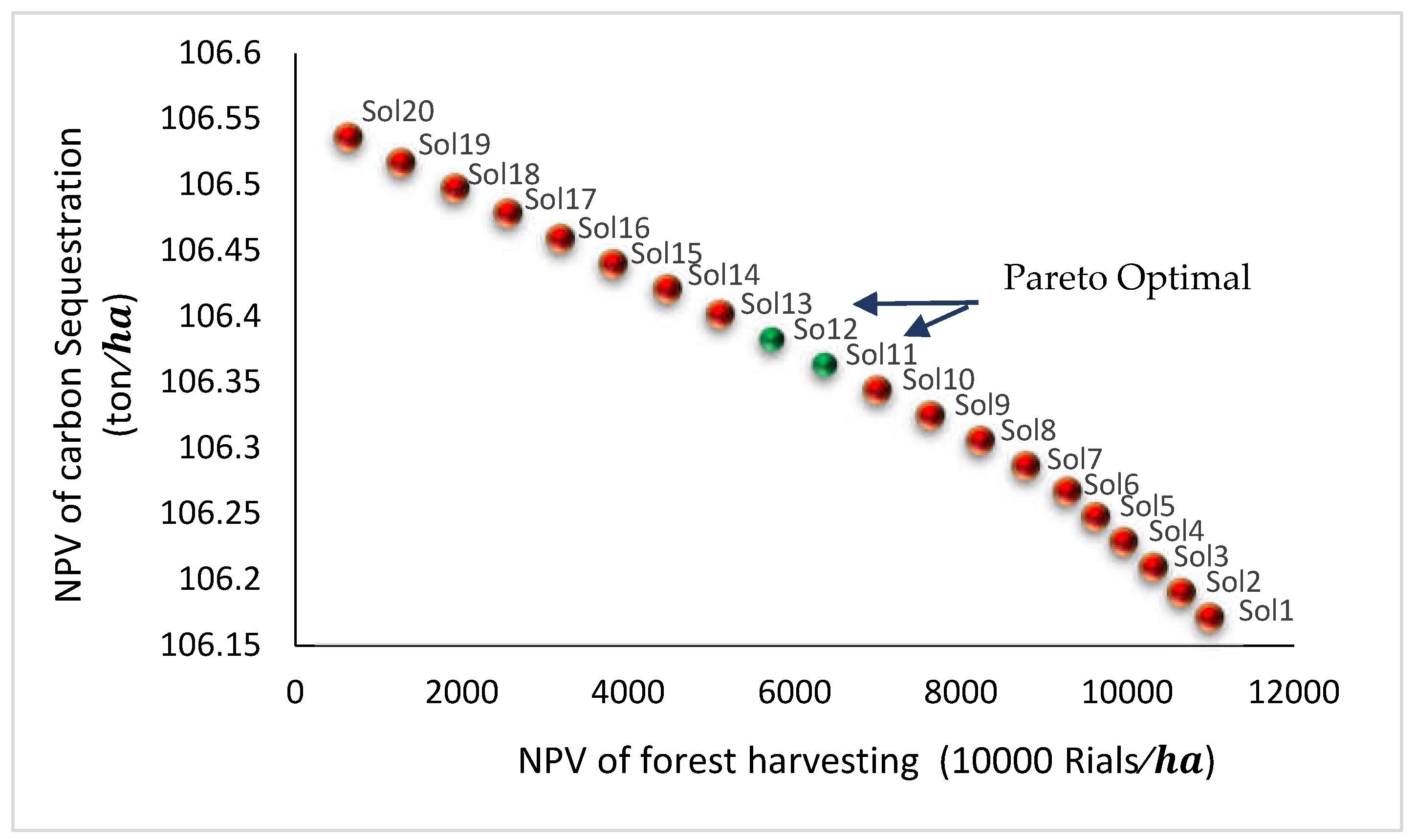
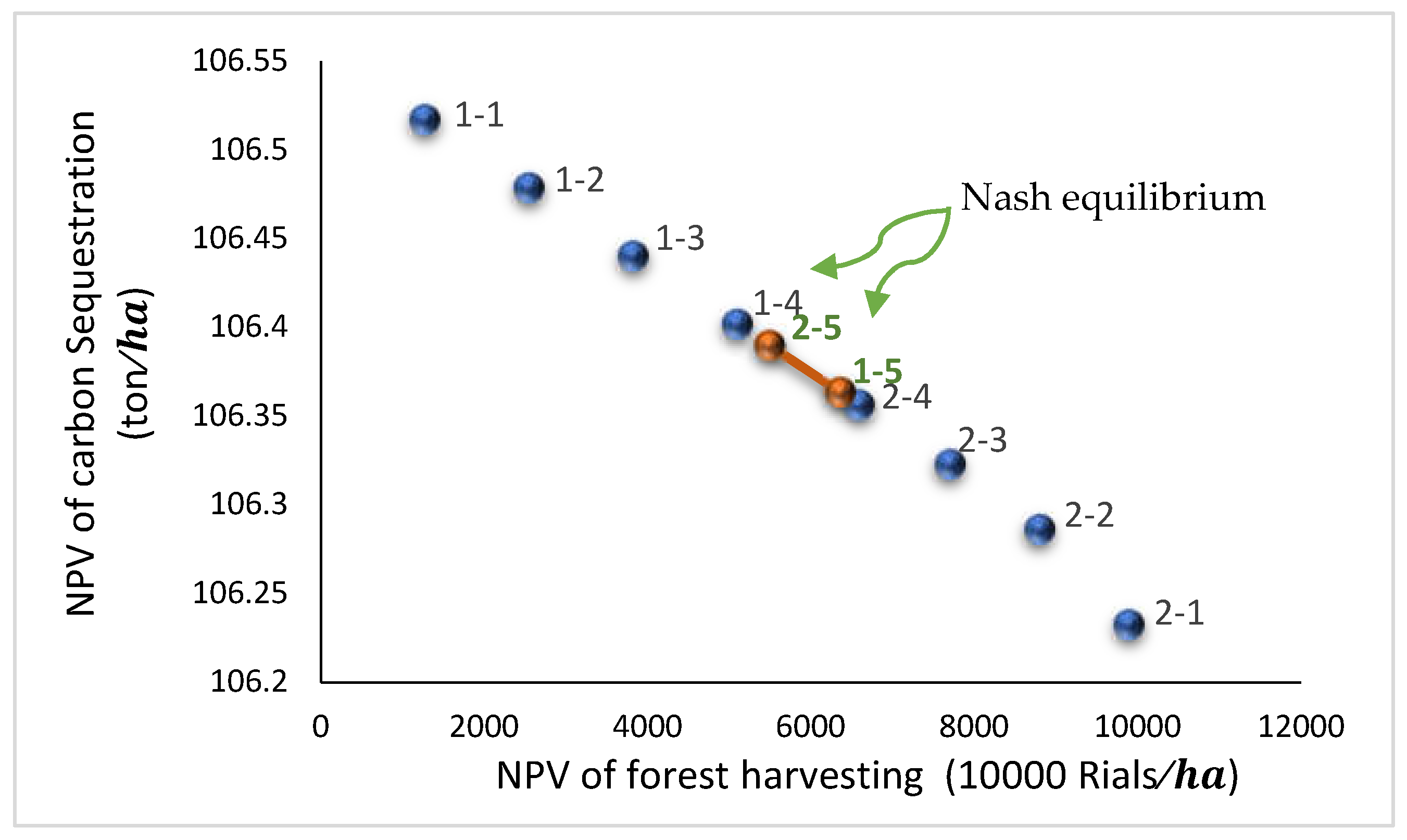
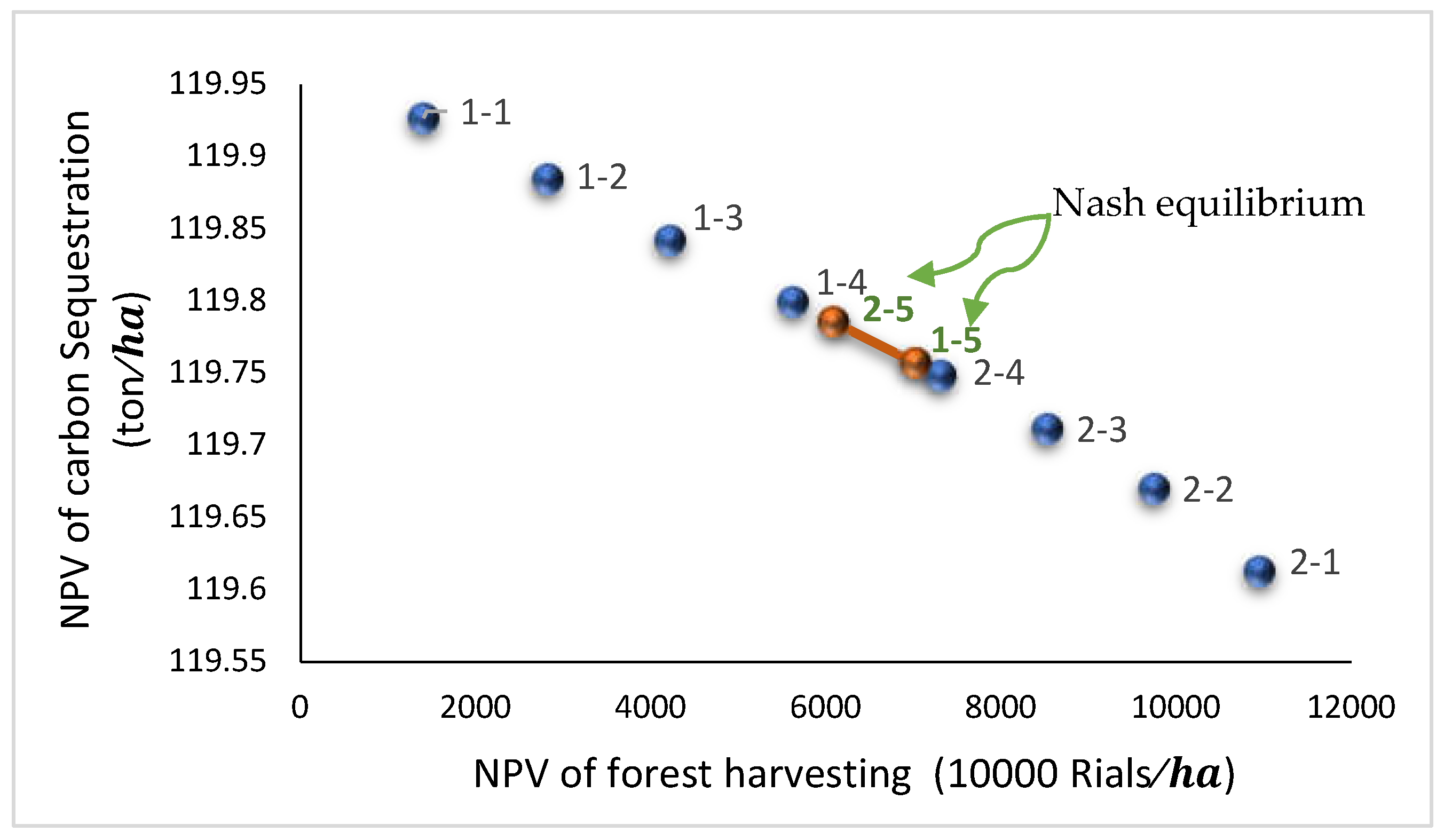
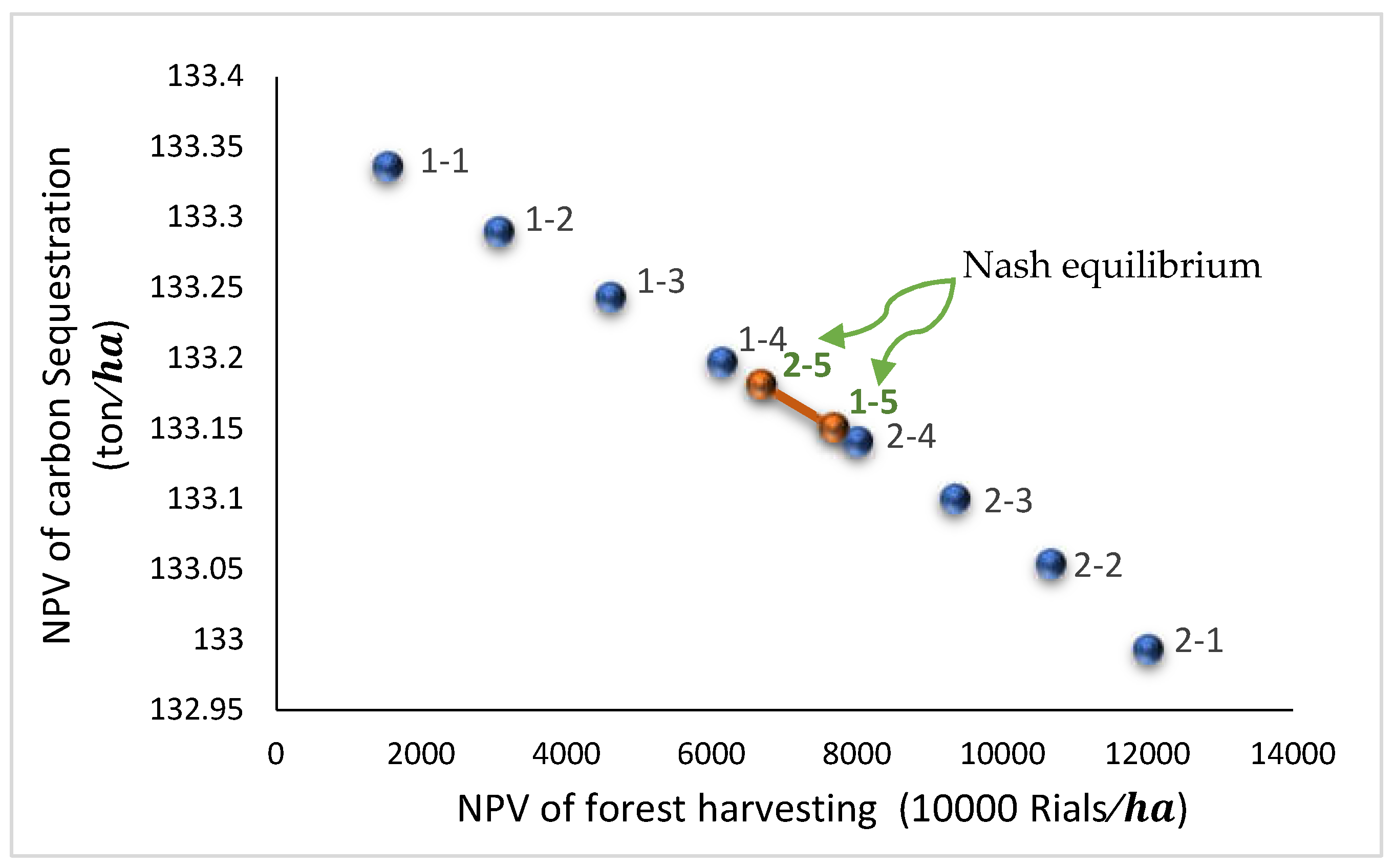
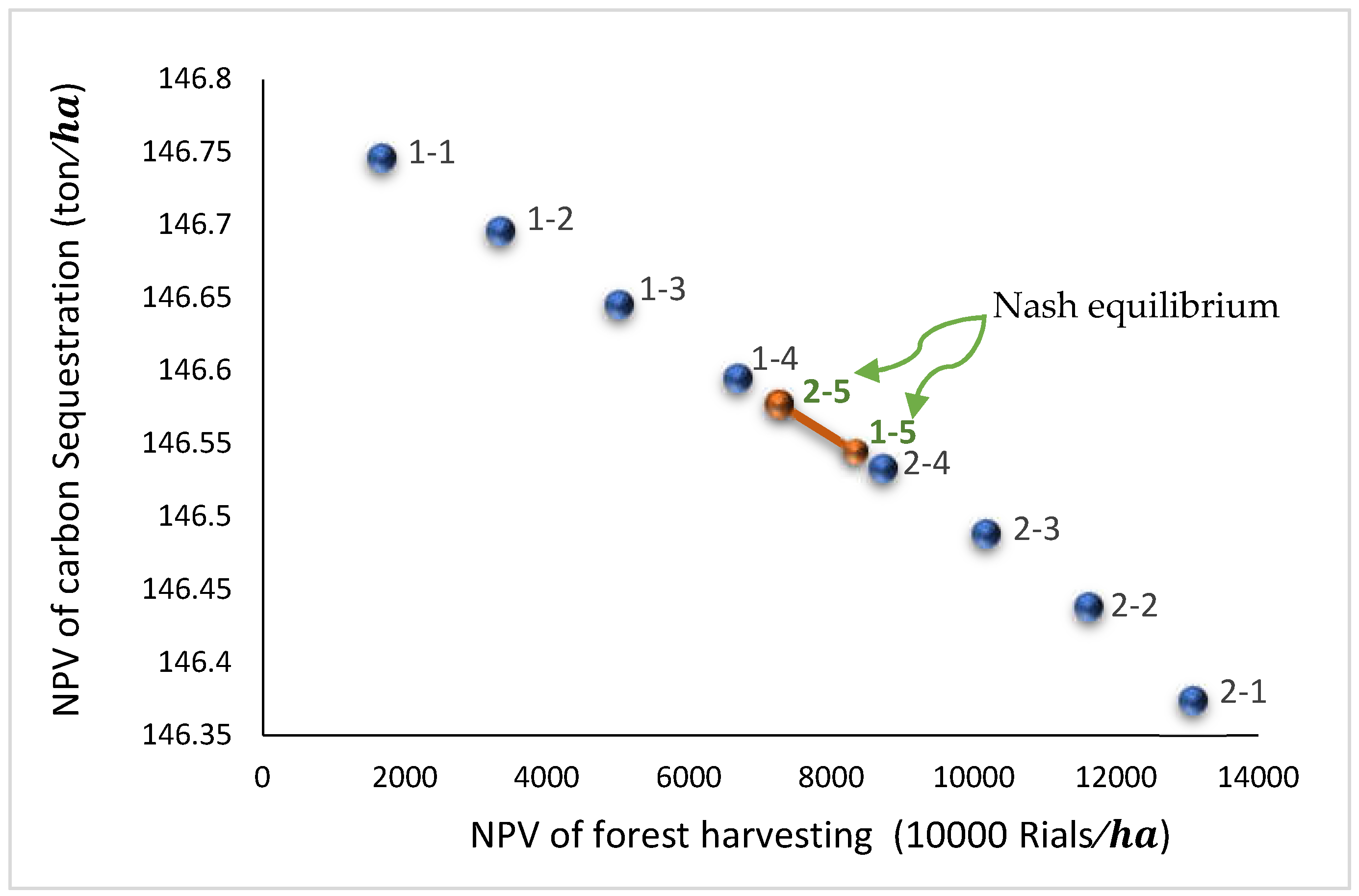
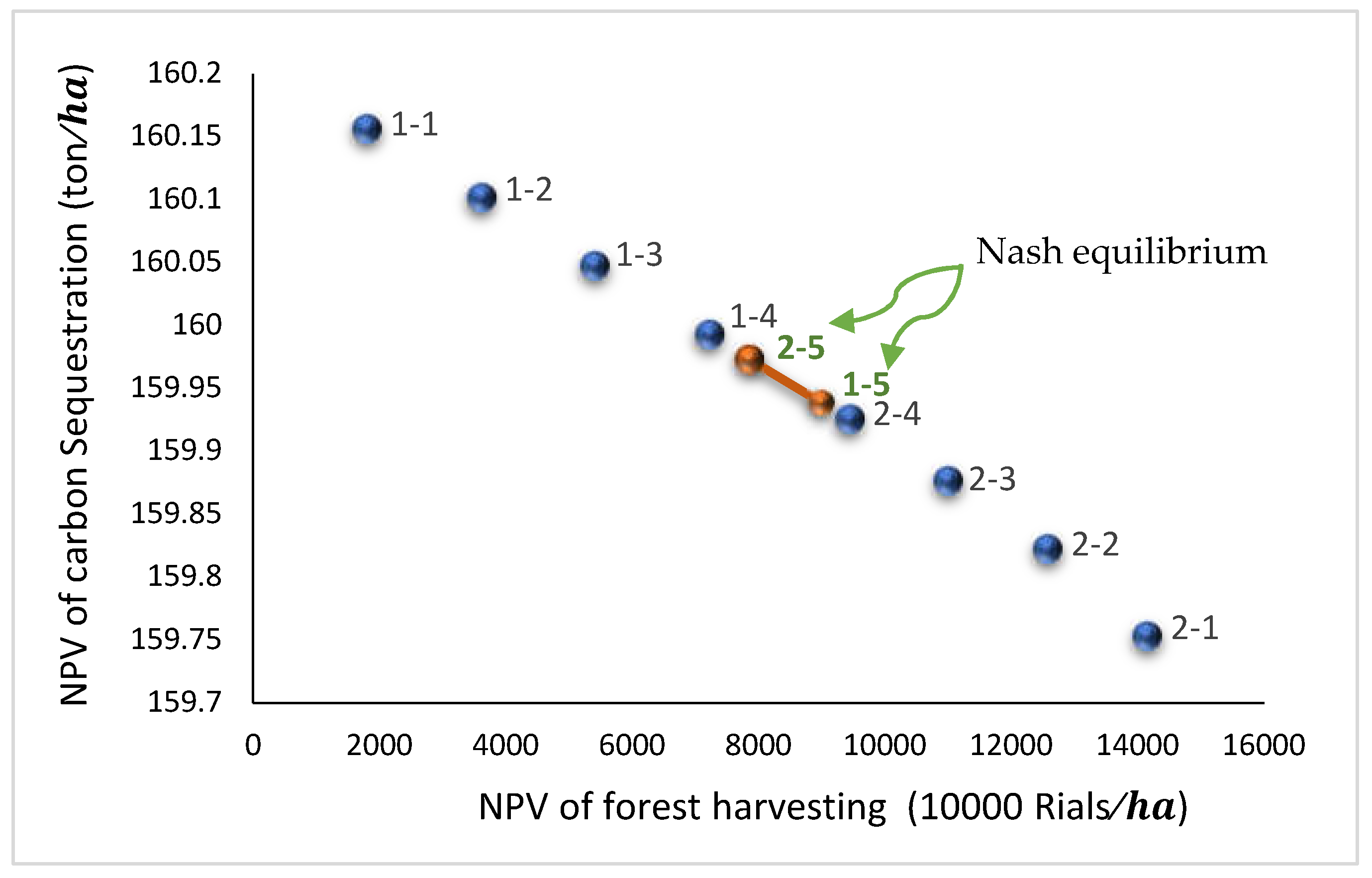
- In the fifth round of bargaining, a Nash equilibrium was reached, indicated by the intersection marked "1-5" and "2-5." At this equilibrium point:
- The economic player achieved an NPV of 6363.748 (10,000 Rials) and carbon sequestration of 106.3633 (tons/ha).
- The environmental player achieved an NPV of 5496.699 (10,000 Rials) and carbon sequestration of 106.3897 tons/ha.
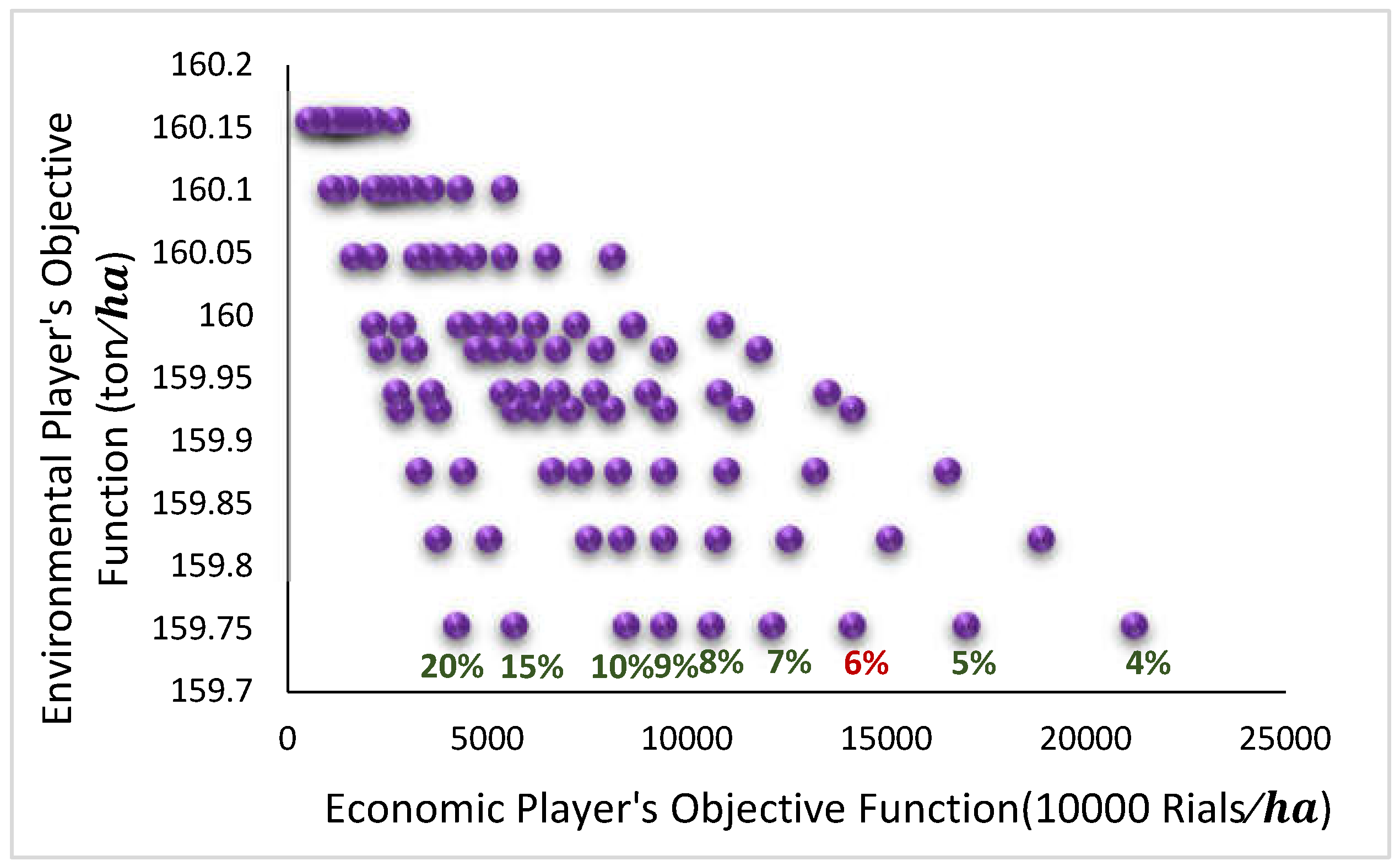
3.8. Sensitivity Analysis
3.8.1. Multi-Objective Model
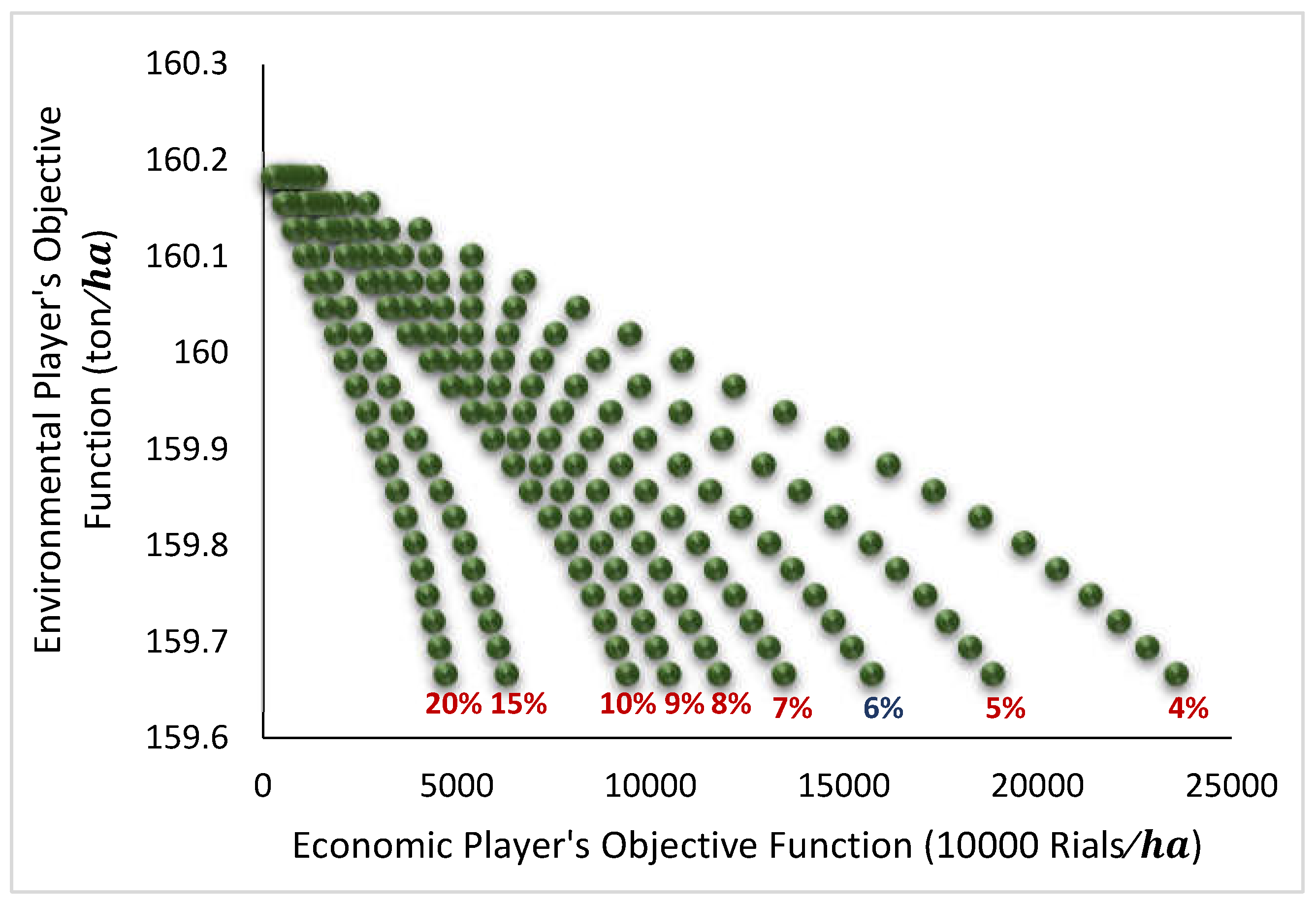
3.8.2. Game Theory Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pohjanmies, T.; Eyvindson, K.; Triviño, M.; Mönkkönen, M. More is more?: Forest management allocation at different spatial scales to mitigate conflicts between ecosystem services. Landscape Ecology. 2017, 32, 2337–2349. [Google Scholar] [CrossRef]
- Mazziotta, A.; Lundström, J.; Forsell, N.; Moor, H.; Eggers, J.; Subramanian, N.; Aquilue, N.; Moran-Ordonez, A.; Brorons, L.; Snall, T. More future synergies and less trade-offs between forest ecosystem services with natural climate solutions instead of bioeconomy solutions. Global Chang Biology. 2022, 28, 6333–6348. [Google Scholar] [CrossRef] [PubMed]
- Nabhani, A.; Mardaneh, E.; Sjølie, H.K. Multi-objective optimization of forest ecosystem services under uncertainty. Ecological Modelling. 2024, 494, 110777. [Google Scholar] [CrossRef]
- Lohmander, P. Optimization in forestry: Motivation, principles, methods and results. Forest Ecology and Management Seminar Series of SLU, Umea. 2011, December 13.
- Marvie Mohajer, M.R. Silvicultur. Press: Tehran University, Iran. 2005, p: 410.
- Karami, H.; Rezvani, M.; Jafari, S. Recent Trends in Deforestation and Biodiversity Loss in Iran’s Northern Forests. Journal of Environmental Management. 2023, 315, 112–125. [Google Scholar] [CrossRef]
- Jazirehi, M.H. Analysis and assessment of Iranian forestry organization, in Management of Northern Forest and Sustainable Development. Journal of Iranian Natural Resources. 2000, 55, 13–45. [Google Scholar]
- Shamekhi, T. Why does the industrial sector coulden›t utilise the ecological potentiel of northern forest. Iranian Journal of Natural Resources. 1993, 46, 79–93. [Google Scholar]
- Purnomo, H.; Yasmi, Y.; Prabhu, R.; Hakim, S.; Jafar, A. Collaborative modelling to support forest management: Qualitative systems analysis at Lumut Mountain, Indonesia Small-scale. Forest Economics, Management and Policy. 2003, 2, 259–275. [Google Scholar] [CrossRef]
- Linkevičius, E.; Borges, J.G.; Doyle, M.; Pülzl, H.; Nordström, E.M.; Vacik, H.; Brukas, V.; Biber, P.; Teder, M.; Kaimre, P.; Synek, M.; Garcia-Gonzalo, J. Linking forest policy issues and decision support tools in Europe. Forest Policy and Economics. 2019, 103, 4–16. [Google Scholar] [CrossRef]
- Nordström, E.M.; Nieuwenhuis, M.; Başkent, E.; Biber, P.; Black, K.; Borges, J.G.; Bugalho, M.; Corradini, G. Forest decision support systems for the analysis of ecosystem services provisioning at the landscape scale under global climate and market change scenarios. European Journal of Forest Research 2019, 138, 561–581. [Google Scholar] [CrossRef]
- Eyvindson, K.; Burgas, D.; Antón-Fernández, C.; Hakanen, J.; Emmerich, M.; Klein, J.; Mönkkönen, M.; Snäll, T.; Caicoya, A.T.; Vergarechea, M.; Blattert, C. MultiOptForest: An interactive multi-objective optimization tool for forest planning and scenario analysis. Open Research Europe. 2023, 3. [Google Scholar] [CrossRef]
- Raquel, S.; Ferenc, S.; Emery, C., Jr.; Abraham, R. Application of game theory for a groundwater conflict in Mexico. Journal of environmental management. 2007, 84, 560–571. [Google Scholar] [CrossRef] [PubMed]
- Lohmander, P. Rational Research in Forest Production and Forest Management with Consideration of Mixed Species Forest Management and Risk. Operations Research for the Future Forest Management, University of Guilan, Iran. 2014, March 8-12.
- Soltani, A.; Sankhayan, P.L.; Hofstad, O. Theory of non-cooperative games as a tool to understand state-local conflicts in forest management. Scandinavian Society of Forest Economics Drøbak, Norway. 2016, 46, 208–216. [Google Scholar]
- Hartgraves, C.R. The role of planning in multiple use management", in: Proceedings of Multiple-use Management of Forest Resources. Clemson Univ., Clemson, SC. 1979, 191-196.
- Bare, B.B.; Briggs, D.G.; Roise, J.P.; and Schreuder, G.F. A survey of systems analysis models in forestry and the forest products industries. European Journal of Operational Research. 1984, 18, 1–18. [Google Scholar] [CrossRef]
- Harrison, T.P.; de Kluyver, C.A. MS/OR and the forest products industry: new directions. Interfaces. 1984, 14, 1–7. [Google Scholar] [CrossRef]
- Chang, S.J.; Buongiorno, J. A programming model for multiple use forestry. Journal of Environmental Management. 1981, 13, 45–58. [Google Scholar] [CrossRef]
- Shaik Md, Y.H.; Robak, E.W. A Forest Management Process to Incorporate Multiple Objectives: a Framework for Systematic Public Input. Forests. 2010, 1, 99–113. [Google Scholar] [CrossRef]
- Mohammadi Limaei, S.; Seddigh Koohi, M.; Rostami Shahraji, T. Goal programming approach for sustainable forest management (Case Study; Iranian Caspian Forests). Journal of Forestry Research. 2014, 25, 429–435. [Google Scholar] [CrossRef]
- Jafari, A.; Najafi, A.; García Melón, M. Decision-making for the selection of a best wood extraction method: An analytic network process approach. Forest Policy and Economics. 2015, 50, 200–209. [Google Scholar] [CrossRef]
- Heaps, T. Convergence of optimal harvesting policies to a normal forest. Journal of Economic Dynamics and Control. 2015, 54, 74–85. [Google Scholar] [CrossRef]
- Arias-Rodil, M.; Dieguez-Aranda, U.; Vazquez-Mendez, M.E. A differentiable optimization model for the management of single-species, even-aged stands. Canadian Journal of Forest Research. 2017, 47(4), 506–514. [Google Scholar] [CrossRef]
- Gonzalez-Gonzalez, J.M.; Vazquez-Mendez, M.E.; Dieguez-Aranda, U. Simultaneous optimization of even flow and land and timber value in forest planning: a continuous approach. Forest Ecosystem. 2021, 8, 1–14. [Google Scholar] [CrossRef]
- Gonzalez-Gonzalez, J.M.; Vazquez-M’endez, M.E.; Dieguez-Aranda, U. Multi-objective models for the forest harvest scheduling problem in a continuous-time framework. Forest Policy and Economics. 2022, 136, 102687. [Google Scholar] [CrossRef]
- Blattert, C.; Mönkkönen, M.; Burgas, D.; Di Fulvio, F.; Caicoya, A.T.; Vergarechea, M.; Klein, J.; Hartikainen, M.; Antón-Fernández, C.; Astrup, R.; Emmerich, M.; Forsell, N.; Lukkarinen, J.; Lundström, J.; Pitzén, S.; Poschenrieder, W.; Primmer, E.; Snäll, T.; Eyvindson, E. Climate targets in European timber-producing countries conflict with goals on forest ecosystem services and biodiversity. Communications Earth & Environment 2023, 4. [Google Scholar] [CrossRef]
- Eyvindson, K.; Hartikainen, M.; Miettinen, K.; Kangas, A. Integrating risk management tools for regional forest planning: an interactive multiobjective value-at-risk approach. Canadian Journal of Forest Research. 2018, 48, 766–773. [Google Scholar] [CrossRef]
- Schroder, S.A.; Tóth, S.F.; Deal, R.L.; Ettl, G.J. Multi-objective optimization to evaluate tradeoffs among forest ecosystem services following fire hazard reduction in the Deschutes National Forest, USA. Ecosystem Services. 2016, 22, 328–347. [Google Scholar] [CrossRef]
- Tóth, S.F.; Ettl, G.J.; Könnyű, N.; Rabotyagov, S.S.; Rogers, L.W.; Comnick, J.M. ECOSEL: Multi-objective optimization to sell forest ecosystem services. Forest Policy and Economics. 2013, 35, 73–82. [Google Scholar] [CrossRef]
- Tóth, S.F.; McDill, M.E. Finding Efficient Harvest Schedules under Three Conflicting Objectives. Forest Science. 2009, 55, 117–131. [Google Scholar] [CrossRef]
- Vergarechea, M.; Astrup, R.; Fischer, C.; Øistad, K.; Blattert, C.; Hartikainen, M.; Eyvindson, K.; Di Fulvio, F.; Forsell, N.; Burgas, D.; Toraño-Caicoya, A.; Mönkkönen, M.; Antón-Fernández, C. Future wood demands and ecosystem services trade-offs: A policy analysis in Norway. Forest Policy and Economics. 2023, 147, 102899. [Google Scholar] [CrossRef]
- Mohammadi Limaei, S. Mixed strategy game theory, application in forest industry. Forest Policy and Economics. 2010, 12, 527–531. [Google Scholar] [CrossRef]
- Holopainen, M.; Mäkinen, A.; Rasinmäki, J.; Hyytiäinen, K.; Bayazidi, S.; Pietilä, I. Comparison of various sources of uncertainty in stand-level net present value estimates. Forest Policy and Economics. 2010, 12, 377–386. [Google Scholar] [CrossRef]
- Alonso-Ayuso, A.; Escudero, L.F.; Guignard, M.; Quinteros, M.; Weintraub, A. Forestry management under uncertainty. Annals of Operations Research. 2011, 190, 17–39. [Google Scholar] [CrossRef]
- Piazza, A.; Pagnoncelli, B.K. The optimal harvesting problem under price uncertainty. Annals of Operations Research. 2014, 217, 425–445. [Google Scholar] [CrossRef]
- Eyvindson, K.; Kangas, A. Evaluating the required scenario set size for stochastic programming in forest management planning: incorporating inventory and growth model uncertainty. Canadian Journal of Forest Research. 2016, 46. [Google Scholar] [CrossRef]
- Alvarez-Miranda, E.; Garcia-Gonzalo, J.; Ulloa-Fierro, F.; Weintraub, A.; Barreiro, S. A multicriteria optimization model for sustainable forest management under climate change uncertainty: An application in Portugal. European Journal of Operational Research. 2018, 269, 79–98. [Google Scholar] [CrossRef]
- Pais, C.; Weintraub, A.; Shen, Z.-J.M. Stochastic forestry planning under market and growth uncertainty. Computers & Operations Research. 2023, 153, 106182. [Google Scholar] [CrossRef]
- Swindel, B. Theory of games and applications in forestry [Management strategies, mathematical models]. USDA Forest Service, General Technical Report SE (USA). 1984, 26.
- Von Neumann, J.; Morgenstern, O. Theory of games and economic behavior; Princeton university press: Princeton, NJ, 1944; p. 625. [Google Scholar]
- Nash, J.F. The bargaining problem. Econometrica. 1950, 18, 155–162. [Google Scholar] [CrossRef]
- Camerer, C.F. Progress in behavioral game theory. Journal of economic perspectives. 1997, 11, 167–188. [Google Scholar] [CrossRef]
- Myerson, R.B. On the Value of Game Theory in Social Science. Rationality and Society. 1992, 4, 62–73. [Google Scholar] [CrossRef]
- Zoghi, M.; Safae, A.; Malekmohammadi, B. Insights on Game Theory in Conflict Analysis of land use change (Case Study: Tehran Dar Abad land area). Geographical Urban Planning Research Journal. 2014, 2, 391–407. [Google Scholar]
- Davis, J.B. Forest Fire Control Decision Making Under Conditions of Uncertainty. Journal of Forestry. 1968, 66, 626–631. [Google Scholar] [CrossRef]
- Pahlavani, P.; Sahraiian, H.R.; Raei, A. Modeling the spreading of forest fire based on a cellular automata using the markov chain and MOLA with a neighborhood filter. Engineering Journal of Geospatial Information Technology. 2017, 5, 99–122. [Google Scholar] [CrossRef]
- Carraro, C.; Marchiori, C.; Sgobbi, A. Negotiating on water: insights from non-cooperative bargaining theory. Environment and Development Economics. 2007, 12, 329–349. [Google Scholar] [CrossRef]
- Parrachino, I.; Zara, S.; Patrone, F. Cooperative Game Theory and its Application to Natural, Environmental, and Water Resource Issues: 3. Application to Water Resources. World Bank Policy Research Working Paper. 2006, 4074. Available at SSRN: https://ssrn.com/abstract=946833.
- Sabuhi, M.; Mojarad, E. Application of Game Theory for Groundwater Resources Management of Atrak. Journal of Agricultural Economics and Development. 2010, 24, 1–12. [Google Scholar]
- Homayounfar, M.; Ganji, A.; Khalili, D.; Mousavi, A.A. A Model for Reservoir Operation Based on the Game Theory. Iran-Water Resources Research. 2010, 6, 14–26. [Google Scholar]
- Mohammadi Limaei, S. Economically optimal values and decisions in Iranian forest management. Ph.D. Thesis, Swedish University of Agriculture Sciences, Umea, 2006; p. 148. [Google Scholar]
- Mohammadi Limaei, S. A game theory approach to the sawnwood and pulpwood markets in the north of Iran. Caspian Journal of Environmental Sciences. 2007, 5, 1–10. [Google Scholar]
- Hejazian, M.; Lotfalian, M.; Lindroos, O.; Mohammadi Limaei, S. Wood transportation machine replacement using goal programming. Scandinavian Journal of Forest Research. 2019, 34, 635–642. [Google Scholar] [CrossRef]
- Rodrigues, A.; Koeppl, H.; Ohtsuki, H.; Satake, A. A game theoretical model of deforestation in human–environment relationships. Journal of theoretical biology. 2009, 258, 127–134. [Google Scholar] [CrossRef]
- Shahi, C.; Shashi, K. An evolutionary game-theoretic approach to the strategies of community members under Joint Forest Management regime. Forest Policy and Economics. 2007, 9, 763–775. [Google Scholar] [CrossRef]
- Lee, C.-S. Multi-objective game-theory models for conflict analysis in reservoir watershed management. Chemosphere. 2012, 87, 608–613. [Google Scholar] [CrossRef]
- Eyvindson, K.; Burgas, D.; Antón-Fernández, C.; Hakanen, J.; Emmerich, M.; Klein, J.; Mönkkönen, M.; Snäll, T.; Caicoya, A.T.; Vergarechea, M.; Blattert, C. MultiOptForest: An interactive multi-objective optimization tool for forest planning and scenario analysis. Open Research Europe. 2023, 3. [Google Scholar] [CrossRef]
- Etemad, S.S.; Mohammadi Limaei, S.; Olsson, L.; Yousefpour, R. Forest management decision-making using goal programming and fuzzy analytic hierarchy process approaches (case study: Hyrcanian forests of Iran). Journal of Forest Science. 2019. 65, 368–379. [CrossRef]
- Shafarood Forestry plan booklet. Forestry Planning of District 7 of Shafarood, Watershed Number 9. Guilan Department of Natural Resources and Watershed Management, Rasht, Iran. 2011, 235. (in Persian).
- Schaefer, M.B. Some aspects of the dynamics of populations important to the management of the commercial marine fisheries. Inter-American Tropical Tuna Commission Bulletin. 1954, 1, 23–56. [Google Scholar] [CrossRef]
- Kabiri Koupaei, K. Carbon sequestration and its spatial pattern in the above-ground woody compartment of a pure and mixed beech stand: A case study of Gorazbon Forest, north of Iran. Ph.D. Thesis, University of Tehran, Karaj, 2009; p. 102. [Google Scholar]
- Snowdon, P.; Raison, R.; Keith, H.; Ritson, P.; Grierson, P.; Adams, M.; Montagu, K.; Bi, H.; Burrows, W.; Eamus, D. Protocol for sampling tree and stand biomass. Australian Greenhouse Office. 2002, 31. [Google Scholar] [CrossRef]
- Mohammadi Limaei, S.; Lohmander, P. Stochastic dynamic programming with Markov chains for optimal sustainable control of the forest sector with continuous cover forestry Iranian. Journal of Operations Research. 2017, 8, 91–96. [Google Scholar] [CrossRef]
- Mohammadi Limaei, S. Economics Optimization of Forest Management. LAP LAMBERT Academic Publication. 2011, p: 140. (February 3, 2011).
- Mavrotas, G. Effective implementation of the ε-constraint method in multi-objective mathematical programming problems. Applied mathematics and computation. 2009, 213, 455–465. [Google Scholar] [CrossRef]
- Parrachino, I.; Zara, S.; Patrone, F. Cooperative Game Theory and its Application to Natural, Environmental, and Water Resource Issues: 3. Application to Water Resources. World Bank Policy Research Working Paper. 2006, 4074. Available at SSRN: https://ssrn.com/abstract=946833.
- Nash, J.F. Noncooperative games. Annals of Mathematics. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Britz, V.; Herings, J.J.; Predtetchinski, A. Theory of the Firm: Bargaining and Competitive Equilibrium. SSRN Electronic Journal 2010, 34. [Google Scholar]
- Ücler, G.; Özsahin, S. Money-Physical Capital Nexus: How Valid Is McKinnon Complementarity Hypothesis In Turkish Economy? Alphanumeric Journal. 2015, 2, 1–12. [Google Scholar] [CrossRef]
- World Bank. Carbon Pricing Dashboard 2020. Available online: https://carbonpricingdashboard.worldbank.org (accessed on 21 February 2021).
- Gold, Coin, and Currency Information Network. Free Market Exchange Rates 2021. Available online: https://www.tgju.org/currency (accessed on 15 January 2021).
- Moradi, S.; Mohammadi Limaei, S.M. Multi-objective game theory model and fuzzy programing approach for sustainable watershed management. Land Use Policy. 2018, 71, 363–371. [Google Scholar] [CrossRef]
- Koltarza, J. Application of Nash equilibrium for developing an optimal forest harvesting strategy in Toruń Forest District. Computer Science and Game Theory, 2024; 11. [Google Scholar] [CrossRef]
- Siangulube, F.S. The Role of Multistakeholder Platforms in Environmental Governance: Analyzing Stakeholder Perceptions in Kalomo District, Zambia, Using Q-Method. Environmental Management. 2024, 74, 13–30. [Google Scholar] [CrossRef]
- Ratner, B.D.; Larson, A.M.; Sarmiento Barletti, J.P.; ElDidi, H.; Catacutan, D.; Flintan, F.; Suhardiman, D.; Falk, T.; Meinzen-Dick, R. Multistakeholder platforms for natural resource governance: Lessons from eight landscape-level cases. Ecology and Society. 2022, 27, 2. [Google Scholar] [CrossRef]
- Madani, K.; Rouhani, O.M.; Mirchi, A.; Gholizadeh, S. A negotiation support system for resolving an international trans-boundary natural resource conflict. Environmental modelling & software. 2014, 51, 240–249. [Google Scholar] [CrossRef]
- Çalışkan, H.; Özden, S. Game Theory Approach to Decision Making Processes in International Forestry Policies. ASEAN Journal of Science and Technology. 2022, 3, 7–13. [Google Scholar]
- Mohammadi Limaei, S.; Mohammadi, Z. Optimal Forest Management Using Stochastic Dynamic Programming Approach–A Case Study from the Hyrcanian Forests of Iran. Journal of Sustainable Forestry. 2023, 42, 120–134. [Google Scholar] [CrossRef]
| Parameters | Explanations |
| The NPV of timber harvesting of species b | |
| Amount of harvesting coefficient for species b | |
| Growth rate of species b | |
| Number of species b per ha | |
| Volume of species b per ha | |
| Maximum number of labour | |
| coefficient used for each labour | |
| Income of each labour | |
| Income coefficient from each labour for harvesting species b | |
| Allowed growth capacity for species b | |
| Growth coefficient for species b | |
| Optimal inventory for species b | |
| Value ofharvestable volume for species b | |
| Coefficient of harvestable volume for Species b | |
| Total NPV | |
| NPV Coefficient | |
| Amount of carbon sequestration | |
| Carbon sequestration coefficient |
| (1) | ||
| (2) | ||
| (3) | ||
| (4) | ||
| (5) | ||
| (6) | ||
| (7) | ||
| (8) | ||
| (9) | ||
| (10) | ||
| (11) | ||
| (12) | ||
| (13) | ||
| (14) |
| Species Name | Variable | Acceptable volume (%) | Acceptable Volume(m3/ha) |
| Beech | X1 | 55 | 251.4 |
| Hornbeam | X2 | 13 | 59.4 |
| Oak | X3 | 16 | 73.1 |
| Alder | X4 | 9 | 41.1 |
| Other industrial species | X5 | 7 | 32 |
| Total | X | 100 | 457 |
| Species Name | Variable | Logarithmic Functions | Predicted volume (m³/ha) | Predicted growth (m³/ha) | Coefficients |
| Beech | X1 | 251.4 | 1.34 | 0.0053 | |
| Hornbeam | X2 | 59.4 | 0.44 | 0.0074 | |
| Oak | X3 | 73.1 | 0.4 | 0.0055 | |
| Alder | X4 | 41.1 | 0.68 | 0.0165 | |
| Other industrial species | X5 | 32 | 0.51 | 0.0159 | |
| Total | X | 457 | 3.37 | - |
| Species Name | Variable | Mean expected stumpage price (10000 Rials/ m3) | Harvestable volume (m3/ha) | NPV of harvestable volume (10000 Rials) |
| Beech | X1 | 667.22 | 0.67 | 7175.56 |
| Hornbeam | X2 | 377.59 | 0.22 | 1333.38 |
| Oak | X3 | 405.46 | 0.2 | 1301.62 |
| Alder | X4 | 571.86 | 0.34 | 3120.91 |
| Other industrial species | X5 | 540.08 | 0.255 | 2210.58 |
| Total | X | - | 1.685 | 15142.05 |
| Objective functions | Solution | |||||
| () Beech (m3/ha) | Hornbeam () (m3/ha) |
() Alder (m3/ha) | () Oak (m3/ha) | () Other (m3/ha) | (m3/ha) | |
| 170 | 77.42 | 3.16 | 37.11 | 16.26 | 303.96 | |
| 190.35 | 72.92 | 20.65 | 38.11 | 20.2 | 342.21 | |
| 210.7 | 68.41 | 38.13 | 39.11 | 24.13 | 380.475 | |
| 231.05 | 63.91 | 55.62 | 40.1 | 28.07 | 418.74 | |
| 251.4 | 59.4 | 73.1 | 41.1 | 32 | 475 | |
| Grid | Solutions | NPV of forest harvesting (Z1) (10000 Rials/ha) |
NPV of carbon sequestration (Z2) (ton/ha) |
Growth (G) (m3/ha) |
Amount of harvest (m3/ha) |
|---|---|---|---|---|---|
|
Grid 1 (303.96 m3/ha) |
Solution 1 | 10993.4 | 106.17 | 1.185 | 1.128 |
| Solution 2 | 10648.08 | 106.19 | 1.24 | 1.073 | |
| Solution 3 | 10302.76 | 106.21 | 1.295 | 1.018 | |
| Solution 4 | 9957.43 | 106.23 | 1.35 | 0.963 | |
| Solution 5 | 9612.11 | 106.25 | 1.4 | 0.913 | |
| Solution 6 | 9266.79 | 106.27 | 1.459 | 0.854 | |
| Solution 7 | 8779.62 | 106.29 | 1.519 | 0.794 | |
| Solution 8 | 8223.06 | 106.31 | 1.581 | 0.732 | |
| Solution 9 | 7626.5 | 106.32 | 1.645 | 0.668 | |
| Solution 10 | 6995.12 | 106.34 | 1.712 | 0.601 | |
| Solution 11 | 6363.75 | 106.36 | 1.778 | 0.535 | |
| Solution 12 | 5732.37 | 106.38 | 1.844 | 0.469 | |
| Solution 13 | 5101 | 106.4 | 1.91 | 0.403 | |
| Solution 14 | 4463.93 | 106.42 | 1.969 | 0.344 | |
| Solution 15 | 3826.22 | 106.44 | 2.026 | 0.287 | |
| Solution 16 | 3188.52 | 106.46 | 2.083 | 0.23 | |
| Solution 17 | 2550.82 | 106.48 | 2.141 | 0.172 | |
| Solution 18 | 1913.11 | 106.5 | 2.198 | 0.115 | |
| Solution 19 | 1275.41 | 106.52 | 2.255 | 0.058 | |
| Solution 20 | 637.7 | 106.54 | 2.313 | 0 |
| Grid | Solutions | NPV of forest harvesting (Z1) (10000 Rials/ha) |
NPV of carbon sequestration (Z2) (ton/ha) |
Growth (G) (m3/ha) |
Amount of harvest (m3/ha) |
|---|---|---|---|---|---|
|
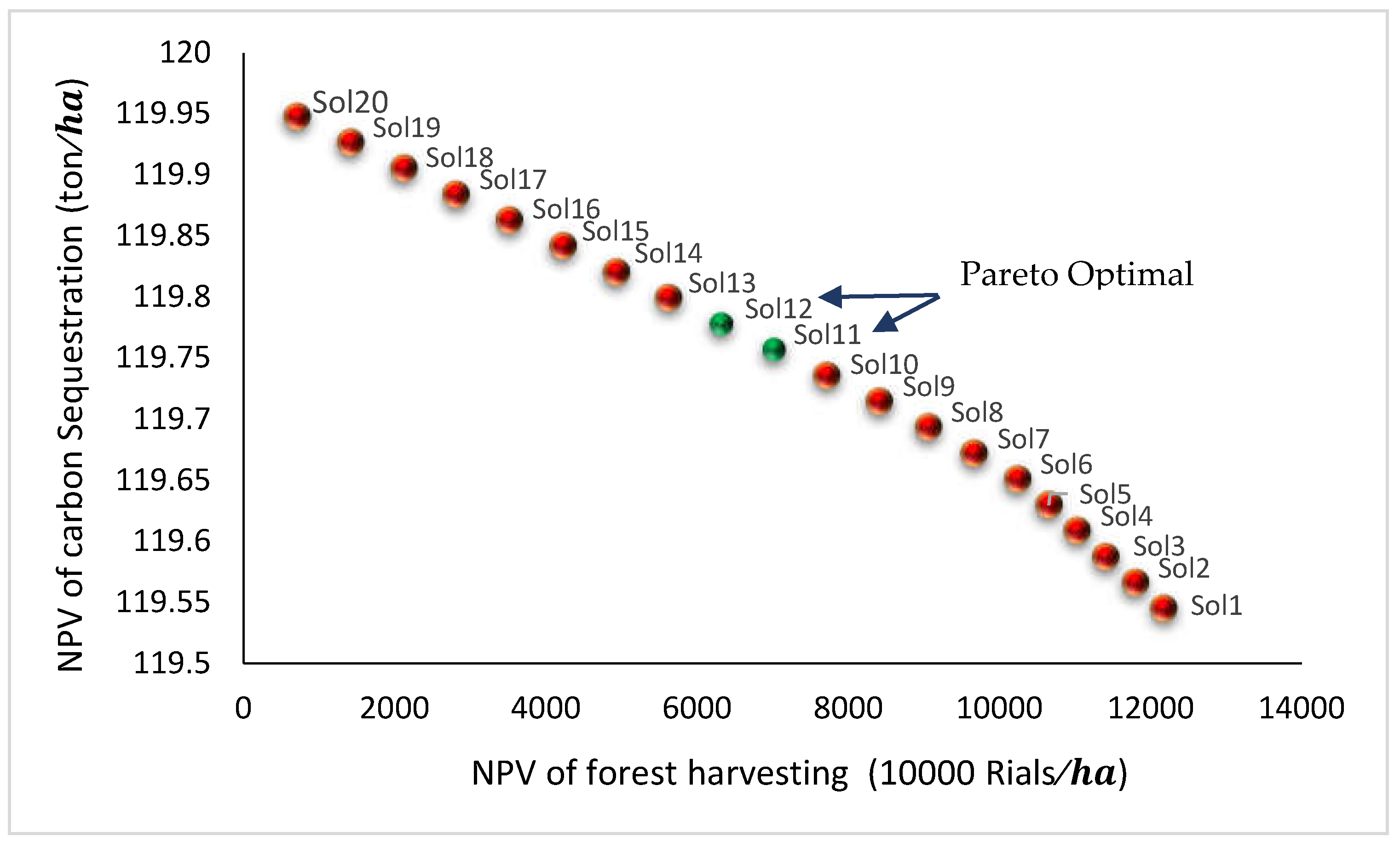
Grid 2 (342.21 m3/ha) |
Solution 1 | 12175.67 | 119.55 | 1.31 | 1.25 |
| Solution 2 | 11794.61 | 119.57 | 1.37 | 1.19 | |
| Solution 3 | 11413.54 | 119.59 | 1.43 | 1.13 | |
| Solution 4 | 11032.47 | 119.61 | 1.49 | 1.07 | |
| Solution 5 | 10651.41 | 119.63 | 1.55 | 1.01 | |
| Solution 6 | 10234.36 | 119.65 | 1.62 | 0.94 | |
| Solution 7 | 9672.23 | 119.67 | 1.68 | 0.88 | |
| Solution 8 | 9058.06 | 119.69 | 1.75 | 0.81 | |
| Solution 9 | 8416.74 | 119.71 | 1.82 | 0.74 | |
| Solution 10 | 7720.01 | 119.74 | 1.89 | 0.67 | |
| Solution 11 | 7023.28 | 119.76 | 1.97 | 0.59 | |
| Solution 12 | 6326.55 | 119.78 | 2.04 | 0.52 | |
| Solution 13 | 5629.71 | 119.8 | 2.11 | 0.45 | |
| Solution 14 | 4926 | 119.82 | 2.18 | 0.38 | |
| Solution 15 | 4222.28 | 119.84 | 2.24 | 0.32 | |
| Solution 16 | 3518.57 | 119.86 | 2.3 | 0.26 | |
| Solution 17 | 2814.86 | 119.88 | 2.37 | 0.19 | |
| Solution 18 | 2111.14 | 119.91 | 2.43 | 0.13 | |
| Solution 19 | 1407.43 | 119.93 | 2.49 | 0.07 | |
| Solution 20 | 703.14 | 119.95 | 2.56 | 0 |
| Grid | Solutions | NPV of forest harvesting (Z1) (10000 Rials/ha) |
NPV of carbon sequestration (Z2) (ton/ha) |
Growth (G) (m3/ha) |
Amount of harvest (m3/ha) |
|---|---|---|---|---|---|
|
Grid 3 (380.475 m3/ha) |
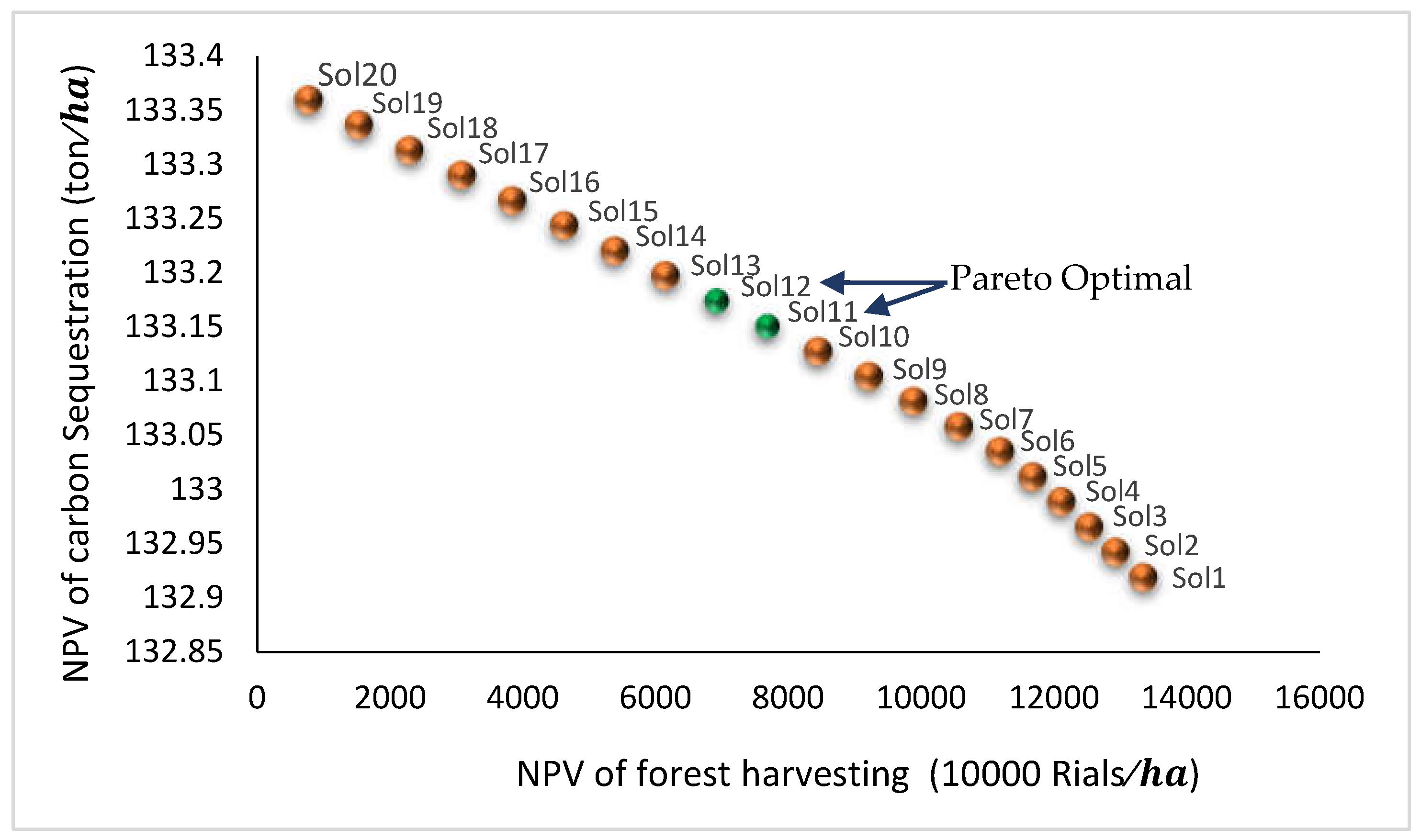
Solution 1 | 13357.95 | 132.92 | 1.44 | 1.36 |
| Solution 2 | 12941.14 | 132.94 | 1.5 | 1.3 | |
| Solution 3 | 12524.32 | 132.97 | 1.57 | 1.23 | |
| Solution 4 | 12107.51 | 132.99 | 1.63 | 1.17 | |
| Solution 5 | 11677.99 | 133.01 | 1.7 | 1.1 | |
| Solution 6 | 11188.32 | 133.03 | 1.77 | 1.03 | |
| Solution 7 | 10564.83 | 133.06 | 1.85 | 0.95 | |
| Solution 8 | 9893.06 | 133.08 | 1.92 | 0.88 | |
| Solution 9 | 9206.98 | 133.1 | 2 | 0.8 | |
| Solution 10 | 8444.9 | 133.13 | 2.08 | 0.72 | |
| Solution 11 | 7682.82 | 133.15 | 2.16 | 0.64 | |
| Solution 12 | 6920.73 | 133.17 | 2.24 | 0.56 | |
| Solution 13 | 6157.79 | 13.2 | 2.32 | 0.48 | |
| Solution 14 | 5388.07 | 133.22 | 2.39 | 0.41 | |
| Solution 15 | 4618.34 | 133.24 | 2.45 | 0.35 | |
| Solution 16 | 3848.62 | 133.27 | 2.52 | 0.28 | |
| Solution 17 | 3078.9 | 133.29 | 2.59 | 0.21 | |
| Solution 18 | 2309.17 | 133.31 | 2.66 | 0.14 | |
| Solution 19 | 1539.45 | 133.34 | 2.73 | 0.07 | |
| Solution 20 | 769.72 | 133.36 | 2.8 | 0 |
| Grid | Solutions | NPV of forest harvesting (Z1) (10000 Rials/ha) |
NPV of carbon sequestration (Z2) (ton/ha) |
Growth (G) (m3/ha) |
Amount of harvest (m3/ha) |
|---|---|---|---|---|---|
|
Grid 4 (418.74 m3/ha) |
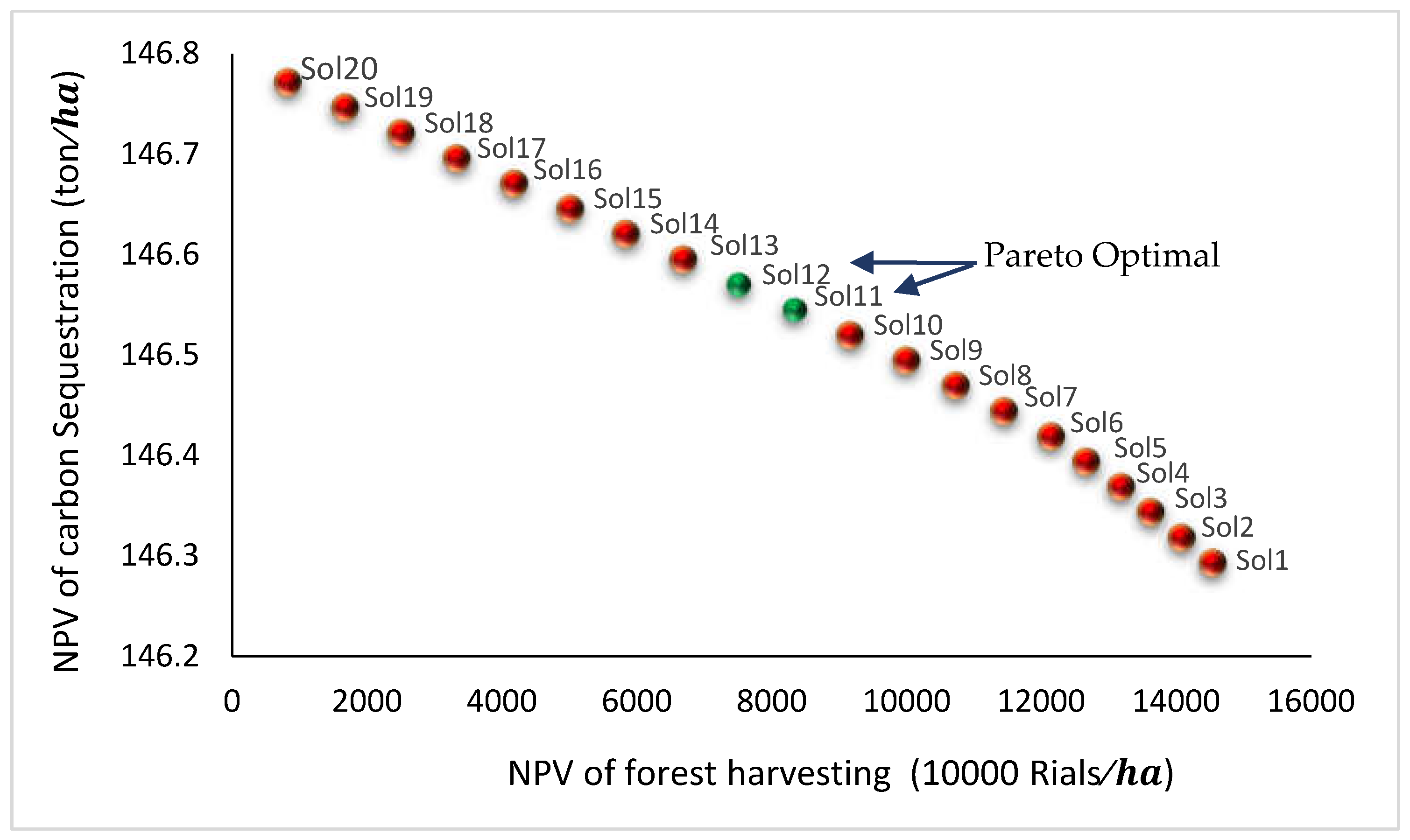
Solution 1 | 14540.22 | 146.29 | 1.56 | 1.48 |
| Solution 2 | 14087.67 | 146.32 | 1.63 | 1.41 | |
| Solution 3 | 13635.11 | 146.34 | 1.7 | 1.34 | |
| Solution 4 | 13182.55 | 146.37 | 1.78 | 1.27 | |
| Solution 5 | 12673.94 | 146.39 | 1.85 | 1.19 | |
| Solution 6 | 12142.27 | 146.42 | 1.93 | 1.11 | |
| Solution 7 | 11457.44 | 146.44 | 2.01 | 1.03 | |
| Solution 8 | 10728.05 | 146.47 | 2.09 | 0.95 | |
| Solution 9 | 9997.23 | 146.49 | 2.17 | 0.87 | |
| Solution 10 | 9169.79 | 146.52 | 2.26 | 0.78 | |
| Solution 11 | 8342.35 | 146.54 | 2.35 | 0.7 | |
| Solution 12 | 7514.91 | 146.57 | 2.43 | 0.61 | |
| Solution 13 | 6685.87 | 146.59 | 2.52 | 0.53 | |
| Solution 14 | 5850.14 | 146.62 | 2.59 | 0.45 | |
| Solution 15 | 5014.4 | 146.65 | 2.67 | 0.38 | |
| Solution 16 | 4178.67 | 146.67 | 2.74 | 0.3 | |
| Solution 17 | 3342.94 | 146.7 | 2.82 | 0.23 | |
| Solution 18 | 2507.2 | 146.72 | 2.89 | 0.15 | |
| Solution 19 | 1671.47 | 146.75 | 2.97 | 0.08 | |
| Solution 20 | 835.73 | 146.77 | 3.04 | 0 |
| Grid | Solutions | NPV of forest harvesting (Z1) (10000 Rials/ha) |
NPV of carbon sequestration (Z2) (ton/ha) |
Growth (G) (m3/ha) |
Amount of harvest (m3/ha) |
|---|---|---|---|---|---|
|
Grid 4 (475 m3/ha) |
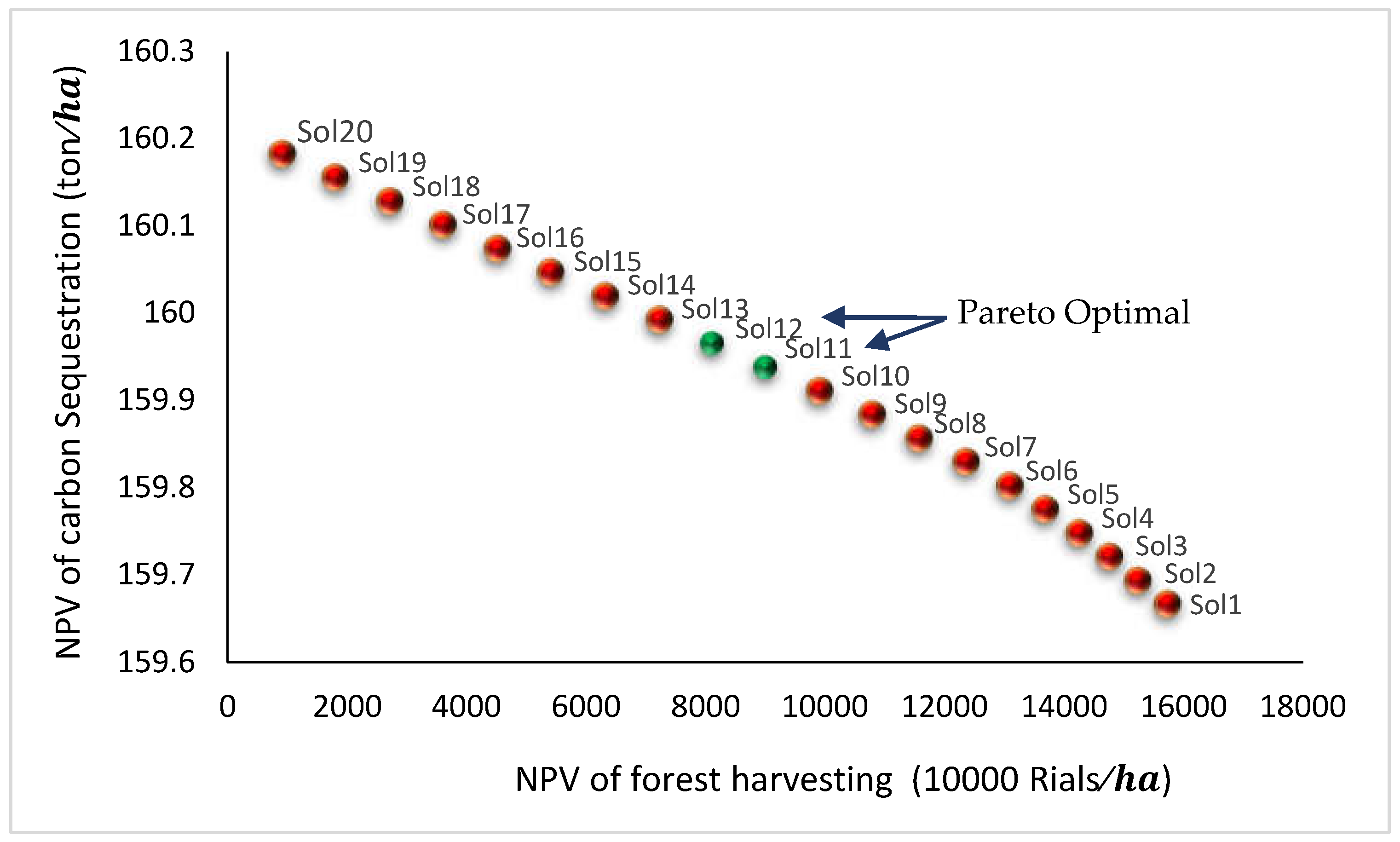
Solution 1 | 15722.5 | 159.67 | 1.69 | 1.6 |
| Solution 2 | 15234.19 | 159.69 | 1.76 | 1.53 | |
| Solution 3 | 14745.89 | 159.72 | 1.84 | 1.45 | |
| Solution 4 | 14243.54 | 159.75 | 1.92 | 1.37 | |
| Solution 5 | 13669.88 | 159.78 | 2 | 1.29 | |
| Solution 6 | 13096.23 | 159.8 | 2.09 | 1.2 | |
| Solution 7 | 12350.05 | 159.83 | 2.18 | 1.11 | |
| Solution 8 | 11536.05 | 159.86 | 2.26 | 1.03 | |
| Solution 9 | 10776.06 | 159.88 | 2.35 | 0.94 | |
| Solution 10 | 9894.68 | 159.9 | 2.44 | 0.85 | |
| Solution 11 | 9001.88 | 159.94 | 2.54 | 0.75 | |
| Solution 12 | 8109.09 | 159.97 | 2.63 | 0.66 | |
| Solution 13 | 7213.95 | 159.99 | 2.72 | 0.57 | |
| Solution 14 | 6312.21 | 159.02 | 2.8 | 0.49 | |
| Solution 15 | 5410.46 | 160.05 | 2.88 | 0.41 | |
| Solution 16 | 4508.72 | 160.07 | 2.96 | 0.32 | |
| Solution 17 | 3606.98 | 160.1 | 3.05 | 0.24 | |
| Solution 18 | 2705.23 | 160.13 | 3.13 | 0.16 | |
| Solution 19 | 1803.49 | 160.16 | 3.21 | 0.08 | |
| Solution 20 | 901.74 | 160.18 | 3.29 | 0 |
| Grid | Game round | Players | NPV of forest harvesting (Z1) (10000 Rials/ha) |
NPV of carbon sequestration (Z2) (ton/ha) |
|---|---|---|---|---|
|
Gride1 (303.96 m3/ha) |
1-1 | Player 1 | 1275.408 | 106.517 |
| 1-2 | Player 2 | 9894.058 | 106.2324 | |
| 2-1 | Player 1 | 2550.815 | 106.4786 | |
| 2-2 | Player 2 | 8794.718 | 106.286 | |
| 3-1 | Player 1 | 3826.223 | 106.4402 | |
| 3-1 | Player 2 | 7695.378 | 106.3228 | |
| 4-1 | Player 1 | 5101.001 | 106.4017 | |
| 4-2 | Player 2 | 6596.038 | 106.3562 | |
| 5-1 | Player 1 | 6363.748 | 106.3633 | |
| 5-2 | Player 2 | 5496.699 | 106.3897 |
| Grid | Game round | Players | NPV of forest harvesting (Z1) (10000 Rials/ha) |
NPV of carbon sequestration (Z2) (ton/ha) |
|---|---|---|---|---|
|
Gride 2 (342.21 m3/ha) |
1-1 | Player 1 | 1407.427 | 119.9267 |
| 1-2 | Player 2 | 10958.1 | 119.6128 | |
| 2-1 | Player 1 | 2814.855 | 119.8843 | |
| 2-2 | Player 2 | 9740.538 | 119.6699 | |
| 3-1 | Player 1 | 4222.282 | 119.8419 | |
| 3-2 | Player 2 | 8522.97 | 119.7114 | |
| 4-1 | Player 1 | 5629.71 | 119.7995 | |
| 4-2 | Player 2 | 7305.403 | 119.7485 | |
| 5-1 | Player 1 | 7023.282 | 119.7571 | |
| 5-2 | Player 2 | 6087.836 | 119.7855 |
| Grid | Game round | Players | NPV of forest harvesting (Z1) (10000 Rials/ha) |
NPV of carbon sequestration (Z2) (ton/ha) |
|---|---|---|---|---|
|
Gride3 (380.48 m3/ha) |
1-1 | Player 1 | 1539.447 | 133.3363 |
| 1-2 | Player 2 | 12022.15 | 132.9933 | |
| 2-1 | Player 1 | 3078.895 | 133.29 | |
| 2-2 | Player 2 | 10686.36 | 133.0539 | |
| 3-1 | Player 1 | 4618.342 | 133.2436 | |
| 3-2 | Player 2 | 9350.562 | 133.1 | |
| 4-1 | Player 1 | 6157.79 | 133.1972 | |
| 4-2 | Player 2 | 8014.768 | 133.1407 | |
| 5-1 | Player 1 | 7682.816 | 133.1508 | |
| 5-2 | Player 2 | 6678.973 | 133.1814 |
| Grid | Game round | Players | NPV of forest harvesting (Z1) (10000 Rials/ha) |
NPV of carbon sequestration (Z2) (ton/ha) |
|---|---|---|---|---|
|
Gride4 (418.74 m3/ha) |
1-1 | Player 1 | 1671.476 | 146.746 |
| 1-2 | Player 2 | 13086.2 | 146.3737 | |
| 2-1 | Player 1 | 3342.935 | 146.6975 | |
| 2-2 | Player 2 | 11632.18 | 146.4379 | |
| 3-1 | Player 1 | 5014.402 | 146.6453 | |
| 3-2 | Player 2 | 10178.15 | 146.488 | |
| 4-1 | Player 1 | 6685.87 | 146.5949 | |
| 4-2 | Player 2 | 8724.133 | 146.533 | |
| 5-1 | Player 1 | 8342.35 | 146.5446 | |
| 5-2 | Player 2 | 7270.11 | 146.5772 |
| Grid | Game round | Players | NPV of forest harvesting (Z1) (10000 Rials/ha) |
NPV of carbon sequestration (Z2) (ton/ha) |
|---|---|---|---|---|
|
Gride5 (457 m3/ha) |
1-1 | Player 1 | 1803.487 | 160.1557 |
| 1-2 | Player 2 | 14150.25 | 159.7526 | |
| 2-1 | Player 1 | 3606.975 | 160.1013 | |
| 2-2 | Player 2 | 12578 | 159.8218 | |
| 3-1 | Player 1 | 5410.462 | 160.047 | |
| 3-2 | Player 2 | 11005.75 | 159.8761 | |
| 4-1 | Player 1 | 7213.949 | 159.9927 | |
| 4-2 | Player 2 | 9433.497 | 159.9252 | |
| 5-1 | Player 1 | 9001.884 | 159.9383 | |
| 5-2 | Player 2 | 7861.248 | 159.9731 |
| Stock (m3/ha) | Game Round | Objective | Solution | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NPV of carbon sequestration (Z2) (ton/ha) | NPV of harvesting (Z2) (10000 Rials/ha) | Growth | Harvest | X1 (Beech) | X2 (Hornbea) | X3 (Alder) | X4 (Oak) | X5 (Other) | ||
| 303.96 | 5-1 | 106.36 | 6363.75 | 1.78 | 0.59 | 170 | 77.42 | 3.16 | 37.11 | 16.26 |
| 303.96 | 5-2 | 106.39 | 5496.7 | 1.87 | 0.5 | |||||
| 342.21 | 5-1 | 119.76 | 7023.28 | 1.97 | 0.65 | 190.35 | 72.92 | 20.65 | 38.11 | 20.2 |
| 342.21 | 5-2 | 119.82 | 6087.84 | 2.06 | 0.56 | |||||
| 380.48 | 5-1 | 133.15 | 7682.82 | 2.16 | 0.71 | 210.7 | 68.41 | 38.13 | 39.11 | 24.13 |
| 380.48 | 5-2 | 133.18 | 6678.97 | 2.26 | 0.61 | |||||
| 418.74 | 5-1 | 146.54 | 8342.35 | 2.35 | 0.77 | 231.05 | 63.91 | 55.62 | 40.1 | 28.07 |
| 418.74 | 5-2 | 146.58 | 7270.11 | 2.46 | 0.66 | |||||
| 457 | 5-1 | 159.94 | 9001.88 | 2.54 | 0.83 | 251.4 | 59.4 | 73.1 | 41.1 | 32 |
| 457 | 5-2 | 159.97 | 7861.25 | 2.66 | 0.71 | |||||
| Stock (m³/ha) | Harvest/Growth (m³/ha) | Players | Beech | Hornbeam | Alder | Oak | Other |
| 303.96 | Growth | Player 1 | 0.45 | 0.57 | 0.017 | 0.47 | 0.3 |
| Player 2 | 0.45 | 0.57 | 0.017 | 0.57 | 0.3 | ||
| Harvest | Player 1 | 0.453 | - | - | 0.139 | - | |
| Player 2 | 0.453 | - | - | 0.048 | - | ||
| 342.21 | Growth | Player 1 | 0.51 | 0.54 | 0.113 | 0.49 | 0.322 |
| Player 2 | 0.51 | 0.54 | 0.113 | 0.58 | 0.322 | ||
| Harvest | Player 1 | 0.507 | - | - | 0.145 | - | |
| Player 2 | 0.507 | - | - | 0.047 | - | ||
| 380.48 | Growth | Player 1 | 0.56 | 0.51 | 0.21 | 0.5 | 0.38 |
| Player 2 | 0.56 | 0.51 | 0.21 | 0.6 | 0.38 | ||
| Harvest | Player 1 | 0.562 | - | - | 0.151 | - | |
| Player 2 | 0.562 | - | - | 0.046 | - | ||
| 418.74 | Growth | Player 1 | 0.62 | 0.47 | 0.3 | 0.51 | 0.45 |
| Player 2 | 0.62 | 0.47 | 0.3 | 0.62 | 0.45 | ||
| Harvest | Player 1 | 0.616 | - | - | 0.157 | - | |
| Player 2 | 0.616 | - | - | 0.044 | - | ||
| 457 | Growth | Player 1 | 0.67 | 0.44 | 0.4 | 0.52 | 0.51 |
| Player 2 | 0.67 | 0.44 | 0.4 | 0.64 | 0.51 | ||
| Harvest | Player 1 | 0.67 | - | - | 0.163 | - | |
| Player 2 | 0.67 | - | - | 0.043 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





