A Theory of Gravity in Minkowski Space

1. Introduction

In GR, gravity is the curvature of spacetime which is a four-dimensional pseudo-Riemannian manifold equipped with a Levi-Civita connection. The action of GR is the Einstein-Hilbert action

$$S_{EH}=\int R\sqrt{-g}{d}^{4}x$$

(1)

where R is the curvature scalar. Although mathematically rich and consistent with experiments, it has some challenges. By challenge, here, we mean the conceptual difficulties of the theory and not quantization! We strongly believe that before asking such profound questions regarding quantization, we must answer some basic yet difficult problems. One problem is the energy problem in GR [1]. There is no energy-momentum tensor of the gravitational field in the full diffeomorphism invariant theory. Even in the linearized theory, it comes with some caveats. An intuitive argument is that since in GR, the gravitational field can be made to vanish in a local inertial frame, we cannot define a tensor for gravity itself. To see this, let us explicitly write the covariant divergence of the energy-momentum tensor as

$${\nabla }_{\mu }{T}^{\mu \nu }={\displaystyle \frac{1}{\sqrt{-g}}}{\partial }_{\mu }\left(\sqrt{-g}{T}^{\mu \nu }\right)+{\Gamma }_{\mu \rho }^{\nu }{T}^{\mu \rho }$$

(2)

The second term on the RHS prevents us from converting the integral of ${\nabla }_{\mu }{T}^{\mu \nu }$ into a boundary term and thus, there is no conservation of momentum and energy! Thus, covariant conservation is not the same as actual conservation. There are three points of view on the energy problem as discussed in [1]

• It is the specific property of GR related to the equivalence principle. Since, in accordance with the principle of general covariance, we must have ${\nabla }_{\mu }{T}^{\mu \nu }=0$, but as shown, this results in the energy problem of the theory.
• It is a serious problem of the theory and GR must be replaced with another theory that has no energy problem.
• It is indeed a serious problem related to some incorrectness of GR, but it has to be solved within the framework of GR itself.

We believe that the conceptual construction of gravity as a dynamic background is the culprit of the problem and we resort to the second point above. We present a theory of gravity in a Minkowski background with gravity as a physical field. Before that, there are two pictures of gravity within GR itself. First, the gravitational redshift (or gravitational time dilation) suggests that GR is indeed a correct theory with gravity as the curvature of spacetime. In contrast, the emission of gravitation radiation with the gravitational field carrying away the energy tends to suggest that the gravitational field has to be a physical field defined on a Minkowski background like the electromagnetic field. Our task is to bring the two pictures on equal footing. The next section discusses the mathematical structure of such a theory.

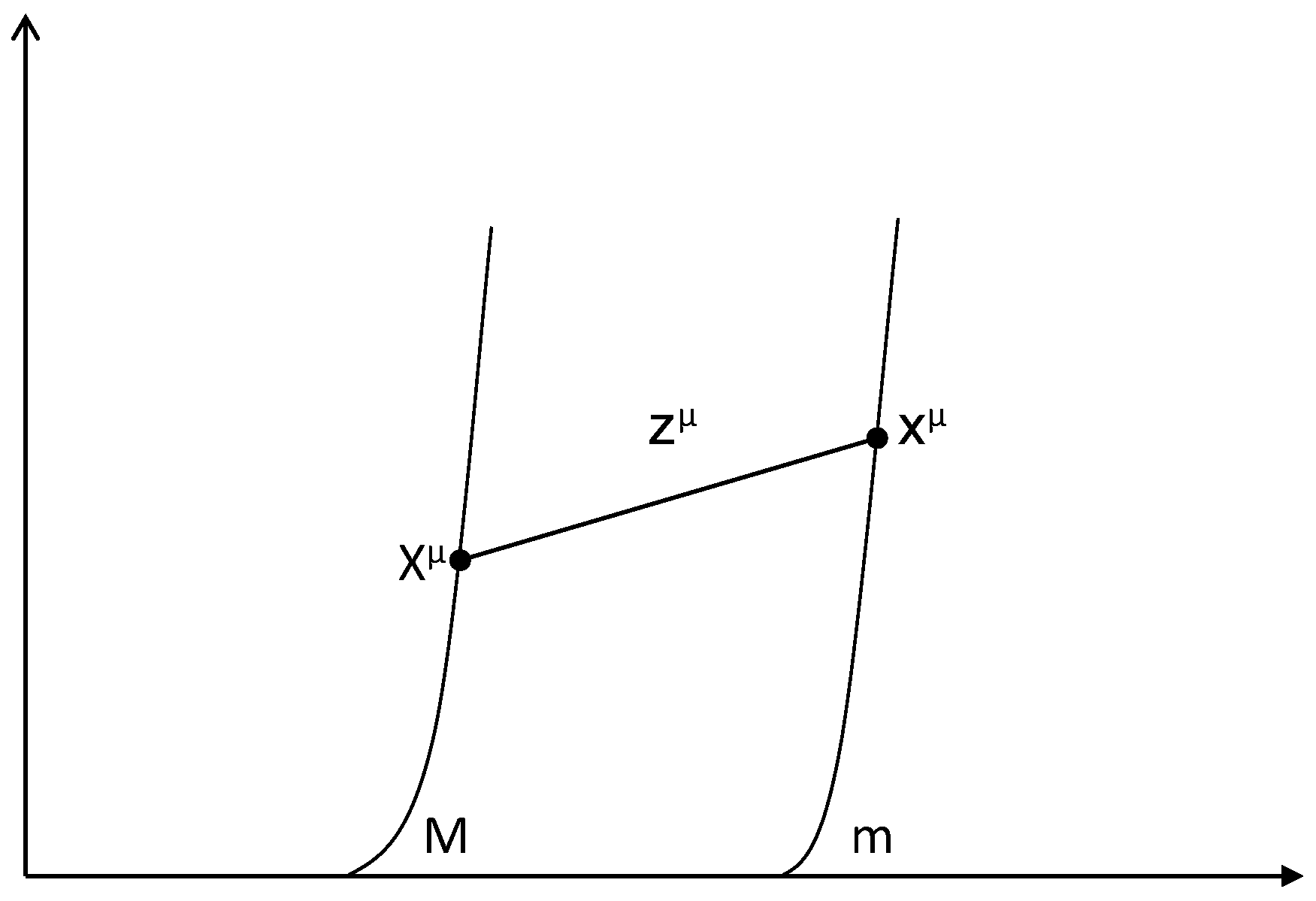
2. Gravity as a Physical Field

The basic tenet of this theory is that gravity is a physical field that affects the worldline of particles such that the particle follows a curved worldline in the flat spacetime background. The effective spacetime interval in the presence of gravity is given as

$$d{s}^2={\eta }_{\mu \nu }d{x}^{\mu }d{x}^{\nu }+A_{\mu \nu }d{X}^{\mu }d{X}^{\nu }$$

(3)

where $x^{\mu }$ are the coordinates of the object of mass m while $X^{\mu }$ are the coordinates of the gravitating mass M on the past light cone of m. ${\eta }_{\mu \nu }$ is the Minkowski metric and $A_{\mu \nu }$ is the gravitational field. Since we are constructing a theory of principle, let us reflect on the physical meaning behind writing (3). We know from Newton’s law that gravity is universal in the sense that it affects all the particles equally. Eq.(3) is the covariantly written version of this universal feature of gravity. In this formulation, the wordline of all the particles given by the first term of (3) are affected similarly by the gravitational field $A_{\mu \nu }$. In Einstein’s view, this idea is straightforwardly implemented by replacing the Minkowski metric with a general pseudo-Riemannian metric, but this forces us to abandon the absolute spacetime of Special Relativity, and we have to give up the idea of a global Lorentz covariance eventually. This seemingly beautiful conceptual leap leads to some problems (atleast in our understanding), such as the energy problem and, more severely, spacetime singularity, naked singularity, white holes, wormholes, and closed timelike curves(time travel!). These ideas are mathematically rich but we believe mathematics doesn’t describe reality, it can take us anywhere and everywhere but might have no physical existence or meaning in our understanding of Nature, which rests only with physics, physical theories built on principles, and ultimately observations.

Let us continue constructing our theory of principle. The Minkowski background defines a null cone for points $x^{\mu }$ and $X^{\mu }$ which satisfies

$$\begin{array}{c}\hfill {\eta }_{\mu \nu }d{z}^{\mu }d{z}^{\nu }=0,\end{array}$$

(4)

$$\begin{array}{c}\hfill z^{\mu }=x^{\mu }-X^{\mu }\end{array}$$

(5)

This relation shows a causal relationship between the worldline of object and mass. This causal relationship has an important role in our theory as it helps us to write $X^{\mu }$ in terms of $x^{\mu }$ (see Figure 1).

The first term in (3) is the worldline of particles in the absence of gravity. The second term in (3) combined with the causal relationship equation (4) gives the effect on the particle’s worldline due to gravitational field $A_{\mu \nu }$. We now need to determine the gravitational field $A_{\mu \nu }$. But first, let us find the trajectory of the particle in the presence of gravity. We will discuss the field equation that would determine $A_{\mu \nu }$ in the next section. The trajectory is one that extremizes the length of the worldline of the particle given by $cd\tau$. Therefore, we start with the action

$$\begin{array}{c}\hfill S=\int d\sigma L\end{array}$$

(6)

$$\begin{array}{c}\hfill =\int d\sigma \sqrt{{\eta }_{\mu \nu }{\dot{x}}^{\mu }{\dot{x}}^{\nu }+A_{\mu \nu }{\dot{X}}^{\mu }{\dot{X}}^{\nu }}\end{array}$$

(7)

To write the Euler-Lagrange equation, we calculate with respect to spacetime coordinate $x^{\mu }$, the following quantities

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial L}{\partial x^{\rho }}}=-{\displaystyle \frac{1}{2L}}\left({\displaystyle \frac{\partial A_{\mu \nu }}{\partial x^{\rho }}}{\dot{X}}^{\mu }{\dot{X}}^{\nu }\right)\end{array}$$

(8)

and since $x^{\mu }$ and $X^{\mu }$ are causally connected by the relation (4), we have

$${\displaystyle \frac{\partial L}{\partial {\dot{x}}^{\rho }}}=-{\displaystyle \frac{1}{L}}{\eta }_{\rho \nu }{\dot{x}}^{\nu }-{\displaystyle \frac{1}{L}}{A}_{\rho \nu }{\dot{x}}^{\nu }+{\displaystyle \frac{1}{L}}{A}_{\rho \nu }{\dot{z}}^{\nu }$$

(9)

Using the Euler-Lagrange equation, we get

$$\begin{array}{c}\hfill {\eta }_{\mu \rho }{\ddot{x}}^{\rho }+A_{\mu \rho }{\ddot{x}}^{\rho }-A_{\mu \rho }{\ddot{z}}^{\rho }+{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\partial A_{\mu \rho }}{\partial x^{\nu }}}+{\displaystyle \frac{\partial A_{\mu \nu }}{\partial x^{\rho }}}-{\displaystyle \frac{\partial A_{\nu \rho }}{\partial x^{\mu }}}\right){\dot{X}}^{\nu }{\dot{X}}^{\rho }]=0\end{array}$$

(10)

Multiplying by the inverse metric ${\eta }^{\mu \sigma }$, we get

$${\displaystyle \frac{d^2{x}^{\sigma }}{d{\tau }^2}}+A_{\rho }^{\sigma }\left({\displaystyle \frac{d^2{x}^{\rho }}{d{\tau }^2}}-{\displaystyle \frac{d^2{z}^{\rho }}{d{\tau }^2}}\right)+{\Gamma }_{\rho \nu }^{\sigma }{\displaystyle \frac{d{X}^{\rho }}{d\tau }}{\displaystyle \frac{d{X}^{\nu }}{d\tau }}=0$$

(11)

where

$${\Gamma }_{\rho \nu }^{\sigma }={\displaystyle \frac{1}{2}}{\eta }^{\mu \sigma }({\partial }_{\nu }{A}_{\mu \rho }+{\partial }_{\rho }{A}_{\mu \nu }-{\partial }_{\mu }{A}_{\nu \rho })$$

(12)

It should be noted that there is no frame in which ${\Gamma }_{\rho \nu }^{\sigma }$ vanishes as it does for a local inertial frame in GR where the connections vanish. This tells that gravity is a real, physical field affecting the worldlines of all particles in a flat Minkowski background. In summary, (3) is the key to our theory. From this, we can formulate all the important aspects we need to describe gravity in this theory.

3. The Field Equation

The action of a spin-2 tensor field propagating in Minkowski space is given by the Fierz-Pauli action [2]. However, Fierz-Pauli’s action describes a linear theory while gravity must be non-linear since gravity interacts with itself. Moreover, the energy-momentum tensor of the gravitational field obtained via Noether’s theorem from Fierz-Pauli Lagrangian is not gauge-invariant. Since our starting point is to solve the energy problem in GR, we discard this theory on this technical ground. The theory we use that describes the spin-2 field is Weyl GEM [3,4]. Weyl GEM arises by demanding local gauge-invariance of the Schrodinger equation under a local phase transformation [4]. The gauge-invariant field tensor in (abelian) Weyl GEM is

$${\mathcal{F}}^{\mu \nu \alpha }={\partial }^{\mu }{A}^{\nu \alpha }-{\partial }^{\nu }{A}^{\mu \alpha }$$

(13)

where the field tensor is anti-symmetric in the first two indices. $A^{\mu \nu }$ is a symmetric gauge potential with the gauge transformation given as

$$A_{\mu \nu }^{\prime }=A_{\mu \nu }+{\partial }_{\mu }{\theta }_{\nu }$$

(14)

The field equation in Weyl GEM is

$${\partial }_{\mu }{\mathcal{F}}^{\mu \nu \alpha }=\kappa {\mathcal{J}}^{\nu \alpha }$$

(15)

where $\kappa$ is a constant, ${\mathcal{J}}^{\mu \alpha }$ is a rank-2 tensor that depends on matter density $c{\rho }^i$ and mass current density $J^{ij}$ [3]. The field equation can be obtained via the action principle by varying the gauge-invariant Lagrangian

$${\mathcal{L}}_{GEM}=-{\displaystyle \frac{c^4}{16\pi G}}{\mathcal{F}}_{\mu \nu \alpha }{\mathcal{F}}^{\mu \nu \alpha }+A_{\mu \alpha }{\mathcal{J}}^{\mu \alpha }$$

(16)

In the weak field limit, the equation of motion (11) gives

$$A_{00}={\displaystyle \frac{2\varphi }{c^2}}$$

(17)

where $\varphi$ is the Newtonian potential. Therefore, in the weak-field limit (15) gives

$$\begin{array}{c}{\partial }_1{\mathcal{F}}^{100}={\nabla }^2{A}_{00}=\kappa {\mathcal{J}}^{00}=\kappa \rho c^2\end{array}$$

(18)

Comparing with the Gauss law of Newtonian gravity, we get, $\kappa ={\displaystyle \frac{8\pi G}{c^4}}$. Therefore, the field equation becomes

$${\partial }_{\mu }{\mathcal{F}}^{\mu \nu \alpha }={\displaystyle \frac{8\pi G}{c^4}}{\mathcal{J}}^{\nu \alpha }$$

(19)

We can also write a non-abelian version of the field equation that includes self-coupling of gravitons [5]. This becomes

$${\mathcal{D}}_{\mu }{\mathcal{F}}^{\mu \nu \alpha }={\displaystyle \frac{8\pi G}{c^4}}{\mathcal{J}}^{\nu \alpha }$$

(20)

where ${\mathcal{D}}_{\mu }$ is the gauge-covariant derivative. Therefore, Weyl GEM is a natural candidate for constructing both abelian and non-abelian gauge theories of gravity in our framework. However, in previous works, GEM describes gravity in the weak field limit of GR. But in our case, it describes gravity in strong regimes too. This difference arises from the way gravity affects the motion of particles. Our theory describes gravity as affecting the spacetime interval, but the change in spacetime interval is not mediated as metric perturbation as it does in GR but as an effect on worldlines of particles by the gravitating mass as encoded in (3). This will become evident when we find the solution in the presence of a static and spherically symmetric mass in the next section. Before that, let us find the energy-momentum tensor of the gravitational field. Using Noether’s theorem, it is given as [3]

$$t_G^{\mu \nu }=-{\displaystyle \frac{c^4}{4\pi G}}\left[{\eta }^{\gamma \mu }{\mathcal{F}}_{\gamma \alpha \beta }{\mathcal{F}}^{\alpha \nu \beta }+{\displaystyle \frac{1}{4}}{\eta }^{\mu \nu }{\mathcal{F}}_{\rho \sigma \theta }{\mathcal{F}}^{\rho \sigma \theta }\right]$$

(21)

with ${\partial }_{\mu }{t}_G^{\mu \nu }=0$ implying local conservation of energy-momentum of gravitational field. Like the energy-momentum tensor of electromagnetic field, this expression is gauge-invariant and therefore represents local energy density of the gravitational field. Therefore, this formalism with the effect of gravity contained in (3) and field equation given by Weyl GEM solves the energy problem of GR and describes gravity in strong regimes too. This is different from both GR(which has the energy problem) and GEM(which only describes the weak-field limit of gravity). To summarize

Table 1. Summary of theories. The theory described in this paper has the advantage that it describes gravity in a strong regime plus it has no energy problem.

	Energy Problem	Describes Strong Regime
General Relativity	Yes	Yes
Weyl GEM	No	No
This Theory	No	Yes

Table 1. Summary of theories. The theory described in this paper has the advantage that it describes gravity in a strong regime plus it has no energy problem.

	Energy Problem	Describes Strong Regime
General Relativity	Yes	Yes
Weyl GEM	No	No
This Theory	No	Yes

4. Static and Spherically Symmetric Solution

For simplicity, we will consider the field equation of abelian Weyl GEM (19). This is physical since self-coupling of gravitons is not expected to affect motion at scales as large as the solar system. They might become important at the quantum scale. Let us also consider the mass to be static. Then

$$\begin{array}{c}\hfill d{X}^{\mu }=(dT,0,0,0)\end{array}$$

(22)

and we take a point in spacetime as

$$\begin{array}{c}\hfill d{x}^{\mu }=(dt,dx,dy,dz)\end{array}$$

(23)

The general form of spacetime interval (3) in the static and spherically symmetric case is

$$d{s}^2=d{t}^2-d{r}^2-d^2{\Omega }_{\left(2\right)}+A_{00}d{T}^2$$

(24)

where $d{\Omega }_{\left(2\right)}^2$ is the metric on $S^2$. The solution of the field equation (19) with one unknown $A_{00}={\varphi }^0$ is $A_{00}={\displaystyle \frac{2\varphi }{c^2}}$. Recall that ${\mathcal{A}}_{\mu \nu }$ is given as

$${\mathcal{A}}_{\mu \nu }=\left(\begin{array}{ccccccc}{\varphi }^0& & {\varphi }^1& & {\varphi }^2& & {\varphi }^3\\ {\varphi }^1& & A^{11}& & A^{12}& & A^{13}\\ {\varphi }^2& & A^{21}& & A^{22}& & A^{23}\\ {\varphi }^3& & A^{31}& & A^{32}& & A^{33}\end{array}\right)$$

(25)

where ${\varphi }^i$ and $A^{ij}$ are gravitational counterparts of scalar potential $\varphi$ and vector potential $A^i$ of electromagnetism. Therefore, in our case of static mass, it essentially means that only the scalar potential is contributing to the gravitational field. This means that using the GEM framework, we can always know what components out of the independent 10 components of the tensor gauge field ${\mathcal{A}}_{\mu \nu }$ are contributing to the gravitational field. In GR, the symmetries of underlying spacetime tell which components of the metric tensor $g_{\mu \nu }$ are contributing to gravity. Now, using the causal relationship equation(4), we obtain

$${(dt-dT)}^2-d{r}^2=0$$

(26)

Thus, we are left with only one unknown parameter $dT$, expressed completely in terms of known spacetime parameters $dt$ and $dr$ as

$$dT=(dt\pm dr)$$

(27)

Therefore, using(24), we get

$$d{s}^2=d{t}^2-d{r}^2-d{\Omega }_{\left(2\right)}^2+{\displaystyle \frac{2\Phi }{c^2}}{(dt-dr)}^2$$

(28)

This coincides with the Whitehead metric [6,7] and as was first shown by Eddington [8] when written in diagonal form, it is equivalent to the Schwarzschild metric of GR. Using the usual Lagrangian procedure, we can easily find the equation of motion which is exactly equivalent to the equation of motion of GR.

5. A Remark on the Accelerated Expansion of the Universe

In GR, we model the universe as an FLRW spacetime with the line element

$$d{s}^2=c^{2}d{t}^2-R^2\left(t\right)\left[{\displaystyle \frac{d{r}^2}{1-k{r}^2}}+r^{2}d{\theta }^2+r^{2}si{n}^2\theta d{\varphi }^2\right]$$

(29)

This line element gives the Friedmann equation where to account for accelerated expansion, we need to introduce the cosmological constant $\Lambda$. To understand accelerated expansion in the case of gravity in Minkowski space, we start by looking at the field equation (19). We immediately observe that a term of form $\Lambda {\zeta }_{\nu \alpha }$ where $\Lambda$ is a constant and ${\zeta }_{\nu \alpha }$ is some constant rank-2 tensor can be added on the left side so both sides remain divergenceless. This can be readily achieved by adding to the Lagrangian (16) a term of form $\Lambda {\zeta }_{\nu \alpha }{A}^{\nu \alpha }$. Note that this term is gauge-invariant under the gauge-transformation (14) since ${\zeta }_{\nu \alpha }$ is a constant tensor. Also, note that this repulsive term results from the vacuum energy of the space itself. To understand the behaviour of the present universe at cosmic scales, such as dark energy, we need to focus on the vacuum solution of the field equation with $\Lambda {\zeta }_{\nu \alpha }$ term. In the past, when matter was dominant, we would need to consider the full non-vacuum solution. However, in the present case, we can ignore the contribution of other energy density and simply solve the vacuum equation with $\Lambda {\zeta }_{\nu \alpha }$ term to finally obtain

$$A_{00}=-{\displaystyle \frac{2GM}{r{c}^2}}-k{r}^2$$

(30)

where k is some constant. Therefore, the gravitational acceleration in this case, in the weak field limit is

$$a=-\nabla A_{00}=-{\displaystyle \frac{GM}{r^2}}+2kr$$

(31)

The second term is effectively the repulsive vacuum energy term that leads to the so-called accelerated expansion of the universe [9] for an appropriate choice of constant k which has to be determined by observation.

6. Discussion on the Early Universe

In this theory, gravity is a physical field defined on Minkowski background and explains the four classical tests of gravity. We also discussed the phenomenon of accelerated expansion in this theory. The way we presented cosmology is very radical than the standard cosmology as there is no spatial expansion rather we can think of the universe as being infinite and accelerated expansion is galaxies physically moving away at increasing speed due to the repulsive gravitational field of the vacuum and expansion is simply galaxies moving away due to the repulsive energy after the Big Bang. So, we picture the universe as an infinite space that always existed while the observable universe is causally connected patch within this universe and had a beginning with the so-called ’Big Bang’. Therefore, we think of the Big Bang as the beginning of the observable universe and not the entire universe which has always existed. Before the Big Bang, all the matter was very close, and the observable universe was very hot. After the Big Bang, the matter density started distributing rapidly in the universe, and when it sufficiently cooled, photons got decoupled and started moving in the infinite universe, which we now observe as the Cosmic Microwave Background(CMB). More importantly, there is no spacetime singularity or Big Bang singularity. Spacetime is the fixed static background defined at all points and at all times. This is also a conceptual advantage of this theory. To explain dark energy, we recall that the repulsive force of the vacuum energy scales linearly with the radial distance. In the very early universe, matter was so close that this did not have any noticeable effect. However, in the present universe, when the observable universe has become sufficiently large, naturally, the repulsive force of the vacuum energy has dominated. This explains why the (observable) universe has started ’expanding’ in an accelerated manner only recently. The horizon problem can be solved by borrowing the idea of Moffat’s Superluminary Universe [10]. The very early universe underwent a Lorentz symmetry-breaking phase for a fraction of time. The speed of light(or the maximum speed of communication) is no longer constrained by the second postulate of special relativity and undergoes a phase transition as

$$c\left(t\right)=c_m\theta (t_c-t)+c_0\theta (t-t_c)$$

(32)

where $\theta$ is the Heaviside step function, and $c_0$ is the present value of the speed of light. Therefore, the metric before and after the phase transition takes the following forms

$$\begin{array}{c}\hfill d{s}^2(t<t_c)=c_m^{2}d{t}^2-d{x}^2-d{y}^2-d{z}^2\end{array}$$

(33)

$$\begin{array}{c}\hfill d{s}^2(t>t_c)=c_0^{2}d{t}^2-d{x}^2-d{y}^2-d{z}^2\end{array}$$

(34)

The geodesic of light is given by $d{s}^2=0$, thus, in the broken symmetry phase

$$d{t}^2={\displaystyle \frac{1}{c_m^2}}\left[d{x}^2+d{y}^2+d{z}^2\right]$$

(35)

If $c_m\to \infty$, $dt=0$ and all the points in the universe are in causal contact. This solves the horizon problem. After the phase transition ($t>t_c$), the Lorentz symmetry is restored, and the speed of light is $c_0$, which is the present value. We believe that the flatness problem is merely an artifact of using GR which is naturally not present in a theory of gravity in Minkowski space.

7. Conclusion

In this paper, we presented a theory of gravity in Minkowski space. The field equation can be written consistently in both linear and non-linear ways using abelian Weyl GEM and non-abelian Weyl GEM respectively. Thus, we brought gravity on the same footing as other field theories. At the core of this theory is the energy problem of GR. The principle of general covariance and giving up the idea of prior geometry leads to the problem that we cannot define the energy-momentum tensor of gravity. The problem becomes noticeable when finding the energy of the gravitational wave. We obtained the solution in the form of the Whitehead metric which is equivalent to the Schwarzschild metric. We also discussed about late time cosmic acceleration and the early universe and its evolution. The key insight is that in the very early Universe, the speed of light underwent a phase transition, where for $t<t_c$, the Lorentz symmetry is broken. In the broken symmetry phase, $c_m\to \infty$ and all the points of the universe were in causal contact. This solves the horizon problem. After the transition ($t>t_c$), the symmetry is restored. There naturally exists no flatness problem in a theory of gravity in Minkowski space, and we believe that it is merely an artefact of using GR or metric theories of gravity where the metric is a dynamical field.