Quantum Space -Time with Energy and Unified Field Theory

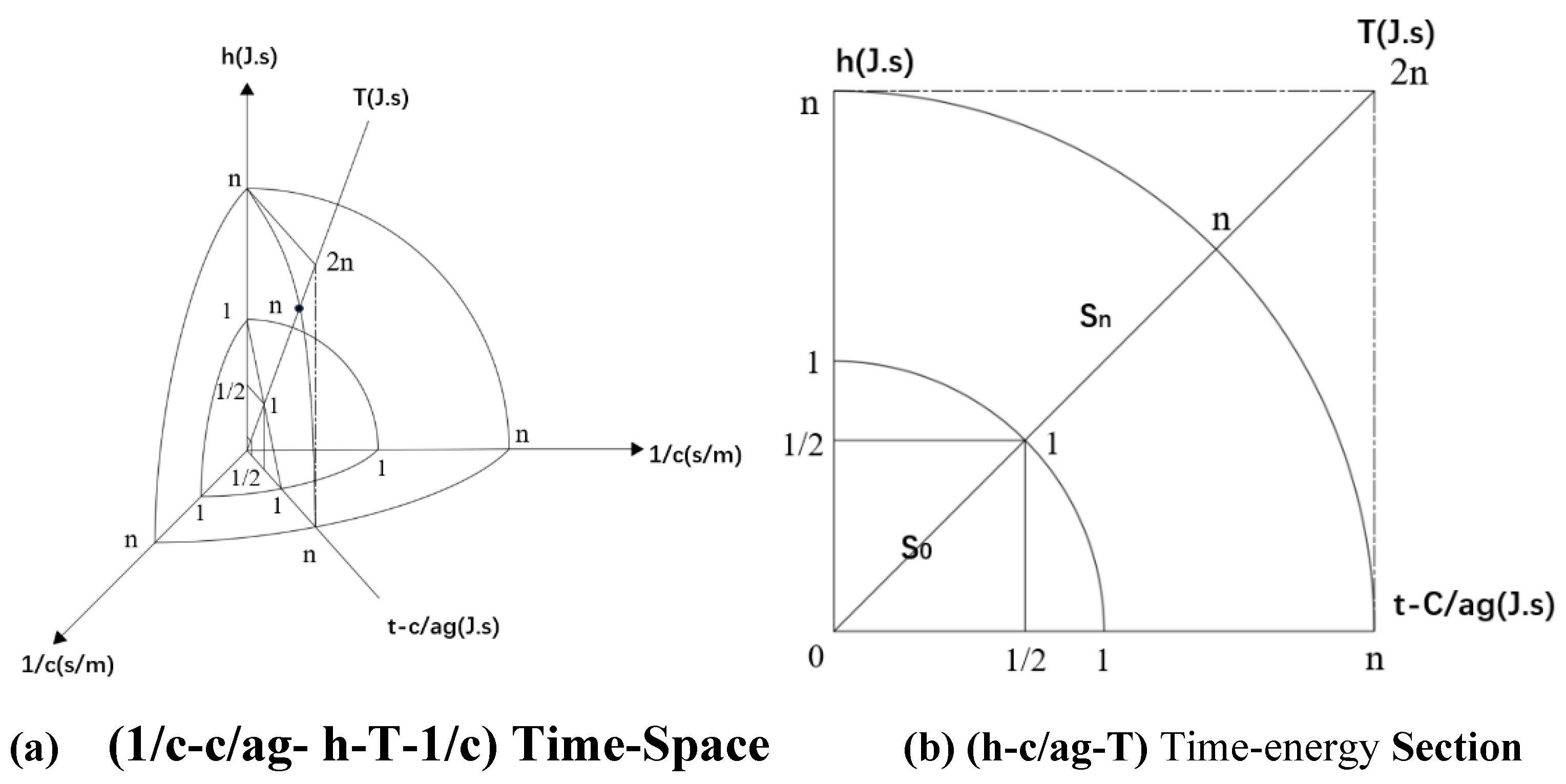
1. Time Quantization

Time is a basic concept in physics. But till now, we have no idea to use mathematical model to describe the structure of “Time”. In Newton’s system, Time is an independent existence with space. In Einstein’s system, Time and Space are bonded together just considering the Velocity of Light is a constant C(m/s). And then for a Quantum system, we consider the energy is discrete and then the “Time contentiousness” disappeared in this system. But It is that the Dimension of Plank’s constant h(J.s) is also including the unit of Time . So, we think that if we may construct a Dimension system of Time-Space with energy based on two priori conditions: the velocity of light is a constant C and the unit of energy with Time is a constant h, Plank constant. And if we can quantized this Time-Space with energy system, Maybe we can get a mathematical model to describe more physics details of the basic structure of Space -Time with energy and get a Unified Field Theory.

$\tau$ can be defined as

$$\tau \sim \mathrm{n}\mathrm{h} (\mathrm{J}.\mathrm{s}) \mathrm{n}~\left(1,2,3,\dots \right)$$

$h$ (J.s) is Planck constant. We can call $\tau as \mathit{T}\mathit{i}\mathit{m}\mathit{e}-\mathit{b}\mathit{e}\mathit{e}\mathit{n}$

$\mathit{t}$can be defined as

$$\mathit{t}~\mathit{n}\left({\displaystyle \frac{\mathit{c}}{a_g}}\right) (\mathrm{J}.\mathrm{s})\mathrm{ }\mathrm{ }\mathrm{n}~(1,2,3,\dots )$$

$C$ is the velocity of Light (m/s), and $a_g$ is the Intensity of field of gravitation (m/s²). We can call $t as \mathit{T}\mathit{i}\mathit{m}\mathit{e}-\mathit{t}\mathit{o}\mathit{ }\mathit{b}\mathit{e}.$

And

$$T~2n (\mathrm{J}.\mathrm{s})\mathrm{ }\mathrm{ }$$

We call $T\mathrm{ }\mathrm{ }\mathit{T}\mathit{i}\mathit{m}\mathit{e}-\mathit{b}\mathit{e}\mathit{i}\mathit{n}\mathit{g}.$

So we got a Time-space with Energy coordinate system (1/c-h(-T -c/ag) -1/c) show as Figure 1(a).

$$〈T〉=〈\tau 〉+〈t〉~n*\left[〈h〉+〈{\displaystyle \frac{\mathit{c}}{a_g}}〉\right]$$

We can define mass M as:

$$M_0~{\displaystyle \frac{h}{C^2}} (\mathrm{k}\mathrm{g}.\mathrm{s})$$

$$\mathrm{M}~n^3{\displaystyle \frac{h}{C^2}} (\mathrm{k}\mathrm{g}.\mathrm{s})$$

and show as Figure 1(b)

at moments $T~2n$(J.s)

$$\mathit{\tau }=\mathit{t}$$

$$nh=nc/a_g$$

$${\displaystyle \frac{1}{a_g}}=h/c (\mathrm{J}.{\mathrm{s}}^2.{\mathrm{m}}^{-1})$$

So we have:

$$M_0{a}_g~1/c (\mathrm{s}.{\mathrm{m}}^{-1})$$

2. Quantum Time Space with Energy

We will define a space-time with energy as:

$$\begin{gathered} M_0{a}_g~1/c (\mathrm{s}.{\mathrm{m}}^{-1}) \\ T~2n (\mathrm{J}.\mathrm{s}) \mathrm{n}~\left(1,2,3,\dots \right) \\ {S}_0~{\displaystyle \frac{1}{4}}*h*{\displaystyle \frac{c}{a_g}}~{({\displaystyle \frac{1}{2}}*h)}^2 S_n~n^2 h*{\displaystyle \frac{c}{a_g}}~{(nh)}^2 \\ {\displaystyle \frac{S_n}{S_0}}={4n}^2 \\ {\displaystyle \frac{M}{M_0}}~n^3 \end{gathered}$$

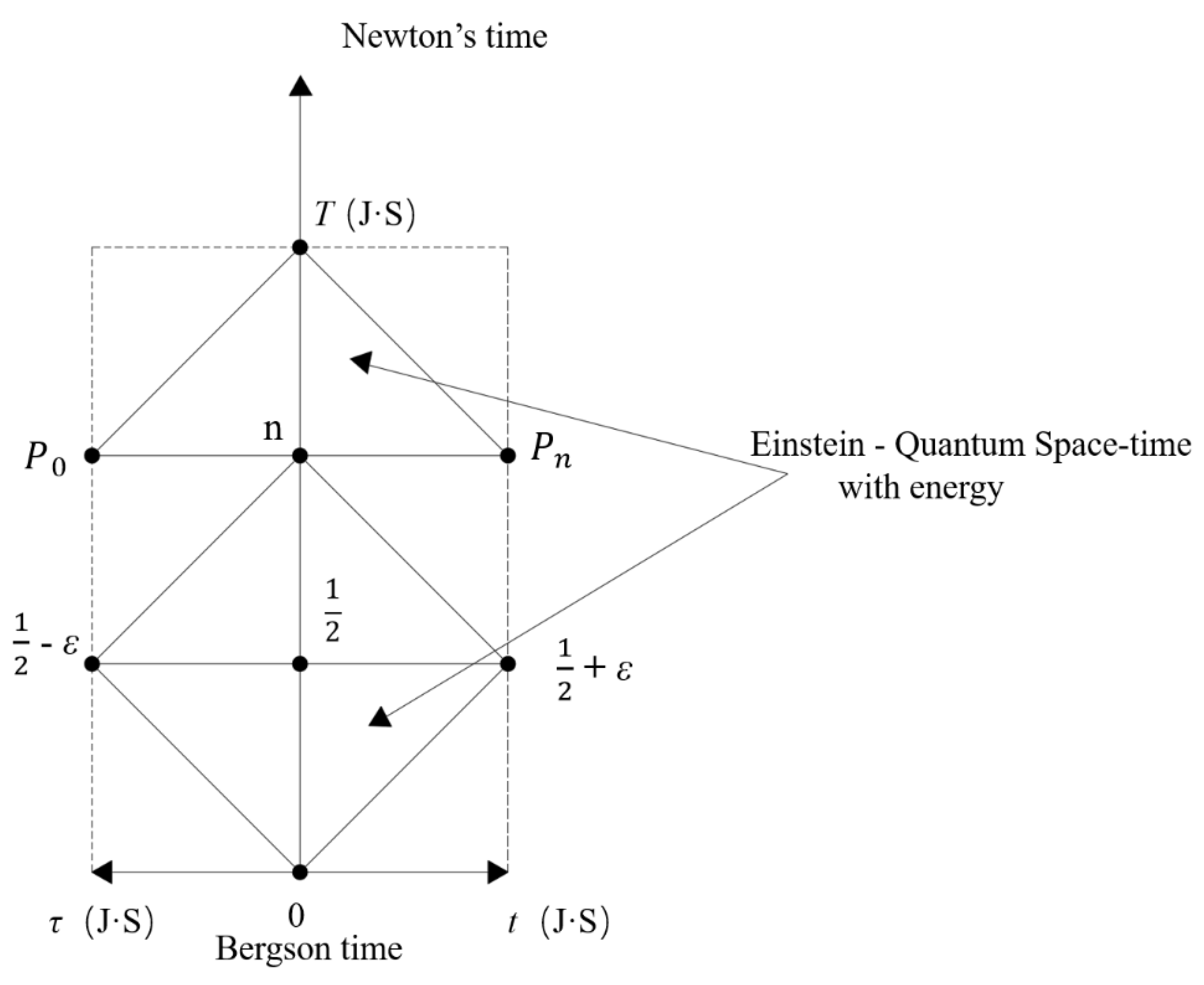
3. The Symmetry Number Structure About Line-1/2 for Unified Field Theory

We can call $\tau (J.S) as \mathit{T}\mathit{i}\mathit{m}\mathit{e}-\mathit{b}\mathit{e}\mathit{e}\mathit{n}$ $t(J.S) as \mathit{T}\mathit{i}\mathit{m}\mathit{e}-\mathit{t}\mathit{o}\mathit{b}\mathit{e}.T\left(J.S\right)as\mathit{T}\mathit{i}\mathit{m}\mathit{e}-\mathit{b}\mathit{e}\mathit{i}\mathit{n}\mathit{g}$. ($\tau ,t,T\in R$).

Abscissa: $\tau \leftarrow 0\to t$ Bergson Time

Vertical ordinate: 0$\to T$ Newton’s Time

1. 

$\mathit{z}\mathit{p}={\displaystyle \frac{1}{2}}\pm \mathit{\epsilon }(\mathit{\epsilon }=\mathit{a}+\mathit{b}\mathit{i} \mathit{a},\mathit{b}\in \mathit{R})$

$$\begin{gathered} \mathbf{0}={\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}-{\displaystyle \frac{\mathbf{1}}{\mathbf{2}}} \\ \mathbf{1}={\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}+{\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}=\left({\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}-\mathsf{\epsilon }\right)+\left({\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}+\mathsf{\epsilon }\right) \end{gathered}$$

This is a model for Quantum Entanglement.

2. 

$\mathit{P}\mathit{n}\pm \mathit{p}\mathbf{0}=\mathbf{2}\mathit{n}$

$$\begin{gathered} \mathit{p}\mathbf{0}\leftrightarrow \left({\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}-\mathsf{\epsilon }\right) \\ \mathit{n}\leftrightarrow {\displaystyle \frac{\mathbf{1}}{\mathbf{2}}} \\ \mathit{p}\mathit{n}\leftrightarrow \left({\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}+\mathsf{\epsilon }\right) \end{gathered}$$

$n\text{~}\left( 1, 2,3,4,\dots \dots \dots .\right)$ All natural numbers excepted 0

$\mathrm{p}0, \mathrm{pn} \text{∈}\mathrm{P}\text{~}\left(2,3,5,7,\dots \dots \dots .\right)$ All prime numbers

$$\mathit{P}\mathit{n}+\mathit{p}\mathbf{0}=\mathbf{2}\mathit{n} n\text{~}\left( 2, 3, 4,\dots \dots \dots .\right)$$

This is a model for gravitation

$$Pn-p0=2n n\text{~}\left(1, 2, 3, 4,\dots \dots \dots .\right)$$

When $\mathit{n}=1$   $\mathit{P}\mathit{n}-\mathit{p}\mathbf{0}=\mathbf{2}$

This is a model for the electromagnetic field.

So we get a Symmetry Number Structure about Line-1/2 for Unified Field Theory as Figure 2. we can call it Einstein-Quantum Space-Time with energy.

4. Discussion

Galilei said that he can creative the Universal only using Space, Time and Logarithm. Einstein thanked that a Unified Field Theory should be a geometrization one. And Roger Penrose pointed out that if we want to get the uniting of the Mass and Time-Space , we need the help of Complex Number[1].The paper [2] discusses that a Unified field theory should be a model with Plank constant、gravitation and the velocity of Light. Wilczek [3] want to use a concept called Quantum Time Crystals to define the Time space with energy.

In Newton’s system, Time is an independent existence with energy.

$$S~E*t$$

In Einstein’s system, Time and Space are bonded together just considering the Velocity of Light is a constant C(m/s).

$$\mathit{S}~1\mathit{*}\left({\displaystyle \frac{\mathit{C}}{{\mathit{a}}_{\mathit{g}}}}\right)$$

${\mathit{a}}_{\mathit{g}}$ is the strength of gravitation (m/s²)

And for a Quantum system, the energy is considered discrete and then the “Time contentiousness” disappeared in this system. But It is that the Dimension of Plank’s constant h (J.s) is also including the unit of Time .

$$\mathit{S}~{\left(\mathit{E}\mathit{*}\mathit{t}\right)}^2={\left(nh\right)}^2$$

h is Plank constant, we can find that the Dimension of Plank’s constant h(J.s) is also including the unit of Time .

In our system, we can get

$$\begin{gathered} {\mathit{S}}^{\mathbf{1}\mathbf{/}\mathbf{2}}~\mathit{E}*\mathbf{t}~\sqrt{\mathit{h}\mathit{*}\left({\displaystyle \frac{\mathit{c}}{\mathit{a}\mathit{g}}}\right)} \\ {\mathit{S}}_{\mathit{n}}/S_0~{\mathbf{4}\mathit{n}}^{\mathbf{2}} \\ {M}_0{a}_g~1/c \end{gathered}$$

And we notice that if Goldbach conjecture 2n=p0+pn (n is a nature number , and p0, pn are primer numbers)and Polignac’s conjecture pn-p0 = 2n (n is a nature number , and p0, pn are primer numbers) be proofed, then

$$\begin{gathered} T~2n=(pn\pm p0) \\ {\displaystyle \frac{S_n}{S_0}}~{4n}^2={(pn\pm p0)}^2 \\ {\displaystyle \frac{M}{M_0}}~n^3={\left({\displaystyle \frac{pn\pm p0}{2}}\right)}^3 \end{gathered}$$

Because of the randomness of prime numbers, This will be a model to explain the randomness of the nature and Quantum Entanglement.

5. Summary

In this paper, We constructed a Space -Time with energy model just considering the velocity of the light C and the Plank constant h. Our Model give a definition of Quantum Space Time as

$$\begin{gathered} {\mathrm{m}}_0~{\displaystyle \frac{h}{C^2}}\text{~}10^{-50} (\mathrm{J}.{\mathrm{m}}^{-2}.{\mathrm{s}}^3) \\ {\displaystyle 1/a_g}~{\displaystyle \frac{h}{C}}\text{~}10^{-42}(\mathrm{J}.{\mathrm{m}}^{-1}.{\mathrm{s}}^2) \\ {S}_0~{\displaystyle \frac{1}{4}}*h*\left({\displaystyle \frac{c}{ag}}\right) ({\mathrm{J}}^2.{\mathrm{s}}^2) \\ T~\mathbf{2}\mathit{n}(\mathrm{J}.\mathrm{s}) \\ {\displaystyle \frac{{\mathit{S}}_{\mathit{n}}}{{\mathit{S}}_{\mathbf{0}}}}~{\mathbf{4}\mathit{n}}^{\mathbf{2}} \\ {\displaystyle \frac{\mathit{M}}{{\mathit{M}}_{\mathbf{0}}}}~{\mathit{n}}^{\mathbf{3}} \end{gathered}$$

This model just provides a basic structure of quantum Space -Time with energy.