Submitted:
25 August 2024
Posted:
27 August 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Literature Review
2.1. Historical Perspectives
2.2. Current Perspectives
2.3. The Need for Alternative Possible Solutions
2.4. Overview of the Modified Ohm’s Law
3. Methodology
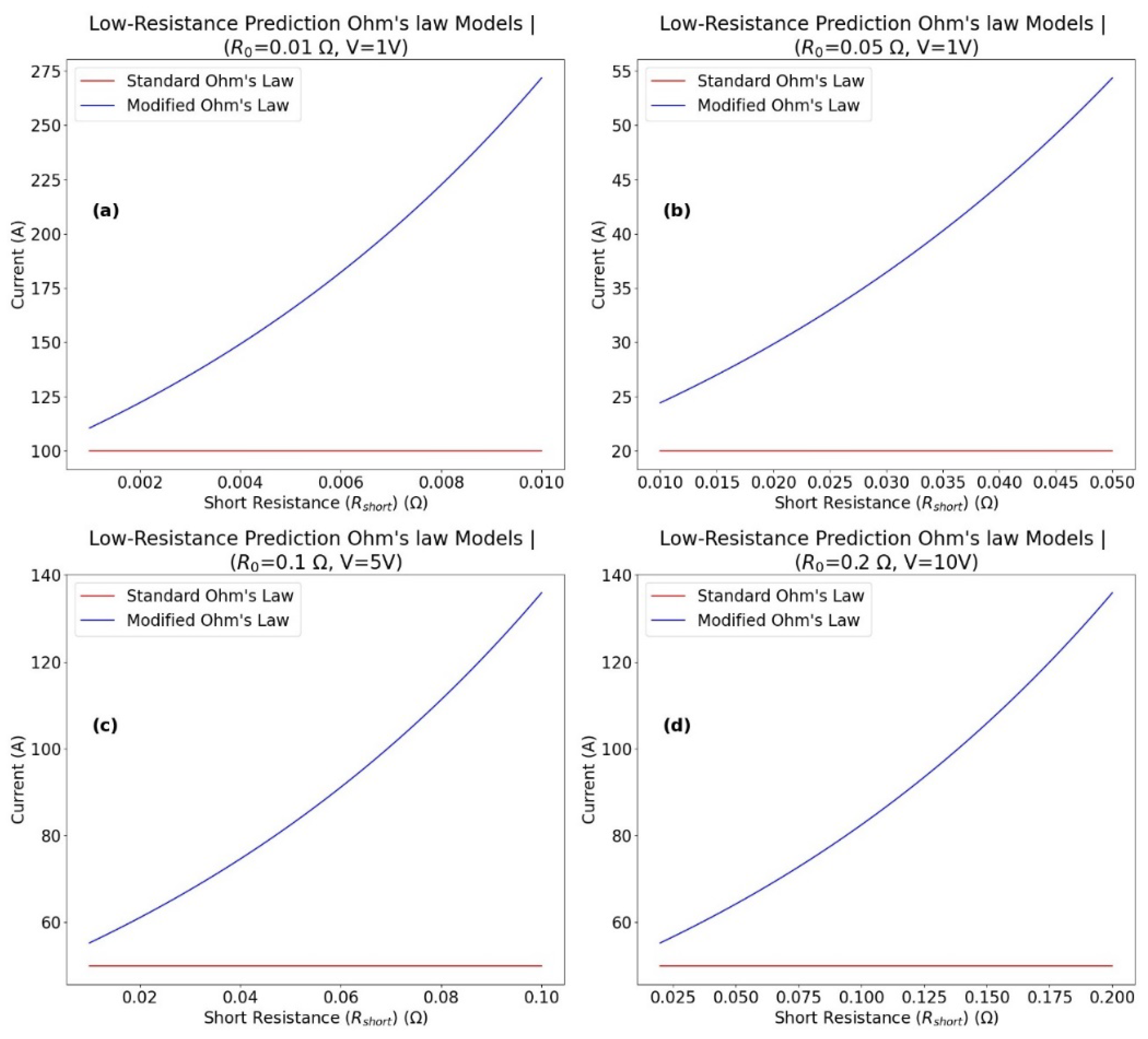
3.1. Low-Resistance Prediction
3.1.1. Simulation Algorithm
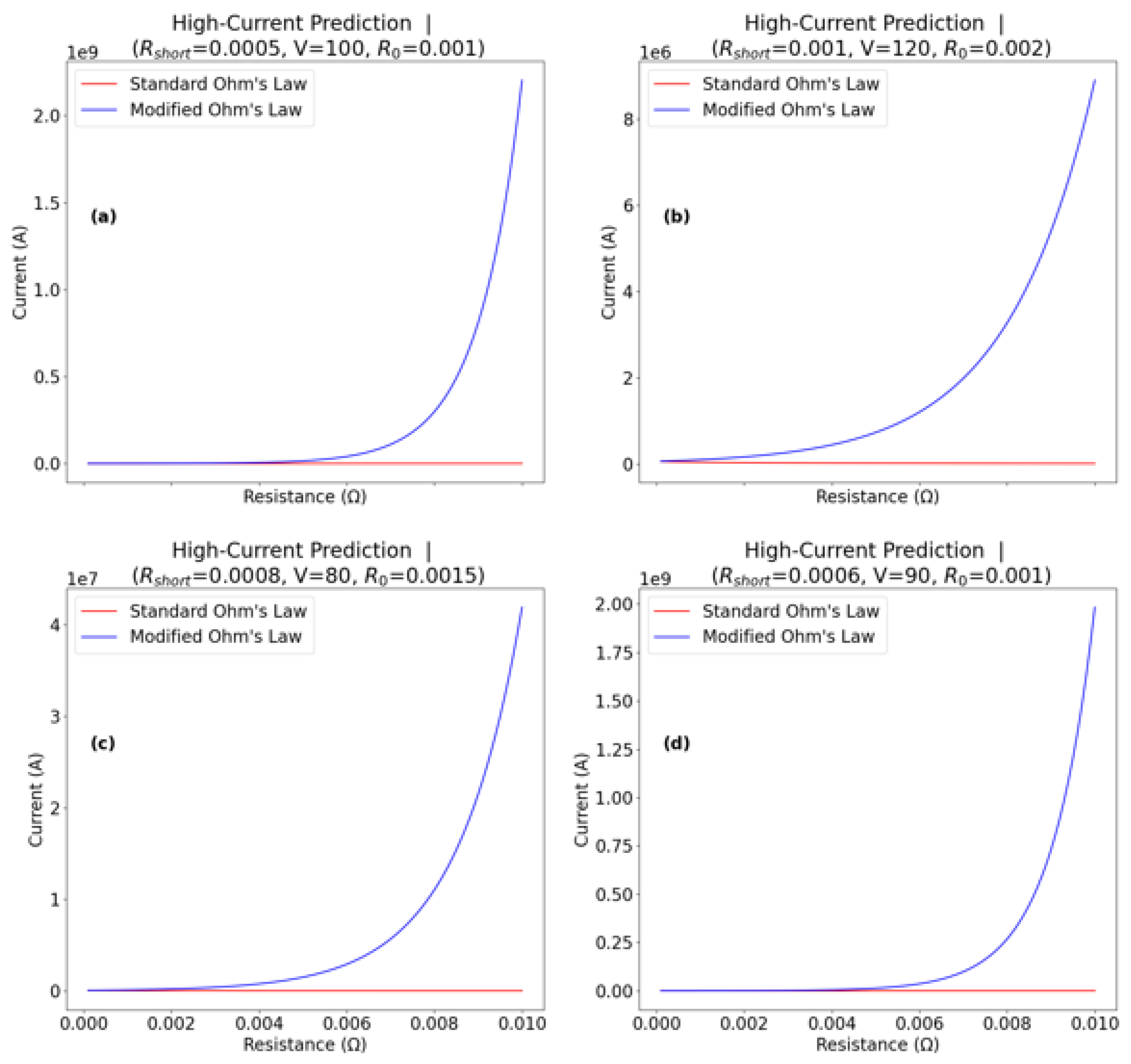
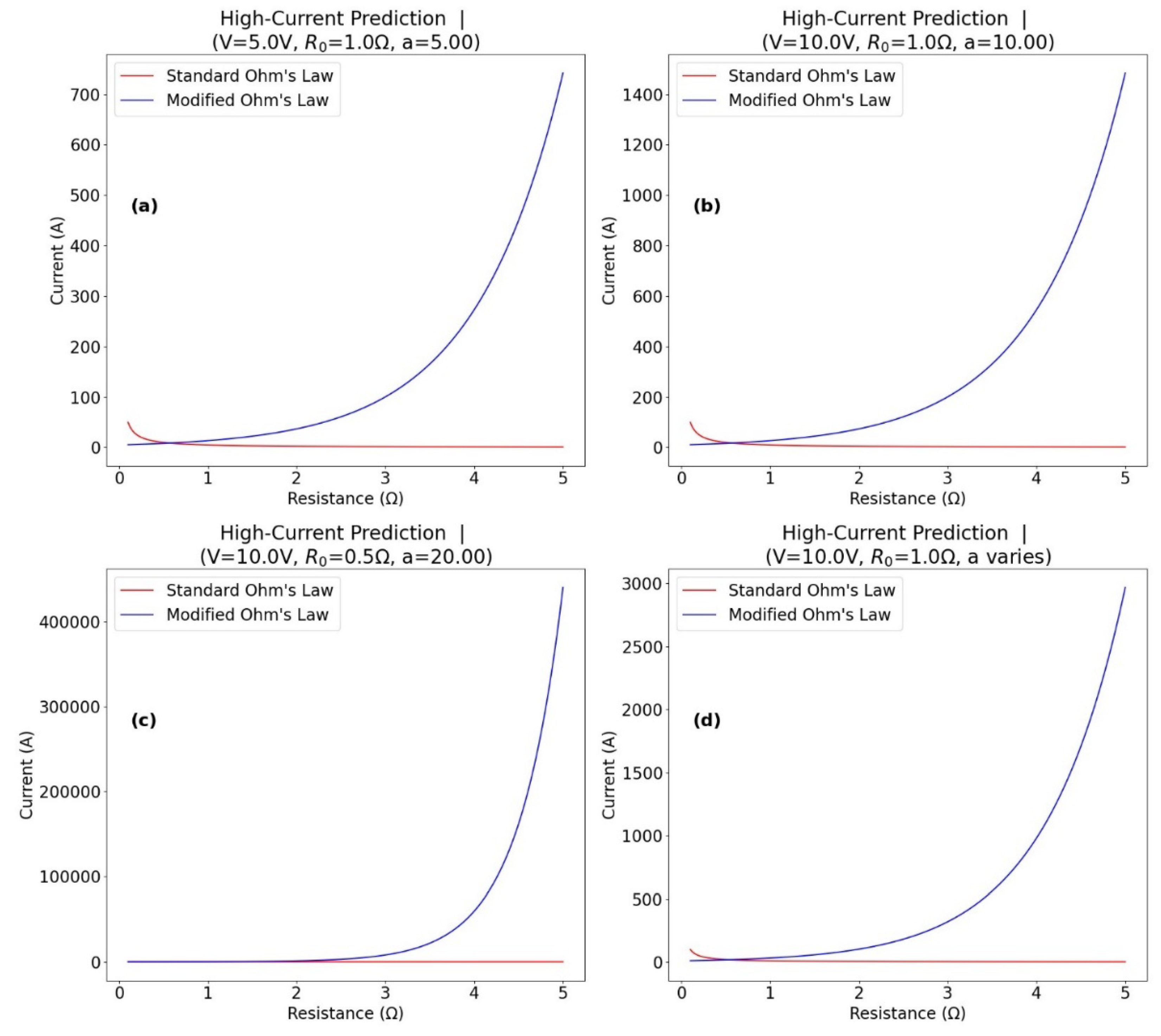
3.2. High Current Prediction
3.3. Practical Scenarios of the Ohm’s Law Variants
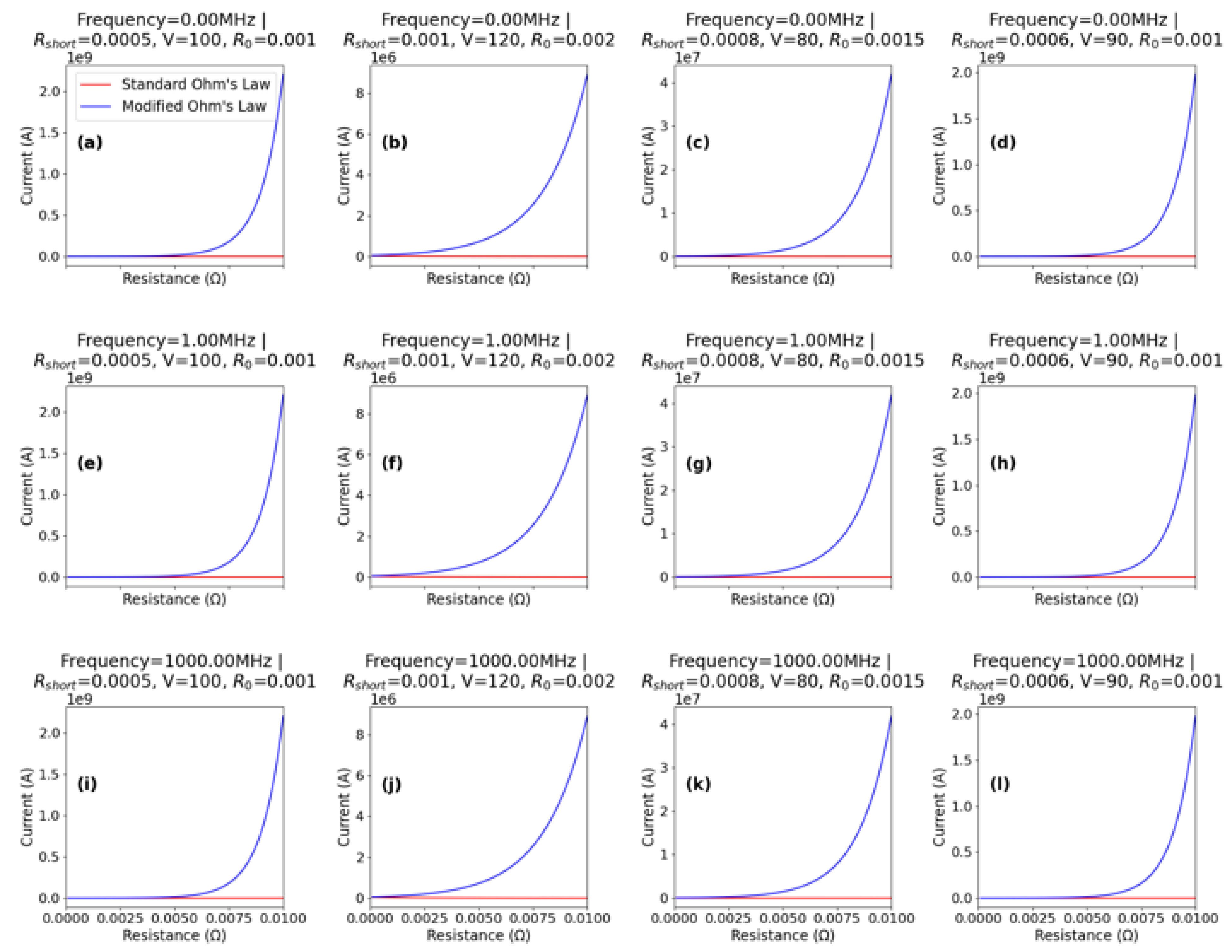
3.3.1. Advanced Design and Analysis of High-Frequency Circuits
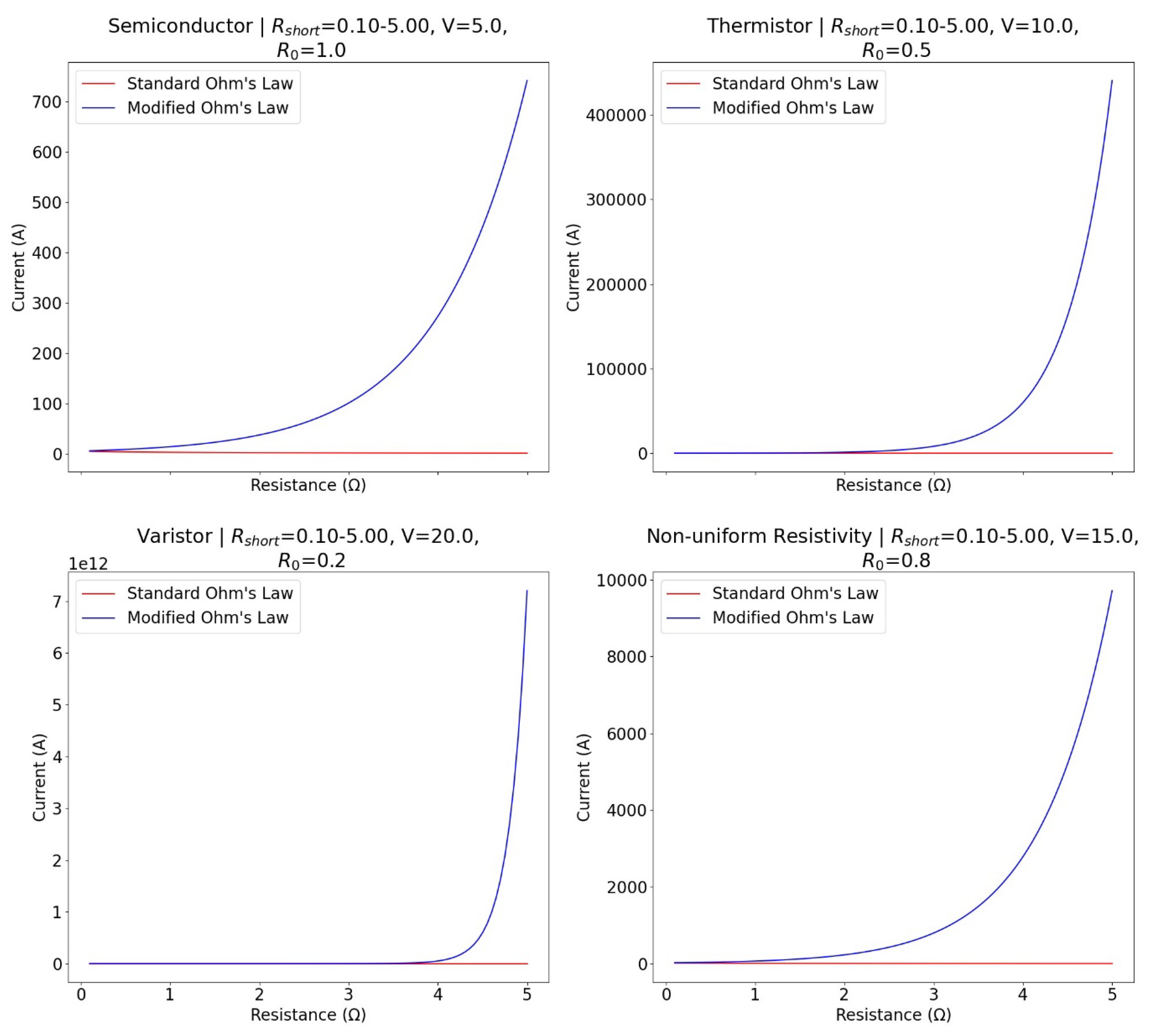
3.3.2. Comparative Analysis of the Ohm’s Law Variants in Various Electronic Devices
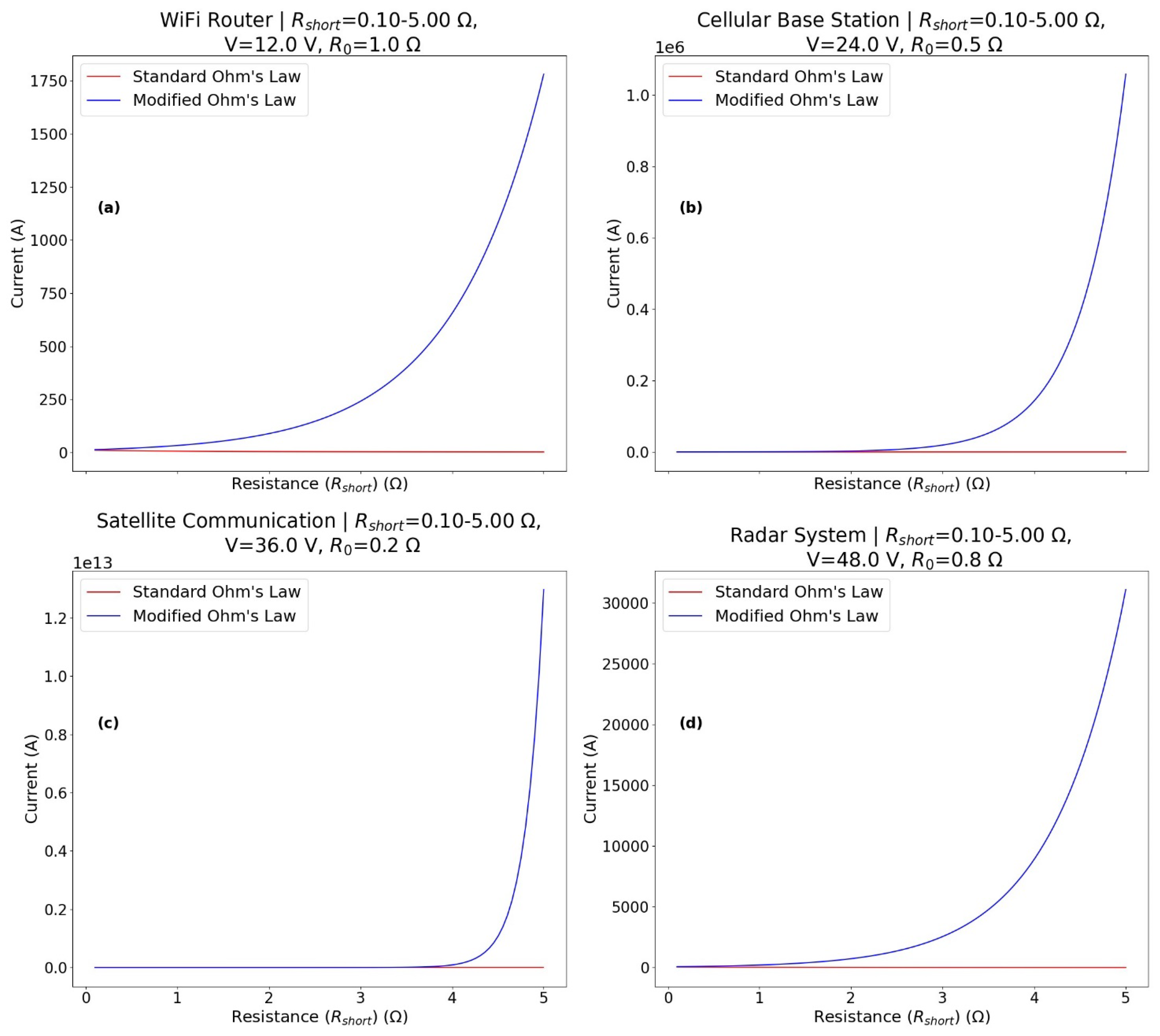
3.3.3. Signal Integrity Analysis in High-Frequency Circuits-A Comparative Case
4. Discussion
4.1. Low-Resistance Predictions
4.2. High-Current Predictions
4.3. Advanced Design and Analysis of High-Frequency Circuits
4.4. Comparative Analysis in Various Electronic Devices
4.5. The Role of Non-Linear Effects in High-Frequency Signal Integrity
4.6. Validating the Modified Model for High-Frequency Circuit Predictions
5. Conclusion
Declaration of Competing Interest
Research involving human/animal participants
Author Contributions
Funding
Appendix A. Methodology Overview and Execution Algorithm
| Method | Execution Algorithm |
|---|---|
| Mathematical Framework |
Derivation of the Modified Ohm’s Law. The exponential correction term was introduced to address non-linear resistance behavior. Key parameters were defined as: (Resistance variation). (Current scaling factor). (Reference resistance). |
| Simulation Framework |
Computational Tools and Techniques. Simulations were conducted using Python with key libraries including NumPy, SciPy, and Matplotlib. The scenarios considered focused on low-resistance measurements and high-current applications. |
| Validation of the Modified Ohm’s Law |
Low-Resistance Measurements. Standard Ohm’s Law. Current was calculated using . Modified Ohm’s Law. Current was calculated using the exponential model, showing enhanced accuracy. Computational and simulation results verified alignment with empirical expectations. |
|
High-Current Applications. Standard Ohm’s Law. Unrealistic infinite currents were predicted as resistance approached zero. Modified Ohm’s Law. The exponential model prevented infinite currents, enhancing safety and practical applicability. |
|
| Advanced Design and Analysis |
Improved Circuit Design. The modified law enabled more accurate designs for high-frequency circuits. Applications were explored in semiconductor devices, thermistors, varistors, and materials with non-uniform resistivities. |
| Signal Integrity in High-Frequency Circuits |
Analysis and Case Studies. The Modified Ohm’s Law improved signal integrity in high-frequency circuits. Practical benefits were illustrated through case studies in communication systems and RF applications. |
| Theoretical and Practical Implications |
Bridging the Gap. The paper discussed how the Modified Ohm’s Law effectively bridged the gap between theoretical models and practical applications. Implications for future research and development in electrical circuit analysis and design. |
References
- Z. Xie, X. Yang, X. Wu, Z. Gong, and Y. Guo, “Research and application of high frequency characteristic of transformers in power line carrier communication,” in 2012 International Conference on Systems and Informatics (ICSAI2012), Yantai, China: IEEE, May 2012, pp. 1556–1560. [CrossRef]
- J. B. Hagen, Radio-Frequency Electronics: Circuits and Applications, 2nd ed. Cambridge University Press, 2009. [CrossRef]
- F. Ellinger et al., “Power-efficient high-frequency integrated circuits and communication systems developed within Cool Silicon cluster project,” in 2013 SBMO/IEEE MTT-S International Microwave & Optoelectronics Conference (IMOC), Rio de Janeiro: IEEE, Aug. 2013, pp. 1–2. [CrossRef]
- J. Semple, D. G. Georgiadou, G. Wyatt-Moon, G. Gelinck, and T. D. Anthopoulos, “Flexible diodes for radio frequency (RF) electronics: a materials perspective,” Semicond. Sci. Technol., vol. 32, no. 12, p. 123002, Dec. 2017. [CrossRef]
- S. V. and G. F. A. Ahammed, “An Overview of Higher Order Frequency Applications in Communication Systems,” Int. J. Adv. Res. Sci. Commun. Technol., pp. 427–432, Dec. 2021. [CrossRef]
- P. Carro, J. De Mingo, P. Garcia-Ducar, and C. Sanchez, “Performance degradation due to antenna impedance variability in DVB-H consumer devices,” IEEE Trans. Consum. Electron., vol. 56, no. 2, pp. 1153–1159, May 2010. [CrossRef]
- M. Nourani and A. Attarha, “Signal Integrity: Fault Modeling and Testing in High-Speed SoCs,” J. Electron. Test., vol. 18, no. 4, pp. 539–554, Aug. 2002. [CrossRef]
- K. Soorya Krishna and M. S. Bhat, “Impedance matching for the reduction of via induced signal reflection in on-chip high speed interconnect lines,” in 2010 INTERNATIONAL CONFERENCE ON COMMUNICATION CONTROL AND COMPUTING TECHNOLOGIES, Oct. 2010, pp. 120–125. [CrossRef]
- V. Barzdenas and A. Vasjanov, “Applying Characteristic Impedance Compensation Cut-Outs to Full Radio Frequency Chains in Multi-Layer Printed Circuit Board Designs,” Sensors, vol. 24, no. 2, Art. no. 2, Jan. 2024. [CrossRef]
- M. Solomentsev and A. J. Hanson, “Modeling Current Distribution Within Conductors and Between Parallel Conductors in High-Frequency Magnetics,” IEEE Open J. Power Electron., vol. 3, pp. 635–650, 2022. [CrossRef]
- P. Ibba, A. Falco, B. D. Abera, G. Cantarella, L. Petti, and P. Lugli, “Bio-impedance and circuit parameters: An analysis for tracking fruit ripening,” Postharvest Biol. Technol., vol. 159, p. 110978, Jan. 2020. [CrossRef]
- D. Chenvidhya, K. Kirtikara, and C. Jivacate, “PV module dynamic impedance and its voltage and frequency dependencies,” Sol. Energy Mater. Sol. Cells, vol. 86, no. 2, pp. 243–251, Mar. 2005. [CrossRef]
- D. Chenvidhya, K. Kirtikara, and C. Jivacate, “A new characterization method for solar cell dynamic impedance,” Sol. Energy Mater. Sol. Cells, vol. 80, no. 4, pp. 459–464, Dec. 2003. [CrossRef]
- X. Qi and R. W. Dutton, “Interconnect Parasitic Extraction of Resistance, Capacitance, and Inductance,” in Interconnect Technology and Design for Gigascale Integration, J. Davis and J. D. Meindl, Eds., Boston, MA: Springer US, 2003, pp. 67–109. [CrossRef]
- A. Kimuya, “THE MODIFIED OHM’S LAW AND ITS IMPLICATIONS FOR ELECTRICAL CIRCUIT ANALYSIS,” Eurasian J. Sci. Eng. Technol., vol. 4, no. 2, pp. 59–70, Dec. 2023. [CrossRef]
- D. J. Shanefield, “Ohm’s Law and Measurements,” in Industrial Electronics for Engineers, Chemists, and Technicians, Elsevier, 2001, pp. 11–25. [CrossRef]
- V. K. Arora, “Failure of Ohm’s Law: Its Implications on the Design of Nanoelectronic Devices and Circuits,” in 2006 25th International Conference on Microelectronics, Belgrade, Serbia and Montenegro: IEEE, 2006, pp. 15–22. [CrossRef]
- A. Kımuya, “MODELING THERMAL BEHAVIOR IN HIGH-POWER SEMICONDUCTOR DEVICES USING THE MODIFIED OHM’S LAW,” Eurasian J. Sci. Eng. Technol., vol. 5, no. 1, pp. 16–43, Jun. 2024. [CrossRef]
- M. Thompson and J. K. Fidler, “Determination of the Impedance Matching Domain of Impedance Matching Networks,” IEEE Trans. Circuits Syst. Regul. Pap., vol. 51, no. 10, pp. 2098–2106, Oct. 2004. [CrossRef]
- V. T. Rathod, “A Review of Electric Impedance Matching Techniques for Piezoelectric Sensors, Actuators and Transducers,” Electronics, vol. 8, no. 2, Art. no. 2, Feb. 2019. [CrossRef]
- A. Reddaf et al., “Modeling of Schottky diode and optimal matching circuit design for low power RF energy harvesting,” Heliyon, vol. 10, no. 6, Mar. 2024. [CrossRef]
- A. Vasjanov and V. Barzdenas, “A Methodology Improving Off-Chip, Lumped RF Impedance Matching Network Response Accuracy,” Electronics, vol. 7, no. 9, p. 188, Sep. 2018. [CrossRef]
- C. Rodriguez, J. Viola, Y. Chen, and J. Alvarez, “Modeling and control of L-type network impedance matching for semiconductor plasma etch,” J. Vac. Sci. Technol. B, vol. 42, no. 2, p. 022212, Mar. 2024. [CrossRef]
- M. Pons, E. Valenzuela, B. Rodríguez, J. A. Nolazco-Flores, and C. Del-Valle-Soto, “Utilization of 5G Technologies in IoT Applications: Current Limitations by Interference and Network Optimization Difficulties—A Review,” Sensors, vol. 23, no. 8, p. 3876, Apr. 2023. [CrossRef]
- H. Attar et al., “5G System Overview for Ongoing Smart Applications: Structure, Requirements, and Specifications,” Comput. Intell. Neurosci., vol. 2022, pp. 1–11, Oct. 2022. [CrossRef]
- M. Meisser, K. Haehre, and R. Kling, “Impedance characterization of high frequency power electronic circuits,” in 6th IET International Conference on Power Electronics, Machines and Drives (PEMD 2012), Bristol, UK: IET, 2012, pp. A122–A122. [CrossRef]
- Tzong-Lin Wu, F. Buesink, and F. Canavero, “Overview of Signal Integrity and EMC Design Technologies on PCB: Fundamentals and Latest Progress,” IEEE Trans. Electromagn. Compat., vol. 55, no. 4, pp. 624–638, Aug. 2013. [CrossRef]
- C. Cuellar, W. Tan, X. Margueron, A. Benabou, and N. Idir, “Measurement method of the complex magnetic permeability of ferrites in high frequency,” in 2012 IEEE International Instrumentation and Measurement Technology Conference Proceedings, Graz, Austria: IEEE, May 2012, pp. 63–68. [CrossRef]
- Shuo Wang and F. C. Lee, “Analysis and Applications of Parasitic Capacitance Cancellation Techniques for EMI Suppression,” IEEE Trans. Ind. Electron., vol. 57, no. 9, pp. 3109–3117, Sep. 2010. [CrossRef]
- M. S. Gupta, “Georg Simon Ohm and Ohm’s Law,” IEEE Trans. Educ., vol. 23, no. 3, pp. 156–162, 1980. [CrossRef]
- K. M. Tenny and M. Keenaghan, “Ohms Law,” in StatPearls, Treasure Island (FL): StatPearls Publishing, 2024. Accessed: Jul. 17, 2024. [Online]. Available: http://www.ncbi.nlm.nih.gov/books/NBK441875/.
- P. Goswami, A. Subudhi, C. Gogate, V. Kshirsagar, and M. Kerawalla, “Advances in superconductivity and superconductors,” Res. J. Eng. Technol. 7 2 67, vol. 7, p. 67, Jun. 2016. [CrossRef]
- N. Klein, “High-frequency applications of high-temperature superconductor thin films,” Rep. Prog. Phys., vol. 65, no. 10, p. 1387, Aug. 2002. [CrossRef]
- R. Flükiger, “Overview of Superconductivity and Challenges in Applications,” Rev. Accel. Sci. Technol., vol. 05, pp. 1–23, Jan. 2012. [CrossRef]
- H. Wu, “Recent development in high temperature superconductor: Principle, materials, and applications,” Appl. Comput. Eng., vol. 63, pp. 153–171, May 2024. [CrossRef]
- J. W. Bray, “Superconductors in Applications; Some Practical Aspects,” IEEE Trans. Appl. Supercond., vol. 19, no. 3, pp. 2533–2539, Jun. 2009. [CrossRef]
- Semiconductors and the Information Revolution. Elsevier, 2009. [CrossRef]
- C. Junior, P. E. Redkva, and B. Sandrino, “Semiconductors in the Digital Age: Evolution, Challenges, and Geopolitical Implications,” Rev. Científica Multidiscip. Núcleo Conhecimento, pp. 133–150, Dec. 2023. [CrossRef]
- K. Zhang and J. Robinson, “Doping of Two-Dimensional Semiconductors: A Rapid Review and Outlook,” MRS Adv., vol. 4, no. 51–52, pp. 2743–2757, Oct. 2019. [CrossRef]
- H. Kim, J. Park, S. Lee, J. Kim, and S. Ahn, “Signal Integrity Analysis of Through-Silicon-Via (TSV) With Passive Equalizer to Separate Return Path and Mitigate the Inter-Symbol Interference (ISI) for Next Generation High Bandwidth Memory,” IEEE Trans. Compon. Packag. Manuf. Technol., vol. 13, no. 12, pp. 1973–1988, Dec. 2023. [CrossRef]
- J. Stejskal, “Conducting polymers are not just conducting: a perspective for emerging technology,” Polym. Int., vol. 69, no. 8, pp. 662–664, Aug. 2020. [CrossRef]
- J. Fan, X. Ye, J. Kim, B. Archambeault, and A. Orlandi, “Signal Integrity Design for High-Speed Digital Circuits: Progress and Directions,” IEEE Trans. Electromagn. Compat., vol. 52, no. 2, pp. 392–400, May 2010. [CrossRef]
- B. Wang and Z. Cao, “A Review of Impedance Matching Techniques in Power Line Communications,” Electronics, vol. 8, no. 9, Art. no. 9, Sep. 2019. [CrossRef]
- K. Song, J. Gao, Z. Wang, E. Ali, M. Bilal, and G. Xie, A Method of Improving Signal Integrity of Solder Joints. 2019.
- D. Kim et al., “Emerging memory electronics for non-volatile radiofrequency switching technologies,” Nat. Rev. Electr. Eng., vol. 1, no. 1, pp. 10–23, Jan. 2024. [CrossRef]
- K. Kojima et al., “High performance organic substrate with high dielectric constant, low loss, and low temperature coefficient of resonant frequency for high frequency RF module applications,” in 2011 IEEE Radio and Wireless Symposium, Phoenix, AZ, USA: IEEE, Jan. 2011, pp. 174–177. [CrossRef]
- L. Zhang et al., “Modulating and tuning relative permittivity of dielectric composites at metamaterial unit cell level for microwave applications,” Mater. Res. Bull., vol. 96, pp. 164–170, Dec. 2017. [CrossRef]
- M. T. Sebastian, R. Ubic, and H. Jantunen, “Low-loss dielectric ceramic materials and their properties,” Int. Mater. Rev., vol. 60, no. 7, pp. 392–412, Oct. 2015. [CrossRef]
- K. Soorya Krishna and M. S. Bhat, “Impedance matching for the reduction of via induced signal reflection in on-chip high speed interconnect lines,” in 2010 INTERNATIONAL CONFERENCE ON COMMUNICATION CONTROL AND COMPUTING TECHNOLOGIES, Nagercoil, India: IEEE, Oct. 2010, pp. 120–125. [CrossRef]
- Z. Cendes, “The development of HFSS,” in 2016 USNC-URSI Radio Science Meeting, Fajardo, PR, USA: IEEE, Jun. 2016, pp. 39–40. [CrossRef]
- X. F. Zhu, Z. H. Yang, B. Li, J. Q. Li, and L. Xu, “High Frequency Circuit Simulator: An Advanced Electromagnetic Simulation Tool for Microwave Sources,” J. Infrared Millim. Terahertz Waves, vol. 30, no. 8, pp. 899–907, Aug. 2009. [CrossRef]
- J. Hoffmann, C. Hafner, P. Leidenberger, J. Hesselbarth, and S. Burger, “Comparison of electromagnetic field solvers for the 3D analysis of plasmonic nano antennas,” Proc SPIE, vol. 7390, Jul. 2009. [CrossRef]
- A. Rezvanitabar, M. S. Kilinc, C. Tekes, E. F. Arkan, M. Ghovanloo, and F. L. Degertekin, “An Adaptive Element-Level Impedance-Matched ASIC With Improved Acoustic Reflectivity for Medical Ultrasound Imaging,” IEEE Trans. Biomed. Circuits Syst., vol. 16, no. 4, pp. 492–501, Aug. 2022. [CrossRef]
- M. Thompson and J. K. Fidler, “Determination of the Impedance Matching Domain of Impedance Matching Networks,” IEEE Trans. Circuits Syst. Regul. Pap., vol. 51, no. 10, pp. 2098–2106, Oct. 2004. [CrossRef]
- T. Duong and J.-W. Lee, “A Dynamically Adaptable Impedance-Matching System for Midrange Wireless Power Transfer with Misalignment,” Energies, vol. 8, no. 8, pp. 7593–7617, Jul. 2015. [CrossRef]
- T. Geyer and D. E. Quevedo, “Multistep Finite Control Set Model Predictive Control for Power Electronics,” IEEE Trans. Power Electron., vol. 29, no. 12, pp. 6836–6846, Dec. 2014. [CrossRef]
- M. Auf Der Maur, G. Penazzi, G. Romano, F. Sacconi, A. Pecchia, and A. Di Carlo, “The Multiscale Paradigm in Electronic Device Simulation,” IEEE Trans. Electron Devices, vol. 58, no. 5, pp. 1425–1432, May 2011. [CrossRef]
- D. Du and K. Ko, Theory of Computational Complexity, 1st ed. Wiley, 2014. [CrossRef]
- A. Ibrahim, M. Salem, M. Kamarol, M. Delgado, and M. K. Mat Desa, “Review of Active Thermal Control for Power Electronics: Potentials, Limitations, and Future Trends,” IEEE Open J. Power Electron., vol. 5, pp. 414–435, Apr. 2024. [CrossRef]
- M. Sofwan, M. Z. Abdullah, and M. K. Abdullah, “Experimental study on the cooling performance of high power LED arrays under natural convection,” IOP Conf. Ser. Mater. Sci. Eng., vol. 50, Dec. 2013. [CrossRef]
- L. Yuan, S. Liu, M. Chen, and X. Luo, “Thermal Analysis of High Power LED Array Packaging with Microchannel Cooler,” in 2006 7th International Conference on Electronic Packaging Technology, Shanghai, China: IEEE, Aug. 2006, pp. 1–5. [CrossRef]
- Q. Chen et al., “Recent advances in thermal-conductive insulating polymer composites with various fillers,” Compos. Part Appl. Sci. Manuf., vol. 178, p. 107998, Mar. 2024. [CrossRef]
- P. Huang et al., “Graphene film for thermal management: A review,” Nano Mater. Sci., vol. 3, Sep. 2020. [CrossRef]
- K. Gorecki and J. Zarebski, “Nonlinear Compact Thermal Model of Power Semiconductor Devices,” IEEE Trans. Compon. Packag. Technol., vol. 33, no. 3, pp. 643–647, Sep. 2010. [CrossRef]
- M. Janicki, Z. Sarkany, and A. Napieralski, “Impact of nonlinearities on electronic device transient thermal responses,” Microelectron. J., vol. 45, no. 12, pp. 1721–1725, Dec. 2014. [CrossRef]
- B. Mukherjee, L. Wang, and A. Pacelli, “A practical approach to modeling skin effect in on-chip interconnects,” in Proceedings of the 14th ACM Great Lakes symposium on VLSI, Boston MA USA: ACM, Apr. 2004, pp. 266–270. [CrossRef]
- O. Yamashita, “Effect of linear and non-linear components in the temperature dependences of thermoelectric properties on the energy conversion efficiency,” Energy Convers. Manag., vol. 50, no. 8, pp. 1968–1975, Aug. 2009. [CrossRef]
- A. M. Darwish, A. J. Bayba, A. Khorshid, A. Rajaie, and H. A. Hung, “Calculation of the Nonlinear Junction Temperature for Semiconductor Devices Using Linear Temperature Values,” IEEE Trans. Electron Devices, vol. 59, no. 8, pp. 2123–2128, Aug. 2012. [CrossRef]
- J. Fan, X. Ye, J. Kim, B. Archambeault, and A. Orlandi, “Signal Integrity Design for High-Speed Digital Circuits: Progress and Directions,” IEEE Trans. Electromagn. Compat., vol. 52, no. 2, pp. 392–400, May 2010. [CrossRef]
- M. Benhaliliba, “Electrical Transport and Current Conduction Mechanisms in ZnO/Si Heterojunction Diode,” Int. J. Robot. Autom. Technol., vol. 8, pp. 60–69, Dec. 2021. [CrossRef]
- E. T. Staikos and T. E. Tsovilis, “An Experimental Methodology for Modeling the Voltage-Dependent Capacitance and Resistance of Varistors: Implications on the Estimation of the Power and Energy Dissipation at Low Frequencies,” IEEE Trans. Power Deliv., vol. 38, no. 6, pp. 4122–4133, Dec. 2023. [CrossRef]
- M. Huff, “Review—Important Considerations Regarding Device Parameter Process Variations in Semiconductor-Based Manufacturing,” ECS J. Solid State Sci. Technol., vol. 10, no. 6, p. 064002, Jun. 2021. [CrossRef]
- F. Lissandrello, N. Lecis, and L. Magagnin, “Investigating the effect of current density in ultra-fast electrolytic zinc phosphate deposition,” Electrochimica Acta, vol. 478, p. 143840, Feb. 2024. [CrossRef]
- A. Lipatov et al., “High Breakdown Current Density in Monolayer Nb 4 C 3 T x MXene,” ACS Mater. Lett., vol. 3, no. 8, pp. 1088–1094, Aug. 2021. [CrossRef]
| Parameter Initialization |
|
| Current Calculation |
|
| Comparative Analysis |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




