A Method for Optimizing Production Layers Regroup Based on Genetic Algorithm

1. Introduction

As waterflooding multi-layer reservoirs get into the high-water-cut stage, due to the strong heterogeneity between layers, inter-layer conflicts become increasingly serious, resulting in imbalanced injection and production, uneven recovery ratio and significant differences of remaining oil distribution among layers, seriously affecting the effectiveness of water injection development [1,2,3]. Production layers regroup is an effective approach for resolving inter-layer conflicts and improving waterflooding efficiency [4,5,6,7].

Scholars have conducted extensive research on the work of production layers regroup. On the basis of accurately understanding the geological and development characteristics of oil reservoirs, scholars such as Jin Y. and Yao B. have used conventional reservoir engineering methods to reasonably divide and combine the production layers for their reservoirs [8,9,10,11,12,13]. Conventional reservoir engineering methods are relatively fast, but the determined layer combination scheme is limited, difficult to compare multiple schemes. Scholars such as Wang S. and Li L. used numerical simulation methods to comprehensively consider various factors that affect the combination of layers, proposed a relatively quantitative classification standard for production layers, and optimized the layer combination of the oilfields [14,15,16]. Although the numerical simulation method can compare and select multiple layer combinations, the early model preparation requires a long time and is not efficient. Scholars such as Li Q. and Wu Y. used mathematical methods such as grey correlation, clustering method, and enumeration to comprehensively consider various factors reflecting the contradictions of reservoir layers, and developed relevant programs for layer combination, achieving rapid layer regrouping and optimization [16,17,18,19,20,21,22]. Mathematical methods can effectively solve the contradiction between efficiency and effectiveness that traditional methods cannot balance, but currently, most methods can only analyze a subset of parameters influencing layers regrouping, or they are limited to selecting the best option from a predefined set rather than seeking the optimal solution to the problem.

Genetic algorithm is a method to search for optimal solutions by simulating the process of natural evolution. This algorithm, through mathematical calculation and computer simulation, converts the problem-solving process into a process similar to the selection, crossover, and mutation of chromosome genes in biological evolution [23]. Genetic algorithm uses probabilistic mechanism for iteration, which makes the method with randomness, and uses evaluation function for heuristic search, which makes the process simple. The mutation mechanism prevents the algorithm from getting trapped in local optima, leading to strong search capabilities. With potential parallelism, it can simultaneously compare multiple individuals, quickly and accurately determine the optimal layer series subdivision scheme. When dealing with complex combination optimization problems, genetic algorithm, compared to some conventional optimization algorithms, usually achieves better results more quickly [24]. Genetic algorithm has been widely applied in fields such as combinatorial optimization, machine learning, signal processing, adaptive control, engineering optimization and artificial life, and is an important intelligent algorithm [25].

This article introduces a smart method for production layers regroup based on genetic algorithm. Comprehensively considering various factors that affect the regroup of layers, based on the combination principle of “smaller intra-group variance and larger inter-group variance of each influencing factor are expected “, genetic algorithm is used to calculate the intra-group variance and inter-group variance of each influencing factor for each initial grouping scheme, and then calculate the fitness values of those schemes. Based on the fitness value, the advantageous schemes with higher fitness values are selected as the basis of the next generation. Then crossover and mutation operations are performed to those advantageous schemes to generate new schemes. Through continuous selection and evolution, until the global optimal solution with the highest fitness value is found, the optimal combination scheme is determined. Unlike selecting a preferable plan from a limited number of predefined combination schemes, this method is an automatic optimization to solve the optimal solution of the problem. It improves both efficiency and accuracy as compared to conventional reservoir engineering methods, numerical simulation methods and most of the mathematical methods.

2. Methodology

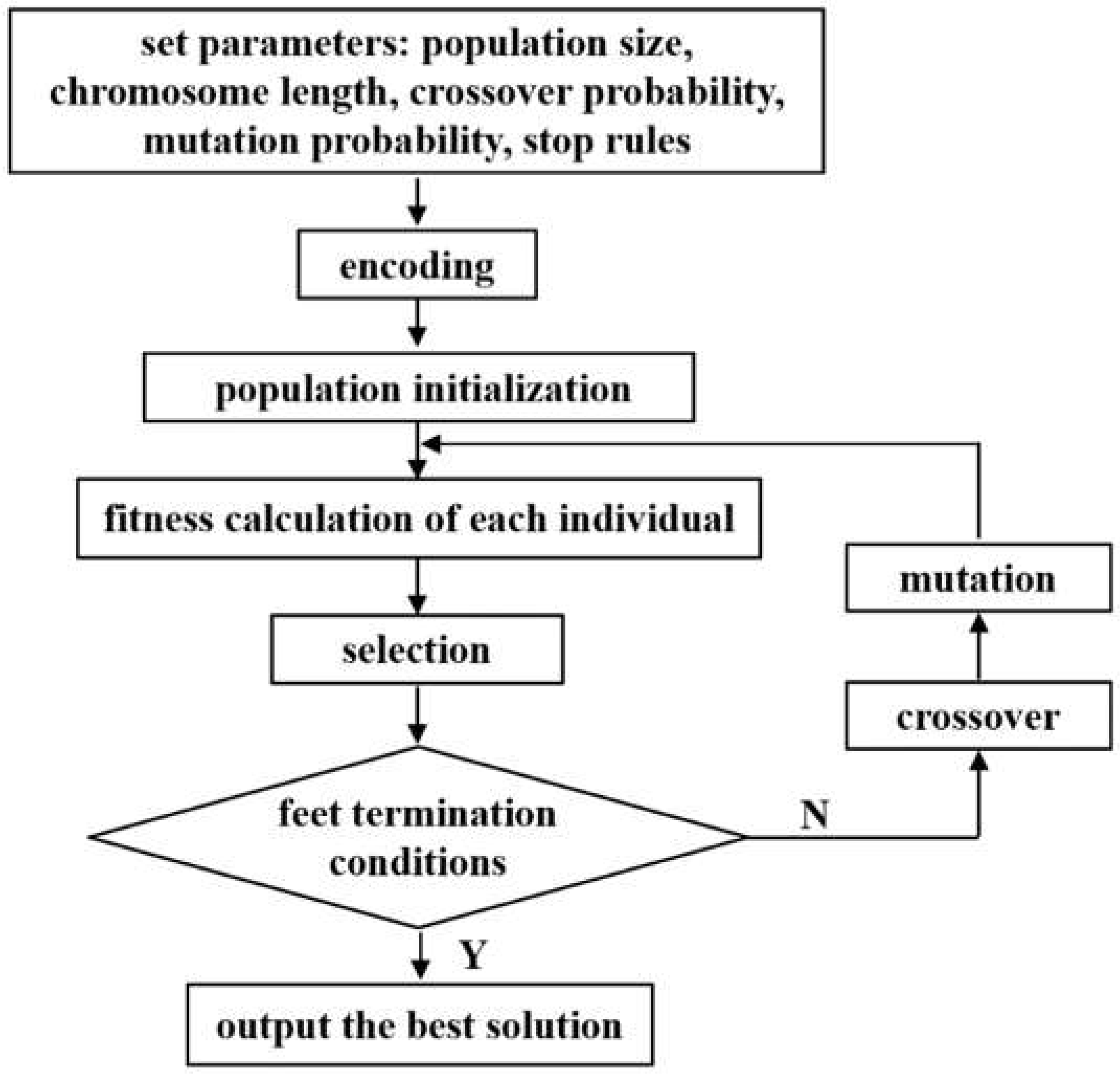
2.1. Genetic Algorithm

Genetic algorithm is a method of finding the optimal solution by simulating natural evolution processes. Figure 1 shows the basic flowchart of genetic algorithm. Genetic algorithm maps the phenotypes of all individuals in the population to numerical values, i.e., encoding, and utilizes randomization techniques to efficiently search for an encoded parameter space. After initializing the population, better approximate solutions are obtained according to the principles of survival of the fittest. The genetic operations of genetic algorithm are selection, crossover, and mutation [23,24]. The selection operation ensures the advantageous individuals of the previous generation population to be inherited, while the crossover and mutation operations are aimed at obtaining more diverse populations, so as to quickly find the optimal solution.

2.2. Optimization of Layers Regrouping Scheme with Genetic Algorithm

This paper applies genetic algorithm to the optimization problem of production layers regrouping in oilfield development, the detailed steps are as follows:

2.2.1. Parameter Preset

The preset parameters include: 1) Population size G, indicating how many regrouping schemes are there in the population; 2) Total number of layer groups S; 3) Total number of layers N; 4) Maximum number of iterations T; 5) Crossover probability P_c; 6) Mutation probability P_m.

2.2.2. Population Initialization

Define the initial population G₀, which consists of G combination schemes. The initial schemes can be randomly generated or set manually (setting a reasonably sound initial population could accelerate the solution process).

As an example, with a total number of layers of 10 and a layer series of 3 (S = 3), a regroup plan could be as Figure 2:

“1” indicates that the layer is included in the group, while “0” indicates that the layer is not included in the group. This is the coding method used in the genetic algorithm. Note: Different layer groups cannot include the same layer.

2.2.3. Calculation of the Fitness Value for Each Regrouping Scheme

The fitness in genetic algorithm is an indicator for the superiority of an individual (that is, each combination scheme). As for the optimization of production layers regroup, regardless of interbed and economic factors, smaller intra-group variance and larger inter-group variance of the influencing factors are expected for the regroup plan. In this paper, these two variances are then combined into a comprehensive variance as the fitness value for each scheme.

The fitness value for each layer groups division scheme is calculated according to the following steps.

(1) calculation of the intra-group variance of the influencing factors

The intra-group variance ${\sigma in}_{i,q}$ of the influencing factors of each layer group is calculated and then the average $\overline{{\sigma in}_q}$ of ${\sigma in}_{i,q}$ for all layer groups is determined through the following formulas.

$${\sigma in}_{i,q}=\sqrt{{\displaystyle \frac{\sum _{j=1}^n{\left(v_{i,j,q}-\overline{v_{i,q}}\right)}^2}{n}}}$$

(1)

$$\overline{v_{i,q}}=\left({\sum }_{j=1}^n{v}_{i,j,q}\right)/n$$

(2)

$$\overline{{\sigma in}_q}=\left({\sum }_{i=1}^S{\sigma in}_{i,q}\right)/S$$

(3)

i, the i-th layer group;

j, the j-th layer in the i-th layer group;

q, the q-th influencing factor;

${\sigma in}_{i,q}$, the standard variance of the q-th influencing factor between each layer in the i-th layer group;

$v_{i,j,q}$, the value of the q-th influencing factor in the j-th layer of the i-th layer group;

$\overline{v_{i,q}}$, the average value of the q-th influencing factor in the i-th layer group;

n, the number of layers in each layer group, could be different between groups;

$\overline{{\sigma in}_q}$, the average value of ${\sigma in}_{i,q}\mathrm{o}\mathrm{f}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{l}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{p}\mathrm{s}$;

S, total number of layer groups.

(2) Calculation of the inter-group variance of the influencing factors

The inter-group variance ${\sigma out}_q$ of the influencing factors is calculated through the following formulas, When calculating the variance of each influencing factor between layer group, set the average value of $\overline{v_{i,q}}$ of each influencing factor across all layers within layer group as the value of that influencing factor in that layer group.

$${\sigma out}_q=\sqrt{{\displaystyle \frac{\sum _{i=1}^S{\left(\overline{v_{i,q}}-\overline{v_q}\right)}^2}{S}}}$$

(4)

$$\overline{v_q}={\displaystyle \frac{\left({\sum }_{i=1}^S\overline{v_{i,q}}\right)}{S}}$$

(5)

${\sigma out}_q,$ the standard variance of the q-th influencing factor between layer groups;

$\overline{v_q}$, the average value of $v_{i,q}$ of all layer groups;

(3) Normalization of intra-group variance and inter-group variance and fitness value calculation for each regrouping scheme.

The two variances above are then normalized and combined into a comprehensive variance as the fitness value for each regrouping plan:

$\overline{{\sigma in}_q}$ and ${\sigma out}_q$ obtained above are normalized as:

$$\ddot{\overline{{\sigma in}_q}}={\displaystyle \frac{\overline{{\sigma in}_q}-\overline{{\sigma in}_{min}}}{\overline{{\sigma in}_{max}}-\overline{{\sigma in}_{min}}}}(q=\mathrm{1,2},...,r)$$

(6)

$$\ddot{{\sigma out}_q}={\displaystyle \frac{{\sigma out}_q-{\sigma out}_{min}}{{\sigma out}_{max}-{\sigma out}_{min}}}\left(q=\mathrm{1,2},...,r\right)$$

(7)

$\ddot{\overline{{\sigma in}_q}}$, normalized value of $\overline{{\sigma in}_q}$;

$\overline{{\sigma in}_{min}}$, the minimum value of $\overline{{\sigma in}_q}$;

$\overline{{\sigma in}_{max}},$ the maximum value of $\overline{{\sigma in}_q}$;

$\ddot{{\sigma out}_q}$, normalized value of ${\sigma out}_q$;

${\sigma out}_{min}$, the minimum value of ${\sigma out}_q$;

${\sigma out}_{max}$, the maximum value of ${\sigma out}_q$.

$\ddot{\overline{{\sigma in}_q}}$ and $\ddot{{\sigma out}_q}$ are then combined into $\sigma$ as the fitness value of the layer regroup scheme:

$\sigma =\sum _{q=1}^r{{\alpha }_q(\lambda }_1(1-\ddot{\overline{{\sigma in}_q}})+{\lambda }_2\ddot{{\sigma out}_q})$; (8)

${\lambda }_1,{\lambda }_2,$ weight coefficients for intra-group variance and inter-group variance, ${\lambda }_1+{\lambda }_2=1$;

${\alpha }_q$, weight coefficient for the q-th influencing factor, $\sum _{q=1}^r{\alpha }_q=1$;

$\sigma$, comprehensive variance, which is the fitness value for the combination scheme.

Noted that, smaller intra-group variance and larger inter-group variance are expected based on the layers regrouping principle, so a smaller $\ddot{\overline{{\sigma in}_q}}$, a larger $1-\ddot{\overline{{\sigma in}_q}}$, a larger $\ddot{{\sigma out}_q}$, and consequently a larger $\sigma$ are expected for an ideal plan.

2.2.4. Genetic Calculation

(1) Selection

Select schemes within the population based on the scheme fitness value. The superior schemes are chosen as the basis for the next calculation.

The roulette wheel selection method is used to define the probability of a scheme being selected [23]:

$$P_k={\displaystyle \frac{{\sigma }_k}{{\sum }_{k=1}^G{\sigma }_k}}$$

(8)

${\sigma }_k,$ the fitness value of the k-th scheme.

Schemes with higher fitness values have a higher probability of being selected. In this case, still select G schemes (the same scheme can be repeatedly selected) to maintain the population size.

(2) Crossover

By utilizing single-point crossover operator, perform random crossovers on the selected schemes obtained through the selection process mentioned above. Randomly select two groups within a scheme, choose a random crossover point, and then perform crossover pairing at that position with the specified crossover probability $P_c$.

(3) Mutation

Perform random mutations for each scheme obtained above after crossover calculation. Randomly select one group within a scheme, choose a random mutation position (i.e., position of the layer), and generate a random number between [0, 1] as a comparison probability. If this probability is less than the mutation probability $P_m$, then the selected mutation position changes from 1 to 0 or from 0 to 1. However, it is important to note that the mutation method here is different from the conventional mutation method in genetic algorithm. It is not a simple change from 1 to 0 or from 0 to 1. In this case, if a layer changes from 1 to 0, then in another group, the same layer must change from 0 to 1, and vice versa. This ensures that different groups do not contain the same layer.

The selection operation mentioned above allows the inheritance of superior schemes, while crossover and mutation operations aim to generate more diversified schemes.

The next generation population G(t+1) is obtained after the selection, crossover, and mutation of population G(t).

Repeat the calculations from section 2.2.3 to 2.2.4 until the termination condition is met. Finally, the scheme with the maximum fitness value during the calculation process is outputted as the optimal scheme.

3. Case Application

A computational program was developed based on the above method, and the layer groups in the waterflooding sandstone reservoir Block X were optimized.

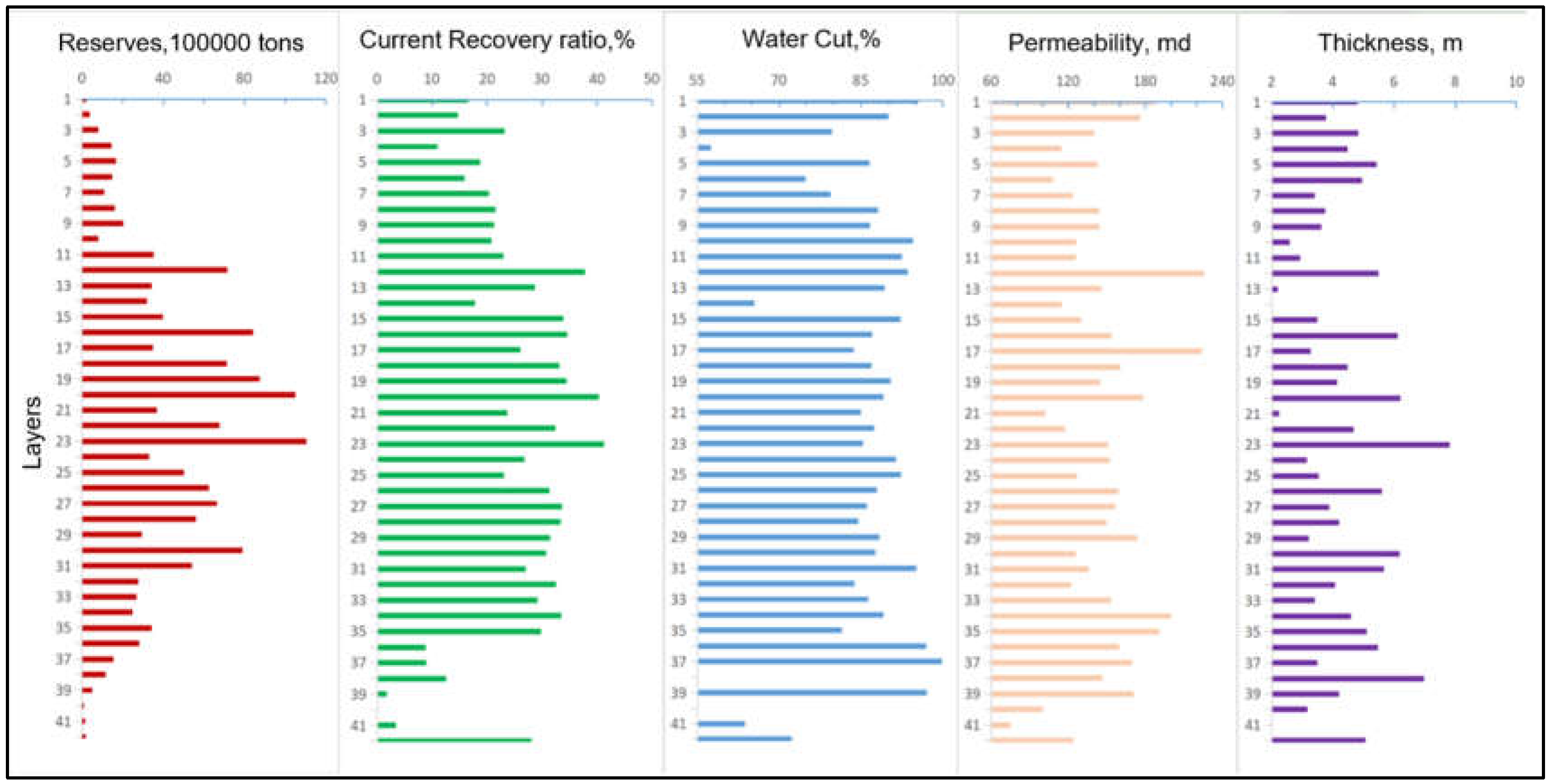
3.1. Overview of the Reservoir

Block X is a waterflooding sandstone reservoir in China (as shown in Figure 3) with 42 individual sand layers vertically and a production history of approximately 35 years. Currently, the cumulative recovery ratio is 30.39%, and the overall water cut is 90.74%, indicating that it has entered a high-water-cut stage. The heterogeneity between layers has resulted in significant variations in the development effect of each layer. For instance, the highest recovery of single layer is 41.25%, while the lowest is only 1.74%. Some layers have no water production, while most have already entered the high-water-cut stage. Geological and development parameters of each layer are illustrated in Figure 4.

3.2. Optimization of Layers Regrouping Scheme with Genetic Algorithm

Firstly, the parameters are set as follows: population size G = 6, total number of layer groups S = 3, total number of layers N = 42, maximum iteration count T = 1000, crossover probability P_c = 0.8, and mutation probability P_m = 0.005.

The initial population is defined as follows: 6 initial layer regrouping schemes are designed based on the parameter values of geological reserves, remaining reserves, current recovery ratio, comprehensive water cut, permeability, and effective thickness, as shown in Table 1.

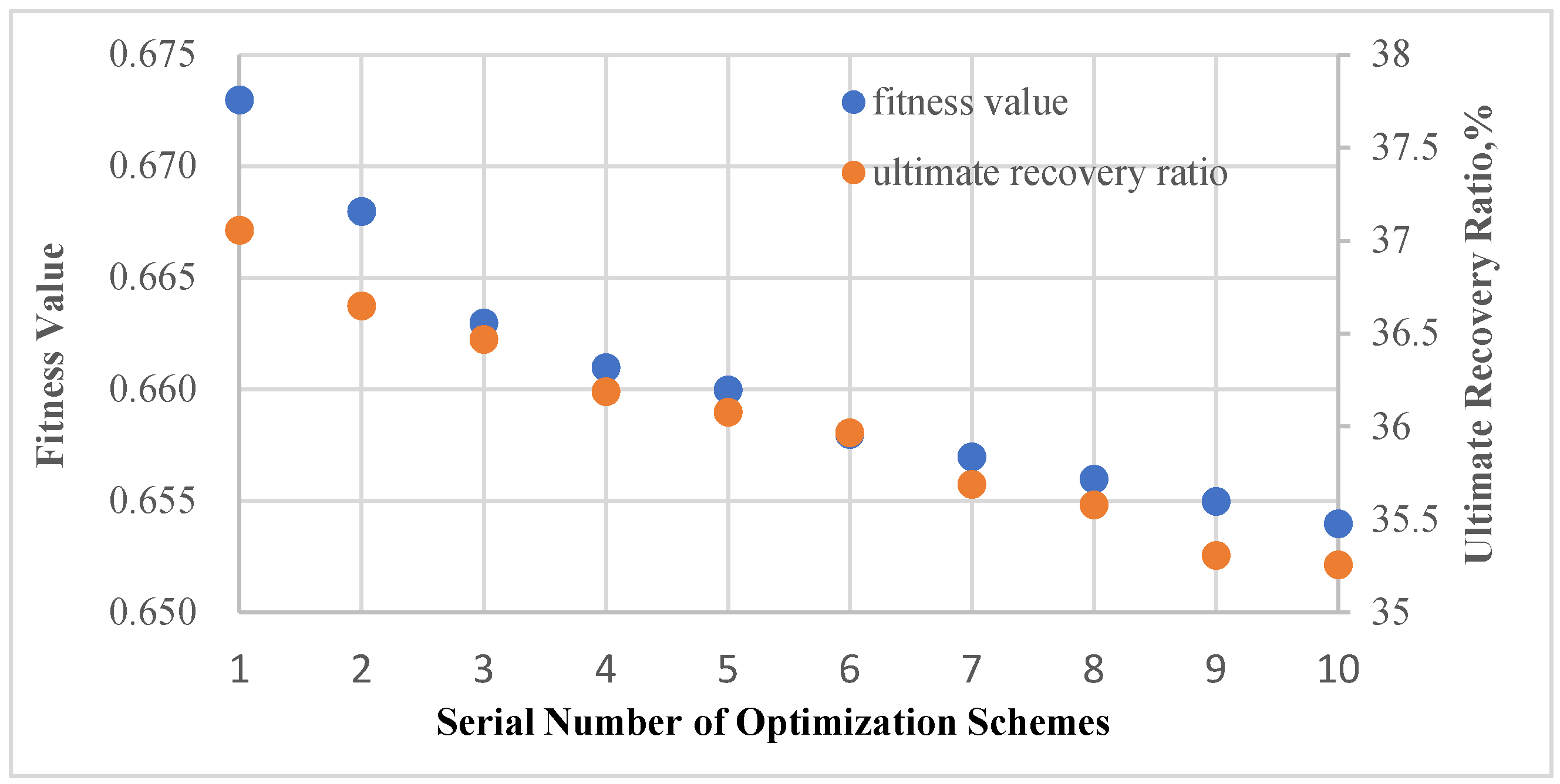
3.3. Optimization Results

On the basis of the initial schemes, a total of 6,000 new schemes were generated through selection, crossover, and mutation. The top 10 optimal schemes are shown in Table 2, with the optimized scheme 1 identified as the optimal grouping scheme (Table 3).

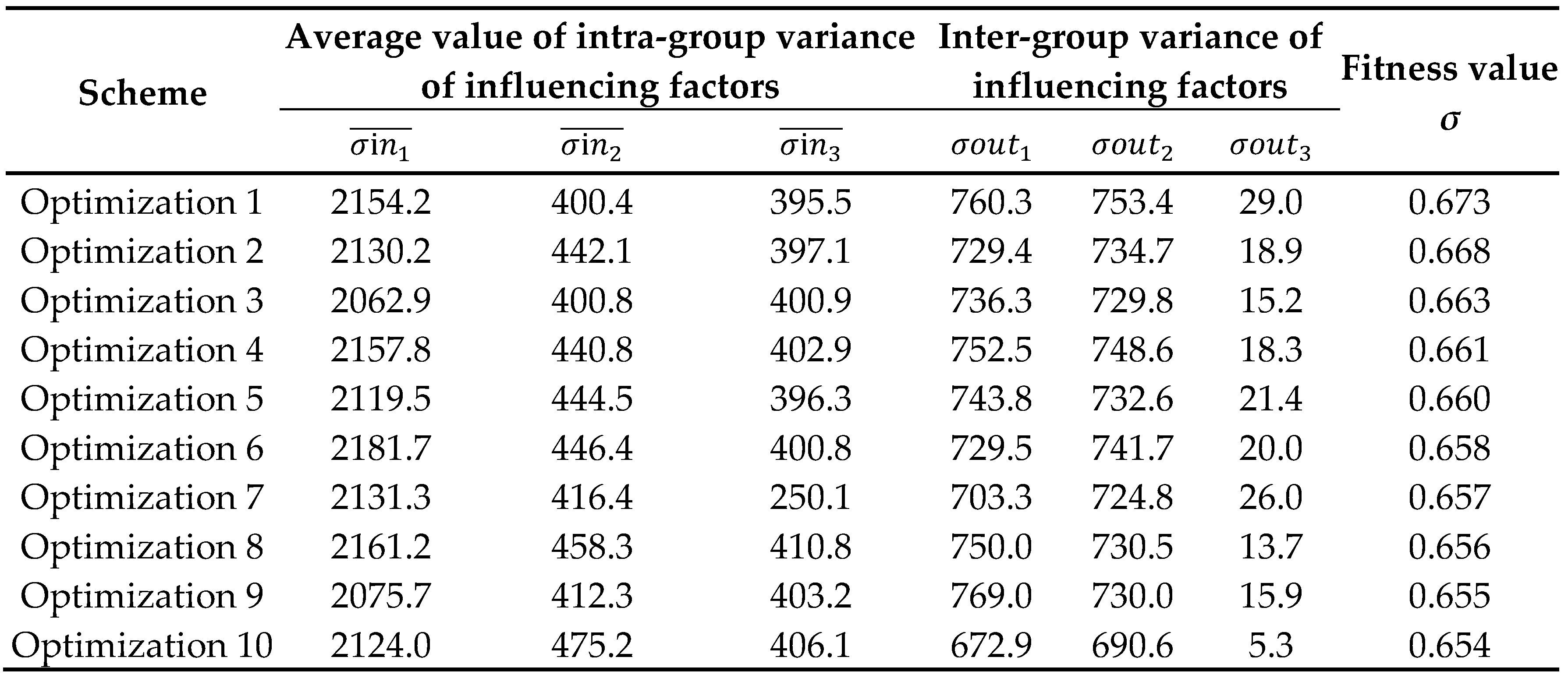
3.4. Reliability Analysis of Optimization Results

To verify the reliability of the optimization method proposed in this paper, by using numerical simulation method, the final recovery ratio of the top 10 optimization schemes were calculated. The comparative results are shown in Table 4 and Figure 5. The conclusions are as follows: first, the optimization schemes achieved higher recoveries than the non-optimization ones; second, the trends of the final recovery rate calculated by numerical simulation and the fitness value calculated by the method in this paper are generally consistent. As the fitness value increases, the final recovery rate gradually increases. Therefore, it can be seen that the calculation results of the optimization algorithm in this paper are reliable. Additionally, the method in this paper takes only about 1 hour for the whole calculating process, while numerical simulation requires one to two weeks. The method presented in this paper greatly improves work efficiency.

4. Deficiencies

This method still has the following deficiencies:

1) It only considers technical indicators and does not take into account the impact of interbed and economic issues.

2) The weight coefficient λ₁ and λ₂, as well as the weight coefficient ${\alpha }_q$ still rely on expertise for assignment.

3) The calculation speed deepens on the reasonable initial schemes to some extent. The more reasonable the initial schemes are, the faster the optimal solution could be obtained.

5. Conclusions

Taking consideration of multiple factors that affect the production layer regroup, such as geological reserves, current recovery ratio, remaining reserves, effective thickness, permeability, porosity and water cut, genetic algorithm is used to calculate the fitness value of the combination scheme. Based on the fitness value, selection, crossover and mutation operations are performed to continuously generate new schemes, until the global optimal solution is found with the biggest fitness value, the optimal scheme is determined.

Unlike selecting a preferable plan from a limited number of predefined combination schemes, this method is an automatic optimization to solve the optimal solution of the problem.

This method can analyze and calculate various factors that influence production layer regrouping beyond those specifically mentioned in this case study. Additional factors can be incorporated into the calculation program as needed.

Comparison with numerical simulation results demonstrates the reliability of this intelligent method, which improves both efficiency and accuracy as compared to conventional reservoir engineering methods, numerical simulation methods and most of the mathematical methods, thus providing effective guidance for the EOR strategies of waterflooding reservoirs in high-water-cut stage.