An In-Depth Analysis of Tsallis Statistics: π ±, K ± Mesons, and Pp̄ Baryon in Inelastic Pp Collisions

1. Introduction

The identification of various stages of dense matter during the evolution of heavy-ion collisions [1] is a crucial task. At extremely high energy or density, a state of matter exists in which quarks and gluons are deconfined, forming Quark-Gluon Plasma (QGP) [2]. This state is also observed in the early universe, occurring microseconds (${10}^{-6}$s) after the Big Bang before condensing into hadrons. Evaluating phase transitions in finite systems has been a longstanding focus, studied for decades through various phenomenological applications.

The Relativistic Heavy-Ion Collider (RHIC) [3] and the Large Hadron Collider (LHC) [4] provide useful tools for identifying the phase structure and investigating the properties of Quantum Chromodynamics (QCD) matter.

According to statistical thermal models, the initial stage of nuclei collisions at RHIC and LHC generates high temperatures, creating a dense "fireball" with a large radius in a short period (about ${10}^{-22}$ seconds). This fireball consists of QGP, which subsequently cools and expands the system. Partons recombine to form a cascade of hadronic matter, and these hadrons continue to interact until these interactions cease, freezing the particle momenta. The temperature at this point decreases to a specific value known as the chemical freeze-out temperature ($T_{ch}$). However, the rescattering process continues to occur, contributing to the ongoing development of collective (hydrodynamical) expansion. Consequently, the matter becomes more dilute, and the mean free path of the given hadrons in elastic reaction processes becomes comparable to the size of the system. At this stage, the rescattering process ceases, resulting in the separation of hadrons from the rest of the system [5,6]. This phase is termed as kinetic or thermal freeze-out stage, and the temperature at this point is denoted as the kinetic or thermal freeze-out temperature ($T_0$). Following this stage, the particle’s energy/momentum spectrum becomes fixed in time, marking the concluding phase of the system’s evolution. If flow effect is included at the stage of kinetic freeze-out along with the degree of excitation of the interacting system, then that temperature is called the effective temperature ($T_{eff}$), and it is generally greater that the $T_0$.

As the purpose of heavy-ion collision is to study the QGP probed through its signatures. However the small collision system like $pp$[7] shows the similar features as observed in heavy-ions like $pPb$[8], $PbPb$[9] and $XeXe$[10] collisions. The signatures like anisotropic radial flow and strangeness enhancement are associated with the formation of quark gluon plasma(QGP) [11], is also observed in $pp$ and $pPb$ systems.

In this paper, we have investigated the thermodynamic characteristics of interacting systems. For this purpose, several statistical models, including the Boltzmann-Gibbs distribution [13], have been employed. Notably, the Tsallis distribution function [14] has proven to be an excellent representation of particle spectra for $p_T$ values. By applying the non-extensive Tsallis distribution function for ALICE data fitting purposes [12], we have determined various thermodynamic parameters such as effective temperature ($T_{eff}$), chemical potential ($\mu$), and volume (V) of the system. The non-extensive Tsallis distribution function is utilized for combined minimum ${\chi }^2$ fits.

2. Methodology

The study of underlying events(UE) [12] is proposed to understand the effect observed in small collision system. The UE consists of initial state radiation (ISR), final state radiation (FSR), beam remnant and multiparticle interactions (MPIs). The particles produced as a function of UE activity allows to probe the properties in MPI suppressed environment. This experiment yields a similar signal to radial flow, but with increased multiplicity due to jet hardening.

At LHC, enormous number of particles are produced. We analysed the primary charged particles, $({\pi }^{+}+{\pi }^{-})$, $(K^{+}+K^{-})$ and $(p+\overline{p})$ as a function of UE at $\sqrt{s}=13TeV$[8] in this work. The UE activity is probed through particle event topology, where leading charged particle carries the highest transverse momentum within $5<p_T^{leading}\le 40GeV/c$ in the pseudorapidity interval of $\left|\eta \right|<0.8$. The lower threshold of $p_T^{leading}$ guarantees the multiple soft scattering while the upper threshold is used to reduce the effects of wide angle radiation which is significant for $p_T>50GeV/c$ and associated with hard scattering.

The three different topological regions away, towards and transverse regions are reported in this paper. These are determined by comparing the azimuthal angles of the leading and associated particles $|△\varphi |$ = ${\varphi }^{leading}-\varphi$. The associated particles lying in the kinematic range of $0.15<p_T<5GeV/c$ and $\left|\eta \right|<0.8$. The away, towards and transverse regions are defined as $|△\varphi |\ge {120}^{\circ }$, ${60}^{\circ }\le |△\varphi |<{120}^{\circ }$ and $|△\varphi |<{60}^{\circ }$. The particles produced in away and toward region contain constituents from away-side and leading jets, whereas the transverse region is sensitive to ISR, FSR and MPI’s.

In this paper, we have used the non extensive Tsallis distribution function [14] to extract the thermodynamic information for primary charged particle $({\pi }^{\pm },K^{\pm }$ and $p\overline{p})$ produced as a function of $R_T$ over a wide range of transverse momentum for pseudorapidity region $\left|\eta \right|=0.8$, at center of mass energy $\sqrt{s}=13TeV$. These primary charged particles have mean life time $\tau$, larger than $1cm/c$ which is produced in interactions or from the decay of particles with life time $\tau$ smaller than $1cm/c$.

2.1. Particle Distribution in Tsallis statistics

Various statistical models are used to extract the thermodynamical parameters like T, and $\mu$ e.g. Boltzmann Gibbs statistics and Tsallis non extensive statistics. Generally two main processes i.e., soft excitation (contributes the soft component of low $p_T$ region) and hard excitation (contributes to the hard component in the $p_T$ region) are involved in transverse momentum spectra [8]. For a soft excitation one could possibly used the Boltzmann-Gibbs statistics, while if the $p_T$ reaches upto $100GeV/c$ in the collision at collider, than one needs to use Tsallis statistics. In this study the transverse momentum spectra of the final state particles produced in $pp$ collision at high energy can be explored using Tsallis statistics[14].The number of particles are given as:

$$N=gV\int {\displaystyle \frac{d^{3}p}{{\left(2\pi \right)}^3}}{[1+(q-1){\displaystyle \frac{E-\mu }{T}}]}^{-({\displaystyle \frac{1}{q}}-1)},$$

(1)

where g, $\mu$ and T are degeneracy, chemical potential and temperature respectively, Where $E=\sqrt{p^2+m^2}$ and q is the fitting parameter which tells us deviation from Boltzmann Gibbs distribution. The particular form which satisfies the thermodynamic consistency is given as:

$$E{\displaystyle \frac{d^{3}N}{d^{3}p}}=gVE{\displaystyle \frac{1}{{\left(2\pi \right)}^2}}{[1+(q-1){\displaystyle \frac{E-\mu }{T}}]}^{-\left({\displaystyle \frac{q}{q-1}}\right)},$$

(2)

$${\displaystyle \frac{d^{2}N}{d{p}_{T}dy}}=gV{\displaystyle \frac{p_T{m}_T}{{\left(2\pi \right)}^2}}{[1+(q-1){\displaystyle \frac{m_{T}coshy-\mu }{T}}]}^{-\left({\displaystyle \frac{q}{q-1}}\right)}$$

(3)

where V is the volume, $m_T=\sqrt{p_T^2+m^2}$ is the transverse mass and y is rapidity.

3. Results

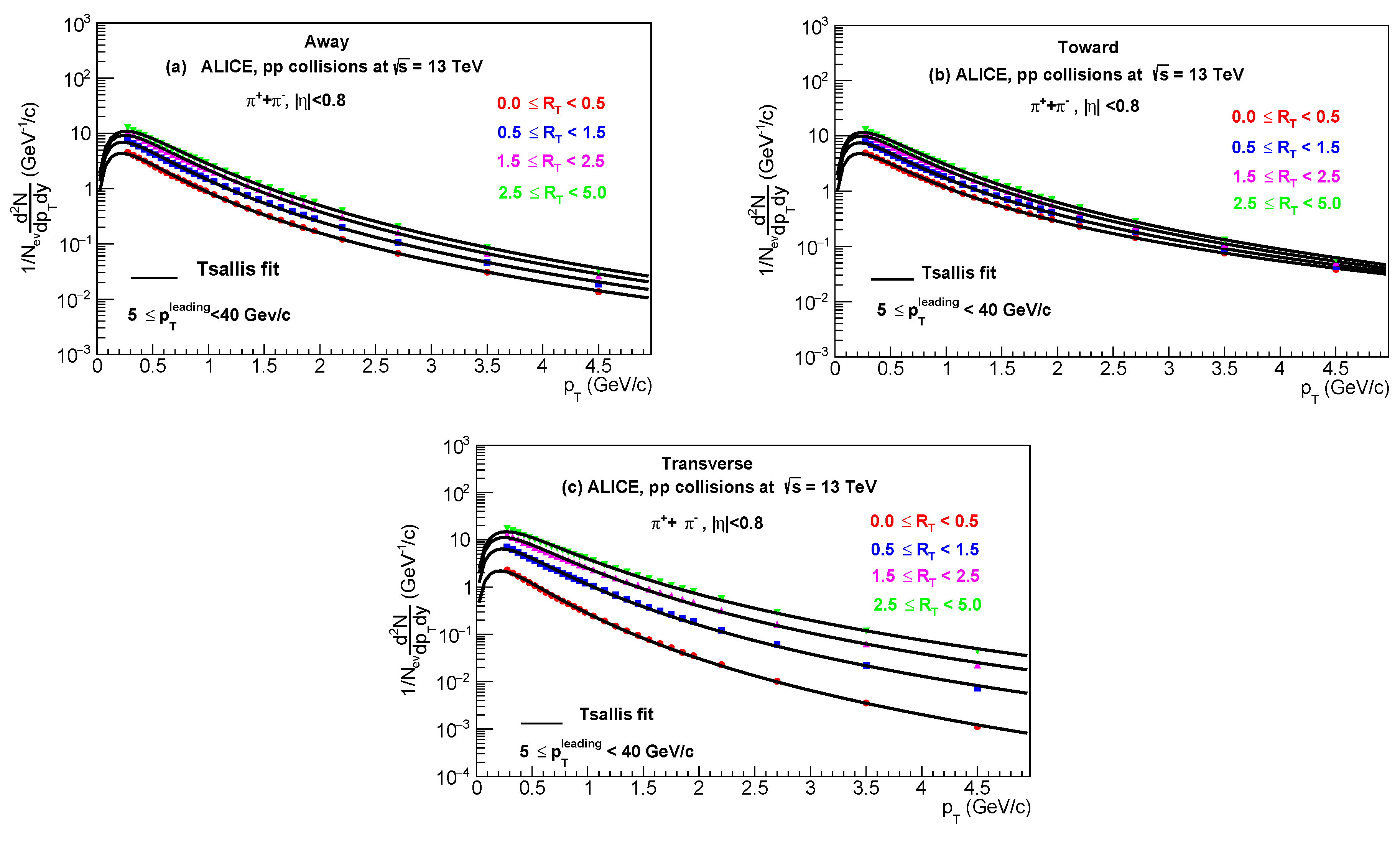
Figure 1a–c depicts the particle yield $1/N_{INEL}{d}^{2}N/d{p}_{T}dy$ as a function of relative transverse momentum classifier $R_T$, for primary charged particles like ${\pi }^{\pm }$ produced in high energy $pp$ collisions at $\sqrt{s_{NN}}=13TeV$ fitted with thermodynamically consistent Tsallis distribution function with chemical potential $\mu$. The observables reported are measured in three different topological region $\left(a\right)$ Away, $\left(b\right)$ Towards and $\left(c\right)$ Transverse region. The circles display the experimental data in the pseudorapidity range of $\left|\eta \right|<0.8$ used in this analysis at LHC by ALICE collaborations [11]. The curve represents the fitting of the data by using eq.(3), the values of extracted parameters; Tsallis temperature, Radius, non-extensive parameter, degeneracy ($T_{eff},R,q,g$) and ${\chi }^2/ndf$ are presented in Table 1.

It is seen clearly that the Tsallis distribution function describes the measured experimental data at the pseudorapidity region of $\left|\eta \right|<0.8$ in $pp$ collisions very well. The best fit corresponds to minimum ${\chi }^2/ndf$. It is observed that the $T_{eff}$ is higher for transverse region due to presence of more UE events like contribution from ISR, FSR and MPIs. While for the away and towards regions, the $T_{eff}$ is lower because of the fragmentation particle production.

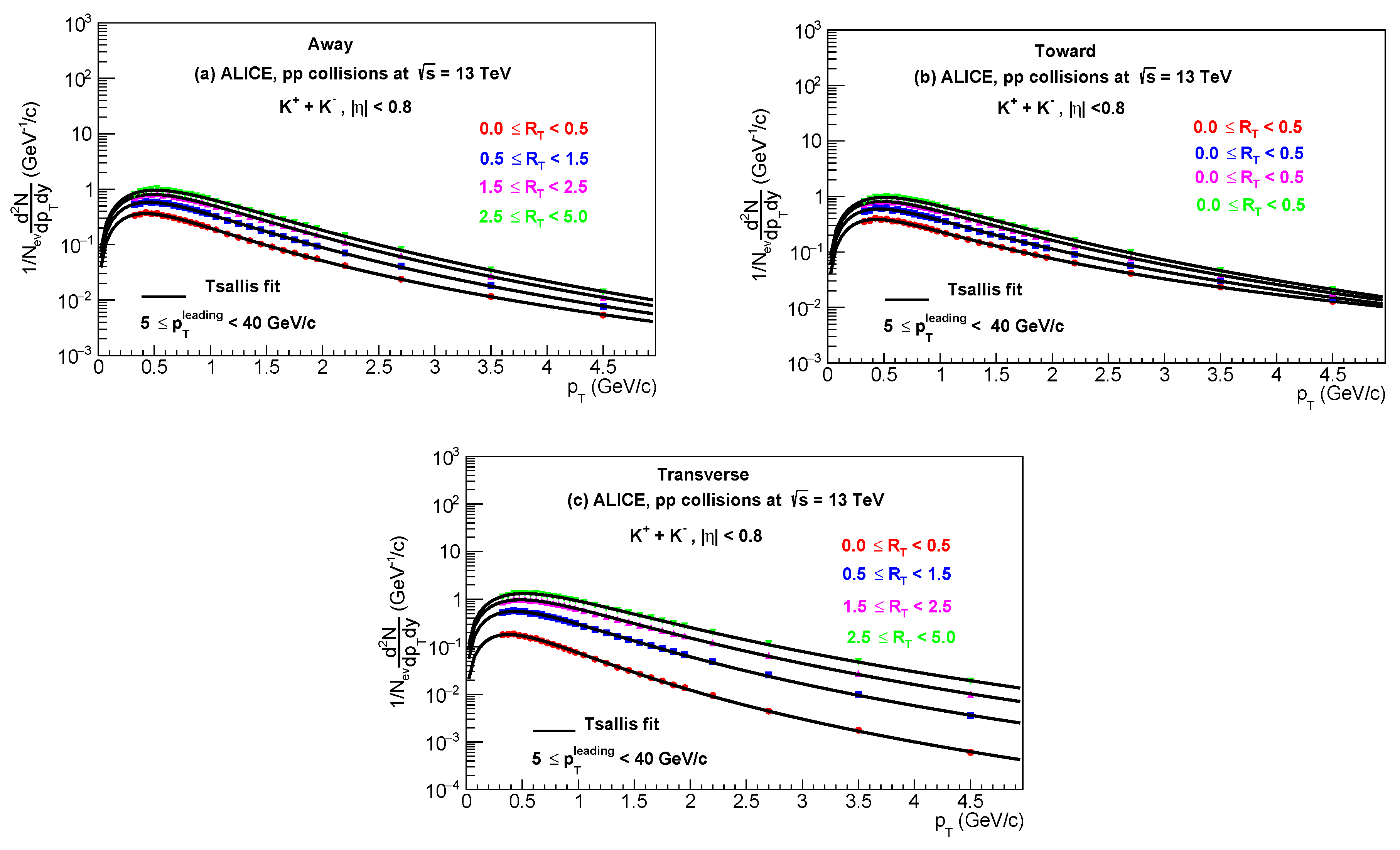
Figure 2a–c presents the particle yield $1/N_{INEL}{d}^{2}N/d{p}_{T}dy$ as a function of relative transverse momentum classifier $R_T$, for strange particles like $K^{\pm }$ produced in high energy $pp$ collisions at $\sqrt{s_{NN}}=13TeV$ fitted with thermodynamically consistent Tsallis distribution function with chemical potential $\mu$. The observables reported are measured in three different topological region $\left(a\right)$ Away, $\left(b\right)$ Towards and $\left(c\right)$ Transverse region. The circles display the experimental data in the pseudorapidity range of $\left|\eta \right|<0.8$ used in this analysis at LHC by ALICE collaborations [11]. The curve represents the fitting of the data by using eq.(3), the values of extracted parameters; Tsallis temperature, Radius, non-extensive parameter, degeneracy ($T,R,q,g$) and ${\chi }^2/ndf$ are presented in Table 2.

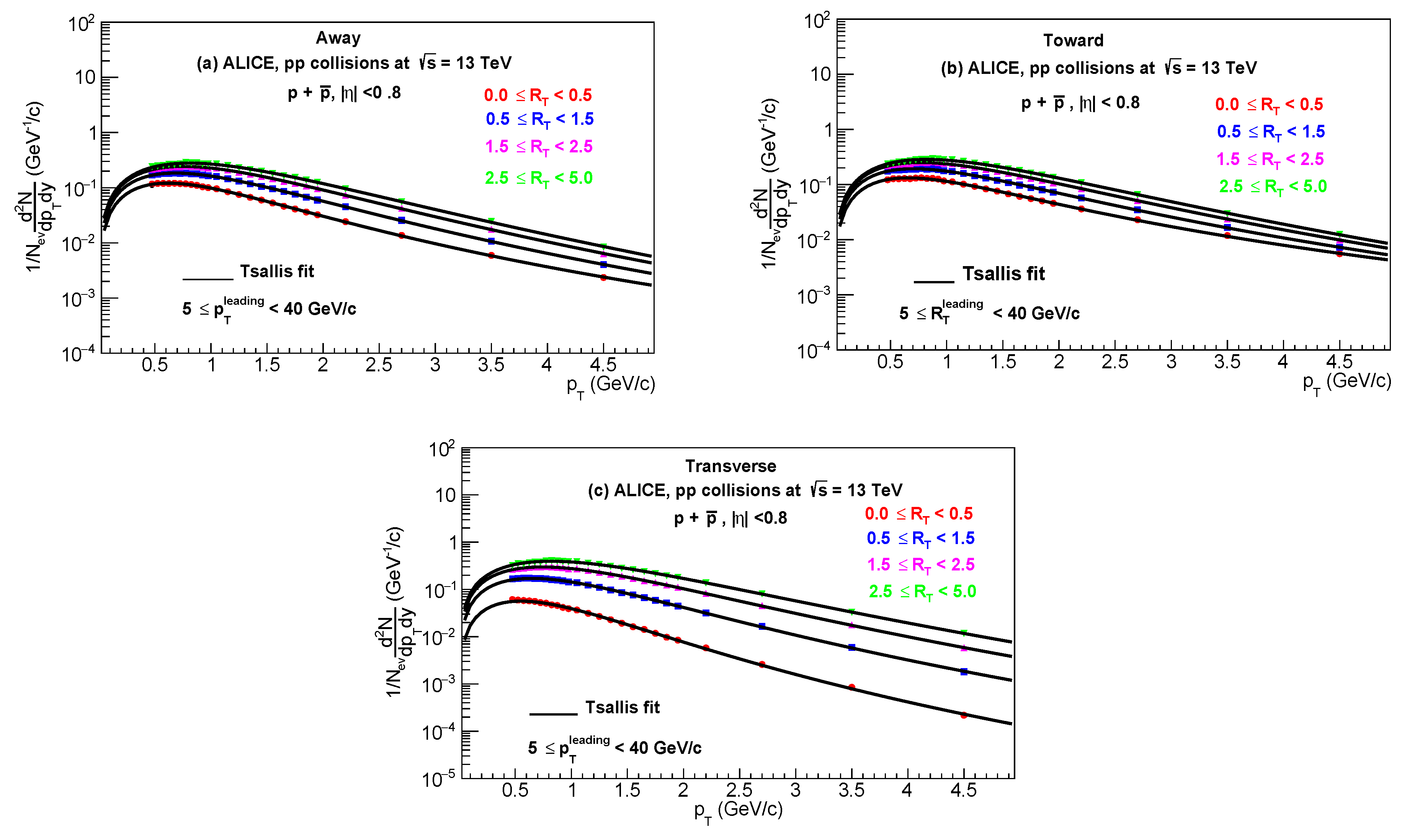
Figure 3a–c shows the particle yield $1/N_{INEL}{d}^{2}N/d{p}_{T}dy$ as a function of relative transverse momentum classifier $R_T$, for primary charged particles like $p\overline{p}$ produced in high energy $pp$ collisions at $\sqrt{s_{NN}}=13TeV$ fitted with thermodynamically consistent Tsallis distribution function with chemical potential $\mu$. The observables reported are measured in three different topological region $\left(a\right)$ Away, $\left(b\right)$ Towards and $\left(c\right)$ Transverse region. The circles display the experimental data in the pseudorapidity range of $\left|\eta \right|<0.8$ used in this analysis at LHC by ALICE collaborations [11]. The curve represents the fitting of the data by using eq. (3), the values of extracted parameters; Tsallis temperature, Radius, non-extensive parameter, degeneracy ($T,R,q,g$) and ${\chi }^2/ndf$ are presented in Table 3.

It is clear from Table 1, Table 2 and Table 3 that the $T_{eff}$ changes with $R_T$ regions. The values for the non-extensive parameter, q ranges between $q=1.137-1.158$, acceptable within the high energy limit and matches to the values obtained in literature [5,15,16].

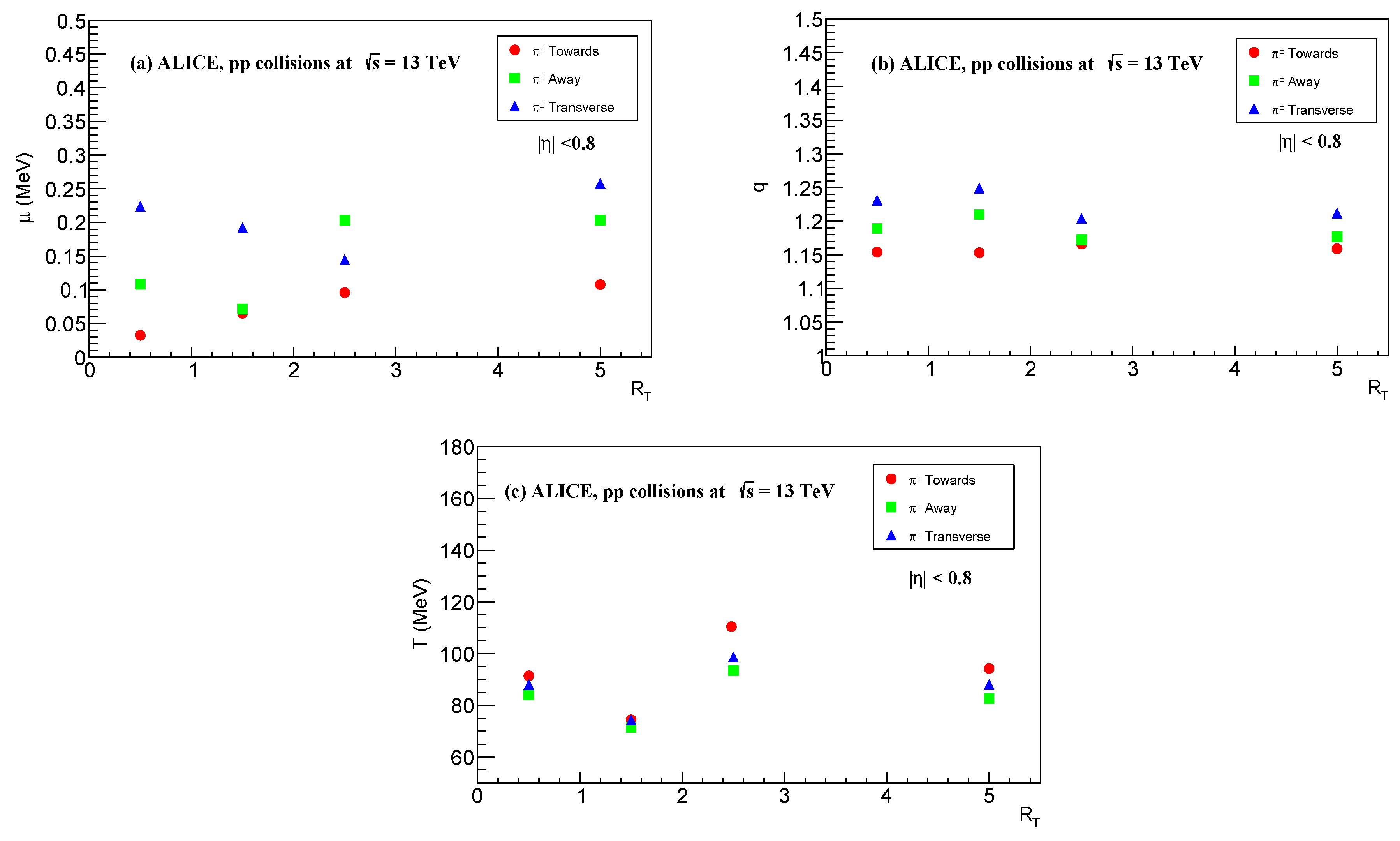
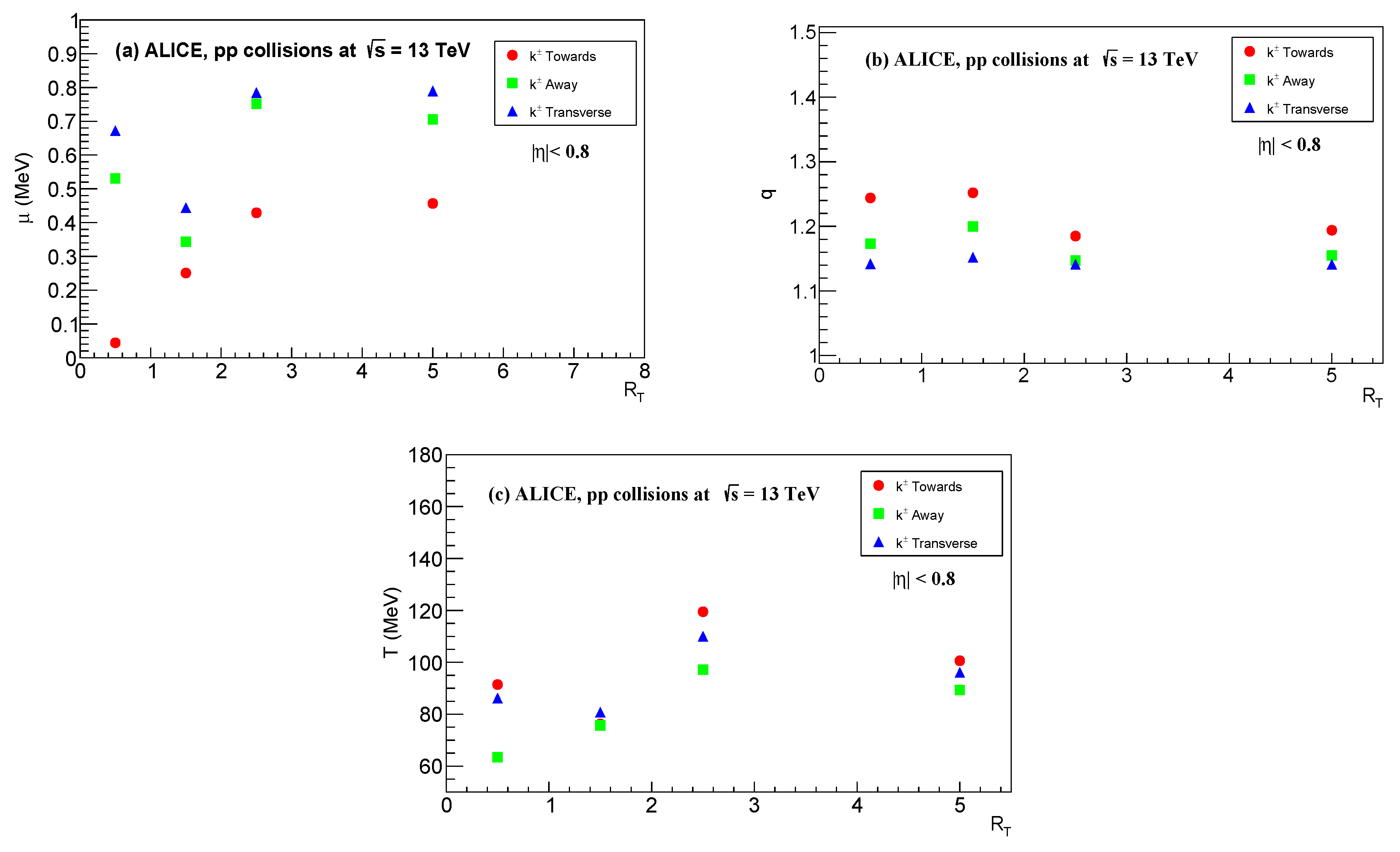
Figure 4a–c depicts the variation of chemical potential $\mu \left(MeV\right)$, non-extensive parameter q and effective temperature $T_{eff}\left(MeV\right)$ with $R_T$ for primary charged particles like ${\pi }^{\pm }$ produced in high energy $pp$ collisions at $\sqrt{s_{NN}}=13TeV$.

Figure 5a–c depicts the variation of chemical potential $\mu$, non-extensive parameter q and temperature $T_{eff}\left(MeV\right)$ with $R_T$ for strange particles like $K^{\pm }$ produced in high energy $pp$ collisions at $\sqrt{s_{NN}}=13TeV$.

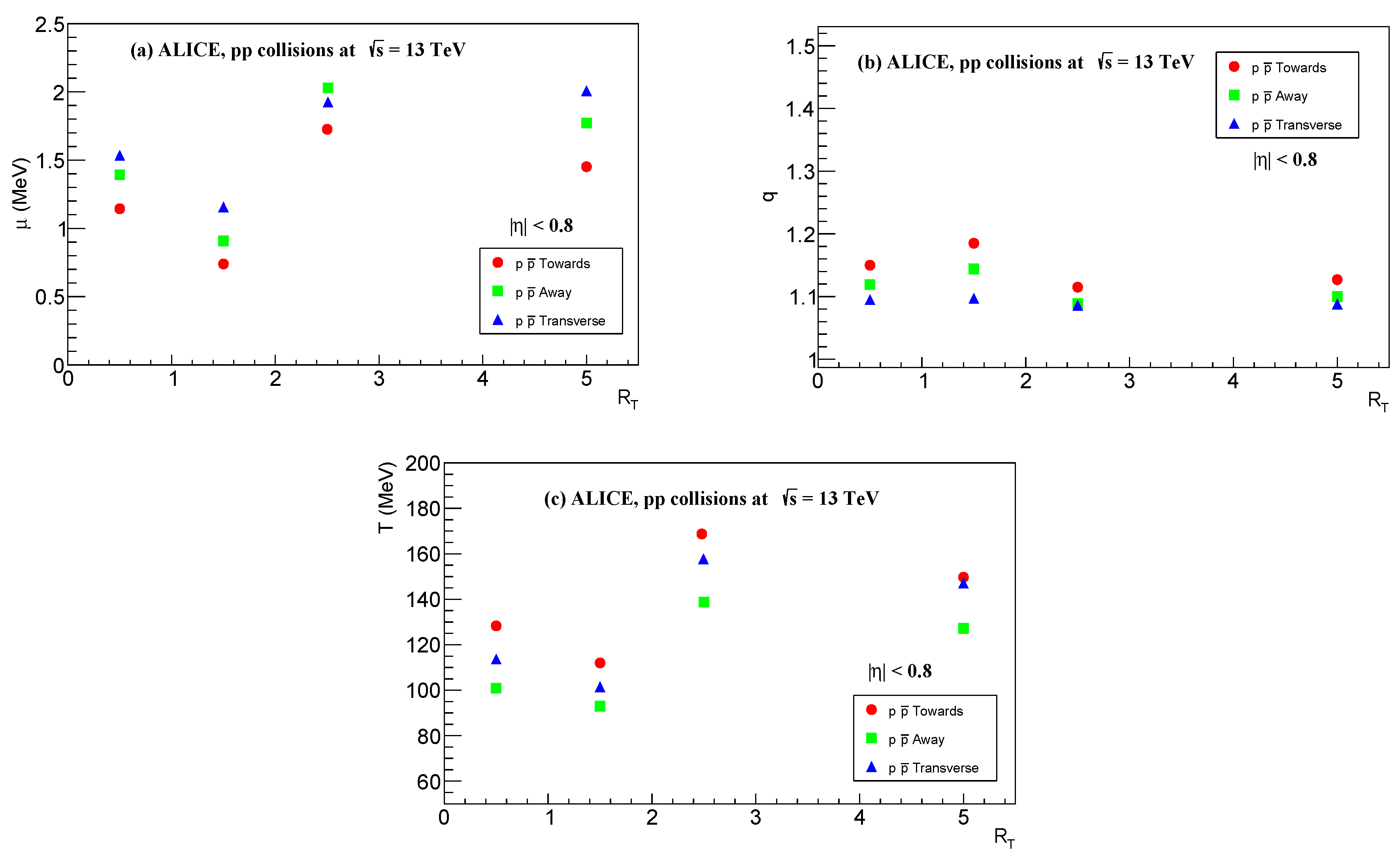
Figure 6a–c depicts the variation of chemical potential $\mu$, non-extensive parameter q and temperature $T_{eff}\left(MeV\right)$ with $R_T$ for baryon like $p\overline{p}$ produced in high energy $pp$ collisions at $\sqrt{s_{NN}}=13TeV$.

4. Conclusion

In this paper we have presented the transverse momentum spectra $1/N_{INEL}{d}^{2}N/d{p}_{T}dy$ of primary charged particles like ${\pi }^{\pm }$, $K^{\pm }$ and $p\overline{p}$ produced in high energy $pp$ collision at center of mass energy of $13TeV$. The momentum spectra of particles is classified according to the $R_T$ classes and fitted with non extensive Tsallis distribution function. Two main parameters i.e. $T_{eff}$ and $\mu$ are under discussion which are very important in the discussion of QCD matter. We have extracted the thermodynamical parameters from the fitted $p_T$ spectra and observed that the $T_{e}ff$ is higher for the transverse region where multiple parton interactions, initial and final state radiations are more sensitive.