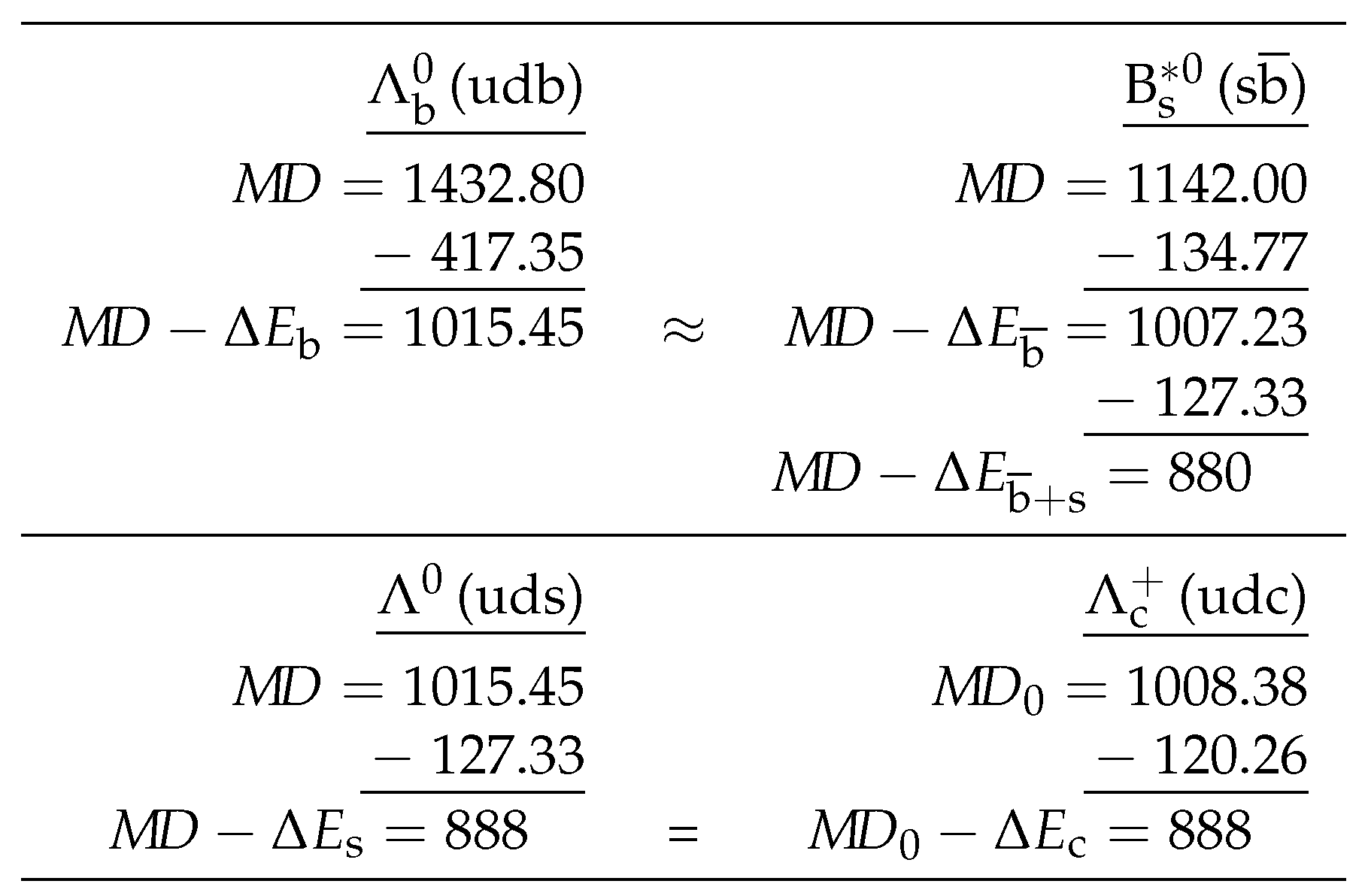CP Violation: Differing Binding Energy Levels of Quarks and Antiquarks, and their Transitions in Λ-baryons and B-mesons

1. Introduction

The lowest energy nucleonic excitations, ${\mathrm{\Lambda }}^0$ and $\mathrm{\Sigma }$, introduce the s quark [1,2] to the world. In a similar fashion, the lowest energy pionic excitations, the kaons, introduce the $\overline{\mathrm{s}}$ antiquark. Using the differences between measured rest-mass deficits $\Delta \left(MD\right)$, i.e., the “energy remainders” after subtracting from the particle rest-masses M the masses of the valence (anti)quarks, viz.

$$MD\equiv M-\sum _{\mathrm{q}}(m_{\mathrm{q}}+m_{\overline{\mathrm{q}}}),$$

(1)

in the lowest-energy transitions between these states, we have previously determined the binding energy levels of the three lowest-energy valence quarks and their antiquarks [3]. We found that the antiquark transitions $\overline{\mathrm{q}}\to \overline{\mathrm{s}}$ (q = u, d) require $2.4\times$ more energy support than the corresponding $\mathrm{q}\to \mathrm{s}$ baryonic transitions, making a strong case for the origin of the charge-parity (CP) violation [4,5,6,7,8,9,10].

In this work, we complete the binding energy levels of valence (anti)quark transitions up to (anti)bottom. There is no room in this diagram for the (anti)top: because of its enormous rest-mass ($m_{\mathrm{t}}=172.5$ GeV [2], expressed as usual in units of energy), this (anti)quark is not singled out in the valence of any known particle.

Determination of the binding energies of c and b quarks and their antiquarks should be based on quark transitions occurring in the lowest-energy charm and bottom excitations above the strange states of baryons and mesons [1,2,3]. Higher excitations contain much more energy that is not used to bind valence (anti)quarks; instead, the excess appears as kinetic energy in the excited states of the particles and their decay fragments [11,12,13,14]. The lowest-energy excitations of the ${\mathrm{\Lambda }}^0$ baryons and the K${}^0$ mesons are

$${\mathrm{\Lambda }}^0\left(\mathrm{uds}\right)\to {\mathrm{\Lambda }}_{\mathrm{c}}^{+}\left(\mathrm{udc}\right),\Delta \left(MD\right)=-7.07\mathrm{MeV},$$

(2)

$${\mathrm{\Lambda }}^0\left(\mathrm{uds}\right)\to {\mathrm{\Lambda }}_{\mathrm{b}}^0\left(\mathrm{udb}\right),\Delta \left(MD\right)=417.35\mathrm{MeV},$$

(3)

and

$${\mathrm{K}}^0\left(\mathrm{d}\overline{\mathrm{s}}\right)\to {\mathsf{\eta }}_{\mathrm{c}}\left(\mathrm{c}\overline{\mathrm{c}}\right),\Delta \left(MD\right)=44.36\mathrm{MeV},$$

(4)

$${\mathrm{K}}^0\left(\mathrm{d}\overline{\mathrm{s}}\right)\to {\mathsf{\eta }}_{\mathrm{b}}\left(\mathrm{b}\overline{\mathrm{b}}\right),\Delta \left(MD\right)=639.16\mathrm{MeV},$$

(5)

respectively. The differences between rest-mass deficits $\Delta \left(MD\right)$ were obtained from the measured $MD$-values [1,2,3] listed here in Table 1 and Table 2, respectively.

The cost of suppressing Coulomb repulsions in ${\mathrm{\Lambda }}_{\mathrm{c}}^{+}$ (1.22 MeV) was also subtracted from the tabulated value of $MD\left({\mathrm{\Lambda }}_{\mathrm{c}}^{+}\right)$, and the reduced value $M{D}_0\left({\mathrm{\Lambda }}_{\mathrm{c}}^{+}\right)=1008.38$ MeV was then used in Equation (2). This cost is precisely the same as that found for repulsive Coulomb forces in protons ($p^{+}$) [3] because the fractional charge makeup is identical in the two particles, viz.

$$Q({\mathrm{\Lambda }}_{\mathrm{c}}^{+}:\mathrm{udc})=Q(p^{+}:\mathrm{udu})=(+2/3,-1/3,+2/3).$$

There is no corresponding cost for the neutral particles because they show no Coulomb repulsion and no tendency of breaking up; in fact, the attractive Coulomb forces that are present in neutral particles certainly contribute to the kinetic energies of the valence quarks and antiquarks [11,12,13,14].

In Section 2, we use Equations (2)–(5) given above to solve for the binding energies of c and b quarks and their antiquarks. In Section 3, we summarize our conclusions, and we compare the energy levels of (anti)quarks in B-mesons and $\mathrm{\Lambda }$-baryons.

2. Binding Energy Levels of Charm and Bottom (Anti)Quarks

2.1. Quark Flips in $\mathrm{\Lambda }$-baryons

The $\mathrm{\Lambda }$-baryons have the same spin-parity $J^{\mathrm{P}}={(1/2)}^{+}$ and no isospin ($I=0$) [15,16,17,18]; thus, the differences $\Delta \left(MD\right)$ in mass deficits shown in Equations (2) and (3) effectively represent the additional energies required to bind the c and b quarks, respectively, relative to the bindings of the s quarks in the lower rest-energy states. We see then from Equations (2) and (3) that

$$E_{\mathrm{s}\to \mathrm{c}}=-7.07\mathrm{MeV},$$

(6)

and

$$E_{\mathrm{s}\to \mathrm{b}}=417.35\mathrm{MeV},$$

(7)

for the $\mathrm{s}\to \mathrm{c}$ and the $\mathrm{s}\to \mathrm{b}$ quark flips, respectively. The negative value of $E_{\mathrm{s}\to \mathrm{c}}$ implies that the c-level lies about 7 MeV below the s-level (see also Table 3).

2.2. Quark Flips between  K${}^0$ and Heavy ${\mathsf{\eta }}_{\mathrm{q}}$ Quarkonia

The neutral kaon and the ${\mathsf{\eta }}_{\mathrm{c}},{\mathsf{\eta }}_{\mathrm{b}}$ quarkonium states have the same spin-parity $J^{\mathrm{P}}=0^{-}$, but K${}^0$ also carries isospin ($I=1/2$) [15,16,17,18]; thus, the differences $\Delta \left(MD\right)$ in mass deficits shown in Equations (4) and (5) lead to the balance equations

$$E_{\mathrm{d}\to \mathrm{c}}+E_{\overline{\mathrm{s}}\to \overline{\mathrm{c}}}+E{I}_{1/2\to 0}=44.36\mathrm{MeV},$$

(8)

and

$$E_{\mathrm{d}\to \mathrm{b}}+E_{\overline{\mathrm{s}}\to \overline{\mathrm{b}}}+E{I}_{1/2\to 0}=639.16\mathrm{MeV},$$

(9)

respectively. The quark-transition energy gaps and the energy released ($E{I}_{1/2\to 0}<0$) in the isospin transition $I=1/2\to 0$ are determined from the solutions obtained in Appendix B of Ref. [3] and in Equations (6) and (7) above: Using the known value of $E_{\mathrm{d}\to \mathrm{s}}=125.69$ MeV, we find that

$$E_{\mathrm{d}\to \mathrm{c}}=E_{\mathrm{d}\to \mathrm{s}}+E_{\mathrm{s}\to \mathrm{c}}=118.62\mathrm{MeV},$$

(10)

$$E_{\mathrm{d}\to \mathrm{b}}=E_{\mathrm{d}\to \mathrm{s}}+E_{\mathrm{s}\to \mathrm{b}}=543.04\mathrm{MeV},$$

(11)

whereas the isospin energy release for $I=1/2\to 0$ has been previously determined [3] to be

$$E{I}_{1/2\to 0}=-38.65\mathrm{MeV}.$$

(12)

Substituting Equations (10)–(12) into (8) and (9), we obtain the antiquark transition energy gaps, viz.

$$E_{\overline{\mathrm{s}}\to \overline{\mathrm{c}}}=-35.61\mathrm{MeV},$$

(13)

and

$$E_{\overline{\mathrm{s}}\to \overline{\mathrm{b}}}=134.77\mathrm{MeV},$$

(14)

as well as the auxiliary result

$$E_{\overline{\mathrm{u}}\to \overline{\mathrm{c}}}=E_{\overline{\mathrm{u}}\to \overline{\mathrm{s}}}+E_{\overline{\mathrm{s}}\to \overline{\mathrm{c}}}=272.45\mathrm{MeV},$$

(15)

where $E_{\overline{\mathrm{u}}\to \overline{\mathrm{s}}}=308.06$ MeV (Appendix C in Ref. [3]). In this case too, the negative value of $E_{\overline{\mathrm{s}}\to \overline{\mathrm{c}}}$ (Equation (13)) implies that the $\overline{\mathrm{c}}$-level lies about 35.6 MeV below the $\overline{\mathrm{s}}$-level in the antiquark energy diagram (see also Table 3).

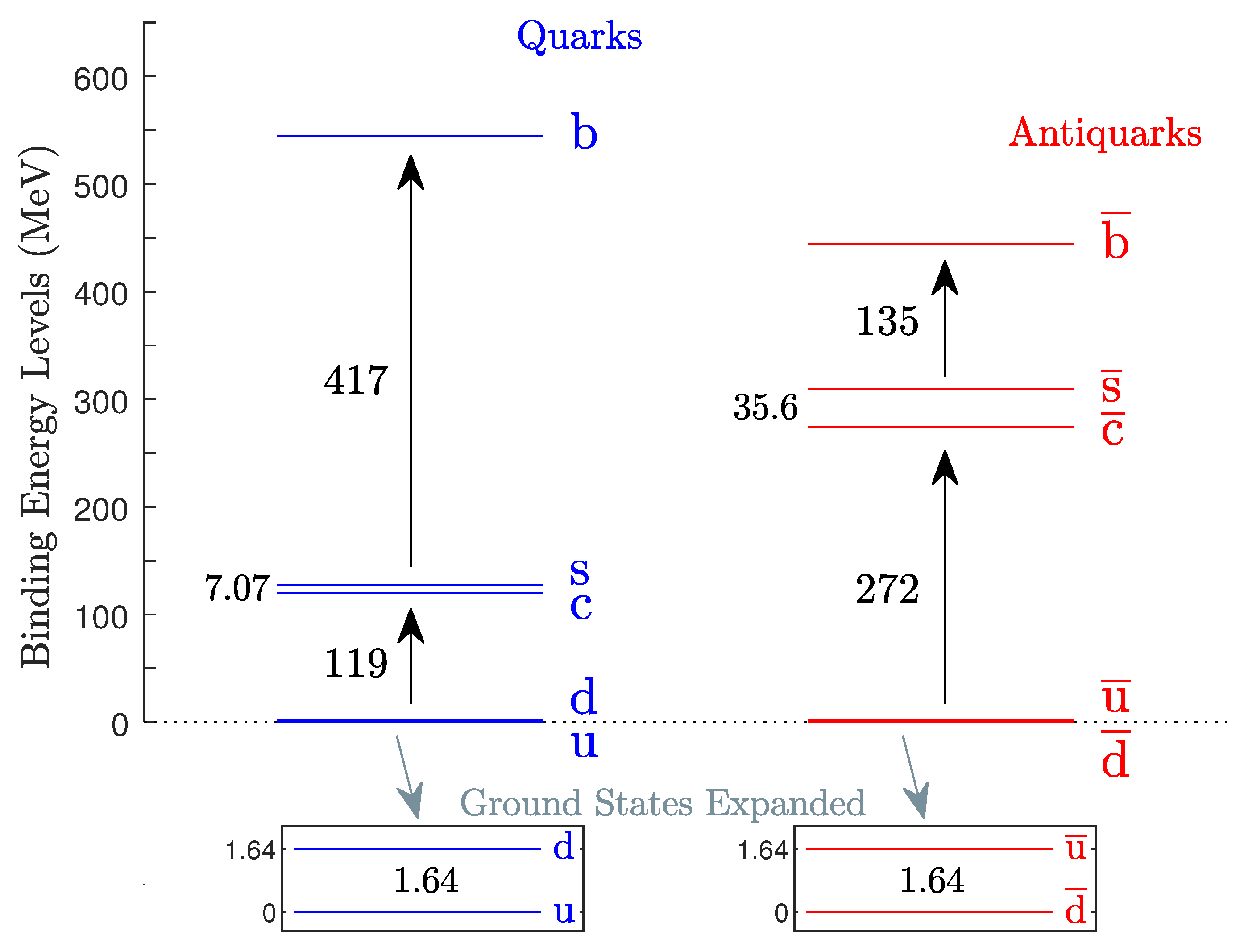
Furthermore, it comes as a surprise that the $\mathrm{s}\to \mathrm{b}$ quark flip is $3\times$ more expensive than the corresponding antiquark flip $\overline{\mathrm{s}}\to \overline{\mathrm{b}}$. The enormous s-b gap of 417 MeV expands the overall range of the quark binding levels, which ends up being 100-MeV wider than the overall range of the antiquark levels.

This result is rather ironic: it seems much easier to produce and maintain bound $\overline{\mathrm{b}}$ antiquarks by flipping $\overline{\mathrm{s}}$ antiquarks—but the process did not really occur in substantial numbers because it is so much more expensive (2.4× more) to produce $\overline{\mathrm{s}}$ and $\overline{\mathrm{c}}$ antiquarks by flipping ground-level antiquark states ($\overline{\mathrm{u}}$ and $\overline{\mathrm{d}}$).

The baryon asymmetry resulting from these processes in the early universe [19,20] must have been particularly pronounced, so much so that the 50%-50% initial conditions commonly assumed in estimates of baryosynthesis in the early universe [21,22,23,24,25,26] appear to have been unjustified in all attempted statistical approaches, frequentist and Bayesian [27,28,29]. From the factor of 2.4 that compares the energy gaps of the (anti)strange transitions, we obtain roughly a percentage of $2.4/3.4=70\%$ baryons versus 30% antibaryons initially produced in the universe, in which case at least 4/7 = 57%, more than half of the baryons, would have avoided annihilation.

3. Conclusions and Comparisons between Particles

3.1. Summary of Conclusions

Combining the above results with the binding energy levels of low rest-energy (anti)quarks, as they were determined previously [3], we summarize in Table 3 the binding energy levels of quarks and antiquarks and the dynamic energy gaps that separate the bound states. The entire energy diagrams for (anti)quarks are also illustrated in Figure 1. From Table 3 and Figure 1, the following characteristic properties are readily seen:

(1a)

The u quark is ground state in the doublet (u, d), whereas $\overline{\mathrm{d}}$ is ground state in the doublet ($\overline{\mathrm{d}}$, $\overline{\mathrm{u}}$).

(1b)

In both doublets, the energy levels are separated by the same amount of energy, a gap of 1.64 MeV.

(2a)

It is $2.3\times$ cheaper to bind a c quark rather than a $\overline{\mathrm{c}}$ antiquark; the c-binding costs 154 fewer MeV.

(2b)

It is also $2.4\times$ cheaper to bind an s quark rather than an $\overline{\mathrm{s}}$ antiquark; the s-binding costs 182 fewer MeV.

(2c)

The cheaper energetics of the second-generation quarks versus the more expensive bindings of antiquarks is strong grounds for CP violation [3,4,5,6,7,8,9,10]. In fact, it seems quite possible that antibaryons, beyond the ground-state antinucleons, were not at all created in the hadron epoch of the universe [19,20,21,22,23,24,25,26], leading to a severe baryon asymmetry from the outset.

(3a)

Surprisingly, binding a flipped b valence quark is very expensive, about $3\times$ more expensive than binding a flipped $\overline{\mathrm{b}}$ valence antiquark: it costs an additional ∼283 MeV, when an s quark makes the transition to the higher state b, relative to the corresponding antiquark transition $\overline{\mathrm{s}}\to \overline{\mathrm{b}}$.

(3b)

The additional cost of 283 MeV is responsible for the expanded energy scale of valence quarks, which turns out to be ∼100-MeV wider than that of valence antiquarks (see Table 3 and Figure 1).

3.2. Comparisons in B mesons and $\mathrm{\Lambda }$ baryons

The above additional cost of 283 MeV is reflected in the experimental $MD$ data [1,2,3] in the following sense: Mesons $\mathrm{c}\overline{\mathrm{b}}$ and $\mathrm{b}\overline{\mathrm{b}}$ aside, the $\overline{\mathrm{b}}$ B-mesons have the highest rest-masses (5280-5415 MeV) among all other mesons; whereas the ${\mathrm{\Lambda }}_{\mathrm{b}}^0$-baryon has the lowest rest-mass (5620 MeV) among all bottom baryons irrespective of spin. The origin of this gap (205-340 MeV) is obscured by the rest-masses of the valence quarks, so it is the mass-deficit values of the particles that reveal the difference in energy content (a bound $\overline{\mathrm{b}}$ antiquark versus a bound b quark):

(i) The $MD$s of the B${}^{*}$-mesons [2] are typically 290-MeV lower than $MD\left({\mathrm{\Lambda }}_{\mathrm{b}}^0\right)=1432.80$ MeV (Table 1), which effectively reflects the energy differential of 283 MeV in supporting a b quark rather than a $\overline{\mathrm{b}}$ antiquark in the valence.

(ii) On the other hand, the $MD$s of the B-mesons are lower by another 45 MeV, which is also the rest-mass difference (e.g., $M\left({\mathrm{B}}^{*0}\right)-M\left({\mathrm{B}}^0\right)=45.5$ MeV), as well as the energy of the photons being emitted in the seen electromagnetic decays

$${\mathrm{B}}^{*}\to \mathrm{B}{\mathsf{\gamma }}_{\left(45\mathrm{MeV}\right)}.$$

(16)

It appears then that B${}^{*}=\mathrm{q}\overline{\mathrm{b}}$ (where q = u, d, s) are metastable states (equation (16)) in which the strong field provides marginal support to the $\overline{\mathrm{b}}$ antiquarks (equation (14)). The mean lifetimes of these decays have not yet been measured, but they should turn out to be brief (∼10${}^{-17}$-10${}^{-20}$ s) due to the spontaneity of the electromagnetic reactions of type (16).

Finally, subtracting the binding energies of b and $\overline{\mathrm{b}}$ from the $MD$s of ${\mathrm{\Lambda }}_{\mathrm{b}}^0$ and B${}_{\mathrm{s}}^{*0}$, respectively, we find that the background field carries an additional 1007-1015 MeV in these particles, which is also the energy in the backgrounds of the lighter $\mathrm{\Lambda }$-baryons (uds and udc) that do not have a b quark in their valences. Only a small fraction of this energy (∼12%) goes into supporting the s and c quarks, leaving in the background fields a remainder of 888 MeV (plus the tiny anti-Coulombic content of 1.22 MeV in ${\mathrm{\Lambda }}_{\mathrm{c}}^{+}$). This somewhat complicated breakdown of binding energies and $MD$s just described is delineated in Table 4, where all listed values are expressed in MeV.

The 888-MeV remainder shown in Table 4 is about 40-MeV lower than that of the nucleonic ground state ($MD\left(n^0\right)=928$ MeV); and it expands to ∼100 MeV in B${}_{\mathrm{s}}^0$-mesons in which $MD\left(B_{\mathrm{s}}^0\right)-\Delta E_{\overline{\mathrm{b}}+\mathrm{s}}=831$ MeV. These background energies indicate that the strong field has an adequate grip on to the excited states of $\mathrm{\Lambda }$ and B particles (in which smaller than nucleonic bindings are required), and these particles are then expected to decay only via electroweak interactions over timescales ∼10${}^{-12}$ s (indeed as shown in Table 9 of Ref. [3] and described in the notes to that table).