Optimization of Functionally Graded Cylindrical Shells for Maximal Eigen-Frequencies

1. Introduction

Historically, eigenfrequencies of cylindrical shells were determined by Rayleigh in 1877 (an infinite isotropic shells), Love [1] (free ends of a finite length shell) and then Koga [2] solved problems of forty five combinations of boundary conditions. Fischer [3] extended the method of Koga to circular shells of composite materials which are specially orthotropic. Shao et al. [4] studied free vibrations of laminated open cylindrical shells with arbitrary boundary conditions.

Structures (beams, plates, shells) made of functionally graded materials (FGM) are composed of two metals or metal and ceramic or two polymers. The physical properties of FGM are usually controlled by the assumed law of variations in some direction. The new class of composite materials (FGM) has been also subjected to the various types of investigations [5,6,7,8,9].

Due to the possible variable porosity and thicknesses of FG structures eigenfrequencies can be controlled and optimized using the appropriate modeling of beams, plates and shells [10,11,12,13]. The cited studies deals mainly with the analysis of so-called axially FG (AFG) materials.

For a such class of materials free vibrations of cylindrical shells are identified by the effects of different parameters, i.e. the thickness, ratio of the internal radius to the mean (or the external) radius and boundary conditions.

In the present paper the shape optimization problems of cylinders are considered. The aim of optimization is to maximize eigenfrequencies of structures varying the cylindrical thickness/shell radius of curvature along the longitudinal direction (AFGMs).

2. Governing Relations

The total energy of the shell is given by:

$$\Pi =U+T$$

(1)

The strain energy U is defined in the classical way, i.e.:

$$U={\int }_{\Omega }{\sigma }_{ij}{\epsilon }_{ij}{H}_{i}d{\xi }_{1}d{\xi }_{2}d{\xi }_3;i,j=\mathrm{1,2},3$$

(2)

whereas the kinetic energy of the shell structure is defined in the following way:

$$T={\displaystyle \frac{1}{2}}{\int }_{\Omega }\rho \left({\xi }_3\right)\left[{\left({\displaystyle \frac{\partial u}{\partial \tau }}\right)}^2+{\left({\displaystyle \frac{\partial \nu }{\partial \tau }}\right)}^2+{\left({\displaystyle \frac{\partial w}{\partial \tau }}\right)}^2\right]H_1{H}_2{H}_{3}d{\xi }_{1}d{\xi }_{2}d{\xi }_3;i,j=\mathrm{1,2},3$$

(3)

For cylindrical shells the curvilinear coordinates ξ₁, ξ₂, and ξ₃ correspond to the longitudinal (x), circumferential (Rθ) and normal coordinate (z) to the mid-surface, respectively. R means the radius of the cylinder. The symbol τ denotes the physical time and ρ is the shell density variable with the shell thickness z for structures made of FGMs.

The relationship between stresses σ_ij and strains ε_ij can be written as follows:

$$\left[\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{33}\\ {\sigma }_{32}\\ {\sigma }_{31}\\ {\sigma }_{12}\end{array}\right]=[Q(z)]\left[\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ {\epsilon }_{33}\\ {\epsilon }_{32}\\ {\epsilon }_{31}\\ {\epsilon }_{12}\end{array}\right]$$

(4)

For FGM materials considering the thickness stretching the stiffness matrix components Q_ij are 3D relations given by:

$$\begin{gathered} \left[Q\left(z\right)\right]= E\left(z\right)/ (1+\nu ) \\ \left[\begin{array}{cccccc}{\displaystyle \frac{1-\nu }{1-2\nu }}& {\displaystyle \frac{\nu }{1-2\nu }}& {\displaystyle \frac{\nu }{1-2\nu }}& 0& 0& 0\\ {\displaystyle \frac{\nu }{1-2\nu }}& {\displaystyle \frac{1-\nu }{1-2\nu }}& {\displaystyle \frac{\nu }{1-2\nu }}& 0& 0& 0\\ {\displaystyle \frac{\nu }{1-2\nu }}& {\displaystyle \frac{\nu }{1-2\nu }}& {\displaystyle \frac{1-\nu }{1-2\nu }}& 0& 0& 0\\ 0& 0& 0& 0.5& 0& 0\\ 0& 0& 0& 0& 0.5& 0\\ 0& 0& 0& 0& 0& 0.5\end{array}\right] \end{gathered}$$

(5)

The elastic modulus E variation characterizes the distribution of porosity along the thickness direction z and is defined in the following way:

$$E\left(z\right)/E_b=\left[\right(E_t/E_b-1\left)f\right(z)+1], f\left(z\right)={\left({\displaystyle \frac{z}{t}}+{\displaystyle \frac{1}{2}}\right)}^n$$

(6)

where the symbols t and b refer to the material properties on top and bottom surfaces, n is power index. ν (const) is the Poissons ratio.

The explicit form of the strain components ε_ij can be expressed in different form as it is discussed by Muc et al. [14]. Using the Love-Kirchhoff hypothesis the strain components can be expressed as follows:

$$\begin{gathered} {\epsilon }_{11}={\displaystyle \frac{1}{H_1}}\left({\displaystyle \frac{\partial {\tilde{U}}_1}{\partial {\xi }_1}}+{\displaystyle \frac{1}{H_2}}{\displaystyle \frac{\partial H_1}{\partial {\xi }_2}}{\tilde{U}}_2+{\displaystyle \frac{1}{H_3}}{\displaystyle \frac{\partial H_1}{\partial {\xi }_3}}{\tilde{U}}_3\right), \\ {\epsilon }_{12}={\displaystyle \frac{H_2}{H_1}}{\displaystyle \frac{\partial }{\partial {\xi }_1}}\left({\displaystyle \frac{{\tilde{U}}_2}{H_2}}\right)+{\displaystyle \frac{H_1}{H_2}}{\displaystyle \frac{\partial }{\partial {\xi }_2}}\left({\displaystyle \frac{{\tilde{U}}_1}{H_1}}\right), \\ {\epsilon }_{13}={\epsilon }_{23}={\epsilon }_{33}=0, \\ \begin{array}{cc}{H}_{\gamma }=A_{\gamma }(1+{\displaystyle \frac{z}{R_{\gamma }}}),\begin{array}{cc}& H_3=1,\begin{array}{cc}& \gamma =\mathrm{1,2}.\end{array}\end{array}& \end{array} \\ {\tilde{U}}_{\gamma }\left({\xi }_1, {\xi }_2,{\xi }_3\right)=u_{\gamma }\left({\xi }_1, {\xi }_2\right)\left(1+{\displaystyle \frac{z}{R_{\gamma }}}\right) {\tilde{U}}_3({\xi }_1, {\xi }_2,{\xi }_3)=u_3\left({\xi }_1, {\xi }_2\right){\xi }_1, \end{gathered}$$

(7)

A_γ mean the Lame coefficients in 2-D curvilinear orthogonal system of coordinates (ξ₁, ξ₂). The strain components ε₂₂ can be obtained by the cyclic permutation of the subscripts 1, 2 and 3.

3. Definition of Design Variables

Optimal design of composite cylindrical shells can be carried in different ways and it depends on the definition of design variables. Therefore, in this area we can distinguish the following approaches:

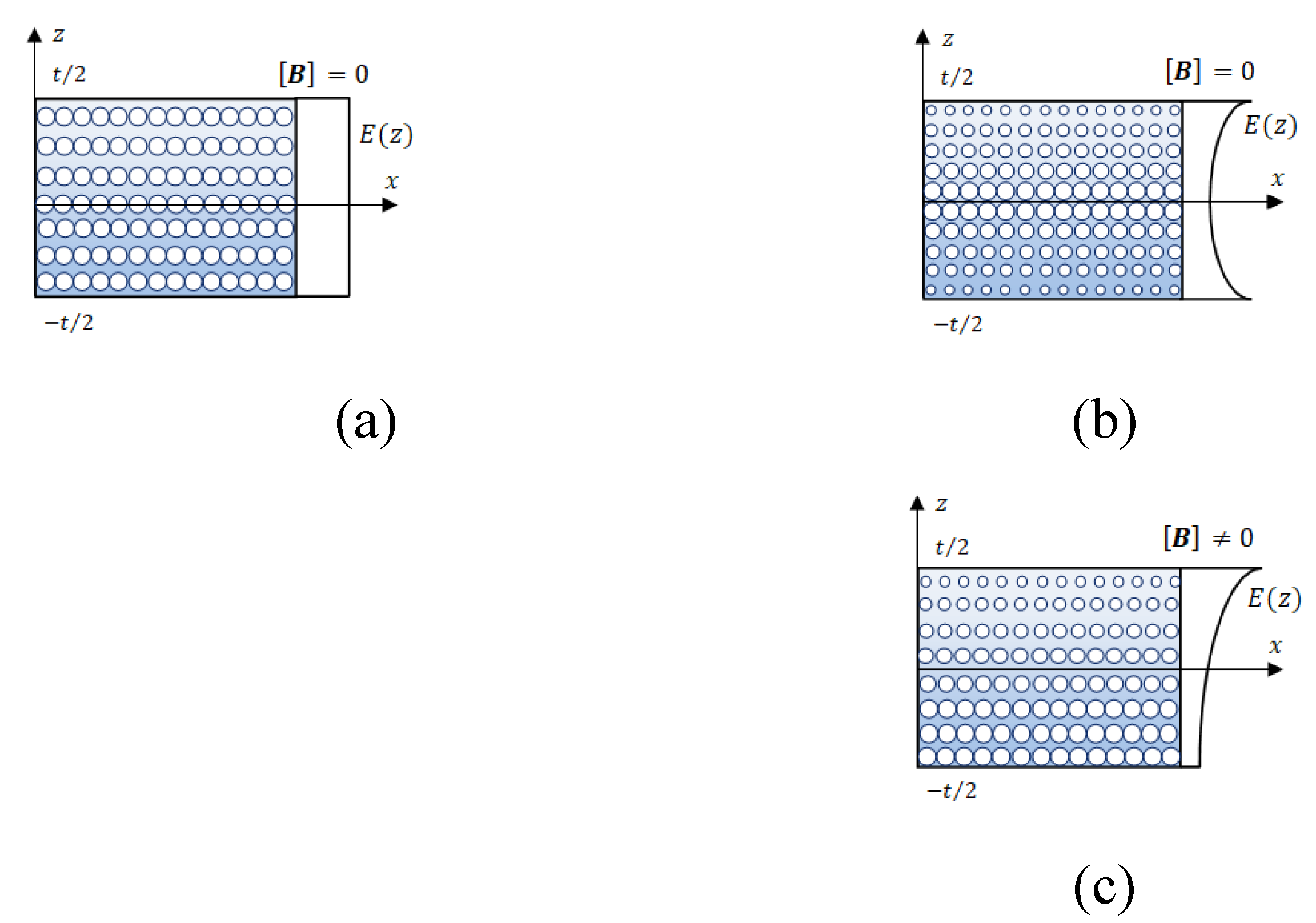
• Material construction of the shell wall – various distributions of FGMs constructions (Figure 1) are discussed in Refs [15,16]; the possible constructions of the shell wall made of nanoplatelets or of carbon nanotubes are presented in Ref [17]

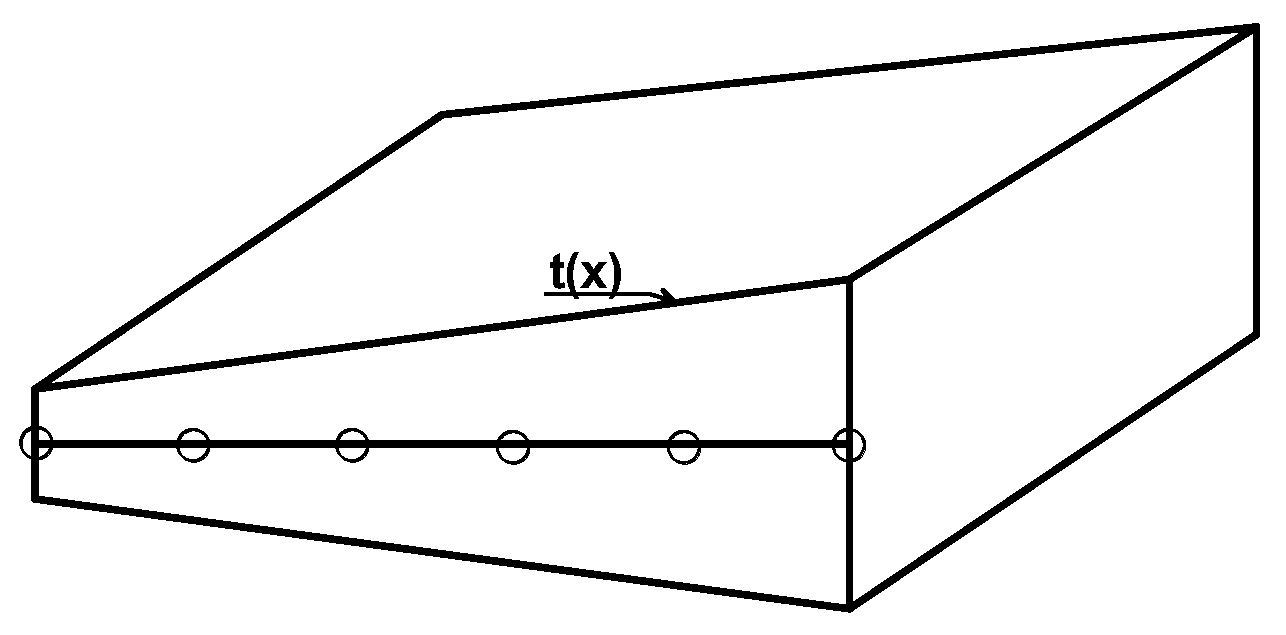
• Thickness variations – the shells thickness t can vary both in the ξ₁, ξ₂, ξ₃ directions; the analysis and the broader discussion of such problems is shown in Refs [18,19] and in Figure 2

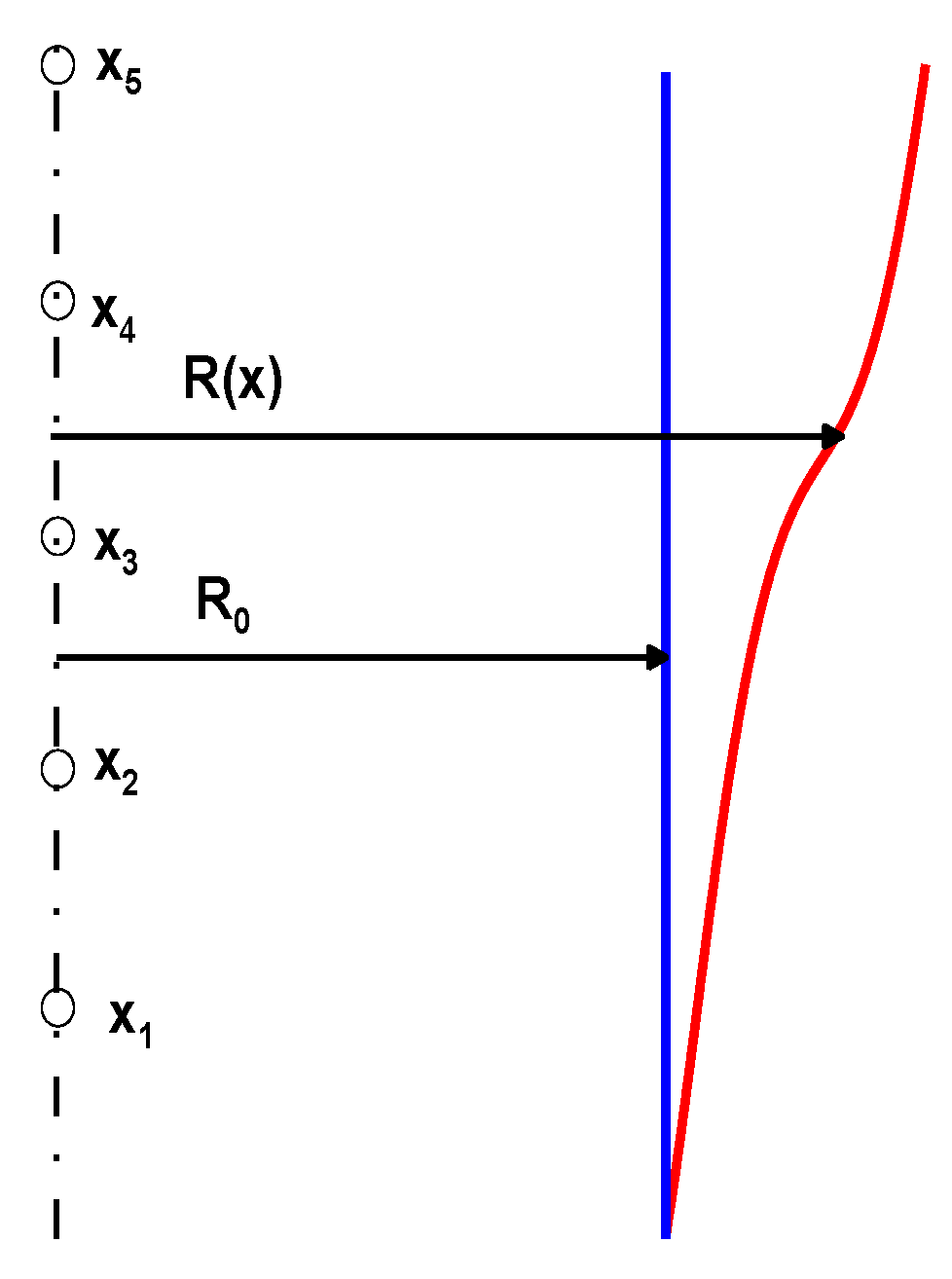
• The radius of the cylindrical shell R can vary both in the longitudinal x and circumferential directions θ and it introduces the new type of design variable connected with the shape optimization problems (a variable shell mid-surface– Figure 3) – see the problems formulated for laminated shells in Ref [18]

The shown above possible definitions of design variables demonstrate the possible optimization problems of maximization (minimization) of eigen-frequencies with respect to different design variables.

The solution of optimization problems can be found with the use of the appropriate optimization algorithms. In our case of the shape optimization problem we propose to apply the evolutionary algorithm method described in details in Ref. [19,20]. However, let us note that the fundamental set of equations derived with use of the Euler method from the functional (1) is nonlinear due to the form of the design variables.

4. Shape Optimization of the Shell Mid-Surface for Axi-Symmetric Cylinders

Very few papers concern the issues of optimization of the mid-surface shape for vibrating rotationally symmetrical or prismatic shells - see [21,22]. This is due to the fact that less attention has been paid to the characteristics of the dynamic response of structures to date, and more to their behavior under the influence of static loads.

The tasks of optimizing the shape of the middle surface of a structure are most often associated with the objective of optimizing the thickness. Due to this fact, various optimization problems can be formulated, consisting of (cf. Barbosa et al. [22] ):

• the demand to meet the condition of a constant value of the volume enclosed by the rotationally symmetric shell - then the thickness of the shell is assumed to be constant,
• the requirement to meet the condition that the volume occupied by the shell material is constant - this corresponds to the condition of the structure weight invariability during the optimization process (the shell wall thickness may change).

In this section, we will present a solution to the optimization problem consisting in the maximization of the lowest natural frequencies of the cylindrical shell. The design variables are the radius R (x) values of the rotationally symmetric shell at the control points. We impose limitations on possible changes in the radius values in the form:

$$0.9R_0\le R\left(x\right)\le 1.15R_0$$

(8)

where R₀ is the radius of the cylindrical shell. The curve Γ defining the shape of the longitudinal line of the shell is determined by specifying pairs of values (x, R (x)) where x is the coordinate of the control point along the length of the forming shell - see Figure 3. The optimization problem was solved using a modified evolutionary strategy (ZSE) introducing five control points. Additionally, due to the symmetry of the problem, a condition was imposed on the concatenated functions in the form of the derivative value of the R (x) function at the point x₅. The natural frequencies are derived with the use of FE method varying also the wave number in the circumferential direction

In the analyzed numerical example, the case of a restrained cylindrical shell with geometrical and mechanical properties was considered. The aim of the considerations is to determine: (i) the optimal shape for isotropic shells, (ii) the influence of orthotropy on the optimal shape, (iii) the influence of the FGM characteristics on the optimal design.

The results of the numerical calculations are presented in Table 1. The optimal shape of the Γ curve describing the surface of the middle rotation-symmetric shell is identical for the isotropic and orthotropic material. However, in the case of an orthotropic material, the lower Young’s modulus corresponds to the longitudinal direction, and the Young’s modulus in the circumferential direction is identical for both types of materials. Due to the form of natural vibrations (vibrations in the circumferential direction are dominant), the identical Young’s modulus in this direction results in the obtained identical shapes of the curve Γ. Various material properties in the longitudinal direction have a fundamental influence on the form of natural vibrations. It also causes some changes in the percentages determining the increase of the lowest natural frequency for the optimal shapes of the center surface of the rotationally symmetric shell.

The increase in the frequency of critical vibrations is primarily caused by the allowable increase in the shell radius. The obtained value of the increment may seem large, but it is a typical increment for this type of task,