Quarks and Leptons Formation from the Spontaneous Fractionation of a Pair of Elementary Particles with Proton Charge Units

1. Introduction

In 1964, Murray Gell-Mann and George Zweig, who were independently working on a theory of the strong interaction, proposed the existence of three subatomic particles. Within this framework they proposed that the strongly interacting particles, hadrons, could have been explained if they had not been elementary but made up of smaller elementary particles that were called quarks at the suggestion of Gell-Mann.

Already in 1961 Gell-Mann had proposed a symmetry scheme that he called “Eightfold Via”, the scheme was based on the mathematical symmetry known as SU(3) and managed to classify hadrons into two fundamental groups: mesons and baryons, an idea that George Zweig had also had in 1964 proposing that both mesons and baryons were constructed from a set of three fundamental particles. Both then went so far as to demonstrate that some properties of hadrons could be explained by treating them as triplets of other constituent particles, quarks. To date, however, there is still no theory that explains how quarks formed in the early universe.

We know that all particles form in pairs but we also know that the UP and DOWN quarks that belong to the so-called first generation of elementary particles in the Standard Model have never been observed to form in pairs independently, it is possible to obtain a quark plasma from collisions at the high energy of hadrons but it is not possible to obtain a creation of a new pair of quarks as happens instead for electron and positron or is proposed for a pair neutrino- antineutrino from a photon [1].

It is usual to assume that in the first moments after the Big Bang, the universe was extremely hot and dense and when the universe cooled, the conditions became optimal to give rise to the building blocks of matter, the quarks and electrons that a few millionths of a second later aggregated to produce protons and neutrons, but this scenario does not explain in any way how and why quarks were formed, therefore, in nature the origin of the quarks is currently a thick mystery.

In this paper is proposed a simple model developed using the principles of the Bridge electromagnetic Theory (BT) [2,3] able to propose a physical phenomenology that justifies the existence of quarks and of the other elementary particles of the first generation of the standard Model. To do that it is necessary to start from a cosmologic model compatible with the BT, able to give a possible answer at two fundamental questions: where do spacetime and primordial matter come from?

An answer was given by the Multi-Bubble Universe model [4,5] (MBU) which explains without the necessity of the Big Bang the birth of spacetime and primordial matter as a spontaneous process starting from the field of nothingness, originally defined by the absence of spacetime and electromagnetic field connected to it. Since the MBU model agrees with numerous observational data relating to the cosmic background, gravity, anomalous rotation speed of the galactic halos, but many predictions are still to be verified, we will consider as a hypothesis the existence of a currently unobserved particle, emitted in pairs (Cf. Ref. [4,5]) by the decay of the balancing graviton predicted by the MBU model, homologous for its properties to a Kaluza-Klein graviton, which should represent the germ from which spacetime and matter originate.

In this work it will be shown that their direct interaction produces a fractionation of the pair into three pairs of fundamental particles compatible with the first generation of the Standard Model. The fractionation process conjectured, here is called X-process, it may have occurred in the early stages of the creation of spacetime by producing hadrons and fundamental leptons.

The BT derives from a phenomenology described in the reference [6,7] according to which a pair of particles, independently by their value of charge $\pm q$, interacting produce a Dipole electromagnetic Source (DEMS) which localizes in the source zone an energy $h^{*}c/\lambda$ and a momentum $h^{*}/\lambda$ in agreement with that one of a photon of wavelength $\lambda$ equal to the minimum interaction distance achieved by the particles. The action associated with such a direct interaction is $h^{*}=2\pi \sigma q^2/c$, with $\sigma =137.035950244954$ equal to the reciprocal value of the theoretical Sommerfeld constant calculated the first time for free interactions in Ref. and successively in Ref. [2], more recently re-calculated in the context of the hydrogen atom formation model and for hydrogenoid atoms [10].

Following the BT, the present article proposes the possibility that a pair of fermions with appropriate characteristics, when they interact with each other, they spontaneously fractionate emulating the formation of the first generation of elementary particles of the Standard Model of matter.

In this article we will show how assuming that there is a pair of particles produced by the decay of the graviton KK with units of electric charge equal to that of the proton $\left(Q=e^{†},\overline{Q}=-e^{†}\right)$, the cross on the electric charged distinguishes the charge of the proton from that of the electron, a DEMS is born as described in BT (See. Ref. [2]), and provided that the two particles have an interaction energy sufficient to give rise to a proton-antiproton pair, that is, that they have an energy $E\ge 2m_p{c}^2$, the pair undergoes a spontaneous fractionation with two equiprobable channels, giving rise to two distinct groups of three pairs of elementary particles. The first group consists of three pairs of fractional charges in the quark-antiquark form $Q\overline{Q}\to d\overline{d}+2u\overline{u}$ while the second group consists in three pairs of leptons, one pair electron-positron and two pairs of electronic neutrino-antineutrino in the form $Q\overline{Q}\to e\overline{e}+2\nu \overline{\nu }$. In this model, neutrinos are expected to have an extremely weak but not zero electric charge because they must be able to interact electromagnetically even if weakly with other matter, so the electron and positron consequently have a lower charge value than that of the original unit from which they are derived. In the following, we will show how both fractional charge groups describe the particles in accordance with the first generation of elementary particles described in the Standard Model.

2. Structure Function of Two Interacting Charge Fragment

The BT (See Ref. [2,3]) is here used to propose a likelihood explanation to the origins of quarks and leptons in the universe. Starting from what has been demonstrated in BT that all DEMS produced by the direct electromagnetic interaction of a free pair of particles with elementary charge $e^{\pm }$ are associated with a Planck unit of action expressed in the Dirac form, to simplify we formally mark the process that gives rise to the DEMS as an operation that returns the action corresponding to the interaction between the charges with the binary symbolic operation giving the Planck action

$$\hslash =e\odot \overline{e}\equiv \sigma {\displaystyle \frac{e^2}{c}}$$

(1)

with $c$ speed of light, $e$ electron charge unit and $\sigma$ reciprocal value of the Sommerfeld constant $\alpha$ is the structure function theoretically calculated by the expression

$$\sigma =\left({\displaystyle \frac{4\pi }{3}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{\mathsf{\Theta }}_t\left(\rho ,\theta \right)d\theta }+{\displaystyle \frac{1}{4\pi {\rho }^2}}\right)$$

(2)

in which

$$\begin{array}{l}{\mathsf{\Theta }}_t\left(\rho ,\theta \right)=16\sqrt{{\displaystyle \frac{1}{{\left(4+{\rho }^2+4\rho \cos \theta \right)}^2}}+{\displaystyle \frac{1}{{\left(4+{\rho }^2-4\rho \cos \theta \right)}^2}}+{\displaystyle \frac{2\left(4-{\rho }^2\right)}{\sqrt{{\left[{\left(4+{\rho }^2\right)}^2-16{\rho }^2{\cos }^2\theta \right]}^3}}}}\\ \cdot \left|{\displaystyle \frac{\left(2+\rho \cos \theta \right)}{\sqrt{{\left(4+{\rho }^2+4\rho \cos \theta \right)}^3}}}+{\displaystyle \frac{\left(2-\rho \cos \theta \right)}{\sqrt{{\left(4+{\rho }^2-4\rho \cos \theta \right)}^3}}}\right|\end{array}$$

(3)

is the transversal component of the Poynting vector of the electromagnetic field of the DEMS (Cf. Ref. [2]). Therefore, in Gauss units the theoretical value of action (1) for an interaction between a pair of charged elementary particles with proton-antiproton electric charge $e^{†}{\overline{e}}^{†}$ is analogously given by ${\hslash }^{†}=e^{†}\odot {\overline{e}}^{†}$ where the numerical value of the action constant depends from the structure function (2) varying as a function of the ratio $\rho =R/\lambda$ between the dipole moment length per unit of charge $R$ and the wavelength $\lambda$ of the DEMS and of the emission angle $\theta$.

For a free electromagnetic interaction between a pair of charged particles, i.e., without external constrains acting on the DEMS, the ratio was been calculated using a stochastic method described in Ref. [29] and its value it is known exactly ${\rho }^{*}=1.275556618599942$, but the value changes if the particles are subjected to the action of external forces. Using this ratio the value of the structure constant is ${\sigma }^{*}=137.035989$ (See Ref. [2]) independently by the value of the charge of the pair of the interacting particles.

Each external constraint acting on the pair during their direct interaction produces a variation of the value of the ratio $\rho$ and consequently of the structure constant as proven in Ref. for an electron-proton capture.

Considering a pair $Q\overline{Q}$ one assumes that when the charges interact produce a DEMS corresponding to a growing electromagnetic spherical bubble delimited by the emitted spherical wave of wavelength $\lambda$ in which the spontaneous fragmentation of the pair occurs dividing the primitive electromagnetic bubble into three sub-DEMS produced by the interaction of a pair of fractional charges $C_i={\chi }_i{e}^{†}$ and ${\overline{C}}_i={\overline{\chi }}_i{e}^{†}$, where ${\chi }_i=\left|{\chi }_i\right|$ and ${\overline{\chi }}_i=-\left|{\chi }_i\right|$with $i=1,2,3$ are the fractional dimensionless charges such a that $0<{\chi }_i<1$, with product of the pair of unitary charges generators $Q\overline{Q}$ given by

$$\left|Q\overline{Q}\right|={\displaystyle \sum _i\left|C_i{\overline{C}}_i\right|}=e^{†2}{\displaystyle \sum _i\left|{\chi }_i{\overline{\chi }}_i\right|}.$$

(4)

Using the Equation (1) for the unit of charge $\left|e^{†}\right|$, the absolute value of the Planck action is given by

$$h=2\pi {\displaystyle \sum _i{C}_i\odot {\overline{C}}_i}=2\pi {\displaystyle \frac{e^{†2}}{c}}{\displaystyle \sum _i{\sigma }_{{\overline{\chi }}_i{\chi }_i}}$$

(5)

with

$${\sigma }_{{\overline{\chi }}_i{\chi }_i}=\left({\displaystyle \frac{4\pi }{3}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{\mathsf{\Theta }}_t\left(\rho ,\theta \right)d\theta }+{\displaystyle \frac{1}{4\pi {\rho }^2}}\right){\chi }_i^2=\sigma {\chi }_i^2$$

(6)

at the vary of the value of the ratio $\rho$ yields the value of the structure constant of the single sub-DEMS.

In general, for any possible interaction $C_i{C}_j$ also with different value of charge or anticharge, the structure constant (6) acquires the form

$${\sigma }_{{\chi }_i{\chi }_j}=\left({\displaystyle \frac{4\pi }{3}}{\displaystyle \underset{0}{\overset{\pi }{\int }}{\mathsf{\Theta }}_t\left({\chi }_i,{\chi }_j,\rho ,\theta \right)d\theta }-{\displaystyle \frac{{\chi }_i{\chi }_j}{4\pi {\rho }^2}}\right)$$

(7)

with field structure function associated to the transversal component of the of the Poynting vector

$$\begin{array}{l}{\mathsf{\Theta }}_t\left({\chi }_i,{\chi }_j,\rho ,\theta \right)=16\sqrt{{\displaystyle \frac{{\chi }_i^2}{{\left(4+{\rho }^2+4\rho \cos \theta \right)}^2}}+{\displaystyle \frac{{\chi }_j^2}{{\left(4+{\rho }^2-4\rho \cos \theta \right)}^2}}+{\displaystyle \frac{2{\chi }_i{\chi }_j\left(4-{\rho }^2\right)}{\sqrt{{\left[{\left(4+{\rho }^2\right)}^2-16{\rho }^2{\cos }^2\theta \right]}^3}}}}\\ \cdot \left|{\displaystyle \frac{{\chi }_i\left(2+\rho \cos \theta \right)}{\sqrt{{\left(4+{\rho }^2+4\rho \cos \theta \right)}^3}}}+{\displaystyle \frac{{\chi }_j\left(2-\rho \cos \theta \right)}{\sqrt{{\left(4+{\rho }^2-4\rho \cos \theta \right)}^3}}}\right|\end{array}$$

(8)

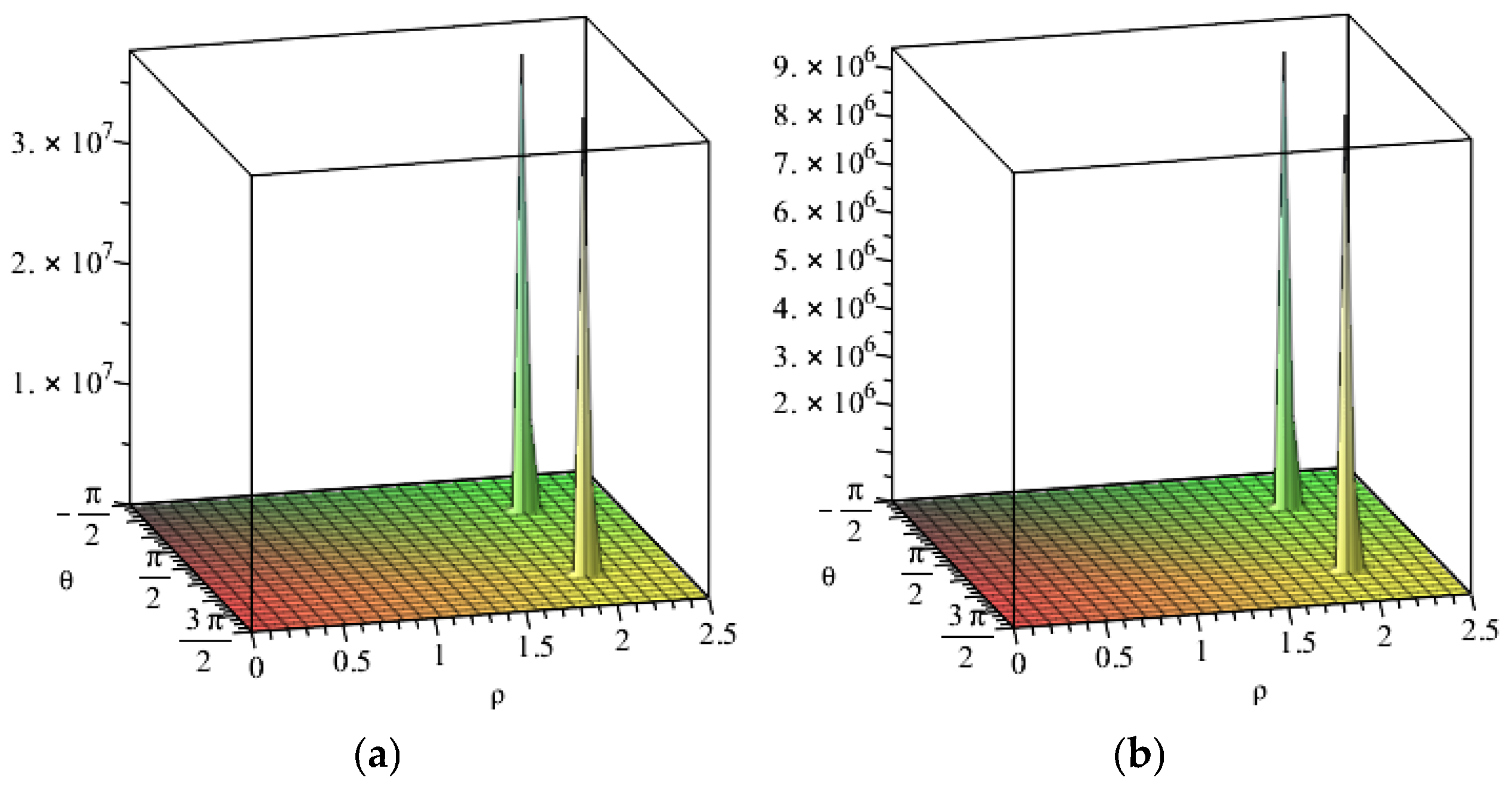
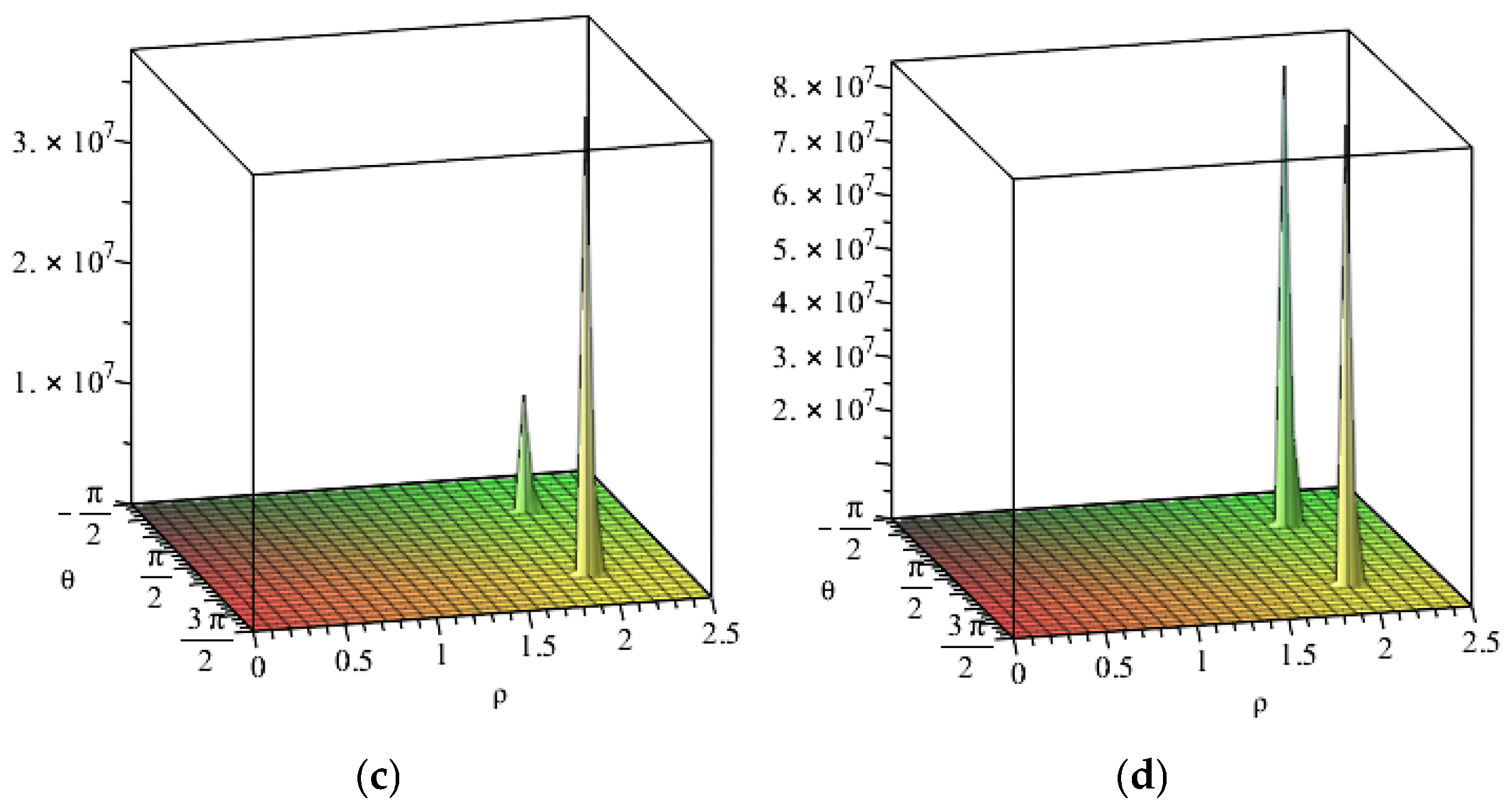
The application of Equation (7) allows to estimate the structure constants for each pair of integer or fractional charges existing in nature. In the (Figure 1a–d) are shown the structure functions (8) for some particular cases.

3. Fragmentation of Unitary Electric Charges of a DEMS

Considering that a DEMS, when formed, continues to exist regardless of the distance of the two interacting charges (see Ref. [1,2]), the following three properties hold:

A—The total action $Q\odot \overline{Q}$ obtained by the free interaction of a pair of interacting particles with integer interacting charges $Q\overline{Q}$is a constant value.

B—The value of the action depends by the value of the interacting charges $Q$ or $\overline{Q}$ and can vary according to the external constrains acting on the charges with the assumption that the total energy of the system must be conserved.

C—The integer charge $Q$ or $\overline{Q}$ of each individual interacting particle can be fractioned but the sum of its parts maintains the initial value.

D—In nature, protons are made up of three particles with fractional charge and different charge signs, according to point (C) above, two of them have the same charge value.

In the case of fractionation in sub-DEMS, the previous properties for a free interaction between two particles of unit charge divided in three pairs of fragments can be rewritten in the form:

(a) Using Equations (4)–(6) the total action of the sub-DEMS produced must not exceed in value the total action of the primary bubble.

$${\displaystyle \sum _i^3{{\chi }_i}^2}\le 1.$$

(9)

(b) The total fractional charge must be equal to that original:

$${\displaystyle \sum _i^3{\chi }_i}=\pm 1$$

(10)

(c) Two of the three charge fragments obtained must have equal value:

$${\chi }_2={\chi }_3$$

(11)

The three previous conditions put into the system

$$\left\{\begin{array}{c}{\chi }_1^2+{\chi }_2^2+{\chi }_3^2\le 1\\ {\chi }_1+{\chi }_2+{\chi }_3=\pm 1\\ {\chi }_2-{\chi }_3=0\end{array}\right.$$

(12a)

can be divided in two independent systems

$$\left\{\begin{array}{l}{\overline{\chi }}_1=-1-2{\overline{\chi }}_3\\ {\overline{\chi }}_2={\overline{\chi }}_3\\ \left(3{\overline{\chi }}_3+2\right){\overline{\chi }}_3\le 0\end{array}\right.$$

(12b)

$$\left\{\begin{array}{l}{\chi }_1=+1-2{\chi }_3\\ {\chi }_2={\chi }_3\\ \left(3{\chi }_3-2\right){\chi }_3\le 0\end{array}\right.$$

(12c)

The third equation of the system (12b) has solutions in the interval $\overline{S}=\left\{{\overline{\chi }}_3\in \left[\begin{array}{cc}-{\displaystyle \frac{2}{3}}& 0\end{array}\right]\right\}\cap {ℝ}^{-}$ for a negative charge generator and in the interval $S=\left\{{\chi }_3\in \left[\begin{array}{cc}0& +{\displaystyle \frac{2}{3}}\end{array}\right]\right\}\cap {ℝ}^{+}$ for a positive charge generator. Considering that a little but finite amount of energy is lost to produce the fractionation, the total action after the fractionation is a bit lower than that resulting after the fractionation, Therefore, one can writes the solution for a negative generator as $\overline{S}=\left\{{\overline{\chi }}_3\in \left[\begin{array}{cc}\underset{{\epsilon }_Q\to \delta Q}{\lim }\left(-{\displaystyle \frac{2}{3}}+{\epsilon }_Q\right)& \underset{{\epsilon }_Q\to \delta Q}{\lim }\left(0-{\epsilon }_Q\right)\end{array}\right]\right\}=\left\{{\overline{\chi }}_3\in \left[\begin{array}{cc}-{{\displaystyle \frac{2}{3}}}^{(+)}& 0^{(-)}\end{array}\right]\right\}$ analogously for the system (12c) for a positive generator $S=\left\{{\chi }_3\in \left[\begin{array}{cc}\underset{{\epsilon }_Q\to \delta Q}{\lim }\left(0+{\epsilon }_Q\right)& \underset{{\epsilon }_Q\to \delta Q}{\lim }\left(+{\displaystyle \frac{2}{3}}-{\epsilon }_Q\right)\end{array}\right]\right\}=\left\{{\chi }_3\in \left[\begin{array}{cc}{0}^{(+)}& +{{\displaystyle \frac{2}{3}}}^{(-)}\end{array}\right]\right\}$ with in both cases $\delta Q<{\epsilon }_Q$ where $\delta Q$ is a non-zero but very close to zero charge constant, the value of which is to be determined. Considering that among all the infinite particular solutions inside the intervals $\overline{S}$ and $S$, the values ${\overline{\chi }}_3$ and ${\chi }_3$ must be those that minimize the difference between the initial action of the particles with integer charge and the final total action of the pairs with fractional charge, for this to happen, only values close to the extremes of the intervals $\overline{S}$ and $S$ satisfy this condition, therefore, the solutions can be written in the form ${\overline{\chi }}_3=\left(-{{\displaystyle \frac{2}{3}}}^{(+)},0^{(-)}\right)$ for the negative generator and ${\chi }_3=\left(+{{\displaystyle \frac{2}{3}}}^{(-)},0^{(+)}\right)$ for the positive generator. The superscriptions $\left(-\right)$ and $\left(+\right)$ at right of the values of charge with theirs eventual multiplicity expresses the sign of the charge tendency defined as multiple of the defect of electric charge $\delta Q$, this symbol at the moment is indicative and does not define an exact value of the charge but represents how each charge value exceeds or is lower than that assigned by the solution justifying also in the leptonic solution the fractioning principle.

Using the two pair of generators and the first two equations of the Equation (12b-12c), one obtains the complete sets of the charge fractioned divided into anticharge and charge for hadronic (H) and leptonic (L) type

$$\begin{array}{l}{\overline{\chi }}_3=\left(-{{\displaystyle \frac{2}{3}}}^{(+)},0^{(-)}\right)\to \left\{\begin{array}{l}\overline{H}=\left(\begin{array}{ccc}+{{\displaystyle \frac{1}{3}}}^{(--)}& -{{\displaystyle \frac{2}{3}}}^{(+)}& -{{\displaystyle \frac{2}{3}}}^{(+)}\end{array}\right)\\ \overline{L}=\left(\begin{array}{ccc}-1^{(++)}& 0^{(-)}& 0^{(-)}\end{array}\right)\end{array}\right.\\ {\chi }_3=\left(+{{\displaystyle \frac{2}{3}}}^{(-)},0^{(+)}\right)\to \left\{\begin{array}{l}H=\left(\begin{array}{ccc}-{{\displaystyle \frac{1}{3}}}^{(++)}& +{{\displaystyle \frac{2}{3}}}^{(-)}& +{{\displaystyle \frac{2}{3}}}^{(-)}\end{array}\right)\\ L=\left(\begin{array}{ccc}+1^{(--)}& 0^{(+)}& 0^{(+)}\end{array}\right)\end{array}\right.\end{array}$$

(13)

the solutions (13) obtained for the systems (12b-12c) are unique and depend on the conservation of charge and action value which, associated with a characteristic fractionation time, corresponds to the conservation of energy.

To simplify the display of the solutions (13), one collects the charges in two matrices, one hadronic

$$H=\left(\begin{array}{c}H\\ \overline{H}\end{array}\right)=\left(\begin{array}{l}\begin{array}{ccc}-{{\displaystyle \frac{1}{3}}}^{(++)}& +{{\displaystyle \frac{2}{3}}}^{(-)}& +{{\displaystyle \frac{2}{3}}}^{(-)}\end{array}\\ {\begin{array}{ccc}+{{\displaystyle \frac{1}{3}}}^{(--)}& -{{\displaystyle \frac{2}{3}}}^{(+)}& -{\displaystyle \frac{2}{3}}\end{array}}^{(+)}\end{array}\right)\iff \left(\begin{array}{l}\begin{array}{ccc}d& u& u\end{array}\\ \begin{array}{ccc}\overline{d}& \overline{u}& \overline{u}\end{array}\end{array}\right)$$

(14)

in which there are three fractional values of the charge generator in correspondence with the existence of two flavours of quarks and one leptonic

$$L=\left(\begin{array}{c}L\\ \overline{L}\end{array}\right)=\left(\begin{array}{l}\begin{array}{ccc}+1^{\left(--\right)}& 0^{\left(+\right)}& 0^{\left(+\right)}\end{array}\\ \begin{array}{ccc}-1^{\left(++\right)}& 0^{\left(-\right)}& 0^{\left(-\right)}\end{array}\end{array}\right)\iff \left(\begin{array}{l}\begin{array}{ccc}\overline{e}& \nu & \nu \end{array}\\ \begin{array}{ccc}e& \overline{\nu }& \overline{\nu }\end{array}\end{array}\right)$$

(15)

Solutions (14) and (15) show that all particles besides the charge value have a charge tendency, i.e., that the charges are not exactly equal to the declared values but that they are slightly lower or higher.

Considering that the charge tendency changes in signs if the sign of the unitary generator changes, charge tendency allows to all the sub-DEMS has got a part of the total energy of the primordial DEMS allowing them to evolve energetically.

The solutions (14) and (15) have as consequence that the proton must have a value of charge an amount $2\delta Q$ greater than the unit charge of the positron, hence for coherence $e^{†}>e$ by reopening a discussion on the real neutrality of atoms and molecules [11,12].

4. Use of the Solutions L and H to Build the First Generation of the Elementary Particles

To describe the quarks in Equation (14), the charge tendency is not essential because the quarks, unlike neutrinos, have a charge to interact with each other particle, their charge tendency may be necessary only considering the behaviour during their interaction in groups of particles forming mesons or baryons, which is not taken into account here. In this work it is sufficient to establish that there is a fractionation mechanism that leads to the existence of hadrons with fractional charges not with the exact same value, therefore with different positive or negative tendencies of the charge value. This mechanism could define the colour charge of quarks allowing direct interaction between quarks of the same type, an example would be $\left(+{{\displaystyle \frac{2}{3}}}^{(-)},+{{\displaystyle \frac{2}{3}}}^{(--)},-{{\displaystyle \frac{1}{3}}}^{(+++)}\right)$ which can be considered for example equivalent to u-RED, u-GREEN and d-BLUE, in such a way that the resulting proton $uud$ formed by the three quarks taken together can form an exact unitary charge particle with zero tendency in agreement with QCD and with a charge only a bit greater than the electron one.

Since the use of the tendency notation for the hadronic solution currently appears redundant, we will use it only when and if necessary.

5. Mixed Solutions

Since the fractionations of the charges of the particles that form the original DEMS occurs on the row of the matrix and the two rows are independent, the only conditions that must be verified are those previously reported in points A-B-C-D, the mixed matrice

$$M=\left(\begin{array}{c}H\\ \overline{L}\end{array}\right)=\left(\begin{array}{l}\begin{array}{ccc}-{\displaystyle \frac{1}{3}}& +{\displaystyle \frac{2}{3}}& +{\displaystyle \frac{2}{3}}\end{array}\\ \begin{array}{ccc}-1^{\left(++\right)}& 0^{\left(-\right)}& 0^{\left(-\right)}\end{array}\end{array}\right)\iff \left(\begin{array}{l}\begin{array}{ccc}d& u& u\end{array}\\ \begin{array}{ccc}e& \overline{\nu }& \overline{\nu }\end{array}\end{array}\right)$$

(16)

and its symmetric

$$\overline{M}=\left(\begin{array}{c}\overline{H}\\ L\end{array}\right)=\left(\begin{array}{l}\begin{array}{ccc}+{\displaystyle \frac{1}{3}}& -{\displaystyle \frac{2}{3}}& -{\displaystyle \frac{2}{3}}\end{array}\\ \begin{array}{ccc}+1^{\left(--\right)}& 0^{\left(+\right)}& 0^{\left(+\right)}\end{array}\end{array}\right)\iff \left(\begin{array}{l}\begin{array}{ccc}\overline{d}& \overline{u}& \overline{u}\end{array}\\ \begin{array}{ccc}\overline{e}& \nu & \nu \end{array}\end{array}\right)$$

(17)

obtained with a mixing of compatible solutions H and L are particularly interesting. Solutions (16) and (17) can exist together because they are two separate solutions of the two generators of charge $(-1,+1)$. The choice of which of the two matrices is the antimatrix is completely arbitrary, in this context the one containing the elementary particles of ordinary matter compatible with the existence of hydrogen atoms has been chosen as the matrix and the one containing the particles compatible with the existence of antihydrogen atoms has been chosen as the antimatrix.

In this case one could have the coexistence in a same electromagnetic bubble of a proton or antiproton and of three leptons violating the creation in pairs of the particles associated to the sub-DEMS. This may be possible if an electromagnetic bubble is formed using two different fractional solutions, one hadronic and one leptonic, i.e., the fractionation takes place by particle of integer charge and not by pair, in this case the interaction occurs by clusters of charge, therefore for rows and the mixed bubble does not violate the invariance of the total charge, of the spin of the bubble and preserves the sum of the baryon and lepton numbers

$$B+L=0$$

(18)

The asymmetric fractionation characterizing the mixed solutions (16) and (17) suggests that with the different charged particles collected in the X-matrix

$${\rm X}=\left(\begin{array}{c}{\begin{array}{ccc}-1^{(++)}& 0^{(-)}& 0\end{array}}^{(-)}\\ \begin{array}{ccc}+1^{(--)}& 0^{(+)}& 0^{(+)}\end{array}\\ \begin{array}{ccc}-{\displaystyle \frac{1}{3}}& +{\displaystyle \frac{2}{3}}& +{\displaystyle \frac{2}{3}}\end{array}\\ \begin{array}{ccc}+{\displaystyle \frac{1}{3}}& -{\displaystyle \frac{2}{3}}& -{\displaystyle \frac{2}{3}}\end{array}\end{array}\right)\iff \left(\begin{array}{c}\begin{array}{ccc}e& \overline{\nu }& \overline{\nu }\end{array}\\ \begin{array}{ccc}\overline{e}& \nu & \nu \end{array}\\ \begin{array}{ccc}d& u& u\end{array}\\ \begin{array}{ccc}\overline{d}& \overline{u}& \overline{u}\end{array}\end{array}\right)$$

(19)

a direct electromagnetic interaction that forms a DEMS is invariant in energy and action only considering pairs of charges formed by clusters obtained by aggregating different elementary particles arranged in the X-matrix (19), each corresponding to a non-elementary particle.

Extending these considerations, charge clusters can be produced using the elementary particles in the matrix (19) in such a way that the initial charge values can be reproduced forming new particles as for example$p\equiv uud$,$\overline{p}\equiv \overline{u}\overline{u}\overline{d}$ or ${\pi }^{+}\equiv u\overline{d}$, ${\pi }^{-}\equiv \overline{u}d$ , but there is also the possibility of produce new heavy clusters with fractional charges of successive generation as ${\overline{d}}^{(II)}=d\overline{d}\overline{d}$, ${\overline{d}}^{(III)}=u\overline{u}\overline{d}$and $d^{(II)}=d\overline{d}d$, $d^{(III)}=u\overline{u}d$ or ${\overline{u}}^{(II)}=d\overline{d}\overline{u}$, ${\overline{u}}^{(III)}=u\overline{u}\overline{u}$and $u^{(II)}=d\overline{d}u$,$u^{(III)}=u\overline{u}u$. These clusters and other possible could be connected to quarks belonging to the second and third generation using more elementary particles. In this sense, generations subsequent to the third would also be possible differing from previous generations only in energy content. This mode is the only one that can be used to keep the charge and action unchanged during the formation of a DEMS between pairs of charged clusters, so it is possible to think that the particles can be aggregated by means of charge clusters that necessarily have different energy and more mass because they are formed by a different number of active sub-DEMS.

Equation (19) puts in evidence a perfect symmetry in particles-antiparticles primary production with an abundance of two neutrinos for each hydrogen atom and two antineutrinos for each anti-hydrogen atom, having four neutrinos for each pair of hydrogen-anti-hydrogen. Considering that at present it is not yet possible to know where and when antihydrogen disappeared, starting with Equation (19) it will be interesting in the future to try to draw all the possible scenarios capable of describing the situation of our universe.

5. Discussion and Conclusions

The particles collected in the matrix X solutions of fractionation, highlight that starting from the principle of conservation of charge and energy in a DEMS produced during the free interaction of the pair with the electric charge of the proton, the fractionation of charge occurs spontaneously, but it cannot occur for particles with an electric charge equal to that of an electron.

The model is able to justify the presence in the universe of four different fermions $(u,d,e,\nu )$ and four different antifermions $(\overline{u},\overline{d},\overline{e},\overline{\nu })$, each associated with a fractional charge and with properties similar to those experimentally known in nature and predicted by the Standard Model. Excluding the value of the mass of the electron, which is well known experimentally, it might be interesting to estimate the mass of quarks and neutrinos, but this is not the purpose of this paper.

Since in BT an elementary particle interacts with other particles only electromagnetically, that can occur only if all the particles have electric charge and consequently mass and inertia [13], therefore, all particles must have charge and mass. The charge of the neutrinos must obviously be very small and currently this value has not yet been evaluated [14].

As a result of the model application, one deduces that the positron has a unit of charge $e$ only slightly lower than that of the proton $e^{†}$, the difference of which is instrumentally difficult to assess (Cf. Ref. [11]).

The introduction of the charge tendency, in addition to allowing a charge, even if very small, to be attributed to the neutrino, suggests a mechanism that justifies the existence of the colour charge of quarks, giving in this case the possibility to two apparently identical particles to interact by binding to each other.

Finally, it may be interesting to consider that in the model, matter and antimatter would have as a distinctive characteristic the sign of the charge generator, when the sign is positive the fractionation produces particles, when the sign is negative the fractionation produces antiparticles. Therefore, the electron would be the antiparticle of the positron, this for a universe full of hydrogen means that there are as many protons as electrons, so since the proton is made up of three quarks $uud$ defined all as particles and one electron defined as antiparticle, defining a matter-antimatter asymmetry number based on the elementary particles $A=\pm k$, a hydrogen atom would be formed by three particles (quarks) with $A_p=3$ and by an antiparticle (electron) $A_e=-1$ with a total asymmetry $A_{p+e}=+2$. If we consider the complete solution of the six fractionated particles that appear in the mixed matrix in Equation (16), in which two antineutrinos are produced together with the electron, this solves the problem of matter-antimatter asymmetry in the universe in terms of particles-antiparticles, in fact hydrogen would consist of a non-elementary particle (p) and an elementary antiparticle (e) which together with the two antineutrinos emitted cancel the number of asymmetry, solving in conceptual terms the problem of the apparent asymmetry in favour of matter in the universe nulling the asymmetry number $A=0$.

The fact that the matter-antimatter asymmetry can be considered zero, however, does not solve the problem of the absence of antihydrogen in the early universe. However, the author believes that the conjecture on the existence of the X-process producing the fractionation, if demonstrated by the identification of a real candidate pair of particles may contribute to finding the way to understand the baryon asymmetry of the universe.