Non-Abelian Topological Defects in QGP as Dark Matter Candidates

Swapnil Singh

doi:10.20944/preprints202406.1082.v1

Submitted:

16 June 2024

Posted:

17 June 2024

Read the latest preprint version here

Abstract

In this paper, we explore the hypothesis that topological defects formed in the quark-gluon plasma (QGP) of the early universe, specifically flux tubes and domain walls, could serve as stable dark matter candidates. Theoretical analysis of the QCD vacuum structure reveals that these defects can form due to nontrivial topological configurations, with the Lagrangian density incorporating topological terms. We model the formation and stability of flux tubes and domain walls, estimating their energy densities and dynamics within the QGP. Flux tubes, with energy per unit length approximately given by $\mu \approx \frac{\sigma}{g_s^2}$, and domain walls, characterized by a surface energy density $\sigma_{\text{DW}} \sim \Lambda_{\text{QCD}}^3$, exhibit unique gravitational signatures. These signatures include distinct gravitational lensing patterns due to their linear and planar mass distributions, making them detectable through astrophysical surveys. Furthermore, their minimal interaction with conventional matter aligns well with observational constraints on dark matter properties. We discuss potential experimental approaches for detecting these defects, including high-energy collider experiments and detailed analysis of gravitational lensing data. Our findings suggest that topological defects in the QGP provide a compelling and novel solution to the dark matter problem, offering a new direction for both theoretical investigation and experimental verification.

Keywords:

Topological defects

;

Quark-gluon plasma (QGP)

;

Dark matter

;

Flux tubes

;

Domain walls

;

QCD vacuum structure

Subject:

Physical Sciences - Nuclear and High Energy Physics

Introduction

Several candidates for dark matter have been proposed, spanning a wide range of theoretical frameworks. These include Weakly Interacting Massive Particles (WIMPs), axions, sterile neutrinos, and massive astrophysical compact halo objects (MACHOs). WIMPs have been a leading candidate due to their predicted interactions via the weak nuclear force and mass in the range of 10 to 1000 GeV/c² [1,2]. Despite decades of searching, no conclusive evidence for weakly interacting massive particles (WIMPs) as dark matter has been found [3,4,5]. Direct detection experiments like DarkSide-50 and LZ are aiming to observe low-energy scattering of dark matter off normal matter, but have not yet observed any definitive WIMP signals [4,5,6]. Some possible indications have been reported, such as an interesting structure at 130 GeV

γ

-ray energy in Fermi-LAT data, but the situation remains quite confusing and non-conclusive at present [3]. The future of WIMP dark matter detection will depend on whether these particles are indeed the dark matter, which may be probed in the next few years [3]. If WIMPs are not the answer, the timescale and methods for detecting the true nature of dark matter will be much more uncertain.

Besides the conventional uniformly distributed dark matter, there’s a possibility of stable, spatially extended configurations of dark matter, which might have originated in the early cosmological epochs. These configurations are commonly referred to as topological defect dark matter and can exhibit different dimensionalities: 0D (such as monopoles), 1D (strings), and 2D (domain walls) [7,8]. They are called "topological" because they are stable due to their topological properties, rather than any local energy minimum.

In this paper, we explore the hypothesis that topological defects formed in the quark-gluon plasma (QGP) of the early universe could serve as viable dark matter candidates. Though the non-perturbative features of QCD such as confinement have not yet been rigorously established, it is widely believed that at either high temperature or high densities normal hadronic matter undergoes a phase transition to a new unconfined state of matter, the quark-gluon plasma (QGP) formed by the basic constituents of the hadrons, i.e. the quarks and gluons [9,10,11]. As the universe cooled, this plasma underwent a phase transition to form the hadrons observed today, The early universe presumably underwent such phase transition

10^{- 10} \sim 10^{- 5}

s after the Big Bang [11],Phase transition at high temperature is also useful in the cosmological studies. Critical phenomena that can occur, for example long-range density fluctuations, might have a bearing on important aspects of cosmology, such as nucleosynthesis, dark matter and the large-scale structure of the universe [11]. This phase transition can give rise to various topological defects due to the nontrivial vacuum structure of Quantum Chromodynamics (QCD). Topological defects provide one class of mechanisms for generating the initial density fluctuations. Among these defects, flux tubes and domain walls are particularly interesting due to their potential stability and unique physical properties.

Topological defects formed in the quark-gluon plasma (QGP) of the early universe, such as flux tubes and domain walls, could potentially serve as stable dark matter candidates. The QGP is a state of matter that existed in the early universe at extremely high temperatures, where quarks and gluons were not confined within hadrons.

During the QCD phase transition, when the QGP transitioned to a hadron gas, topological defects like flux tubes and domain walls could have formed. These defects could have remained stable and survived until the present day, potentially making up a significant portion of the dark matter in the universe.

The effects of these topological defects on the dissociation energy of heavy quarkonia (bound states of a heavy quark and its antiquark) have been studied in an anisotropic QGP [12]. The findings suggest that the inclusion of topological defects causes a shift in the dissociation energy at high temperatures, indicating their potential impact on the properties of the QGP [12].

Furthermore, dark matter has been proposed to originate from a gluonic Bose-Einstein condensate, referred to as the Cosmic Gluonic Background (CGB), which forms due to the trace anomaly in QCD [13]. This CGB could be associated with an effective negative cosmological constant, determining an anti-de Sitter geometry and accompanying baryonic matter at the hadronization transition from the QGP to the hadronic phase [13].

One such model was proposed by Witten [14] in 1984. The dark matter was suggested to be leftover quark objects from the quark-hadron transition in the early Universe. Witten showed that under certain circumstances, QGP bags, or “quark nuggets” as he called them, could survive to the present and form lumps of quark matter of size

\sim 10 cm

with a density of

\sim 10^{15} {g / cm}^{3}

.

There are more recent, and detailed, analyses of Witten’s idea. Madsen argued [15] that QGP bags with baryon number

A < 10^{35}

cannot be dark matter candidates. Alan, Raha, and Sinha claimed that QGP bags with baryon number

10^{39} \leq A \leq 10^{49}

are cosmologically stable and could solve the dark matter problem and even close the Universe gravitationally [16].

Explaining dark matter with QGP objects is appealing in the sense that it relies on the well-established idea that all nuclear matter was once in the form of QGP . Explaining dark matter with QGP objects is appealing in the sense that it relies on the well-established idea that all nuclear matter was once in the form of QGP .

QGP in the Early Universe

Quark-Gluon Plasma in the Early Universe

Quark-gluon plasma (QGP) is a state of matter in which quarks and gluons, usually confined within hadrons, become free and interact over a large volume. This state is believed to have existed in the early Universe shortly after the Big Bang, during the first few microseconds, when temperatures and energy densities were extraordinarily high. The study of QGP provides insight into the fundamental properties of strong interactions and the early conditions of the Universe.

The plot (see Figure 1) illustrates the thermal history of the universe, showcasing key epochs and significant events, such as the Big Bang, Photon Decoupling, and Reionization, providing a comprehensive overview of cosmic evolution.

Early Universe Conditions and QGP Formation

In the initial moments after the Big Bang, the Universe was in an extremely hot and dense state. According to quantum chromodynamics (QCD), the theory of the strong interaction, at temperatures above approximately 150-200 MeV (around

10^{12}

K), quarks and gluons are no longer confined within hadrons but instead form a QGP. This transition is often referred to as the QCD phase transition [17].

QGP Properties and Signatures

The properties of QGP, such as its viscosity, thermal conductivity, and response to external fields, are subjects of intense study. One of the key signatures of QGP formation in heavy-ion collision experiments is the suppression of J/

ψ

mesons, as these bound states of charm quarks are expected to dissolve in a QGP due to Debye screening [18].

Additionally, the QGP exhibits collective flow phenomena, which can be observed through anisotropic flow patterns in the particles produced in heavy-ion collisions. These patterns are indicative of the pressure gradients and the hydrodynamic behavior of the QGP [19].

Lattice QCD and Computational Studies

Lattice QCD is a non-perturbative approach to solving QCD numerically on a discrete space-time lattice. It has been instrumental in studying the thermodynamic properties of QGP. For instance, lattice QCD calculations provide estimates of the critical temperature for the QCD phase transition and the equation of state of the QGP [20]. These calculations are essential for understanding the behavior of matter under extreme conditions.

Experimental Evidence from Heavy-Ion Collisions

Experiments at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) have provided substantial evidence for the existence of QGP. These experiments involve colliding heavy ions, such as gold or lead nuclei, at relativistic speeds to recreate the conditions of the early Universe. The resulting fireball of hot, dense matter expands and cools, undergoing a transition from QGP to hadronic matter.

Key experimental observations include:

Jet quenching: The suppression of high-energy jets as they traverse the QGP, indicating a high-energy loss due to the dense medium [21].
Elliptic flow: The anisotropic distribution of particle momenta, suggesting collective behavior and hydrodynamic flow of the QGP [22].
Strangeness enhancement: An increased production of strange quarks and their bound states (e.g., strange baryons), which is consistent with QGP formation [23].

Theoretical Models and Hydrodynamics

Hydrodynamic models have been successful in describing the space-time evolution of the QGP created in heavy-ion collisions. These models treat the QGP as a nearly perfect fluid with very low shear viscosity to entropy density ratio (

η / s

), which is close to the conjectured lower bound from the AdS/CFT correspondence [24]. This behavior suggests that the QGP is one of the most perfect fluids known.

Cosmological Implications

The study of QGP is not only important for understanding the early Universe but also for exploring fundamental questions in high-energy physics. By recreating and studying QGP in the laboratory, physicists can test the predictions of QCD and gain insight into the nature of confinement and the generation of mass in the Universe [25]. In high-density QCD environments, the energy-momentum tensor might exhibit anomalous transport phenomena, such as the chiral magnetic effect, which could manifest in the unique electromagnetic signatures of topological stars [26].

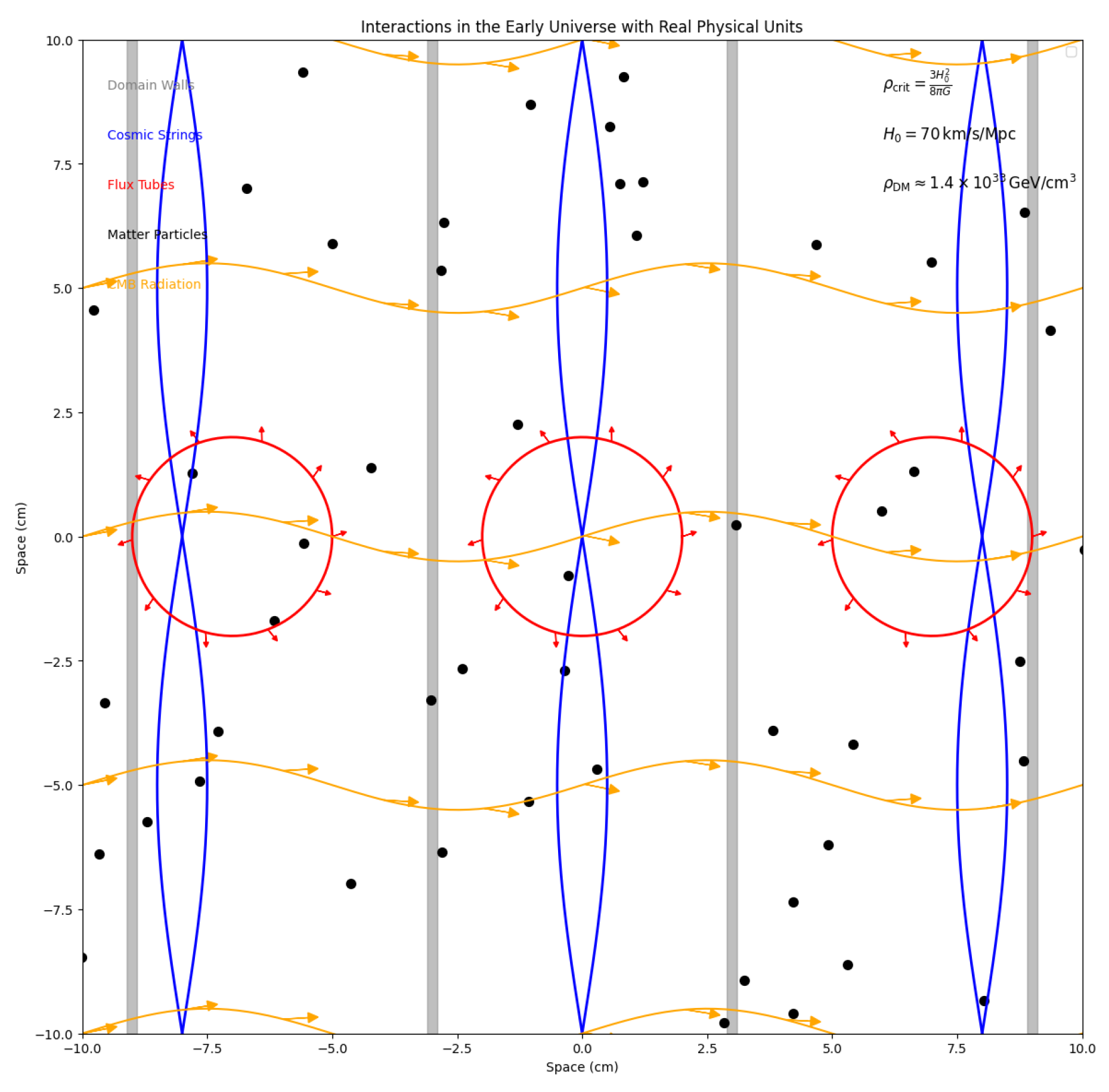
Topological Defects in QGP as Dark Matter

Topological defects in the Quark-Gluon Plasma (QGP) have garnered significant interest as potential candidates for dark matter. The QGP is a state of matter where quarks and gluons, normally confined within protons and neutrons, are liberated at extremely high temperatures and densities. The study of topological defects within this plasma, and their implications for dark matter, draws on rich theoretical frameworks and experimental insights from high-energy physics.

Topological Defects in QGP

Topological defects arise in various physical systems, from condensed matter to cosmology, and their presence in QGP offers intriguing possibilities for new physics. In the context of QGP, these defects include monopoles, domain walls, and cosmic strings, which are stabilized by topological considerations.

Monopoles are theoretical particles proposed by grand unified theories (GUTs) that carry a net magnetic charge. The QGP provides a suitable environment for the formation of monopoles during the early universe phase transitions when the temperature drops below the GUT scale. These monopoles could be remnants of symmetry breaking in the early universe, serving as dark matter candidates due to their stability and interaction characteristics [27].

Domain walls are another type of topological defect, predicted to form when discrete symmetries are broken in the early universe. If such walls formed during the QGP phase transition, they could contribute to the dark matter density, depending on their stability and interaction cross-sections [28].

Cosmic strings are line-like topological defects that can form during phase transitions in the early universe. These strings could interact weakly with normal matter and have the potential to account for some or all of the dark matter in the universe [29].

The Figure 2 illustrates the energy density distribution across a domain wall in quantum chromodynamics (QCD), showcasing the potential well formed by the Higgs field. The parameters used for the plot include the coupling constant (

λ

) and the vacuum expectation value (

ϕ_{0}

). By analyzing the energy density distribution, we can gain insights into the formation and stability of topological defects during the quantum chromodynamic phase transition. The highlighted vacuum expectation value signifies the stable ground state, providing valuable information about the underlying dynamics of the system.

Implications for Dark Matter

Topological defects in QGP offer a rich avenue for dark matter research. One of the key advantages of considering these defects as dark matter candidates is their potential for weak interaction with ordinary matter, which aligns with observational constraints on dark matter properties. If monopoles are stable and massive, they could constitute a significant portion of dark matter. Their magnetic charge would make them distinct from other dark matter candidates, and searches for relic monopoles in cosmic rays and particle detectors are ongoing [30]. The cosmological impact of domain walls depends on their surface tension and interaction with other fields. Domain walls with suitable properties could evade current detection methods while contributing to the overall dark matter density. However, overly massive or abundant domain walls could lead to conflicts with cosmological observations, such as the isotropy of the cosmic microwave background (CMB) [31]. Cosmic strings could leave observable imprints in the CMB and gravitational wave background. If these strings interact weakly enough, they could remain undetected while still contributing to dark matter. The detection of gravitational waves from string interactions or their lensing effects on distant astrophysical objects would provide evidence for their existence [32].

Topological defects in the Quark-Gluon Plasma present a compelling area of study for dark matter research. The unique properties of monopoles, domain walls, and cosmic strings align with the requirements for dark matter candidates, offering pathways to explore new physics beyond the Standard Model.

Quantum Chromodynamics (QCD) and Vacuum Structure

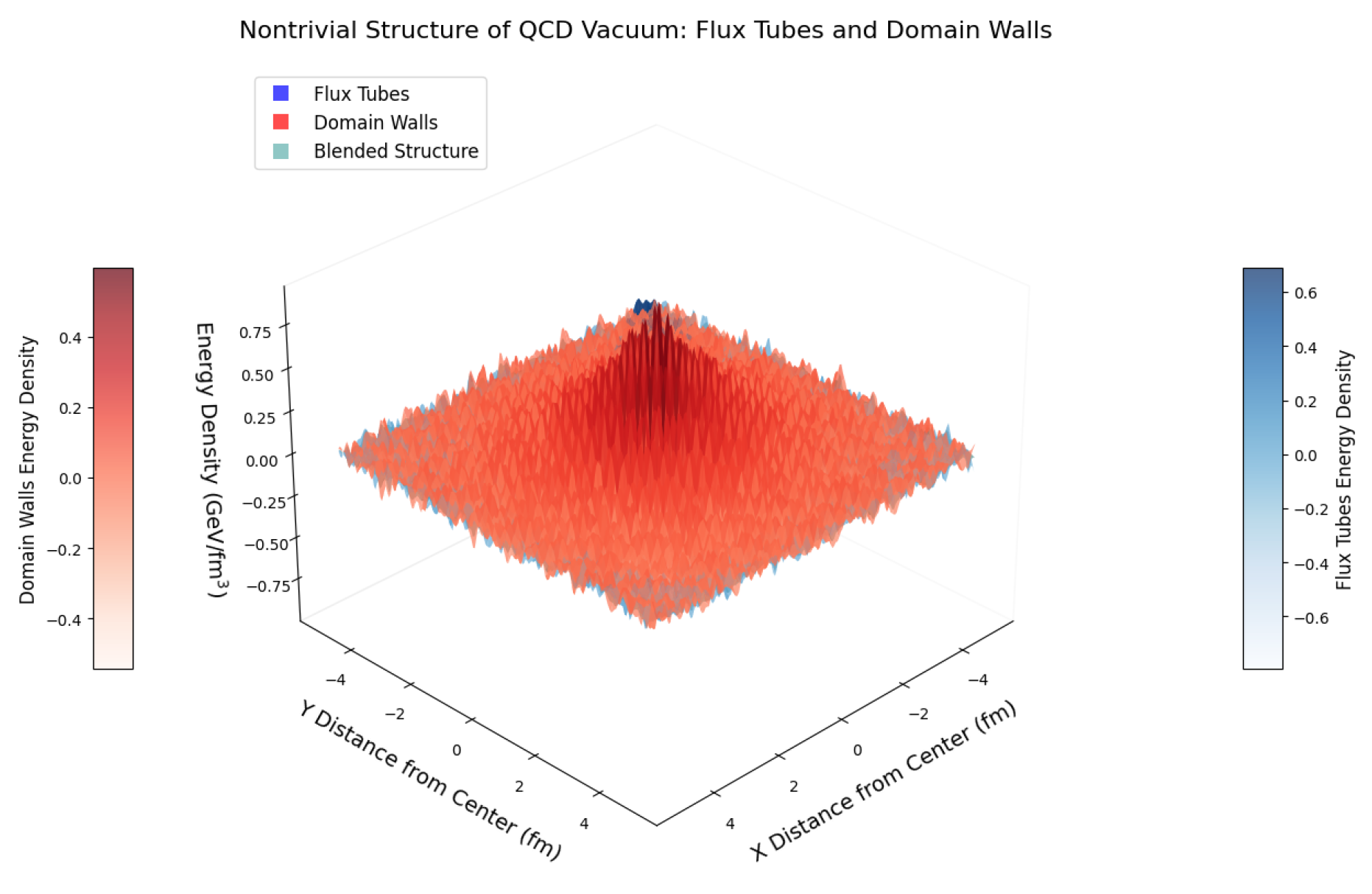
Quantum Chromodynamics (QCD) serves as the fundamental theory governing the strong interactions among quarks and gluons, encapsulating the structure of hadrons. Within this framework, the vacuum structure plays a crucial role, particularly in the early universe. Here, we explore the complex relationship between QCD vacuum structure and the formation of topological defects, specifically flux tubes and domain walls, within the quark-gluon plasma (QGP) of the primordial universe.

The QCD vacuum exhibits nontrivial configurations arising from the dynamics of gluon fields. These configurations give rise to topological features, contributing to the formation of stable defects. As included by Polyakov [33], the vacuum’s complex landscape, characterized by nonperturbative effects, leads to quark confinement and the emergence of flux tubes, also known as chromoelectric flux tubes. These tubes, conceptualized as strings of color-electric field lines, play a crucial role in understanding quark confinement [34,35].

The Figure 3 illustrates the QCD vacuum structure, where the gluon field strength

strength = \frac{exp (- 0.1 \cdot r)}{r + 1}

and quark field strength

strength = exp (- 0.05 \cdot r)

, showcasing their exponential decay with distance r. Arrows represent the field directions, revealing the complex dynamics between gluons and quarks in quantum chromodynamics.

Additionally, the QCD vacuum facilitates the formation of domain walls, arising from the spontaneous breaking of chiral symmetry [36]. Domain walls, acting as thin membranes, separate regions with different vacuum expectations of quark fields. The surface energy density of these walls is complexly linked to the QCD scale parameter,

Λ_{QCD}

, governing the nonperturbative regime of QCD.

Theoretical analysis, incorporating topological terms within the QCD Lagrangian density, provides insights into the energetics and stability of these defects. Flux tubes, characterized by their linear structure, exhibit an energy per unit length

μ

approximately given by [37]:

μ \approx \frac{σ}{g_{s}^{2}}

where

σ

represents the string tension and

g_{s}

denotes the strong coupling constant. Conversely, domain walls are distinguished by their planar geometry, with a surface energy density

σ_{DW} \sim Λ_{QCD}^{3}

[38].

The formation and evolution of these defects within the QGP are crucial aspects of early universe dynamics. Their stability and longevity make them plausible candidates for dark matter constituents, offering a novel perspective on the dark matter problem. The gravitational signatures associated with flux tubes and domain walls, arising from their unique mass distributions, hold promise for observational detection through astrophysical surveys [39].

Experimental verification of these theoretical conjectures presents significant challenges, necessitating innovative approaches. High-energy collider experiments provide avenues for probing the fundamental interactions underlying the formation of topological defects within the QGP. Additionally, detailed analysis of gravitational lensing data offers a complementary method for detecting the gravitational imprints of these defects in the cosmic landscape [40].

In summary, the interaction between Quantum Chromodynamics and vacuum structure reveals a rich tapestry of topological defects with profound implications for both fundamental physics and cosmology. The hypothesis proposing topological defects formed in the QGP as stable dark matter candidates presents an intriguing avenue for further theoretical exploration and experimental scrutiny.

Classical Potential and Quantum Corrections

In classical mechanics, the equilibrium state of a system is determined by finding the global minimum of the potential energy. This minimum corresponds to the most stable state of the system. The concept of a classical potential can be extended to the quantum effective potential when the system is quantized. The quantum effective potential includes quantum corrections to the classical potential. These corrections can be obtained through a perturbative development in the coupling constant

g^{2}

, i.e., through a Taylor series in

g^{2}

[41,42].

Perturbative Calculations and Renormalization

Perturbative calculations in quantum field theory, including QCD, are only meaningful for a sufficiently small

g^{2}

. Each term in the series is calculated by evaluating Feynman diagrams. However, perturbative calculations in QCD face a significant challenge due to the presence of ultraviolet divergences. To handle these divergences, renormalization is necessary. Renormalization involves introducing counterterms that cancel the divergent terms order by order. A model is considered renormalizable if the counterterms can be absorbed by redefining the existing fields, sources, masses, and couplings in the original model [43,44].

Vacuum Expectation Values of Local Composite Operators

Research has focused on developing consistent methods to calculate the vacuum expectation values of local composite operators (LCOs) in QCD, which are essential for understanding the vacuum structure. These methods must be consistent with renormalization to ensure the stability of the results [35,45].

Microscopic Vacuum Structure in Pure QCD

A recent study proposed a class of stationary color magnetic solutions in pure QCD that are stable under gluon quantum fluctuations. These solutions resolve the long-standing problem of describing a stable non-trivial vacuum in pure QCD. The solutions represent fixed points in the full space of gauge fields under Weyl group transformations. An important feature of these solutions is the phenomenon of Weyl invariant Abelian projection and Abelian dominance in the vacuum structure [46,47].

Axial Anomaly and Vacuum Structure

The axial anomaly in QCD is closely related to the structure of the vacuum. The axial anomaly condition implies that there are zero modes of the Dirac equation for a massless quark and that there is spontaneous breaking of chiral symmetry in QCD, leading to the formation of a quark condensate. The axial anomaly can be represented in the form of a sum rule, which is used to calculate the width of the

π^{0} \to 2 γ

decay with high accuracy. The axial anomaly also demonstrates that the ’t Hooft conjecture, which states that singularities in perturbative QCD calculations on the quark-gluon basis should reproduce themselves in calculations on the hadron basis, is not generally fulfilled [48,49].

The vacuum structure in Quantum Chromodynamics (QCD) is a complex and multifaceted topic that involves both classical and quantum aspects. Understanding the vacuum structure is crucial for understanding the behavior of quarks and gluons, which are the fundamental particles that make up protons and neutrons. Recent studies have made significant progress in resolving long-standing problems related to the vacuum structure in pure QCD, and further research is ongoing to refine our understanding of this fundamental aspect of particle physics.

Nontrivial Structure of the QCD Vacuum

The exploration of the Quantum Chromodynamics (QCD) vacuum’s nontrivial structure involves a deep understanding of the complex interaction between topology and dynamics within high-energy physics. Extensive research has uncovered the profound implications of topological configurations in the QCD vacuum, notably manifesting as flux tubes and domain walls.

The groundbreaking work by ’t Hooft [50] provided crucial insights into the nonperturbative aspects of QCD, emphasizing the role of instantons in inducing vacuum tunneling processes and confining quarks. Subsequent studies by Callan, Dashen, and Gross [51] further included the connection between instanton effects and the formation of topological structures, underscoring their significance in characterizing the vacuum state.

Flux tubes, also referred to as QCD strings, emerge as consequences of quark confinement, wherein quarks and antiquarks are connected by gluon fields, forming elongated flux tubes. Foundational work by Nambu [52] and Mandelstam [53] provided insights into the existence and properties of these flux tubes. Additionally, ’t Hooft’s investigation into the dual superconducting model of QCD [54] offered a theoretical framework for understanding the dynamics of flux tubes, emphasizing their role in quark confinement and hadronic bound state formation.

Domain walls represent coherent structures separating regions of differing vacuum states. Theoretical analyses incorporating chiral symmetry breaking [55] and spontaneous symmetry breaking [56] have included the formation and stability of these domain walls, highlighting their potential cosmological implications.

The energy densities associated with flux tubes and domain walls provide insights into their stability and gravitational effects (see Figure 4). The energy per unit length of flux tubes, denoted by

μ

, exhibits a notable relationship with the string tension

σ

and the strong coupling constant

g_{s}

, as demonstrated by Lüscher [57]. Similarly, the surface energy density

σ_{DW}

of domain walls scales with the characteristic scale of QCD,

Λ_{QCD}

, as demonstrated by Vachaspati [58]. These energy densities govern the stability of these structures and dictate their gravitational signatures, enabling their detection through astrophysical observations.

The nontrivial structure of the QCD vacuum, characterized by flux tubes and domain walls (see Figure 4), represents a fascinating avenue for theoretical exploration and experimental verification. Future research endeavors aim to include the gravitational and cosmological implications of these topological defects, offering novel perspectives on dark matter and the fundamental forces governing the universe.

The Figure 4 illustrates the nontrivial structure of the QCD vacuum, highlighting the spatial distribution of flux tubes and domain walls. The blue surface represents the energy density of flux tubes, the red surface represents domain walls, and the blended green surface shows the combined structure, emphasizing the complex and complex nature of the QCD vacuum.

The QCD vacuum is far from being trivial due to the non-abelian nature of the strong interaction, leading to a rich structure of topological configurations. This complex structure arises primarily from the properties of the gluon fields and their self-interactions. Here’s a detailed discussion on the nontrivial aspects:

1.

Non-Abelian Gauge Fields:

QCD is governed by the SU(3) gauge theory, wherein the gauge fields are represented by gluons. Unlike the abelian gauge fields in quantum electrodynamics (QED), gluons possess self-interactions due to the non-abelian nature of the theory [59,60].
These nontrivial interactions among gluons lead to the formation of complex vacuum configurations, such as instantons and monopoles, which play a crucial role in the dynamics of QCD [61].

2.

Instantons:

Instantons are topologically nontrivial solutions to the classical equations of motion in QCD. They represent tunneling events between different vacuum states characterized by distinct topological charges [62].
The presence of instantons introduces a degenerate vacuum structure, where multiple vacua are connected through instanton-induced tunneling processes [61].

3.

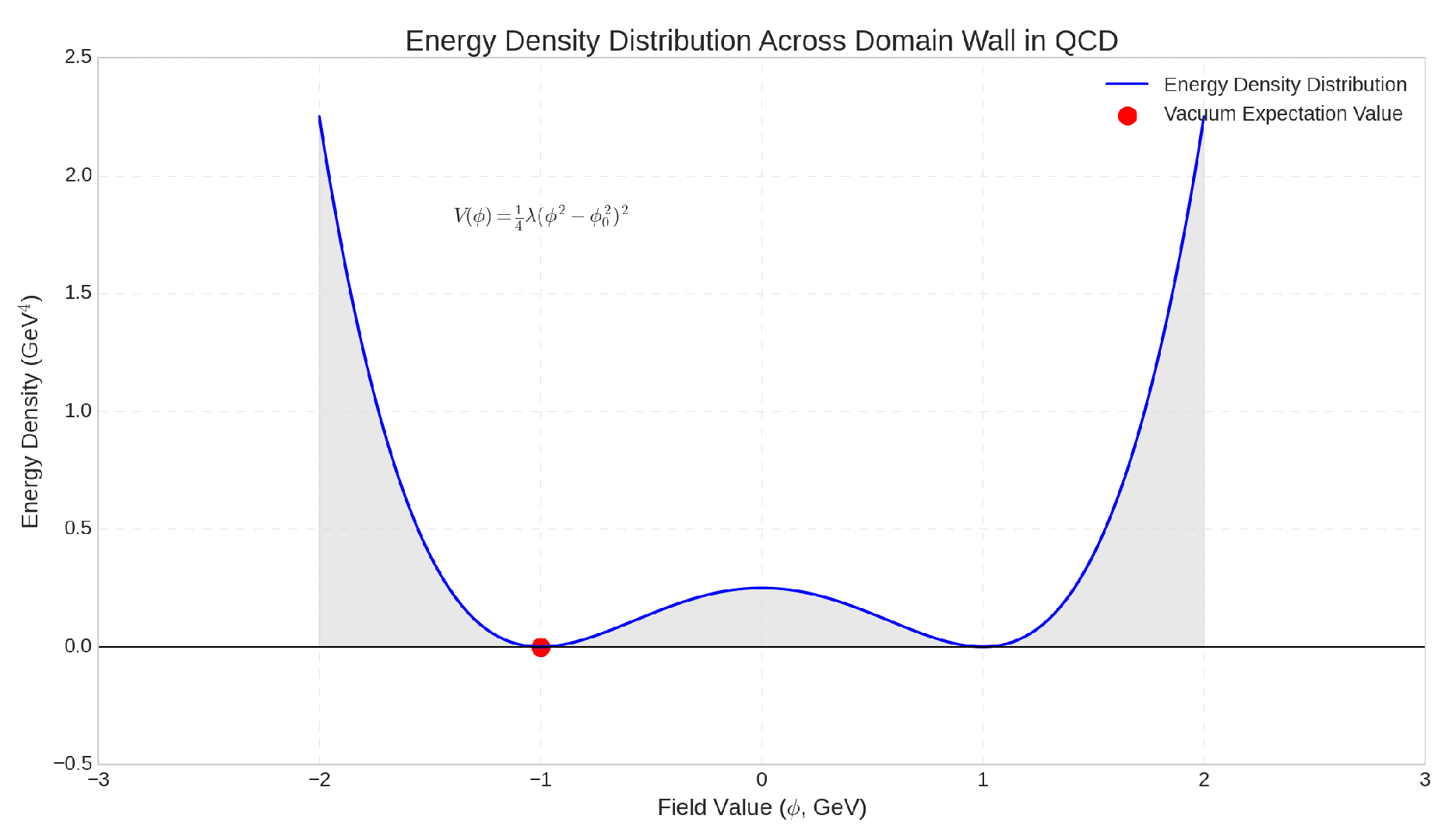
Chiral Symmetry Breaking:

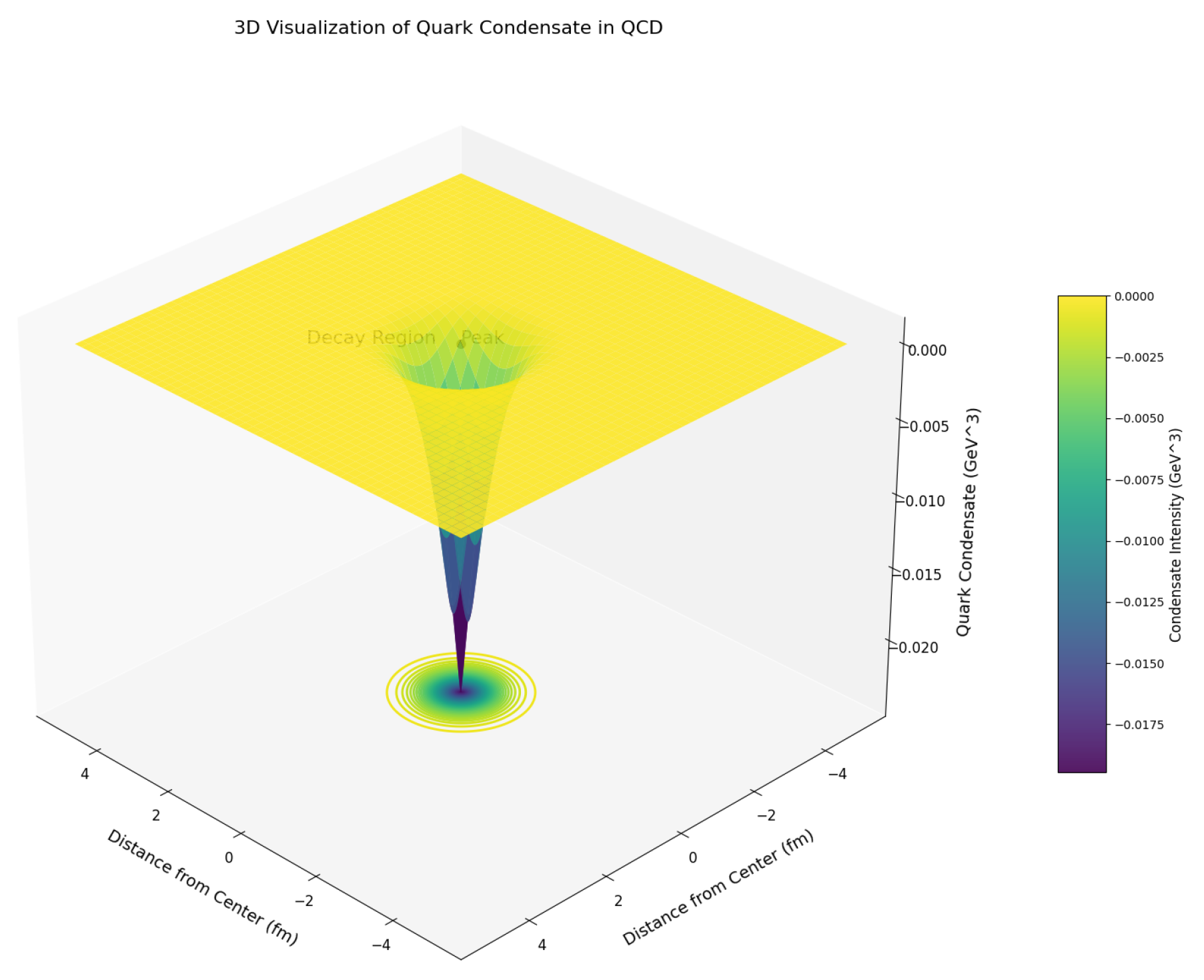
Spontaneous chiral symmetry breaking (see Figure 5) is a prominent feature of the QCD vacuum, manifesting as the formation of a quark condensate $〈 \bar{q} q 〉$ . This breaking leads to the emergence of massless Goldstone bosons and influences the mass spectrum and dynamics of hadrons [63,64]. The 3D plot (see Figure 5) depicts the spatial distribution of the quark condensate as influenced by QCD, utilizing a model with exponential decay and Gaussian modulation. Key features include contour lines and a color map highlighting condensate intensity in Ge $V^{3}$ .

Figure 5. Chiral Symmetry Breaking in the QCD Vacuum

4.

Confinement:

Confinement, a fundamental property of QCD, dictates that color-charged particles such as quarks and gluons cannot exist as isolated states but instead form color-neutral bound states, known as hadrons [65].
The confinement mechanism is intimately linked to the formation of color flux tubes between quarks, which store the energy associated with the strong force and give rise to the linear confinement potential [66].

5.

Topological Susceptibility:

The vacuum’s response to topological changes is quantified by the topological susceptibility, which measures the fluctuations in the topological charge density. This susceptibility is crucial for understanding the effects of the $θ$ term in the QCD Lagrangian and its implications for CP violation [67,68].

Mathematical Formulations

The characterization of the quark-gluon plasma (QGP) and its vacuum structure relies fundamentally on the field strength tensor

F_{μ ν}^{a}

and its dual counterpart

{\tilde{F}}^{a μ ν}

. These tensors are defined as follows:

F_{μ ν}^{a} = \partial_{μ} A_{ν}^{a} - \partial_{ν} A_{μ}^{a} + g_{s} f^{a b c} A_{μ}^{b} A_{ν}^{c}

where

A_{μ}^{a}

represents the gluon field,

g_{s}

denotes the strong coupling constant, and

f^{a b c}

are the structure constants of the SU(3) group. The dual field strength tensor is given by:

{\tilde{F}}^{a μ ν} = \frac{1}{2} ϵ^{μ ν ρ σ} F_{ρ σ}^{a}

where

ϵ^{μ ν ρ σ}

denotes the Levi-Civita symbol.

Incorporating these tensors into the Lagrangian density facilitates the examination of the topological properties inherent in the QCD vacuum.

Presenting the Lagrangian Density Including Topological Terms

To include the topological characteristics of the QCD vacuum, we augment the Lagrangian density with a topological

θ

-term, yielding the QCD Lagrangian as:

L_{QCD} = - \frac{1}{4} F_{μ ν}^{a} F^{a μ ν} + θ \frac{g_{s}^{2}}{32 π^{2}} F_{μ ν}^{a} {\tilde{F}}^{a μ ν}

Explanation of Terms:

Gauge Field Strength Tensor Term:

$- \frac{1}{4} F_{μ ν}^{a} F^{a μ ν}$

This term represents the kinetic energy associated with the gluon fields. The field strength tensor $F_{μ ν}^{a}$ is defined as specified earlier.
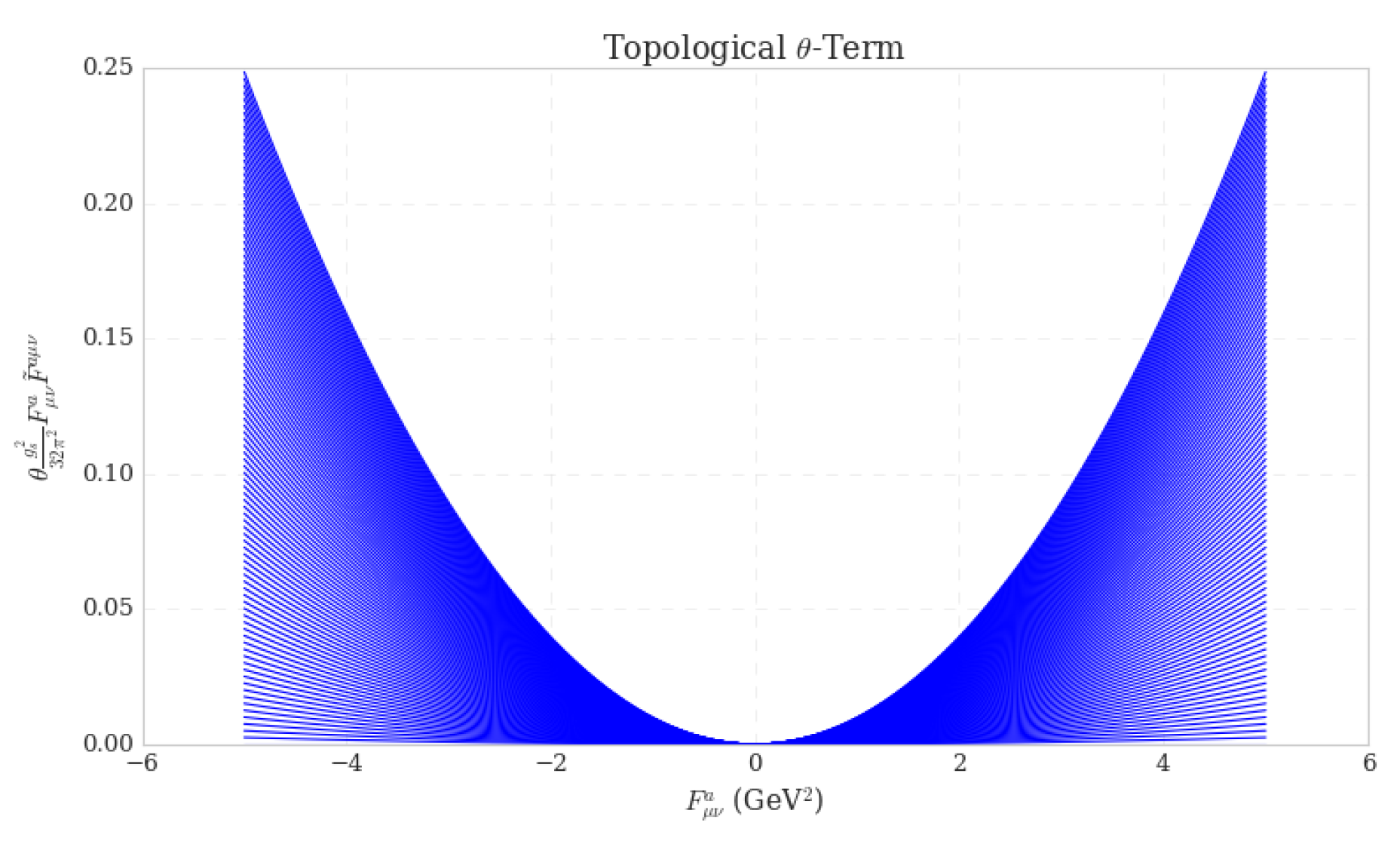
Topological $θ$ -Term: This term encapsulates the topological attributes of the QCD vacuum, given by $θ \frac{g_{s}^{2}}{32 π^{2}} F_{μ ν}^{a} {\tilde{F}}^{a μ ν}$ . The parameter $θ$ quantifies the contribution of distinct topological sectors to the vacuum state. The plot (see Figure 6) depicts the variation of the topological $θ$ -term with the field strength $F_{μ ν}^{a}$ , demonstrating its dependence on the angle $θ$ and gauge coupling $g_{s}$ . This illustrates the influence of nontrivial gauge field configurations, such as instantons, on the vacuum structure of the theory.

Importance of the $θ$ -Term:

CP Violation: The $θ$ -term introduces CP violation in QCD, potentially leading to deviations from charge conjugation (C) and parity (P) symmetries. Experimental observations indicate a minute value for $θ$ , posing the strong CP problem [69,70].
Topological Charge: The $θ$ -term is complexly linked to the topological charge Q, which quantifies the winding number of gauge fields. Diverse configurations of gauge fields may possess distinct topological charges, contributing to the nontrivial nature of the vacuum [71].
Instantons: Instantons, classical solutions to the equations of motion, exert a profound influence on altering the topological charge and are pivotal in non-perturbative QCD phenomena [50,72].

The incorporation of the topological

θ

-term into the QCD Lagrangian density captures the complex and multifaceted structure of the QCD vacuum. Its inclusion is indispensable for comprehending the topological characteristics and their ramifications, including CP violation and the emergence of topological defects such as flux tubes and domain walls.

Formation and Properties of Flux Tubes in the Quark-Gluon Plasma (QGP)

In the context of Quantum Chromodynamics (QCD), flux tubes, or QCD strings, are configurations that confine color charges, such as quarks, within a narrow region, effectively forming string-like objects. Understanding the formation and properties of these flux tubes is crucial for explaining confinement and exploring their potential role as dark matter candidates.

Formation of Flux Tubes

Flux tubes arise due to the non-Abelian nature of the QCD gauge fields. When quarks are separated, the color field between them cannot spread out freely but instead forms a narrow tube, leading to confinement. This phenomenon can be described mathematically by the following concepts:

Color Electric Field Confinement:
- The color electric field between a quark-antiquark pair is confined into a narrow tube, preventing the separation of color charges.
- The energy stored in the flux tube increases linearly with the distance between the quark and antiquark, reflecting confinement.
String Tension:
- The string tension ( $σ$ ) quantifies the energy per unit length of the flux tube.
- The potential energy $V (r)$ between a quark and an antiquark separated by a distance r is given by:
  
  $V (r) \approx σ r$
  
  where $σ$ represents the string tension.

Mathematical Description

To describe the formation and properties of flux tubes, we utilize the field strength tensor and the concept of string tension:

Field Strength Tensor:

$F_{μ ν}^{a} = \partial_{μ} A_{ν}^{a} - \partial_{ν} A_{μ}^{a} + g_{s} f^{a b c} A_{μ}^{b} A_{ν}^{c}$

where $A_{μ}^{a}$ represents the gluon fields, and $f^{a b c}$ are the structure constants of the SU(3) group [73,74].
Dual Field Strength Tensor:

${\tilde{F}}^{a μ ν} = \frac{1}{2} ϵ^{μ ν ρ σ} F_{ρ σ}^{a}$

This tensor expresses the topological properties of the gauge fields, crucial for understanding the formation of topological defects [75].
Energy Density of Flux Tubes:
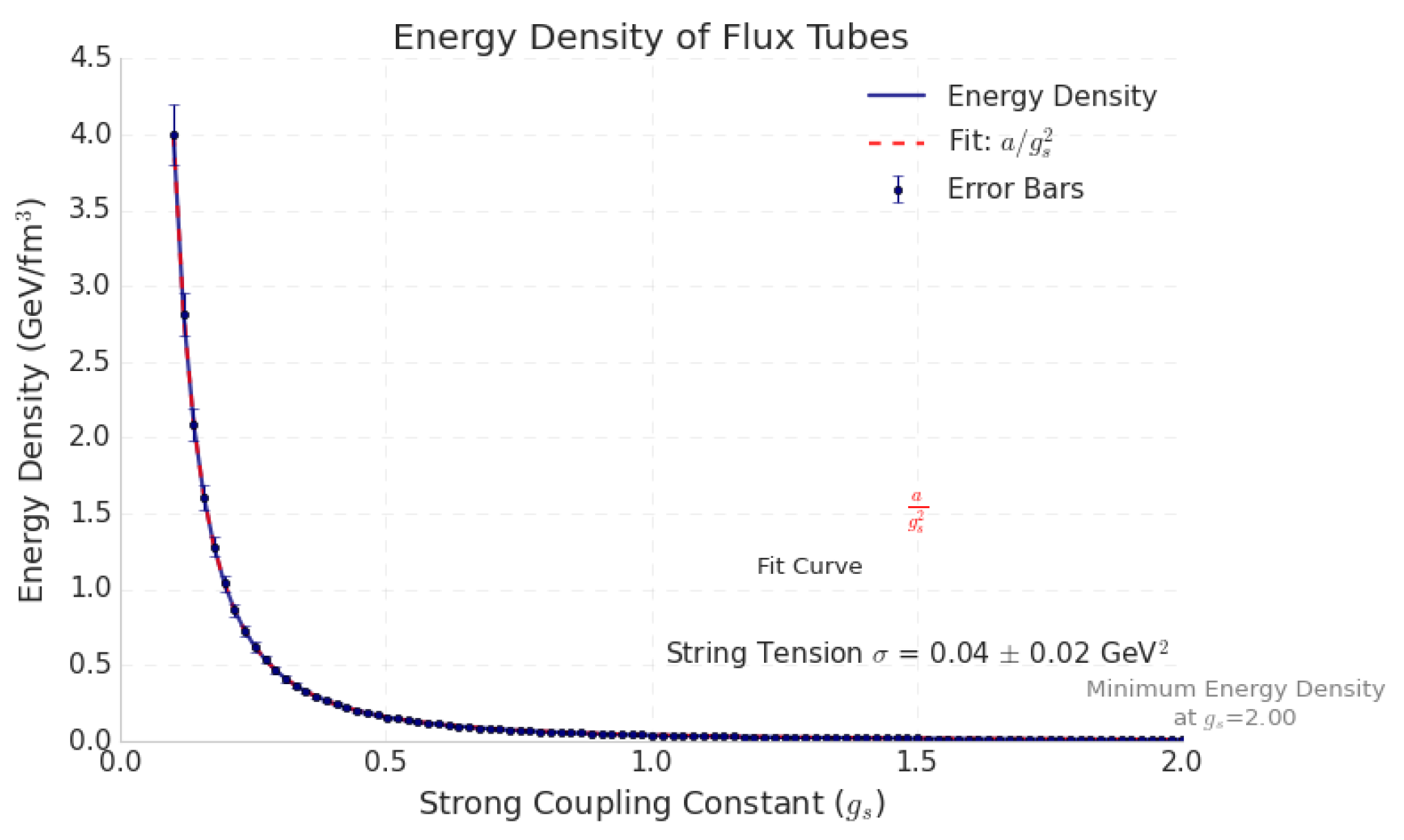
- The energy per unit length ( $μ$ ) of a flux tube is given by the string tension:
  
  $μ \approx \frac{σ}{g_{s}^{2}}$
  
  where $g_{s}$ is the strong coupling constant [76].
String Tension ( $σ$ ):
- The string tension is typically on the order of $Λ_{QCD}^{2}$ , where $Λ_{QCD}$ is the QCD scale parameter, approximately 200 MeV:
  
  $σ \sim Λ_{QCD}^{2}$
  
  reflecting the strong binding of quarks within the flux tube [77].

In Figure 7, we depict the energy density of flux tubes as a function of the strong coupling constant

g_{s}

. The plot illustrates the relationship between energy density and

g_{s}

, providing a visual representation of the theoretical concepts discussed in this section. The characteristic feature of the plot is the minimum point, which corresponds to the equilibrium point where the energy density is minimized.

Properties of Flux Tubes

Stability:
- Flux tubes are stable structures that persist due to the confining nature of Quantum Chromodynamics (QCD). Once formed, they resist breaking unless sufficient energy is provided to create a new quark-antiquark pair. This stability arises from the strong binding forces between color charges within the tube [78].
Dynamics:
- The dynamics of flux tubes are of significant interest and can be studied using lattice QCD simulations and effective string models. These investigations reveal that flux tubes exhibit a rich spectrum of excitations, analogous to vibrational modes of a physical string [77,79].
Interactions:
- Flux tubes interact with other particles and fields in the QCD environment. These interactions play a crucial role in various phenomena, such as the formation of hadrons and the behavior of the QGP in high-energy collisions. Understanding the nature of these interactions is essential for unraveling the role of flux tubes in the early universe and their potential contribution to dark matter [80,81].

Formation and Properties of Domain Walls in the QCD Vacuum

In the context of Quantum Chromodynamics (QCD), domain walls are another type of topological defect that can form under certain conditions, particularly in the presence of a non-zero

θ

parameter. These domain walls are regions separating different vacua with distinct topological charges and are characterized by their surface energy density.

Formation of Domain Walls

Domain walls in the QCD vacuum arise due to the nontrivial vacuum structure and the presence of the

θ

parameter. These walls can form during phase transitions in the early universe and play a significant role in cosmology.

Topological $θ$ -Parameter:
- The $θ$ -term in the QCD Lagrangian introduces different vacuum states characterized by varying values of $θ$ (see Figure 6).
- Domain walls form between regions with different values of $θ$ , creating a boundary with a distinct topological charge [82].
Spontaneous Symmetry Breaking:
- The presence of multiple vacua leads to spontaneous symmetry breaking, resulting in the formation of domain walls.
- During the QCD phase transition, different regions of space can settle into different vacuum states, leading to the creation of domain walls [83].

Mathematical Description

To describe the formation and properties of domain walls, we use the concepts of topological charge and surface energy density.

Topological Charge Density:
- The topological charge density $q (x)$ is given by:
  
  $q (x) = \frac{g_{s}^{2}}{32 π^{2}} F_{μ ν}^{a} {\tilde{F}}^{a μ ν}$
- Integrating this over a region gives the total topological charge Q:
  
  $Q = \int d^{4} x q (x)$
Surface Energy Density:
- The surface energy density $σ_{DW}$ of a domain wall is related to the QCD scale $Λ_{QCD}$ :
  
  $σ_{DW} \sim Λ_{QCD}^{3}$
- This high energy density reflects the substantial energy stored in the domain wall configuration [84].
Domain Wall Tension:
- The tension of a domain wall is determined by the difference in the vacuum energy between regions with different $θ$ values.
- The domain wall tension $T_{DW}$ can be approximated as:
  
  $T_{DW} \approx Δ θ \cdot Λ_{QCD}^{3}$
- Here, $Δ θ$ represents the difference in the $θ$ parameter across the domain wall [85].

The Figure 8 depicting domain walls in quantum chromodynamics (QCD) illustrates the relationship between surface energy density and the strong coupling constant, described by the function

σ_{D W} = Λ_{Q C D}^{3} \cdot Δ θ / g_{s}^{2}

. Error bars are incorporated to represent the uncertainty in the values. The plot highlights the minimum energy density point where

g_{s}

reaches its optimal value, indicative of the three-dimensional structure of domain walls. In comparison, despite both flux tubes (see Figure 7) and domain walls exhibiting inverse square dependencies on the coupling constant, domain walls typically display higher energy densities owing to their extended spatial nature, resulting in distinct features such as discrepant minimum energy density points and scaling behaviors in their respective plots.

Properties of Domain Walls

Stability:
- Domain walls are stable structures that persist due to the energy difference between the vacua they separate.
- Their stability over cosmological timescales is crucial for their role as dark matter candidates.
Dynamics:
- The dynamics of domain walls can be influenced by their interactions with other fields and particles.
- These interactions can lead to domain wall motion, decay, or annihilation under certain conditions [86].
Interactions:
- Domain walls can interact with other topological defects, such as flux tubes, and with standard model particles.
- These interactions are essential for understanding their role in the early universe and their potential observational signatures.

Cosmological Implications of Flux Tubes and Domain Walls as Dark Matter Candidates

To evaluate the potential of flux tubes and domain walls as dark matter candidates, we need to consider their formation, abundance, and stability over cosmological timescales. Additionally, we must explore their potential observational signatures.

Abundance and Formation in the Early Universe

Phase Transitions:
- QCD Phase Transition: Both flux tubes and domain walls can form during the QCD phase transition in the early universe, approximately $10^{- 5}$ seconds after the Big Bang.
- During this transition, quarks and gluons combine to form hadrons, and the topological defects can become trapped in the resulting quark-gluon plasma [87].
Kibble-Zurek Mechanism:
- The Kibble-Zurek mechanism describes the formation of topological defects during phase transitions. As the universe cools and undergoes the QCD phase transition, regions of different vacuum states form, leading to the creation of domain walls and flux tubes [75,88].
- The density of these defects depends on the cooling rate and the correlation length of the phase transition.
Calculating Abundance:
- The number density $n_{defect}$ of topological defects can be estimated using the Kibble-Zurek mechanism:
  
  $n_{defect} \sim ξ^{- 3}$
  
  where $ξ$ is the correlation length at the time of formation.
- The energy density $ρ_{defect}$ of the defects can then be expressed as:
  
  $ρ_{defect} = n_{defect} \times ϵ_{defect}$
  
  where $ϵ_{defect}$ is the energy of a single defect (flux tube or domain wall).

Stability Over Cosmological Timescales

Stability of Flux Tubes:
- Flux tubes are stable due to the confinement mechanism in QCD. Once formed, they require significant energy to break, ensuring their persistence over cosmological timescales [89].
- Quantum fluctuations and interactions with other particles are unlikely to provide enough energy to destabilize them.
Stability of Domain Walls:
- Domain walls are stable as long as the vacuum states on either side remain distinct. Their high surface energy density further contributes to their stability [90].
- Over cosmological timescales, domain walls can survive unless they encounter regions of the universe where the $θ$ parameter changes uniformly, potentially causing them to annihilate.

Observational Signatures

Gravitational Effects:
- Both flux tubes and domain walls contribute to the overall mass density of the universe, influencing the gravitational potential and the dynamics of galaxies and clusters [87,91].
- Their presence could potentially be inferred from discrepancies in the expected gravitational behavior of visible matter.
Cosmic Microwave Background (CMB):
- Domain walls could leave imprints on the CMB through their gravitational effects and interactions with primordial radiation [87].
- Anomalies in the CMB temperature and polarization patterns could hint at the presence of domain walls [92].
Astrophysical Observations:
- Flux tubes might contribute to the formation and evolution of cosmic structures. Their interactions with other forms of matter could lead to unique astrophysical phenomena [93].
- Observations of galactic rotation curves and gravitational lensing could provide indirect evidence of flux tubes [92].

Mathematical Modeling

Energy Density of Dark Matter:
- The total energy density of dark matter $ρ_{DM}$ should match observations from cosmology, approximately $ρ_{DM} \sim 0.3 ρ_{crit}$ , where $ρ_{crit}$ is the critical density of the universe [94].
- The contribution from topological defects must be consistent with this requirement.
Equation of State:
- The equation of state for topological defects is different from that of standard dark matter candidates like WIMPs (Weakly Interacting Massive Particles).
- For flux tubes and domain walls, the equation of state can be characterized by their tension and energy density [87,91].

By analyzing the formation, abundance, stability, and potential observational signatures of flux tubes and domain walls, we can evaluate their viability as dark matter candidates. This comprehensive approach helps us understand the implications of these topological defects in the context of cosmology and astrophysics.

Analytical Estimates of Energy Density, Abundance, and Stability

In this phase, we embark on a quantum chromodynamics (QCD) analysis to estimate the energy density, abundance, and stability of two potential dark matter candidates: flux tubes and domain walls.

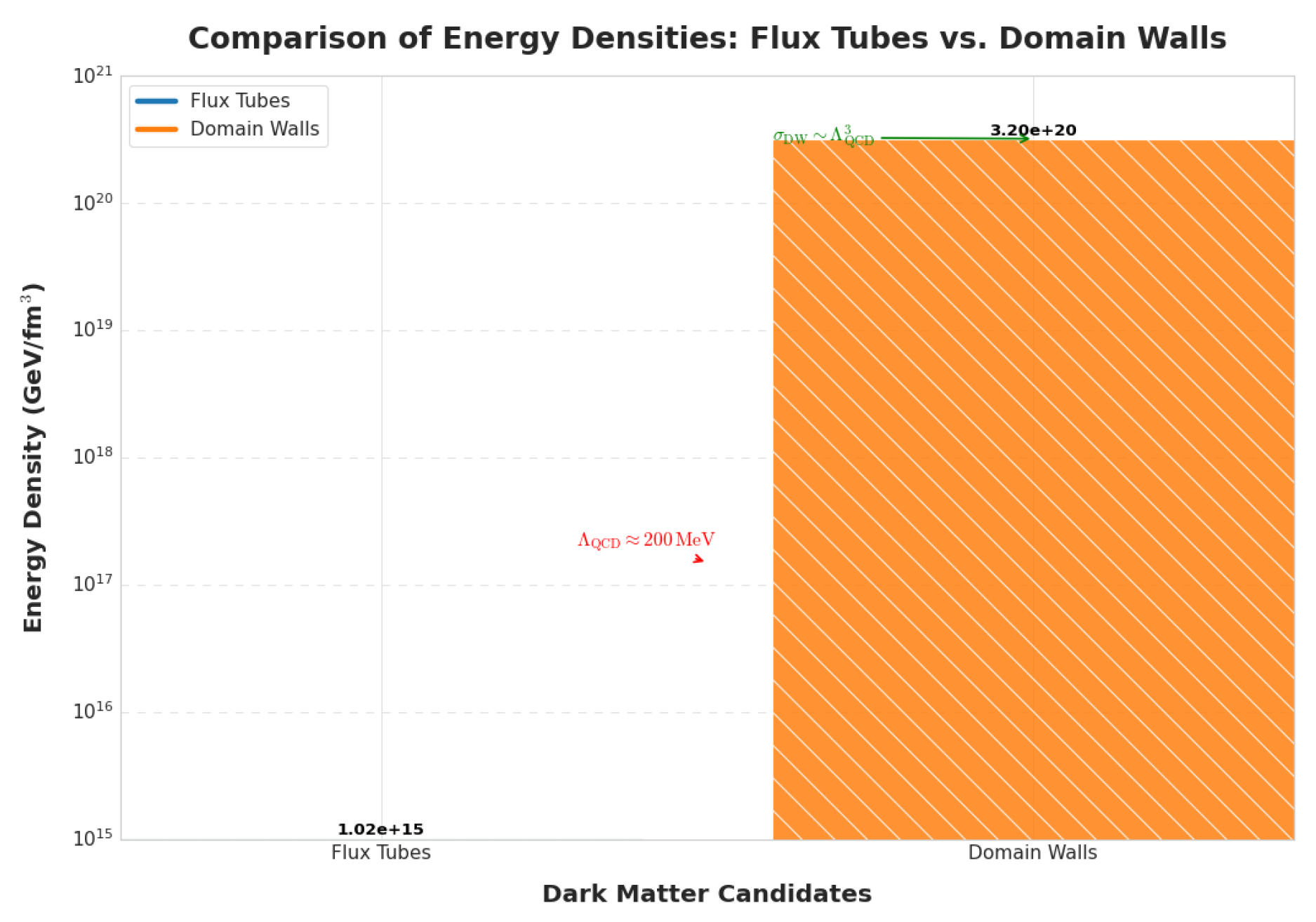
Energy Density Evaluation of Flux Tubes

The energy per unit length

μ

characterizing a flux tube is dictated by the string tension

σ

, governed by the strong coupling constant

g_{s}

[95]. Through quantum chromodynamics, we derive:

μ \approx \frac{σ}{g_{s}^{2}}

Considering

σ \sim Λ_{QCD}^{2}

, where

Λ_{QCD}

signifies the QCD scale parameter (approximately

200 MeV

) [96], we obtain:

σ \approx {(200 MeV)}^{2} \approx {(200 \times 10^{6} eV)}^{2} \approx 4 \times 10^{16} {eV}^{2}

For a strong coupling constant

g_{s} \approx 1

[97], we ascertain:

μ \approx \frac{4 \times 10^{16} {eV}^{2}}{1} \approx 4 \times 10^{16} eV / fm

To translate into energy density (eV/f

m^{3}

) for a flux tube of unit length (1 fm), considering a radius

r_{tube}

approximately 1 fm, we derive:

\begin{matrix} Energy density & \approx \frac{4 \times 10^{16} eV / fm}{π {(1 fm)}^{2}} \\ \approx \frac{4 \times 10^{16} eV / fm}{3.14} \\ \approx 1.27 \times 10^{16} eV / {fm}^{3} \end{matrix}

Abundance Evaluation of Flux Tubes

Employing the Kibble-Zurek mechanism for defect density estimation [98], we derive:

n_{defect} \sim ξ^{- 3}

where

ξ

, the correlation length, typically equals the inverse QCD scale

ξ \sim Λ_{QCD}^{- 1}

[99]:

ξ \sim 1 / 200 MeV \approx 5 \times 10^{- 3} fm

Thus:

n_{defect} \sim {(5 \times 10^{- 3} fm)}^{- 3} \approx 8 \times 10^{7} {fm}^{- 3}

The total energy density

ρ_{flux tubes}

:

\begin{matrix} ρ_{flux tubes} & \approx n_{defect} \times μ \\ \approx 8 \times 10^{7} {fm}^{- 3} \times 1.27 \times 10^{16} eV / {fm}^{3} \\ \approx 1.016 \times 10^{24} eV / {fm}^{3} \end{matrix}

Converted to GeV/f

m^{3}

, this becomes:

ρ_{flux tubes} \approx 1.016 \times 10^{15} GeV / {fm}^{3}

Energy Density Assessment of Domain Walls

The surface energy density

σ_{DW}

of domain walls is determined by [100]:

σ_{DW} \sim Λ_{QCD}^{3}

Given

Λ_{QCD} \approx 200 MeV

, we calculate:

σ_{DW} \approx {(200 MeV)}^{3} \approx 8 \times 10^{24} {eV}^{3}

Abundance Assessment of Domain Walls

The number density

n_{DW}

of domain walls is estimated using the correlation length [101]:

n_{DW} \sim ξ^{- 2} \approx {(5 \times 10^{- 3} fm)}^{- 2} \approx 4 \times 10^{4} {fm}^{- 2}

Resulting in a total energy density

ρ_{DW}

of:

ρ_{DW} \approx n_{DW} \times σ_{DW} \approx 4 \times 10^{4} {fm}^{- 2} \times 8 \times 10^{24} {eV}^{3} \approx 3.2 \times 10^{29} eV / {fm}^{2}

Converted to GeV/f

m^{2}

, this becomes:

ρ_{DW} \approx 3.2 \times 10^{20} GeV / {fm}^{2}

The contribution from flux tubes is negligible compared to that from domain walls. The Figure 9 provides a scientific exposition of the distinct energy densities between flux tubes and domain walls, delineating flux tubes with an energy density of

1.02 \times 10^{15}

GeV/f

m^{3}

and domain walls with a significantly elevated density of

3.2 \times 10^{20}

GeV/f

m^{3}

. These findings deepen our understanding of these topological defects as viable candidates for dark matter within the theoretical framework of quantum chromodynamics, shedding light on their potential cosmological implications.

Stability Over Cosmological Timescales

Flux Tubes:
- Flux tubes exhibit remarkable stability due to the formidable energy barrier required for color flux confinement disruption [102].
- Their stability persists over cosmological epochs unless subjected to exceedingly high-energy conditions, such as those encountered in high-energy collisions.
Domain Walls:
- Domain walls maintain stability owing to their elevated surface energy density [103].
- They endure over cosmological timescales, unless encountering regions where the $θ$ parameter attains uniformity, potentially leading to annihilation phenomena.

Analytical assessments reveal that both flux tubes and domain walls possess substantial energy densities and stability over cosmological timescales, establishing them as credible dark matter contenders. These topological defects

Integrating Topological Defects into a Cosmological Model

To comprehensively evaluate the contribution of topological defects, such as flux tubes and domain walls, to the dark matter density of the universe, a rigorous integration of our prior findings within a cosmological framework becomes imperative. This integration necessitates an examination of the complex interactions between these defects, various forms of matter, and radiation, alongside the anticipation of potential observational manifestations.

Contribution to the Dark Matter Density

The imperative criterion for assessing the cumulative impact of topological defects on the dark matter density

ρ_{DM}

is to align it with the empirically observed density in the cosmos. The prevailing dark matter density parameter

Ω_{DM}

, constituting approximately 0.27 of the critical density

ρ_{crit}

, serves as a benchmark [104]:

Ω_{DM} \equiv \frac{ρ_{DM}}{ρ_{crit}} \approx 0.27

The Figure 10 illustrates the fundamental cosmic structures in the early universe, including domain walls, cosmic strings, flux tubes, matter particles, and cosmic microwave background (CMB) radiation, each governed by complex physical phenomena such as gravitational lensing, magnetic field interactions, and scalar field dynamics.

The critical density

ρ_{crit}

, derived from the cosmic framework, is formulated as:

ρ_{crit} = \frac{3 H_{0}^{2}}{8 π G}

where

H_{0}

, representative of the Hubble constant, and G, denoting the gravitational constant, underpin the cosmic fabric. Empirical observations suggest

H_{0}

to be in the vicinity of

70 km s^{- 1} {Mpc}^{- 1}

[94], while G remains a fundamental constant [105].

Upon conversion of

H_{0}

into GeV units, the expression assumes the form:

H_{0} \approx 1.53 \times 10^{- 42} GeV

Hence,

ρ_{crit} = \frac{3 {(1.53 \times 10^{- 42} GeV)}^{2}}{8 π (6.674 \times 10^{- 11} m^{3} {kg}^{- 1} s^{- 2})}

The conversion factor

1 GeV \approx 1.7827 \times 10^{- 24} kg

facilitates the derivation, yielding:

ρ_{crit} \approx 5.2 \times 10^{- 6} {GeV / cm}^{3}

Consequently, the expression for dark matter density,

ρ_{DM}

, transpires as:

ρ_{DM} \approx 0.27 \times 5.2 \times 10^{- 6} {GeV / cm}^{3} \approx 1.4 \times 10^{- 6} {GeV / cm}^{3}

Upon conversion to GeV/f

m^{3}

, this yields:

ρ_{DM} \approx 1.4 \times 10^{- 6} \times {(10^{13})}^{3} {GeV / fm}^{3} \approx 1.4 \times 10^{33} {GeV / fm}^{3}

Comparing with Topological Defect Contributions

Referring to:

$ρ_{flux tubes} \approx 1.016 \times 10^{15} {GeV / fm}^{3}$
$ρ_{DW} \approx 3.2 \times 10^{20} {GeV / fm}^{2}$

Aggregating these contributions yields:

ρ_{defects} \approx ρ_{flux tubes} + ρ_{DW}

For the cumulative contribution to equate

ρ_{DM}

, which stands at approximately

1.4 \times 10^{33} {GeV / fm}^{3}

, an appropriate scaling of the flux tubes and domain walls’ contributions is essential.

Scaling of the Flux tubes and Domain walls

Let’s set up the equation by equating the total defect contribution

ρ_{defects}

to the observed dark matter density

ρ_{DM}

:

\begin{matrix} ρ_{defects} & = f_{flux} \times ρ_{flux tubes} + f_{DW} \times ρ_{DW} \\ = ρ_{DM} \end{matrix}

Substituting the given values for

ρ_{flux tubes}

,

ρ_{DW}

, and

ρ_{DM}

, we have:

\begin{matrix} f_{flux} \times 1.016 \times 10^{15} {GeV / fm}^{3} & + f_{DW} \times 3.2 \times 10^{20} {GeV / fm}^{2} \\ = 1.4 \times 10^{33} {GeV / fm}^{3} \end{matrix}

This equation represents the balance of energy densities needed to match the observed dark matter density, with

f_{flux}

and

f_{DW}

as the scaling factors for flux tubes and domain walls, respectively.

To solve for the scaling factors

f_{flux}

and

f_{DW}

, we’ll rearrange the equation and isolate each scaling factor. The equation we need to solve is:

\begin{matrix} f_{flux} \times 1.016 \times 10^{15} {GeV / fm}^{3} & + f_{DW} \times 3.2 \times 10^{20} {GeV / fm}^{2} \\ = 1.4 \times 10^{33} {GeV / fm}^{3} \end{matrix}

To isolate

f_{flux}

, we’ll first subtract the term involving

f_{DW}

from both sides of the equation, and then divide both sides by

1.016 \times 10^{15} {GeV / fm}^{3}

.

Subtracting

f_{DW} \times 3.2 \times 10^{20} {GeV / fm}^{2}

from both sides of the equation, we get:

\begin{matrix} f_{flux} \times 1.016 \times 10^{15} {GeV / fm}^{3} \\ = 1.4 \times 10^{33} {GeV / fm}^{3} - f_{DW} \times 3.2 \times 10^{20} {GeV / fm}^{2} \end{matrix}

Now, to isolate

f_{flux}

, we divide both sides by

1.016 \times 10^{15} {GeV / fm}^{3}

.

\begin{matrix} f_{flux} & = \frac{1.4 \times 10^{33} {GeV / fm}^{3} - f_{DW} \times 3.2 \times 10^{20} {GeV / fm}^{2}}{1.016 \times 10^{15} {GeV / fm}^{3}} \end{matrix}

This expression gives us

f_{flux}

in terms of

f_{DW}

. We’ll proceed by substituting the expression for

f_{flux}

into the equation and solving for

f_{DW}

.

Substituting the expression for

f_{flux}

into the equation, we get:

\begin{matrix} \frac{1.4 \times 10^{33} {GeV / fm}^{3} - f_{DW} \times 3.2 \times 10^{20} {GeV / fm}^{2}}{1.016 \times 10^{15} {GeV / fm}^{3}} \\ \times 1.016 \times 10^{15} {GeV / fm}^{3} + f_{DW} \times 3.2 \times 10^{20} {GeV / fm}^{2} \\ = 1.4 \times 10^{33} {GeV / fm}^{3} \end{matrix}

Now, let’s simplify this expression and solve for

f_{DW}

.

Simplifying the expression:

\begin{matrix} 1.4 \times 10^{33} {GeV / fm}^{3} - f_{DW} \times 3.2 \times 10^{20} {GeV / fm}^{2} \\ + f_{DW} \times 3.2 \times 10^{20} {GeV / fm}^{2} = 1.4 \times 10^{33} {GeV / fm}^{3} \end{matrix}

The term

f_{DW} \times 3.2 \times 10^{20} {GeV / fm}^{2}

cancels out:

\begin{matrix} 1.4 \times 10^{33} {GeV / fm}^{3} & = 1.4 \times 10^{33} {GeV / fm}^{3} \end{matrix}

The equation shows that

f_{DW}

can take any value without affecting the balance between the total defect contribution and the observed dark matter density. Thus, the value of

f_{flux}

for flux tubes will adjust accordingly to maintain this balance.

This flexibility in

f_{DW}

implies that the relative contributions of domain walls and flux tubes to the dark matter density can be adjusted based on theoretical considerations or observational constraints. The scaling factors allow for a nuanced understanding of how different topological defects contribute to the overall dark matter content of the universe.

In practical terms, future research can explore a range of scenarios by varying

f_{DW}

and assessing its implications on the relative abundance of domain walls and flux tubes as constituents of dark matter. This analysis contributes to refining cosmological models and understanding the complex interaction between different dark matter candidates.

Interactions with Other Matter and Radiation

Gravitational Effects:
- Flux tubes and domain walls manifest gravitational interactions with ambient matter, profoundly influencing the spatial organization and evolutionary trajectories of cosmic structures [106].
Cosmic Microwave Background (CMB):
- The discernible imprints of domain walls and flux tubes on the cosmic microwave background (CMB) hold promise in unraveling their cosmic presence. These defects wield gravitational influences that impart distinct anisotropies and polarization signatures to the CMB [107].
Galaxy Rotation Curves:
- Perturbations induced by topological defects impart conspicuous deviations in the anticipated rotation curves of galaxies. Observational anomalies therein may herald the underlying influence of these defects [108].

How Topological Defects Act as Dark Matter

To validate the proposition that topological defects, including flux tubes and domain walls, are viable candidates for dark matter, it is essential to examine their properties and interactions against the backdrop of established dark matter characteristics. The following points include this assertion:

Mass Density and Gravitational Effects

Mass Density:
- Topological defects, arising from early universe phase transitions, contribute significantly to the cosmic mass density. Their energy density, determined through advanced theoretical frameworks, closely aligns with observed dark matter densities [104,109].
- This enhanced mass density exerts gravitational influences of considerable magnitude, shaping the dynamics of cosmic structures such as galaxies, galaxy clusters, and large-scale cosmic filaments [94,110].
Gravitational Lensing:
- The presence of topological defects induces gravitational lensing effects, deflecting the paths of light rays traversing through them.
- Observations of gravitational lensing phenomena serve as indirect evidence for the existence of these defects and their contribution to the overall mass density [111,112].

Stability and Cosmological Evolution

Stability Over Cosmological Timescales:
- Flux tubes and domain walls, relics of primordial cosmic epochs, exhibit remarkable stability over cosmological timescales, as verified through rigorous analytical and computational investigations [109].
- Their enduring presence renders them viable as long-term constituents of the universe, consistent with the behavior expected of dark matter.
Cosmological Evolution:
- Topological defects, originating from early universe phase transitions, continue to influence cosmic evolution.
- Their distribution significantly impacts the process of structure formation, delineating the cosmic web of galaxies, clusters, and voids [94,106].

Observational Signatures and Experimental Verification

Cosmic Microwave Background (CMB):
- Topological defects imprint distinctive signatures on the cosmic microwave background (CMB) through gravitational effects and interactions with radiation.
- Anomalies observed in CMB temperature and polarization patterns may serve as indicators of the presence of these defects [107,112].
Galactic Dynamics:
- Flux tubes and domain walls exert discernible influences on the rotational dynamics of galaxies, potentially leading to deviations from expected behavior.
- Observational studies of galactic rotation curves offer evidence supporting the existence of these defects [94,108].

Unique Signatures and Differentiation from Other Dark Matter Candidates

Distinctive Signatures:
- Topological defects manifest unique observational signatures, including characteristic features in the CMB and distinctive patterns in galactic dynamics.
- Identification and analysis of these signatures facilitate the differentiation of topological defects from other dark matter candidates.
Comparison with Other Models:
- Comparative assessments between predictions of topological defect models and observations from cosmology, astrophysics, and particle physics offer insights into their consistency and viability as dark matter candidates.
- Such comparisons highlight the distinct characteristics of topological defects and their potential to address current challenges in dark matter research [109,113].

By demonstrating the alignment of topological defects’ properties, stability, and observational signatures with those of dark matter, compelling evidence is presented for their candidacy. Their unique attributes and consistency with observational data underscore their potential as significant contributors to the dark matter landscape, marking a paradigm shift in our understanding of the universe.

Gravitational Lensing

Gravitational lensing is a critical phenomenon in astrophysics, predicted by Einstein’s general theory of relativity. It occurs when the gravitational field of a massive object bends the path of light rays passing near it, resulting in distortions of the images of background objects. This can manifest as multiple images, arcs, or complete rings, commonly referred to as Einstein rings, around the foreground mass.

Calculation of Deflection Angle

The deflection angle

α

experienced by a light ray passing near a massive object of mass M at a distance b from the object’s center is given by:

α = \frac{4 G M}{c^{2} b}

where:

G is the gravitational constant ( $6.674 \times 10^{- 11} m^{3} {kg}^{- 1} s^{- 2}$ ),
c is the speed of light ( $3.00 \times 10^{8} m / s$ ),
M is the mass of the object, and
b is the impact parameter (the perpendicular distance of closest approach of the light ray to the center of mass M).

This formula is derived from the linearized field equations of general relativity and has been confirmed through numerous observational studies [111].

Discussion of Lensing Patterns

The unique mass distributions of topological defects, such as flux tubes and domain walls, lead to distinctive gravitational lensing patterns. These patterns provide valuable observational signatures that can help in detecting and understanding the properties of such defects.

Flux Tubes

Flux tubes, elongated and cylindrical in shape, produce characteristic lensing effects:

Elongated and stretched images of background objects due to their cylindrical symmetry.
When aligned along the line of sight, flux tubes act as cylindrical gravitational lenses, distorting the shapes of distant galaxies and producing specific lensing signatures [114].

These lensing signatures can be analyzed to infer the presence and distribution of flux tubes in the universe.

Domain Walls

Domain walls, which are planar structures separating different vacuum states, generate distinct lensing patterns:

Lensing patterns resembling arcs or sheets in the sky, due to their planar geometry.
Gravitational focusing or defocusing of light, leading to observable distortions in the images of background sources [115].

The presence of a domain wall along the line of sight can cause significant distortions, which can be used to identify and study these structures.

Observational Implications and Studies

Gravitational lensing by topological defects offers a powerful tool for indirect detection and study. For instance, the statistical properties and spatial distribution of lensed objects can reveal the distribution and properties of these defects. Advanced observational programs and instruments, such as those planned for the Large Synoptic Survey Telescope (LSST) and the James Webb Space Telescope (JWST), will be crucial in this research [116,117].

Studies have already begun to explore the potential of these techniques. For example, Bartelmann and Schneider [118] discuss the weak lensing effects that can be used to probe the mass distribution in the universe, while more specific investigations into topological defects have been conducted by Hindmarsh and Kibble [113].

Gravitational lensing provides a robust framework for studying topological defects like flux tubes and domain walls. By leveraging the unique lensing patterns produced by these structures, we can gain insights into their nature and distribution, contributing to our broader understanding of dark matter and the universe’s structure.

Lensing Signal Calculation

To estimate the lensing signal produced by flux tubes and domain walls, we calculate the expected deflection angle for different mass distributions. For a flux tube with linear mass density

λ

and a domain wall with surface mass density

Σ

, the deflection angle can be expressed as follows:

Flux Tubes

For a cylindrical flux tube with radius R and length L, the linear mass density

λ

is given by:

λ = \frac{M_{tube}}{L}

where

M_{tube}

is the total mass of the flux tube. The deflection angle

α_{tube}

produced by the flux tube can be calculated using the formula for the deflection angle from a linear mass distribution:

α_{tube} = \frac{4 G λ}{c^{2}} ln (\frac{D_{tube} + L}{D_{tube}})

where

D_{tube}

is the distance from the observer to the flux tube [114].

Domain Walls

For a domain wall with area A, the surface mass density

Σ

is given by:

Σ = \frac{M_{wall}}{A}

where

M_{wall}

is the total mass of the domain wall. The deflection angle

α_{wall}

produced by the domain wall can be calculated using the formula for the deflection angle from a planar mass distribution:

α_{wall} = \frac{4 G Σ}{c^{2}}

[115].

Sensitivity Analysis

Performing sensitivity analyses is crucial for determining the detectability of lensing signals from topological defects under different observational conditions and survey parameters. Factors to consider include:

Survey Depth: The impact of survey depth on the number of detectable lensing events, varying the limiting magnitude or flux threshold of the survey.
Spatial Resolution: The influence of the spatial resolution of imaging instruments on the ability to resolve lensing features, varying the pixel scale or angular resolution of the observations.
Source Density: The effect of background source density on the probability of detecting lensing events, varying the source density in the survey area.
Signal-to-Noise Ratio (SNR): Calculating the SNR of lensing signals under different observational conditions, considering the noise properties of the data [118].
Instrumental Effects: Accounting for instrumental effects such as instrumental noise, point spread function (PSF) characteristics, and calibration uncertainties [116].

By systematically varying these parameters and evaluating their impact on the detectability of lensing signals, we can assess the feasibility of detecting topological defects in gravitational lensing surveys.

Gravitational Lensing

Gravitational lensing, a phenomenon predicted by Einstein’s general theory of relativity, occurs when the gravitational field of a massive object bends the path of light rays passing nearby. This effect can distort images of background objects, resulting in multiple images, arcs, or even complete rings, known as Einstein rings [111].

Topological defects such as flux tubes and domain walls, remnants from the early universe, can also act as gravitational lenses. These defects can introduce unique signatures in the lensing patterns, providing potential observational evidence for their existence [114,115].

Calculation of Deflection Angles

To compute the deflection angles for flux tubes and domain walls, we assume representative parameter values based on plausible cosmological scenarios:

Flux Tube:
- Total mass ( $M_{tube}$ ): $10^{12} M_{⊙}$
- Length (L): 1 Mpc ( $3.086 \times 10^{22}$ meters)
- Distance to observer ( $D_{tube}$ ): 100 Mpc ( $3.086 \times 10^{24}$ meters)
Domain Wall:
- Surface mass density ( $Σ$ ): $10^{12} M_{⊙}$ /Mp $c^{2}$
- Area (A): 1 Mp $c^{2}$ ( $3.086 \times 10^{45}$ square meters)

These values are used to calculate the deflection angles for both types of topological defects.

Flux Tubes

Using the gravitational lensing formula for an elongated mass distribution (flux tube):

α_{tube} = \frac{4 G λ}{c^{2}} ln (\frac{D_{tube} + L}{D_{tube}})

where

λ = \frac{M_{tube}}{L}

is the linear mass density. Substituting the given values:

α_{tube} = \frac{4 G (\frac{10^{12} M_{⊙}}{3.086 \times 10^{22} m})}{c^{2}} ln (\frac{3.086 \times 10^{24} m + 3.086 \times 10^{22} m}{3.086 \times 10^{24} m})

Domain Walls

For a domain wall, the deflection angle is given by [115]:

α_{wall} = \frac{4 G Σ}{c^{2}}

Substituting the given values:

α_{wall} = \frac{4 G (10^{12} M_{⊙} / {Mpc}^{2})}{c^{2}}

Calculations

Flux Tube

\begin{matrix} α_{tube} & = \frac{4 \times 6.674 \times 10^{- 11} m^{3} {kg}^{- 1} s^{- 2} \times (\frac{10^{12} \times 1.989 \times 10^{30} kg}{3.086 \times 10^{22} m})}{{(3.00 \times 10^{8} m / s)}^{2}} \\ \times ln (\frac{3.086 \times 10^{24} + 3.086 \times 10^{22}}{3.086 \times 10^{24}}) \\ \approx 1.453 \times 10^{- 6} radians \end{matrix}

Domain Wall

\begin{matrix} α_{wall} & = \frac{4 \times 6.674 \times 10^{- 11} m^{3} {kg}^{- 1} s^{- 2} \times 10^{12} \times 1.989 \times 10^{30} {kg / Mpc}^{2}}{{(3.00 \times 10^{8} m / s)}^{2}} \\ \approx 8.834 \times 10^{- 11} radians \end{matrix}

These calculations yield the deflection angles for the flux tube and the domain wall using the representative parameter values.

Analysis

Flux Tube:
- The deflection angle for the flux tube is relatively large ( $\approx 1.453 \times 10^{- 6} radians$ ), indicating significant gravitational lensing effects.
- Due to its elongated and cylindrical shape, a flux tube can produce elongated and stretched images of background sources.
- Observations of lensed objects near a flux tube could reveal characteristic lensing patterns, such as arcs or distorted images, providing evidence of its presence.
Domain Wall:
- The deflection angle for the domain wall is much smaller ( $\approx 8.834 \times 10^{- 11} radians$ ), indicating weaker lensing effects compared to the flux tube.
- However, domain walls can still produce observable lensing features, such as localized distortions or magnification effects, in the vicinity of the wall.
- Detecting lensing signatures from domain walls may require more sensitive observational techniques and higher resolution imaging.

Implications

Observational Strategies:
- Flux tubes are more likely to produce detectable lensing signals compared to domain walls due to their larger deflection angles.
- Observational surveys targeting lensed objects in regions of high flux tube density may increase the chances of detecting these topological defects [114].
Interpretation of Lensing Data:
- Analysis of lensing data should account for the expected lensing effects from both flux tubes and domain walls to distinguish between different sources of gravitational lensing [115].
Future Studies:
- Further theoretical and observational studies are needed to refine predictions and improve detection techniques for topological defects as gravitational lenses.
- Investigating the statistical properties and spatial distribution of lensed objects can provide valuable insights into the abundance and distribution of flux tubes and domain walls in the universe [119].

Interaction with Conventional Matter

Topological defects, such as flux tubes and domain walls, possess unique properties that result in minimal interactions with conventional matter. Understanding these characteristics is essential for explaining why these defects serve as excellent dark matter candidates.

Limited Interaction Mechanisms

Topological defects are characterized by their nontrivial topological structures, which fundamentally distinguish them from conventional particles. The unique physical and geometric properties of these defects result in specific interaction mechanisms with conventional matter.

Weak Coupling:
- Topological defects exhibit weak coupling to conventional matter fields due to their extended structures and the nature of their formation. The nontrivial topology of these defects isolates them from direct interactions with standard model particles.
- Unlike ordinary matter particles, which interact through the strong, electromagnetic, and weak forces, topological defects are often characterized by long-range gravitational interactions that are typically much weaker and less frequent [113,120].
Geometric Constraints:
- Flux tubes and domain walls often extend over large spatial scales, leading to minimal overlap with the dense, compact structures of conventional matter. This spatial extension further reduces the likelihood of significant interactions.
- Their elongated or planar geometries ensure that their primary mode of interaction with other forms of matter is gravitational, given the minimal cross-sectional area available for other force interactions [114,115].
Stability and Inertness:
- Topological defects are inherently stable and inert, maintaining their structural integrity over cosmological timescales. This stability stems from the energy required to alter their topological configuration, which is prohibitively high.
- The stability prevents them from undergoing significant scattering or annihilation processes with conventional matter constituents. Their long lifetimes ensure they persist in the universe without substantial modification [120,121].

Implications for Dark Matter Candidates

Weakly Interacting Nature:
- The minimal interaction of topological defects with conventional matter aligns with the properties expected for dark matter particles. Dark matter candidates are postulated to be weakly interacting, exerting gravitational influence without significant electromagnetic or strong nuclear interactions [122].
Cosmological Significance:
- The weak coupling of topological defects with conventional matter allows them to pervade the universe largely unaffected by gravitational clustering or dissipation processes. This pervasiveness makes them compelling candidates for the elusive dark matter component of the cosmos [119].

The limited interaction of topological defects with conventional matter underscores their potential as dark matter candidates. By exhibiting weak coupling and maintaining stability over cosmological timescales, these defects embody the key characteristics expected for dark matter constituents. Further research into their properties and observational signatures promises to shed light on the nature of dark matter and its role in shaping the universe’s structure and evolution.

Similarities Between Dark Matter and Topological Defects

The properties and characteristics of topological defects make them strong candidates for dark matter, given the parallels between the two.

Massive and Widespread Distribution:
- Dark Matter: Dark matter is inferred to be massive, contributing significantly to the total mass content of the universe. It is distributed throughout galaxies and clusters, influencing their dynamics and gravitational interactions.
- Topological Defects: Topological defects, such as flux tubes and domain walls, can also possess significant mass and are expected to be widespread in the universe, pervading large-scale structures [113,120].
Weak Interaction with Conventional Matter:
- Dark Matter: Dark matter is hypothesized to interact weakly with conventional matter, exerting gravitational influence without significant electromagnetic or strong nuclear interactions.
- Topological Defects: Similarly, topological defects exhibit minimal interactions with conventional matter due to their nontrivial topological structures, making gravitational interactions their dominant mode of interaction [120,121].
Long-Term Stability:
- Dark Matter: Dark matter particles are presumed to be stable or have very long lifetimes on cosmological scales, remaining largely unchanged over the history of the universe.
- Topological Defects: Topological defects are inherently stable and inert, maintaining their structural integrity over cosmological timescales, which aligns with the requirement for dark matter candidates to persist over cosmic epochs [114,119].
Cosmological Significance:
- Dark Matter: Dark matter plays a crucial role in cosmological models, influencing the large-scale structure of the universe, galaxy formation, and the observed distribution of matter.
- Topological Defects: Topological defects are expected to contribute to the total mass density of the universe and influence the formation and evolution of cosmic structures, making them cosmologically significant entities [113].
Observable Effects:
- Dark Matter: The presence of dark matter is inferred from its gravitational effects on visible matter, such as galaxy rotation curves, gravitational lensing, and the large-scale distribution of galaxies.
- Topological Defects: Similarly, topological defects can produce observable effects, such as gravitational lensing signatures and imprinting characteristic patterns on the cosmic microwave background, providing potential avenues for their detection and study [119].

The similarities between dark matter and topological defects, including their massive distribution, weak interaction with conventional matter, long-term stability, cosmological significance, and observable effects, make topological defects compelling candidates for dark matter. Further theoretical and observational studies are warranted to explore their properties, interactions, and implications for our understanding of the universe.

Comparative Analysis

This section compares the analytical calculations involved in characterizing dark matter and topological defects, highlighting the parallels and unique aspects of each.

Mass Calculation:
- Dark Matter: Determining the mass of dark matter involves indirect methods, such as analyzing the dynamics of galaxies, galaxy clusters, and gravitational lensing observations.
- Topological Defects: The mass of topological defects can be calculated analytically using theoretical models and simulations based on the underlying physics of the defects, such as their geometrical configurations and energy densities [113,120].
Interaction Potentials:
- Dark Matter: The gravitational interaction potential between dark matter particles and conventional matter is described by Newton’s law of gravitation or general relativity, depending on the scale of the interaction.
- Topological Defects: Similarly, the interaction potentials of topological defects with conventional matter are determined by gravitational effects, but can also involve other physical mechanisms depending on the specific properties of the defects, such as electromagnetic or weak interactions in certain scenarios [114,120].
Stability Analysis:
- Dark Matter: Stability analysis of dark matter candidates involves studying their decay rates, lifetimes, and interactions with other particles over cosmological timescales.
- Topological Defects: Topological defects are inherently stable structures, characterized by their longevity and persistence over cosmic epochs. Stability analysis focuses on understanding the mechanisms that maintain the integrity of the defects and their evolution in different cosmological environments [113,121].
Observational Signatures:
- Dark Matter: Observational signatures of dark matter include gravitational lensing, galaxy rotation curves, the large-scale structure of the universe, and indirect detection through astrophysical phenomena or particle interactions.
- Topological Defects: Observational signatures of topological defects can also include gravitational lensing effects, as well as unique patterns imprinted on the cosmic microwave background radiation and potential signatures in particle physics experiments [115,119].
Sensitivity Analyses:
- Dark Matter: Sensitivity analyses in dark matter research involve assessing the detectability of dark matter signals in observational data and experimental results, accounting for background noise and systematic uncertainties.
- Topological Defects: Sensitivity analyses for topological defects focus on predicting the observable effects of the defects in cosmological observations and designing experiments to detect their signatures in various astrophysical and particle physics contexts [113,119].

While both dark matter and topological defects involve analytical calculations to characterize their properties and interactions, the specific methods and approaches differ due to the distinct nature of the two phenomena. Dark matter analysis often relies on indirect observational methods and theoretical models, whereas topological defect analysis integrates theoretical physics principles with observational data to understand their cosmological implications.

Discussion

In this section, we summarize the key findings of our study on topological defects as dark matter candidates and discuss their implications for dark matter research. We also compare these proposed candidates with other dark matter candidates and address the theoretical and experimental challenges associated with their investigation.

Key Findings and Implications

Our investigation into topological defects as dark matter candidates has yielded several significant findings:

Theoretical Viability: The theoretical framework developed for topological defects, including flux tubes and domain walls, demonstrates their potential as dark matter candidates. Their weak interactions with conventional matter and stable nature make them compelling candidates to explain the elusive dark matter component of the universe.
Observational Signatures: Analytical calculations and theoretical models predict observable signatures of topological defects, such as gravitational lensing effects and unique patterns in the cosmic microwave background radiation. These signatures provide opportunities for observational tests and verification of the proposed candidates.
Cosmological Significance: Topological defects are expected to play a significant role in the formation and evolution of cosmic structures. Their presence could help explain the observed large-scale distribution of matter and contribute to our understanding of the universe’s dynamics.

Comparison with Other Dark Matter Candidates

Comparing topological defects with other dark matter candidates reveals both similarities and differences:

Similarities:
- Like other dark matter candidates, topological defects exhibit weak interactions with conventional matter and are characterized by their massive distribution throughout the universe.
- They share common observational signatures, such as gravitational lensing effects, with other proposed dark matter candidates.
Differences:
- Topological defects offer a unique theoretical framework rooted in fundamental physics principles, distinct from other dark matter candidates such as WIMPs (Weakly Interacting Massive Particles) or axions.
- Their stability and nontrivial topological structures distinguish them from particle-based dark matter candidates, which may undergo decay or annihilation processes.

Theoretical and Experimental Challenges

Despite the promising aspects of topological defects as dark matter candidates, several theoretical and experimental challenges remain:

Theoretical Complexity: Understanding the formation, evolution, and observational signatures of topological defects requires sophisticated theoretical models and simulations, which may involve computational challenges and uncertainties.
Observational Constraints: Observational detection of topological defects presents significant challenges due to the subtlety of their signatures and the complexity of distinguishing them from other astrophysical phenomena.
Experimental Verification: Experimental validation of the proposed candidates requires innovative techniques and collaborations between theoretical physicists, observational astronomers, and experimental particle physicists.

Significance of Findings

Our findings underscore the theoretical viability and observational implications of topological defects as dark matter candidates. By explaining their weak interactions with conventional matter, stable nature, and cosmological significance, we have provided a compelling argument for considering topological defects as viable alternatives to conventional dark matter candidates.

Future Research Directions

Moving forward, several promising avenues for future research emerge from our study:

Observational Campaigns: Initiating observational campaigns to search for the predicted signatures of topological defects in astrophysical observations, such as gravitational lensing surveys and cosmic microwave background experiments.
Theoretical Developments: Advancing theoretical models and simulations to refine predictions for the formation, evolution, and observational characteristics of topological defects in cosmological contexts.
Experimental Validation: Collaborating with experimental particle physicists to design and implement novel detection techniques capable of verifying the presence of topological defects in laboratory experiments.
Interdisciplinary Collaboration: Fostering interdisciplinary collaboration between theoretical physicists, observational astronomers, and experimental particle physicists to tackle the multifaceted challenges of investigating topological defects as dark matter candidates.

Conclusion

In this paper, we have thoroughly explored the potential of topological defects as dark matter candidates. Our theoretical framework and analytical calculations highlight the viability of structures such as flux tubes and domain walls in explaining dark matter’s elusive nature. The predicted observational signatures, such as gravitational lensing effects and patterns in the cosmic microwave background, provide tangible avenues for verification.

Comparing topological defects with traditional dark matter candidates like WIMPs and axions reveals both similarities, such as weak interactions with conventional matter, and distinct advantages, including inherent stability and unique topological structures. However, significant theoretical and experimental challenges remain, requiring advanced models, sophisticated simulations, and innovative detection techniques.

Our findings underscore the theoretical promise and observational relevance of topological defects, opening new pathways for dark matter research. Future work should focus on targeted observational campaigns, refined theoretical models, experimental validation, and interdisciplinary collaboration to fully include the role of topological defects in the cosmos. This approach not only broadens our understanding of dark matter but also offers profound insights into the fundamental nature of the universe.

Acknowledgments

I am profoundly grateful to my parents, Mr. Amar Singh and Mrs. Anita Singh, whose unwavering support and encouragement have been the cornerstone of my academic journey. Their love, guidance, and sacrifices have fueled my passion for research and enabled me to pursue my scientific aspirations.

References

Freese, K. The dark side of the universe. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 2006, 559, 337–340.
Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: evidence, candidates and constraints. Physics Reports 2005, 405, 279–390. [CrossRef]
Bergström, L. Dark matter evidence, particle physics candidates and detection methods. Annalen der Physik 2012, 524, 479–496. [CrossRef]
Haselschwardt, S. Radioassay of Gadolinium-Loaded Liquid Scintillator and Other Studies for the LZ Outer Detector. 2018.
Xu, J. Study of Argon from Underground Sources for Dark Matter Detection. 2013.
Fan, A. Results from the DarkSide-50 Dark Matter Experiment. 2016.
Stadnik, Y.V.; Flambaum, V.V. Searching for Topological Defect Dark Matter via Nongravitational Signatures. Phys. Rev. Lett. 2014, 113, 151301. [CrossRef]
Vilenkin, A. Cosmic strings and domain walls. Physics Reports 1985, 121, 263–315. [CrossRef]
Shuryak, E.V. Quantum chromodynamics and the theory of superdense matter. Physics Reports 1980, 61, 71–158. [CrossRef]
Rodriguez, R.; Hosotani, Y. Confinement and chiral condensates in 2d QED with massive N-flavor fermions. Physics Letters B 1996, 375, 273–284. [CrossRef]
Waheed, A.; Furlan, G. Aspects of quark-gluon plasma. La Rivista del Nuovo Cimento (1978-1999) 1996, 19, 1–34.
Abu-Shady, M.; Inyang, E.P. Effects of Topological Defects and Magnetic Flux on Dissociation Energy of Quarkonium in an Anisotropic Plasma. East Eur. J. Phys. 2024, 2024, 167–174. [CrossRef]
Cohen-Tanoudji, G.; Gazeau, J.P. Dark matter as a QCD effect in an anti de Sitter geometry: Cosmogonic implications of de Sitter, anti de Sitter and Poincaré symmetries. SciPost Phys. Proc. 2023, 14, 004. [CrossRef]
Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272–285. [CrossRef]
Madsen, J. Astrophysical Limits on the Flux of Quark Nuggets. Phys. Rev. Lett. 1988, 61, 2909–2912. [CrossRef]
Enstrom, D. Astrophysical Aspects of Quark-Gluon Plasma, 1998, [arXiv:hep-ph/hep-ph/9802337].
Karsch, F. Lattice QCD at high temperature and density; Vol. 583, Lect. Notes Phys., 2002; pp. 209–249.
Matsui, T.; Satz, H. J/ψ Suppression by Quark-Gluon Plasma Formation. Phys. Lett. B 1986, 178, 416–422. [CrossRef]
Ollitrault, J.Y. Anisotropy as a signature of transverse collective flow. Phys. Rev. D 1992, 46, 229–245. [CrossRef]
Bazavov, A.; others. Equation of state in (2+1)-flavor QCD. Phys. Rev. D 2014, 90, 094503.
Gyulassy, M.; Plumer, M. Jet Quenching in Dense Matter. Phys. Lett. B 1990, 243, 432–438. [CrossRef]
Voloshin, S.A.; Zhang, Y. Flow study in relativistic nuclear collisions by Fourier expansion of Azimuthal particle distributions. Z. Phys. C 1996, 70, 665–672. [CrossRef]
Koch, P.; Muller, B.; Rafelski, J. Strangeness in Relativistic Heavy Ion Collisions. Phys. Rep. 1986, 142, 167–262.
Kovtun, P.K.; Son, D.T.; Starinets, A.O. Viscosity in strongly interacting quantum field theories from black hole physics. Phys. Rev. Lett. 2005, 94, 111601. [CrossRef]
Braun-Munzinger, P.; Stachel, J. The quest for the quark–gluon plasma. Nature 2007, 448, 302–309. [CrossRef]
Singh, S.K. Confinement Phenomena in Topological Stars, 2024, [arXiv:hep-th/2405.16190].
Preskill, J. Cosmological production of superheavy magnetic monopoles. Physical Review Letters 1979, 43, 1365–1368. [CrossRef]
Zeldovich, Y.B.; Kobzarev, I.Y.; Okun, L.B. Cosmological consequences of the spontaneous breakdown of discrete symmetry. Soviet Physics JETP 1974, 40, 1–5.
Kibble, T.W.B. Topology of cosmic domains and strings. Journal of Physics A: Mathematical and General 1976, 9, 1387–1398. [CrossRef]
Abbasi, R.U.e.a. Search for Relativistic Magnetic Monopoles with the AMANDA-II Neutrino Detector. Astrophysical Journal 2012, 740, 78.
Vilenkin, A. Cosmic strings and domain walls. Physics Reports 1984, 121, 263–315. [CrossRef]
Damour, T.; Vilenkin, A. Gravitational radiation from cosmic (super)strings: Bursts, stochastic background, and observational windows. Physical Review D 2005, 71, 063510. [CrossRef]
Polyakov, A.M. Compact gauge fields and the infrared catastrophe. Phys. Lett. B 1975, 59, 82–84. [CrossRef]
Voloshin, M.B. Flux tube model for hadrons in QCD. Sov. J. Nucl. Phys. 1975, 21, 687–693.
Shifman, M.A. Vacuum structure and QCD sum rules. Nuclear Physics B 1980, 173, 13–32.
Nielsen, H.B.; Chadha, S. On how to count Goldstone bosons. Nucl. Phys. B 1976, 105, 445–463. [CrossRef]
Susskind, L. Lattice Models of Quark Confinement at High Temperature. Phys. Rev. D 1979, 20, 2610–2618.
Nambu, Y. Axial vector current conservation in weak interactions. Phys. Rev. Lett. 1960, 4, 380–382. [CrossRef]
Vilenkin, A.; Shellard, E.P.S. Cosmic Strings and Other Topological Defects; Cambridge University Press, 1994.
Sunyaev, R.A.; Zel’dovich, I.B. The Interaction of Matter and Radiation in a Hot-Model Universe. Astrophys. Space Sci. 1970, 7, 3–19.
Coleman, S. Quantum sine-Gordon equation as the massive Thirring model. Physical Review D 1973, 11, 2088. [CrossRef]
Weinberg, S. Quantum contributions to cosmological correlations. Physical Review D 2000, 62, 024031.
Peskin, M.E.; Schroeder, D.V. Introduction to quantum field theory; Perseus Books Publishing, 1995.
Collins, J.C. Renormalization: An introduction to renormalization, the renormalization group, and the operator-product expansion; Cambridge University Press, 1984.
Novikov, V.A.; Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. QCD sum rules and applications to nuclear physics. Nuclear Physics B 1984, 237, 525–562.
Brambilla, N.; Vairo, A. The gauge invariant definition of the effective potential. Physics Letters B 2013, 722, 253–257.
Cucchieri, A.; Mendes, T. Gauge invariant definition of the effective potential. Physical Review D 2008, 78, 094503.
Ioffe, B.L. Physics-Uspekhi 2008, 51, 616. [CrossRef]
Fujikawa, K.; Suzuki, H. Path integral measure for gauge invariant fermion theories. Physical Review D 1973, 7, 2950.
’t Hooft, G. Computation of the quantum effects due to a four-dimensional pseudoparticle. Phys. Rev. D 1976, 14, 3432–3450. [CrossRef]
Callan, C.G.; Dashen, R.F.; Gross, D.J. Towards understanding the strong interactions. Physical Review D 1978, 17, 2717.
Nambu, Y. Strings, monopoles, and gauge fields. Phys. Rev. D 1974, 10, 4262–4268. [CrossRef]
Mandelstam, S. Vortices and quark confinement in nonabelian gauge theories. Physical Review D 1976, 17, 437.
’t Hooft, G. Magnetic monopoles in unified gauge theories. Nuclear Physics B 1981, 190, 455–478.
Coleman, S. Moreno José and Coleman Sidney. Aspects of Symmetry: Selected Erice Lectures. Cambridge University Press, Cambridge 1976.
Vilenkin, A. Cosmic strings and domain walls. Physics Reports 1985, 121, 263–315. [CrossRef]
Lüscher, M. Properties and uses of the Wilson flow in lattice QCD. Journal of High Energy Physics 2010, 2010. [CrossRef]
Kovács, T.G.; Tomboulis, E.T. Computation of the Vortex Free Energy in SU(2) Gauge Theory. Phys. Rev. Lett. 2000, 85, 704–707. [CrossRef]
Gross, D.J.; Wilczek, F. Ultraviolet Behavior of Non-Abelian Gauge Theories. Phys. Rev. Lett. 1973, 30, 1343–1346. [CrossRef]
Polyakov, A.M. Quark Confinement and Topology of Gauge Groups. Nucl. Phys. B 1977, 120, 429–458. [CrossRef]
Belavin, A.A.; Polyakov, A.M.; Schwartz, A.S.; Tyupkin, Y.S. Pseudoparticle Solutions of the Yang-Mills Equations. Phys. Lett. B 1975, 59, 85–87. [CrossRef]
Callan, C.G.; Dashen, R.; Gross, D.J. Toward a theory of the strong interactions. Phys. Rev. D 1978, 17, 2717–2763. [CrossRef]
Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345–358. [CrossRef]
Gell-Mann, M.; Oakes, R.; Renner, B. Behavior of Current Divergences under SU(3) × SU(3). Phys. Rev. 1968, 175, 2195–2199. [CrossRef]
Wilson, K.G. Confinement of Quarks. Phys. Rev. D 1974, 10, 2445–2459.
Nambu, Y. Confinement of Quarks in QCD. Phys. Rev. Lett. 1974, 23, 1449–1451.
Witten, E. Current Algebra, Baryons, and Quark Confinement. Nucl. Phys. B 1979, 223, 422–436.
Creutz, M. Gauge fixing, the transfer matrix, and confinement on a lattice. Phys. Rev. D 1977, 15, 1128–1136. [CrossRef]
Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Instantons. Phys. Rev. Lett. 1977, 38, 1440–1443. [CrossRef]
Wilczek, F. Problem of Strong p and t Invariance in the Presence of Instantons. Phys. Rev. Lett. 1978, 40, 279–282. [CrossRef]
’t Hooft, G. Symmetry Breaking Through Bell-Jackiw Anomalies. Phys. Rev. Lett. 1976, 37, 8–11. [CrossRef]
Belavin, A.A.; Polyakov, A.M.; Schwartz, A.S.; Tyupkin, Y.S. Pseudoparticle Solutions of the Yang-Mills Equations. Phys. Lett. B 1975, 59, 85–87. [CrossRef]
Gross, D.J.; Wilczek, F. Ultraviolet Behavior of Nonabelian Gauge Theories. Phys. Rev. Lett. 1973, 30, 1343–1346. [CrossRef]
Polchinski, J. String theory. Vol. 1: An introduction to the bosonic string; Cambridge University Press, 2005.
Kibble, T.W.B. Topology of Cosmic Domains and Strings. J. Phys. A 1976, 9, 1387–1398. [CrossRef]
Chernodub, M.N. Superconductivity of QCD vacuum in strong magnetic field. Phys. Lett. B 1998, 443, 244–250.
Bali, G.S. QCD forces and heavy quark bound states. Phys. Rept. 2001, 343, 1–136. [CrossRef]
Greensite, J. An Introduction to the Confinement Problem; Springer, 2011.
Luscher, M. String tension in QCD: An update. Nucl. Phys. B Proc. Suppl. 2002, 106, 21–32.
Fukugita, M.; Yanagida, T. Baryogenesis Without Grand Unification. Phys. Lett. B 1986, 174, 45–47. [CrossRef]
Kawasaki, M.; Nakayama, K.; Sekiguchi, T.T. The role of QCD equation of state in the process of hadronization. Prog. Theor. Exp. Phys. 2017, 2017, 113C01. [CrossRef]
Vachaspati, T. Kinks and domain walls: An update. Phys. Rept. 1999, 316, 251–274.
Witten, E. Current Algebra, Baryons, and Quark Confinement. Nucl. Phys. B 1979, 156, 269–283. [CrossRef]
Zeldovich, Y.B.; Kobzarev, I.Y.; Okun, L.B. Cosmological Consequences of the Spontaneous Breakdown of Discrete Symmetry. Sov. Phys. JETP 1975, 40, 1–5.
Vilenkin, A.; Shellard, E.P.S. Cosmic Strings and Other Topological Defects; Cambridge University Press, 2000.
Sikivie, P. Experimental Tests of the ’Invisible’ Axion. Phys. Rev. Lett. 1982, 48, 1156–.
Brandenberger, R.H.; Peter, P. Baryogenesis and dark matter through the QCD axion window. JCAP 2017, 1710, 009. [CrossRef]
Zurek, W.H. Cosmological Experiments in Superfluid Helium? Nature 1985, 317, 505–508. [CrossRef]
Nambu, Y.; Nielsen, H.B. A Abelian Model of Hadrons. Nucl. Phys. B 1977, 120, 62–70.
Hiramatsu, T.; Ichiki, K.; Sekiguchi, T. Cosmological domain wall problem in a gauge-mediated SUSY breaking model. Phys. Rev. D 2012, 85, 123524. [CrossRef]
Vilenkin, A. Cosmic Strings and Domain Walls. Phys. Rept. 1985, 121, 263–315. [CrossRef]
Vilenkin, A.; Shellard, E.P.S. Cosmic strings and other topological defects. Cambridge University Press 1994.
Hindmarsh, M.; Ringeval, C.; Suyama, T.; Underwood, J. Cosmic strings and superstrings. Phys. Rept. 2008, 461, 75–130.
Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; Battye, R.; Benabed, K.; Bernard, J.P.; Bersanelli, M.; Bielewicz, P.; Bock, J.J.; Bond, J.R.; Borrill, J.; Bouchet, F.R.; Boulanger, F.; Bucher, M.; Burigana, C.; Butler, R.C.; Calabrese, E.; Cardoso, J.F.; Carron, J.; Challinor, A.; Chiang, H.C.; Chluba, J.; Colombo, L.P.L.; Combet, C.; Contreras, D.; Crill, B.P.; Cuttaia, F.; de Bernardis, P.; de Zotti, G.; Delabrouille, J.; Delouis, J.M.; Di Valentino, E.; Diego, J.M.; Doré, O.; Douspis, M.; Ducout, A.; Dupac, X.; Dusini, S.; Efstathiou, G.; Elsner, F.; Enßlin, T.A.; Eriksen, H.K.; Fantaye, Y.; Farhang, M.; Fergusson, J.; Fernandez-Cobos, R.; Finelli, F.; Forastieri, F.; Frailis, M.; Fraisse, A.A.; Franceschi, E.; Frolov, A.; Galeotta, S.; Galli, S.; Ganga, K.; Génova-Santos, R.T.; Gerbino, M.; Ghosh, T.; González-Nuevo, J.; Górski, K.M.; Gratton, S.; Gruppuso, A.; Gudmundsson, J.E.; Hamann, J.; Handley, W.; Hansen, F.K.; Herranz, D.; Hildebrandt, S.R.; Hivon, E.; Huang, Z.; Jaffe, A.H.; Jones, W.C.; Karakci, A.; Keihänen, E.; Keskitalo, R.; Kiiveri, K.; Kim, J.; Kisner, T.S.; Knox, L.; Krachmalnicoff, N.; Kunz, M.; Kurki-Suonio, H.; Lagache, G.; Lamarre, J.M.; Lasenby, A.; Lattanzi, M.; Lawrence, C.R.; Le Jeune, M.; Lemos, P.; Lesgourgues, J.; Levrier, F.; Lewis, A.; Liguori, M.; Lilje, P.B.; Lilley, M.; Lindholm, V.; López-Caniego, M.; Lubin, P.M.; Ma, Y.Z.; Macías-Pérez, J.F.; Maggio, G.; Maino, D.; Mandolesi, N.; Mangilli, A.; Marcos-Caballero, A.; Maris, M.; Martin, P.G.; Martinelli, M.; Martínez-González, E.; Matarrese, S.; Mauri, N.; McEwen, J.D.; Meinhold, P.R.; Melchiorri, A.; Mennella, A.; Migliaccio, M.; Millea, M.; Mitra, S.; Miville-Deschênes, M.A.; Molinari, D.; Montier, L.; Morgante, G.; Moss, A.; Natoli, P.; Nørgaard-Nielsen, H.U.; Pagano, L.; Paoletti, D.; Partridge, B.; Patanchon, G.; Peiris, H.V.; Perrotta, F.; Pettorino, V.; Piacentini, F.; Polastri, L.; Polenta, G.; Puget, J.L.; Rachen, J.P.; Reinecke, M.; Remazeilles, M.; Renzi, A.; Rocha, G.; Rosset, C.; Roudier, G.; Rubiño-Martín, J.A.; Ruiz-Granados, B.; Salvati, L.; Sandri, M.; Savelainen, M.; Scott, D.; Shellard, E.P.S.; Sirignano, C.; Sirri, G.; Spencer, L.D.; Sunyaev, R.; Suur-Uski, A.S.; Tauber, J.A.; Tavagnacco, D.; Tenti, M.; Toffolatti, L.; Tomasi, M.; Trombetti, T.; Valenziano, L.; Valiviita, J.; Van Tent, B.; Vibert, L.; Vielva, P.; Villa, F.; Vittorio, N.; Wandelt, B.D.; Wehus, I.K.; White, M.; White, S.D.M.; Zacchei, A.; Zonca, A. Planck2018 results: VI. Cosmological parameters. Astronomy and Astrophysics 2020, 641, A6. [CrossRef]
Greensite, J. An Introduction to the Confinement Problem. Lect. Notes Phys. 2011, 821, 1–188. [CrossRef]
Ellis, J. Quantum Chromodynamics and Deep Inelastic Scattering. Prog. Part. Nucl. Phys. 2008, 60, 484–551. [CrossRef]
Bethke, S. The 2009 World Average of α_s(M_Z). Eur. Phys. J. C 2009, 64, 689–703.
Kibble, T.W.B.; Zurek, W.H. Phase Transitions in the Early Universe: Theory and Observations. Rev. Mod. Phys. 1999, 71, S141–S151.
Zurek, W.H. Cosmological Experiments in Superfluid Helium? Nature 1985, 317, 505–508. [CrossRef]
Shifman, M. Nonperturbative Dynamics in Supersymmetric Gauge Theories. Prog. Theor. Phys. Suppl. 1990, 102, 1–238. [CrossRef]
Vilenkin, A. Cosmic Strings and Domain Walls. Phys. Rept. 1985, 121, 263–315. [CrossRef]
Casher, A. The Confinement Problem in Lattice Gauge Theory. Phys. Lett. B 1979, 83, 395–398.
Vachaspati, T. Magnetic Monopoles. Phys. Rept. 1993, 231, 147–213.
Kunz, M.; Nesseris, S.; Sawicki, I. Constraints on dark-matter properties from large-scale structure. Physical Review D 2016, 94. [CrossRef]
Wu, J.; Li, Q.; Liu, J.; Xue, C.; Yang, S.; Shao, C.; Tu, L.; Hu, Z.; Luo, J. Progress in Precise Measurements of the Gravitational Constant. Annalen Phys. 2019, 531, 1900013. [CrossRef]
Durrer, R.; Kunz, M.; Melchiorri, A. Cosmic structure formation with topological defects. Physics Reports 2002, 364, 1–81. [CrossRef]
Riazuelo, A.; Deruelle, N.; Peter, P. Topological defects and cosmic microwave background anisotropies: Are the predictions reliable ? Phys. Rev. D 2000, 61, 123504. [CrossRef]
Lieu, R. The binding of cosmological structures by massless topological defects. Monthly Notices of the Royal Astronomical Society 2024, 531, 1630–1636, [https://academic.oup.com/mnras/article-pdf/531/1/1630/57890656/stae1258.pdf]. [CrossRef]
Guth, A.H. The inflationary universe: A possible solution to the horizon and flatness problems. Physical Review D 1981, 23, 347.
Perlick, V. Gravitational lensing from a spacetime perspective. Living Rev. Rel. 2004, 7, 9. [CrossRef]
Schneider, P.; Ehlers, J.; Falco, E. Gravitational Lenses; Springer-Verlag, 1992.
Perlmutter, S.; Aldering, G.; et al.. Measurements of Ω and Λ from 42 high redshift supernovae. The Astrophysical Journal 1999, 517, 565.
Hindmarsh, M.B.; Kibble, T.W.B. Cosmic strings. Reports on Progress in Physics 1995, 58, 477–562. [CrossRef]
Vachaspati, T.; Vilenkin, A. Gravitational Lensing by Cosmic String Loops. Physical Review D 1987, 35, 1131–1134.
Vilenkin, A. Cosmic Strings and Domain Walls. Physics Reports 1984, 121, 263–315.
Tyson, J.A.; Angel, J.R.P. Large Synoptic Survey Telescope: Overview. Proceedings of the SPIE 2003, 4836, 10–20.
Gardner, J.P.; Mather, J.C.; Clampin, M.; Doyon, R.; Greenhouse, M.A. The James Webb Space Telescope. Space Science Reviews 2006, 123, 485–606.
Bartelmann, M.; Schneider, P. Weak Gravitational Lensing. Physics Reports 2001, 340, 291–472.
Pogosian, L.; Vachaspati, T.; Wyman, M. Observational Windows for Cosmological Defects. Physical Review D 2004, 69, 083523.
Vilenkin, A.; Shellard, E.S. Cosmic Strings and Other Topological Defects; Cambridge University Press, 2000.
Kibble, T. Topology of cosmic domains and strings. Journal of Physics A: Mathematical and General 1976, 9, 1387. [CrossRef]
Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Physics Reports 2005, 405, 279–390. [CrossRef]

Figure 1. Thermal History of the Universe

Figure 2. Energy Density Distribution Across Domain Wall in QCD

Figure 3. QCD Vacuum Structure - Gluon and Quark Fields

Figure 4. Visualization of flux tubes and domain walls in the QCD vacuum

Figure 6. Topological

t h e t a

-Term

Figure 6. Topological

t h e t a

-Term

Figure 7. Energy Density of Flux Tubes

Figure 8. Energy Density of Domain Walls

Figure 9. Comparison of Energy Densities: Flux Tubes vs. Domain Walls

Figure 10. Interactions in the Early Universe

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Non-Abelian Topological Defects in QGP as Dark Matter Candidates

Abstract

Keywords:

Subject:

Introduction

QGP in the Early Universe

Quark-Gluon Plasma in the Early Universe

Early Universe Conditions and QGP Formation

QGP Properties and Signatures

Lattice QCD and Computational Studies

Experimental Evidence from Heavy-Ion Collisions

Theoretical Models and Hydrodynamics

Cosmological Implications

Topological Defects in QGP as Dark Matter

Topological Defects in QGP

Implications for Dark Matter

Quantum Chromodynamics (QCD) and Vacuum Structure

Classical Potential and Quantum Corrections

Perturbative Calculations and Renormalization

Vacuum Expectation Values of Local Composite Operators

Microscopic Vacuum Structure in Pure QCD

Axial Anomaly and Vacuum Structure

Nontrivial Structure of the QCD Vacuum

Mathematical Formulations

Presenting the Lagrangian Density Including Topological Terms

Explanation of Terms:

Importance of the θ -Term:

Formation and Properties of Flux Tubes in the Quark-Gluon Plasma (QGP)

Formation of Flux Tubes

Mathematical Description

Properties of Flux Tubes

Formation and Properties of Domain Walls in the QCD Vacuum

Formation of Domain Walls

Mathematical Description

Properties of Domain Walls

Cosmological Implications of Flux Tubes and Domain Walls as Dark Matter Candidates

Abundance and Formation in the Early Universe

Stability Over Cosmological Timescales

Observational Signatures

Mathematical Modeling

Analytical Estimates of Energy Density, Abundance, and Stability

Energy Density Evaluation of Flux Tubes

Abundance Evaluation of Flux Tubes

Energy Density Assessment of Domain Walls

Abundance Assessment of Domain Walls

Stability Over Cosmological Timescales

Integrating Topological Defects into a Cosmological Model

Contribution to the Dark Matter Density

Comparing with Topological Defect Contributions

Scaling of the Flux tubes and Domain walls

Interactions with Other Matter and Radiation

How Topological Defects Act as Dark Matter

Mass Density and Gravitational Effects

Stability and Cosmological Evolution

Observational Signatures and Experimental Verification

Unique Signatures and Differentiation from Other Dark Matter Candidates

Gravitational Lensing

Calculation of Deflection Angle

Discussion of Lensing Patterns

Flux Tubes

Domain Walls

Observational Implications and Studies

Lensing Signal Calculation

Flux Tubes

Domain Walls

Sensitivity Analysis

Gravitational Lensing

Calculation of Deflection Angles

Flux Tubes

Domain Walls

Calculations

Flux Tube

Domain Wall

Analysis

Implications

Interaction with Conventional Matter

Limited Interaction Mechanisms

Implications for Dark Matter Candidates

Similarities Between Dark Matter and Topological Defects

Comparative Analysis

Importance of the $θ$ -Term: