One-Dimensional Relativistic Self-Gravitating Systems

Preprint

Review

One-Dimensional Relativistic Self-Gravitating Systems

Altmetrics

Downloads

157

Views

Comments

A peer-reviewed article of this preprint also exists.

Robert B. Mann^*

This version is not peer-reviewed

Submitted:

09 June 2024

Posted:

13 June 2024

You are already at the latest version

Alerts

Abstract

One of the oldest problems in physics is that of calculating the motion of N particles under a specified mutual force: the N-body problem. Much is known about this problem if the specified force is non-relativistic gravity, and considerable progress has been made by considering the problem in one spatial dimension. Here I review what is known about the relativistic gravitational N-body problem. Reduction to one spatial dimension has the feature that gravitational radiation is absent, thereby allowing for a clear comparison between the physics of one-dimensional relativistic and non-relativistic self-gravitating systems. After describing how to obtain a relativistic theory of gravity coupled to N point particles, I discuss in turn the 2-body, 3-body, 4-body, and N-body problems. Quite general exact solutions can be obtained for the 2-body problem, unlike the situation in general relativity in 3 spatial dimensions for which only highly specified solutions exist. The 3-body problem exhibits mild forms of chaos, and provides one of the first theoretical settings in which relativistic chaos can be studied. For N4 other interesting features emerge. Relativistic self-gravitating systems have a number of interesting problems awaiting further investigation, providing us with a new frontier for exploring relativistic many-body systems.

Keywords:

Subject: Physical Sciences - Theoretical Physics

Dedicated to the memory of Tadayuki Ohta, who introduced me to this fascinating subject.

1. Introduction

One of the oldest problems in physics is the N-body problem: determination of the motion of a system of N particles mutually interacting through specified forces. This problem appears in a broad variety of subfields of physics, including cosmology, stellar dynamics, planetary motion, atomic physics, and nuclear physics. The N-body problem is a particular challenge if the interactions are purely gravitational. Although an exact solution is known for the 2-body problem in pure Newtonian gravity in three spatial dimensions, there is no closed form solution for large N, even for

N = 3

[1], though particular solutions exist in restricted cases [2]. No exact solution is known in the general-relativistic case even for

N = 2

, since it experiences dissipation of energy in the form of gravitational radiation.

One-dimensional self-gravitating systems (OGS) have played an important role in advancing our understanding of the gravitational N-body problem [3]. Such systems have been of interest for over half a century, where they have played an important role in astrophysics and cosmology for more than 30 years [4]. Apart from being prototypes for studying the behaviour of gravity in higher dimensions, they also approximate the behaviour in 3 spatial dimensions of some physical systems. Examples include very long-lived core-halo configurations that model a dense massive core in near-equilibrium, surrounded by a halo of high kinetic energy stars that feebly interact with the core [4,5,6]. Other examples include cosmological models [7,8] the dynamics of stars in a direction orthogonal to the plane of a highly flattened galaxy [9], shells of matter interacting with a spherical globular cluster [10], and collisions of flat parallel domain walls moving in directions orthogonal to their surfaces.

Although the connection between the idealized OGS and natural astrophysical systems can be tenuous, the accuracy and ease with which their dynamical evolution may be simulated has remained the principal motivation for continued study of the OGS. Unlike 3-dimensional self-gravitating systems, in which the motion of the (point) masses must be numerically integrated, the OGS admits direct computation of the particle (or sheet, or shell) crossings. This provides accurate computation of the evolution of the system over many dynamical time scales. Furthermore, a number of interesting questions concerning the statistical properties of the OGS remain open, including whether or not it can attain a state of true equilibrium from arbitrary initial conditions [5], its ergodic behaviour, the circumstances (if any) under which equipartition of energy can be attained [11], and the appearance of fractal behaviour [3,12].

For three decades, studies of the OGS have been in a non-relativistic context, assuming Newtonian gravity with its standard causal structure [3,7,8,11,13,14,15,16,17,18,19,20,21]. Research into relativistic one-dimensional self-gravitating systems (ROGS) was generally ignored. In large part this was because relativistic effects do not play a dominant role in stellar dynamics, but it was also due to the lack of a theoretical framework for relativistic gravity in one spatial dimension. The Einstein tensor is identically zero in this

(1 + 1)

-dimensional spacetime context, and so Einstein’s equation at face value would simply imply vanishing stress-energy. However reduction of the number of spatial dimensions in a relativistic context can be expected to be quite useful since gravitational radiation (at least due to spin-2 gravitons) cannot exist in less than 3 spatial dimensions. However most (if not all) of the remaining conceptual features of relativistic gravity are retained in lower dimensions, and so one might hope to obtain insight into the nature of relativistic classical and quantum gravitation in a wide variety of physical situations by studying the ROGS.

It is straightforward to find a set of equations governing the motion of particles – these are furnished by the geodesic equations. In addition to this, what is needed to study ROGS is a set of equations governing the dynamics of the spacetime metric in a self-consistent way. Early versions of

(1 + 1)

–dimensional gravity [22,23] set the Ricci curvature scalar equal to a constant, yielding trivial dynamics for the spacetime metric (although containing sufficiently interesting features [24] such that this theory is still of interest today [25] ). Intensive investigation of a wide variety of gravitational theories ensued a few years later, primarily motivated by a quest to understand quantum gravity in a simplified context [26]. The overwhelming majority of such investigations were concerned with the (quantum) dynamics of the spacetime metric, and not with the dynamical motion of particles in such spacetimes.

At about the same time that interest

(1 + 1)

-dimensional quantum gravity began, investigations of the ROGS also began. The purpose of this article is to review the origins, results, and status of relativistic one-dimensional self-gravitating systems. After a brief review of the OGS, I begin by reviewing how the

D \to 2

limit of D-dimensional general relativity [27] can be self-consistently coupled to point particles, thereby yielding the ROGS. The equations of motion for the particles are obtained using the canonical formalism, which I describe in some detail. I shall then consider in turn the 2-body, 3-body, 4-body, and N-body ROGS, discussing their distinctions from the OGS, their salient features, their chaotic behaviour, and their statistical properties, as relevant. I conclude by discussing a number of interesting open problems for relativistic one-dimensional self-gravitating systems. While other constants will retain their values throughout, the speed of light c will generally be set to unity, and only explicitly written where relevant for instructive purposes.

2. Non-Relativistic Self-Gravitating Systems

For a system of particles the Hamiltonian in Newtonian gravity in two dimensions is

H = \sum_{a} \frac{p_{a}^{2}}{2 m_{a}} + π G \sum_{a, b = 1}^{N} m_{a} m_{b} | z_{a} - z_{b} |

(1)

where

m_{a}

z_{a}

and

p_{a}

are the mass, the coordinate location, and the momentum of a-th particle, respectively, and G is the gravitational constant. The potential between any two particles is proportional to the product of their masses and the spatial separation between them, as expected from dimensionally continuing the well-known potential

V = - G_{d} \sum_{a \neq b}^{N} \frac{m_{a} m_{b}}{| z_{a} - z_{b} |^{d - 2}}

(2)

of Newtonian gravity in d spatial dimensions, where

G_{1} = π G

. When

d = 1

the potential in (1) vanishes, and so the restriction

a \neq b

in (1) is not required.

The equations of motion of the OGS (1) are given by Hamilton’s equations

\begin{matrix} {\dot{z}}_{a} & = & \frac{\partial H}{\partial p_{a}} = \frac{p_{a}}{m_{a}} \end{matrix}

(3)

\begin{matrix} {\dot{p}}_{a} & = & - \frac{\partial H}{\partial z_{a}} = - 2 π G \sum_{b} m_{a} m_{b} \frac{\partial | z_{a} - z_{b} |}{\partial z_{a}} \\ = & - 2 π G \sum_{b} m_{a} m_{b} sgn (z_{a} - z_{b}) \end{matrix}

(4)

yielding

{\ddot{z}}_{a} = - 2 π G \sum_{b} m_{b} sgn (z_{a} - z_{b})

(5)

for the acceleration of the a-th particle.

We see that each particle experiences a constant force from each of the other particles, where the sign (- or +) of the force from any given particle depends on whether

z_{a} > z_{b}

or vice-versa. The force is therefore always attractive: if

z_{a}

is to the right of

z_{b}

(

z_{a} > z_{b}

) then particle a will accelerate leftward toward

z_{b}

(and b rightward toward a) until they meet, after which time

z_{a}

is to the left of

z_{b}

(

z_{a} < z_{b}

) and the force changes sign, accelerating particle a rightward. This scenario assumes that the particles can pass through each other without any influence, as would be appropriate for parallel sheets of particulate matter where collisions between the particles can be neglected. It is of course possible to include additional structure – for example, modelling the particles as impenetrable points would make them bounce off of each other – but this would detract from the study of pure gravitational effects. Such additional structure will not be considered in this article, apart from the inclusion of attractive and repulsive electromagnetic interactions.

Consider the case

N = 2

. If the particles are initially separated by some distance d, they will move toward each other with constant acceleration until they cross, after which the acceleration of each flips sign. The particles fly apart increasingly slowly until they reach a maximal separation d, after which they move toward each other again with increasing speed. After crossing a second time, the particles separate, moving with decreasing speed until they return to their original positions. Assuming no other interactions, the motion then repeats perpetually. Prior to crossing, the entire scenario is equivalent to that of a body of mass m falling near the surface of the Earth.

For N particles, every particle initially undergoes constant acceleration until the first two particles cross. This causes a sign flip in the force between each particle in the crossing pair, thereby changing the magnitudes (and perhaps signs) of the accelerations of each due to the presence of the other particles. As more particles cross, this changes the accelerations of more and more particles, in general yielding chaotic motion.

The simplest example of this occurs for

N = 3

. This 3-body OGS has been shown to exhibit a mild form of chaos [3]. This OGS can be mapped to a single-particle moving in 2 spatial dimensions in a hexagonal-well potential

V (x, y)

, whose sides are impenetrable flat sheets. If the masses of all particles are equal then the shape is that of a regular hexagon; unequal masses distort this symmetry so that the sides are of unequal length [28,29]. Alternatively, the 3-body OGS can be regarded as a single-particle under the influence of a constant gravitational field in 2 spatial dimensions that bounces off of a symmetric wedge of angle

2 θ

, where this angle parametrizes the relative inequality of the masses [3].

Constructing a relativistic of the Hamiltonian (1) is somewhat subtle. This is the subject of the next section.

3. Relativistic Gravity Coupled to Point Particles

In three spatial dimensions a self-gravitating system would consist of a set of N particles minimally coupled to Einstein gravity. Its action in n-dimensions is [30]

\begin{matrix} I_{n} = \int d^{n} x [\frac{1}{2 κ_{n}} \sqrt{- g} (R - 2 Λ_{n}) - \sum_{a = 1}^{N} m_{a} \int d τ_{a} {\{- g_{μ ν} (x) \frac{d z_{a}^{μ}}{d τ_{a}} \frac{d z_{a}^{ν}}{d τ_{a}}\}}^{1 / 2} δ^{(n)} (x - z_{a} (τ_{a}))] \end{matrix}

(6)

where

| Λ_{n} | = \frac{(n - 2) (n - 1)}{2 ℓ^{2}}

is the cosmological constant (whose sign

+ / -

respectively corresponds to asymptotically de Sitter/Anti de Sitter spacetime),

κ_{n} = 8 π G_{n} / c^{4}

is the gravitational coupling and R is the Ricci scalar. Systems of astrophysical interest have

n = 4

. Notwithstanding issues connected with collisions between the particles, the field equations that follow from this action embody what we expect from a self-gravitating system: the curvature of spacetime governs how the particles move along the trajectories

z_{a} (τ_{a})

, and the masses and motion of these particles in turn govern how spacetime dynamically curves.

A ROGS that resembles a relativistic three-dimensional self-gravitating system as closely as possible should therefore have the following features.

The stress-energy of the particles generates spacetime curvature in as simple a manner as possible.
The curvature of spacetime guides the motion of each particle in accord with the equivalence principle, in the absence of any extraneous forces.
The dynamics of the system is self-consistent.

One might expect to obtain the ROGS by simply setting

n = 2

in (6) (1 space dimension, 1 time dimension), but this will not work: the Ricci scalar is a total derivative in

(1 + 1)

dimensions, in turn implying that the Einstein tensor is identically zero for any metric.

However there is a way of taking the

n \to 2

limit of the action (6) [27]. Consider the action

\begin{matrix} I_{n}^{E H} & = & \frac{1}{2 κ_{n}} (\int d^{n} x \sqrt{- \tilde{g}} \tilde{R} - \int d^{n} x \sqrt{- g} R) \\ = & \frac{1}{2 κ_{n}} \int d^{n} x [e^{ϵ Ψ / 2} [(R - (ϵ + 1) □ Ψ) - \frac{1}{4} ϵ (ϵ + 1) {(\partial Ψ)}^{2}] - R] \end{matrix}

(7)

where

\tilde{g} = e^{Ψ} g

is a conformally rescaled metric and

ϵ = n - 2

. Expanding in powers of

ϵ

yields

I_{2}^{E H} = \frac{n - 2}{4 κ_{n}} \int d^{2} x \sqrt{- g} [Ψ R - Ψ □ Ψ - \frac{1}{2} {(\nabla Ψ)}^{2}]

(8)

and so by setting

κ_{2} = \frac{2 κ_{n}}{n - 2}

we obtain

I_{2}^{E H} \equiv lim_{n \to 2} I_{n}^{E H} = \frac{1}{2 κ_{2}} \int d^{2} x \sqrt{- g} [Ψ R + \frac{1}{2} {(\nabla Ψ)}^{2}]

(9)

upon discarding total divergences. The limit

n \to 2

in (6) is straightforward for the other two terms, yielding

\begin{matrix} I & = & \int d^{2} x \sqrt{- g} [\frac{1}{2 κ} (Ψ R + \frac{1}{2} {(\nabla Ψ)}^{2} - 2 Λ) \\ - \sum_{a = 1}^{N} m_{a} \int d τ_{a} {\{- g_{μ ν} (x) \frac{d z_{a}^{μ}}{d τ_{a}} \frac{d z_{a}^{ν}}{d τ_{a}}\}}^{1 / 2} δ^{(2)} (x - z_{a} (τ_{a}))] \end{matrix}

(10)

as the action for the ROGS, where

κ = κ_{2}

and

Λ = Λ_{2} = \pm \frac{1}{ℓ^{2}}

Note that this procedure incorporates an an additional field

Ψ

in the gravitational action. This might seem to be in tension with the second desirable feature in the list above. However the field equations derived from the variations

δ Ψ

and

δ g_{μ ν}

are

R - g^{μ ν} \nabla_{μ} \nabla_{ν} Ψ = R - \frac{1}{\sqrt{- g}} \partial_{μ} (\sqrt{- g} g^{μ ν} \partial_{ν} Ψ) = 0

(11)

\frac{1}{2} \nabla_{μ} Ψ \nabla_{ν} Ψ - \frac{1}{4} g_{μ ν} \nabla^{λ} Ψ \nabla_{λ} Ψ + g_{μ ν} \nabla^{λ} \nabla_{λ} Ψ - \nabla_{μ} \nabla_{ν} Ψ = κ T_{μ ν} - g_{μ ν} Λ

(12)

where

\begin{matrix} T_{μ ν} & = & - \frac{2}{\sqrt{- g}} \frac{δ L_{M}}{δ g^{μ ν}} = \sum_{a} m_{a} \int d τ_{a} \frac{1}{\sqrt{- g}} g_{μ σ} g_{ν ρ} \frac{d z_{a}^{σ}}{d τ_{a}} \frac{d z_{a}^{ρ}}{d τ_{a}} δ^{(2)} (x - z_{a} (τ_{a})) \end{matrix}

(13)

where the last term in (10) is the matter Lagrangian

L_{M}

. Taking the trace of (12) and inserting the result into (11) gives

R + 2 Λ = κ T_{μ}^{μ} .

(14)

which shows that the evolution of the metric depends only on the stress-energy, and decouples from the evolution of

Ψ

. The variation

δ z_{a}^{μ}

yields

\frac{d}{d τ_{a}} \{g_{μ ν} (z_{a}) \frac{d z_{a}^{ν}}{d τ_{a}}\} - \frac{1}{2} g_{ν λ, μ} (z_{a}) \frac{d z_{a}^{ν}}{d τ_{a}} \frac{d z_{a}^{λ}}{d τ_{a}} = 0

(15)

which is the geodesic equation, or rather equations since there is one per particle.

The system (14,15) forms a closed relativistic self-gravitating system of N point particles. Spacetime curvature is determined from the stress-energy of the particulate matter from (14); in turn the evolution of the particles is determined by the spacetime curvature via (15).

The theory given by the action (10) is known as

R = T

theory [31,32,33] . Its classical properties, including gravitational collapse, black holes, cosmological solutions, solitonic properties, and thermodynamics have been extensively studied [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68]. Its chief interest lies in the fact that it captures the essence of classical general relativity in two spacetime dimensions, and has

(1 + 1)

–dimensional analogs of many of its properties [34,69,70]. Moreover, it has a well-defined Newtonian limit [32,34]. This is in contrast to generic scalar-tensor theories [71], where the dilaton does not decouple from the evolution of the gravitational field.

The quantum properties of

R = T

theory have also received attention from a variety of perspectives [36,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88]. There is also a supersymmetric version of the theory [89], which has supersymmetric black hole solutions [90,91,92]. Recently experiments have been carried out [93,94] that test certain aspects of the theory, albeit in a simulated context.

The remainder of this article is concerned with the N-body problem and its solutions as determined from the equations that follow from the action (10). The canonical approach is the most useful way to obtain these equations. This is the subject of the next section.

4. Canonical Formalism for Particle Dynamics

To obtain the ROGS Hamiltonian, the canonical Arnowitt-Deser-Misner (ADM) formalism [95,96,97] can be employed, as with the ADM formalism in

(3 + 1)

–dimensional theory. The result of this procedure is that constraints are eliminated, coordinate conditions are imposed, and the reduced Hamiltonian is given as a spatial integral of the second derivative of

Ψ

, which is a function of the dynamical variables (

z_{a}

p_{a}

) of the particles [98]. Consequently the Hamiltonian is completely determined in terms of the coordinates and momenta of the particles.

4.1. Neutral Particles

Consider first the N-body system whose interactions are purely gravitational. Writing the metric as

d s^{2} = - N_{0}^{2} d t^{2} + γ {(d x + \frac{N_{1}}{γ} d t)}^{2}

(16)

its extrinsic curvature is

K = {(2 N_{0} γ)}^{- 1} (2 \partial_{1} N_{1} - γ^{- 1} N_{1} \partial_{1} γ - \partial_{0} γ) = \sqrt{γ} κ (π - Π / γ)

(17)

where

π

and

Π

are the respective conjugate momenta to

γ

and

Ψ

. Using this the action integral (10) can be written as

I = \int d^{2} x \{\sum_{a} p_{a} {\dot{z}}_{a} δ (x - z_{a} (x^{0})) + π \dot{γ} + Π \dot{Ψ} + N_{0} R^{0} + N_{1} R^{1}\}

(18)

where

\begin{matrix} R^{0} & = & - κ \sqrt{γ} γ π^{2} + 2 κ \sqrt{γ} π Π + \frac{1}{4 κ \sqrt{γ}} {(Ψ^{'})}^{2} - \frac{1}{κ} {(\frac{Ψ^{'}}{\sqrt{γ}})}^{'} \end{matrix}

\begin{matrix} - \frac{Λ}{κ} \sqrt{γ} - \sum_{a} \sqrt{\frac{p_{a}^{2}}{γ} + m_{a}^{2}} δ (x - z_{a} (x^{0})) \end{matrix}

(19)

\begin{matrix} R^{1} & = & \frac{γ^{'}}{γ} π - \frac{1}{γ} Π Ψ^{'} + 2 π^{'} + \sum_{a} \frac{p_{a}}{γ} δ (x - z_{a} (x^{0})) \end{matrix}

(20)

where

\partial_{0}

is denoted by

(\dot{​})

and

\partial_{1}

by a symbol

(​^{'})

Performing the canonical reduction is a somewhat involved procedure, but is fully analogous to the

(3 + 1)

-dimensional case [99,100]. Suppressing the details, the coordinate conditions

γ = 1 and Π = 0

(21)

can be consistently chosen, and subsequently the action integral reduces to [98]

I_{R} = \int d x^{2} \{\sum_{a} p_{a} {\dot{z}}_{a} δ (x - z_{a}) - H\} .

(22)

where, writing

▵ Ψ \equiv Ψ^{″}

H = \int d x H = - \frac{1}{κ} \int d x ▵ Ψ

(23)

which can be verified using a superpotential approach based on Noether’s theorem [101]. The auxiliary field

Ψ

is determined by solving [98,102,103]

▵ Ψ - \frac{1}{4} {(Ψ^{'})}^{2} + κ^{2} π^{2} + Λ + κ \sum_{a} \sqrt{p_{a}^{2} + m_{a}^{2}} δ (x - z_{a}) = 0,

(24)

2 π^{'} + \sum_{a} p_{a} δ (x - z_{a}) = 0

(25)

which follow from reducing the constraint equations (19) and (20) via the canonical reduction procedure. Note that

Ψ

is a function of the dynamical variables (

z_{a}

p_{a}

) of the particles, as stated above.

The expression (23) is analogous to the reduced Hamiltonian in

(3 + 1)

dimensional general relativity [97,99,100]. Equation (24) can be shown to be an energy balance condition: the energy of the gravitational field (expressed in terms of

(Ψ, π)

and the cosmological constant

Λ

) plus the relativistic energy of motion of the particles must add to zero. Likewise, (25) expresses the fact that the total momentum of the gravitational field and the particles must add to zero.

Two interesting approximations can be obtained from (23) and the constraint equations. One is an expansion in powers of the coupling

κ

– the weak-field expansion. The other is an expansion in inverse powers of c – the post-Newtonian expansion.

The

κ

-expansion can be carried out by solving (24) for

▵ Ψ

and inserting the result into (23). Setting

Λ = 0

for simplicity, this yields

\begin{matrix} H & = & \sum_{a} \sqrt{p_{a}^{2} + m_{a}^{2}} \{1 - \frac{1}{4} Ψ (z_{a}) + \frac{1}{32} Ψ (z_{a}) Ψ (z_{a})\} \\ + \frac{κ}{2} \sum_{a} p_{a} χ (z_{a}) \{1 - \frac{1}{4} Ψ (z_{a})\} + \frac{κ^{2}}{8} \sum_{a} \sqrt{p_{a}^{2} + m_{a}^{2}} χ (z_{a}) χ (z_{a}) \\ = & \sum_{a} \sqrt{p_{a}^{2} + m_{a}^{2}} + \frac{κ}{8} \sum_{a} \sum_{b} (\sqrt{p_{a}^{2} + m_{a}^{2}} \sqrt{p_{b}^{2} + m_{b}^{2}} - p_{a} p_{b}) r_{a b} \\ + \frac{ϵ κ}{8} \sum_{a} \sum_{b} (\sqrt{p_{a}^{2} + m_{a}^{2}} p_{b} - p_{a} \sqrt{p_{b}^{2} + m_{b}^{2}}) (z_{a} - z_{b}) \\ + \frac{1}{4} {(\frac{κ}{4})}^{2} \{\sum_{a} \sqrt{p_{a}^{2} + m_{a}^{2}} {[\sum_{b} p_{b} r_{a b} + ϵ \sum_{b} \sqrt{p_{b}^{2} + m_{b}^{2}} (z_{a} - z_{b})]}^{2} \\ - \sum_{a} p_{a} [\sum_{b} p_{b} r_{a b} + ϵ \sum_{b} \sqrt{p_{b}^{2} + m_{b}^{2}} (z_{a} - z_{b})] [\sum_{c} \sqrt{p_{c}^{2} + m_{c}^{2}} r_{a c} + ϵ \sum_{c} p_{c} (z_{a} - z_{c})] \\ + \sum_{a} \sum_{b} [\sqrt{p_{a}^{2} + m_{a}^{2}} \sqrt{p_{b}^{2} + m_{b}^{2}} r_{a b} - ϵ p_{a} \sqrt{p_{b}^{2} + m_{b}^{2}} (z_{a} - z_{b})] \\ \times [\sum_{c} \sqrt{p_{c}^{2} + m_{c}^{2}} r_{b c} + ϵ \sum_{c} p_{c} (z_{b} - z_{c})] \\ - \sum_{a, b} [\sqrt{p_{a}^{2} + m_{a}^{2}} p_{b} r_{a b} - ϵ p_{a} p_{b} (z_{a} - z_{b})] [\sum_{c} p_{c} r_{b c} + ϵ \sum_{c} \sqrt{p_{c}^{2} + m_{c}^{2}} (z_{b} - z_{c})]\} \end{matrix}

(26)

to second order in

κ

, where

χ

is defined by

χ^{'} \equiv π

. In order to obtain (26) the boundary term

S_{b} = {[- \frac{1}{4 κ} Ψ Ψ^{'} + κ χ χ^{'} - \frac{κ}{8} \{Ψ {(χ^{2})}^{'} - Ψ^{'} χ^{2}\} + \frac{1}{32 κ} Ψ^{2} Ψ^{'}]}_{- \infty}^{\infty}

(27)

must vanish. Here there is a subtle problem in comparison to the

(3 + 1)

–dimensional setting because the dimensionless potential

G m | x | / c^{2}

becomes infinite at spatial infinity. It is straightforward to show that if the function

f (x) \equiv Ψ^{2} - 4 κ^{2} χ^{2}

and its first derivative vanish for

| x | > > | z_{a} |

for all a then the surface term (27) vanishes, since it is a sum of terms proportional to

f^{'}

and

(4 - Ψ) f^{'} + f Ψ^{'}

The

κ

-expansion is the successive approximation of the ROGS in the background of Minkowskian space-time. At each order in

κ

the relativistic form is preserved, and so this approximation is appropriate for describing relativistic motion of the particles in weak gravitational fields.

The post-Newtonian expansion is an approximation powers of

1 / c

. Temporarily restoring

t \to c t

we note that both

p_{a}^{2} / m_{a}^{2}

and

\sqrt{κ}

are of the order of

c^{- 2}

. This yields

\begin{matrix} H & = & \sum_{a} m_{a} c^{2} + \sum_{a} \frac{{\tilde{p}}_{a}^{2}}{2 m_{a}} + \frac{κ}{8} \sum_{a} \sum_{b} m_{a} m_{b} {\tilde{r}}_{a b} \\ - \sum_{a} \frac{{\tilde{p}}_{a}^{4}}{8 m_{a}^{3} c^{2}} + \frac{κ c^{2}}{8} \sum_{a} \sum_{b} m_{a} \frac{{\tilde{p}}_{b}^{2}}{m_{b}} {\tilde{r}}_{a b} - \frac{κ c^{2}}{8} \sum_{a} \sum_{b} {\tilde{p}}_{a} {\tilde{p}}_{b} {\tilde{r}}_{a b} \\ + \frac{1}{4} {(\frac{κ c^{3}}{4})}^{2} \sum_{a} \sum_{b} \sum_{c} m_{a} m_{b} m_{c} \{{\tilde{r}}_{a b} {\tilde{r}}_{a c} - ({\tilde{z}}_{a} - {\tilde{z}}_{b}) ({\tilde{z}}_{a} - {\tilde{z}}_{c})\} \end{matrix}

(28)

from (26), where the canonical variables

(z_{a}, p_{a})

have been redefined

\begin{matrix} z_{a} ⟶ {\tilde{z}}_{a} = z_{a} p_{a} ⟶ {\tilde{p}}_{a} = p_{a} - \frac{ϵ κ}{4} \sum_{b} m_{a} m_{b} r_{a b} \end{matrix}

(29)

to eliminate a spurious term of order

1 / c

, with

r_{a b} = (z_{a} - z_{b})

. Under this redefinition the Poisson brackets amongst the canonical variables remain unchanged. It is straightforward to show that the canonical equations of motion

\begin{matrix} {\dot{\tilde{z}}}_{a} = \frac{\partial H}{\partial {\tilde{p}}_{a}} {\dot{\tilde{p}}}_{a} = - \frac{\partial H}{\partial {\tilde{z}}_{a}} \end{matrix}

(30)

are equivalent to the geodesic equation (15) [98].

For illustrative purposes, consider a single static source at the origin with

Λ = 0

. The constraint equations (24) and (25) become

\begin{matrix} - \frac{1}{κ} ▵ Ψ & = & κ π^{2} - \frac{1}{4 κ} {(Ψ^{'})}^{2} + M δ (x) \end{matrix}

(31)

\begin{matrix} π^{'} & = & 0 \end{matrix}

(32)

and the Hamiltonian equations that follow from (18) are

\begin{matrix} \dot{π} + N_{0} [\frac{3 κ}{2} π^{2} + \frac{1}{8 κ} {(Ψ^{'})}^{2}] + N_{1} π^{'} + \frac{1}{2 κ} N_{0}^{'} Ψ^{'} + N_{1}^{'} π & = & 0 \end{matrix}

(33)

\begin{matrix} \dot{Ψ} + 2 κ N_{0} π - N_{1} Ψ^{'} & = & 0 \end{matrix}

(34)

\begin{matrix} κ π N_{0} + N_{1}^{'} & = & 0 \end{matrix}

(35)

\begin{matrix} \partial_{1} (\frac{1}{2} N_{0} Ψ^{'} + N_{0}^{'}) & = & 0 \end{matrix}

(36)

Solutions to these equations that ensure the boundary conditions

S_{b} = 0

hold are

\begin{matrix} Ψ & = & - \frac{κ M}{2} | x | + \frac{ϵ κ M}{2} t \end{matrix}

(37)

\begin{matrix} π & = & χ^{'} = - \frac{ϵ}{4} M (χ = - \frac{ϵ M}{4} x) \end{matrix}

(38)

\begin{matrix} N_{0} & = & e^{\frac{κ M}{4} | x |} \end{matrix}

(39)

\begin{matrix} N_{1} & = & ϵ \frac{x}{| x |} (e^{\frac{κ M}{4} | x |} - 1) \end{matrix}

(40)

where

ϵ

is a constant of integration, with

ϵ^{2} = 1

. Solutions with

ϵ = 1

are related by time-reversal to those with

ϵ = - 1

. This factor guarantees the invariance of the whole theory under the time reversal. We also see from (37) that even for a static source the auxiliary field is not static.

The Hamiltonian is

\begin{matrix} H & = & - \frac{1}{κ} \int d x ▵ Ψ = M \end{matrix}

(41)

showing that the total energy is the mass, and

\begin{matrix} g_{00} & = & - N_{0}^{2} + N_{1}^{2} = 1 - 2 e^{\frac{κ M}{4} | x |} < - 1 \end{matrix}

indicating that this static point-particle solution has no event horizon.

4.2. Charged Particles

It is also possible to include non-gravitational interactions into the ROGS. Electromagnetism is an obvious choice to consider, and in fact the derviation of the canonically reduced Hamiltonian for charged particles is parallel to that of the previous subsection for the uncharged case [104]. Here I shall highlight aspects of the charged case that are distinct from the uncharged case.

The action integral for gravitational and electromagnetic fields coupled with N charged point masses is

\begin{matrix} I & = & \int d^{2} x [\frac{1}{2 κ} \sqrt{- g} g^{μ ν} \{Ψ R_{μ ν} + \frac{1}{2} \nabla_{μ} Ψ \nabla_{ν} Ψ - g_{μ ν} Λ\} \\ - A_{μ} F_{, ν}^{μ ν} + \frac{1}{4 \sqrt{- g}} F^{μ ν} F^{α β} g_{μ α} g_{ν β} \\ + \sum_{a} \int d τ_{a} \{- m_{a} {(- g_{μ ν} (x) \frac{d z_{a}^{μ}}{d τ_{a}} \frac{d z_{a}^{ν}}{d τ_{a}})}^{1 / 2} + e_{a} \frac{d z_{a}^{μ}}{d τ_{a}} A_{μ} (x)\} δ^{2} (x - z_{a} (τ_{a}))] \end{matrix}

(42)

where

A_{μ}

and

F^{μ ν}

are the vector potential and the field strength, and

e_{a}

and

τ_{a}

are the charge and the proper time of a-th particle, respectively. The field equations that follow from the action (42) are

\begin{matrix} R - g^{μ ν} \nabla_{μ} \nabla_{ν} Ψ = 0 \end{matrix}

(43)

\begin{matrix} \frac{1}{2} \nabla_{μ} Ψ \nabla_{ν} Ψ - \frac{1}{4} g_{μ ν} \nabla^{λ} Ψ \nabla_{λ} Ψ + g_{μ ν} \nabla^{λ} \nabla_{λ} Ψ - \nabla_{μ} \nabla_{ν} Ψ = κ T_{μ ν} - g_{μ ν} Λ \end{matrix}

(44)

\begin{matrix} F_{, ν}^{μ ν} = \sum_{a} e_{a} \int d τ_{a} \frac{d z_{a}^{μ}}{d τ_{a}} δ^{2} (x - z_{a} (τ_{a})) \end{matrix}

(45)

\begin{matrix} \frac{1}{\sqrt{- g}} F_{μ ν} = \partial_{μ} A_{ν} - \partial_{ν} A_{μ}, \end{matrix}

(46)

\begin{matrix} m_{a} [\frac{d}{d τ_{a}} \{g_{μ ν} (z_{a}) \frac{d z_{a}^{ν}}{d τ_{a}}\} - \frac{1}{2} g_{ν λ, μ} (z_{a}) \frac{d z_{a}^{ν}}{d τ_{a}} \frac{d z_{a}^{λ}}{d τ_{a}}] = e_{a} \frac{d z_{a}^{ν}}{d τ_{a}} \{A_{ν, μ} (z_{a}) - A_{μ, ν} (z_{a})\} \end{matrix}

(47)

where the stress-energy is

T_{μ ν} = \sum_{a} m_{a} \int d τ_{a} \frac{1}{\sqrt{- g}} g_{μ σ} g_{ν ρ} \frac{d z_{a}^{σ}}{d τ_{a}} \frac{d z_{a}^{ρ}}{d τ_{a}} δ^{2} (x - z_{a} (τ_{a})) + \frac{1}{(- g)} \{F_{μ α} F_{ν β} g^{α β} - \frac{1}{4} g_{μ ν} F_{α β} F^{α β}\}

(48)

whose conservation is guaranteed from (44). Note that in (1+1) dimensions no magnetic component of the field exists. Inserting the trace of (44) into (43) yields (14) as before. This equation, along with (45), (46), and (47) form a closed system of equations for gravity, electromagnetism, and charged N-body matter.

Using the form (16) of the metric, the variational principle yields the set of equations

\begin{matrix} \dot{π} & + & N_{0} \{\frac{3 κ}{2} \sqrt{γ} π^{2} - \frac{κ}{\sqrt{γ}} π Π + \frac{1}{8 κ \sqrt{γ} γ} {(Ψ^{'})}^{2} + \frac{1}{4 \sqrt{γ}} (E^{2} + 2 \frac{Λ}{κ}) \\ - \sum_{a} \frac{p_{a}^{2}}{2 γ^{2} \sqrt{\frac{p_{a}^{2}}{γ} + m_{a}^{2}}} δ (x - z_{a} (t))\} \\ + & N_{1} \{- \frac{1}{γ^{2}} Π Ψ^{'} + \frac{π^{'}}{γ} + \sum_{a} \frac{p_{a}}{γ^{2}} δ (x - z_{a} (t))\} + N_{0}^{'} \frac{1}{2 κ \sqrt{γ} γ} Ψ^{'} + N_{1}^{'} \frac{π}{γ} = 0, \end{matrix}

(49)

\begin{matrix} \dot{γ} - N_{0} (2 κ \sqrt{γ} γ π - 2 κ \sqrt{γ} Π) + N_{1} \frac{γ^{'}}{γ} - 2 N_{1}^{'} = 0, \end{matrix}

(50)

\begin{matrix} R^{0} = 0, \end{matrix}

(51)

\begin{matrix} R^{1} = 0, \end{matrix}

(52)

\begin{matrix} \dot{Π} + \partial_{1} (- \frac{1}{γ} N_{1} Π + \frac{1}{2 κ \sqrt{γ}} N_{0} Ψ^{'} + \frac{1}{κ \sqrt{γ}} N_{0}^{'}) = 0, \end{matrix}

(53)

\begin{matrix} \dot{Ψ} + N_{0} (2 κ \sqrt{γ} π) - N_{1} (\frac{1}{γ} Ψ^{'}) = 0, \\ {\dot{p}}_{a} + \frac{\partial N_{0}}{\partial z_{a}} \sqrt{\frac{p_{a}^{2}}{γ} + m_{a}^{2}} - \frac{N_{0}}{2 \sqrt{\frac{p_{a}^{2}}{γ} + m_{a}^{2}}} \frac{p_{a}^{2}}{γ^{2}} \frac{\partial γ}{\partial z_{a}} - \frac{\partial N_{1}}{\partial z_{a}} \frac{p_{a}}{γ} \end{matrix}

(54)

\begin{matrix} ​ + N_{1} \frac{p_{a}}{γ^{2}} \frac{\partial γ}{\partial z_{a}} + \int d x N_{0} \sqrt{γ} E \frac{\partial E}{\partial z_{a}} = 0, \end{matrix}

(55)

\begin{matrix} \dot{z_{a}} - N_{0} \frac{\frac{p_{a}}{γ}}{\sqrt{\frac{p_{a}^{2}}{γ} + m_{a}^{2}}} + \frac{N_{1}}{γ} = 0 . \end{matrix}

(56)

\begin{matrix} \frac{\partial E}{\partial t} + \sum_{a} e_{a} \frac{d z_{a}}{d t} δ (x - z_{a} (t)) = 0, \end{matrix}

(57)

\begin{matrix} \sqrt{- g} E = - \frac{\partial φ}{\partial x} - \frac{\partial A}{\partial t} \end{matrix}

(58)

where

A_{μ} = (- φ, A) E = F^{01}

(59)

and the quantities

\begin{matrix} R^{0} & = & - κ \sqrt{γ} γ π^{2} + 2 κ \sqrt{γ} π Π + \frac{1}{4 κ \sqrt{γ}} {(Ψ^{'})}^{2} - \frac{1}{κ} {(\frac{Ψ^{'}}{\sqrt{γ}})}^{'} - \frac{1}{2} \sqrt{γ} (E^{2} + 2 \frac{Λ}{κ}) \end{matrix}

\begin{matrix} - \sum_{a} \sqrt{\frac{p_{a}^{2}}{γ} + m_{a}^{2}} δ (x - z_{a} (t)) \end{matrix}

(60)

\begin{matrix} R^{1} & = & \frac{γ^{'}}{γ} π - \frac{1}{γ} Π Ψ^{'} + 2 π^{'} + \sum_{a} \frac{p_{a}}{γ} δ (x - z_{a} (t)) \end{matrix}

(61)

\begin{matrix} \frac{\partial E}{\partial x} & = & \sum_{a} e_{a} δ (x - z_{a} (t)) \end{matrix}

(62)

vanish due to the constraints. The set of equations (49) – (58) are equivalent to the set of Equations (43) – (47).

Note that in (55) and (56), all metric components (

N_{0}

N_{1}

γ

) are evaluated at the point

x = z_{a}

with

\frac{\partial f}{\partial z_{a}} \equiv {\frac{\partial f (x)}{\partial x}|}_{x = z_{a}} .

Furthermore, in (1+1) dimensions the electric field has no independent degrees of freedom. For charged particles moving within a finite region

(| x | < L)

, the electric field in an outer region

(| x | > L)

E = \pm \frac{1}{2} \sum_{a} e_{a}

E = 0

in the outer region for a system of zero total charge.

The canonical reduction of this system proceeds in a manner similar to the uncharged case. The coordinate conditions (21) can again be chosen and the reduced action is still given by (22). The reduced Hamiltonian is again given by (23), but now the constraints become

▵ Ψ - \frac{1}{4} {(Ψ^{'})}^{2} + κ^{2} π^{2} + \frac{1}{2} (κ E^{2} + 2 Λ) + κ \sum_{a} \sqrt{p_{a}^{2} + m_{a}^{2}} δ (x - z_{a}) = 0,

(63)

2 π^{'} + \sum_{a} p_{a} δ (x - z_{a}) = 0 .

(64)

The consistency of this canonical reduction is proven by showing that the canonical equations of motion derived from the reduced Hamiltonian (23) are identical with the Equations (55) and (56) [98,104].

5. The 2-Body Problem

As stated in the introduction, an exact solution to the two body problem is known in Newtonian theory, but not in general relativity due to dissipation of energy in the form of gravitational radiation. Hence analysis of a two body system in general relativity (e.g., binary pulsars) necessarily involves resorting to approximation methods such as a post-Newtonian expansion [99,105]. Quite remarkably, there are a number of exact solutions [103,104,104,106,107,108] to the 2-body problem in the ROGS theory described above. While this is in part understandable due to the lack of gravitational radiation (there are no gravitons in

(1 + 1)

dimensions), the non-linearity of the system does not obviously admit exact solutions, and in fact a general dilaton theory of gravity will not have them.

5.1. Solution for 2 Charged Particles

Here we present the exact solution for the charged case [104], since from it the electrically neutral case is recovered by setting

e_{1} = e_{2} = 0

. The standard approach for obtaining a solution is to find an explicit expression for the Hamiltonian (23) by solving (63) and (64). From this the equations of motion can be derived, which in turn can be solved to obtain the trajectories of the particles.

Noting that the electric field appears in the combination

(E^{2} + 2 Λ / κ)

in all equations, it is convenient to set

V (x) \equiv E^{2} - C and Λ_{e} \equiv - 2 Λ - κ C

(65)

with

C \equiv \frac{1}{4} {(\sum_{a} e_{a})}^{2}

. The quantity

Λ_{e}

is an effective cosmological constant that includes the contribution from the electric field. This situation arises because, analogous to the way in which a 4-form behaves in

(3 + 1)

dimensions [109], in

(1 + 1)

dimensions the electromagnetic field strength is a 2-form, and so contributes to the stress-energy tensor in the same manner as a cosmological constant in compact spatial regions.

Defining

ϕ

Ψ = - 4 ln | ϕ |,

(66)

the constraints (63) and (64) for a two-particle system become

\begin{matrix} ▵ ϕ - \frac{1}{4} \{κ^{2} {(χ^{'})}^{2} + \frac{κ}{2} V - \frac{1}{2} Λ_{e}\} ϕ & = & \frac{κ}{4} \{\sqrt{p_{1}^{2} + m_{1}^{2}} ϕ (z_{1}) δ (x - z_{1}) \\ + \sqrt{p_{2}^{2} + m_{2}^{2}} ϕ (z_{2}) δ (x - z_{2})\} \end{matrix}

(67)

▵ χ = - \frac{1}{2} \{p_{1} δ (x - z_{1}) + p_{2} δ (x - z_{2})\}

(68)

along with (62) for the electric field, whose solution is

E = \frac{1}{2} \partial_{x} \sum_{a} e_{a} | x - z_{a} (t) | .

(69)

It is also straightforward to solve (68); the result is

χ = - \frac{1}{4} \{p_{1} | x - z_{1} | + p_{2} | x - z_{2} |\} - ϵ X x + ϵ C_{χ}

(70)

where X and

C_{χ}

are constants of integration and, as in (37),

ϵ

(

ϵ^{2} = 1

) ensures that the time reversal properties of

χ

are explicitly manifest. By definition,

ϵ

changes sign under time reversal and thus so does

χ

Suppose that

z_{2} < z_{1}

. We can divide space into three regions:

z_{1} < x

((+) region),

z_{2} < x < z_{1}

((0) region) and

x < z_{2}

((-) region). From (69) and (70) one sees that in each region

χ^{'}

and V are constant:

V = \{\begin{matrix} 0 & (+) region, \\ - \frac{1}{2} e_{1} e_{2} & (0) region, \\ 0 & (-) region, \end{matrix}

(71)

χ^{'} = \{\begin{matrix} - ϵ X - \frac{1}{4} (p_{1} + p_{2}) & (+) region, \\ - ϵ X + \frac{1}{4} (p_{1} - p_{2}) & (0) region, \\ - ϵ X + \frac{1}{4} (p_{1} + p_{2}) & (-) region \end{matrix}

(72)

Obtaining the solution to (67) is somewhat more complicated [103], entailing a proper choice of boundary conditions that ensure finiteness of the Hamiltonian and the vanishing of surface terms which arise in transforming the action. The result is [104]

\begin{matrix} ϕ_{+} & = & {(\frac{K_{1}}{M_{1}})}^{\frac{1}{2}} e^{- \frac{1}{4} (K_{01} z_{1} - K_{02} z_{2}) + \frac{1}{2} K_{+} (x - z_{1})} \\ ϕ_{0} & = & \frac{e^{- \frac{1}{4} (K_{01} z_{1} - K_{02} z_{2})}}{4 K_{0}} \{{(K_{1} M_{1})}^{1 / 2} e^{- \frac{1}{2} K_{0} (x - z_{1})} + {(K_{2} M_{2})}^{1 / 2} e^{\frac{1}{2} K_{0} (x - z_{2})}\} \\ ϕ_{-} & = & {(\frac{K_{2}}{M_{2}})}^{\frac{1}{2}} e^{- \frac{1}{4} (K_{01} z_{1} - K_{02} z_{2}) - \frac{1}{2} K_{-} (x - z_{2})} \end{matrix}

(73)

where

\{\begin{matrix} K_{+} & = \sqrt{κ^{2} {(X + \frac{ϵ}{4} ({\tilde{p}}_{1} + {\tilde{p}}_{2}))}^{2} - \frac{1}{2} Λ_{e}} & (+) region \\ K_{0} & = \sqrt{κ^{2} {(X - \frac{ϵ}{4} ({\tilde{p}}_{1} - {\tilde{p}}_{2}))}^{2} - \frac{κ}{2} e_{1} e_{2} - \frac{1}{2} Λ_{e}} & (0) region \\ K_{-} & = \sqrt{κ^{2} {(X - \frac{ϵ}{4} ({\tilde{p}}_{1} + {\tilde{p}}_{2}))}^{2} - \frac{1}{2} Λ_{e}} & (-) region \end{matrix}

(74)

with

{\tilde{p}}_{i} = p_{i} sgn (z_{1} - z_{2})

, and

\begin{matrix} K_{1} & \equiv & 2 K_{0} + 2 K_{-} - κ \sqrt{p_{2}^{2} + m_{2}^{2}} \\ K_{2} & \equiv & 2 K_{0} + 2 K_{+} - κ \sqrt{p_{1}^{2} + m_{1}^{2}} \\ K_{01} & \equiv & K_{0} - K_{+} + \frac{κ ϵ}{2} {\tilde{p}}_{1}, \\ K_{02} & \equiv & K_{0} - K_{-} - \frac{κ ϵ}{2} {\tilde{p}}_{2}, \\ M_{1} & \equiv & κ \sqrt{p_{1}^{2} + m_{1}^{2}} + 2 K_{0} - 2 K_{+} \\ M_{2} & \equiv & κ \sqrt{p_{2}^{2} + m_{2}^{2}} + 2 K_{0} - 2 K_{-} \end{matrix}

(75)

The Hamiltonian (23) becomes

\begin{matrix} H & = & - \frac{1}{κ} \int d x ▵ Ψ = \frac{4}{κ} {[\frac{ϕ^{'}}{ϕ}]}_{- \infty}^{\infty} = \frac{2 (K_{+} + K_{-})}{κ} \end{matrix}

(76)

and is explicitly determined in terms of the canonical variables once the solution X to

K_{1} K_{2} = M_{1} M_{2} e^{K_{0} | z_{1} - z_{2} |}

(77)

is obtained. This relation is a (not obvious) consequence of solving (67), and can more explicitly be written as

\begin{matrix} ​ & (4 K_{0}^{2} + [κ \sqrt{p_{1}^{2} + m_{1}^{2}} - 2 K_{+}] [κ \sqrt{p_{2}^{2} + m_{2}^{2}} - 2 K_{-}]) \tanh (\frac{1}{2} K_{0} | z_{1} - z_{2} |) \\ = - 2 K_{0} ([κ \sqrt{p_{1}^{2} + m_{1}^{2}} - 2 K_{+}] + [κ \sqrt{p_{2}^{2} + m_{2}^{2}} - 2 K_{-}]) \end{matrix}

(78)

which is the determining equation of the Hamiltonian.

Note that

K_{\pm}

must both be real in order that the Hamiltonian (76) have a definite meaning. This imposes a restriction on X corresponding to a value of the effective cosmological constant

Λ_{e}

. But

K_{0}

is not necessarily real; indeed for sufficiently strong electromagnetic repulsion (sufficiently large positive

e_{1} e_{2}

)

K_{0}

will be imaginary. In this case in the (0) region the solution for

ϕ

becomes

ϕ_{0} (x) = A_{s} \sin \frac{1}{2} {\tilde{K}}_{0} x + A_{c} ​cos \frac{1}{2} {\tilde{K}}_{0} x,

(79)

instead of (73), where

\begin{matrix} {\tilde{K}}_{0} & = & - i K_{0} = \sqrt{\frac{κ}{2} e_{1} e_{2} + \frac{1}{2} Λ_{e} - κ^{2} {(X - \frac{ϵ}{4} ({\tilde{p}}_{1} - {\tilde{p}}_{2}))}^{2}} \end{matrix}

(80)

yielding a new determining equation of the Hamiltonian

\begin{matrix} (4 {\tilde{K}}_{0}^{2} - [κ \sqrt{p_{1}^{2} + m_{1}^{2}} - 2 K_{+}] [κ \sqrt{p_{2}^{2} + m_{2}^{2}} - 2 K_{-}]) ​tan (\frac{1}{2} {\tilde{K}}_{0} | z_{1} - z_{2} |) \\ = 2 {\tilde{K}}_{0} ([κ \sqrt{p_{1}^{2} + m_{1}^{2}} - 2 K_{+}] + [κ \sqrt{p_{2}^{2} + m_{2}^{2}} - 2 K_{-}]) \end{matrix}

(81)

instead of (78). Indeed (81) and (79) can respectively be obtained from (78) and (73) by formally replacing

K_{0}

with

i {\tilde{K}}_{0}

Consequently (77) is applicable for all values of

K_{0}

. This transcendental equation determines H in terms of the momenta and positions of the particles. Although (77) cannot be explicitly written in terms of known functions, it can be used to obtain exactly the canonical equations of motion for

z_{i}

and

p_{i}

, which are [104]

\begin{matrix} {\dot{p}}_{1} & = & - \frac{\partial H}{\partial z_{1}} = - \frac{2}{κ} (\frac{Y_{+}}{K_{+}} + \frac{Y_{-}}{K_{-}}) \frac{K_{0} K_{1} K_{2}}{J} \end{matrix}

(82)

\begin{matrix} {\dot{z}}_{1} & = & \frac{\partial H}{\partial p_{1}} = ϵ \frac{Y_{+}}{K_{+}} + \frac{8}{J} (\frac{Y_{+}}{K_{+}} + \frac{Y_{-}}{K_{-}}) \frac{K_{0} K_{1}}{M_{1}} \{\frac{p_{1}}{\sqrt{p_{1}^{2} + m_{1}^{2}}} - ϵ \frac{Y_{+}}{K_{+}}\} \end{matrix}

(83)

\begin{matrix} {\dot{p}}_{2} & = & \frac{2}{κ} (\frac{Y_{+}}{K_{+}} + \frac{Y_{-}}{K_{-}}) \frac{K_{0} K_{1} K_{2}}{J} \end{matrix}

(84)

\begin{matrix} {\dot{z}}_{2} & = & - ϵ \frac{Y_{-}}{K_{-}} + \frac{8}{J} (\frac{Y_{+}}{K_{+}} + \frac{Y_{-}}{K_{-}}) \frac{K_{0} K_{2}}{M_{2}} \{\frac{p_{2}}{\sqrt{p_{2}^{2} + m_{2}^{2}}} + ϵ \frac{Y_{-}}{K_{-}}\} \end{matrix}

(85)

where

\begin{matrix} Y_{\pm} & \equiv & κ [X \pm \frac{ϵ}{4} (p_{1} + p_{2})] \\ Y_{0} & \equiv & κ [X - \frac{ϵ}{4} (p_{1} - p_{2})] \end{matrix}

(86)

and

\begin{matrix} J & = & 2 \{(\frac{Y_{0}}{K_{0}} + \frac{Y_{+}}{K_{+}}) K_{1} + (\frac{Y_{0}}{K_{0}} + \frac{Y_{-}}{K_{-}}) K_{2}\} \\ - 2 \{(\frac{Y_{0}}{K_{0}} - \frac{Y_{+}}{K_{+}}) \frac{1}{M_{1}} + (\frac{Y_{0}}{K_{0}} - \frac{Y_{-}}{K_{-}}) \frac{1}{M_{2}}\} K_{1} K_{2} - \frac{Y_{0}}{K_{0}} K_{1} K_{2} (z_{1} - z_{2}) . \end{matrix}

(87)

These canonical equations ensure the conservation of the Hamiltonian and the total momentum

p_{1} + p_{2}

. They can also be shown [104] to be equivalent to the geodesic Equations (55) and (56), which become

\begin{matrix} {\dot{p}}_{a} & = & - \frac{\partial N_{0}}{\partial z_{a}} \sqrt{p_{a}^{2} + m_{a}^{2}} + \frac{\partial N_{1}}{\partial z_{a}} p_{a} + \frac{1}{2} \sum_{b} e_{a} e_{b} N_{0} \frac{\partial}{\partial z_{a}} | z_{a} - z_{b} |, \end{matrix}

(88)

\begin{matrix} \dot{z_{a}} & = & N_{0} \frac{p_{a}}{\sqrt{p_{a}^{2} + m_{a}^{2}}} - N_{1} . \end{matrix}

(89)

under the coordinate conditions (21), where

\frac{\partial N_{0, 1}}{\partial z_{i}} \equiv \frac{1}{2} \{{\frac{\partial N_{0, 1}}{\partial x}|}_{x = z_{i} + 0} + {\frac{\partial N_{0, 1}}{\partial x}|}_{x = z_{i} - 0}\} .

(90)

defines the partial derivatives at

z_{1}, z_{2}

. Equations (49), (50), (53) and (54) yield the metric under the coordinate conditions (21) [104].

5.2. Test Particle Limit

Figure 1. A plot of the relativistic trajectory (blue) of a test particle in comparison to the non-relativistic case (red). The Hamiltonian for each case is set to

H = 1.125 m

and

μ = 0.1 m

Figure 1. A plot of the relativistic trajectory (blue) of a test particle in comparison to the non-relativistic case (red). The Hamiltonian for each case is set to

H = 1.125 m

and

μ = 0.1 m

To make sense of the solutions contained in (77) it is useful to first consider the test particle limit in which

m_{1} = μ < < m = m_{2}

and both particles have zero charge. Setting the latter to be a static source at the origin, with

z_{2} = 0 = p_{2}

, the defining Equation (77) becomes

(\sqrt{p^{2} + μ^{2}} - H) (m + ϵ \tilde{p} - H) = (\sqrt{p^{2} + μ^{2}} - ϵ \tilde{p}) m e^{\frac{κ}{4} (H - ϵ \tilde{p}) | z |}

(91)

where

z_{1} = z

and

p_{1} = p

. The corresponding non-relativistic Hamiltonian is

H = m + μ + \frac{κ m μ}{4} | z | + \frac{p^{2}}{2 μ}

(92)

obtained by expanding (91) for

p < < m

κ m | z | < < 1

. Typically the sum

m c^{2} + μ c^{2}

of the rest-energies (where we have set

c = 1

in the above) is subtracted from the non-relativistic Hamiltonian (92). However for proper comparison of the energy to the relativisitic case these terms need to be retained.

Figure 1 shows a comparison between the relativistic case (91) and non-relativistic case (92) in the phase space of the test particle. Even for relatively small values of the total energy, the non-relativistic motion (red) is notably distinct. For the given value of

H = 1.125 m

and an initial condition of

z = 0

, the initial momentum

p = 0.075 m

in the relativistic case as compared to

p = 0.071 m

in the non-relativisitic case. In both cases the static mass m attracts the test particle, but in the relativistic case its momentum initially decreases less rapidly. However this situation changes once the particle reaches its maximal separation from m. This occurs at

κ m | z | = 1

in the non-relativistic case, but at the shorter separation

κ m | z | = 0.89

in the relativistic case – relativistic gravitational attraction is stronger for the same total energy. One can observe the rather counter-intuitive feature that the particle is then attracted back to the source even though it has positive momentum in the relativistic case! The loss of momentum is more rapid than in the non-relativistic case, and continues to be so until the test particle returns to the origin, after which (in both cases) the motion repeats.

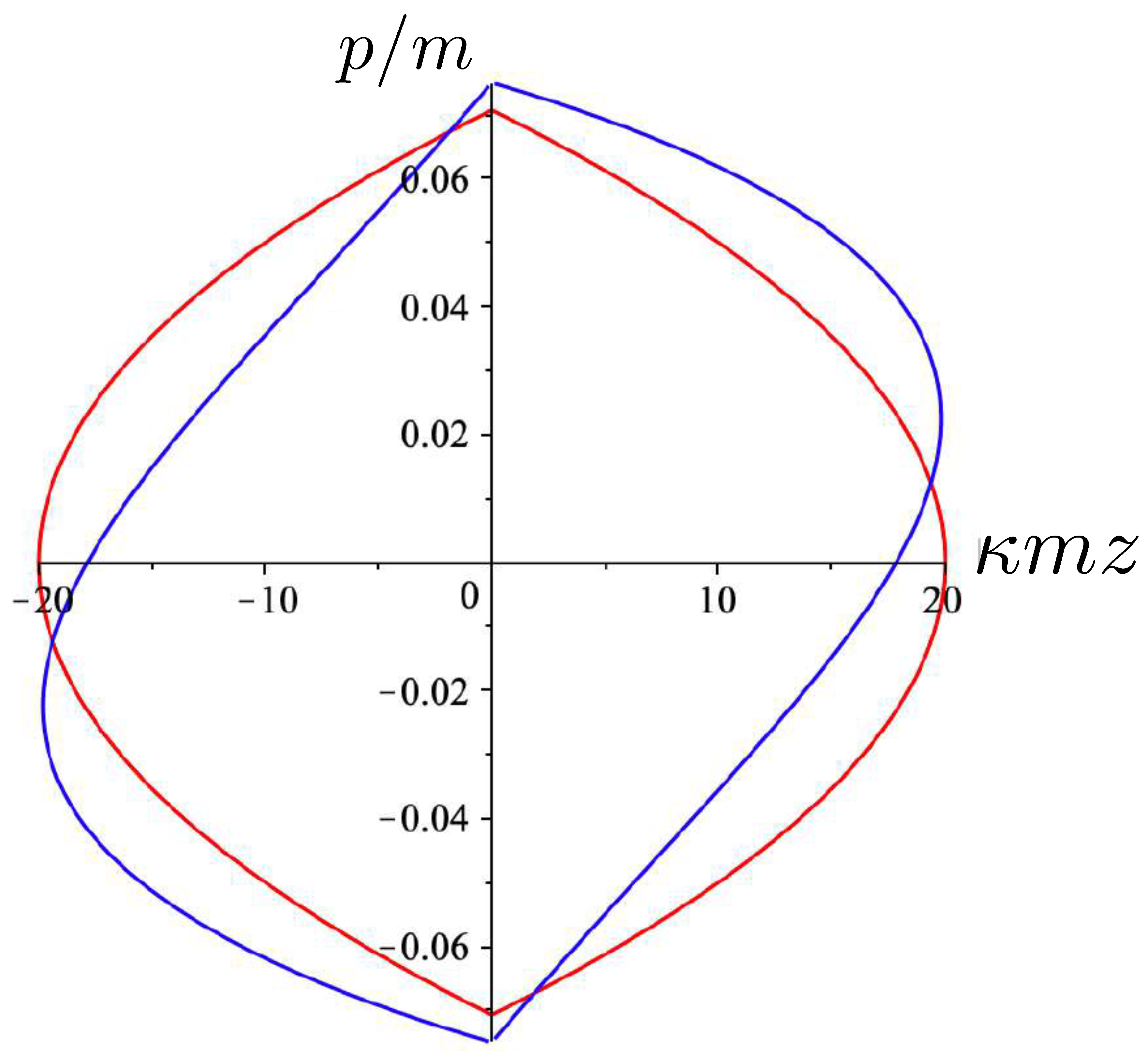
5.3. Exact Equal Mass Two-Body Motion for $Λ = 0$

For neutral bodies of equal mass the determining Equation (77) can be solved explicitly for

Λ = 0

, yielding [106,107]

H = \sqrt{p^{2} + m^{2}} + ϵ p sgn (r) - \frac{8 W [- \frac{κ}{8} (| r | \sqrt{p^{2} + m^{2}} - ϵ p r) \exp (\frac{κ}{8} (| r | \sqrt{p^{2} + m^{2}} - ϵ p r)]}{κ | r |}

(93)

in the center of inertia system

p_{1} = - p_{2} = p

, where

r = z_{1} - z_{2}

. Here

W (x)

is the Lambert W function [110]

y \cdot e^{y} = x \Rightarrow y = W (x)

(94)

which has two real branches

W_{0}

and

W_{- 1}

for real x.

Since the Hamiltonian (93) is exact for arbitrary values of m and p to infinite order in

κ

the whole structure of the theory can be studied, from the weak field to the strong field limits. As in the test particle case, a phase space trajectory in

(r, p)

space can be obtained by setting

H = H_{0}

. Alternatively, the equations of motion (82), (83), (84) and (85) yield

\begin{matrix} \dot{p} & = & - \frac{\frac{κ}{4} (H - 2 ϵ \tilde{p}) (H - ϵ \tilde{p} - \sqrt{p^{2} + m^{2}})}{2 - \frac{κ r}{4} (H - ϵ \tilde{p} - \sqrt{p^{2} + m^{2}})} sgn (r), \end{matrix}

(95)

\begin{matrix} \dot{r} & = & 2 ϵ \{1 - \frac{H - 2 ϵ \tilde{p}}{2 - \frac{κ r}{4} (H - ϵ \tilde{p} - \sqrt{p^{2} + m^{2}})} \cdot \frac{1}{\sqrt{p^{2} + m^{2}}}\} sgn (r), \end{matrix}

(96)

and can be solved numerically. However superficial coordinate singularities appear where the denominator

\{2 - κ r (H - ϵ \tilde{p} - \sqrt{p^{2} + m^{2}}) / 4\}

vanishes, corresponding to

W (x) = - 1

. This is the transit point between two branches

W_{0}

and

W_{- 1}

. and are a consequence of t being a coordinate time.

This problem can be dealt with by describing the trajectories in terms of the proper time

τ_{a}

of each particle. Using (89) this is

\begin{matrix} d τ_{a}^{2} & = & d t^{2} \{N_{0} {(z_{a})}^{2} - {(N_{1} (z_{a}) + {\dot{z}}_{a})}^{2}\} = d t^{2} N_{0} {(z_{a})}^{2} \frac{m_{a}^{2}}{p_{a}^{2} + m_{a}^{2}} (a = 1, 2) \end{matrix}

(97)

becoming

d τ = d τ_{1} = d τ_{2} = \frac{(H - 2 ϵ \tilde{p}) m}{\{2 - \frac{κ r}{4} (H - 2 ϵ \tilde{p})\} (\sqrt{p^{2} + m^{2}} - ϵ \tilde{p}) \sqrt{p^{2} + m^{2}}} d t

(98)

for both particles in the equal mass case. The canonical Equations (95) and (96) then become

\begin{matrix} \frac{d p}{d τ} & = & - \frac{κ}{4 m} \sqrt{p^{2} + m^{2}} \{H (\sqrt{p^{2} + m^{2}} - ϵ \tilde{p}) - m^{2}\} sgn (r) \end{matrix}

(99)

\begin{matrix} \frac{d r}{d τ} & = & \frac{2 ϵ}{m} (\sqrt{p^{2} + m^{2}} - ϵ \tilde{p}) \{\frac{[2 - \frac{κ r}{4} (H - ϵ \tilde{p} - \sqrt{p^{2} + m^{2}})] \sqrt{p^{2} + m^{2}}}{H - 2 ϵ \tilde{p}} - 1\} sgn (r) \end{matrix}

(100)

which remarkably have an exact solution.

This is procured as follows. Noting that H is constant, (99) is an ordinary differential equation that can be solved for

p (τ)

. The trajectory

r (τ)

can then be obtained by solving (77) or by directly solving (100) after substituting the solution for p, yielding an exact expression for the proper separation of the two bodies as a function of their mutual proper time. The result is [107]

\begin{matrix} p (τ) & = & \frac{ϵ m}{2} (f_{0} (τ) - \frac{1}{f_{0} (τ)}) sgn (r) \end{matrix}

(101)

\begin{matrix} r (τ) & = & \frac{16 sgn (r)}{κ \{H - m (f_{0} - \frac{1}{f_{0}})\}} \tanh^{- 1} [\frac{H - m (f_{0} + \frac{1}{f_{0}})}{H - m (f_{0} - \frac{1}{f_{0}})}], \end{matrix}

(102)

with

f_{0} (τ) = \frac{H}{m} [1 - \frac{\sqrt{p_{0}^{2} + m^{2}} - ϵ p_{0} sgn (r) - \frac{m^{2}}{H}}{\sqrt{p_{0}^{2} + m^{2}} - ϵ p_{0} sgn (r)} e^{\frac{ϵ κ m}{4} (τ - τ_{0})}],

(103)

where

p_{0}

is the initial momentum at

τ = τ_{0}

In Figure 2 the trajectory r is plotted for various values of

H_{0}

as a function of the mutual proper time of the two equal mass particles, with the corresponding phase space trajectories plotted underneath. For small

H_{0}

we see the distorted oval-shaped trajectory similar to that in Figure 1. The corresponding motion (shown as the solid curve in the upper diagram) is oscillatory, corresponding to the two particles flying apart to some maximal separation and then merging together to repeat the motion with their positions interchanged. As

H_{0}

increases we observe considerable distortion in the phase-space trajectory. The motion becomes increasingly asymmetric over a given half-period, with the maximal separation occurring at relatively smaller values of

τ

. For most of the motion

p > 0

; once

p < 0

the particles rapidly merge together to then repeat the motion with their positions switched.

As the energy

H_{0}

of the 2-body system increases, the departure from non-relativistic motion is quite striking. This is illustrated in Figure 3 for

H_{0} = 25 m

. We see that the period of the relativistic motion is only slightly longer than a half-period of its non-relativistic counterpart. Furthermore, the relativistic system is much more tightly bound, with the maximal separation approximately half that of the non-relativistic case.

5.4. Exact Two-Body Motion with Equal Masses and Arbitrary Charges

Turning now to the charged system, in the center of inertia frame

p_{1} = - p_{2} = p

the determining Equations (78) and (81) become

(J_{Λ}^{2} + B^{2}) \tanh (\frac{κ}{8} J_{Λ} | r |) = 2 J_{Λ} B,

(104)

and

({\tilde{J}}_{Λ}^{2} - B^{2}) \tan (\frac{κ}{8} {\tilde{J}}_{Λ} | r |) = - 2 {\tilde{J}}_{Λ} B,

(105)

respectively, where

\begin{matrix} J_{Λ} = \sqrt{{(\sqrt{H^{2} + \frac{8 Λ_{e}}{κ^{2}}} - 2 ϵ \tilde{p})}^{2} - \frac{8 e_{1} e_{2}}{κ} - \frac{8 Λ_{e}}{κ^{2}}} \\ {\tilde{J}}_{Λ} = \sqrt{\frac{8 e_{1} e_{2}}{κ} + \frac{8 Λ_{e}}{κ^{2}} - {(\sqrt{H^{2} + \frac{8 Λ_{e}}{κ^{2}}} - 2 ϵ \tilde{p})}^{2}} \\ B = H - 2 \sqrt{p^{2} + m^{2}} . \end{matrix}

(106)

Each case further subdivides into two parts:

\begin{matrix} \tanh (\frac{κ}{16} J_{Λ} | r |) & = & \frac{B}{J_{Λ}} (\tanh - type A) \end{matrix}

(107)

\begin{matrix} \tanh (\frac{κ}{16} J_{Λ} | r |) & = & \frac{J_{Λ}}{B} (\tanh - type B) \end{matrix}

(108)

for (104) and

\begin{matrix} ​tan (\frac{κ}{16} {\tilde{J}}_{Λ} | r |) & = & - \frac{B}{{\tilde{J}}_{Λ}} (​tan - type A) \end{matrix}

(109)

\begin{matrix} ​tan (\frac{κ}{16} {\tilde{J}}_{Λ} | r |) & = & \frac{{\tilde{J}}_{Λ}}{B} (​tan - type B) \end{matrix}

(110)

for (105). If both

Λ_{e} = 0

and

e_{a} = 0

then (108) has no solutions since

J_{Λ} / B

exceeds unity.

The canonical equations of motion

\begin{matrix} \dot{p} & = & - \frac{κ J_{Λ}^{2} (J_{Λ}^{2} - B^{2})}{16 C} sgn (r), \end{matrix}

(111)

\begin{matrix} \dot{r} & = & 2 ϵ \sqrt{1 + \frac{8 Λ_{e}}{κ^{2} H^{2}}} (1 - \frac{J_{Λ}^{2}}{C}) sgn (r) + \frac{2 J_{Λ}^{2}}{C} \frac{p}{\sqrt{p^{2} + m^{2}}} . \end{matrix}

(112)

where

C = \frac{1}{\sqrt{1 + \frac{8 Λ_{e}}{κ^{2} H^{2}}}} \{\sqrt{1 + \frac{8 Λ_{e}}{κ^{2} H^{2}}} J_{Λ}^{2} - (\sqrt{H^{2} + \frac{8 Λ_{e}}{κ^{2}}} - 2 ϵ \tilde{p}) (B + \frac{κ}{16} (J_{Λ}^{2} - B^{2}) r)\}

(113)

are the same for all four types. Coordinate singularities are present here as before, and these can again be dealt with by choosing the time coordinate to be the common proper time (97), which in this case is

d τ = d τ_{1} = d τ_{2} = \frac{m}{\sqrt{p^{2} + m^{2}}} \frac{J_{Λ}^{2}}{C} d t

(114)

yielding

\begin{matrix} \frac{d p}{d τ} = - \frac{κ \sqrt{p^{2} + m^{2}} (J_{Λ}^{2} - B^{2})}{16 m} sgn (r) \end{matrix}

(115)

\begin{matrix} \frac{d r}{d τ} = \frac{2 ϵ}{m} \{\frac{\sqrt{p^{2} + m^{2}} C}{J_{Λ}^{2}} - (\sqrt{p^{2} + m^{2}} - ϵ \tilde{p})\} sgn (r) \end{matrix}

(116)

for the canonical equations of motion (111) and (112).

Solving (115) gives a solution of the form (101), but where

f (τ) = \{\begin{matrix} \frac{\frac{H}{m} (1 + \sqrt{γ_{H}}) \{1 - η e^{\frac{ϵ κ m}{4} \sqrt{γ_{m}} (τ - τ_{0})}\}}{γ_{e} + \sqrt{γ_{m}} + (\sqrt{γ_{m}} - γ_{e}) η e^{\frac{ϵ κ m}{4} \sqrt{γ_{m}} (τ - τ_{0})}} & γ_{m} > 0 \\ \frac{1 + \sqrt{γ_{H}}}{\frac{m}{H} γ_{e} + \frac{σ}{m - σ \frac{ϵ κ H}{8} (τ - τ_{0})}} & γ_{m} = 0 \\ ​ \\ \frac{\frac{H}{m} (1 + \sqrt{γ_{H}})}{γ_{e} + \sqrt{- γ_{m}} \frac{σ + \frac{m^{2}}{H} \sqrt{- γ_{m}} tan [\frac{ϵ κ m}{8} \sqrt{- γ_{m}} (τ - τ_{0})]}{\frac{m^{2}}{H} \sqrt{- γ_{m}} - σ tan [\frac{ϵ κ m}{8} \sqrt{- γ_{m}} (τ - τ_{0})]}} & γ_{m} < 0 \end{matrix}

(117)

with

\begin{matrix} γ_{H} = 1 + \frac{8 Λ_{e}}{κ^{2} H^{2}} γ_{e} = 1 + \frac{2 e_{1} e_{2}}{κ m^{2}} γ_{m} = γ_{e}^{2} + \frac{8 Λ_{e}}{κ^{2} m^{2}} \end{matrix}

(118)

\begin{matrix} σ = (1 + \sqrt{γ_{H}}) (\sqrt{p_{0}^{2} + m^{2}} - ϵ p_{0} sgn (r)) - \frac{m^{2}}{H} γ_{e} η = \frac{σ - \frac{m^{2}}{H} \sqrt{γ_{m}}}{σ + \frac{m^{2}}{H} \sqrt{γ_{m}}} \end{matrix}

(119)

and

p_{0}

is the initial momentum at

τ = τ_{0}

. These solutions are valid provided

1 + \frac{8 Λ_{e}}{κ^{2} H^{2}} \geq 0

(120)

which is satisfied for all

Λ_{e} > 0

, and for

Λ_{e} < 0

imposes the constraint

H \geq \sqrt{- \frac{8 Λ_{e}}{κ^{2}}}

(121)

on the Hamiltonian.

The solution for

r (τ)

is then

r (τ) = \{\begin{matrix} \frac{16 sgn (r) \tanh^{- 1} [\frac{κ (H - m |f (τ) + \frac{1}{f (τ)}|)}{\sqrt{{(\sqrt{κ^{2} H^{2} + 8 Λ_{e}} - m κ (f (τ) - \frac{1}{f (τ)}))}^{2} - 8 κ e_{1} e_{2} - 8 Λ_{e}}}]}{\sqrt{{(\sqrt{κ^{2} H^{2} + 8 Λ_{e}} - m κ (f (τ) - \frac{1}{f (τ)}))}^{2} - 8 κ e_{1} e_{2} - 8 Λ_{e}}} & (​tanh - type A) \\ \frac{16 sgn (r) \tanh^{- 1} [\frac{\sqrt{{(\sqrt{κ^{2} H^{2} + 8 Λ_{e}} - m κ (f (τ) - \frac{1}{f (τ)}))}^{2} - 8 κ e_{1} e_{2} - 8 Λ_{e}}}{κ (H - m |f (τ) + \frac{1}{f (τ)}|)}]}{\sqrt{{(\sqrt{κ^{2} H^{2} + 8 Λ_{e}} - m κ (f (τ) - \frac{1}{f (τ)}))}^{2} - 8 κ e_{1} e_{2} - 8 Λ_{e}}} & (​tanh - type B) \end{matrix}

(122)

for the tanh-type solutions, and

r (τ) = \{\begin{matrix} \frac{16 sgn (r) (\tan^{- 1} [\frac{κ (m |f (τ) + \frac{1}{f (τ)}| - H)}{\sqrt{8 Λ_{e} + 8 κ e_{1} e_{2} - {(\sqrt{κ^{2} H^{2} + 8 Λ_{e}} - m κ (f (τ) - \frac{1}{f (τ)}))}^{2}}}] + n π)}{\sqrt{8 Λ_{e} + 8 κ e_{1} e_{2} - {(\sqrt{κ^{2} H^{2} + 8 Λ_{e}} - m κ (f (τ) - \frac{1}{f (τ)}))}^{2}}} (​tan - type A) \\ \frac{16 sgn (r) (\tan^{- 1} [\frac{\sqrt{8 Λ_{e} + 8 κ e_{1} e_{2} - {(\sqrt{κ^{2} H^{2} + 8 Λ_{e}} - m κ (f (τ) - \frac{1}{f (τ)}))}^{2}}}{κ (H - m |f (τ) + \frac{1}{f (τ)}|)}] + n π)}{\sqrt{8 Λ_{e} + 8 κ e_{1} e_{2} - {(\sqrt{κ^{2} H^{2} + 8 Λ_{e}} - m κ (f (τ) - \frac{1}{f (τ)}))}^{2}}} (​tan - type B) \end{matrix}

(123)

for the tan-type solutions.

5.4.1. Neutral Particle Motion

For electrically neutral particles, with

e_{1} = e_{2} = 0

the quantity

Λ_{e} = - 2 Λ

. In this case the gravitational attraction of the masses competes with cosmic expansion or attraction, depending on the sign of

Λ_{e}

It is instructive to examine the motion for a range of masses. To this end, an arbitrary fiducial mass

m_{0}

can be chosen, which sets a calibration scale for all other quantities. Typical scenarios are illustrated in Figure 4 and Figure 5.

For

Λ_{e} < 0

the curvature

R < 0

in the absence of stress-energy (from (14)) corresponding to cosmic attraction, depicted in Figure 4. The particles always remain bound, and for large values of m undergo oscillation about their centre of inertia in a manner not too different from that shown in Figure 2 for small

H_{0}

. However for very small m a rather surprising situation arises: a sharp extremum develops early in each half-period followed by a second, broader extremum. The first extremum is visible in Figure 4 for the

m = 0.05 m_{0}

curve, but also appears for smaller values of m; it is not visible for

m = 0.001 m_{0}

due to plotting precision.

In all cases in Figure 4 the two particles start at

r = 0

with equal opposing momentum and and depart in opposite directions. For small enough m they quickly reach a maximum separation and then go back toward one another for a certain period of proper time. At some point they each reverse direction, moving apart more slowly until they attain a second maximal separation. They then reverse direction again, returning to their starting point where the motion then repeats itself with the particles interchanged.

This peculiar behavior, first observed in [102,103], is due to a subtle interplay between the gravitational attraction and relativistic motion of the particles in a spacetime with cosmic attraction. It is demonstrative of unexpected relativistic behaviour that self-gravitating systems can exhibit.

Λ_{e} > 0

R > 0

in the absence of stress-energy, and a de Sitter-like cosmic expansion ensues. The situation for various values of m is illustrated in Figure 5. For large enough m the motion is bounded. As m decreases, the period of the motion becomes larger, until at a critical value of

m ≲ 4.729

the period becomes infinite. Here the cosmic expansion is balances the gravitational attraction of the particles, and for smaller values of m dominates. The bound behaviour is fully analogous to that of an overdense universe that expands to some maximal value of the scale factor and then recontracts; the unbound behaviour is analogous to that of an underdense universe whose deceleration parameter is insufficient to prevent full cosmic dilution.

All of the above behaviour is described by the tanh-type solutions. However there is a countably infinite set of unbounded motions described by the tan-type solutions. Some examples are shown in Figure 6 for the phase-space. For

0 < Λ_{e} < Λ_{c}

both bounded and unbounded motions exist for fixed value of

H = H_{0}

, shown in the left panel of Figure 6. The bounded motion consists of the distorted oscillations noted previously, whereas the unbounded motion consists of two particles simply approaching each other at some minimal value of

| r |

after which they reverse direction and proceed toward infinity. The dotted curves come from the upper expression in (123) and the dashed curves from the lower one. As

Λ_{e} \to Λ_{c}

the bulges of the solid tanh-type A curve and the dotted tan-type A curve come close, making contact at the critical value

Λ_{e} = Λ_{c}

. For

Λ_{e} > Λ_{c}

these two curves bifurcate into the solid curves shown in the right panel of Figure 6: the particles cross one another before receding toward infinity. The upper solid curve represents the motion in which

p \to p_{\pm} = \frac{(\pm \sqrt{κ^{2} H^{2} + 8 Λ_{e}} + \sqrt{8 Λ_{e}})}{2 κ}

(124)

r \to \pm \infty

One peculiar feature of the unbounded motion is that the two particles diverge to infinite separation at finite proper time. The trajectory

x (t)

of a null ray emitted from particle 2 at time T is governed by

d τ = 0

, yielding

\frac{d x}{d t} = \pm N_{0} (x (t), z_{1} (t), z_{2} (t), p (t)) - N_{1} (x (t), z_{1} (t), z_{2} (t), p (t))

(125)

for the equation of the light signal directed toward (+) or away from (-) particle 1. Numerically solving (125) yields the trajectories shown in Figure 7, which plots the trajectories of null rays emitted from particle 2 at various times T. For small

κ m_{0} T ≲ 3.4)

, the particles are in causal contact, as shown by the dotted curve of positive slope in the left panel of Figure 7. At

κ m_{0} T \approx 3.4

the light ray just barely catches up to particle 1, which itself is almost in light-like motion; this is shown by the dashed curve of positive slope. Beyond this time the particles are no longer in causal contact. For larger T, the null ray of positive slope quickly asymptotes to a line parallel to the asymptotic worldline of particle 1, shown by the dashed curve. The light rays emitted away from particle 1 all asymptote to curves parallel to the trajectory of particle 2. As T becomes even larger, the null ray emitted in the direction of particle 1 experiences a repulsive effect, ultimately reversing direction as shown in the right panel of Figure 7. For

κ m_{0} T \approx 4.82

the null ray emitted toward particle 1 asymptotes to

r = 0

. For larger values of T null rays emitted in the positive direction eventually reverse their motion and asymptote to curves that are parallel to the asymptotic trajectory of particle 2, shown by the dashed and dot-dashed lines in the left panel of Figure 7. The trajectories of the light signals emitted away from particle 1 cannot be distinguished in the plot from the trajectory of particle 2.

This behaviour can be captured in a flat-space model as follows. Consider the 2-velocity

u^{μ} = (h (σ τ), \sqrt{h^{2} (σ τ) - 1})

(126)

where

h (σ τ)

is some function and

d s^{2} = - d t^{2} + d x^{2}

(127)

is the flat metric. The general expression for the 2- acceleration is

a^{μ} = \frac{d u^{μ}}{d τ} = σ h^{'} (1, \frac{h}{\sqrt{f^{2} (σ τ) - 1}})

(128)

whose magnitude is

a \cdot a = \frac{{(σ h^{'})}^{2}}{h^{2} (σ τ) - 1}

(129)

where

h^{'} = d h (τ) / d τ

. Noting that

u \cdot u = 1

and

a \cdot u = 0

we have the following possible scenarios:

As $τ \to \infty$ , $h \to h_{0}$ where $h_{0}$ is finite. In this case the particle never becomes lightlike.
As $τ \to \infty$ , $h \to \infty$ . In this case the particle becomes lightlike, but this happens in an infinite amount of proper time (and coordinate time). The standard example is $h = cosh (σ τ)$ , the constant acceleration example.
The function $h \to \infty$ as $τ \to τ_{0}$ , where $τ_{0}$ is finite. In this case the particle asymptotes to a lightlike trajectory in a finite amount of proper time, but an infinite amount of coordinate time; an example is $h = sec (σ τ)$ . The acceleration increases as a function of proper time, diverging at $τ = τ_{0}$ . This last situation is realized by the exact solutions (123) with $Λ > Λ_{c}$ .

The proper time

τ_{\infty}

at which the particles attain infinite separation

r ⟶ \infty

τ_{\infty} = \frac{4}{κ m \sqrt{γ_{m}}} \log (\frac{H_{0} (1 + \sqrt{γ_{H}}) - (p_{+} + \sqrt{p_{+}^{2} + m^{2}}) (1 + \sqrt{γ_{m}})}{η [H_{0} (1 + \sqrt{γ_{H}}) - (p_{+} + \sqrt{p_{+}^{2} + m^{2}}) (\sqrt{γ_{m}} - 1)]})

(130)

for any given m, where

p_{+}

is given by (124).

5.4.2. Charged Particle Motion with $Λ_{e} = 0$

There are two qualtiatively distinct cases of charged particle motion: attractive, when the particles have opposite sign charges, and repulsive, when the charges have the same sign. The situation becomes further complicated for nonzero

Λ_{e}

, and so it is more instructive to first consider

Λ_{e} = 0

. Since the charges appear in all solutions as the product

e_{1} e_{2}

, it is sufficient to set

e_{1} = - e_{2} = q

for the attractive case and

e_{1} = e_{2} = q

for the repulsive case.

For

Λ_{e} = 0

(117) simplifies to

\begin{matrix} f_{e} (τ) & = & \frac{H}{m γ_{e}} \{1 - η_{e} e^{\frac{ϵ κ m}{4} γ_{e} (τ - τ_{0})}\} \end{matrix}

(131)

where

η_{e} = \frac{\sqrt{p_{0}^{2} + m^{2}} - ϵ p_{0} sgn (r) - \frac{m^{2}}{H} γ_{e}}{\sqrt{p_{0}^{2} + m^{2}} - ϵ p_{0} sgn (r)}

from (118) and (119) and

p (τ)

has the form (101) with

f_{0} \to f_{e}

; the relative distance

r (τ)

is likewise obtained from (107) - (110).

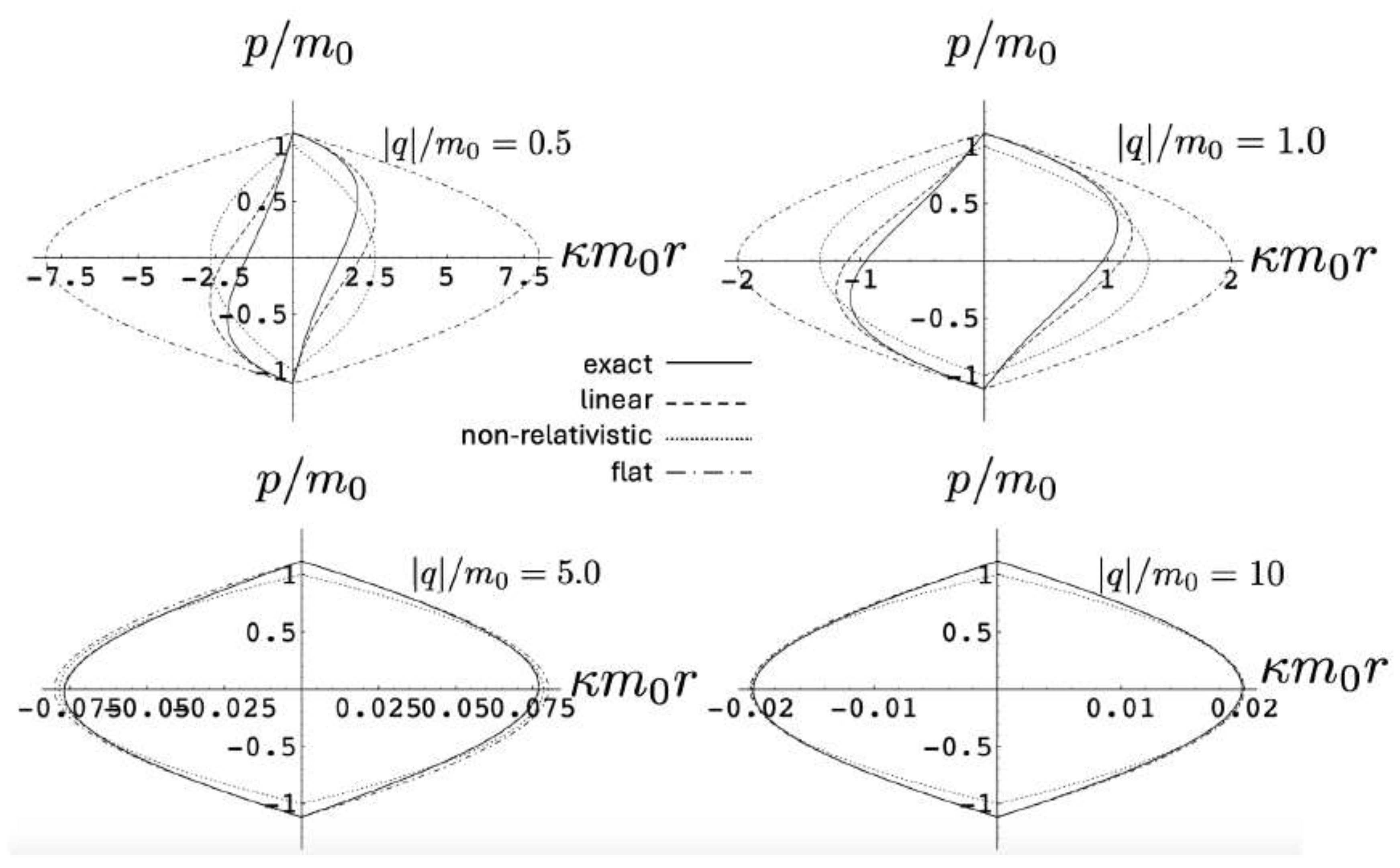
5.4.2.1 `The attractive case`: $e_{1} = - e_{2} = q$

The quantity

κ^{2} {(H - m f (τ) + \frac{m}{f (τ)})}^{2} - 8 κ e_{1} e_{2} > 0

in the attractive case and the two particles always remain bound, with the motion described by the tanh-type solution (107). As expected, as

| q |

increases the particles are more tightly bound. This is clear from Figure 8, where the maximal separation of the particles decreases as

| q |

increases, due to the additional electromagnetic attraction. The frequency of the motion correspondingly increases.

The period is determined from the initial value of

p_{0} = \sqrt{{(H / 2)}^{2} - m^{2}}

r = 0

T = \frac{16}{κ m γ_{e}} \tanh^{- 1} (\frac{γ_{e} \sqrt{H^{2} - 4 m^{2}}}{(2 - γ_{e}) H}) .

(132)

Although the above expression diverges when

γ_{e} = \frac{2 H}{2 p_{0} + H}

, this situation is never realized in the attractive case, since

γ_{e} < 1

whereas

\frac{2 H}{2 p_{0} + H} > 1

It is instructive to compare the exact relativistic motion to the motion in three approximations :

the non-relativistic motion described by the Hamiltonian

$H = 2 m + \frac{p^{2}}{m} + \frac{q^{2}}{2} | r | + \frac{κ m^{2}}{4} | r |,$

(133)
the linear approximation in $κ$ , whose Hamiltonian is

$\begin{matrix} H & = & 2 \sqrt{p^{2} + m^{2}} + \frac{1}{2} q^{2} | r | + \frac{κ}{4} \{(2 p^{2} + m^{2} - 2 ϵ \tilde{p} \sqrt{p^{2} + m^{2}}) | r | \\ + \frac{1}{2} q^{2} (\sqrt{p^{2} + m^{2}} - ϵ \tilde{p}) r^{2} + \frac{1}{24} q^{4} {| r |}^{3}\}, \end{matrix}$

(134)
the $κ \to 0$ limit, which is special-relativistic electrodynamics in (1+1)-dimensional flat space-time ; its Hamiltonian is

$H = 2 \sqrt{p^{2} + m^{2}} + \frac{q^{2}}{2} | r | .$

(135)

This comparison is illustrated in Figure 9 for

H_{0} = 3 m_{0}

for

q / m_{0} = 0.5, 1, 5

and 10. For small

q = 0.5

both the exact solution (solid curve) and the linear approximation (dashed curve) follow S-shaped trajectories, whereas the non-relativistic (dotted curve) and flat electrodynamics (dot-dashed curve) trajectories have symmetric oval shapes. As

| q |

the effect of gravity becomes relatively weak and all trajectories tend to coincide with the trajectory of flat electrodynamics.

5.4.2.2 `The repulsive case`: $e_{1} = e_{2} = q$ , $| q | \leq q_{c}$

In this case the electromagnetic force is repulsive and competes with the attractive gravitational force. There is a critical value

q_{c} = \sqrt{\frac{κ}{8}} (H - \sqrt{H^{2} - 4 m^{2}}),

(136)

of the charge, obtained from setting

J^{2} = {(H - 2 ϵ \tilde{p})}^{2} - 8 q^{2} / κ = 0

. If

| q | < q_{c}

, bounded and unbounded motions can occur, described respectively by the tanh-type (

J^{2} > 0

) and tan-type solutions (

J^{2} < 0

) for

r (τ)

. Alternatively, (136) gives the critical value of H for fixed

κ

and q, or the critical value of

κ

for fixed H and q, both corresponding to the transition from bounded to unbounded motion.

The two possibilities are illustrated in Figure 10, which plots

r (τ)

plots for fixed

H_{0} = 3 m_{0}

(left) or fixed

| q | / m_{0} = 0.1

(right). We see for fixed

H_{0}

that the period becomes larger as

| q |

increases; once the critical value

q_{c} / m_{0} = 0.2700907567

is exceeded the motion becomes unbounded and the separation of the two particles diverges at finite

τ

. Likewise, if

| q |

is fixed, then a similar transition takes place at a threshold value of

H_{0} = H_{c}

; for the particular choice given here,

H_{c} / m_{0} = 7.21249

The existence of two types of motion for fixed H and q has no non-relativistic analogue, and is a qualitatively new aspect of the relativistic gravitation. An illustration is provided in Figure 11, showing

r (τ)

for

H_{0} = 3 m_{0}

and

| q | / m_{0} = 0.25 < q_{c} / m_{0}

. Both bounded motion and a sequence of possible unbounded motions can exist. The tan-type A and B motions have the specific feature that

r (τ)

diverges (the particles attain infinite separation) at finite proper time (but at infinite coordinate time).

5.4.2.3 `The repulsive case`: $e_{1} = e_{2} = q$ , $| q | > q_{c}$

Only unbounded motion is permitted in this case since the electromagnetic repulsive force overwhelms the attractive gravitational force if

| q | > q_{c}

. The

r (τ)

trajectories are qualitatively similar to the unbounded motions depicted in Figure 11; to understand the distinctions between unbounded motion for this case and that for the

| q | \leq q_{c}

case it is instructive to consider the phase space plots.

Consider first the physical region of

(| q |, p)

parameter space, shown in Figure 12 for

H_{0} = 3 m_{0}

. From (106), the shaded area is the region

J^{2} > 0

and

B > 0

, where tanh-type A and tanh-type B give the actual trajectories. The boundary of this area is fixed by

p = - \sqrt{2 / κ} | q | + H_{0} / 2

and

p = \pm p_{0} = \pm \sqrt{{(H_{0} / 2)}^{2} - m^{2}}

(

= \pm \sqrt{5} m_{0} / 2

for the specific choice in Figure 12). The values of

| q |

at the intersections of these boundary lines are

q_{d}

(for the negative solution) and

q_{c}

(the critical value (136)) for the positive one. The tanh-type B solution is realized in a very narrow region between the dashed (

J - B = 0

) and solid (

p = - \sqrt{2 / κ} | q | + H_{0} / 2

) curves in the shaded region. The tan-type A and B trajectories are realized in the unshaded

J^{2} < 0

region.

The dotted line in Figure 12 denotes a constant

| q | / m_{0}

line whose intercepts with the diagonal lines

p = \pm \sqrt{2 / κ} | q | + H_{0} / 2

are

p_{1} / m_{0}

and

p_{2} / m_{0}

. In the subcritical region

0 < | q | < q_{c}

this dotted line would be to the left of

q_{c} / m_{0}

. The tanh-type A solutions are realized in the shaded region with

- p_{0} < p < p_{0}

, and the associated

r (τ)

trajectory is given by the solid line in Figure 11. In the unshaded region

p_{2} < p < p_{1}

between the diagonal lines and to the left of

q_{c} / m_{0}

, both tan-type A and B are realized; the associated

r (τ)

trajectories are respectively given by the dotted and dashed lines in Figure 11. The region

p_{0} < p < p_{2}

is forbidden.

In the supercritical region

q_{c} < | q | < q_{d}

all values of p in the range

- p_{0} < p < p_{1}

are allowed, and the associated phase space trajectories are shown in the left panel of Figure 13. The single bounded motion N in the right panel of Figure 11 merges with the unbounded motion A0 at

| q | = q_{c}

to yield two new unbounded trajectories

N 1

(corresponding to the unshaded region

p_{2} < p < p_{1}

), and

N 2

(corresponding to the shaded region

- p_{0} < p < p_{2}

) in Figure 13. The remaining unbounded motions

A_{n}

and

B_{n} (n = 1, 2, \dots)

are all described by respectively by the tan-type A and B solutions. In both Figure 11 and Figure 13 the analogous trajectories in flat space electrodynamics(the dot-dashed curves) are shown to illustrate the strongly deforming effects of gravity on the trajectories.

Finally for

| q | > q_{d}

all solutions are tan-type A and B since

p_{2} < - p_{0}

. Sample phase space trajectories are shown in the right panel of Figure 13. A characteristic cusp appears at

r = 0

in the

N 1

and

N 2

trajectories. For the B trajectories the motion switches between B0 (for

- p_{0} \leq p \leq p_{0}

) and B1 (for

p_{2} \leq p \leq - p_{0}

and

p_{0} \leq p \leq p_{1}

); the full motion is denoted B01.

B 12

is likewise composed of a combination of B1 and B2.

Another interesting aspect of the supercritical

| q | > q_{c}

case is that

H < 2 m

is possible – the total energy can be less than the rest energy of the particles! For

H < 2 m

only

J^{2} < 0

is possible and the shaded region in Figure 12 is absent. Consequently only unbounded motion is possible; some trajectories in phase space for this case are shown in Figure 14. All types of unbounded motions

A_{n}

and

B_{n}

are realized. Note that all trajectories curve more toward the r-axis (due to the additional effect of gravitational attraction) relative to that of flat space electrodynamics. They are also shifted in the positive p direction due to the p-dependence of the gravitational potential.

In 1+1 flat-space electrodynamics the total energy of the system is restricted to

H \geq 2 m

for attractive charges , but no such restriction on H exists for repulsive charges. We see that in a general relativistic theory the same situation prevails.

The time-reversed trajectories corresponding to these cases can all be obtained by setting

ϵ = - 1

, and trajectories in the

r < 0

region are obtained from those in

r > 0

by reversing the signs of both r and p.

5.4.3. Charged Particle Motion with $Λ_{e} \neq 0$

This is the most general case for two-body motion in the electrovacuum. The dynamics is governed by a combination of gravitational attraction, electromagnetic attraction/repulsion, and the cosmological constant. The signs of

γ_{m}

and

κ^{2} {(H_{0} - m f (τ) + \frac{m}{f (τ)})}^{2} - 8 κ e_{1} e_{2} - 8 Λ_{e}

characterize the solutions.

The possible range of motions is now rich and complicated [104], and a set of sample trajectories is presented in Figure 15. One of the noteworthy special cases occurs particular range of negative

Λ_{e}

and small mass (or large

H / m_{0}

), where the trajectories have a double-peaked structure. This is shown in the top panel of Figure 15 and is particularly noticeable for

Λ_{e} / {(κ m_{0})}^{2} = - 0.5

, shown as the solid curve. The particles begin at

r = 0

with equal and opposite initial momenta, reach a maximum separation, and then reverse direction due to the combined attractive electromagentic and graviational forces. But they soon reverse direction again, moving apart until reaching a second maximum after which they return to the starting point. For small values of

| q |

the double peak structure is present, but for sufficiently large

| q |

it disappears.

This peculiar behavior takes place due to the induced momentum-dependent potential in conjunction with the dual force attraction in the cosmological vacuum. An expansion of the Hamiltonian in terms of

κ

and

Λ_{e} / κ^{2}

\begin{matrix} H & = & 2 \sqrt{p^{2} + m^{2}} + \frac{κ}{4} {(\sqrt{p^{2} + m^{2}} - ϵ \tilde{p})}^{2} | r | + \frac{κ^{2}}{4^{2}} {(\sqrt{p^{2} + m^{2}} - ϵ \tilde{p})}^{3} r^{2} \\ + \frac{7 κ^{3}}{6 \times 4^{3}} {(\sqrt{p^{2} + m^{2}} - ϵ \tilde{p})}^{4} {| r |}^{3} - \frac{Λ_{e}}{2 κ} \cdot \frac{ϵ \tilde{p}}{\sqrt{p^{2} + m^{2}}} | r | - \frac{Λ_{e}}{16} \cdot \frac{ϵ \tilde{p} m^{2}}{p^{2} + m^{2}} r^{2} \\ + \frac{Λ_{e}^{2}}{4 κ^{3}} \cdot \frac{ϵ \tilde{p}}{{(p^{2} + m^{2})}^{3 / 2}} | r | + \cdot \cdot \cdot \end{matrix}

(137)

illustrates that negative

Λ_{e}

acts effectively as an attractive force leading to bounded (periodic) motions, whereas positive

Λ_{e}

acts effectively as a repulsive force.

For

Λ_{e} < 0

there can be both bounded and unbounded motion in the electromagnetically repulsive case depending on the size of

| q |

. For small

| q |

cosmological attraction is smaller, whereas for large

| q |

the opposite situation prevails. There is an intermediate range of

| q |

for a given

Λ_{e}

where both bounded and unbounded motion is possible [104]. Sample trajectories are shown in the middle panel of Figure 15.

In the electromagnetically attractive case, for

Λ_{e} > 0

there can again be both bounded and unbounded motion depending on the size of

| q |

. In this case attraction due to a sufficiently large value of

| q |

will overwhelm cosmological repulsion. These effects depend on the relative size of H as compared to

\sqrt{κ^{2} m^{2} / 2 Λ_{e} + 4 m^{2}}

; if H is larger than this latter quantity then there is again an intermediate range of

| q |

where both bounded and unbounded motions exist [104]. Sample trajectories are shown in the bottom panel of Figure 15.

Finally the case of joint electromagnetic and cosmological repulsion yield trajectories similar to those in Figure 11.

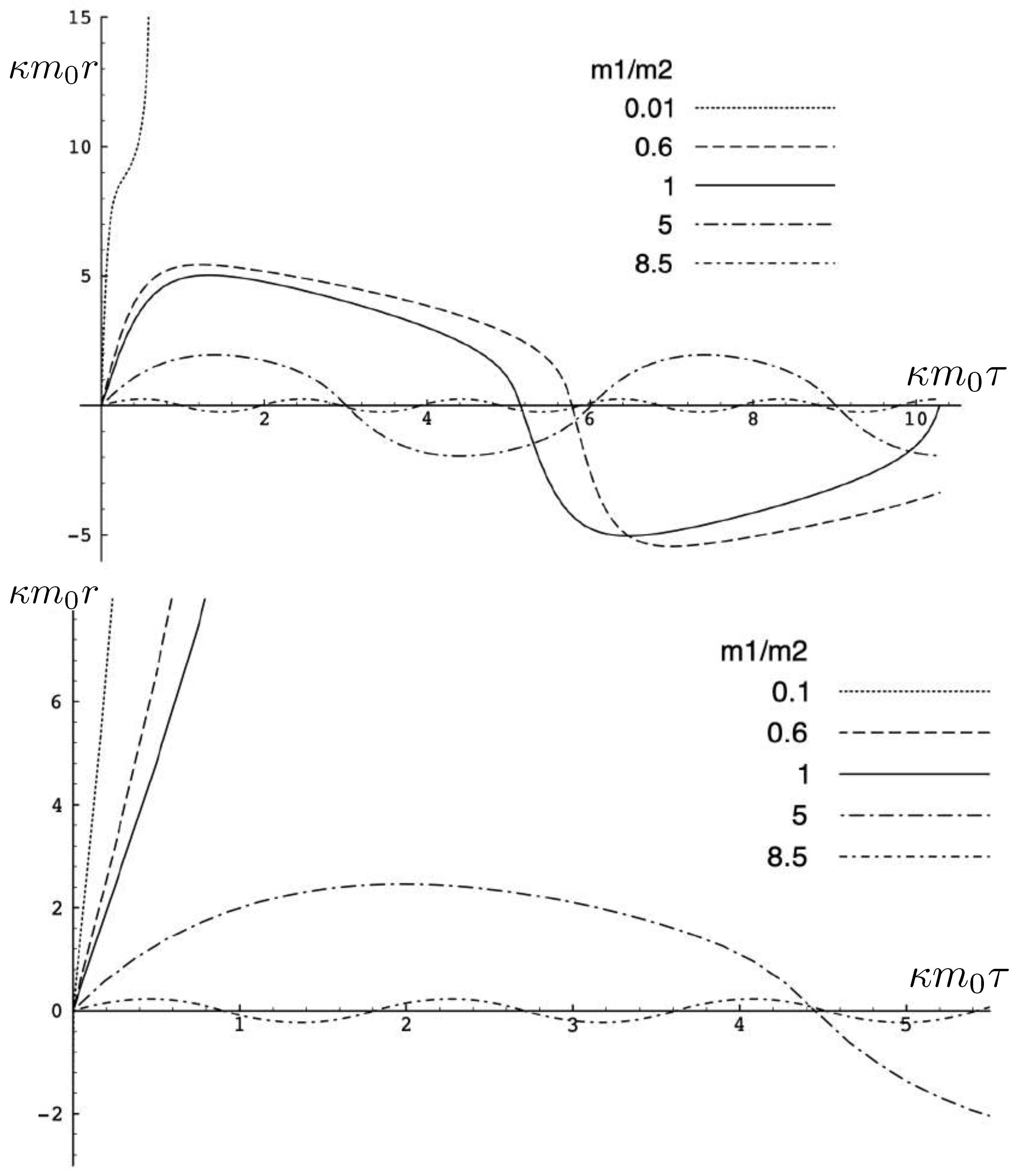
5.5. Exact Two-Body Motion with Unequal Masses

For unequal masses the proper time (97) of each particle

\begin{matrix} d τ_{1} = d t \frac{16 Y K_{0} K_{1} m_{1}}{J K M_{1} \sqrt{p^{2} + m_{1}^{2}}} d τ_{2} = d t \frac{16 Y K_{0} K_{2} m_{2}}{J K M_{2} \sqrt{p^{2} + m_{2}^{2}}} \end{matrix}

(138)

differs, where

K \equiv K_{+} = K_{-}

and

Y \equiv Y_{+} = Y_{-}

. While there are a variety of choices of time parameter one could use to describe the motion, the most natural one appears to be [103,104]

d \tilde{τ} \equiv d t \frac{16 Y K_{0}}{J K} {(\frac{K_{1} K_{2} m_{1} m_{2}}{M_{1} M_{2} \sqrt{p^{2} + m_{1}^{2}} \sqrt{p^{2} + m_{1}^{2}}})}^{1 / 2},

(139)

which is symmetric with respect to

1 \leftrightarrow 2

and reduces to the proper time (114) when

m_{1} = m_{2}

The parameter space now has an additional variable and analysis of the various types of motions is correspondingly more detailed. However the general rubric of the four types of motion depending on cosmological attraction/repulsion and electromagnetic attraction/repulsion continues to hold.

A number of the more interesting sample cases are illustrated in Figure 16 and Figure 17. When

m_{1}

is large,

m_{2}

behaves like a test body and the two particles oscillate about their centre of inertia for all values of the parameters shown. The gravitational attraction is stronger and both the period and proper maximal separation between the particles becomes shorter.

For

Λ_{e} < 0

, as the mass ratio decreases the maximal separation and period both get larger as shown in Figure 16. However eventually the attractive effect due to the cosmological constant begins to dominate, and for quite small mass ratios the period and proper maximal separation decrease and the double peak structures emerge. For larger

| q |

(top panel) the electromagnetic attraction is stronger yielding correspondingly shorter periods and maximal separations as compared to the smaller

| q |

case (bottom panel).

If there is either cosmological or electromagnetic repulsion (or both) then unbounded motion is possible, as shown in Figure 17. Large

m_{1}

yields bounded motion as before, but for a small enough mass ratio the repulsive effect dominates and the particles fly apart to infinity. Maximal separations and periods are larger for cosmological and electromagnetic repulsion, as shown in the bottom panel of Figure 17.

5.6. Static Balance

(3 + 1)

dimensions exact solutions to the 2-body problem in general relativity have been unobtainable, primarily because gravitational radiation carries energy away from the system. However a condition of static balance – in which gravitational attraction is exactly balanced by electromagnetic repulsion – was attained for two bodies [111,112] and later for N bodies on a line [113]. This condition is

e_{i} = \pm \sqrt{4 π G} m_{i},

(140)

which is more stringent than the corresponding condition

G m_{1} m_{2} - \frac{e_{1} e_{2}}{4 π} = 0

(141)

in Newtonian theory. Whether or not (140) is a is a necessary condition for static balance remains an open question.

The corresponding static balance condition in (1+1) dimensions can be straightforwardly obtained from the determining Equation (77): it is simply the extremum of H with respect to r. Setting

\partial H / \partial r = 0

yields, after some algebra,

\frac{κ}{2} (\sqrt{p^{2} + m_{1}^{2}} - ϵ \tilde{p}) (\sqrt{p^{2} + m_{2}^{2}} - ϵ \tilde{p}) - e_{1} e_{2} = 0

(142)

which is the force-balance condition. If

p = 0

then

\frac{κ}{2} m_{1} m_{2} - e_{1} e_{2} = 0

(143)

which is the static balance condition [108]. This condition is identical with that of (141) in Newtonian theory in (1+1) dimensions.

However there is a more general solution to (142), which is

p_{c} = \pm \frac{| {(\frac{κ}{2})}^{2} m_{1}^{2} m_{2}^{2} - e_{1}^{2} e_{2}^{2} |}{\sqrt{2 κ e_{1} e_{2}} \sqrt{(\frac{κ}{2} m_{1}^{2} + e_{1} e_{2}) (\frac{κ}{2} m_{2}^{2} + e_{1} e_{2})}} .

(144)

provided

e_{1} e_{2} > 0

, where

p = p_{c}

is the (constant) value of the momentum for which the repulsive electromagnetic and attractive gravitational forces between both particles are the same.

Non-relativistically (143) is the force-balance condition that includes both the static case and uniform motion. However in the relativistic case these two are different. In general the force-balance condition (142) depends on the momentum and allows for uniform motion in the centre of inertia system in which both particles either approach or recede with constant momentum (144). The static balance condition (143) is the special case for which

p_{c} = 0

6. The 3-Body Problem

The 3-body problem for a relativistic self-gravitating system is an interesting subject of study, in large part because its non-relativistic counterpart models several interesting physical systems. These include two elastically colliding billiard balls in a uniform gravitational field [114], perfectly elastic collisions of a particle with a wedge in a uniform gravitational field [3], and a “linear baryon” (a bound state of three quarks along a line) [115]. These systems can even be tested experimentally [116].

The first study of 3-body motion in a fully relativistic context was carried out over 20 years ago [28,29], with extensions to include unequal masses [117], a cosmological constant [118], and charge [119] subsequently undertaken. The most effective means to study the dynamics of the 3-body ROGS is to work in the canonical formalism [98]. This approach yields an exact expression for the Hamiltonian in terms of the four physical degrees of freedom of the system: the two proper separations of the point particles and their conjugate momenta.

The non-relativistic system can be shown to be equivalent to that of a single particle moving in a hexagonal-well potential in 2 spatial dimensions. The 3-body ROGS has an exact relativistic generalization of this hexagonal-well problem, providing insight into intrinsically non-perturbative relativistic effects. For equal mass particles, the cross-sectional shape of the well is that of a regular hexagon in the non-relativistic case. Unequal masses distort this symmetry to that of a ‘squashed’ hexagon, whose sides have differing length. The hexagonal symmetry is maintained relativistically, with the sides of the hexagon curved outward.

Poincaré sections can be used to examine the global structure of the phase space. The relativistic plots are qualitatively similar to their non-relativistic counterparts, but distorted toward the lower-right of the phase plane. This is due relativistic gravitational momentum that continuously distorts the basic structure of the Poincaré plot.

6.1. 3-Body Constraint Equations

The constraints (63) and (64) for a 3-body system become

\begin{matrix} ▵ ϕ - \frac{κ^{2}}{4} {(χ^{'})}^{2} ϕ & = & \frac{κ}{4} \{\sqrt{p_{1}^{2} + m_{1}^{2}} ϕ (z_{1}) δ (x - z_{1}) + \sqrt{p_{2}^{2} + m_{2}^{2}} ϕ (z_{2}) δ (x - z_{2}) \end{matrix}

\begin{matrix} ​ + \sqrt{p_{3}^{2} + m_{3}^{2}} ϕ (z_{3}) δ (x - z_{3})\} \end{matrix}

(145)

\begin{matrix} ▵ χ & = & - \frac{1}{2} \{p_{1} δ (x - z_{1}) + p_{2} δ (x - z_{2}) + p_{3} δ (x - z_{3})\} \end{matrix}

(146)

where the general solution to this latter equation is

χ = - \frac{1}{4} \{p_{1} | x - z_{1} | + p_{2} | x - z_{2} | + p_{3} | x - z_{3} |\} - ϵ X x + ϵ C_{χ} .

(147)

As before

ϵ

(

ϵ^{2} = 1

) flips sign under time-reversal, and X and

C_{χ}

are constants of integration.

The strategy for solving (145) is similar to the 2-body case: spacetime is divided into four regions

z_{1} < x (+) region

z_{2} < x < z_{1} (1) region

z_{3} < x < z_{2} (2) region

x < z_{3} (-) region

assuming

z_{3} < z_{2} < z_{1}

. Within each of these regions

χ^{'}

is constant

χ^{'} = \{\begin{matrix} - ϵ X - \frac{1}{4} (p_{1} + p_{2} + p_{3}) & (+) region \\ - ϵ X + \frac{1}{4} (p_{1} - p_{2} - p_{3}) & (1) region \\ - ϵ X + \frac{1}{4} (p_{1} + p_{2} - p_{3}) & (2) region \\ - ϵ X + \frac{1}{4} (p_{1} + p_{2} + p_{3}) & (-) region \end{matrix}

(148)

and (145) has the solution

\{\begin{matrix} ϕ_{+} (x) = A_{+} e^{\frac{κ}{2} K_{+} x} + B_{+} e^{- \frac{κ}{2} K_{+} x} \\ ϕ_{1} (x) = A_{1} e^{\frac{κ}{2} K_{1} x} + B_{1} e^{- \frac{κ}{2} K_{1} x} \\ ϕ_{2} (x) = A_{2} e^{\frac{κ}{2} K_{2} x} + B_{2} e^{- \frac{κ}{2} K_{2} x} \\ ϕ_{-} (x) = A_{-} e^{\frac{κ}{2} K_{-} x} + B_{-} e^{- \frac{κ}{2} K_{-} x} \end{matrix}

(149)

in each region, where

\begin{matrix} K_{+} \equiv X + \frac{ϵ}{4} (p_{1} + p_{2} + p_{3}) K_{-} \equiv X - \frac{ϵ}{4} (p_{1} + p_{2} + p_{3}) \\ K_{1} \equiv X - \frac{ϵ}{4} (p_{1} - p_{2} - p_{3}) K_{2} \equiv X - \frac{ϵ}{4} (p_{1} + p_{2} - p_{3}) \end{matrix}

(150)

In order that a full solution to (145) respect boundary conditions that ensure finiteness of the Hamiltonian, the function

ϕ

must satisfy the following matching conditions

\begin{matrix} ϕ_{+} (z_{1}) = ϕ_{1} (z_{1}) ϕ_{1} (z_{2}) = ϕ_{2} (z_{2}) ϕ_{-} (z_{3}) = ϕ_{2} (z_{3}) \end{matrix}

(151a)

\begin{matrix} ϕ_{+}^{'} (z_{1}) - ϕ_{1}^{'} (z_{1}) = \frac{κ}{4} \sqrt{p_{1}^{2} + m_{1}^{2}} ϕ (z_{1}) \end{matrix}

(151b)

\begin{matrix} ϕ_{1}^{'} (z_{2}) - ϕ_{2}^{'} (z_{2}) = \frac{κ}{4} \sqrt{p_{2}^{2} + m_{2}^{2}} ϕ (z_{2}) \end{matrix}

(151c)

\begin{matrix} ϕ_{2}^{'} (z_{3}) - ϕ_{-}^{'} (z_{3}) = \frac{κ}{4} \sqrt{p_{3}^{2} + m_{3}^{2}} ϕ (z_{3}) . \end{matrix}

(151d)

at the locations of the particles

x = z_{1}, z_{2}, z_{3}

. Satisfying these conditions is a straightforward but tedious exercise, yielding the result

\begin{matrix} L_{1} L_{2} L_{3} & = & M_{12} M_{21} L_{3}^{*} e^{\frac{κ}{4} s_{12} [(L_{1} + M_{12}) z_{13} - (L_{2} + M_{21}) z_{23}]} \\ + M_{23} M_{32} L_{1}^{*} e^{\frac{κ}{4} s_{23} [(L_{2} + M_{23}) z_{21} - (L_{3} + M_{32}) z_{31}]} \\ + M_{31} M_{13} L_{2}^{*} e^{\frac{κ}{4} s_{31} [(L_{3} + M_{31}) z_{32} - (L_{1} + M_{13}) z_{12}]} \end{matrix}

(152)

or more compactly

L_{1} L_{2} L_{3} = \sum_{i j k} |ϵ^{i j k}| M_{i j} M_{j i} L_{k}^{*} e^{\frac{κ}{4} s_{i j} [(L_{i} + M_{i j}) z_{i k} - (L_{j} + M_{j i}) z_{j k}]}

(153)

for the full determining equation of the Hamiltonian, where

\begin{matrix} M_{i j} & = & M_{i} - ϵ p_{i} s_{i j}, M_{i} = \sqrt{p_{i}^{2} + m_{i}^{2}} \end{matrix}

(154)

\begin{matrix} L_{i} & = & H - M_{i} - ϵ (\sum_{j} p_{j} s_{j i}) L_{i}^{*} = (1 - \prod_{j < k \neq i} s_{i j} s_{i k}) M_{i} + L_{i} \end{matrix}

(155)

with

z_{i j} = (z_{i} - z_{j})

s_{i j} =

sgn

(z_{i j})

, and

ϵ^{i j k}

the 3-dimensional Levi-Civita tensor. Equation (153) reproduces the correct determining equation for any permutation of the particles.

The components of the metric can be determined from (49) – (54). Of greater relevance are the canonical equations of motion (30), which become

\begin{matrix} {\dot{z}}_{1} \{L_{2} L_{3} + L_{1} L_{3} + L_{1} L_{2} \\ - [M_{2} - ϵ p_{2} s_{21}] [M_{1} - ϵ p_{1} s_{12}] [1 + \frac{κ}{4} L_{3}^{*} | z_{12} |] e^{\frac{κ}{4} s_{12} [(L_{1} + M_{12}) z_{13} - (L_{2} + M_{21}) z_{23}]} \\ - [M_{3} - ϵ p_{3} s_{31}] [M_{1} - ϵ p_{1} s_{13}] [1 + \frac{κ}{4} L_{2}^{*} | z_{13} |] e^{\frac{κ}{4} s_{13} [(L_{1} + M_{23}) z_{12} + (L_{3} + M_{32}) z_{23}]} \\ - [M_{2} - ϵ p_{2} s_{23}] [M_{3} - ϵ p_{3} s_{32}] [1 + \frac{κ}{4} L_{1}^{*} | z_{23} |] e^{\frac{κ}{4} s_{23} [(L_{3} + M_{31}) z_{13} - (L_{2} + M_{13}) z_{12}]}\} \\ = [M_{2} - ϵ p_{2} s_{21}] [(\frac{\partial M_{1}}{\partial p_{1}} - ϵ s_{12}) L_{3}^{*} - (M_{1} - ϵ p_{1} s_{12}) (ϵ s_{13} + \frac{κ}{4} L_{3}^{*} (ϵ z_{12}))] \\ \times e^{\frac{κ}{4} s_{12} [(L_{1} + M_{12}) z_{13} - (L_{2} + M_{21}) z_{23}]} \\ + [M_{3} - ϵ p_{3} s_{31}] [(\frac{\partial M_{1}}{\partial p_{1}} - ϵ s_{13}) L_{2}^{*} - (M_{1} - ϵ p_{1} s_{13}) {ϵ s_{12} + \frac{κ}{4} L_{2}^{*} (ϵ z_{13})}] \\ \times e^{\frac{κ}{4} s_{13} [(L_{1} + M_{23}) z_{12} + (L_{3} + M_{32}) z_{23}]} \\ + [M_{2} - ϵ p_{2} s_{23}] [M_{3} - ϵ p_{3} s_{32}] [- s_{12} s_{13} \frac{\partial M_{1}}{\partial p_{1}} + \frac{κ}{4} s_{23} L_{1}^{*} [ϵ | z_{12} | - ϵ | z_{13} |]] \\ \times e^{\frac{κ}{4} s_{23} [(L_{3} + M_{31}) z_{13} - (L_{2} + M_{13}) z_{12}]} \\ + \frac{\partial M_{1}}{\partial p_{1}} L_{2} L_{3} + ϵ (s_{12} L_{1} L_{3} + s_{13} L_{2} L_{1}) \end{matrix}

(156)

for

{\dot{z}}_{1}

, with similar expressions for

{\dot{z}}_{2}

and

{\dot{z}}_{3}

. Differentiating (152) with respect to

z_{1}

yields

\begin{matrix} {\dot{p}}_{1} \{L_{2} L_{3} + L_{1} L_{3} + L_{1} L_{2} \\ - [M_{2} - ϵ p_{2} s_{21}] [M_{1} - ϵ p_{1} s_{12}] [1 + \frac{κ}{4} L_{3}^{*} | z_{12} |] e^{\frac{κ}{4} s_{12} [(L_{1} + M_{12}) z_{13} - (L_{2} + M_{21}) z_{23}]} \\ - [M_{3} - ϵ p_{3} s_{31}] [M_{1} - ϵ p_{1} s_{13}] [1 + \frac{κ}{4} L_{2}^{*} | z_{13} |] e^{\frac{κ}{4} s_{13} [(L_{1} + M_{23}) z_{12} + (L_{3} + M_{32}) z_{23}]} \\ - [M_{2} - ϵ p_{2} s_{23}] [M_{3} - ϵ p_{3} s_{32}] [1 + \frac{κ}{4} L_{1}^{*} | z_{23} |] e^{κ / 4 s_{23} [(L_{3} + M_{3} - ϵ p_{3} s_{32}) z_{13} - (L_{2} + M_{2} - ϵ p_{2} s_{23}) z_{12}]}\} \\ = [M_{2} - ϵ p_{2} s_{21}] [M_{1} - ϵ p_{1} s_{12}] [\frac{κ}{4} s_{12} L_{3}^{*} [H + ϵ (p_{2} - p_{1}) s_{12} + ϵ p_{3} s_{13}]] \\ \times e^{\frac{κ}{4} s_{12} [(L_{1} + M_{12}) z_{13} - (L_{2} + M_{21}) z_{23}]} \\ + [M_{3} - ϵ p_{3} s_{31}] [M_{1} - ϵ p_{1} s_{13}] [\frac{κ}{4} s_{13} L_{2}^{*} [H + ϵ p_{2} s_{12} + ϵ (p_{3} - p_{1}) s_{13}]] \\ \times e^{\frac{κ}{4} s_{13} [(L_{1} + M_{23}) z_{12} + (L_{3} + M_{32}) z_{23}]} \\ + [M_{2} - ϵ p_{2} s_{23}] [M_{3} - ϵ p_{3} s_{32}] [\frac{κ}{4} s_{23} L_{1}^{*} p_{1} (s_{12} - s_{13})] e^{\frac{κ}{4} s_{23} [(L_{3} + M_{31}) z_{13} - (L_{2} + M_{13}) z_{12}]} \end{matrix}

(157)

for

{\dot{p}}_{1}

, again with similar expressions for

{\dot{p}}_{2}

and

{\dot{p}}_{3}

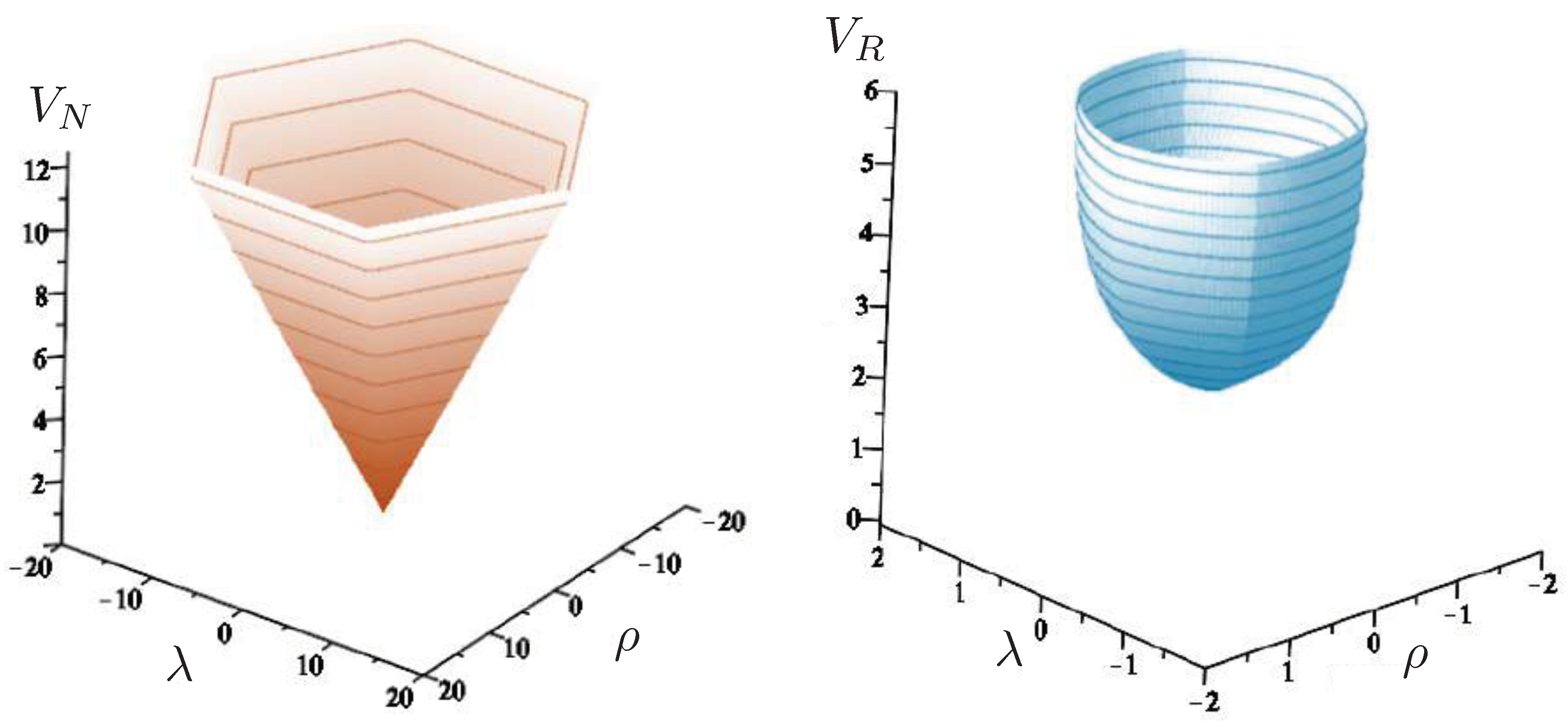
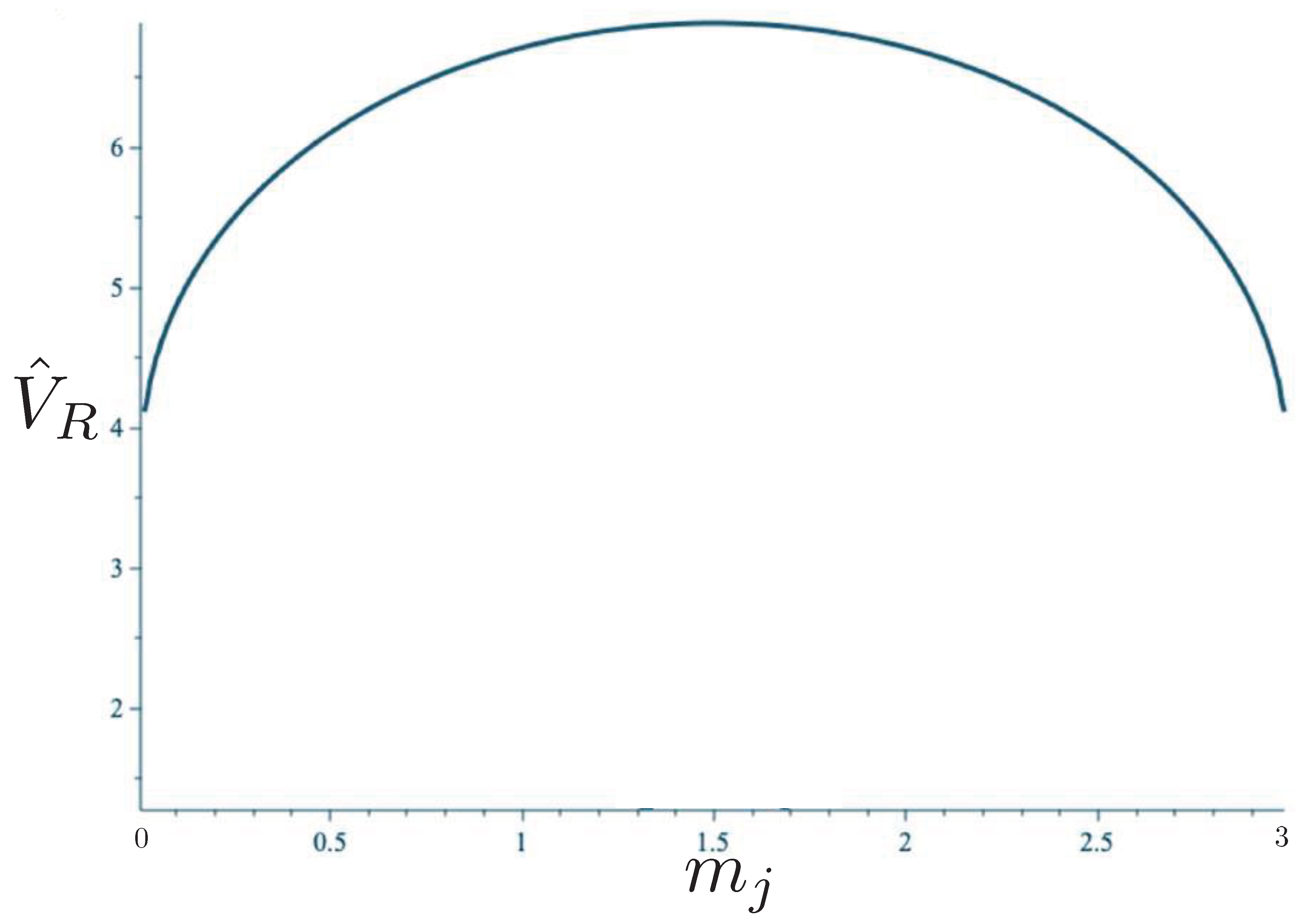
6.2. Effective Potential

The determining Equation (152) indicates that the Hamiltonian is a function of only four independent variables: the two separations between the particles and their conjugate momenta. Writing

\begin{matrix} z_{1} - z_{2} & = \sqrt{2} ρ \end{matrix}

(158)

\begin{matrix} z_{1} + z_{2} - 2 z_{3} & = \sqrt{6} λ \end{matrix}

(159)

\begin{matrix} z_{1} + z_{2} + z_{3} & = Z \end{matrix}

(160)

in turn implies the conjugate momenta

\begin{matrix} p_{ρ} & = & \frac{1}{\sqrt{2}} (p_{1} - p_{2}) \end{matrix}

(161)

\begin{matrix} p_{λ} & = & \frac{1}{\sqrt{6}} (p_{1} + p_{2} - 2 p_{3}) \end{matrix}

(162)

\begin{matrix} p_{Z} & = & \frac{1}{3} (p_{1} + p_{2} + p_{3}) \end{matrix}

(163)

obtained by imposing the requirement

{q_{A}, p_{b}} = δ_{AB}

(164)

where A,B

= ρ, λ, Z

The coordinates

ρ

and

λ

describe the motions of the three particles about their center of mass. The remaining conjugate pair

(Z, p_{Z})

respectively correspond to the centre of mass and its conjugate momenta in the non-relativistic limit. The Hamiltonian is independent of these variables and so

p_{Z}

can be set to zero without loss of generality; similarly the origin can be chosen to be

Z = 0

The Hamiltonian can be therefore be regarded as a function

H = H (ρ, λ, p_{ρ}, p_{λ})

of the four canonical degrees of freedom. The determining equation can be rewritten as

L_{+} L_{-} L_{0} = M_{+ -} M_{- +} L_{0}^{*} e^{\frac{κ}{4} s_{0} H_{0}} + M_{- 0} M_{01} L_{+}^{*} e^{\frac{κ}{4} s_{-} H_{-}} + M_{0 +} M_{+ 0} L_{-}^{*} e^{\frac{κ}{4} s_{+} H_{+}}

(165)

where

\begin{matrix} H_{0} & \equiv & (L_{1} + M_{12}) z_{13} - (L_{2} + M_{21}) z_{23} \\ = & \sqrt{2} H ρ - ϵ (2 |ρ| p_{ρ} + [|λ + \frac{ρ}{\sqrt{3}}| - |λ - \frac{ρ}{\sqrt{3}}|] p_{λ}) \end{matrix}

(166)

\begin{matrix} H_{-} & \equiv & (L_{2} + M_{23}) z_{21} - (L_{3} + M_{32}) z_{31} \\ = & H (λ - \frac{ρ}{\sqrt{3}}) - ϵ ([|ρ| - \frac{\sqrt{3}}{2} |λ + \frac{ρ}{\sqrt{3}}|] (\frac{p_{λ}}{\sqrt{3}} + p_{ρ}) + \frac{3}{2} (p_{λ} - \frac{p_{ρ}}{\sqrt{3}}) |λ - \frac{ρ}{\sqrt{3}}|) \end{matrix}

(167)

\begin{matrix} H_{+} & \equiv & (L_{3} + M_{31}) z_{32} - (L_{1} + M_{13}) z_{12} \\ = & - H (λ + \frac{ρ}{\sqrt{3}}) - ϵ ([|ρ| - \frac{\sqrt{3}}{2} |λ - \frac{ρ}{\sqrt{3}}|] (\frac{p_{λ}}{\sqrt{3}} - p_{ρ}) - \frac{3}{2} (p_{λ} + \frac{p_{ρ}}{\sqrt{3}}) |λ + \frac{ρ}{\sqrt{3}}|) \end{matrix}

(168)

and

\begin{matrix} M_{0} & = & \sqrt{\frac{2}{3}} \sqrt{p_{λ}^{2} + m_{0}^{2}} M_{\pm} = \frac{1}{\sqrt{2}} \sqrt{{(\frac{p_{λ}}{\sqrt{3}} \pm p_{ρ})}^{2} + 2 m_{\pm}^{2}} \end{matrix}

(169)

\begin{matrix} L_{\pm} & = & H - M_{\pm} \pm \frac{ϵ}{\sqrt{2}} [(\frac{p_{λ}}{\sqrt{3}} \mp p_{ρ}) s_{0} \pm \frac{2}{\sqrt{3}} p_{λ} s_{\pm}] \end{matrix}

(170)

\begin{matrix} L_{0} & = & H - M_{0} - \frac{ϵ}{\sqrt{2}} [(\frac{p_{λ}}{\sqrt{3}} + p_{ρ}) s_{+} + (\frac{p_{λ}}{\sqrt{3}} - p_{ρ}) s_{-}] \end{matrix}

(171)

\begin{matrix} M_{\pm \mp} & = & M_{\pm} \mp \frac{ϵ}{\sqrt{2}} (\frac{p_{λ}}{\sqrt{3}} \pm p_{ρ}) s_{0}, M_{\pm 0} = M_{\pm} - \frac{ϵ}{\sqrt{2}} (\frac{p_{λ}}{\sqrt{3}} \pm p_{ρ}) s_{\pm} \end{matrix}

(172)

\begin{matrix} M_{0 \pm} & = & M_{o} + \frac{ϵ \sqrt{2}}{\sqrt{3}} p_{λ} s_{\pm} L_{0}^{*} = (1 - s_{+} s_{-}) M_{0} + L_{0} \end{matrix}

(173)

\begin{matrix} L_{\pm}^{*} & = & (1 \mp s_{0} s_{\pm}) M_{\pm} + L_{\pm} \end{matrix}

(174)

It is instructive to carry out an expansion of (165) in inverse powers of the speed of light c, which is the post-Newtonian (pN) expansion. This gives

\begin{matrix} H_{p N} & = & 3 m c^{2} + \frac{p_{ρ}^{2} + p_{λ}^{2}}{2 m} + \frac{κ m^{2} c^{4}}{\sqrt{8}} [|ρ| + \frac{\sqrt{3}}{2} (|λ + \frac{ρ}{\sqrt{3}}| + |λ - \frac{ρ}{\sqrt{3}}|)] - \frac{{(p_{ρ}^{2} + p_{λ}^{2})}^{2}}{16 m^{3} c^{2}} + \frac{κ c^{2}}{\sqrt{8}} | ρ | p_{ρ}^{2} \\ + \frac{κ c^{2}}{16 \sqrt{2}} [3 (|λ + \frac{ρ}{\sqrt{3}}| + |λ - \frac{ρ}{\sqrt{3}}|) (\sqrt{3} p_{λ}^{2} + p_{ρ}^{2}) + 6 (|λ + \frac{ρ}{\sqrt{3}}| - |λ - \frac{ρ}{\sqrt{3}}|) p_{ρ} p_{λ}] \\ + \frac{κ^{2} m^{3} c^{6}}{16} [\frac{|ρ| \sqrt{3}}{2} (|λ + \frac{ρ}{\sqrt{3}}| + |λ - \frac{ρ}{\sqrt{3}}|) + \frac{3}{4} |λ + \frac{ρ}{\sqrt{3}}| |λ - \frac{ρ}{\sqrt{3}}| - \frac{3}{4} (λ^{2} + ρ^{2})] \end{matrix}

(175)

where factors of the speed of light c have been restored (recall

κ = \frac{8 π G}{c^{4}}

). To leading order in

1 / c

H = H_{N} \equiv 3 m c^{2} + \frac{p_{ρ}^{2} + p_{λ}^{2}}{2 m} + \frac{κ m^{2} c^{4}}{\sqrt{8}} [|ρ| + \frac{\sqrt{3}}{2} (|λ + \frac{ρ}{\sqrt{3}}| + |λ - \frac{ρ}{\sqrt{3}}|)] + \dots

(176)

which is the non-relativstic hexagonal-well Hamiltonian of a single particle [115] plus the total rest mass of the system. This latter quantity, while non-relativistically irrelevant, is useful to retain in order to straightforwardly compare energies and motions and energies of the relativistic (R) and non-relativistic (N) systems.

The Hamiltonian (176) describes the non-relativistic motion of a single particle of mass m (referred to as the hex-particle) in a linearly-increasing potential well in the

(ρ, λ)

plane, whose cross-sectional shape is that of a regular hexagon. To extend this to the pN and R cases, the potential can be defined by the relation

V (ρ, λ) = H (p_{ρ} = 0, p_{λ} = 0)

. From (165) we then obtain

\begin{matrix} (V_{R} - m_{1} c^{2}) (V_{R} - m_{2} c^{2}) (V_{R} - m_{3} c^{2}) \\ = (V_{R} - s_{+} s_{-} m_{3} c^{2}) m_{1} m_{2} c^{4} exp [\frac{\sqrt{2} κ R}{4} V_{R} |sin θ|] \\ + (V_{R} - s_{ρ} s_{+} m_{1} c^{2}) m_{2} m_{3} c^{4} exp [\frac{\sqrt{2} κ R}{4} V_{R} |sin (θ - \frac{π}{3})|] \\ + (V_{R} + s_{ρ} s_{-} m_{2} c^{2}) m_{3} m_{1} c^{4} exp [\frac{\sqrt{2} κ R}{4} V_{R} |sin (θ + \frac{π}{3})|] \end{matrix}

(177)

for the R potential, where

ρ = R sin θ λ = R cos θ

(178)

has been used to render the hexagonal symmetry manifest, and

s_{\pm} = sgn (\sqrt{3} λ \pm ρ)

s_{ρ} = sgn (ρ)

. The corresponding pN potential is

\begin{matrix} {\tilde{V}}_{p N} & = (m_{1} + m_{2} + m_{3}) c^{2} + \frac{κ c^{4}}{4 \sqrt{2}} (2 m_{1} m_{2} |\tilde{ρ}| + m_{1} m_{3} |\sqrt{3} \tilde{λ} + \tilde{ρ}| + m_{2} m_{3} |\sqrt{3} \tilde{λ} - \tilde{ρ}|) \\ + \frac{1}{2 c^{2}} {(\frac{κ c^{4}}{4})}^{2} m_{1} m_{2} m_{3} ((1 - {\tilde{s}}_{ρ} {\tilde{s}}_{1}) |\tilde{ρ}| |\sqrt{3} \tilde{λ} + \tilde{ρ}| + (1 + {\tilde{s}}_{ρ} {\tilde{s}}_{2}) |\tilde{ρ}| |\sqrt{3} \tilde{λ} - \tilde{ρ}| \\ + \frac{1}{2} (1 - {\tilde{s}}_{1} {\tilde{s}}_{2}) |\sqrt{3} \tilde{λ} + \tilde{ρ}| |\sqrt{3} \tilde{λ} - \tilde{ρ}|) \end{matrix}

(179)

where

\tilde{ρ}

and

\tilde{λ}

are defined as in (158) and (159) using the

{\tilde{z}}_{a}

coordinates of (29). As

c \to \infty

κ \to 0

, and we recover

\begin{matrix} V_{N} & = (m_{1} + m_{2} + m_{3}) c^{2} + \frac{2 π G}{\sqrt{2}} (2 m_{1} m_{2} |ρ| + m_{1} m_{3} |\sqrt{3} λ + ρ| + m_{2} m_{3} |\sqrt{3} λ - ρ|) \end{matrix}

(180)

which is hexagonal well potential of the N-system.

A comparison of

V_{N}

and

V_{R}

is given in Figure 18. At very low energies they are indistinguishable, but striking differences emerge with increasing energy. For all energies equipotential lines of

V_{N}

form the shape of a regular hexagon in the

(ρ, λ)

plane, with the sides rising linearly in all directions, forming the hexagonal-well potential noted earlier. The post-Newtonian potential

V_{p N}

retains the hexagonal symmetry, but distorts the sides to be parabolically concave. The relativistic potential

V_{R}

also retains the hexagonal symmetry, but the sides of the hexagon become convex, even at energies only slightly larger than the rest mass. The overall size of the hexagon at a given value of

V_{R}

is considerably smaller since its growth is extremely rapid compared to the other two cases. Its cross-sectional size reaches a maximum at

V_{R} = V_{R c} = 6.711968022 m c^{2}

, after which it decreases in diameter like

ln (V_{R}) / V_{R}

with increasing

V_{R}

. The relativistic potential is therefore an hexagonal carafe, whose neck narrows as

V_{R}

increases. The part of the potential for which

V_{R} > V_{R c}

is in an intrinsically non-perturbative relativistic regime: the motion for values of

V_{R}

larger than this cannot be understood as a perturbation from some classical limit of the motion. A comparison of the equipotential lines for each case in Figure 19 highlights these distinctions.

Furthermore, since there are couplings between the momentum and position of the hex-particle, the potential does not fully govern the motion in both the pN and R systems. In the pN system there is a momentum-dependent steepening of the walls of the hexagon to leading order in

1 / c^{2}

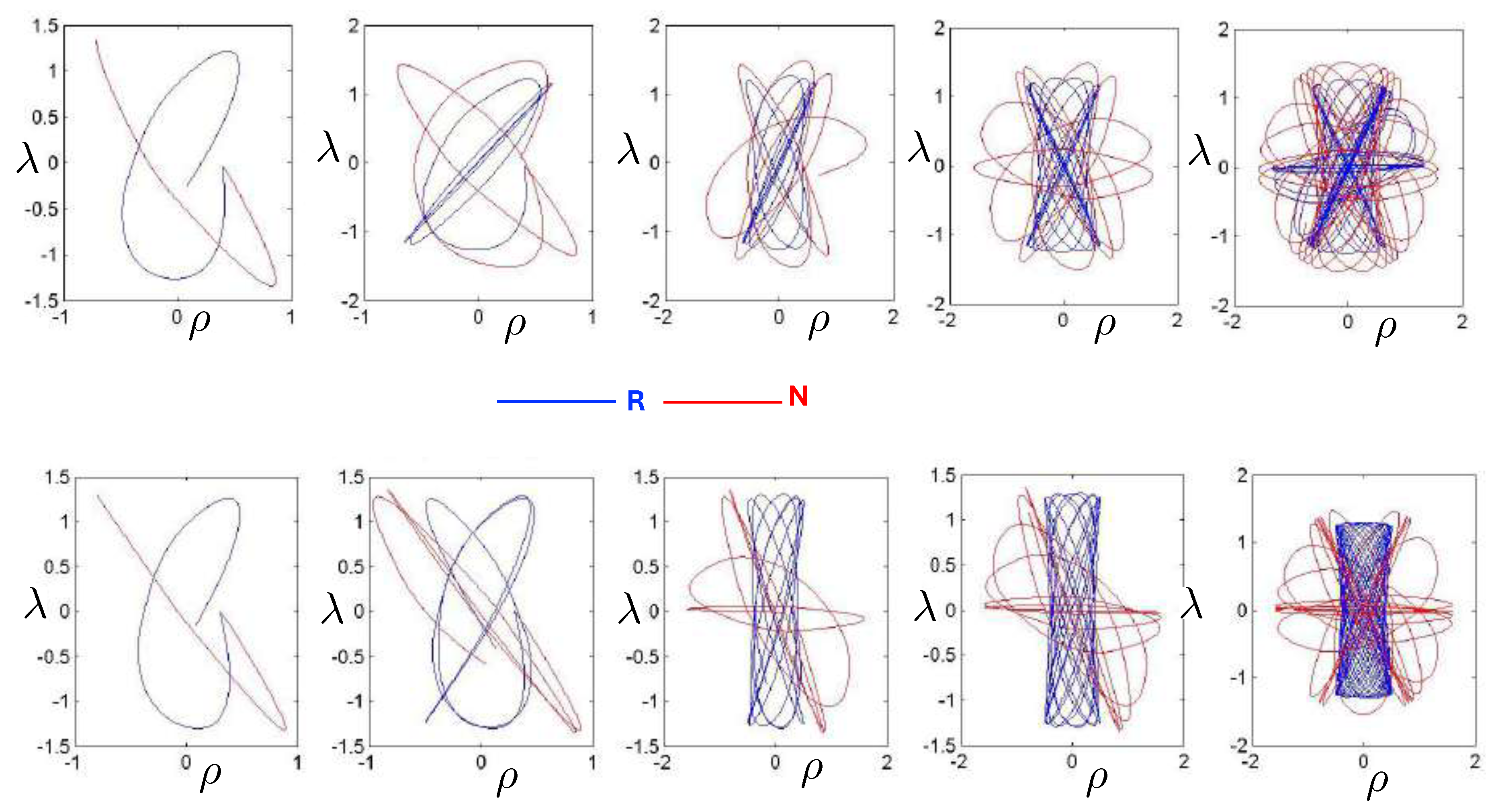
6.3. Relativistic Equal Mass 3-Body Trajectories

An analysis of the 3-body system is best carried out by considering the motion of the hex-particle in the

(ρ, λ)

plane. In the Hamiltonian formalism the motion is given by two conjugate pairs of differential equations for

(ρ, p_{ρ})

and

(λ, p_{λ})

that are continuous everywhere except across the three hexagonal bisectors

ρ = 0

ρ - \sqrt{3} λ = 0

, and

ρ + \sqrt{3} λ = 0

. These bisectors respectively correspond to the crossings of particles 1 and 2, 2 and 3, or 1 and 3, and divide the hexagon into sextants.

The non-relativistic analogue of this system is that of a ball that elastically collides with a wedge whilst experiencing a constant gravitational force [3,16]. A bounce at one of the edges of the wedge corresponds to a crossing one of the three hexagonal bisectors, and a discrete mapping can be constructed that describes the particle’s angular and radial velocities each time it collides with one of the edges. The systems are nearly identical in the equal mass case since a crossing between two equal mass particles cannot be distinguished from an elastic collision between them.

The interesting dynamics of the system arises due to these crossings, or alternatively due to the non-smoothness of the potential along the bisectors. Two types of motion can be distinguished [3]: A-motion, in which the hex-particle crosses a single bisector twice in succession (the same pair of particles cross twice in a row) and B-motion, corresponding to the hex-particle crossing two successive sextant boundaries (one particle crosses each of its compatriots in succession). Any given motion is characterized by a symbol sequence, a sequence of letters A and B, with a finite exponent n denoting n-repetitions and an overbar denoting an infinite repeated sequence. For example the expression

A^{2} B^{3}

denotes three A-motions (two adjacent particles cross twice in a row twice in succession) followed by three B-motions (one particle crosses the other two in succession, which then cross each other). The expression

{(A^{n} B^{m})}^{p}

denotes the motion

A^{n} B^{m}

repeated p times, and

\bar{(A^{n} B^{m})}

denotes infinitely many repeats of this motion. There is an ambiguity in classifying either the final or the initial crossing since the whether or not a motion is of A-type or B-type is contingent upon the previous crossing; this ambiguity can be resolved by taking the initial crossing of any sequence of motions as being unlabeled.

Since the same initial conditions for the N, pN, and R systems do not yield the same conserved energy H, comparison of these cases necessitates a choice: one can either compare at fixed values of the energy (FE conditions), modifying the initial conditions as appropriate (as required by the conservation laws for each system), or else fix the initial conditions, comparing trajectories at differing values of H (fixed-momenta (FM) conditions). Numerically it is useful to rescale

p_{i} = M_{t o t} c \hat{p_{i}} z_{i} = \frac{4}{κ M_{t o t} c^{2}} \hat{z_{i}}

(181)

in which case the equations of motion become

\begin{matrix} \frac{\partial η}{\partial \hat{p_{i}}} & = & \frac{1}{c} \frac{\partial H}{\partial p_{i}} = \frac{4}{κ M_{t o t} c^{3}} \frac{d {\hat{z}}_{i}}{d t} = \frac{d {\hat{z}}_{i}}{d \hat{t}} \end{matrix}

(182)

\begin{matrix} \frac{\partial η}{\partial \hat{z_{i}}} & = & (\frac{4}{κ M_{t o t}^{2} c^{4}}) \frac{\partial H}{\partial z_{i}} = - \frac{4}{κ M_{t o t} c^{3}} \frac{d \hat{p_{i}}}{d t} = - \frac{d \hat{p_{i}}}{d \hat{t}} \end{matrix}

(183)

where

M_{t o t} = 3 m

is the total mass of the system,

t = \frac{4}{κ M_{t o t} c^{3}} \hat{t}

, and

{\hat{z}}_{i}

and

{\hat{p}}_{i}

are the respective dimensionless positions and momenta. The quantities

M_{i}

and

L_{i}

likewise rescale

\begin{matrix} M_{i} & = & M_{t o t} c^{2} (\sqrt{{\hat{p_{i}}}^{2} + {\hat{m_{i}}}^{2}} + \hat{p_{i}}) = M_{t o t} c^{2} {\hat{M}}_{i} \end{matrix}

(184)

\begin{matrix} L_{i} & = & M_{t o t} c^{2} (η + 1 - \sqrt{{\hat{p_{i}}}^{2} + {\hat{m_{i}}}^{2}} - ϵ (\sum_{j} {\hat{p}}_{j} s_{j i})) = M_{t o t} c^{2} {\hat{L}}_{i} \end{matrix}

(185)

where

η + 1 = H / M_{t o t} c^{2}

\hat{m_{i}} = (\frac{m_{i}}{M_{t o t}})

One consideration in describing the motion is that the proper time (97) differs for each particle, even in the equal mass case. The simplest choice (but not the only one) is to work with the coordinate time t.

The plots in this section were obtained numerically [29,117], with a time step in the numerical code having a value

\hat{t} = 1

. Absolute and relative error tolerances of

ϵ_{a b s} = ϵ_{r e l} = 10^{- 8}

were imposed so that the estimated error in each of the dynamical variables

ρ (i), λ (i), p_{ρ} (i)

, and

p_{λ} (i)

at each step i in the numerical integration is

ϵ (i) \leq max (ϵ_{r e l} |y (i)|, ϵ_{a b s})

6.3.1. General Features of the Motion

For each of the N, pN, and R systems the motions fall into one of three principal classes: annuli, pretzel and chaotic. Within each class the orbits either (i) eventually densely cover the portion of

(ρ, λ)

space they occupy, or (ii) do not. A symbol sequence consisting of a finite sequence repeated infinitely many times would be in case (ii) whereas all chaotic orbits (by definition) are in case (i). Quasi-regular orbits are also in case (i); for these the symbol sequence consists of repeats of the same finite sequence, but with an A-motion added or removed at irregular intervals. In phase space the two types of orbits are separated by separatrixes (trajectories joining a pair of hyperbolic fixed points). Regular orbits lie inside the ‘elliptical’ region surrounding an elliptical fixed point whereas quasi-regular orbits lie outside such a region.

Quasi-periodic trajectories closely resemble their related periodic counterparts, except that the orbit does not exactly repeat itself. Consequently a quasi-periodic orbit eventually densely covers some region of phase space despite its high degree of regularity, manifest by its periodic symbol sequence. A particle moving on a torus

S^{1} \times S^{1}

is a textbook example. Its motion is characterized by its angular velocity around each copy of

S^{1}

; if the ratio of these is rational, the motion will be periodic, whereas the motion will be quasi-periodic if the ratio is irrational. For the 3-body case non-periodic orbits with fixed symbol sequences are quasi-periodic, and appear as a collection of closed circles, ovals, or crescents in the Poincaré section (discussed in the next subsection). Quasi-regular orbits have symbol sequences that are not fixed.

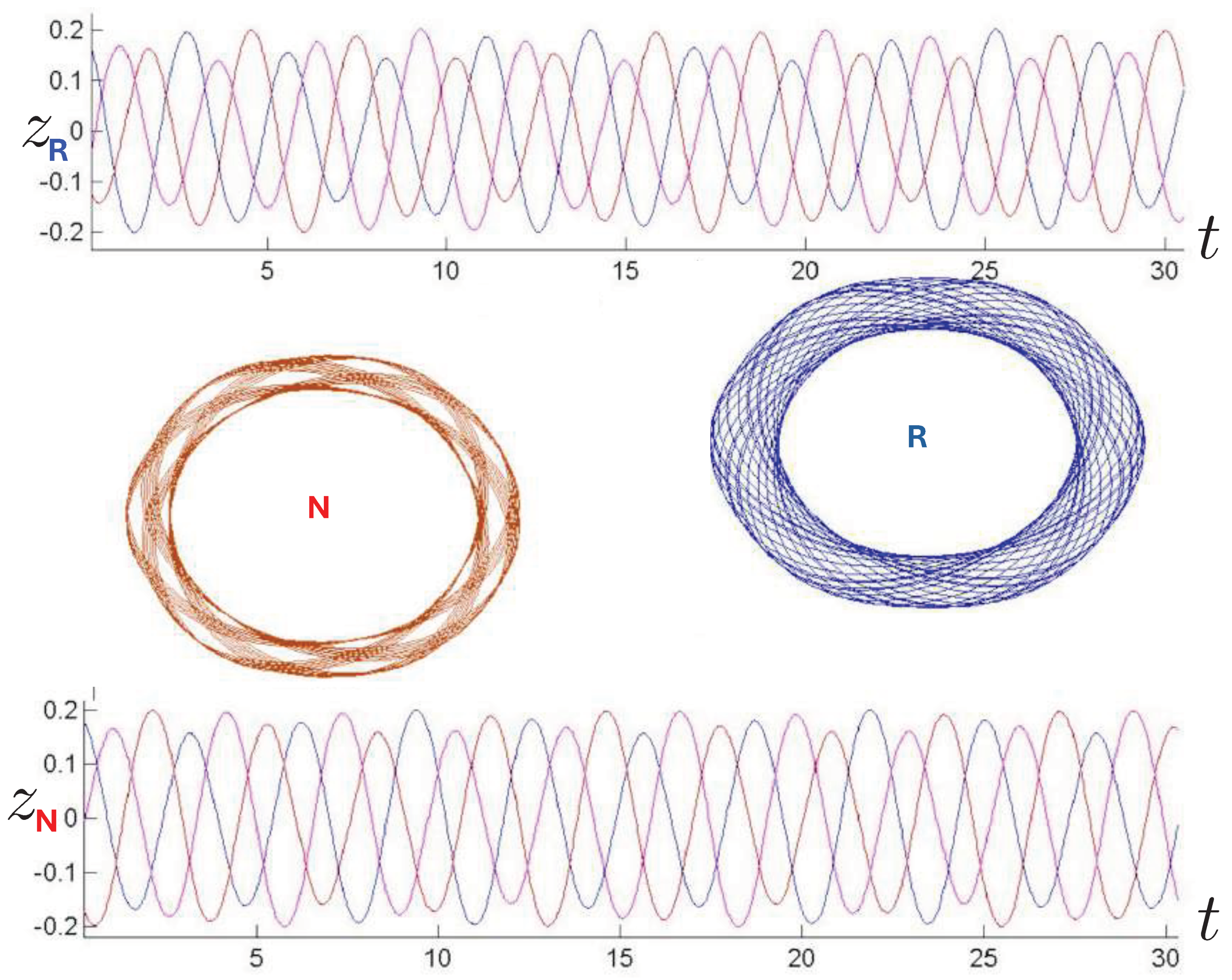
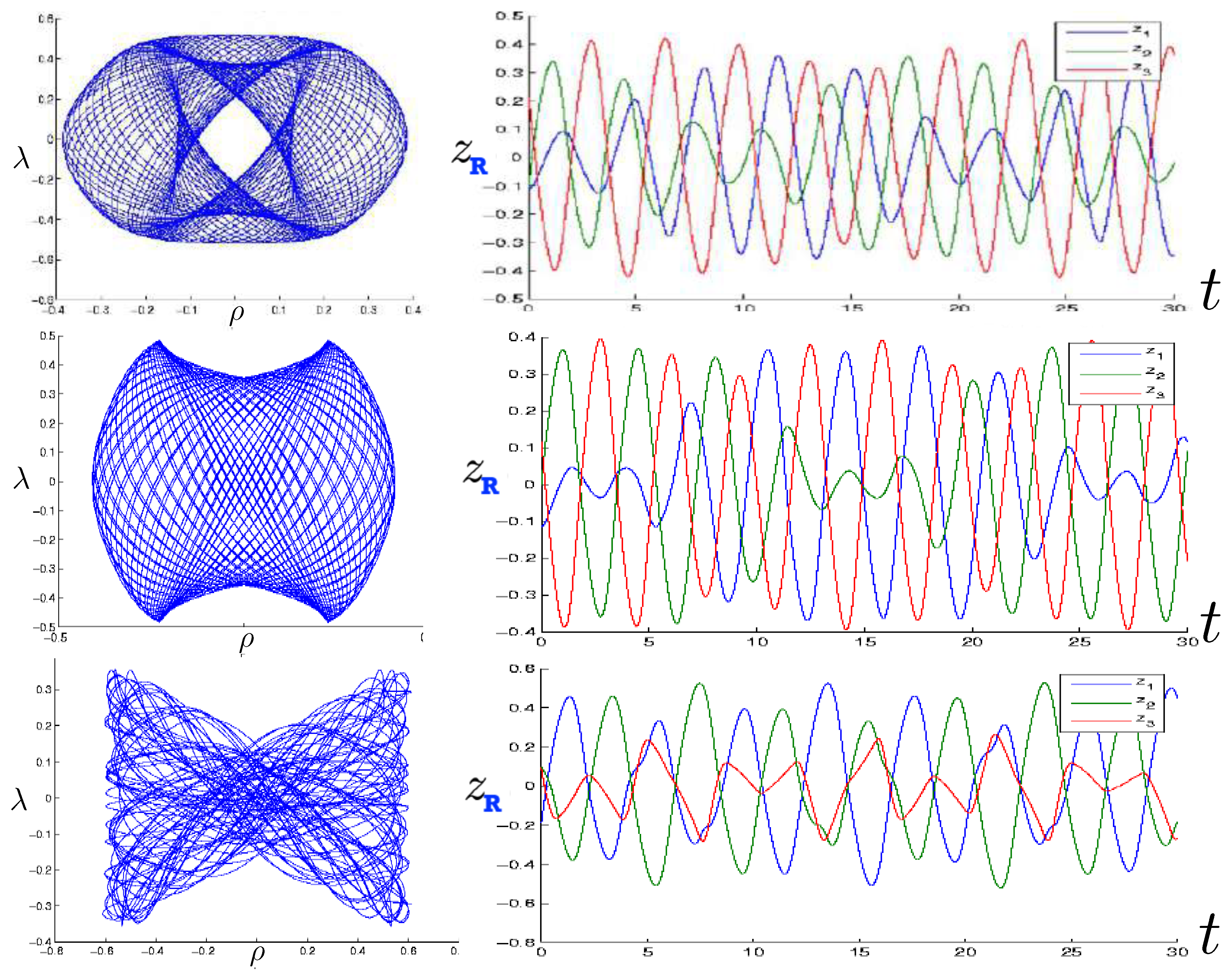
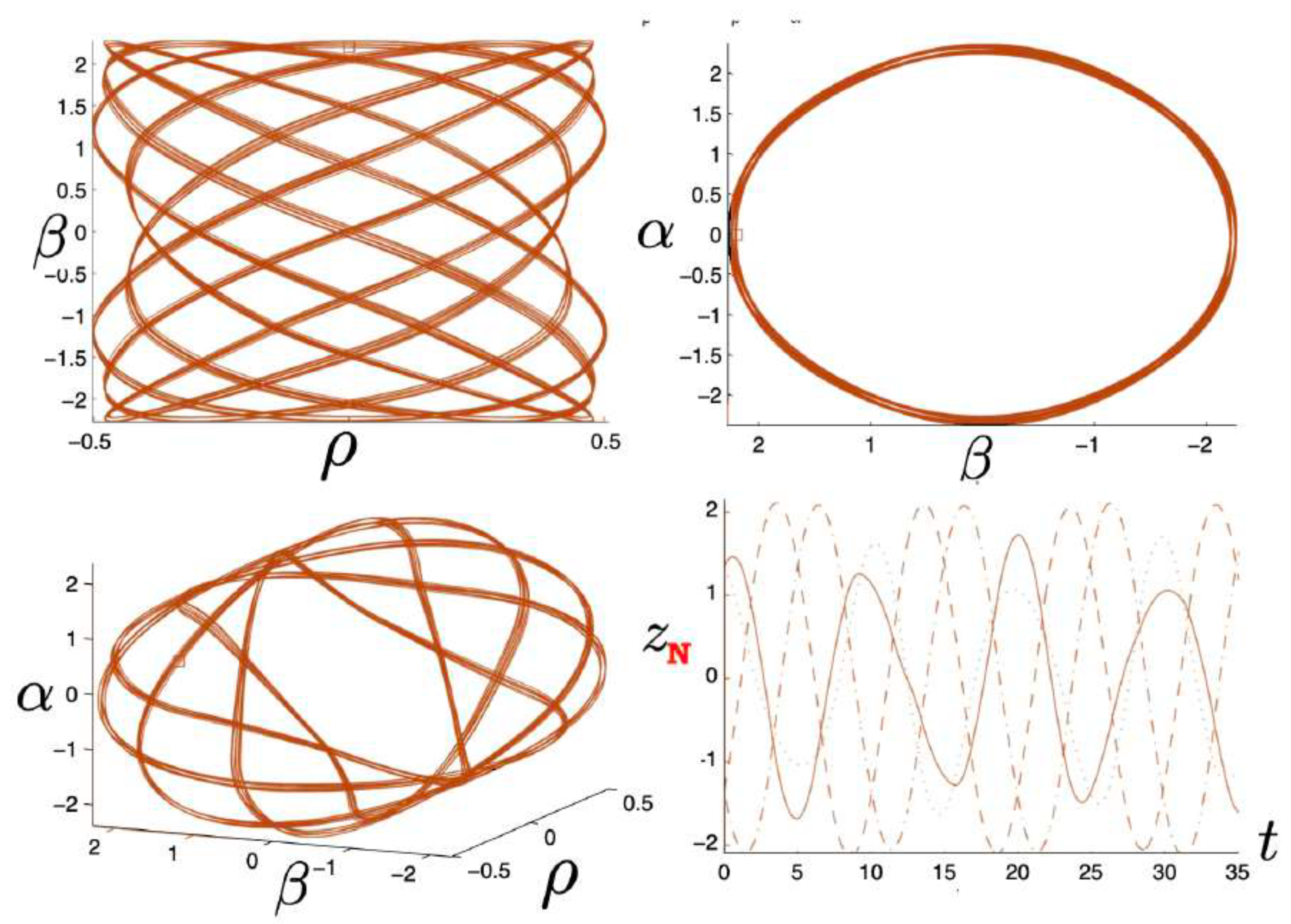
6.3.2. Annulus Orbits

Annulus orbits have the symbol sequence

\bar{B}

and consist of an annulus encircling the origin in the

ρ - λ

plane. In these orbits the hex-particle never crosses the same bisector twice in succession.

Most annulus orbits are quasi-periodic and fill in the entire ring. However a few repeat themselves after some number of rotations about the origin, and a wide variety of patterns are possible contingent upon the initial conditions for the N, pN, and R systems. No qualitative distinctions between N and pN annuli were observed within numerically attainable values of

η

[28,29].

An example of annulus orbits for the N and R systems (for FE conditions), along with the positions of each of the three bodies as a function of time, is shown in Figure 20 (periodic) and Figure 21 (near-chaotic). Periodic orbits are numerically difficult to find, so the orbits in Figure 20 are actually very close to periodic orbits; this allows the pattern of the periodic orbit to be visible. At similar energies the R hex-particle covers the

(ρ, λ)

plane more densely than its N counterpart, and has a higher frequency of oscillation. The higher frequency for the R system was seen in the previous section for two bodies and appears to hold generally for the 3-body system as well. The increased trajectory density for FE conditions in the R system consequently follows, since the same number of time steps were used for both.

These features of higher frequency and trajectory density are more apparent in Figure 22, which provides a comparison of orbits using FM initial conditions. For these conditions the R system (blue) has slightly higher energy than its N counterpart (red). The N system is less dense, covers a smaller region of the

(ρ, λ)

plane, and does not venture as close to the origin, characteristics that becoming increasingly pronounced for increasing

η

, provided that the R energy remains larger than its N counterpart. This is not guaranteed for FM conditions, as the bottom diagram in Figure 22 illustrates: here the N system has about 14% more energy than its R counterpart, and so covers a larger region of the

(ρ, λ)

plane.

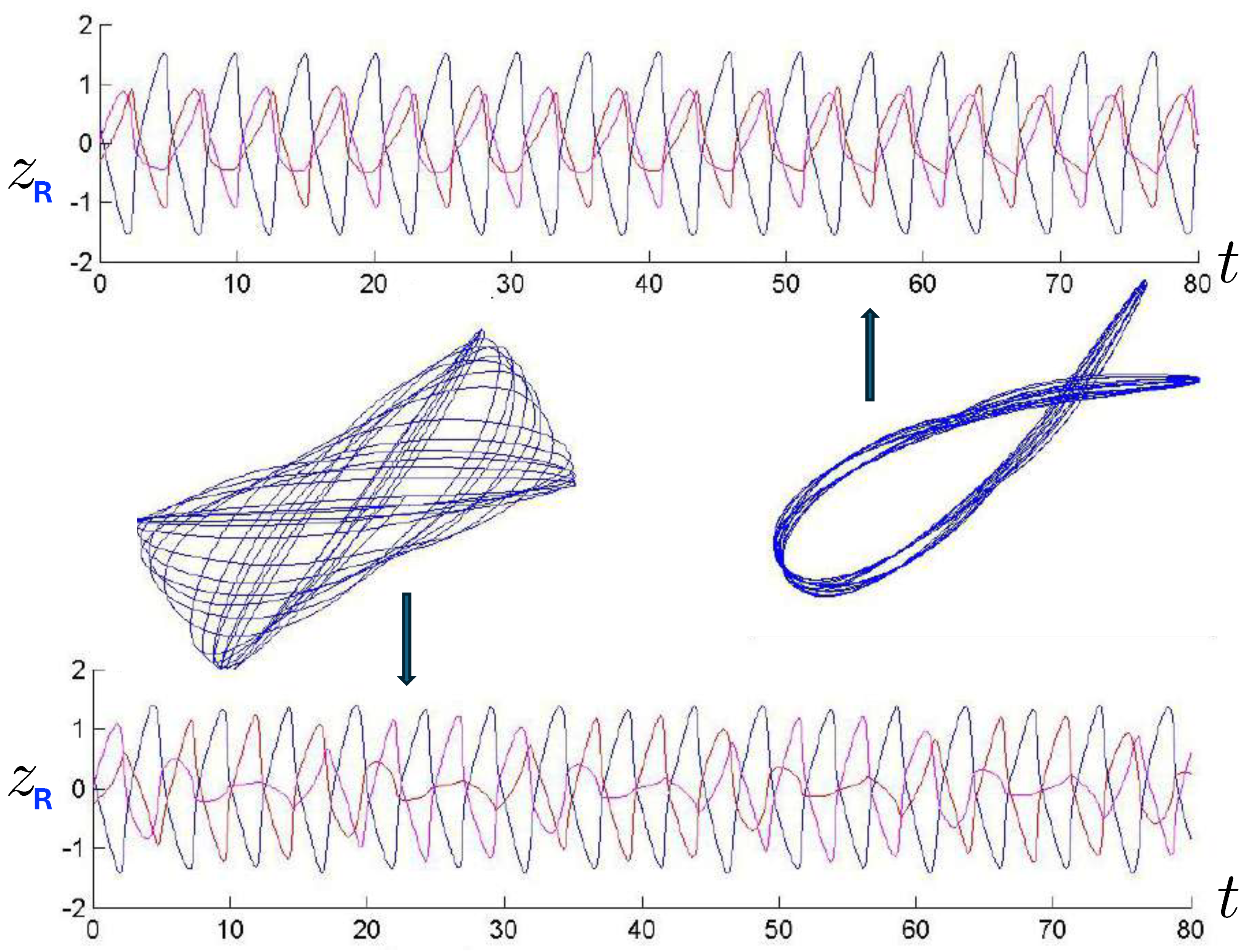
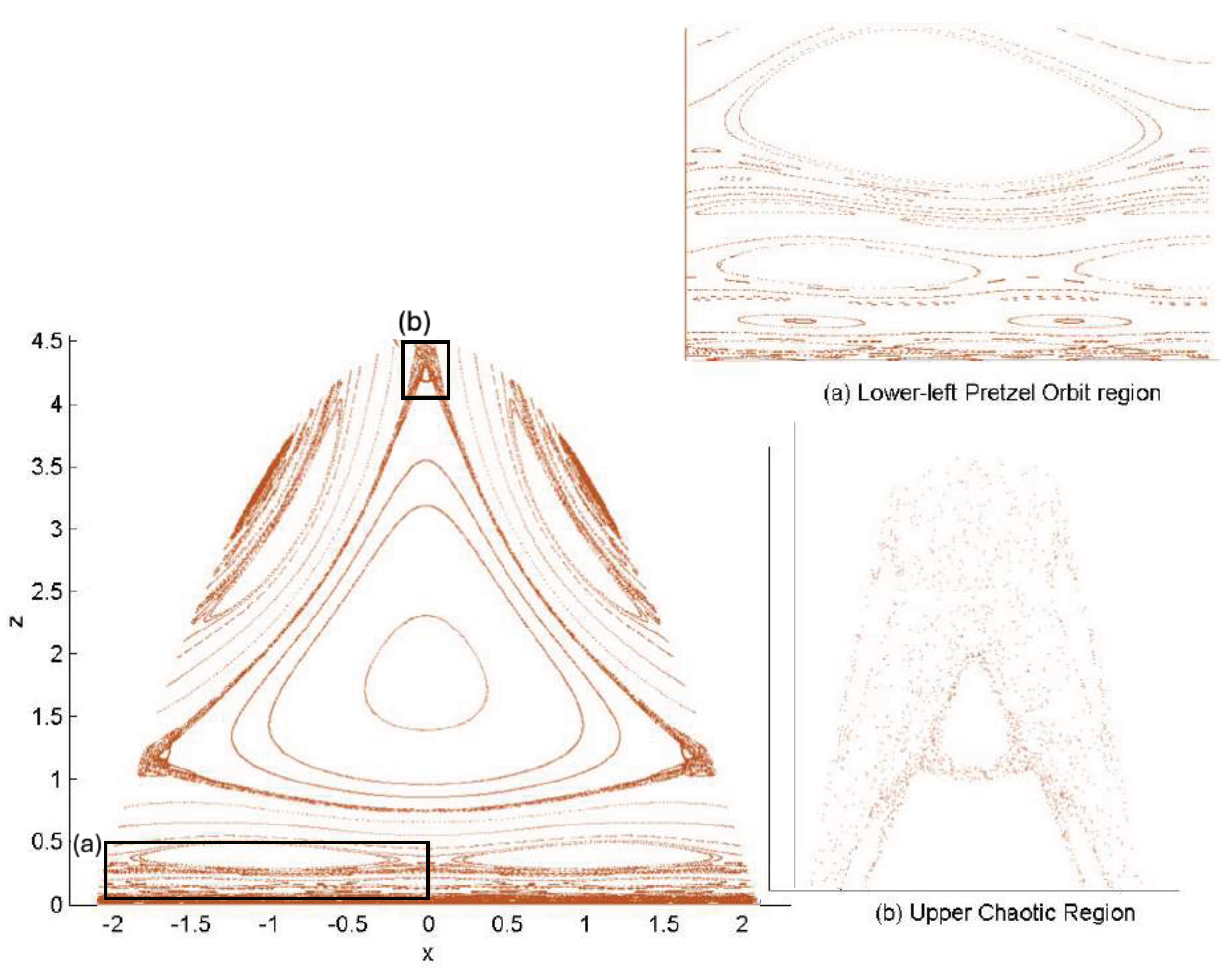
6.3.3. Pretzel Orbits

Pretzel orbits have the generic symbol sequence

\prod_{i j k} {(A^{n_{i}} B^{3 m_{j}})}^{l_{k}}

, where

n_{i}, m_{j}, l_{k} \in Z^{+}

, with some

l_{k}

possibly infinite, and consist of orbits in which the hex-particle essentially oscillates back and forth about one of the three bisectors for some segments of its motion. A typical example is shown in Figure 23. For both the N and R systems, we see that two of the three bodies form a stable bound subsystem, which in turn orbits the third analogous to a 2-body system. The N system exhibits parabolic regularity for both the 2-body subsystem and the full system, whereas the R system has shoulder-like distortions observed previously in the 2-body case.

This formation of a stable (or quasi-stable) bound subsystem is characteristic of pretzel orbits, and the range of possible trajectories is extremely diverse. Many families of regular orbits exist. These generally have one base element in their symbol sequence (e.g.,

A B^{3}

) and a sequence of elements formed by appending an A to each existing sequence of A’s (for example,

{A B^{3}, A^{2} B^{3}, A^{3} B^{3}, . . .}

. The

B^{3}

sequence corresponds to a 180-degree rotation of the hex-particle about the origin, yielding a broad variety of twisted, pretzel-like figures. This is a notable distinction from the wedge system [3,16], for which B and

B^{2}

sequences are also observed; only

B^{3}

sequences are present in all pretzel orbits.

Distinctions between the R, pN and N systems are strongest for pretzel orbits. Both regular orbits (with an infinitely repeating symbol sequence) and irregular orbits that densely fill a cylindrical tube in the

(ρ, λ)

plane occur. Orbits in the R system generally have kinks about the

λ = 0

line that are absent in their N and pN counterparts; a cylindrical-shaped trajectory in the N system looks like an hourglass in the R system, for example. Furthermore, periodic and quasi-periodic orbits in the N system have counterparts with the same symbol sequence in the R system but not in the pN system, which exhibits chaotic behaviour not seen in the N and R systems.

A comparison of the time-evolution of trajectories in the N and R systems is shown in Figure 24 for FE conditions at small and large values of

η

. For small

η

(

η = 0.05

) there is very little distinction between the N and R motions, consistent with the smooth non-relativistic limit of (152). Significantly different trajectories occur for larger values

η

(

η = 0.85

). In the R system the oscillation frequency is higher and the pattern ‘weaves’ relative to the near-cylindrical shape in the N-system once enough time steps have occured. The R trajectory is more tightly confined, commensurate with the 2-body motion seen in the previous section.

In Figure 25 we display the sensitivity of trajectories to initial conditions. The fish-like diagram has an

A B^{6}

symbol sequence: two of the particles oscillate quasi-regularly about each other (shown in the upper

z (t)

plot), with this pair undergoing larger-amplitude and lower-frequency oscillations with the third. A slight change of the initial FE conditions yields the strudel-like figure on the left. Now one particle alternates its oscillations with the other two, maintaining a near-constant amplitude throughout.

By controlling the FM initial conditions interesting sequences of hex-particle orbits can be obtained. An example is given in Figure 26, which compares snake-like orbits in the N (red) and R (blue) systems. These quasi-regular orbits have symbol sequences

\{\bar{A^{i} B^{3}}\}

. In both systems the orbits have two sharp turning points separated by some number n of bumps. In the N system these have been shown to exist for arbitrary n [3], and it has been conjectured the same is true for the R and pN systems [29]. The figures in the R system develop an hourglass shape narrowing about

λ = 0

, and cover a much narrower region in the

ρ

direction (note the scale in the bottom sequence of plots). The N orbits, by contrast, are circumscribed by a cylinder.

The symbol sequence

A B^{3}

results in boomerang-like figures, shown in Figure 27, where the qualitatively different physics due to relativistic effects is manifest. At low energies (

η = 0.2

) the N (red) and R(blue) systems have similar boomerang shapes. However as

η

increases, orbits in the R system develop two distinct turning points at different distances from the

ρ = 0

axis for

λ > 0

, with symmetric counterparts for

λ < 0

. This feature is particularly evident for

η = 0.75

. A kink at the right-hand-side of the boomerang emerges, becoming increasingly pronounced with increasing

η

. The underlying reason behind the development of this structure is not clear.

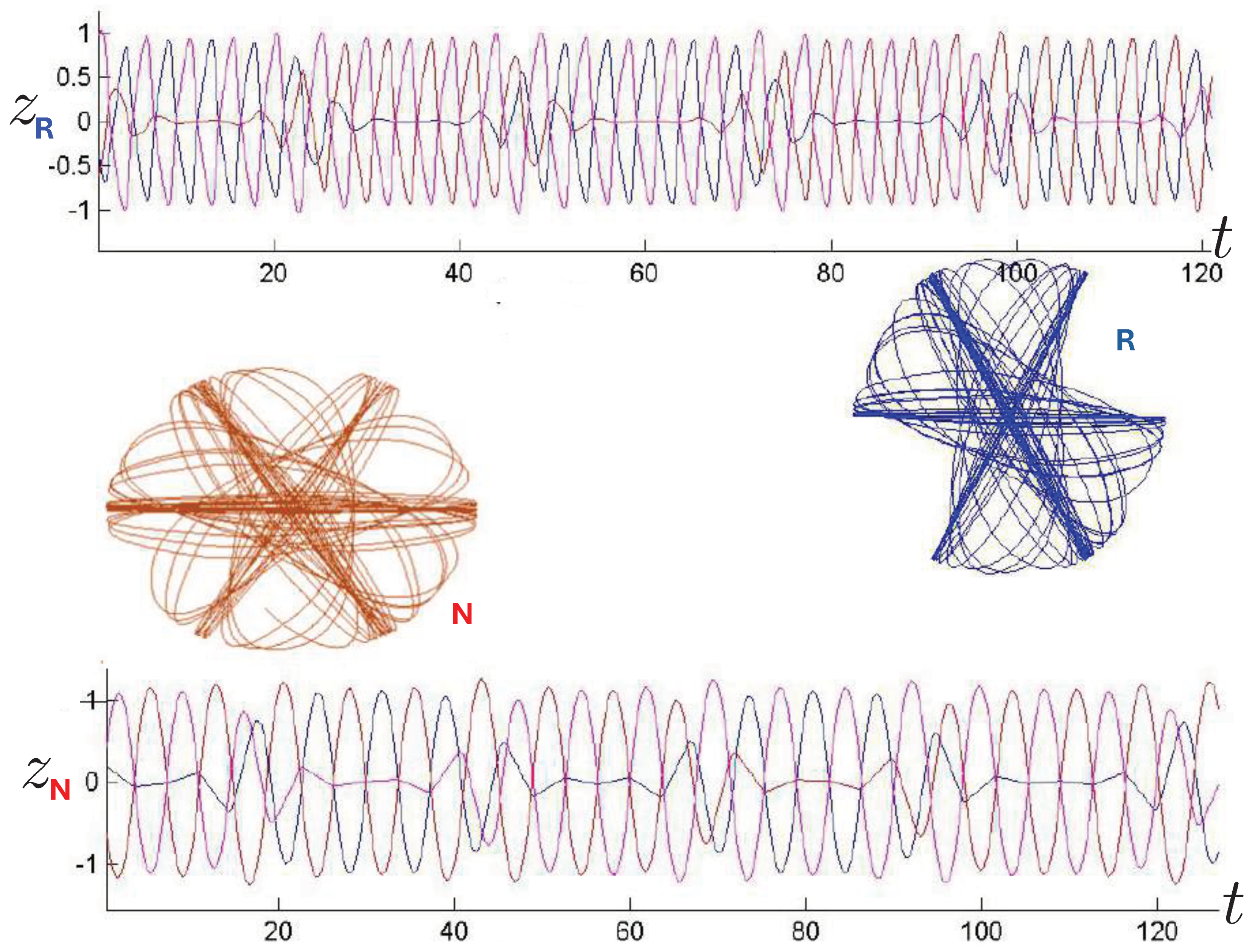
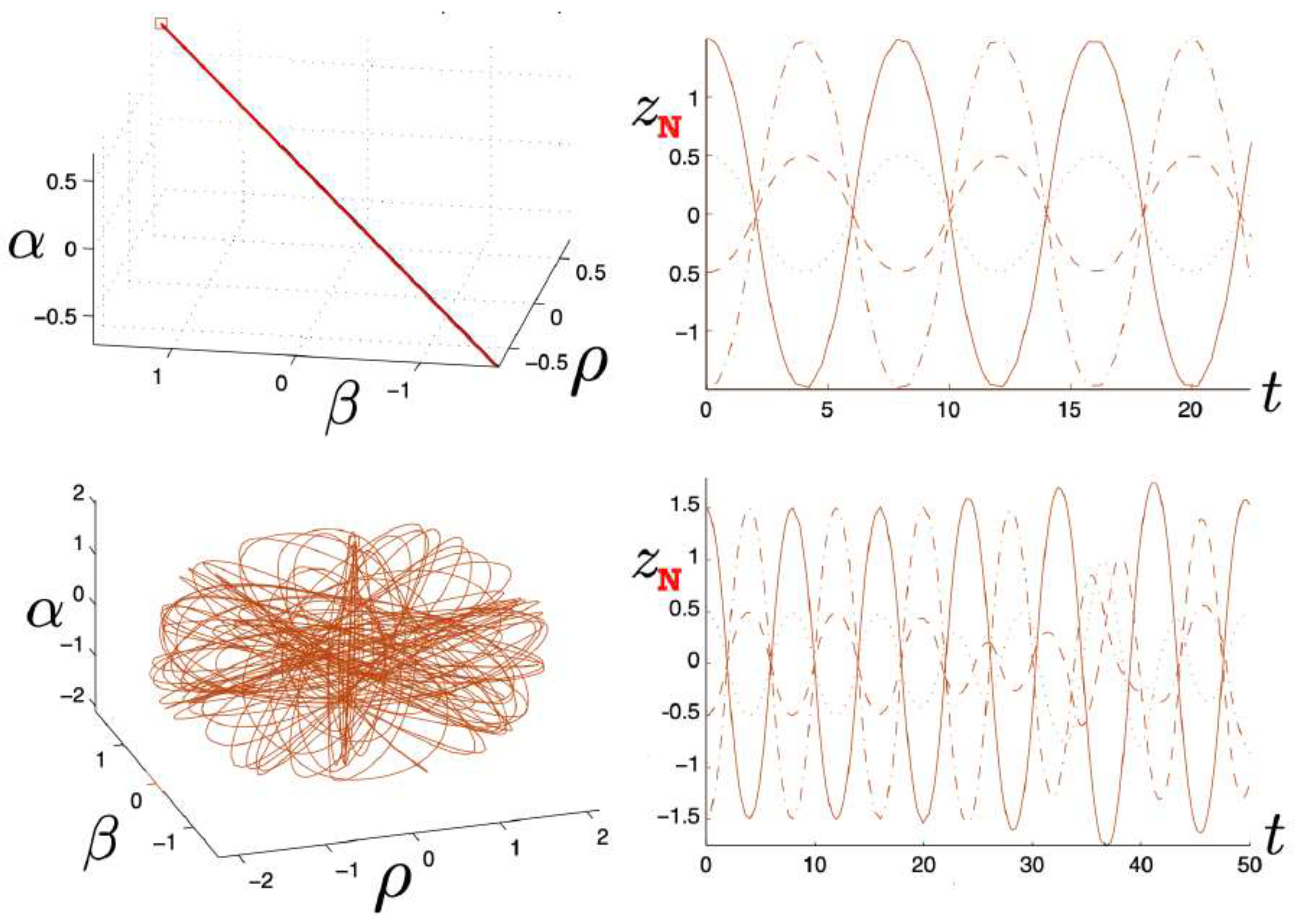
6.3.4. Chaotic Orbits

Chaotic orbits are those for which the hex-particle wanders between A-motions and B-motions in an apparently irregular fashion. Unlike the annuli and pretzel orbits, chaotic orbits eventually wander into all areas of the

ρ - λ

plane. Chaos emerges at the transition between annulus and pretzel orbits, where the hex-particle passes very close to the origin, for each system.

Figure 28 illustrates a typical case for the N and R systems. Two particles undergo a large-amplitude oscillation with the third one (the middle ‘m’ particle) mildly oscillating near the centre of momentum. At irregular intervals this third particle switches places with one of the other two, and the pattern repeats. The m-particle alternates in an irregular fashion, leading to chaos.

A comparison of the time development of chaotic trajectories in both the N and R systems is shown in Figure 29. The upper sequence shows how a chaotic trajectory can develop in the R system (blue) whilst the N system (red) forms a densely filled annulus for the same FE initial conditions with

η = 0.5

. The lower sequence shows how a chaotic trajectory can develop in the N system (red) whilst the R system (blue) forms a densely filled pretzel, for the same FE initial conditions, again for

η = 0.5

. In both cases the R trajectory attains its final pattern much more rapidly than its N counterpart, a manifestion of the difference in frequencies noted earlier.

The transition from an annulus to a pretzel orbit through a chaotic region for the R system is shown in Figure 30. Proceeding from from left-to-right and top-to-bottom with decreasing initial angular momentum for the hex-particle, the system begins as an annulus, passes through a set of chaotic orbits, and then becomes a pretzel. The chaotic trajectories through the origin (or very close to it), a characteristic feature for this region of chaos in all three systems. In the R system the transitional region shrinks as

η

increases [29].

There is a striking distinction between the pN system and the (N,R) systems for the chaotic class of motions. Unlike the latter two, the pN exhibits an additional area of chaos in the pretzel region. This feature will become evident in the next subsection.

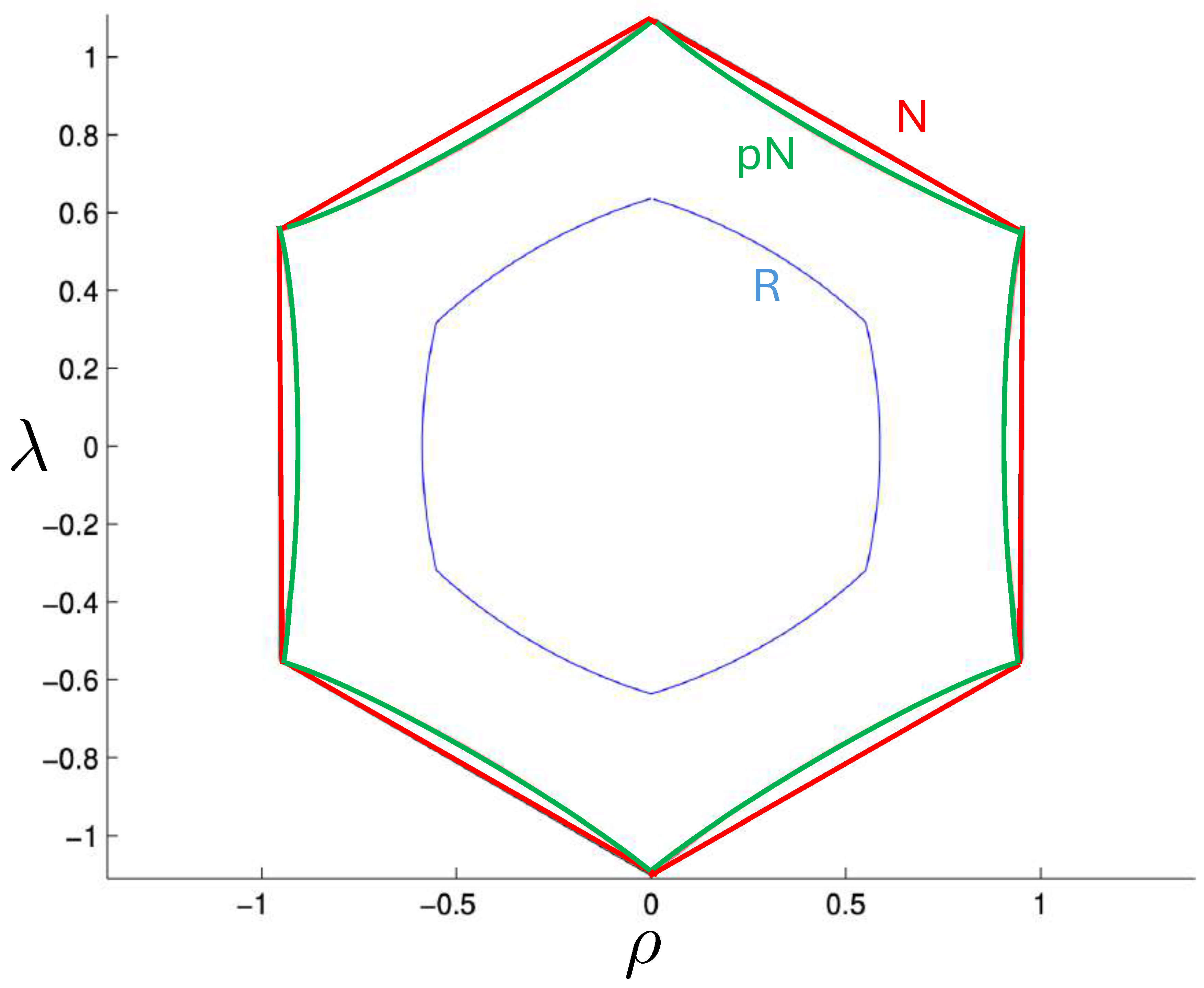
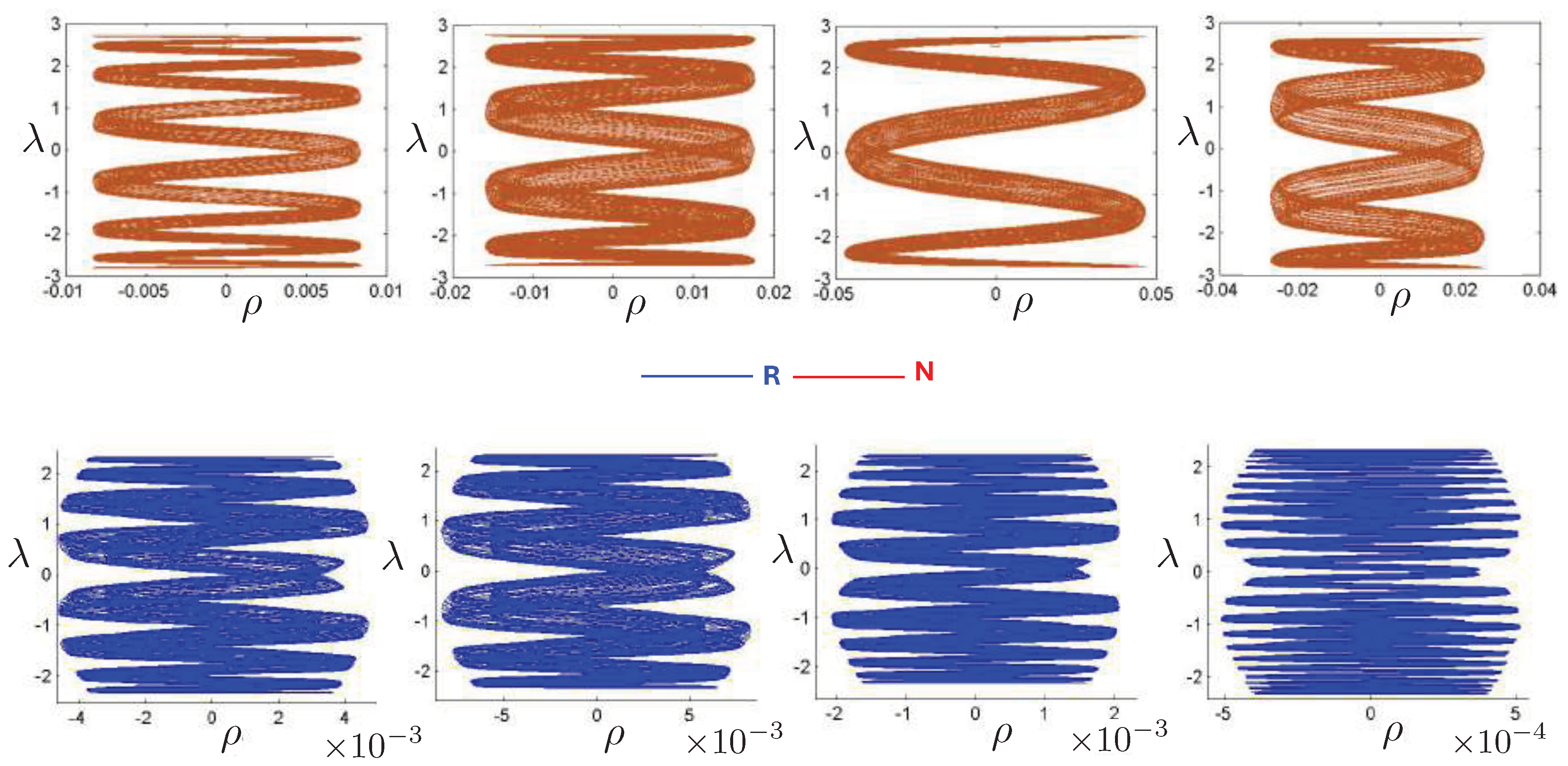
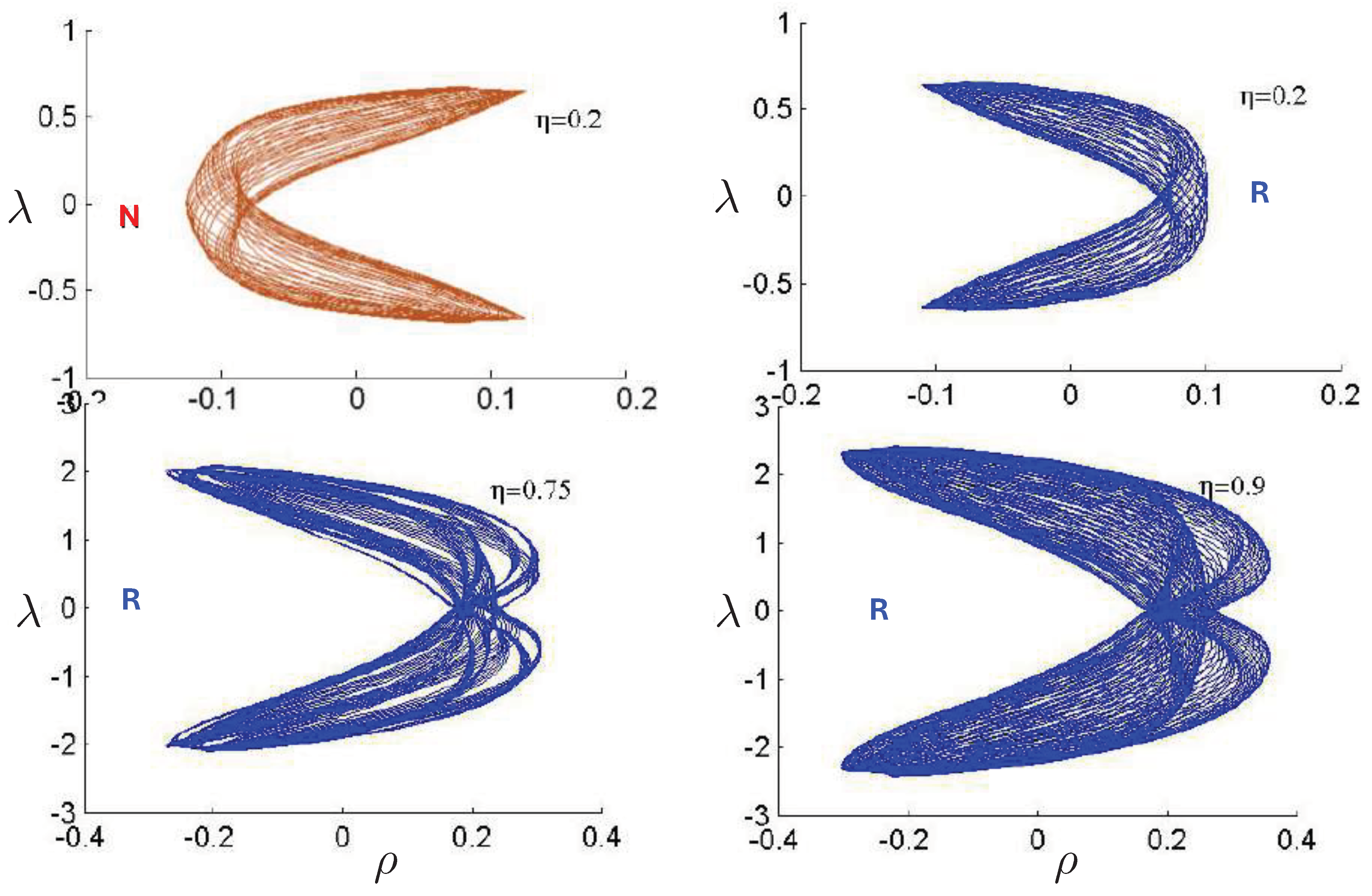
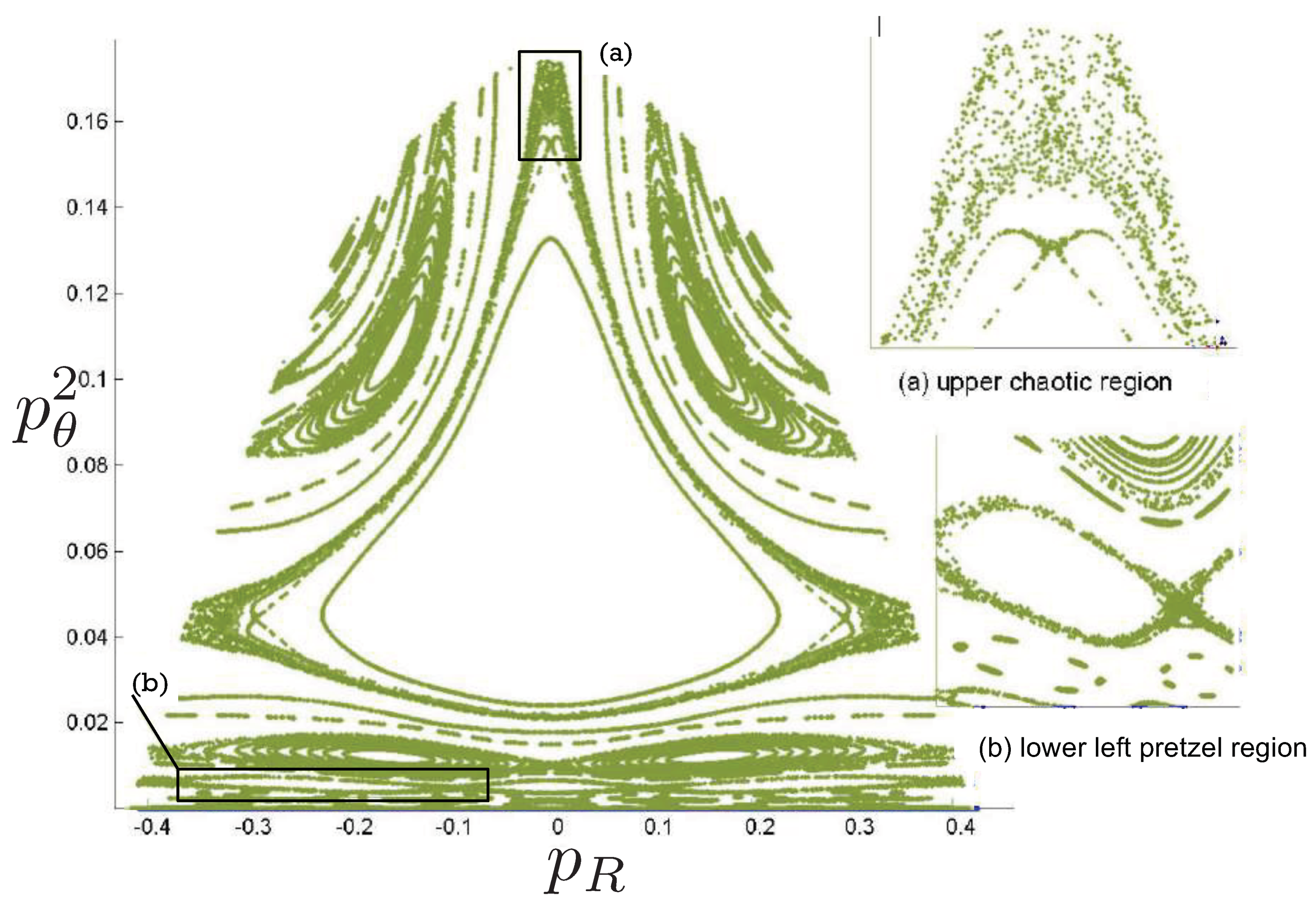
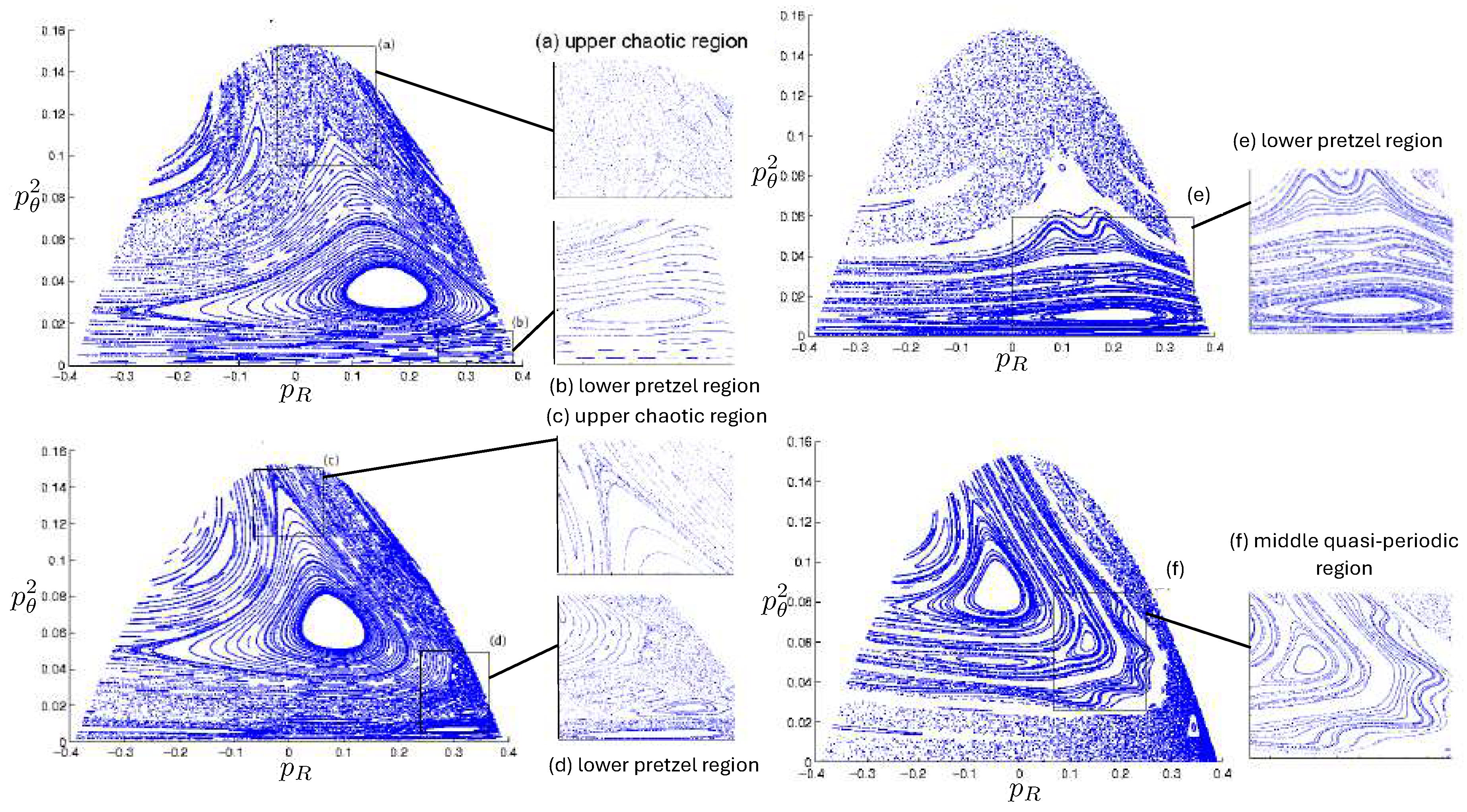
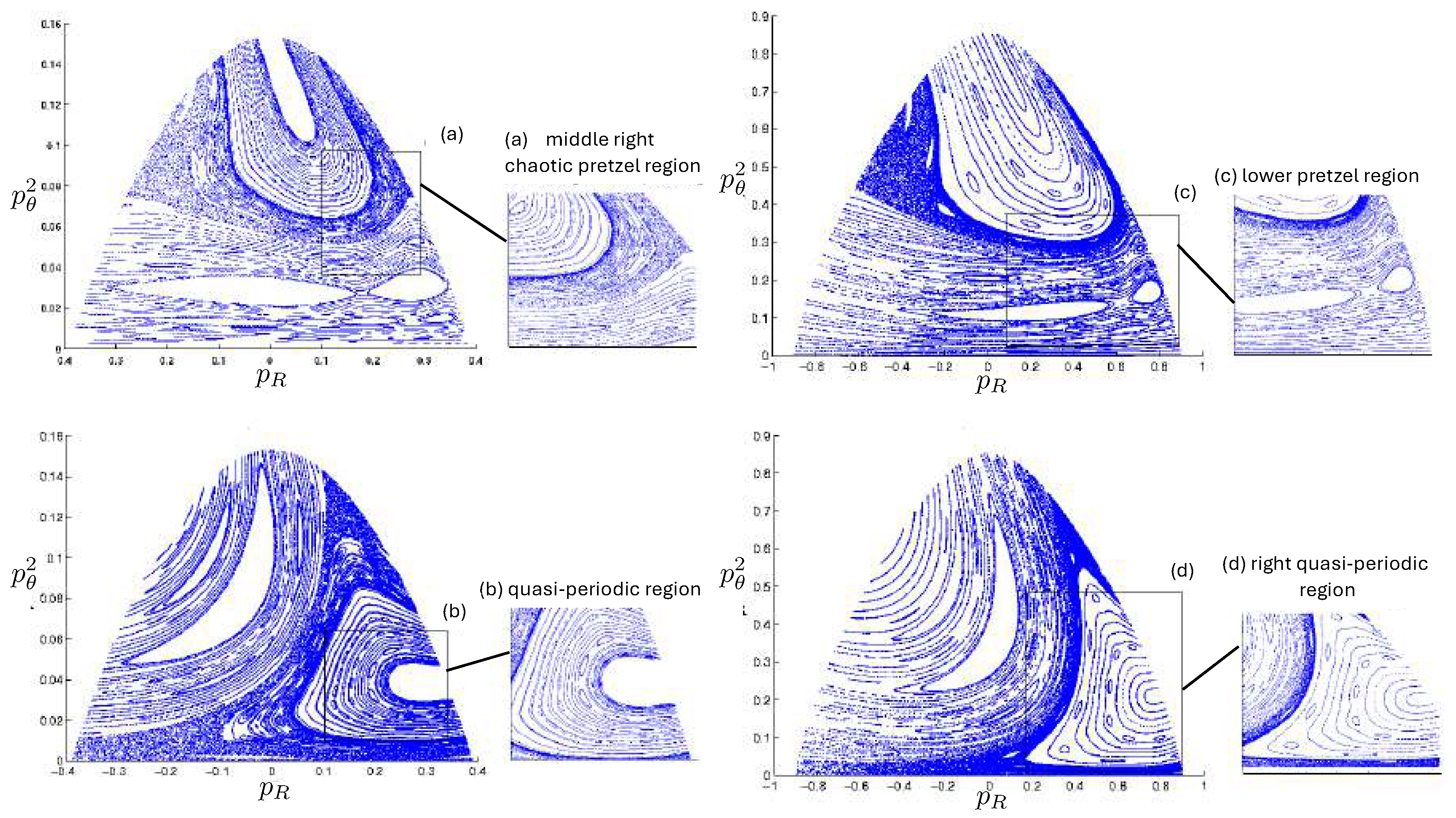
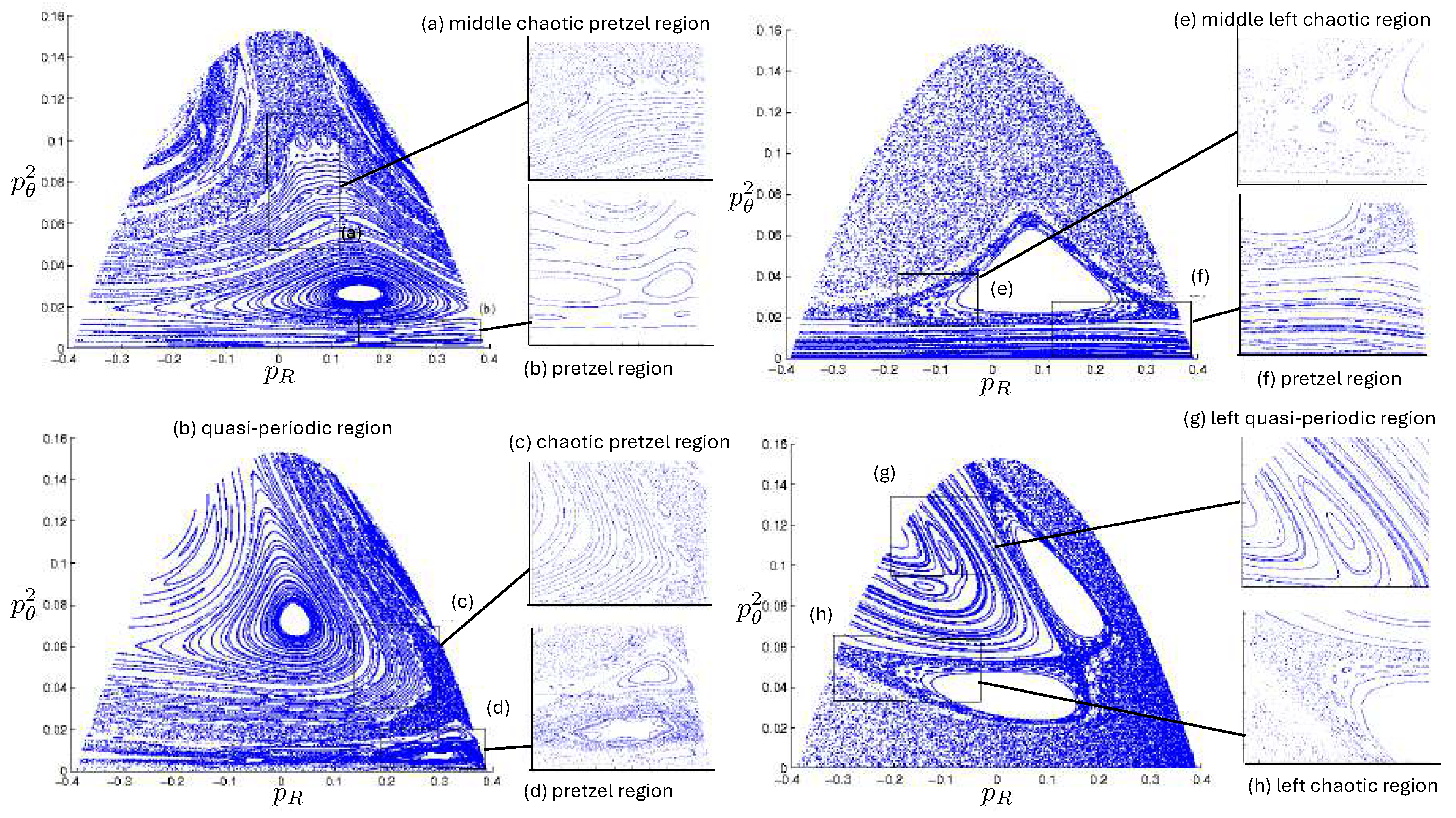
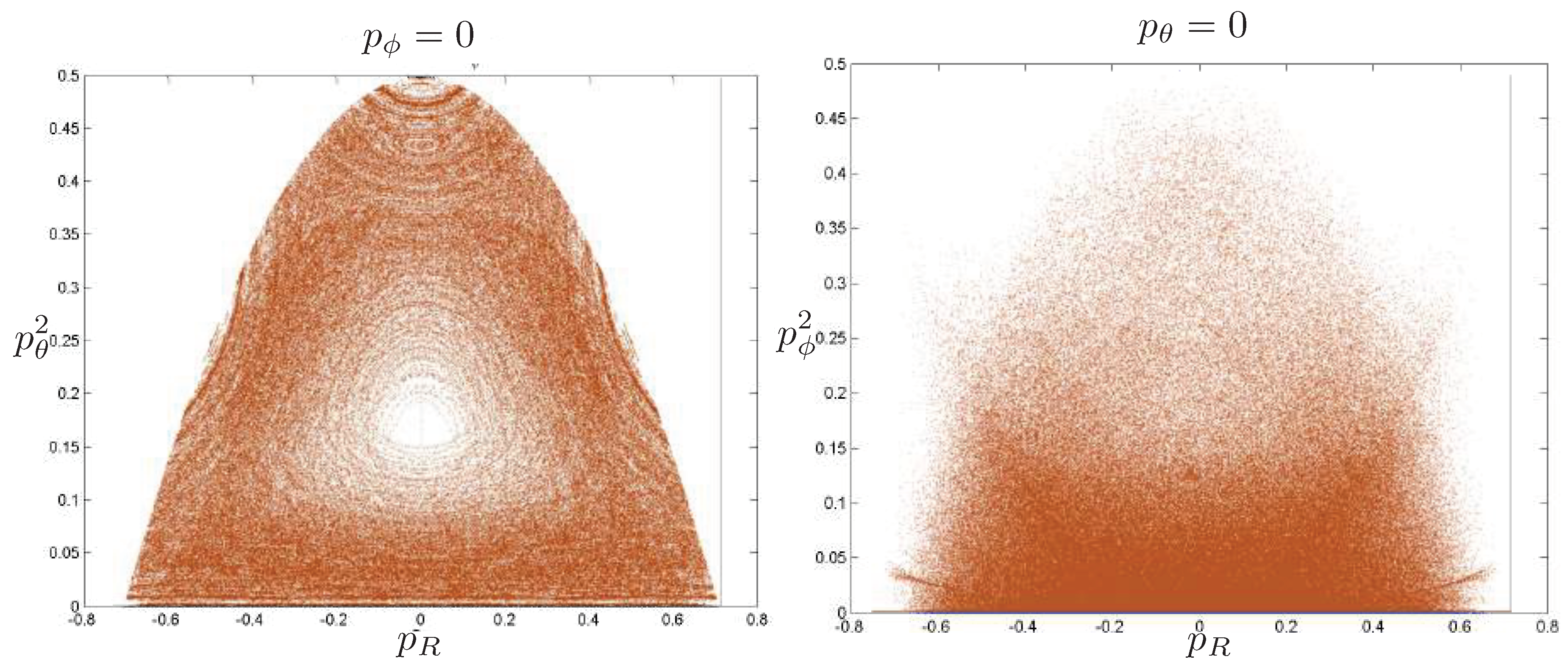
6.4. Poincaré Plots

Poincaré sections for each of the N, pN, and R systems can be constructed by plotting the square of the angular momentum

p_{θ}^{2}

, against the radial momentum

p_{R}

(both scaled to be dimensionless as per (181)) of the hex-particle each time it crosses a bisector. Since all bisectors are equivalent in the equal mass case, all crossings can be plotted on the same surface of section. The plots then indicate regions of chaos, as well as periodicity and quasi-periodicity.

Since the Hamiltonian is time-independent, the total energy is a constant of the motion, and the phase space is a 3-dimensional hypersurface in 4 dimensions for each system. The system is said to be integrable if an additional constant of the motion exists, in which case its trajectories are restricted to two-dimensional surfaces in the available phase space.

The types of motion that integrable systems can exhibit are either periodic or quasi-periodic. Periodic (1-dimensional) orbits have trajectories that always appear as lines or dots on the Poincaré section, since by definition they comprise the intersection of two 2-dimensional surfaces. By contrast, the extra degree of freedom for a non-integrable system permits orbits to visit all regions of phase space. In this case the system typically displays strongly chaotic behavior and the associated trajectories appear as filled in areas on the Poincaré plot.

Small perturbations of an integrable system admit small regions of chaos, though most of its orbits remain confined to two-dimensional surfaces. The chaotic regions grow as the perturbation increases in magnitude and eventually become connected areas on the Poincaré section, a phenomenon known as a Kolmogorov, Arnold and Moser (KAM) transition [120,121,122,123]. For sufficiently large perturbations, systems typically become almost fully ergodic [124], though islands of regularity may persist for quite some time prior to this and typically have an intricate fractal structure.

The Poincaré plots for the N, R and pN systems appear respectively in Figure 31, Figure 32, and Figure 33, using the same conventions as in [3] up to an overall normalization for each section. The energy conservation relation (176), which is

p_{R}^{2} + p_{θ}^{2} \leq \frac{2}{3} η

(186)

determines the outer boundary of each plot, where the presence of

η

reflects the different normalizations for each system. When the potential energy is zero, equality in (186) holds, corresponding to the hex-particle being at the origin. Any departure from the origin reduces the values of

(p_{R}, p_{θ})

and so yields the phase-space limit.

Figure 31 for the N system reproduces the results for the wedge problem [3]. Here

H - 3 m c^{2}

is normalized to unity and the RHS of (186) is 1. In the equal mass case the 3-body problem corresponds to motion of a body falling toward a wedge whose sides are each at angles

30^{o}

relative to the vertical axis. The energy constraint after an A-collision has taken place yields another boundary

{(p_{R} - 2 \sqrt{3} | p_{θ} |)}^{2} \leq 1 - p_{θ}^{2}

(187)

whose satisfaction yields all points in phase space that have undergone an A-collision (the A-region). Points violating (187) are those for which a B-collision has taken place (the B-region). Since the interaction is gravitational, collisions with the third particle cannot ultimately be avoided. Consequently the A-region has no fixed points and any point in the A-region will inevitably venture into the B-region. However fixed points can occur in a subset of the B-region: here B-collisions are infinitely repeated, corresponding to the annulus orbits.

In the N system the centre of the plot in Figure 31 is a fixed point surrounded by a subregion of near-integrable curves. The annulus orbits are all contained within the large triangle surrounding this region. The closed circles in this annulus region correspond to quasi-periodic orbits about the periodic annuli with higher period, such as in Figure 20. The boundary of the annulus region is a thin region of chaos, most prominent at the corners as shown in the lower right inset. These chaotic regions are confined and not simply connected.

The region beyond this is the pretzel region, which has circles bounding the quasi-periodic near-integrable regions; these exhibit repeated self-similarity, shown in the upper right inset. The two large circles observed just below the annulus region correspond to the boomerang-shaped orbits (

\bar{A B^{3}}

) shown in Figure 27. The next set of circles will be

\bar{A^{2} B^{3}}

, and so on. Between these sets of circles are collections of crescents with sequences

\bar{A B^{3} A^{2} B^{3}}

\bar{A B^{3} A B^{3} A^{2} B^{3}}

, etc. Each circle is actually a continuum of possible circles, whose diameter depends on the initial conditions. At the center of this family of circles is a dot corresponding to the periodic orbit in question.

Somewhat remarkably, the highly nonlinear R system, shown for two different values of

η

in Figure 32 retains all of the qualitative features of the N system, at least up to the range of

η

numerically accessible. The annulus, pretzel and chaotic regions all retain their same basic structure, though asymmetrically deformed. This deformation increases as

η

increases and occurs because the Hamiltonian given by Equation (152) is invariant under the discrete symmetry

(p_{i}, ϵ) \to (- p_{i}, - ϵ)

instead of the

p_{i} \to - p_{i}

symmetry in the N system. The discrete constant

ϵ = \pm 1

is a measure of the flow of time of the gravitational field relative to the particle momenta. In Figure 32

ϵ = + 1

; the opposite choice would create the same distortion but towards the lower left. The situation is reminiscent of the 2-body case of the previous section, where the gravitational coupling to the kinetic-energy causes a distortion of the trajectory from an otherwise symmetric pattern. Whether or not KAM breakdown occurs for higher

η

values remains an interesting open question.

As compared to the N and R plots, the pN system, shown in Figure 33 is notably different. It retains the

p_{i} \to - p_{i}

symmetry of the N system but appears to undergo a KAM transition at

η \sim 0.3

, shown in Figure 34. For small

η

the distinction with the N system is mild, but for

η = . 21

, the lines across the bottom of the figure slightly widen. Larger regions of chaos become evident around the edges of the groups of ellipses in the lower regions of the figure for

η = 0.26

. Further increasing

η \to . 3

, the lower part of the Poincaré section becomes engulfed by a chaotic sea; only a few non-connected islands of regular motion remain. No such behavior is seen in R system for similar values of

η

. These distinctions are not artifacts due to differences in scalings between the systems. The underlying feature that enforces structure on the phase space in the R system but not in the pN system remains to be understood.

6.5. Unequal Masses

For unequal masses the hexagon becomes squashed, with two opposite corners moving inward, changing both the slopes of the straight edges and their relative lengths; relativistic corrections maintain this basic distortion, but with the straight edges becoming parabolic [117]. The exact R potential is given by (177), with its pN and N counterparts respectively given by (179) and (180).

The R potential is similar to the N potential except that the sides of the hexagon become concave, and have a much steeper slope as the radial variable in the

(ρ, λ)

space increases. For

V_{R} = {\hat{V}}_{R}

such that

ln (\frac{({\hat{V}}_{R} - m_{j} c^{2}) ({\hat{V}}_{R} - (M_{tot} - m_{j}) c^{2})}{(M_{tot} - m_{j}) m_{j} c^{4}}) = {\hat{V}}_{R} [\frac{1}{({\hat{V}}_{R} - m_{j} c^{2})} + \frac{1}{({\hat{V}}_{R} - (M_{tot} - m_{j}) c^{2})}]

(188)

(for

j = 1, 2

or 3), the slope of the R potential becomes infinite. In the equal mass case this occurs at

{\hat{V}}_{R} \approx 6.71197 m c^{2}

, where

m = M_{tot} / 3

. The maximal possible critical value of the potential occurs when one of the masses

m_{j} = M_{tot} / 2

, for which

{\hat{V}}_{R} \approx 6.886682 m_{j} c^{2}

. For

m ⟶ 0, M_{tot}

the potential

{\hat{V}}_{R} ⟶ M_{tot} c^{2}

– no energy is available for motion. A plot of

{\hat{V}}_{R}

as a function of

m_{j}

is shown in Figure 35. For values of

V_{R} > {\hat{V}}_{R}

the size of the distorted hexagon decreases like

(ln V_{R}) / V_{R}

The overall shape of the R potential is that of a distorted hexagonal carafe, whose distortion is analogous to that of the N potential, as shown in Figure 36. The relatively steeper growth of the R potential as a function of distance from the origin is manifest by the smaller scales for

ρ

and

λ

in the right-hand panel.

6.5.1. Trajectories

Expressing relative masses as a ratio

m_{1} : m_{2} : m_{3}

, annulus, pretezel and chaotic trajectories are obtained and the symbol sequence always takes the form

\prod_{i, j, k} {(A^{m_{i}}, B^{3 n_{j}})}^{l_{k}}

(189)

as in the equal mass case. Equation (189) implies that B motion always comes in multiples of three; no motions have been observed that depart from this situation [117].

The situation where two masses are equal (

m_{1} : m_{2} : m_{3} = 1 : 1 : α

) is instructive, and plots of the relative motion of the particles for both the N and R systems is given in Figure 37 for decreasing values of

α

. For equal mass (

α = 1

) there is annulus motion: no particle ever crosses another twice in a row. But as

m_{3}

decreases (

α

decreases) its frequency of oscillation decreases while its amplitude increases with respect to the other two, which provide a gravitationally bound subsystem. The binding becomes tighter as

α

decreases, more so for the R system. Eventually the binding becomes so tight that the more massive particles execute an additional A motion before crossing the third particle, and the hex-particle transitions from annulus to pretzel motion. The greater the mass difference, the more difficult it is to set up initial conditions at a given energy so that particles 1 and 2 do not cross more than once during the long period oscillation of particle 3.

Large and small values of

α

are likewise instructive, and plots for

α = 100

(particle 3 very massive) and

α = 0.01

(particles 1 and 2 very massive) are respectively shown in Figure 38 and Figure 39. As expected, for large

α

the heavy particle 3 barely moves as the other two oscillate about it, depicted in Figure 38. However the passing of the other two particles causes small perturbations in the motion of the heavy body, shown in the insets. The perturbation is smooth and regular in the N system whereas in the R system the velocity of the large mass increases much more suddenly, leading to a more erratic and jerky trajectory.

For small

α

(Figure 39) a stable gravitationally bound subsystem is formed by the two heavy particles, with the third oscillating about their center of inertia. The oscillation amplitude is much larger and frequency much smaller in the N system than in the R system, commensurate with the two-body system in Section 5. The effect of the light particle 3 is to cause oscillatory motion of the center of mass of the two more massive particles, which is clear from the insets in the the N and R systems. This perturbation is almost imperceptible due to the two heavy particles being twice as massive as the single particle in the

α = 100

case (Figure 38); consequently they are less susceptible to changes in motion from the smaller mass body.

6.5.2. Poincaré Plots

As with the equal mass case, the annulus and pretzel trajectories are in similar regions of the Poincaré plot, separated by a region of chaos, but the shapes and sizes of the different regions change. The R system is topologically similar to the N system, but with the various regions distorted in a manner similar to the equal mass case.

Figure 40 compares the Poincaré sections for the N and R systems for the mass ratio

1 : 1 : 0.1

for

η = 0.3

. The triangular annulus region moves towards the top the surface of section and becomes smaller in both systems. This latter effect is a manifestation of the difficulty in attaining annulus motion noted above, when one particle is much less massive than the other two.

If one particle is much more massive than the other two, the annulus region gets larger and extends towards the lower region of the plot, as shown in Figure 41 in both the R and N systems for the mass ratio

1 : 1 : 10

. In this situation the hex-particle needs less angular momentum to attain an annulus orbit in the

(ρ

λ)

plane. Somewhat like a two-planet solar system in one-dimension, the two lighter bodies behave like two separate 2 body systems, with the heavy particle taking the role of the second body for each, as shown in Figure 38. Furthermore, additional regions of chaos appear that are absent in the equal mass case.

An example of a Poincaré plot when all three masses are unequal is shown in Figure 42 for the N and R systems, with mass ratio

1 : 5 : 10

. Since none of the bodies have the same mass, the symmetry about the

p_{R} = 0

axis in the N system is gone. Different regions are not as clearly segregated as in the

m_{1} = m_{2}

case, and instead extend over a larger region of the plot. A region of chaos separating outer pretzel regions from the inner annulus region is marked by A in the left diagram, and above and below B are new regions of chaos amongst pretzel trajectories.

The R system further distorts the N diagram to the lower right. The chaotic region separating annulus and pretzel trajectories is now two loops that were created by a single trajectory, both marked by a 1. The annulus region is confined to the area inside both of these loops (marked by a 2), where a single annulus trajectory will visit both regions.

The key feature of the unequal mass case, for both the N and R systems, is the presence of additional chaotic regions that are absent in the equal mass case in the corresponding constant energy hyper-surface. These additional chaotic regions appear within the pretzel regions of the corresponding equal mass plot, and are characterized by broadened lines in the pretzel region, evident in each of Figure 40, Figure 41 and Figure 42. The origin of this additional chaos is not understood.

The unequal mass case is equivalent to the two-dimensional symmetric wedge billiard system in a uniform gravitational field [3], with the relative masses of the particles directly related to the wedge angle

θ

tan θ = \frac{\sqrt{1 + 2 α^{- 2}}}{1 + 2 α^{- 1}}

(190)

where

α

is as defined as above, and

θ = π / 6

corresponds to

α = 1

, the equal mass case. The angle of the wedge is related to the angle between the bisectors of the hexagonal well. The only distinction between the wedge system and the 3-body system is the absence of collisions in the the latter. If all masses are equal there is no distinction between a collision and a crossing of two bodies (apart from particle labelling) and so the Poincaré maps become identical in this case.

In both the N and R systems, there is an increase in the amount of chaos as the difference in the masses increases. Earlier studies explored a limited range of mass ratios, however, and it remains an open question as to whether or not one or both systems will undergo a transtion to global chaos, or if integrable and near integrable regions exist for all mass ratios.

6.6. Charge and Cosmological Constant

Including a cosmological constant [118] and endowing the particles with charges [125] significantly increases the parameter space. The solutions to (63) and (64) still yield (65), but now

V = \{\begin{matrix} 0 \\ - e_{1} e_{2} - e_{1} e_{3} \\ - e_{1} e_{3} - e_{2} e_{3} \\ 0 \end{matrix} \begin{matrix} in region (1) \\ in region (2) \\ in region (3) \\ in region (4) \end{matrix}\}

(191)

where space is divided into four regions, chosen so that

z_{1} < z_{2} < z_{3}

region (1) being to the left of particle 1 and region (4) to the right of particle 3. The determining equation becomes

\begin{matrix} [(({\hat{M}}_{1} + {\hat{K}}_{1 +}) {\hat{K}}_{3 +}^{2} + ({\hat{M}}_{3} + {\hat{K}}_{4}) {\hat{K}}_{2 +}^{2}) tanh (\frac{{\hat{K}}_{3 +} z_{32}}{4}) tanh (\frac{{\hat{K}}_{2 +} z_{21}}{4}) \\ + ({\hat{M}}_{1} + {\hat{K}}_{1 +}) ({\hat{M}}_{3} + {\hat{K}}_{4}) {\hat{M}}_{2} tanh (\frac{{\hat{K}}_{3 +} z_{32}}{4}) tanh (\frac{{\hat{K}}_{2 +} z_{21}}{4}) \\ + (({\hat{M}}_{1} + {\hat{M}}_{2} + {\hat{K}}_{1 +}) ({\hat{M}}_{3} + {\hat{K}}_{4}) + {\hat{K}}_{3 +}^{2}) {\hat{K}}_{2 +} tanh (\frac{1}{4} {\hat{K}}_{3 +} z_{32}) \\ + (({\hat{M}}_{1} + {\hat{K}}_{1 +}) ({\hat{M}}_{2} + {\hat{M}}_{3} + {\hat{K}}_{4}) + {\hat{K}}_{2 +}^{2}) {\hat{K}}_{3 +} tanh (\frac{1}{4} {\hat{K}}_{2 +} z_{21}) \\ + ({\hat{M}}_{1} + {\hat{M}}_{2} + {\hat{M}}_{3} + {\hat{K}}_{1 +} + {\hat{K}}_{4}) {\hat{K}}_{2 +} {\hat{K}}_{3 +}] \\ = 0 \end{matrix}

(192)

where

z_{i j} \equiv (z_{i} - z_{j})

s_{i j} \equiv sgn (z_{i j})

and

\begin{matrix} {\hat{M}}_{i} & = & κ \sqrt{p_{i}^{2} + m_{i}^{2}} \end{matrix}

(193)

\begin{matrix} {\hat{K}}_{1 \pm} & \equiv & \sqrt{κ^{2} {[X - \frac{ϵ}{4} (\sum_{a = 1}^{3} p_{a} s_{a 1} \pm p_{1})]}^{2} - \frac{Λ_{e}}{2}} \end{matrix}

(194)

\begin{matrix} {\hat{K}}_{2 \pm} & \equiv & \sqrt{κ^{2} {[X - \frac{ϵ}{4} (\sum_{a = 1}^{3} p_{a} s_{a 2} \pm p_{2})]}^{2} - \frac{κ}{2} (e_{1} e_{2} + e_{1} e_{3}) - \frac{Λ_{e}}{2}} \end{matrix}

(195)

\begin{matrix} {\hat{K}}_{3 \pm} & \equiv & \sqrt{κ^{2} {[X - \frac{ϵ}{4} (\sum_{a = 1}^{3} p_{a} s_{a 3} \pm p_{3})]}^{2} - \frac{κ}{2} (e_{1} e_{3} + e_{2} e_{3}) - \frac{Λ_{e}}{2}} \end{matrix}

(196)

\begin{matrix} {\hat{K}}_{4} & = & - 2 \sqrt{κ^{2} {[X + \frac{ϵ}{4} (p_{1} + p_{2} + p_{3})]}^{2} - \frac{Λ_{e}}{2}} \end{matrix}

(197)

with

H = \frac{4}{κ} \sqrt{κ^{2} X^{2} - \frac{Λ_{e}}{2}} \geq \frac{4}{κ} \sqrt{- \frac{Λ_{e}}{2}}

(198)

which defines the constant of integration X. This relation is the same as (76) when the charges are zero. The inequality follows since H and

X \geq 0

must both be real, defining a negative critical value

Λ_{n e g c r i t} \equiv - \frac{κ^{2} H^{2}}{8} \leq Λ_{e}

(199)

Permutation of the particles yields same determining equation with indicies appropriately switched.

There are six inequivalent configurations: (0 0 0), (+ 0 0), (+ + 0), (+ - 0), (+ + -) and (+ + +), where 0 denotes a neutral particle, since the potential is invariant for

e_{i} \to - e_{i}

and the charge configurations interchange as the particles cross. The first of these has been considered in the previous subsections. The second of these, unless

Λ_{e} = 0

, is equivalent to three neutral particles with a cosmological constant. If one particle is neutral the relative magnitudes of the charges are irrelevant since only products of their magnitudes matter. The effect of the electromagnetic energy is to yield a charge-dependent constant vacuum energy between the particles, with the size of the region and the magnitude of the vacuum energy changing as the particles move about. If one particle is neutral then the magnitude of the vacuum energy between the particles does not change.

The parameter space has been explored in considerable detail [118,125]. As it is so vast only a few key results shall be presented.

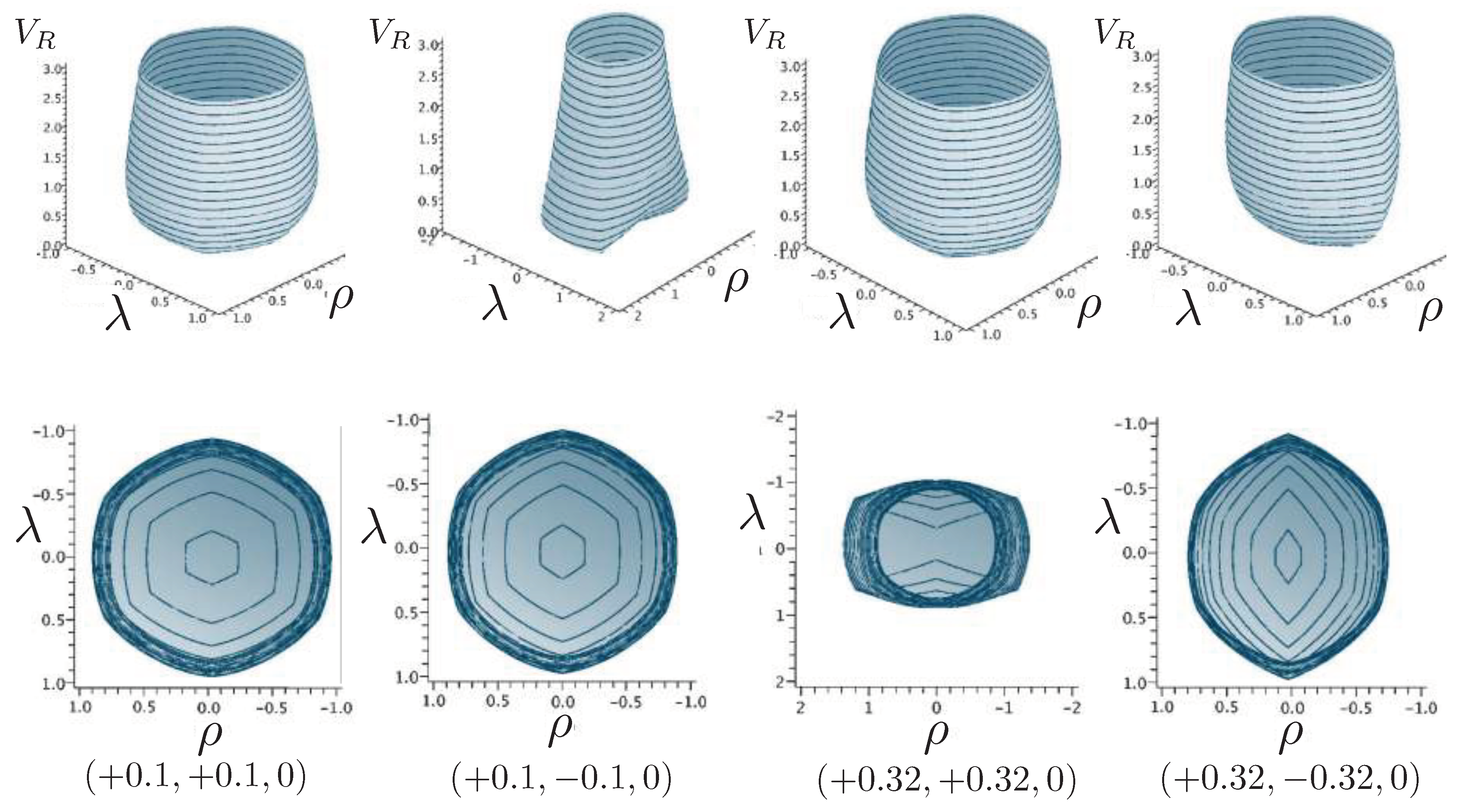
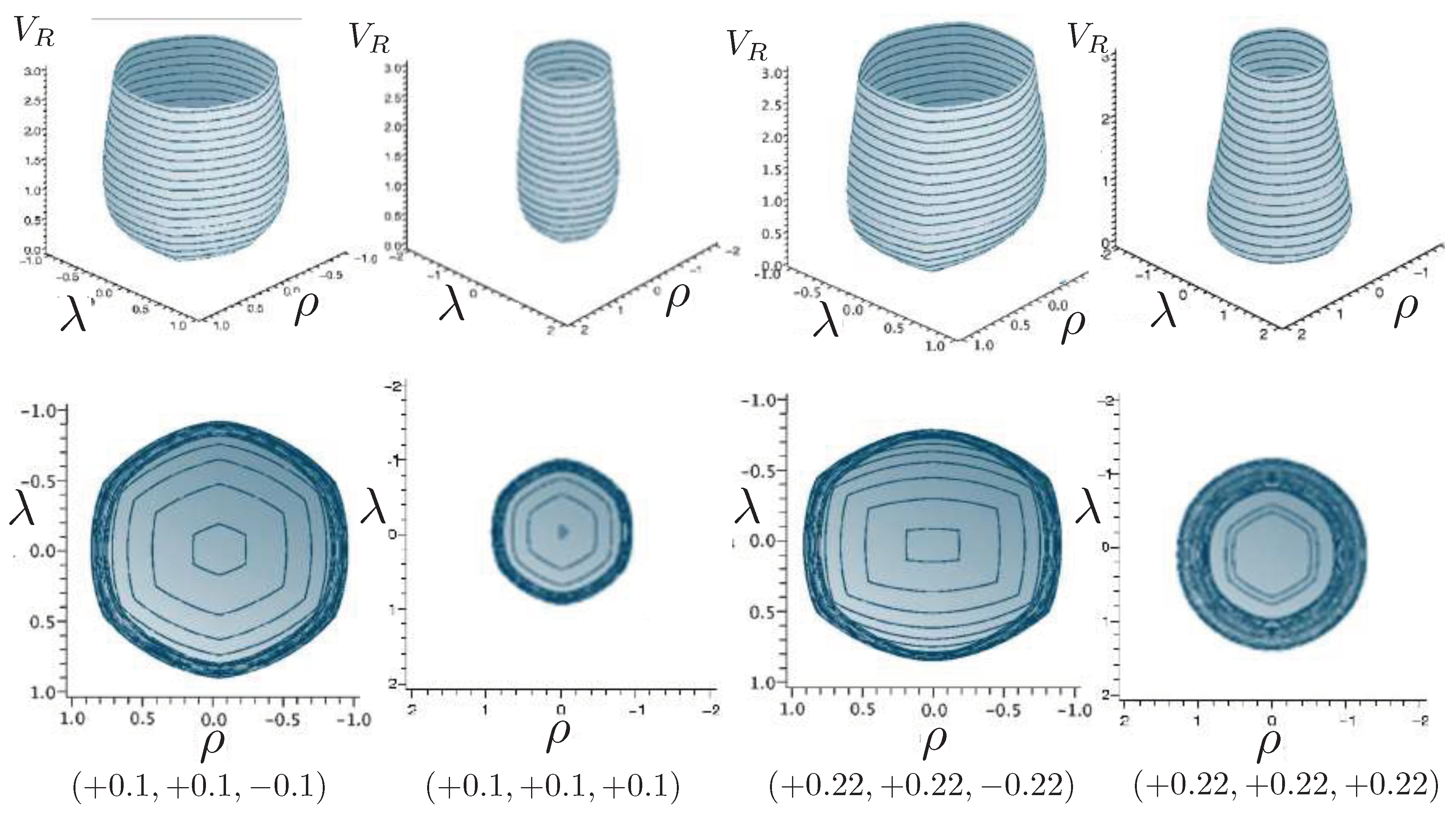
6.6.1. Neutral Configurations with $Λ_{e} \neq 0$

For a nonzero cosmological constant, the case of three neutral particles is equivalent to that of the (+ 0 0) configuration. In general

Λ_{e}

significantly modifies the chaotic properties of the relativistic 3-body system in markedly different ways, depending on its sign. The following analysis sets all masses to be equal.

For

Λ_{e} < 0

there is a rapid decrease in the size of the chaotic regions. These become even even smaller than in the N system in the Poincaré plot. Given the high degree of non-linearity this is quite surprising. This is manifest even at fairly small energies, illustrated in Figure 43 for

H = 1.2 M_{tot} c^{2}

The upper diagram in Figure 43 corresponds to the

Λ_{e} = 0

case, similar to the lower diagram in Figure 32 but with tracks (green curves) showing how different types of orbits move as

Λ_{e}

changes from a negative value (lower left diagram) to a positive one (lower right diagram). These four different quasiperiodic (or stable) orbits are shown in Figure 44 and change as

Λ_{e}

changes. Orbit (a) is located in the centre of the annulus region, whereas orbits (b), (c), and (d) produce a set of points on the Poincaré plot that follow the contours of the triangular shaped region. The stable and quasistable orbits remain so as

Λ_{e}

becomes more negative, but

Λ_{e} > 0

stable orbits can become chaotic. The transition point depends on the initial conditions of the orbit or its specific location in phase space. These results support the intuitive higher-dimensional understanding of a negative cosmological constant as a parameter that provides stronger gravitational binding, leading to an increase of the integrability of the dynamics and thus an increase in the stability of trajectories.

Remarkably, as

Λ_{e} \to Λ_{n e g c r i t}

the chaotic regions nearly vanish. Since the area of the chaotic regions in the Poincaré section were found to be roughly proportional to

|\frac{Λ_{e}}{Λ_{n e g c r i t}}|

for the range of possible energies that could be numerically investigated, it has been conjectured that this holds for arbitrarily large values of H. Conversely, the area of the chaotic regions in the Poincaré section increases as

Λ_{e}

becomes increasingly positive, shown in the lower right panel of Figure 43. This occurs within the regions corresponding to the pretzel orbits and in the regions between annulus and pretzel orbits. This phenomenon has likewise been conjectured to occur at all energies [118].

6.6.2. Charged Configurations

The charged 3-body case allows study of additional novel phenomena such as localized vacuum energy and the breaking the full hexagonal symmetry. Concerning the former, since the electromagnetic coupling between any pair of charges induces a vacuum energy between them, we can study how this localization of vacuum energy modifies effects with

Λ_{e} \neq 0

. Concerning the latter, the shape of the hexagonal potential becomes elongated unless all particles have the same charge, as in the unequal mass case [117].

Diagrams of representative cases for the potential (relative to the total rest mass) are shown in Figure 45 and Figure 46, taking (for simplicity) all charges to be equal in magnitude.

When all particles have identical charge the potential has hexagonal symmetry, but for different charges this symmetry becomes skewed. As shown in the first and third columns in Figure 45, the potential is stretched along the

λ = 0

axis in the (+ + ne) case, corresponding to the decrease in the electric potential as particles 1 and 2 separate. This results in an increase in the magnitude of

ρ

. As the magnitude of the charge increases the width of the potential at lower energies likewise increases and the sides of the hexagonal cross section become more concave. The value of

V_{R c}

at which the cross section of V is largest is also reduced. The same effects occur for the (+ 0 +) and (0 + +) configurations, but with the potential compressed along the

ρ + \sqrt{3} λ = 0

and

ρ - \sqrt{3} λ = 0

axis respectively.

By contrast in the (+ - 0) case, shown in the second and fourth columns in Figure 45, the potential is compressed along the

λ = 0

axis. This corresponds to a decrease in electric potential with increasing

ρ

When two of the particles have positive charges and the third negative (+ + -), shown in the first and third columns in Figure 46, the hexagon becomes elongated in the

ρ

direction as the magnitude of the charge increases. If all three particles have equal positive charge (+ + +), hexagonal symmetry is preserved as shown in the second and fourth columns in Figure 46. The width of the potential increases at lower energies and its sides become more convex as the magnitude of the charge increases.

As before, annulus, pretzel, and chaotic trajectories are present depending on the initial conditions; samples are shown in Figure 47. We can gain more insight by considering Poincaré plots, shown in Figure 48 (+ + 0), Figure 49 (+ - 0), and Figure 50 (+ + -).

If one particle is neutral, only the product of the charges is relevant and not their individual magnitudes; their relative sign determines the sign of V from (191). The region between the two charged particles has constant vacuum energy throughout the motion, but the size of this region changes as the particles move. Consequently using equal magnitude charges has no loss of generality.

For the (+ + 0) case in Figure 48 there are two different Poincaré plots: one corresponding to the crossing of the two identical charged particles and the other corresponding to the neutral particle crossing either of the identical particles. Comparing to the lower right panel of Figure 48, we see that chaotic behaviour emerges more rapidly with increasing repulsive charge than increasing energy, with the chaotic regions much more widespread in Figure 48. The chaotic behaviour is notably enhanced, filling the pretzel regions and pushing the annulus region in the opposite direction as the charge increases, leaving almost no circular periodic motions.

For three bodies of distinct charge, the relative magnitudes of the charges do matter, since the magnitude of the vacuum energy between them now changes as they interchange positions. The (+ - 0) case depicted in Figure 49 is very different from that induced by a negative cosmological constant, shown in the lower left panel of Figure 43, where the amount of chaos is much less as compared to the non-relativistic case. In Figure 49 there is an increase in chaos throughout a band between the pretzel and annulus regions, even for comparatively small values of the total energy. As the energy increases (right panel) the expansion of the pretzel areas pushes out the annulus region. Some of the chaotic areas between the quasi annulus and pretzel regions transform into the substructures of the repeating circles.

The (+ + -) case in Figure 50 is yet again different. The recurring circles stay around the annulus region even for higher charges, and do not change into connected areas, though the annulus region is pushed to dissolve into the left pretzel region in the lower graphs and the lower pretzel in the upper graphs with a thin band of chaos between the two regions. The magnitude of the vacuum energy between the positive charges changes between 0 and

2 e^{2}

, the former occuring whenever the negatively charged particle is between the other two. This leads to more widespread chaotic behaviour comparted to the (+ - ne) configuration, due to repeated changes in vacuum energy for a given total energy.

The behaviour of the charged case is quite rich and varied. A number of other scenarios have been studied at low energies [125], but exploration of high-energy behaviour has yet to be carried out.

7. The 4-Body Problem

The N particle OGS can be mapped to a single particle moving in

N - 1

dimensions in a linear potential whose equipotential surfaces are that of an

N - 1

simplex. Since the largest number of spatial dimensions that can be directly visualized is three, the

N = 4

system – the 4-body OGS – is of particular interest. Curiously, it has received almost no attention – only the non-relativistic system has been studied [126]. The relativistic 4-body system has yet to be investigated.

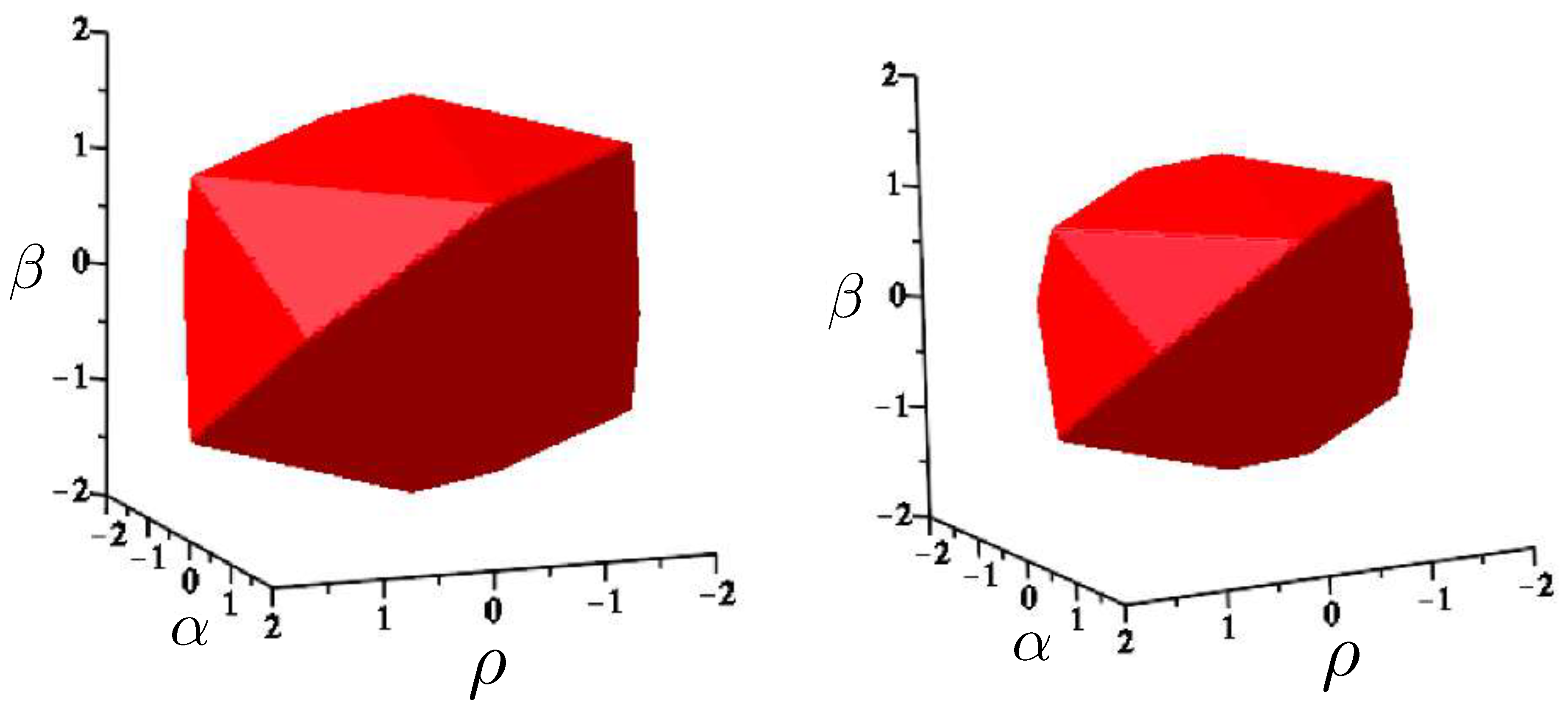
7.1. 4-Body Potential

The Hamiltonian for the non-relativistic 4-body problem is given by (1) with

N = 4

. There are now six independent degrees of freedom: the three separations between the particles and their conjugate momenta. Writing

\begin{matrix} z_{12} = \sqrt{2} ρ & z_{34} = \sqrt{2} α \\ z_{13} = \frac{1}{\sqrt{2}} (ρ + \sqrt{3} β - α) & z_{23} = \frac{1}{\sqrt{2}} (- ρ + \sqrt{3} β - α) \\ z_{24} = \frac{1}{\sqrt{2}} (- ρ + \sqrt{3} β + α) & z_{14} = \frac{1}{\sqrt{2}} (ρ + \sqrt{3} β + α) \end{matrix}

(200)

where

z_{i j} = z_{i} - z_{j}

, the conjugate momenta are

\begin{matrix} p_{1} = \frac{1}{\sqrt{2}} (p_{ρ} + \frac{\sqrt{3}}{2} p_{β}) & p_{2} = \frac{1}{\sqrt{2}} (- p_{ρ} + \frac{\sqrt{3}}{2} p_{β}) \\ p_{3} = \frac{1}{\sqrt{2}} (p_{α} - \frac{\sqrt{3}}{2} p_{β}) & p_{4} = \frac{1}{\sqrt{2}} (- p_{α} - \frac{\sqrt{3}}{2} p_{β}) \end{matrix}

(201)

with conservation of momentum allowing us to set

p_{1} + p_{2} + p_{3} + p_{4} = 0

; the centre of mass can be fixed at the origin without loss of generality. When one of

z_{12}

z_{23}

, or

z_{13}

vanish (two particles are placed directly on top of one another) this reduces to the 3-body case studied in the previous section.

In the equal mass case the Hamiltonian (1) becomes

\begin{matrix} H & = \frac{1}{2 m} (p_{ρ}^{2} + p_{α}^{2} + \frac{3}{2} p_{β}^{2}) + \frac{8 π G m^{2}}{\sqrt{8}} [|ρ| + |α| + \frac{1}{2} |ρ + α + \sqrt{3} β| \\ + \frac{1}{2} |ρ - α + \sqrt{3} β| + \frac{1}{2} |ρ + α - \sqrt{3} β| + \frac{1}{2} |ρ - α - \sqrt{3} β|] \end{matrix}

(202)

which is the Hamiltonian of a single particle (the box-particle) moving in three spatial dimensions in a linear potential whose shape is that of a 3-simplex.

The potential

V (ρ, β, α) = H (p_{ρ} = 0, p_{β} = 0, p_{α} = 0)

(203)

has equipotential surfaces which are that of a cube of pyramid-shaped sides, shown in Figure 51. As V increases the simplex likewise increases, as is clear from the comparing the two diagrams. A cross-section of this surface through any of the edges of one of these pyramids yields a hexagon with sides of unequal length. For such cross-sections the system reduces to that of 3-body case with unequal masses since two particles will occupy the same position.

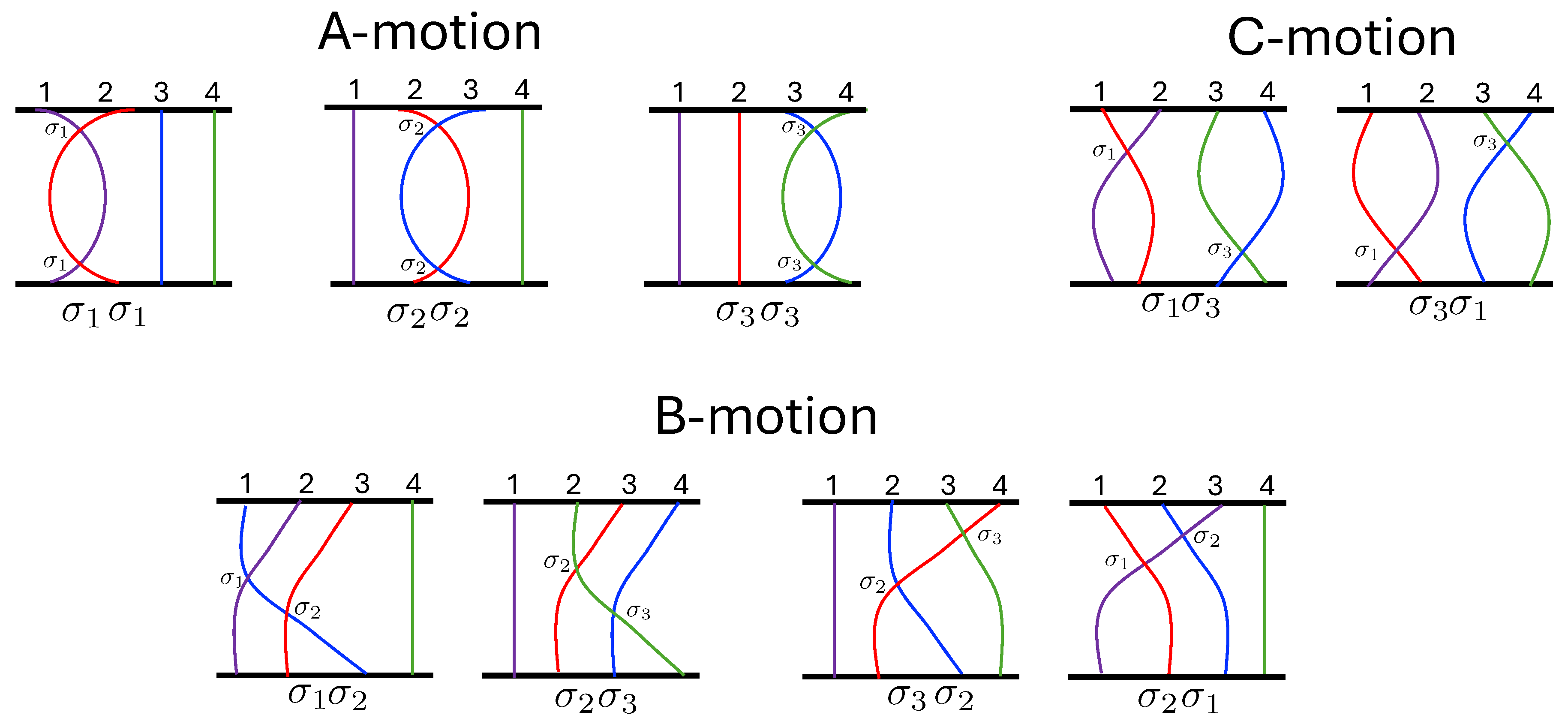
7.2. Motion Classification

The 4-body system has an interesting structure that can be described in terms of braid operators. This generalizes the A-type and B-type motions of the 3-body case.

As in the 2-body and 3-body cases, each particle moves with a constant acceleration that is proportional to the difference between the total mass on its right and left sides prior to any collision. Assuming the particles move through each other, after a collision, the mass difference experienced by any given particle will in general change, and consequently the accelerations of the particles also changes. From the viewpoint of the box particle, any crossing of a pair of particles corresponds to the box particle crossing a plane bisecting the 3-simplex through its vertices and edges. There are a total of six such planes, obtained by setting any one of the six quantities in (200) to zero. The planes occur in pairs whose line of intersection is along each of the three principal axes.

Any sequence of crossings of N bodies can be described using braid Group notation [127] using the set

{σ_{1}, σ_{2}, \dots, σ_{N - 1}}

, with

σ_{j} = σ_{j}^{- 1}

since crossing direction is irrelevant. The positions of the particles (and not the particle themselves) are are ordered as

(1, 2, 3, . . ., N)

, where the left-most particle is at position 1, next 2, and so on with the right-most particle being at position N. Note that it is the particular sequence of collisions that is important; any permutation of the operators would result in loss of information about the motion in the system.

Applying this to the 3-body system, the braid operators are

{σ_{1}, σ_{2}}

and the motion can be classified into

\begin{matrix} σ_{1} σ_{1}, σ_{2} σ_{2} & A motion \\ σ_{1} σ_{2}, σ_{2} σ_{1} & B motion \end{matrix}

(204)

or in other words the only interesting types of motion are when the same pair of particles crosses twice in a row (A-motion) or when one particle crosses each of its compatriots in succession (B-motion).

In the 4-body case, there are only 3 possible crossings –

{z_{12}, z_{23}, z_{34}}

– at any given instant, and the braid operators

{σ_{1}, σ_{2}, σ_{3}}

, respectively correspond to an interchange between the right-most, middle, and left-most pair of bodies. In this case we have

\begin{matrix} σ_{1} σ_{1}, σ_{2} σ_{2}, σ_{3} σ_{3} & A motion \\ σ_{1} σ_{2}, σ_{2} σ_{1}, σ_{2} σ_{3}, σ_{3} σ_{2} & B motion \\ σ_{1} σ_{3}, σ_{3} σ_{1} & C motion \end{matrix}

(205)

which is depicted in Figure 52. The A and B motions represent the same physical situations as in the 3-body case, but the C motion is new: two particles cross one another and then the other two cross one another.

Multiple collisions can occur. In the 3-body system this happens when the hex particle crosses the origin, corresponding to all three bodies meeting at the same point at some instant of time. The analog of this in the 4-body case occurs when the box particle crosses the line of intersection of any two bisecting planes of the 3-simplexes. There are two kinds of these 3-body collisions described by

{σ_{1^{3}}, σ_{2^{3}}}

. There are also two kinds of 4-body collisions described by

{σ_{1^{4}}, σ_{1^{2} 3^{2}}}

. The former corresponds to all 4 bodies meeting at a single point, equivalent to the box particle crossing the origin. The latter occurs when one pair of particles cross at one point and the other pair cross at a different point at the the same time, corresponding to the box particle crossing one of the three lines connecting opposite vertices of the pyramids in the simplex (see Figure 51).

7.3. Equal Mass Trajectories

It can be straightforwardly shown that if one of the box-particle’s position and momentum coordinates are initially zero, they will remain zero throughout the motion, and that all the phenomena seen in the 3-body case in the previous section are recovered [126]. The more interesting situation is when the box particle exhibits motion in all spatial directions.

A comparison is shown in Figure 53, where the

α, p_{α}

remains fixed in the upper plots, but in the lower plots either

α

(lower left) or

p_{α}

(lower right) deviates from zero. The motion in the

α

direction simply perturbs the patterns in the upper figures, effectively giving a “thickness” to the original hex-particle patterns.

By carefully choosing the initial conditions it is possible to obtain genuinely novel periodic orbits in three dimensions, as shown in Figure 54. This trajectory has a pretzel form when projected onto two of the planes

(ρ, β)

(upper left) and

(ρ, α)

(not shown) and has annulus form when projected onto the third

(β, α)

plane (upper right). The full three-dimensional orbit is shown in the lower left panel (with no perspective so that lines further away do not appear smaller). The motion here is

\bar{{(C B^{2} C B^{2} C B^{6})}^{2} C B^{6}}

and has no analogue in the 3-body system. Motions of each particle are shown in the lower right panel, and have two bodies undergoing small amplitude oscillations (solid and dotted lines) with the other two undergoing larger amplitude oscillation (dash and dot-dash lines).

The upper panels of Figure 55 show a situitation where the four particles begin at zero momentum and are equally spaced. As expected they are all attracted together and cross at the same point, repeating this pattern indefinitely. The symbol sequence is undefined since all four particles always ‘collide’ at the same time step. The box particle oscillates along a line in

(ρ, β, α)

space (upper left), with all particles crossing at the origin simultaneously. The outer two particles (solid, dot-dash) undergo large amplitude oscillations and the inner two (dash, dotted) undergo small amplitude oscillations. However the motion is unstable: a slight change in any of the initial conditions (via either a small perturbation in position or momentum) throws the system into chaos. This is shown in the bottom two panels of Figure 55 where the initial value of

ρ

is slightly increased. All particle trajectories (lower right) continually vary their oscillation amplitudes. This is evident within 30 time steps, where we see the dashed line grow in amplitude whilst the dot-dash one shrinks.

7.4. Poincaré Plots

The most natural extension of a Poincaré plot to the 4-body case is use spherical coordinates, plotting the radial momentum

p_{R}

against the squares of the two angular momenta

p_{θ}^{2}

and

p_{ϕ}^{2}

. Writing

\begin{matrix} sin ϕ & = & \frac{β}{\sqrt{ρ^{2} + β^{2}}}, cos ϕ = \frac{ρ}{\sqrt{ρ^{2} + β^{2}}} \\ sin θ & = & \frac{\sqrt{ρ^{2} + β^{2}}}{\sqrt{ρ^{2} + β^{2} + α^{2}}}, cos θ = \frac{α}{\sqrt{ρ^{2} + β^{2} + α^{2}}} \end{matrix}

(206)

R is the distance from the origin to the point of crossing in

(ρ, β, α)

space and

(θ, ϕ)

are the polar and azimuthal angles of this point. The unit vectors for these spherical coordinates are

\hat{R} = [\begin{matrix} cos ϕ sin θ \\ sin ϕ sin θ \\ cos θ \end{matrix}], \hat{ϕ} = [\begin{matrix} - sin ϕ \\ cos ϕ \\ 0 \end{matrix}], \hat{θ} = [\begin{matrix} cos ϕ cos θ \\ sin ϕ cos θ \\ - sin θ \end{matrix}]

(207)

The associated momenta are

\begin{matrix} p_{R} & = & \frac{p_{ρ} ρ + p_{β} β + p_{α} α}{\sqrt{ρ^{2} + β^{2} + α^{2}}} = \hat{R} \cdot \vec{p} \\ p_{ϕ} & = & \frac{- p_{ρ} β + p_{β} ρ}{\sqrt{ρ^{2} + β^{2}}} = \hat{ϕ} \cdot \vec{p} \\ p_{θ} & = & \frac{p_{ρ} ρ α + p_{β} β α - p_{α} (ρ^{2} + β^{2})}{\sqrt{(ρ^{2} + β^{2} + α^{2}) (ρ^{2} + β^{2})}} = \hat{θ} \cdot \vec{p} \end{matrix}

(208)

and (208) can be used to compute

p_{R}

p_{ϕ}^{2}

and

p_{θ}^{2}

whenever two of the four particles cross one another.

Constructing complete Poincaré plots is a challenge for two reasons. First, the standard approach of choosing a range of initial conditions that fill in the important regions is computationally much more formidable since with five independent variables the number of possible plots is very large. This can be dealt with by automating the generation of data over a specific range of initial conditions, but a significant reduction in the number of time steps must be employed for computational tractability. Visualizing the large number of discrete points in 3-dimensional space is the second challenge. The plots in Figure 56 were constructed by separating out the space into millions of minute three-dimensional boxes, assigning a value corresponding to the number of Poincare points that fall inside and a position corresponding to the location of the box. Although this limits the ability to zoom in to observe self-similar structures, highly saturated regions of chaos tend to show up well.

Figure 56 shows two special slices:

p_{ϕ} = 0

(the “bottom” slice) and

p_{θ}^{2} < 0.0005

(the “side” slice). Out of 12 million points generated, 400,000 are in the bottom slice and 500,000 are in the side slice. In the latter case any trajectory with

p_{θ} = 0

would remain in a cone rooted at the origin, and so the above bound on

p_{θ}^{2}

imposes the constraint of

p_{θ}

being “close” to zero.

The bottom slice in Figure 56 bears a resemblance to the non-relativistic 3-body case shown in Figure 31, exhibiting mixed regions of chaos and integrability. By constrast, the side slice does not display the same patterns and fractal-like properties as the bottom slice. Whether this is due to an insufficient number of time steps, a failure to cover a sufficient range of initial conditions or an intrinsic lack of any patterns is not yet known.

The non-relativistic 4-body problem has a number of other interesting aspects [126]. These include apparently chaotic motion in some projections with quasi-periodic motion in others, novel Poincaré plots for particular classes of orbits, and Lyapunov exponents that asymptote to constant values ranging between

10^{- 2}

for chaotic trajectories,

10^{- 3} - 10^{- 4}

for quasi-periodic trajectories and

10^{- 5}

(the limits of numerical precision) for periodic trajectories [126]. More complete studies remain to be carried out, not only for the non-relativistic system, but for its relativistic counterpart.

8. The N-Body Problem

Studies of the N-body OGS for

N > 4

generally have been concerned with its statistical properties. Many unanswered questions remain despite extensive study. Its ergodic and equipartition properties are still not well understood. Whether or not the OGS can attain a true equilibrium state from arbitrary initial conditions is also not clear. These issues remain outstanding in large part because the attractive interactions are cumulatively long range, unlike typical thermodynamic systems that have repulsive and short range interactions between their constituents.

However some statistical properties of the OGS are known. The single-particle distribution function in both the canonical and microcanonical ensemble has been derived [4]. These distribution functions reduce to the isothermal solution of the Vlasov equation in the large N limit.

Even less is known about the N-body ROGS, with only one study of its statistical properties having been carried out to date [128]. In this section a few of the basic results of this system will be summarized.

8.1. Motion Classification

Braid operators

{σ_{1}, σ_{2}, \dots, σ_{N}}

can be used to classify motion in the N-body system. A sequence of m pair crossings will be described by

σ_{f (1)} σ_{f (2)} σ_{f (3)} . . . σ_{f (m)}

(209)

where

1 \leq f (x) \leq (N - 1)

for all

1 \leq x \leq m

is a discrete integer function and

σ_{f (x)}

means that the bodies currently in positions

f (x)

and

f (x) + 1

cross. Crossing directions are irrelevant, and for a given trajectory any given sequence of m braid operators forms a unique ordered list of crossings.

It is possible to define a a metric that describes the relative “distance” between any pair of crossings via

g (x) \equiv | Δ f (x) | = | f (x + 1) - f (x) |

(210)

which implies

0 \leq g (x) \leq (N - 2)

for all

1 \leq x \leq (m - 1)

. The motion can be then classified as follows:

\begin{matrix} g (x) & Motion Class \\ 0 & A \\ 1 & B \\ 2 & C \\ 3 & D \\ . . . \end{matrix}

(211)

denoting each type by increasing letters of the alphabet. A-motion corresponds to any 2 crossings in nearest proximity – two particles cross each other twice in succession. B-motion corresponds to any 2 crossings in next-nearest proximity – two particles cross each other, and then one of them crosses its other nearest neighbour. C-motion corresponds to any 2 crossings in next-to-next-nearest proximity: two particles cross each other and then a neighbouring pair cross each other. This continues until the left-most pair of particles cross one another followed by the crossing of the right-most pair (or vice-versa), which is the extreme case. In the 4-body case, for example,

σ_{1} σ_{2} σ_{1} σ_{3} σ_{2}

, yields from (205) the symbol sequence

B B C B

. Computing successive values of

g (x)

(

1, 1, 2, 1

) gives same result.

A collision of m particles simultaneously corresponds to a single particle crossing through an

(N - m)

-dimensional surface in the interior of the

(N - 1)

simplex. Such collisions can be further classified by extending the braid group notation with the set

{σ_{1^{m}}, σ_{2^{m}}, \dots, σ_{{(N + 1 - m)}^{m}}}

. The subscript denotes which set of particles is involved, beginning with the left-most; the superscripts denote the number of particles in the collision, with the superscript “2” dropped when pairwise collisions occur. For example

σ_{8^{5}}

denotes a 5-particle collision that involves particles 8-12. All collisions yield crossings with the exception of the initial conditions causing m particles to occupy the same point throughout the motion (as in the upper left panel of Figure 55 in the 4-body case). In this situation the system reduces to that of an (unequal mass)

(N - m)

-body problem.

After a multiple particle collision it is always possible to predict the new order of particles given their preceding order. Defining rightward velocity as positive, for two adjacent particles a small time just before the collision, the left one must have a larger velocity than right one or else the latter would be moving away and not toward the left one and no collision would occur. Applying this reasoning to every adjacent pair implies that on moving from left to right the velocity of each particle decreases in the sequence, with the left-most particle having the largest velocity. Immediately after the collision the original order will be reversed, since the previously left-most particle will be travelling rightward faster than all other particles in the collision and emerge afterwards as the right-most particle, and so on for all particles in the collision. If any of the n particles does not satisfy the increasing velocity condition there will be fewer than n particles in the multiple collision.

8.2. Post-Newtonian Canonical Ensemble

The canonical one-particle distribution function can be shown to be

f_{c}^{R} (p, z) = \frac{1}{Z N!} \int \int d p d z δ (\bar{p}) δ (\bar{z}) exp (- β H) N^{- 1} \sum_{a} δ (z - z_{a}) δ (p - p_{a})

(212)

by making use of momentum conservation and translation invariance [128], where H is the Hamiltonian of the system. This quantity is straightforward to compute for the N system [4], since its Hamiltonian (1) is at most quadratic in the canonical variables. However the Hamiltonian (76) for the R system is a highly non-linear function of these variables, and computation of (212) is not obvious. For practical reasons, the post-Newtonian Hamiltonian

H_{p N}

in (28) has been used to gain insight into the statistical properties of the ROGS [128].

The quantity

\begin{matrix} Z & = \frac{1}{N!} \int \int d p d z δ (\bar{p}) δ (\bar{z}) exp (- β H_{p N}) \end{matrix}

(213)

is the partition function. A somewhat tedious calculation yields the result [128]

\begin{matrix} Z = \frac{exp [- β M c^{2} - \frac{3 (N - 1)}{2} ln (β m c^{2}) - \{\frac{(5 N + 3) (N - 1) + 8 N \sum_{k = 1}^{N - 1} \sum_{l = k + 1}^{N - 1} \frac{(l - k)}{l (N - k)}}{8 N β m c^{2}}\}]}{\sqrt{N} {(\sqrt{2 π} G / c^{3})}^{(N - 1)} {[(N - 1)!]}^{2}} \end{matrix}

(214)

to lowest relativistic order, where

M = \sum_{a = 1}^{N} m_{a}

. The average energy is then

\begin{matrix} 〈E〉 & = & - \frac{\partial}{\partial β} ln Z \\ = & M c^{2} + \frac{3}{2 β} (N - 1) - \frac{(5 N + 3) (N - 1) + 8 N \sum_{k = 1}^{N - 1} \sum_{l = k + 1}^{N - 1} \frac{(l - k)}{l (N - k)}}{8 β^{2} M c^{2}} \end{matrix}

(215)

to the relevant order in

c^{- 2}

. For fixed

M = N m

the relativistic correction grows quadratically with N and is negative. Consequently average energy of the ROGS is lower than its non-relativistic counterpart at the same temperature.

When the thermal energy

k T = β^{- 1}

is sufficiently small relative to the rest energy

M c^{2}

of the system, the average energy

ζ \equiv \frac{(E - M c^{2})}{M c^{2}}

is not much different from its non-relativistic value of

\frac{3 (N - 1)}{2 β M c^{2}}

. As

β

decreases the value of

〈ζ〉

increases more slowly than its non-relativistic counterpart, and reaches a maximum at

β = β_{\max} \equiv \frac{(5 N + 3) (N - 1) + 8 N \sum_{k = 1}^{N - 1} \sum_{l = k + 1}^{N - 1} \frac{(l - k)}{l (N - k)}}{6 (N - 1) M c^{2}} \underset{N > > 1}{\to} (\frac{7}{2} - \frac{2 π^{2}}{9}) \frac{N}{M c^{2}}

(216)

which is half the value of its non-relativistic counterpart. This maximum value is plotted in Figure 57 as a function of N, and asymptotes to the constant value

〈ζ〉 = . 573940872

N \to \infty

. For

β > β_{\max}

the average energy

ζ

decreases with increasing

β

, vanishing at

β = \frac{1}{2} β_{\max}

. The post-Newtonian expansion (28) breaks down well before this value of

β

The canonical momentum distribution function can be obtained by integrating the single particle distribution function. The result is

\begin{matrix} ϑ_{c n} (p) & = & \int_{- \infty}^{\infty} d z f_{c n} (p, z) \\ = & \sqrt{\frac{(N β)}{2 π m (N - 1)}} exp [- \frac{N β p^{2}}{2 m (N - 1)}] \\ \times (1 + \frac{1}{β m c^{2}} (\frac{N β^{2} p^{4} (N^{2} - 3 N + 3)}{8 m^{2} {(N - 1)}^{3}} - \frac{β p^{2} (4 N^{2} - 7 N + 6)}{4 m {(N - 1)}^{2}} + \frac{5 N (N - 1) + 3}{8 N (N - 1)})) \end{matrix}

(217)

and corrects the standard non-relativistic Gaussian expression by a polynomial in

p^{2}

The preceding expression can be rewritten in terms of dimensionless variables

η \equiv \frac{p}{m V} V^{2} \equiv \frac{4 (E - M c^{2})}{3 M} = \frac{4 ζ c^{2}}{3}

(218)

and is plotted in Figure 58.

The central momentum density grows with increasing

ζ

, but falls off more rapidly than its non-relativistic counterpart does. However for

η > 2

, the momentum density grows exponentially relative to its non-relativistic counterpart, overtaking it for sufficiently large

η

. This is clearly seen in the right-hand panels of Figure 58. The differences become less pronounced as N increases, although the basic features remain the same for all N.

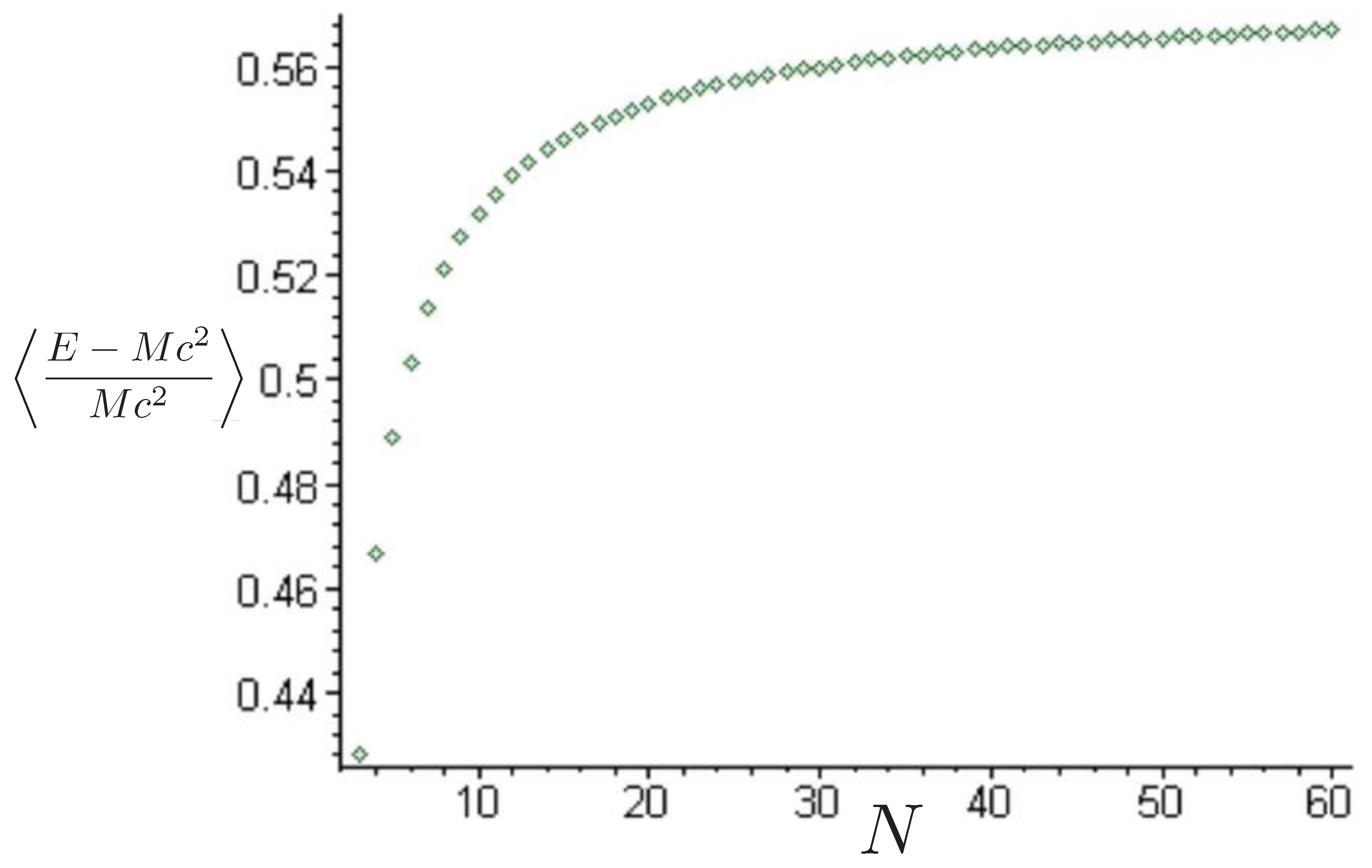
8.3. Other Statistical Features

Computation of other quantities, such as the canonical density distribution, the full single particle canonical distribution, and the microcanonical distribution functions involve a considerable amount of tedious algebra. Some general features emerge from this analysis [128]. One is that relativistic effects cool the system: at a given energy, the ROGS temperature is smaller than the OGS temperature. Another is that ROGS density and distribution functions become more sharply peaked than their OGS counterparts as

ζ

increases for any given N. For sufficiently large values of the position parameter z,

ρ_{OGS} > ρ_{ROGS}

for both the canonical and microcanonical distribution functions. The momentum densities exhibit different behaviour, with

ϑ_{OGS} > ϑ_{ROGS}

for small values to intermediate values

η

, but for large enough

η

, the inequality is reversed and

ϑ_{OGS} < ϑ_{ROGS}

Further exploration of the N-body ROGS will be challenging. A natural first step would be a consideration of the charged and cosmological systems at the post-Newtonian level. The unequal mass case is likely similarly tractable, though it will be considerably more difficult. However a full understanding almost certainly require a numerical approach, particularly to go beyond leading order corrections in

1 / c^{2}

9. The Circular N-Body Problem

Thus far the discussion has been concerned with lineal topology. For non-relativistic gravity this is the only option. The OGS equations (4) for a general potential V are

\begin{matrix} V^{''} & = & 4 π G m δ (x - z (t)) \end{matrix}

(219)

\begin{matrix} \dot{p} & = & - V^{'} (z) \end{matrix}

(220)

\begin{matrix} \dot{z} & = & \frac{p}{m} \end{matrix}

(221)

for a single particle. The first equation implies

V = 2 π G m |x|

, which has a vanishing derivative at

x = 0

and yielding

p = z = 0

as a consistent single particle solution. However if the topology is circular then both

V (L) = V (- L)

and

V^{'} (L) = V^{'} (- L)

for some L, where

2 L

is the circumference of the circle. These matching conditions have no solution unless another point source of negative mass is introduced. For N bodies modelled as compact smeared sources the problem remains: the potential grows linearly with increasing distance from the source(s) and the matching conditions cannot be satisfied for physically reasonable (i.e., positive mass) sources.

However the ROGS, being in a dynamical spacetime, does not suffer from this problem, since the spacetime can expand or contract in response to the presence of sources. It is possible to solve the canonical equations of motion and obtain both single particle [129] and exact N-body static equilibrium solutions [130,131]. This latter solution corresponds to a spacetime that expands/contracts in response to N equal mass bodies at equidistant proper separations from one another. These are the first N-body dynamic equilibrium solutions in any relativistic theory of gravity.

The action is still given by (10) but the extrinsic curvature K in (17) is now taken to be a time coordinate

τ (t)

. This allows the elimination of

π

from all canonical field equations. The reduced canonical action (22) instead becomes

I_{R} = \int d^{2} x \{\sum_{a} p_{a} {\dot{z}}_{a} δ (x - z_{a}) + Π \frac{\partial}{\partial t} (Ψ + ln γ) - H\},

(222)

where now

H = \int d x H = \frac{2 \dot{τ}}{κ} \int d x \sqrt{γ}

(223)

which is the circumference functional of the circle when

\dot{τ}

is constant. The N-body system is now time-dependent. The spatial metric can be chosen so that

γ = γ (t)

, as in general relativity on

(2 + 1)

-dimensional spatially compact manifolds [132]. The Hamiltonian will be time-independent if a time parametrization is chosen so that

\dot{τ} \sqrt{γ}

is constant.

Equilibrium solutions correspond to a situation in which all particles are motionless at various points around the circle. Consequently they are characterized by

\dot{z_{a}} = 0 = p_{a}

, and so the canonical field equations (49) – (54) become [130,131]

\begin{matrix} 2 Π^{'} - Π Ψ^{'} = 0; & ​ \end{matrix}

(224)

\begin{matrix} Ψ^{''} - \frac{1}{4} {(Ψ^{'})}^{2} - {(κ Π)}^{2} + γ (τ^{2} - Λ_{e}) + κ \sum_{a} \sqrt{γ} m δ (x - z_{a} (x^{0})) = 0 & ​ \end{matrix}

(225)

\begin{matrix} N_{0}^{''} - \dot{τ} γ - N_{0} \{(τ^{2} - Λ_{e}) γ + κ / 2 \sum_{a} \sqrt{γ} m δ (x - z_{a} (x^{0}))\} = 0 & ​ \end{matrix}

(226)

\begin{matrix} N_{1}^{'} - \dot{γ} / 2 + γ τ N_{0} = 0 & ​ \end{matrix}

(227)

\begin{matrix} \dot{Π} + \partial_{1} (- \frac{1}{γ} N_{1} Π + \frac{1}{2 κ \sqrt{γ}} N_{0} Ψ^{'} + \frac{1}{κ \sqrt{γ}} N_{0}^{'}) = 0 & ​ \end{matrix}

(228)

\begin{matrix} \dot{Ψ} + 2 N_{0} (κ \frac{Π}{\sqrt{γ}} + τ) - N_{1} (\frac{1}{γ} Ψ^{'}) = 0 & ​ \end{matrix}

(229)

with

{\frac{\partial N_{0}}{\partial x}|}_{x = z_{a}} = 0 N_{1} (z_{a}) = 0

(230)

which follows from the geodesic equations.

Solutions to (224–229) must be appropriately matched at the locations

z_{a}

of each particle and the identification point

|x| = L

. The solutions for

Ψ

and

N_{0}

must be continuous but are not differentiable at the particle locations; for example

{lim}_{ϵ \to 0} [Ψ^{'} (z_{a} + ϵ) - Ψ^{'} (z_{a} - ϵ)] = κ \sqrt{γ} m

. Setting

r = |z_{a} - z_{a + 1}| = \frac{2 L}{N}

corresponding to N bodies of equal mass m at equal time-varying proper separations, the solution is

\sqrt{γ} = \frac{N}{L \sqrt{τ^{2} - Λ_{e}}} arctanh (\frac{ξ \sqrt{\frac{κ^{2} M^{2}}{16 N^{2}} + (ξ^{2} - 1) (τ^{2} - Λ_{e})} - \frac{κ M}{4 N}}{\frac{κ^{2} M^{2}}{16 N^{2}} + ξ^{2} (τ^{2} - Λ_{e})} \sqrt{τ^{2} - Λ_{e}})

(231)

for the metric function

γ (t)

, where

ξ

is an integration constant,

{\hat{c}}^{2} \equiv γ (τ^{2} - Λ_{e}) = c_{+}^{2} > 0

, and

M = m N

is the total mass of the system.

The remaining functions are

\begin{matrix} κ Π & = & \frac{\pm c_{+} \sqrt{β^{2} - 1}}{\frac{sinh (\frac{c_{+} L}{N})}{sinh (c_{+} L)} \sum_{a = 1}^{n} cosh (c_{+} (| x - z_{a} | - L)) - β} \end{matrix}

(232)

\begin{matrix} Ψ & = & - 2 ln (β - \frac{sinh (\frac{c_{+} L}{N})}{sinh (c_{+} L)} \sum_{a = 1}^{n} cosh (c_{+} (| x - z_{a} | - L))) - 2 ln (\frac{κ Π_{0} (t)}{c_{+} \sqrt{β^{2} - 1}}) \end{matrix}

(233)

\begin{matrix} N_{0} & = & \frac{\dot{τ} γ}{c_{+}^{2} β} (\frac{sinh (\frac{c_{+} L}{N})}{sinh (c_{+} L)} \sum_{a = 1}^{n} cosh (c_{+} (| x - z_{a} | - L))) - β) \end{matrix}

(234)

\begin{matrix} N_{1} & = & γ \frac{\dot{c_{+}}}{c_{+}} x - \frac{γ^{2} τ \dot{τ}}{c_{+}^{3} β} \frac{sinh (\frac{c_{+} L}{N})}{sinh (c_{+} L)} \sum_{a = 1}^{n} ϵ (x - z_{a}) [sinh (c_{+} (| x - z_{a} | - L)) + sinh (c_{+} L)] \end{matrix}

(235)

where

\begin{matrix} β & = & \frac{4 N}{κ M} \sqrt{\frac{κ^{2} M^{2}}{16 N^{2}} + (ξ^{2} - 1) (τ^{2} - Λ_{e})} \end{matrix}

(236)

and

ϵ (x) = \frac{|x|}{x}

is a step function with

ϵ (0) = 0

The system is cyclically symmetric, with

N_{1} (L) = N_{1} (- L)

, and so we can choose the origin to be halfway between any two particles in the

N =

even case or on a particle in the

N =

odd case. The spatial periodicity of the solution can be better seen using the relation

\sum_{a = 1}^{n} cosh (c_{+} (| x - z_{a} | - L)) = cosh (c_{+} f (x)) \frac{sinh (c_{+} L)}{sinh (\frac{c_{+} L}{N})}

(237)

where

f (x)

is the saw-tooth function that peaks with a value of

L / N

(in other words,

f (z_{a}) = L / N

) at the particle locations and vanishes half-way between the particles (i.e.,

f (\frac{z_{a} - z_{a + 1}}{2}) = 0

). A simple shift of the origin in the cosh function and a subsequent manipulation of the sum yields the equivalence.

{\hat{c}}^{2} = c_{-}^{2} < 0

the another class of solutions exists with

\sqrt{γ} = \frac{N}{L \sqrt{Λ_{e} - τ^{2}}} [arctan (\frac{ξ \sqrt{\frac{κ^{2} M^{2}}{16 N^{2}} + (1 - ξ^{2}) (Λ_{e} - τ^{2})} - \frac{κ M}{4 N}}{\frac{κ^{2} M^{2}}{16 N^{2}} - ξ^{2} (Λ_{e} - τ^{2})} \sqrt{Λ_{e} - τ^{2}}) + k π]

(238)

and

c_{+} \to i c_{-}

in (232) – (235). The integration constant

|ξ| < \sqrt{1 + \frac{{(κ M)}^{2}}{16 Λ_{e} N^{2}}}

as a due to the periodicity of

N_{1} (x, t)

and k is an integer. No solutions exist for

c^{2} = 0

The solution (231–235) (and its

c^{2} < 0

counterpart) corresponds to an expanding/contracting spacetime of a circle with N bodies at equal time-varying proper separations from one another around the circle. The solution for the spatial metric is equivalent to that of single-particle solution [129] upon rescaling

L \to L / N

and

M \to M / N

. However this rescaling equivalence does not hold for the remaining functions. For

Λ_{e} = 0

the spacetime expands but perpetually decelerates due to the presence of the point masses. If

Λ_{e} < 0

the proper circumference of the circle expands from zero to some maximal size and then recontracts. The most interesting behaviour occurs if

Λ_{e} > 0

. In this case the cosmological expansion opposes decelerating effects due to the point masses and the spacetime can expand from zero size to finite value, evolve from some minimal/maximal circumference to a maximal/minimal size, or undergo perpetual oscillation.

A generalization of this solution to one in which there are an even number of bodies with charge alternating in sign but equal in magnitude also has been obtained [131]. This solution, and its neutral counterpart in (231–235) almost certainly describe an unstable equilibrium, since the masses are all equal and the particles are evenly separated. Perturbations from equilibrium would be interesting to investigate, as they would form model inhomogeneous self-gravitating cosmological systems. This remains an interesting avenue for further study.

10. Conclusions

Relativistic one-dimensional self-gravitating systems provide an interesting (and in the view of this author) undervalued theoretical laboratory for studying a number of physical effects of which rather little is known. These include exact 2-body motion, static N-body equilibrium, relativistic thermodynamics and statistical mechanics, relativistic chaos, and the interplay between gravity, electromagnetism, and cosmological evolution. I shall close this review with a brief overview of seven different research avenues that warrant further study.

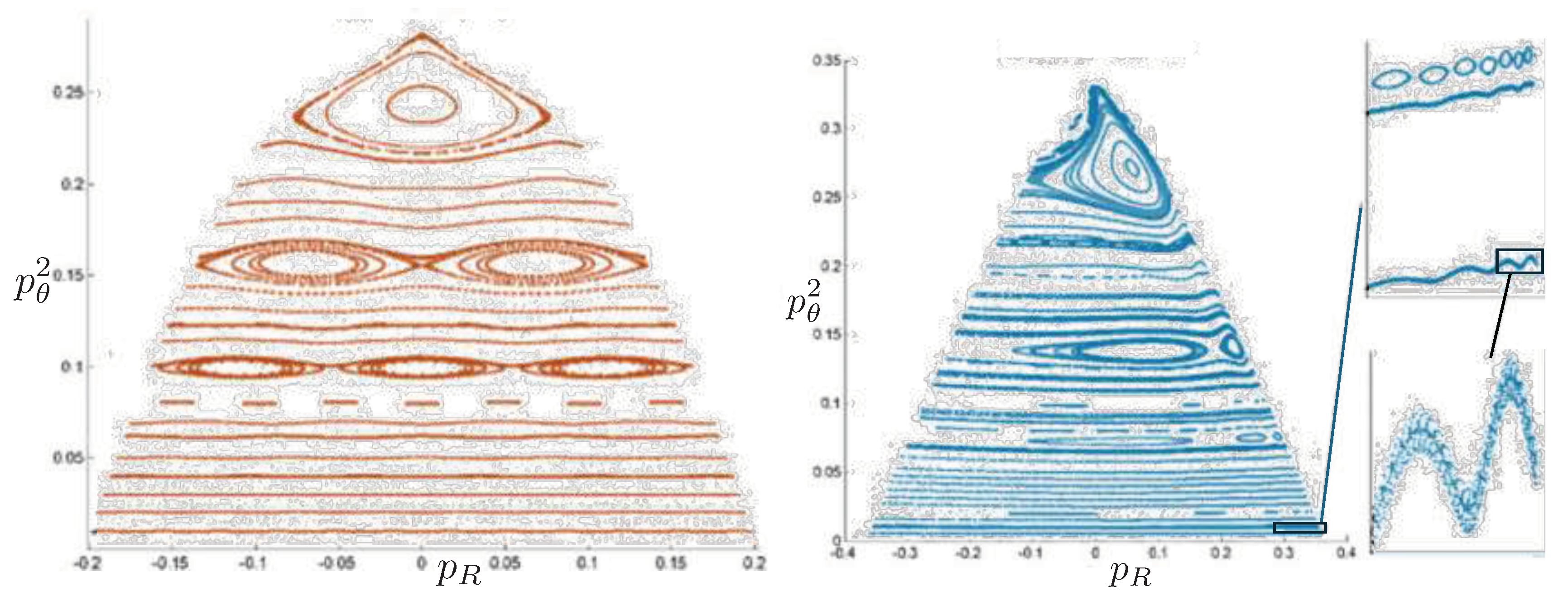
Relativistic Chaos at High Energy

All studies of relativistic 3-body chaos have been at energies below the cross-sectional maximum of the potential $V_{R}$ in (177). The regions of chaos in the R system are distortions of their N system counterparts, but do not increase. It would be of great interest to know what the chaotic behaviour is for energies larger than the cross-sectional maximum, where very strong relativistic effects are present. Will the chaotic regions in the Poincaré plots grow or shrink? Such studies would provide further insight into the effects of strong gravity on chaotic systems.
4-body Chaos

The largest value of N in the N-body problem for which equipotential surfaces can be visualized is $N = 4$ . As noted in Section 7, only the N system has been investigated for its motions and chaotic behaviour. The R system has yet to be investigated along these lines. It is conceivable that qualitatively new features will be observed in this case.
Fully relativistic Statistical Mechanics

The scope for exploration here is very broad. Only the statistical properties of the neutral pN system have been studied. The effects of charge and cosmological expansion are not known, and a full study of the statistical properties of the R system remain to be carried out. This latter problem will be quite technically challenging, since the distributions functions cannot be analytically integrated. Some novel blend of analytic and numerical methods will need to be employed.
Circular N-body Dynamics

A novel feature of the N-body ROGS is that it admits two distinct spatial topologies: linear and circular. In the latter case there are no dynamical solutions for $N \geq 2$ . These will likely need to be found numerically. It would be particularly interesting to investigate 3-body chaos in this setting to see what effects circular topology has on chaotic phenomena.
The 2-dimensional N-body problem

Since there is no gravitational radiation in 2 spatial dimensions the N-body problem in this setting is of considerable interest, all the more so since general relativity will provide the foundation for the field equations. This problem has been considered from a topological perspective [133], from which an implicit solution for the metric and the motion of N particles was obtained [134]. The solution becomes explicit for $N = 2$ . However the relationship between this approach and the canonical approach has only been explored to a limited extent [135,136]. A thorough analysis should be carried out, particularly since particle collisions can form black holes [137] and quite possibly lead to other interesting spacetime effects.
Extensions to Dilaton Gravity

The $R = T$ theory (10) has provided the context for exploring the relativistic N-body problem since it is the $D \to 2$ limit of general relativity [27]. However a broad class of 2-dimensional theories of gravity exist [71] and are of physical interest for a variety of reasons. Exploring the N-body problem in this broader context could lead to new physical insights into chaos, relativity, and quantum gravity.
The Quantum N-body Problem

The Hamiltonian (76) is the exact energy functional of all degrees of freedom in the relativistic charged 2-body system. Consequently its quantization will be tantamount to fully quantization of gravity coupled to charged matter in one spatial dimension. The N system can be fully quantized, with energy eigenfunctions given in terms of Airy functions, and the associated eigenvalues in terms of their zeroes. Perturbative solutions to the quantum pN system have been obtained [138], but a full analysis of the quantum R system has yet to be carried out. This problem is of considerable interest, since there is experimental evidence that the energy states of neutrons are given by the eigenstates of the N system [139], confirming the test-mass limit of the quantum N-system. A better understanding of the quantum R-system could conceivably lead to experimental tests of relativistic quantum gravity.

Funding

This work was supported in part by the Natural Sciences and Engineering Research Council of Canada.

Data Availability Statement

Files used to generate the various graphs presented in this paper are available on request.

Acknowledgments

I am grateful to the students and collaborators that have contributed to the work presented in this review: Sven Bachmann, Fiona Burnell, Philip Chak, Pierre Farrugia, Peter Gustainis, Ryan Kerner, Michael Koop, Andrew Lauritzen, Justin Malecki, Geoff Potvin, Daniel Robbins, Simon Ross, Marco Raiteri, Mina Rohanazadegan, Tony Scott, Mike Trott, Alex Yale, and Matt Young. And I am especially grateful to Tadayuki Ohta (now deceased) for introducing me to the N-body problem and the canonical methods that allowed us to explore this interesting aspect of gravitational physics.

Conflicts of Interest

I declare no conflicts of interest connected with the work presented in this article.

Abbreviations

The following abbreviations are used in this manuscript:

OGS	One-dimensional Self Gravitating System
ROGS	Relativistic One-dimensional Self Gravitating System
N system	Non-relativistic System
pN system	post-Newtonian System
R system	Relativistic System

References

Barrow-Green, J. The Princeton Companion to Mathematics; Princeton University Press, 2010; p. 726––728. [CrossRef]
Šuvakov, M.; Dmitrašinović, V. Three Classes of Newtonian Three-Body Planar Periodic Orbits. Phys. Rev. Lett. 2013, 110, 114301. arXiv:1303.0181. [CrossRef]
Lehtihet, H.; Miller, B. Numerical study of a billiard in a gravitational field. Physica D: Nonlinear Phenomena 1986, 21, 93–104. [CrossRef]
Rybicki, G.B. EXACT STATISTICAL MECHANICS OF A ONE-DIMENSIONAL SELF-GRAVITATING SYSTEM. Astrophys. Space Sci. 14: No. 1, 56-72(Nov 1971). [CrossRef]
Yawn, K.R.; Miller, B.N. Equipartition and Mass Segregation in a One-Dimensional Self-Gravitating System. Phys. Rev. Lett. 1997, 79, 3561–3564. [CrossRef]
Wright, H.L.; Miller, B.N.; Stein, W.E. The Relaxation Time of a One-Dimensional Self-Gravitating System. Astrophys. Space Sci. 1982, 84, 421–429. [CrossRef]
Rouet, J.; Feix, M.; Navet, M. One-dimensional numerical simulation and homogeneity of the expanding universe. Vistas in Astronomy 1990, 33, 357–370. [CrossRef]
Shiozawa, Y.; Miller, B.N. Cosmology in one dimension: A two-component model. Chaos Solitons Fractals 2016, 91, 86–91. arXiv:1506.06777. [CrossRef]
Oort, J.H. The force exerted by the stellar system in the direction perpendicular to the galactic plane and some related problems. Bull. Astron. Institutes Neth. 1932, 6, 249.
Hénon, M. Intial Collapse and Dynamical Mixing of a Spherical Cluster. Liege International Astrophysical Colloquia, 1967, Vol. 15, Liege International Astrophysical Colloquia, p. 243.
Valageas, P. Thermodynamics and dynamics of a 1d gravitational system. Astron. Astrophys. 2006, 450, 445, [astro-ph/0601390]. [CrossRef]
Koyama, H.; Konishi, T. Emergence of power - law correlation in 1-dimensional self - gravitating system. Phys. Lett. A 2001, 279, 226–230, [astro-ph/0008208]. [CrossRef]
Whelan, N.D.; Goodings, D.A.; Cannizzo, J.K. Two balls in one dimension with gravity. Phys. Rev. A 1990, 42, 742–754. [CrossRef]
Bukta, D.; Karl, G.; Nickel, B.G. The linear baryon. Canadian Journal of Physics 2000, 78, 449, [arXiv:nlin.CD/chao-dyn/9910026]. arXiv:1506.06777. [CrossRef]
Valageas, P. Relaxation of a 1D gravitational system. Phys. Rev. E 2006, 74, 016606, [astro-ph/0604263]. [CrossRef]
Anderson, K.; Villet, C. Computational Study of the Dynamics of an Asymmetric Wedge Billiard. International Journal of Bifurcation and Chaos 2021, 31, 2130006. [CrossRef]
Wojtkowski, M.P. A system of one-dimensional balls with gravity. Communications in Mathematical Physics 1990, 126, 507 – 533. [CrossRef]
Miller, B.N.; Youngkins, V.P. Dynamics of a pair of spherical gravitating shells. Chaos: An Interdisciplinary Journal of Nonlinear Science 1997, 7, 187–197, [https://pubs.aip.org/aip/cha/article-pdf/7/1/187/18301044/187_1_online.pdf]. [CrossRef]
Gabrielli, A.; Joyce, M.; Sicard, F. One-dimensional gravity in infinite point distributions. Phys. Rev. E 2009, 80, 041108. arXiv:0812.4249. [CrossRef]
Gabrielli, A.; Joyce, M. Gravitational force in an infinite one-dimensional Poisson distribution. Phys. Rev. E 2010, 81, 021102. arXiv:0909.5034. [CrossRef]
Manfredi, G.; Rouet, J.L.; Miller, B.; Shiozawa, Y. Cosmology in One Dimension: Vlasov Dynamics. Phys. Rev. E 2016, 93, 042211. arXiv:1505.06948. [CrossRef]
Teitelboim, C. Gravitation and Hamiltonian Structure in Two Space-Time Dimensions. Phys. Lett. B 1983, 126, 41–45. [CrossRef]
Jackiw, R. Lower Dimensional Gravity. Nucl. Phys. B 1985, 252, 343–356. [CrossRef]
Brown, J.D.; Henneaux, M.; Teitelboim, C. Black Holes in Two Space-time Dimensions. Phys. Rev. D 1986, 33, 319–323. [CrossRef]
Penington, G.; Shenker, S.H.; Stanford, D.; Yang, Z. Replica wormholes and the black hole interior. JHEP 2022, 03, 205. arXiv:1911.11977. [CrossRef]
Harvey, J.A.; Strominger, A. Quantum aspects of black holes. Spring School on String Theory and Quantum Gravity (To be followed by Workshop on String Theory 8-10 Apr), 1993, pp. 175–223, [hep-th/9209055].
Mann, R.B.; Ross, S.F. The D —> 2 limit of general relativity. Class. Quant. Grav. 1993, 10, 1405–1408, [gr-qc/9208004]. [CrossRef]
Burnell, F.J.; Mann, R.B.; Ohta, T. Chaos in a relativistic three-body selfgravitating system. Phys. Rev. Lett. 2003, 90, 134101, [gr-qc/0208044]. [CrossRef]
Burnell, F.J.; Malecki, J.J.; Mann, R.B.; Ohta, T. Chaos in an exact relativistic three-body selfgravitating system. Phys. Rev. E 2004, 69, 016214, [gr-qc/0301099]. [CrossRef]
Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley and Sons: New York, 1972.
Mann, R.B.; Shiekh, A.; Tarasov, L. Classical and Quantum Properties of Two-dimensional Black Holes. Nucl. Phys. B 1990, 341, 134–154. [CrossRef]
Mann, R.B. Lower dimensional black holes. Gen. Rel. Grav. 1992, 24, 433–449. [CrossRef]
Mann, R.B. Lowest dimensional gravity. 4th Canadian Conference on General Relativity and Relativistic Astrophysics, 1991.
Sikkema, A.E.; Mann, R.B. Gravitation and Cosmology in Two-dimensions. Class. Quant. Grav. 1991, 8, 219–236. [CrossRef]
Mann, R.B.; Steele, T.G. Thermodynamics and quantum aspects of black holes in (1+1)-dimensions. Class. Quant. Grav. 1992, 9, 475–492. [CrossRef]
Mann, R.B.; Morsink, S.M.; Sikkema, A.E.; Steele, T.G. Semiclassical gravity in (1+1)-dimensions. Phys. Rev. D 1991, 43, 3948–3957. [CrossRef]
Lemos, J.P.S.; Sa, P.M. Nonsingular constant curvature two-dimensional black hole. Mod. Phys. Lett. A 1994, 9, 771–774, [gr-qc/9309023]. [CrossRef]
Lemos, J.P.S.; Sa, P.M. The Two-dimensional analog of general relativity. Class. Quant. Grav. 1994, 11, L11–L14, [gr-qc/9310041]. [CrossRef]
Verbin, Y. Lower dimensional gravity. Phys. Rev. D 1994, 50, 7318–7322. [CrossRef]
Stoetzel, B. Two-dimensional gravitation and Sine-Gordon solitons. Phys. Rev. D 1995, 52, 2192–2201, [gr-qc/9501033]. [CrossRef]
Creighton, J.D.E.; Mann, R.B. Quasilocal thermodynamics of two-dimensional black holes. Phys. Rev. D 1996, 54, 7476–7482. [CrossRef]
Ivanov, B.V. Electrically induced gravity in two-dimensions. Phys. Lett. A 1996, 210, 255–257. [CrossRef]
Landsberg, P.T.; Mann, R.B. Thermodynamic classifications and dilatonic black holes. Gen. Rel. Grav. 1997, 29, 1269–1281. [CrossRef]
Yan, J.; Qiu, X.M. Sinh-Gordon matter field and a solvable model in two-dimensional gravity. Gen. Rel. Grav. 1998, 30, 1319–1329. [CrossRef]
Moayedi, S.K.; Darabi, F. Families of exact solutions of a 2-D gravity model minimally coupled to electrodynamics. J. Math. Phys. 2001, 42, 1229–1235, [gr-qc/0012062]. [CrossRef]
Yan, J.; Wang, S.J.; Tao, B.Y. A solvable model in two-dimensional gravity coupled to a nonlinear matter field. Commun. Theor. Phys. 2001, 35, 19–21.
Alves, M.; Barcelos-Neto, J.; Novello, M.; Salim, J.M. Time dependent cosmological constant in the Jackiw-Teitelboim cosmology. EPL 2003, 61, 715–720, [hep-th/0207239]. [CrossRef]
Djama, T. 2D(1+1) quantum gravity: Gravitational quantum stationary Hamilton-Jacobi equation 2004. [hep-th/0406255].
Boozer, A.D. Nordstrom gravity coupled to point particles in (1+1) dimensions. Phys. Rev. D 2010, 81, 064022. [CrossRef]
Boozer, A.D. Nordstrom gravity in (1+1) dimensions coupled to matter. Phys. Rev. D 2011, 84, 024035. [CrossRef]
Estrada-Jiménez, S.; Gómez-Díaz, J.R.; López-Ortega, A. Quasinormal modes of a two-dimensional black hole. Gen. Rel. Grav. 2013, 45, 2239–2250. arXiv:1308.5943. [CrossRef]
Laurent, G. Locally Inertial Approximations of Balance Laws Arising in (1+1)-Dimensional General Relativity. SIAM J. Appl. Math. 2015, 75, 1301–1328. [CrossRef]
Frassino, A.M.; Mann, R.B.; Mureika, J.R. Lower-Dimensional Black Hole Chemistry. Phys. Rev. D 2015, 92, 124069. arXiv:1509.05481. [CrossRef]
Takahashi, K.; Kobayashi, T. Generalized 2D dilaton gravity and kinetic gravity braiding. Class. Quant. Grav. 2019, 36, 095003. arXiv:1812.08847. [CrossRef]
Alonso Izquierdo, A.; García Fuertes, W.; Mateos Guilarte, J. Self-gravitating kinks in two-dimensional pseudo-Riemannian universes. Phys. Rev. D 2020, 101, 036020. arXiv:1911.08167. [CrossRef]
Ai, W.Y. A note on the novel 4D Einstein–Gauss–Bonnet gravity. Commun. Theor. Phys. 2020, 72, 095402. arXiv:2004.02858. [CrossRef]
Fernandes, P.G.S.; Carrilho, P.; Clifton, T.; Mulryne, D.J. Derivation of Regularized Field Equations for the Einstein-Gauss-Bonnet Theory in Four Dimensions. Phys. Rev. D 2020, 102, 024025. arXiv:2004.08362. [CrossRef]
Hennigar, R.A.; Kubizňák, D.; Mann, R.B.; Pollack, C. On taking the D → 4 limit of Gauss-Bonnet gravity: theory and solutions. JHEP 2020, 07, 027. arXiv:2004.09472. [CrossRef]
Casadio, R.; Micu, O.; Mureika, J. Compact sources and cosmological horizons in lower dimensional bootstrapped Newtonian gravity. Class. Quant. Grav. 2021, 38, 065020. arXiv:2008.13465. [CrossRef]
Zhong, Y. Revisit on two-dimensional self-gravitating kinks: superpotential formalism and linear stability. JHEP 2021, 04, 118. arXiv:2101.10928. [CrossRef]
Zhong, Y.; Li, F.Y.; Liu, X.D. K-field kinks in two-dimensional dilaton gravity. Phys. Lett. B 2021, 822, 136716. arXiv:2108.10166. [CrossRef]
Yan, J. The phonon mass and the Hawking temperature in the two-dimensional acoustic black hole model. Phys. Lett. B 2021, 818, 136359. [CrossRef]
Gera, S.; Sengupta, S. Two-dimensional gravity from vanishing metrical dimensions. Phys. Rev. D 2021, 104, 124050. arXiv:2110.06252. [CrossRef]
Zhong, Y. Normal modes for two-dimensional gravitating kinks. Phys. Lett. B 2022, 827, 136947. arXiv:2112.08683. [CrossRef]
Lima, F.C.E.; Almeida, C.A.S. Aspects of Kink-Like Structures in 2D Dilaton Gravity. Fortsch. Phys. 2023, 71, 2300051. arXiv:2205.11570. [CrossRef]
Feng, J.; Zhong, Y. Scalar perturbation of gravitating double-kink solutions. EPL 2022, 137, 49001. arXiv:2202.02946. [CrossRef]
Andrade, I.; Bazeia, D.; Lobão Jr., A.S.; Menezes, R. Generalized Jackiw-Teitelboim gravity in presence of Block brane-like models*. Chin. Phys. C 2022, 46, 125102. arXiv:2208.04210. [CrossRef]
Zhong, Y.; Guo, H.; Liu, Y.X. Kink solutions in generalized 2D dilaton gravity. Phys. Lett. B 2024, 849, 138471. arXiv:2308.13786. [CrossRef]
Christensen, D.; Mann, R.B. The Causal structure of two-dimensional space-times. Class. Quant. Grav. 1992, 9, 1769–1786, [hep-th/9203050]. [CrossRef]
Chan, K.C.K.; Mann, R.B. Cosmological models in two space-time dimensions. Class. Quant. Grav. 1993, 10, 913–930, [gr-qc/9210015]. [CrossRef]
Grumiller, D.; Kummer, W.; Vassilevich, D.V. Dilaton gravity in two-dimensions. Phys. Rept. 2002, 369, 327–430, [hep-th/0204253]. [CrossRef]
Morsink, S.M.; Mann, R.B. Black hole radiation of Dirac particles in (1+1)-dimensions. Class. Quant. Grav. 1991, 8, 2257–2268. [CrossRef]
Mann, R.B. Quantum evaporation of Liouville black holes. Proceedings of the Cornelius Lanczos Centenary Conference, 1991, pp. 545–547.
Mann, R.B. Liouville black holes. Nucl. Phys. B 1994, 418, 231–256, [hep-th/9308034]. [CrossRef]
Klosch, T.; Strobl, T. Classical and quantum gravity in (1+1)-Dimensions. Part 1: A Unifying approach. Class. Quant. Grav. 1996, 13, 965–984, [gr-qc/9508020]. [Erratum: Class.Quant.Grav. 14, 825 (1997)], . [CrossRef]
Darabi, F.; Moayedi, S.K.; Ahmadi, A.R. Exact solutions of Dirac equation on (1+1)-dimensional spacetime coupled to a static scalar field. Int. J. Theor. Phys. 2010, 49, 1232–1235, [quant-ph/0507119]. [CrossRef]
Farrugia, P.S.; Mann, R.B.; Scott, T.C. N-body Gravity and the Schroedinger Equation. Class. Quant. Grav. 2007, 24, 4647–4660, [gr-qc/0611144]. [CrossRef]
Mann, R.B.; Mureika, J.R. (1+1)-Dimensional Entropic Gravity. Phys. Lett. B 2011, 703, 167–171. arXiv:1105.5925. [CrossRef]
Mureika, J.R.; Nicolini, P. Aspects of noncommutative (1+1)-dimensional black holes. Phys. Rev. D 2011, 84, 044020. arXiv:1104.4120. [CrossRef]
Bilal, K.; El Boukili, A.; Nach, M.; Sedra, M.B. Liouville Black Hole In A Noncommutative Space 2011. arXiv:1109.3206.
Mureika, J.; Nicolini, P. Self-completeness and spontaneous dimensional reduction. Eur. Phys. J. Plus 2013, 128, 78. arXiv:1206.4696. [CrossRef]
Cruz, M.; Gonzalez-Espinoza, M.; Saavedra, J.; Vargas-Arancibia, D. Scalar perturbations of two-dimensional Horava–Lifshitz black holes. Eur. Phys. J. C 2016, 76, 75. arXiv:1508.00650. [CrossRef]
Pedernales, J.S.; Beau, M.; Pittman, S.M.; Egusquiza, I.L.; Lamata, L.; Solano, E.; del Campo, A. Dirac Equation in ( 1+1 )-Dimensional Curved Spacetime and the Multiphoton Quantum Rabi Model. Phys. Rev. Lett. 2018, 120, 160403. arXiv:1707.07520. [CrossRef]
Casadio, R.; Giusti, A.; Mureika, J. Lower dimensional corpuscular gravity and the end of black hole evaporation. Mod. Phys. Lett. A 2019, 34, 1950174. arXiv:1805.10444. [CrossRef]
Collas, P.; Klein, D. The Dirac Equation in Curved Spacetime: A Guide for Calculations; SpringerBriefs in Physics, Springer, 2019. arXiv:1809.02764. [CrossRef]
Ghosh, S. Duality Between Dirac Fermions in Curved Spacetime and Optical solitons in Non-Linear Schrodinger Model: Magic of 1+1-Dimensional Bosonization. Eur. Phys. J. C 2019, 79, 980. arXiv:1903.03391. [CrossRef]
Yang, R.Q.; Liu, H.; Zhu, S.; Luo, L.; Cai, R.G. Simulating quantum field theory in curved spacetime with quantum many-body systems. Phys. Rev. Res. 2020, 2, 023107. arXiv:1906.01927. [CrossRef]
Deger, A.; Horner, M.D.; Pachos, J.K. AdS/CFT correspondence with a three-dimensional black hole simulator. Phys. Rev. B 2023, 108, 155124. arXiv:2211.15305. [CrossRef]
Knutt-Wehlau, M.E.; Mann, R.B. Supergravity from a massive superparticle and the simplest super black hole. Nucl. Phys. B 1998, 514, 355–378, [hep-th/9708126]. [CrossRef]
Knutt-Wehlau, M.E.; Mann, R.B. Super black hole from cosmological supergravity with a massive superparticle. Phys. Lett. B 1998, 435, 25–30, [hep-th/9801203]. [CrossRef]
Knutt-Wehlau, M.E.; Mann, R.B. Cosmological supergravity from a massive superparticle and supercosmological black holes. Class. Quant. Grav. 1999, 16, 937–952, [hep-th/9809082]. [CrossRef]
Kamnitzer, J.; Mann, R.B. SuperLiouville black holes. Nucl. Phys. B 2001, 609, 429–441, [hep-th/0103016]. [CrossRef]
Chen, Q.; Chu, Y.; Cai, J. Simulating superluminal propagation of Dirac particles using trapped ions. Phys. Rev. A 2022, 105, 042609. arXiv:2110.01155. [CrossRef]
Shi, Y.H.; others. Quantum simulation of Hawking radiation and curved spacetime with a superconducting on-chip black hole. Nature Commun. 2023, 14, 3263. arXiv:2111.11092. [CrossRef]
Deser, S.; Arnowitt, R.; Misner, C.W. Consistency of Canonical Reduction of General Relativity. J. Math. Phys. 1960, 1, 434. [CrossRef]
Arnowitt, R.L.; Deser, S.; Misner, C.W. Canonical variables for general relativity. Phys. Rev. 1960, 117, 1595–1602. [CrossRef]
Arnowitt, R.L.; Deser, S.; Misner, C.W. The Dynamics of general relativity. Gen. Rel. Grav. 2008, 40, 1997–2027, [gr-qc/0405109]. [CrossRef]
Ohta, T.; Mann, R.B. Canonical reduction of two-dimensional gravity for particle dynamics. Class. Quant. Grav. 1996, 13, 2585–2602, [gr-qc/9605004]. [CrossRef]
Ohta, T.; Okamura, H.; Kimura, T.; Hiida, K. Coordinate Condition and Higher Order Gravitational Potential in Canonical Formalism. Prog. Theor. Phys. 1974, 51, 1598. [CrossRef]
Ohta, T.; Kimura, T. The Theory of Classical and Quantum Gravity (ch. 6); McGraw-Hill (in Japanese), 1989; p. ch. 6.
Mann, R.B.; Potvin, G.; Raiteri, M. Energy for N body motion in two-dimensional gravity. Class. Quant. Grav. 2000, 17, 4941–4958, [gr-qc/0008072]. [CrossRef]
Mann, R.B.; Robbins, D.; Ohta, T. Exact relativistic two-body motion in lineal gravity. Phys. Rev. Lett. 1999, 82, 3738–3741, [gr-qc/9811061]. [CrossRef]
Mann, R.B.; Robbins, D.; Ohta, T. Exact solutions of relativistic two-body motion in lineal gravity. Phys. Rev. D 1999, 60, 104048, [gr-qc/9906066]. [CrossRef]
Mann, R.B.; Robbins, D.; Ohta, T.; Trott, M.R. Exact solutions to the motion of two charged particles in lineal gravity. Nucl. Phys. B 2000, 590, 367–426, [gr-qc/0005082]. [CrossRef]
Damour, T. THE PROBLEM OF MOTION IN NEWTONIAN AND EINSTEINIAN GRAVITY. 300 Years of Gravity: A Conference to Mark the 300th Anniversary of the Publication of Newton’s Principia, 1986.
Mann, R.B.; Ohta, T. Exact solution for the metric and the motion of two bodies in (1+1)-dimensional gravity. Phys. Rev. D 1997, 55, 4723–4747, [gr-qc/9611008]. [CrossRef]
Mann, R.B.; Ohta, T. Exact solution for relativistic two-body motion in dilaton gravity. Class. Quant. Grav. 1997, 14, 1259–1266, [gr-qc/9607016]. [CrossRef]
Mann, R.B.; Ohta, T. Exact charged two-body motion and the static balance condition in lineal gravity. Class. Quant. Grav. 2000, 17, 4059, [gr-qc/0105030]. [CrossRef]
Aurilia, A.; Kissack, R.S.; Mann, R.B.; Spallucci, E. Relativistic Bubble Dynamics: From Cosmic Inflation to Hadronic Bags. Phys. Rev. D 1987, 35, 2961. [CrossRef]
Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function 1996. 5, 329–359. [CrossRef]
Majumdar, S.D. A Class of Exact Solutions of Einstein’s Field Equations. Phys. Rev. 1947, 72, 390–398. [CrossRef]
Papaetrou, A. A Static solution of the equations of the gravitational field for an arbitrary charge distribution. Proc. Roy. Irish Acad. A 1947, 51, 191–204.
Gautreau, R.; Hoffmann, R.; Armenti, A. Static multiparticle systems in general relativity. Nuovo Cimento 7B.
Whelan, N.D.; Goodings, D.A.; Cannizzo, J.K. Two balls in one dimension with gravity. Phys. Rev. A 1990, 42, 742–754. [CrossRef]
Bukta, D.; Karl, G.; Nickel, B.G. The linear baryon. Can. J. Phys. 2000, 78, 449–459. [CrossRef]
Milner, V.; Hanssen, J.L.; Campbell, W.C.; Raizen, M.G. Optical Billiards for Atoms. Phys. Rev. Lett. 2001, 86, 1514–1517. [CrossRef]
Malecki, J.J.; Mann, R.B. Three body dynamics in a (1+1)-dimensional relativistic selfgravitating system. Phys. Rev. E 2004, 69, 066208, [gr-qc/0306046]. [CrossRef]
Koop, M.J.; Mann, R.B.; Bachmann, S. Chaos in a 3-body Self-Gravitating Cosmological Spacetime. Phys. Rev. D 2007, 76, 104051, [astro-ph/0607070]. [CrossRef]
Koop, M.J.; Mann, R.B.; Rohanizadegan, M. Chaotic behavior in a charged three-body self-gravitating system. Journal of Mathematical Physics 2009, 50, 082703, [https://pubs.aip.org/aip/jmp/article-pdf/doi/10.1063/1.3190103/15818967/082703_1_online.pdf]. [CrossRef]
Kolmogorov, A. Dokl. Akad. Nauk. SSSR 1954, 98, 525.
Arnol’d, V.I.V.I.; Avez, A.A. Ergodic problems of classical mechanics / [by] V. I. Arnold and A. Avez.; The Mathematical physics monograph series, Benjamin: New York, 1968.
Arnol’d, V.I. SMALL DENOMINATORS AND PROBLEMS OF STABILITY OF MOTION IN CLASSICAL AND CELESTIAL MECHANICS. Russian Mathematical Surveys 1963, 18, 85. [CrossRef]
Moser, J. Nachr. Akad. Wiss. Goettingen Math. Phys. 1962, K1, 1.
Reichl, L.E.; Zheng, W.M., NONLINEAR RESONANCE AND CHAOS IN CONSERVATIVE SYSTEMS. In Directions in Chaos — Volume 1; pp. 17–90, https://www.worldscientific.com/doi/pdf/10.1142/97898144157120002. [CrossRef]
Koop, M.; Mann, R.; Rohanizadegan, M. Chaotic behavior in a charged three-body self-gravitating system. Journal of Mathematical Physics 2009, 50. [CrossRef]
Laurtizen, A.; Gustainis, P.; Mann, R.B. The 4-Body Problem in a (1+1)-Dimensional Self-Gravitating System 2013. arXiv:1306.3594.
Birman, J.S., Recent Developments in Braid and Link Theory. In Mathematical Conversations: Selections from The Mathematical Intelligencer; Springer New York: New York, NY, 2001; pp. 381–392. [CrossRef]
Mann, R.B.; Chak, P. Statistical mechanics of relativistic one-dimensional selfgravitating systems. Phys. Rev. E 2002, 65, 026128, [gr-qc/0101106]. [CrossRef]
Mann, R.B. Particles on a circle in canonical lineal gravity. Class. Quant. Grav. 2001, 18, 3427–3462, [gr-qc/0105008]. [CrossRef]
Kerner, R.; Mann, R.B. Dynamical N body equilibrium in circular dilaton gravity. Class. Quant. Grav. 2003, 20, L133–L138, [gr-qc/0206029]. [CrossRef]
Kerner, R.; Mann, R.B. Dynamical charged N-body equilibrium in circular dilaton gravity. Class. Quant. Grav. 2004, 21, 5789–5818, [gr-qc/0410059]. [CrossRef]
Moncrief, V. Reduction of the Einstein equations in (2+1)-dimensions to a Hamiltonian system over Teichmuller space. J. Math. Phys. 1989, 30, 2907–2914. [CrossRef]
Bellini, A.; Valtancoli, P. Exact quasistatic particle scattering in (2+1) gravity. Phys. Lett. B 1995, 348, 44–50. [CrossRef]
Bellini, A.; Ciafaloni, M.; Valtancoli, P. Solving the n body problem in (2+1) gravity. Nucl. Phys. B 1996, 462, 453–492, [hep-th/9511207]. [CrossRef]
Yale, A.; Mann, R.B.; Ohta, T. Analysis of Two-Particle Systems in 2 + 1 Gravity Through Hamiltonian Dynamics. Class. Quant. Grav. 2010, 27, 245005. arXiv:1010.4568. [CrossRef]
Ciafaloni, M.; Munier, S. Hamiltonian solutions of the 3-body problem in (2+1)-gravity. Class. Quant. Grav. 2011, 28, 195018. arXiv:1012.3263. [CrossRef]
Matschull, H.J. Black hole creation in (2+1)-dimensions. Class. Quant. Grav. 1999, 16, 1069–1095, [gr-qc/9809087]. [CrossRef]
Mann, R.B.; Young, M.B. Perturbative quantum gravity coupled to particles in (1+1)-dimensions. Class. Quant. Grav. 2007, 24, 951–964, [gr-qc/0610116]. [CrossRef]
Nesvizhevsky, V.V.; others. Study of the neutron quantum states in the gravity field. Eur. Phys. J. C 2005, 40, 479–491, [hep-ph/0502081]. [CrossRef]

Figure 2. Top: a plot of the relativistic trajectories of neutral particles of equal mass as a function of their mutual proper time for various values of the conserved energy

H_{0}

. All motions begin at

r = 0

with an initial momentum given by solving (93). Bottom: The corresponding phase-space plots for the top diagram. Note that the curves for the largest value of

H_{0}

extend outside the range of the figure.

Figure 2. Top: a plot of the relativistic trajectories of neutral particles of equal mass as a function of their mutual proper time for various values of the conserved energy

H_{0}

. All motions begin at

r = 0

with an initial momentum given by solving (93). Bottom: The corresponding phase-space plots for the top diagram. Note that the curves for the largest value of

H_{0}

extend outside the range of the figure.

Figure 3. A comparison of relativistic and non-relativistic trajectories of neutral particles of equal mass as a function of their mutual proper time at a large value of the conserved energy

H_{0}

. Both motions begin at

r = 0

with an initial momentum given by solving (93) (solid line) and its corresponding counterpart (92) with

z = r

and

μ = m

Figure 3. A comparison of relativistic and non-relativistic trajectories of neutral particles of equal mass as a function of their mutual proper time at a large value of the conserved energy

H_{0}

. Both motions begin at

r = 0

with an initial momentum given by solving (93) (solid line) and its corresponding counterpart (92) with

z = r

and

μ = m

Figure 4. A sequence of equal mass curves in the cosmic-attractive case for

\frac{Λ_{e}}{κ^{2} m_{0}^{2}} = - 1.5

and

\frac{H_{0}}{m_{0}} = 16

. There is a second extremum in each half-period for m = 0.05

m_{0}

Figure 4. A sequence of equal mass curves in the cosmic-attractive case for

\frac{Λ_{e}}{κ^{2} m_{0}^{2}} = - 1.5

and

\frac{H_{0}}{m_{0}} = 16

. There is a second extremum in each half-period for m = 0.05

m_{0}

Figure 5. A sequence of equal mass curves in the cosmic-expansive case for

\frac{Λ_{e}}{κ^{2} m_{0}^{2}} = 1.5

and

\frac{H_{0}}{m_{0}} = 16

. The motion becomes unbound for masses m < 4.73

m_{0}

Figure 5. A sequence of equal mass curves in the cosmic-expansive case for

\frac{Λ_{e}}{κ^{2} m_{0}^{2}} = 1.5

and

\frac{H_{0}}{m_{0}} = 16

. The motion becomes unbound for masses m < 4.73

m_{0}

Figure 6. Phase space trajectories of bounded and the unbounded motions for

H_{0} = 2.1 m_{0}

and

\frac{Λ_{e}}{κ^{2} m_{0}^{2}} = 1.0

(left) and

\frac{Λ_{e}}{κ^{2} m_{0}^{2}} = 1.5

(right).

Figure 6. Phase space trajectories of bounded and the unbounded motions for

H_{0} = 2.1 m_{0}

and

\frac{Λ_{e}}{κ^{2} m_{0}^{2}} = 1.0

(left) and

\frac{Λ_{e}}{κ^{2} m_{0}^{2}} = 1.5

(right).

Figure 7. Trajectories of unbounded motion for the same parameters as in Figure 6. At early times the two particles are in casual contant (left panel), but null rays emitted from particle 2 for proper times

κ m_{0} T \geq 3.4

will never reach particle 1, as shown by the dashed and dot-dashed lines of positive slope in the left panel. Null rays emitted in the opposite direction asymptote to curves that are parallel to the asymptotic trajectory of particle 2. As the emission time T from particle 2 increases, the null rays experience increasing effective repulsion, with those emitted toward particle 1 eventually reversing their directions to asymptote to curves that are parallel to the asymptotic trajectory of particle 2, as shown in the right panel. The null rays emitted in the opposite direction follow too close to the trajectory of particle 2 to be distinguished in the figure in the right panel.

κ m_{0} T \geq 3.4

Figure 8. Left: The exact

r (τ)

plots for

H_{0} = 3 m_{0}

and four different values of

| q | / m_{0}

. Right: Phase space trajectories correponding to the

r (τ)

plots at the left.

Figure 8. Left: The exact

r (τ)

plots for

H_{0} = 3 m_{0}

and four different values of

| q | / m_{0}

. Right: Phase space trajectories correponding to the

r (τ)

plots at the left.

Figure 9. A comparison of phase space trajectories of

H_{0} = 3 m_{0}

for exact, linear, non-relativistic and flat electrodynamics for various values of

| q |

Figure 9. A comparison of phase space trajectories of

H_{0} = 3 m_{0}

for exact, linear, non-relativistic and flat electrodynamics for various values of

| q |

Figure 10. A comparison of sub-critical repulsive motion from two perspectives. Left: Plots for various values of

| q | / m_{0}

for

H_{0} = 3 m_{0}

– the threshold value for escape is

| q | / m_{0} = 0.2700907567

. Right: Plots for various values of

H_{0} / m_{0}

for

| q | / m_{0} = 0.1

– the threshold value for escape is

H_{0} / m_{0} = 7.21249

Figure 10. A comparison of sub-critical repulsive motion from two perspectives. Left: Plots for various values of

| q | / m_{0}

for

H_{0} = 3 m_{0}

– the threshold value for escape is

| q | / m_{0} = 0.2700907567

. Right: Plots for various values of

H_{0} / m_{0}

for

| q | / m_{0} = 0.1

– the threshold value for escape is

H_{0} / m_{0} = 7.21249

Figure 11. An illustration of the possible bounded motion (solid) and unbounded motions (dotted and dashed) for the same values of

H_{0} = 3 m_{0}

and

| q | / m_{0} = 0.25 < q_{c} / m_{0}

depicted in position space (left) and phase space (right). The initial value

r (0)

determined which of these motions is realized. The flat-space (

κ = 0

) electrodynamic phase space trajectory is shown in the right panel for comparison.

Figure 11. An illustration of the possible bounded motion (solid) and unbounded motions (dotted and dashed) for the same values of

H_{0} = 3 m_{0}

and

| q | / m_{0} = 0.25 < q_{c} / m_{0}

depicted in position space (left) and phase space (right). The initial value

r (0)

determined which of these motions is realized. The flat-space (

κ = 0

) electrodynamic phase space trajectory is shown in the right panel for comparison.

Figure 12. The physical region of the

(| q |, p)

parameter space for

H_{0} / m_{0} = 3

in the repulsive charged case.

Figure 12. The physical region of the

(| q |, p)

parameter space for

H_{0} / m_{0} = 3

in the repulsive charged case.

Figure 13. Phase space trajectories for

| q | > q_{c}

and

H_{0} / m_{0} = 3

Left: Unbounded motions for

| q | / m_{0} = 0.3

. Right: Unbounded motions for

| q | / m_{0} = 2

. A comparison to the motion in flat space electrodynamics (

κ = 0

) is given in the left panel.

Figure 13. Phase space trajectories for

| q | > q_{c}

and

H_{0} / m_{0} = 3

Left: Unbounded motions for

| q | / m_{0} = 0.3

. Right: Unbounded motions for

| q | / m_{0} = 2

. A comparison to the motion in flat space electrodynamics (

κ = 0

) is given in the left panel.

Figure 14. Phase space trajectories of unbounded motions for

H_{0} / m_{0} = 1 < 2

and

| q | / m_{0} = 1

Figure 14. Phase space trajectories of unbounded motions for

H_{0} / m_{0} = 1 < 2

and

| q | / m_{0} = 1

Figure 15. Trajectories of equal mass charged particles for

Λ_{e} \neq 0

. Top:

r (τ)

for

H / m_{0} = 500

| q | / m_{0} = 5

(attractive), and various values of

Λ_{e} < 0

. Middle:

r (τ)

for

H / m_{0} = 2.5

Λ_{e} / {(κ m_{0})}^{2} = - 0.694

for various values of

| q |

(repulsive). Bottom:

r (τ)

for

H / m_{0} = 3.0

Λ_{e} / {(κ m_{0})}^{2} = 1

for various values of

| q |

(attractive). Cases with

Λ_{e} > 0

with electromagnetic repulsion have trajectories similar to those in Figure 11.

Figure 15. Trajectories of equal mass charged particles for

Λ_{e} \neq 0

. Top:

r (τ)

for

H / m_{0} = 500

| q | / m_{0} = 5

(attractive), and various values of

Λ_{e} < 0

. Middle:

r (τ)

for

H / m_{0} = 2.5

Λ_{e} / {(κ m_{0})}^{2} = - 0.694

for various values of

| q |

(repulsive). Bottom:

r (τ)

for

H / m_{0} = 3.0

Λ_{e} / {(κ m_{0})}^{2} = 1

for various values of

| q |

(attractive). Cases with

Λ_{e} > 0

with electromagnetic repulsion have trajectories similar to those in Figure 11.

Figure 16. Trajectories

r (τ)

of unequal mass charged particles in the electromagnetically attractive case for a variety of mass ratios with

H / m_{0} = 10

Λ_{e} / {(κ m_{0})}^{2} = - 1

, and

m_{2} = m_{0}

. Top:

| q | / m_{0} = 1

. Bottom:

| q | / m_{0} = 0.1

Figure 16. Trajectories

r (τ)

of unequal mass charged particles in the electromagnetically attractive case for a variety of mass ratios with

H / m_{0} = 10

Λ_{e} / {(κ m_{0})}^{2} = - 1

, and

m_{2} = m_{0}

. Top:

| q | / m_{0} = 1

. Bottom:

| q | / m_{0} = 0.1

Figure 17. Trajectories

r (τ)

of unequal mass charged particles in the electromagnetically repulsive case for a variety of mass ratios with

H / m_{0} = 10

and

m_{2} = m_{0}

. Top:

| q | / m_{0} = 0.6

and

Λ_{e} / {(κ m_{0})}^{2} = - 1

(cosmological attraction) Bottom:

| q | / m_{0} = 0.1

and

Λ_{e} / {(κ m_{0})}^{2} = 0.1

(cosmological repulsion).

Figure 17. Trajectories

r (τ)

of unequal mass charged particles in the electromagnetically repulsive case for a variety of mass ratios with

H / m_{0} = 10

and

m_{2} = m_{0}

. Top:

| q | / m_{0} = 0.6

and

Λ_{e} / {(κ m_{0})}^{2} = - 1

(cosmological attraction) Bottom:

| q | / m_{0} = 0.1

and

Λ_{e} / {(κ m_{0})}^{2} = 0.1

(cosmological repulsion).

Figure 18. The shape of the non-relativistic potential (left) and relativistic potential (right) of the hex-particle in the equal mass case.

Figure 19. Equipotential lines at

V = 4 m c^{2}

for the non-relativistic potential (red), post-Newtonian potential (green), and relativistic potential (blue) in the equal mass case.

Figure 19. Equipotential lines at

V = 4 m c^{2}

for the non-relativistic potential (red), post-Newtonian potential (green), and relativistic potential (blue) in the equal mass case.

Figure 20. Annulus orbits (N-red, R-blue) shown in conjunction with their corresponding 3-particle trajectories

z (t)

(blue, red, magenta) for 30 time steps (top: relativistic, bottom: non-relativistic). The quasi-regular annulus orbits are for FE initial conditions with

η = 1.1

and run for 200 time steps. They are far from being chaotic. The R motion is further from periodicity, leaving far fewer open regions in the

(ρ, λ)

plane.

Figure 20. Annulus orbits (N-red, R-blue) shown in conjunction with their corresponding 3-particle trajectories

z (t)

(blue, red, magenta) for 30 time steps (top: relativistic, bottom: non-relativistic). The quasi-regular annulus orbits are for FE initial conditions with

η = 1.1

and run for 200 time steps. They are far from being chaotic. The R motion is further from periodicity, leaving far fewer open regions in the

(ρ, λ)

plane.

Figure 21. Near-chaotic annulus orbits (N-red, R-blue) shown in conjunction with their corresponding 3-particle trajectories

z (t)

(blue, red, magenta) for 80 time steps (top: relativistic, bottom: non-relativistic). These near-chaotic orbits were run for 200 time steps using FE initial conditions with

η = 1.5

. The R trajectory is closer to chaos than the N trajectory.

Figure 21. Near-chaotic annulus orbits (N-red, R-blue) shown in conjunction with their corresponding 3-particle trajectories

z (t)

(blue, red, magenta) for 80 time steps (top: relativistic, bottom: non-relativistic). These near-chaotic orbits were run for 200 time steps using FE initial conditions with

η = 1.5

. The R trajectory is closer to chaos than the N trajectory.

Figure 22. A comparsion of annulus orbits at identical FM conditions, for three similar values of

η

, all for 200 time steps. N trajectories (red) typically have less energy than R trajectories (blue) and so cover a smaller region of the

(ρ, λ)

plane. However for some initial conditions the N system has a larger energy (bottom figure) and so covers a correspondingly larger region.

Figure 22. A comparsion of annulus orbits at identical FM conditions, for three similar values of

η

, all for 200 time steps. N trajectories (red) typically have less energy than R trajectories (blue) and so cover a smaller region of the

(ρ, λ)

plane. However for some initial conditions the N system has a larger energy (bottom figure) and so covers a correspondingly larger region.

Figure 23. Regular pretzel orbits for FE conditions for the R (blue) and N (red) systems, each run for 120 time steps, with their corresponding 3-particle trajectories

z (t)

(blue, red, magenta) truncated at 35 time steps (top: relativistic, bottom: non-relativistic). The collision sequences are

A B^{3}

(R) and

A^{2} B^{3}

(N), and differ due to FE initial conditions.

Figure 23. Regular pretzel orbits for FE conditions for the R (blue) and N (red) systems, each run for 120 time steps, with their corresponding 3-particle trajectories

z (t)

(blue, red, magenta) truncated at 35 time steps (top: relativistic, bottom: non-relativistic). The collision sequences are

A B^{3}

(R) and

A^{2} B^{3}

(N), and differ due to FE initial conditions.

Figure 24. Time evolution of the hex-particle for a pretzel orbit, shown simultaneously in the N (red) and R (blue) systems at t=3,11,25,and 35 time steps (moving left to right on both rows) at FE conditions. For low energies (

η = 0.05

, top) the trajectories in the two systems are very similar, but at high energies (

η = 0.85

, bottom) they differ significantly. In the latter case the R orbit evolves with a higher collision frequency and stabilizes into a quasi-periodic cylindrical pattern. In contrast to this, the N trajectory extends considerably further from the origin and will eventually form a densely filled cylinder.

η = 0.05

, top) the trajectories in the two systems are very similar, but at high energies (

η = 0.85

Figure 25. A comparision of pretzel orbits of the relativistic system for slightly different FE conditions, each run for 200 time steps, with their corresponding 3-particle trajectories

z (t)

(blue, red, magenta) truncated at 80 time steps. A regular

A B^{6}

orbit pattern (top) yields the fish-like structure at the right, whereas slightly different initial conditions (bottom) result in the studel-like figure at the left. Here two particles are in a large-amplitude bound state, with the particle undergoing lower-amplitude irregular oscillations with this pair.

Figure 25. A comparision of pretzel orbits of the relativistic system for slightly different FE conditions, each run for 200 time steps, with their corresponding 3-particle trajectories

z (t)

(blue, red, magenta) truncated at 80 time steps. A regular

A B^{6}

Figure 26. A comparison of quasi-regular snake-like orbits for the N (red) and R (blue) systems, run for 200 time steps. These orbits have the symbol sequence

A^{m} B^{3}

for m odd, and in both systems each trajectory has two sharp turning points separated by some number n of bumps. The value of n increases with decreasing initial angular momentum in the

(ρ, λ)

plane. For the N system FM initial conditions were used, with the square (barely visible near the top of each figure) indicating the starting point. In the R system FE initial conditions were used with

η = 0.75

. The R orbits have a narrow hourglass shape, whereas the N orbits in the upper row lie in a cylinder notably larger in size in the

ρ

direction.

Figure 26. A comparison of quasi-regular snake-like orbits for the N (red) and R (blue) systems, run for 200 time steps. These orbits have the symbol sequence

A^{m} B^{3}

for m odd, and in both systems each trajectory has two sharp turning points separated by some number n of bumps. The value of n increases with decreasing initial angular momentum in the

(ρ, λ)

η = 0.75

. The R orbits have a narrow hourglass shape, whereas the N orbits in the upper row lie in a cylinder notably larger in size in the

ρ

direction.

Figure 27. A comparison of orbits with the symbol sequence

A B^{3}

for 200 time steps with FM initial conditions. The N system (red) is shown at the upper left and the R system (blue) in the remaining three plots for different values of

η

. As

η

increases, the R trajectories develop a kink along the

λ = 0

axis, displaying a double-banding pattern with two turning points at two distinct distances from the

ρ

axis about

λ = 0

Figure 27. A comparison of orbits with the symbol sequence

A B^{3}

for 200 time steps with FM initial conditions. The N system (red) is shown at the upper left and the R system (blue) in the remaining three plots for different values of

η

. As

η

increases, the R trajectories develop a kink along the

λ = 0

axis, displaying a double-banding pattern with two turning points at two distinct distances from the

ρ

axis about

λ = 0

Figure 28. A comparison of chaotic orbits for the N (red) and R (blue) systems in the region of phase space separating annulus and pretzel trajectories for 300 time steps, with their corresponding 3-particle trajectories

z (t)

(blue, red, magenta) truncated at 120 time steps. FE initial conditions were used, but with different initial values of

(ρ, λ, p_{ρ})

for each system. Most of the time the middle (‘m’) particle remains nearly motionless between the other two particles, which oscillated about the centre of inertia with large amplitude. However slight irregularities between the number of crossings for which one particle remains almost stationary results in the identity of the m-particle perpetually changing its identity, leading to chaos.

z (t)

(blue, red, magenta) truncated at 120 time steps. FE initial conditions were used, but with different initial values of

(ρ, λ, p_{ρ})

Figure 29. A comparison of the time-development of N (red) and R (blue) trajectories at

η = 0.5

for FE initial conditions, shown (in both rows) from left to right at

t = 5, 15, 30, 80

and 110 units. For one set of identical FE conditions, the R trajectory is chaotic whereas its N counterpart forms a densely filled annulus (top row). For a different set of identical FE conditions (with the same

η

), the N trajectory is chaotic whereas its R counterpart forms a densely filled cylinder in the pretzel class.

Figure 29. A comparison of the time-development of N (red) and R (blue) trajectories at

η = 0.5

for FE initial conditions, shown (in both rows) from left to right at

t = 5, 15, 30, 80

η

), the N trajectory is chaotic whereas its R counterpart forms a densely filled cylinder in the pretzel class.

Figure 30. Transition in the R system from an annulus to a pretzel orbit through a chaotic region, with

η = 0.5

. The initial angular momentum in the

(ρ, λ)

plane decreases from the upper left panel to the lower right one. Each plot is for FE initial conditions with 450 time steps. The chaotic trajectories pass very close to or through the origin.

Figure 30. Transition in the R system from an annulus to a pretzel orbit through a chaotic region, with

η = 0.5

. The initial angular momentum in the

(ρ, λ)

plane decreases from the upper left panel to the lower right one. Each plot is for FE initial conditions with 450 time steps. The chaotic trajectories pass very close to or through the origin.

Figure 31. The Poincaré plot of the N system. The squares denote the parts of the plot magnified in the insets.

Figure 32. Poincaré plots of the R system. In the upper plot

η = 0.1

; in the lower plot

η = 0.5

. The upper insets provide close-ups of the chaotic region at the top of the diagram, which is similar to the N system, but distorted in shape. The lower insets are close-ups of the structure in the pretzel; it likewise is distorted relative to the N system, with the distortions growing as

η

increases.

Figure 32. Poincaré plots of the R system. In the upper plot

η = 0.1

; in the lower plot

η = 0.5

η

increases.

Figure 33. The Poincaré plot of the pN system at

η = 0.21

. Qualitatively similar to the N system in terms of symmetry, its chaotic regions are larger, and the pretzel region is on the threshold of KAM breakdown.

Figure 33. The Poincaré plot of the pN system at

η = 0.21

. Qualitatively similar to the N system in terms of symmetry, its chaotic regions are larger, and the pretzel region is on the threshold of KAM breakdown.

Figure 34. A series of successive close-ups of the lower section of the Poincaré plot of the N system. This illustrates the self-similar structure in the pretzel region that repeats at increasingly small scales. The limiting factor at very small scales is the number of trajectories that we included in the plot.

Figure 35. Critical values of the relativistic potential

{\hat{V}}_{R}

plotted in units of

M_{tot} c^{2}

(here set equal to 3) as a function of a given particle mass

m_{j}

. The maximum value The maximum critical value occurs in the case when

m_{j} = M_{t o t} / 2

. As

m_{j} \to 0

M_{tot}

the minimal value

{\hat{V}}_{R} \to M_{tot}

is attained.

Figure 35. Critical values of the relativistic potential

{\hat{V}}_{R}

plotted in units of

M_{tot} c^{2}

(here set equal to 3) as a function of a given particle mass

m_{j}

. The maximum value The maximum critical value occurs in the case when

m_{j} = M_{t o t} / 2

. As

m_{j} \to 0

M_{tot}

the minimal value

{\hat{V}}_{R} \to M_{tot}

is attained.

Figure 36. Cross-sections of the N potential (left) and R potential (right) at

V \approx 1.3 M_{t o t} c^{2}

for different particle mass ratios: solid - 1:1:1; dashed - 1:1:4; dotted - 4:4:1; dash-dotted - 1:4:8. All discontinuities lie on one of the three bisectors

ρ = 0

ρ = \sqrt{3} λ

, or

ρ = - \sqrt{3} λ

regardless of the mass ratio in both systems. The smaller scales for

ρ

and

λ

are indicative of the steeper growth of the R potential as a function of distance from the origin.

Figure 36. Cross-sections of the N potential (left) and R potential (right) at

V \approx 1.3 M_{t o t} c^{2}

for different particle mass ratios: solid - 1:1:1; dashed - 1:1:4; dotted - 4:4:1; dash-dotted - 1:4:8. All discontinuities lie on one of the three bisectors

ρ = 0

ρ = \sqrt{3} λ

, or

ρ = - \sqrt{3} λ

regardless of the mass ratio in both systems. The smaller scales for

ρ

and

λ

are indicative of the steeper growth of the R potential as a function of distance from the origin.

Figure 37. Plots of the relative position

z (t)

of each particle with respect to the center of mass in the N system (top) and R system (bottom). Particles 1 (solid), 2 (dotted), and 3 (dashed) have relative masses in the ratio

1 : 1 : α

. The same initial values of

(ρ, λ, p_{​} ρ, p_{​} λ)

are used in each plot, with (153) used to fix the total energy

η + 1

for the R system and its non-relativistic limit used to fix

η

in the N system. The top figure is an annulus trajectory (

\bar{B}

) while the next two are pretzels (

\bar{B^{9} A}

\bar{{(B^{3} A^{2})}^{4} B^{3} A^{3}}

) in the N system, whereas the bottom figure is a pretzel (

\bar{{(B^{6} A)}^{7} B^{3}}

) in the R system, and the two above that are both annuli in the R system. The smaller the value of

α

, the more tightly bound are particles 1 and 2 in each system, with relatively tighter binding in the R system as can be seen by comparing the bottom figure with the third one from the top.

Figure 37. Plots of the relative position

z (t)

of each particle with respect to the center of mass in the N system (top) and R system (bottom). Particles 1 (solid), 2 (dotted), and 3 (dashed) have relative masses in the ratio

1 : 1 : α

. The same initial values of

(ρ, λ, p_{​} ρ, p_{​} λ)

are used in each plot, with (153) used to fix the total energy

η + 1

for the R system and its non-relativistic limit used to fix

η

in the N system. The top figure is an annulus trajectory (

\bar{B}

) while the next two are pretzels (

\bar{B^{9} A}

\bar{{(B^{3} A^{2})}^{4} B^{3} A^{3}}

) in the N system, whereas the bottom figure is a pretzel (

\bar{{(B^{6} A)}^{7} B^{3}}

) in the R system, and the two above that are both annuli in the R system. The smaller the value of

α

, the more tightly bound are particles 1 and 2 in each system, with relatively tighter binding in the R system as can be seen by comparing the bottom figure with the third one from the top.

Figure 38. A comparison of the relative motion of the particles with respect to the center of mass plotted as a function of time for the R system (top,

η = 0.2793

) and N system (bottom,

η = 0.1748

). Particles 1 (solid), 2 (dotted), and 3 (dashed) have relative masses in the ratio

1 : 1 : 100

. Small perturbations in the motion of the large mass due to the crossing of the smaller masses are shown in the insets.

Figure 38. A comparison of the relative motion of the particles with respect to the center of mass plotted as a function of time for the R system (top,

η = 0.2793

) and N system (bottom,

η = 0.1748

). Particles 1 (solid), 2 (dotted), and 3 (dashed) have relative masses in the ratio

1 : 1 : 100

. Small perturbations in the motion of the large mass due to the crossing of the smaller masses are shown in the insets.

Figure 39. A comparison of the relative motion of the particles with respect to the center of mass plotted as a function of time for the R system (top,

η = 0.2244

) and N system (bottom,

η = 0.2512

). Particles 1 (solid), 2 (dotted), and 3 (dashed) have relative masses in the ratio

1 : 1 : = 0.01

. The respective upper insets show the motion of the stable, two body sub-system made up of the two heavy particles, whereas the effect of encounters with the light particle are shown in the respective lower insets.

Figure 39. A comparison of the relative motion of the particles with respect to the center of mass plotted as a function of time for the R system (top,

η = 0.2244

) and N system (bottom,

η = 0.2512

). Particles 1 (solid), 2 (dotted), and 3 (dashed) have relative masses in the ratio

1 : 1 : = 0.01

Figure 40. Poincaré plots with mass ratio

1 : 1 : 0.1

for the N (left) and R (right) systems, both with

η = 0.3

The insets show the onset of chaos in the pretzel region for the R system.

Figure 40. Poincaré plots with mass ratio

1 : 1 : 0.1

for the N (left) and R (right) systems, both with

η = 0.3

The insets show the onset of chaos in the pretzel region for the R system.

Figure 41. Poincaré plots with mass ratio

1 : 1 : 10

for the N (left) and R (right) systems, both with

η = 0.3

. Additional regions of chaos in the pretzel region appear that are not present in the corresponding regions of the equal mass Poincaré sections, shown in the insets.

Figure 41. Poincaré plots with mass ratio

1 : 1 : 10

for the N (left) and R (right) systems, both with

η = 0.3

. Additional regions of chaos in the pretzel region appear that are not present in the corresponding regions of the equal mass Poincaré sections, shown in the insets.

Figure 42. Poincaré plots with a mass ratio of 1:5:10 for the N (left) and R (right) systems, both for

η = 0.3

. The region of chaos separating annulus trajectories (inside) and predominantly pretzel trajectories (outside) is marked by A, whereas the densely filled area directly above and below B is a new region of chaos amongst the pretzel trajectories. In the R system (right), the densely filled regions (marked by a 1) were created by a single trajectory separating the annulus and pretzel orbits, while the chaotic regions (marked by a 2) were created by a trajectory within the pretzel region.

Figure 42. Poincaré plots with a mass ratio of 1:5:10 for the N (left) and R (right) systems, both for

η = 0.3

Figure 43. Poincare plots for

H = 1.2 M_{tot}

for three different values of

\frac{Λ_{e}}{κ^{2} M_{tot}^{2}}

: 0 (top),

- 0.175

(lower left), and

0.6

(lower right). The green curves track the orbits (a -d) shown in Figure 44, and indicate their trajectories in the plot as

\frac{Λ_{e}}{κ^{2} M_{tot}^{2}}

changes from

- 0.175

0.6

; the arrow indicates the direction of increasing

Λ_{e}

. The insets show closeups of the trajectories near chaotic regions. The lower left plot shows that chaos diminishes at

Λ_{e}

becomes more negative, whereas in the lower right diagram orbits (b) and (c) have become chaotic and so do not appear; only the locations of orbits (a) and (d) are shown.

Figure 43. Poincare plots for

H = 1.2 M_{tot}

for three different values of

\frac{Λ_{e}}{κ^{2} M_{tot}^{2}}

: 0 (top),

- 0.175

(lower left), and

0.6

(lower right). The green curves track the orbits (a -d) shown in Figure 44, and indicate their trajectories in the plot as

\frac{Λ_{e}}{κ^{2} M_{tot}^{2}}

changes from

- 0.175

0.6

; the arrow indicates the direction of increasing

Λ_{e}

. The insets show closeups of the trajectories near chaotic regions. The lower left plot shows that chaos diminishes at

Λ_{e}

becomes more negative, whereas in the lower right diagram orbits (b) and (c) have become chaotic and so do not appear; only the locations of orbits (a) and (d) are shown.

Figure 44. Four representative periodic and quasi-periodic orbits, labelled (a) a stable (nearly circular) orbit located in the centre of the annulus region, denoted by a ∘’ symbol (upper left), (b) an annulus orbit located around the outside edge of the triangular annulus region, denoted by a ‘△’ symbol (upper right), (c) a quasi-periodic pretzel orbit located halfway between the centre of the annulus region and the first large outer annulus regions, denoted by a ‘□’ symbol (lower left), and (d) a banana-shaped

A B^{3}

orbit located in the centre of that region, denoted by the ‘+’ symbol (lower right).

A B^{3}

orbit located in the centre of that region, denoted by the ‘+’ symbol (lower right).

Figure 45. Plots of the potential for one neutral and two charged particles. Values of

\frac{e}{\sqrt{κ} M_{t o t}}

for each case are given at the bottom. Solid lines denote equipotentials.

Figure 45. Plots of the potential for one neutral and two charged particles. Values of

\frac{e}{\sqrt{κ} M_{t o t}}

for each case are given at the bottom. Solid lines denote equipotentials.

Figure 46. Plots of the potential for three charged particles. Values of

\frac{e}{\sqrt{κ} M_{t o t}}

for each case are given at the bottom. Solid lines denote equipotentials.

Figure 46. Plots of the potential for three charged particles. Values of

\frac{e}{\sqrt{κ} M_{t o t}}

for each case are given at the bottom. Solid lines denote equipotentials.

Figure 47. Sample trajectories in the charged case with FE conditions, for

H / M_{t o t} = 1.2

Λ_{e} = 0

, and

\frac{e}{\sqrt{κ} M_{t o t}} = (0.1, 0.1, - 0.1)

(top and middle) and

(0.2, 0.2, - 0.2)

(bottom). Each figure was run for 200 time steps; the corresponding three-particle trajectories at the right were truncated after 30 time steps.

Figure 47. Sample trajectories in the charged case with FE conditions, for

H / M_{t o t} = 1.2

Λ_{e} = 0

, and

\frac{e}{\sqrt{κ} M_{t o t}} = (0.1, 0.1, - 0.1)

(top and middle) and

(0.2, 0.2, - 0.2)

(bottom). Each figure was run for 200 time steps; the corresponding three-particle trajectories at the right were truncated after 30 time steps.

Figure 48. Poincaré plots of the system at

H / M_{t o t} = 1.2

corresponding to the crossings of (upper) the two positively charged particles and (lower) of the neutral particle with a positively charged particle. In the left panel

\frac{e}{\sqrt{κ} M_{t o t}} = (+ 0.1, + 0.1, 0)

; in the right panel

\frac{e}{\sqrt{κ} M_{t o t}} = (+ 0.17, + 0.17, 0)

. The left upper insets (a,c) show a close up of the upper chaotic regions; the left lower insets show the pretzel regions. The insets at the right show a close up of the structure in pretzel region.

Figure 48. Poincaré plots of the system at

H / M_{t o t} = 1.2

corresponding to the crossings of (upper) the two positively charged particles and (lower) of the neutral particle with a positively charged particle. In the left panel

\frac{e}{\sqrt{κ} M_{t o t}} = (+ 0.1, + 0.1, 0)

; in the right panel

\frac{e}{\sqrt{κ} M_{t o t}} = (+ 0.17, + 0.17, 0)

. The left upper insets (a,c) show a close up of the upper chaotic regions; the left lower insets show the pretzel regions. The insets at the right show a close up of the structure in pretzel region.

Figure 49. Poincaré plots of the system for charges

\frac{e}{\sqrt{κ} M_{t o t}} = (+ 0.2, - 0.2, 0)

; corresponding to the crossings of (upper) the two charged particles and (lower) the neutral particle with the positively charged particle. In the left panel

H / M_{t o t} = 1.2

; in the right panel

H / M_{t o t} = 1.8

. The upper insets (a,c) show a close up of pretzel regions; the lower insets (b,d) show quasi-periodic regions.

Figure 49. Poincaré plots of the system for charges

\frac{e}{\sqrt{κ} M_{t o t}} = (+ 0.2, - 0.2, 0)

; corresponding to the crossings of (upper) the two charged particles and (lower) the neutral particle with the positively charged particle. In the left panel

H / M_{t o t} = 1.2

; in the right panel

H / M_{t o t} = 1.8

. The upper insets (a,c) show a close up of pretzel regions; the lower insets (b,d) show quasi-periodic regions.

Figure 50. Poincaré plots of the system at

H / M_{t o t} = 1.2

corresponding to the crossings of (upper) the two positively charged particles and (lower) of the negative particle with a positively charged particle. In the left panel

\frac{e}{\sqrt{κ} M_{t o t}} = (+ 0.1, + 0.1, - 0.1)

; in the right panel

\frac{e}{\sqrt{κ} M_{t o t}} = (+ 0.223, + 0.223, - 0.223)

. The left upper insets (a,c) show close ups of chaotic regions; the left lower insets (b,d) show pretzel regions. The upper and lower insets (e,h) at the right show close ups of chaotic regions; the lower and upper insets (f,g) of pretzel and quasi-periodic regions.

Figure 50. Poincaré plots of the system at

H / M_{t o t} = 1.2

corresponding to the crossings of (upper) the two positively charged particles and (lower) of the negative particle with a positively charged particle. In the left panel

\frac{e}{\sqrt{κ} M_{t o t}} = (+ 0.1, + 0.1, - 0.1)

; in the right panel

\frac{e}{\sqrt{κ} M_{t o t}} = (+ 0.223, + 0.223, - 0.223)

Figure 51. Two equipotential surfaces of the box-particle Newtonian potential in the equal mass case, with the right panel showing a smaller value of V and the left one showing a larger value.

Figure 52. 4-body braid operations

Figure 53. Annulus (left) and pretzel (right) orbits for the non-relativistic 4-body system for 500 time steps and

\frac{H}{M_{t o t}} = 2

. For the upper plots the initial conditions are

ρ = 0,

α = 0,

p_{ρ} = 0.5,

p_{β} = 0,

p_{α} = 0

(left) and

ρ = 1,

α = 0,

p_{ρ} = 0,

p_{β} = 0,

p_{α} = 0

(right), with

β

calculated so that (202) initially is satisfied. The initial conditions for the lower plots are

ρ = 0,

α = 0.1,

p_{ρ} = 0.5,

p_{β} = 0, p_{α} = 0

(left) and

ρ = 1,

α = 0,

p_{ρ} = 0,

p_{β} = 0,

p_{α} = 0.1

(right). The respective Lyapunov exponents are 1.214×

10^{- 2}

(annulus, lower left) and 7.350×

10^{- 3}

(pretzel, lower right). The small square boxes in each diagram denote the initial conditions.

Figure 53. Annulus (left) and pretzel (right) orbits for the non-relativistic 4-body system for 500 time steps and

\frac{H}{M_{t o t}} = 2

. For the upper plots the initial conditions are

ρ = 0,

α = 0,

p_{ρ} = 0.5,

p_{β} = 0,

p_{α} = 0

(left) and

ρ = 1,

α = 0,

p_{ρ} = 0,

p_{β} = 0,

p_{α} = 0

(right), with

β

calculated so that (202) initially is satisfied. The initial conditions for the lower plots are

ρ = 0,

α = 0.1,

p_{ρ} = 0.5,

p_{β} = 0, p_{α} = 0

(left) and

ρ = 1,

α = 0,

p_{ρ} = 0,

p_{β} = 0,

p_{α} = 0.1

(right). The respective Lyapunov exponents are 1.214×

10^{- 2}

(annulus, lower left) and 7.350×

10^{- 3}

(pretzel, lower right). The small square boxes in each diagram denote the initial conditions.

Figure 54. A three-dimensional periodic orbit (middle left) that has pretzel form when projected into the

(ρ, β)

(upper left) and

(ρ, α)

(not shown) planes and annulus form when onto the

(β, α)

plane (upper right), using FE (

H / M_{t o t} = 1

) conditions, where initially

ρ = α = 0

β = 2.2

and

p_{ρ} = 0.15

p_{α} = 0.37509

, and

p_{β} = 0

. Particle trajectories are shown the in the lower right.

Figure 54. A three-dimensional periodic orbit (middle left) that has pretzel form when projected into the

(ρ, β)

(upper left) and

(ρ, α)

(not shown) planes and annulus form when onto the

(β, α)

plane (upper right), using FE (

H / M_{t o t} = 1

) conditions, where initially

ρ = α = 0

β = 2.2

and

p_{ρ} = 0.15

p_{α} = 0.37509

, and

p_{β} = 0

. Particle trajectories are shown the in the lower right.

Figure 55. An example of how a regular motion (upper left) can become chaotic (lower left) from a small change in initial conditions, with corresponding particle trajectories shown at the right. In all figures FE conditions are used with

H / M_{t o t} = 0.625

, and initially

(p_{ρ}, p_{β}, p_{α}) = (0, 0, 0)

, and

(β, α) = (1.633, 0.70711)

. In the upper two figures

ρ = 0.70711

initially, but in the lower two figures

ρ = 0.70712

initially. The small box in each of the left figures marks the initial position of the box particle. The upper figures show regular motion, but the lower ones show a rapid onset of chaos.

H / M_{t o t} = 0.625

, and initially

(p_{ρ}, p_{β}, p_{α}) = (0, 0, 0)

, and

(β, α) = (1.633, 0.70711)

. In the upper two figures

ρ = 0.70711

initially, but in the lower two figures

ρ = 0.70712

initially. The small box in each of the left figures marks the initial position of the box particle. The upper figures show regular motion, but the lower ones show a rapid onset of chaos.

Figure 56. Slices of the complete Poincare plot, with the bottom (

p_{ϕ} = 0

) slice at left and the side (

p_{θ} = 0

) slice at right. The bottom slice bears some resemblance to the the 3-body non-relativistic case in Figure 31 but the side slice does not display similar fractal-like structures. Approximately 500,000 points were used to generate these figures.

Figure 56. Slices of the complete Poincare plot, with the bottom (

p_{ϕ} = 0

) slice at left and the side (

p_{θ} = 0

Figure 57. Maximum value of the average relativistic energy as a function of N to leading order in

1 / c^{2}

Figure 57. Maximum value of the average relativistic energy as a function of N to leading order in

1 / c^{2}

Figure 58. Plots of the momentum distribution (217) as a function of

η = \frac{p}{m V}

(left column) and its value relative to the non-relativistic case (right column) for three different values of N and various values of

ζ

Figure 58. Plots of the momentum distribution (217) as a function of

η = \frac{p}{m V}

(left column) and its value relative to the non-relativistic case (right column) for three different values of N and various values of

ζ

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

One-Dimensional Relativistic Self-Gravitating Systems

Abstract

1. Introduction

2. Non-Relativistic Self-Gravitating Systems

3. Relativistic Gravity Coupled to Point Particles

4. Canonical Formalism for Particle Dynamics

4.1. Neutral Particles

4.2. Charged Particles

5. The 2-Body Problem

5.1. Solution for 2 Charged Particles

5.2. Test Particle Limit

5.3. Exact Equal Mass Two-Body Motion for Λ = 0

5.4. Exact Two-Body Motion with Equal Masses and Arbitrary Charges

5.4.1. Neutral Particle Motion

5.4.2. Charged Particle Motion with Λ e = 0

5.4.2.1 The attractive case: e 1 = − e 2 = q

5.4.2.2 The repulsive case: e 1 = e 2 = q , | q | ≤ q c

5.4.2.3 The repulsive case: e 1 = e 2 = q , | q | > q c

5.4.3. Charged Particle Motion with Λ e ≠ 0

5.5. Exact Two-Body Motion with Unequal Masses

5.6. Static Balance

6. The 3-Body Problem

6.1. 3-Body Constraint Equations

6.2. Effective Potential

6.3. Relativistic Equal Mass 3-Body Trajectories

6.3.1. General Features of the Motion

6.3.2. Annulus Orbits

6.3.3. Pretzel Orbits

6.3.4. Chaotic Orbits

6.4. Poincaré Plots

6.5. Unequal Masses

6.5.1. Trajectories

6.5.2. Poincaré Plots

6.6. Charge and Cosmological Constant

6.6.1. Neutral Configurations with Λ e ≠ 0

6.6.2. Charged Configurations

7. The 4-Body Problem

7.1. 4-Body Potential

7.2. Motion Classification

7.3. Equal Mass Trajectories

7.4. Poincaré Plots

8. The N-Body Problem

8.1. Motion Classification

8.2. Post-Newtonian Canonical Ensemble

8.3. Other Statistical Features

9. The Circular N-Body Problem

10. Conclusions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe

5.3. Exact Equal Mass Two-Body Motion for $Λ = 0$

5.4.2. Charged Particle Motion with $Λ_{e} = 0$

5.4.2.1 `The attractive case`: $e_{1} = - e_{2} = q$

5.4.2.2 `The repulsive case`: $e_{1} = e_{2} = q$ , $| q | \leq q_{c}$

5.4.2.3 `The repulsive case`: $e_{1} = e_{2} = q$ , $| q | > q_{c}$

5.4.3. Charged Particle Motion with $Λ_{e} \neq 0$

6.6.1. Neutral Configurations with $Λ_{e} \neq 0$