Submitted:
10 June 2024
Posted:
11 June 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction and State of the Art
- First-generation PV systems, which are fully commercialized, employ wafer-based crystalline silicon (c-Si) technology, comprising either single crystalline (sc-Si) or multicrystalline (mc-Si) structures.
- Second-generation PV systems, in the early stages of market deployment, encompass thin-film PV technologies, primarily including three main families: (1) amorphous (a-Si) and micromorph silicon (a-Si/μc-Si); (2) cadmium telluride (CdTe); and (3) copper indium selenide (CIS) and copper indium-gallium diselenide (CIGS).
- Third-generation PV systems comprise technologies such as concentrating PV (CPV) and organic PV cells, which are still in the demonstration phase or have not yet attained widespread commercialization, alongside novel concepts currently in development.
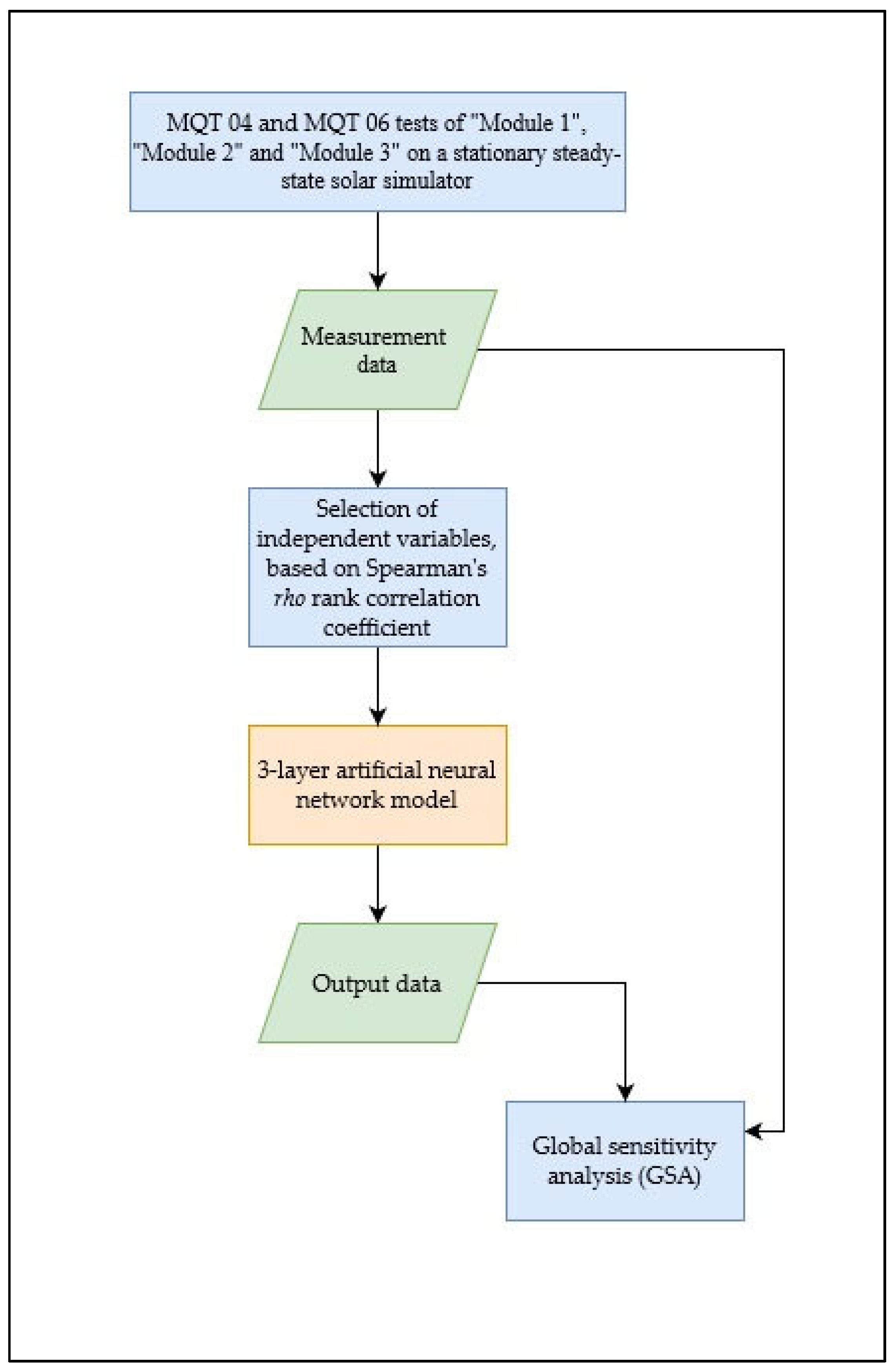
2. Materials and Methods
2.1. Testing Methods for PV Modules
- MQT 04 - Measurement of temperature coefficients - The test consists of measuring the temperature coefficients of current, voltage and peak power in accordance with PN-EN 60904-10. The purpose of the test is to determine the temperature coefficients of PV modules at different irradiances. When performing the test, a device for controlling the temperature of the module is required [34].
- MQT 06 - Performance under STC and NOCT conditions - The test consists of determining the electrical performance of the module under standard test conditions. Measurement under STC (Standard Test Conditions) is used to verify the information on the module's nameplate. The solar source should be a natural solar source or a BBA-class solar simulator, or better [34].
2.2. Characteristics of the Tested PV Modules
2.3. Experimental Description and Test Methods
- a)
- Coefficient of determinacy ():
- b)
- Mean absolute error (MAE):
- c)
- Root mean square error (RMSE):
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Maka, A.O.M.; Alabid, J.M. Solar Energy Technology and Its Roles in Sustainable Development. Clean Energy 2022, 6, 476–483. [Google Scholar] [CrossRef]
- Aktaş, A.; Kirçiçek, Y. Solar System Characteristics, Advantages, and Disadvantages. In Solar Hybrid Systems; Elsevier, 2021; pp. 1–24.
- Winter, A.; Hager, M.D.; Newkome, G.R.; Schubert, U.S. The Marriage of Terpyridines and Inorganic Nanoparticles: Synthetic Aspects, Characterization Techniques, and Potential Applications. Adv. Mater. 2011, 23, 5728–5748. [Google Scholar] [CrossRef] [PubMed]
- Bdour, M.; Al-Sadi, A. Analysis of Different Microcracks Shapes and the Effect of Each Shape on Performance of PV Modules. IOP Conf. Ser. Mater. Sci. Eng. 2020, 876, 012005. [Google Scholar] [CrossRef]
- Mohammad Bagher, A. Types of Solar Cells and Application. Am. J. Opt. Photonics 2015, 3, 94. [Google Scholar] [CrossRef]
- Green, M.A. Silicon Photovoltaic Modules: A Brief History of the First 50 Years. Prog. Photovoltaics Res. Appl. 2005, 13, 447–455. [Google Scholar] [CrossRef]
- El Chaar, L.; Lamont, L.A.; El Zein, N. Review of Photovoltaic Technologies. Renew. Sustain. Energy Rev. 2011, 15, 2165–2175. [Google Scholar] [CrossRef]
- Goetzberger, A.; Hebling, C.; Schock, H.-W. Photovoltaic Materials, History, Status and Outlook. Mater. Sci. Eng. R Reports 2003, 40, 1–46. [Google Scholar] [CrossRef]
- Marques Lameirinhas, R.A.; Torres, J.P.N.; de Melo Cunha, J.P. A Photovoltaic Technology Review: History, Fundamentals and Applications. Energies 2022, 15, 1823. [Google Scholar] [CrossRef]
- Asdrubali, F.; Umberto, D. High Efficiency Plants and Building Integrated Renewable Energy Systems. In Handbook of Energy Efficiency in Buildings; Elsevier, 2019; pp. 441–595.
- Sahu, A.; Garg, A.; Dixit, A. A Review on Quantum Dot Sensitized Solar Cells: Past, Present and Future towards Carrier Multiplication with a Possibility for Higher Efficiency. Sol. Energy 2020, 203, 210–239. [Google Scholar] [CrossRef]
- Lee, T.D.; Ebong, A.U. A Review of Thin Film Solar Cell Technologies and Challenges. Renew. Sustain. Energy Rev. 2017, 70, 1286–1297. [Google Scholar] [CrossRef]
- Nakamura, M.; Yamaguchi, K.; Kimoto, Y.; Yasaki, Y.; Kato, T.; Sugimoto, H. Cd-Free Cu(In,Ga)(Se,S) 2 Thin-Film Solar Cell With Record Efficiency of 23.35%. IEEE J. Photovoltaics 2019, 9, 1863–1867. [Google Scholar] [CrossRef]
- Sinke, W.C. Development of Photovoltaic Technologies for Global Impact. Renew. Energy 2019, 138, 911–914. [Google Scholar] [CrossRef]
- Pinho Correia Valério Bernardo, C.; Marques Lameirinhas, R.A.; Neto Torres, J.P.; Baptista, A. Comparative Analysis between Traditional and Emerging Technologies: Economic and Viability Evaluation in a Real Case Scenario. Mater. Renew. Sustain. Energy 2023, 12, 1–22. [Google Scholar] [CrossRef]
- Hwang, I.; Um, H.-D.; Kim, B.-S.; Wober, M.; Seo, K. Flexible Crystalline Silicon Radial Junction Photovoltaics with Vertically Aligned Tapered Microwires. Energy Environ. Sci. 2018, 11, 641–647. [Google Scholar] [CrossRef]
- Weckend, S.; Wade, A.; Heath, G. End of Life Management: Solar Photovoltaic Panels; Golden, CO (United States), 2016.
- Sangwongwanich, A.; Yang, Y.; Sera, D.; Blaabjerg, F. Lifetime Evaluation of Grid-Connected PV Inverters Considering Panel Degradation Rates and Installation Sites. IEEE Trans. Power Electron. 2018, 33, 1225–1236. [Google Scholar] [CrossRef]
- Manimekalai, P.; Harikumar, R.; Raghavan, S. An Overview of Batteries for Photovoltaic (PV) Systems. Int. J. Comput. Appl. 2013, 82, 28–32. [Google Scholar] [CrossRef]
- Pinho Correia Valério Bernardo, C.; Marques Lameirinhas, R.A.; Neto Torres, J.P.; Baptista, A. The Shading Influence on the Economic Viability of a Real Photovoltaic System Project. Energies 2023, 16, 2672. [Google Scholar] [CrossRef]
- Karthikeyan, V.; Sirisamphanwong, C.; Sukchai, S.; Sahoo, S.K.; Wongwuttanasatian, T. Reducing PV Module Temperature with Radiation Based PV Module Incorporating Composite Phase Change Material. J. Energy Storage 2020, 29, 101346. [Google Scholar] [CrossRef]
- Nabil, T.; Mansour, T.M. Augmenting the Performance of Photovoltaic Panel by Decreasing Its Temperature Using Various Cooling Techniques. Results Eng. 2022, 15, 100564. [Google Scholar] [CrossRef]
- Gupta, V.; Sharma, M.; Pachauri, R.K.; Dinesh Babu, K.N. Comprehensive Review on Effect of Dust on Solar Photovoltaic System and Mitigation Techniques. Sol. Energy 2019, 191, 596–622. [Google Scholar] [CrossRef]
- Agyekum, E.B.; PraveenKumar, S.; Alwan, N.T.; Velkin, V.I.; Shcheklein, S.E. Effect of Dual Surface Cooling of Solar Photovoltaic Panel on the Efficiency of the Module: Experimental Investigation. Heliyon 2021, 7, e07920. [Google Scholar] [CrossRef] [PubMed]
- Murtadha, T.K. Installing Clear Acrylic Sheet to Reduce Unwanted Sunlight Waves That Photovoltaic Panels Receive. Results Eng. 2023, 17, 100875. [Google Scholar] [CrossRef]
- Du, B.; Hu, E.; Kolhe, M. Performance Analysis of Water Cooled Concentrated Photovoltaic (CPV) System. Renew. Sustain. Energy Rev. 2012, 16, 6732–6736. [Google Scholar] [CrossRef]
- Mallick, T.K.; Eames, P.C.; Norton, B. Using Air Flow to Alleviate Temperature Elevation in Solar Cells within Asymmetric Compound Parabolic Concentrators. Sol. Energy 2007, 81, 173–184. [Google Scholar] [CrossRef]
- Xiao, M.; Tang, L.; Zhang, X.; Lun, I.; Yuan, Y. A Review on Recent Development of Cooling Technologies for Concentrated Photovoltaics (CPV) Systems. Energies 2018, 11, 3416. [Google Scholar] [CrossRef]
- Siecker, J.; Kusakana, K.; Numbi, B.P. A Review of Solar Photovoltaic Systems Cooling Technologies. Renew. Sustain. Energy Rev. 2017, 79, 192–203. [Google Scholar] [CrossRef]
- Hoque, E.; Shipon, F.A.; Das, A.; Raihan, Z. Development of an Integrated PV Solar Panel Cooling System by Using Fin, DC Fan, Thermoelectric Regenerator and Water Sprayer. In Proceedings of the International Conference on Mechanical, Industrial and Materials Engineering (ICMIME); 2022; p. 225.
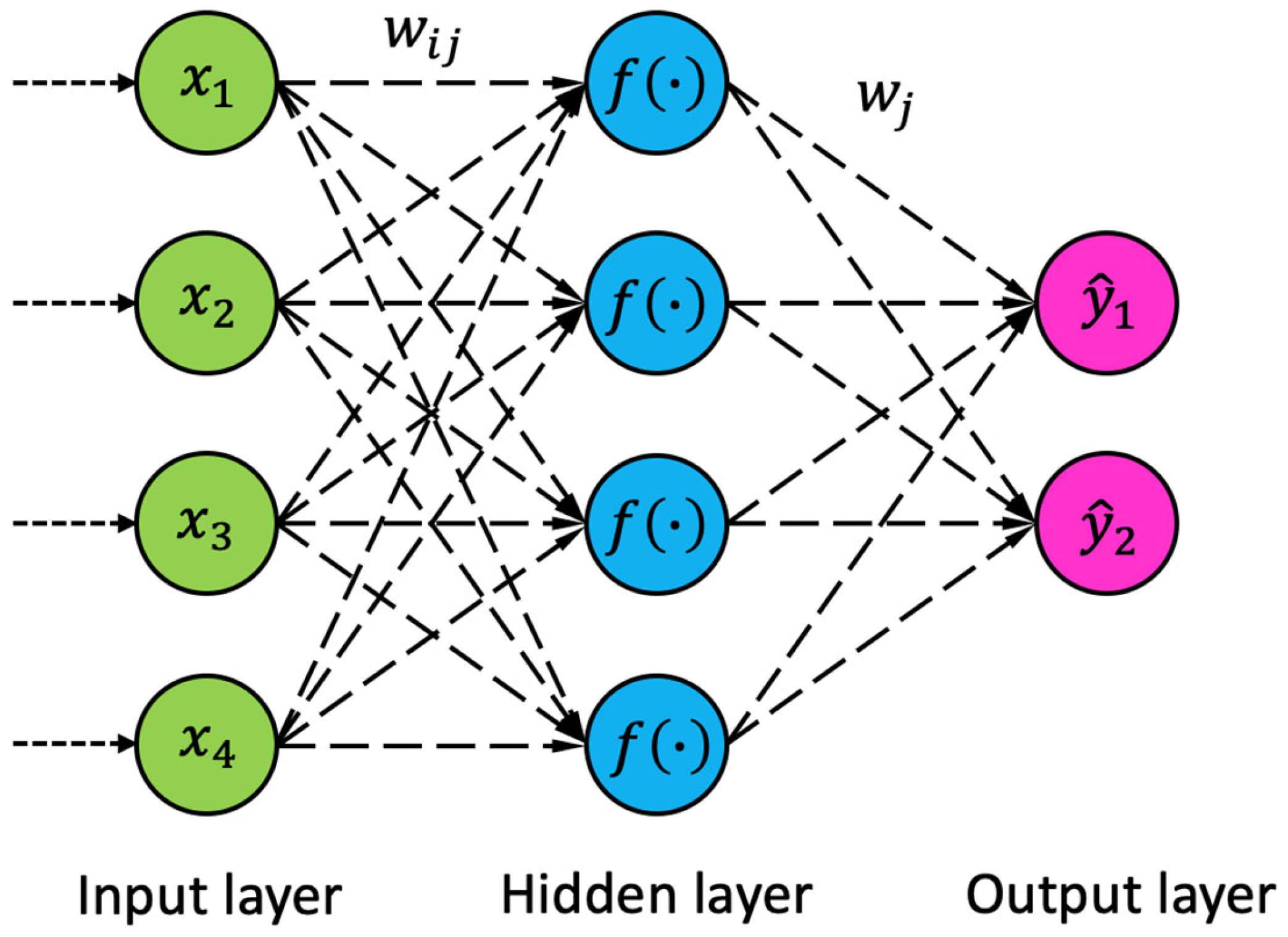
- Gunasekar, N.; Mohanraj, M.; Velmurugan, V. Artificial Neural Network Modeling of a Photovoltaic-Thermal Evaporator of Solar Assisted Heat Pumps. Energy 2015, 93, 908–922. [Google Scholar] [CrossRef]
- Rodríguez, F.; Fleetwood, A.; Galarza, A.; Fontán, L. Predicting Solar Energy Generation through Artificial Neural Networks Using Weather Forecasts for Microgrid Control. Renew. Energy 2018, 126, 855–864. [Google Scholar] [CrossRef]
- Kaya, M.; Hajimirza, S. Application of Artificial Neural Network for Accelerated Optimization of Ultra Thin Organic Solar Cells. Sol. Energy 2018, 165, 159–166. [Google Scholar] [CrossRef]
- PN-EN IEC 61215-1-2:2021-11 Photovoltaic (PV) Modules for Terrestrial Applications - Construction Qualification and Type Approval - Part 1-2: Particular Requirements for Testing of Thin-Film Photovoltaic (PV) Modules Manufactured on the Basis of Cadmium Telluride (CdTe). 2021.
- PN-EN 60721-2-1:2014-10 Classification of Environmental Conditions - Part 2-1: Environmental Conditions Found in Nature - Temperature and Humidity. 2014.
- Data from the Manufacturer of “Module 1”.
- Data from the Manufacturer of “Module 2”.
- Data from the Manufacturer of “Module 3”.
- Colarossi, D.; Tagliolini, E.; Principi, P.; Fioretti, R. Design and Validation of an Adjustable Large-Scale Solar Simulator. Appl. Sci. 2021, 11, 1964. [Google Scholar] [CrossRef]
- Spearman, C. Theory of General Factor. Br. J. Psychol. Gen. Sect. 1946, 36, 117–131. [Google Scholar] [CrossRef]
- Rutkowski, L.; Cpalka, K. Flexible Neuro-Fuzzy Systems. IEEE Trans. Neural Networks 2003, 14, 554–574. [Google Scholar] [CrossRef] [PubMed]
- Hecht-Nielsen, R. Kolmogorov’s Mapping Neural Network Existence Theorem. First IEEE Int. Conf. Neural Networks 1987, 3, 11–14. [Google Scholar]
- Hassoun, M.H. Fundamentals of Artificial Neural Networks; MIT Press, 1995; ISBN 978-0262082396.
- Bieganowski, A.; Józefaciuk, G.; Bandura, L.; Guz, Ł.; Łagód, G.; Franus, W. Evaluation of Hydrocarbon Soil Pollution Using E-Nose. Sensors 2018, 18, 2463. [Google Scholar] [CrossRef] [PubMed]
- Khorramifar, A.; Rasekh, M.; Karami, H.; Lozano, J.; Gancarz, M.; Łazuka, E.; Łagód, G. Determining the Shelf Life and Quality Changes of Potatoes (Solanum Tuberosum) during Storage Using Electronic Nose and Machine Learning. PLoS One 2023, in print (accepted).
- Guz, Ł.; Łagód, G.; Jaromin-Gleń, K.; Suchorab, Z.; Sobczuk, H.; Bieganowski, A. Application of Gas Sensor Arrays in Assessment of Wastewater Purification Effects. Sensors 2014, 15, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Szeląg, B.; Drewnowski, J.; Łagód, G.; Majerek, D.; Dacewicz, E.; Fatone, F. Soft Sensor Application in Identification of the Activated Sludge Bulking Considering the Technological and Economical Aspects of Smart Systems Functioning. Sensors 2020, 20, 1941. [Google Scholar] [CrossRef] [PubMed]
- Trabelsi, M.; Massaoudi, M.; Chihi, I.; Sidhom, L.; Refaat, S.S.; Huang, T.; Oueslati, F.S. An Effective Hybrid Symbolic Regression–Deep Multilayer Perceptron Technique for PV Power Forecasting. Energies 2022, 15, 9008. [Google Scholar] [CrossRef]
- Changsong, C.; Shanxu, D.; Tao, C.; Bangyin, L. Online 24-h Solar Power Forecasting Based on Weather Type Classification Using Artificial Neural Network. Sol. Energy 2011, 85, 2856–2870. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M. A 24-h Forecast of Solar Irradiance Using Artificial Neural Network: Application for Performance Prediction of a Grid-Connected PV Plant at Trieste, Italy. Sol. Energy 2010, 84, 807–821. [Google Scholar] [CrossRef]
- Cao, S.; Cao, J. Forecast of Solar Irradiance Using Recurrent Neural Networks Combined with Wavelet Analysis. Appl. Therm. Eng. 2005, 25, 161–172. [Google Scholar] [CrossRef]
- Hontoria, L.; Aguilera, J.; Zufiria, P. Generation of Hourly Irradiation Synthetic Series Using the Neural Network Multilayer Perceptron. Sol. Energy 2002, 72, 441–446. [Google Scholar] [CrossRef]
- Mihalakakou, G.; Santamouris, M.; Asimakopoulos, D.N. The Total Solar Radiation Time Series Simulation in Athens, Using Neural Networks. Theor. Appl. Climatol. 2000, 66, 185–197. [Google Scholar] [CrossRef]
- Sfetsos, A.; Coonick, A.H. Univariate and Multivariate Forecasting of Hourly Solar Radiation with Artificial Intelligence Techniques. Sol. Energy 2000, 68, 169–178. [Google Scholar] [CrossRef]
- Mellit, A.; Benghanem, M.; Arab, A.H.; Guessoum, A. A Simplified Model for Generating Sequences of Global Solar Radiation Data for Isolated Sites: Using Artificial Neural Network and a Library of Markov Transition Matrices Approach. Sol. Energy 2005, 79, 469–482. [Google Scholar] [CrossRef]
- Elsaraiti M, Merabet, A. Solar power forecasting using deep learning techniques. IEEE Access 2022;10:31692–8.
- Vennila C, Titus A, Sudha T, Sreenivasulu U, Reddy N, Jamal K, et al. Forecasting solar energy production using machine learning. Int J Photoenergy 2022:2022.
- Sudharshan K, Naveen C, Vishnuram P, Krishna Rao Kasagani DVS, Nastasi B. Sys-tematic review on impact of different irradiance forecasting techniques for solar energy prediction. Energies 2022;15(17):6267.
- Pombo DV, Bindner HW, Spataru SV, Sørensen PE, Bacher P. Increasing the accu-racy of hourly multi-output solar power forecast with physics-informed machine learning. Sensors 2022;22(3):749.
- Li Z, Xu R, Luo X, Cao X, Du S, Sun H. Short-term photovoltaic power predic-tion based on modal reconstruction and hybrid deep learning model. Energy Rep 2022;8:9919–32.
- Gumar AK, Demir F. Solar photovoltaic power estimation using meta-optimized neu-ral networks. Energies 2022;15(22):8669.
- Alkhayat G, Hasan SH, Mehmood R. SENERGY: a novel deep learning-based auto-selective approach and tool for solar energy forecasting. Energies 2022;15(18):6659.
- Zazoum B. Solar photovoltaic power prediction using different machine learning methods. Energy Rep 2022;8:19–25.
- Almaghrabi S, Rana M, Hamilton M, Rahaman MS. Forecasting regional level solar power generation using advanced deep learning approach. In: 2021 international joint conference on neural networks (IJCNN). IEEE; 2021. p. 1–7.
- Zhou H, Liu Q, Yan K, Du Y. Deep learning enhanced solar energy forecasting with AI-driven IoT. Wirel Commun Mob Comput 2021;2021.
- Fara L, Diaconu A, Craciunescu D, Fara S. Forecasting of energy production for photovoltaic systems based on arima and ann advanced models. Int J Photoenergy 2021:2021.
- Konstantinou M, Peratikou S, Charalambides AG. Solar photovoltaic forecasting of power output using LSTM networks. Atmosphere 2021;12(1):124.
- Alkhayat G, Mehmood R. A review and taxonomy of wind and solar energy forecast-ing methods based on deep learning. Energy AI 2021;4:100060.
- Shamshirband S, Rabczuk T, Chau K-W. A survey of deep learning techniques: ap-plication in wind and solar energy resources. IEEE Access 2019;7:164650–66.
- Abdelhakim EH, Bourouhou A. Forecasting of PV power application to PV power penetration in a microgrid. https://doi .org /10 .1109 /EITech .2016 .7519644, 2016. 468–473.
- Alamin YI, Anaty MK, Álvarez Hervás JD, Bouziane K, Pérez García M, Yaagoubi R, et al. Very short-term power forecasting of high concentrator photovoltaic power facility by implementing artificial neural network. Energies 2020;13(13):3493.
- Mellit A, Massi Pavan A, Ogliari E, Leva S, Lughi V. Advanced methods for photo-voltaic output power forecasting: a review. Appl Sci 2020;10(2):487.
- Zhang X, Li Y, Lu S, Hamann HF, Hodge B-M, Lehman B. A solar time based analog ensemble method for regional solar power forecasting. IEEE Trans Sustain Energy 2018;10(1):268–79.



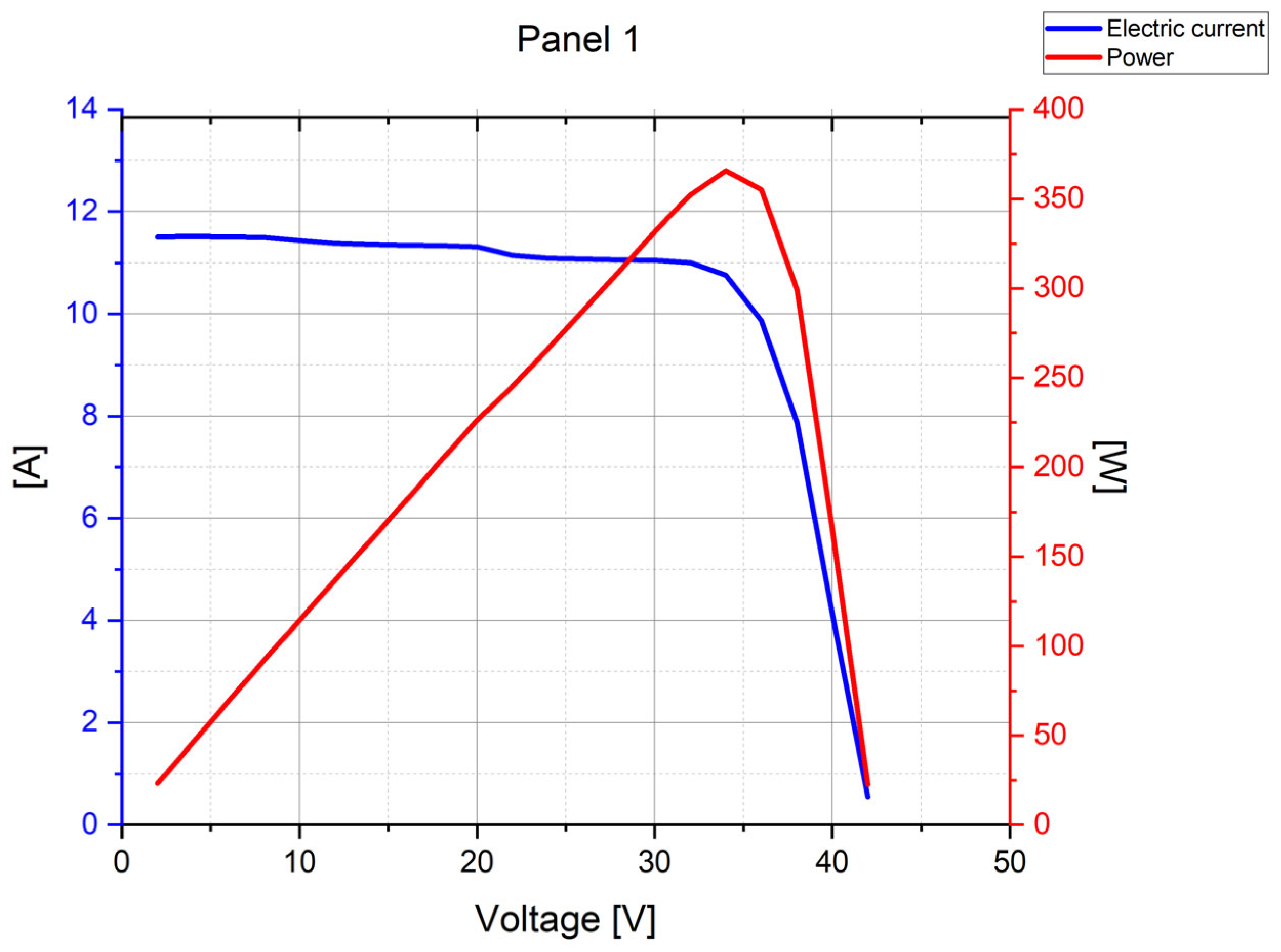
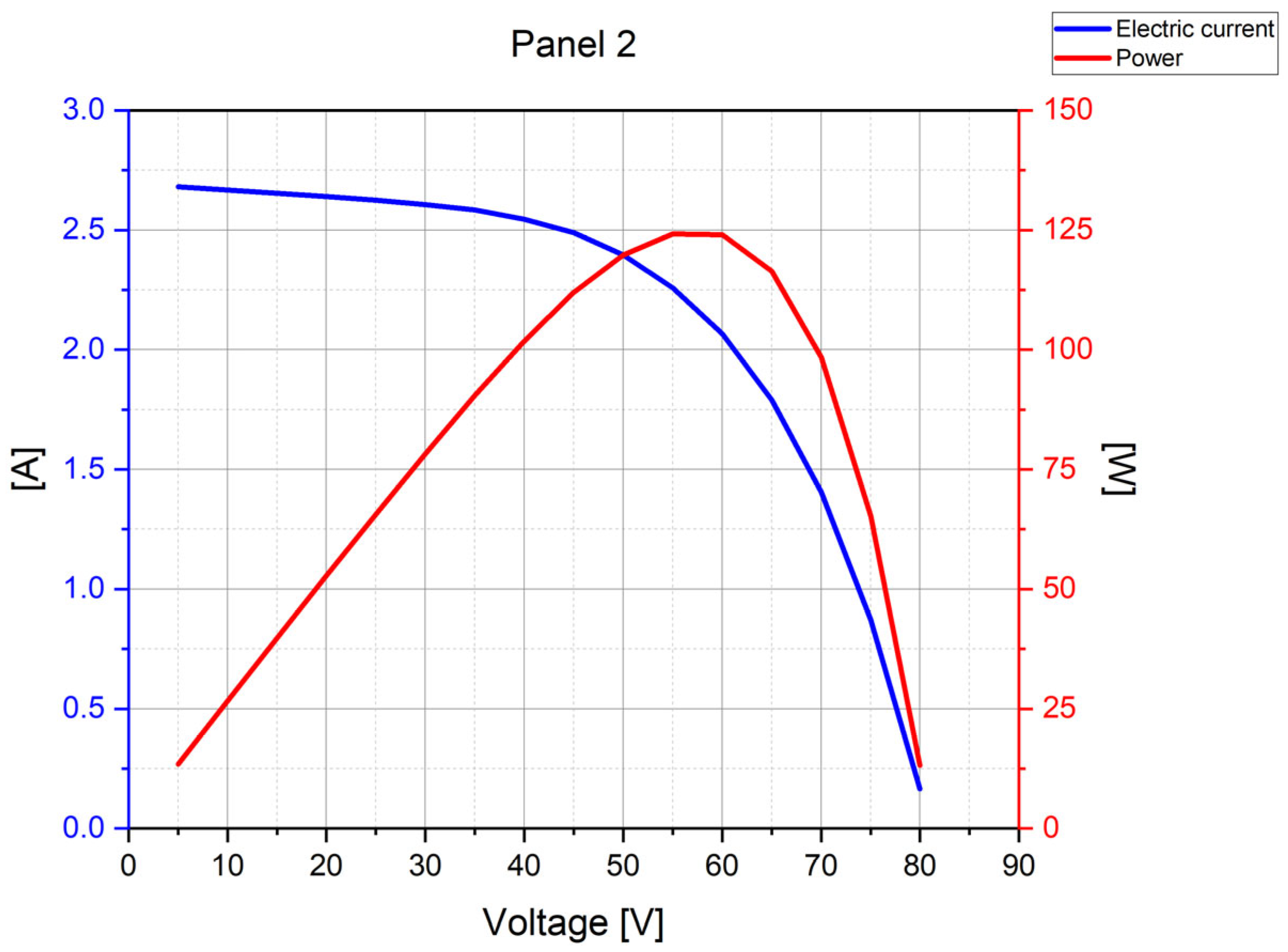
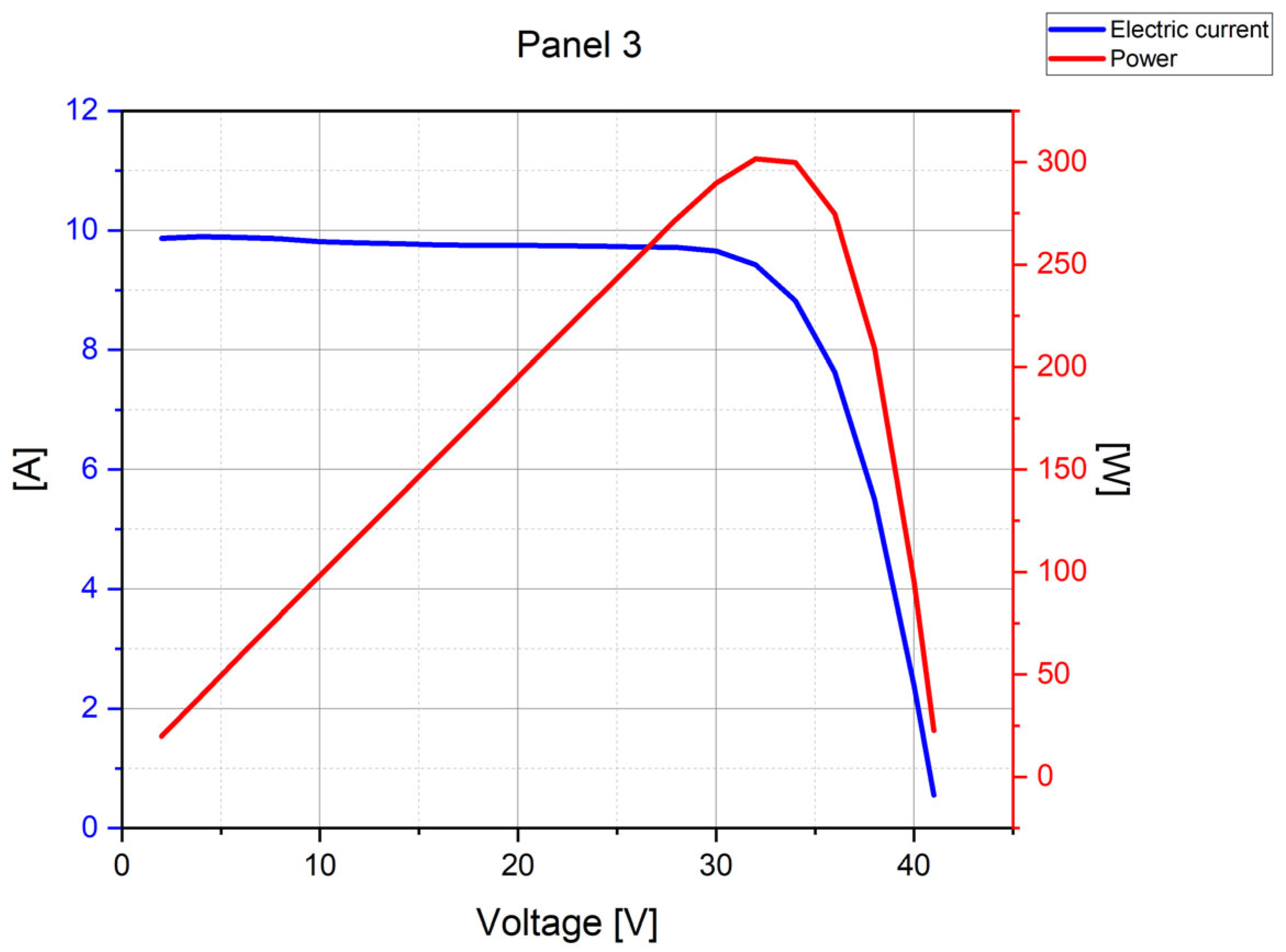
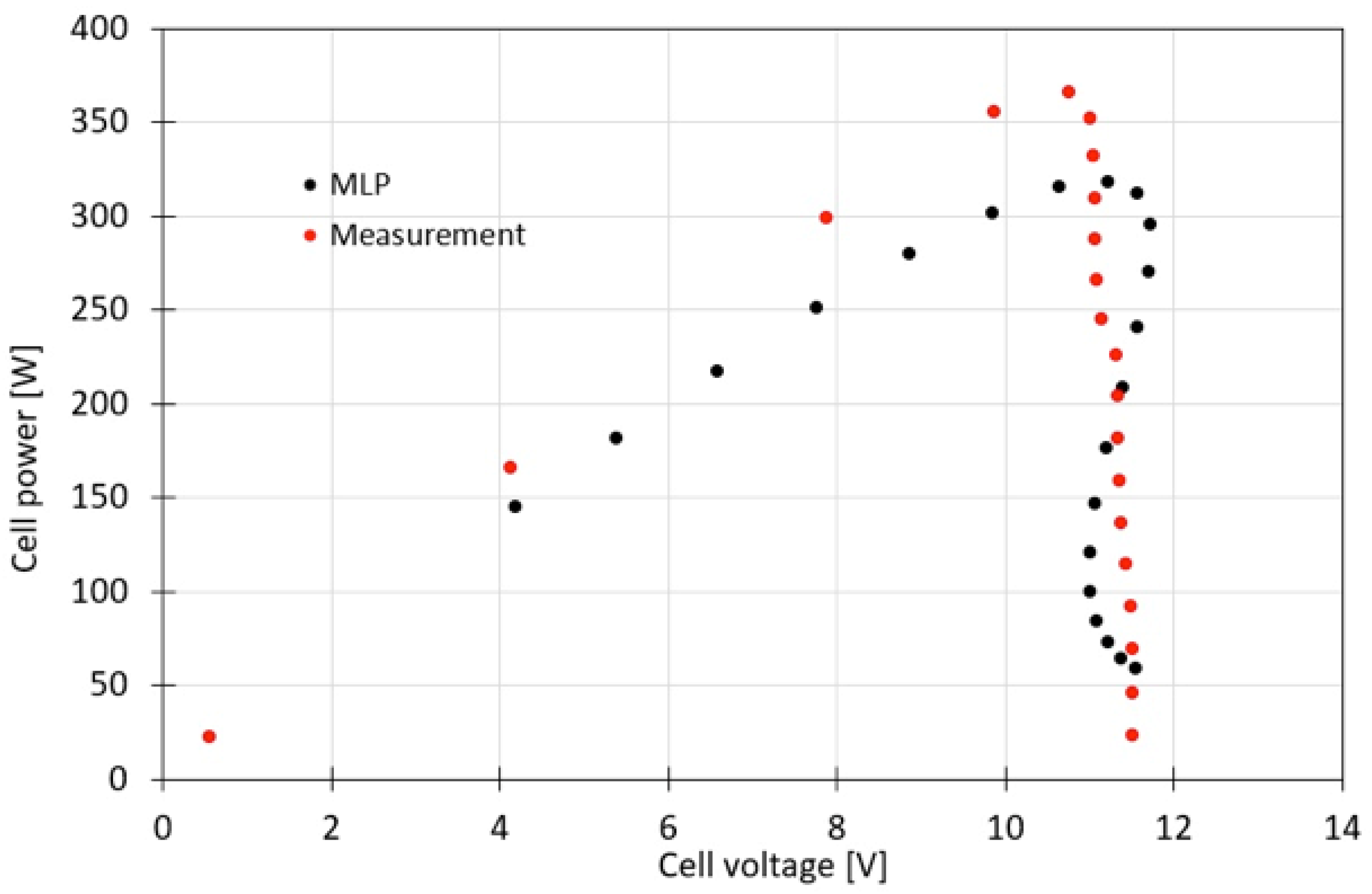
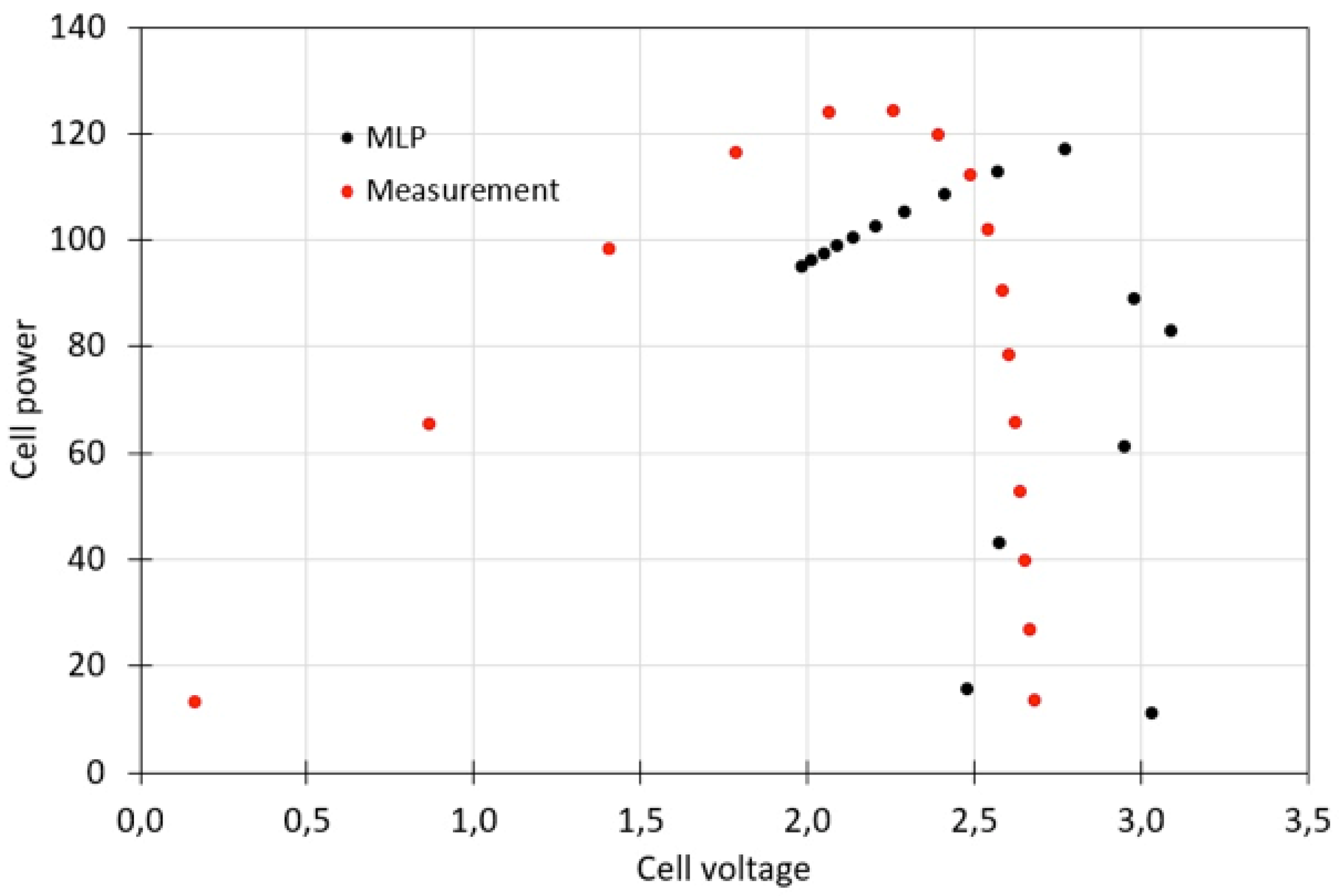

| Parameter | PV modules tested | ||||
|---|---|---|---|---|---|
| Module 1 | Module 2 | Module 3 | |||
| Max Power | Pmax | [W] | 365 | 145 | 315 |
| Idle voltage | Voc/V | [V] | 40.7 | 59.5 | 40.53 |
| Module efficiency | Eff | [%] | 20.0 | 13.3 | 19.3 |
| Max power voltage | Vmpp | [V] | 34.1 | 60.4 | 33.2 |
| Max power current | Impp | [A] | 10.7 | 2.4 | 9.5 |
| Short-circuit current | Isc | [A] | 11.4 | 2.7 | 10.0 |
| Open-circuit voltage | Voc | [V] | 40.7 | 85.2 | 40.5 |
| Parameter | Module 1 | Module 2 | Module 3 |
|---|---|---|---|
| Pmax [W] | 367.302 | 125.332 | 303.844 |
| Isc [A] | 11.454 | 2.692 | 9.818 |
| Voc [V] | 44.996 | 86.334 | 49.71 |
| Impp [A] | 10.654 | 2.166 | 9.192 |
| Vmpp [V] | 34.47 | 57.804 | 32.838 |
| Filling Factor [-] | 0.712 | 0.538 | 0.622 |
| Measurement | 5V | 15V | 25V | 35V | 40V |
|---|---|---|---|---|---|
| “Module 1” | |||||
| Power | |||||
| Measurement 1 [W] | 57.8901 | 171.1275 | 275.1322 | 365.42124 | 161.8382 |
| Measurement 2 [W] | 57.6934 | 170.9794 | 274.2930 | 362.1189 | 169.96 |
| Measurement 3 [W] | 57.3698 | 169.8569 | 280.7647 | 361.1334 | 168.7743 |
| Measurement 4 [W] | 57.5227 | 169.8666 | 281.0866 | 359.4855 | 161.9976 |
| Measurement 5 [W] | 57.3990 | 169.6859 | 274.4320 | 354.4239 | 165.2108 |
| Average [W] | 57.57503 | 170.3033 | 277.1417 | 360.5166 | 165.5562 |
| Current | |||||
| Measurement 1 [A] | 11.5763 | 11.409 | 11.0057 | 10.452 | 4.0459 |
| Measurement 2 [A] | 11.5389 | 11.399 | 10.9726 | 10.3584 | 4.249 |
| Measurement 3 [A] | 11.4748 | 11.325 | 11.2311 | 10.3311 | 4.2193 |
| Measurement 4 [A] | 11.507 | 11.3253 | 11.2439 | 10.2844 | 4.0499 |
| Measurement 5 [A] | 11.4799 | 11.3129 | 10.978 | 10.1403 | 4.1303 |
| Average [A] | 11.5154 | 11.3543 | 11.0863 | 10.3132 | 4.1389 |
| “Module 2” | |||||
| Power | |||||
| Measurement 1 [W] | 13.4401 | 65.8343 | 113.0481 | 119.1181 | 17.9283 |
| Measurement 2 [W] | 13.3214 | 65.1509 | 111.2806 | 114.9977 | 11.3292 |
| Measurement 3 [W] | 13.4363 | 65.8609 | 112.2522 | 116.6261 | 10.9828 |
| Measurement 4 [W] | 13.3855 | 65.2238 | 111.2941 | 115.5224 | 13.8337 |
| Measurement 5 [W] | 13.4530 | 65.9243 | 112.1763 | 115.5607 | 11.9393 |
| Average [W] | 13.4073 | 65.5988 | 112.0102 | 116.3650 | 13.2026 |
| Current | |||||
| Measurement 1 [A] | 2.6882 | 2.6334 | 2.5122 | 1.8326 | 0.2241 |
| Measurement 2 [A] | 2.6644 | 2.606 | 2.4729 | 1.7692 | 0.1416 |
| Measurement 3 [A] | 2.6873 | 2.6344 | 2.4945 | 1.7942 | 0.1373 |
| Measurement 4 [A] | 2.677 | 2.609 | 2.4732 | 1.777 | 0.1729 |
| Measurement 5 [A] | 2.6906 | 2.637 | 2.4928 | 1.7778 | 0.1492 |
| Average [A] | 2.6815 | 2.624 | 2.4891 | 1.7902 | 0.165 |
| “Module 3” | |||||
| Power | |||||
| Measurement 1 [W] | 49.4636 | 146.4109 | 243.2909 | 296.5507 | 107.8788 |
| Measurement 2 [W] | 49.5614 | 146.6602 | 243.8605 | 286.7913 | 89.9354 |
| Measurement 3 [W] | 49.5627 | 146.8454 | 243.7230 | 288.4221 | 102.8483 |
| Measurement 4 [W] | 49.4132 | 146.5157 | 242.7928 | 281.0666 | 84.2467 |
| Measurement 5 [W] | 49.2112 | 146.1223 | 242.8360 | 283.3992 | 92.6678 |
| Average [W] | 49.4424 | 146.5109 | 243.3006 | 287.2460 | 95.5154 |
| Current | |||||
| Measurement 1 [A] | 9.8910 | 9.7619 | 9.7318 | 8.4882 | 2.6970 |
| Measurement 2 [A] | 9.9170 | 9.7782 | 9.7545 | 8.2108 | 2.2484 |
| Measurement 3 [A] | 9.9121 | 9.7907 | 9.7494 | 8.2570 | 2.5712 |
| Measurement 4 [A] | 9.8839 | 9.7686 | 9.7121 | 8.0493 | 2.1062 |
| Measurement 5 [A] | 9.8459 | 9.7419 | 9.7138 | 8.1150 | 2.3167 |
| Average [A] | 9.8900 | 9.7683 | 9.7323 | 8.2241 | 2.3879 |
| U | Tc | Tp | Pmax | Voc/V | eff | Vmpp | Impp | Isc | |
|---|---|---|---|---|---|---|---|---|---|
| U | 1.00 | 0.73 | 0.25 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 |
| Tc | 1.00 | 0.29 | 0.79 | 0.33 | 0.79 | 0.33 | 0.79 | 0.79 | |
| Tp | 1.00 | 0.44 | 0.31 | 0.44 | 0.31 | 0.44 | 0.44 | ||
| Pmax | 1.00 | 0.36 | 1.00 | 0.36 | 1.00 | 1.00 | |||
| Voc/V | 1.00 | 0.36 | 1.00 | 0.36 | 0.36 | ||||
| eff | 1.00 | 0.36 | 1.00 | 1.00 | |||||
| Vmpp | 1.00 | 0.36 | 0.36 | ||||||
| Impp | 1.00 | 1.00 | |||||||
| Isc | 1.00 |
| Set | Tp | Tc | ||||
|---|---|---|---|---|---|---|
| Training | 0.94 | 24.68 | 36.06 | 0.97 | 0.53 | 1.17 |
| Test | 0.98 | 13.87 | 14.87 | 1.00 | 0.23 | 0.32 |
| Validation | 0.87 | 39.62 | 46.31 | 0.98 | 0.75 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





