Submitted:
28 May 2024
Posted:
29 May 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Problem Statements
3. Main Results
4. Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LKF | Lyapunov-Krasovskii functional |
| WBII | Wirtinger-based integral inequality |
| LMI | Linear matrix inequality |
| BOD | biochemical oxygen demand |
| DO | dissolved oxygen |
References
- Niculescu, S. I. Delay Effects on Stability: A Robust Control Approach. Springer Science & Business Media 2001, 269. [Google Scholar]
- Richard, J. P. Time-delay systems: an overview of some recent advances and open problems. Automatica 2003, 39, 1667–1694. [Google Scholar] [CrossRef]
- Kwon, O. M.; Park, M. J.; Park, J. H.; Lee, S. M. Enhancement on stability criteria for linear systems with interval time-varying delays. International Journal of Control Automation and Systems 2016, 14, 12–20. [Google Scholar] [CrossRef]
- Zhang, X. M.; Han, Q. L.; Seuret, A.; Gouaisbaut, F.; He, Y. Overview of recent advances in stability of linear systems with time-varying delays. IET Control Theory and Applications 2019, 13, 1–16. [Google Scholar] [CrossRef]
- Park, M. J.; Kwon, O. M.; Ryu, J. H. Advanced stability criteria for linear systems with time-varying delays. Journal of the Franklin Institute-Engineering and Applied Mathematics 2018, 355, 520–543. [Google Scholar]
- Zeng, H. B.; Lin, H. C.; He, Y.; Teo, K. L.; Wang, W. Hierarchical stability conditions for time-varying delay systems via an extended reciprocally convex quadratic inequality. Journal of the Franklin Institute-Engineering and Applied Mathematics 2020, 357, 9930–9941. [Google Scholar] [CrossRef]
- Xu, S. Y.; Lam, J. A survey of linear matrix inequality techniques in stability analysis of delay systems. International Journal of Systems Science 2008, 39, 1095–1113. [Google Scholar] [CrossRef]
- Zhang, C. K.; He, Y.; Jiang, L.; Wu, M.; Zeng, H. B. Stability analysis of systems with time-varying delay via relaxed integral inequalities. Systems & Control Letters 2016, 92, 52–61. [Google Scholar] [CrossRef]
- He, Y.; Wang, Q. G.; Lin, C.; Wu, M. Augmented Lyapunov functional and delay-dependent stability criteria for neutral systems. International Journal of Robust and Nonlinear Control 2005, 15, 923–933. [Google Scholar] [CrossRef]
- Sun, J.; Liu, G. P.; Chen, J.; Rees, D. Improved delay-range-dependent stability criteria for linear systems with time-varying delays. Automatica 2016, 92, 52–61. [Google Scholar] [CrossRef]
- Kwon, O. M.; Park, M. J.; Park, J. H.; Lee, S. M.; Cha, E. J. Improved results on stability of linear systems with time-varying delays via wirtinger-based integral inequality. Journal of the Franklin Institute-Engineering and Applied Mathematics 2014, 351, 5386–5398. [Google Scholar] [CrossRef]
- Qian, W.; Li, T.; Cong, S.; Fei, S. M. Stability analysis for interval time-varying delay systems based on time-varying bound integral method. Journal of the Franklin Institute-Engineering and Applied Mathematics 2014, 351, 4892–4903. [Google Scholar] [CrossRef]
- Lee, S. H.; Park, M. J.; Kwon, O. M.; Choi, S. G. Less conservative stability criteria for general neural networks through novel delay-dependent functional. Applied Mathematics and Computation 2022, 420, 126886. [Google Scholar] [CrossRef]
- Zhao, X.; Lin, C.; Chen, B.; Wang, Q. G. Stability analysis for linear time-delay systems using new inequality based on the second-order derivative. Journal of the Franklin Institute-Engineering and Applied Mathematics 2019, 356, 8770–8784. [Google Scholar] [CrossRef]
- Gu, K. Q. An integral inequality in the stability problem of time-delay systems. Proc. of the 39th IEEE Conference on Decision and Control, Sydney, Australia, (12-15 December 2000), 2805-2810.
- Seuret, A.; Gouaisbaut, F. Wirtinger-based integral inequality: Application to time-delay systems. Automatica 2013, 49, 2860–2866. [Google Scholar] [CrossRef]
- Gu, K. Q. A further refinement of discretized lyapunov functional method for the stability of time-delay systems. International Journal of Control 2001, 74, 967–976. [Google Scholar] [CrossRef]
- Park, M. J.; Kwon, O. M.; Park, J. H.; Lee, S. M.; Cha, E. J. Stability of time-delay systems via wirtinger-based double integral inequality. Automatica 2015, 55, 204–208. [Google Scholar] [CrossRef]
- Park, P. G.; Lee, W. I.; Lee, S. Y. Auxiliary function-based integral inequalities for quadratic functions and their applications to time-delay systems. Journal of the Franklin Institute-Engineering and Applied Mathematics 2015, 352, 1378–1396. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Stability of linear systems with time-varying delays using bessel-legendre inequalities. IEEE Transactions on Automatic Control 2018, 63, 225–232. [Google Scholar] [CrossRef]
- Park, M. J.; Kwon, O. M.; Ryu, J. H. Generalized integral inequality: Application to time-delay systems. Applied Mathematics Letters 2018, 77, 6–12. [Google Scholar] [CrossRef]
- Zeng, H. B.; Liu, X. G.; Wang, W. A generalized free-matrix-based integral inequality for stability analysis of time-varying delay systems. Applied Mathematics and Computation 2019, 354, 1–8. [Google Scholar] [CrossRef]
- Park, P. G.; Ko, J. W.; Jeong, C. Reciprocally convex approach to stability of systems with time-varying delays. Automatica 2011, 47, 235–238. [Google Scholar] [CrossRef]
- Zhang, X. M.; Han, Q. L.; Seuret, A.; Gouaisbaut, F. An improved reciprocally convex inequality and an augmented lyapunov-krasovskii functional for stability of linear systems with time-varying delay. Automatica 2017, 84, 221–226. [Google Scholar] [CrossRef]
- Seuret, A.; Liu, K.; Gouaisbaut, F. Generalized reciprocally convex combination lemmas and its application to time-delay systems. Automatica 2017, 84, 221–226. [Google Scholar] [CrossRef]
- Zhang, R. M.; Zeng, D. Q.; Park, J. H.; Zhong, S. M.; Liu, Y. J.; Zhou, X. New approaches to stability analysis for time-varying delay systems. Journal of the Franklin Institute-Engineering and Applied Mathematics 2019, 356, 4174–4189. [Google Scholar]
- Kim, S. H.; Park, P.; Jeong, C. Robust h stabilisation of networked control systems with packet analyser. IET Control Theory and Applications 2019, 356, 4174–4189. [Google Scholar]
- Lee, S. Y.; Lee, W. I.; Park, P. Improved stability criteria for linear systems with interval time-varying delays: Generalized zero equalities approach. Applied Mathematics and Computation 2017, 292, 336–348. [Google Scholar] [CrossRef]
- Kwon, O. M.; Lee, S. H.; Park, M. J.; Lee, S. M. Augmented zero equality approach to stability for linear systems with time-varying delay. Applied Mathematics and Computation 2020, 381, 125329. [Google Scholar] [CrossRef]
- Li, Z. C.; Yan, H. C.; Zhang, H.; Zhan, X. S.; Huang, C. Z. Improved inequality-based functions approach for stability analysis of time delay system. Automatica 2019, 108, 108416. [Google Scholar] [CrossRef]
- Li, Z. C.; Yan, H. C.; Zhang, H.; Peng, Y.; Park, J. H.; He, Y. Stability analysis of linear systems with time-varying delay via intermediate polynomial-based functions. Automatica 2020, 113, 108756. [Google Scholar] [CrossRef]
- Zhang, C. K.; Long, F.; He, Y.; Yao, W.; Jiang, L.; Wu, M. A relaxed quadratic function negative-determination lemma and its application to time-delay systems. Automatica 2020, 113, 108764. [Google Scholar] [CrossRef]
- Sheng, Z. L.; Lin, C.; Chen, B.; Wang, Q. G. Asymmetric lyapunov-krasovskii functional method on stability of time-delay systems. International Journal of Robust and Nonlinear Control 2021, 31, 2847–2854. [Google Scholar] [CrossRef]
- De Oliveira, M. C.; Skelton, R. E. Stability tests for constrained linear systems. Perspectives in Robust Control 2007, 1–10. [Google Scholar]
- Liu, Y.; Hu, L. S.; Shi, P. A novel approach on stabilization for linear systems with time-varying input delay. Applied Mathematics and Computation 2012, 218, 5937–5947. [Google Scholar] [CrossRef]
- Lee, C. S.; Leitmann, G. Continuous feedback guaranteeing uniform ultimate boundedness for uncertain linear delay systems - an application to river pollution-control. Computers & Mathematics with Applications 1988, 16, 929–938. [Google Scholar] [CrossRef]
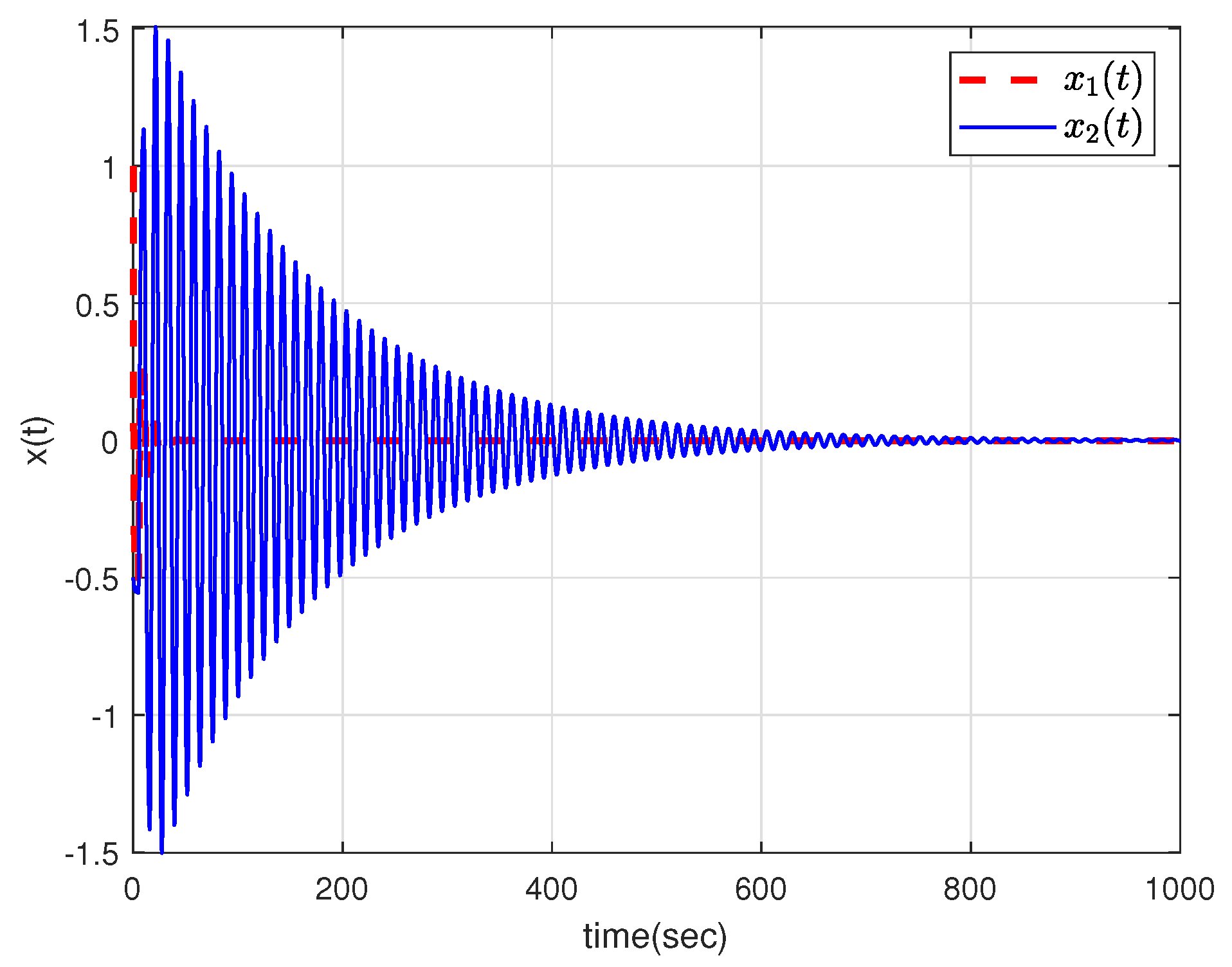
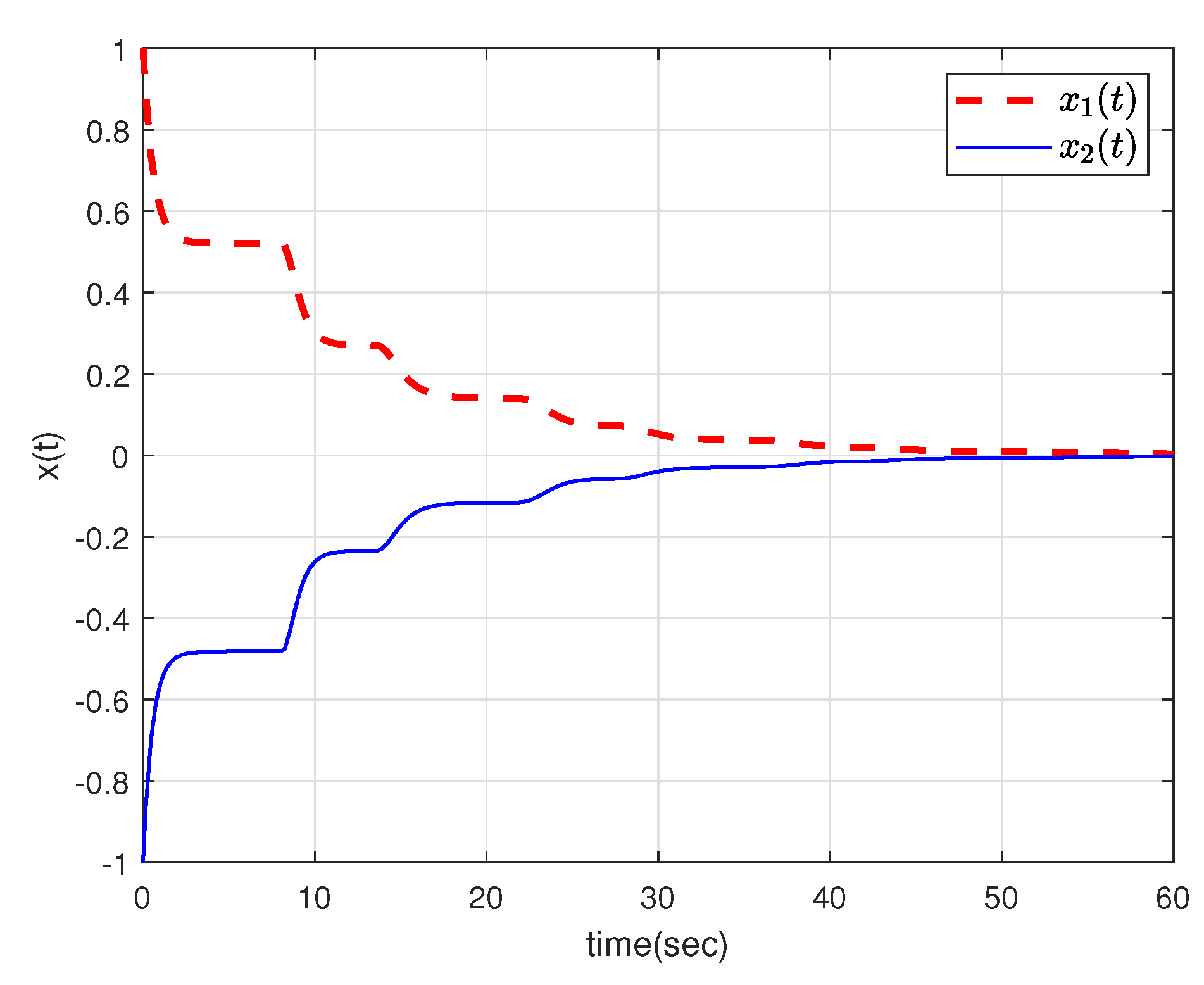
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| [10] | 4.1935 | 4.4932 | 4.3979 | 4.1978 | 5.0275 |
| [35] | 4.4045 | 4.5729 | 4.5406 | 4.2367 | 5.0440 |
| [3] | 4.7561 | 4.7746 | 4.7931 | 4.7567 | 5.1372 |
| Corollary 1 | 4.7577 | 4.7715 | 4.7634 | 4.7273 | 5.1373 |
| Theorem 1 | 4.7952 | 4.8132 | 4.8110 | 4.7850 | 5.1511 |
| Theorem 2 | 4.7951 | 4.8132 | 4.8109 | 4.7849 | 5.1500 |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| [10] | 2.3058 | 2.5663 | 3.3408 | 4.1690 | 5.0275 |
| [35] | 2.3513 | 2.6987 | 3.4186 | 4.2097 | 5.0440 |
| [3] | 2.4904 | 2.7994 | 3.4977 | 4.2939 | 5.1372 |
| Corollary 1 | 2.4752 | 2.8111 | 3.4997 | 4.2946 | 5.1373 |
| Theorem 1 | 2.5739 | 2.9247 | 3.5561 | 4.3134 | 5.1412 |
| Theorem 2 | 2.5739 | 2.9247 | 3.5593 | 4.3133 | 5.1406 |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| [3] | 5.1893 | 6.0899 | 7.0461 | 8.0461 | 9.0461 |
| Corollary 1 | 3.8906 | 4.8426 | 5.8413 | 6.8413 | 7.8413 |
| Theorem 1 | 5.4731 | 6.2440 | 7.1456 | 8.0755 | 9.0564 |
| Theorem 2 | 5.6896 | 6.3537 | 7.1932 | 8.0908 | 9.0578 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





